The Behavior of Wind Turbines Equipped with Induction Generators and Stator Converters Under Significant Variations in Wind Speed
Abstract
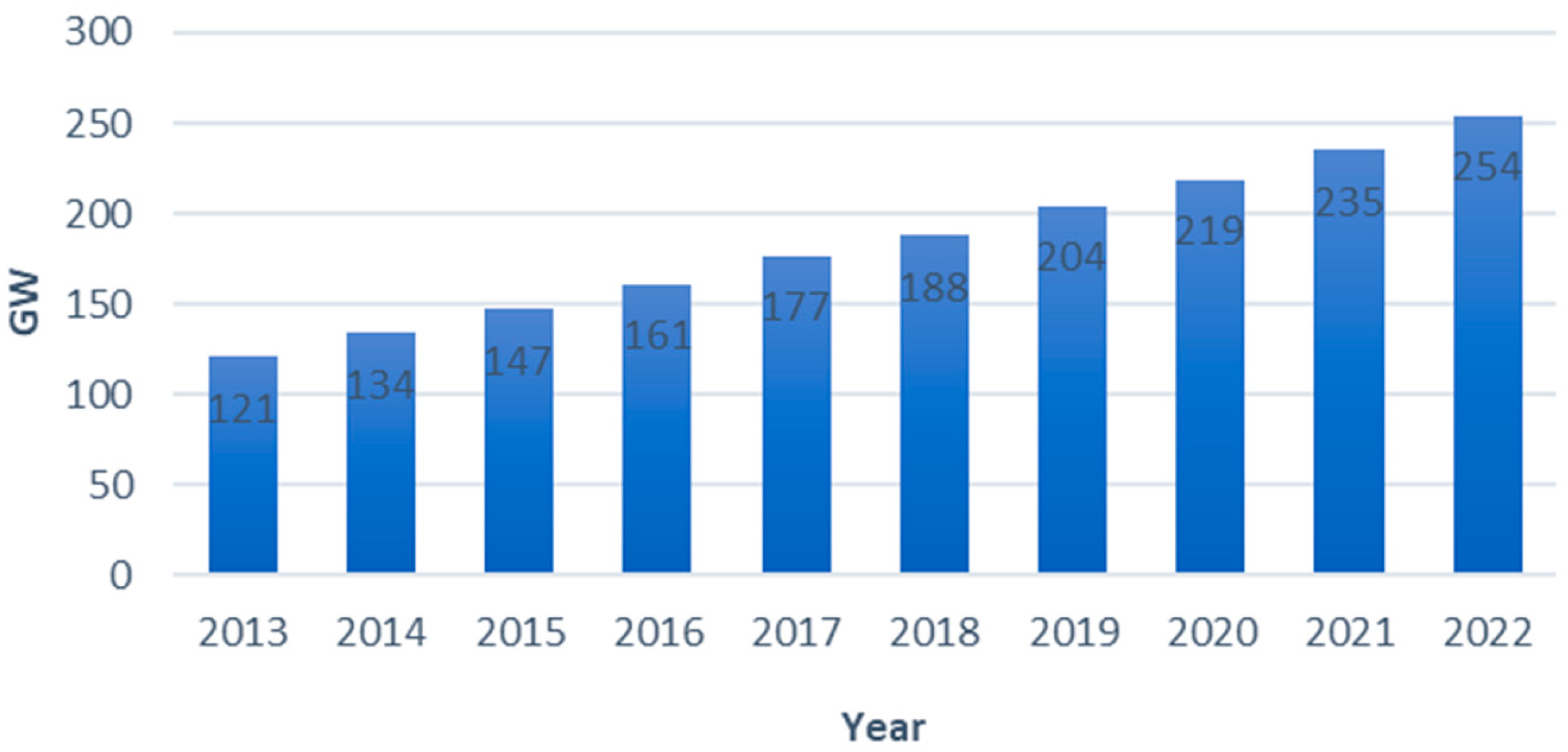
1. Introduction
- -
- The high cost of the initial investment, particularly in cases where there are no government subsidies for the large-scale implementation of these solutions;
- -
- The shortage of qualified human resources capable of installing, operating, and maintaining electricity generation systems;
- -
- The inadequate communication among the parties involved regarding the benefits associated with the implementation of renewable energy generation systems;
- -
- The low reliability of transport networks, which prevents multiple individuals or legal entities from injecting any power into the grid.
- -
- The use of a small power turbine operating at maximum power in free air [11];
- -
- Reversing the aerodynamic model of the turbine based on the estimated values of the turbine’s torque and rotor speed [12];
- -
- Estimating the rotor speed of the turbine and its torque, utilizing the inverse aerodynamic model and nonlinear control theory [13].
- -
- The implementation of an advanced torque controller, which relies on an efficient estimation of wind speed, has been shown to enhance the accuracy of wind speed estimation by 2–7% compared to alternative methods [15];
- -
- The application of a PID controller, with results assessed through performance index parameters in the time domain [16];
- -
- The use of a controller that, based on the power curve corresponding to various wind speeds, aims to track the optimal power curve identified by the control system [17];
- -
- The application of modified virtual inertial controllers, which also serve to enhance the damping capacity of power oscillations within the energy system [18];
- -
- The application of vector control oriented by stator flux, achieving a reduction in the generator’s impact on system stability [19].
- -
- Presentation of the current state of research concerning the behavior of wind turbines under significant variations in wind speed;
- -
- Determining the potential power output based on the characteristics of the wind turbine and the power curve as a function of angular velocity;
- -
- Determining the power output of the induction generator and constructing the power characteristic as a function of angular velocity, based on its rated values;
- -
- Establishing the optimal angular mechanical speed by utilizing the mathematical model of the turbine based on its technical parameters, specifically the wind speed;
- -
- Determining the maximum value of the power supplied by the wind turbine.
2. Properties and Characteristics of the Analyzed Wind Turbine
3. Mathematical Models of the Induction Generator and the Three-Blade Horizontal Axis Turbine
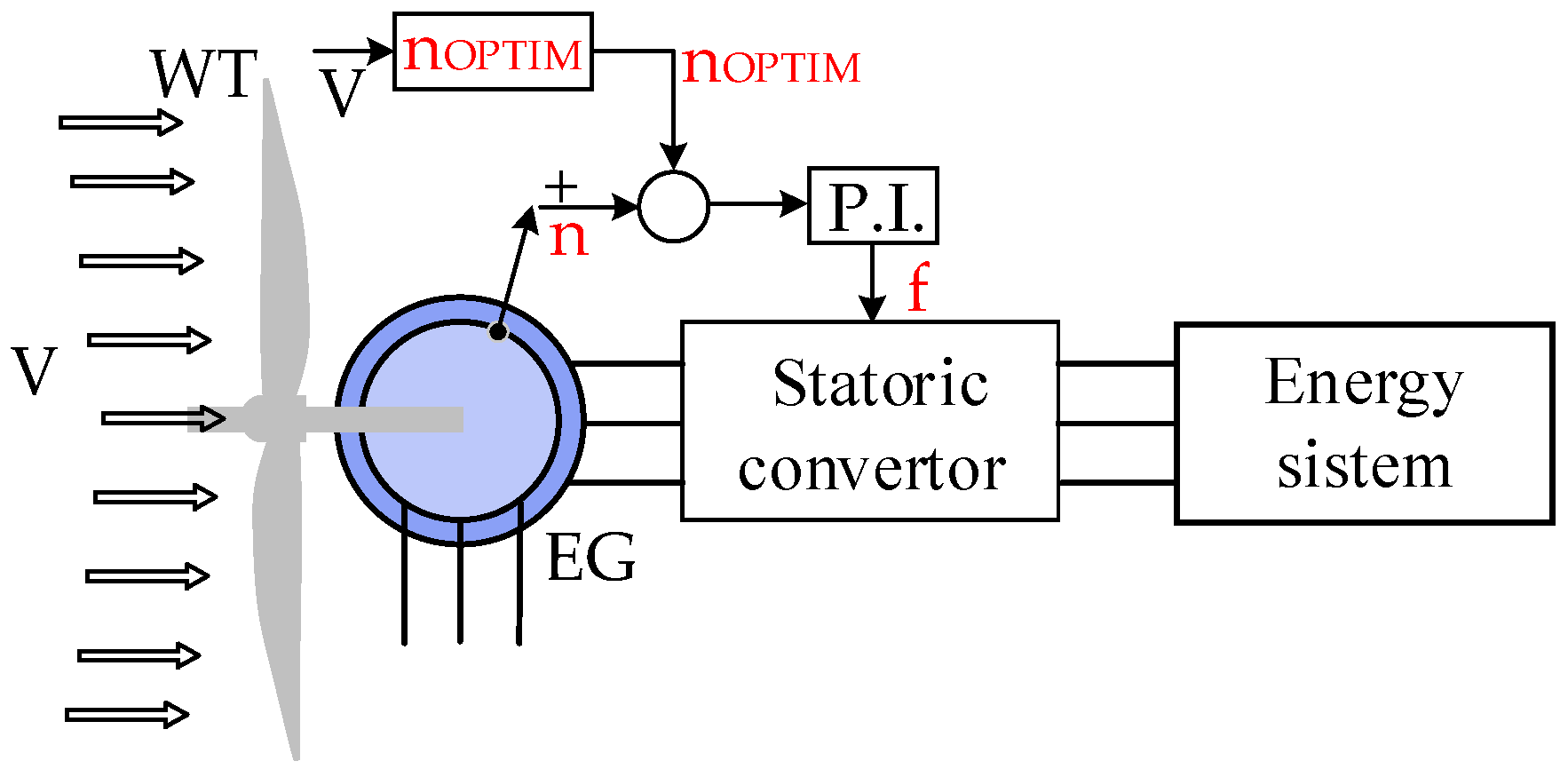
3.1. The Mathematical Model of the Induction Generator
- The moment of inertia, J = 0.34 kgm2;
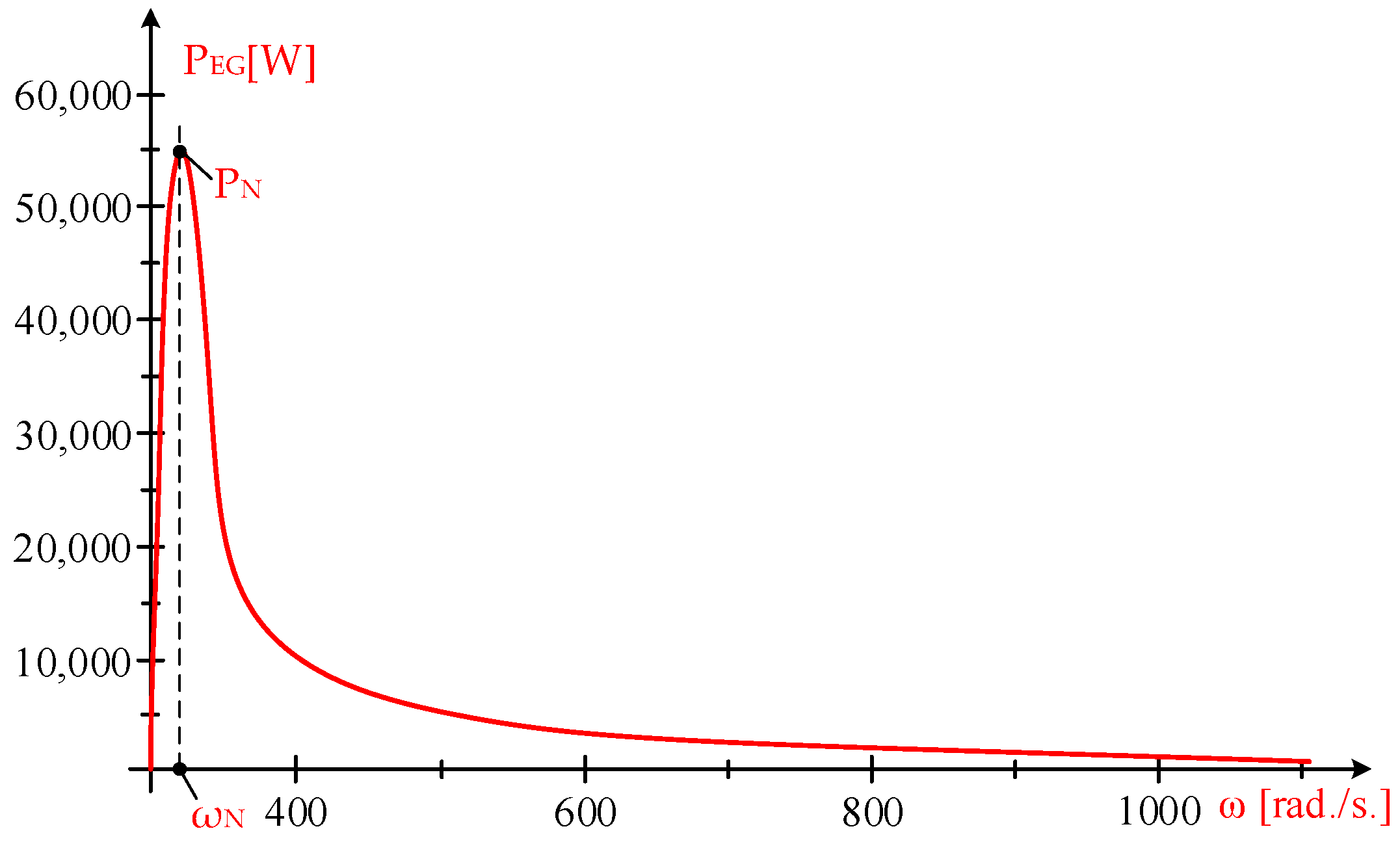
- The nominal power PN = PEG = 55 kW;
- The rated voltage UN = 400 V;
- The nominal current IN = 98 A;
- The number of poles 2p1 = 2;
- Nominal speed nN = 2940 rpm;
- The nominal sliding sN = 0.02.
3.2. The Mathematical Model of the Turbine
- (1)
- The maximum power value is achieved at ωOPTIM by setting the derivative of power to zero:
- (2)
- The maximum power value of the WT corresponds to the optimal MAS, ωOPTIM:
- (3)
- The value of the ratio ωOPTIM/ωMAXIM leads to Equation (3).
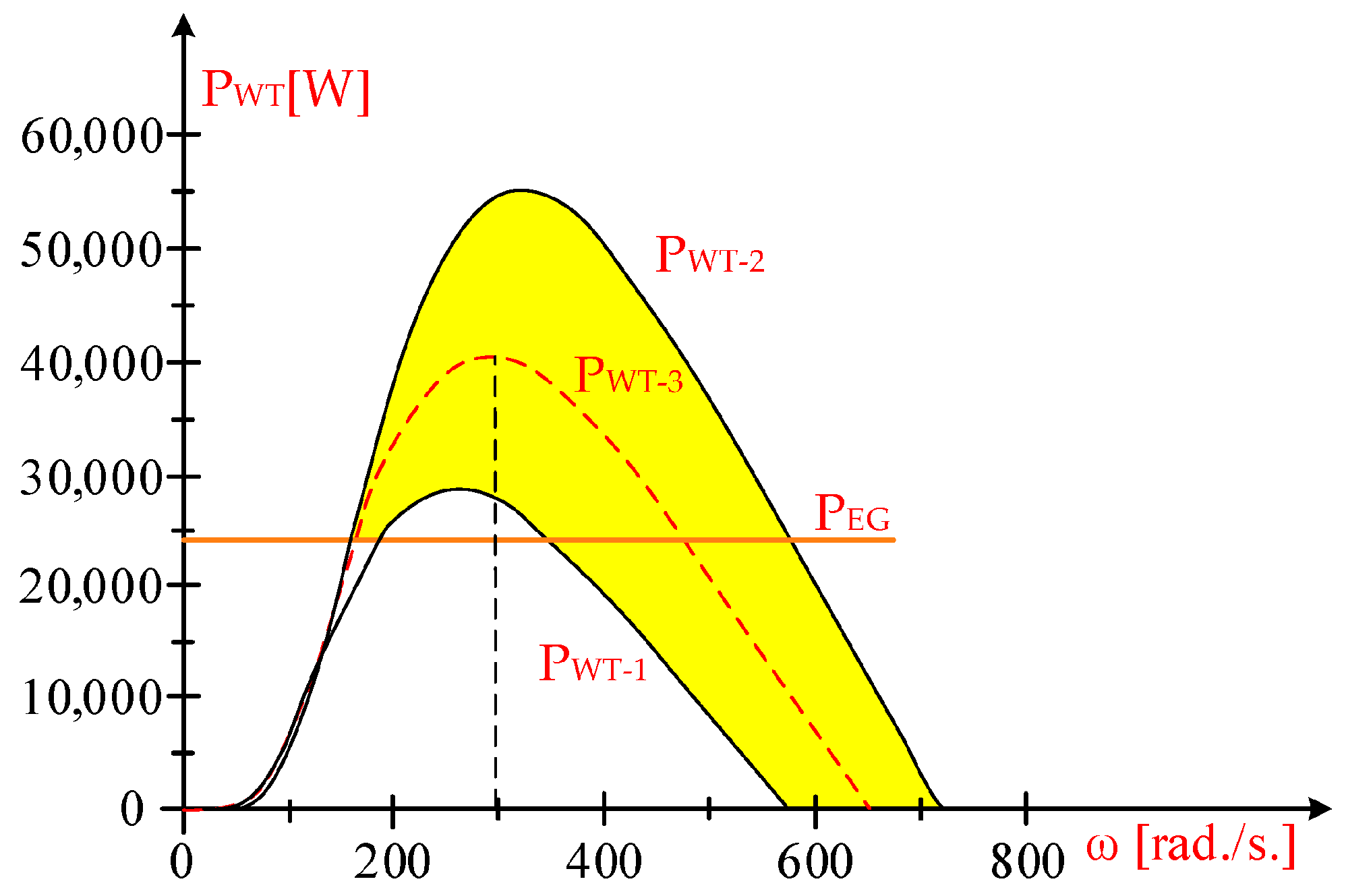
4. System Operation in the Optimal Zone: Analysis of Various Dependencies
4.1. The Dependencies of Frequency, Steady-State Current, and Power Factor in Relation to Wind Speed
- For V = 3 m/s:
- For V = 4 m/s:
- For V = 5 m/s:
- For V = 6 m/s:
- For V = 7 m/s:
- For V = 8 m/s:
- For V = 9 m/s:
- For V = 10 m/s:
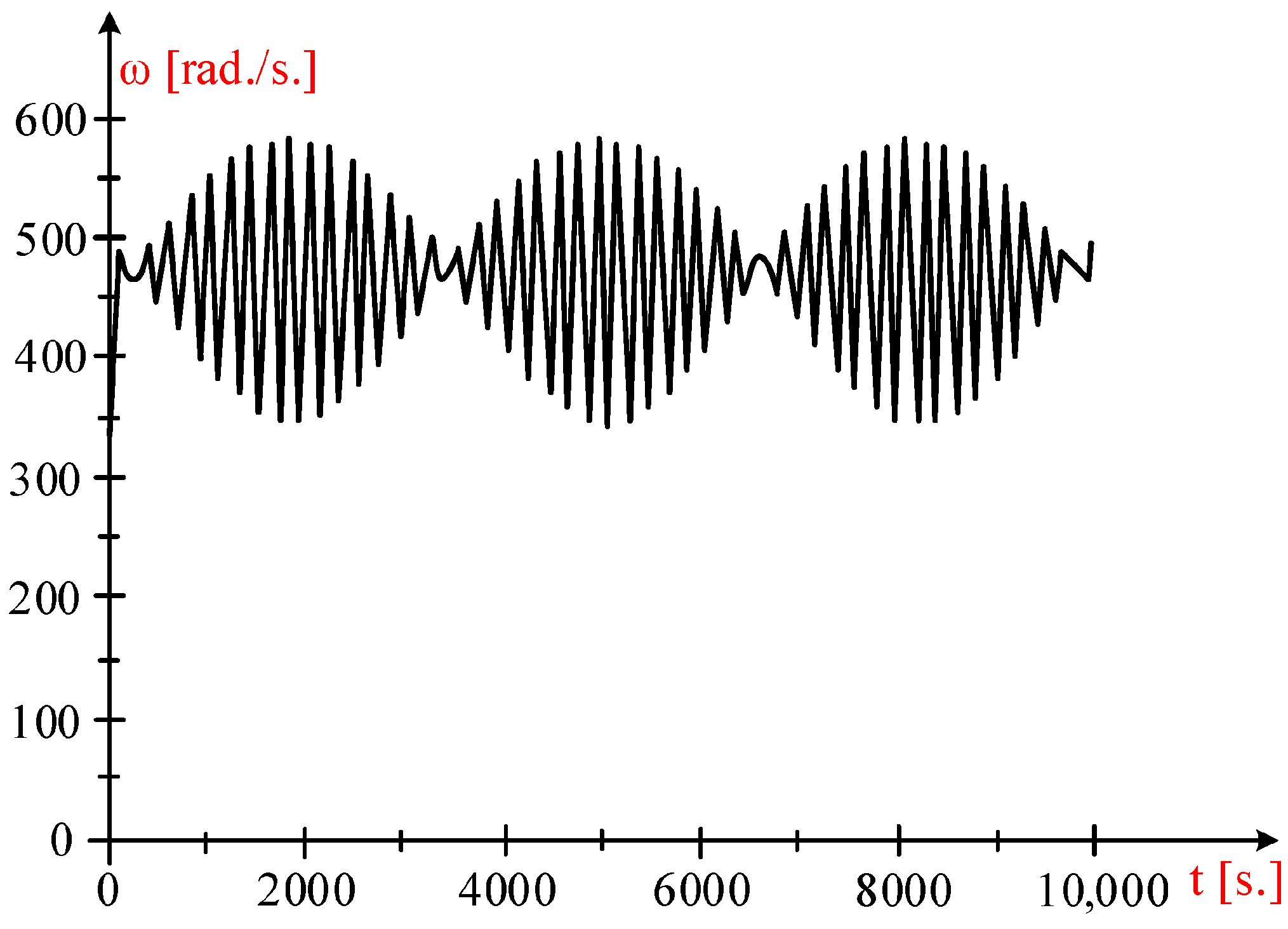
4.2. Wind System Behavior at Time-Varying Wind Speeds by Estimating the Wind Energy Captured by the Turbine
- For V1 = 8 m/s:
- For V2 = 10 m/s:
- For V3 = 9 m/s:
- (1)
- The amount of electric energy supplied to the grid is 41.206% lower than the maximum wind energy that can be harnessed by the turbines:
- (2)
- The wind energy harnessed by the turbine at PEG = 24,057 W is 41.17% than the maximum wind energy that the turbine is capable of capturing:
5. Discussion
5.1. Results
- Mathematical models for the generator and turbine have been established based on technical data from a 55 kW turbine;
- The generator’s power was determined at a variable frequency while maintaining a constant stator flux;
- The dependencies of the stator current and frequency on wind speed have been determined;
- The wind-turbine-captured wind energy values were compared with the electrical energy supplied to the grid.
5.2. Fundamental Aspects
- When the load on the electric generator remains constant, the electrical energy supplied to the grid is more than twice as small as the maximum wind energy that can be harnessed by a wind turbine;
- The operation of the turbine at its maximum power points necessitates the adjustment of the generator’s power output by regulating the stator frequency, thereby achieving optimal rotational speed.
5.3. Discussions
- Utilizing a power converter within the stator circuit enables the turbine to operate at its maximum power point;
- For optimal control, it is essential to accurately understand the dependence of the optimal mechanical angular speed on wind velocity.
6. Conclusions
- -
- Deduction of mathematical models for the 55 kW turbine and the induction generator from the technical data of the turbine (power characteristics, power dependence on rotational speed).
- -
- Analysis of the behavior of the induction generator under variable frequencies and controlled stator flux.
- -
- Determination of wind speed dependencies for the stator frequency and current as well as the power factor in the MPP operation mode of the turbine.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WT | wind turbine |
| MPP | maximum power point |
| MAS | mechanical angular speed |
| EG | electric generator |
| PID | proportional, integrative, derivative |
| V | wind speed |
| J | equivalent moment of inertia |
| PWT | power given by WT relative to the shaft of the electric generator |
| PWT-MAX | maximum power value from the wind turbine |
| PEG | power of the electric generator |
| PN | rated power |
| EE | electric energy supplied to the grid |
| EW | wind energy |
| EW-MAX | maxim wind energy |
| MWT | moment provided by WT, relative to the EG shaft |
| MEG | electromagnetic moment at the EG shaft |
| UN | rated voltage |
| US | stator voltage |
| IN | nominal current |
| IS | stator current |
| IR | rotor current |
| RS | stator resistance |
| RR | rotor resistance |
| Xsc | short-circuit reactance |
| XR | rotor reactance |
| XM | magnetizing reactance |
| N1 | number of turns per phase in the stator |
| N2 | number of turns per phase in the rotor |
| fN | nominal frequency |
| ω | mechanical angular velocity |
| ωN | nominal mechanical angular velocity |
| ωOPTIM | optimal mechanical angular velocity |
| ωMAXIM | maxim mechanical angular velocity |
| k | transformation ratio |
| kT | transmission multiplication ratio |
| kp | proportionality factor |
| p1 | number of poles |
| nN | nominal speed |
| n1 | rotational speed of the spinning field |
| n | rotor’s rotational speed |
| sN | nominal sliding |
| cos φ | generator power factor |
| a, b, c | parameters of the wind turbine |
References
- Ciucci, M. Energia Din Surse Regenerabile. Available online: https://www.europarl.europa.eu/factsheets/ro/sheet/70/energia-din-surse-regenerabile (accessed on 22 May 2025).
- Electricity and Heat Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_and_heat_statistics (accessed on 21 June 2025).
- Evolution of Wind Energy in Europe. Available online: https://www.iberdrola.com/sustainability/wind-power-evolution-europe (accessed on 21 June 2025).
- Bishoge, O.K.; Zhang, L.L.; Mushi, W.G. The Potential Renewable Energy for Sustainable Development in Tanzania: A Review. Clean Technol. 2019, 1, 70–88. [Google Scholar] [CrossRef]
- Sachin, G.; Shree, K.M.; Shivam, K.; Deepesh, A. A Consolidation Review of Major Wind Turbine Models in Global Market. In Proceedings of the 2020 International Conference on Power Electronics & IoT Applications in Renewable Energy and Its Control (PARC), Mathura, India, 28–29 February 2020. [Google Scholar]
- Khajah, A.M.H.A.; Philbin, S.P. Techno-Economic Analysis and Modelling of the Feasibility of Wind Energy in Kuwait. Clean Technol. 2022, 4, 14–34. [Google Scholar] [CrossRef]
- Sajadi, A.; Clark, K.; Loparo, K.A. Statistical Steady-State Stability Analysis for Transmission System Planning for Offshore Wind Power Plant Integration. Clean Technol. 2020, 2, 311–332. [Google Scholar] [CrossRef]
- Sorandaru, C.; Ancuti, M.-C.; Musuroi, S.; Svoboda, M.; Muller, V.; Geza Erdodi, M. Fundamental Issue for Wind Power Systems Operating at Variable Wind Speeds: The Dependence of the Optimal Angular Speed on the Wind Speed. In Proceedings of the 2022 International Conference and Exposition on Electrical And Power Engineering (EPE), Iasi, Romania, 20–22 October 2022. [Google Scholar]
- Routray, A.; Hur, S.H. Power regulation of a wind farm through flexible operation of tur-bines using predictive control. Energies 2024, 313, 133917. [Google Scholar]
- Carstea, C.; Butaru, F.; Ancuti, M.-C.; Musuroi, S.; Deacu, A.; Babaita, M. Wind Power Plants Operation at Variable Wind Speeds. In Proceedings of the 2020 IEEE 14th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 21–23 May 2020. [Google Scholar]
- Sorandaru, C.; Musuroi, S.; Frigura-Iliasa, F.M.; Vatau, D.; Dordescu, M. Analysis of the Wind System Operation in the Optimal Energetic Area at Variable Wind Speed over Time. Sustainability 2019, 11, 1249. [Google Scholar] [CrossRef]
- Huynh, P.; Tungare, S.; Banerjee, A. Maximum Power Point Tracking for Wind Turbine Using Integrated Generator–Rectifier Systems. IEEE Trans. Power Electron. 2020, 56, 730–739. [Google Scholar]
- Hussain, J.; Mishra, M.K. An Efficient Wind Speed Computation Method Using Sliding Mode Observers in Wind Energy Conversion System Control Applications. IEEE Trans. Ind. Appl. 2020, 56, 730–739. [Google Scholar] [CrossRef]
- Edrah, M.; Zhao, X.; Hung, W.; Qi, P.; Marshall, B.; Karcanias, A. Effects of POD Control on a DFIG Wind Turbine Structural System. IEEE Trans. Energy Convers. 2020, 35, 765–774. [Google Scholar] [CrossRef]
- Deng, X.; Yang, J.; Sun, Y.; Song, D.; Yang, Y.; Joo, Y.H. An Effective Wind Speed Estimation Based Extended Optimal Torque Control for Maximum Wind Energy Capture. IEEE Access 2020, 8, 65959–65969. [Google Scholar] [CrossRef]
- Karthik, R.; Sri Hari, A.; Pavan Kumar, Y.V.; John Pradeep, D. Modelling and Control Design for Variable Speed Wind Turbine Energy System. In Proceedings of the 2020 International Conference on Artificial Intelligence and Signal Processing (AISP), Amaravati, India, 10–12 January 2020. [Google Scholar]
- Xingjia, Y.; Yingming, L.; Jieqiu, B.; Zuoxia, X. Research and simulation of direct drive wind turbine VSCF characteristic. In Proceedings of the IEEE International Conference on Automation and Logistics, Qingdao, China, 1–3 September 2008. [Google Scholar]
- Ravanji, M.H.; Parniani, M. Stability Assessment of DFIG-Based Wind Turbines Equipped with Modified Virtual Inertial Controller under Variable Wind Speed Conditions. In Proceedings of the 43rd Annual Conference of the IEEE-Industrial-Electronics-Society (IECON), Beijing, China, 29 October–1 November 2017. [Google Scholar]
- Soued, S.; Ramadan, H.S.; Becherif, M. Effect of Doubly Fed Induction Generator on Transient Stability Analysis under Fault Conditions. In Proceedings of the 6th International Conference on Emerging and Renewable Energy—Generation and Automation (ICEREGA), Sousse, Tunisia, 28–30 October 2018. [Google Scholar]
- Hua, Y.; Yujun, D.; Liye, X.; Qionglin, L.; Chen, Z.; Yi, W. Hydro-Tower Pumped Storage-based Wind Power Generator: Short-term Dynamics and Controls. In Proceedings of the 2nd Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 20–22 October 2023. [Google Scholar]
- Jannet, J.; Fouizi, M. Model of wind turbine-pumped storage hydro plant. In Proceedings of the 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018. [Google Scholar]
- Papakonstantinou, A.G.; Konstanteas, A.I.; Papathanassiou, S.A. Solutions to Enhance Frequency Regulation in an Island System With Pumped-Hydro Storage Under 100% Renewable Energy Penetration. IEEE Access 2023, 11, 76675–76690. [Google Scholar] [CrossRef]
- Yingyu, A.; Li, Y.; Zhang, J.; Wang, T.; Liu, C. Enhanced Frequency Regulation Strategy for Wind Turbines Based on Over-speed De-loading Control. In Proceedings of the 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020. [Google Scholar]
- Fan, F.; Crisostomi, E.; Zhang, B.; Thomopulos, D. Rotor Speed Fluctuation Analysis for Rapid De-Loading of Variable Speed Wind Turbines. In Proceedings of the IEEE 20th Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 16–18 June 2020. [Google Scholar]
- Ravanji, M.H.; Parniani, M. Small-Signal Stability Analysis of DFIG-based Wind Turbines Equipped with Auxiliary Control Systems under Variable Wind Speed. In Proceedings of the 20th IEEE International Conference on Environment and Electrical Engineering (EEEIC)/4th IEEE Industrial and Commercial Power Systems Europe Conference (I and CPS Europe), Electr Network, Madrid, Spain, 9–12 June 2020. [Google Scholar]
- Rebello, E.; Watson, D.; Rodgers, M. Performance Analysis of a 10 MW Wind Farm in Providing Secondary Frequency Regulation: Experimental Aspects. IEEE Trans. Power Syst. 2019, 34, 3090–3097. [Google Scholar] [CrossRef]
- EC Wind 55kW Wind Turbine. Available online: https://eco-energ.co.uk/wind/ec-wind-55kw-wind-turbine/ (accessed on 21 June 2025).
- Dobrin, E.; Ancuti, M.-C.; Musuroi, S.; Sorandaru, C.; Ancuti, R.; Lazar, M.A. Dynamics of the Wind Power Plants at Small Wind Speeds. In Proceedings of the 2020 IEEE 14th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 21–23 May 2020. [Google Scholar]
- Pesut, N.D.; Ciric, R.M. An efficient method for speed control of induction wind turbine generator with dual AC-DC-AC converter. Wind Eng. 2022, 46, 993–1008. [Google Scholar] [CrossRef]
- Ge, M.W.; Ke, W.M.; Chen, H.X. Pitch control strategy before the rated power for variable speed wind turbines at high altitudes. J. Hydrodynam. 2019, 31, 379–388. [Google Scholar] [CrossRef]
- Micon M 300-55. Available online: https://en.wind-turbine-models.com/turbines/1305-micon-m-300-55 (accessed on 1 April 2025).
- Baala, Y.; Bri, S. DFIG-Based Wind Turbine Control Using High-Gain Observer. In Proceedings of the 1st International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 16–19 April 2020. [Google Scholar]
- Vadi, S.; Gürbüz, F.B.; Bayindir, R.; Hossain, E. Design and Simulation of a Grid Connected Wind Turbine with Permanent Magnet Synchronous Generator. In Proceedings of the 8th IEEE International Conference on Smart Grid, Paris, France, 17–19 June 2020. [Google Scholar]
- Gao, G.; Chen, W. Design Challenges of Wind Turbine Generators. In Proceedings of the 29th Electrical Insulation Conference, Montreal, QC, Canada, 31 May–3 June 2009. [Google Scholar]
- Han, Y.; Kim, S.; Ha, J.-I.; Lee, W.-J. A Doubly Fed Induction Generator Controlled in Single-Sided Grid Connection for Wind Turbines. IEEE Trans. Energy Convers. 2013, 28, 413–424. [Google Scholar] [CrossRef]
- Chioncel, C.P.; Spunei, E.; Tirian, G.-O. Visualizing the Maximum Energy Zone of Wind Turbines Operating at Time-Varying Wind Speeds. Sustainability 2024, 16, 2659. [Google Scholar] [CrossRef]
- Chioncel, C.P.; Spunei, E.; Tirian, G.-O. Wind Turbines Around Cut-In Speed: Startup Optimization and Behavior Analysis Reported to MPP. Appl. Sci. 2025, 15, 3026. [Google Scholar] [CrossRef]
- Chioncel, C.P.; Tirian, O.G.; Dordescu, M.; Spunei, E. Optimization of wind turbine operation in variable wind speed conditions. In Proceedings of the 7th International Conference on Energy Efficiency and Agricultural Engineering (EE and AE), Ruse, Bulgaria, 12–14 November 2020. [Google Scholar]
- Wu, Z.Q.; Hou, L.C.; Cao, B.L.; Ma, B.Y.; Hu, X.Y. Cooperative Control for Wind Turbines Based on Hamilton System Under Limited Input. Int. J. Control Autom. Syst. 2023, 21, 2605–2614. [Google Scholar] [CrossRef]
- Chioncel, C.P.; Ciucurita, S.; Spunei, E. Control of Wind-Power Systems Operating at Variable Wind Speeds to Optimize Energy Capture. Energies 2024, 18, 2574. [Google Scholar] [CrossRef]
- Siemens, Motor 55 KW at DOL Operation. Available online: https://ausschreibungstexte.siemens.com/tiplv/Data/E/Drive_Technology,_Automat/Dr/Low_/I/1LE1_-_SIMOTICS_GP_and_SIMOTICS_SD_standard_motors_%280,/I/2/Motor__DPMD_AAF229_001_000__kW_at_DOL_operation,__DPMD_AAD769_001_000__housing,_FS___DPMD_AAA726_001_000_,__DPMD_ACB254_001_000_,__DPMD_AA/(LV_HVT8GHVAWMTMVFSCP1DTHS657W_1LE1504-2CA23-4AA4) (accessed on 28 June 2025).
- Babescu, M. Masina Sincrona—Modelare—Identificare—Simulare; Publisher Polityehnica Timisoara: Timisoara, Romania, 2003; ISBN 973-625-021-0. [Google Scholar]
- Chioncel, C.P.; Spunei, E.; Tirian, G.-O. The problem of power variations in wind turbines operating under variable wind speeds over time and the need for wind energy storage systems. Energies 2024, 17, 5079. [Google Scholar] [CrossRef]



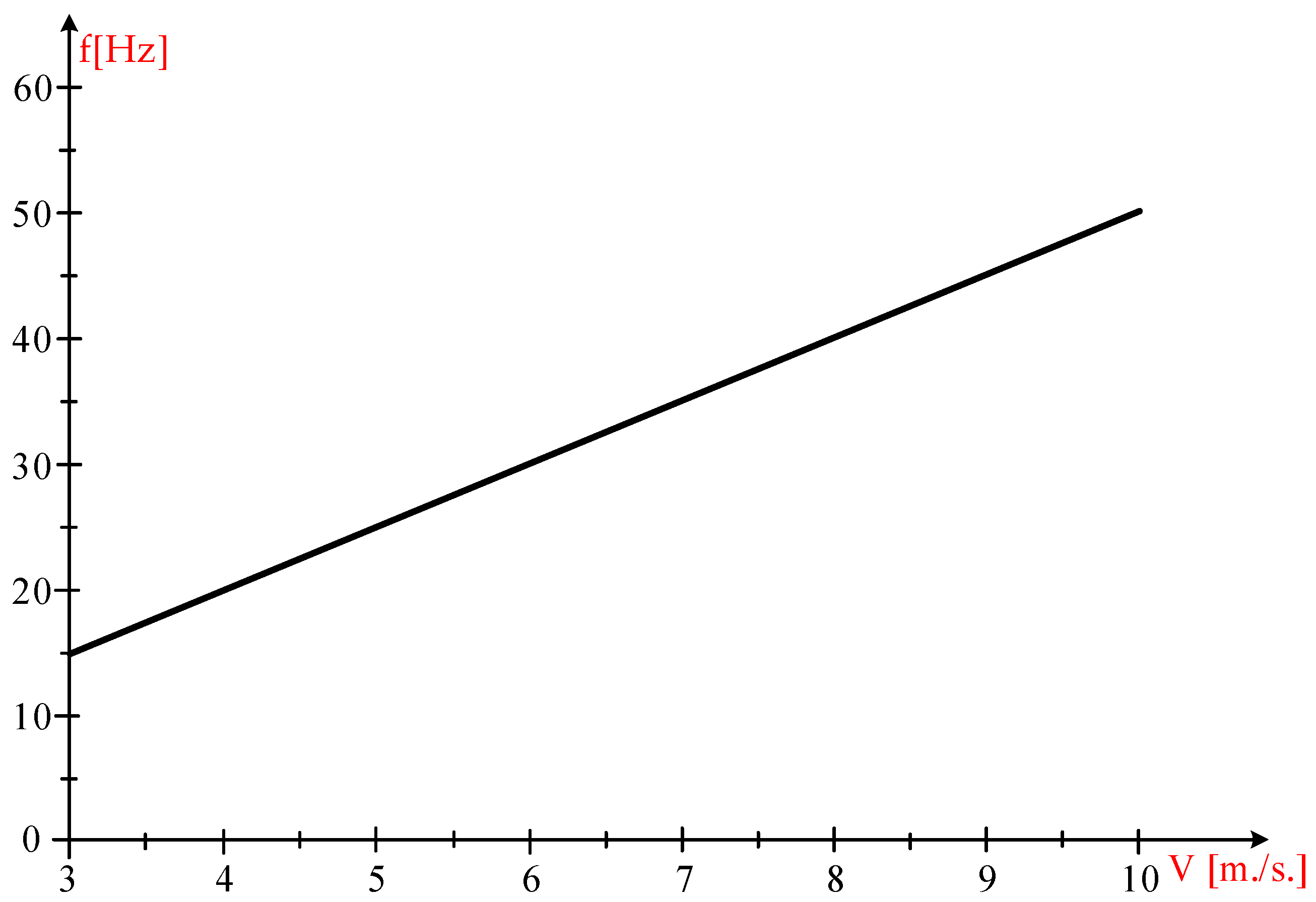

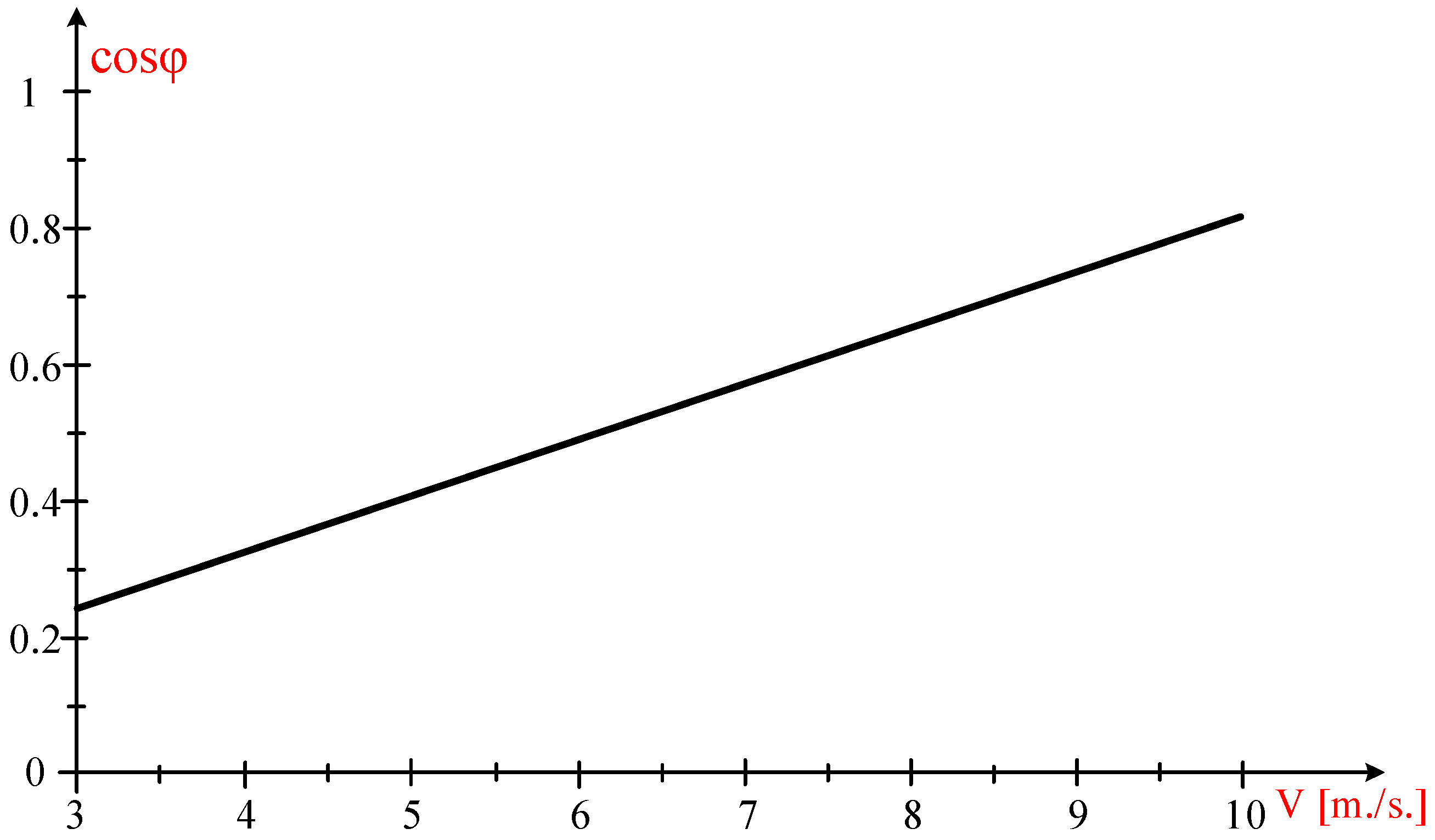
| V [m/s] | f [Hz] |
|---|---|
| 3 | 15.233 |
| 4 | 20.493 |
| 5 | 25.321 |
| 6 | 30.344 |
| 7 | 35.347 |
| 8 | 40.325 |
| 9 | 45.26 |
| 10 | 50.877 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chioncel, C.P.; Tirian, G.-O.; Spunei, E. The Behavior of Wind Turbines Equipped with Induction Generators and Stator Converters Under Significant Variations in Wind Speed. Appl. Sci. 2025, 15, 7700. https://doi.org/10.3390/app15147700
Chioncel CP, Tirian G-O, Spunei E. The Behavior of Wind Turbines Equipped with Induction Generators and Stator Converters Under Significant Variations in Wind Speed. Applied Sciences. 2025; 15(14):7700. https://doi.org/10.3390/app15147700
Chicago/Turabian StyleChioncel, Cristian Paul, Gelu-Ovidiu Tirian, and Elisabeta Spunei. 2025. "The Behavior of Wind Turbines Equipped with Induction Generators and Stator Converters Under Significant Variations in Wind Speed" Applied Sciences 15, no. 14: 7700. https://doi.org/10.3390/app15147700
APA StyleChioncel, C. P., Tirian, G.-O., & Spunei, E. (2025). The Behavior of Wind Turbines Equipped with Induction Generators and Stator Converters Under Significant Variations in Wind Speed. Applied Sciences, 15(14), 7700. https://doi.org/10.3390/app15147700








