1. Introduction
With the widespread adoption of location-based services and the increasing availability of user mobility data, location prediction [
1,
2,
3]—the task of forecasting the future position a user is likely to visit based on their historical movement trajectory—has gained significant attention in recent years. It plays a critical role in various real-world applications such as personalized recommendation systems [
4], intelligent navigation [
5], urban planning [
6], and location-aware advertising [
7]. In many studies, the location prediction is also referred to as a point-of-interest (POI) recommendation, where a POI denotes specific geographical entities like restaurants, parks, or stores that users may check into and visit, as shown in
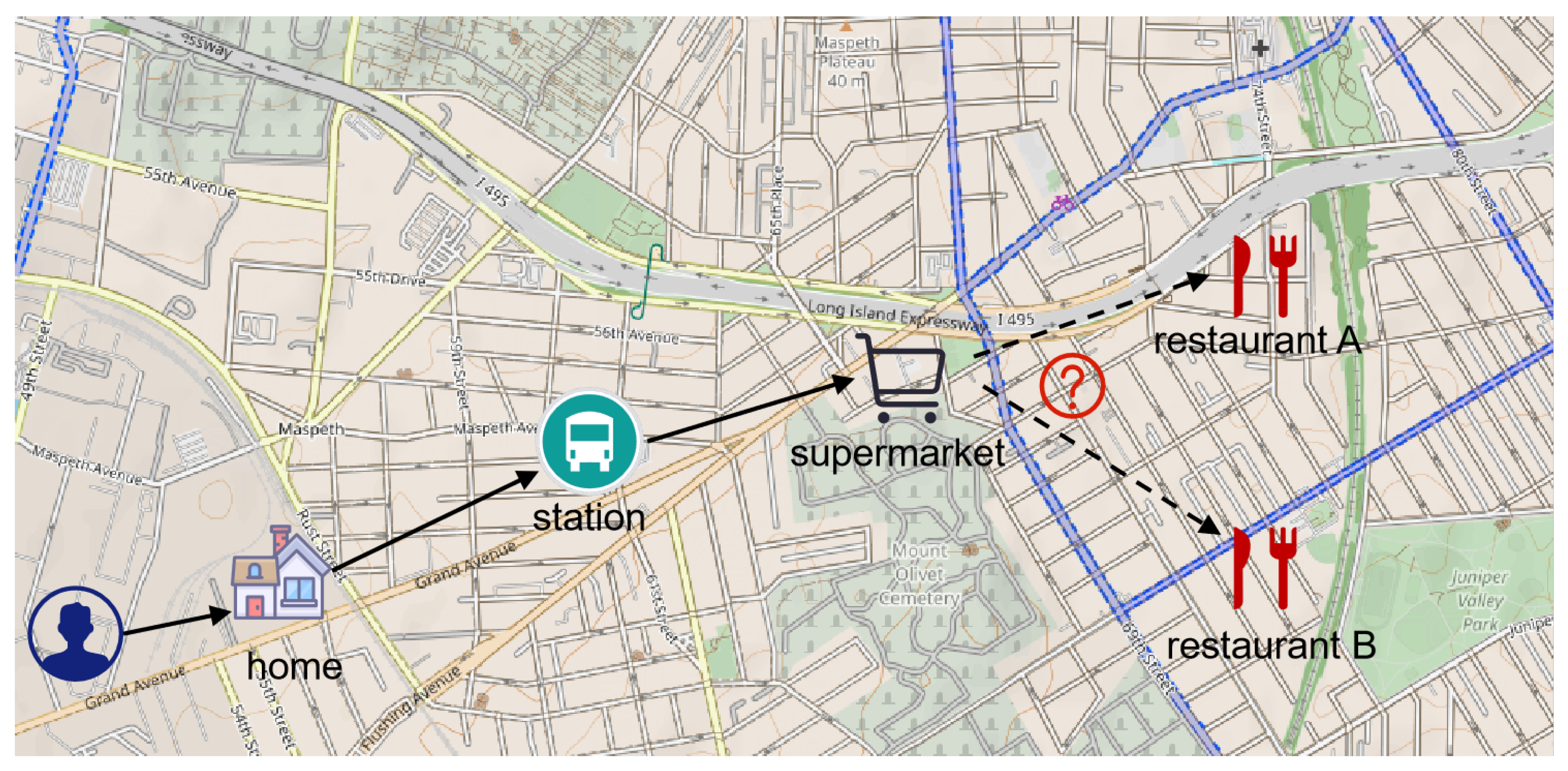
Figure 1. It aims to infer user preferences and contextual patterns from historical trajectory data and predict which location predictions users are most likely to visit next. Location prediction addresses the fundamental problem: leveraging users’ spatiotemporal behavioral history to anticipate their next geographical action.
Numerous models have been developed to address this task, which can broadly be categorized into four main groups. The first group comprises traditional approaches such as collaborative filtering (CF) [
8,
9] and matrix factorization (MF) [
10,
11], which capture co-visitation or preference patterns but often struggle with sequential or spatial dynamics. The second category includes recurrent neural network (RNN)-based models [
12,
13,
14,
15], which utilize temporal sequence modeling to learn the evolution of user preferences over time. However, these models often face limitations in capturing long-term dependencies and complex spatial interactions. The third group introduces attention-based models [
16,
17,
18,
19] that dynamically assign weights to different historical check-ins or contextual factors, improving the ability to model user intent. Finally, graph-based [
20,
21,
22] and hypergraph-based methods [
23,
24,
25] have emerged as powerful tools for modeling high-order and non-Euclidean user-location prediction relationships by representing check-in sequences and spatial clusters as graphs or hypergraphs. These approaches offer enhanced flexibility in representing multifaceted interactions but still face challenges in disentangling diverse behavioral influences effectively. In recent studies, contrastive learning has also been coupled with advanced probabilistic methods such as Variational Bayes [
26]. These methods provide a robust framework for sparse recovery, enabling more efficient learning in high-dimensional spaces.
Despite the substantial advancements in location prediction, three critical challenges remain unresolved, limiting the effectiveness of current models:
First, a prevalent limitation lies in the entanglement of heterogeneous behavioral signals—such as collective user preferences, sequential transition patterns, and geographical proximity—into a unified latent representation. This monolithic embedding often obscures the distinct contribution of each factor, making it difficult to interpret the underlying decision-making process and reducing the model’s ability to adapt to varying user behaviors across contexts.
Second, although some recent approaches [
27,
28,
29] leverage graph-based or multi-relational structures to capture diverse interaction patterns, they frequently fall short in terms of explicit disentanglement. Instead of modeling each behavioral perspective independently, these models often integrate multiple views into a single graph structure or latent space without clearly separating their semantic roles. As a result, the learned representations tend to be entangled and coarse-grained, which hampers the model’s ability to capture fine-grained, view-specific dynamics essential for accurate location prediction.
Third, even in models [
30,
31] that do acknowledge multiple views, there is a notable lack of mechanisms for explicit alignment or contrastive integration across these perspectives. Without encouraging consistency or highlighting distinctions among views, the model fails to fully exploit the complementary nature of multi-perspective information. This deficiency becomes especially pronounced in scenarios characterized by data sparsity and noisy check-in records, where robust and discriminative representations are crucial for generalization. Consequently, the inability to systematically disentangle and reconcile different behavioral signals remains a bottleneck in achieving accurate location predictions.
To address the above challenges in location prediction, we propose a novel framework named Multi-Perspective Hypergraphs with Contrastive Learning (MPHCL), which captures and disentangles user preferences by integrating three key behavioral dimensions. The framework comprises three individual graphs: (1) the collective preference hypergraph for collaborative preferences within the user community, (2) the geospatial context hypergraph for spatial correlations between locations, and (3) the global transition flow graph for mobility patterns based on visit sequences. This multi-perspective approach enables nuanced disentanglement of behavioral factors influencing user mobility. We introduce a unified hypergraph representation learning network that ensures the independence of each perspective during embedding, utilizing a node–hyperedge–node message passing framework and across-hyperedge propagation to prevent feature entanglement. Additionally, a cross-view contrastive learning mechanism aligns multi-view representations by treating embeddings of the same user or location across different views as positive pairs while considering others as negative. This approach enhances consistency, strengthens the robustness of learned embeddings, especially under sparse or noisy data, and facilitates effective integration of diverse signals. Consequently, MPHCL provides a comprehensive and personalized understanding of user intent, leading to improved performance in location prediction tasks.
In short, our main contributions are summarized as follows:
We propose a novel Multi-Perspective Hypergraphs with Contrastive Learning (MPHCL) model for location prediction, which disentangles user preferences by leveraging hypergraphs from three perspectives. Our unified hypergraph representation learning network incorporates a two-step information propagation scheme to capture high-order locations, including within-hyperedge feature aggregation and across-hyperedge feature propagation. Additionally, we introduce a cross-view contrastive learning mechanism that enhances view-specific user and location prediction representations through self-supervised signals.
We leverage graph Laplacian matrices to perform effective spectral reasoning over the constructed hypergraphs, which allows for the propagation of user preferences along directed paths in the process of graph learning.
Extensive experiments on two real-world datasets have verified the prediction performance of our proposed MPHCL model compared with various state-of-the-art methods.
4. Methodology
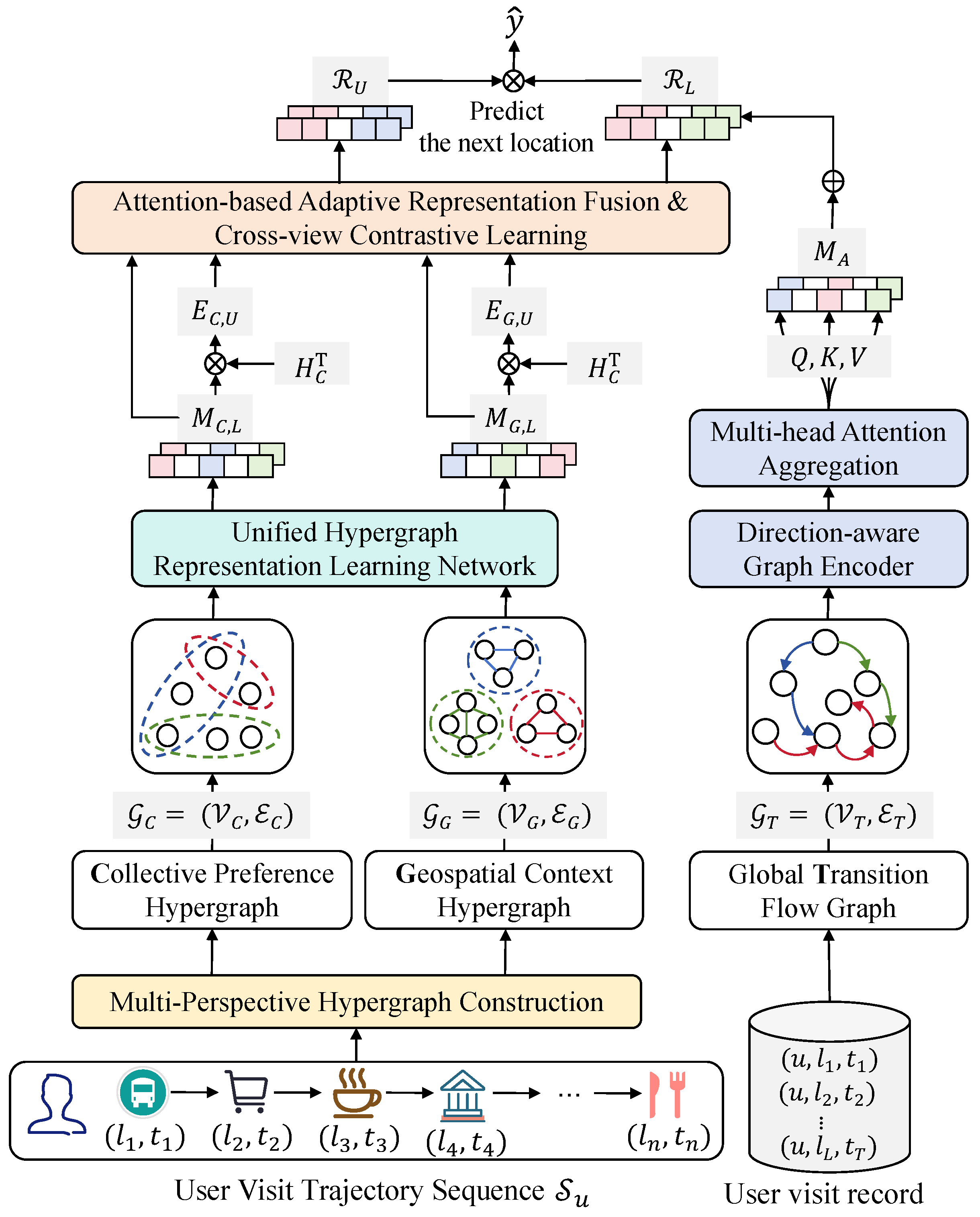
The overall framework of the proposed Multi-Perspective Hypergraphs with Contrastive Learning (MPHCL) model for location prediction is illustrated in
Figure 3. The collective preference hypergraph captures collaborative user behavior, the geospatial context hypergraph reflects the spatial relationships between locations, and the global transition flow graph models the sequential dependencies in user visits. The model employs a two-step information propagation mechanism to capture high-order dependencies within each hypergraph. Additionally, the cross-view contrastive learning module aligns the embeddings from different views, maximizing agreement across user and location representations. This architecture enables the model to integrate complementary information from multiple perspectives for more accurate location predictions.
4.1. Multi-Perspective Hypergraph Construction
In the realm of location prediction, understanding the intricate interaction relationships between users and locations is paramount. These relationships are multifaceted, encompassing (1) user-location interactions, (2) transitional dynamics that reflect the relationships among different locations, and (3) geographical correlations that emerge from the physical proximity of these locations. To capture and model these complex dynamics effectively, previous studies have introduced methodologies that treat users and locations as discrete nodes within a graph framework, wherein the interconnections between them are represented as edges.
However, traditional graph structures involve notable limitations [
35], as they predominantly focus on pairwise relationships. This approach restricts the ability to capture higher-order interactions, i.e., those that involve multiple nodes concurrently, which are often crucial for understanding the underlying semantic context. For instance, the social dynamics surrounding a user’s engagement with multiple locations or the interrelationships among a cluster of geographically proximate locations may involve intricate interactions that a conventional graph representation cannot adequately express.
Given these constraints, we recognize the necessity of a more sophisticated framework that can accommodate the complexities of these relationships. Inspired by the highly flexible and versatile nature of hypergraphs [
36], we propose a novel approach that entails the design of three distinct hypergraphs. These hypergraphs are not merely enhancements of traditional structures but, rather, represent a paradigm shift in how we conceptualize relational data within the location prediction sphere. Each hypergraph is meticulously crafted to encapsulate different aspects of user–location interactions, thereby facilitating a richer representation of the relational patterns.
4.1.1. Collective Preference Hypergraph
In order to effectively capture the high-order interactions between users and locations, we construct a collective preference hypergraph,
, where
denotes the set of locations, and
represents the collection of user-specific trajectories encoded as hyperedges. Each hyperedge,
, comprises the locations visited by user
u and is weighted by a diagonal matrix
, where each hyperedge weight,
, provides trajectory length normalization to counterbalance varying visitation frequencies. Hyperedges are formed based on the check-in trajectories of individual users. Specifically, each user’s visit history is represented as a hyperedge, where each hyperedge connects the locations that the user has visited. These hyperedges are weighted by the length of the user’s trajectory to normalize the visitation frequencies, ensuring that users with more frequent visits do not dominate the learning process. The user-location visit pattern is encoded by the incidence matrix
, with elements defined as follows:
The vertex degrees are computed as , while the hyperedge degrees are given by , forming diagonal degree matrices and .
The intra-sequence co-visitation structure is captured by the weighted adjacency matrix
, which encodes the relational strength between locations. To capture inter-sequence user dependencies based on shared location visitation, we define a hyperedge similarity metric using cosine similarity as follows:
where
denotes the column of
corresponding to hyperedge
.
Information propagation over the collective preference hypergraph is governed by the hypergraph Laplacian , enabling the learning of diffusion-aware representations. Furthermore, a spectral analysis of the kernel allows for the identification of latent user clusters exhibiting similar behavioral patterns across the location space. The proposed collective preference hypergraph facilitates the modeling of both local user trajectory structures and global co-visitation patterns.
4.1.2. Geospatial Context Hypergraph
The construction of the geographical view hypergraph is a sophisticated process that entails the formulation of a hypergraph designed to represent the geographical relationships among different locations while adhering to specific spatial constraints. Formally, we denote a geospatial context hypergraph as
, where
represents the set of locations. Locations that are within a predefined distance threshold, calculated using the Haversine distance, are connected via hyperedges. These hyperedges capture the spatial relationships between geographically close locations, reflecting the proximity effect in user preferences. Within this hypergraph
, a hyperedge is established to connect locations that lie within a predetermined distance threshold
. This threshold is critical for accurately capturing the proximity of interactions and is derived from the Haversine distance metric
, which is mathematically expressed as follows:
where
represents two locations,
denotes latitudes of locations
,
signifies longitudes of locations
, and
is the Earth’s radius.
In our model, we utilize the Haversine distance metric to capture geographical proximity between locations, as it accurately accounts for the curvature of the Earth. Unlike the Euclidean norm, which assumes a flat plane and is suitable only for small-scale distances, the Haversine distance calculates the shortest path along the surface of a sphere, making it ideal for modeling real-world spatial relationships between locations. This ensures that the proximity relationships between locations are represented more realistically, especially for large geographical areas.
Consequently, the incidence matrix serves as a crucial role in depicting the geographical interactions among locations. Specifically, if the Haversine distance between and satisfies the condition , we designate . Conversely, if the distance exceeds the threshold, we set . This binary representation encapsulates the existence of geographical relationships and enables the exploration of patterns in spatial clustering that significantly influence user behaviors and preferences.
The proposed geospatial context hypergraph is not merely a mathematical construct, and it embodies critical geographical influences that play a vital role in shaping user preferences in real-world contexts. By integrating this spatial dimension, we can elucidate how users traverse their environments, uncovering visitation patterns often dictated by geographical proximity. This structure thus effectively reflects user geographical preferences, allowing us to analyze how proximity impacts user decision-making processes when selecting the next locations.
So far, we have constructed two hypergraphs from diverse perspectives, namely the collective preference hypergraph and the geospatial context hypergraph . Next, we will propose a disentangled hypergraph representation learning network to explicitly model and derive enriched representations of locations. Employing a disentangled learning framework, we can isolate the contributions of each viewpoint, facilitating a comprehensive understanding of user dynamic visit preferences.
4.2. Global Transition Flow Graph
While traditional hypergraphs can effectively capture high-order and undirected associations among entities, they are inherently limited in representing directional semantics, such as location-to-location transitions in user visit trajectories. In contrast to the collective preference hypergraph, which models co-visitation, we define a Global Transition Flow Graph
to encode directed transition dynamics between locations. Here, the vertex set
denotes the set of locations, while the edge set
captures the sequential transitions observed in all user visit records, where each
corresponds to an ordered set of location transitions
made by user
u. Hyperedges represent transitions between locations based on sequential visit data. Each hyperedge in this graph connects a pair of locations, representing the direct transitions from one location to another in a user’s trajectory. These transitions are directed to preserve the movement dynamics of users. To represent such directional transitions, we define the incidence matrix
, where
if location
serves as a source or target in the transition
, and its role is further differentiated via a pair of incidence matrices
that explicitly capture source and target locations, respectively. Specifically, they are defined as follows:
Using these directed incidence matrices, we define a transition-aware matrix as , where is a diagonal matrix assigning weights to each transitional edge, commonly normalized by the number of transitions observed in each user’s trajectory. It captures the directed transition strength from source locations to target locations.
To enable spectral reasoning over this directed global transition flow graph
, we define a transition-aware Laplacian matrix as follows:
where
and
are the diagonal degree matrices of source nodes and transition edges, respectively. This spectral operator allows us to propagate preferences along directed paths in the trajectory space, thus enabling a fine-grained analysis of transition dependencies. The transition-aware Laplacian matrix captures the directed transition dynamics between locations by incorporating both source and target location information. Spectral reasoning over this matrix allows for the propagation of user preferences along directed paths in the global transition flow graph, enabling the model to capture the directed nature of user mobility. This spectral analysis provides a means to analyze global transition patterns and predict future locations based on the directionality of previous transitions.
The proposed global transition flow graph , therefore, captures the global structure of location transitions across all users and facilitates the discovery of dynamic behavioral patterns and next-location prediction signals.
4.2.1. Direction-Aware Graph Encoder
To extract semantically rich transition-aware representations from , we propose a direction-aware graph encoder. Unlike standard GCNs, which treat edges as undirected, this encoder explicitly models the asymmetry in user movement behavior. For each location node , we separately aggregate features from its incoming and outgoing transitions to learn a direction-sensitive embedding.
Formally, let
denote the current embedding matrix of locations. We define the directional aggregation from source and target directions as follows:
where
and
are learnable weight matrices for outgoing and incoming transitions, respectively,
and
are diagonal normalization matrices, and
is a non-linear activation function such as ReLU.
The final node representation is obtained by fusing the two directions:
where
is a learnable parameter or a fixed balancing factor. While other fusion strategies, such as concatenation, attention-based fusion, and MLP-based fusion, could be applied, we observed that the weighted combination method offered the best trade-off between model performance and complexity.
This dual-path aggregation helps encode both “where users come from” and “where they are likely to go,” which is essential for modeling temporal dependencies and user intent in next-location prediction.
4.2.2. Multi-Head Attention Aggregation
To further enhance representation capability, we adopt a Multi-head Attention Aggregation mechanism that adaptively weighs different transition contexts. Inspired by the transformer architecture, we compute
h attention heads as follows:
where
are the query, key, and value matrices of the
k-th head. The final representation is obtained as follows:
where
is a learnable projection matrix, and
denotes the position-aware attention matrix.
This design allows the model to capture diverse spatial–temporal transition semantics and improves the robustness and expressiveness of location representations for downstream prediction tasks.
4.3. Unified Hypergraph Representation Learning Network
In this section, we propose a novel approach to learn disentangled representations of location prediction from three distinct hypergraphs, employing advanced aggregation and propagation methods within hypergraph convolutional networks (HGCNs) [
23,
37]. These networks aim to capture the complex dependencies between users and location predictions through multiple views.
Before encoding, given the user set U and location set L, we initialize the user embeddings and location embeddings via a look-up table, where stands for a embedded function designed by stacking multiple full connection layers, d denotes the embedding dimension, is the number of users, and represents the number of locations. Each element and . The embedding matrices and are updated during training using gradient-based optimization.
These embeddings are propagated through the hypergraph convolution network in subsequent steps, where the aggregation function considers interactions between users and location predictions across multiple views, enhancing their feature representations. The propagation process of traditional hypergraph learning involves an iterative refinement of embeddings, computed as follows:
where
is the adjacency matrix corresponding to hyperedge
e,
is the embedding at the
k-th layer for the hyperedge
e, and
denotes a nonlinear activation function, such as ReLU.
However, the traditional hypergraph learning only considers the feature aggregation of adjacent nodes within a hyperedge and ignore the interaction of non-adjacent nodes across different hyperedges.
In this paper, we will focus on the interaction between non-adjacent nodes across different hyperedges and propose a disentangled hypergraph representation learning network. It selectively emphasizes more informative connections between nodes across different hyperedges and computes weighted sums of neighboring node embeddings, dynamically adjusting weights based on the relative importance of each connection.
Specifically, the proposed unified hypergraph representation learning network incorporates a two-step information propagation scheme to capture high-order locations iteratively. This scheme is based on a node–hyperedge–node propagation model, where hyperedges act as intermediaries for node aggregation within the hypergraph and for propagating information across the hyperedges. The propagation process is composed of two main operations: (a) within-hyperedge feature aggregation and (b) across-hyperedge feature propagation.
4.3.1. Within-Hyperedge Feature Aggregation
For each hyperedge,
, we aggregate the embeddings of the nodes that belong to this hyperedge. This aggregation operation generates a medium message,
, which summarizes the information of all nodes in the hyperedge. The aggregation is mathematically represented as follows:
where
is the aggregation function applied to the node embeddings
l, with each
representing the embedding of node
l. The function
can take various forms, such as a summation, average, or maximum, depending on the specific characteristics of the hypergraph:
where
denotes the number of nodes in hyperedge
e. This aggregation step captures the joint information of all nodes within a given hyperedge, generating a summary message for that hyperedge.
4.3.2. Across-Hyperedge Feature Propagation
Since each node
l may be connected to multiple hyperedges, we aggregate the messages from these related hyperedges to refine the node’s embedding. Take the collective preference hypergraph
for example; the propagation of information from hyperedges back to nodes is represented as follows:
where
is the propagation function, which aggregates the medium messages
from all hyperedges
e that are related to node
l.
This across-hyperedge feature propagation step enables the refinement of node embedding by incorporating information from neighboring hyperedges, capturing the multi-level relationships that exist within the hypergraph structure. The proposed disentangled hypergraph representation learning network operates iteratively, with the embeddings being refined across multiple layers. Let
denote the embedding of node
l at the
ℓ-th layer of the model. The embedding at each layer is updated by combining the propagated message from the previous layer and the newly aggregated information:
where
is the information from the previous layer, and the addition of the previous layer’s embedding helps maintain residual connections. The residual connections are crucial to prevent over-smoothing, a common issue in graph neural networks (GNNs), ensuring that the node embeddings retain distinctiveness even after multiple aggregation layers.
Finally, to generate the final representation for node
l, the embeddings from all layers are averaged, formulated as follows:
The total number of layers is denoted as L. After performing the multi-layer propagation and aggregation operations, we obtain the refined collective location embedding matrix for collective preference hypergraph . These representations capture the underlying structure of the collaborative hypergraph, effectively encoding the complex interactions between users and locations.
For the aggregation functions and , we implement them using mean pooling. This choice of aggregation method has been proven to be both effective in capturing the relationships within collaborative and geographical views of the data. Specifically, mean pooling ensures that the aggregated message from each hyperedge is balanced, averaging the information from all nodes within a hyperedge without favoring any particular node.
Similar to the collective preference hypergraph , we further model geographical dependencies of locations. These modules are stacked over L layers to capture high-order neighborhood dependencies, with residual connections introduced to mitigate the over-smoothing problem.
Through above processes, we can obtain the refined collective location embedding matrix for the collective preference hypergraph and the refined geospatial location embedding matrix for the geospatial context hypergraph , where denotes the number of locations, and d is the embedding dimension.
4.4. Attention-Based Adaptive Representation Fusion
In the previous section, to comprehensively capture user preferences from diverse perspectives, we propose a disentangled hypergraph representation learning network approach that learns distinct location embeddings for three fundamental dimensions, i.e., collective preference and geospatial context. These embeddings, denoted as and , respectively, are formulated in the latent space . Each embedding encapsulates distinct factors that influence user behavior within its respective dimension, thereby enabling the modeling of intricate user preferences.
To further establish user-specific embeddings tailored to these perspectives, we use the incidence matrix
of collective preference hypergraph
, which encodes the relationships between users and locations in the collaborative dimensions. Specifically, the user embeddings
and
are computed by aggregating the location embeddings
and
through the incidence matrix
. Mathematically, this process can be formulated as follows:
where
represents the transposed incidence matrix enabling the projection of location embeddings into user-specific spaces.
To achieve a unified representation of user preferences that adaptively considers the relative importance of different behavioral perspectives, we introduce an attention-based fusion mechanism. Rather than using fixed scalar coefficients, we learn attention weights dynamically based on the user embeddings derived from the collective and geographical views.
Formally, given the two user-specific embeddings
, we compute the fused user representation
as follows:
where
is the learned attention weight for each user, broadcasting across the embedding dimensions.
We compute the attention weights
using a two-layer feedforward network with non-linear activation:
where
denotes vector concatenation,
and
are learnable weight matrices, and
is the hidden layer dimension. The softmax operation is applied row-wise to ensure normalized attention distribution across views.
Alternatively, for a more compact implementation, a scalar attention weight per user can be computed using a single-layer attention module:
where
and
are learnable parameters, and
is the sigmoid function.
This attention-based fusion mechanism allows the model to dynamically weigh collaborative and geographical information according to user-specific behavioral patterns, thereby yielding more personalized and adaptive user representations.
While adaptive fusion of user embeddings is critical due to the heterogeneity in user behaviors across perspectives, the aggregation of location embeddings can be simplified. Since location predictions inherently exhibit less variability across dimensions, a linear summation of location embeddings is sufficient for constructing their unified representation. Thus, we define the fused location representation
:
This linear aggregation assumes that the characteristics of location predictions are uniformly distributed across dimensions, enabling efficient computation while preserving representational fidelity.
4.5. Cross-View Contrastive Learning
Contrastive learning [
38,
39] is a prominent self-supervised learning approach that focuses on understanding the similarities and differences among data points. Its fundamental principle involves bringing similar sample pairs closer together in the embedding space while simultaneously pushing dissimilar pairs further apart. In this work, we propose a unified cross-view contrastive learning framework designed to enhance view-specific user and location prediction representations through self-supervised signals, effectively capturing the underlying cooperative associations among collective preference, sequential transition, and geospatial context perspectives.
We incorporate a disentangled hypergraph representation learning module that generates distinct embeddings for each user and location prediction across the aforementioned views. These multi-view representations are subsequently aligned through a cross-view contrastive objective within an adaptive representation fusion module.
Specifically, from the user perspective, we treat embeddings of the same user across different views as positive pairs, while embeddings from different users are regarded as negative pairs. To facilitate this alignment, we employ the InfoNCE loss function [
40], which maximizes the agreement between the representations from different views. In the context of contrastive learning, inspired by [
23], we explore the relationships among user representations derived from collaborative, transitional, and geographical perspectives. The following Equation (
24) defines contrastive losses that help optimize our model by emphasizing similarities and dissimilarities among these different views. For instance,
represents the contrastive loss of the same user,
u, between collaborative and geospatial views.
where
,
represents user embeddings from different perspectives of user
u,
is a cosine similarity function, and
is a temperature hyperparameters of the contrastive learning.
From the location perspective, we replace user
with location
and define the contrastive losses,
, for the collaborative and geospatial views:
To obtain the final self-supervised contrastive loss for the entire model, we weighted aggregate the contrastive loss from both user and location perspectives:
where
is a weighting coefficient to balance the contrastive loss between the user and location.
This comprehensive self-supervised loss enhances the consistency and discriminative capability of multi-view representations. Moreover, to mitigate the overfitting issue and enhance robustness, we adopt a hypergraph augmentation strategy by applying hyperedge dropout on the constructed collective preference, sequential transition, and geospatial context hypergraphs. This dropout, controlled by a ratio , introduces structural perturbations and promotes generalizable representation learning under noisy conditions.
4.6. Prediction and Optimization
With the fused user representation and fused location representation , where and denote the total number of users and locations respectively, we compute the interaction score between user and location predictions based on their dot product in the latent space.
Specifically, the predicted interaction probability is computed via a softmax function, as , indicating the likelihood of the user visiting that location at the given timestamp. This probabilistic prediction is computed by the dot product of the fused user and location representations in the latent space, followed by a softmax function, ensuring that the output is a normalized probability distribution across the top-k locations.
The recommendation objective is formulated as in Equation (
27), a binary cross-entropy loss over all user-location prediction pairs.
where
indicates whether user
u visited location
l (1 for visited, 0 otherwise).
To enhance the learning signal, we adopt a multi-task objective by incorporating a self-supervised contrastive loss,
, and a regularization term to mitigate overfitting. The final total loss function is defined as follows:
where
is a hyperparameter controlling the relative importance of the self-supervised signal, and
denotes the set of all trainable parameters in the proposed MPHCL model.
5. Experiments
5.1. Dataset
We conduct experiments on two widely used real-world location-based social network (LBSN) datasets [
41]: Foursquare-NYC (abbreviated as NYC) and Foursquare-TKY (abbreviated as TKY). These datasets were independently collected from New York City and Tokyo City, respectively, and span a continuous period of 11 months. The user check-in data is obtained from the Foursquare platform and includes detailed temporal and spatial information on user visits to various location predictions.
To ensure data quality, we apply a series of preprocessing steps. First, we chronologically sort all user interactions and filter out unpopular location predictions that have been visited by fewer than 5 users. Next, we segment each user’s complete check-in history into sessions, where each session contains all check-ins that occur within a 24-hour window. Sessions with fewer than three check-in records are discarded to ensure meaningful interaction sequences. Additionally, we exclude inactive users whose total number of sessions is fewer than three.
We use the first 80% of sessions from each user for training, while the remaining 20% are reserved for testing. To prevent information leakage during evaluation, we only include location predictions in the test set that occur after all check-ins in the corresponding user’s training data. The detailed statistics of the preprocessed datasets are provided in
Table 1.
5.2. Data Distribution Analysis
To analyze user mobility patterns and the spatial density of location predictions, we visualize the visit frequency and location distribution across two real-world datasets: NYC and TKY.
Figure 4 presents the heatmap of visit frequency, where each pixel corresponds to a geographical location
, and the color intensity reflects the total number of user visits to the corresponding location prediction.
The NYC dataset contains
locations and the TKY dataset contains
locations. The redder the region on the heatmap, the higher the accumulated visit frequency. From
Figure 4a, it is evident that user activities in NYC are highly concentrated in the Manhattan area, particularly around midtown and the Upper West Side. In contrast,
Figure 4b shows that visit frequencies in Tokyo are densely distributed in the
Tokyo Metropolis, which serves as the central area of user interaction.
To further examine the spatial density of location predictions, we show the number distribution of locations, where each circular marker represents a spatial cluster of locations, annotated with the count of locations within that region. In particular,
Figure 5a shows that the
Upper West Side of Manhattan (highlighted with a blue bounding box) contains approximately 286 locations, representing a high local density. Similarly,
Figure 5b highlights an area in Tokyo Metropolis that includes 655 locations. These distributions reflect significant spatial clustering and long-tail distributions, where a small number of urban areas contain the majority of location predictions.
5.3. Evaluation Metrics
We employ the following three popular metrics to assess the performance of various methods.
Recall@K measures the proportion of ground truth locations successfully retrieved among the top-K predictions. For a given test instance,
i, let
denote the ground truth location, and let
denote the list of top-K predicted locations. Recall@K is defined as in Equation (
29).
where
N is the total number of test instances, and
is the indicator function that returns 1 if the condition is true and 0 otherwise. This Recall@K metric emphasizes whether the true next location is included in the top-K list, regardless of its exact position in the list.
The normalized discounted cumulative gain (NDCG@K) measures a position-aware metric that assesses the quality of the ranking by considering the position of the relevant location prediction in the predicted list. It penalizes relevant items that appear lower in the ranked list. For each test instance,
i, the DCG (discounted cumulative gain) at rank
K is computed as in Equation (
30).
where
denotes the location prediction ranked at position
j in the top-K predicted list
. The ideal DCG (IDCG) corresponds to the DCG when the ground truth location prediction appears at the top position as in Equation (
31).
and thus, the NDCG@K is defined as in Equation (
32).
this NDCG@K metric not only considers whether the true location prediction is present in the predicted list but also rewards higher ranks more significantly.
The mean reciprocal rank (MRR) evaluates the average reciprocal rank of the ground truth in the prediction list, and its calculation is as in Equation (
33).
where
N is the number of queries, and
represents the rank position of the ground truth for the
i-th query.
To ensure statistical reliability and fairness, each experiment is repeated 10 times, and we report the average values of Recall@K and NDCG@K and MRR. We evaluate the model performance at two commonly .
5.4. Parameter Settings
For our proposed MPHCL model, we utilize the Adam optimizer with a learning rate of
, a weight decay of
, and a hyperedge dropout rate of
. The embedding dimension for both users and locations is searched from the range
. To explore model depth, the number of layers in the hypergraph convolutional network is chosen from the candidate set
, allowing us to examine the influence of multi-hop message aggregation. With respect to spatial filtering, we empirically set the geographical distance threshold from the range
= 1.0 km, 2.0 km, 2.5 km, 3 km, considering urban scale and user mobility. In our cross-view contrastive learning module, the temperature parameter is selected from the range
to control the smoothness of the similarity distribution. The optimal parameter selection will be presented in
Section 5.7.
5.5. Baseline Model
We compare the performance of our proposed Multi-Perspective Hypergraphs with Contrastive Learning (MPHCL) model with ten state-of-the-art baselines, which are popular for location prediction.
NeuNext [
14] employs a spatio-temporal gated architecture that enhances traditional LSTM networks with time and distance gates to model user-location interaction sequences. It introduces two distinct pairs of time and distance gates to separately capture both short-term and long-term user interests.
LSTPM [
15] is designed to effectively capture and represent users’ long-term preferences by utilizing a context-aware non-local network combined with a geo-nonlocal structure. It allows the model to account for the nuanced ways in which user interests evolve over time, taking into consideration various contextual factors. Furthermore, LSTPM incorporates a geo-dilated LSTM architecture to adeptly model users’ short-term interests.
LightGCN [
42] presents a streamlined graph convolutional architecture specifically designed for collaborative filtering by removing non-essential processes, such as feature transformation and nonlinear activation.
EEDN [
43] utilizes a hybrid hypergraph convolution encoder designed to model interactions between users and locations. It integrates a matrix factorization decoder to facilitate effective feature alignment.
STAN [
16] employs a sophisticated bi-layer attention mechanism designed to capture the spatiotemporal correlations present in user trajectories, which allows the model to analyze and understand how users interact with different locations and items over time.
GETNext [
17] introduces a comprehensive global trajectory flow map aimed at uncovering prevalent patterns in user movement. By leveraging GCNs, it transforms these attributes into latent embeddings, which facilitate a deeper understanding of user behavior dynamics.
CTRNext [
44] integrates a trajectory semantic similarity module alongside a multihead self-attention mechanism to capture collaborative signals derived from the check-in behaviors of similar users. This approach enables the model to analyze and understand the semantic relationships between user trajectories, thereby enhancing its ability to identify patterns and preferences shared among users with comparable behaviors.
MSTHN [
24] utilizes a multi-faceted spatial-temporal enhanced hypergraph network to capture intricate local interactions and high-order global collaborative signals. Furthermore, a user temporal preference augmentation module combines both local and global representations, improving the model’s capacity to adjust to dynamic user behavior.
SLS-REC [
45] adopts a self-supervised graph neural architecture that explicitly models both long-term static and short-term dynamic user interests through a multi-view spatio-temporal learning strategy. The model constructs a Hawkes-process-based attention hypergraph to capture complex, high-order temporal and spatial dependencies for short-term interest modeling.
STHGCN [
25] leverages hypergraphs and aggregates multi-hop trajectory information to model the intricate relationships between user check-ins and their trajectories. This advanced framework integrates spatio-temporal data to provide a comprehensive understanding of user movement patterns.
5.6. Performance Comparasion
Table 2 and
Table 3 provide an in-depth comparison of our MPHCL model when benchmarked against ten baseline models. The consistent differences in computation results between NYC and TKY can primarily be attributed to the differences in urban density, geographical layout, cultural and behavioral variations, and data sparsity. These factors influence how well the model can generalize to each city’s unique characteristics, leading to the observed performance differences.
Figure 6 and
Figure 7 are visual representations of
Table 2 and
Table 3. Early methods, such as NeuNext and LSTPM, focus on sequence modeling based on LSTM architectures augmented with temporal and spatial gating mechanisms. While these models are effective in capturing short-term and long-term user interests to some extent, they do not explicitly model spatial relations or collaborative signals between users. Consequently, their performance remains suboptimal. On the NYC dataset, NeuNext achieves Recall@10 of 0.2549 and MRR of 0.2355, while LSTPM shows marginal improvement with Recall@10 of 0.2671 and MRR of 0.2460. These results reflect their limited representational power in capturing complex behavioral patterns.
To overcome the weaknesses of purely sequential models, a second group of models such as EEDN, STAN, and GETNext integrates graph-based or attention-based mechanisms. These approaches incorporate spatial and semantic contexts more effectively. For instance, GETNext utilizes a global trajectory flow graph to model transitions between location predictions, which leads to improved performance with Recall@10 reaching 0.3739 on the NYC dataset. However, these models still operate largely within conventional graph frameworks, restricting their ability to capture high-order relationships and resulting in a plateau in performance around the 0.37–0.38 mark for Recall@10. This demonstrates that while adding attention or spatial graph structures improves results, these gains remain limited due to the inherent modeling constraints.
Recent advances such as MSTHN, SLS-REC, and STHGCN further push the boundaries by incorporating hypergraph structures, enabling them to model high-order collaborative signals among location predictions and users more effectively. These models interpret user sessions or trajectory clusters as hyperedges, allowing them to capture rich interactions that are otherwise lost in traditional graphs. For example, STHGCN achieves Recall@10 of 0.4377 and MRR of 0.3709 on NYC, which represents a significant improvement over earlier graph-based approaches. Nonetheless, these models often focus on a single perspective, such as spatial movement or local sequential patterns, and lack the capacity to coordinate multiple behavioral views.
Our proposed MPHCL framework addresses these gaps by simultaneously modeling three distinct perspectives of user behavior through separate hypergraphs, thereby capturing a more comprehensive understanding of user intent. More importantly, MPHCL introduces a contrastive learning objective across these views, encouraging the alignment of user embeddings derived from different perspectives. This facilitates the learning of robust and coherent representations that are more adaptable to dynamic user behaviors. The final representations are integrated through a learnable aggregation mechanism that dynamically adjusts the contribution of each view, further enhancing personalization.
Empirical results on two benchmark datasets, NYC and TKY, clearly demonstrate the superiority of MPHCL. On the NYC dataset, MPHCL achieves Recall@10 of 0.4786, NDCG@10 of 0.3965, and MRR of 0.3865, significantly outperforming the strongest baseline STHGCN, which achieves 0.4377, 0.3732, and 0.3709, respectively. A similar trend is observed on the TKY dataset, where MPHCL reaches Recall@10 of 0.3925 and MRR of 0.2950, again achieving state-of-the-art results across all metrics. Notably, while earlier methods stagnate around Recall@10 values in the mid-30s, MPHCL breaks through this ceiling, reaching values near 48 on the NYC dataset, illustrating a substantial leap in recommendation accuracy.
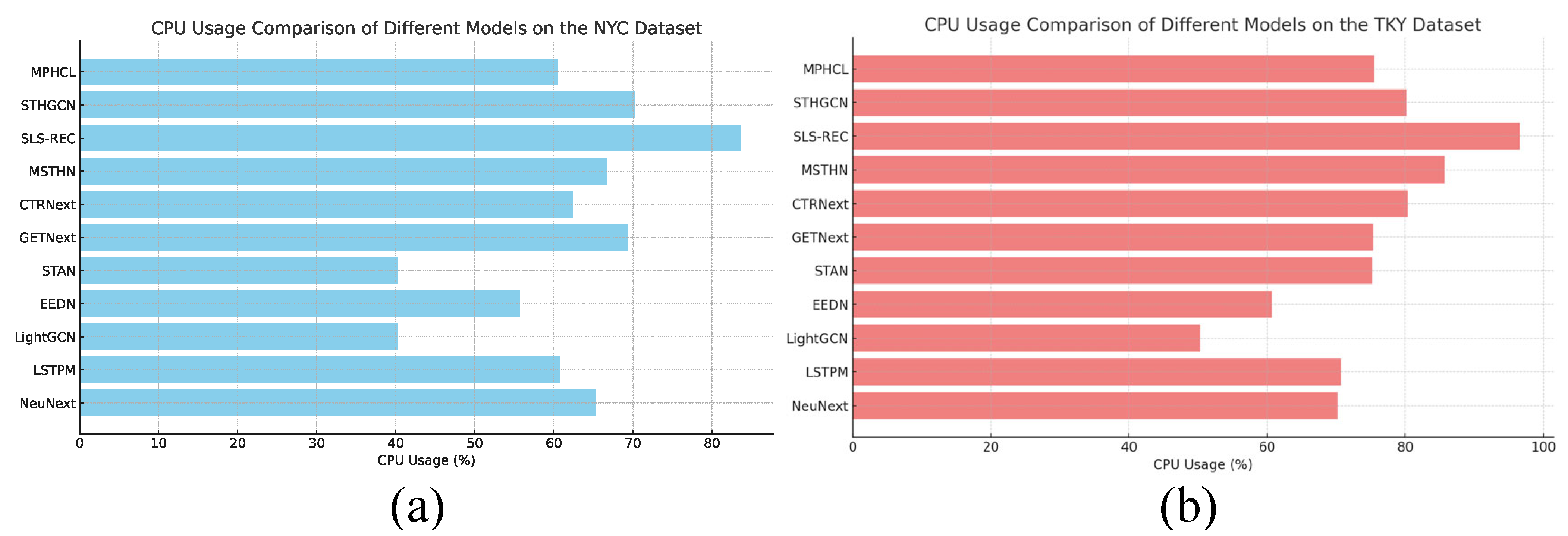
Figure 8 shows the CPU usage comparison of different models. Specifically, our proposed MPHCL model demonstrates a relatively low CPU usage of 60% on the NYC dataset and 75% on the TKY dataset. These results indicate that MPHCL not only performs competitively in terms of prediction accuracy but also operates efficiently, making it suitable for real-time applications with mobile users who update their location data frequently.
5.7. Hyperparameter Analysis
We analyze the impact of the temperature hyperparameter and the distance threshold on the model performance, measured by Recall@5, on both the NYC and TKY datasets. The temperature hyperparameter is commonly used in contrastive learning frameworks (e.g., InfoNCE loss), where it controls the concentration level of the similarity distribution. Specifically, a smaller sharpens the distribution, amplifying differences between similar and dissimilar pairs, while a larger smooths it. In our case, we observe that the optimal value is , which balances these effects and leads to the highest recall performance across different distance thresholds.
In
Figure 9a, we observe that, when
, Recall@5 reaches its peak for all values of
. Among these,
yields the best performance. This can be attributed to the spatial characteristics of NYC, where location predictions are densely clustered, particularly in Manhattan. Hence, a relatively small distance threshold is sufficient to capture the relevant local geographical context.
In contrast,
Figure 9b shows that, while
is still optimal, the best-performing distance threshold is
, slightly larger than that of NYC. This is because the location predictions in Tokyo are more geographically dispersed across a wider urban area. As a result, a larger
is necessary to incorporate a broader spatial context and effectively capture semantic relationships in the data.
In summary, while the optimal temperature hyperparameter remains consistent across datasets at , the optimal distance threshold varies due to differences in location prediction density and spatial distribution. NYC benefits from a smaller due to its compact urban layout, whereas TKY requires a larger threshold to accommodate its broader geographical spread.
To investigate the sensitivity of our Disentangled Hypergraph Representation Learning Network to architectural configurations, we conduct a comprehensive evaluation over varying embedding dimensions
and layer numbers
, as shown in
Figure 10.
The performance surface formed by varying d and L reveals the following key observations:
(1) On the NYC dataset, the model attains the maximum performance Recall@5 = 0.4350 at . This setting, corresponding to an intermediate embedding size and a two-layer network, strikes an effective balance between representation capacity and overfitting risk.
(2) On the TKY dataset, the optimal setting shifts slightly to a deeper architecture, Recall@5 = 0.3630 at . Despite the difference in optimal depth, both datasets consistently favor an embedding dimension of , suggesting this size as a robust choice across domains.
(3) We observe a non-monotonic relationship between both d and L with performance. When the embedding size is too small (e.g., ), the model suffers from insufficient representational capacity, leading to degraded performance due to its inability to capture complex hyper-relational patterns. As d increases, performance improves, peaking at , after which further increases (e.g., ) lead to a decline. This degradation for larger d is attributed to feature redundancy, which not only increases the computational cost but may also introduce noise, harming generalization. A similar pattern is observed with respect to network depth L. Shallow networks () tend to under-express structural dependencies, while overly deep networks () suffer from over-smoothing or optimization difficulties. The optimal number of layers thus lies at a moderate depth.
(4) In conclusion, the experimental results empirically demonstrate that a moderate embedding size () coupled with a shallow-to-moderate network depth ( or ) offers the best trade-off between model expressiveness and generalization. This validates the importance of carefully tuning these architectural hyperparameters for achieving optimal performance in disentangled hypergraph representation learning.
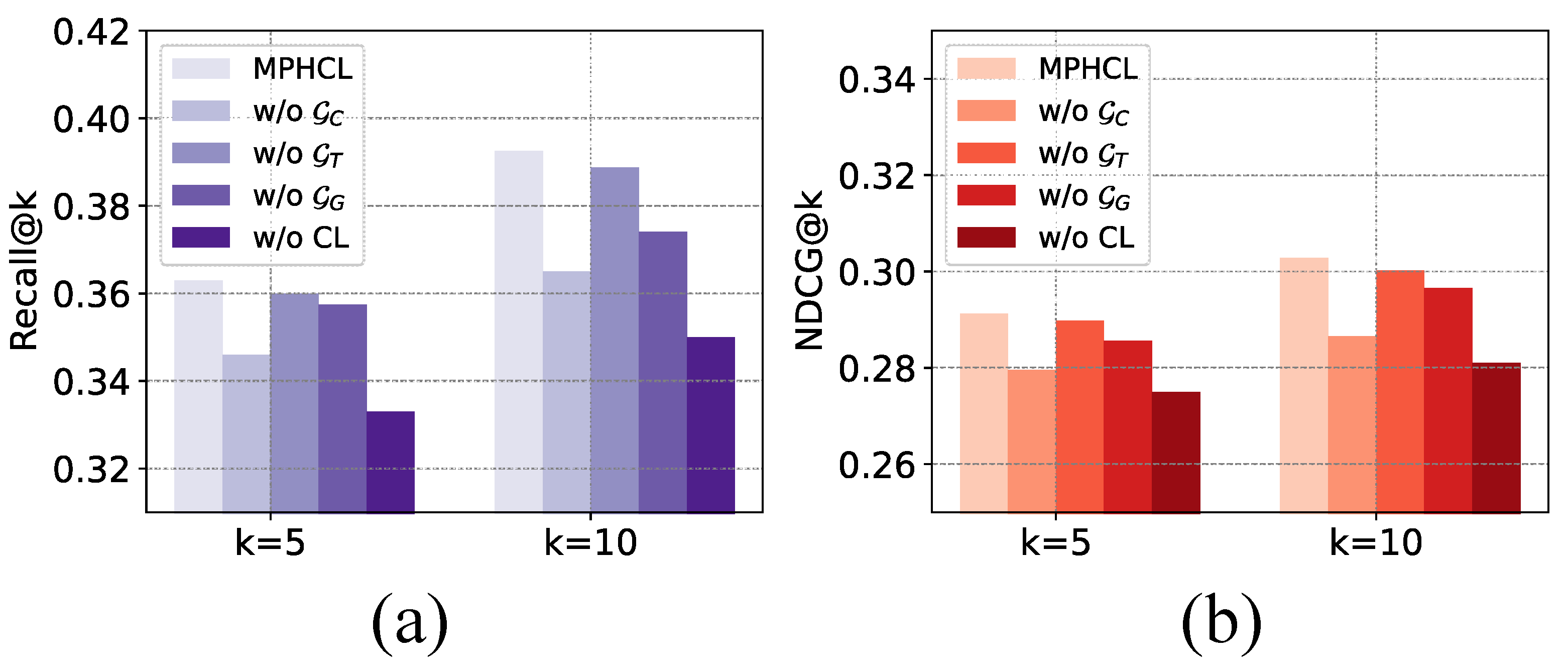
5.8. Ablation Study
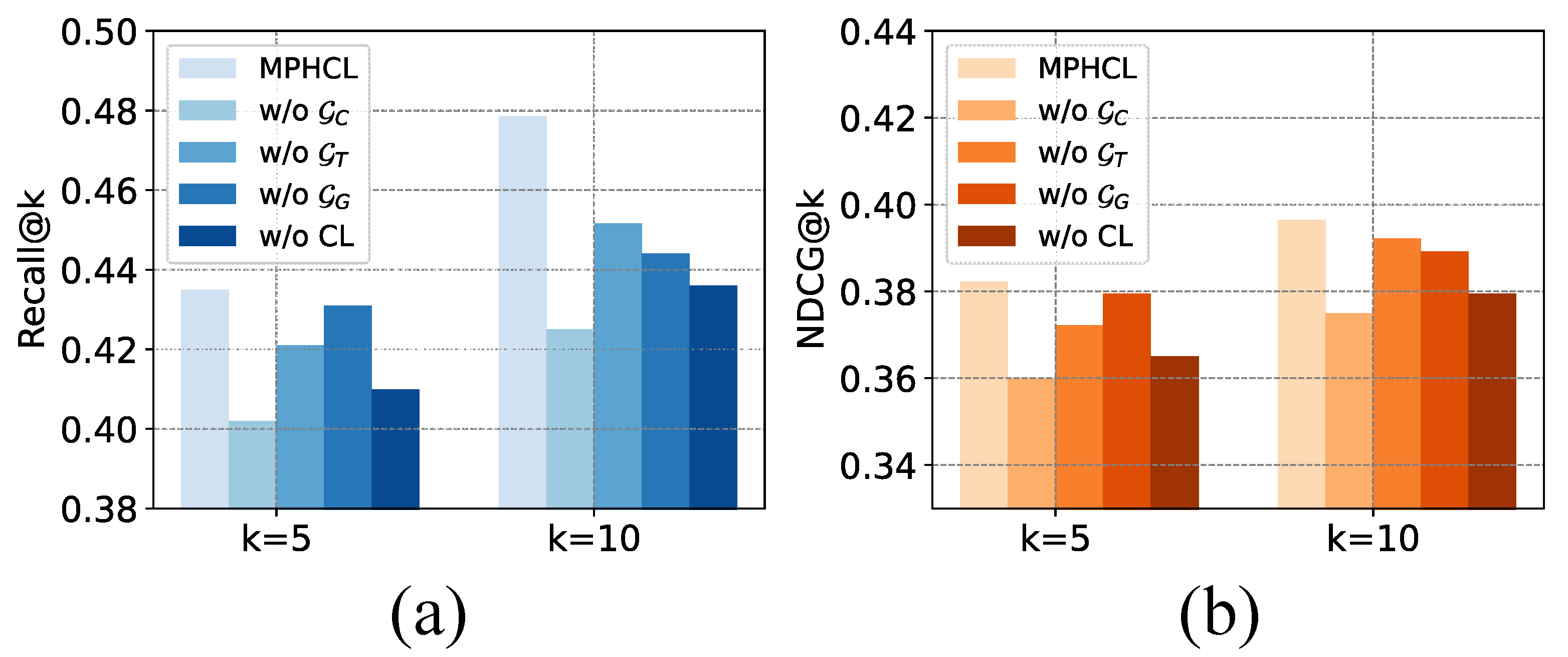
To comprehensively evaluate the effectiveness of each individual module within our proposed MPHCL framework, we conduct a detailed ablation study on two representative datasets—NYC and TKY—as illustrated in
Figure 11 and
Figure 12. The full MPHCL model is denoted as the baseline, while “w/o X” indicates the model variant without component X. For each variant, we compare the performance using Recall@K and NDCG@K metrics.
w/o represents removing the collective preference hypergraph.
w/o represents removing the global transition flow graph.
w/o represents removing the geospatial context hypergraph.
w/o CL represents removing cross-view contrastive learning from the full MPHCL model.
The key four findings are summarized as follows:
On the NYC dataset, the removal of the collective preference hypergraph () leads to the most pronounced decline in both Recall@K and NDCG@K scores. This indicates that capturing collaborative signals among users and items through high-order relations plays a central role in recommendation accuracy within dense urban environments like NYC, where user behaviors tend to be highly co-dependent. The contrastive learning module is the second most impactful, demonstrating that enforcing representational consistency and discrimination among hypergraph views significantly improves generalization. By contrast, the geospatial context hypergraph () and global transition flow graph () contribute to more modest gains. Notably, the global transition flow graph shows the least degradation when removed, implying that short-term behavioral transitions play a relatively minor role in this context, possibly due to the less sequentially structured urban mobility patterns of NYC users.
In the TKY dataset, the contrastive learning module emerges as the most crucial component, with its absence resulting in the most substantial drop in both performance metrics. This can be attributed to the relatively sparse and more heterogeneous nature of user behaviors in Tokyo, where enforcing consistency across hypergraph-structured views becomes essential for learning robust representations. The collective preference hypergraph follows as the second most important component, reflecting the residual importance of collaborative user-item interactions. Interestingly, in contrast to NYC, the geospatial context hypergraph contributes more than the global transition flow graph, highlighting the stronger influence of location-based preferences in TKY’s wider spatial layout. These results suggest that different urban characteristics and user interaction patterns lead to varying dependencies on spatial, sequential, and collaborative cues.
Across both datasets, a consistent pattern emerges in how the ranking cutoff K affects the relative importance of modules. At , where top-ranked predictions are emphasized, the global transition flow graph tends to be more influential than the geospatial context hypergraph, especially in the NYC dataset. This suggests that recent user behaviors and transition dynamics play a larger role in fine-grained recommendation scenarios. However, as K increases to 10, the Geospatial Context Hypergraph becomes more impactful. This shift can be explained by the fact that geographic cues, though more stable and less temporally sensitive, contribute to broader diversity in larger recommendation lists, while the directed nature of sequential transitions is more localized and immediate in its influence.
Finally, despite dataset-specific differences, several general conclusions can be drawn. For NYC, the collective preference hypergraph dominates in importance, aligning with the city’s denser and more homogeneous behavioral patterns, where user co-preferences are strong and informative. For TKY, the contrastive learning component proves to be the most essential, underscoring its role in overcoming data sparsity and enhancing the expressiveness of learned embeddings. Additionally, the geospatial context hypergraph shows greater relative importance in TKY due to the city’s broader geographic dispersion, where modeling spatial proximity is vital for meaningful recommendations. In both cases, the full MPHCL model consistently outperforms all its ablated counterparts, thereby validating the synergistic effect of jointly modeling collaborative, global transition flow, and spatial patterns under a contrastive learning framework.
5.9. In-Depth Study
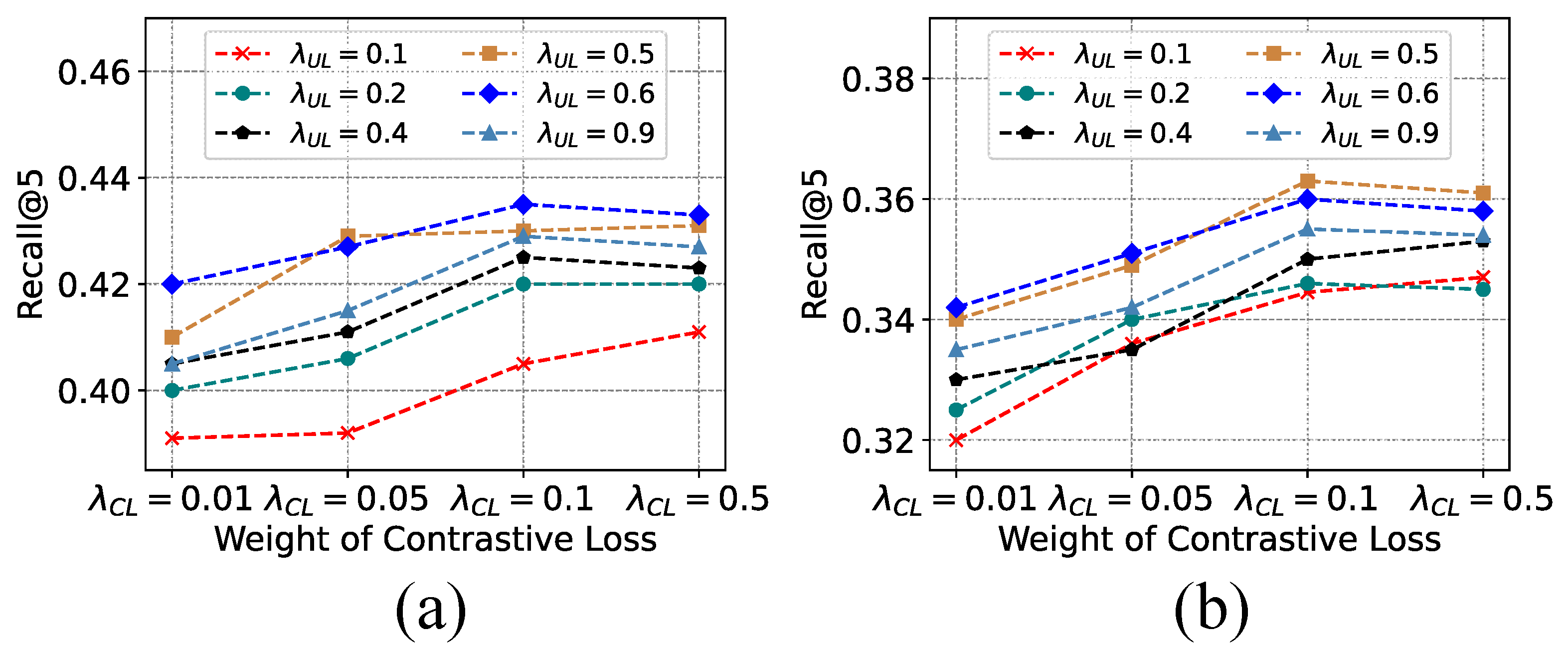
To further explore the influence of contrastive learning on model performance, we conduct a deep investigation into the effect of varying the contrastive loss weight. As shown in
Figure 13, we compare different configurations of contrastive loss (
) and the fusion coefficient (
) for user and location views, across two datasets: (a) NYC and (b) TKY. The Recall@5 scores under different parameter settings reveal key insights into how these components contribute to the overall recommendation performance.
From the results, it is evident that contrastive learning significantly enhances the model’s ability to capture useful representations, particularly in the NYC dataset. As increases, Recall@5 consistently improves across most settings, confirming the importance of contrastive objectives in aligning representations under different contexts. This trend persists, albeit less prominently, in the TKY dataset, suggesting contrastive learning also plays a beneficial role in sparser or differently distributed spatial environments.
In addition to the contrastive loss weight, the fusion weight —which balances the contributions of the user view and the location view—also shows a noticeable effect. For the NYC dataset, the best performance is achieved when , indicating that the user-centric view is slightly more influential than the location-centric view. In contrast, the TKY dataset achieves optimal performance around , suggesting both views contribute equally and should be treated with the same level of importance.
These findings suggest that, in denser urban environments like NYC, where users frequently interact with a diverse set of locations, the personalization aspect (user view) is more critical. Conversely, in less dense or differently structured environments like Tokyo, user preferences and location characteristics are more balanced in importance. This nuanced understanding supports the necessity of adaptively weighting contrastive signals based on regional characteristics and data density.
To further validate the effectiveness of our geospatial modeling,
Figure 14 and
Figure 15 visualize the learned geographical view hypergraph
on the NYC and TKY dataset. The left panel overlays the correlation of different locations on an actual city map, revealing highly dense and complex spatial dependence. The right panel presents a structural abstraction of the hypergraph, illustrating the connectivity among locations and the spatial relationships captured by our MPHCL model. The hypergraph constructed for the NYC dataset contains 3835 nodes and 2160 edges, with an average degree of 0.5632. This relatively low average degree, despite the large number of nodes, highlights the sparsity and diversity of user interactions across the spatial landscape. Such complexity underscores the need for robust context modeling, which our contrastive framework effectively captures.
5.10. Discussion
Our approach could also support transport network design by providing accurate predictions of user mobility patterns, which can be leveraged to optimize the placement of transport hubs, designing dynamic routing systems, and improving the efficiency of public transport services. By accurately forecasting user preferences for specific locations, our model can help in designing systems that are more aligned with actual user behavior, thus enhancing the overall efficiency of transportation networks.
In travel demand modeling and next-location prediction, it is common to face challenges due to insufficient or sparse data. To address this, big data, particularly floating car data (FCD), has emerged as a valuable resource for calibrating model parameters. FCD provides comprehensive vehicle movement data, which helps to more accurately estimate travel demand and predict users’ future movements by capturing traffic patterns across both spatial and temporal dimensions. The FCD data might serve as an external, complementary source of information that helps refine predictions when user trajectory data is sparse or noisy. To further enhance the model’s performance in scenarios with limited information, we plan to incorporate FCD in future work. By using real-time vehicle trajectory data, FCD can aid in calibrating user behavior patterns. This data can help us capture flow patterns in geographically diverse areas, improving the accuracy of user visits to the next location, especially in data-sparse or noisy environments.
6. Conclusions
In this study, we proposed MPHCL, a novel multi-perspective learning framework designed to address the inherent limitations of existing location prediction models, which often conflate heterogeneous behavioral signals into entangled latent spaces. By constructing dedicated hypergraphs that reflect collaborative preferences, global transition flow dynamics, and geospatial contexts, respectively, MPHCL captures high-order relationships that traditional graph-based and sequence models overlook. The proposed disentangled hypergraph representation learning network employs a two-step propagation scheme—within-hyperedge and across-hyperedge aggregation—to effectively isolate and refine the semantic contribution of each behavioral factor. Moreover, we integrate a cross-view contrastive learning module that encourages alignment between view-specific embeddings, thus enhancing the coherence, robustness, and generalizability of learned representations. Comprehensive experiments on two datasets confirm that MPHCL consistently achieves superior performance across all evaluation metrics compared to a broad range of strong baselines, including RNN-based, GCN-based, and hypergraph-based models. The average recall improvement ranges from 7.05% to 7.81%, the average NDCG improvement ranges from 5.77% to 12.60%, and the average MRR improvement ranges from 4.21% to 10.45%. Ablation studies further demonstrate the individual effectiveness of each module, while sensitivity analyses highlight the importance of hyperparameter selection for spatial and representational granularity.