Abstract
Cyclical footage, a fundamental parameter in tunnel construction, has received limited attention despite its critical role in ensuring excavation stability and safety. To investigate the underlying mechanisms by which different cyclical footage values influence the stability of deeply buried tunnels, the Fast Lagrangian Analysis of Continua in Three Dimensions (FLAC3D) was employed to simulate the spatiotemporal evolution of tunnel responses during excavation. The simulation results reveal that each cyclical footage scenario produces a “segmental decline” pattern in tunnel displacement. Unlike shallow tunnels, where peak displacement typically occurs near the tunnel face, in deep tunnels the maximum Y-direction displacement appears at the center of the excavation face. Furthermore, as cyclical footage increases, the displacement extent first expands and then contracts. The stress release process is found to be minimally affected by cyclical footage, with vertical strain in the tunnel roof nearly fully released within 1 m ahead of the excavation face. Therefore, deploying tunnel support structures beyond this 1 m zone may enhance their effectiveness. This study provides a theoretical reference for optimizing excavation parameters in deep tunnels and contributes to reducing the likelihood of support failure during underground construction.
1. Introduction
The length of cyclical footage (the length of each boring during the excavation of the tunnel, CF) has always been one of the major issues impacting construction safety and efficiency. Similarly, it is a key aspect in ensuring the stability of the tunnel and fully utilizing the self-bearing capability of the surrounding rock [1,2]. Construction and other circumstances unavoidably cause the installation of support systems to lag behind the excavation process. In order to assure the stability of the tunnel and fully utilize the self-bearing capacity of the surrounding rock, it is critical to select an optimal CF throughout the tunnel excavation process [3,4,5]. However, there are currently no highly exact and universally applicable criteria for selecting the optimal CF during construction process, which may result in an engineering project blind spots [6]. The cost of building will rise, the duration will be longer, and there will be more construction disturbances if the CF length exceeds the range of proper values. When the length of the CF is smaller than the range of appropriate values, the tunnel’s stability decreases construction risk rises, and the degree of construction disruption rises. As a result, mastering the influence of different CF on the overall stability of a tunnel is of enormous scientific and engineering importance.
Wang et al. [6] developed a calculation formula for excavation footage in homogeneous soil based on Taishaji loose media theory, expanded it to layered soil, and compared it to the findings of finite difference simulation to address the problem that excavation footage is difficult to determine. Hoek and Carranza-Torres et al. [7,8,9] regarded the CF as an important parameter affecting the characteristic curve of the supporting structure in the convergence constraint method. Da et al. [10] suggested a method for analyzing the spatial–temporal effects of soft rock excavation processes in fault fracture zones and optimizing tunnel excavation footage in large fault fracture zones in the research area. Qiao et al. [3] developed a cyclic footage calculation technique based on logarithmic spiral failure mode for the face’s advanced core soil and proved the relationship between cyclic footage and internal friction. Other characteristics include angle, cohesiveness, support pressure, excavation height, and so on. Cai et al. [11] used ABAQUS software to perform numerical trial calculations to determine the dilatation angle closest to the actual tunnel surrounding rock, established the tunnel excavation numerical model of Mohr–Coulomb model taking dilatation angle into account, and completed the excavation progress optimization study through comparison selection. Based on the Hoek–Brown yield criterion, Zhao et al. [12] adopted the finite element numerical simulation method to conduct three-dimensional numerical simulation of the tunnel construction process under the condition of different excavation step lengths, and analyzed the response law of cross section and working face displacement in the process of tunnel advancing. Lee et al. [13] conducted an in-depth analysis on cyclic footage using a series of small experiments and Particle Flow Code in Three Dimensions (PFC3D) numerical simulation software, and identified five types of tunneling and supporting behaviors modes applicable to weak rock mass. Yan et al. [14] used Finite Difference Method (FDM), considering mining stress and geological conditions at the same time, and put forward the determination method of cyclic screening suitable for coal mine excavation. Skrzypkowski et al. [15] proposed a vault support selection approach for hard coal seam driving faces that takes into account discontinuous deformation of fault shape. It is discovered that if the tunnel face is to be protected in time, the relationship between ventilation criterion, geometric value of the machine employed, and geo-mechanically computation taking rock load must be considered. Liang et al. [16], based on limit theory and unified strength theory, considering the influence of cyclic tunneling and inter-mediate principal stress on the stability of tunneling face, the three-dimensional failure mode and corresponding velocity field of tunneling face are proposed. Chen et al. [17] invented a new type of jet cracker, which improved the length of cyclic footage and blasting efficiency. Goh et al. [18] evaluated the effects of excavation length, depth, and other parameters on the maximum wall deflection generated by the supported excavation using a series of finite element analyses. Shin et al. [19] explore the safety technology of long span tunnel excavation considering multi-surface excavation and the minimum length of each round using the analytical approach and the numerical analysis method. The monthly excavation lengths and work items for the TBM tunnel field construction were examined by Jin et al. [20] based on the borehole reports to determine the predicted increase in monthly excavation lengths based on the lowest operational shift loss rates in the nine fields. Si et al. [21] determined the influence range of airflow disturbance after coal and gas protrusion accident in ventilation system, and proposed the airflow disturbance index related to the length of dug tunnel and protrusion pressure factor. The stability of the tunnel working face and vault was examined by Tian et al. [22] in order to obtain the formula for determining the unsupported span of a shallow buried tunnel in soft rock strata. This analysis was based on the shallow buried tunnel envelope pressure calculation model. Other scholars have also looked at the stability of roads from different angles, which may be helpful as a reference. Mahdevari et al. [23] proposed a new model to predict the unstable zone of underground tunnels and provide a standard for the criterion of tunnel stability. Mo et al. [24] had obtained the buckling mechanism of coal mine tunnel floor by numerical simulation and found the property that the displacement and damage mode are sensitive to the deformation modulus. Mandal et al. [25], through a series of simulation tests, evaluated the convergence of the top plate of the continuous coal mining machine digging the underground tunnel. Darvishi et al. [26] used numerical simulations to study the change in the stability of the main gate tunnel when two longwall panels were mined simultaneously.
In general, researchers have mostly focused on the stability control analysis of the tunnel boring process, while there are fewer reports on the selection of CF under high stress conditions. In this study, based on Fast Lagrangian Analysis of Continua in Three Dimensions (FLAC3D), a full-section boring simulation of high-stress tunnel under different CF is carried out. The focus is on analyzed the spatial and temporal evolution characteristics of the data of the tunnel displacement and stress, and revealed the deformation patterns in different position of the tunnel.
2. Materials and Methods
Cyclical footage (CF) is the length of each planned excavation in the tunnel boring process, as shown in Figure 1. It not only determines the efficiency of excavation, but also plays a key influence on the bearing capacity of the surrounding rock after excavation [16]. At present, in the actual application of the field, CF is mostly determined by the combination of field test and engineering experience, with emphasis on the consideration of factors such as peripheral rock mass grade, tunnel depth, and section size, but there is still a great deal of blindness.
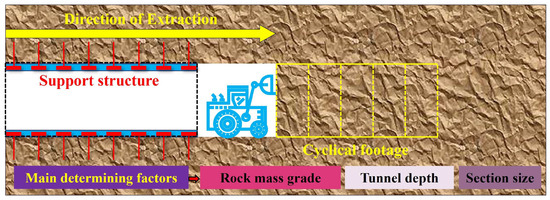
Figure 1.
Schematic diagram of tunnel excavation cyclical footage.
ITASCA created the numerical simulation program FLAC. An version of the two-dimensional finite difference program FLAC2D, FLAC3D [27] uses the explicit Lagrangian algorithm and mixed-discrete partitioning to properly mimic the flow of materials and plastic failure. It can examine the plastic flow of soil, rock, and other materials as well as mimic their mechanical properties. Currently, FLAC3D is utilized extensively in geotechnical engineering analysis due to its quick computation speed, accuracy, and wide range of applications [15]. Therefore, in this study, FLAC3D was utilized to carry out the simulation study of different CF scenarios for tunnels under high stress conditions.
2.1. Model Build and Parameters Select
The overall size of the model is 30 m × 30 m × 30 m (length, width, height). The shape of the tunnel section is rectangular, and the length is 4 m × 4 m (length and height). The total tunnel length of waiting to be excavated is 15 m. To avoid the interference of other factors, the whole stratum of the model is assumed to be a uniform medium body, and there are no special geological conditions such as joints and fractures. The model units are all regular hexahedra, the dimension is 0.5 m × 0.5 m × 0.5 m (length, width, height), a total of 216,000 zones. Typical surrounding rock tunnel parameters of class are taken as an example, and partially adjusted to make them more representative [28]. The specific parameter values are shown in Table 1. The numerical model of tunnel and surrounding rock is shown in Figure 2, and the monitoring points, monitoring line and area names are shown in Figure 3.

Table 1.
Mechanical parameters of model.
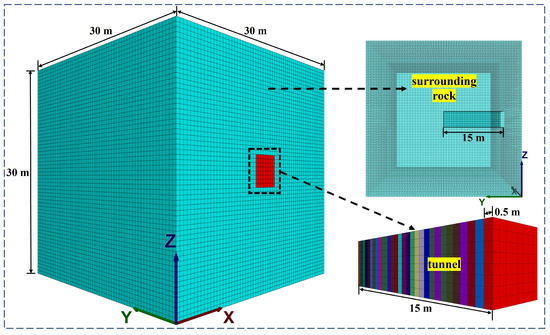
Figure 2.
Numerical model of tunnel and surrounding rock.
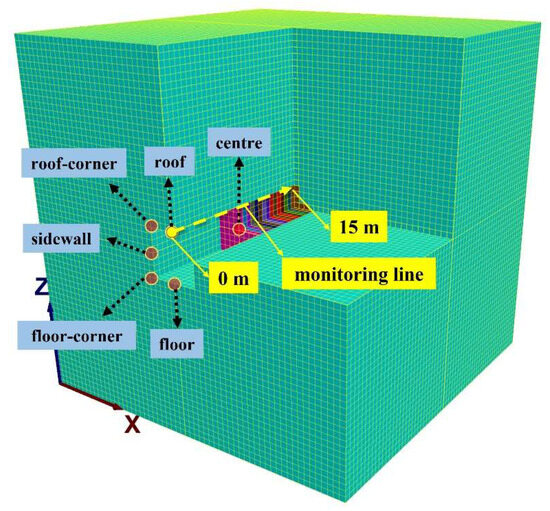
Figure 3.
Monitoring layout schematic.
The FLAC3D program comes with isotropic elasticity, Drucker–Prager plasticity, Mohr–Coulomb plasticity, strain-hardening/softening Mohr–Coulomb plasticity and Hoek–Brown plasticity, etc. constitutive model [29]. The Mohr–Coulomb failure criterion [7,30] is a typical and widely used failure model for brittle materials such as rock and concrete, and it works well in a low confinement state of compression. For overall consideration, in this study, the commonly used Mohr–Coulomb plasticity constitutive model was selected for simulation.
2.2. Model Displacement and Stress Boundary Conditions
The length of each direction of the selected 3D numerical model is more than 5 times of the radius of the excavation tunnel. According to the Saint-Venant principle [31,32,33], the model can be regarded as a semi-infinite body. Hence, fixed displacement constraints can be applied to the bottom, left, right, front, and back surfaces of the model, and the top is a free surface. The stress of 30 MPa is evenly assigned to the X, Y, and Z directions of the model. At the same time, a load of 30 MPa is applied to the top, and the gravity acceleration of 9.8 m/s2 is set to form the initial ground stress field. The specific boundary conditions are shown in Figure 4, and the initial stress field of model is shown in Figure 5.
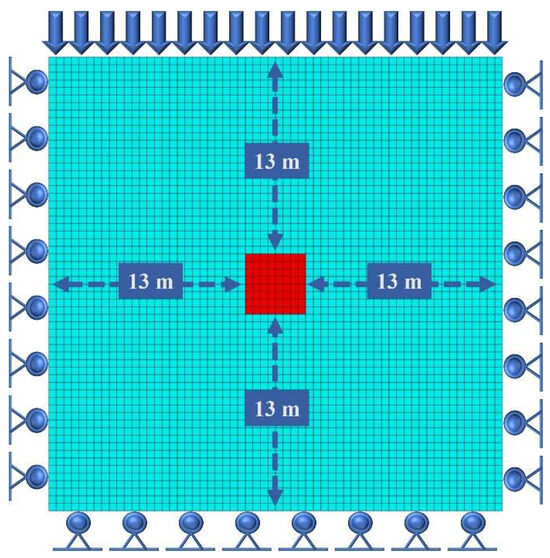
Figure 4.
Model boundary conditions.
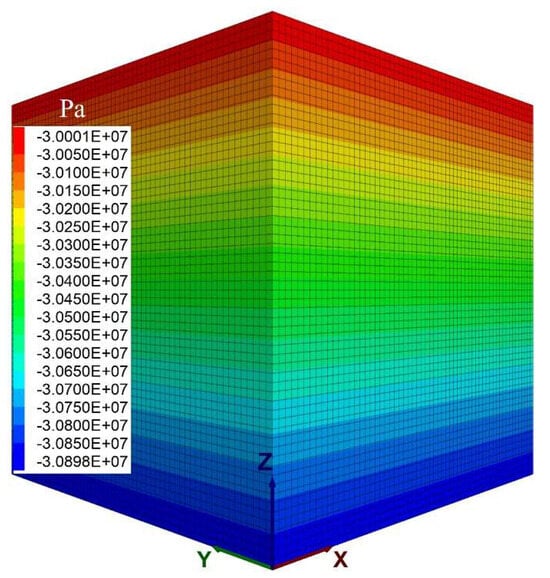
Figure 5.
Initial stress field of model.
2.3. Simulation Test Scheme
Based on the actual engineering application and the length of grid division of the model, a total of 5 schemes are used to carry out full-section excavation without support in the unit of 0.5 m, 1.0 m, 1.5 m, 3 m, 5 m, and 7.5 m when the mechanical ratio is . After the model converges, the relevant data will be saved and then the next step of excavation will be carried out. Specific simulation calculation steps are shown in Figure 6.
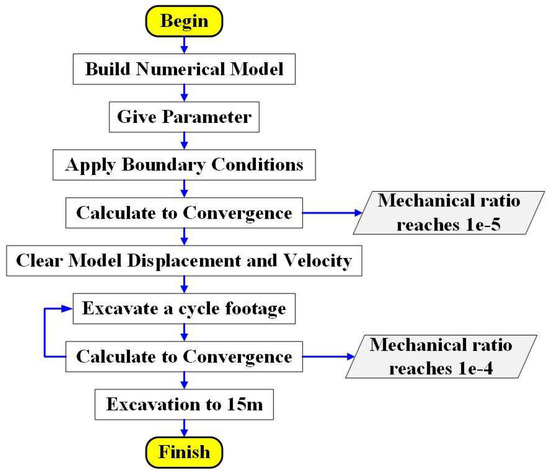
Figure 6.
Simulation calculation steps.
3. Results
3.1. Process Analysis of Result
When the model is fully excavated and balanced, the number of computational steps required varies for different cyclic footage schemes. The computational steps required to equilibrate the initial stress field of the model is 1070. The longest computational steps are cyclic footage scheme of 0.5 m, which is 12,311, and the shortest computational steps is cyclic footage scheme of 7.5 m, which is 5587. The computational steps are negatively correlated with the length of cyclic footage. The details are shown in Figure 7 and the maximum unbalance force is shown in Figure 8. “Mechanical unbalanced maximum” is an indicator for evaluating model convergence in numerical simulation. It presents a large value at the initial calculation of the model and gradually decreases as the model calculation progresses (assuming the model itself can converge). The tunnel excavation length in this simulation is 15 m. Therefore, different numbers of calculations will be performed under different CF schemes. At this time, the peak values under different CF schemes are all 15/CF. Therefore, the number of peak values under different CF schemes (0.5 m, 1 m, 1.5 m, 3 m, 5 m, 7.5 m) are 30, 15, 10, 5, 3, and 2 respectively. In addition, it can be seen that after each CF excavation calculation, the model has converged.
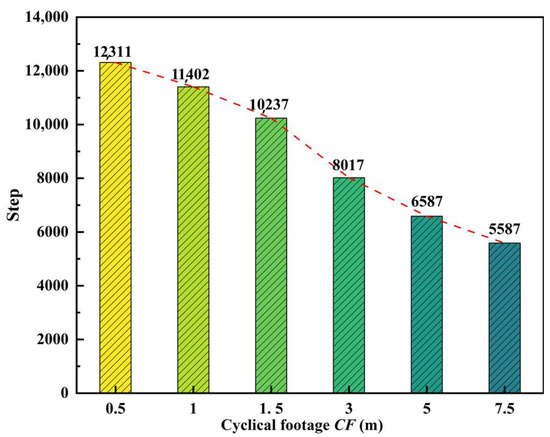
Figure 7.
Computational steps required to equilibrate the model with different cyclic footages.
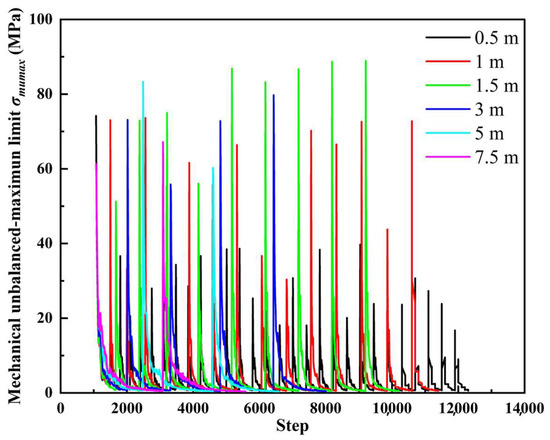
Figure 8.
Mechanical unbalanced maximum in model with different cyclic footages.
3.2. Displacement Analysis of Result
Analyze the displacement of tunnel under different CF, displacement of the tunnel section as shown in Figure 9, with the increase of CF, the decrease of the total computational step, the maximal displacement magnitude of tunnel has also been gradually decreases, and the maximal displacement are distributed in the center of the location of the initial excavation of tunnel roof and sidewall center, from 0.5 m to 7.5 m maximum displacement magnitude is respectively: 93.4 mm, 89.4 mm, 85.4 mm, 81.6 mm, 79.8 mm, and 77.4 mm. Except the CF of 0.5 m, the displacement magnitude of other CF shows a significant “segmental decline” characteristic, which is strongly related to the distribution of CF.
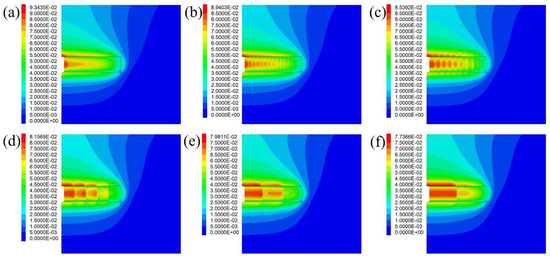
Figure 9.
Displacement magnitude with different cyclic footages: (a) 0.5 m; (b) 1 m; (c) 1.5 m; (d) 3 m; (e) 5 m; (f) 7.5 m. Units in all figures are m.
In the center of the tunnel roof, decorated throughout the model line, the position after the completion of the 15 m full excavation of displacement magnitude space evolution characteristics is obtained; the results are shown in Figure 10. Within the scope of the top 10 m, the length of the displacement magnitude changes more gently; at about the 15 m constraints (both attachments), there are rapid changes in size, and the displacement magnitude increases with depth. The displacement influence brought by tunnel driving gradually decreases until it approaches zero. Y-displacement in the working face is shown in Figure 11; the maximum value is in the center of the working face, and with the increase of circular footage, the maximum value is in 0.5 m CF, and the minimum value is in 1.5 m cyclic footage.
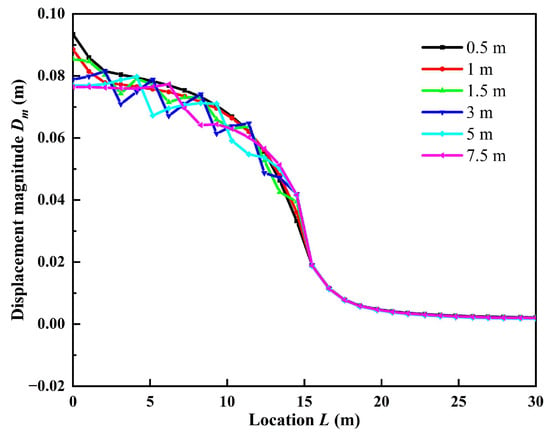
Figure 10.
Longitudinal deformation profile of tunnel.
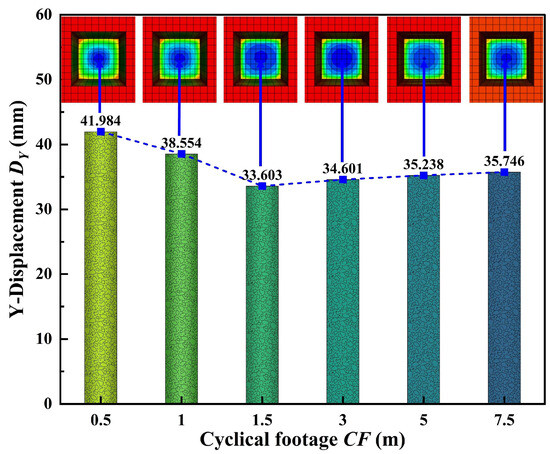
Figure 11.
Y-displacement on working face with tunnel excavation of 15 m.
The time evolution characteristics of displacements at different positions of the working face were recorded by “history” command, and the results are shown in Figure 12. After each excavation, displacements at different positions first increased rapidly and then gradually became balanced. At the same time, as the excavation position was closer and closer to the working face at 15 m, the excavation of each CF has an increasing influence on the displacement of each part of the 15 m working face.
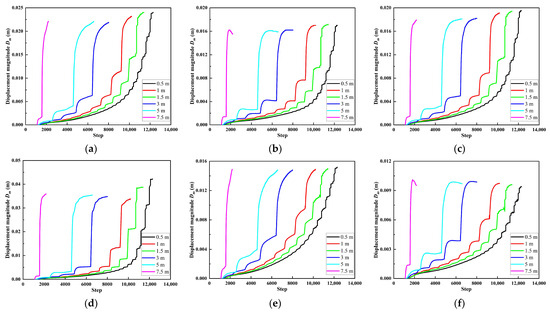
Figure 12.
Displacement magnitude of working face with tunnel excavation of 15 m: (a) roof; (b) floor; (c) sidewall; (d) center; (e) roof-corner; (f) floor-corner.
3.3. Stress Analysis of Result
The place in the center of the tunnel roof decorated throughout the excavation tunnel roof line, and obtained the position after the completion of the 15 m full excavation space evolution characteristics of vertical stress; the results are shown in Figure 13. The internal stress in the range of 0 m to 14 m under all CF has been basically released. The vertical stress evolution characteristics under different CF show that the vertical stress release on the roof of the footage under CF is relatively small. Under the constraint of model length and parameters, the stress is basically released at around 1 m, and the residual stress is about 6 MPa under the constraint of around 0.5 m, and the remaining stress at the stress constraint is about 14 MPa. Therefore, in tunnel support, the lagging constraint should be greater than 1 m, otherwise the supporting structure will be easily damaged under high stress. As shown in Figure 14, the maximum value of YY-stress on the working face is in the center of the working face, and the variation trend is consistent with that of Y-displacement. The maximum value is achieved in 5 m/7.5 m cyclic footage, while the minimum value is achieved in 1.5 m CF.
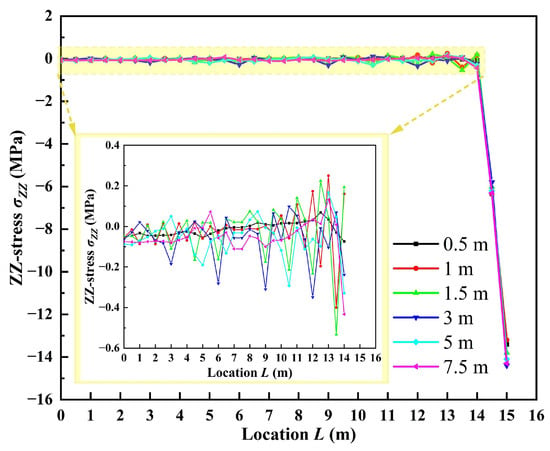
Figure 13.
Vertical stress monitoring result of tunnel roof.
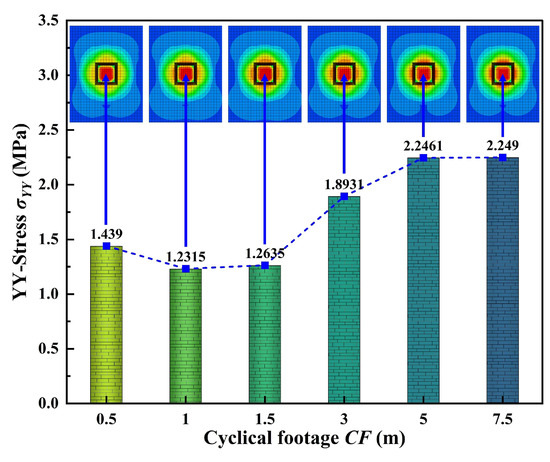
Figure 14.
YY-stress on working face with tunnel excavation of 15 m.
Meanwhile, the time evolution characteristics of stress (XX, YY, ZZ) in three directions at different positions of the working face at 15 m were recorded by “history” command, and the results are shown in Figure 15. As the tunnel is dug, the stresses change, thus creating a mining stress field [34,35], and the stress is transferred to the deeper area. The stress transferred forms stress clusters, and from the transferred stress area, the stress relaxation zone is formed, remote areas affected by mining, with minimal or no part of this area that is still not the original rock stress zone. The stress concentration factor in the stress concentration zone can reach 1.5, and in the stress relaxation zone, the stress is almost completely released. The relevant images were analyzed and the results of stress analysis on the working face were obtained as shown in Table 2.
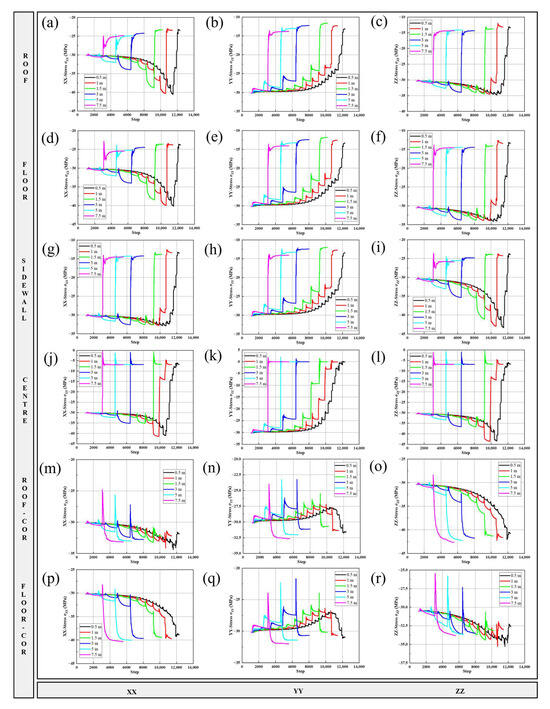
Figure 15.
Time evolution process of stress in different parts of working face: (a) Roof of stress-XX; (b) Roof of stress-YY; (c) Roof of stress-ZZ; (d) Floor of stress-XX; (e) Floor of stress-YY; (f) Floor of stress-ZZ; (g) Sidewall of stress-XX; (h) Sidewall of stress-YY; (i) Sidewall of stress-ZZ; (j) Center of stress-XX; (k) Center of stress-YY; (l) Center of stress-ZZ; (m) Roof-Corner of stress-XX; (n) Roof-Corner of stress-YY; (o) Roof-Corner of stress-ZZ; (p) Floor-Corner of stress-XX; (q) Floor-Corner of stress-YY; (r) Floor-Corner of stress-ZZ.

Table 2.
Time evolution feature of stress in different parts of working face.
The vertical stress of the tunnel roof in different locations of the monitoring curve as shown in Figure 16. Each step excavation releases (3 m) closer to the area of vertical stress of the roof. This part of the stress is transferred to deeper depths, resulting in an increase in stress in the deeper region, from about 30 MPa to 35 MPa, while the stress concentration decreased slightly with the increase in cyclic footage. Therefore, in the case of unsupported full-section excavation, the smaller the cyclical feed, the longer the excavation cyclic footage, and the greater the stress transfer. With the continuous tunneling, the stability of the face will continue to decrease, and the construction period will also increase greatly. The larger the CF is, the greater the stress released by an excavation will be. The sudden change of stress will cause great damage to the surrounding rock, and the self-bearing capacity of the tunnel will be greatly threatened, seriously endangering the safety of the tunnel.
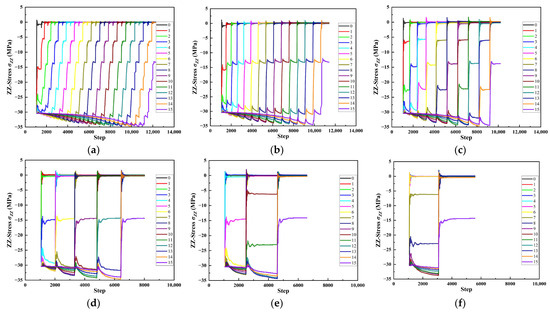
Figure 16.
Vertical stress monitoring curves at different positions of tunnel roof: (a) 0.5 m; (b) 1 m; (c) 1.5 m; (d) 3 m; (e) 5 m; (f) 7.5 m.
3.4. Plastic Zone Analysis of Result
The distribution of plastic zones is shown in Figure 17 (The suffixes “-n” and “-p” of shear and tension refer to the yield state. “-n” refers to the yield state in which the final calculation is completed, and “-p” refers to the state that has been entered during the convergence calculation process). The existing plastic zones after tunnel excavation are all shear failures, and some areas enter the tensile failure state before convergence. In addition, the plastic zone of CF scheme (1.5 m) is the most uniform. With the increase of CF length, the (shear-n, shear-p, tension-p) areas gradually increase. The statistics of plastic zone volume (shear-n) under different CF schemes are shown in Figure 18, and the order of volume size schemes is: 1.5 m > 5 m > 1 m > 3 m > 0.5 m > 7.5 m.
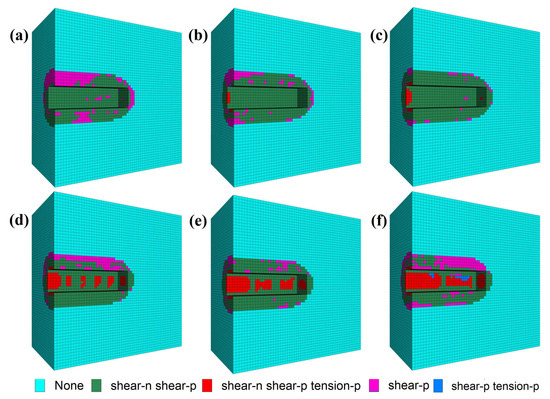
Figure 17.
Distribution of plastic zone with different CFs: (a) 0.5 m; (b) 1 m; (c) 1.5 m; (d) 3 m; (e) 5 m; (f) 7.5 m.
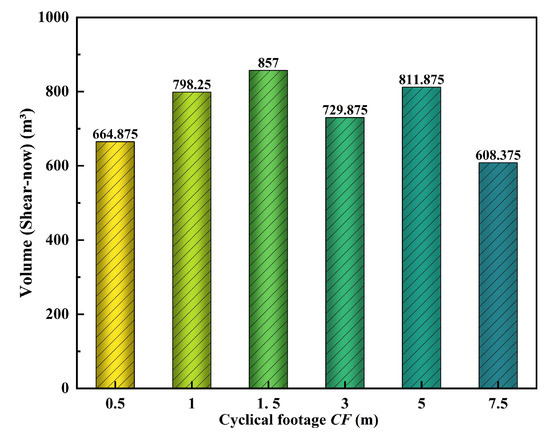
Figure 18.
Plastic zone volume (shear-now) of model in different CFs.
3.5. Comprehensive Comparison Analysis of Result
According to the results of displacement, stress, and plastic zone volume, when the cyclic footage is 1.5 m, Y-stress displacement in the face is the smallest, Y-stress is small, stress release speed is moderate, plastic zone distribution is uniform, the type is single, the length of displacement conforms to the project reality, and the construction difficulty is low. The tunnel driving process under 1.5 m cyclic footage is analyzed in detail. Displacement, stress and maximum shear stress, maximum principal stress, and maximum shear strain increment in three directions were obtained, and the results are shown in Figure 19.
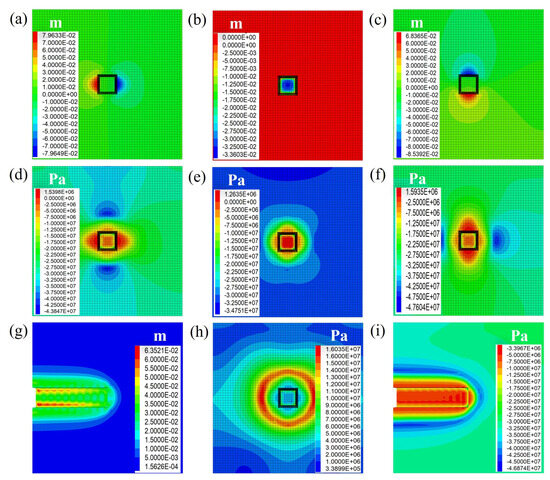
Figure 19.
Correlation cloud image of cyclic footage of 1.5 m: (a) Displacement-X; (b) Displacement-Y; (c) Displacement-Z; (d) Stress-XX; (e) Stress-YY; (f) Stress-ZZ; (g) Maximum shear strain increment; (h) Maximum shear stress; (i) Maximum principal stress.
4. Discussion
“Unsuitable” CF length will limit efficient and safe of tunnel excavation. In tunnel design, mine technicians and mining experts generally focus on pillar dimensions [36], support technology [37], stress control [38], etc., with little attention paid to the “raw” parameters of the tunneling process, i.e., the CF. Reference [16] considered the effect of CF during the study of the stability of the excavated surface, but it was not the focus of their study, and they did not give a recommendation for choosing the length of the cyclic progression. Reference [14] proposes a new method for determining the length of CF in coal mines, using the maximum principal stress in the tunnel roof as the main consideration, and states that most engineers [39,40] have recognized that the choice of CF has a considerable influence on the likelihood of collapse of the working face and the tunnel, as well as on the stability of the main support in the vicinity of the working face. Unfortunately, however, to the best of our knowledge, studies focusing on this parameter are still relatively few.
The selection of CF not only affects the rate of the boring process, but is also closely related to the bearing capacity of the tunnel itself. CF can not only affect the displacement distribution of the tunnel (Figure 8 and Figure 9), but also has a more significant effect on the vertical displacement (Y-Displacement) (Figure 10) and vertical stress (Stress-YY) (Figure 13) of the palm face, and this effect is not linear. It is clearly seen that when the CF length is 1.5 m, both the displacement values and stress state are better than other CF lengths. This gives us some insights: We can use numerical simulation software to establish a model that fits the actual engineering scenario, select correct and reasonable parameters, carry out simulation and analysis of the stability of the tunnel under different CF length schemes, obtain the corresponding displacement and stress parameters, and carry out a comprehensive comparative analysis to obtain the optimal CF length. This approach can overcome the limitations of theoretical derivation, or engineering experience in determining the worthiness of CF, and can avoid the cost of money and time consumed by similar simulation tests.
However, pure numerical simulations are often unconvincing, so experiments are usually required to verify the simulation results. Unfortunately, we are currently unable to conduct experimental tests according to the simulation scenarios, which is too “time-consuming and labor-intensive”. Therefore, we should recommend the formulation of a complete set of specifications to define the above process, including but not limited to the degree of quantification of the test scenarios and the calibration of the consistency of the results. In addition, this study only refers to the simulation process under rectangular tunnels, but in actual production, there are many other common tunnel section shapes. All these issues will be the focus of our next work.
5. Conclusions
The following are the main conclusions drawn from the numerical simulations carried out in this study under different cyclical footage (CF) schemes for deep high-stress tunnel:
- (1)
- The maximum displacement is positively correlated with the calculated steps, and is distributed in the center of the roof and the center of the sidewall at the initial excavation position of the tunnel. The displacement is closely related to the length of CF and shows a significant “segmental decline” characteristic. Therefore, “timely support” is necessary to ensure the stability of the tunnel.
- (2)
- The maximum displacement in the tunnel face direction exists at the center of the tunnel face, and its displacement shows a trend of first decreasing and then increasing with the increase of CF. Under the conditions of this simulation, the plastic zone with CF length of 1.5 m is the most homogeneous, which is basically “shear-now” and has a volume of 857 m3.
- (3)
- The CF length has less influence on the vertical stress release process (spatial effect of excavation) of the tunnel roof, and the stress release is basically completed at a distance of about 1 m from the working face (Under the conditions of this simulation), so it is recommended that the tunnel support should lag behind the working face by more than 1 m.
- (4)
- According to the stability analysis results (displacement, stress, plastic zone, etc.) under different cyclical footage lengths, combined with engineering practice and economic, time efficiency, it is considered that 1.5 m is the best cyclical footage length under the model established in this study. The optimal CF under other engineering conditions can be determined by referring to the ideas in this article.
Author Contributions
Conceptualization, S.L., Y.H., B.D. and D.L.; methodology, S.L., Y.H., B.D. and D.L.; software, S.L. and D.L.; validation, Y.H. and B.D.; formal analysis, Y.H.; investigation, Y.H., B.D. and D.L.; resources, B.D.; data curation, D.L.; writing—original draft preparation, S.L. and Y.H.; writing—review and editing, B.D. and D.L.; visualization, S.L. and Y.H.; supervision, B.D. and D.L.; project administration, D.L. and B.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Key Project of Education Department of Hunan Province (22A0293), the Hengyang Science and Technology Planning Project (202330046116) and the Regional Joint Fund of Hunan Province (2025JJ70183).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All relevant data can be obtained by sending email to the corresponding author.
Acknowledgments
We thank Dong Liu and Shupeng Zhou of 3rd Construction Co., Ltd. of China Construction 5th Engineering Bureau for their guidance and help in paper writing and engineering experience.
Conflicts of Interest
Author Shang Li and Yuzhou Hou were employed by the 3rd Construction Co., Ltd. of China Construction 5th Engineering Bureau. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zoo, Y.; Lee, W.S.; Kim, C.-Y. The Influence of the Round Length on the Stability of Tunnel Face and Unsupported Span. In Underground Space Use. Analysis of the Past and Lessons for the Future, Two Volume Set; CRC Press: Boca Raton, FL, USA, 2005; pp. 231–236. ISBN 0-429-10748-X. [Google Scholar]
- Baudendistel, M. Significance of the Usupported Span in Tunnelling. Signif. Usupported Span Tunn. 1985, 85, 103–108. [Google Scholar]
- Liang, Q.; Sun, Z.B.; Pan, Q.J. Analysis of Round Length Based on Upper Bound Method and Limit Equilibrium in Tunnel Excavation. China J. Highw. Transp. 2016, 29, 96. [Google Scholar]
- He, M.; Xie, H.; Peng, S.; Jiang, Y.-D. Study on Rock Mechanics in Deep Mining Engineering. Yanshilixue Yu Gongcheng XuebaoChin. J. Rock Mech. Eng. 2005, 24, 2803–2813. [Google Scholar]
- Fairhurst, C. Some Challenges of Deep Mining. Engineering 2017, 3, 527–537. [Google Scholar] [CrossRef]
- Zhi-da, W.; Xiao-nan, G. Calculation method of digging length in underpass with underground excavation under shallow cover. Rock Soil Mech. 2010, 31, 2637–2642. [Google Scholar]
- Hoek, E. Estimating Mohr-Coulomb Friction and Cohesion Values from the Hoek-Brown Failure Criterion. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1990, 27, 227–229. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Practical Estimates of Rock Mass Strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Fairhurst, C. The Elasto-Plastic Response of Underground Excavations in Rock Masses That Satisfy the Hoek–Brown Failure Criterion. Int. J. Rock Mech. Min. Sci. 1999, 36, 777–809. [Google Scholar] [CrossRef]
- Da, L.I.; Yong-sheng, L.I.; Zhan-fu, L.U.O. Study of Footage Optimization Method of Tunneling Cycle under Complicated Conditions. Rock Soil Mech. 2013, 34, 498–502. [Google Scholar]
- Meguid, M.A.; Saada, O.; Nunes, M.A.; Mattar, J. Physical Modeling of Tunnels in Soft Ground: A Review. Tunn. Undergr. Space Technol. 2008, 23, 185–198. [Google Scholar] [CrossRef]
- Zhao, X.; Jiang, J.; Lan, B. An Integrated Method to Calculate the Spatial Distribution of Overburden Strata Failure in Longwall Mines by Coupling GIS and FLAC3D. Int. J. Min. Sci. Technol. 2015, 25, 369–373. [Google Scholar] [CrossRef]
- Lee, Y.-Z.; Schubert, W. Determination of the Round Length for Tunnel Excavation in Weak Rock. Tunn. Undergr. Space Technol. 2008, 23, 221–231. [Google Scholar] [CrossRef]
- Yan, S.; Wang, R.; Bai, J.; Wu, W.; Elmo, D. An Alternative Approach to Determine Cycle Length of Tunnel Excavation in Coal Mines. J. Ambient Intell. Humaniz. Comput. 2020, 11, 553–560. [Google Scholar] [CrossRef]
- Skrzypkowski, K.; Zagórski, K.; Zagórska, A.; Apel, D.B.; Wang, J.; Xu, H.; Guo, L. Choice of the Arch Yielding Support for the Preparatory Tunnel Located near the Fault. Energies 2022, 15, 3774. [Google Scholar] [CrossRef]
- Liang, Q.; Liu, J.; Wang, J.; Zeng, X.-T.; Wu, S.-G. Three-Dimensional Stability of Cyclical Footage Area in Tunnel Face. KSCE J. Civ. Eng. 2022, 26, 955–965. [Google Scholar] [CrossRef]
- Chen, W.; Ma, H.; Shen, Z.; Wang, D. Experiment Research on the Rock Blasting Effect with Radial Jet Cracker. Tunn. Undergr. Space Technol. 2015, 49, 249–252. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Fan, Z.; Wengang, Z.; Yanmei, Z.; Hanlong, L. A Simple Estimation Model for 3D Braced Excavation Wall Deflection. Comput. Geotech. 2017, 83, 106–113. [Google Scholar] [CrossRef]
- Shin, S.-J.; Shin; Cho, K.H.; Seo, D.-H. A study on the increasing advance length by pre-supported tunnelling method in heavily fractured rock condition. J. Korean Urban Railw. Soc. 2018, 6, 111–123. [Google Scholar] [CrossRef]
- Jin, C.J. Park Analysis of Monthly Excavation Length Depending on Ground Condition and TBM Diameter. J. Korean Soc. Disaster Inf. 2014, 10, 141–150. [Google Scholar]
- Si, J.; Li, L.; Cheng, J.; Wang, Y.; Hu, W.; Li, T.; Li, Z. Characteristics of Airflow Reversal of Excavation Tunnel after a Coal and Gas Outburst Accident. Energies 2021, 14, 3645. [Google Scholar] [CrossRef]
- Tian, X.; Song, Z.; Zhou, G.; Zhang, X. A Theoretical Calculation Method of the Unsupported Span for the Shallow Tunnel in the Soft Stratum. Adv. Civ. Eng. 2020, 2020, 7989036. [Google Scholar] [CrossRef]
- Mahdevari, S.; Khodabakhshi, M.B. A Hybrid PSO-ANFIS Model for Predicting Unstable Zones in Underground Tunnels. Tunn. Undergr. Space Technol. 2021, 117, 104167. [Google Scholar] [CrossRef]
- Mo, S.; Sheffield, P.; Corbett, P.; Ramandi, H.L.; Oh, J.; Canbulat, I.; Saydam, S. A Numerical Investigation into Floor Buckling Mechanisms in Underground Coal Mine Tunnels. Tunn. Undergr. Space Technol. 2020, 103, 103497. [Google Scholar] [CrossRef]
- Mandal, P.K.; Das, A.J.; Kumar, N.; Bhattacharjee, R.; Tewari, S.; Kushwaha, A. Assessment of Roof Convergence during Driving Tunnels in Underground Coal Mines by Continuous Miner. Int. J. Rock Mech. Min. Sci. 2018, 108, 169–178. [Google Scholar] [CrossRef]
- Darvishi, A.; Ataei, M.; Rafiee, R. Investigating the Effect of Simultaneous Extraction of Two Longwall Panels on a Maingate Gateroad Stability Using Numerical Modeling. Int. J. Rock Mech. Min. Sci. 2020, 126, 104172. [Google Scholar] [CrossRef]
- Zhai, Y. An Update of the 3D Analytical Solution for the Design of Barricades Made of Waste Rocks. Int. J. Rock Mech. Min. Sci. 2022, 158, 105176. [Google Scholar] [CrossRef]
- Itasca Consulting Group. FLAC3D: Fast Lagrangian Analysis of Continua in 3 Dimensions; Itasca Consulting Group: Minneapolis, MN, USA, 2013; pp. 175–180. Available online: https://search.worldcat.org/title/flac3d-fast-lagrangian-analysis-of-continua-in-3-dimensions/oclc/50411345 (accessed on 6 July 2025).
- Cameron-Clarke, I.S.; Budavari, S. Correlation of Rock Mass Classification Parameters Obtained from Borecore and In-Situ Observations. Eng. Geol. 1981, 17, 19–53. [Google Scholar] [CrossRef]
- Hou, M.Z.; Li, M.; Gou, Y.; Feng, W. Numerical Simulation and Evaluation of the Fracturing and Tight Gas Production with a New Dimensionless Fracture Conductivity (FCD) Model. Acta Geotech. 2021, 16, 985–1000. [Google Scholar] [CrossRef]
- Labuz, J.F.; Zang, A. Mohr–Coulomb Failure Criterion. Rock Mech. Rock Eng. 2012, 45, 975–979. [Google Scholar] [CrossRef]
- Toupin, R.A. Saint-Venant’s Principle. Arch. Ration. Mech. Anal. 1965, 18, 83–96. [Google Scholar] [CrossRef]
- Horgan, C.O.; Knowles, J.K. Recent Developments Concerning Saint-Venant’s Principle. In Advances in Applied Mechanics; Hutchinson, J.W., Wu, T.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 1983; Volume 23, pp. 179–269. [Google Scholar]
- Cai, W.; Zhu, H.; Liang, W. Three-Dimensional Stress Rotation and Control Mechanism of Deep Tunneling Incorporating Generalized Zhang–Zhu Strength-Based Forward Analysis. Eng. Geol. 2022, 308, 106806. [Google Scholar] [CrossRef]
- Jie, L.I.U.; EN-yuan, W.; EN-lai, Z.; Wen-quan, X.U.; Shao-bin, H.U. Distribution and Variation of Mining-Induced Stress Field in Deep Workface. J. Min. Saf. Eng. 2014, 31, 60. [Google Scholar]
- Jiang, Z.; Guo, W.; Xie, S. Coal Pillar Size Determination and Surrounding Rock Control for Gob-Side Entry Driving in Deep Soft Coal Seams. Processes 2023, 11, 2331. [Google Scholar] [CrossRef]
- Shan, R.; Li, T.; Liu, W.; Chen, Y.; Shi, S.; Li, G. Study on Asymmetric Support of Anchor Cable with C-Shaped Tube in Inclined Coal Seam Tunnel. Appl. Sci. 2023, 13, 8088. [Google Scholar] [CrossRef]
- Xie, J.; Ning, S.; Zhu, W.; Wang, X.; Hou, T. Influence of Key Strata on the Evolution Law of Mining-Induced Stress in the Working Face under Deep and Large-Scale Mining. Minerals 2023, 13, 983. [Google Scholar] [CrossRef]
- Chen, Z.H. Stress Distribution Characteristics in Rock Surrounding Heading Face and Its Relationship with Temporary Supporting. Appl. Mech. Mater. 2014, 568–570, 1684–1689. [Google Scholar] [CrossRef]
- Stone, R. Design of Primary Ground Support during Tunnel Development Using Empirical Databases. Int. J. Min. Sci. Technol. 2016, 26, 131–137. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).