Detection of Psychomotor Retardation in Youth Depression: A Machine Learning Approach to Kinematic Analysis of Handwriting
Abstract
1. Introduction
- A novel decision-support screening tool based on kinematic handwriting analysis of a simple repetitive handwriting task in youth DD is proposed for the first time.
- DD versus control group classification results, using machine learning with reduced feature sets, are systematically compared.
- Optimal feature subsets are identified, and the most frequently recurring features are analyzed.
2. Materials and Methods
2.1. Subjects
2.2. Experimental Protocol
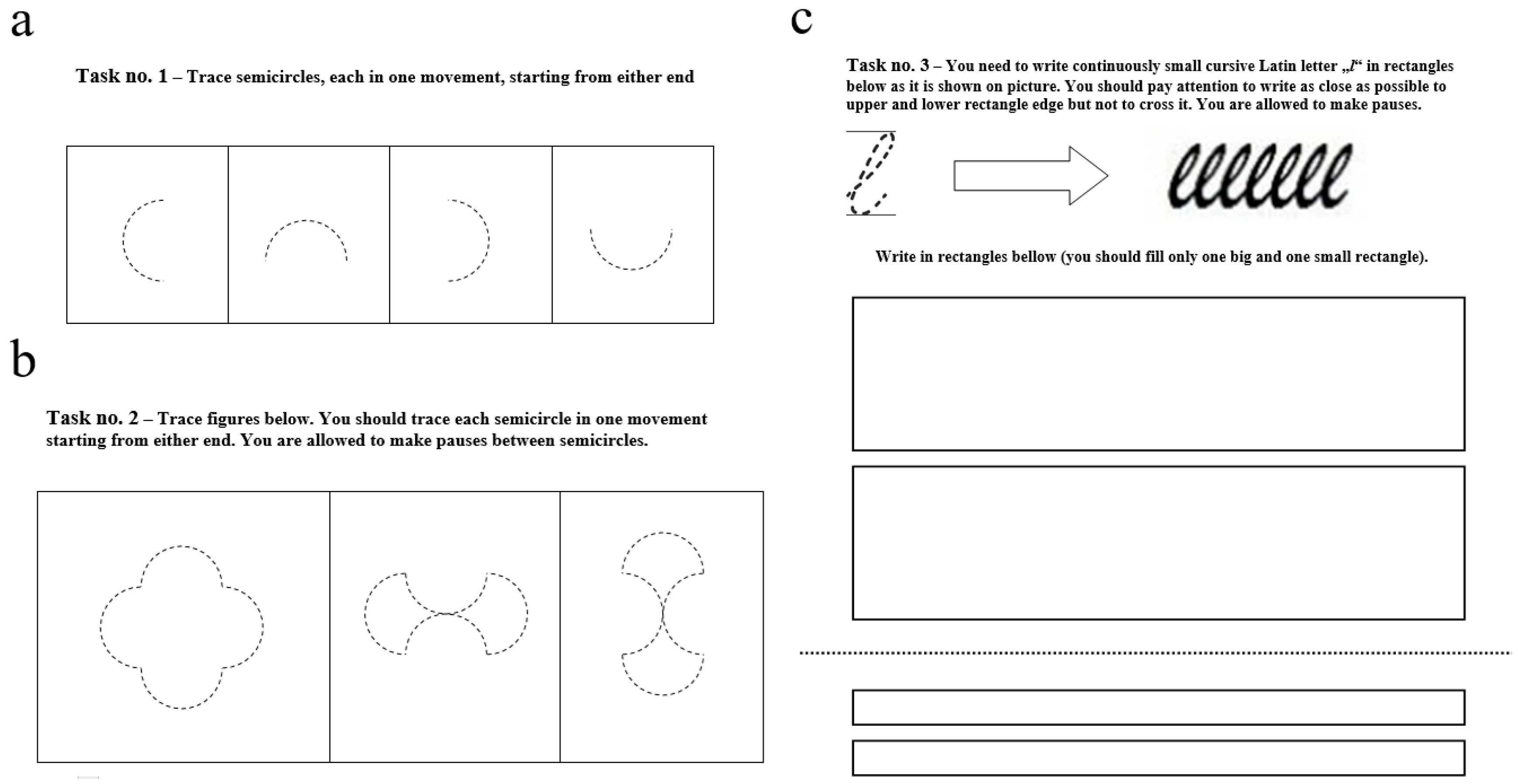
- First task—Tracing Single Semicircles: Participants were instructed to trace four semicircles, each completed in a single stroke. The semicircles were presented as dashed outlines within separate squares and rotated clockwise by 90° increments.
- Second task—Tracing Composite Figures: Participants traced three composite figures, each consisting of four semicircles oriented differently. The dimensions and orientations matched those in Task 1, and the figures were also presented as dashed outlines within individual squares
- Third task—Repetitive Handwriting of a Cursive Letter: Participants continuously wrote the lowercase cursive Latin letter “l” within two rectangles: a larger rectangle measuring 40 × 160 mm (LR subtask) and a smaller rectangle measuring 9 × 160 mm (SR subtask). The number of letters was not predefined; participants stopped writing at their own discretion.
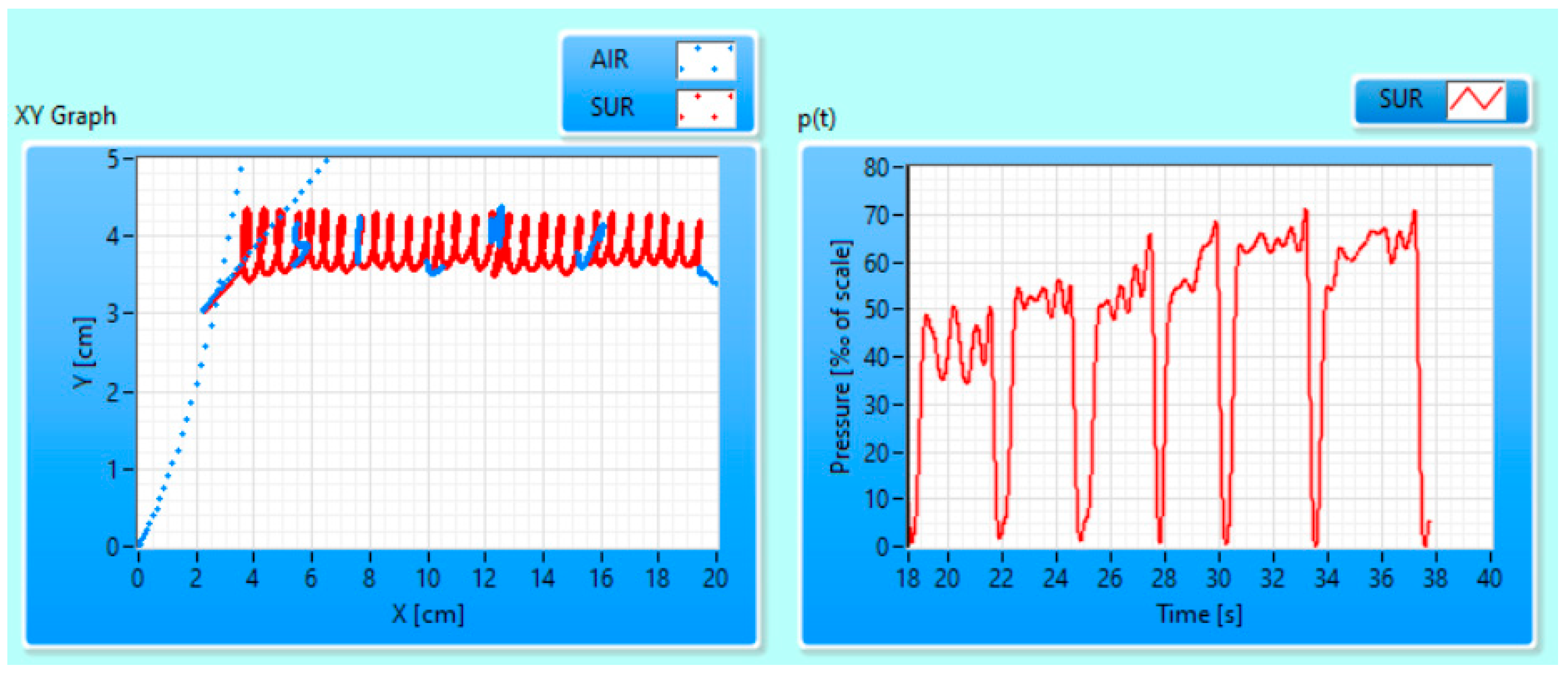
2.3. Letter Segmentation and Feature Extraction
- Calculation of velocity per y-axis Vy(t) = dY(t)/dt for the whole SR subtask;
- Finding local maximums of Vy(t) and using these maximums as letter boundaries within the SR subtask.
- The absolute difference between LL for the “letter” and the median LL in the entire subtask does not exceed 20% of the median LL;
- Vy(t) during the “letter” drawing time contains local minima.
2.4. Statistical Analysis
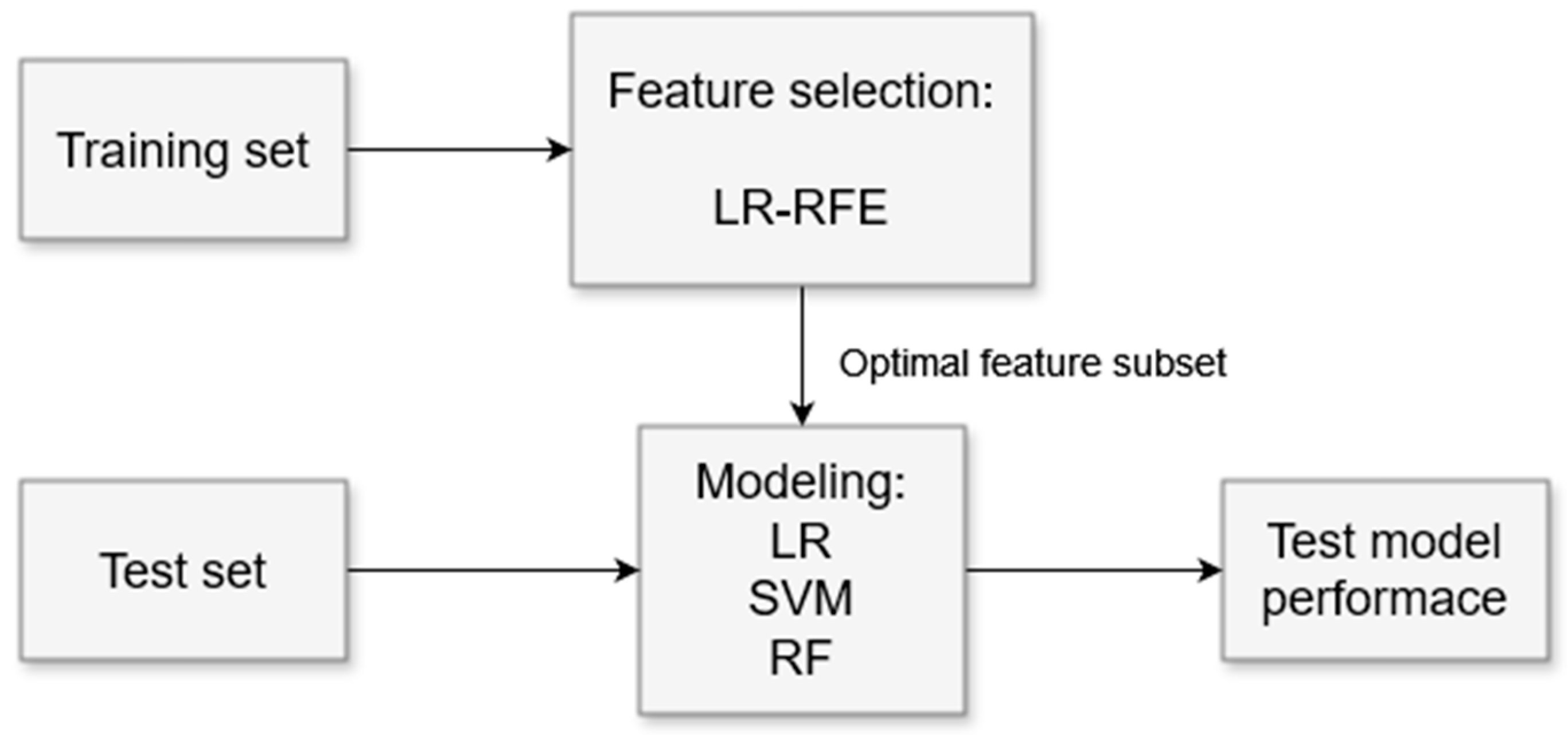
2.5. Machine Learning Analysis
3. Results
4. Discussion
4.1. “Letter” Segmentation
4.2. Feature Selection
4.3. Machine Learning
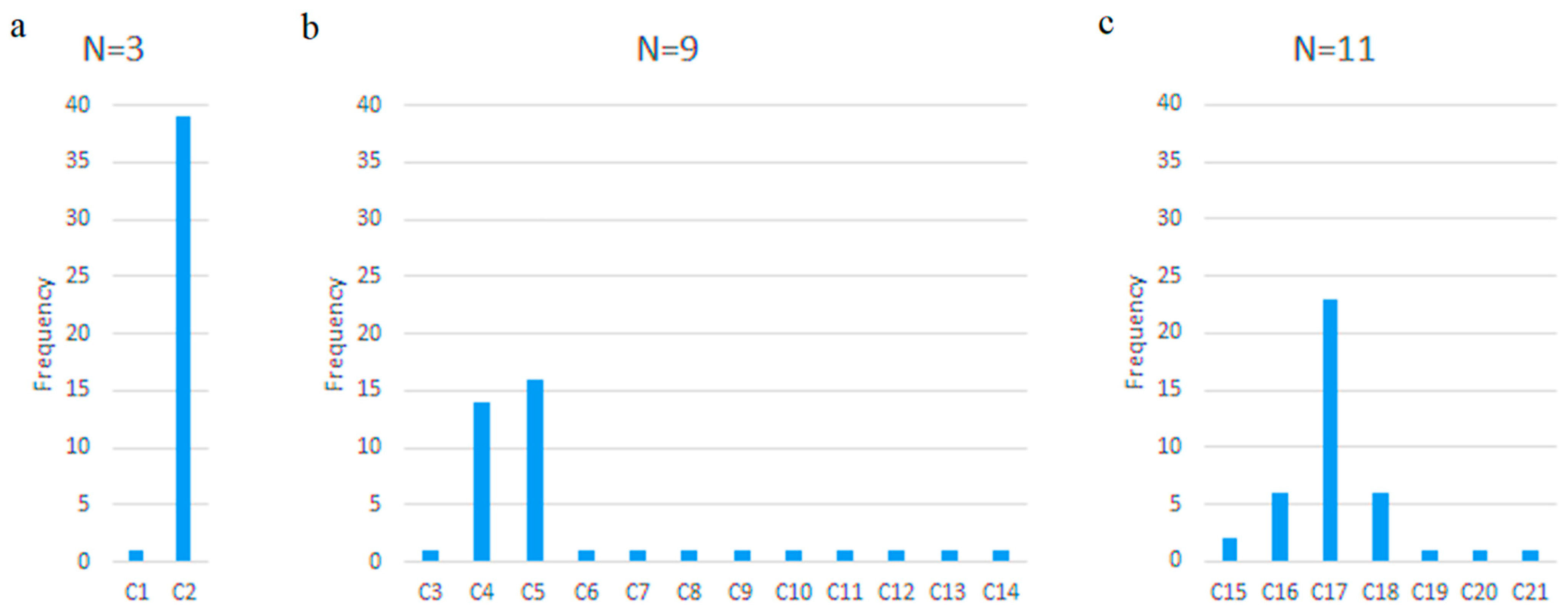
- N = 3—when LR and SVM achieved their highest classification accuracy;
- N = 9—the smallest N after which LR maintained “stable” accuracy (~74%);
- N = 11—the smallest N after which SVM maintained “stable” accuracy (~74%);
- N = 40—classification without RFE, where RF achieved the highest accuracy.
4.4. Optimal Features
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| YLDs | Years Lived with Disability |
| DD | Depressive Disorder |
| SSRI | Selective Serotonin Reuptake Inhibitors |
| TCA | Tricyclic Antidepressants |
| EHI | Edinburgh Handedness Inventory |
| SMFQ | Short Mood and Feelings Questionnaire |
| SCARED | Screen for Child Anxiety-Related Emotional Disorders |
| LOOCV | Leave-One-Out Cross-Validation |
| RFE | Recursive Feature Elimination |
| LR | Logistic Regression |
| SVM | Support Vector Machine |
| RF | Random Forest |
Appendix A
Appendix B
| Parameter | Value |
|---|---|
| Penalty | ‘elasticnet’ |
| Dual | False |
| Tolerance (tol) | 0.0001 |
| Inverse regularization (C) | 1.0 |
| Fit intercept | True |
| Intercept scaling | 1 |
| Class weight | None |
| Random state | None |
| Solver | ‘saga’ |
| Max iterations | 100 |
| Multiclass | ‘deprecated’ |
| Verbose | 0 |
| Warm start | False |
| Number of jobs (n_jobs) | None |
| L1 ratio | 0.5 |
| Parameter | Value |
|---|---|
| Inverse regularization (C) | 1.0 |
| Kernel | ‘linear’ |
| Polynomial degree | 3 |
| Gamma | ‘scale’ |
| Coefficient 0 (coef0) | 0.0 |
| Shrinking | True |
| Probability estimation | False |
| Tolerance (tol) | 0.001 |
| Cache size | 200 |
| Class weight | None |
| Verbose | False |
| Max iterations | -1 |
| Decision function shape | ‘ovr’ |
| Break ties | False |
| Random state | None |
| Parameter | Value |
|---|---|
| Number of trees (n_estimators) | 100 |
| Criterion | ‘gini’ |
| Maximum depth | None |
| Min samples to split | 2 |
| Min samples per leaf | 1 |
| Min weight fraction leaf | 0.0 |
| Max features | ‘sqrt’ |
| Max leaf nodes | None |
| Min impurity decrease | 0.0 |
| Bootstrap | True |
| Out-of-bag score (oob_score) | False |
| Number of jobs (n_jobs) | None |
| Random state | None |
| Verbose | 0 |
| Warm start | False |
| Class weight | None |
| Cost-complexity pruning (ccp_alpha) | 0.0 |
| Max samples | None |
| Monotonic constraints | None |
Appendix C
| No. | Feature | CONTROL Mean ± Se | DD Mean ± Se | p-Value | |ρ| 1 |
|---|---|---|---|---|---|
| 0 | Vx_cv 2 | 1.623 ± 0.185 | 2.060 ± 0.168 | 2.539 × 10−4 | 0.063 |
| 1 | Vx_max 3 | 2.456 ± 0.030 | 2.306 ± 0.033 | 1.150 × 10−4 | 0.122 |
| 2 | Vx_pct75 4 | 1.840 ± 0.027 | 1.680 ± 0.027 | 3.618 × 10−6 | 0.151 |
| 3 | Vx_pct90 5 | 2.340 ± 0.030 | 2.176 ± 0.031 | 1.810 × 10−5 | 0.137 |
| 4 | Vy_std 6 | 2.305 ± 0.018 | 1.884 ± 0.017 | 2.686 × 10−48 | 0.523 |
| 5 | Vy_max | 3.403 ± 0.024 | 2.879 ± 0.024 | 5.493 × 10−43 | 0.490 |
| 6 | Vy_min 7 | −3.359 ± 0.027 | −2.799 ± 0.025 | 1.594 × 10−42 | 0.484 |
| 7 | Vy_pct10 8 | −3.111 ± 0.028 | −2.582 ± 0.026 | 2.164 × 10−40 | 0.452 |
| 8 | Vy_pct75 | 2.282 ± 0.020 | 1.785 ± 0.021 | 1.056 × 10−51 | 0.530 |
| 9 | Vy_pct90 | 3.081 ± 0.023 | 2.531 ± 0.022 | 5.866 × 10−52 | 0.531 |
| 10 | V_med 9 | 2.651 ± 0.025 | 2.235 ± 0.025 | 1.424 × 10−28 | 0.395 |
| 11 | V_mean | 2.543 ± 0.021 | 2.171 ± 0.022 | 8.148 × 10−30 | 0.403 |
| 12 | V_std | 0.918 ± 0.009 | 0.770 ± 0.009 | 9.576 × 10−27 | 0.388 |
| 13 | V_max | 3.966 ± 0.032 | 3.422 ± 0.031 | 1.992 × 10−28 | 0.405 |
| 14 | V_pct25 10 | 1.905 ± 0.025 | 1.623 ± 0.025 | 2.567 × 10−15 | 0.278 |
| 15 | V_pct75 | 3.261 ± 0.025 | 2.759 ± 0.025 | 6.889 × 10−38 | 0.458 |
| 16 | V_pct90 | 3.696 ± 0.029 | 3.173 ± 0.030 | 9.517 × 10−31 | 0.416 |
| 17 | Ax_med | 0.006 ± 0.001 | 0.003 ± 0.001 | 5.372 × 10−5 | 0.125 |
| 18 | Ax_pct90 | 0.079 ± 0.002 | 0.073 ± 0.002 | 4.049 × 10−4 | 0.084 |
| 19 | Ay_min | −0.174 ± 0.003 | −0.137 ± 0.003 | 4.374 × 10−20 | 0.334 |
| 20 | Ay_pct10 | −0.162 ± 0.003 | −0.125 ± 0.002 | 1.307 × 10−20 | 0.344 |
| 21 | A_std | 0.086 ± 0.002 | 0.063 ± 0.001 | 3.528 × 10−24 | 0.355 |
| 22 | A_pct25 | −0.067 ± 0.001 | −0.047 ± 0.001 | 5.628 × 10−34 | 0.384 |
| 23 | A_pct75 | 0.074 ± 0.001 | 0.052 ± 0.001 | 2.063 × 10−27 | 0.357 |
| 24 | A_pct90 | 0.115 ± 0.002 | 0.087 ± 0.002 | 1.321 × 10−20 | 0.334 |
| 25 | Jx_med | 0.000 ± 0.000 | −0.000 ± 0.000 | 6.664 × 10−8 | 0.158 |
| 26 | Jy_std | 0.006 ± 0.000 | 0.005 ± 0.000 | 8.880 × 10−11 | 0.219 |
| 27 | Jy_max | 0.009 ± 0.000 | 0.008 ± 0.000 | 6.201 × 10−9 | 0.179 |
| 28 | Jy_pct25 | −0.006 ± 0.000 | −0.004 ± 0.000 | 3.829 × 10−13 | 0.246 |
| 29 | Jy_pct75 | 0.006 ± 0.000 | 0.004 ± 0.000 | 9.180 × 10−12 | 0.228 |
| 30 | Jy_pct90 | 0.008 ± 0.000 | 0.007 ± 0.000 | 3.136 × 10−10 | 0.195 |
| 31 | J_med | −0.004 ± 0.000 | −0.002 ± 0.000 | 1.975 × 10−20 | 0.282 |
| 32 | J_min | −0.009 ± 0.000 | −0.008 ± 0.000 | 3.825 × 10−10 | 0.203 |
| 33 | J_pct10 | −0.008 ± 0.000 | −0.006 ± 0.000 | 2.671 × 10−13 | 0.230 |
| 34 | J_pct25 | −0.007 ± 0.000 | −0.005 ± 0.000 | 7.068 × 10−15 | 0.251 |
| 35 | J_pct75 | 0.002 ± 0.000 | 0.002 ± 0.000 | 1.029 × 10−4 | 0.106 |
| 36 | J_pct90 | 0.011 ± 0.000 | 0.008 ± 0.000 | 9.278 × 10−23 | 0.271 |
| 37 | Jp_min | −0.003 ± 0.000 | −0.003 ± 0.000 | 6.233 × 100 | 0.076 |
| 38 | Jp_pct10 | −0.002 ± 0.000 | −0.001 ± 0.000 | 5.454 × 10−4 | 0.063 |
| 39 | LS 11 | 2.543 ± 0.021 | 2.171 ± 0.022 | 8.148 × 10−30 | 0.403 |
Appendix D
| Optimal Feature Subset | Abbreviation |
|---|---|
| Vx_max, Vy_pct75, V_std | C1 |
| Vy_std, Vy_pct75, V_pct25 | C2 |
| Vx_max, Vy_std, Vy_max, Vy_pct75, V_std, V_max, V_pct25, V_pct90, LS | C3 |
| Vx_max, Vy_std, Vy_max, Vy_pct75, Vy_pct90, V_std, V_max, V_pct25, LS | C4 |
| Vx_max, Vy_std, Vy_pct1, Vy_pct75, V_mean, V_std, V_max, V_pct25, LS | C5 |
| Vx_max, Vy_std, Vy_pct75, Vy_pct90, V_mean, V_std, V_pct25, V_pct90, LS | C6 |
| Vx_max, Vy_std, Vy_max, Vy_pct75, V_mean, V_std, V_max, V_pct25, LS | C7 |
| Vx_max, Vy_std, Vy_pct75, Vy_pct90, V_med, V_mean, V_std, V_pct25, LS | C8 |
| Vx_max, Vy_std, Vy_max, Vy_pct1, Vy_pct75, V_std, V_max, V_pct25, LS | C9 |
| Vx_max, Vy_std, Vy_max, Vy_pct1, Vy_pct75, V_std, V_max, V_pct25, LS | C10 |
| Vx_max, Vy_std, Vy_max, Vy_pct1, Vy_pct75, V_std, V_max, V_pct25, LS | C11 |
| Vx_max, Vy_std, Vy_max, Vy_pct1, Vy_pct75, V_std, V_max, V_pct25, LS | C12 |
| Vx_max, Vy_std, Vy_max, Vy_pct1, Vy_pct75, V_std, V_max, V_pct25, LS | C13 |
| Vx_max, Vy_std, Vy_max, Vy_pct1, Vy_pct75, V_std, V_max, V_pct25, LS | C14 |
| Vx_max, Vx_pct90, Vy_std, Vy_max, Vy_pct75, V_mean, V_std, V_max, V_pct25, V_pct90, LS | C15 |
| Vx_max, Vy_std, Vy_max, Vy_pct75, Vy_pct90, V_med, V_mean, V_std, V_max, V_pct25, LS | C16 |
| Vx_max, Vy_std, Vy_max, Vy_pct1, Vy_pct75, Vy_pct90, V_mean, V_std, V_max, V_pct25, LS | C17 |
| Vx_max, Vy_std, Vy_max, Vy_pct75, Vy_pct90, V_mean, V_std, V_max, V_pct25, V_pct90, LS | C18 |
| Vx_max, Vy_std, Vy_max, Vy_min, Vy_pct75, Vy_pct90, V_mean, V_std, V_pct25, V_pct90, LS | C19 |
| Vx_max, Vy_std, Vy_max, Vy_pct75, V_med, V_mean, V_std, V_max, V_pct25, V_pct90, LS | C20 |
| Vx_max, Vy_std, Vy_pct1, Vy_pct75, Vy_pct90, V_mean, V_std, V_max, V_pct25, V_pct90, LS | C21 |
Appendix E

References
- WHO. Depressive Disorder (Depression). Available online: https://www.who.int/news-room/fact-sheets/detail/depression (accessed on 11 June 2024).
- Liu, Q.; He, H.; Yang, J.; Feng, X.; Zhao, F.; Lyu, J. Changes in the global burden of depression from 1990 to 2017: Findings from the Global Burden of Disease study. J. Psychiatr. Res. 2020, 126, 134–140. [Google Scholar] [CrossRef]
- Kupcova, I.; Danisovic, L.; Klein, M.; Harsanyi, S. Effects of the COVID-19 pandemic on mental health, anxiety, and depression. BMC Psychol. 2023, 11, 108. [Google Scholar] [CrossRef] [PubMed]
- Yan, G.; Zhang, Y.; Wang, S.; Yan, Y.; Liu, M.; Tian, M.; Tian, W. Global, regional, and national temporal trend in burden of major depressive disorder from 1990 to 2019: An analysis of the global burden of disease study. Psychiatry Res. 2024, 337, 115958. [Google Scholar] [CrossRef] [PubMed]
- Sacco, R.; Camilleri, N.; Eberhardt, J.; Umla-Runge, K.; Newbury-Birch, D. A systematic review and meta-analysis on the prevalence of mental disorders among children and adolescents in Europe. Eur. Child Adolesc. Psychiatry 2024, 33, 2877–2894. [Google Scholar] [CrossRef] [PubMed]
- Polanczyk, G.V.; Salum, G.A.; Sugaya, L.S.; Caye, A.; Rohde, L.A. Annual research review: A meta-analysis of the worldwide prevalence of mental disorders in children and adolescents. J. Child Psychol. Psychiatry 2015, 56, 345–365. [Google Scholar] [CrossRef]
- Solmi, M.; Radua, J.; Olivola, M.; Croce, E.; Soardo, L.; Salazar de Pablo, G.; Il Shin, J.; Kirkbride, J.B.; Jones, P.; Kim, J.H.; et al. Age at onset of mental disorders worldwide: Large-scale meta-analysis of 192 epidemiological studies. Mol. Psychiatry 2022, 27, 281–295. [Google Scholar] [CrossRef]
- Castelpietra, G.; Knudsen, A.K.S.; Agardh, E.E.; Armocida, B.; Beghi, M.; Iburg, K.M.; Logroscino, G.; Ma, R.; Starace, F.; Steel, N.; et al. The burden of mental disorders, substance use disorders and self-harm among young people in Europe, 1990-2019: Findings from the Global Burden of Disease Study 2019. Lancet Reg. Health Eur. 2022, 16, 100341. [Google Scholar] [CrossRef]
- American Psychiatric Association and American Psychiatric Association (Ed.) Diagnostic and Statistical Manual of Mental Disorders: DSM-5, 5th ed.; American Psychiatric Association: Washington, DC, USA, 2013; pp. 591–643. [Google Scholar]
- WHO. ICD-11 for Mortality and Morbidity Statistics. Available online: https://icd.who.int/browse/2024-01/mms/en#1563440232 (accessed on 19 October 2024).
- Paquet, A.; Lacroix, A.; Calvet, B.; Girard, M. Psychomotor semiology in depression: A standardized clinical psychomotor approach. BMC Psychiatry 2022, 22, 474. [Google Scholar] [CrossRef]
- Elkjær, E.; Mikkelsen, M.B.; Michalak, J.; Mennin, D.S.; O’Toole, M.S. Motor alterations in depression and anxiety disorders: A systematic review and meta-analysis. J. Affect. Disord. 2022, 317, 373–387. [Google Scholar] [CrossRef]
- König, A.; Tröger, J.; Mallick, E.; Mina, M.; Linz, N.; Wagnon, C.; Karbach, J.; Kuhn, C.; Peter, J. Detecting subtle signs of depression with automated speech analysis in a non-clinical sample. BMC Psychiatry 2022, 22, 830. [Google Scholar] [CrossRef]
- Mergl, R.; Juckel, G.; Rihl, J.; Henkel, V.; Karner, M.; Tigges, P.; Schröter, A.; Hegerl, U. Kinematical analysis of handwriting movements in depressed patients. Acta Psychiatr. Scand. 2004, 109, 383–391. [Google Scholar] [CrossRef] [PubMed]
- Baune, B.T.; Fuhr, M.; Air, T.; Hering, C. Neuropsychological functioning in adolescents and young adults with major depressive disorder—A review. Psychiatry Res. 2014, 218, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Bennabi, D.; Vandel, P.; Papaxanthis, C.; Pozzo, T.; Haffen, E. Psychomotor retardation in depression: A systematic review of diagnostic, pathophysiologic, and therapeutic implications. BioMed Res. Int. 2013, 2013, 158746. [Google Scholar] [CrossRef]
- Buyukdura, J.S.; McClintock, S.M.; Croarkin, P.E. Psychomotor retardation in depression: Biological underpinnings, measurement, and treatment. Prog. Neuropsychopharmacol. Biol. Psychiatry 2011, 35, 395–409. [Google Scholar] [CrossRef]
- Wells, F.L. Motor retardation as a manic-depressive symptom. Am. J. Psychiatry 1909, 66, 1–52. [Google Scholar] [CrossRef]
- Shevell, M. Global developmental delay and mental retardation or intellectual disability: Conceptualization, evaluation, and etiology. Pediatr. Clin. N. Am. 2008, 55, 1071–1084. [Google Scholar] [CrossRef]
- Esposito, A.; Raimo, G.; Maldonato, M.; Vogel, C.; Conson, M.; Cordasco, G. Behavioral Sentiment Analysis of Depressive States. In Proceedings of the 2020 11th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), Mariehamn, Finland, 23–25 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 209–214. [Google Scholar]
- Raimo, G.; Buonanno, M.; Conson, M.; Cordasco, G.; Faundez-Zanuy, M.; McConvey, G.; Marrone, S.; Marulli, F.; Vinciarelli, A.; Esposito, A. Handwriting and Drawing for Depression Detection: A Preliminary Study. In Applied Intelligence and Informatics; Springer: Cham, Switzerland, 2022; pp. 320–332. [Google Scholar]
- Zhang, L.; Fan, Y.; Jiang, J.; Li, Y.; Zhang, W. Adolescent Depression Detection Model Based on Multimodal Data of Interview Audio and Text. Int. J. Neural Syst. 2022, 32, 2250045. [Google Scholar] [CrossRef] [PubMed]
- Sobin, C.; Sackeim, H. Psychomotor symptoms of depression. Am. J. Psychiatry 1997, 154, 4–17. [Google Scholar] [CrossRef]
- Ivančević, N. Kinematic Analysis of Handwriting in Neurological, Psychiatric and Neurodevelopmental Disorders of Childhood and Adolescence. Ph.D. Dissertation, Biomedical Engineering and Technologies, University of Belgrade, Belgrade, Serbia, 2021. [Google Scholar]
- Asselborn, T.; Gargot, T.; Kidziński, Ł.; Johal, W.; Cohen, D.; Jolly, C.; Dillenbourg, P. Automated human-level diagnosis of dysgraphia using a consumer tablet. Npj Digit. Med. 2018, 1, 42. [Google Scholar] [CrossRef]
- Gavenciak, M.; Mucha, J.; Mekyska, J.; Galaz, Z.; Zvoncakova, K.; Faundez-Zanuy, M. Computer-Aided Diagnosis of Graphomotor Difficulties Utilizing Direction-Based Fractional Order Derivatives. Cogn. Comput. 2024, 17, 13. [Google Scholar] [CrossRef]
- Brossard-Racine, M.; Majnemer, A.; Shevell, M.; Snider, L.; Bélanger, S.A. Handwriting capacity in children newly diagnosed with Attention Deficit Hyperactivity Disorder. Res. Dev. Disabil. 2011, 32, 2927–2934. [Google Scholar] [CrossRef] [PubMed]
- Rosenblum, S.; Epsztein, L.; Josman, N. Handwriting Performance of Children with Attention Deficit Hyperactive Disorders: A Pilot Study. Phys. Occup. Ther. Pediatr. 2008, 28, 219–234. [Google Scholar] [CrossRef]
- Soleimani, R.; Kousha, M.; Zarrabi, H.; Tavafzadeh-Haghi, S.M.; Jalali, M.M. The Impact of Methylphenidate on Motor Performance in Children with both Attention Deficit Hyperactivity Disorder and Developmental Coordination Disorder: A Randomized Double-Blind Crossover Clinical Trial. Iran. J. Med. Sci. 2017, 42, 354–361. [Google Scholar] [PubMed]
- Cook, J. From movement kinematics to social cognition: The case of autism. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2016, 371, 20150372. [Google Scholar] [CrossRef] [PubMed]
- Cordasco, G.; Scibelli, F.; Faundez-Zanuy, M.; Likforman-Sulem, L.; Esposito, A. Handwriting and Drawing Features for Detecting Negative Moods. In Quantifying and Processing Biomedical and Behavioral Signals; Esposito, A., Faundez-Zanuy, M., Morabito, F.C., Pasero, E., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 73–86. ISBN 978-3-319-95095-2. [Google Scholar]
- Rosenblum, S.; Werner, P.; Dekel, T.; Gurevitz, I.; Heinik, J. Handwriting process variables among elderly people with mild Major Depressive Disorder: A preliminary study. Aging Clin. Exp. Res. 2010, 22, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Schröter, A.; Mergl, R.; Bürger, K.; Hampel, H.; Möller, H.-J.; Hegerl, U. Kinematic analysis of handwriting movements in patients with Alzheimer’s disease, mild cognitive impairment, depression and healthy subjects. Dement. Geriatr. Cogn. Disord. 2003, 15, 132–142. [Google Scholar] [CrossRef]
- Rahman, A.U.; Halim, Z. Identifying dominant emotional state using handwriting and drawing samples by fusing features. Appl. Intell. 2023, 53, 2798–2814. [Google Scholar] [CrossRef]
- Likforman-Sulem, L.; Esposito, A.; Faundez-Zanuy, M.; Clémençon, S.; Cordasco, G. EMOTHAW: A Novel Database for Emotional State Recognition From Handwriting and Drawing. IEEE Trans. Hum.-Mach. Syst. 2017, 47, 273–284. [Google Scholar] [CrossRef]
- Greco, C.; Raimo, G.; Amorese, T.; Cuciniello, M.; Mcconvey, G.; Cordasco, G.; Faundez-Zanuy, M.; Vinciarelli, A.; Callejas-Carrion, Z.; Esposito, A. Discriminative Power of Handwriting and Drawing Features in Depression. Int. J. Neural Syst. 2024, 34, 2350069. [Google Scholar] [CrossRef]
- Dragovic, M. Towards an improved measure of the Edinburgh Handedness Inventory: A one-factor congeneric measurement model using confirmatory factor analysis. Laterality Asymmetries Body Brain Cogn. 2004, 9, 411–419. [Google Scholar] [CrossRef]
- Milenkovic, S.; Dragovic, M. Modification of the Edinburgh Handedness Inventory: A replication study. Laterality 2013, 18, 340–348. [Google Scholar] [CrossRef]
- Thabrew, H.; Stasiak, K.; Bavin, L.-M.; Frampton, C.; Merry, S. Validation of the Mood and Feelings Questionnaire (MFQ) and Short Mood and Feelings Questionnaire (SMFQ) in New Zealand help-seeking adolescents. Int. J. Methods Psychiatr. Res. 2018, 27, e1610. [Google Scholar] [CrossRef] [PubMed]
- Arab, A.; El Keshky, M.; Hadwin, J.A. Psychometric Properties of the Screen for Child Anxiety Related Emotional Disorders (SCARED) in a Non-Clinical Sample of Children and Adolescents in Saudi Arabia. Child Psychiatry Hum. Dev. 2016, 47, 554–562. [Google Scholar] [CrossRef]
- Ivančević, N.; Novičić, M.; Miler, V.; Janković, M.; Stevanovic, D.; Nikolić, B.; Popović, M.; Jancic, J. Does handedness matter? Writing and tracing kinematic analysis in healthy adults. Psihologija 2019, 52, 413–435. [Google Scholar] [CrossRef]
- Miler-Jerković, V.; Kojić, V.; Popović, M.B. An Information and Reliability Analysis of handwriting Kinematics. In Proceedings of the 2nd International Conference on Electrical, Electronic and Computing Engineering IcETRAN, Silver Lake, Serbia, 8–11 June 2015; pp. 1–4. [Google Scholar]
- Džepina, V.; Ivančević, N.; Miler-Jerković, V.; Nikolić, B.; Stevanović, D.; Janković, M.M. GT Analyzer—A Basic Tool for Handwriting Movement Data. In Proceedings of the 9th International Conference on Electrical, Electronic and Computing Engineering IcETRAN, Novi Pazar, Serbia, 6–9 June 2022; pp. 1–5. [Google Scholar]
- Yan, J.H.; Hinrichs, R.N.; Payne, V.G.; Thomas, J.R. Normalized Jerk: A Measure to Capture Developmental Characteristics of Young Girls’ Overarm Throwing. J. Appl. Biomech. 2000, 16, 196–203. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Bartlett, M.S.; Fowler, R.H. Properties of sufficiency and statistical tests. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1937, 160, 268–282. [Google Scholar] [CrossRef]
- Zimmerman, D.W. Invalidation of Parametric and Nonparametric Statistical Tests by Concurrent Violation of Two Assumptions. J. Exp. Educ. 1998, 67, 55–68. [Google Scholar] [CrossRef]
- Cross, C.L.; Daniel, W.W. Analysis of Variance. In Biostatistics: A Foundation for Analysis in the Health Sciences, 11th ed.; Wiley: Hoboken, NJ, USA, 2018; pp. 267–354. ISBN 978-1-119-49657-1. [Google Scholar]
- Granitto, P.M.; Furlanello, C.; Biasioli, F.; Gasperi, F. Recursive feature elimination with random forest for PTR-MS analysis of agroindustrial products. Chemom. Intell. Lab. Syst. 2006, 83, 83–90. [Google Scholar] [CrossRef]
- Wong, T.-T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Parush, S.; Pindak, V.; Hahn-Markowitz, J.; Mazor-Karsenty, T. Does fatigue influence children’s handwriting performance? Work 1998, 11, 307–313. [Google Scholar] [CrossRef]
- Kushki, A.; Schwellnus, H.; Ilyas, F.; Chau, T. Changes in kinetics and kinematics of handwriting during a prolonged writing task in children with and without dysgraphia. Res. Dev. Disabil. 2011, 32, 1058–1064. [Google Scholar] [CrossRef] [PubMed]
- Drotár, P.; Mekyska, J.; Rektorová, I.; Masarová, L.; Smékal, Z.; Faundez-Zanuy, M. Evaluation of handwriting kinematics and pressure for differential diagnosis of Parkinson’s disease. Artif. Intell. Med. 2016, 67, 39–46. [Google Scholar] [CrossRef]
- Xia, S.; Yang, Y. A Model-Free Feature Selection Technique of Feature Screening and Random Forest-Based Recursive Feature Elimination. Int. J. Intell. Syst. 2023, 2023, 2400194. [Google Scholar] [CrossRef]
- Visted, E.; Sørensen, L.; Vøllestad, J.; Osnes, B.; Svendsen, J.L.; Jentschke, S.; Binder, P.-E.; Schanche, E. The Association Between Juvenile Onset of Depression and Emotion Regulation Difficulties. Front. Psychol. 2019, 10, 2262. [Google Scholar] [CrossRef] [PubMed]
- De Los Reyes, A.; Youngstrom, E.A.; Pabón, S.C.; Youngstrom, J.K.; Feeny, N.C.; Findling, R.L. Internal consistency and associated characteristics of informant discrepancies in clinic referred youths age 11 to 17 years. J. Clin. Child Adolesc. Psychol. 2011, 40, 36–53. [Google Scholar] [CrossRef]
- Nisenson, M.; Lin, V.; Gansner, M. Digital Phenotyping in Child and Adolescent Psychiatry: A Perspective. Harv. Rev. Psychiatry 2021, 29, 401–408. [Google Scholar] [CrossRef]
- Haley, F.; Andrews, J.; Moghaddam, N. Acceptability of Remote Monitoring Technologies for Early Warning of Major Depression. J. Technol. Behav. Sci. 2025. [Google Scholar] [CrossRef]
- Le, H.-N.; George, T.; University, W.; Boyd, R. Prevention of major depression: Early detection and early intervention in the general population. Clin. Neuropsychiatry 2006, 3, 6–22. [Google Scholar]
- Otte, C.; Gold, S.M.; Penninx, B.W.; Pariante, C.M.; Etkin, A.; Fava, M.; Mohr, D.C.; Schatzberg, A.F. Major depressive disorder. Nat. Rev. Dis. Primer 2016, 2, 16065. [Google Scholar] [CrossRef] [PubMed]
- Rueckriegel, S.M.; Blankenburg, F.; Burghardt, R.; Ehrlich, S.; Henze, G.; Mergl, R.; Hernáiz Driever, P. Influence of age and movement complexity on kinematic hand movement parameters in childhood and adolescence. Int. J. Dev. Neurosci. 2008, 26, 655–663. [Google Scholar] [CrossRef] [PubMed]
- Sabbe, B.; van Hoof, J.; Hulstijn, W.; Zitman, F. Depressive retardation and treatment with fluoxetine: Assessment of the motor component. J. Affect. Disord. 1997, 43, 53–61. [Google Scholar] [CrossRef]


| Characteristics | DD 1 | Control | p-Value | ||
|---|---|---|---|---|---|
| Mean | SD | Mean | SD | ||
| Age (years) | 14.6 | 1.6 | 15.9 | 0.4 | 0.002 |
| EHI score 2 | 53.8 | 56.0 | 51.8 | 55.2 | 0.989 |
| SMFQ 3 | 13.0 | 6.8 | 6.4 | 5.1 | 0.002 |
| SCARED 4 | 37.5 | 15.7 | 22.8 | 12.3 | 0.002 |
| Duration of disturbances (months) | 17.7 | 10.6 | / | / | / |
| Antidepressant therapy duration (weeks) | 15.8 | 17.0 | / | / | / |
| n | % | n | % | p-value | |
| Number of subjects | 20 | 100 | 20 | 100 | / |
| Antidepressant therapy | 11 | 55 | / | / | / |
| Right-handed subjects | 18 | 90 | 17 | 85 | 0.012 |
| Male subjects | 4 | 20 | 10 | 50 | 0.140 |
| Variable | Derivative Variable | Total Variable |
|---|---|---|
| X position, X(t) | 1st, 2nd, 3rd derivative of X(t): Velocity per x-axis, Vx(t) Acceleration per x-axis, Ax(t) Jerk per x-axis, Jx(t) | Total velocity, V(t) Total acceleration, A(t) Total jerk, J(t) |
| Y position, Y(t) | 1st, 2nd, 3rd derivative of Y(t): Velocity per y-axis, Vy(t) Acceleration per y-axis, Ay(t) Jerk per y-axis, Jy(t) | |
| Pressure, p(t) | 1st, 2nd, 3rd derivative of p(t): | |
| Total variables = 15 | ||
| Abbreviation | Unit | Letter Feature |
|---|---|---|
| LL | [cm] | Letter length |
| LT | [s] | Letter drawing time |
| LS | [cm/s] | Letter drawing speed |
| NCV | [n.u.] | Number of changes in velocity |
| RNCV | [n.u.] | Number of changes in velocity relative to letter drawing time (NCV/LT) |
| NST | [n.u.] | Time spent during drawing on-surface normalized by the letter drawing time (ON-SURFACE TIME/LT) |
| NIP | [n.u.] | Number of changes in pressure direction |
| NCA | [n.u.] | Number of changes in acceleration |
| RNCA | [s−1] | Number of changes in acceleration relative to letter drawing time (NCA/LT) |
| NIV | [n.u.] | Number of changes in velocity direction |
| NJ | [n.u.] | J(t)—total jerk; LT—letter drawing time; LL—letter length |
| NS | [n.u.] | Number of strokes in the “letter” segment |
| No. | Feature | CONTROL Mean ± Se | DD Mean ± Se | p-Value | |ρ| |
|---|---|---|---|---|---|
| 1 | Vy_pct90 | 3.081 ± 0.023 | 2.531 ± 0.022 | 5.866 × 10−52 | 0.531 |
| 2 | Vy_pct75 | 2.282 ± 0.020 | 1.785 ± 0.021 | 1.057 × 10−51 | 0.530 |
| 3 | Vy_std | 2.305 ± 0.018 | 1.884 ± 0.017 | 2.686 × 10−48 | 0.523 |
| 4 | Vy_max | 3.403 ± 0.024 | 2.879 ± 0.024 | 5.493 × 10−43 | 0.490 |
| 5 | Vy_min | −3.359 ± 0.027 | −2.799 ± 0.025 | 1.594 × 10−42 | 0.484 |
| Classifier | N | Letter Accuracy [%] | Letter Recall [%] | Letter Precision [%] | Subject Accuracy [%] |
|---|---|---|---|---|---|
| LR | 3 | 76.7 | 77.4 | 77.1 | 82.5 |
| 9 | 74.1 | 74.5 | 74.3 | 77.5 | |
| 11 | 74.1 | 74.0 | 74.0 | 77.5 | |
| 40 | 71.4 | 65.3 | 68.5 | 70.0 | |
| SVM | 3 | 76.2 | 77.6 | 77.0 | 80.0 |
| 9 | 73.3 | 73.4 | 73.4 | 77.5 | |
| 11 | 74.0 | 74.0 | 74.0 | 77.5 | |
| 40 | 73.7 | 72.4 | 73.1 | 77.5 | |
| RF | 3 | 72.0 | 73.6 | 72.7 | 77.5 |
| 9 | 69.0 | 71.0 | 69.8 | 75.0 | |
| 11 | 69.0 | 71.6 | 70.0 | 75.0 | |
| 40 | 75.3 | 78.2 | 76.9 | 82.5 |
| Optimal Combination Subset | Abbreviation |
|---|---|
| Vy_std, Vy_pct75, V_pct25 | C2 |
| Vy_std, Vy_pct75, V_pct25, Vx_max, Vy_pct1, V_mean, V_std, V_max, LS | C5 |
| Vy_std, Vy_pct75, V_pct25, Vx_max, Vy_pct1, V_mean, V_std, V_max, LS, Vy_max, Vy_pct90, | C17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Džepina, V.; Ivančević, N.; Rosić, S.; Nikolić, B.; Stevanović, D.; Jančić, J.; Janković, M.M. Detection of Psychomotor Retardation in Youth Depression: A Machine Learning Approach to Kinematic Analysis of Handwriting. Appl. Sci. 2025, 15, 7634. https://doi.org/10.3390/app15147634
Džepina V, Ivančević N, Rosić S, Nikolić B, Stevanović D, Jančić J, Janković MM. Detection of Psychomotor Retardation in Youth Depression: A Machine Learning Approach to Kinematic Analysis of Handwriting. Applied Sciences. 2025; 15(14):7634. https://doi.org/10.3390/app15147634
Chicago/Turabian StyleDžepina, Vladimir, Nikola Ivančević, Sunčica Rosić, Blažo Nikolić, Dejan Stevanović, Jasna Jančić, and Milica M. Janković. 2025. "Detection of Psychomotor Retardation in Youth Depression: A Machine Learning Approach to Kinematic Analysis of Handwriting" Applied Sciences 15, no. 14: 7634. https://doi.org/10.3390/app15147634
APA StyleDžepina, V., Ivančević, N., Rosić, S., Nikolić, B., Stevanović, D., Jančić, J., & Janković, M. M. (2025). Detection of Psychomotor Retardation in Youth Depression: A Machine Learning Approach to Kinematic Analysis of Handwriting. Applied Sciences, 15(14), 7634. https://doi.org/10.3390/app15147634






