Design and Analysis of a Hybrid MPPT Method for PV Systems Under Partial Shading Conditions
Abstract
1. Introduction
- The dynamic response of the system is remarkably improved for rapidly changing irradiance levels,
- Maximum operating point determination capability of the developed algorithm is high when compared to existing methods in the current literature,
- The number of oscillations under steady-state operation is significantly reduced,
- The accuracy of the perturbation direction is increased by the proposed method.
2. Materials and Methods
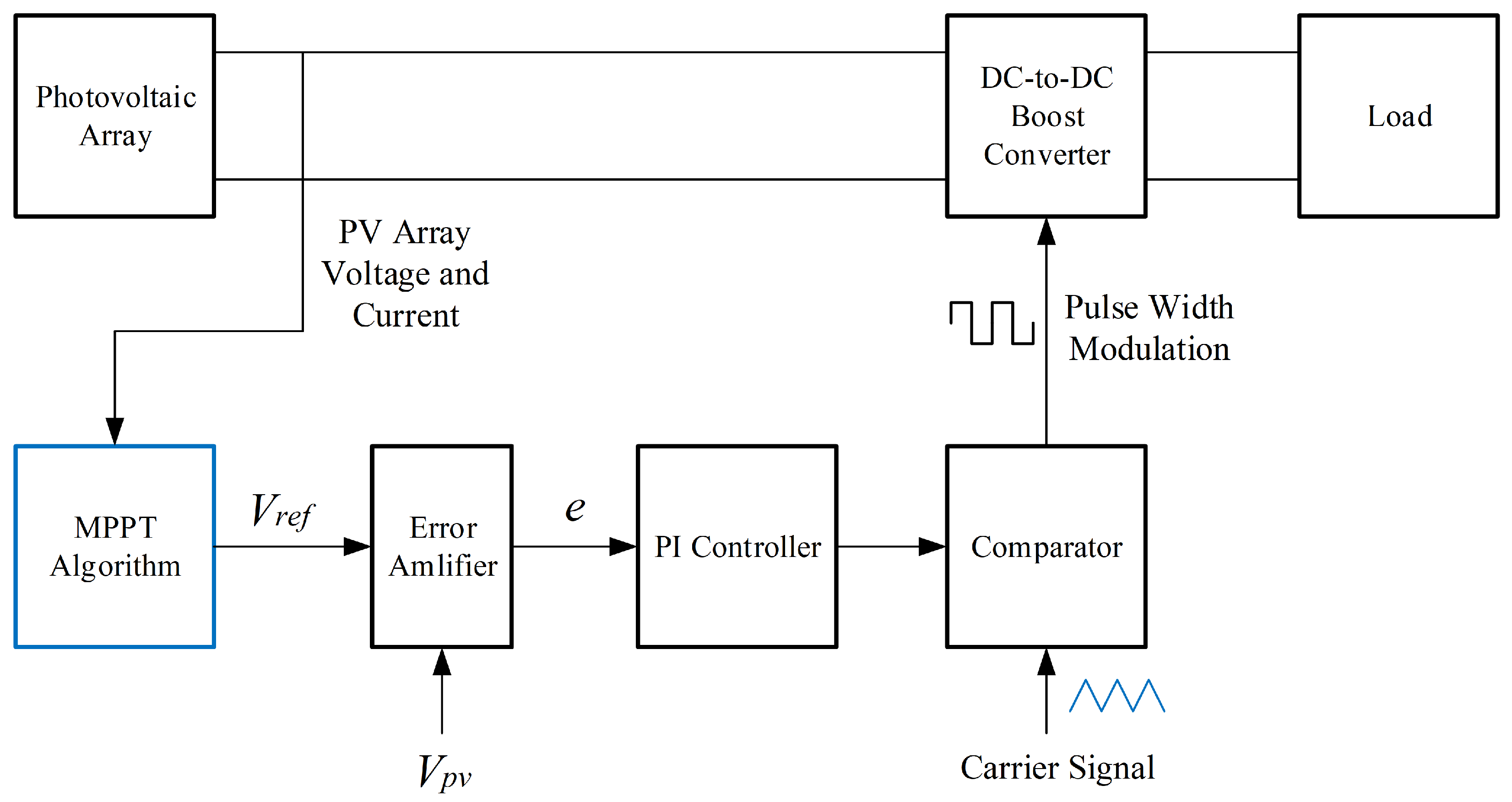
2.1. Design of the Proposed PV System
2.2. Design of DC-DC Boost Converter
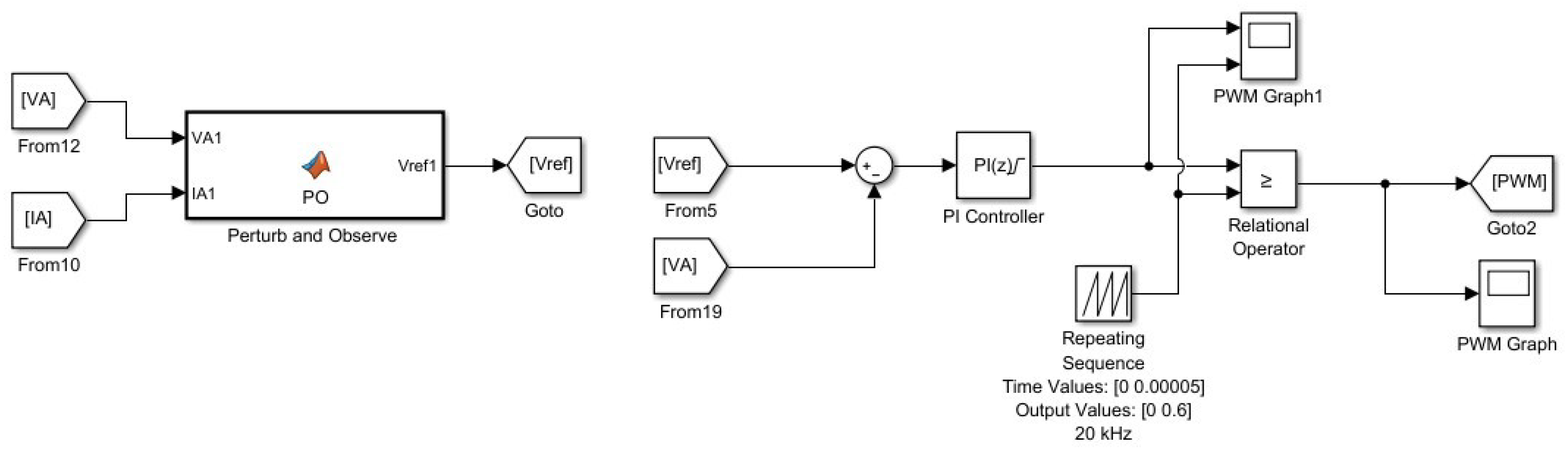
2.3. Design of the Proposed MPPT Algorithms
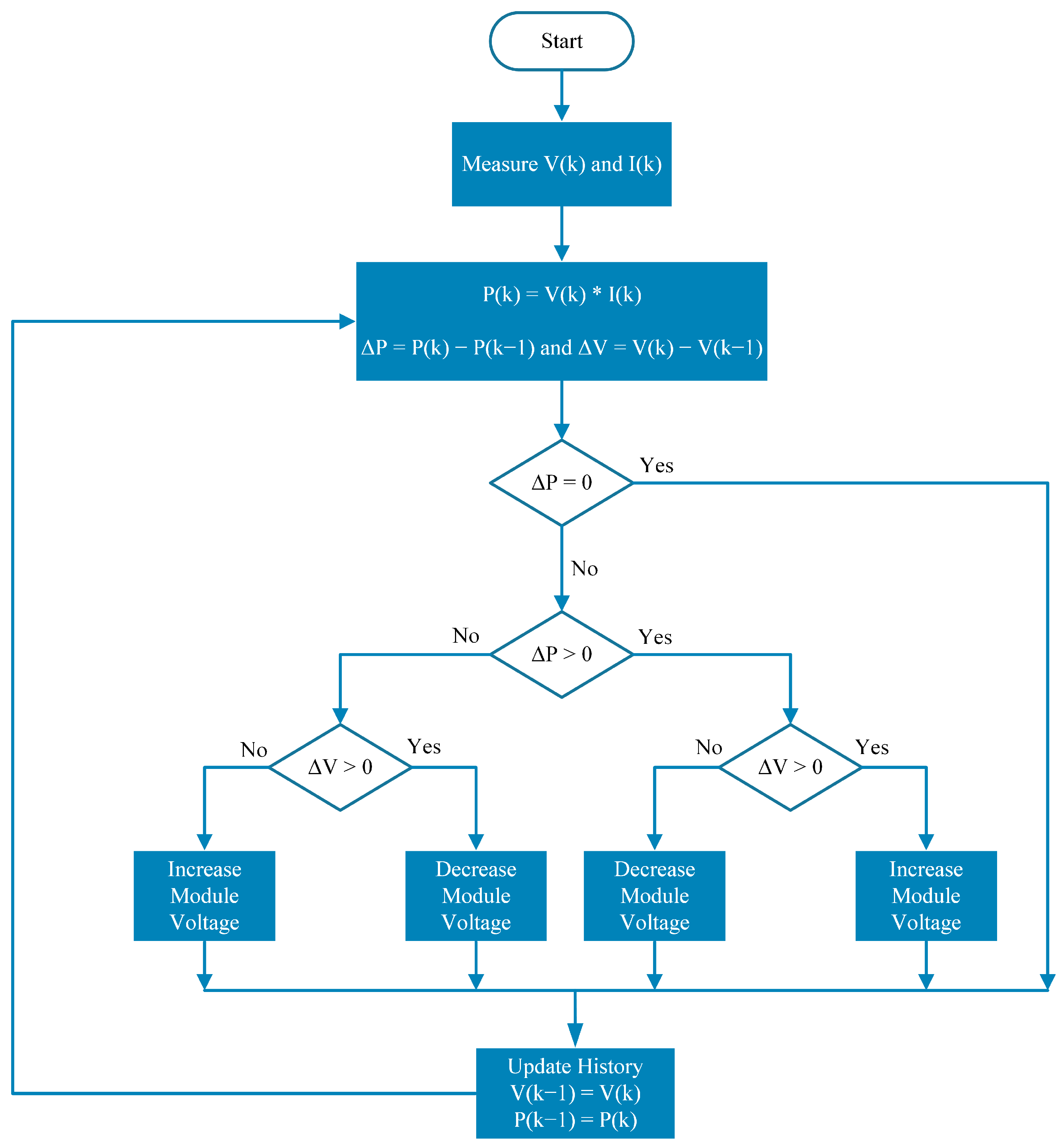
2.3.1. Design of Perturb & Observe MPPT Algorithm
2.3.2. Design of Kalman Filter and Perturb & Observe Hybrid MPPT Algorithm
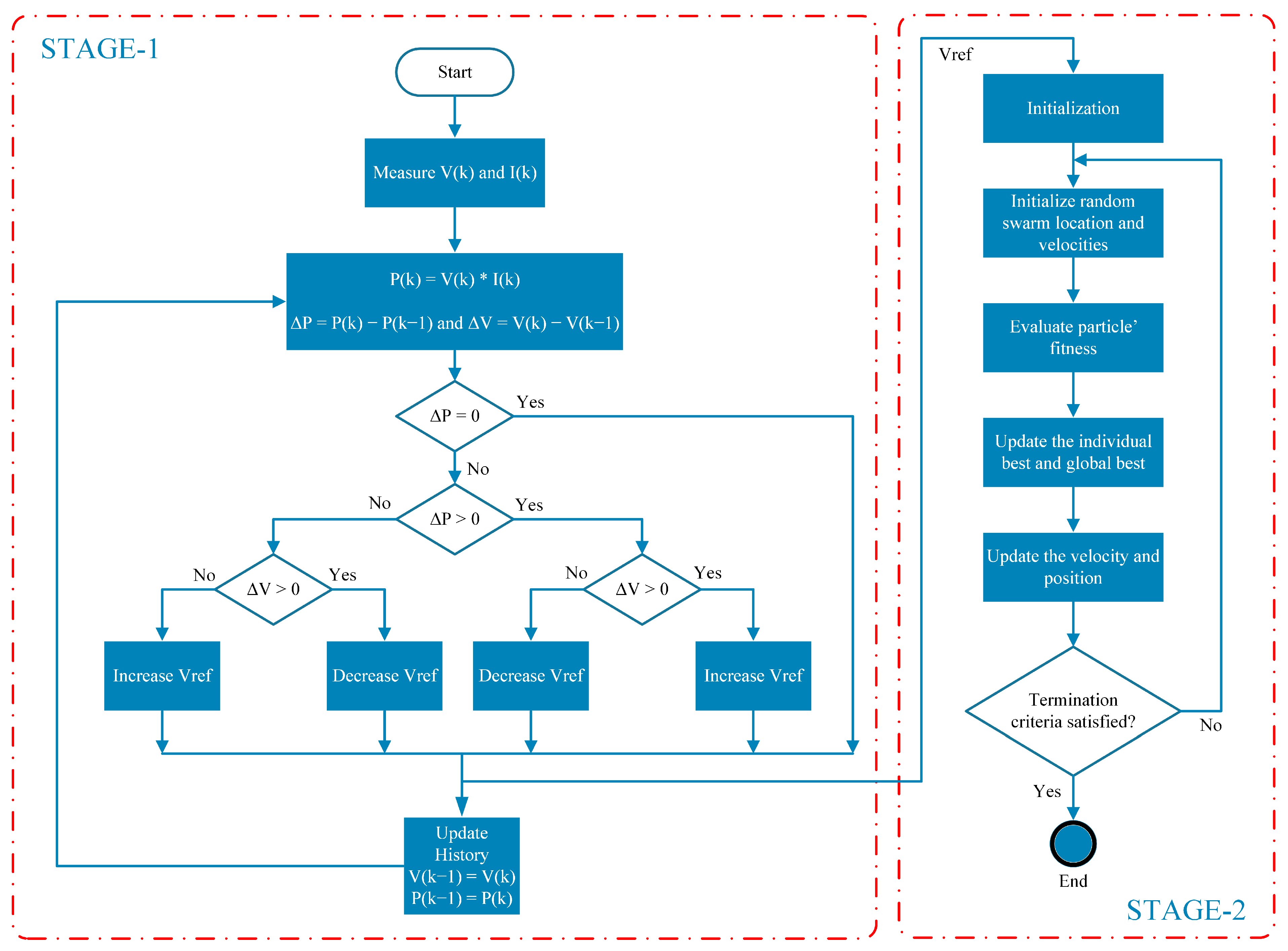
2.3.3. The Proposed Algorithm: Design of the Perturb & Observe and Particle Swarm Optimization MPPT Algorithm
3. Results and Discussion
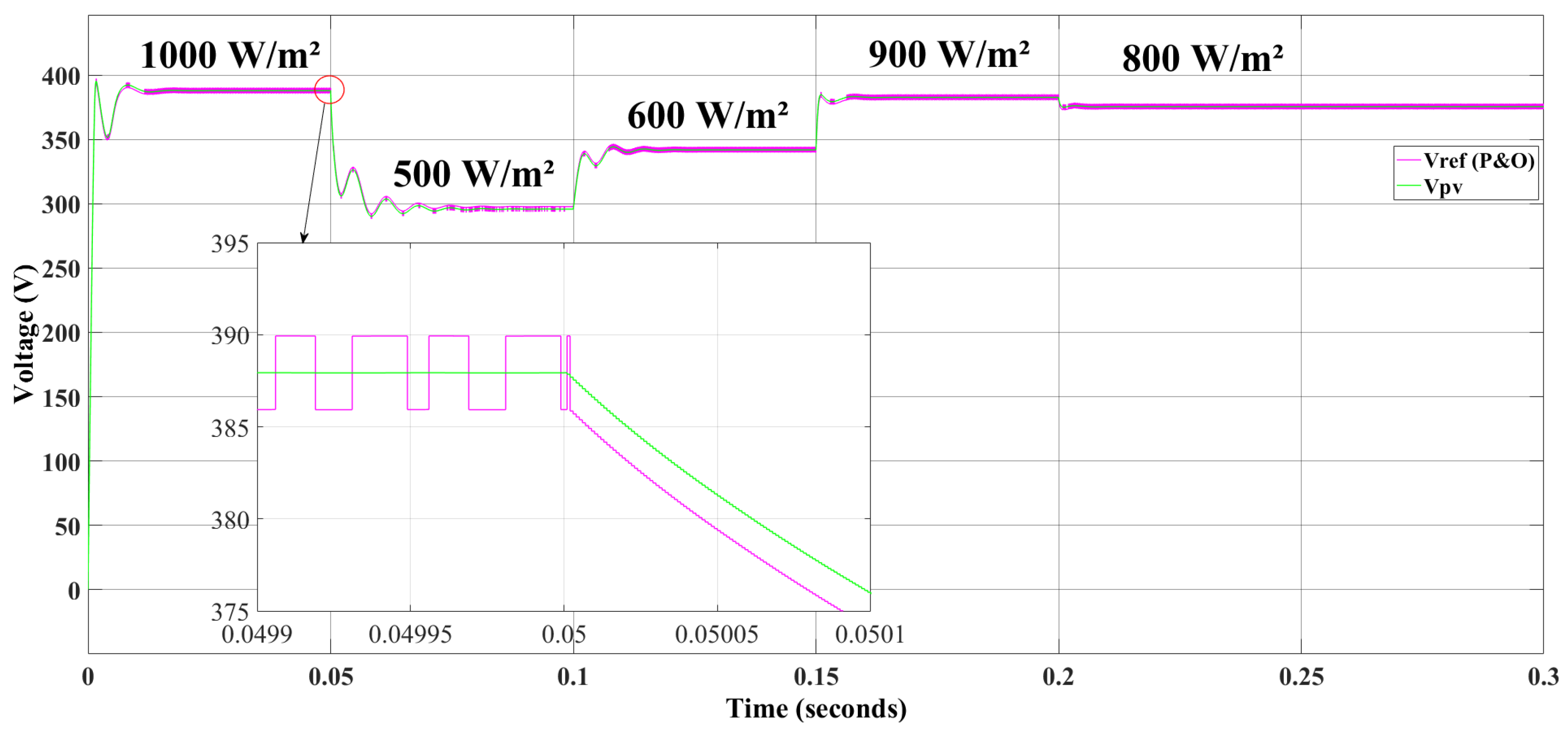
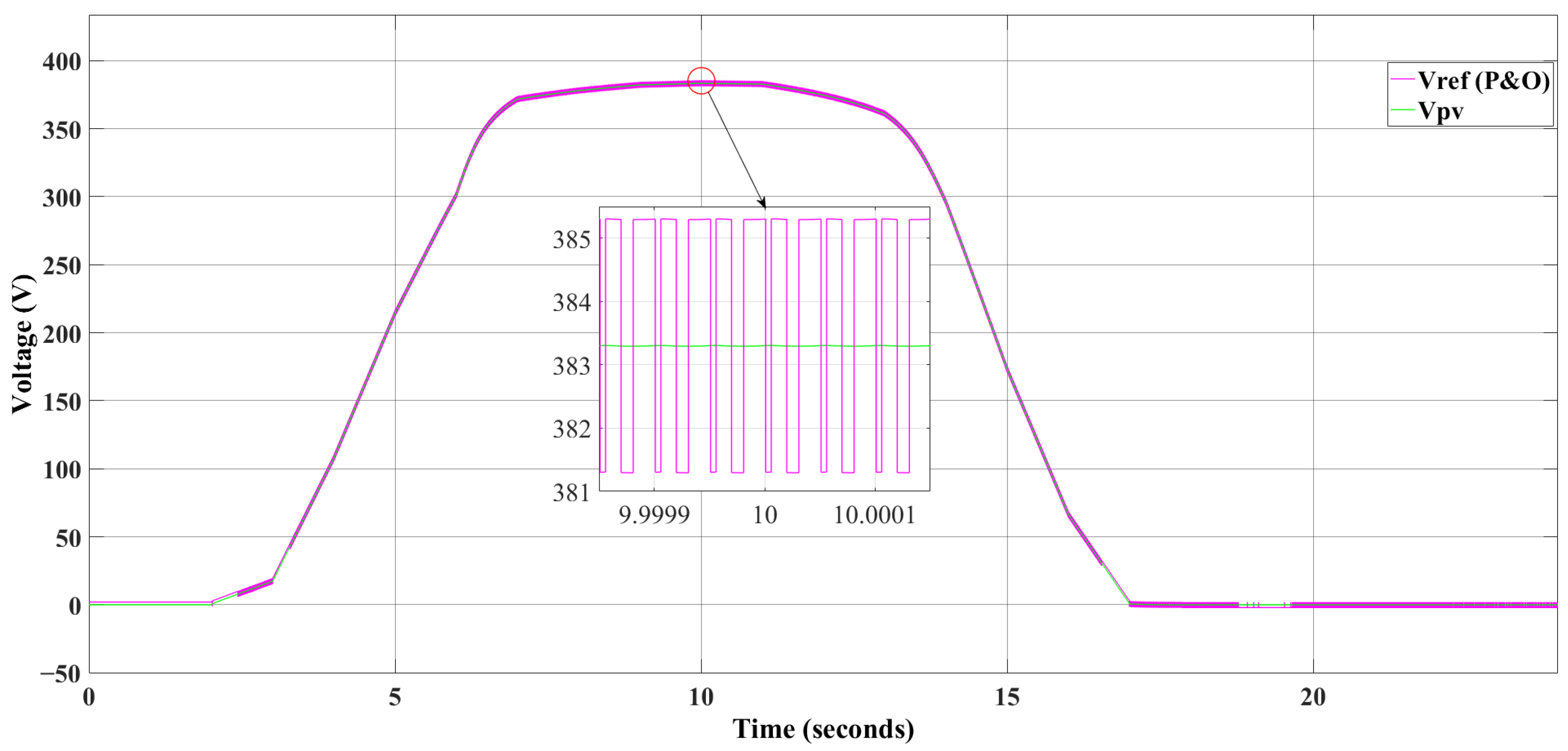
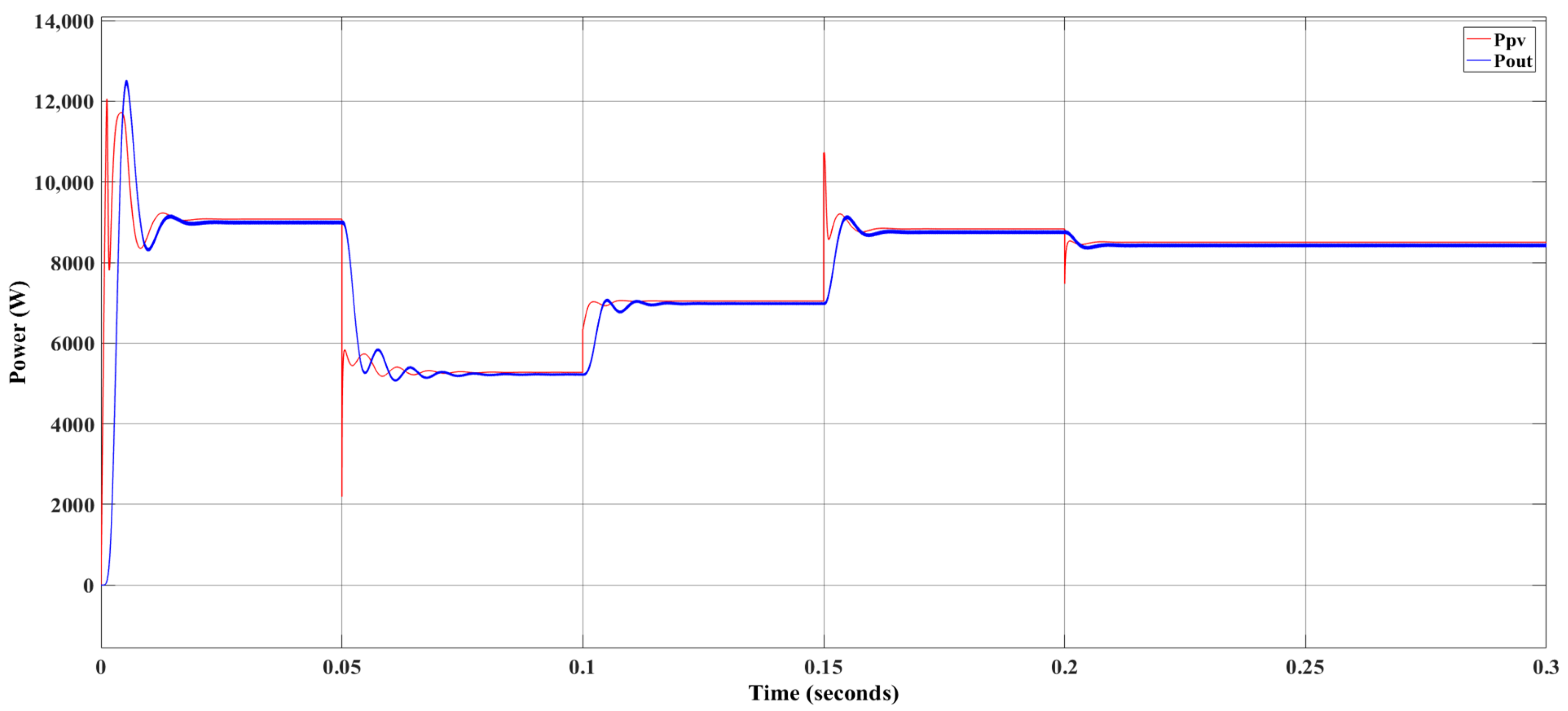
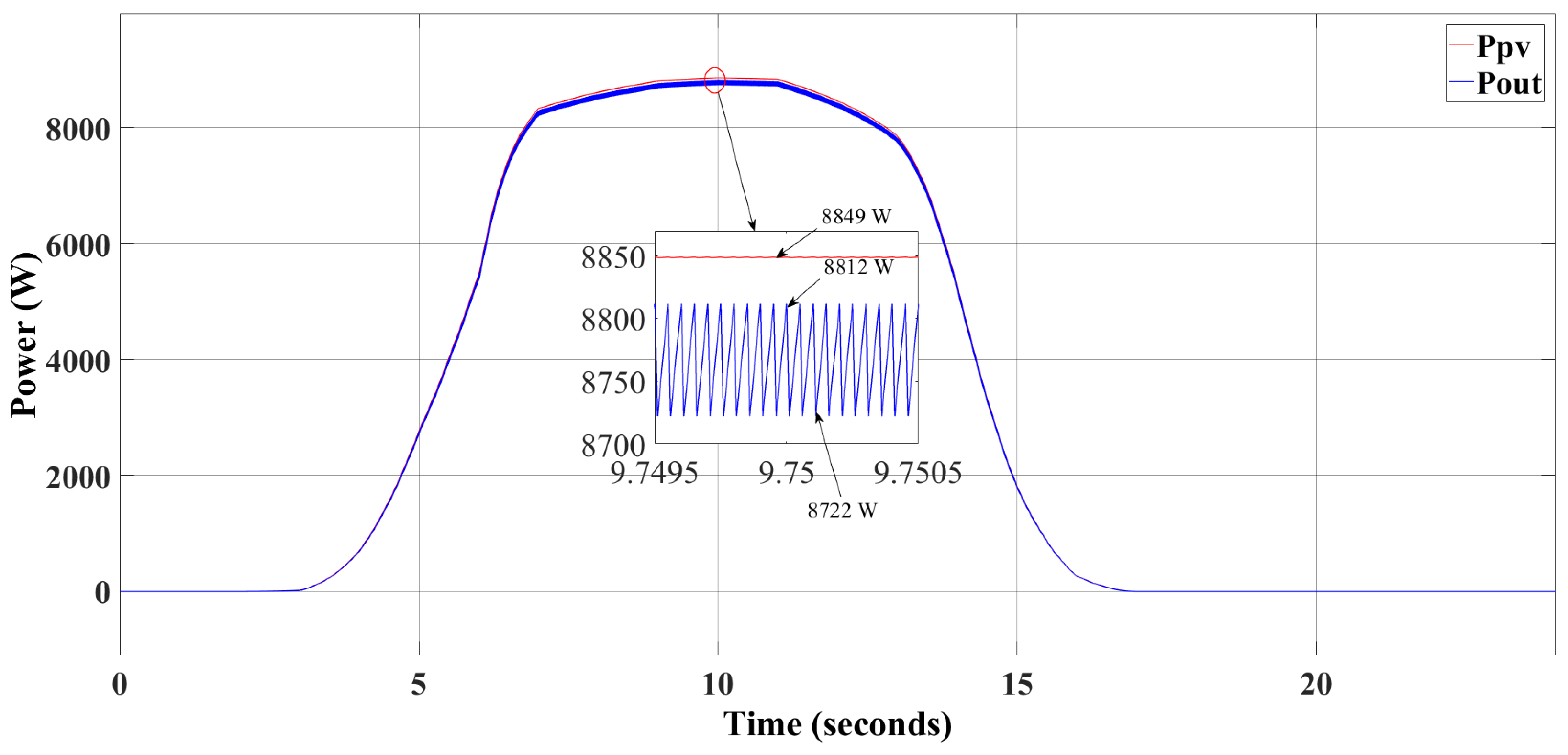
3.1. Operating Scenario of the Overall System: Perturb & Observe MPPT Algorithm
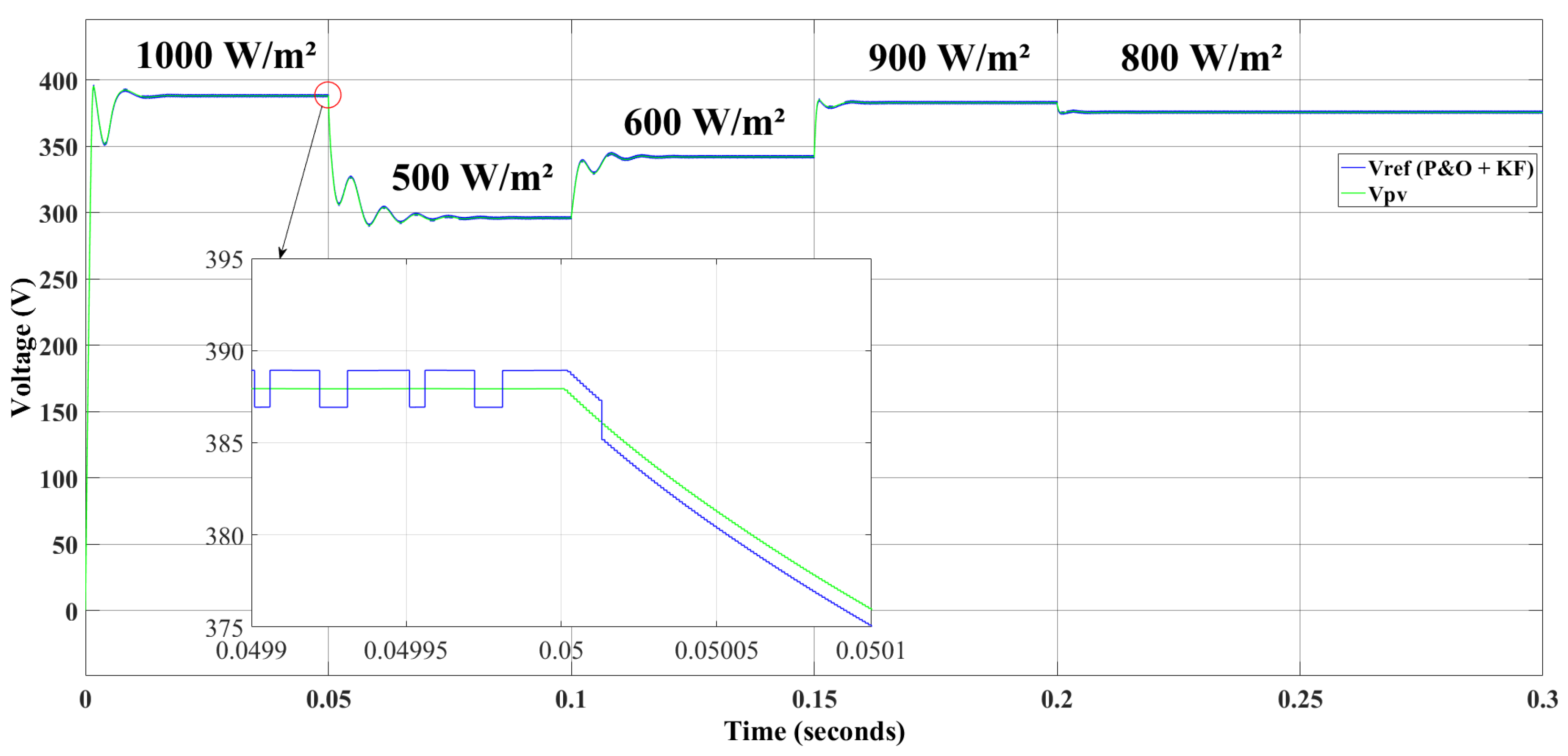
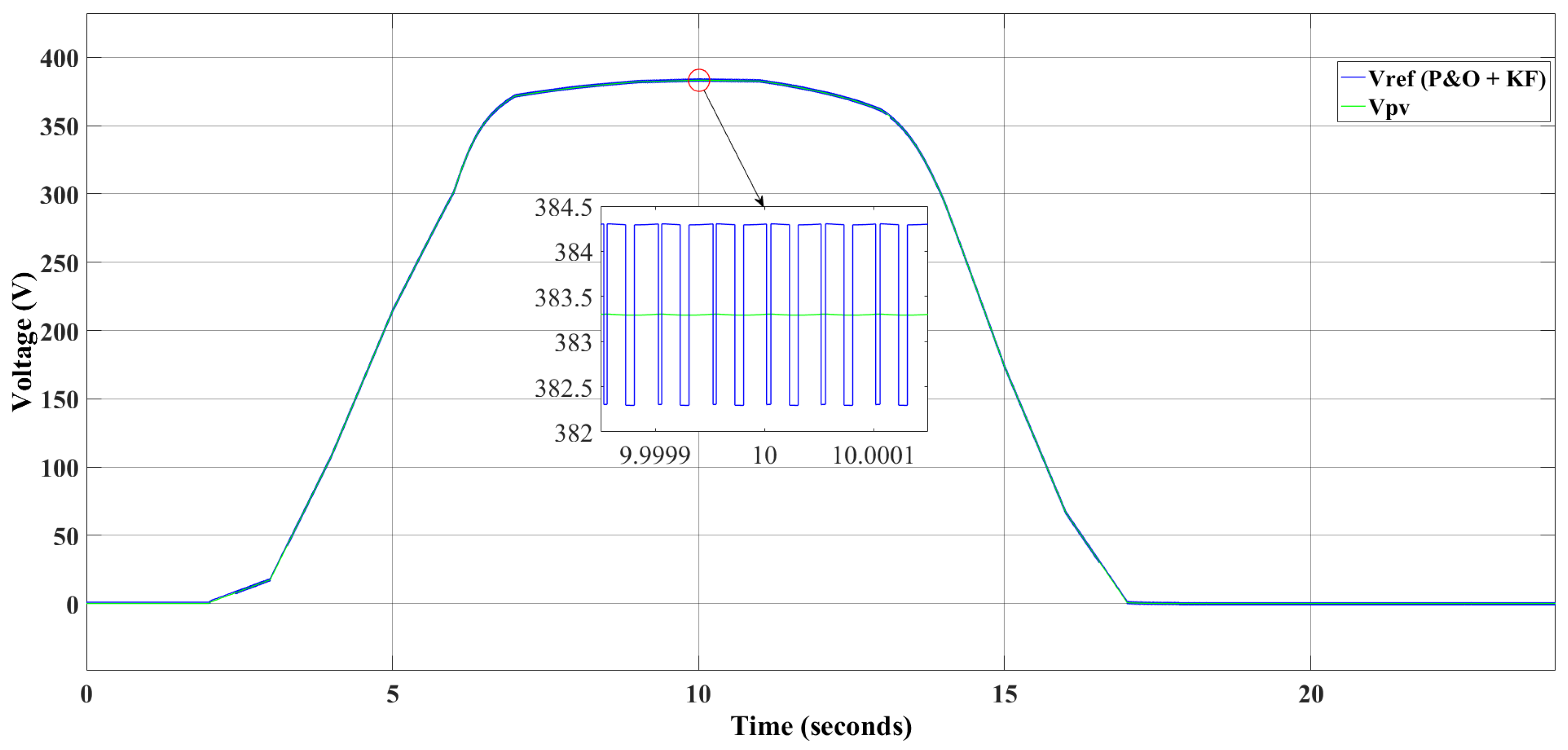
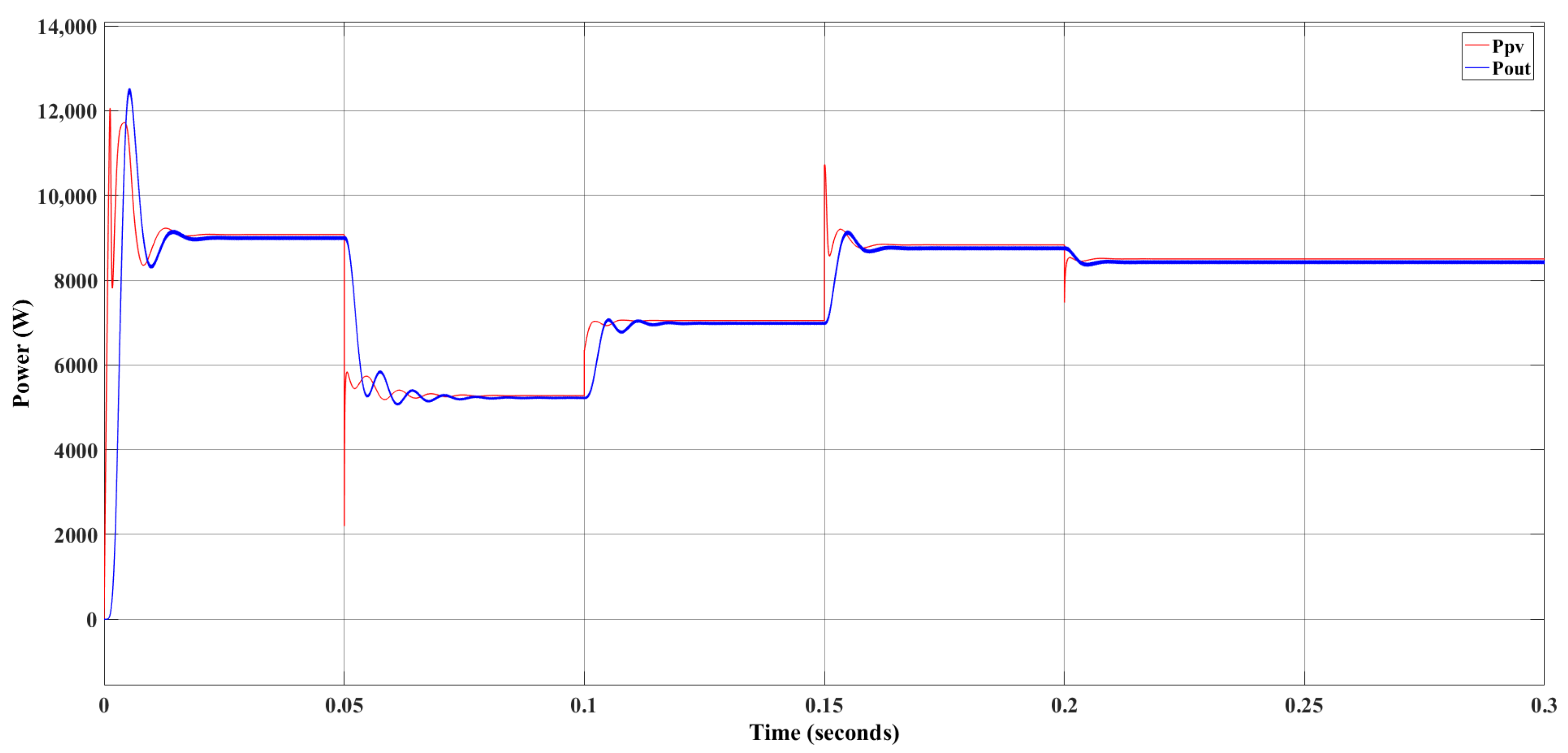
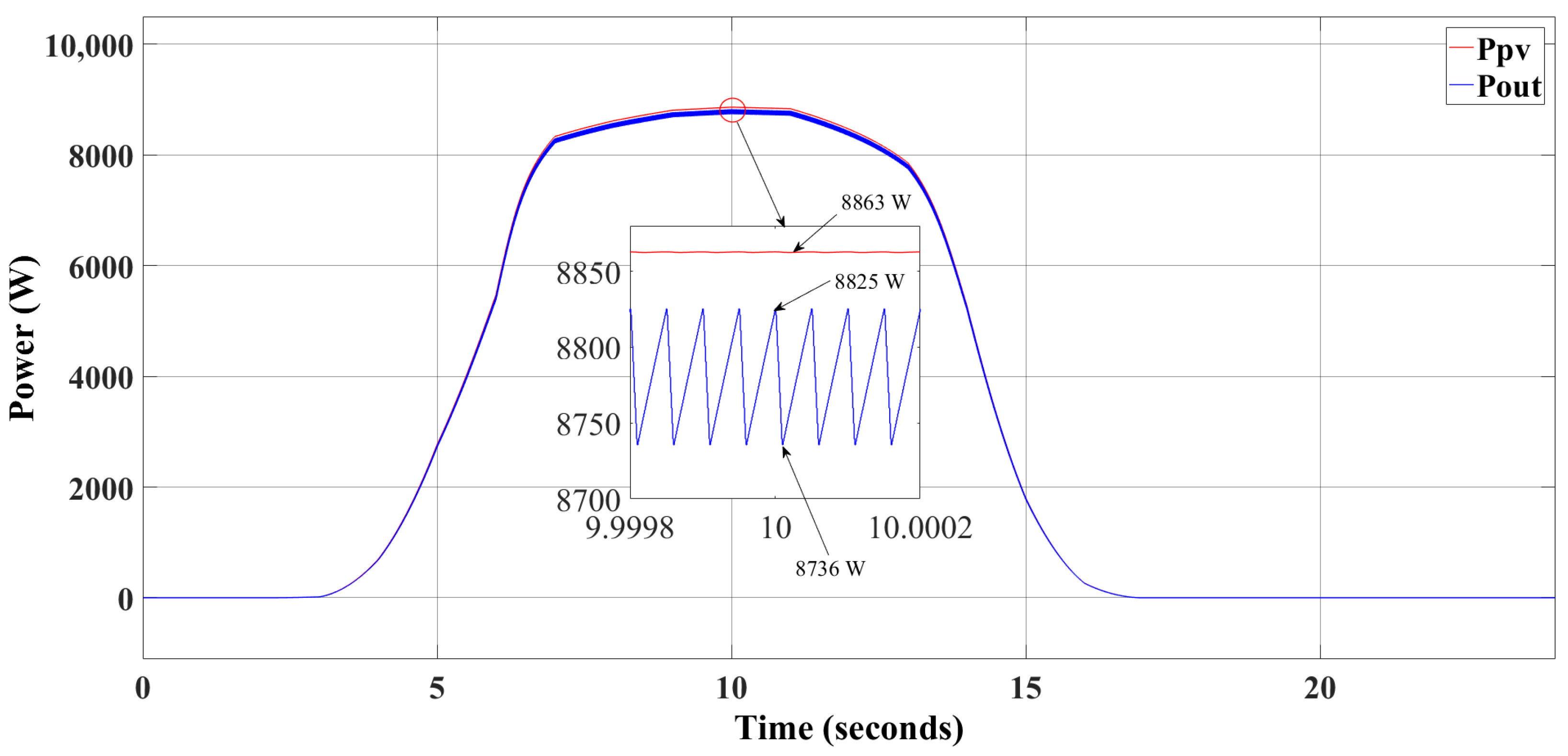
3.2. Operating Scenario of the Overall System: Kalman Filter and the Perturb & Observe Hybrid MPPT Algorithm
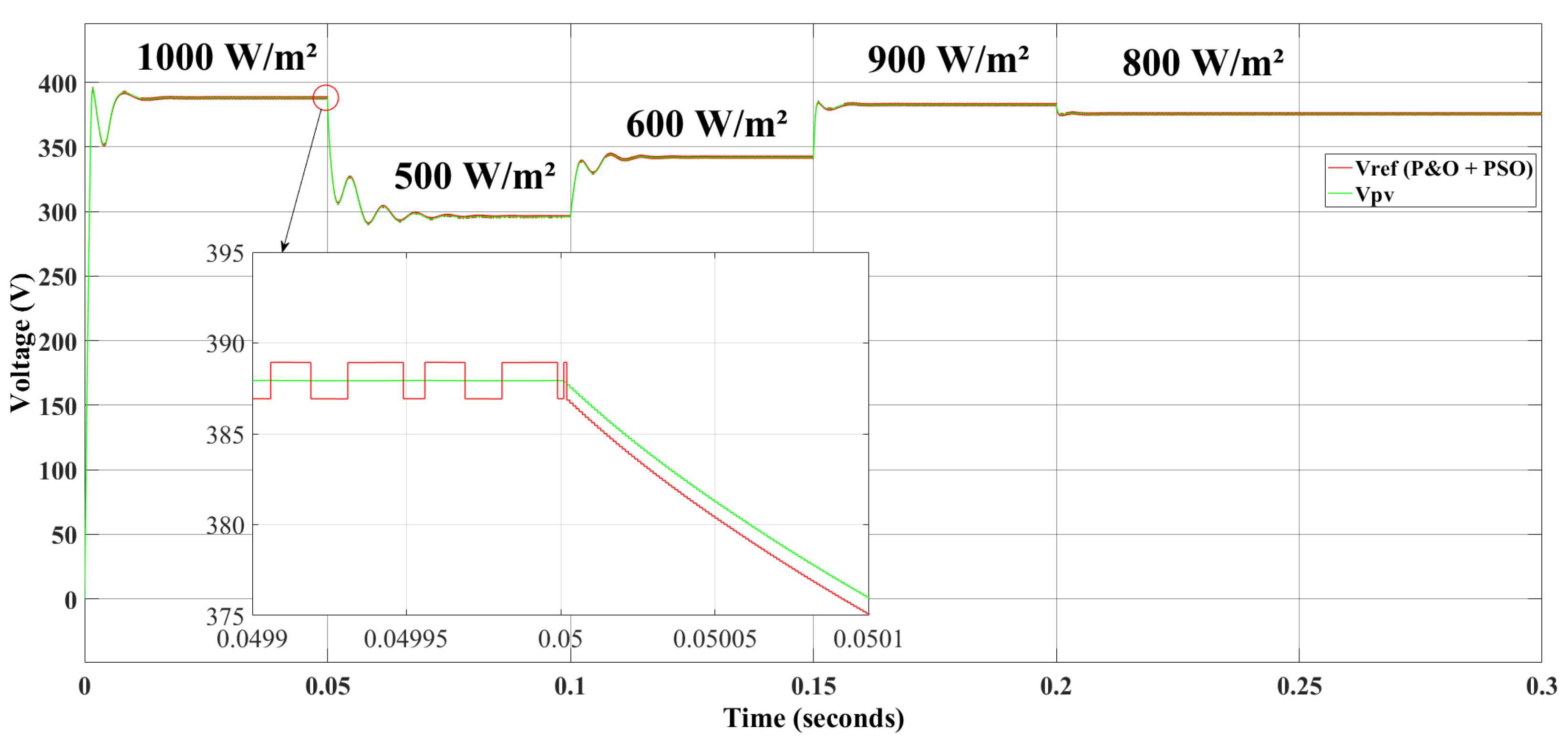
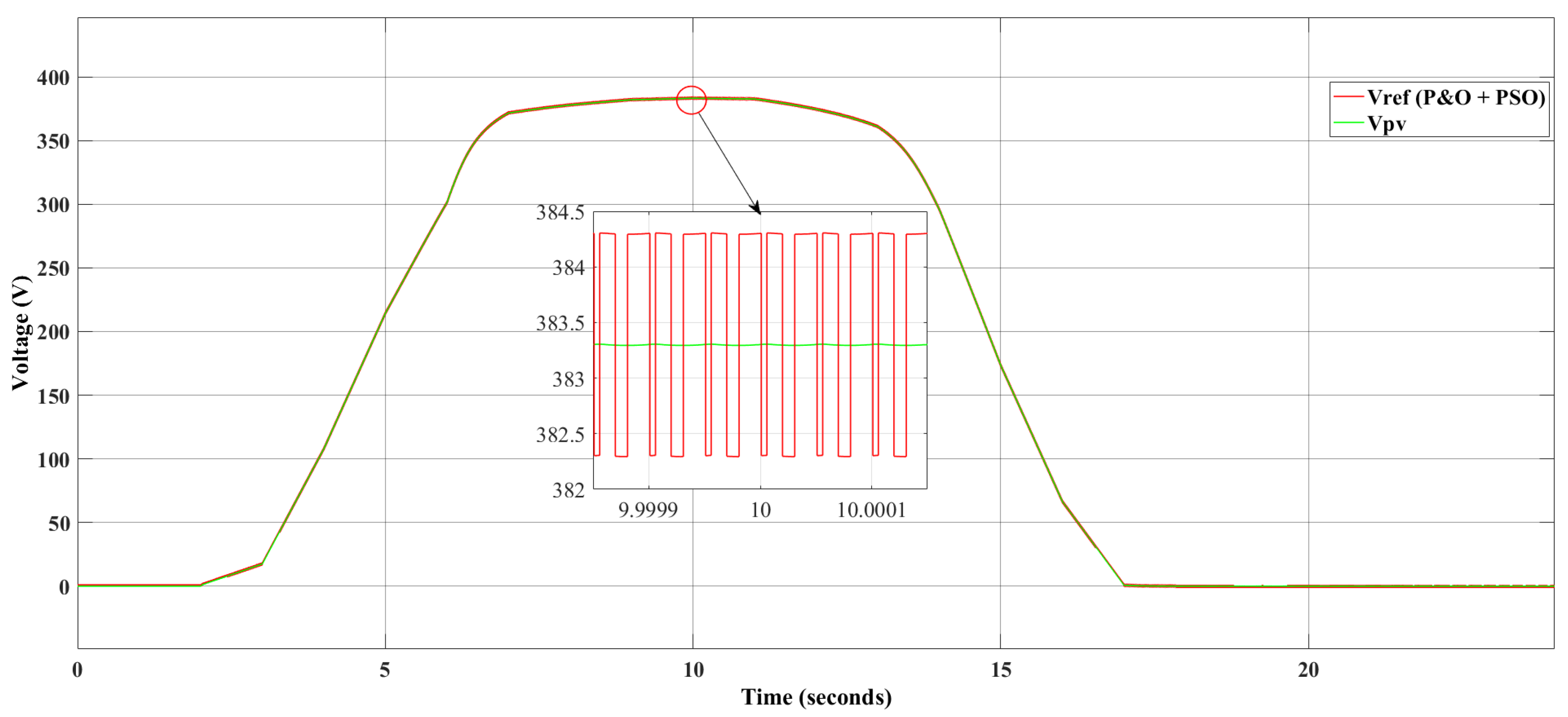
3.3. Operating Scenario of the Overall System: Perturb & Observe and Particle Swarm Optimization Hybrid MPPT Algorithm
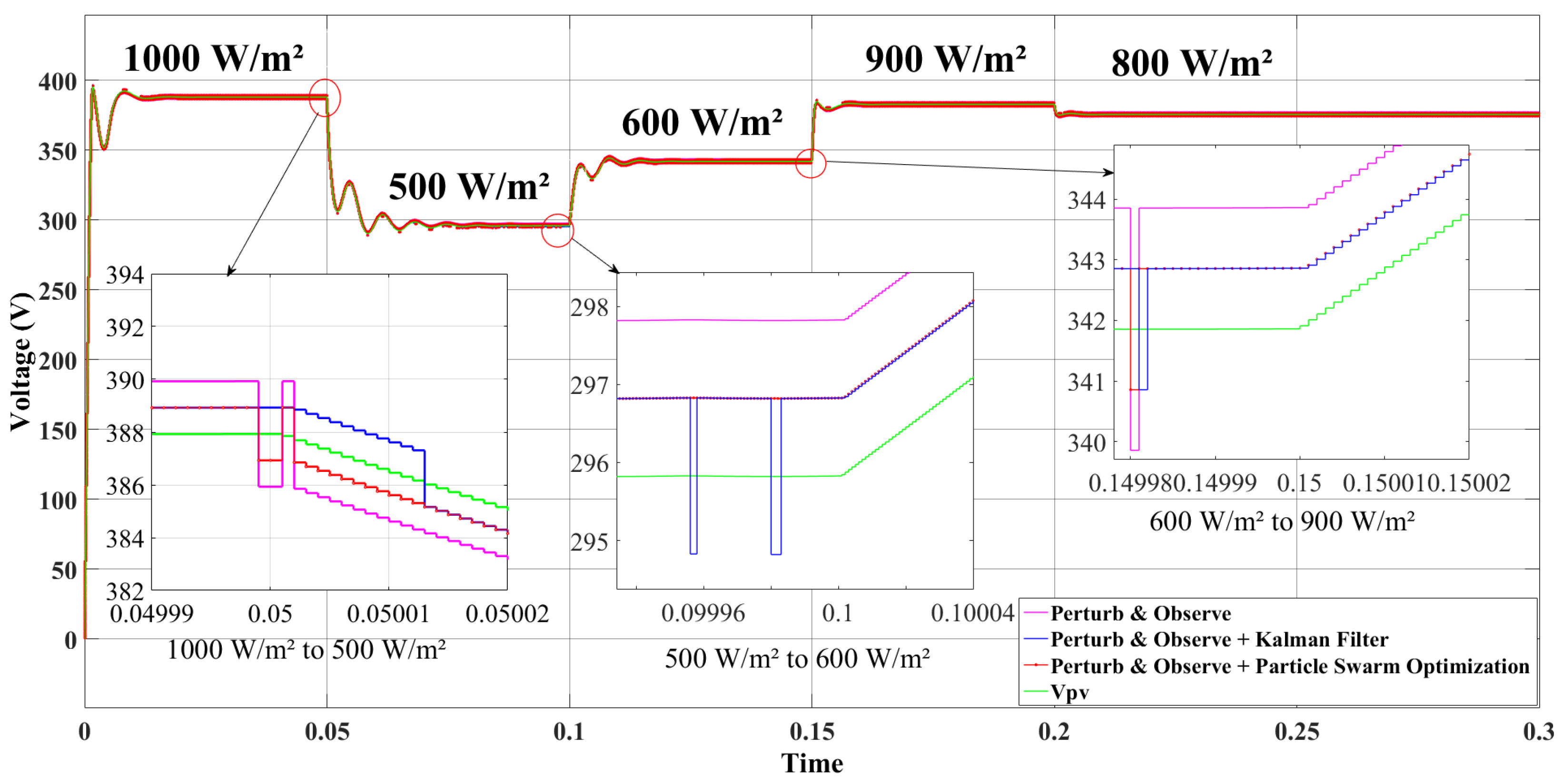
3.4. Comparison of the Proposed Method with the Other Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Networks |
| CPS | Crow Pattern Search |
| CS | Cuckoo Search |
| DE | Differential Evolution |
| FLC | Fuzzy Logic Controller |
| FOCV | Fractional Open Circuit Voltage |
| DE | Differential Evolution |
| FSCC | Fractional Short Circuit Current |
| GA | Genetic Algorithm |
| GWO | Grey Wolf Optimization |
| HC | Hill Climbing |
| IC | Incremental Conductance |
| IGBT | Insulated-Gate Bipolar Transistor |
| KF | Kalman Filter |
| LuT | Look up Table |
| MPC | Model Predictive Control |
| MPP | Maximum Power Point |
| MPPT | Maximum Power Point Tracking |
| P&O | Perturb & Observe |
| PI | Proportional-Integral |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| PWM | Pulse Width Modulation |
| SFLA | Shuffled Frog Leaping Algorithm |
| SSA | Salp Swarm Algorithm |
| STC | Standard Test Conditions |
| WO | Whale Optimization |
References
- El-Helw, H.M.; Magdy, A.; Marei, M.I. A hybrid maximum power point tracking technique for partially shaded photovoltaic arrays. IEEE Access 2017, 5, 11900–11908. [Google Scholar] [CrossRef]
- Joisher, M.; Singh, D.; Taheri, S.; Espinoza-Trejo, D.R.; Pouresmaeil, E.; Taheri, H. A hybrid evolutionary-based MPPT for photovoltaic systems under partial shading conditions. IEEE Access 2020, 8, 38481–38492. [Google Scholar] [CrossRef]
- Al-Ezzi, A.S.; Ansari, M.N.M. Photovoltaic solar cells: A review. Appl. Syst. Innov. 2022, 5, 67. [Google Scholar] [CrossRef]
- Dambhare, M.V.; Butey, B.; Moharil, S.V. Solar photovoltaic technology: A review of different types of solar cells and its future trends. In Proceedings of the International Conference on Research Frontiers in Sciences (ICRFS 2021), Nagpur, India, 5–6 February 2021. [Google Scholar]
- Gao, C.; Chen, H. Electricity from renewable energy resources: Sustainable energy transition and emissions for developed economies. Util. Policy 2023, 82, 101543–101554. [Google Scholar] [CrossRef]
- International Energy Agency. Global Energy Review 2025; Technical Report; International Energy Agency: Paris, France, 2025; Available online: https://www.iea.org/reports/global-energy-review-2025 (accessed on 25 June 2025).
- Motahhir, S.; Chtita, S.; Chouder, A.; Hammoumi, A.E. Enhanced energy output from a PV system under partial shaded conditions through grey wolf optimizer. Clean. Eng. Technol. 2022, 9, 100533–100543. [Google Scholar] [CrossRef]
- Singh, V.; Tiwari, A. Study and comparison of various types of converters used for solar PV: A review. In Proceedings of the 2018 International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018. [Google Scholar]
- Bingöl, O.; Özkaya, B. Analysis and comparison of different PV array configurations under partial shading conditions. Sol. Energy 2018, 160, 336–343. [Google Scholar] [CrossRef]
- Eke, R.; Demircan, C. Shading effect on the energy rating of two identical PV systems on a building façade. Sol. Energy 2015, 122, 48–57. [Google Scholar] [CrossRef]
- Schuss, C.; Kotikumpu, T.; Eichberger, B.; Rahkonen, T. Impact of dynamic environmental conditions on the output behaviour of photovoltaics. In Proceedings of the 20th IMEKO TC4 International Symposium and 18th International Workshop on ADC Modelling and Testing Research on Electric and Electronic Measurement for the Economic Upturn, Benevento, Italy, 15–17 September 2014. [Google Scholar]
- Kumari, P.A.; Geethanjali, P. Parameter estimation for photovoltaic system under normal and partial shading conditions: A survey. Renew. Sustain. Energy Rev. 2018, 84, 1–11. [Google Scholar] [CrossRef]
- Hahn, D.; Daßler, D.; Schindler, S.; Götz, D.; Gottschalg, R.; Dassler, D.; Hanifi, H. Evaluation of shading tolerance of PV modules with different module designs for mobile application by simulation, indoor and outdoor. In Proceedings of the 36th European Photovoltaic Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2019. [Google Scholar]
- Brecl, K.; Bokalič, M.; Topič, M. Annual energy losses due to partial shading in PV modules with cut wafer-based Si solar cells. Renew. Energy 2021, 168, 195–203. [Google Scholar] [CrossRef]
- Bi, Z.; Ma, J.; Man, K.; Smith, J.; Yue, Y.; Wen, H. Global MPPT method for photovoltaic systems operating under partial shading conditions using the 0.8 VOC model. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe, Genova, Italy, 11–14 June 2019. [Google Scholar]
- Trzmiel, G.; Głuchy, D.; Kurz, D. The impact of shading on the exploitation of photovoltaic installations. Renew. Energy 2020, 153, 480–498. [Google Scholar] [CrossRef]
- Torkian, F.; Ghandehari, R. Power recovery of the PV arrays under partial shading by a power electronic compensator. Sol. Energy 2022, 237, 284–292. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, T.; Wang, J.; Shu, H.; Yu, T.; Zhang, X.; Yao, W.; Sun, L. Comprehensive overview of maximum power point tracking algorithms of PV systems under partial shading condition. J. Clean. Prod. 2020, 268, 121983–122007. [Google Scholar] [CrossRef]
- Zhu, W.; Shang, L.; Li, P.; Guo, H. Modified hill climbing MPPT algorithm with reduced steady-state oscillation and improved tracking efficiency. J. Eng. 2018, 2018, 1878–1883. [Google Scholar] [CrossRef]
- Lasheen, M.; Abdel-Salam, M. Maximum power point tracking using hill climbing and ANFIS techniques for PV applications: A review and a novel hybrid approach. Energy Convers. Manag. 2018, 171, 1002–1019. [Google Scholar] [CrossRef]
- Motsoeneng, P.; Bamukunde, J.; Chowdhury, S. Comparison of perturb & observe and hill climbing MPPT schemes for PV plant under cloud cover and varying load. In Proceedings of the 10th International Renewable Energy Congress (IREC 2019), Sousse, Tunisia, 26–28 March 2019. [Google Scholar]
- Kwan, T.H.; Wu, X. The lock-on mechanism MPPT algorithm as applied to the hybrid photovoltaic cell and thermoelectric generator system. Appl. Energy 2017, 204, 873–886. [Google Scholar] [CrossRef]
- Sulthan, S.M.; Devaraj, D.; Sri Revathi, B.; Mohammed Mansoor, O.; Raj, V. Development and analysis of a two stage Hybrid MPPT algorithm for solar PV systems. Energy Rep. 2023, 9, 1502–1512. [Google Scholar] [CrossRef]
- Yüksek, G.; Mete, A.N. A hybrid variable step size MPPT method based on P&O and INC methods. In Proceedings of the 2017 10th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017. [Google Scholar]
- Irmak, E.; Güler, N. A model predictive control-based hybrid MPPT method for boost converters. Int. J. Electron. 2020, 107, 1–16. [Google Scholar] [CrossRef]
- Lemmassi, A.; Derouich, A.; Hanafi, A.; Byou, A.; Benmessaoud, M.; El Quanjli, N. Low-cost MPPT for triple-junction solar cells used in nanosatellites: A comparative study between P&O and INC algorithms. e-Prime—Adv. Electr. Eng. Electron. Energy 2024, 7, 100426. [Google Scholar] [CrossRef]
- Sher, H.A.; Murtaza, A.F.; Noman, A.; Addoweesh, K.E.; Al-Haddad, K.; Chiaberge, M. A new sensorless hybrid MPPT algorithm based on fractional short-circuit current measurement and P&O MPPT. IEEE Trans. Sustain. Energy 2015, 6, 1426–1434. [Google Scholar] [CrossRef]
- Shetty, D.; Sabhahit, J.N. Grey wolf optimization and incremental conductance based hybrid MPPT technique for solar powered induction motor driven water pump. Int. J. Renew. Energy Dev. 2024, 13, 52–61. [Google Scholar] [CrossRef]
- Chiu, C.S.; Ngo, S. Hybrid SFLA MPPT design for multi-module partial shading photovoltaic energy systems. Int. J. Electron. 2023, 110, 199–220. [Google Scholar] [CrossRef]
- Kacimi, N.; Grouni, S.; Idir, A.; Boucherit, M.S. New improved hybrid MPPT based on neural network-model predictive control-Kalman Filter for photovoltaic system. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 1230–1241. [Google Scholar] [CrossRef]
- Basiński, K.; Ufnalski, B.; Grzesiak, L.M. Hybrid MPPT algorithm for PV systems under partially shaded conditions using a stochastic evolutionary search and a deterministic hill climbing. Power Electron. Drives 2017, 2, 49–59. [Google Scholar] [CrossRef]
- Assam, B.; Messalti, S.; Harrag, A. New improved hybrid MPPT based on backstepping-sliding mode for PV system. J. Eur. Des Syst. Autom. 2019, 52, 317–323. [Google Scholar] [CrossRef]
- Rizzo, S.A.; Scelba, G. A hybrid global MPPT searching method for fast variable shading conditions. J. Clean. Prod. 2021, 298, 126775. [Google Scholar] [CrossRef]
- Ghosh, S. IBS - P&O hybrid MPPT algorithm for solar PV applications. In Proceedings of the 2019 IEEE PES GTD Grand International Conference and Exposition Asia (GTD Asia), Bangkok, Thailand, 19–23 March 2019. [Google Scholar]
- Tao, H.; Ghahremani, M.; Ahmed, F.W.; Jing, W.; Nazir, M.S.; Ohshima, K. A novel MPPT controller in PV systems with hybrid whale optimization-PS algorithm based ANFIS under different conditions. Control Eng. Pract. 2021, 112, 104809. [Google Scholar] [CrossRef]
- Hassan, A.; Bass, O.; Masoum, M.A. An improved genetic algorithm based fractional open circuit voltage MPPT for solar PV systems. Energy Rep. 2023, 9, 1535–1548. [Google Scholar] [CrossRef]
- Ncir, N.; Akchioui, N.E.; Fathi, A.E. Enhancing photovoltaic system modeling and control under partial and complex shading conditions using a robust hybrid DE-FFNN MPPT strategy. Renew. Energy Focus 2023, 47, 100504. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Norouzi, H.; Alkhalaf, S.; Ali, Z.M.; Dadfar, S.; Furukawa, N. Enhancement of MPPT controller in PV-BES system using incremental conductance along with hybrid crow-pattern search approach based ANFIS under different environmental conditions. Sustain. Energy Technol. Assess. 2022, 50, 101812. [Google Scholar] [CrossRef]
- Hilali, A.; El Marghichi, M.; Makhad, M.; Loulijat, A.; El Quanjli, N.; Mossa, M.A.; Almalki, M.M.; Alghamdi, T.A.H. Optimization of solar water pumping systems through a combined approach based on MPPT-Bat and DTC. PLoS ONE 2024, 19, e0309330. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A grey wolf-assisted perturb & observe MPPT algorithm for a PV system. IEEE Trans. Energy Convers. 2017, 32, 340–347. [Google Scholar] [CrossRef]
- Chao, K.H.; Rizal, M.N. A hybrid MPPT controller based on the genetic algorithm and ant colony optimization for photovoltaic systems under partially shaded conditions. Energies 2021, 14, 2902. [Google Scholar] [CrossRef]
- Salim, J.A.; Albaker, B.M.; Alwan, M.S.; Hasanuzzaman, M. Hybrid MPPT approach using cuckoo search and grey wolf optimizer for PV systems under variant operating conditions. Glob. Energy Interconnect. 2022, 5, 627–644. [Google Scholar] [CrossRef]
- Elymany, M.M.; Enany, M.A.; Elsonbaty, N.A. Hybrid optimized-ANFIS based MPPT for hybrid microgrid using zebra optimization algorithm and artificial gorilla troops optimizer. Energy Convers. Manag. 2024, 299, 117809. [Google Scholar] [CrossRef]
- Nabipour, M.; Razaz, M.; Seifossadat, S.G.; Mortazavi, S.S. A new MPPT scheme based on a novel fuzzy approach. Renew. Sustain. Energy Rev. 2017, 74, 1147–1169. [Google Scholar] [CrossRef]
- Rizzo, S.A.; Salerno, N.; Scelba, G.; Sciacca, A. Enhanced hybrid global MPPT algorithm for PV systems operating under fast-changing partial shading conditions. Int. J. Renew. Energy Res. 2018, 8, 221–229. [Google Scholar] [CrossRef]
- Padmanaban, S.; Priyadarshi, N.; Bhaskar, M.S.; Holm-Nielsen, J.B.; Ramachandaramurthy, V.K.; Hossain, E. A hybrid ANFIS-ABC based MPPT controller for PV system with anti-islanding grid protection: Experimental realization. IEEE Access 2019, 7, 103377–103389. [Google Scholar] [CrossRef]
- Çelik, Ö.; Teke, A. A hybrid MPPT method for grid connected photovoltaic systems under rapidly changing atmospheric conditions. Electr. Power Syst. Res. 2017, 152, 194–210. [Google Scholar] [CrossRef]
- Li, Y.; Samad, S.; Ahmed, F.W.; Abdulkareem, S.S.; Hao, S.; Rezvani, A. Analysis and enhancement of PV efficiency with hybrid MSFLA–FLC MPPT method under different environmental conditions. J. Clean. Prod. 2020, 271, 122195. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Holm-Nielsen, J.B.; Blaabjerg, F.; Bhaskar, M.S. An experimental estimation of hybrid ANFIS-PSO-based MPPT for PV grid integration under fluctuating sun irradiance. IEEE Syst. J. 2020, 14, 1218–1229. [Google Scholar] [CrossRef]
- Mezdi, K.E.; Magri, A.E.; Watil, A.; Myasse, I.E.; Bahatti, L.; Lajouad, R.; Ouabi, H. Nonlinear control design and stability analysis of hybrid grid-connected photovoltaic-battery energy storage system with ANN-MPPT method. J. Energy Storage 2023, 72, 108747. [Google Scholar] [CrossRef]
- Ge, X.; Ahmed, F.W.; Rezvani, A.; Aljojo, N.; Samad, S.; Foong, L.K. Implementation of a novel hybrid BAT-fuzzy controller based MPPT for grid-connected PV-battery system. Control Eng. Pract. 2020, 98, 104380. [Google Scholar] [CrossRef]
- Pradhan, C.; Senapati, M.K.; Malla, S.G.; Nayak, P.K.; Gjengedal, T. Coordinated power management and control of standalone PV-hybrid system with modified IWO-based MPPT. IEEE Syst. J. 2020, 15, 3585–3596. [Google Scholar] [CrossRef]
- Balaji, V.; Fathima, A.P. Hybrid algorithm for MPPT tracking using a single current sensor for partially shaded PV systems. Sustain. Energy Technol. Assess. 2022, 53, 102415. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Hu, Z.; Norouzi, H.; Jiang, M.; Dadfar, S.; Kashiwagi, T. Novel hybrid modified krill herd algorithm and fuzzy controller based MPPT to optimally tune the member functions for PV system in the three-phase grid-connected mode. ISA Trans. 2022, 129, 214–229. [Google Scholar] [CrossRef]
- Boujelben, N.; Masmoudi, F.; Djemel, M.; Derbel, N. Design and comparison of quadratic boost and double cascade boost converters with boost converter. In Proceedings of the 2017 14th International Multi-Conference on Systems, Signals & Devices (SSD), Marrakech, Morocco, 28–31 March 2017. [Google Scholar]
- Adnan, M.F.; Oninda, M.A.M.; Nishat, M.M.; Islam, N. Design and simulation of a DC-DC boost converter with PID controller for enhanced performance. Int. J. Eng. Res. Technol. (IJERT) 2017, 6, 27–32. [Google Scholar] [CrossRef]
- Neto, D.T.S.; Salles, M.B.C.; Salazar, P.D.P.; Cardoso, J.R. A Kalman Filter based MPPT algorithm. SBSE2020 2021, 1, 1–6. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Yatim, A.H.; Yusuf, S.T. An improved PSO-based MPPT control strategy for photovoltaic systems. Int. J. Photoenergy 2014, 2014, 818232. [Google Scholar] [CrossRef]


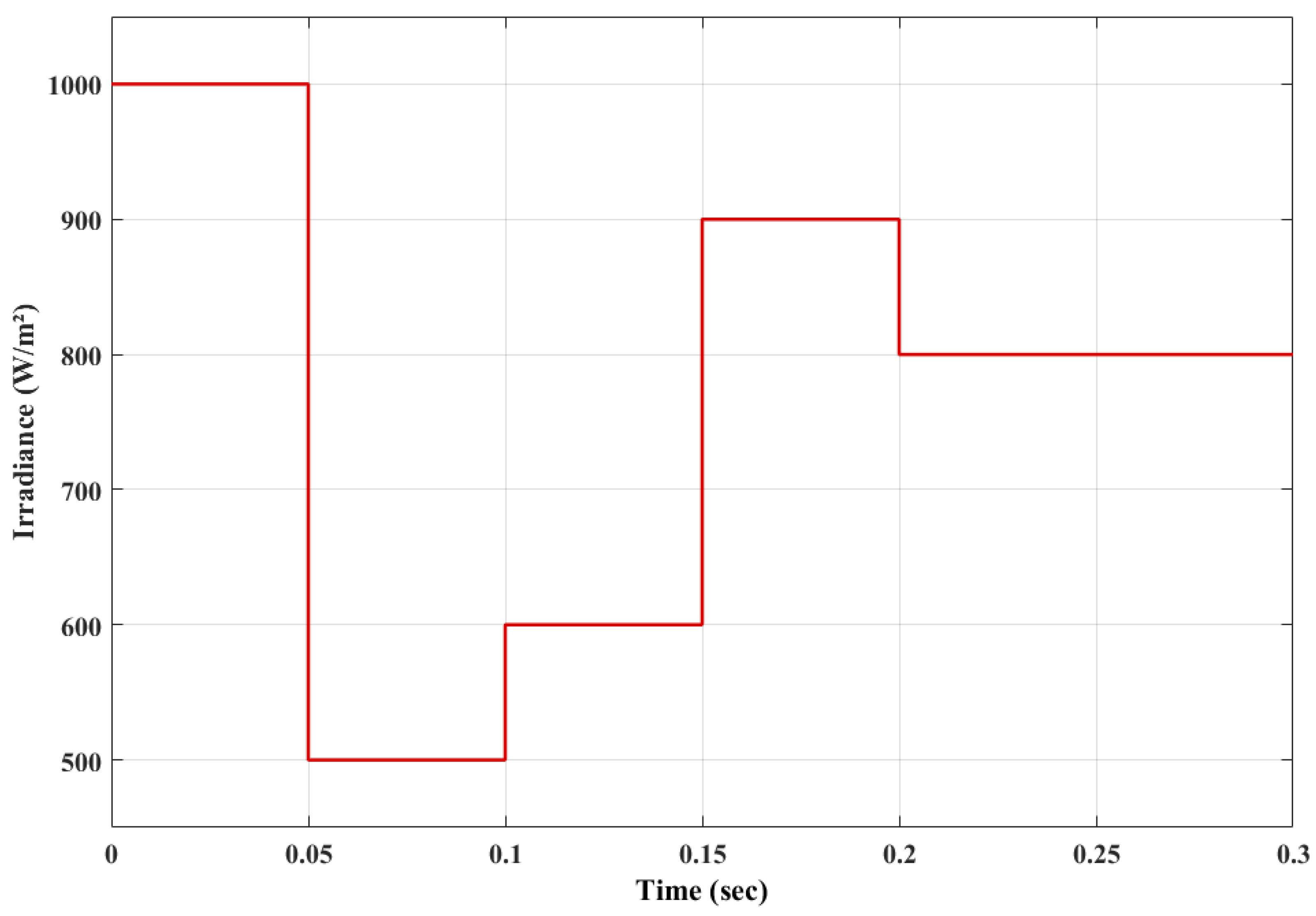
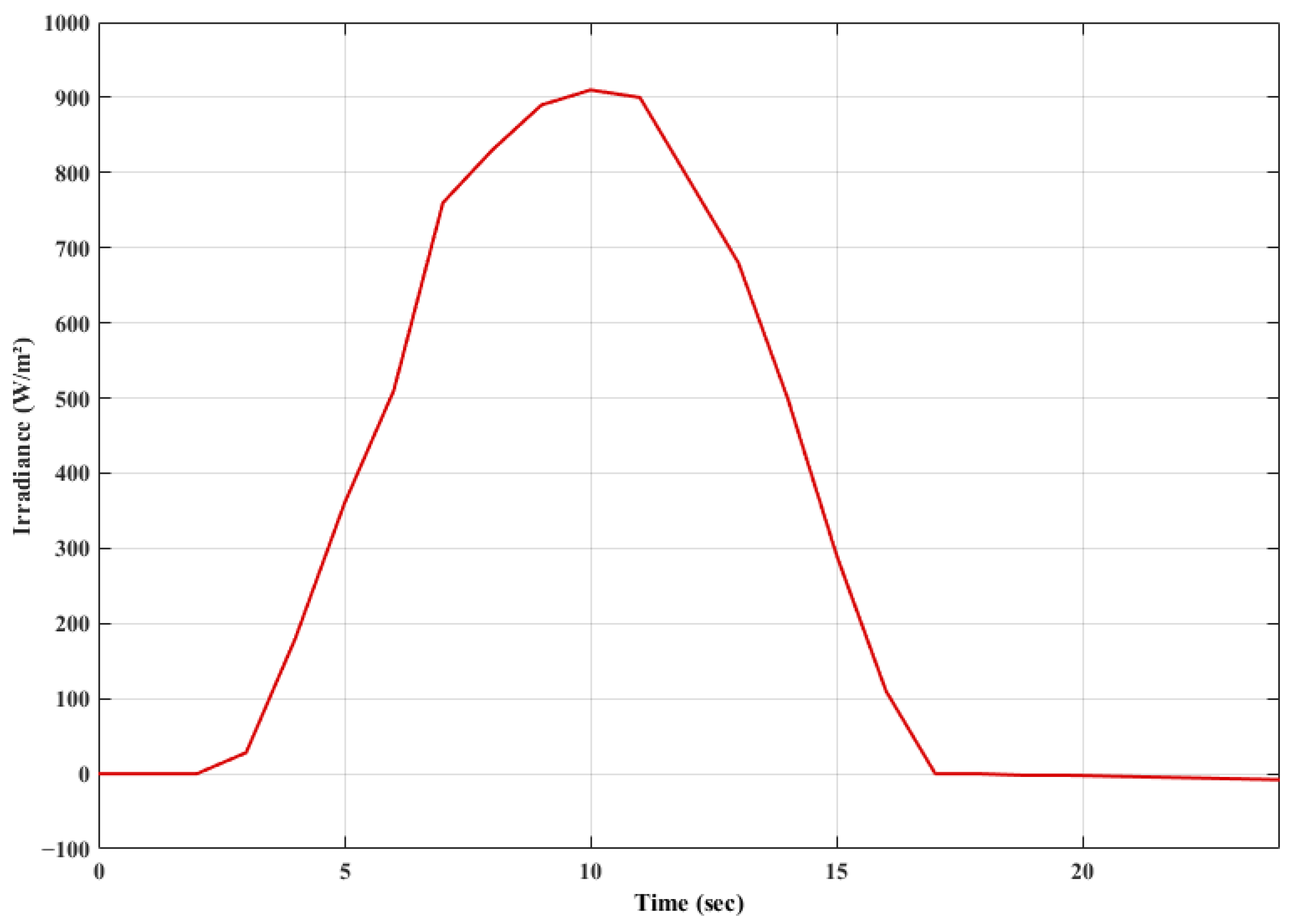
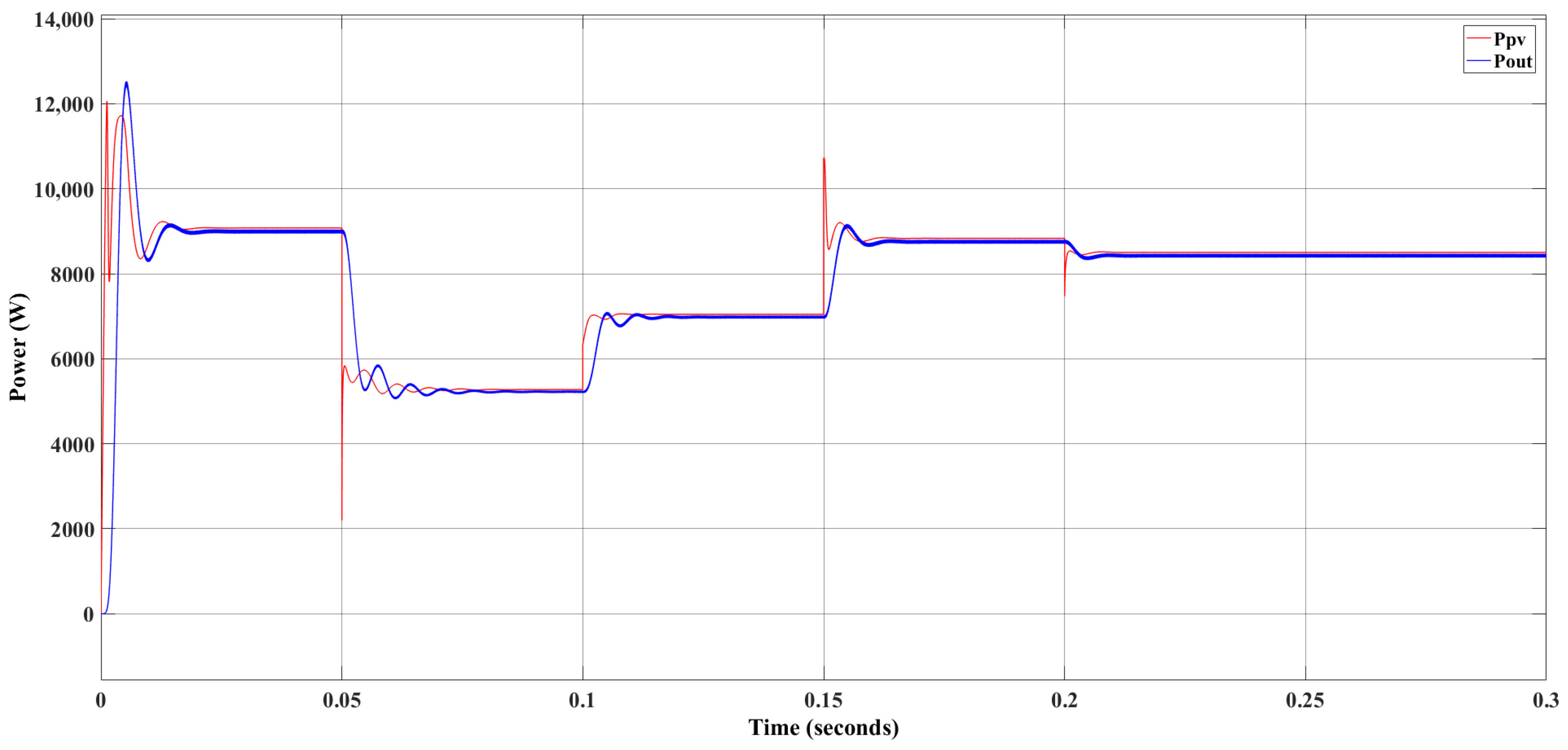
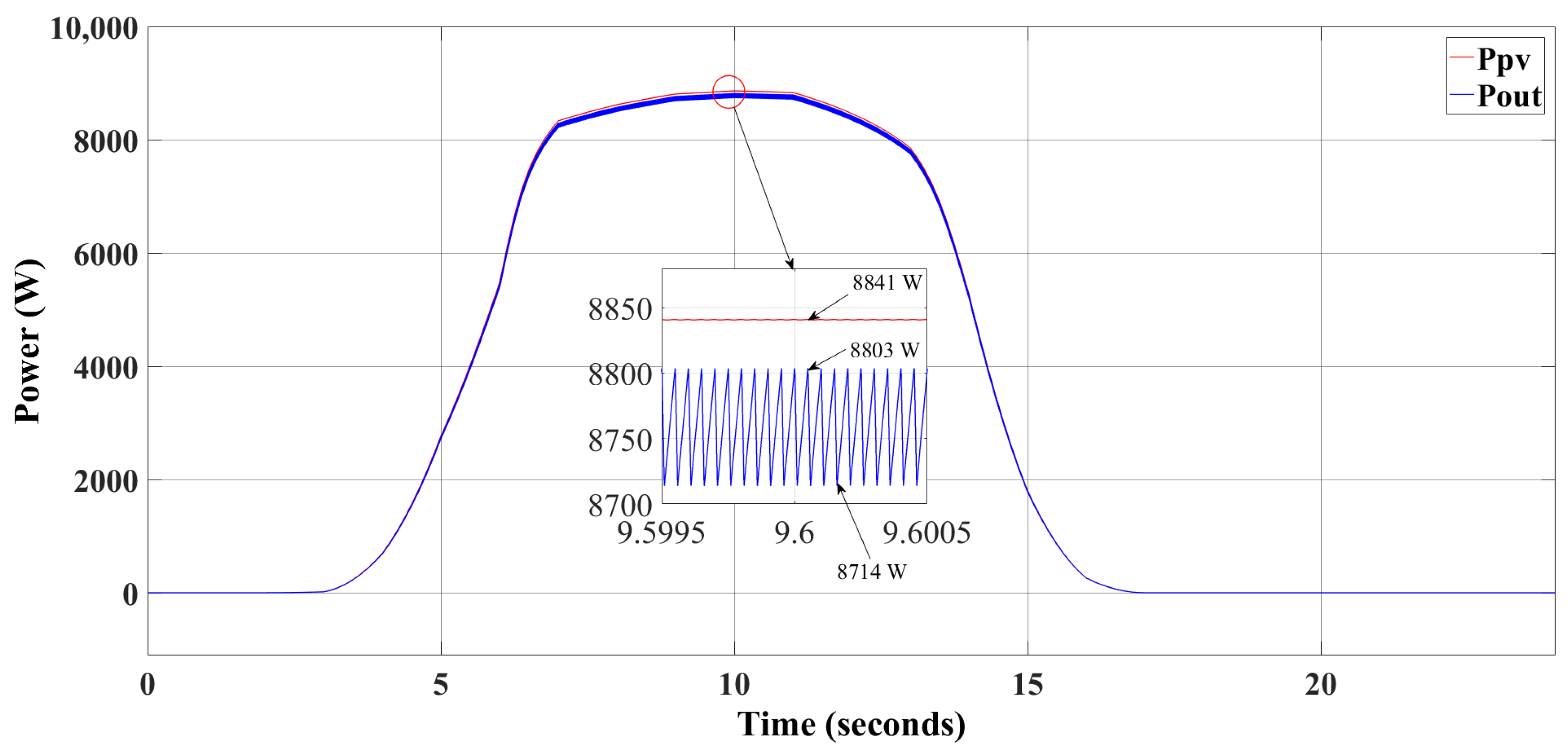

| MPPT Algorithm | Merits | Demerits |
|---|---|---|
| Lock-On Mechanism MPPT [23] | Low MPP tracking oscillation, high performance, steady performance, adaptive duty cycle ratio measurement. | Computational complexity, need for two SEPIC converters, need to extra equipments. |
| P&O-LuT Hybrid MPPT [24] | Fast MPP tracking, fast response to changes in weather conditions, high MPPT accuracy, high efficiency. | Need for extra memory. |
| Variable Step Size MPPT based on P&O and IC [25] | Low MPP tracking oscillation, fast MPP tracking, dynamic step size. | Processing load due to continuous calculation of the number of steps. |
| P&O-MPC Hybrid MPPT [26] | Fast response time, high performance, high efficiency, control without comparison structure. | Processing load due to the number of steps, computational complexity. |
| P&O and IC MPPT [27] | Low cost system design, easy to apply MPPT, high MPPT accuracy, high efficiency, appropriate to changes in weather conditions. | Special equipment may be required for spatial conditions. |
| P&O-FSCC Hybrid MPPT [28] | Fast MPP tracking, high efficiency, appropriate for changes in weather conditions, irradiance sensorless structure, intelligent weather forecasting. | Need for fast switching equipment, temporary cancellation of PV panel and possibility of power loss. |
| GWO-IC Hybrid MPPT [29] | Fast MPP tracking, fast response to changes in weather conditions, high efficiency. | Processing load due to continuous calculation of the number of steps, need special parameter selection required. |
| SFLA-IC Hybrid MPPT [30] | Low computational time, low computational complexity, steady performance. | Processing load due to the number of steps and may require good hardware, special parameter selection required. |
| ANN-MPC-KF Hybrid MPPT [31] | Fast response to changes in weather conditions, low overshoot, high performance, high power output, high efficiency, fast MPP tracking, high MPPT accuracy. | Processing load due to the number of steps and may require good hardware, the ANN algorithm may need to be trained with sufficient data, special parameter selection required. |
| Stochastic Evolutionary Search-Specific HC MPPT [32] | Low cost system design, low computational complexity. | Special parameter selection required. |
| Backstepping-Sliding Mode MPPT [33] | Low MPP tracking oscillation, low overshoot, high performance. | Computational complexity, processing load due to the number of steps and may require good hardware. |
| Hybrid Two-Stage Global MPPT [34] | Fast response to changes in weather conditions, low energy usage, appropriate to changes in weather conditions. | The ANN algorithm may need to be trained with sufficient data. |
| Improvised Binary Sequence-P&O Hybrid MPPT [35] | Fast response to changes in weather conditions, appropriate to changes in weather conditions, precise MPP tracking. | Special limitation selection required. |
| WO-Pattern Search Algorithm based on ANFIS [36] | High power output, high efficiency, fast MPP tracking. | Computational complexity, the ANFIS algorithm may need to be trained with sufficient data, special parameter selection required. |
| GA based FOCV MPPT [37] | Fast MPP tracking, high efficiency, low MPP tracking oscillation. | Computational complexity, special parameter selection required. |
| DE-Feed Forward Neural Network Hybrid MPPT [38] | Fast MPP tracking, high efficiency, precise MPP tracking. | Computational complexity, the Feed Forward Neural Network algorithm may need to be trained with sufficient data, processing load due to the number of steps and may require good hardware. |
| ANFIS based CPS-IC Hybrid MPPT [39] | High output power, low sampling rate, low power ripple. | Computational complexity, the ANFIS algorithm may need to be trained with sufficient data, special parameter selection required. |
| Bat Metaheuristic Optimizer MPPT [40] | Low MPP tracking error, low MPP tracking oscillation, fast MPP tracking, fast response to changes in weather conditions, high efficiency. | Computational complexity, need to extra sensors, special parameter selection required. |
| GWO-P&O Hybrid MPPT [41] | Fast MPP tracking, precise MPP tracking, high MPPT accuracy. | Processing load due to number of steps, special parameter selection required. |
| Genetic Algorithm-Ant Bee Colony Hybrid MPPT [42] | High MPPT accuracy, low computational time, few calculation steps. | Processing load due to the number of steps and may require good hardware, special parameter selection required. |
| CS-GWO Hybrid MPPT [43] | Fast MPP tracking, zero oscillation in constant state, more effectiveness than GWO, highly dependable. | Computational complexity, special parameter selection required. |
| Zebra Optimization Algorithm and Artificial Gorilla Troops Optimization based ANFIS MPPT [44] | High performance, low computational time, effective hybrid design. | Computational complexity, the ANFIS algorithm may need to be trained with sufficient data, special parameter selection required. |
| Adaptive Fuzzy Logic Controller MPPT [45] | High MPPT accuracy, high performance, low power ripple. | Special parameter selection required, risk of control complexity. |
| ANN-HC Hybrid MPPT [46] | Low computational comlexity, few equipment needed, appropriate to changes in weather conditions. | The ANN algorithm may need to be trained with sufficient data. |
| ANFIS-Ant Bee Colony Hybrid MPPT [47] | Low total harmonic distortion, safe grid connection, fast response to changes in weather conditions, high efficiency, precise MPP tracking. | Processing load due to the number of steps and may require good hardware, the ANFIS algorithm may need to be trained with sufficient data, special parameter selection required. |
| P&O-ANN Hybrid MPPT [48] | High power factor, low total harmonic distortion, precise MPP tracking, low oscillation in a steady state, fast MPP tracking, high efficiency, appropriate to changes in weather conditions. | The ANN algorithm may need to be trained with sufficient data, special parameter selection required. |
| MSFLA-FLC Hybrid MPPT [49] | Precise MPP tracking, high efficiency, fast MPP tracking, high power output, integration of battery energy storage. | Computational complexity, special parameter selection required. |
| ANFIS-PSO Hybrid MPPT [50] | Precise MPP tracking, fast MPP tracking, low total harmonic distortion, low computational comlexity, no need for extra sensors, zeta converter integration. | Processing load due to the number of steps and may require good hardware, the ANFIS algorithm may need to be trained with sufficient data, special parameter selection required. |
| ANN MPPT [51] | Few measurements, precise MPP tracking, low MPP tracking error, fast response to changes in weather conditions, integration of battery energy storage. | Computational complexity, the ANN algorithm may need to be trained with sufficient data. |
| Bat-Fuzzy Logic Hybrid MPT [52] | High efficiency, fast response to changes in weather conditions, low MPP tracking oscillation, precise MPP tracking, high MPPT accuracy, easy to implement, integration of the grid and batteries. | Special parameter selection required, risk of control complexity. |
| Modified Invasive Weed Optimization-P&O Hybrid MPPT [53] | Low voltage ripple, high MPPT accuracy, grid-compatible. | Processing load due to the number of steps and may require good hardware. |
| SSA-P&O Hybrid MPPT [54] | Fast MPP tracking, low MPP tracking oscillation, appropriate to changes in weather conditions, easy to implement, needs only one sensor. | Computational complexity, special parameter selection required. |
| Musical Chair MPPT [55] | High performance, low computational time, low oscillation in steady state, high MPPT accuracy. | Special parameter selection required. |
| Modified Krill Swarm Algorithm-FLC Hybrid MPPT [56] | Precise MPP tracking, fast response to changes in weather conditions, dependable power source. | Computational complexity, special parameter selection required. |
| Parameter | Value |
|---|---|
| Maximum Output Power at STC | 11.76 kW (Pmax) |
| Number of Panels (Series) | 7 |
| Number of Strings (Parallel) | 4 |
| Total Number of Panels | 28 |
| Total Output Voltage | 346.71 V (Vmpp) |
| Total Output Current | 33.92 A (Impp) |
| Parameter | Value |
|---|---|
| Input Voltage (Vin) | 346.71 V |
| Output Voltage (Vout) | 540 V |
| Input Current (Iin) | 33.92 A |
| Output Current (Iout) | 21.78 A |
| Voltage Ripple () | 5.4 V |
| Current Ripple () | 2.18 A |
| Inductor Value (L) | 0.018 H |
| Capacitor Value (C) | 72.18 µF |
| Load Resistor Value (RL) | 24.79 Ω |
| Inductor Current Ripple () | 0.34 A |
| Switching Frequency (fsw) | 20 kHz |
| MPPT | Energy Production at MPP |
|---|---|
| Perturb & Observe MPPT | 8.825 kWh |
| Perturb & Observe and Kalman Filter Hybrid MPPT | 8.812 kWh |
| Proposed Perturb & Observe and Particle Swarm Optimization Hybrid MPPT | 8.803 kWh |
| MPPT Algorithm | Undershoot Voltage | Convergence Time | Tracking Accuracy |
|---|---|---|---|
| Perturb & Observe MPPT | 3 V | 8 ms | Medium |
| Perturb & Observe and Kalman Filter Hybrid MPPT | 2 V | 6 ms | Medium |
| Proposed Perturb & Observe and Particle Swarm Optimization Hybrid MPPT | 1.5 V | 5 ms | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Timur, O.; Uzundağ, B.K. Design and Analysis of a Hybrid MPPT Method for PV Systems Under Partial Shading Conditions. Appl. Sci. 2025, 15, 7386. https://doi.org/10.3390/app15137386
Timur O, Uzundağ BK. Design and Analysis of a Hybrid MPPT Method for PV Systems Under Partial Shading Conditions. Applied Sciences. 2025; 15(13):7386. https://doi.org/10.3390/app15137386
Chicago/Turabian StyleTimur, Oğuzhan, and Bayram Kaan Uzundağ. 2025. "Design and Analysis of a Hybrid MPPT Method for PV Systems Under Partial Shading Conditions" Applied Sciences 15, no. 13: 7386. https://doi.org/10.3390/app15137386
APA StyleTimur, O., & Uzundağ, B. K. (2025). Design and Analysis of a Hybrid MPPT Method for PV Systems Under Partial Shading Conditions. Applied Sciences, 15(13), 7386. https://doi.org/10.3390/app15137386






