Dynamic Response Mitigation of Offshore Jacket Platform Using Tuned Mass Damper Under Misaligned Typhoon and Typhoon Wave
Abstract
1. Introduction
2. Research Methodology and TMD Fundamentals
2.1. Overall Research Methodology
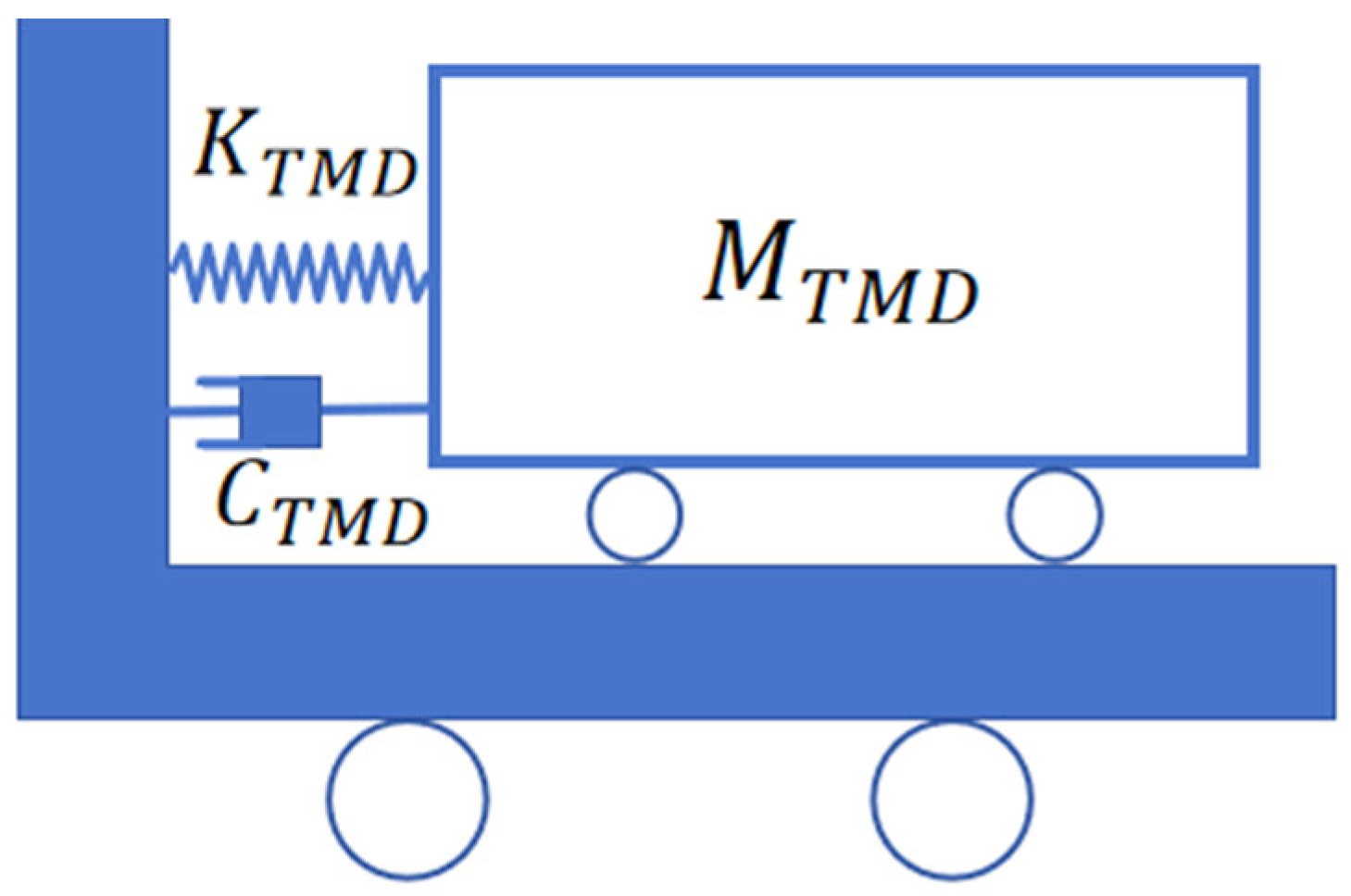
2.2. Theoretical Framework of TMD
3. Offshore Platform Overview and Finite Element Model
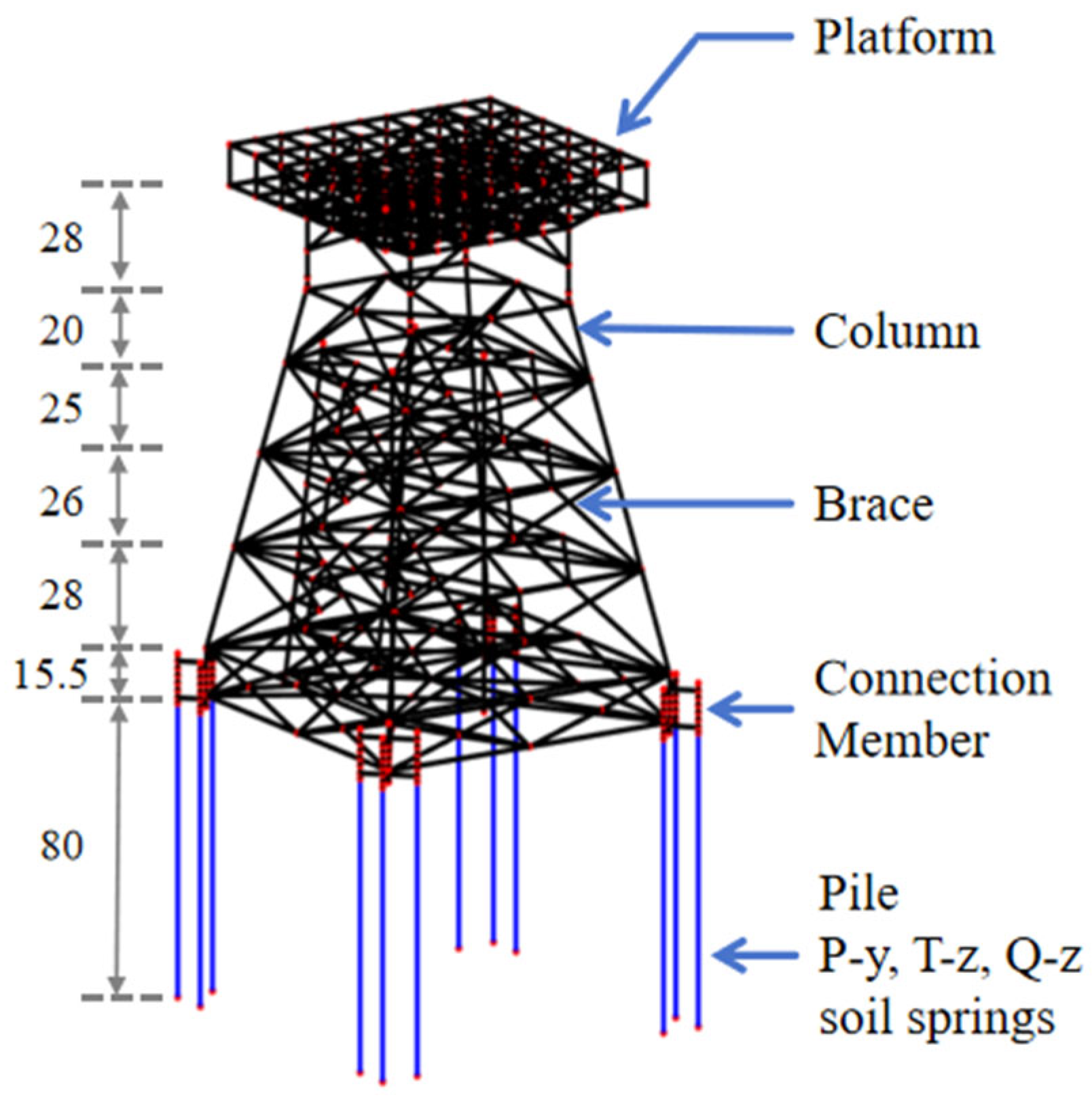
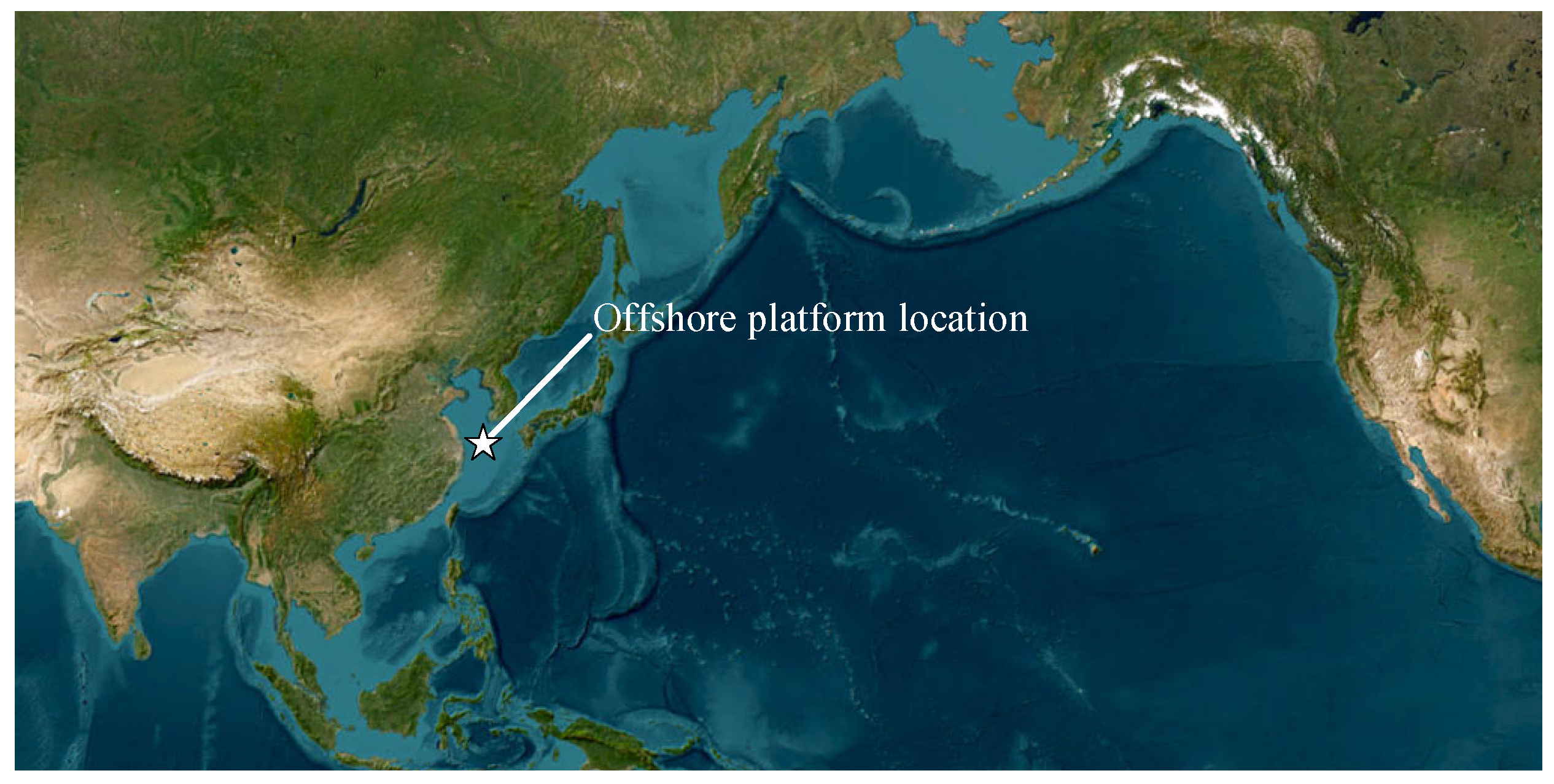
3.1. Deep-Water Offshore Platform
3.2. Finite Element Model
3.3. Soil–Structure Interaction
3.4. Pile-Water Interface
4. Typhoon-Induced Wind and Wave Loading
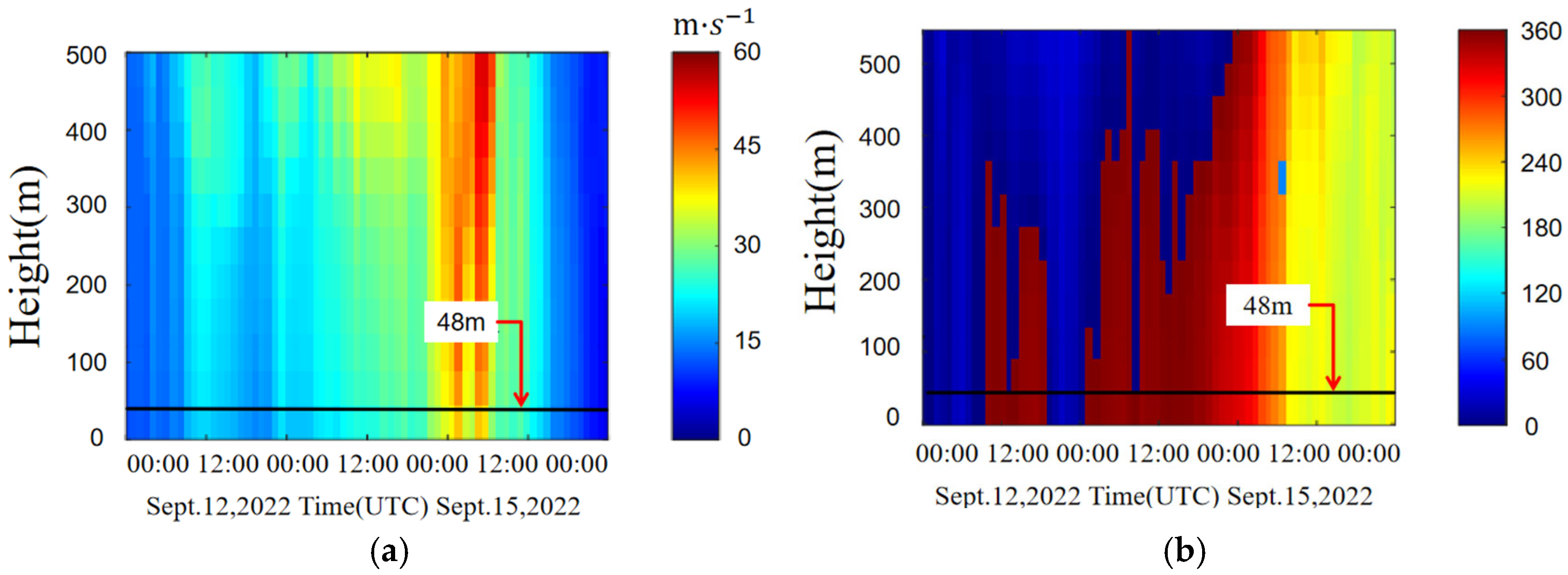
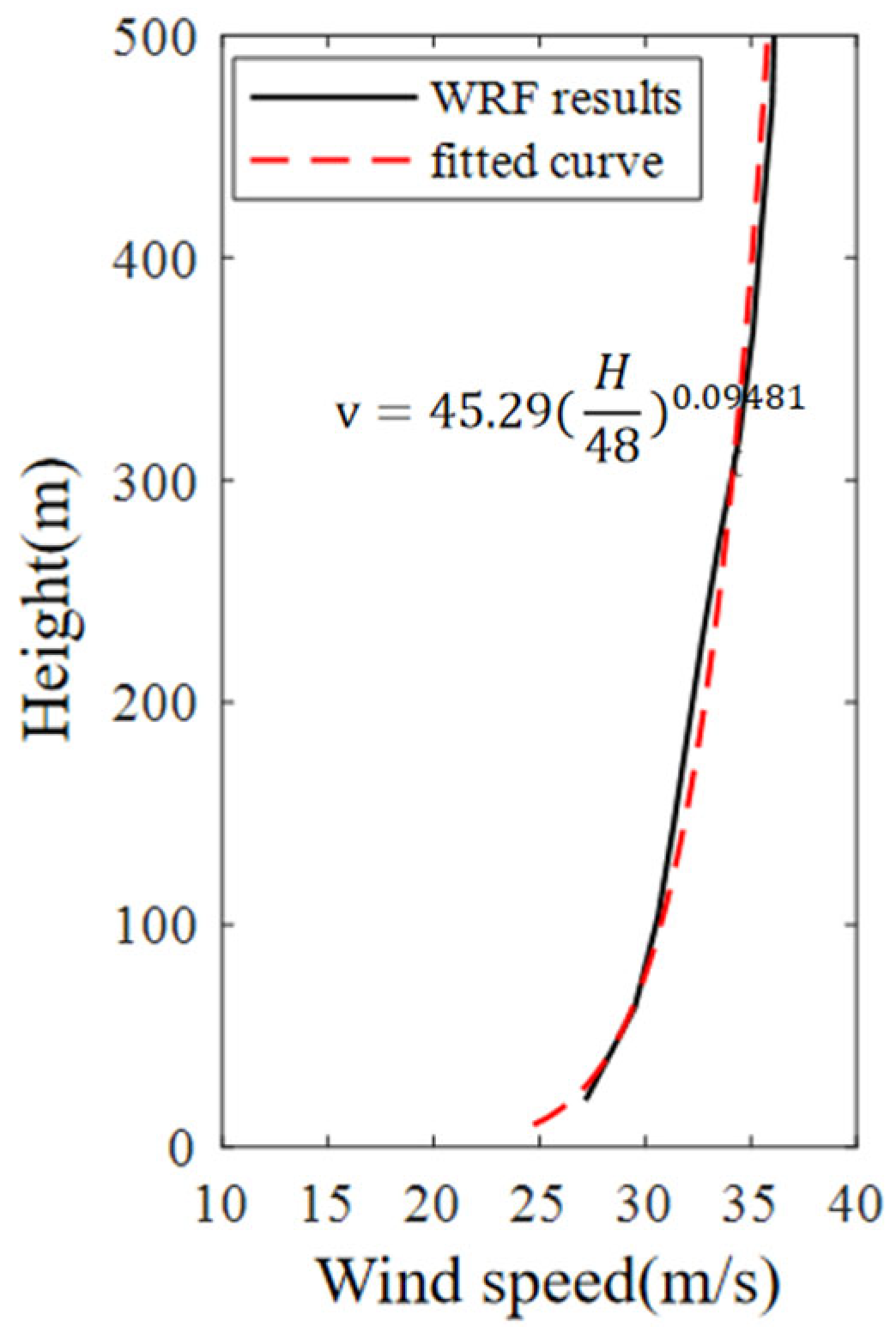
4.1. Typhoon-Induced Wind Loading
4.2. Typhoon-Induced Wave Loading
5. Dynamic Loading Mitigation of Offshore Platform Using TMD
5.1. Metocean Conditions
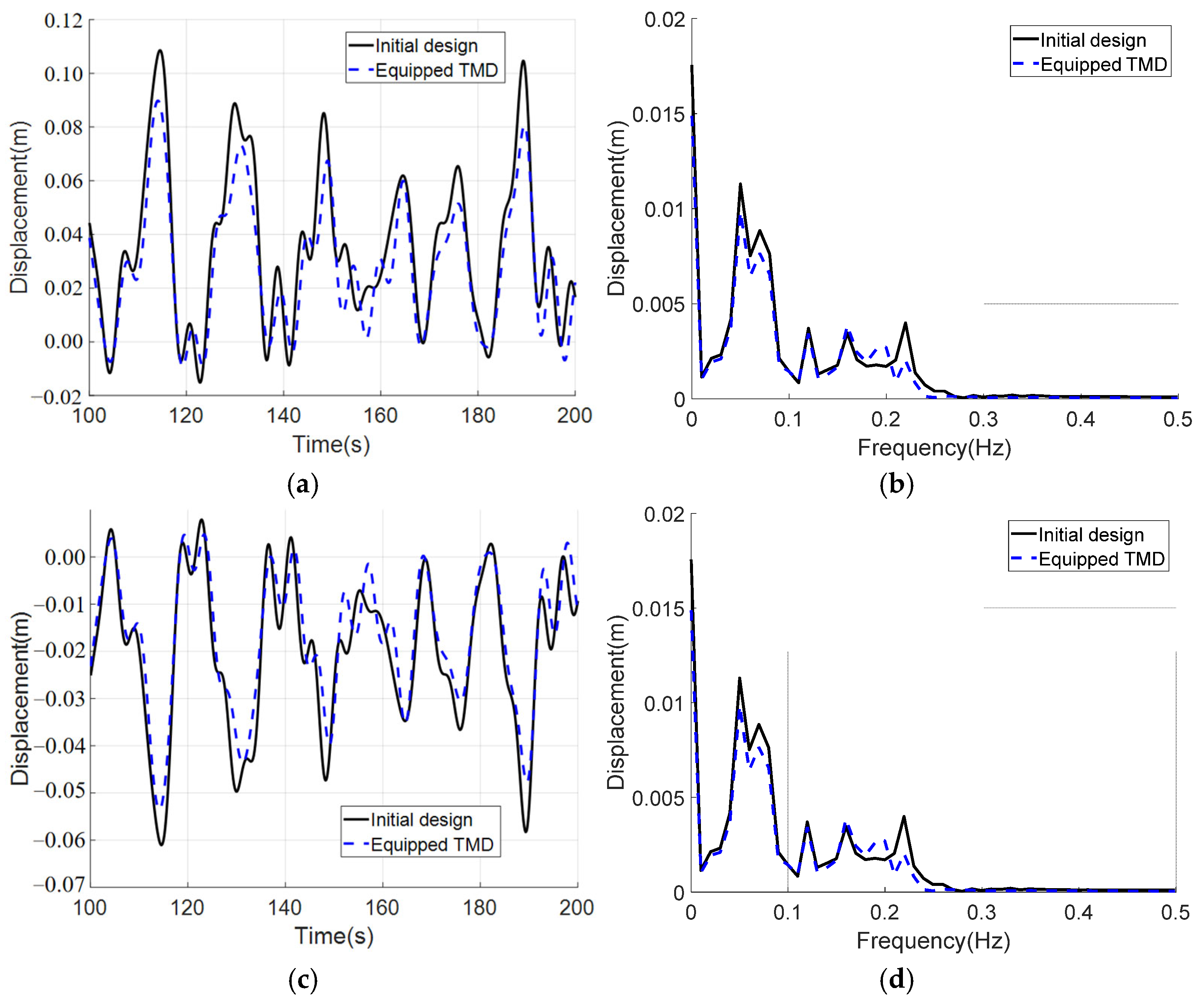
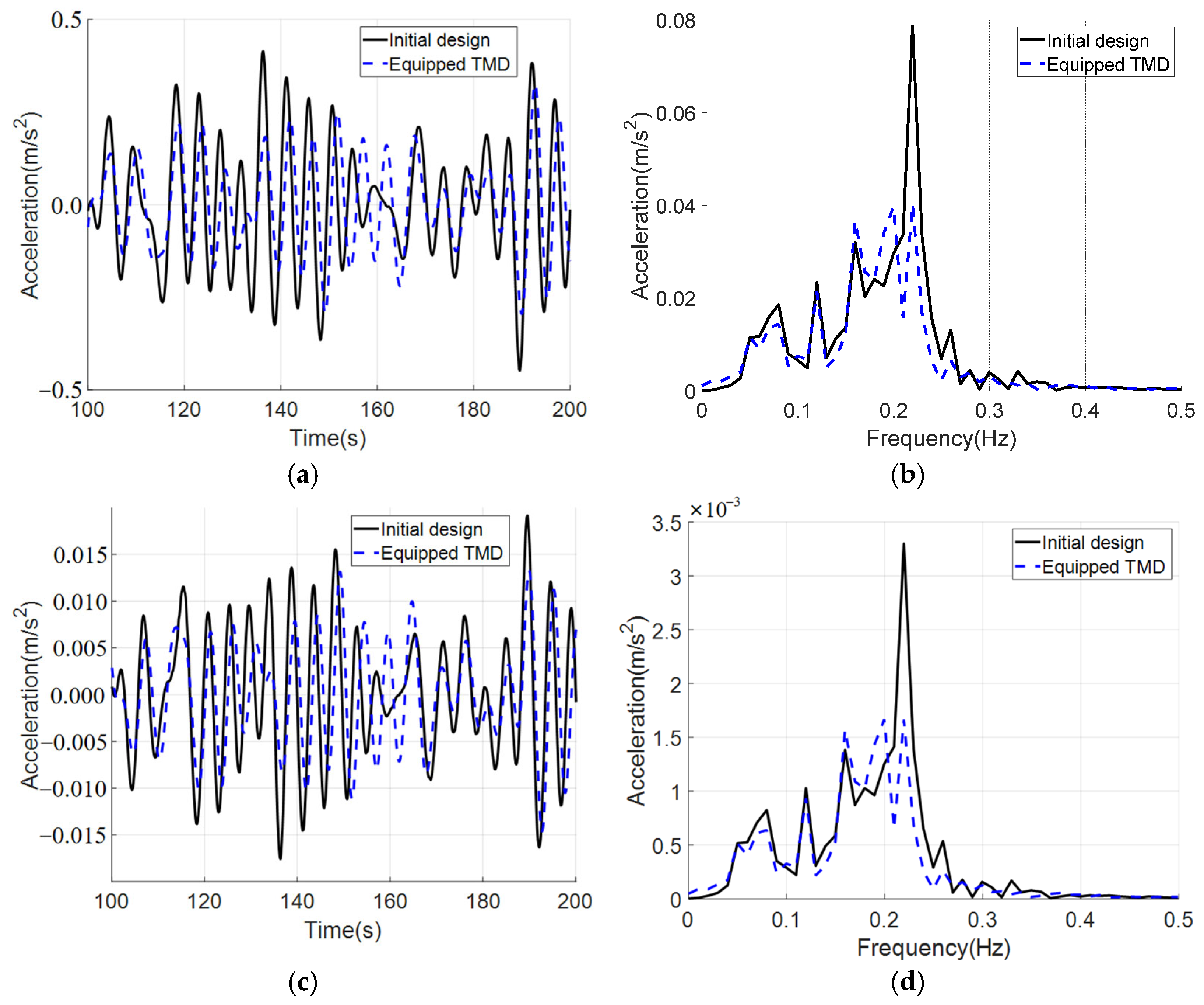
5.2. Dynamic Responses and Discussion
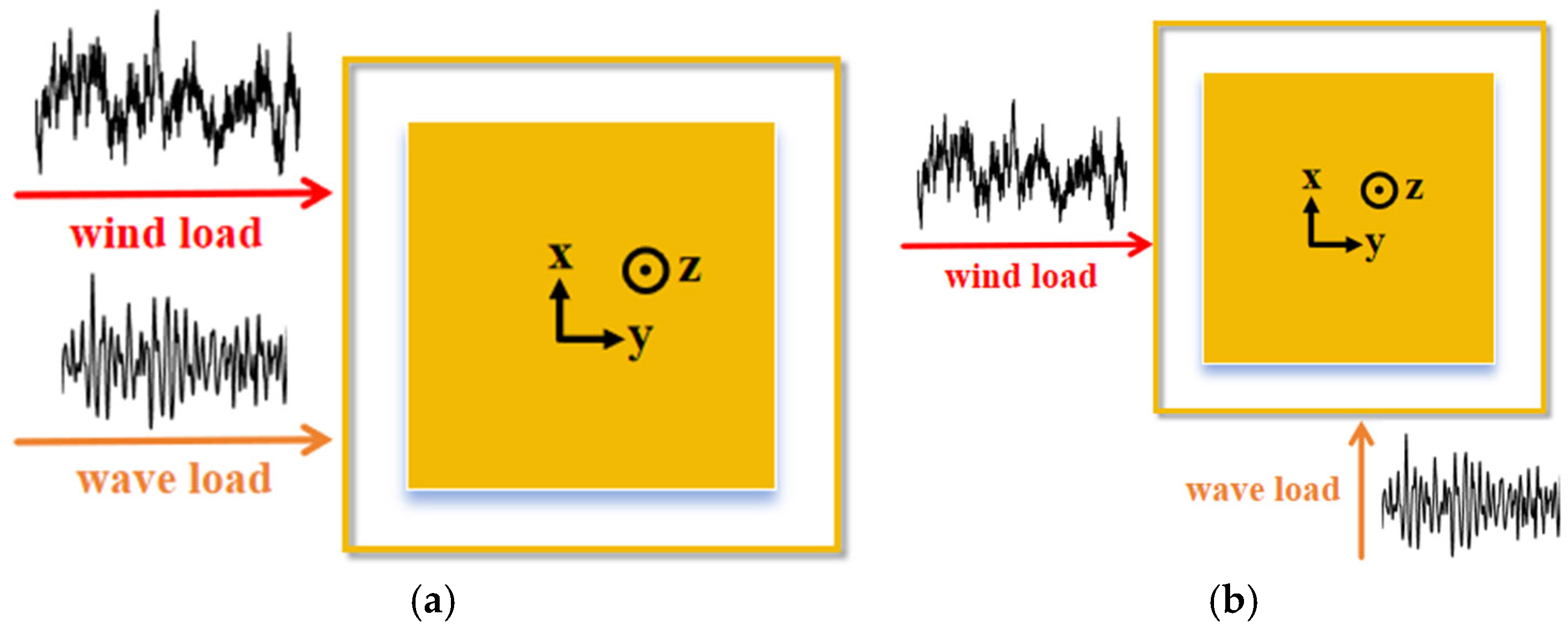
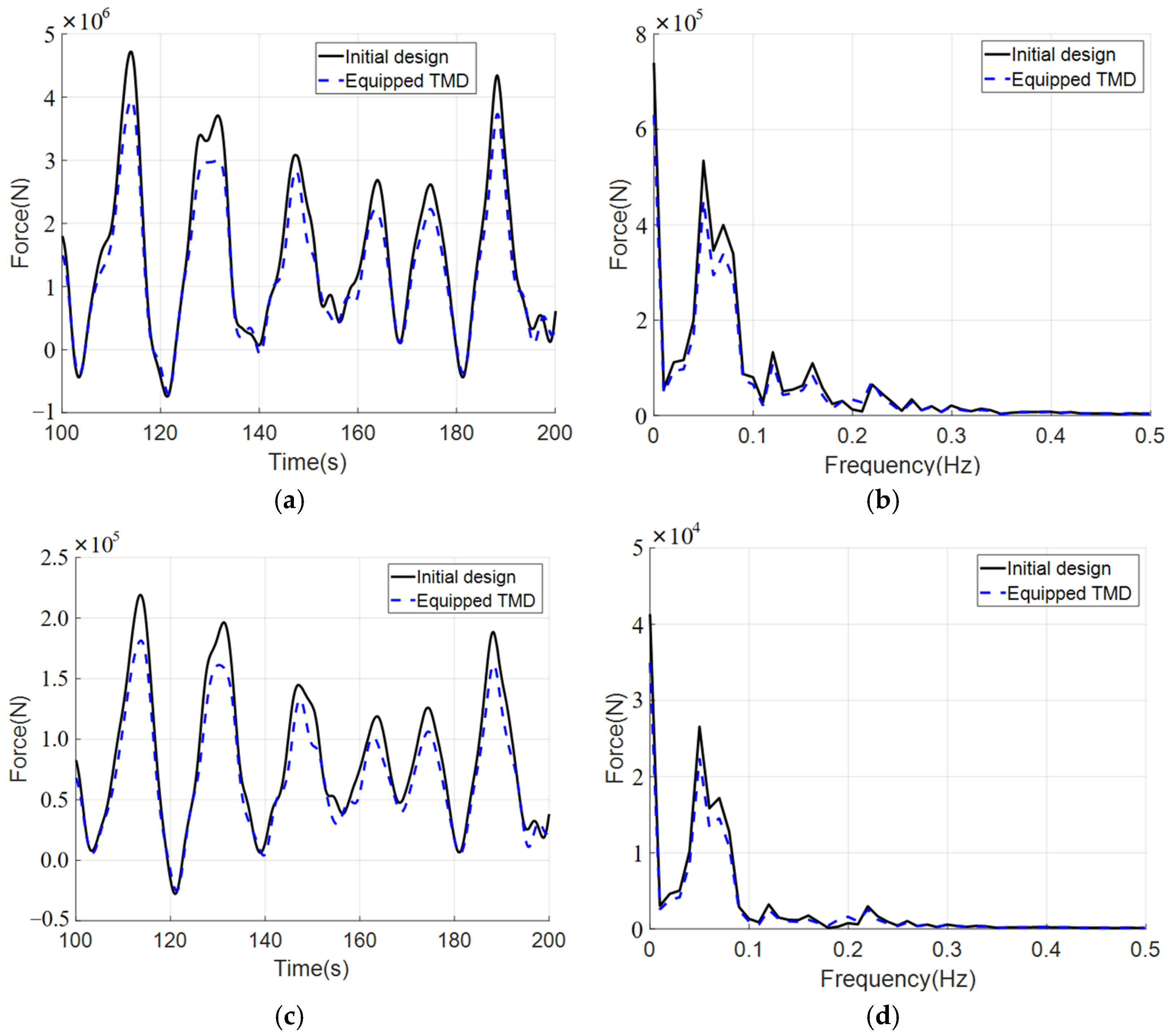
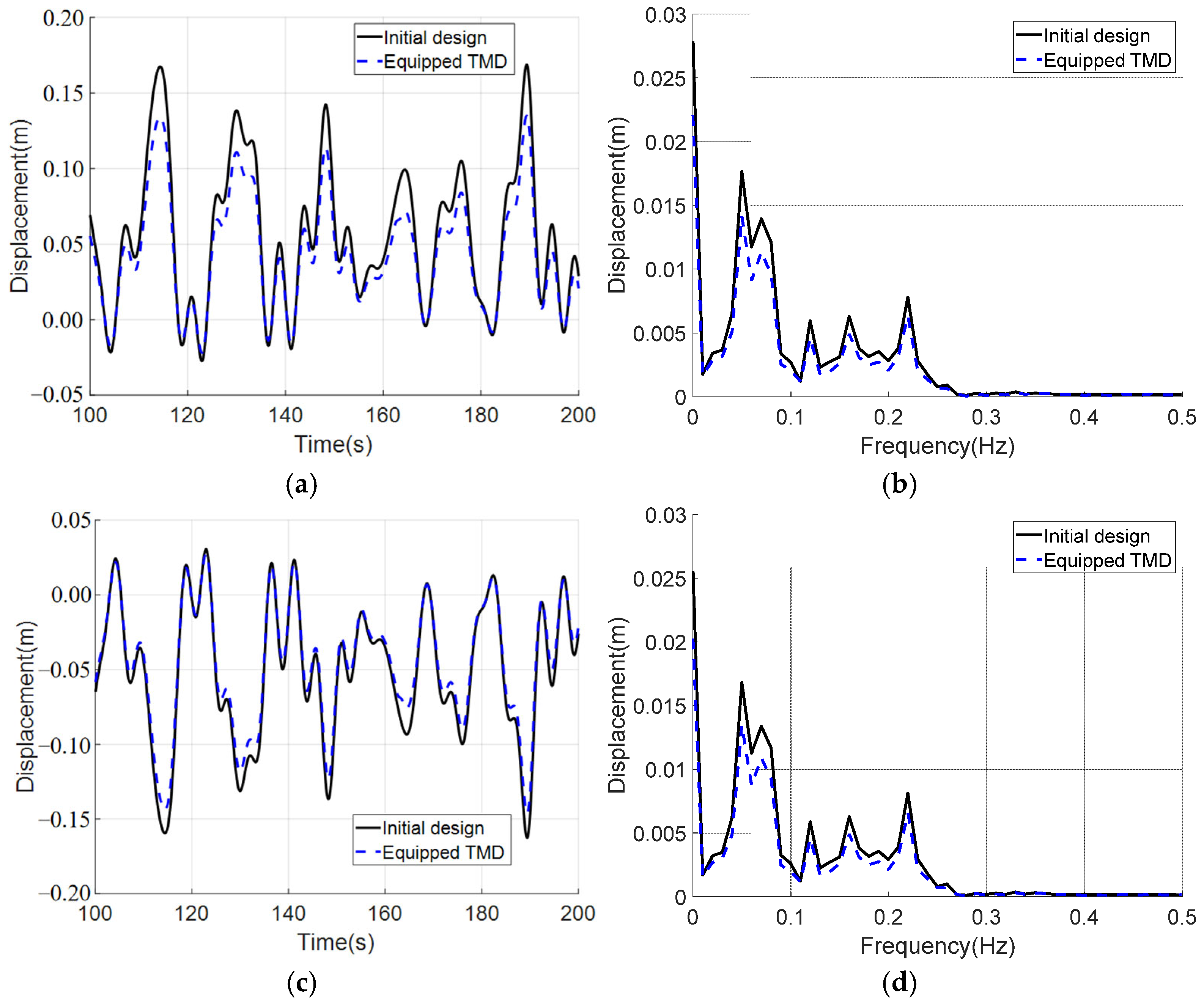
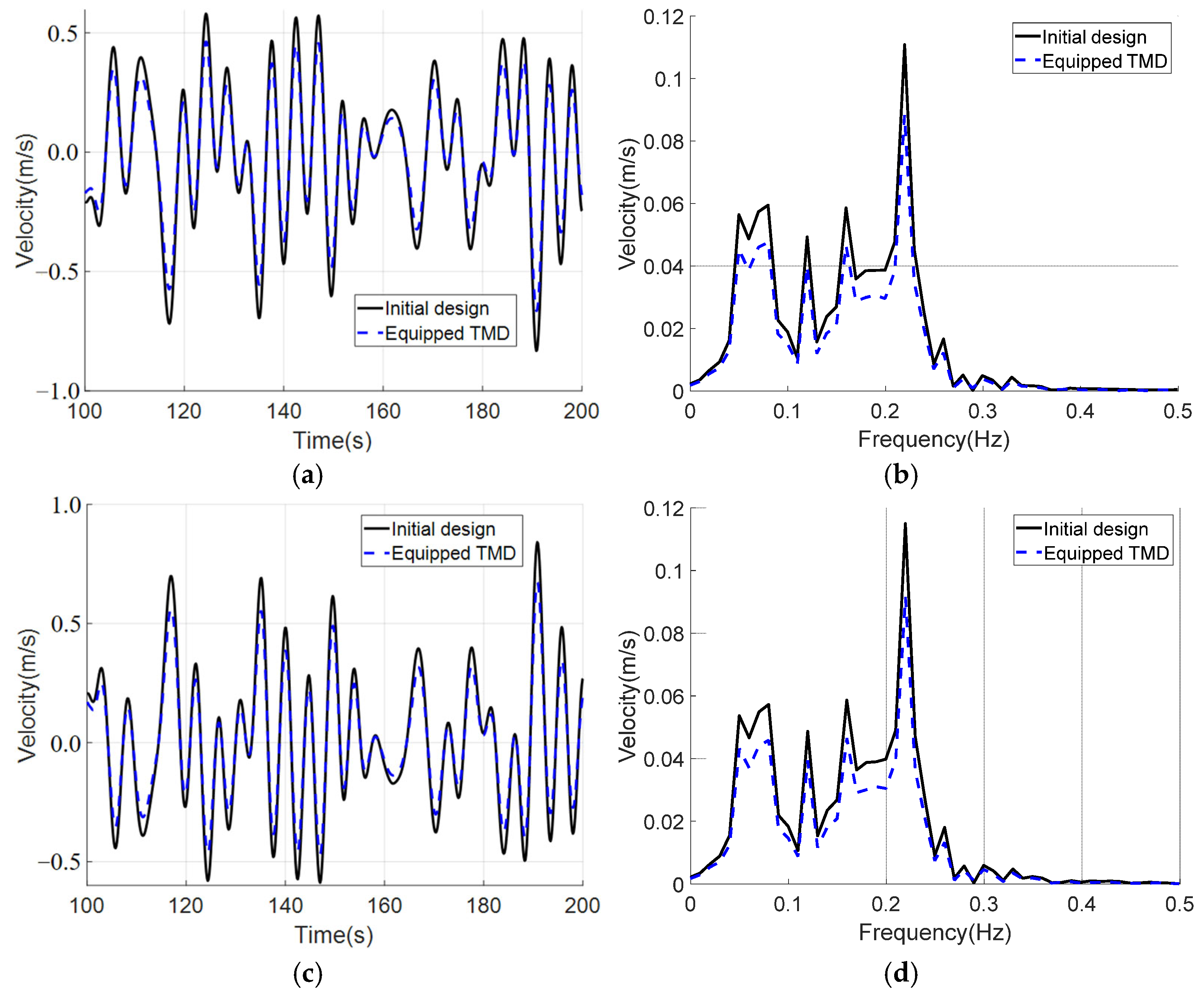
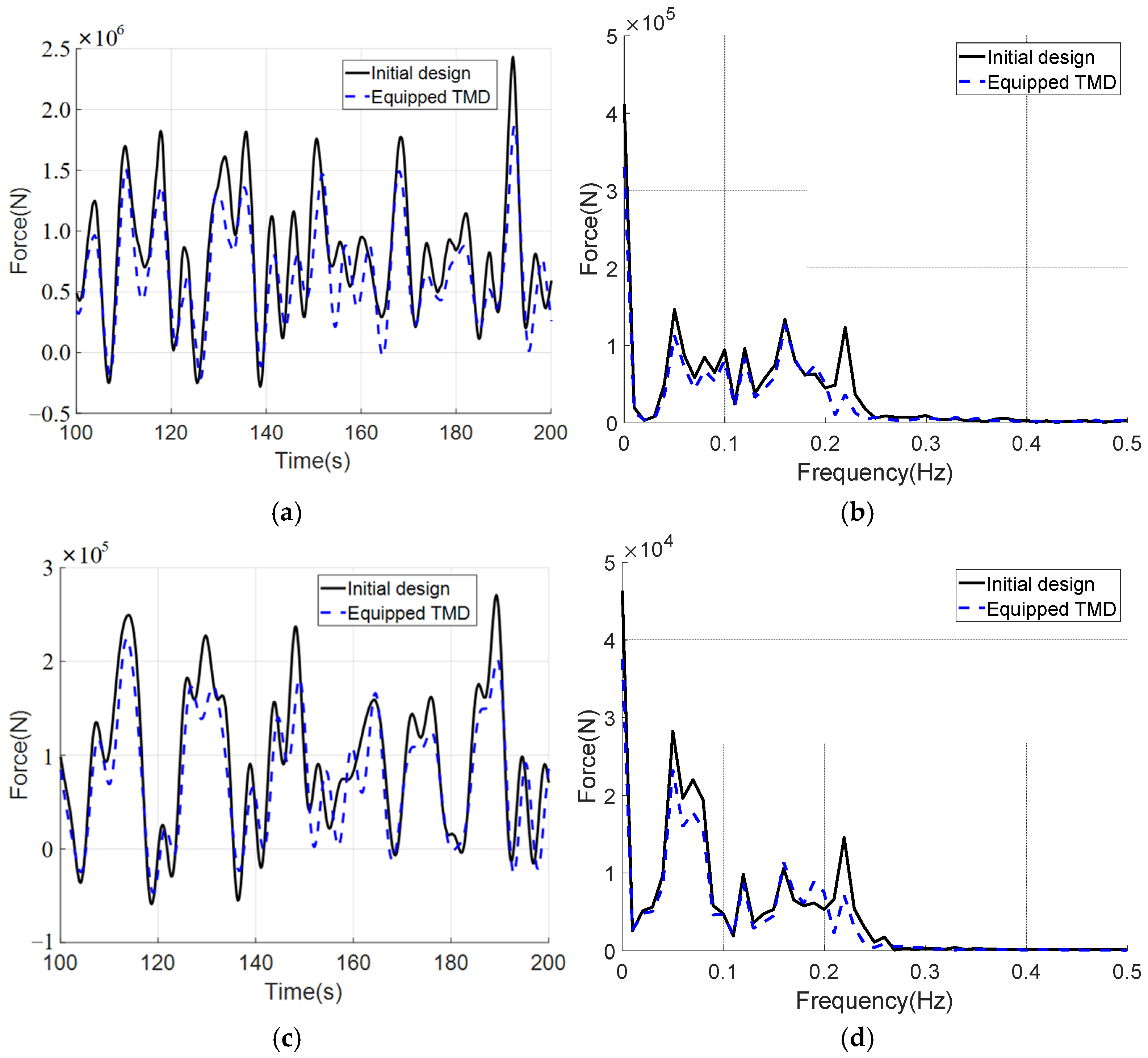
5.2.1. Aligned Typhoon and Typhoon-Wave
5.2.2. Misaligned Typhoon and Typhoon-Wave
5.2.3. Experiment on Frequency Detuning Sensitivity of TMD
5.2.4. The Influence of Key Design Parameters on the Applicability of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Havigh, S.N.; Askar, M.B. The process of fatigue analysis on fixed metal offshore platforms. Mar. Sci. 2017, 7, 10–16. [Google Scholar] [CrossRef]
- Peng, B.-F.; Chang, B.; Llorente, C. Nonlinear dynamic soil-pile-structure interaction analysis of a deepwater platform for ductility level earthquakes. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2005; p. OTC–17274-MS. [Google Scholar] [CrossRef]
- Liu, J.; Ma, X.; Zhang, X.; Zhang, Z.; Liu, G. Axial vibration of deep-water drilling risers under lifting conditions. J. Pet. Sci. Eng. 2022, 209, 109903. [Google Scholar] [CrossRef]
- Huang, X.; Yang, B. Towards novel energy shunt inspired vibration suppression techniques: Principles, designs and applications. Mech. Syst. Signal Process. 2023, 182, 109496. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M.; Tang, G.-Y. Active Control of Offshore Steel Jacket Platforms; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Yang, F.; Sedaghati, R.; Esmailzadeh, E. Vibration suppression of structures using tuned mass damper technology: A state-of-the-art review. J. Vib. Control 2022, 28, 812–836. [Google Scholar] [CrossRef]
- Frahm, H. Device for Damping Vibrations of Bodies. U.S. Patent 989,958, 18 April 1911. [Google Scholar]
- Wu, Q.; Zhao, X.; Zheng, R.; Minagawa, K. High Response Performance of a Tuned-Mass Damper for Vibration Suppression of Offshore Platform under Earthquake Loads. Shock Vib. 2016, 2016, 7383679. [Google Scholar] [CrossRef]
- Guo, W.; Li, H.N.; Liu, G.H.; Yu, Z.W. A simplified optimization strategy for nonlinear tuned mass damper in structural vibration control. Asian J. Control 2012, 14, 1059–1069. [Google Scholar] [CrossRef]
- Bui, H.-L.; Tran, N.-A. Multi-objective optimal design of TMDs for increasing critical flutter wind speed of bridges. J. Wind Eng. Ind. Aerodyn. 2022, 225, 104992. [Google Scholar] [CrossRef]
- Leung, A.Y.; Zhang, H.; Cheng, C.; Lee, Y. Particle swarm optimization of TMD by non-stationary base excitation during earthquake. Earthq. Eng. Struct. Dyn. 2008, 37, 1223–1246. [Google Scholar] [CrossRef]
- Nie, W.; Liu, S.; Yin, H.; Lu, S.; Zhao, D.; Xu, H. Application of the Improved Multipopulation Genetic Algorithm in the TMD Controlled System considering Soil-Structure Interaction. Adv. Civ. Eng. 2022, 2022, 8212766. [Google Scholar] [CrossRef]
- Xu, T.; Li, Y.; Leng, D. Mitigating jacket offshore platform vibration under earthquake and ocean waves utilizing tuned inerter damper. Bull. Earthq. Eng. 2023, 21, 1627–1650. [Google Scholar] [CrossRef]
- Delavar, M.A.; Bargi, K. Seismic response control of offshore platforms equipped with optimum localization of SMA. engrxiv 2020. [Google Scholar] [CrossRef]
- Gavgani, S.A.M.; Homami, P.; Darbanian, R.; Moharrerzadeh, K. Probabilistic assessment of optimum tuned mass damper in offshore platforms considering fluid–structure interaction. Mar. Syst. Ocean Technol. 2024, 19, 57–67. [Google Scholar] [CrossRef]
- Jin, Q.; Li, X.; Sun, N.; Zhou, J.; Guan, J. Experimental and numerical study on tuned liquid dampers for controlling earthquake response of jacket offshore platform. Mar. Struct. 2007, 20, 238–254. [Google Scholar] [CrossRef]
- Sardar, R.; Chakraborty, S. Wave vibration control of jacket platform by tuned liquid dampers. Ocean Eng. 2022, 247, 110721. [Google Scholar] [CrossRef]
- Paul, S.; Datta, T.; Kapuria, S. Control of fixed offshore jacket platform using semi-active hydraulic damper. J. Offshore Mech. Arct. Eng. 2009, 131, 041106. [Google Scholar] [CrossRef]
- Patil, K.; Jangid, R. Passive control of offshore jacket platforms. Ocean Eng. 2005, 32, 1933–1949. [Google Scholar] [CrossRef]
- Tabeshpour, M.R.; Rokni, H.J. Frequency domain long-term efficiency of viscous damper in jacket platforms under random wave load. Arab. J. Sci. Eng. 2017, 42, 4523–4534. [Google Scholar] [CrossRef]
- Janbazi Rokni, H.; Tabeshpour, M.R. Spectral fatigue analysis of jacket platform under wave load equipped with viscous damper. J. Mar. Sci. Technol. 2019, 24, 855–870. [Google Scholar] [CrossRef]
- Espinoza, G.; Benedetti, F.; Alvarez-Mendoza, P.; Bonilla, E. Influence of the seismic excitation frequencies content on the behavior of a tuned mass damper in low-rise building considering soil-structure interaction. Lat. Am. J. Solids Struct. 2018, 15, e75. [Google Scholar] [CrossRef]
- Pastia, C.; Luca, S.-G. Vibration control of a frame structure using semi-active tuned mass damper. Bul. Institutului Politeh. Lasi Sect. Constr. Arhit. 2013, 59, 31. [Google Scholar]
- Ju, S.H.; Su, F.C.; Jiang, Y.T.; Chiu, Y.C. Ultimate load design of jacket-type offshore wind turbines under tropical cyclones. Wind Energy 2019, 22, 685–697. [Google Scholar] [CrossRef]
- Fan, T.-Y.; Lin, C.-Y.; Huang, C.-C.; Chu, T.-L. Time-domain fatigue analysis of multi-planar tubular joints for a jacket-type substructure of offshore wind turbines. Int. J. Offshore Polar Eng. 2020, 30, 112–119. [Google Scholar] [CrossRef]
- Bai, Y.; Yan, H.-B.; Cao, Y.; Kim, Y.; Yang, Y.-Y.; Jiang, H. Time-dependent reliability assessment of offshore jacket platforms. Ships Offshore Struct. 2016, 11, 591–602. [Google Scholar] [CrossRef]
- Shahin, M.A. State-of-the-art review of some artificial intelligence applications in pile foundations. Geosci. Front. 2016, 7, 33–44. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Curras, C.J.; Kutter, B.L.; Wilson, D.W.; Abghari, A. Seismic soil-pile-structure interaction experiments and analyses. J. Geotech. Geoenviron. Eng. 1999, 125, 750–759. [Google Scholar] [CrossRef]
- Liang, Z.; Jeng, D.-S. The instantaneous seabed liquefaction around offshore pile-type foundation and seabed protection under combined wave and current loading. Ocean Eng. 2022, 257, 111649. [Google Scholar] [CrossRef]
- Haghroosta, T.; Ismail, W.; Ghafarian, P.; Barekati, S. The efficiency of the Weather Research and Forecasting (WRF) model for simulating typhoons. Nat. Hazards Earth Syst. Sci. 2014, 14, 2179–2187. [Google Scholar] [CrossRef]
- Iuso, G.; Virone, G.; Cafiero, G.; Bonisoli, E.; Lisitano, D.; Venturini, S. Aeroelastic-structural coupling in antenna prototype for windy open-space. In Proceedings of the COUPLED VIII: Proceedings of the VIII International Conference on Computational Methods for Coupled Problems in Science and Engineering; Sitges, Spain, 3–5 June 2019, pp. 481–492.
- IEC 61400-1:2019; Wind Energy Generation Systems—Part 1: Design Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2019.
- Teng, L.; Hang, X.; Wang, L.; Wang, L.; Guo, Z. Interactive Validation of Real-Time Hybrid Wave Basin Test for Fowts Using an Aero-Hydro-Servo Multibody Program Zwind. SSRN 2025. [Google Scholar] [CrossRef]
- Otoniel Canuet, L.F. Atmospheric Turbulence Profile Modeling for Satellite-Ground Laser Communication; Universitat Politècnica de Catalunya: Barcelona, Spain, 2015. [Google Scholar]
- Van Binh, L.; Ishihara, T.; Van Phuc, P.; Fujino, Y. A peak factor for non-Gaussian response analysis of wind turbine tower. J. Wind Eng. Ind. Aerodyn. 2008, 96, 2217–2227. [Google Scholar] [CrossRef]
- Cao, T. A Theoretical and Numerical Study of Turbulent Wind-Wave Interaction; University of Minnesota: Minneapolis, MN, USA, 2020. [Google Scholar]
- Zhang, S.-f.; Chen, C.; Zhang, Q.-x.; Zhang, D.-m.; Zhang, F. Wave loads computation for offshore floating hose based on partially immersed cylinder model of improved Morison formula. Open Pet. Eng. J. 2015, 8, 130–137. [Google Scholar] [CrossRef][Green Version]
- Shayesteh Bilondi, M.R.; Yazdani, H.; Khatibinia, M. Seismic energy dissipation-based optimum design of tuned mass dampers. Struct. Multidiscip. Optim. 2018, 58, 2517–2531. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 2017, 44, 129–156. [Google Scholar] [CrossRef]





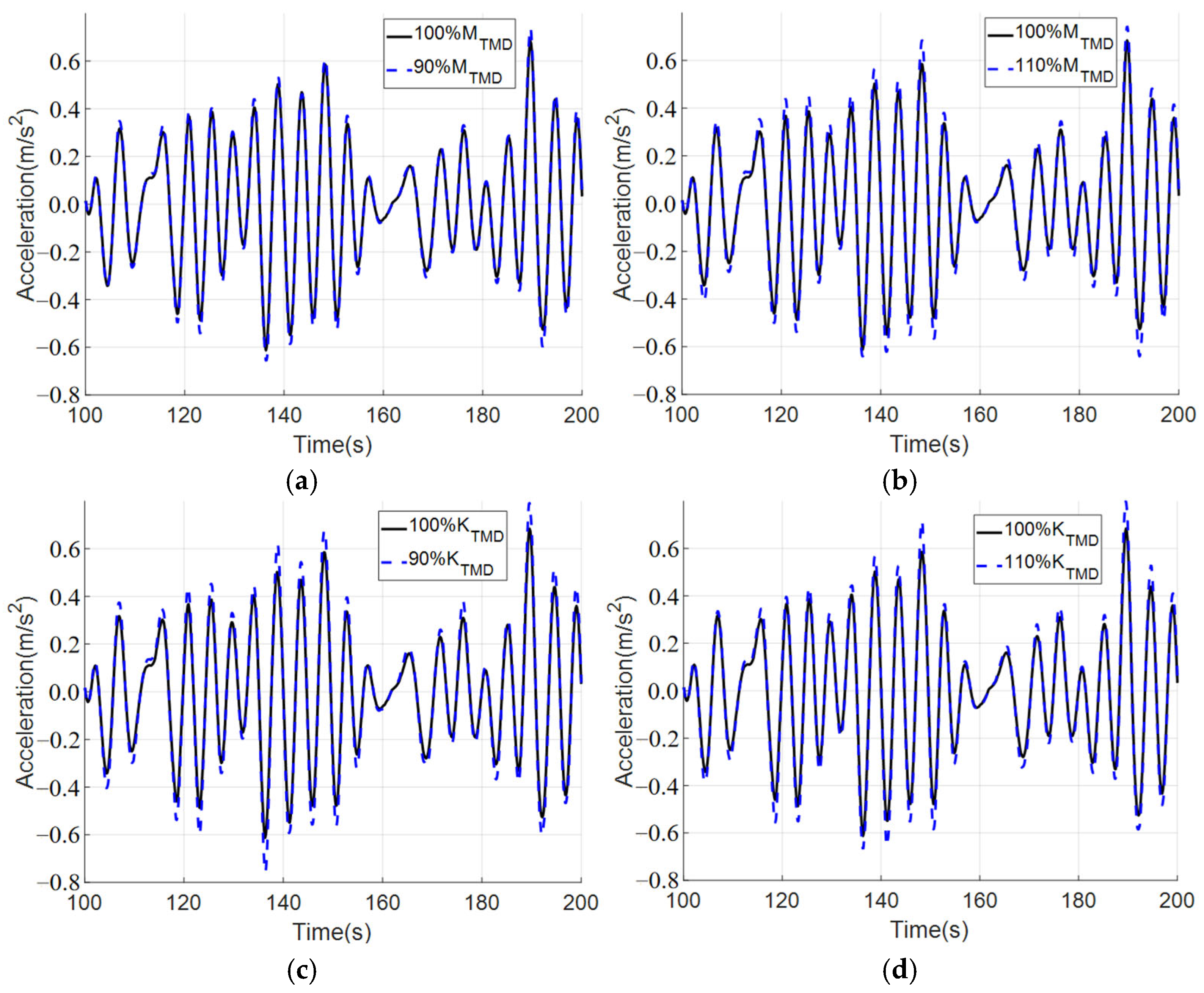
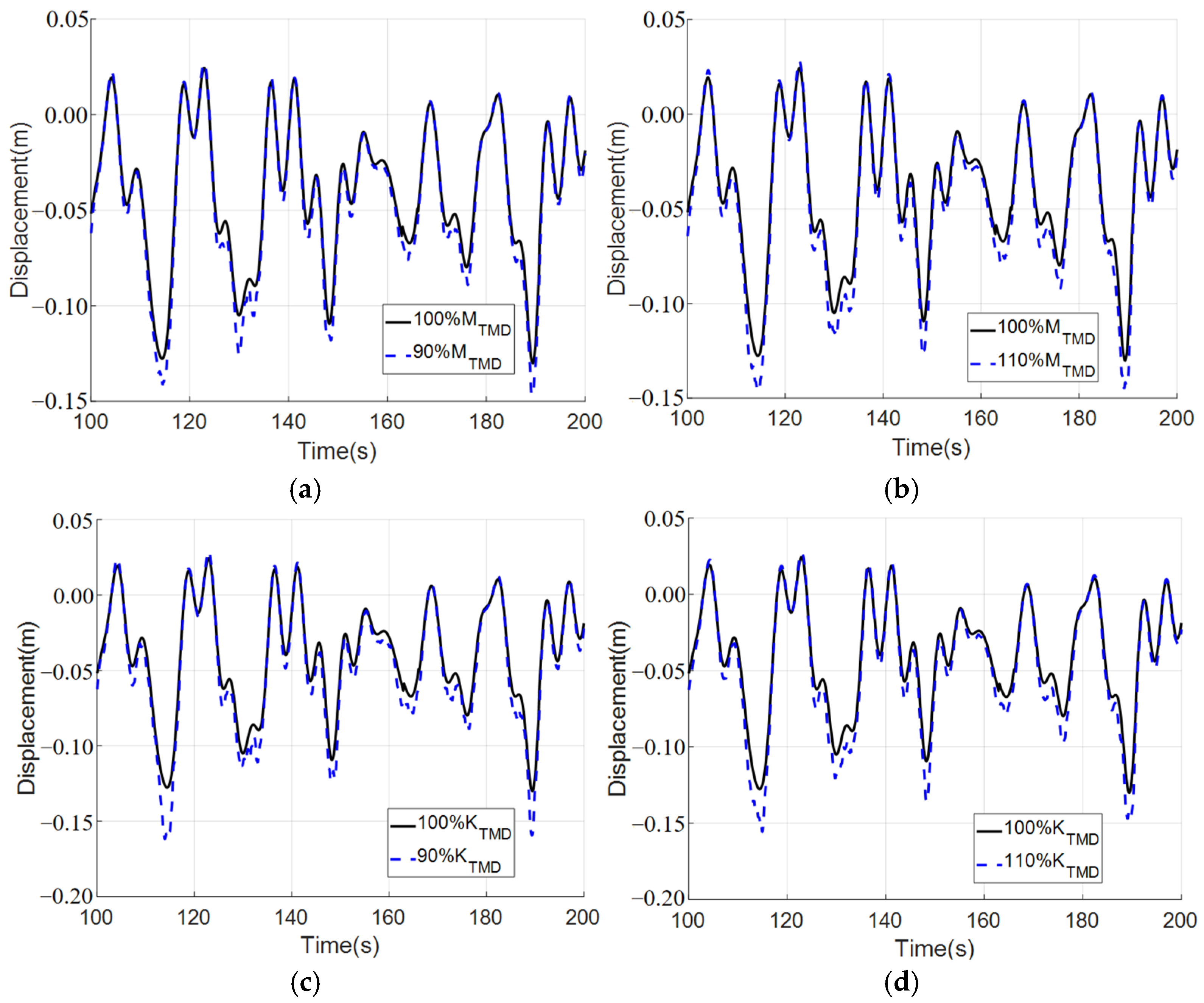
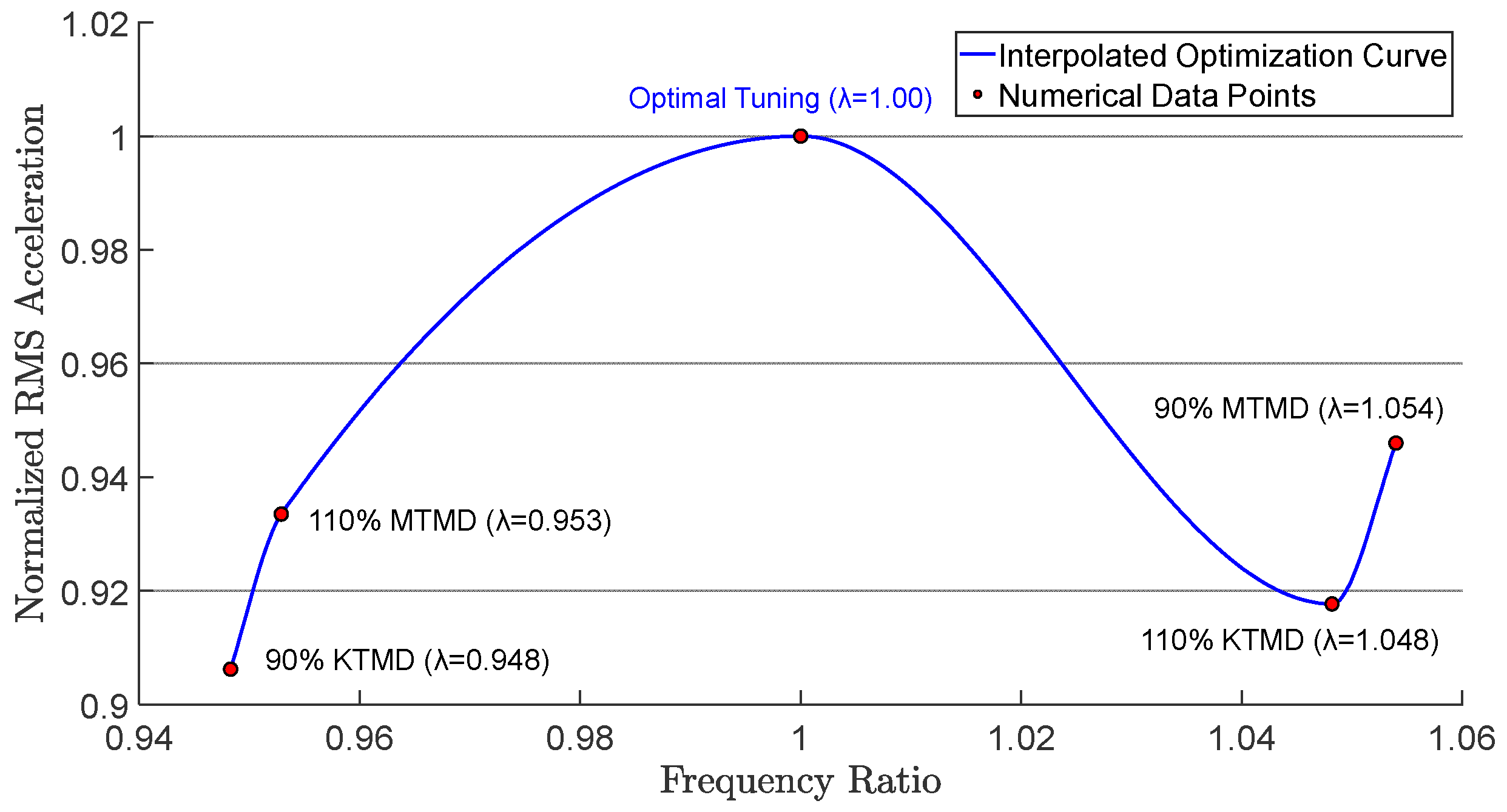
| Water Level (m) | Hs (m) | Tp (s) | Current Velocity (m/s) |
|---|---|---|---|
| 110.18 | 32.2 | 18.9 | 1.905 |
| No. | Soil | Depth (m) | Effective Weight (kN/m3) | Friction Angle (°) | Undrained Shear Strength (kPa) | |
|---|---|---|---|---|---|---|
| Top (m) | Bottom (m) | |||||
| 1 | Sand | 0 | 10 | 9 | 23° | - |
| 2 | Sand | 10 | 14.2 | 9.2 | 23.5° | - |
| 3 | Sand | 14.2 | 21.5 | 9.5 | 26.5° | - |
| 4 | Sand | 21.5 | 33.1 | 9.6 | 27° | - |
| 5 | Clay | 33.1 | 51.1 | 8.8 | - | 96 |
| 6 | Sand | 51.1 | 53.1 | 9.7 | 29° | - |
| 7 | Clay | 53.1 | 65.1 | 9 | - | 134 |
| 8 | Sand | 65.1 | 67.9 | 9.8 | 30° | - |
| 9 | Clay | 67.9 | 75.5 | 9.2 | - | 163 |
| 10 | Clay | 75.5 | 81.9 | 9.2 | - | 179 |
| 11 | Sand | 81.9 | 82.8 | 9.9 | 30.5° | - |
| Disturbance Parameter | ∆foff | ∆doff | ∆aoff | ||
|---|---|---|---|---|---|
| Mean Value | Maximum | Mean Value | Maximum | ||
| 90% MTMD | 5.4% | −4.38% | −3.21% | −5.40% | −4.41% |
| 110% MTMD | −4.71% | −6.95% | −3.22% | −6.65% | −4.76% |
| 90% KTMD | −5.17% | −8.60% | −5.38% | −9.38% | −6.40% |
| 110% KTMD | 4.82% | −7.30% | −8.06% | −8.23% | −5.31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, K.; Zhu, G.; Lv, G.; Yu, H.; Wang, L.; Huang, M.; Wang, L. Dynamic Response Mitigation of Offshore Jacket Platform Using Tuned Mass Damper Under Misaligned Typhoon and Typhoon Wave. Appl. Sci. 2025, 15, 7321. https://doi.org/10.3390/app15137321
Jiang K, Zhu G, Lv G, Yu H, Wang L, Huang M, Wang L. Dynamic Response Mitigation of Offshore Jacket Platform Using Tuned Mass Damper Under Misaligned Typhoon and Typhoon Wave. Applied Sciences. 2025; 15(13):7321. https://doi.org/10.3390/app15137321
Chicago/Turabian StyleJiang, Kaien, Guangyi Zhu, Guoer Lv, Huafeng Yu, Lizhong Wang, Mingfeng Huang, and Lilin Wang. 2025. "Dynamic Response Mitigation of Offshore Jacket Platform Using Tuned Mass Damper Under Misaligned Typhoon and Typhoon Wave" Applied Sciences 15, no. 13: 7321. https://doi.org/10.3390/app15137321
APA StyleJiang, K., Zhu, G., Lv, G., Yu, H., Wang, L., Huang, M., & Wang, L. (2025). Dynamic Response Mitigation of Offshore Jacket Platform Using Tuned Mass Damper Under Misaligned Typhoon and Typhoon Wave. Applied Sciences, 15(13), 7321. https://doi.org/10.3390/app15137321








