Research on the Bearing Characteristics of Narrow Coal Pillars in Double-Roadway Excavation Under the Influence of Full Dynamic Pressure
Abstract
1. Introduction
2. Regional Engineering Background
3. Theoretical Calculation of the Narrow Coal Pillar Width for Double-Roadway Excavation
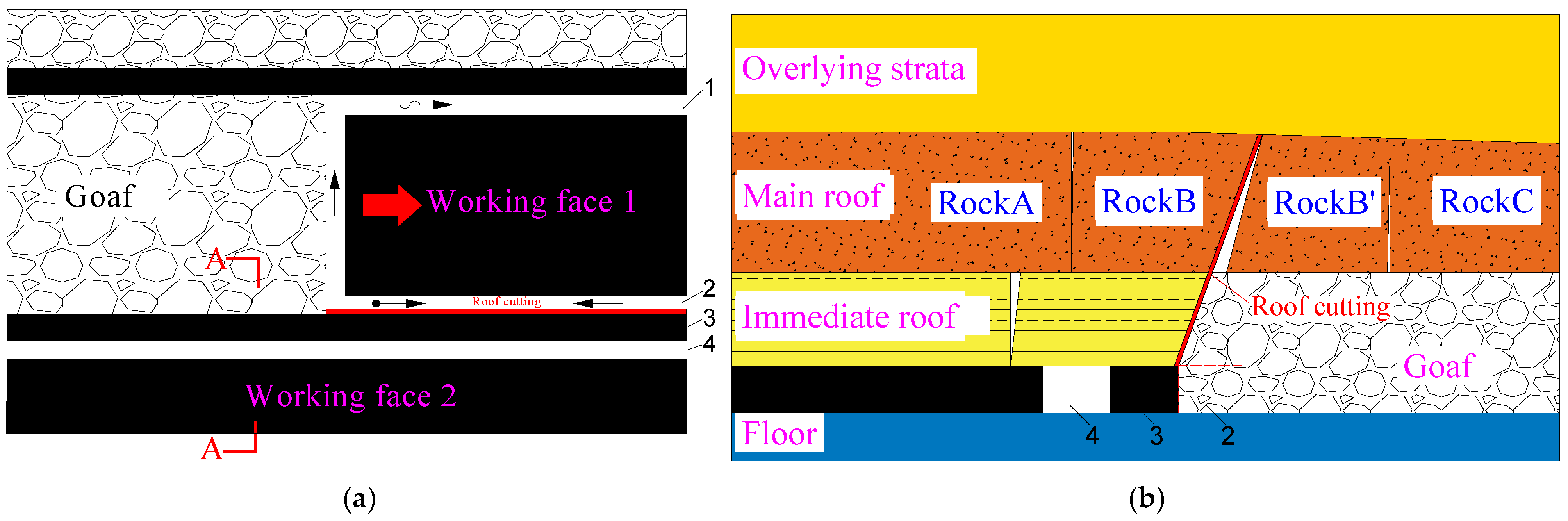
3.1. NCPDRE Layout
3.2. Mechanical and Structural Modeling of the Immediate Roof
3.3. Theoretical Calculation of Narrow Coal Pillar Width
4. Study of the Bearing Characteristics of NCPDRE
4.1. Numerical Simulation Modelling
4.1.1. Determination of the Parameters of the Goaf Collapse Zone
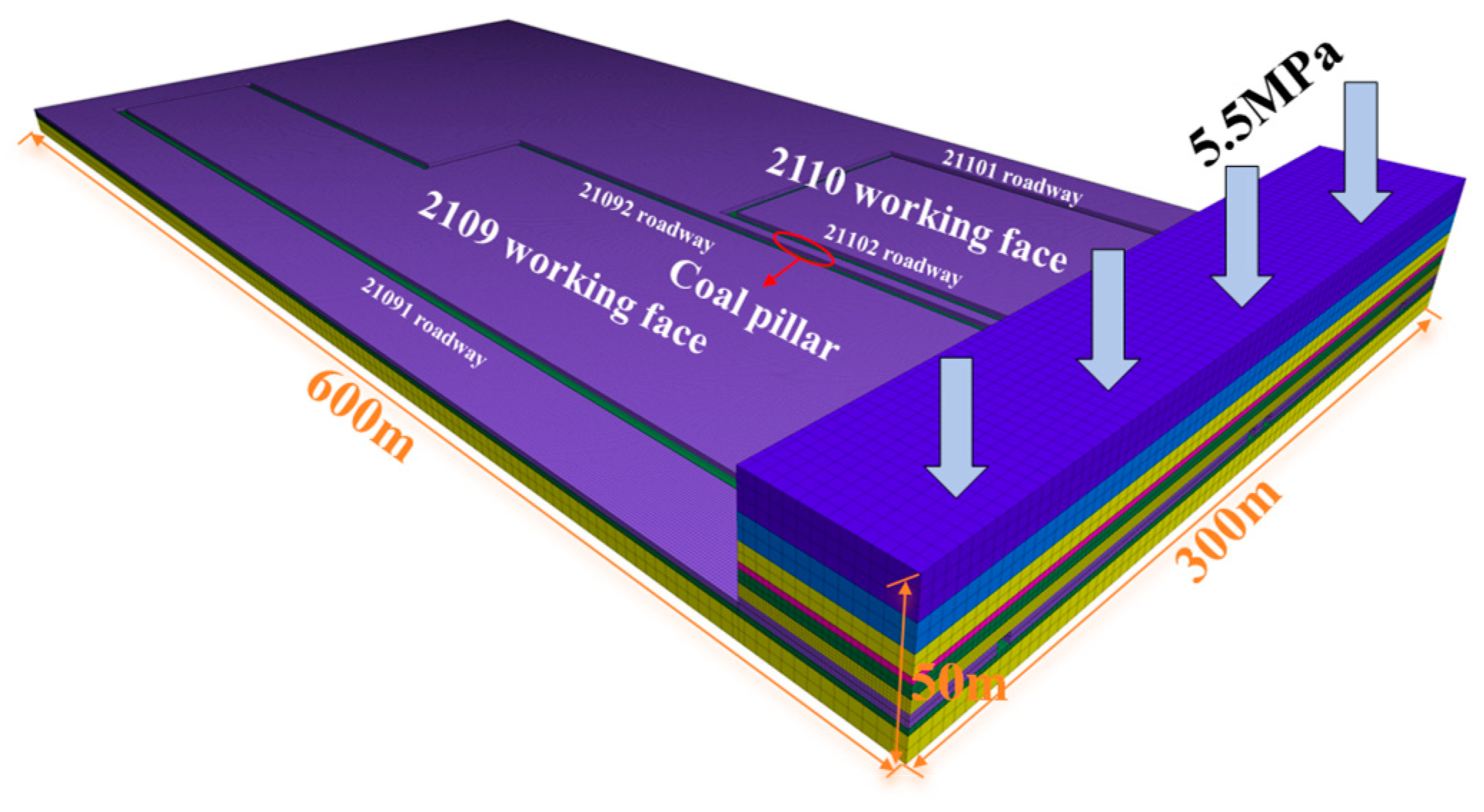
4.1.2. Numerical Simulation Model and Simulation Scheme
4.2. Research on the Bearing Characteristics of Coal Pillars Under the Influence of Full Dynamic Pressure
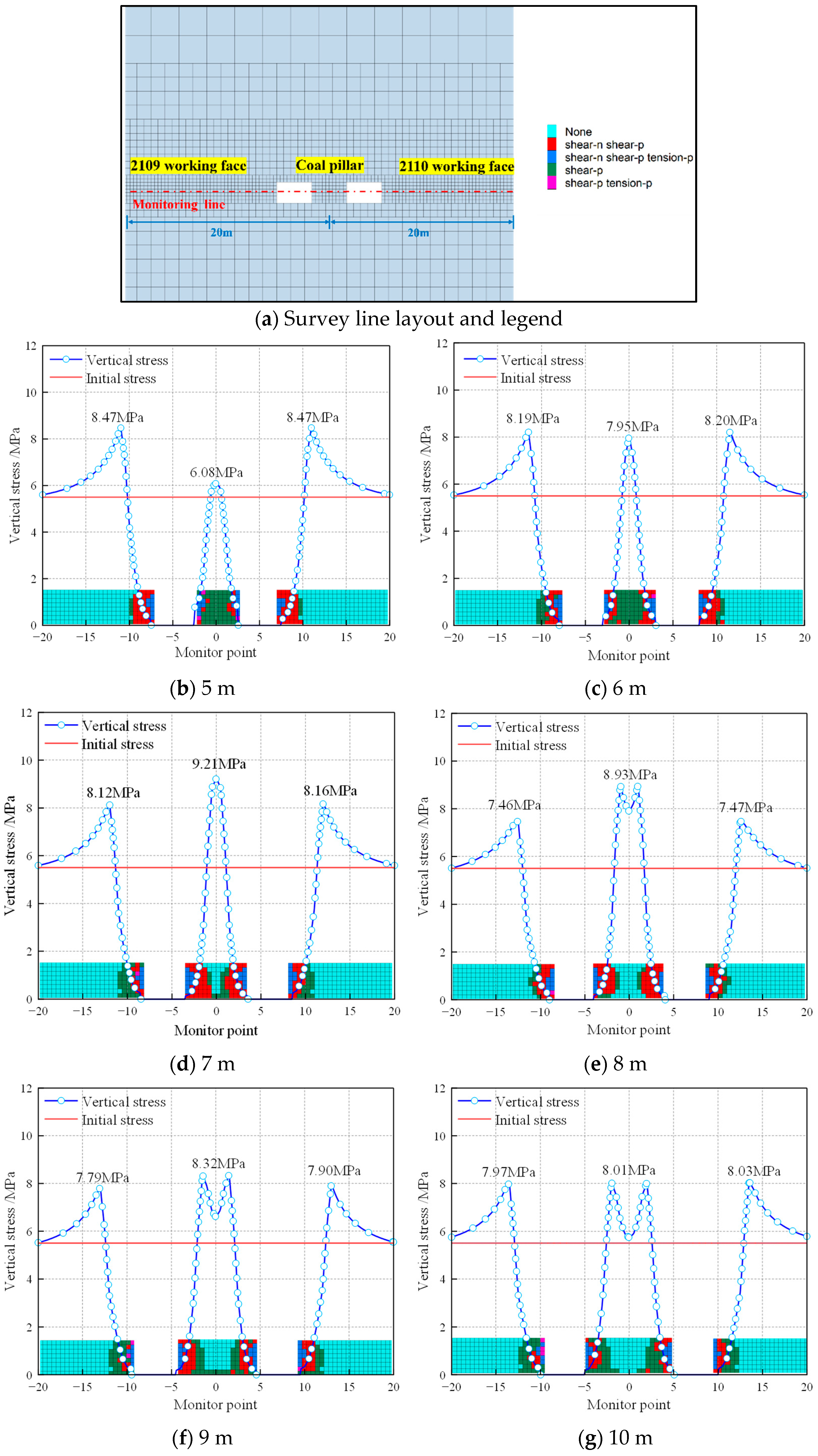
4.2.1. Bearing Characteristics of Different Coal Pillar Widths During Double-Roadway Excavation
- (1)
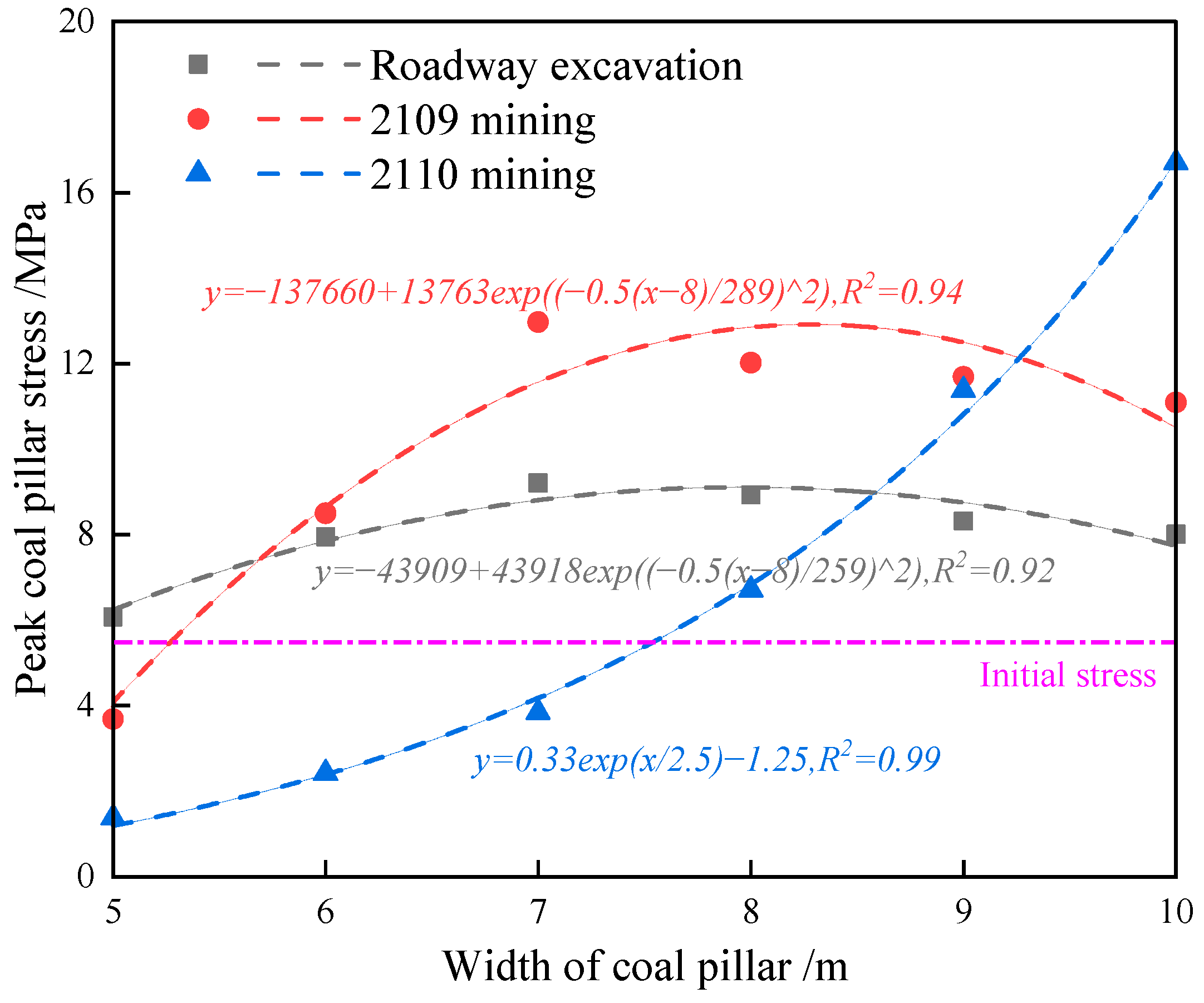
- When the coal pillar width was 5 m, the vertical stress within the coal pillar reached 6.08 MPa, slightly exceeding the initial stress of 5.5 MPa (1.11 times). At this point, the coal pillar reached its yield limit, with a predominance of grids in the plastic failure zone and fewer grids in the undamaged elastic region.
- (2)
- When the coal pillar width increased to 6 m, the vertical stress increased to 7.95 MPa, significantly higher than the initial stress (1.45 times). The bearing capacity of the coal pillar also increased to 1.45 MPa.
- (3)
- With a coal pillar width of 7 m, the peak stress increased to 9.21 MPa (1.67 times the initial stress). The number of grids in the elastic zone further increased, while the plastic zone remained intact, forming an elastic core area with a width of 1 m.
- (4)
- For a coal pillar height of 8 m, the peak stress exhibited a bimodal distribution, reaching 8.93 MPa (1.62 times the initial stress). The width of the elastic core area expanded to 2 m, with a significant increase in the number of grids in the elastic zone and a marked reduction in the number of grids in the plastic zone.
- (5)
- When the coal pillar widths were 9 m and 10 m, the peak stress remained bimodal, with values of 8.32 MPa (1.51 times the initial stress) and 8.01 MPa (1.46 times the initial stress). Compared to the 8 m coal pillar, the peak stress and stress concentration coefficient decreased substantially, while the width of the elastic core area increased to 3 m and 4 m. This led to a significant increase in the number of grids in the elastic zone, enhancing the bearing capacity and stability of the coal pillar.
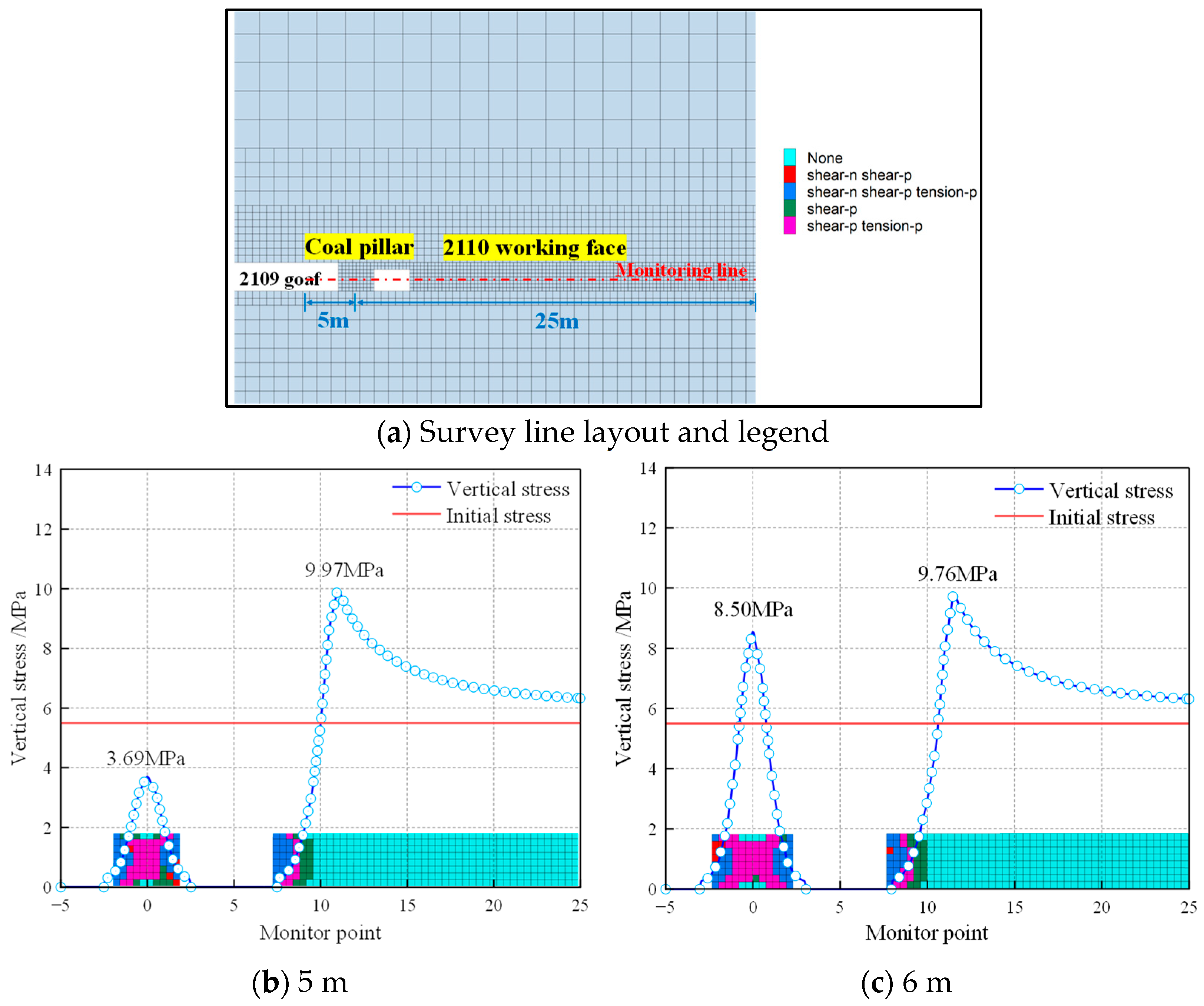
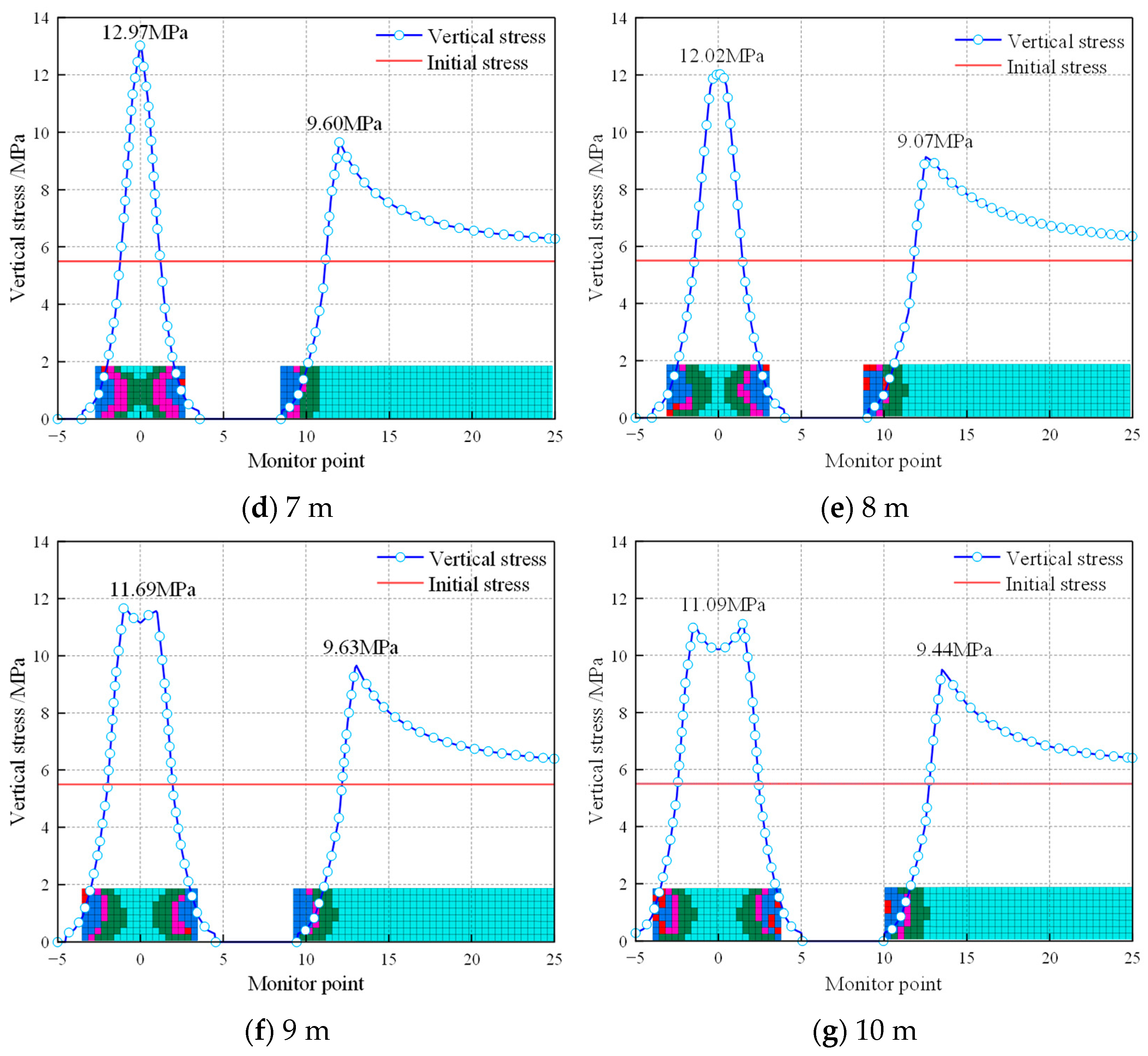
4.2.2. Bearing Characteristics of Different Coal Pillar Widths During the Mining of the 2109 Working Face
- (1)
- For a 5 m coal pillar, the vertical stress measured 3.69 MPa, which was below the initial stress (0.67 times). This indicates the occurrence of yield failure in the coal pillar, predominantly characterized by a plastic failure network structure, with minimal presence in the elastic zone.
- (2)
- In the 6 m coal pillar, the peak stress reached 8.5 MPa, exceeding the initial stress (1.55 times). This suggests that the coal pillar retained some bearing capacity, with a minor elastic component present and incomplete plastic failure development.
- (3)
- When the coal pillar measured 7 m, the peak stress increased to 12.97 MPa (2.36 times the initial stress). While the bearing capacity became more pronounced, the coal pillar remained unstable due to extensive plastic failure grids and plastic infiltration.
- (4)
- For the 8 m coal pillar, the stress curve exhibited an approximate double-peak pattern, with a peak stress of 12.02 MPa (2.19 times the initial stress). The elastic core width measured merely 1 m, showing increased width and grid count in the elastic zone compared to the 7 m pillar, alongside a significant reduction in plastic zone grids.
- (5)
- In the 9 m and 10 m coal pillars, the peak stress demonstrated a distinct bimodal pattern, measuring 11.69 MPa (2.13 times the initial stress) and 11.09 MPa (2.02 times the initial stress), which were reduced compared with the 8 m coal pillar. By contrast, the width of the elastic core area and the number of grids in the elastic zone significantly increased, and the bearing capacity and stability were improved.
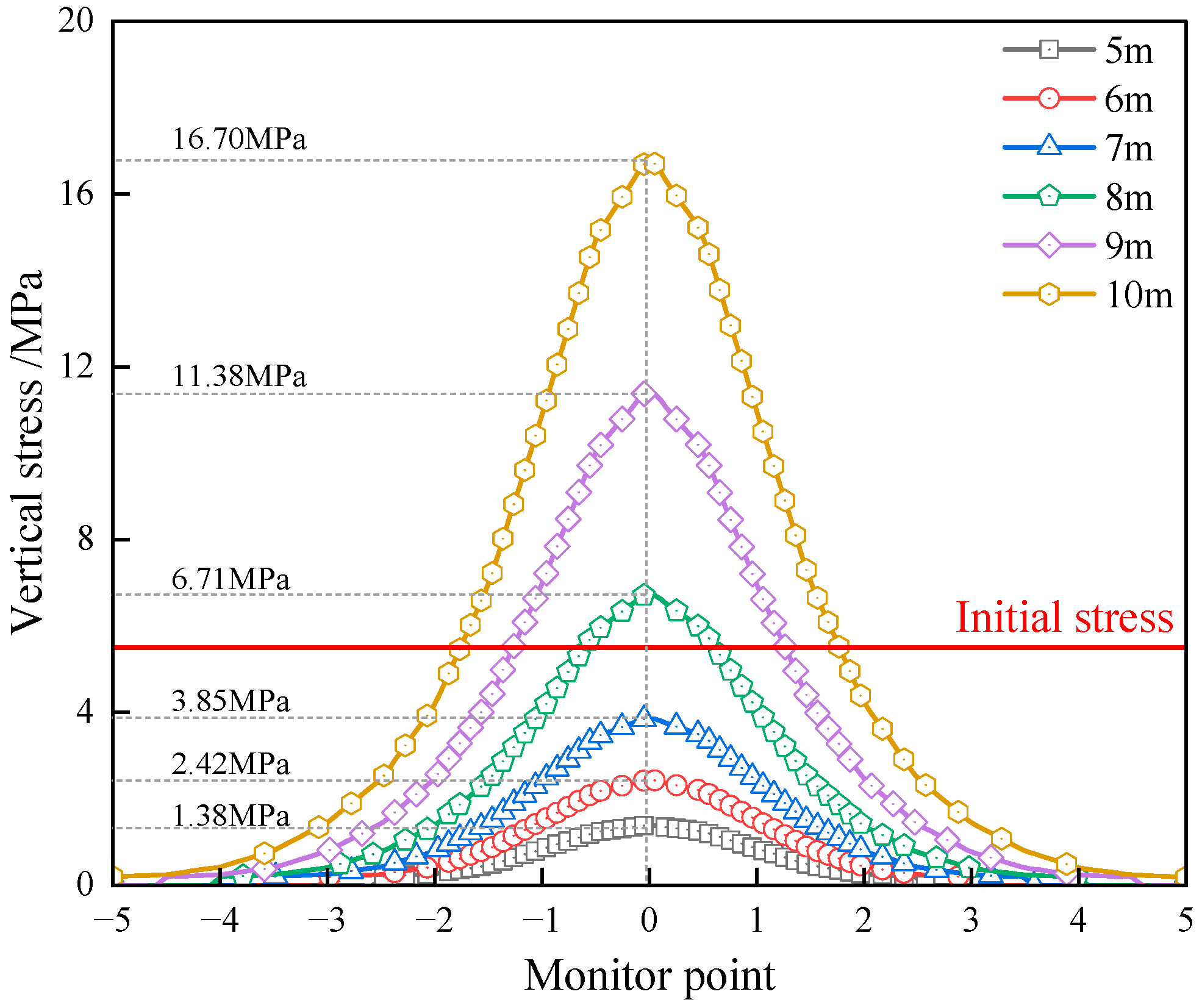
4.2.3. Bearing Characteristics of Different Coal Pillar Widths During the Mining of the 2110 Working Face
- (1)
- The vertical stress curves of coal pillars with varying widths during secondary mining exhibited unimodal distributions that were symmetrical about the coal pillar’s centerline. As the width of the coal pillar increased, both the vertical stress curve and its peak value demonstrated corresponding growth. The maximum vertical stress for 5 m to 7 m coal pillars remained significantly below the initial stress. In contrast, the 8 m coal pillar showed a maximum vertical stress slightly exceeding the initial stress, while the 9 m and 10 m coal pillars exhibited maximum vertical stresses that were 2.07 and 3.04 times the initial stress.
- (2)
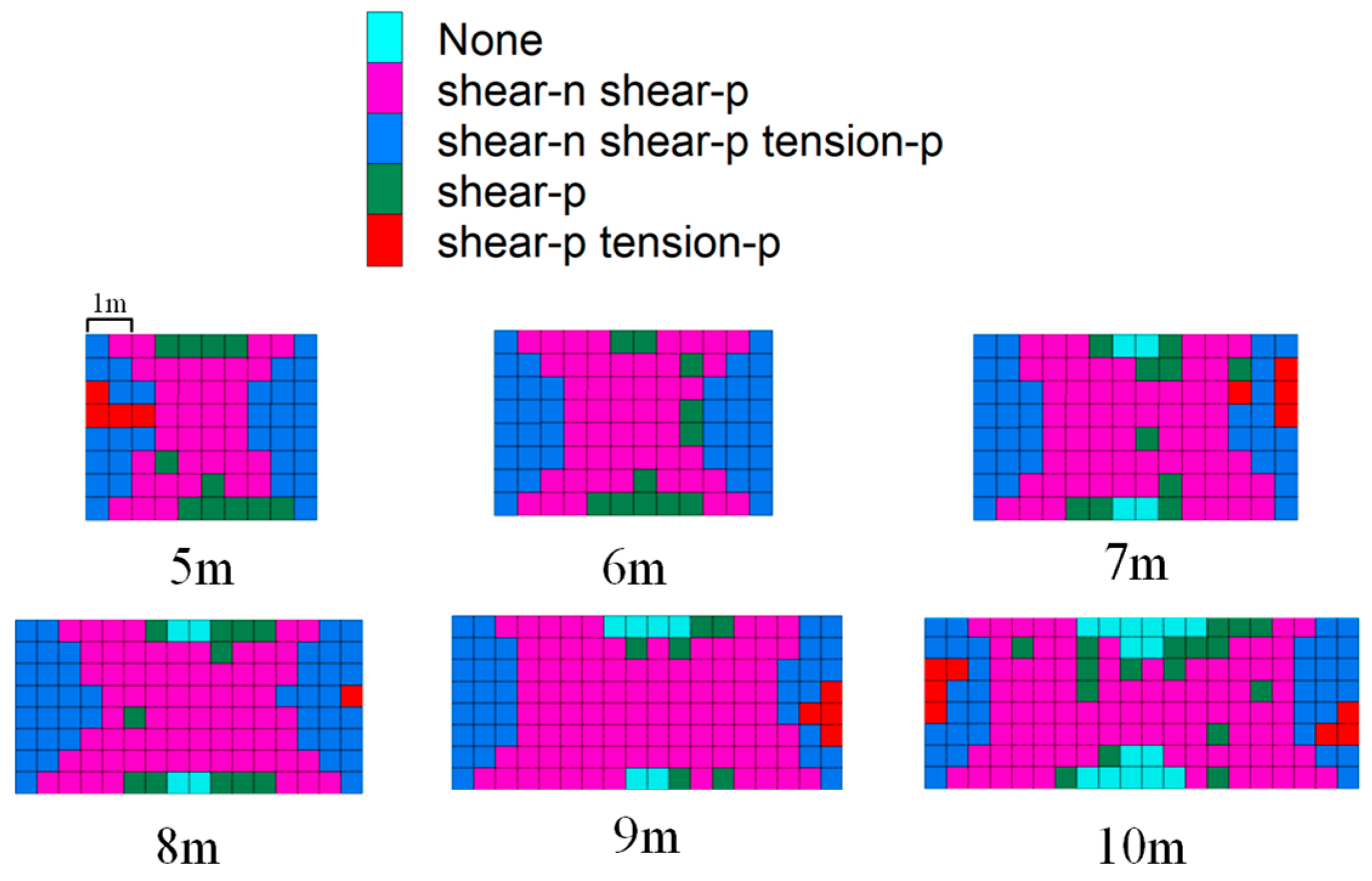
- The analysis of the plastic zone contour diagram reveals that the lattice structures of both 5 m and 6 m coal pillars underwent plastic failure. When the coal pillar width exceeded 7 m, the majority of the lattice structures experienced plastic failure, with only a limited number of elastic lattices remaining. The plastic zones beneath each coal pillar width were fully penetrated, leaving no elastic core area. However, as the coal pillar width increased, there was a gradual augmentation in the number of lattice structures within the elastic zone.
4.3. Analysis of Coal Pillar Stability Under the Influence of Full Dynamic Pressure
- (1)
- Following the primary mining operation, with the exception of the 5 m coal pillar, which exhibited a stress reduction of 2.39 MPa, all other width categories demonstrated stress increments of 0.55 MPa, 3.76 MPa, 3.09 MPa, 3.37 MPa, and 3.08 MPa. Notably, the stress increase in coal pillars of 7 m and above in width showed minimal variation. Concurrently, the elastic zone and its proportional extent across different width categories experienced measurable reductions. These observations indicate that while coal pillars of 6 m and above maintained load-bearing capacity under first mining stress conditions, the internal plastic zone underwent progressive development. This suggests a dual state of maintained structural integrity coupled with internal plastic deformation.
- (2)
- Subsequent to the second mining phase, comparative analysis revealed stress reductions of 2.31 MPa, 6.08 MPa, 9.12 MPa, 5.31 MPa, and 0.31 MPa in 5 m to 9 m coal pillars, respectively, in contrast to a 5.61 MPa increase in the 10 m pillar. The vertical stress in 5 m–7 m coal pillars fell below initial stress levels, indicating structural failure and complete loss of bearing capacity, as evidenced by the absence or minimal presence of elastic zones. Conversely, the 8 m and 9 m coal pillars, while maintaining stress levels above initial values, demonstrated reduced peak stress, signifying their transition into the plastic yield stage. Although these pillars retained residual bearing capacity, their elastic zones remained substantially diminished.
5. Field Industrial Experiment
6. Conclusions
- (1)
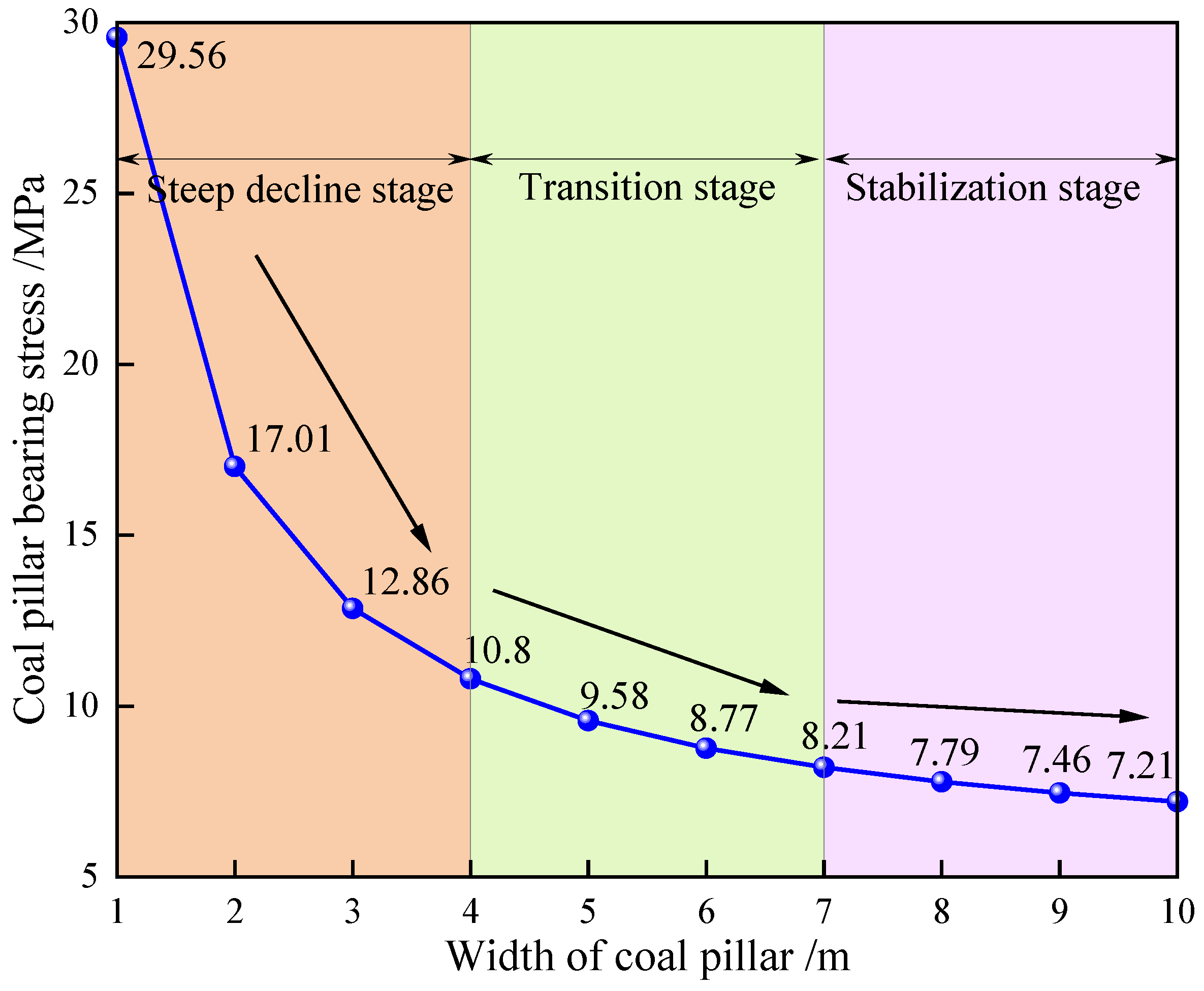
- A comprehensive mechanical model of the immediate roof following upper section working face mining was developed, incorporating the derived relationship between the coal pillar bearing load and the immediate roof length. The bearing stress characteristics of coal pillars in Qingwa Coal Mine were categorized into three distinct phases: the steep decline stage (0–4 m), transition stage (4–7 m), and stabilization stage (>7 m). Coal pillars within the stabilization phase’s width range demonstrated measurable strength surplus capacity, indicating enhanced structural integrity.
- (2)
- Through numerical simulation analysis, the bearing characteristics of 5 m–10 m coal pillars were systematically examined across roadway excavation, first mining, and second mining. The investigation revealed that, for 5 m–7 m pillars, significant internal stress superposition occurred, manifesting as a single-hump distribution pattern with progressively increasing peak stress. Conversely, 8 m–10 m pillars exhibited reduced internal stress superposition, characterized by a double-hump distribution pattern with gradually decreasing peak stress. During the first mining operation, the vertical stress distribution within the pillars transitioned from single-hump to double-hump configurations as the width increased. Second mining analysis demonstrated complete plastic failure in the 5 m and 6 m coal pillar meshes, while the 7 m and wider pillars showed extensive plastic damage with fully penetrated plastic zones across all width categories.
- (3)
- Under the influence of full dynamic pressure, the 5–7 m coal pillars yielded and were destroyed, whereas the 8 m and above coal pillars had certain residual bearing capacity, compared with the first mining. After the second mining, the elastic zone grid of each width of the coal pillar was sharply reduced. The 5 m and 6 m coal pillars were no longer in the elastic grid, whereas the elastic zone grid area and proportion of the 7 m and above coal pillars were very low. In order to avoid plastic zone penetration after the first mining, it was determined that the optimal width of NCPDRE was 8 m.
- (4)
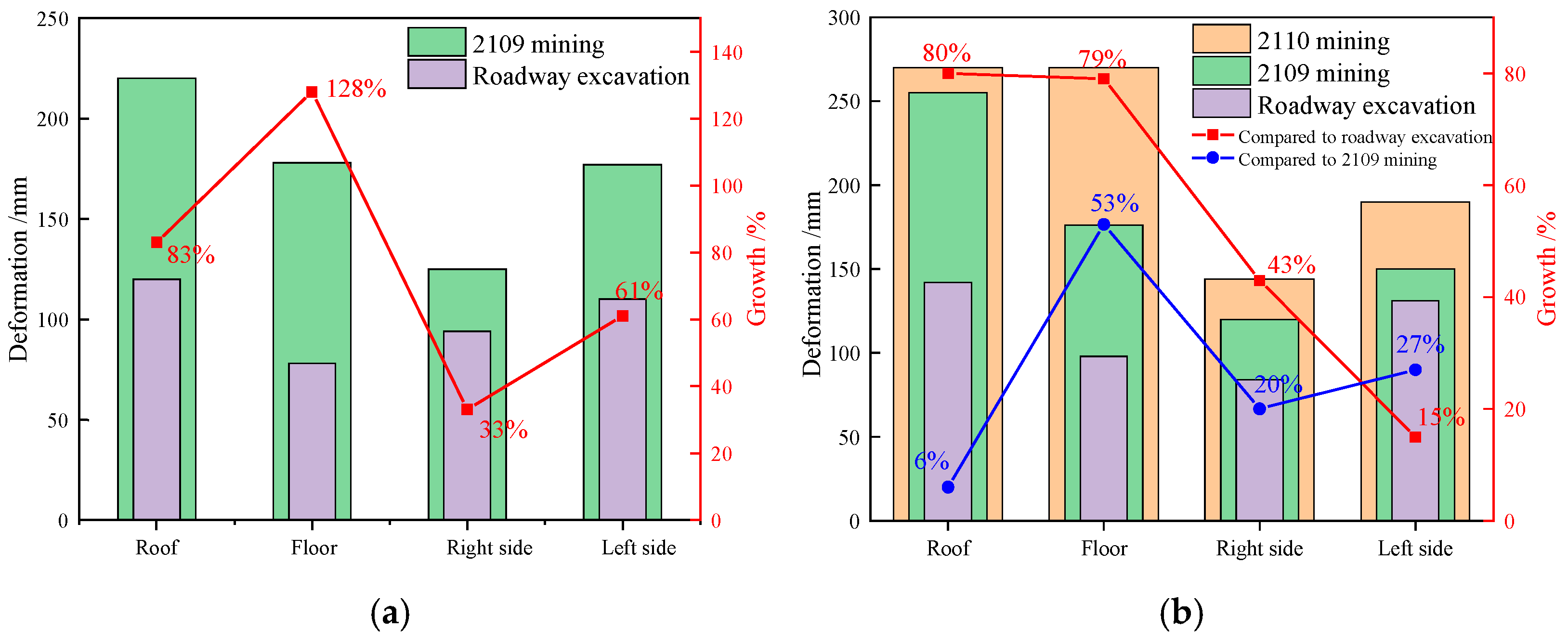
- The observation and analysis of the displacement of the roadway surface under the influence of full dynamic pressure showed that the first mining had a greater influence on the displacement of the roof and floor of the roadway, followed by the solid coal side, whereas the displacement of the coal pillar side was smaller; the second mining had a greater influence on the floor, followed by the coal pillar side and the solid coal side, whereas the displacement of the roof had a smaller influence.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ge, S.; Liu, S.; Liu, J.; Wang, B.; An, X.; Xiang, L. Effectiveness of secure supply and carbon reduction in the coal sector for strengthening the energy power of China. Strateg. Study CAE 2024, 26, 40–51. [Google Scholar]
- Wang, S. Thoughts about the main energy status of coal and green mining in China. China Coal 2020, 46, 11–16. [Google Scholar]
- Ge, S.; Fan, J.; Liu, S.; Song, M.; Xian, Y.; Wang, B.; Teng, T. Low carbon modern coal-based energy technology system and development strategy. J. China Coal Soc. 2024, 49, 203–223. [Google Scholar]
- Yuan, L. Strategic conception of carbon neutralization in coal industry. Strateg. Study CAE 2023, 25, 103–110. [Google Scholar] [CrossRef]
- Yu, Y.; Liang, H.; Chen, Y.; Zhao, X. Study on spatiotemporal effect and control technology of roadway driving face to mining. Coal Technol. 2018, 37, 18–21. [Google Scholar]
- Jia, H.; Zhang, Z.; Liu, S.; Peng, B.; Yu, H.; Shao, S.; Wang, Y. Research on dissimilation characteristics and control method of failure of surrounding rock in the roadway with repeated mining of steep and ultra-close multiple coal seam. Coal Sci. Technol. 2025, 53, 67–79. [Google Scholar]
- Kumar, R.; Mandal, P.K.; Ghosh, N.; Das, A.J.; Banerjee, G. Design of Stable Parallelepiped Coal Pillars Considering Geotechnical Uncertainties. Rock Mech. Rock Eng. 2023, 56, 6581–6602. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Xu, G.; Gao, X.; Liu, Q.; Li, Z.; Liu, J. Lateral abutment pressure distribution and evolution in wide pillars under the first mining effect. Int. J. Min. Sci. Technol. 2023, 33, 309–322. [Google Scholar] [CrossRef]
- Tai, Y.; Yu, B.; Xia, B.; Li, Z.; Xia, H. Research on stress release for the gob-side roadway using the roof-cutting technology with a chainsaw arm. R. Soc. Open Sci. 2020, 7, 191663. [Google Scholar] [CrossRef]
- Xia, Z.; Yao, Q.; Xu, Q.; Ma, J.; Liu, Z. Numerical-modeling-based assessment of the impact of two-end-type cable support on failure characteristics of yield pillars. Eng. Fail. Anal. 2021, 128, 105619. [Google Scholar] [CrossRef]
- Wang, M.; Wang, W.; Xu, Y.; Xie, G.; Qin, J.; Liu, H.; Wei, S.; Xu, Q. Study on the new layout pattern about the gob-side entry under dynamic pressure and its surrounding rock stability control. Energy Sci. Eng. 2024, 12, 1389–1410. [Google Scholar] [CrossRef]
- Bai, W.; Xu, Q.; Li, Y.; Li, T. Reasonable width of coal pillar between roadways during double lane driving with large mining height. Saf. Coal Mines 2019, 50, 212–215. [Google Scholar]
- Huang, W.; Liu, S.; Gao, M.; Hou, T.; Wang, X.; Zhao, T.; Sui, L.; Xie, Z. Improvement of Reinforcement Performance and Engineering Application of Small Coal Pillars Arranged in Double Roadways. Sustainability 2023, 15, 292. [Google Scholar] [CrossRef]
- He, Y.; Li, J. Stress Distribution and Optimum Spacing Determination of Double-Withdrawal-Channel Surrounding Rocks: A Case Study of Chinese Coal Mine. Shock Vib. 2021, 2021, 9973634. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, F.; Wang, C.; Li, X.; Li, Q. Stability and control of surrounding rock in double lane tunneling with deep high stress. China Min. Mag. 2022, 31, 104–112. [Google Scholar]
- Li, C.; Xin, D.; Liu, Y.; Chen, T. A Case Study on Strong Strata Behaviors Mechanism of Mining Reserved Roadway and Its Prevention Techniques. Processes 2023, 11, 1341. [Google Scholar] [CrossRef]
- Qian, D.; Jiao, H.; Deng, J.; Yang, J.; Jiao, M.; Xian, G.; Yu, C.; Zhu, Y.; Liu, J.; Huang, S.; et al. Instability Mechanism, Pressure Relief, and Long Anchorage Control Countermeasures for Surrounding Rock of Strong Mining Roadway at Large Mining Height Working Face. Minerals 2023, 13, 391. [Google Scholar] [CrossRef]
- Liu, S.; Bai, J.; Wang, X.; Wang, G.; Wu, B.; Li, Y.; Zhao, J. Study on the Stability of Coal Pillars Under the Disturbance of Repeated Mining in a Double-Roadway Layout System. Front. Earth Sci. 2021, 9, 754747. [Google Scholar] [CrossRef]
- Han, B.; Zhang, C.; Zhang, C.; Wang, S. Mechanism of pressure relief for double roadway arrangement in thick coal seam. J. Taiyuan Univ. Technol. 2024, 55, 989–999. [Google Scholar]
- Wu, X.; Liu, H.; Li, J.; Guo, X.; Lu, K.; Wang, J. Temporal-spatial evolutionary law of plastic zone and stability control in repetitive mining roadway. J. China Coal Soc. 2020, 45, 3389–3400. [Google Scholar]
- Wu, X.; Wang, J.; Chen, S.; Zhang, Y.; Bu, Q. Regulation principle and stability control of plastic zone in repeated mining roadway. Rock Soil Mech. 2022, 43, 205–217. [Google Scholar]
- Wu, X.; Pang, Z.; Zhao, S.; Zhang, Y.; Lv, K.; Wang, S. Scale-span evolution law mechanical mechanism of surrounding rock cracks in repeated mining roadway. J. China Coal Soc. 2024, 49, 579–592. [Google Scholar]
- Wu, X.; Wang, J.; Guo, X.; Wang, E.; Cao, J. Morphological characteristics and quantitative discriminant method of superimposed plastic zone expansion of surrounding rock of repeated mining roadway. J. China Univ. Min. Technol. 2024, 53, 46–58+105. [Google Scholar]
- Liu, J.; Lv, K.; Wu, Z.; Zhao, B.; Wang, P.; Sun, X.; Cao, J. Study on failure mechanism and control of surrounding rock of secondary mining roadway in thick and hard roof coal seam. Met. Mine 2024, 12, 77–87. [Google Scholar]
- Fan, L.; Chang, J.; Wang, W.; Yuan, C.; Wu, H.; Qi, C. Research on the influencing factors and evolution law of structural stability of surrounding rock of mining roadway. J. Min. Saf. Eng. 2025, 42, 589–600. [Google Scholar]
- Skrzypkowski, K. Comparative Analysis of the Mining Cribs Models Filled with Gangue. Energies 2020, 13, 5290. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Yang, A.; Feghali, P.; Skrzypkowski, K. Structural Evaluation of Cable Bolts under Static Loading. Appl. Sci. 2023, 13, 1326. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Bai, J.; Wu, B.; Wu, W. Research on the failure mechanism and control technology of surrounding rock in gob-side entry driving under unstable overlying strata. Eng. Fail. Anal. 2022, 138, 106361. [Google Scholar] [CrossRef]
- He, M.; Zhu, G.; Guo, Z. Longwall mining “cutting cantilever beam theory” and 110 mining method in China—The third mining science innovation. J. Rock Mech. Geotech. Eng. 2015, 7, 483–492. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Jiang, J.; Sun, Z. Y-shaped ventilation air leakage law of working face of gob-side entry retaining by cutting roof to release pressure. J. Min. Saf. Eng. 2021, 38, 625–633. [Google Scholar]
- Liu, X.; Hua, X.; Yang, P.; Huang, Z. A study of the mechanical structure of the direct roof during the whole process of non-pillar gob-side entry retaining by roof cutting. Energy Explor. Exploit. 2020, 38, 1706–1724. [Google Scholar] [CrossRef]
- Guo, Y.; Lu, C.; He, Z.; Song, J. Numerical and Field Investigations of Tremors Induced by Thick-Hard Strata Fracture. Appl. Sci. 2022, 12, 11151. [Google Scholar] [CrossRef]
- Wang, M.; Xu, Y.; Xu, Q.; Shan, C.; Li, Z.; Nan, H.; Li, Y.; Liu, H.; Chu, T. Stability control of overburden and coal pillars in the gob-side entry under dynamic pressure. Int. J. Rock Mech. Min. Sci. 2023, 170, 105490. [Google Scholar] [CrossRef]
- Xia, B.; Gong, T.; Yu, B.; Zhou, L. Numerical simulation method for stope underground pressure in whole process of longwall mining. J. China Coal Soc. 2017, 42, 2235–2244. [Google Scholar]
- Shan, C.; Qi, S.; Xie, G.; Qin, J.; Li, Y.; Huang, P.; Zhang, Q.; Ren, G. Study on Multi-scale strength and Control of Coal Pillar in Gob Side Entry of Fully Mechanized Top Coal Caving Face in “Double Hard’ Seam. Coal Technol. 2023, 42, 63–68. [Google Scholar]
- Sabapathy, R.; Mandal, P.K.; Paul, P.S.; Das, A.J. Evaluation of potentiality of coal bump hazard in underground coal mines through numerical modelling and binary logistic regression approach with field validation. Bull. Eng. Geol. Environ. 2025, 84, 333. [Google Scholar] [CrossRef]
- Matinpour, F.; Majdi, A. Determining the abutment angle in longwall coal mining using NLMR, GEP and GEO techniques. Earth Sci. Inform. 2025, 18, 358. [Google Scholar] [CrossRef]
- Salamon, M.D.G. Mechanism of caving in longwall coal mining. In Rock Mechanics Contributions and Challenges, Proceedings of the 31st U.S. Symposium, Golden, CO, USA, 18–20 June 1990; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Bai, M.; Kendorski, F.S.; Van Roosendaal, D.J. Chinese and North American high-extraction underground coal mining strata behavior and water protection experience and guidelines. In Proceedings of the Conference on Ground Control in Mining, Morgantown, WV, USA, 1–3 August 1995. [Google Scholar]
- Zhang, Y. Research and Application of Reserved Narrow Coal Pillar Roof Cutting and Pressure Relief Technology in Qingyun Coal Industry. Shandong Coal Sci. Technol. 2023, 41, 27–31. [Google Scholar]




| Immediate Roof Lithology | Compressive Strength/MPa | c1 | c2 |
|---|---|---|---|
| hard | >40 | 2.1 | 16 |
| medium hard | 20–40 | 4.7 | 19 |
| weak | <20 | 6.2 | 32 |
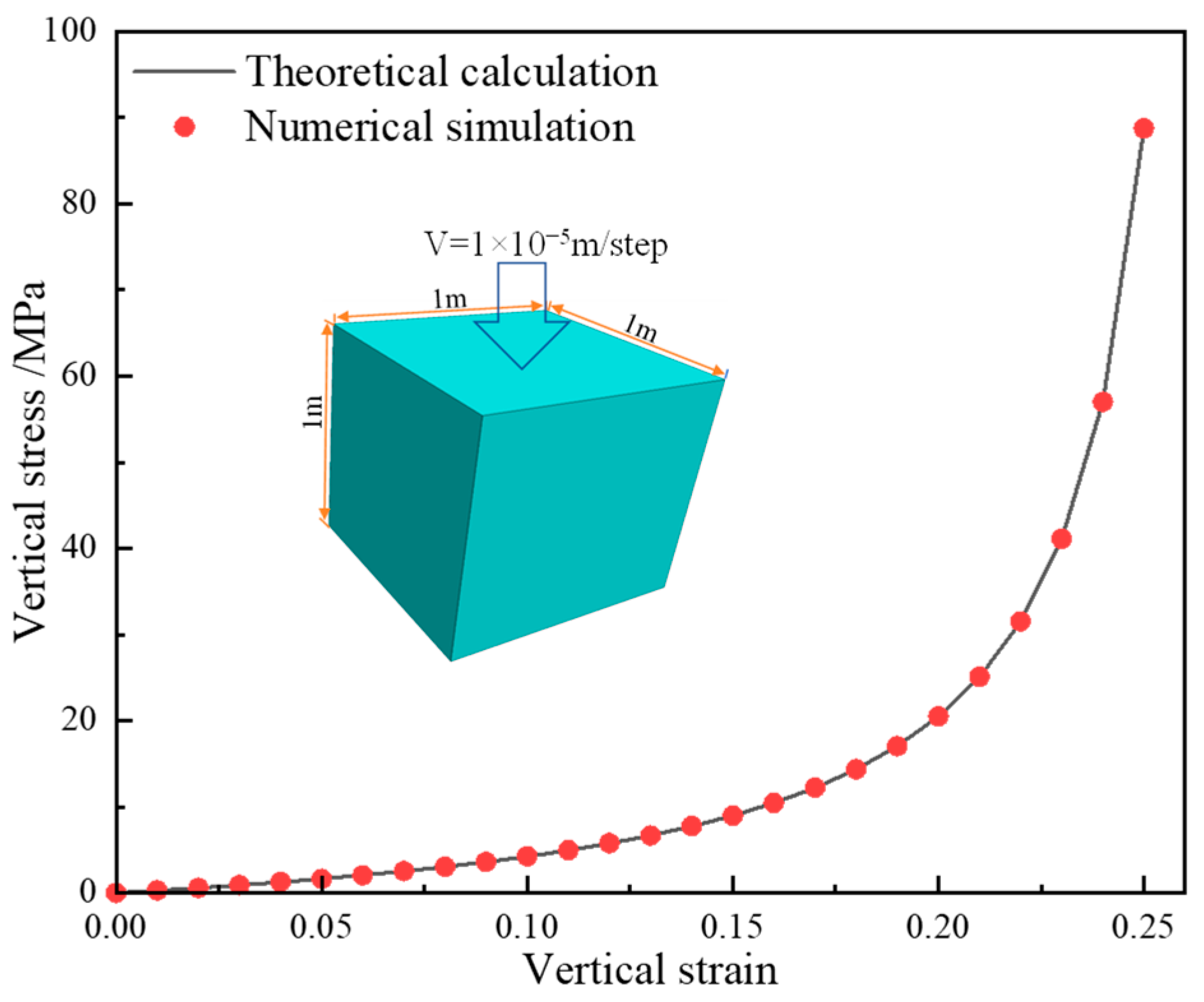
| Vertical strain εZ | 0 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 |
| Vertical stress σZ/MPa | 0 | 1.63 | 4.23 | 8.98 | 20.48 | 88.77 |
| Vertical strain εZ | 0 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 |
| Volume strain εp | 0 | 0.0375 | 0.075 | 0.1125 | 0.15 | 0.1875 |
| cap pressure pc/MPa | 0 | 0.54 | 1.41 | 2.99 | 6.83 | 29.59 |
| Bulk/GPa | Shear/GPa | Density/(kg × m−3) | Internal Friction Angle/° |
|---|---|---|---|
| 5.56 | 4.7 | 1800 | 20 |
| Layer | Bulk/GPa | Shear/GPa | Poisson’s Ratio | Internal Friction Angle f/° | Cohesion C/MPa |
|---|---|---|---|---|---|
| Siltstone | 2.01 | 1.76 | 0.27 | 38.05 | 0.71 |
| 2#Coal | 0.21 | 0.22 | 0.21 | 18.49 | 0.25 |
| Mudstone | 0.51 | 0.54 | 0.21 | 23.64 | 0.34 |
| Fine sandstone | 3.33 | 3.02 | 0.26 | 46.74 | 1.29 |
| Sandstone | 2.42 | 2.80 | 0.17 | 43.45 | 1.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, W.; Zhang, H.; Han, Z.; Tang, H.; Pei, J.; Wu, S.; Xu, D. Research on the Bearing Characteristics of Narrow Coal Pillars in Double-Roadway Excavation Under the Influence of Full Dynamic Pressure. Appl. Sci. 2025, 15, 7148. https://doi.org/10.3390/app15137148
Gu W, Zhang H, Han Z, Tang H, Pei J, Wu S, Xu D. Research on the Bearing Characteristics of Narrow Coal Pillars in Double-Roadway Excavation Under the Influence of Full Dynamic Pressure. Applied Sciences. 2025; 15(13):7148. https://doi.org/10.3390/app15137148
Chicago/Turabian StyleGu, Wei, Hao Zhang, Zhenfei Han, Haokun Tang, Jingyong Pei, Shixin Wu, and Dalong Xu. 2025. "Research on the Bearing Characteristics of Narrow Coal Pillars in Double-Roadway Excavation Under the Influence of Full Dynamic Pressure" Applied Sciences 15, no. 13: 7148. https://doi.org/10.3390/app15137148
APA StyleGu, W., Zhang, H., Han, Z., Tang, H., Pei, J., Wu, S., & Xu, D. (2025). Research on the Bearing Characteristics of Narrow Coal Pillars in Double-Roadway Excavation Under the Influence of Full Dynamic Pressure. Applied Sciences, 15(13), 7148. https://doi.org/10.3390/app15137148





