Formation of a Freezing Wall Around a Vertical Shaft Under Localized Freezing
Abstract
1. Introduction
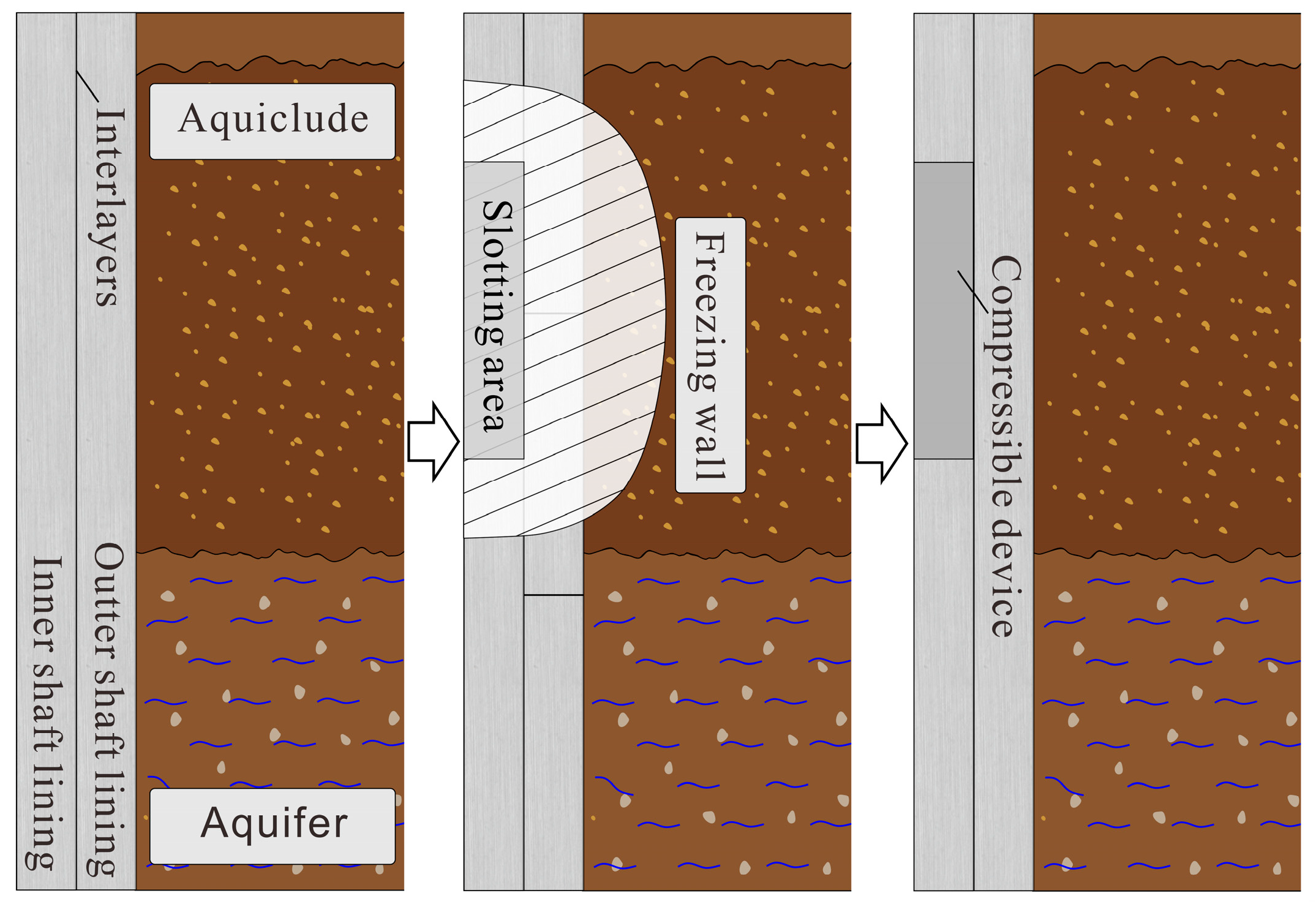
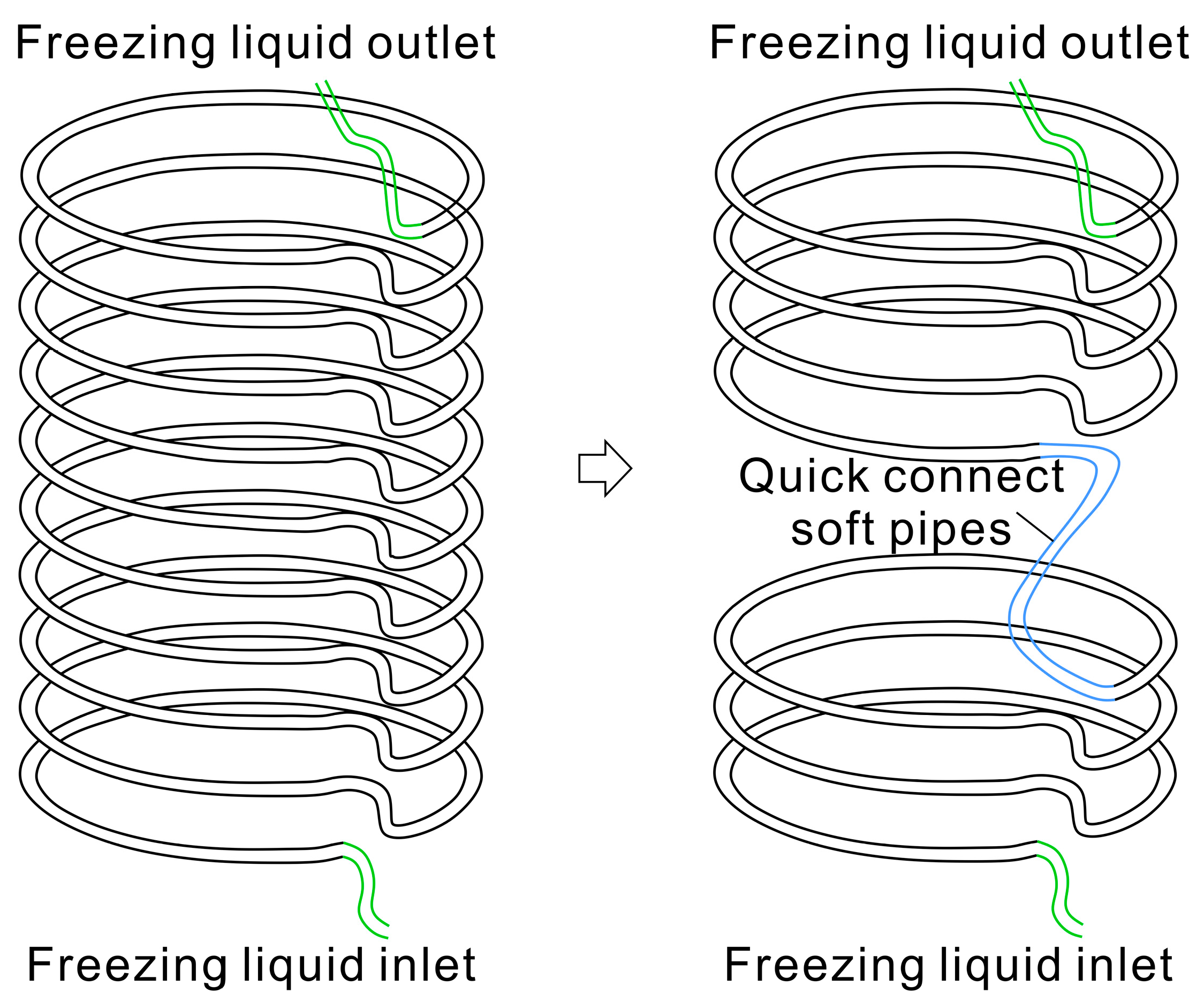
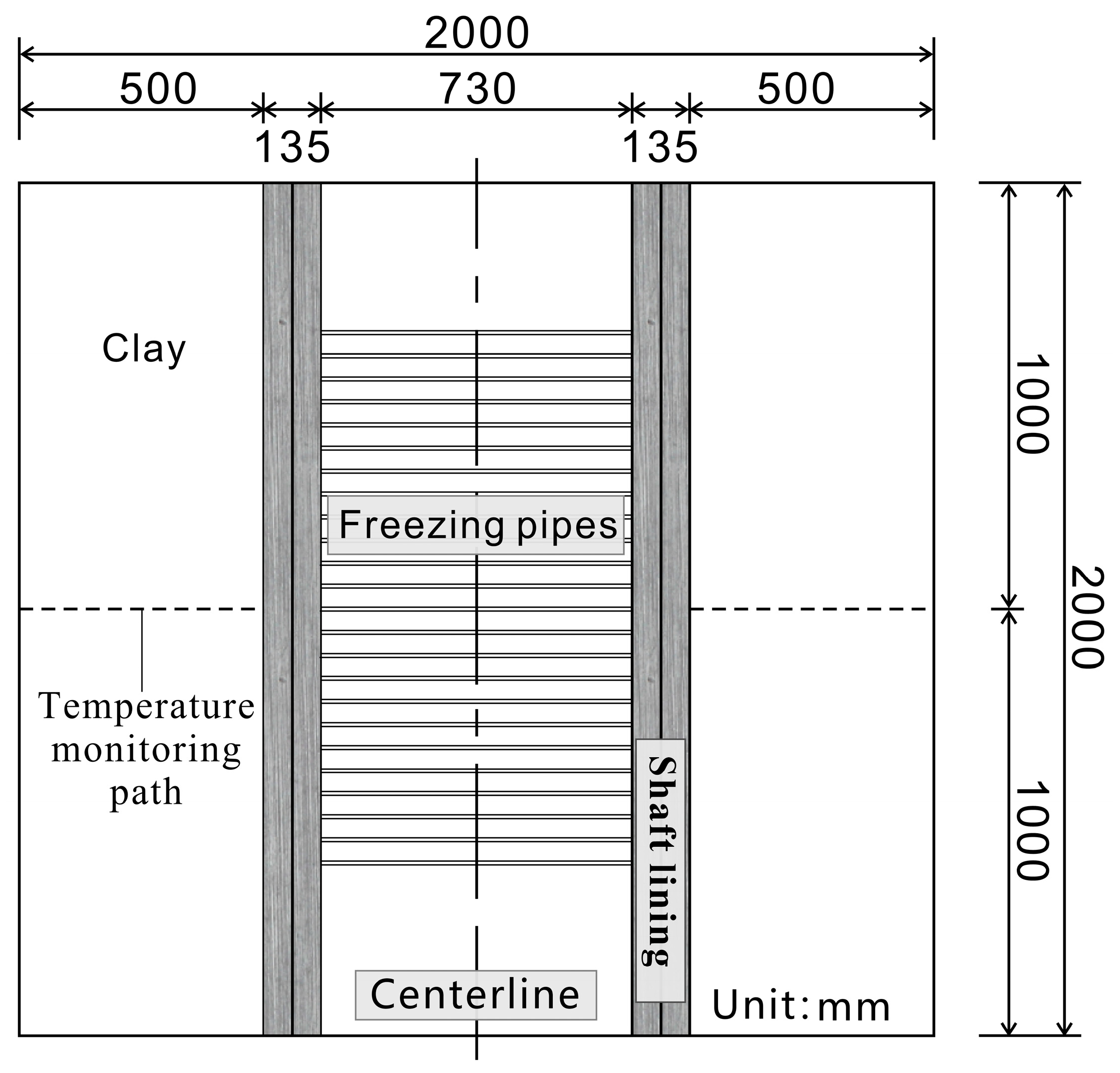
2. Technology of Shaft Lining Localized Freezing
3. Numerical Methodology
3.1. Governing Equation
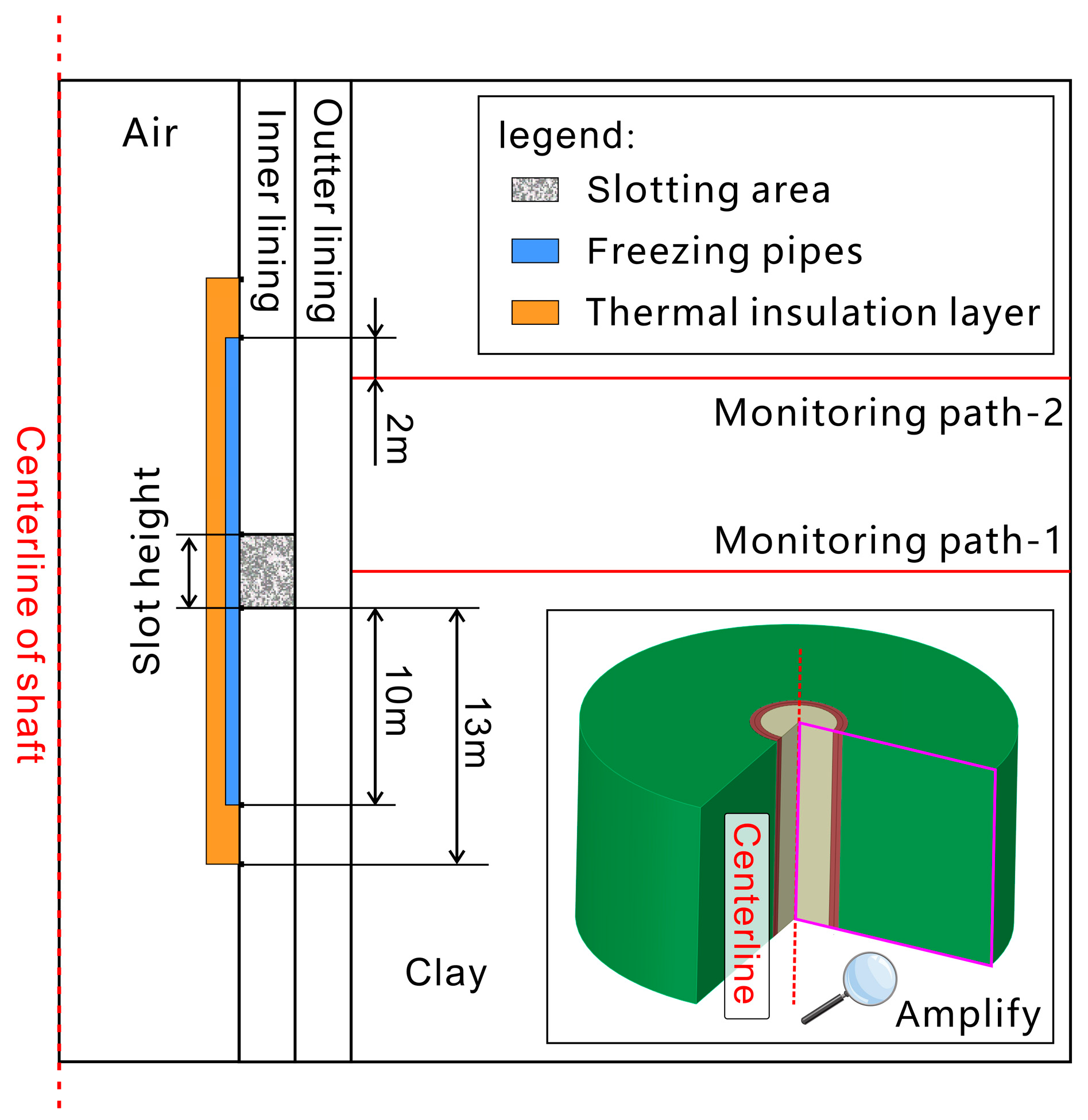
3.2. Initial and Boundary Conditions
3.3. Numerical Simulation Scheme
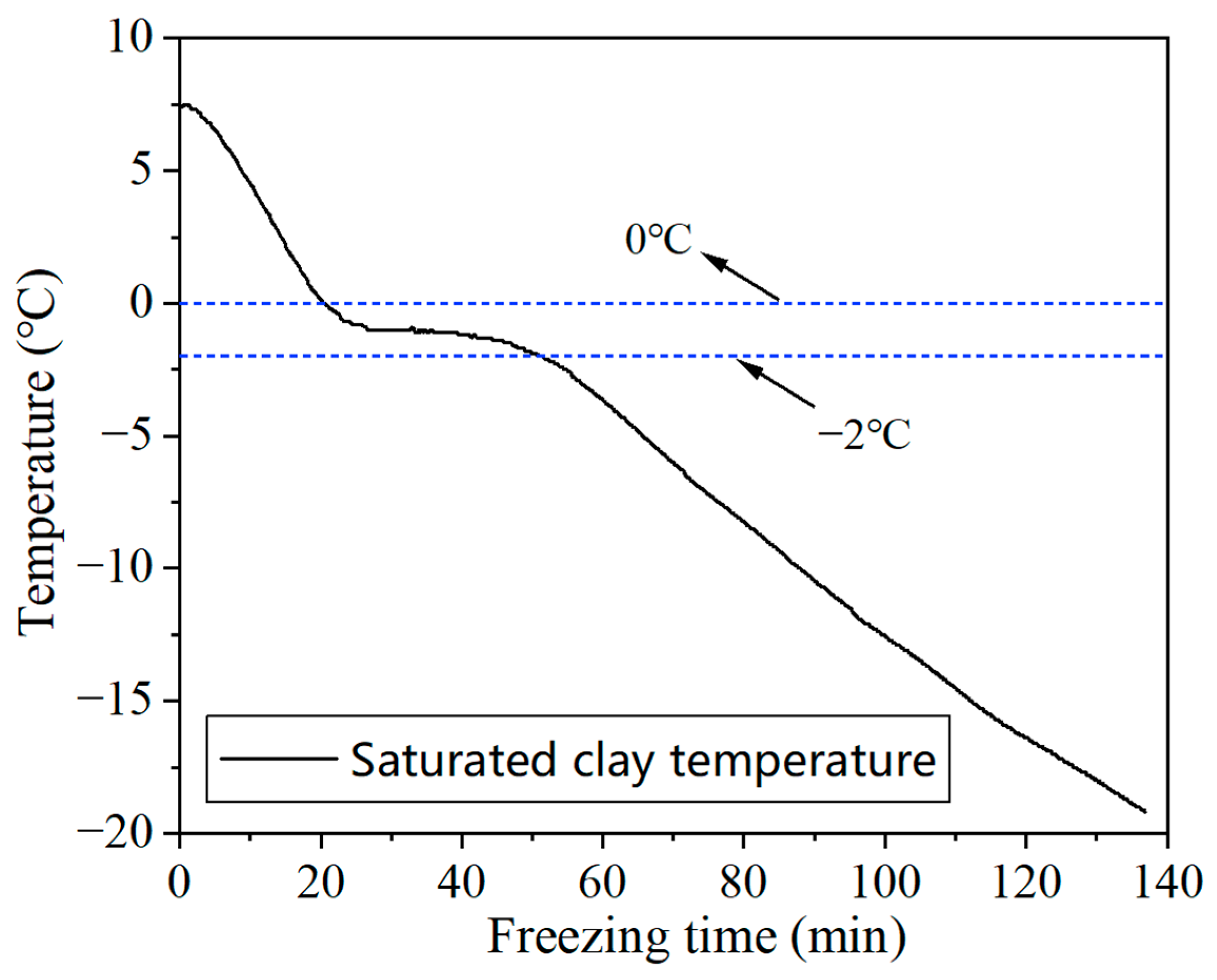
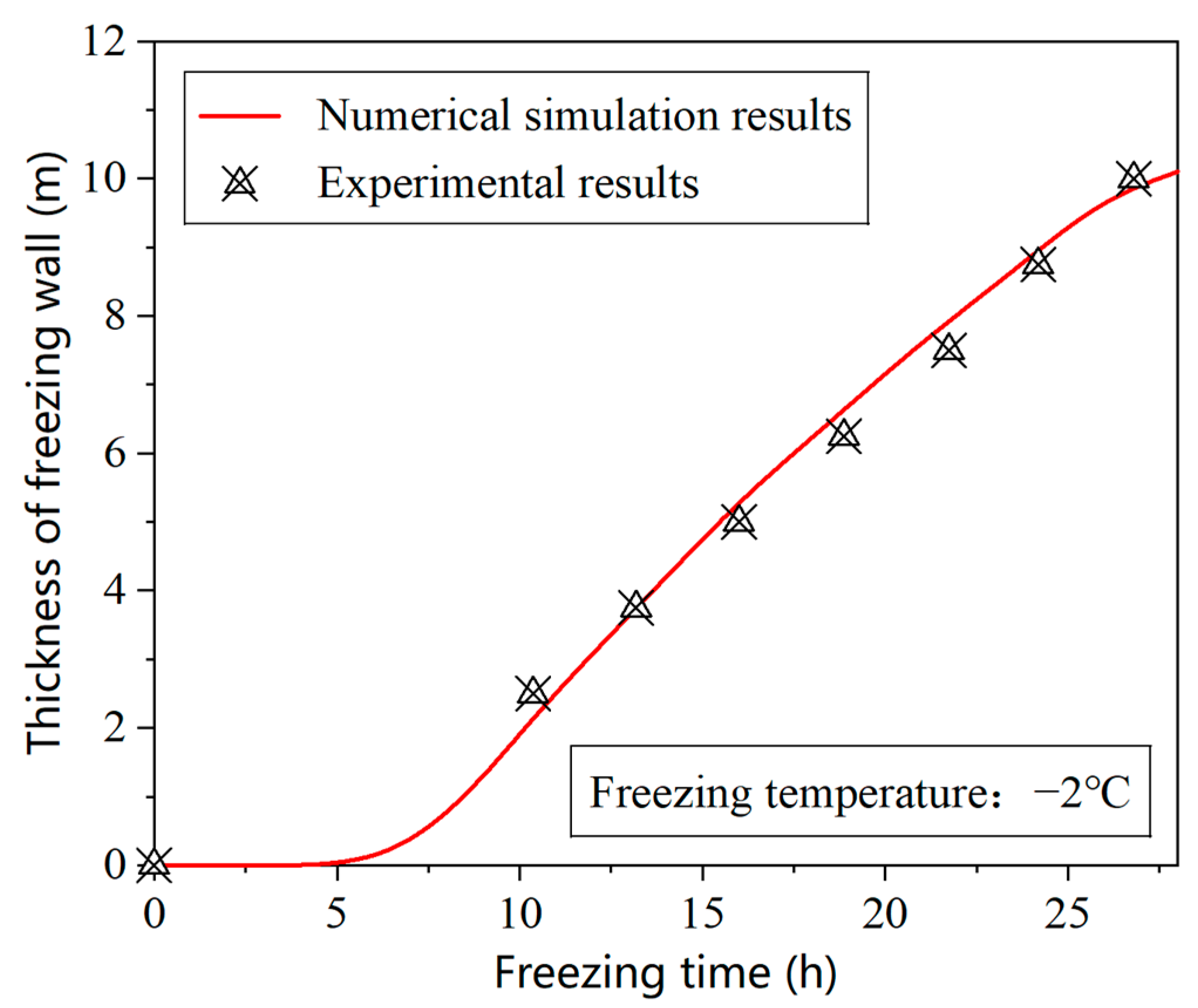
3.4. Model Validation
4. Results and Discussion
4.1. Evolution of the Freezing Wall During the Active Freezing Period
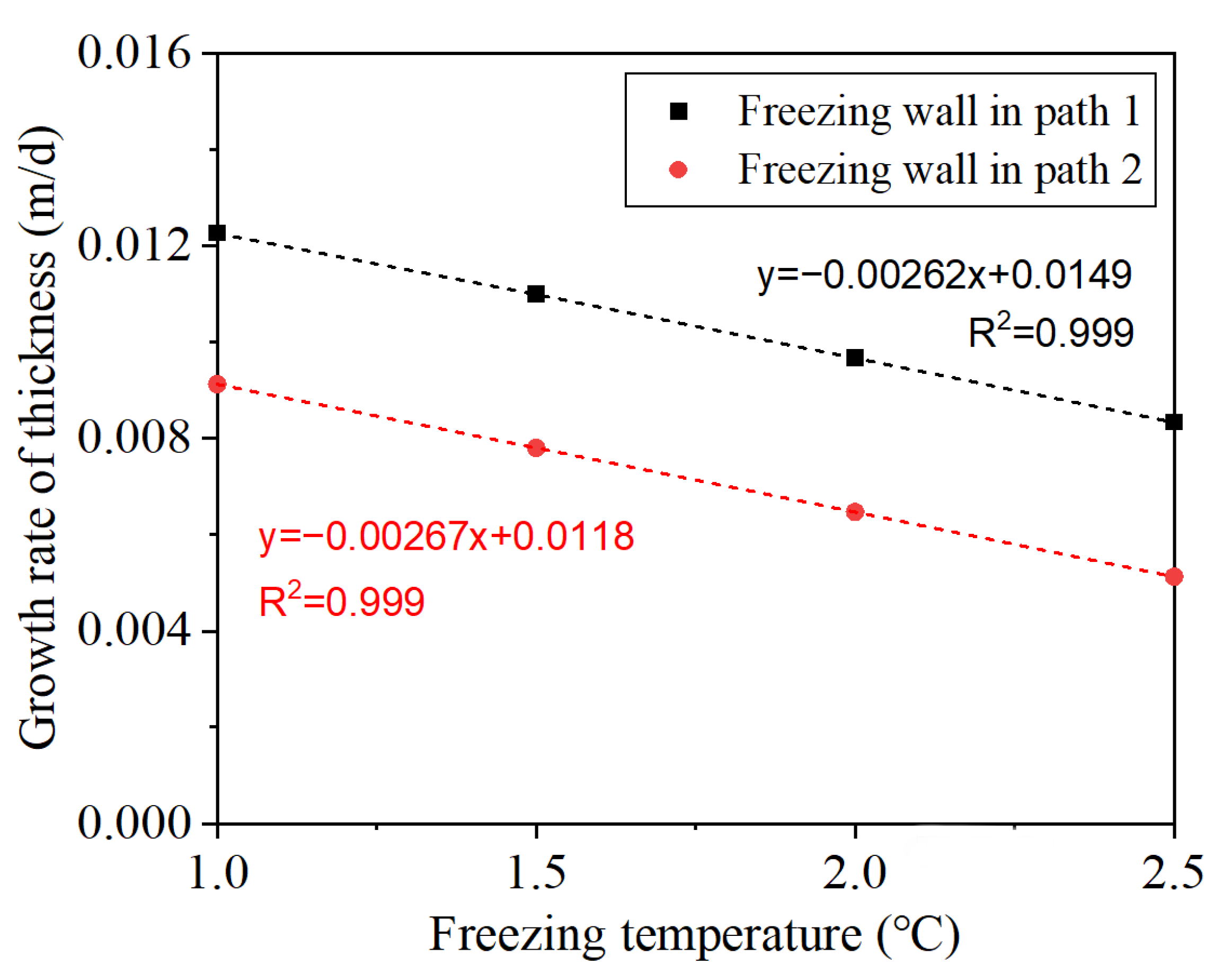
4.1.1. Morphology of the Freezing Wall Under Typical Parameters
4.1.2. Influence of Engineering Factors on the Evolution of the Freezing Wall
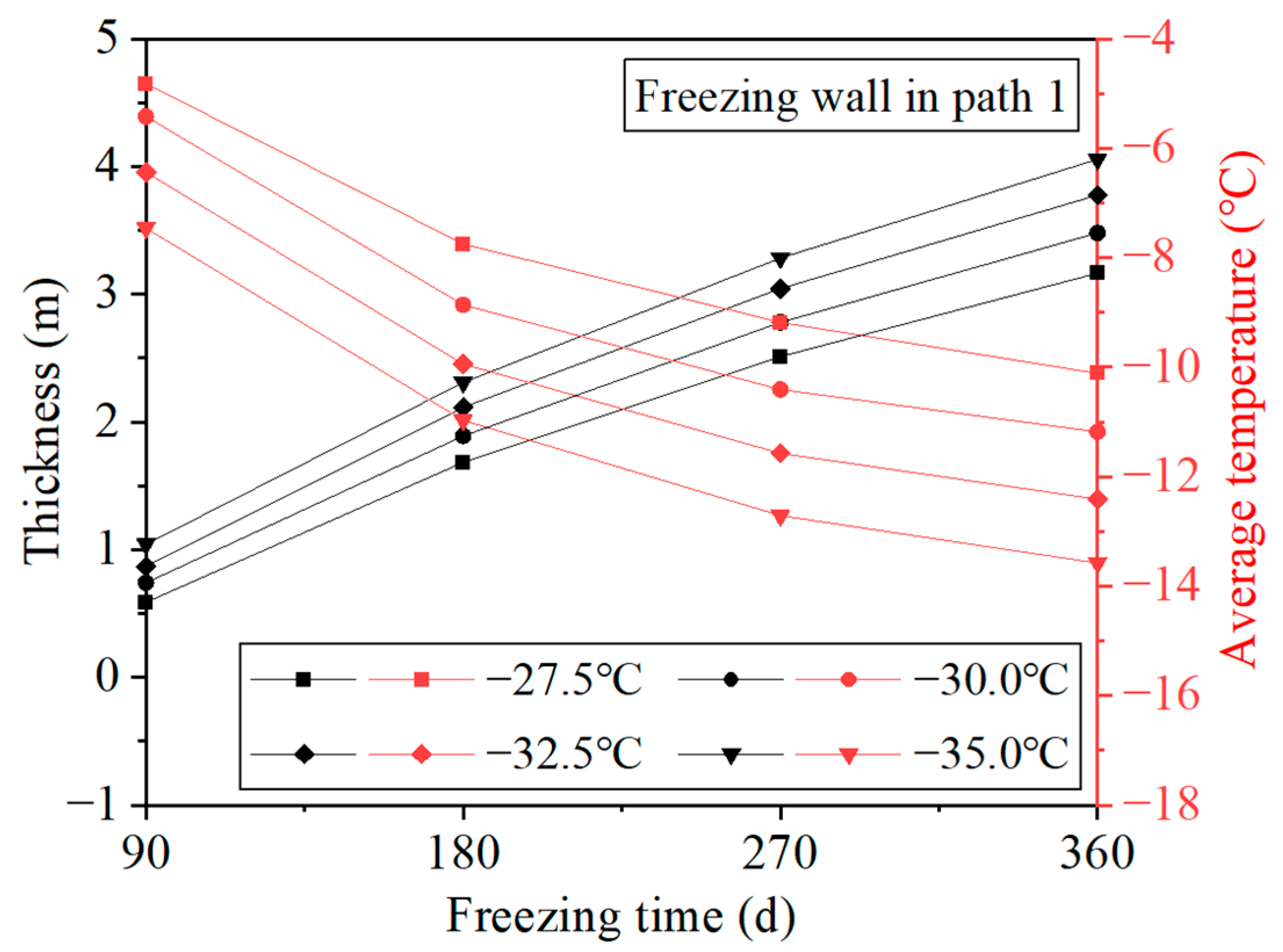
Freezing Temperature
Shaft Lining Thickness
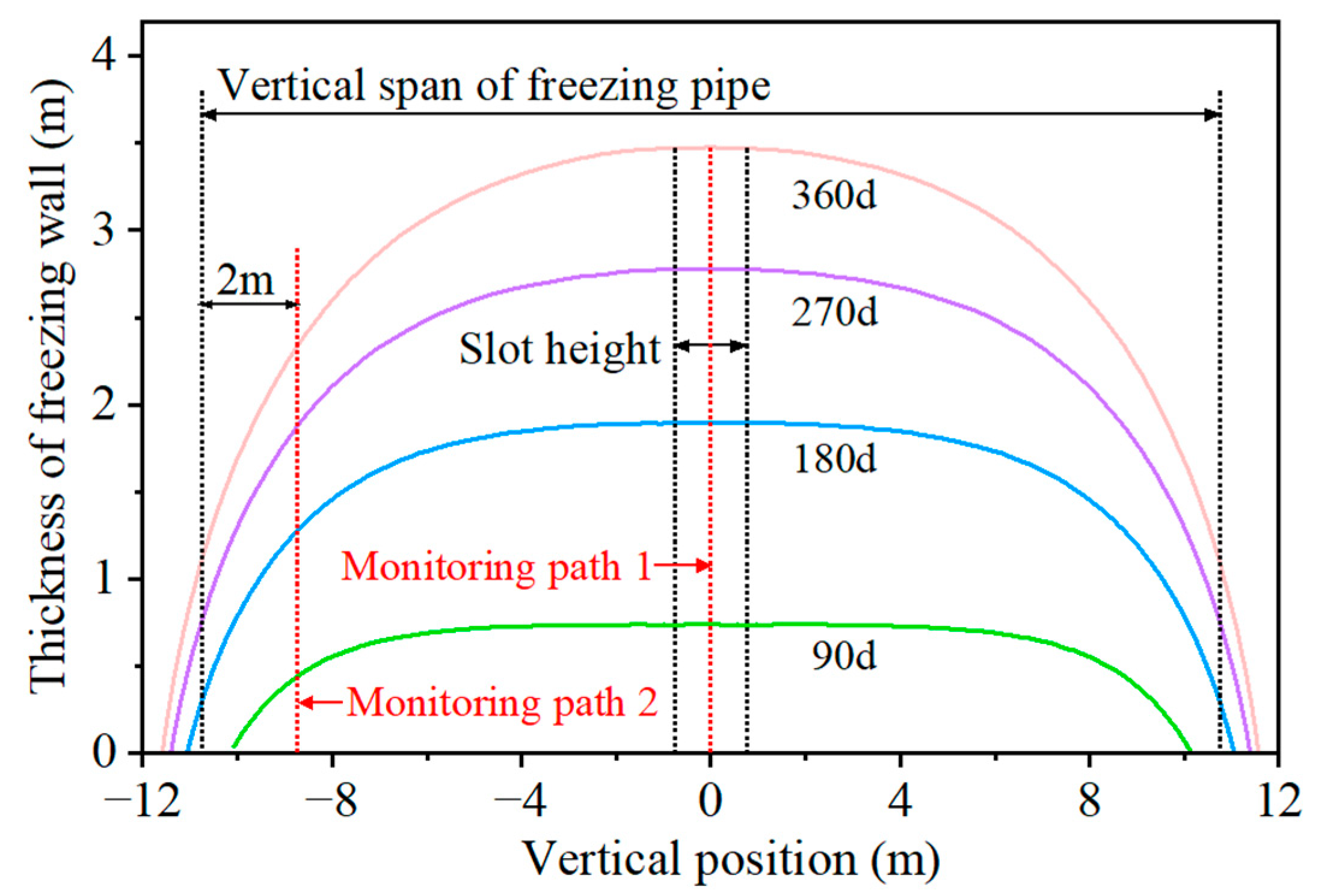
4.2. Evolution of the Freezing Wall During the Slotting Period
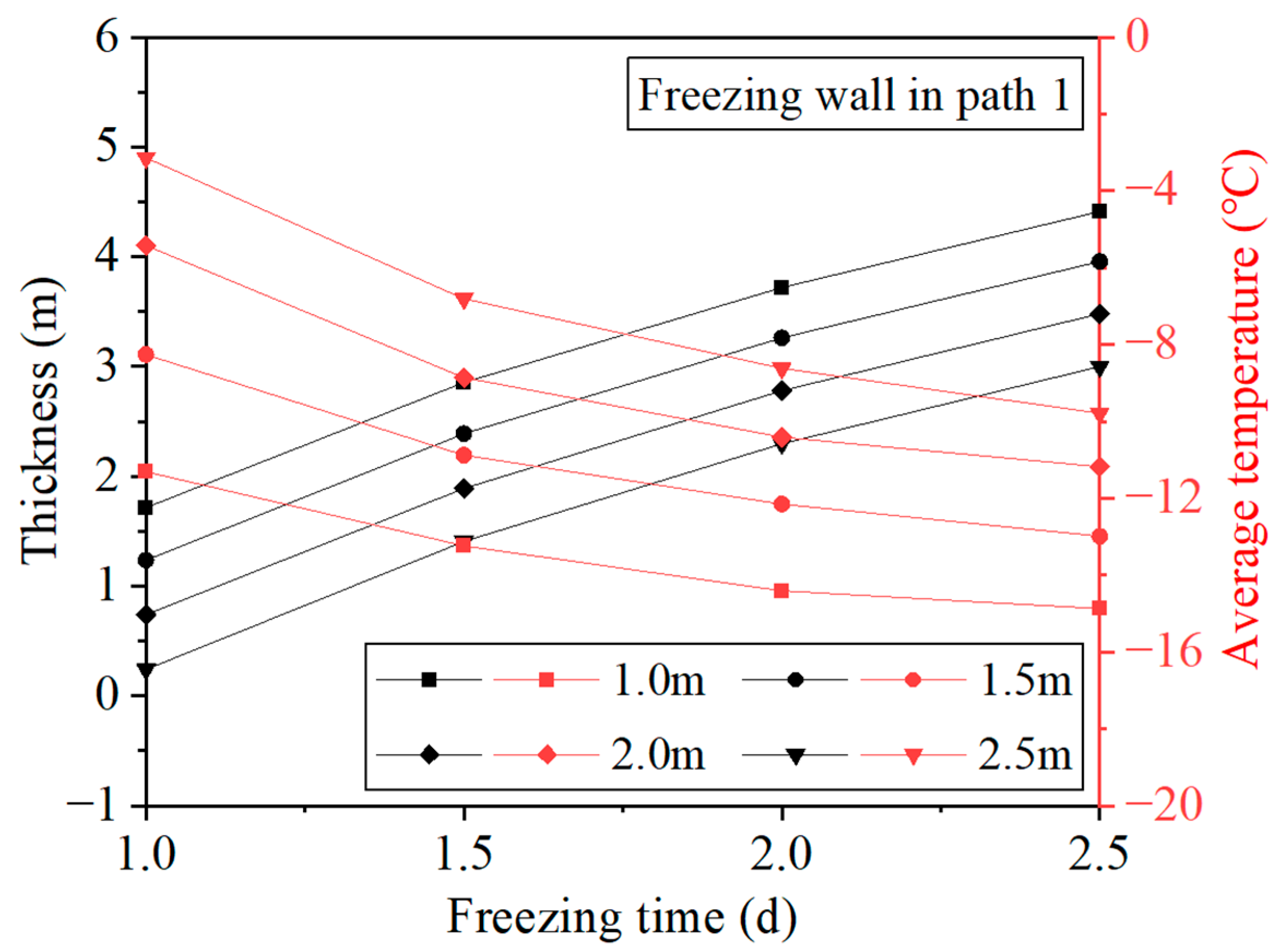
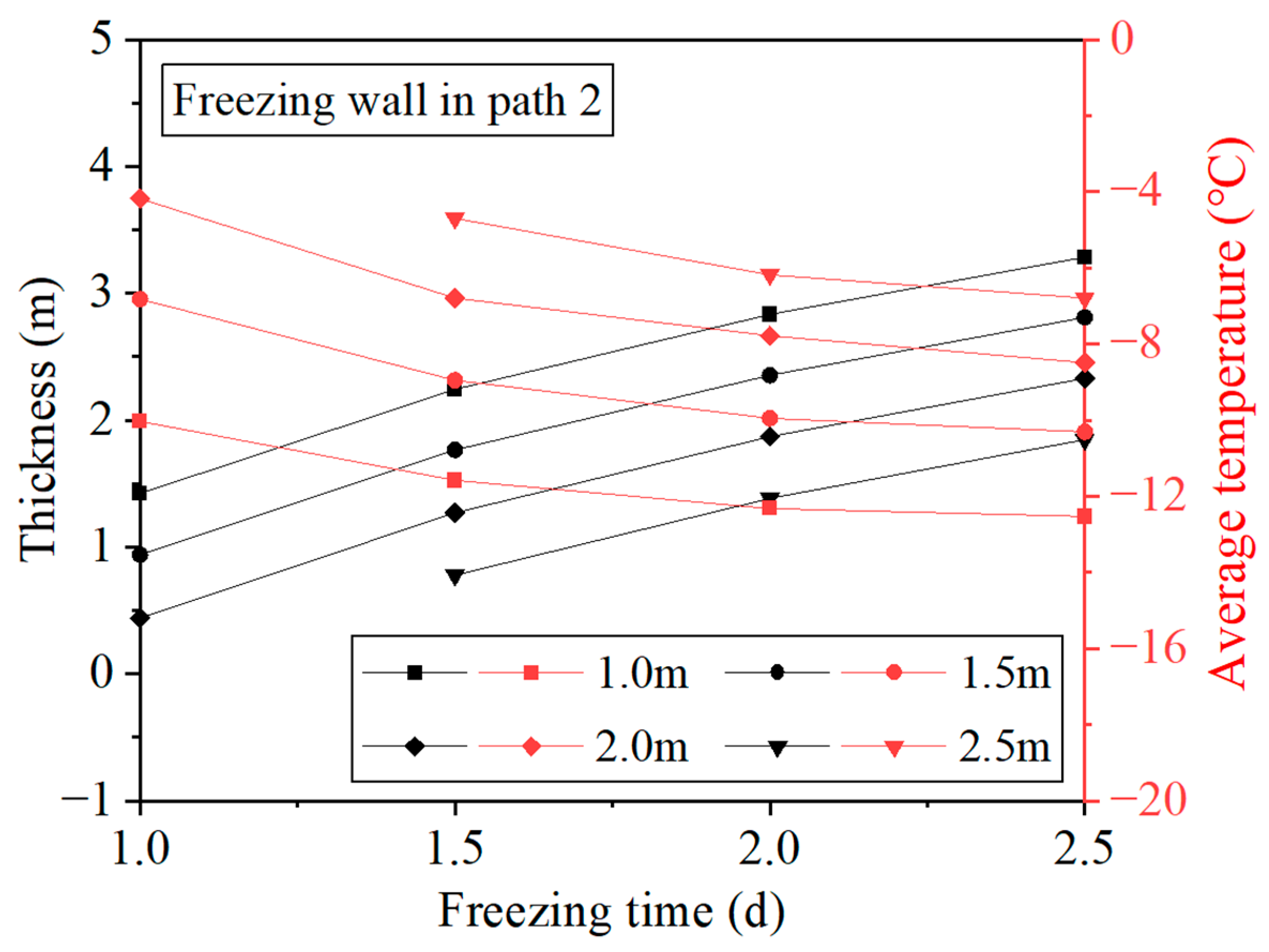
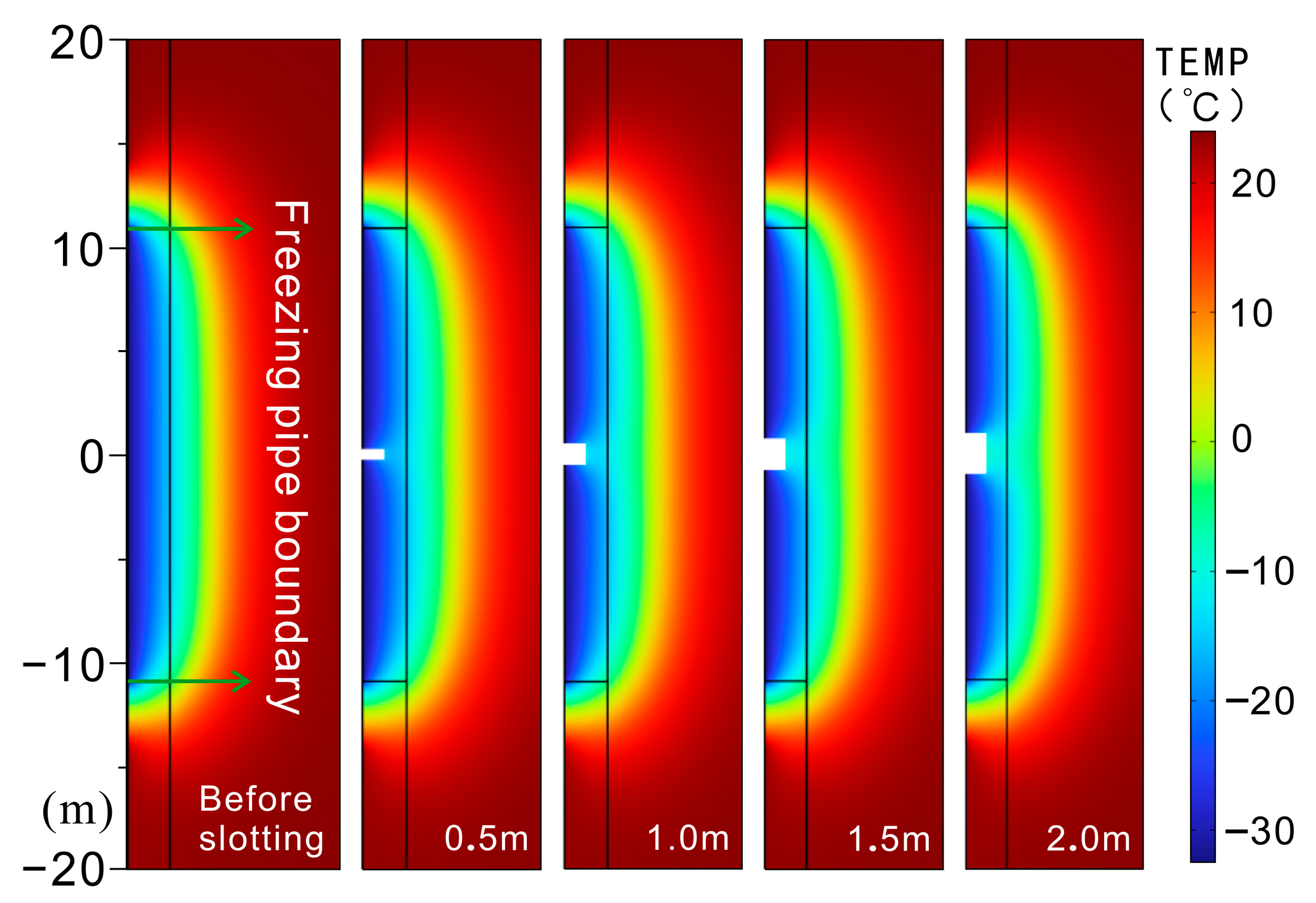
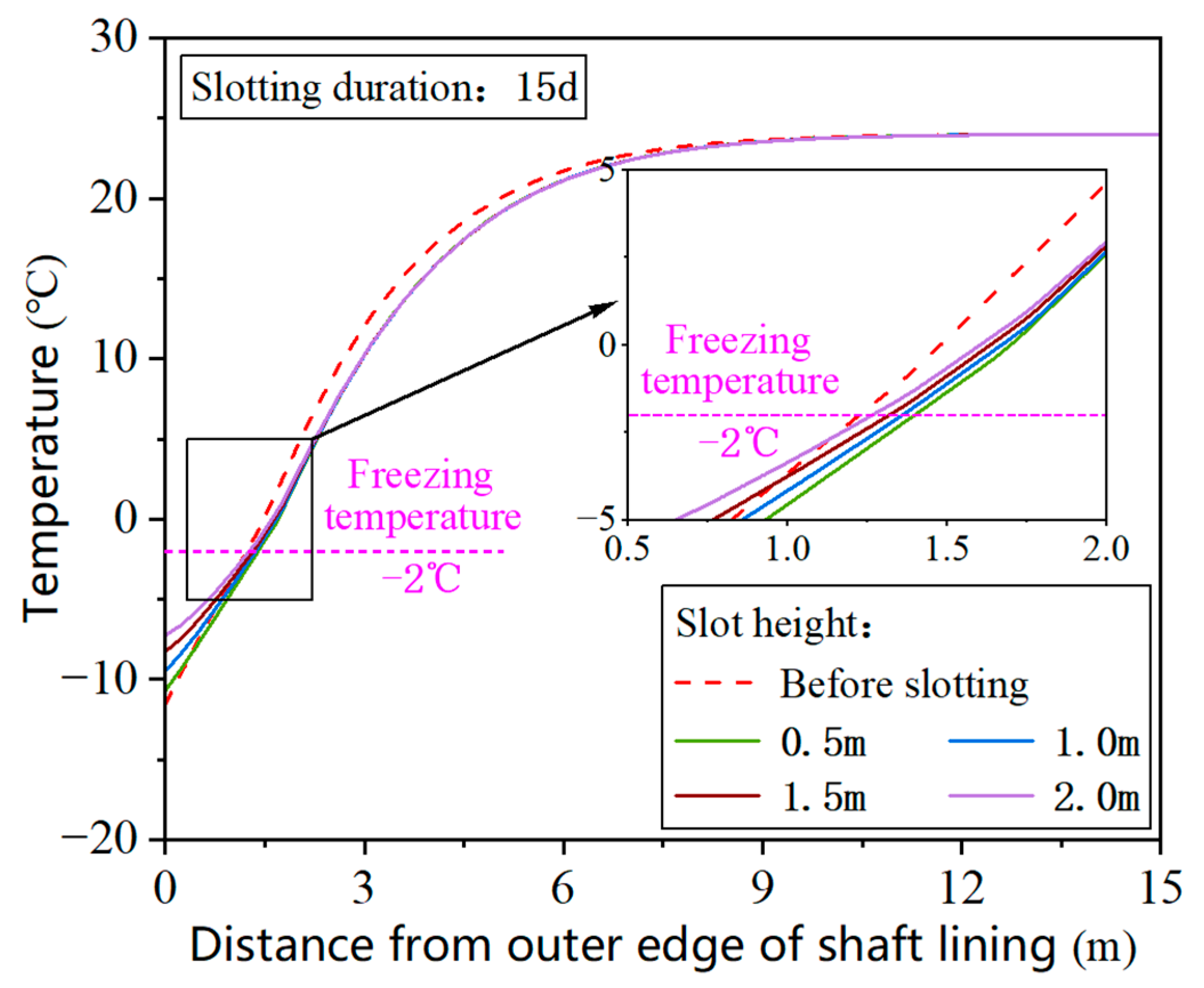
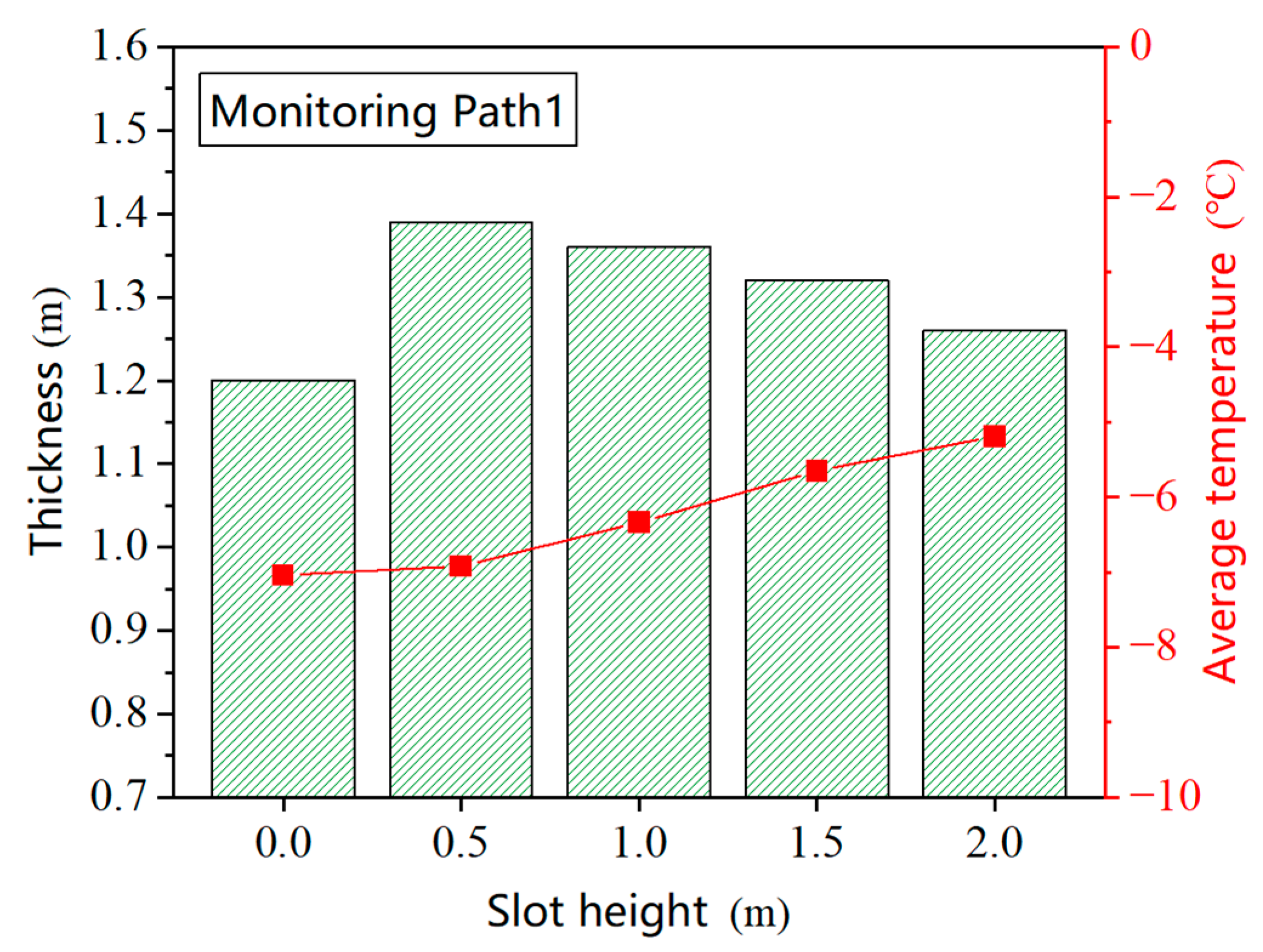
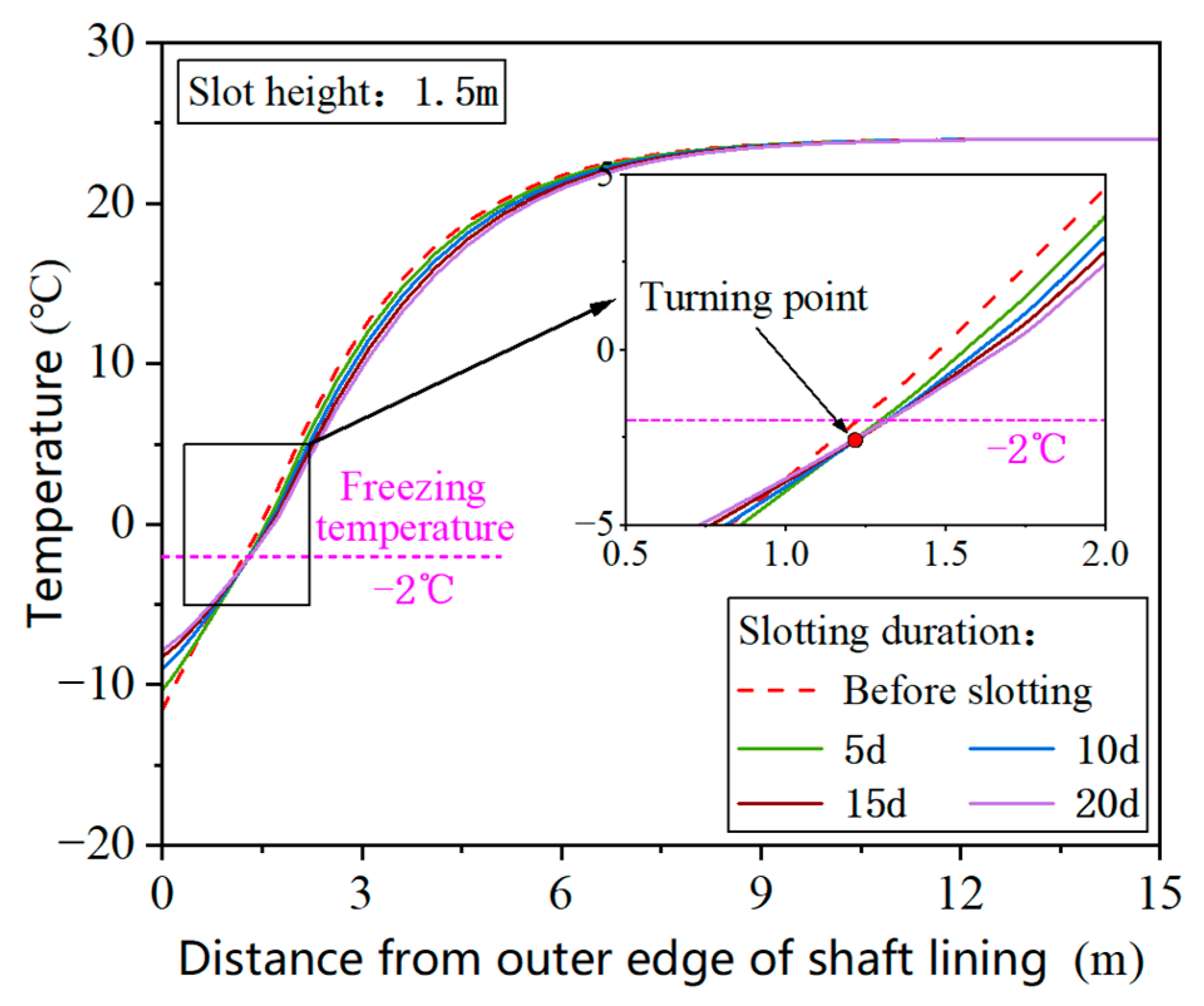
4.2.1. Influence of Slot Height on the Evolution of the Freezing Wall
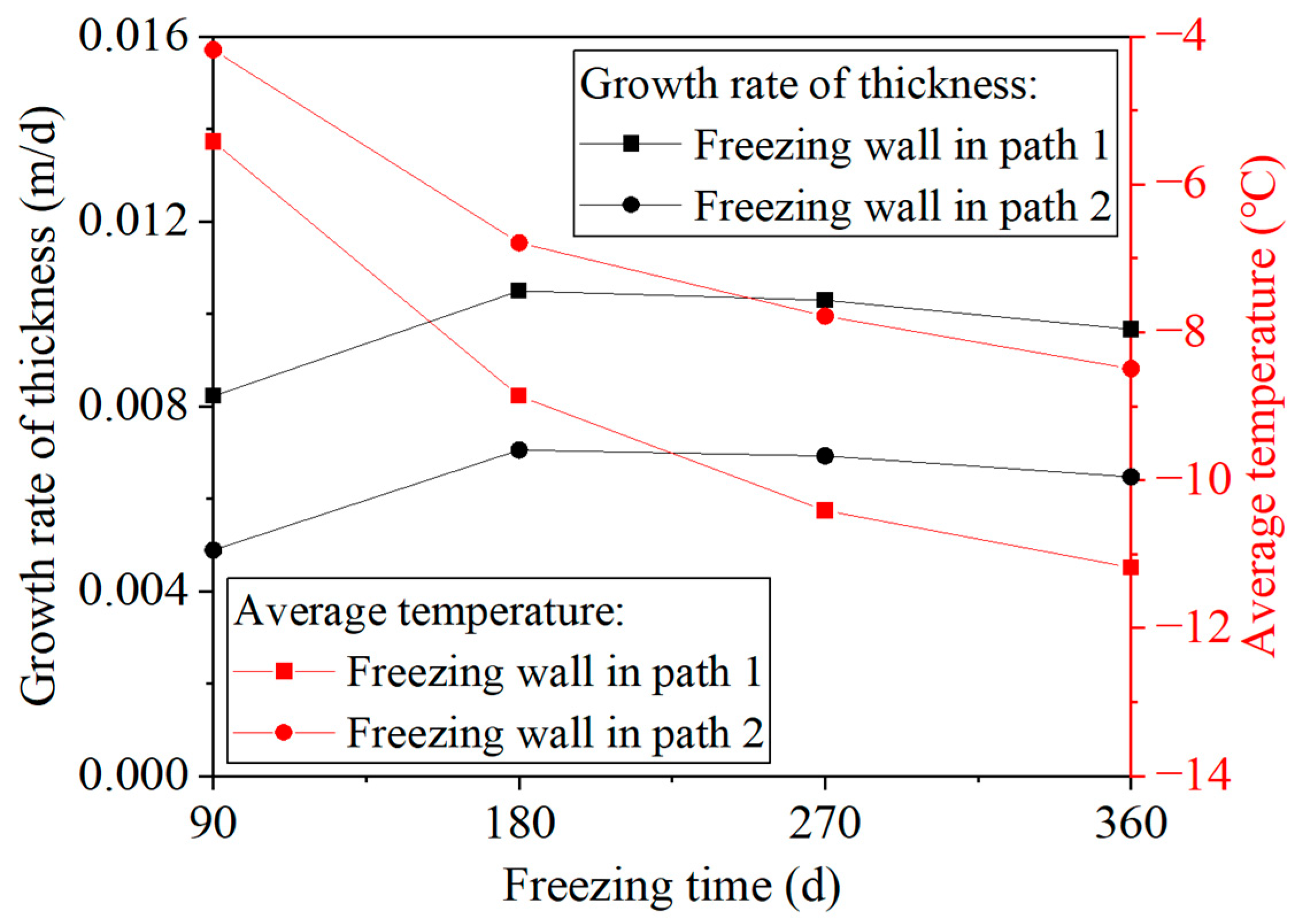
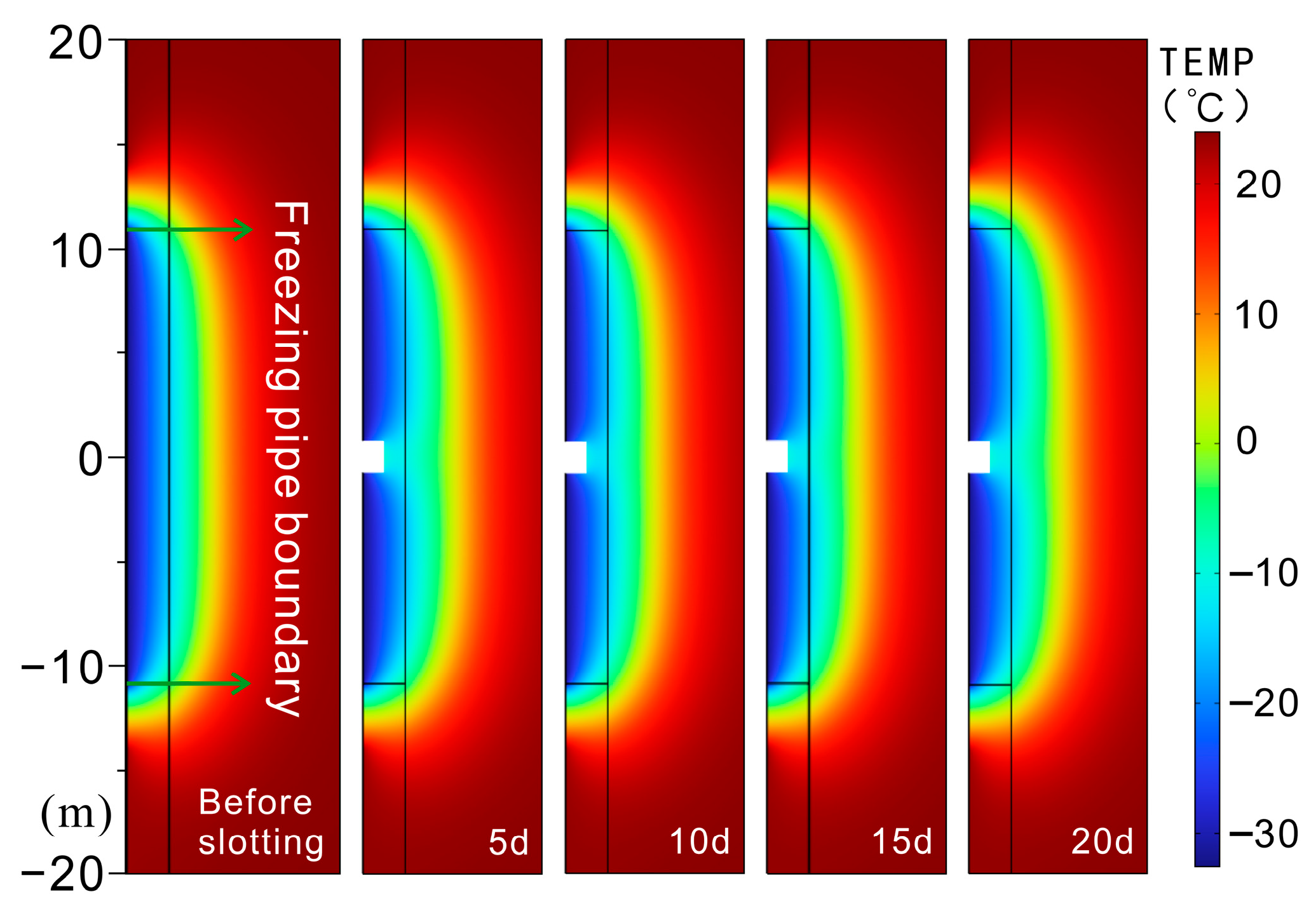
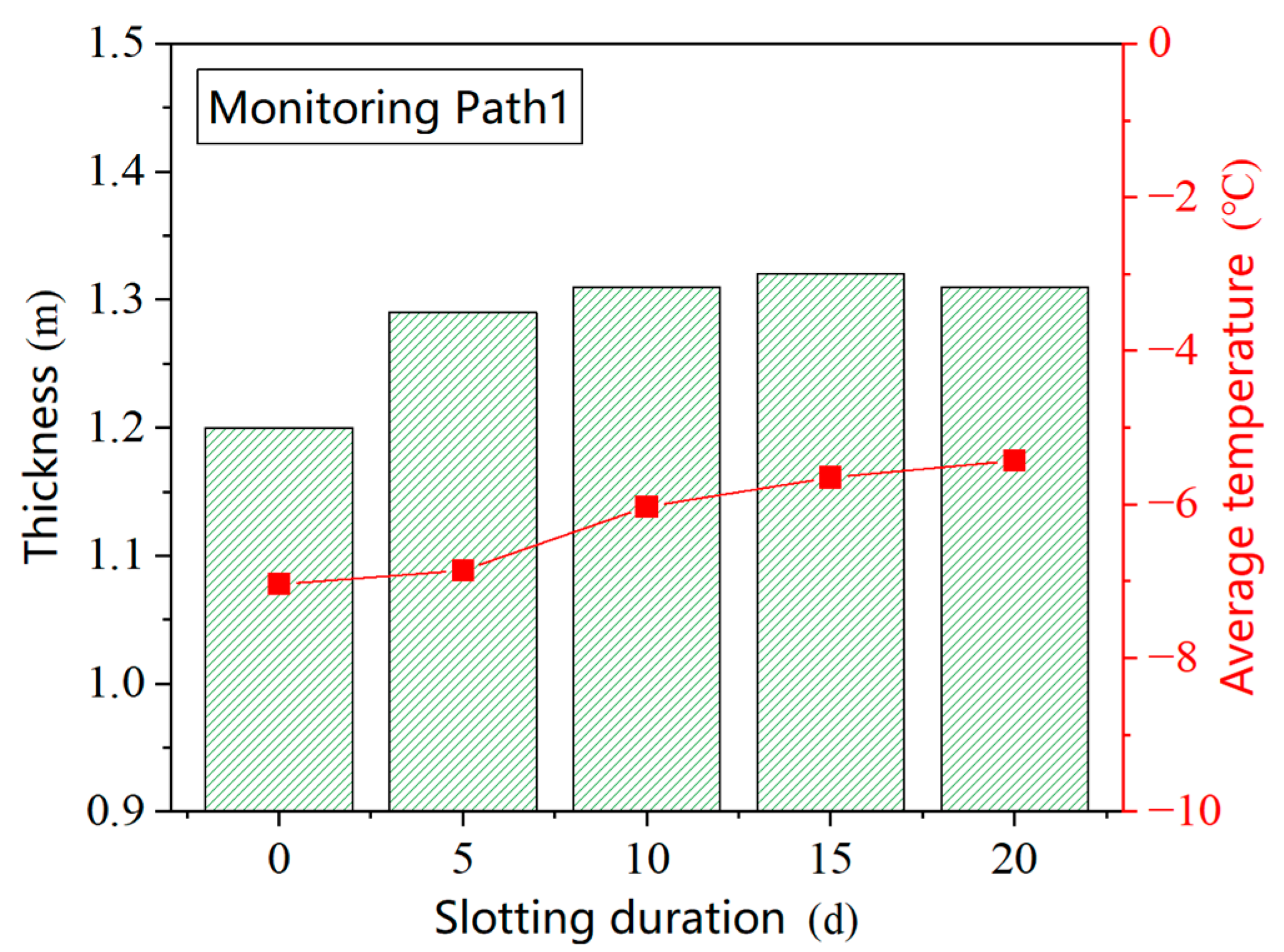
4.2.2. Influence of Slotting Duration on the Evolution of the Freezing Wall
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, W.H.; Huang, S.X.; Wang, Y.S.; Li, W.; Yang, Z.J.; Ren, Y.L.; Han, T.; Zhang, C.; Zhang, T.; Luo, T.T.; et al. Development and prospect of freezing shaft lining technology for vertical mine shafts in China. J. China Coal Soc. 2025, 50, 92–114. (In Chinese) [Google Scholar]
- Qing, Y.; Ikuta, S.; Shimada, H.; Sasaoka, T.; Matsui, K. Application of Underground Continuous Impervious Curtain to Shaft Lining Rupture Treatment in Eastern Chinese Coal Mines. Mem. Fac. Eng. Kyushu Univ. 2012, 72, 39–53. [Google Scholar]
- Wu, Y.; Zhu, S.Y.; Li, X.Z.; Zhang, H.; Huang, Z. Distribution characteristics of the additional vertical stress on a shaft wall in thick and deep alluvium: A simulation analysis. Nat. Hazards 2019, 96, 353–368. [Google Scholar] [CrossRef]
- Yu, G.C. The prevention of cracking and water leakage in the concrete inner lining of frozen shafts. Int. J. Min. Geol. Eng. 1986, 4, 247–251. [Google Scholar]
- Zhang, J.; Zhang, X.; Guo, X.; Jiang, J.; Wu, L. Water in rush Analysis and Manage Measures of Shaft Sinking by Freezing Method. Disaster Adv. 2012, 5, 452–456. [Google Scholar]
- Zhang, L.; Cong, Y.; Jiang, H.; Erdi, A.; Wang, Z. Failure criterion for concrete shafts in deep alluvium zones based on plastic ultimate strain and its application. Environ. Earth Sci. 2021, 80, 207. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, J.; Zhou, T.; Yong, W.X. Evaluation of vertical shaft stability in underground mines: Comparison of three weight methods with uncertainty theory. Nat. Hazards 2021, 109, 1457–1479. [Google Scholar] [CrossRef]
- Yu, Q.; Miao, H.; He, X.; Lin, M.; Guo, R.; Zhang, K. Experimental study on influence of additional stress induced by hydrophobic drainage on vertical shaft-lining. Min. Metall. Explor. 2023, 40, 667–689. [Google Scholar] [CrossRef]
- Ma, F.S.; Deng, Q.H.; Cunningham, D.; Yuan, R.M.; Zhao, H.J. Vertical shaft collapse at the Jinchuan Nickel Mine, Gansu Province, China: Analysis of contributing factors and causal mechanisms. Environ. Earth Sci. 2013, 69, 21–28. [Google Scholar] [CrossRef]
- Sun, Q.H.; Ma, F.S.; Guo, J.; Li, G.; Feng, X.L. Deformation Failure Mechanism of Deep Vertical Shaft in Jinchuan Mining Area. Sustainability 2020, 12, 2226. [Google Scholar] [CrossRef]
- Li, W.P.; Li, X.Q. Mechanism of rupture of shaft linings in coal mine areas buried by thick over-soils in East China. Géotechnique 2005, 55, 237–244. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhang, L.; Han, Y.W. Study on the Mechanism and Repair Technology of Vertical Shaft Wall Rupture in Huayuan Coal Mine. Shandong Coal Sci. Technol. 2023, 41, 192–198. (In Chinese) [Google Scholar]
- Wu, Z.; Wang, X.D.; Wu, G.H.; Zhu, M.C. Mechanism and control technology of water inrush from shaft freezing holes after thawing. Coal Geol. Explor. 2015, 43, 35–42. (In Chinese) [Google Scholar]
- Zhelnin, M.; Kostina, A.; Plekhov, O.; Levin, L. Numerical simulation of soil stability during artificial freezing. Procedia Struct. Integr. 2019, 17, 316–323. [Google Scholar] [CrossRef]
- Chen, W.; Wan, W.; He, H.; Liao, D.X.; Liu, J. Temperature Field Distribution and Numerical Simulation of Improved Freezing Scheme for Shafts in Loose and Soft Stratum. Rock Mech. Rock Eng. 2024, 57, 2695–2725. [Google Scholar] [CrossRef]
- Yao, Z.S.; Cai, H.B.; Xue, W.P.; Wang, X.J.; Wang, Z.J. Numerical simulation and measurement analysis of the temperature field of artificial freezing shaft sinking in Cretaceous strata. API Adv. 2019, 9, 025209. [Google Scholar] [CrossRef]
- Pilecki, Z.; Krawiec, K.; Pilecka, E.; Nagy, S.; Latka, T. Temperature anomaly as an indicator of groundwater flow prior to the shaft sinking with the use of artificial ground freezing. Eng. Geol. 2025, 347, 107916. [Google Scholar] [CrossRef]
- Sanger, F.J. Ground freezing in construction. J. Soil Mech. Found. Div. 1968, 94, 131–158. [Google Scholar] [CrossRef]
- Sanger, F.J.; Sayles, F.H. Thermal and Rheological Computations for Artificially Frozen Ground Construction. Dev. Geotech. Eng. 1979, 26, 311–337. [Google Scholar]
- Yang, W.H.; Huang, J.H. Numerical Analysis on the Heat Flux Density of a Freezing Pipe with Constant Outer Surface Temperature. J. Glaciol. Geocryol. 2006, 3, 401–405. (In Chinese) [Google Scholar]
- Hu, J.; Wang, X.B.; Jiang, B.R. Numerical Analysis of Temperature Field of Vertical Frozen Soil Wall Reinforcement at Shield Shaft. Adv. Mater. Res. 2014, 918, 218–223. [Google Scholar] [CrossRef]
- Li, H. Analysis of the Mechanical Characteristics of the Existing and Newly Built Shaft Wall During the Freezing Repair of the Damaged Shaft. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2021. (In Chinese). [Google Scholar]
- Cheng, H.; Zhou, R.H.; Yao, Z.S.; Ju, X.B.; Wang, X.J. Study on shaft damage control technology of water inrush and sand burst in drilling process with thick topsoil and thin bedrock. Coal Sci. Technol. 2021, 49, 176–185. (In Chinese) [Google Scholar]
- Zhelnin, M.; Kostina, A.; Prokhorov, A.; Plekhov, O.; Semin, M.; Levin, L. Coupled thermo-hydro-mechanical modeling of frost heave and water migration during artificial freezing of soils for mineshaft sinking. J. Rock Mech. Geotech. Eng. 2022, 14, 537–559. [Google Scholar] [CrossRef]
- Wang, Y.S.; Yang, R. Monitoring and analysis of the stress and deformation of shaft lining and the influence of freezing tube fracture in deep topsoil. Cold Reg. Sci. Technol. 2022, 193, 103420. [Google Scholar] [CrossRef]
- Levin, L.; Golovatyi, I.; Zaitsev, A.; Pugin, A.; Semin, M. Thermal monitoring of frozen wall thawing after artificial ground freezing: Case study of Petrikov Potash Mine. Tunn. Undergr. Space Technol. 2021, 107, 103685. [Google Scholar] [CrossRef]
- Liu, Y.; Li, K.Q.; Li, D.Q.; Tang, X.S.; Gu, S.X. Coupled thermal–hydraulic modeling of artificial ground freezing with uncertainties in pipe inclination and thermal conductivity. Acta Geotech. 2022, 17, 257–274. [Google Scholar] [CrossRef]
- Han, C.; Xu, J.; Zhang, W.; Wei, J.; Yang, F.; Yin, H.; Xie, D. Assessment and grouting of water inrush induced by shaft-freezing holes in the Yingpanhao coal mine, Inner Mongolia, China. Mine Water Environ. 2022, 41, 16–29. [Google Scholar] [CrossRef]
- Li, W.N.; Yang, X.; Lu, C.D.; Li, Q.X.; Fang, P.; Wu, X.; Huang, H.Y.; Fan, H.P.; Yao, N.P.; Tian, H.L.; et al. Modeling and optimization of trajectory deviation for compound directional drilling in coal mines. Neurocomputing 2025, 618, 129029. [Google Scholar] [CrossRef]
- Zhang, J.; Li, F.; Liu, S.; Wu, W.D.; Yu, X. Early age cracking potential of inner lining of coal mine frozen shaft. Energy Rep. 2022, 8, 16–24. [Google Scholar] [CrossRef]
- Song, C.Y. Research and Application of Slotting and Directional Blasting Technology for the Shrinkable Layer of Vertical Well Wall. Shandong Coal Sci. Technol. 2024, 42, 41–51. (In Chinese) [Google Scholar]
- Wang, X.J.; Yao, Z.S.; Rong, C.X.; Cai, H.B.; Cheng, H. Design and model test of shaft lining compressible connector in deep hydrophobic alluvium. Procedia Environ. Sci. 2012, 12, 864–870. [Google Scholar]
- COMSOL Co., Ltd. LiveLink for MATLAB User’s Guide COMSOL Multiphysics® V.6.0. COMSOL AB; COMSOL Co., Ltd.: Stockholm, Sweden, 2021. [Google Scholar]
- Ren, Y.L. Study on bearing capacity of cylindraceous double-concrete shaft lining. Adv. Mater. Res. 2012, 368, 3022–3027. [Google Scholar] [CrossRef]





| Properties | Concrete | Dry Clay | Air | Water | Ice |
|---|---|---|---|---|---|
| Density (kg/m3) | 2524 | 1571 | 1.225 | 1000 | 920 |
| Capacity (J/(kg·°C)) | 921 | 472 | 1006 | 4182 | 2060 |
| Thermal conductivity (W/(m·°C)) | 2.65 | 1.74 | 0.0242 | 0.60 | 2.14 |
| Parameter | Symbol | Typical Value | Variable Values |
|---|---|---|---|
| Freezing temperature (°C) | −30 | −27.5, −32.5, −35 | |
| Total thickness of shaft lining (m) | H | 2 | 1, 1.5, 2.5 |
| Height of slotting zone (m) | h | 1.5 | 0.5, 1, 2 |
| Duration of slotting (d) | S | 15 | 5, 10, 20 |
| Thickness (m) | 90 d | 180 d | 270 d | 360 d |
|---|---|---|---|---|
| Path 1 | 0.74 | 1.89 | 2.78 | 3.48 |
| Path 2 | 0.44 | 1.27 | 1.87 | 2.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, Y.; Yang, W.; Yang, Z.; Zhang, C.; Han, T.; Luo, T.; Ma, Y.; Zou, C. Formation of a Freezing Wall Around a Vertical Shaft Under Localized Freezing. Appl. Sci. 2025, 15, 7144. https://doi.org/10.3390/app15137144
Zhang Y, Wang Y, Yang W, Yang Z, Zhang C, Han T, Luo T, Ma Y, Zou C. Formation of a Freezing Wall Around a Vertical Shaft Under Localized Freezing. Applied Sciences. 2025; 15(13):7144. https://doi.org/10.3390/app15137144
Chicago/Turabian StyleZhang, Yu, Yuhang Wang, Weihao Yang, Zhijiang Yang, Chi Zhang, Tao Han, Tingting Luo, Yongjie Ma, and Cheng Zou. 2025. "Formation of a Freezing Wall Around a Vertical Shaft Under Localized Freezing" Applied Sciences 15, no. 13: 7144. https://doi.org/10.3390/app15137144
APA StyleZhang, Y., Wang, Y., Yang, W., Yang, Z., Zhang, C., Han, T., Luo, T., Ma, Y., & Zou, C. (2025). Formation of a Freezing Wall Around a Vertical Shaft Under Localized Freezing. Applied Sciences, 15(13), 7144. https://doi.org/10.3390/app15137144







