Study on the Choice of a Suitable Material Model for the Numerical Simulation of the Incremental Forming Process of Polymeric Materials
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
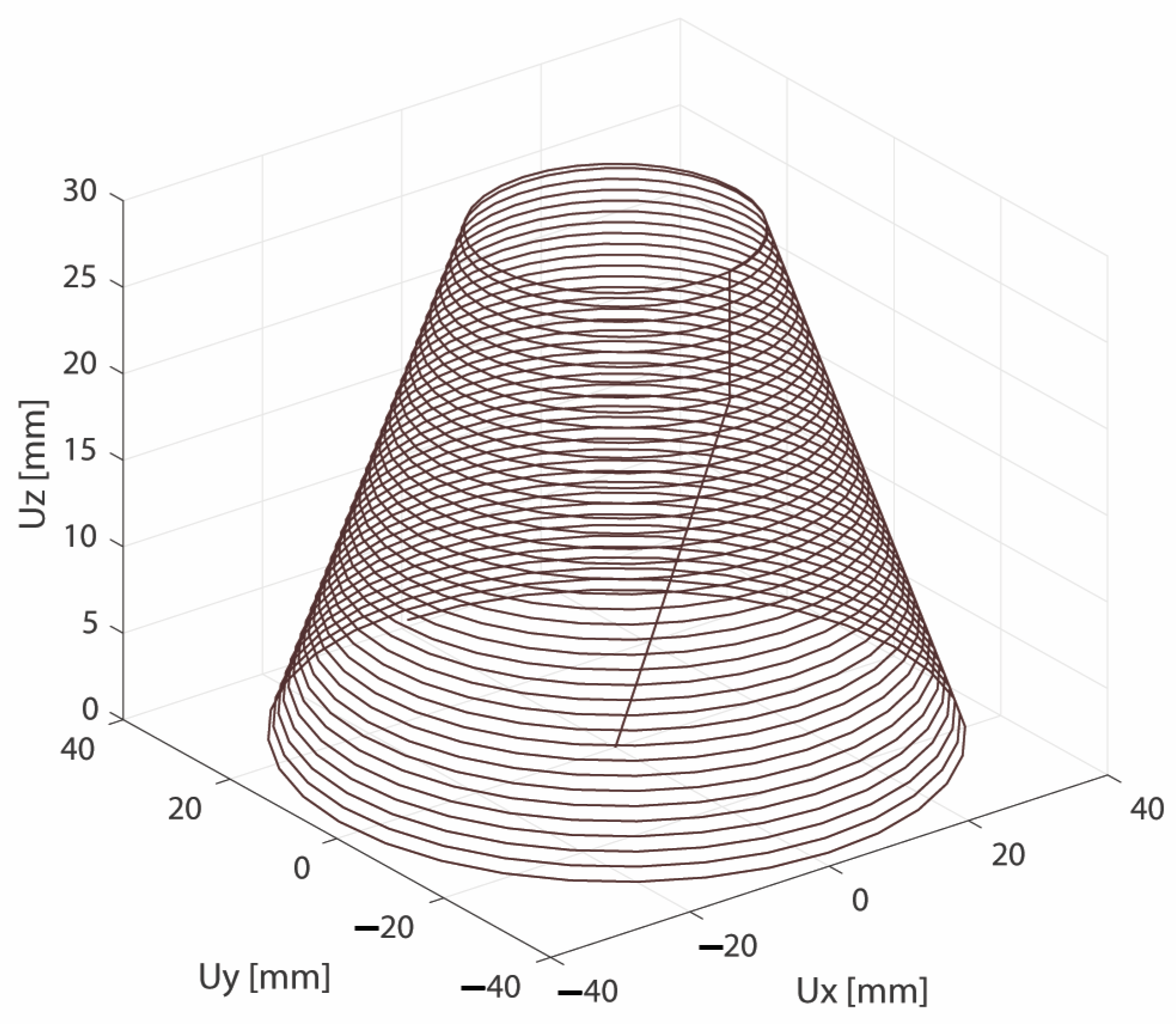
2.1. Numerical Simulation
2.2. Experimental Layout
3. Results and Discussion
4. Conclusions
- Finite element simulation of the incremental forming process for polymeric materials yields results that closely align with experimental data, demonstrating strong agreement in both the distribution and magnitude of strain and thickness reduction.
- The force variation curves obtained through finite element simulation closely match the experimental results, with only minor discrepancies observed between the numerical and experimental values.
- To achieve higher accuracy in simulating the incremental forming process, material model 24 in Ls-Dyna is recommended for polyamide and model 89 is recommended for polyethylene when predicting specific strains and thickness reduction. However, for more accurate force prediction during the forming process, material model 89 is recommended for both polymer types.
- When the appropriate material model is applied, the discrepancy between experimental and simulated results for specific strains and thickness reduction (excluding minor strain) remains within a maximum of 2.55% for polyamide and 4.21% for polyethylene.
- Using the appropriate material model, the maximum deviation between experimental and simulated process forces is 2.54% for polyamide and 2.71% for polyethylene, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite element method |
| SPIF | Single-point incremental forming |
| TPIF | Two-point incremental forming |
| VUMAT | Vectorized user material |
| ANOVA | Analysis of variance |
| VBO | Viscoplasticity based on overstress |
| PA | Polyamide |
| HDPE | High-density polyethylene |
| PC | Polycarbonate |
| PVC | Polyvinyl chloride |
References
- Barimani-Varandi, A.; Nasrabadi, M.K.; Ravan, B.A.; Javadi, M. Rapid prototyping of aircraft canopy based on the incremental forming process. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 2811. [Google Scholar] [CrossRef]
- Bagudanch, I.; García-Romeu, M.L.; Ferrer, I.; Ciurana, J. Customized cranial implant manufactured by incremental sheet forming using a biocompatible polymer. Rapid Prototyp. J. 2018, 24, 120–129. [Google Scholar] [CrossRef]
- Diabb Zavala, J.M.; Leija Gutiérrez, H.M.; Segura-Cárdenas, E.; Mamidi, N.; Morales-Avalos, R.; Villela-Castrejón, J.; Elías-Zúñiga, A. Manufacture and mechanical properties of knee implants using SWCNTs/UHMWPE composites. J. Mech. Behav. Biomed. Mater. 2021, 120, 104554. [Google Scholar] [CrossRef] [PubMed]
- Hassan, M.; Hussain, G.; Wei, H.; Qadeer, A.; Al Kahtani, M. Progress on single-point incremental forming of polymers. Int. J. Adv. Manuf. Technol. 2021, 114, 1–26. [Google Scholar] [CrossRef]
- Durante, M.; Formisano, A.; Lambiase, F. Formability of polycarbonate sheets in single-point incremental forming. Int. J. Adv. Manuf. Technol. 2019, 102, 2049–2062. [Google Scholar] [CrossRef]
- Rosca, N.; Trzepiecinski, T.; Oleksik, V. Minimizing the Forces in the Single Point Incremental Forming Process of Polymeric Materials Using Taguchi Design of Experiments and Analysis of Variance. Materials 2022, 15, 6453. [Google Scholar] [CrossRef] [PubMed]
- Rosca, N.; Oleksik, M.; Rosca, L.; Avrigean, E.; Trzepiecinski, T.; Najm, S.M.; Oleksik, V. Minimizing the Main Strains and Thickness Reduction in the Single Point Incremental Forming Process of Polyamide and High-Density Polyethylene Sheets. Materials 2023, 16, 1644. [Google Scholar] [CrossRef] [PubMed]
- Beşliu, I.; Tamaşag, I.; Slătineanu, L. An Experimental Study on Incremental Forming Process of Polycarbonate Sheets. Macromol. Symp. 2021, 395, 2000282. [Google Scholar] [CrossRef]
- Kong, F.; Cha, G.; Yan, A.; Pu, Y. An improvement study on incremental forming resilience of PP plate. Bol. Tec. 2017, 55, 110–115. [Google Scholar]
- Jaglan, A.; Dogra, N.; Kumar, A.; Kumar, P. Finite Element Simulation Approach in Incremental Sheet Forming Process. In Handbook of Flexible and Smart Sheet Forming Techniques: Industry 4.0 Approaches; Wiley: Hoboken, NJ, USA, 2023; pp. 129–139. [Google Scholar]
- Ibrahim, A.K. A comparative study of simulation models on incremental forming process by using the enhancement tools. Mater. Sci. Forum 2019, 957, 93–102. [Google Scholar]
- Conte, R.; Serratore, G.; Ambrogio, G.; Gagliardi, F. Numerical analyses of long fiber–reinforced polymeric sheets processed by Single Point Incremental Forming. Int. J. Adv. Manuf. Technol. 2022, 123, 1203–1214. [Google Scholar] [CrossRef]
- Sy, L.V.; Hue, P.T.M. Implement a modified viscoplasticity based on overstress model into numerical simulation of the incremental sheet forming process. Lect. Notes Electr. Eng. 2017, 415, 23–33. [Google Scholar]
- Xu, P.; Li, X.; Feng, F.; Li, X.; Yang, Y. Experimental and numerical studies on two-point incremental forming of woven fabric composite sheet. J. Manuf. Process. 2023, 85, 205–215. [Google Scholar] [CrossRef]
- Rai, S.; Kumar, R.; Nirala, H.K.; Francis, K.; Agrawal, A. Experimental and simulation study of single point incremental forming of polycarbonate. ASME Int. Manuf. Sci. Eng. Conf. 2019, 6, MSEC2019-3026. [Google Scholar]
- García-Collado, A.; Medina-Sanchez, G.; Gupta, M.K.; Dorado-Vicente, R. Application of the finite element method to the incremental forming of polymer sheets: The thermomechanical coupled model and experimental validations. Polymers 2020, 12, 1715. [Google Scholar] [CrossRef] [PubMed]
- Ostasevicius, V.; Eidukynas, D.; Grigaliunas, V.; Jurenas, V.; Paleviciute, I.; Gudauskis, M. Investigation of advanced robotized polymer sheet incremental forming process. Sensors 2021, 21, 7459. [Google Scholar] [CrossRef] [PubMed]
- Medina-Sanchez, G.; Garcia-Collado, A.; Carou, D.; Dorado-Vicente, R. Force prediction for incremental forming of polymer sheets. Materials 2018, 11, 1597. [Google Scholar] [CrossRef] [PubMed]
- Formisano, A.; Durante, M. A numerical-experimental investigation of the wrinkling defect in incremental forming of thin polycarbonate sheets. Int. Rev. Model. Simul. 2019, 12, 206–211. [Google Scholar] [CrossRef]
- Kulkarni, S.S.; Mocko, G.M. A finite element simulation model of convective heat-assisted single-point incremental forming of thermoplastics. Int. J. Adv. Manuf. Technol. 2020, 111, 3305–3317. [Google Scholar] [CrossRef]
- Formisano, A.; Boccarusso, L.; Durante, M. Optimization of Single-Point Incremental Forming of Polymer Sheets through FEM. Materials 2023, 16, 451. [Google Scholar] [CrossRef] [PubMed]
- Ls-Dyna Keyword User’s Manual, Vol. II, Material Models, Version R13.1.0.0; Livermore Software Technology Corporation: Livermore, CA, USA, 2012.
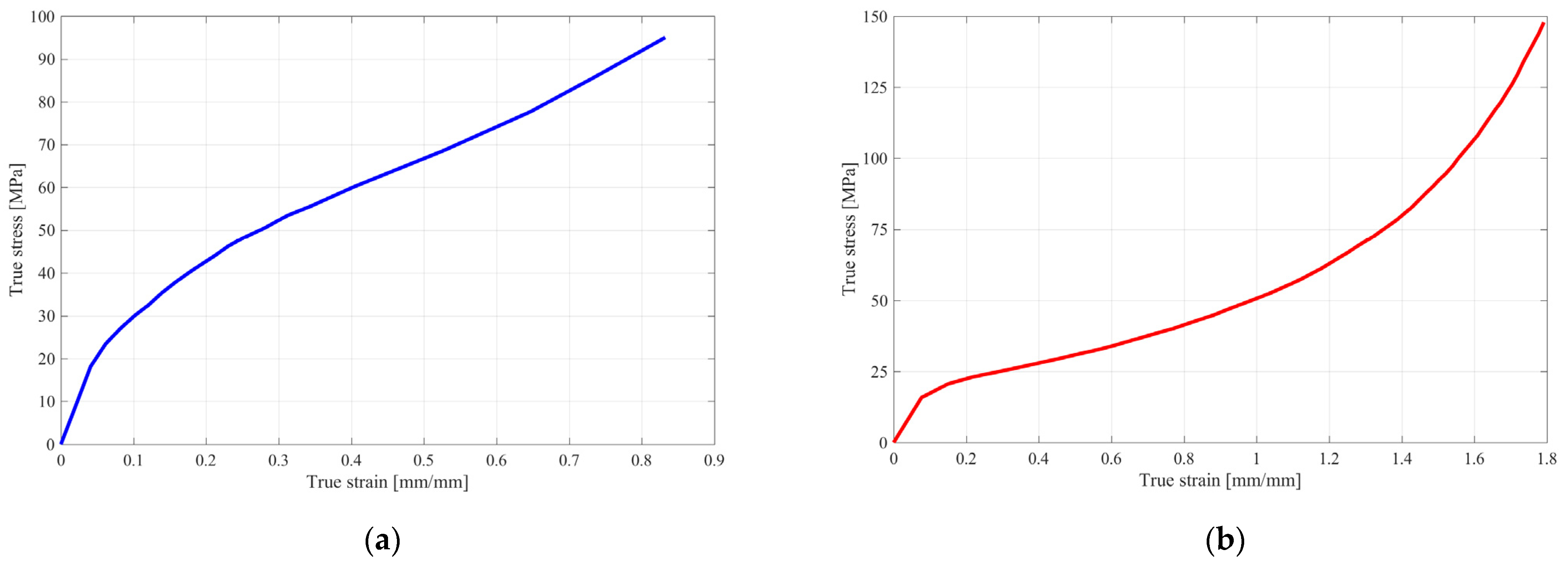


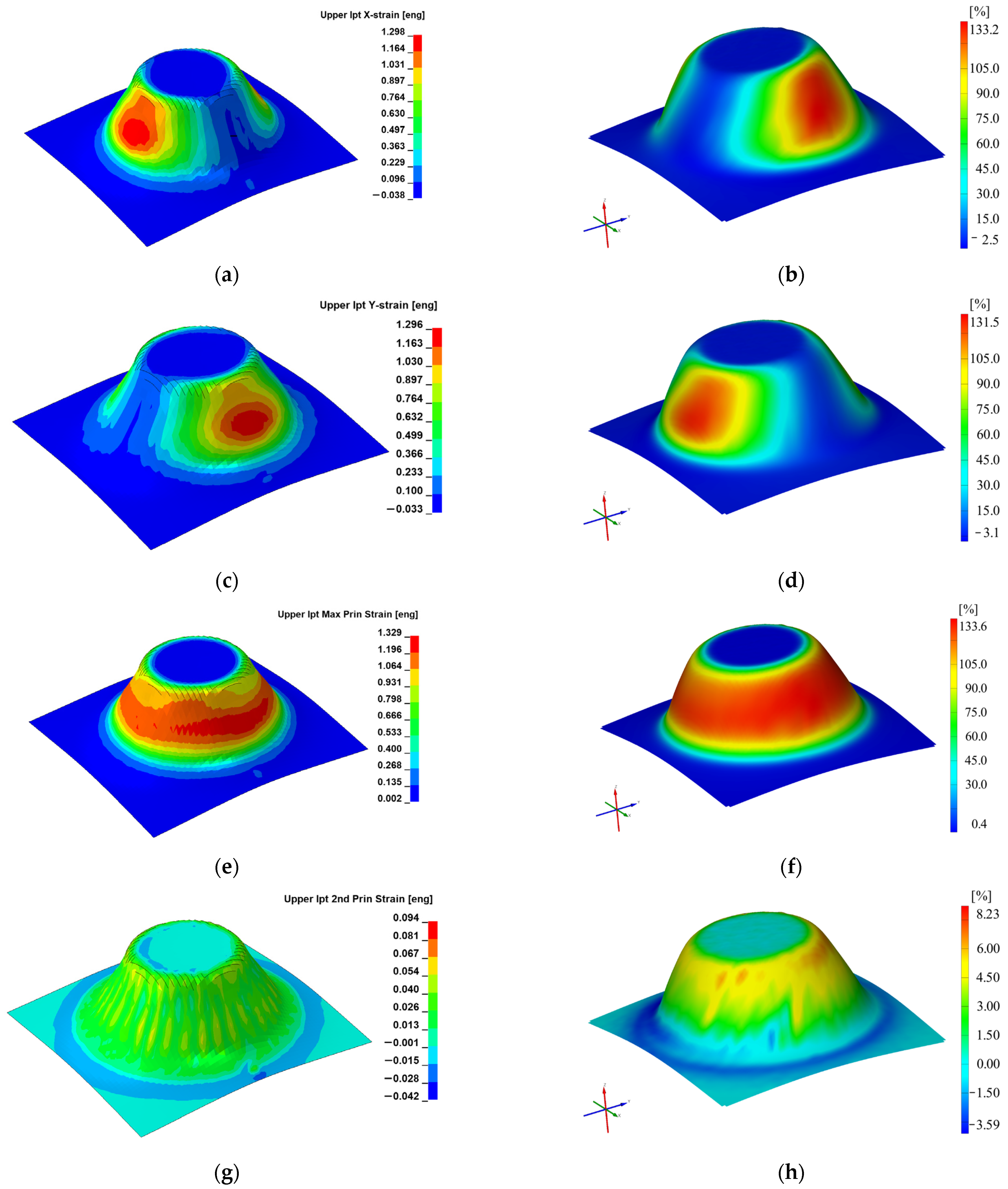
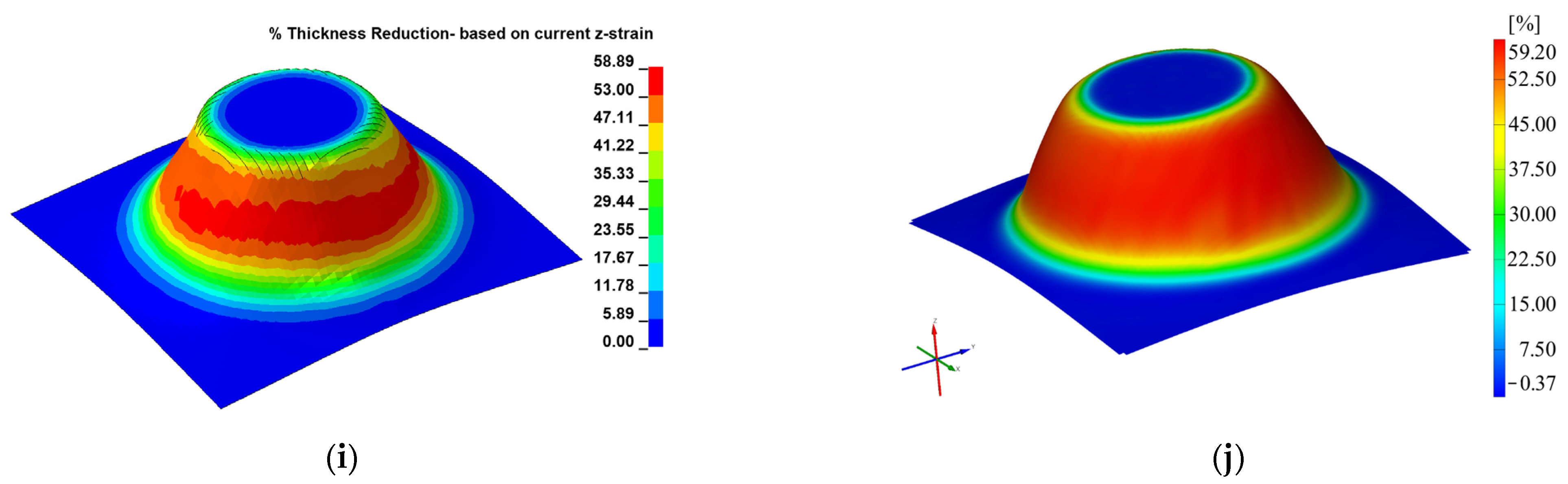
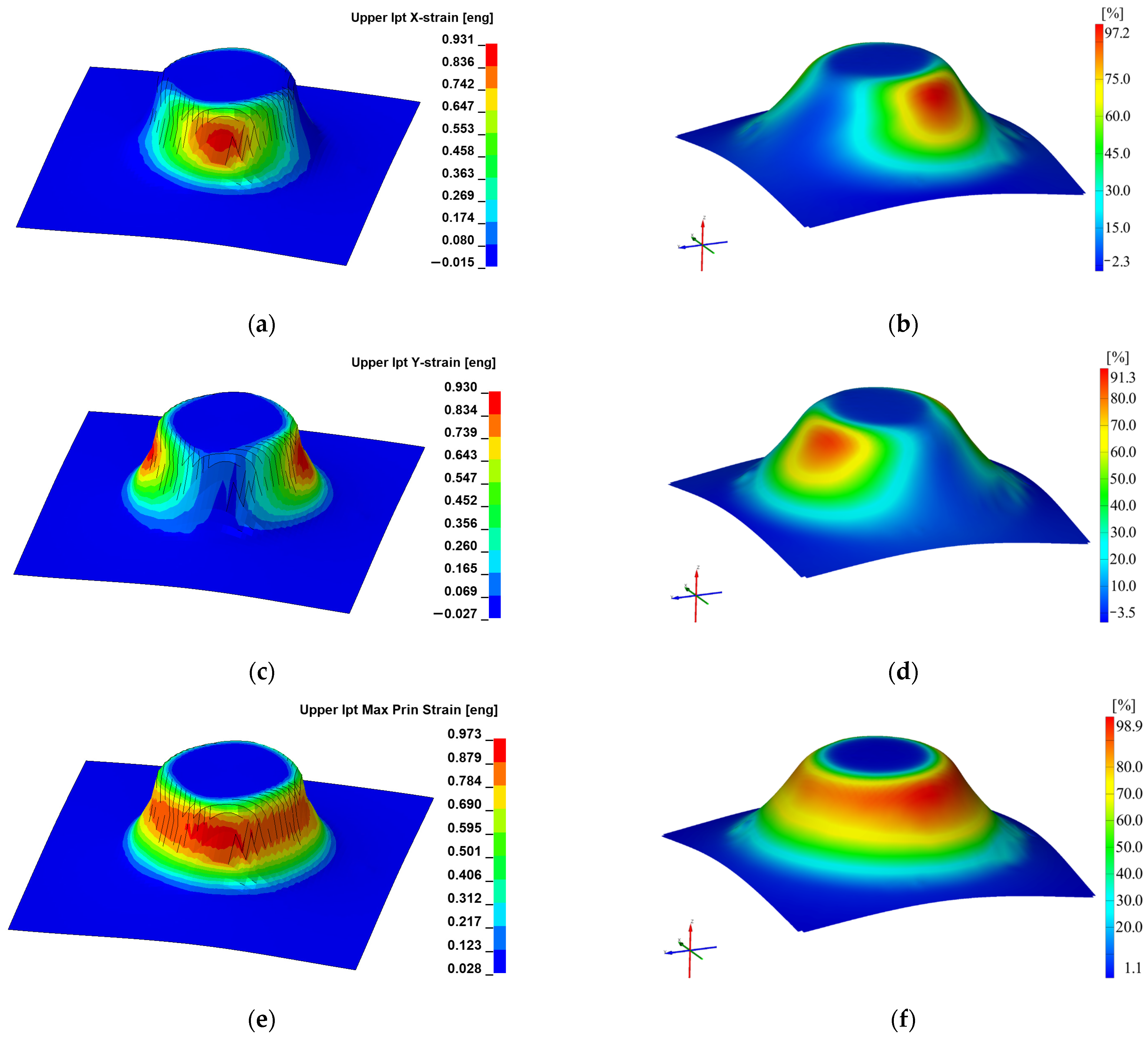
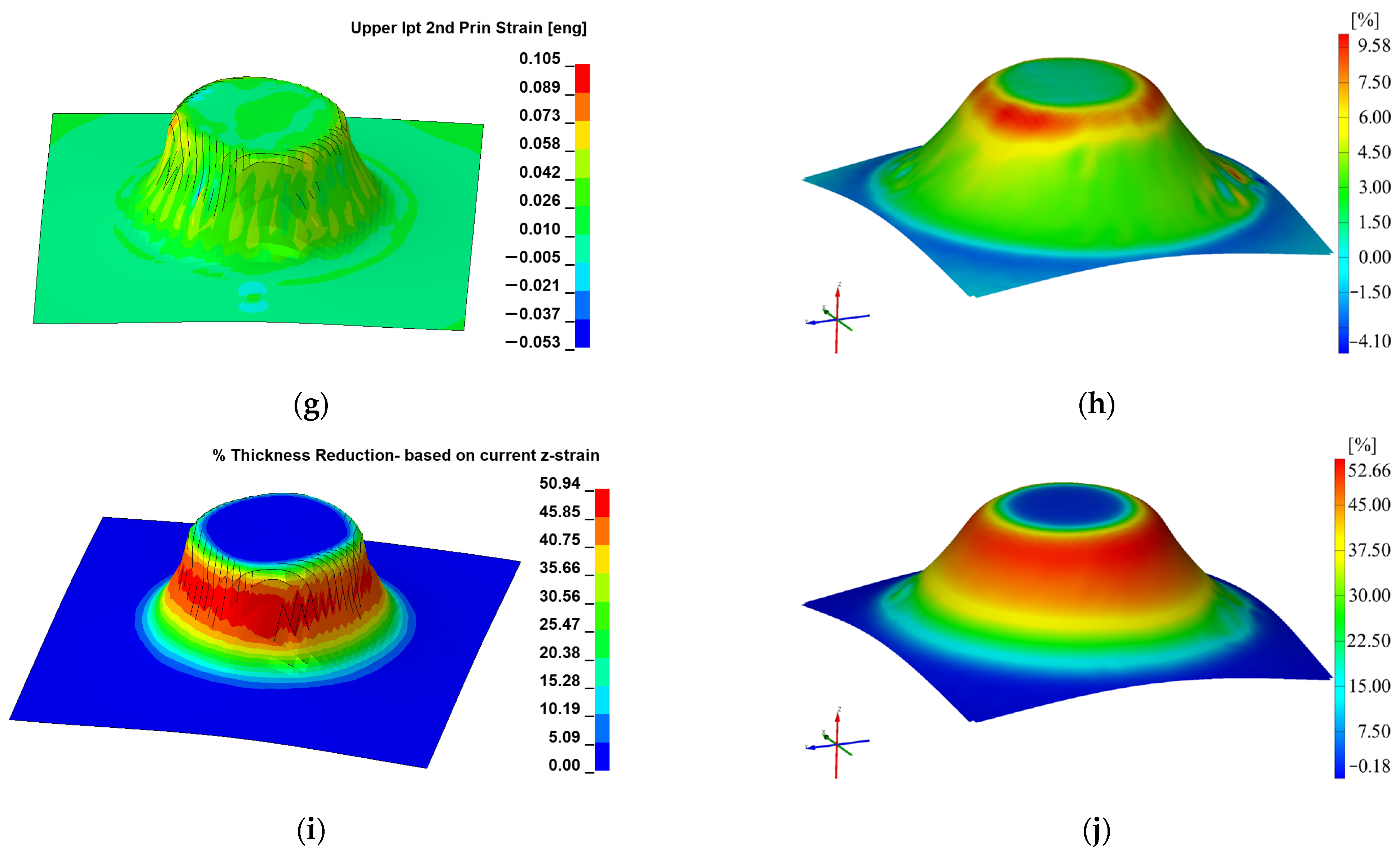
| Material Type | Material Model | Strain on x Direction εx | Strain on y Direction εy | Major Strain ε1 | Minor Strain ε2 | Thickness Reduction |
|---|---|---|---|---|---|---|
| [%] | [%] | [%] | [%] | [%] | ||
| PA | 24 | 129.80 | 129.60 | 132.90 | 9.44 | 58.89 |
| PA | 89 | 127.30 | 127.90 | 129.80 | 9.51 | 57.43 |
| Experimental PA | 133.20 | 131.50 | 133.60 | 8.23 | 59.20 | |
| PE | 24 | 92.70 | 92.56 | 94.32 | 10.21 | 50.28 |
| PE | 89 | 93.11 | 92.99 | 97.33 | 10.47 | 50.94 |
| Experimental PE | 97.20 | 91.30 | 98.90 | 9.58 | 52.66 | |
| Material Type | Material Model | Strain on x Direction εx [%] | Strain on y Direction εy [%] | Major Strain ε1 [%] | Minor Strain ε2 [%] | Thickness Reduction [%] |
|---|---|---|---|---|---|---|
| PA | 24 | 2.55 | 1.44 | 0.52 | 14.70 | 0.52 |
| 89 | 4.21 | 2.74 | 2.84 | 15.55 | 2.99 | |
| PE | 24 | 4.63 | 1.38 | 4.63 | 6.58 | 4.52 |
| 89 | 4.21 | 1.85 | 1.59 | 9.29 | 3.27 |
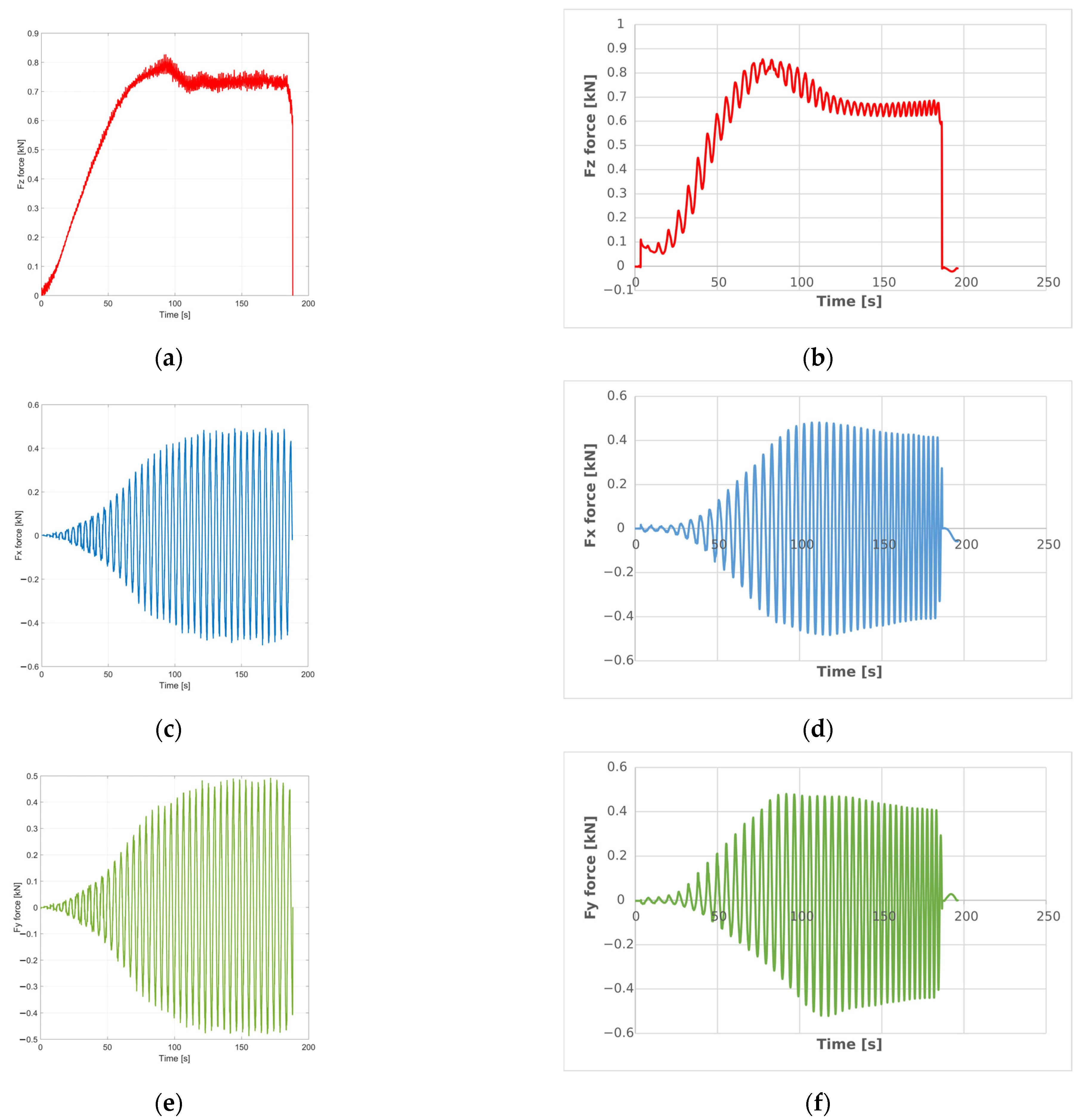
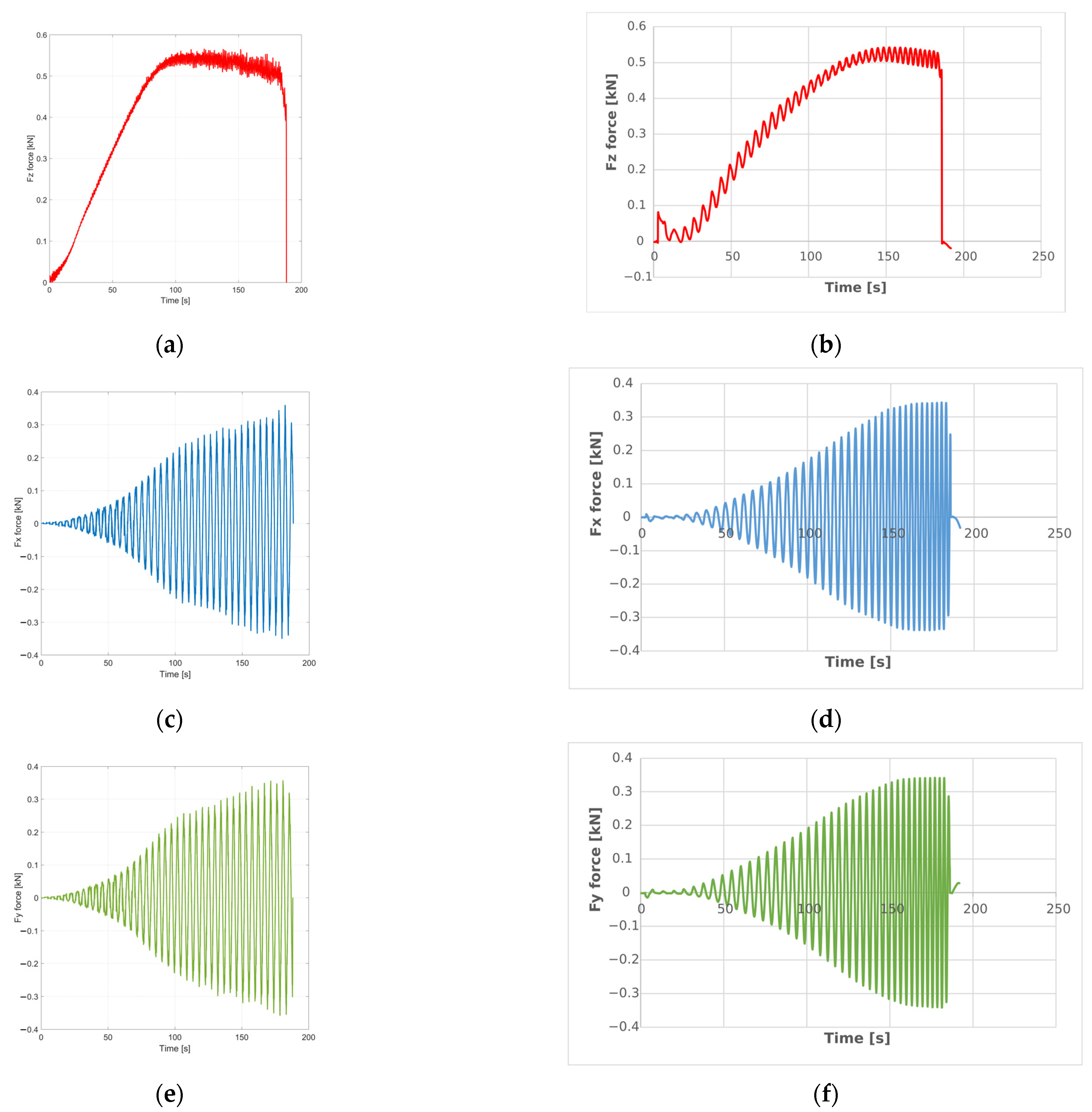
| Material Type | Material Model | Fz Force [kN] | Fx Force [kN] | Fy Force [kN] |
|---|---|---|---|---|
| PA | 24 | 0.91 | 0.50 | 0.50 |
| PA | 89 | 0.89 | 0.49 | 0.49 |
| Experimental PA | 0.87 | 0.48 | 0.48 | |
| PE | 24 | 0.57 | 0.36 | 0.36 |
| PE | 89 | 0.56 | 0.35 | 0.35 |
| Experimental PE | 0.54 | 0.34 | 0.34 | |
| Material Type | Material Model | Fz Force [%] | Fx Force [%] | Fy Force [%] |
|---|---|---|---|---|
| PA | 24 | 4.23 | 4.74 | 4.56 |
| 89 | 1.83 | 2.24 | 2.54 | |
| PE | 24 | 4.78 | 4.68 | 4.30 |
| 89 | 2.43 | 2.71 | 2.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosca, N.; Najm, S.M.; Avrigean, E.; Oleksik, M.; Trzepieciński, T.; Oleksik, V. Study on the Choice of a Suitable Material Model for the Numerical Simulation of the Incremental Forming Process of Polymeric Materials. Appl. Sci. 2025, 15, 7094. https://doi.org/10.3390/app15137094
Rosca N, Najm SM, Avrigean E, Oleksik M, Trzepieciński T, Oleksik V. Study on the Choice of a Suitable Material Model for the Numerical Simulation of the Incremental Forming Process of Polymeric Materials. Applied Sciences. 2025; 15(13):7094. https://doi.org/10.3390/app15137094
Chicago/Turabian StyleRosca, Nicolae, Sherwan Mohammed Najm, Eugen Avrigean, Mihaela Oleksik, Tomasz Trzepieciński, and Valentin Oleksik. 2025. "Study on the Choice of a Suitable Material Model for the Numerical Simulation of the Incremental Forming Process of Polymeric Materials" Applied Sciences 15, no. 13: 7094. https://doi.org/10.3390/app15137094
APA StyleRosca, N., Najm, S. M., Avrigean, E., Oleksik, M., Trzepieciński, T., & Oleksik, V. (2025). Study on the Choice of a Suitable Material Model for the Numerical Simulation of the Incremental Forming Process of Polymeric Materials. Applied Sciences, 15(13), 7094. https://doi.org/10.3390/app15137094








