Enhancing Neural Network Interpretability Through Deep Prior-Guided Expected Gradients
Abstract
1. Introduction
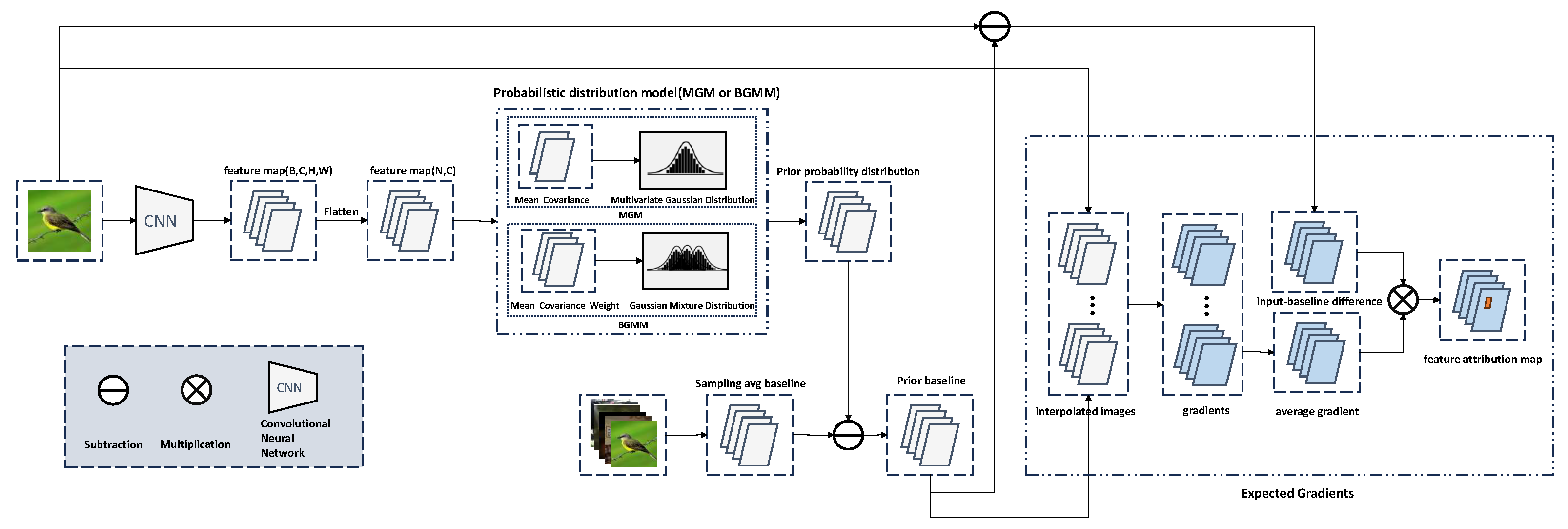
- A deep prior-guided EG framework, DeepPrior-EG, is proposed to address the longstanding misalignment between baselines and the concept of missingness. It initiates gradient path integration from learned prior baselines, computing expected gradients along the trajectory to the input image. These priors are extracted from intrinsic deep features of CNN layers.
- Two prior modeling strategies are developed within the framework: a multivariate Gaussian model (MGM) capturing high-dimensional feature interdependencies, and a Bayesian nonparametric Gaussian mixture model (BGMM) that adaptively infers mixture complexity to represent heterogeneous feature distributions.
- An explanation-driven retraining paradigm is implemented, wherein the model is fine-tuned using insights derived from the framework. This enhances robustness and reduces interference from irrelevant background features.
- DeepPrior-EG is thoroughly evaluated using diverse qualitative and quantitative interpretability metrics. Results demonstrate its superiority in attribution quality and interpretive fidelity, with the BGMM variant achieving state-of-the-art performance.
2. Related Work
2.1. Gradient-Based Explanation Methods
2.2. Integrated Gradients
2.3. Expected Gradients
3. Methodology
3.1. Motivation and Proposed Framework
- Inherent Prior Encoding: CNNs naturally encode hierarchical priors through layered architectures, capturing low-level features (edges/textures) and high-level semantics (object shapes/categories), enabling effective modeling of complex nonlinear patterns.
- Superior Feature Learning: Unlike traditional methods (SIFT/HOG) limited to low-level geometric features, CNNs automatically learn task-specific representations through end-to-end training, eliminating manual feature engineering.
- Noise-Robust Representation: By mapping high-dimensional pixels to compact low-dimensional spaces, CNNs reduce data redundancy while enhancing feature robustness.
- Transfer Learning Efficiency: Pretrained models (ResNet/VGG) on large datasets (ImageNet) provide transferable general features, improving generalization and reducing training costs.
3.2. Multivariate Gaussian Model for Deep Priors
- Feature Flattening: Given feature map , reshape into matrix () shown in Equation (11).
3.3. Bayesian Gaussian Mixture Models for Deep Priors
- Feature Flattening: Reshape convolutional feature map into matrix () through Equation (16).
- vs. GMM: Avoids preset K and singular covariance issues through nonparametric regularization;
- vs. KDE: Explicitly models multimodality versus kernel-based density biases;
- vs. VAE: Maintains strict likelihood-based generation unlike decoder-induced distribution shifts.
3.4. Theoretical Analysis of Axiomatic Compliance
4. Experiments
4.1. ImageNet Dataset
4.2. Evaluation Metrics
- KPM/KAM: These metrics measure the ability of the model to recover positive or important features, respectively. These metrics highlight the extent to which explanations emphasize feature contributions that positively influence predictions. For KPM, all features are initially masked, and then those with positive partial derivatives are gradually unmasked (while negative-derivative features remain masked). The model’s output changes are plotted, and the area under this curve (AUC) is computed—a larger AUC indicates that the explanation method more accurately identifies features that enhance predictions. Similarly, KAM begins with full masking but sequentially unmasks features in descending order of their absolute importance (e.g., gradient magnitudes). The resulting AUC reflects how well the explanation ranks globally significant features, with higher values denoting better alignment with true feature importance.
- RPM/RNM: These metrics assess the impact of removing important features on model predictions. These metrics quantify how sensitive the model is to the absence of critical features, thereby evaluating the robustness of the explanation method. RPM starts with all positive-derivative features unmasked and negative ones masked, then progressively masks the positive features (in order of importance). The output curve’s AUC measures the drop in predictions caused by removing these features—larger AUC values imply the explanation correctly highlights influential positive contributors. Conversely, RNM begins with negative-derivative features unmasked and positive ones masked, then masks the negative features sequentially. Here, a larger AUC signifies better detection of features that suppress predictions when removed.
- RAM: This metric provides a general measure of feature importance based on absolute values, capturing the overall contribution of features irrespective of their directionality. Starting with all features unmasked, RAM progressively masks them in descending order of absolute importance (e.g., gradient magnitudes). The model’s output changes are tracked, and the AUC is derived from the resulting curve. A larger AUC indicates that the explanation method more accurately prioritizes features by their true impact, whether positive or negative.
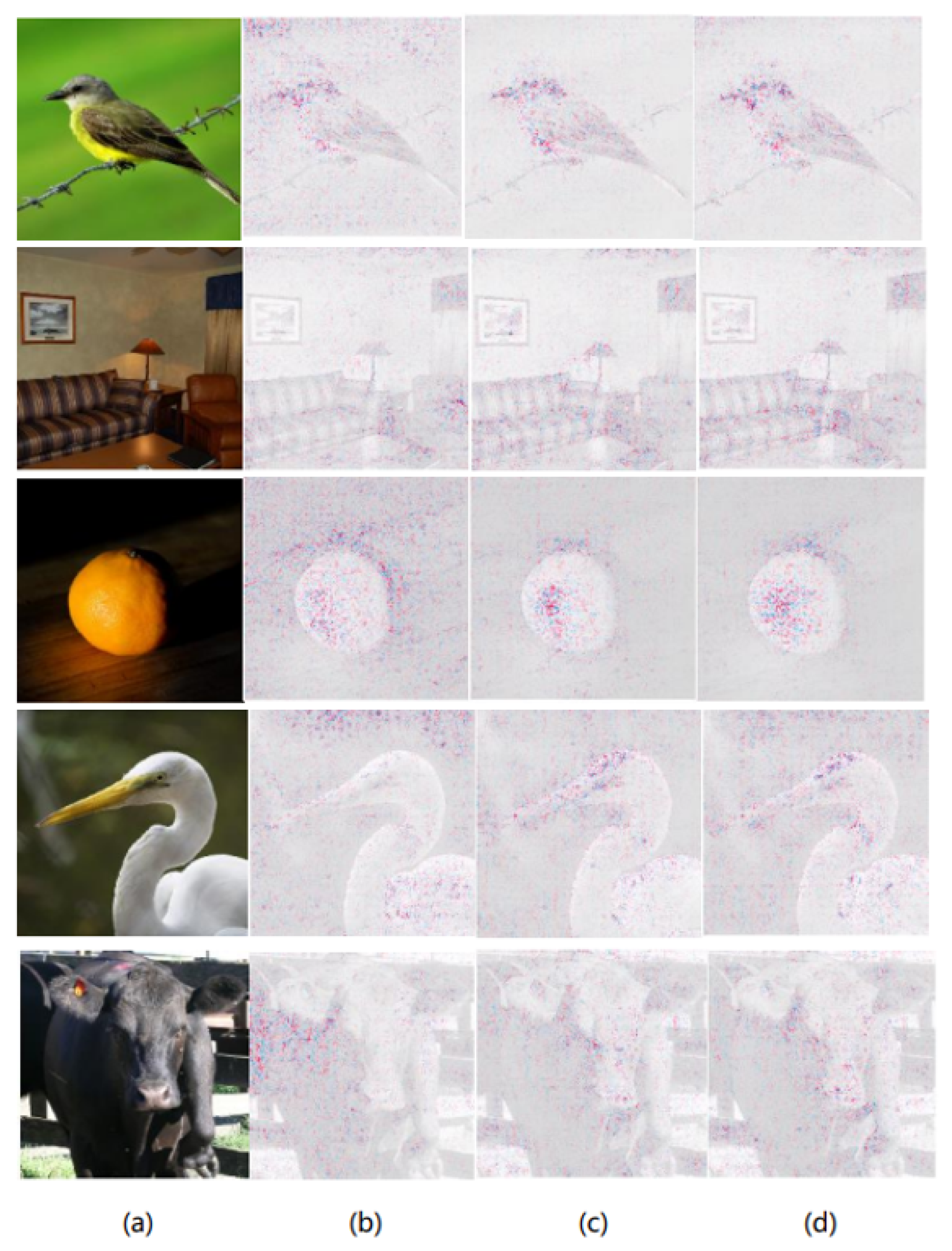
4.3. Results
4.3.1. Evaluation on ImageNet
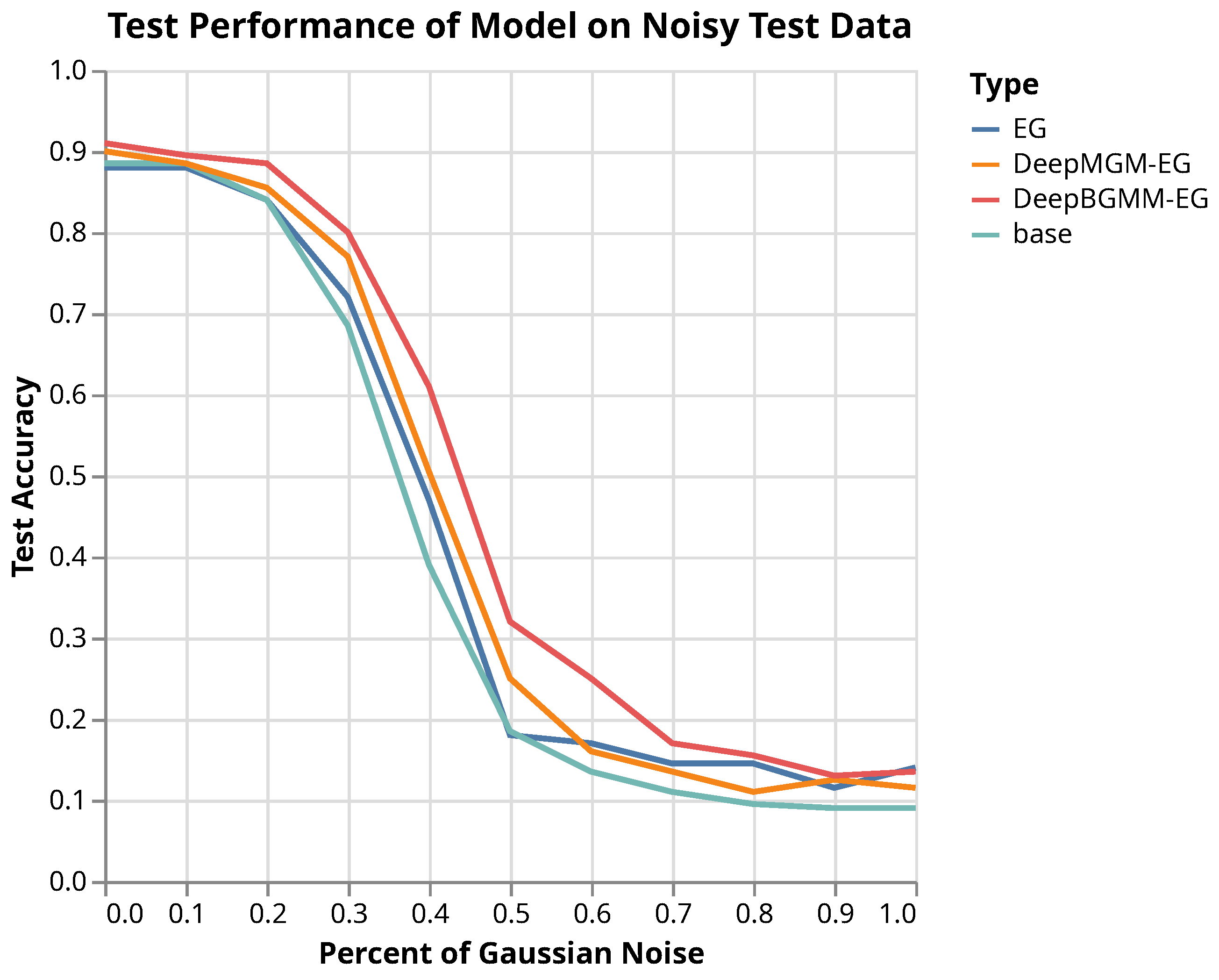
4.3.2. Improvement of Model Robustness to Noise via Attribution Priors
5. Discussion
5.1. Comparative Analysis of Shape Priors
5.2. Evaluation of Class Activation Mapping Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Fu, T.; Du, Y.; Gao, W.; Huang, K.; Liu, Z.; Chandak, P.; Liu, S.; Van Katwyk, P.; Deac, A.; et al. Scientific discovery in the age of artificial intelligence. Nature 2023, 2, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Alowais, S.A.; Alghamdi, S.S.; Alsuhebany, N.; Alqahtani, T.; Alshaya, A.I.; Almohareb, S.N.; Aldairem, A.; Alrashed, M.; Bin Saleh, K.; Badreldin, H.A.; et al. Revolutionizing healthcare: The role of artificial intelligence in clinical practice. BMC Med. Educ. 2023, 2, 689. [Google Scholar] [CrossRef]
- Khaleel, M.; Ahmed, A.A.; Alsharif, A. Artificial Intelligence in Engineering. Brill. Res. Artif. Intell. 2023, 2, 32–42. [Google Scholar] [CrossRef]
- Nazir, S.; Dickson, D.M.; Akram, M.U. Survey of explainable artificial intelligence techniques for biomedical imaging with deep neural networks. Comput. Biol. Med. 2023, 2, 106668. [Google Scholar] [CrossRef]
- Hassija, V.; Chamola, V.; Bajpai, B.C.; Naren; Zeadally, S. Security issues in implantable medical devices: Fact or fiction? Sustain. Cities Soc. 2021, 2, 102552. [Google Scholar] [CrossRef]
- Wichmann, F.A.; Geirhos, R. Are deep neural networks adequate behavioral models of human visual perception? Annu. Rev. Vis. Sci. 2023, 2, 501–524. [Google Scholar] [CrossRef] [PubMed]
- Hassija, V.; Chamola, V.; Mahapatra, A.; Singal, A.; Goel, D.; Huang, K.; Scardapane, S.; Spinelli, I.; Mahmud, M.; Hussain, A. Interpreting black-box models: A review on explainable artificial intelligence. Cogn. Comput. 2024, 2, 45–74. [Google Scholar] [CrossRef]
- Slack, D.; Hilgard, A.; Singh, S.; Lakkaraju, H. Reliable post hoc explanations: Modeling uncertainty in explainability. Adv. Neural Inf. Process. Syst. 2021, 2, 9391–9404. [Google Scholar]
- Ai, Q.; Narayanan, R.L. Model-agnostic vs. model-intrinsic interpretability for explainable product search. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Queensland, Australia, 1–5 November 2021; pp. 5–15. [Google Scholar]
- Song, Y.Y.; Ying, L.U. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 2, 130. [Google Scholar]
- Su, X.; Yan, X.; Tsai, C.L. Linear regression. Wiley Interdiscip. Rev. Comput. Stat. 2012, 2, 275–294. [Google Scholar] [CrossRef]
- LaValley, M.P. Logistic regression. Circulation 2008, 2, 2395–2399. [Google Scholar] [CrossRef]
- Vesic, A.; Marjanovic, M.; Petrovic, A.; Strumberger, I.; Tuba, E.; Bezdan, T. Optimizing extreme learning machine by animal migration optimization. In Proceedings of the 2022 IEEE Zooming Innovation in Consumer Technologies Conference (ZINC), Novi Sad, Serbia, 25–26 May 2022; pp. 261–266. [Google Scholar]
- Golubovic, S.; Petrovic, A.; Bozovic, A.; Antonijevic, M.; Zivkovic, M.; Bacanin, N. Gold price forecast using variational mode decomposition-aided long short-term model tuned by modified whale optimization algorithm. In Proceedings of the International Conference on Data Intelligence and Cognitive Informatics, Tirunelveli, India, 27–28 June 2023; Springer: Singapore, 2023; pp. 69–83. [Google Scholar]
- Rigatti, S.J. Random forest. J. Insur. Med. 2017, 2, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Kontschieder, P.; Fiterau, M.; Criminisi, A.; Bulo, S.R. Deep neural decision forests. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1467–1475. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Fernando, T.; Gammulle, H.; Denman, S.; Sridharan, S.; Fookes, C. Deep learning for medical anomaly detection—A survey. ACM Comput. Surv. (CSUR) 2021, 2, 1–37. [Google Scholar] [CrossRef]
- Sundararajan, M.; Taly, A.; Yan, Q. Gradients of counterfactuals. arXiv 2016, arXiv:1611.02639. [Google Scholar]
- Shrikumar, A.; Greenside, P.; Kundaje, A. Learning important features through propagating activation differences. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3145–3153. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.R.; Samek, W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 2015, 2, e0130140. [Google Scholar] [CrossRef] [PubMed]
- Erion, G.; Janizek, J.D.; Sturmfels, P.; Lundberg, S.M.; Lee, S.-I. Improving performance of deep learning models with axiomatic attribution priors and expected gradients. Nat. Mach. Intell. 2021, 2, 620–631. [Google Scholar] [CrossRef]
- Hamarneh, G.; Li, X. Watershed segmentation using prior shape and appearance knowledge. Image Vis. Comput. 2009, 2, 59–68. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9446–9454. [Google Scholar]
- Do, C.B. The Multivariate Gaussian Distribution. Sect. Notes, Lect. Mach. Learn. CS 2008, 229, 1–10. [Google Scholar]
- Nosrati, M.S.; Hamarneh, G. Incorporating prior knowledge in medical image segmentation: A survey. arXiv 2016, arXiv:1607.01092. [Google Scholar]
- Zhao, X.; Huang, W.; Huang, X.; Robu, V.; Flynn, D. Baylime: Bayesian local interpretable model-agnostic explanations. In Proceedings of the Uncertainty in Artificial Intelligence, Online, 27–30 July 2021; pp. 887–896. [Google Scholar]
- Buono, V.; Mashhadi, P.S.; Rahat, M.; Tiwari, P.; Byttner, S. Expected Grad-CAM: Towards gradient faithfulness. arXiv 2024, arXiv:2406.01274. [Google Scholar]
- Kim, B.; Wattenberg, M.; Gilmer, J.; Cai, C.; Wexler, J.; Viegas, F. Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (tcav). In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 2668–2677. [Google Scholar]
- Smilkov, D.; Thorat, N.; Kim, B.; Viégas, F.; Wattenberg, M. Smoothgrad: Removing noise by adding noise. arXiv 2017, arXiv:1706.03825. [Google Scholar]
- Ross, A.S.; Hughes, M.C.; Doshi-Velez, F. Right for the right reasons: Training differentiable models by constraining their explanations. arXiv 2017, arXiv:1703.03717. [Google Scholar]
- Baehrens, D.; Schroeter, T.; Harmeling, S.; Kawanabe, M.; Hansen, K.; Müller, K.R. How to explain individual classification decisions. J. Mach. Learn. Res. 2010, 2, 1803–1831. [Google Scholar]
- Enguehard, J. Sequential Integrated Gradients: A simple but effective method for explaining language models. arXiv 2023, arXiv:2305.15853. [Google Scholar]
- Sayres, R.; Taly, A.; Rahimy, E.; Blumer, K.; Coz, D.; Hammel, N.; Krause, J.; Narayanaswamy, A.; Rastegar, Z.; Wu, D.; et al. Using a deep learning algorithm and integrated gradients explanation to assist grading for diabetic retinopathy. Ophthalmology 2019, 2, 552–564. [Google Scholar] [CrossRef]
- Lu, J. A survey on Bayesian inference for Gaussian mixture model. arXiv 2021, arXiv:2108.11753. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Petsiuk, V. Rise: Randomized Input Sampling for Explanation of black-box models. arXiv 2018, arXiv:1806.07421. [Google Scholar]




| Method | KPM | KNM | KAM | RPM | RNM | RAM |
|---|---|---|---|---|---|---|
| EG | 1.0952 | −1.1014 | 0.9653 | 1.2502 | −1.2558 | 1.4305 |
| LIFT | 1.1027 | −1.1283 | 0.9288 | 1.2120 | −1.2316 | 1.4432 |
| DeepBGMM-EG | 1.1193 | −1.1279 | 0.9580 | 1.2224 | −1.2340 | 1.4361 |
| DeepMGM-EG | 1.1192 | −1.1283 | 0.9565 | 1.2217 | −1.2333 | 1.4342 |
| Method | KPM | KNM | KAM | RPM | RNM | RAM |
|---|---|---|---|---|---|---|
| EG | 1.2418 | −1.2390 | 1.0217 | 2.4655 | −2.4639 | 2.8490 |
| LIFT | 1.0055 | −0.8827 | 0.9758 | 2.7043 | −2.6894 | 2.8403 |
| DeepBGMM-EG | 1.2603 | −1.2412 | 1.0244 | 2.3692 | −2.3510 | 2.7601 |
| DeepMGM-EG | 1.2540 | −1.2416 | 1.0131 | 2.4678 | −2.4566 | 2.8758 |
| Method | KPM | KNM | KAM | RPM | RNM | RAM |
|---|---|---|---|---|---|---|
| EG | 1.0952 | −1.1014 | 0.9653 | 1.2502 | −1.2558 | 1.4305 |
| DeepBGMM-EG | 1.1193 | −1.1279 | 0.9580 | 1.2224 | −1.2340 | 1.4361 |
| Shape-EG | 1.1018 | −1.1044 | 0.9649 | 1.2485 | −1.2504 | 1.4317 |
| Method | Insertion | Deletion |
|---|---|---|
| Lime | 0.1178 | 0.1127 |
| Grad-CAM | 0.1233 | 0.1290 |
| Baylime | 0.1178 | 0.1127 |
| EG | 0.6849 | 0.1206 |
| DeepBGMM-EG | 0.6849 | 0.1202 |
| DeepMGM-EG | 0.6842 | 0.1204 |
| Shape-EG | 0.6841 | 0.1207 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.-Y.; Gong, X.-J. Enhancing Neural Network Interpretability Through Deep Prior-Guided Expected Gradients. Appl. Sci. 2025, 15, 7090. https://doi.org/10.3390/app15137090
Guo S-Y, Gong X-J. Enhancing Neural Network Interpretability Through Deep Prior-Guided Expected Gradients. Applied Sciences. 2025; 15(13):7090. https://doi.org/10.3390/app15137090
Chicago/Turabian StyleGuo, Su-Ying, and Xiu-Jun Gong. 2025. "Enhancing Neural Network Interpretability Through Deep Prior-Guided Expected Gradients" Applied Sciences 15, no. 13: 7090. https://doi.org/10.3390/app15137090
APA StyleGuo, S.-Y., & Gong, X.-J. (2025). Enhancing Neural Network Interpretability Through Deep Prior-Guided Expected Gradients. Applied Sciences, 15(13), 7090. https://doi.org/10.3390/app15137090







