Interpretable Machine Learning for Legume Yield Prediction Using Satellite Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
- Data acquisition: Crop yield data for lupin are collected from various fields.
- Data pre-processing and feature engineering: Spectral reflectance data are initially acquired through Sentinel-2 multispectral imagery. Then, 13 commonly used VIs are calculated based on 9 spectral bands. The resulting dataset is cleaned and prepared. Outliers are removed following the interquartile range (IQR) technique. Identification of highly correlated features follows through Spearman correlation analysis, while also Z-score normalization of input features takes place. Finally, data augmentation with Synthetic Minority Over-sampling Technique for Regression (SMOTER) is applied to address imbalanced data distribution.
- ML model training: Six ML regression models are trained as a means of capturing relationships among the features. In all cases, GridSearchCV and 5-fold cross-validation with shuffling are utilized for hyperparameter tuning and performance evaluation via relevant metrics.
- Model interpretation: An interpretability analysis utilizing SHAP values is then performed on the most accurate ML model to identify the factors affecting individual predictions.
2.1. Data Acquisition
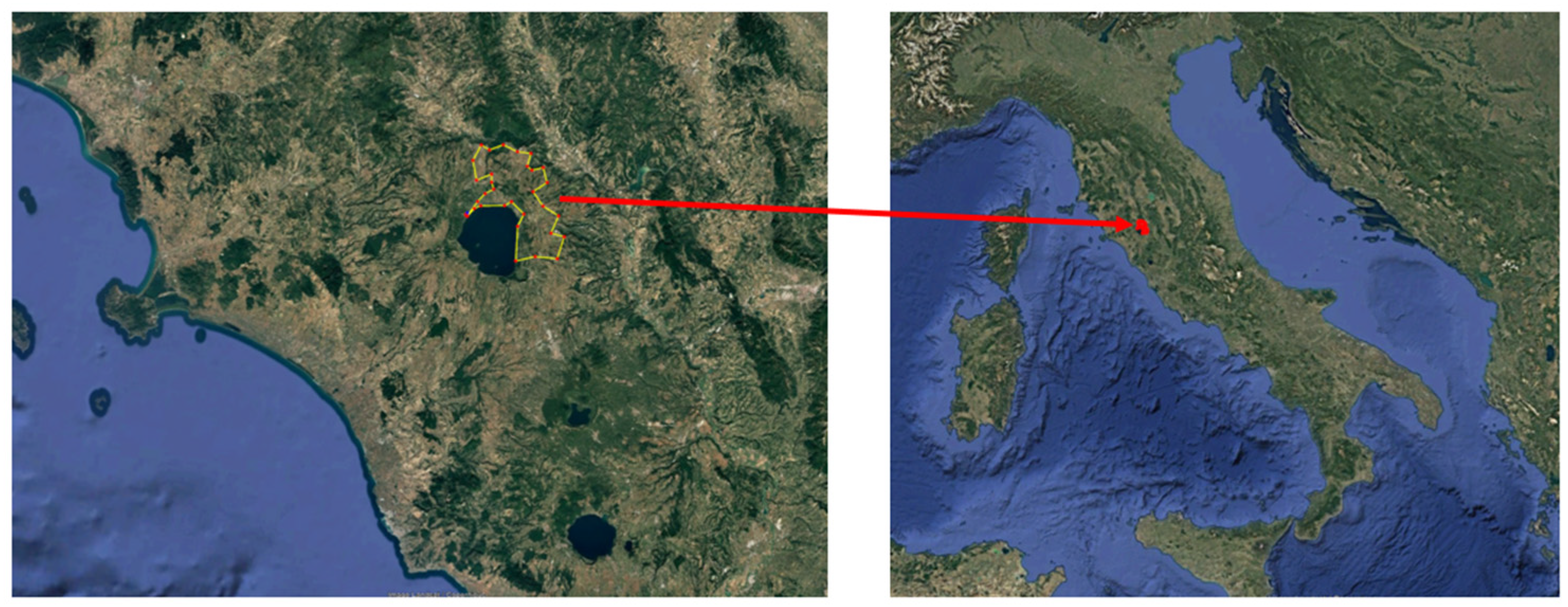
2.1.1. Ground-Truth Crop Yield Data
2.1.2. Remote Sensing Data: Sentinel-2 Spectral Bands
- (Blue, 490 nm);
- (Green, 560 nm);
- (Red, 665 nm);
- (Red Edge 1, 705 nm);
- (Red Edge 2, 740 nm);
- (Red Edge 3, 783 nm);
- (Narrow Near-Infrared, 865 nm);
- (Short-Wave Infrared 1, 1610 nm);
- (Short-Wave Infrared 2, 2190 nm).
2.2. Feature Selection and Preprocessing
2.2.1. Computation of Vegetation Indices
2.2.2. Outlier Removal
2.2.3. Addressing Multicollinearity in the Dataset
2.2.4. Normalization of Input Features
2.2.5. Data Augmentation
2.3. Machine Learning Used for Yield Prediction
2.3.1. Tested Machine Learning Algorithms
2.3.2. Performance Metrics
2.4. Model Interpretation
3. Results
3.1. Comparison of Machine Learning Performance
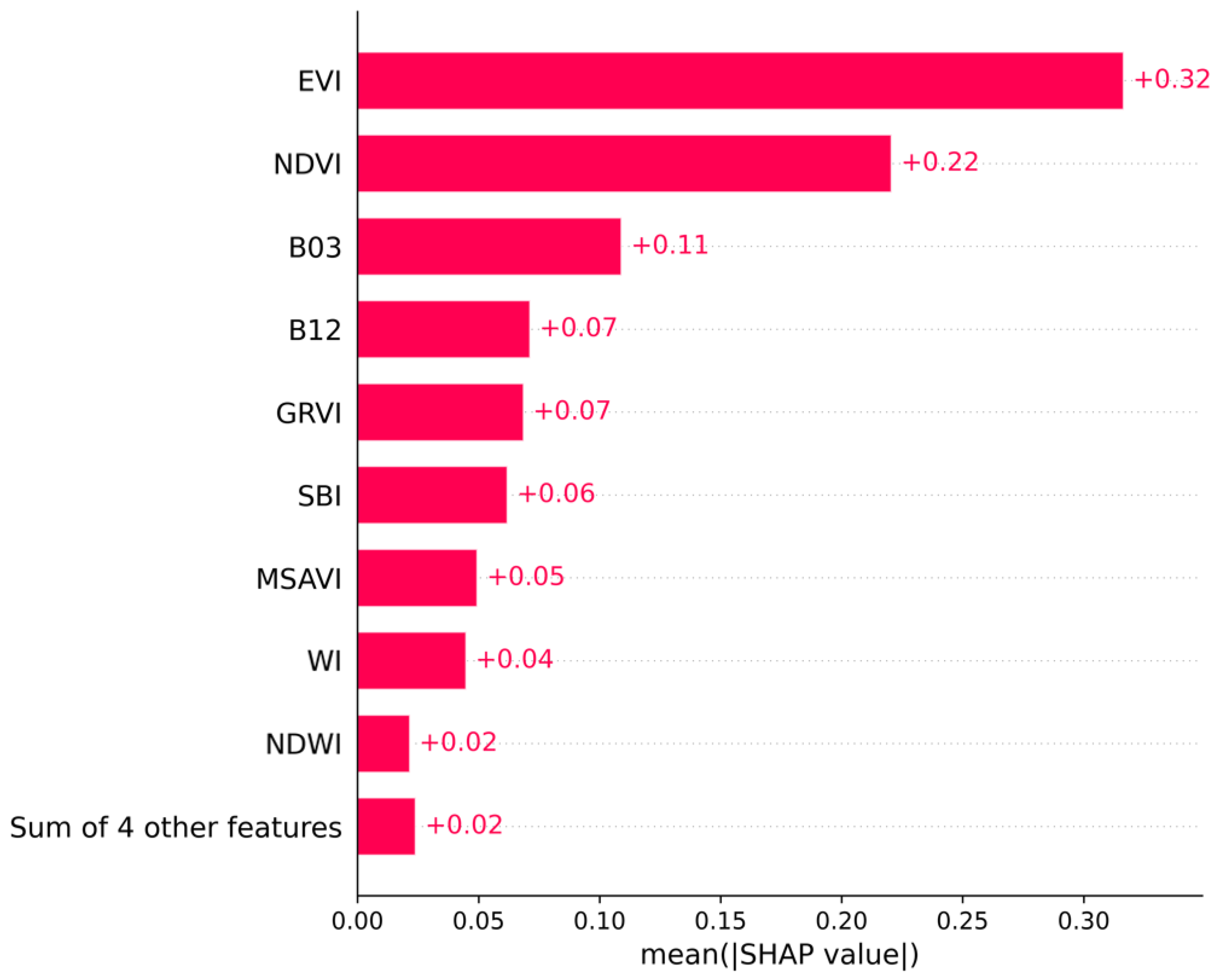
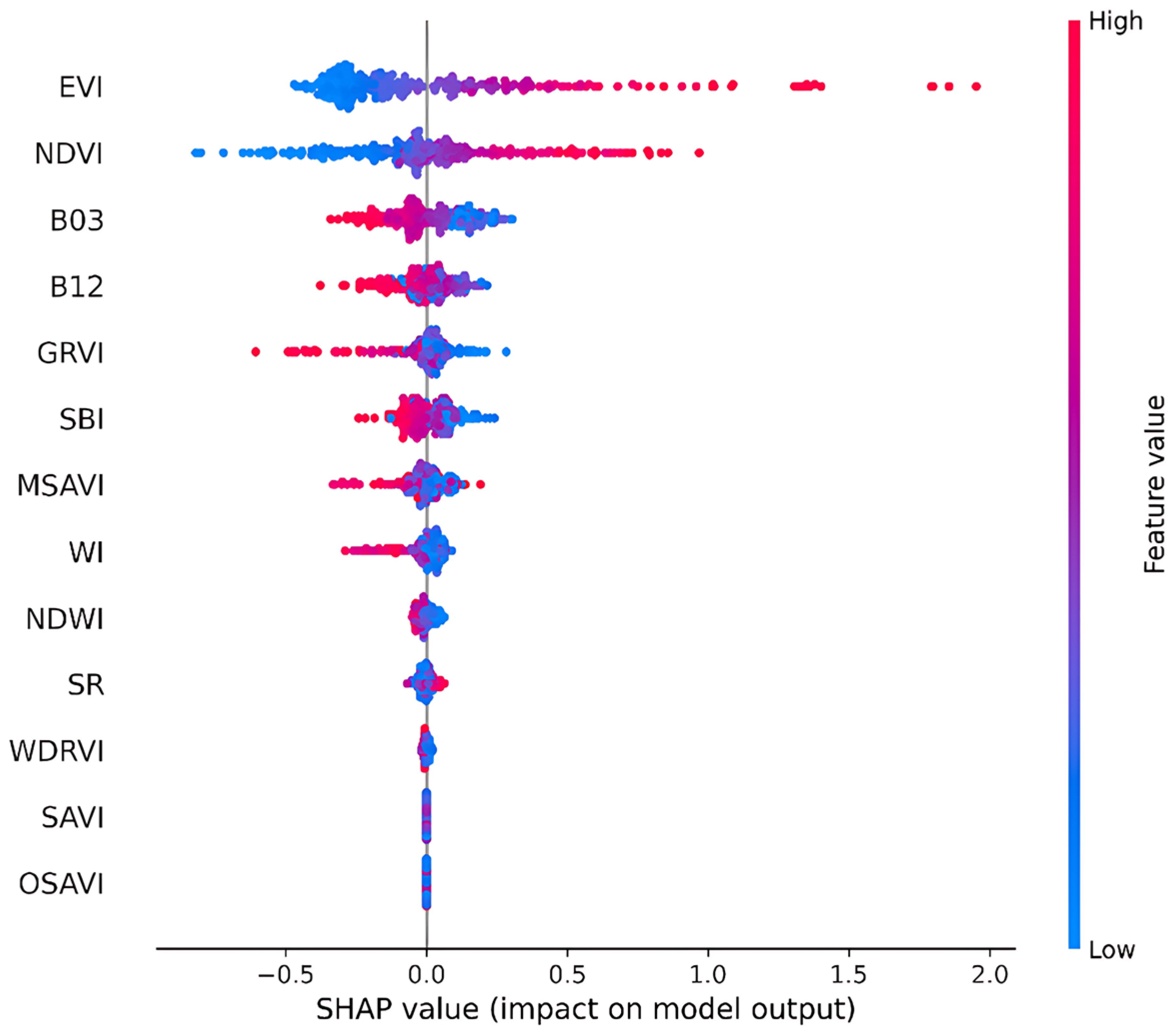
3.2. SHAP-Based Interpretation of XGBoost Feature Contributions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matthews, L.; Strauss, J.A.; Reinsch, T.; Smit, H.P.J.; Taube, F.; Kluss, C.; Swanepoel, P.A. Legumes and livestock in no-till crop rotations: Effects on nitrous oxide emissions, carbon sequestration, yield, and wheat protein content. Agric. Syst. 2025, 224, 104218. [Google Scholar] [CrossRef]
- Liu, R.; Flanagan, B.M.; Ratanpaul, V.; Gidley, M.J. Valorising legume protein extraction side-streams: Isolation and characterisation of fibre-rich and starch-rich co-products from wet fractionation of five legumes. Food Hydrocoll. 2025, 164, 111191. [Google Scholar] [CrossRef]
- Dela, M.; Shanka, D.; Dalga, D. Biofertilizer and NPSB fertilizer application effects on nodulation and productivity of common bean (Phaseolus vulgaris L.) at Sodo Zuria, Southern Ethiopia. Open Life Sci. 2023, 18, 20220537. [Google Scholar] [CrossRef]
- Folina, A.; Stavropoulos, P.; Mavroeidis, A.; Roussis, I.; Kakabouki, I.; Tsiplakou, E.; Bilalis, D. Optimizing Fodder Yield and Quality Through Grass–Legume Relay Intercropping in the Mediterranean Region. Plants 2025, 14, 877. [Google Scholar] [CrossRef]
- Tita, D.; Mahdi, K.; Devkota, K.P.; Devkota, M. Climate change and agronomic management: Addressing wheat yield gaps and sustainability challenges in the Mediterranean and MENA regions. Agric. Syst. 2025, 224, 104242. [Google Scholar] [CrossRef]
- Benos, L.; Makaritis, N.; Kolorizos, V. From Precision Agriculture to Agriculture 4.0: Integrating ICT in Farming—Information and Communication Technologies for Agriculture—Theme III: Decision; Bochtis, D.D., Sørensen, C.G., Fountas, S., Moysiadis, V., Pardalos, P.M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 79–93. ISBN 978-3-030-84152-2. [Google Scholar]
- Filippi, P.; Han, S.Y.; Bishop, T.F.A. On crop yield modelling, predicting, and forecasting and addressing the common issues in published studies. Precis. Agric. 2024, 26, 8. [Google Scholar] [CrossRef]
- Parashar, N.; Johri, P.; Khan, A.A.; Gaur, N.; Kadry, S. An Integrated Analysis of Yield Prediction Models: A Comprehensive Review of Advancements and Challenges. Comput. Mater. Contin. 2024, 80, 389–425. [Google Scholar] [CrossRef]
- Petropoulos, T.; Benos, L.; Busato, P.; Kyriakarakos, G.; Kateris, D.; Aidonis, D.; Bochtis, D. Soil Organic Carbon Assessment for Carbon Farming: A Review. Agriculture 2025, 15, 567. [Google Scholar] [CrossRef]
- Cheng, E.; Zhang, B.; Peng, D.; Zhong, L.; Yu, L.; Liu, Y.; Xiao, C.; Li, C.; Li, X.; Chen, Y.; et al. Wheat yield estimation using remote sensing data based on machine learning approaches. Front. Plant Sci. 2022, 13, 1090970. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Darra, N.; Anastasiou, E.; Kriezi, O.; Lazarou, E.; Kalivas, D.; Fountas, S. Can Yield Prediction Be Fully Digitilized? A Systematic Review. Agronomy 2023, 13, 567. [Google Scholar] [CrossRef]
- Jiang, H.; Jiang, L.; He, L.; Murengami, B.G.; Jing, X.; Misiewicz, P.A.; Cheein, F.A.; Fu, L. Yield prediction of root crops in field using remote sensing: A comprehensive review. Comput. Electron. Agric. 2024, 227, 109600. [Google Scholar] [CrossRef]
- Ali, A.M.; Abouelghar, M.; Belal, A.A.; Saleh, N.; Yones, M.; Selim, A.I.; Amin, M.E.S.; Elwesemy, A.; Kucher, D.E.; Maginan, S.; et al. Crop Yield Prediction Using Multi Sensors Remote Sensing (Review Article). Egypt. J. Remote Sens. Sp. Sci. 2022, 25, 711–716. [Google Scholar] [CrossRef]
- Kasampalis, D.A.; Alexandridis, T.K.; Deva, C.; Challinor, A.; Moshou, D.; Zalidis, G. Contribution of Remote Sensing on Crop Models: A Review. J. Imaging 2018, 4, 52. [Google Scholar] [CrossRef]
- Nearing, G.S.; Crow, W.T.; Thorp, K.R.; Moran, M.S.; Reichle, R.H.; Gupta, H.V. Assimilating remote sensing observations of leaf area index and soil moisture for wheat yield estimates: An observing system simulation experiment. Water Resour. Res. 2012, 48, W05525. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Xu, X.; Zhao, C.; Jin, X.; Yang, G.; Feng, H. Assimilation of Two Variables Derived from Hyperspectral Data into the DSSAT-CERES Model for Grain Yield and Quality Estimation. Remote Sens. 2015, 7, 12400–12418. [Google Scholar] [CrossRef]
- Clevers, J.; Vonder, O.; Jongschaap, R.; Desprats, J.F.; King, C.; Prévot, L.; Bruguier, N. Using SPOT data for calibrating a wheat growth model under mediterranean conditions. Agronomie 2002, 22, 687–694. [Google Scholar] [CrossRef]
- Joshi, A.; Pradhan, B.; Gite, S.; Chakraborty, S. Remote-Sensing Data and Deep-Learning Techniques in Crop Mapping and Yield Prediction: A Systematic Review. Remote Sens. 2023, 15, 2014. [Google Scholar] [CrossRef]
- Meghraoui, K.; Sebari, I.; Pilz, J.; Ait El Kadi, K.; Bensiali, S. Applied Deep Learning-Based Crop Yield Prediction: A Systematic Analysis of Current Developments and Potential Challenges. Technologies 2024, 12, 43. [Google Scholar] [CrossRef]
- Peng, D.; Zhou, L.; Huang, J.; Zhou, B.; Wang, F. Rice yield estimation based on MODIS EVI and measured data derived from statistical sampling plots at province level. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2011, 27, 106–114. [Google Scholar] [CrossRef]
- Bazzi, H.; Ciais, P.; Makowski, D.; Baghdadi, N. Advancing winter wheat yield anomaly prediction with high-resolution satellite-based gross primary production. One Earth 2025, 8, 101146. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, K.; Sun, L.; Xie, Y.; Song, X.-P. Satellite-based soybean yield prediction in Argentina: A comparison between panel regression and deep learning methods. Comput. Electron. Agric. 2024, 221, 108978. [Google Scholar] [CrossRef]
- Ashfaq, M.; Khan, I.; Alzahrani, A.; Tariq, M.U.; Khan, H.; Ghani, A. Accurate Wheat Yield Prediction Using Machine Learning and Climate-NDVI Data Fusion. IEEE Access 2024, 12, 40947–40961. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep Gaussian Process for Crop Yield Prediction Based on Remote Sensing Data. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar] [CrossRef]
- Kuwata, K.; Shibasaki, R. Estimating crop yields with deep learning and remotely sensed data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 858–861. [Google Scholar]
- Wolanin, A.; Mateo-García, G.; Camps-Valls, G.; Gómez-Chova, L.; Meroni, M.; Duveiller, G.; Liangzhi, Y.; Guanter, L. Estimating and understanding crop yields with explainable deep learning in the Indian Wheat Belt. Environ. Res. Lett. 2020, 15, 24019. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Luo, Y.; Zhang, L.; Zhang, J.; Li, Z.; Tao, F. Wheat yield predictions at a county and field scale with deep learning, machine learning, and google earth engine. Eur. J. Agron. 2021, 123, 126204. [Google Scholar] [CrossRef]
- Tian, H.; Wang, P.; Tansey, K.; Zhang, J.; Zhang, S.; Li, H. An LSTM neural network for improving wheat yield estimates by integrating remote sensing data and meteorological data in the Guanzhong Plain, PR China. Agric. For. Meteorol. 2021, 310, 108629. [Google Scholar] [CrossRef]
- Tian, H.; Wang, P.; Tansey, K.; Han, D.; Zhang, J.; Zhang, S.; Li, H. A deep learning framework under attention mechanism for wheat yield estimation using remotely sensed indices in the Guanzhong Plain, PR China. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102375. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z.; Kang, Y.; Özdoğan, M. Corn yield prediction and uncertainty analysis based on remotely sensed variables using a Bayesian neural network approach. Remote Sens. Environ. 2021, 259, 112408. [Google Scholar] [CrossRef]
- Xie, Y.; Huang, J. Integration of a Crop Growth Model and Deep Learning Methods to Improve Satellite-Based Yield Estimation of Winter Wheat in Henan Province, China. Remote Sens. 2021, 13, 4372. [Google Scholar] [CrossRef]
- Fernandes, J.L.; Ebecken, N.F.F.; Esquerdo, J.C.D.M. Sugarcane yield prediction in Brazil using NDVI time series and neural networks ensemble. Int. J. Remote Sens. 2017, 38, 4631–4644. [Google Scholar] [CrossRef]
- Li, Y.; Li, R.; Ji, R.; Wu, Y.; Chen, J.; Wu, M.; Yang, J. Research on Factors Affecting Global Grain Legume Yield Based on Explainable Artificial Intelligence. Agriculture 2024, 14, 438. [Google Scholar] [CrossRef]
- Manafifard, M. A new hyperparameter to random forest: Application of remote sensing in yield prediction. Earth Sci. Inform. 2024, 17, 63–73. [Google Scholar] [CrossRef]
- Ishaq, R.A.F.; Zhou, G.; Jing, G.; Shah, S.R.A.; Ali, A.; Imran, M.; Jiang, H. Obaid-ur-Rehman Geospatial Robust Wheat Yield Prediction Using Machine Learning and Integrated Crop Growth Model and Time-Series Satellite Data. Remote Sens. 2025, 17, 1140. [Google Scholar] [CrossRef]
- Joshi, A.; Pradhan, B.; Chakraborty, S.; Varatharajoo, R.; Gite, S.; Alamri, A. Deep-Transfer-Learning Strategies for Crop Yield Prediction Using Climate Records and Satellite Image Time-Series Data. Remote Sens. 2024, 16, 4804. [Google Scholar] [CrossRef]
- Zhao, Y.; He, J.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Wheat Yield Robust Prediction in the Huang-Huai-Hai Plain by Coupling Multi-Source Data with Ensemble Model under Different Irrigation and Extreme Weather Events. Remote Sens. 2024, 16, 1259. [Google Scholar] [CrossRef]
- Jeong, S.; Ko, J.; Ban, J.; Shin, T.; Yeom, J. Deep learning-enhanced remote sensing-integrated crop modeling for rice yield prediction. Ecol. Inform. 2024, 84, 102886. [Google Scholar] [CrossRef]
- Benos, L.; Tagarakis, A.C.; Dolias, G.; Berruto, R.; Kateris, D.; Bochtis, D. Machine Learning in Agriculture: A Comprehensive Updated Review. Sensors 2021, 21, 3758. [Google Scholar] [CrossRef]
- Qin, X.; Wu, B.; Zeng, H.; Zhang, M.; Tian, F. Global Gridded Crop Production Dataset at 10 km Resolution from 2010 to 2020. Sci. Data 2024, 11, 1377. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Qu, Y.; Geng, H.; Xin, Q.; Huang, J.; Peng, S.; Zhang, L. Mapping annual 10-m maize cropland changes in China during 2017–2021. Sci. Data 2023, 10, 765. [Google Scholar] [CrossRef]
- Wuyun, D.; Sun, L.; Chen, Z.; Li, Y.; Han, M.; Shi, Z.; Ren, T.; Zhao, H. A 10-meter resolution dataset of abandoned and reclaimed cropland from 2016 to 2023 in Inner Mongolia, China. Sci. Data 2025, 12, 317. [Google Scholar] [CrossRef]
- Nuttall, J.G.; Wallace, A.J.; Delahunty, A.J.; Perry, E.M.; Clancy, A.B.; Panozzo, J.F.; Fitzgerald, G.J.; Walker, C.K. Lentil grain quality and segregation opportunities in-field using remote sensing. Agron. J. 2024, 116, 121–140. [Google Scholar] [CrossRef]
- Das, P.; Jha, G.K.; Lama, A.; Parsad, R. Crop Yield Prediction Using Hybrid Machine Learning Approach: A Case Study of Lentil (Lens culinaris Medik.). Agriculture 2023, 13, 596. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, 3rd ed.; 2025. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 10 June 2025).
- Ryo, M. Explainable artificial intelligence and interpretable machine learning for agricultural data analysis. Artif. Intell. Agric. 2022, 6, 257–265. [Google Scholar] [CrossRef]
- Benos, L.; Tsaopoulos, D.; Tagarakis, A.C.; Kateris, D.; Busato, P.; Bochtis, D. Explainable AI-Enhanced Human Activity Recognition for Human–Robot Collaboration in Agriculture. Appl. Sci. 2025, 15, 650. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Bebeli, P.J.; Lazaridi, E.; Chatzigeorgiou, T.; Suso, M.-J.; Hein, W.; Alexopoulos, A.A.; Canha, G.; van Haren, R.J.F.; Jóhannsson, M.H.; Mateos, C.; et al. State and Progress of Andean Lupin Cultivation in Europe: A Review. Agronomy 2020, 10, 1038. [Google Scholar] [CrossRef]
- Jiménez-Jiménez, S.I.; Marcial-Pablo, M.d.J.; Ojeda-Bustamante, W.; Sifuentes-Ibarra, E.; Inzunza-Ibarra, M.A.; Sánchez-Cohen, I. VICAL: Global Calculator to Estimate Vegetation Indices for Agricultural Areas with Landsat and Sentinel-2 Data. Agronomy 2022, 12, 1518. [Google Scholar] [CrossRef]
- Jeong, S.; Ko, J.; Yeom, J.-M. Predicting rice yield at pixel scale through synthetic use of crop and deep learning models with satellite data in South and North Korea. Sci. Total Environ. 2022, 802, 149726. [Google Scholar] [CrossRef]
- Yang, W.; Nigon, T.; Hao, Z.; Dias Paiao, G.; Fernández, F.G.; Mulla, D.; Yang, C. Estimation of corn yield based on hyperspectral imagery and convolutional neural network. Comput. Electron. Agric. 2021, 184, 106092. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of Green-Red Vegetation Index for Remote Sensing of Vegetation Phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Muruganantham, P.; Wibowo, S.; Grandhi, S.; Samrat, N.H.; Islam, N. A Systematic Literature Review on Crop Yield Prediction with Deep Learning and Remote Sensing. Remote Sens. 2022, 14, 1990. [Google Scholar] [CrossRef]
- Dash, C.S.K.; Behera, A.K.; Dehuri, S.; Ghosh, A. An outliers detection and elimination framework in classification task of data mining. Decis. Anal. J. 2023, 6, 100164. [Google Scholar] [CrossRef]
- Fletcher, A.A.; Kelly, M.S.; Eckhoff, A.M.; Allen, P.J. Revisiting the intrinsic mycobiome in pancreatic cancer. Nature 2023, 620, E1–E6. [Google Scholar] [CrossRef]
- Behkamal, B.; Entezami, A.; De Michele, C.; Arslan, A.N. Investigation of Temperature Effects into Long-Span Bridges via Hybrid Sensing and Supervised Regression Models. Remote Sens. 2023, 15, 3503. [Google Scholar] [CrossRef]
- Liao, Z.; He, B.; Quan, X. Modified enhanced vegetation index for reducing topographic effects. J. Appl. Remote Sens. 2015, 9, 96068. [Google Scholar] [CrossRef]
- Aparicio-Ibáñez, J.; Pimentel, R.; Bonet-García, F.J.; Polo, M.J. Using NDVI-derived vegetation vigour as a proxy for soil water content in Mediterranean-mountain traditional water management systems: Seasonal variability and restoration impacts. Ecol. Indic. 2025, 174, 113468. [Google Scholar] [CrossRef]
- Ebrahimy, H.; Wang, Y.; Zhang, Z. Utilization of synthetic minority oversampling technique for improving potato yield prediction using remote sensing data and machine learning algorithms with small sample size of yield data. ISPRS J. Photogramm. Remote Sens. 2023, 201, 12–25. [Google Scholar] [CrossRef]
- Jawa, M.; Meena, S. Software Effort Estimation Using Synthetic Minority Over-Sampling Technique for Regression (SMOTER). In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022; pp. 1–6. [Google Scholar]
- Belhaouari, S.B.; Islam, A.; Kassoul, K.; Al-Fuqaha, A.; Bouzerdoum, A. Oversampling techniques for imbalanced data in regression. Expert Syst. Appl. 2024, 252, 124118. [Google Scholar] [CrossRef]
- Polychronopoulos, N.D.; Moustris, K.; Karakasidis, T.; Sikora, J.; Krasinskyi, V.; Sarris, I.E.; Vlachopoulos, J. Machine learning for screw design in single-screw extrusion. Polym. Eng. Sci. 2025, 65, 2607–2623. [Google Scholar] [CrossRef]
- Asiminari, G.; Benos, L.; Kateris, D.; Busato, P.; Achillas, C.; Pearson, C.G.S.S.; Bochtis, D. Simplifying Field Traversing Efficiency Estimation Using Machine Learning and Geometric Field Indices. AgriEngineering 2025, 7, 75. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards A Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy 2021, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Erion, G.G.; Li, S.-I. Consistent Individualized Feature Attribution for Tree Ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Zhang, P.; Jia, Y.; Shang, Y. Research and application of XGBoost in imbalanced data. Int. J. Distrib. Sens. Netw. 2022, 18, 15501329221106936. [Google Scholar] [CrossRef]
- Srinivasu, P.N.; Jaya Lakshmi, G.; Gudipalli, A.; Narahari, S.C.; Shafi, J.; Woźniak, M.; Ijaz, M.F. XAI-driven CatBoost multi-layer perceptron neural network for analyzing breast cancer. Sci. Rep. 2024, 14, 28674. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, X.; Ran, X.; Li, Z.; Cao, W. Prioritizing Causation in Decision Trees: A Framework for Interpretable Modeling. Eng. Appl. Artif. Intell. 2024, 133, 108224. [Google Scholar] [CrossRef]
- Johnson, S.; Perumalsamy, D. Application of XGBoost algorithm and grid search hyperparameter tuning to study health effects among individuals in the industrial area. Multimed. Tools Appl. 2025. [Google Scholar] [CrossRef]
- Arbi, S.J.; Rehman, Z.; Hassan, W.; Khalid, U.; Ijaz, N.; Maqsood, Z.; Haider, A. Optimized machine learning-based enhanced modeling of pile bearing capacity in layered soils using random and grid search techniques. Earth Sci. Inform. 2025, 18, 332. [Google Scholar] [CrossRef]
- Polychronopoulos, N.D.; Sarris, I.; Vlachopoulos, J. Implementation of Machine Learning in Flat Die Extrusion of Polymers. Molecules 2025, 30, 1879. [Google Scholar] [CrossRef]
- Chen, H.; Lundberg, S.M.; Lee, S.-I. Explaining a series of models by propagating Shapley values. Nat. Commun. 2022, 13, 4512. [Google Scholar] [CrossRef]
- Tagarakis, A.C.; Ketterings, Q.M.; Lyons, S.; Godwin, G. Proximal Sensing to Estimate Yield of Brown Midrib Forage Sorghum. Agron. J. 2017, 109, 107–114. [Google Scholar] [CrossRef]
- Tagarakis, A.C.; Ketterings, Q.M. In-Season Estimation of Corn Yield Potential Using Proximal Sensing. Agron. J. 2017, 109, 1323–1330. [Google Scholar] [CrossRef]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Minh, V.Q.; Trung, N.H. A comparative analysis of multitemporal MODIS EVI and NDVI data for large-scale rice yield estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]
- Mutanga, O.; Masenyama, A.; Sibanda, M. Spectral saturation in the remote sensing of high-density vegetation traits: A systematic review of progress, challenges, and prospects. ISPRS J. Photogramm. Remote Sens. 2023, 198, 297–309. [Google Scholar] [CrossRef]
- Yang, F.; Feng, L.; Liu, Q.; Wu, X.; Fan, Y.; Raza, M.A.; Cheng, Y.; Chen, J.; Wang, X.; Yong, T.; et al. Effect of interactions between light intensity and red-to- far-red ratio on the photosynthesis of soybean leaves under shade condition. Environ. Exp. Bot. 2018, 150, 79–87. [Google Scholar] [CrossRef]
- Krishna, G.; Sahoo, R.N.; Singh, P.; Patra, H.; Bajpai, V.; Das, B.; Kumar, S.; Dhandapani, R.; Vishwakarma, C.; Pal, M.; et al. Application of thermal imaging and hyperspectral remote sensing for crop water deficit stress monitoring. Geocarto Int. 2021, 36, 481–498. [Google Scholar] [CrossRef]
- Ewusi-Wilson, R.; Yendaw, J.A.; Sebbeh-Newton, S.; Ike, E.; Ayeh, F.J.F. Explainable Artificial Intelligence Estimation of Maximum Dry Density in Soil Compaction Based on Basic Soil Properties and Compaction Energy. Transp. Infrastruct. Geotechnol. 2025, 12, 94. [Google Scholar] [CrossRef]
- Morais, T.G.; Jongen, M.; Tufik, C.; Rodrigues, N.R.; Gama, I.; Serrano, J.; Domingos, T.; Teixeira, R.F.M. Estimation of Annual Productivity of Sown Rainfed Grasslands Using Machine Learning. Grass Forage Sci. 2025, 80, e12707. [Google Scholar] [CrossRef]
- Tagarakis, A.C.; Benos, L.; Kyriakarakos, G.; Pearson, S.; Sørensen, C.G.; Bochtis, D. Digital Twins in Agriculture and Forestry: A Review. Sensors 2024, 24, 3117. [Google Scholar] [CrossRef]
- Diaz-Gonzalez, F.A.; Vuelvas, J.; Correa, C.A.; Vallejo, V.E.; Patino, D. Machine learning and remote sensing techniques applied to estimate soil indicators—Review. Ecol. Indic. 2022, 135, 108517. [Google Scholar] [CrossRef]
- Ren, P.; Xiao, Y.; Chang, X.; Huang, P.-Y.; Li, Z.; Gupta, B.B.; Chen, X.; Wang, X. A Survey of Deep Active Learning. ACM Comput. Surv. 2021, 54, 1–40. [Google Scholar] [CrossRef]
- Fu, Y.; Zhu, X.; Li, B. A survey on instance selection for active learning. Knowl. Inf. Syst. 2013, 35, 249–283. [Google Scholar] [CrossRef]


| Algorithm | ||||
|---|---|---|---|---|
| DT | 0.3297 | 0.1970 | 0.4438 | 0.6393 |
| XGBoost | 0.2399 | 0.1149 | 0.3389 | 0.8756 |
| RF | 0.2900 | 0.1661 | 0.4076 | 0.6959 |
| SVR | 0.2404 | 0.1129 | 0.3360 | 0.7933 |
| KNN | 0.2624 | 0.1646 | 0.4057 | 0.6987 |
| MLPR | 0.2467 | 0.1125 | 0.3354 | 0.8141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petropoulos, T.; Benos, L.; Berruto, R.; Miserendino, G.; Marinoudi, V.; Busato, P.; Zisis, C.; Bochtis, D. Interpretable Machine Learning for Legume Yield Prediction Using Satellite Remote Sensing Data. Appl. Sci. 2025, 15, 7074. https://doi.org/10.3390/app15137074
Petropoulos T, Benos L, Berruto R, Miserendino G, Marinoudi V, Busato P, Zisis C, Bochtis D. Interpretable Machine Learning for Legume Yield Prediction Using Satellite Remote Sensing Data. Applied Sciences. 2025; 15(13):7074. https://doi.org/10.3390/app15137074
Chicago/Turabian StylePetropoulos, Theodoros, Lefteris Benos, Remigio Berruto, Gabriele Miserendino, Vasso Marinoudi, Patrizia Busato, Chrysostomos Zisis, and Dionysis Bochtis. 2025. "Interpretable Machine Learning for Legume Yield Prediction Using Satellite Remote Sensing Data" Applied Sciences 15, no. 13: 7074. https://doi.org/10.3390/app15137074
APA StylePetropoulos, T., Benos, L., Berruto, R., Miserendino, G., Marinoudi, V., Busato, P., Zisis, C., & Bochtis, D. (2025). Interpretable Machine Learning for Legume Yield Prediction Using Satellite Remote Sensing Data. Applied Sciences, 15(13), 7074. https://doi.org/10.3390/app15137074








