A Riemannian Dichotomizer Approach on Symmetric Positive Definite Manifolds for Offline, Writer-Independent Signature Verification
Abstract
1. Introduction
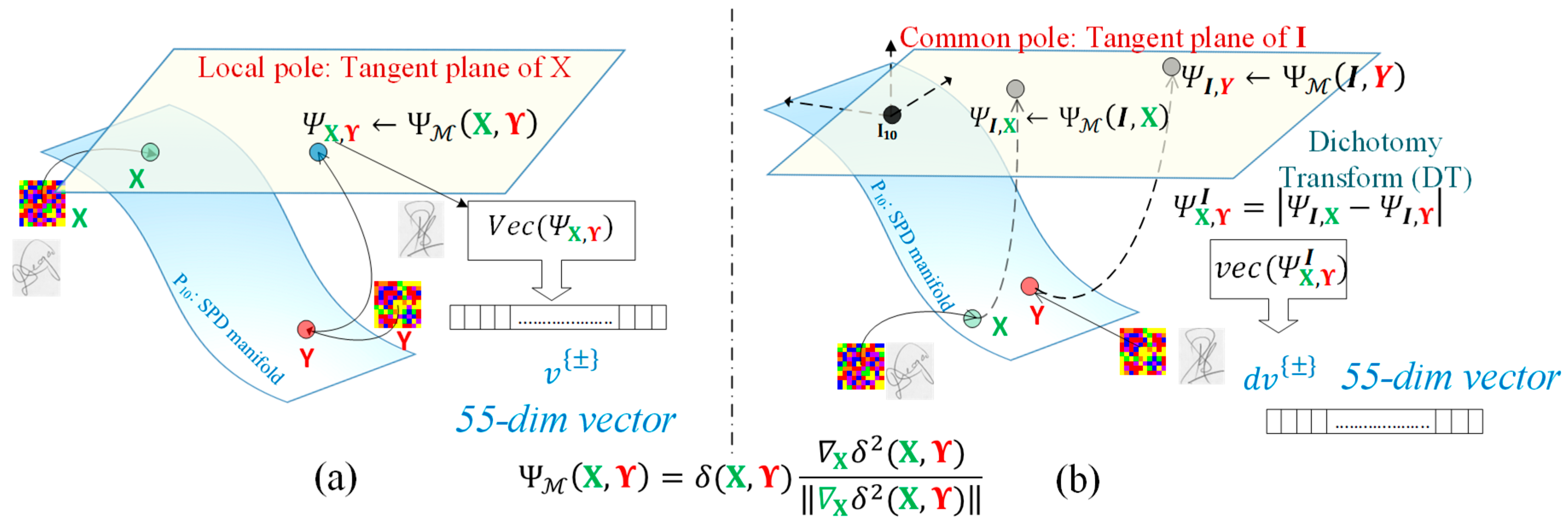
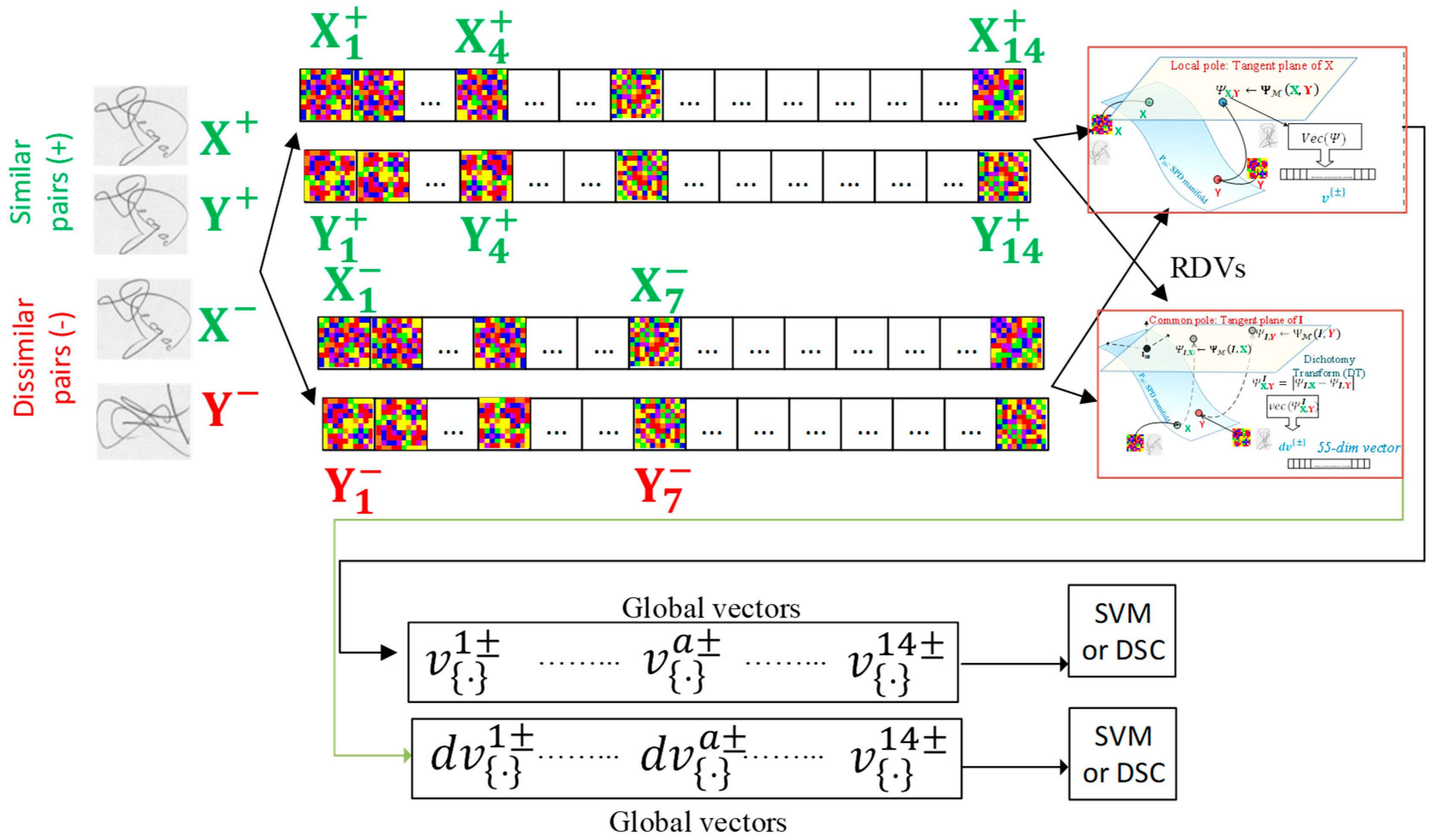
- We provide a mathematical framework for modeling the leap from the Euclidean-oriented DT to its Riemannian equivalent, Riemannian dissimilarity vectors (RDVs) , which are employed for the first time in the literature for addressing WI-SV. The Euclidean-oriented DT is typically performed with the use of the subtraction operator between vector descriptors. In the context of the Riemannian framework, the concept of a bipoint, i.e., oriented pairs of points, which is an antecedent of a vector, offers a novel perspective on the interpretation of subtractions [57]. As a result, the proposed RDVs are formed as the result of the Riemannian equivalent for vector space subtraction between two SPD manifold entities . The RDVs are expressed by a manifold dissimilarity function, , which is a map to the tangent bundle of the SPD manifold. For classification tasks, the resulting RDVs (in the form of symmetric matrices) are converted to a vectored from ( or ) with the use of a vector operator .
- We present and compare two alternative methodologies for constructing the RDVs between two signature covariance matrices, , namely the local and the global common pole approach. In the case of the local approach, the RDV is formed by the local tangent vectors . Intuitively, the local RDV approach encodes the notion of the dissimilarity between by means of an appropriate subtraction operation (. In the case of the global common pole approach, the common pole is used to evaluate the RDV dissimilarity (, ( for each one of the with respect to the identity matrix . Then, the Euclidean-based DT, applied directly to the , , evaluates the global common pole RDV . To both local and global common pole RDVs, we then apply the operator in order to create any of the two or vectored forms for classification purposes.
- We employ and compare the efficiency of the RDVs under two different popular frameworks in order to realize the WI-SV system. The first one consists of a binary support vector machine (SVM), while the second utilizes a decision stump learning algorithm equipped with a Decision Stump Committee (DSC) structure under the Gentle Ada Boost framework initially proposed by [28] and among others employed also for WI-SV purposes in [37]. The experimental setup consists of blind disjoint learning and testing sets in both intra-lingual and cross-lingual test sets.
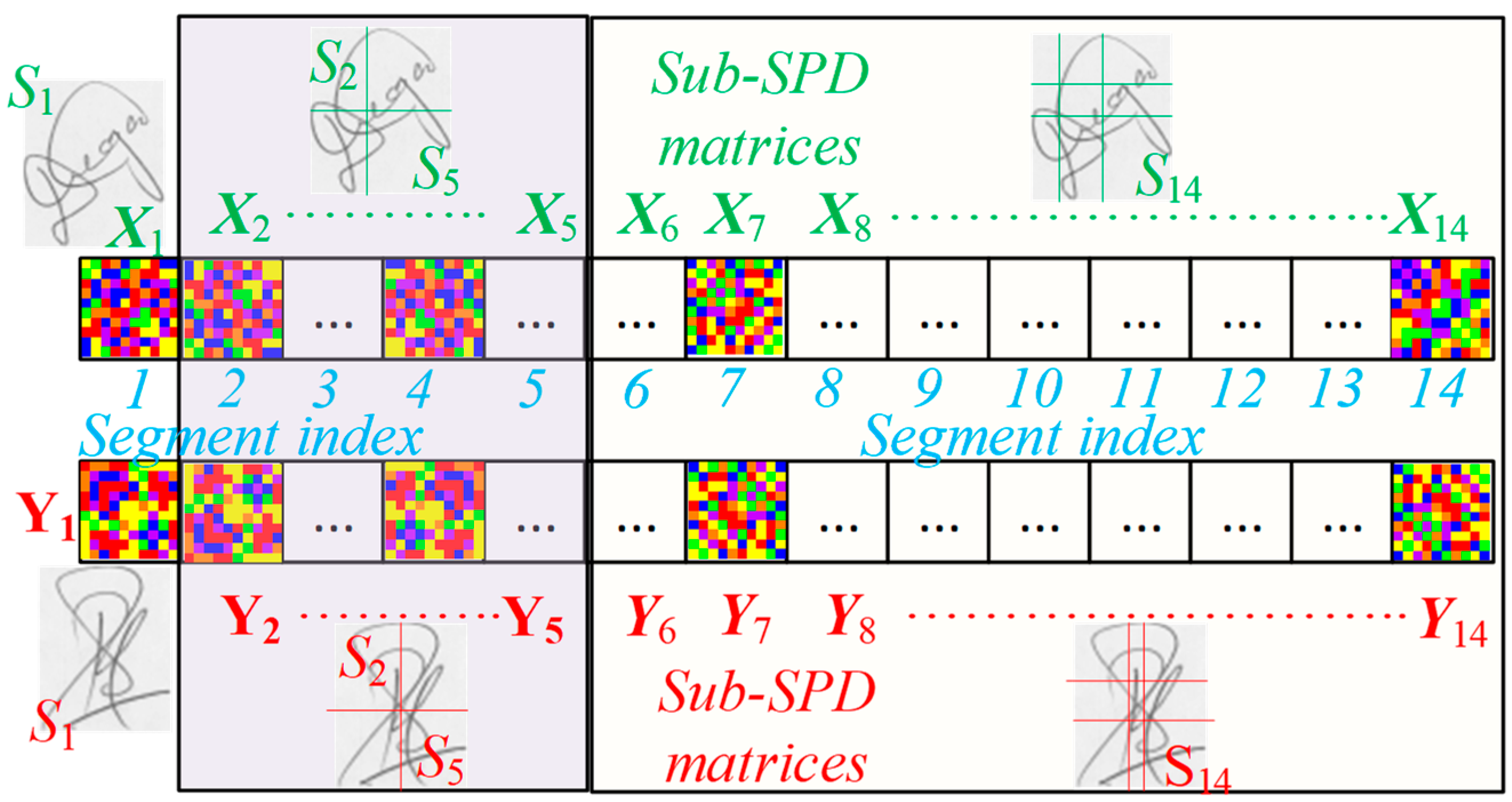
- We follow two distinct methodologies for the purpose of fusing the resultant local or global common pole . For this purpose, related coordinates between equimass spatial segments between a pair of signature images are selected; thus, a pair of covariance matrices, , is evaluated for any two visual segments. Then, the local or common pole RDVs of a sequence of image segments can be fused under two modes: (a) a serial one, in which the resulting scores from each segment are combined in order to create a score as a function of the segments and (b) a parallel one in which vectored forms or are appended in order to form an extended vector with larger dimensionality, accompanied by one score.
2. WI-SV-Related Work and Overview
2.1. Related Work
2.2. Overview of the Proposed Method
3. Materials and Methods
3.1. Theoretical Elements and Mathematical Tools of the SPD Manifold
3.2. Euclidean and Riemannian Dissimilarity Frameworks
3.3. WI-SV in the Case of the Riemannian Dissimilarity Framework
4. Experimental Setup
4.1. The Datasets
4.2. Signature Image to Covariance Matrix
- A family of Gabor filters in different directions and frequencies.
- A family of difference of Gaussians (DoG).
4.3. The Learning Framework
4.4. The Models—Verifiers
| Algorithm 1: Learning a WI-SV verifier with the SVM. |
|
| Algorithm 2: Learning a WI-SV verifier with the DSC-BFS. |
|
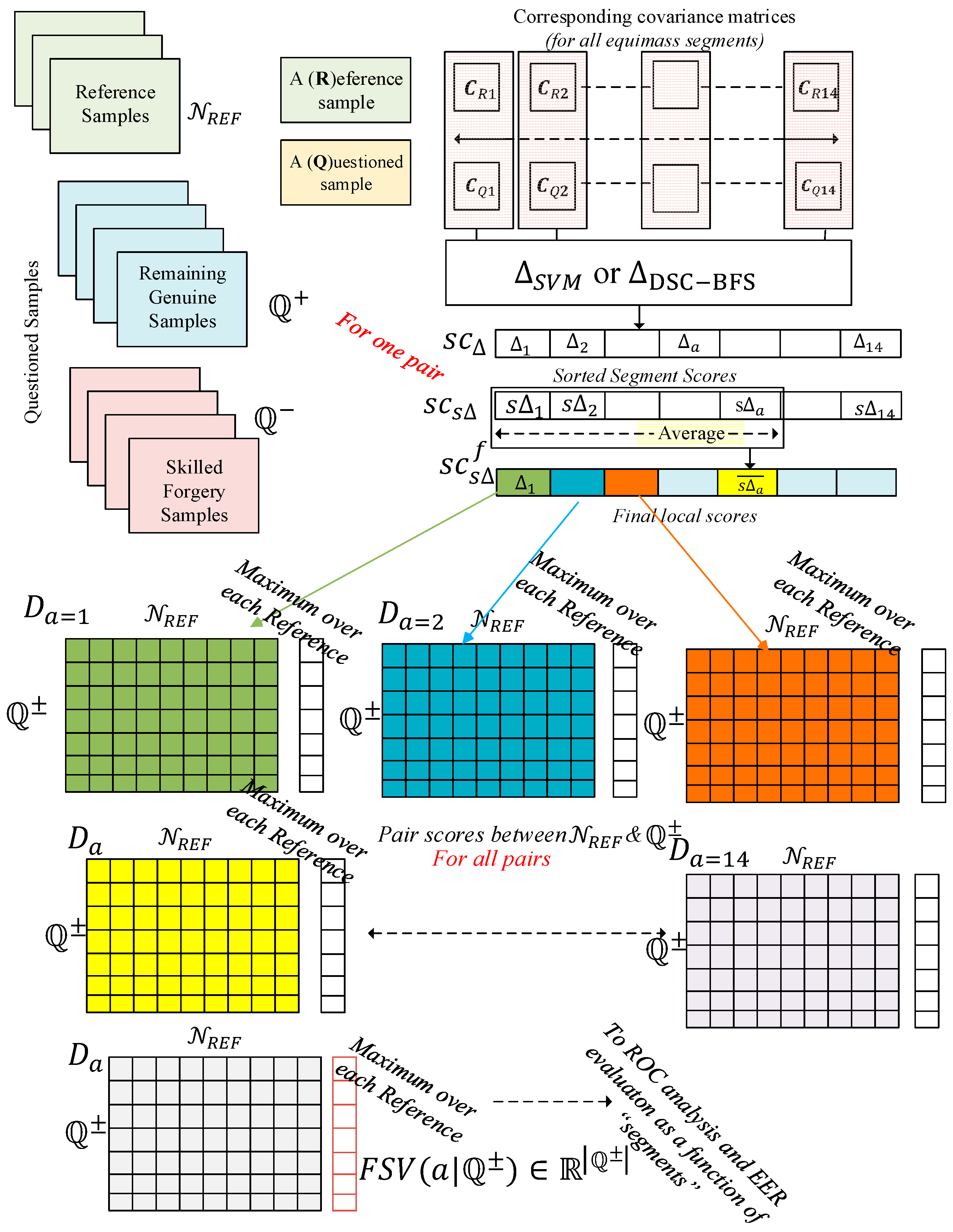
4.5. Description of the Testing Protocol
- Sort in a descending order, thus creating the score vector.
- Generate the final score vector by (a) assigning its first component to the original value and (b) assigning its value as
5. Results and Discussion
5.1. Intra-Lingual Experiments
- With respect to the employment of the SVM or the DSC-BFS as the signature verifier, it is evident that all datasets exhibit superior performance under the SVM classifier when compared to the DSC-BFS in terms of average . Furthermore, the SVM module demonstrates higher robustness with respect to SPD measures A, S, and J. This is evidenced by a higher proportion of cases exhibiting lower results in comparison to the DSC-BFS cases.
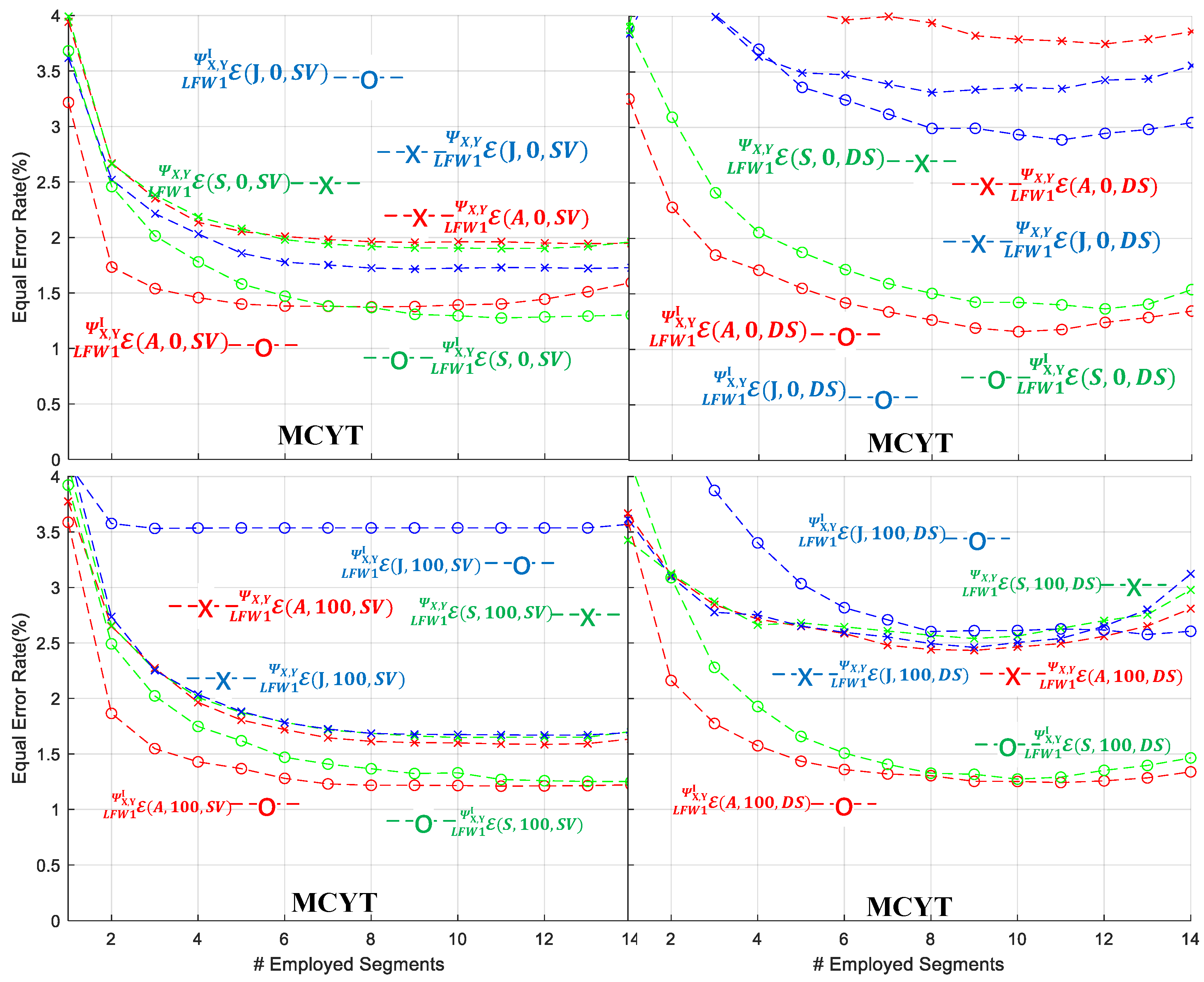
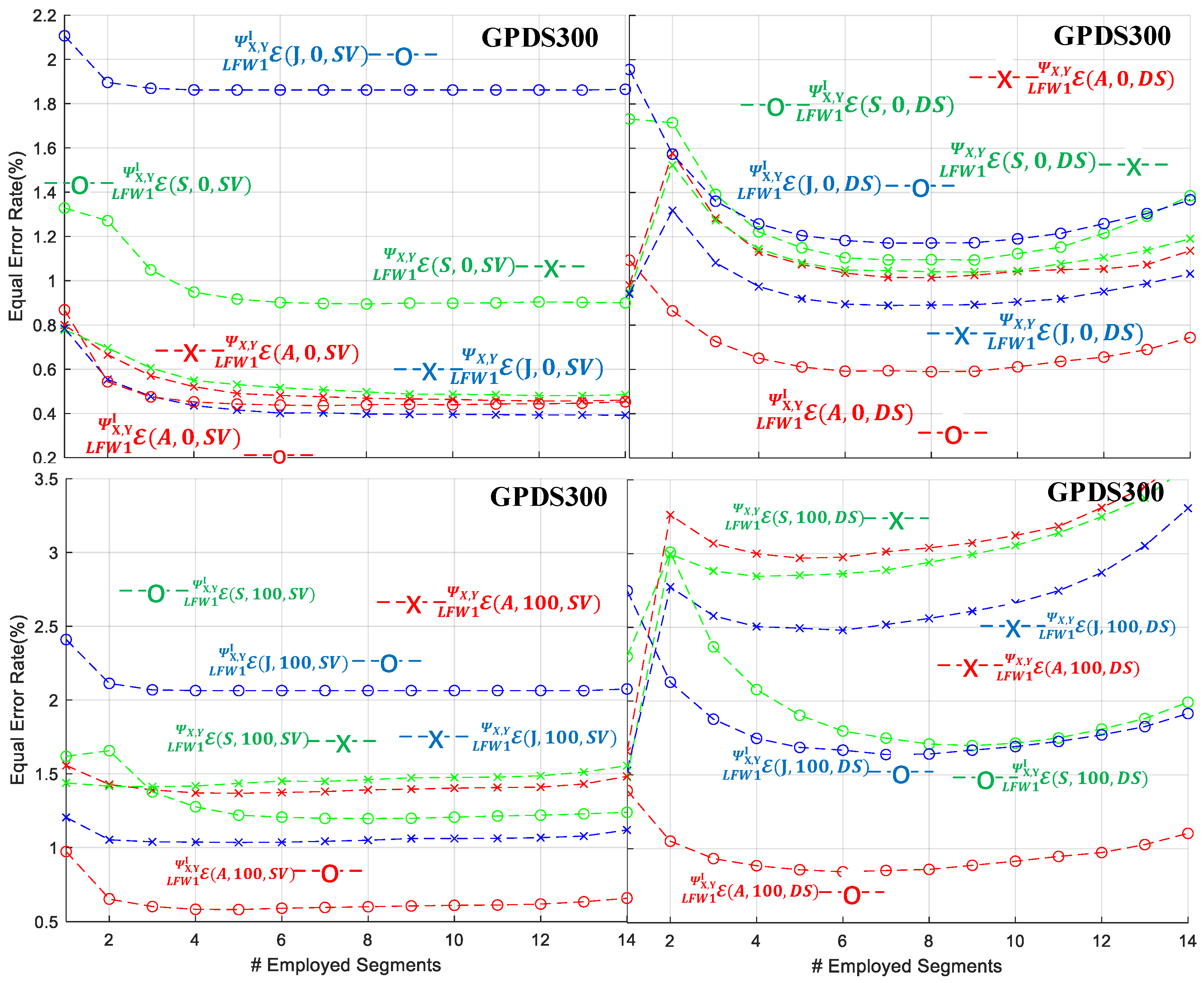
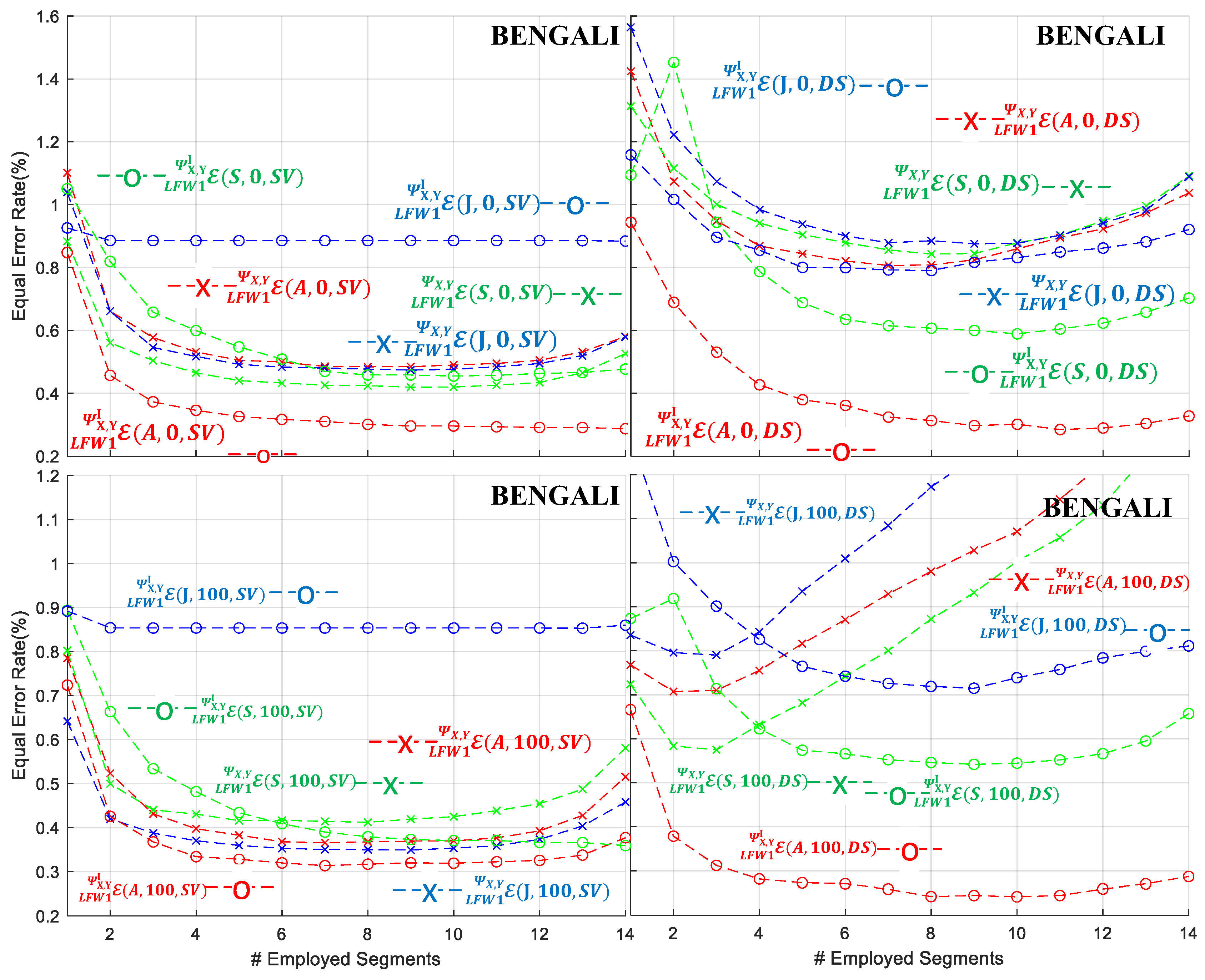
- With respect to the use of the local or common pole RDVs highlighted in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 it is evident that, with the notable exception of the HINDI dataset, SVM verifier and , clearly the common pole RDV provides the best average in all cases. A possible explanation for the higher discriminative capabilities of the common pole RDV approach is that, in the local approach, the RDVs are created without having fixed poles, thus making the conditioned class outputs of the operator somehow incompatible with each other. Although special care in the form of a parallel transport action could provide a candidate solution, the use of signature images and corresponding covariance matrices that are placed everywhere in the SPD manifold does not allow us to designate a vantage point besides the already utilized in the RDV.
- With respect to the vs. negative class formation, it is apparent that for the majority of the cases the setup provides the lowest average rates more robustly. This outcome has been anticipated, given the construction of each individual dataset under similar acquisition and a priori conditions. Consequently, the classifier models learned through the learning procedure with the setup of simulated (or skilled) forgery samples inherently exhibit generalization capabilities during the testing stage [55,56].
- With respect to the use of the AIRM, Stein, or Jeffrey measure for the formation of the RVDs, again it is more than evident that, with the notable exception of the HINDI/SVM/, the use of AIRM is more effective compared to the use of the Stein and Jeffrey measures. This should not be considered as a surprise, since the use of AIRM has been reported to optimally operate in a number of cases, including signature verification [56].
- For the case of the LFW2/TFW2 protocol in which a larger 770-dimensional vector is utilized, Table 4, Table 5 and Table 6 present the corresponding average error rates. For comparing the results between the serial LFW1 and parallel LFW2 protocols, we complement the contents of Table 4, Table 5 and Table 6 by reporting the optimal LFW1/TFW1 average as extracted from Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 for the cases and for the segment index to ensure fairness and robustness through all datasets.
5.2. Cross-Lingual Experiments
- With respect to the employment of the SVM against the DSC-BFS, the results indicate that the two forms of classifiers demonstrate comparable performance levels, exhibiting marginal disparities in their operational capabilities.
- With respect to the local or common pole RDVs, it is again evident that clearly the common pole RDV provides the best average in the majority of the cases.
- With respect to the vs. negative class formation, an enhancement in the verification performance of the learned verifiers is observed for the when compared to the Thus, contrary to the elevated verification leverage of the on the cases, the development of the classifiers under the assumption on the cases yields more robust models.
- The common pole RDV accompanied by the local LFW1/TFW1 protocol provides lower verification error rates.
- For the case of testing signatures emerging from fixed a priori acquisition conditions and signature styles (e.g., Western, Asian) as in the protocol, the use of the seems to be more efficient. On the other hand, in the case of having unknown a priori acquisition conditions and signature styles as in the protocol, the use of the seems to be more efficient.
- For the protocol and the local LFW1/TFW1, efficiency seems to be an increasing function of segment index . As an example, the MCYT dataset achieves lower than 1% when the segment index has greater values than eight (8). For the protocol, such efficient behavior is not observed. This aggregation of scores, as a function of the segment index , can be intuitively seen as the attempt of a computer vision system to incorporate the knowledge of the most similar parts of the signature pairs in a qualitative and quantitative way. Therefore, the incorporation of a large number of segments can be useful in cases of testing pairs of signatures for which we do not have any ground truth regarding their acquisition conditions or origins. In the case that this kind of ground truth is known, then a moderate selection of segment scores provides the optimal verification error rates.
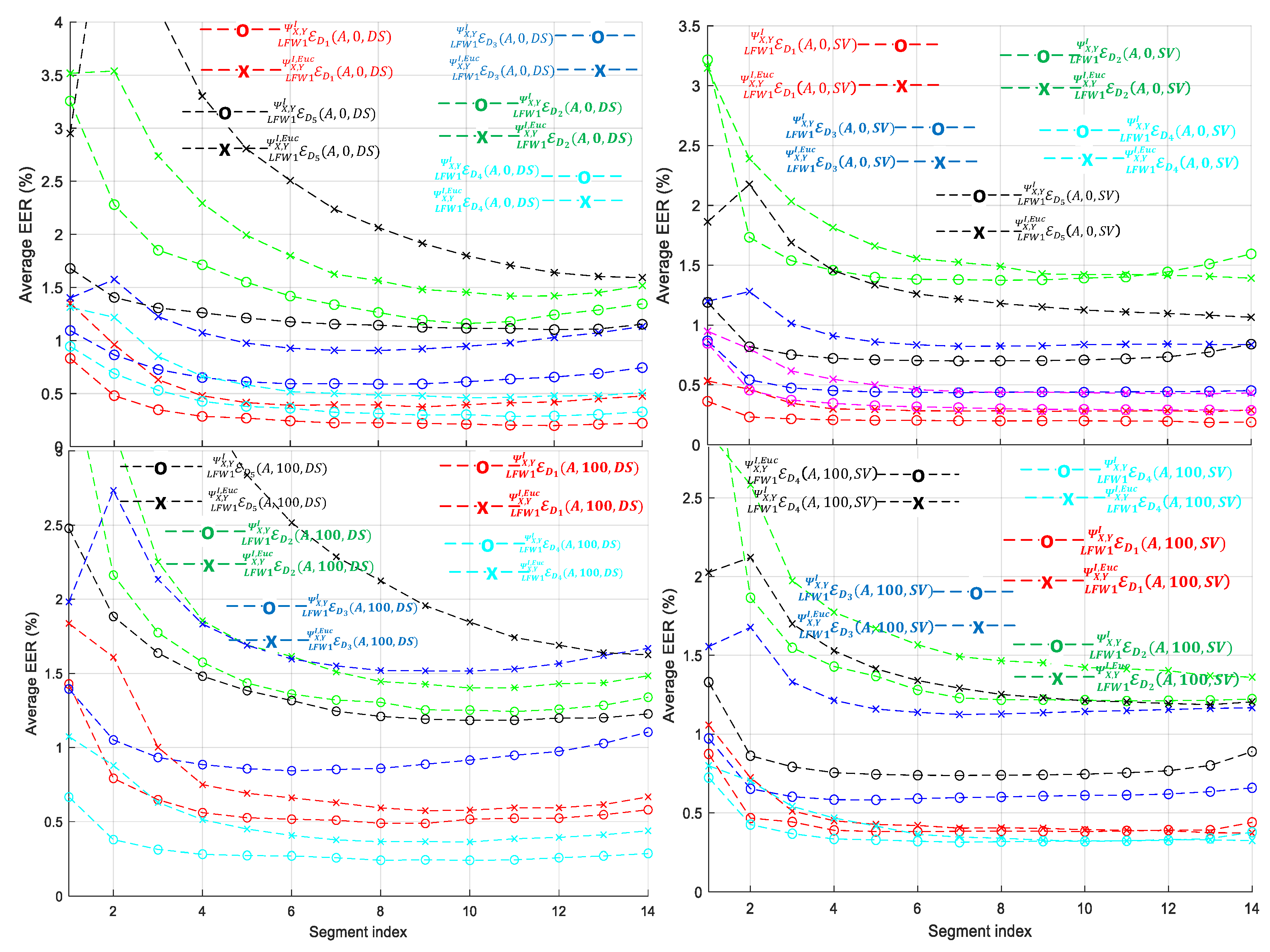
5.3. Comparisons with Euclidean Representations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIRM | Affine Invariant Riemannian Metric |
| WI-SV | Writer-Independent Signature Verification |
| WD-SV | Writer-Dependent Signature Verification |
| RDV | Riemannian Dissimilarity vectors |
| SPD | Symmetric Positive Definite |
| BFS | Boosting Feature Selection |
| DSC | Decision Stump Committee |
| SVM | Support Vector Machine |
| DT | Dichotomy Transform |
| G-G | Genuine to Genuine |
| G-RF | Genuine to Random Forgery |
| G-SF | Genuine to Skilled Forgery |
| EER | Equal Error Rate |
| FAR | False Acceptance Rate |
| FRR | False Rejection Rate |
| CEDAR | Center of Excellence for Document Analysis and Recognition |
| MCYT | Ministerio de Ciencia y Tecnologia, |
| GPDS | Grupo de Procesado Digital de la Señal |
| BHSig260 | Bangla and Hindi Signature Dataset |
References
- Jain, A.K.; Deb, D.; Engelsma, J.J. Biometrics: Trust, But Verify. IEEE Trans. Biom. Behav. Identity Sci. 2022, 4, 303–323. [Google Scholar] [CrossRef]
- Dargan, S.; Kumar, M. A comprehensive survey on the biometric recognition systems based on physiological and behavioral modalities. Expert Syst. Appl. 2020, 143, 113114. [Google Scholar] [CrossRef]
- Hameed, M.M.; Ahmad, R.; Kiah, M.L.M.; Murtaza, G. Machine learning-based offline signature verification systems: A systematic review. Signal Process. Image Commun. 2021, 93, 116139. [Google Scholar] [CrossRef]
- Deviterne-Lapeyre, M.; Ibrahim, S. Interpol questioned documents review 2019–2022. Forensic Sci. Int. Synerg. 2023, 6, 100300. [Google Scholar] [CrossRef]
- Singla, A.; Mittal, A. Exploring offline signature verification techniques: A survey based on methods and future directions. Multimed. Tools Appl. 2024, 84, 2835–2875. [Google Scholar] [CrossRef]
- Diaz, M.; Ferrer, M.A.; Impedovo, D.; Malik, M.I.; Pirlo, G.; Plamondon, R. A Perspective Analysis of Handwritten Signature Technology. ACM Comput. Surv. 2018, 51, 1–39. [Google Scholar] [CrossRef]
- Engin, D.; Kantarcı, A.; Arslan, S.; Ekenel, H.K. Offline Signature Verification on Real-World Documents. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 3518–3526. [Google Scholar]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. In Proceedings of the Advances in Neural Information Processing Systems (NIPS 1993), Denver, CO, USA, 29 November–2 December 1993. [Google Scholar]
- Impedovo, D.; Pirlo, G.; Plamondon, R. Handwritten Signature Verification: New Advancements and Open Issues. In Proceedings of the 2012 International Conference on Frontiers in Handwriting Recognition, Bari, Italy, 18–20 September 2012; pp. 367–372. [Google Scholar]
- Stauffer, M.; Maergner, P.; Fischer, A.; Riesen, K. A Survey of State of the Art Methods Employed in the Offline Signature Verification Process. In New Trends in Business Information Systems and Technology: Digital Innovation and Digital Business Transformation; Springer: Cham, Switzerland, 2021; pp. 17–30. [Google Scholar]
- Impedovo, D.; Pirlo, G. Automatic signature verification in the mobile cloud scenario: Survey and way ahead. IEEE Trans. Emerg. Top. Comput. 2018, 9, 554–568. [Google Scholar] [CrossRef]
- Faundez-Zanuy, M.; Fierrez, J.; Ferrer, M.A.; Diaz, M.; Tolosana, R.; Plamondon, R. Handwriting Biometrics: Applications and Future Trends in e-Security and e-Health. Cogn. Comput. 2020, 12, 940–953. [Google Scholar] [CrossRef]
- Lai, S.; Jin, L.; Zhu, Y.; Li, Z.; Lin, L. SynSig2Vec: Forgery-Free Learning of Dynamic Signature Representations by Sigma Lognormal-Based Synthesis and 1D CNN. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 6472–6485. [Google Scholar] [CrossRef]
- Okawa, M. Online signature verification using single-template matching with time-series averaging and gradient boosting. Pattern Recognit. 2020, 102, 107227. [Google Scholar] [CrossRef]
- Vorugunti, C.S.; Guru, D.S.; Mukherjee, P.; Pulabaigari, V. OSVNet: Convolutional Siamese Network for Writer Independent Online Signature Verification. In Proceedings of the 2019 International Conference on Document Analysis and Recognition (ICDAR), Sydney, Australia, 20–25 September 2019; pp. 1470–1475. [Google Scholar]
- Alpar, O. Online signature verification by continuous wavelet transformation of speed signals. Expert Syst. Appl. 2018, 104, 33–42. [Google Scholar] [CrossRef]
- Tolosana, R.; Vera-Rodriguez, R.; Ortega-Garcia, J.; Fierrez, J. Preprocessing and Feature Selection for Improved Sensor Interoperability in Online Biometric Signature Verification. IEEE Access 2015, 3, 478–489. [Google Scholar] [CrossRef]
- Shih, M.-C.; Huang, T.-L.; Shih, Y.-H.; Shuai, H.-H.; Liu, H.-T.; Yeh, Y.-R.; Huang, C.-C. DetailSemNet: Elevating Signature Verification Through Detail-Semantic Integration. In Proceedings of the European Conference on Computer Vision (ECCV), Milan, Italy, 29 September–4 October 2024; Springer: Cham, Switzerland, 2025; pp. 449–466. [Google Scholar]
- Li, H.; Wei, P.; Ma, Z.; Li, C.; Zheng, N. TransOSV: Offline Signature Verification with Transformers. Pattern Recognit. 2024, 145, 109882. [Google Scholar] [CrossRef]
- Abosamra, G.; Oqaibi, H. A Signature Recognition Technique with a Powerful Verification Mechanism Based on CNN and PCA. IEEE Access 2024, 12, 40634–40656. [Google Scholar] [CrossRef]
- Viana, T.B.; Souza, V.L.F.; Oliveira, A.L.I.; Cruz, R.M.O.; Sabourin, R. A multi-task approach for contrastive learning of handwritten signature feature representations. Expert Syst. Appl. 2023, 217, 119589. [Google Scholar] [CrossRef]
- Thakur, U.; Sharma, A. Offline handwritten mathematical recognition using adversarial learning and transformers. Int. J. Doc. Anal. Recognit. (IJDAR) 2023, 27, 147–158. [Google Scholar] [CrossRef]
- Zheng, L.; Wu, D.; Xu, S.; Zheng, Y. HTCSigNet: A Hybrid Transformer and Convolution Signature Network for offline signature verification. Pattern Recognit. 2024, 159, 111146. [Google Scholar] [CrossRef]
- Arab, N.; Nemmour, H.; Chibani, Y. A new synthetic feature generation scheme based on artificial immune systems for robust offline signature verification. Expert Syst. Appl. 2023, 213, 119306. [Google Scholar] [CrossRef]
- Muhtar, Y.; Muhammat, M.; Yadikar, N.; Aysa, A.; Ubul, K. FC-ResNet: A Multilingual Handwritten Signature Verification Model Using an Improved ResNet with CBAM. Appl. Sci. 2023, 13, 8022. [Google Scholar] [CrossRef]
- Maruyama, T.M.; Oliveira, L.S.; Britto, A.S.; Sabourin, R. Intrapersonal Parameter Optimization for Offline Handwritten Signature Augmentation. IEEE Trans. Inf. Forensics Secur. 2021, 16, 1335–1350. [Google Scholar] [CrossRef]
- Diaz, M.; Ferrer, M.A.; Eskander, G.S.; Sabourin, R. Generation of Duplicated Off-Line Signature Images for Verification Systems. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 951–964. [Google Scholar] [CrossRef]
- Rivard, D.; Granger, E.; Sabourin, R. Multi-feature extraction and selection in writer-independent off-line signature verification. Int. J. Doc. Anal. Recognit. 2013, 16, 83–103. [Google Scholar] [CrossRef]
- Eskander, G.S.; Sabourin, R.; Granger, E. Hybrid writer-independent writer-dependent offline signature verification system. IET Biom. 2013, 2, 169–181. [Google Scholar] [CrossRef]
- Souza, V.L.F.; Oliveira, A.L.I.; Cruz, R.M.O.; Sabourin, R. A white-box analysis on the writer-independent dichotomy transformation applied to offline handwritten signature verification. Expert Syst. Appl. 2020, 154, 113397. [Google Scholar] [CrossRef]
- Longjam, T.; Kisku, D.R.; Gupta, P. Writer independent handwritten signature verification on multi-scripted signatures using hybrid CNN-BiLSTM: A novel approach. Expert Syst. Appl. 2023, 214, 119111. [Google Scholar] [CrossRef]
- Long, J.; Xie, C.; Gao, Z. High discriminant features for writer-independent online signature verification. Multimed. Tools Appl. 2023, 82, 38447–38465. [Google Scholar] [CrossRef]
- Bird, J.J.; Naser, A.; Lotfi, A. Writer-independent signature verification; Evaluation of robotic and generative adversarial attacks. Inf. Sci. 2023, 633, 170–181. [Google Scholar] [CrossRef]
- Manna, S.; Chattopadhyay, S.; Bhattacharya, S.; Pal, U. SWIS: Self-Supervised Representation Learning for Writer Independent Offline Signature Verification. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; pp. 1411–1415. [Google Scholar]
- Chattopadhyay, S.; Manna, S.; Bhattacharya, S.; Pal, U. SURDS: Self-Supervised Attention-guided Reconstruction and Dual Triplet Loss for Writer Independent Offline Signature Verification. In Proceedings of the 2022 26th International Conference on Pattern Recognition (ICPR), Montreal, QC, Canada, 21–25 August 2022; pp. 1600–1606. [Google Scholar]
- Parcham, E.; Ilbeygi, M.; Amini, M. CBCapsNet: A novel writer-independent offline signature verification model using a CNN-based architecture and capsule neural networks. Expert Syst. Appl. 2021, 185, 115649. [Google Scholar] [CrossRef]
- Zois, E.N.; Alexandridis, A.; Economou, G. Writer independent offline signature verification based on asymmetric pixel relations and unrelated training-testing datasets. Expert Syst. Appl. 2019, 125, 14–32. [Google Scholar] [CrossRef]
- Galbally, J.; Gomez-Barrero, M.; Ross, A. Accuracy evaluation of handwritten signature verification: Rethinking the random-skilled forgeries dichotomy. In Proceedings of the 2017 IEEE International Joint Conference on Biometrics (IJCB), Denver, CO, USA, 1–4 October 2017; pp. 302–310. [Google Scholar]
- Santos, C.; Justino, E.J.R.; Bortolozzi, F.; Sabourin, R. An off-line signature verification method based on the questioned document expert’s approach and a neural network classifier. In Proceedings of the Ninth International Workshop on Frontiers in Handwriting Recognition, Kokubunji, Japan, 26–29 October 2004; pp. 498–502. [Google Scholar]
- Oliveira, L.; Justino, E.; Sabourin, R. Off-line Signature Verification Using Writer-Independent Approach. In Proceedings of the 2007 International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007; pp. 2539–2544. [Google Scholar]
- Bertolini, D.; Oliveira, L.S.; Justino, E.; Sabourin, R. Reducing forgeries in writer-independent off-line signature verification through ensemble of classifiers. Pattern Recognit. 2010, 43, 387–396. [Google Scholar] [CrossRef]
- Eskander, G.S.; Sabourin, R.; Granger, E. Adaptation of Writer-Independent Systems for Offline Signature Verification. In Proceedings of the 2012 International Conference on Frontiers in Handwriting Recognition, Bari, Italy, 18–20 September 2012; pp. 434–439. [Google Scholar]
- Ren, J.-X.; Xiong, Y.-J.; Zhan, H.; Huang, B. 2C2S: A two-channel and two-stream transformer based framework for offline signature verification. Eng. Appl. Artif. Intell. 2023, 118, 105639. [Google Scholar] [CrossRef]
- Lu, X.; Huang, L.; Yin, F. Cut and Compare: End-to-end Offline Signature Verification Network. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 3589–3596. [Google Scholar]
- Wei, P.; Li, H.; Hu, P. Inverse Discriminative Networks for Handwritten Signature Verification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5764–5772. [Google Scholar]
- Dey, S.; Dutta, A.; Toledo, J.I.; Ghosh, S.K.; Lladós, J.; Pal, U. SigNet: Convolutional Siamese Network for Writer Independent Offline Signature Verification. arXiv 2017, arXiv:1707.02131. [Google Scholar]
- Cha, S.-H.; Srihari, S. Writer Identification: Statistical Analysis and Dichotomizer. In Advances in Pattern Recognition; Ferri, F., Iñesta, J., Amin, A., Pudil, P., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1876, pp. 123–132. [Google Scholar]
- Pekalska, E.; Duin, R.P.W. Dissimilarity-based classification for vectorial representations. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; pp. 137–140. [Google Scholar]
- Pekalska, E.; Duin, R.P.W. Beyond Traditional Kernels: Classification in Two Dissimilarity-Based Representation Spaces. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2008, 38, 729–744. [Google Scholar] [CrossRef]
- Duin, R.W.; Loog, M.; Pȩkalska, E.; Tax, D.J. Feature-Based Dissimilarity Space Classification. In Recognizing Patterns in Signals, Speech, Images and Videos; Ünay, D., Çataltepe, Z., Aksoy, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6388, pp. 46–55. [Google Scholar]
- Faraki, M.; Harandi, M.T.; Porikli, F. A Comprehensive Look at Coding Techniques on Riemannian Manifolds. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5701–5712. [Google Scholar] [CrossRef] [PubMed]
- Zois, E.N.; Said, S.; Tsourounis, D.; Alexandridis, A. Subscripto multiplex: A Riemannian symmetric positive definite strategy for offline signature verification. Pattern Recognit. Lett. 2023, 167, 67–74. [Google Scholar] [CrossRef]
- Giazitzis, A.; Diaz, M.; Zois, E.N.; Ferrer, M.A. Janus-Faced Handwritten Signature Attack: A Clash Between a Handwritten Signature Duplicator and a Writer Independent, Metric Meta-learning Offline Signature Verifier. In Proceedings of the 18th International Conference on Document Analysis and Recognition, Athens, Greece, 30 August–4 September 2024; Springer: Cham, Switzerland, 2024; pp. 216–232. [Google Scholar]
- Giazitzis, A.; Zois, E.N. SigmML: Metric meta-learning for Writer Independent Offline Signature Verification in the Space of SPD Matrices. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024; pp. 6300–6310. [Google Scholar]
- Zois, E.N.; Tsourounis, D.; Kalivas, D. Similarity Distance Learning on SPD Manifold for Writer Independent Offline Signature Verification. IEEE Trans. Inf. Forensics Secur. 2024, 19, 1342–1356. [Google Scholar] [CrossRef]
- Giazitzis, A.; Zois, E.N. Metric meta-learning and intrinsic Riemannian embedding for writer independent offline signature verification. Expert Syst. Appl. 2025, 261, 125470. [Google Scholar] [CrossRef]
- Pennec, X.; Fillard, P.; Ayache, N. A Riemannian Framework for Tensor Computing. Int. J. Comput. Vis. 2006, 66, 41–66. [Google Scholar] [CrossRef]
- Souza, V.L.F.; Oliveira, A.L.I.; Sabourin, R. A Writer-Independent Approach for Offline Signature Verification using Deep Convolutional Neural Networks Features. In Proceedings of the 2018 7th Brazilian Conference on Intelligent Systems (BRACIS), Sao Paulo, Brazil, 22–25 October 2018; pp. 212–217. [Google Scholar]
- Kumar, A.; Bhatia, K. Offline Handwritten Signature Verification Using Decision Tree. In Cyber Technologies and Emerging Sciences; Springer: Singapore, 2023; pp. 305–313. [Google Scholar]
- Huang, Z.; Wang, R.; Li, X.; Liu, W.; Shan, S.; Gool, L.V.; Chen, X. Geometry-Aware Similarity Learning on SPD Manifolds for Visual Recognition. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2513–2523. [Google Scholar] [CrossRef]
- Wang, R.; Wu, X.J.; Chen, Z.; Hu, C.; Kittler, J. SPD Manifold Deep Metric Learning for Image Set Classification. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 8924–8938. [Google Scholar] [CrossRef]
- Sra, S. A new metric on the manifold of kernel matrices with application to matrix geometric means. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012; 25, pp. 1–9. [Google Scholar]
- Wang, Z.; Vemuri, B.C. An affine invariant tensor dissimilarity measure and its applications to tensor-valued image segmentation. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; p. I-228-233. [Google Scholar]
- Faraki, M.; Harandi, M.T.; Porikli, F. More about VLAD: A leap from Euclidean to Riemannian manifolds. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4951–4960. [Google Scholar]
- Jégou, H.; Perronnin, F.; Douze, M.; Sánchez, J.; Pérez, P.; Schmid, C. Aggregating Local Image Descriptors into Compact Codes. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1704–1716. [Google Scholar] [CrossRef]
- Tuzel, O.; Porikli, F.; Meer, P. Pedestrian Detection via Classification on Riemannian Manifolds. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1713–1727. [Google Scholar] [CrossRef]
- Pennec, X. 3—Manifold-valued image processing with SPD matrices. In Riemannian Geometric Statistics in Medical Image Analysis; Pennec, X., Sommer, S., Fletcher, T., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 75–134. [Google Scholar]
- Kalera, M.K.; Srihari, S.; Xu, A. Offline signature verification and identification using distance statistics. Int. J. Pattern Recognit. Artif. Intell. 2004, 18, 1339–1360. [Google Scholar] [CrossRef]
- Vargas, J.F.; Ferrer, M.A.; Travieso, C.M.; Alonso, J.B. Off-line signature verification based on grey level information using texture features. Pattern Recognit. 2011, 44, 375–385. [Google Scholar] [CrossRef]
- Ortega-Garcia, J.; Fierrez-Aguilar, J.; Simon, D.; Gonzalez, J.; Faundez-Zanuy, M.; Espinosa, V.; Satue, A.; Hernaez, I.; Igarza, J.J.; Vivaracho, C.; et al. MCYT baseline corpus: A bimodal biometric database. IEE Proc. Vis. Image Signal Process. 2003, 150, 395–401. [Google Scholar] [CrossRef]
- Pal, S.; Alaei, A.; Pal, U.; Blumenstein, M. Performance of an Off-Line Signature Verification Method Based on Texture Features on a Large Indic-Script Signature Dataset. In Proceedings of the 2016 12th IAPR Workshop on Document Analysis Systems (DAS), Santorini, Greece, 11–14 April 2016; pp. 72–77. [Google Scholar]
- Zois, E.N.; Tsourounis, D.; Theodorakopoulos, I.; Kesidis, A.L.; Economou, G. A Comprehensive Study of Sparse Representation Techniques for Offline Signature Verification. IEEE Trans. Biom. Behav. Identity Sci. 2019, 1, 68–81. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Iba, W.; Langley, P. Induction of One-Level Decision Trees. In Machine Learning Proceedings 1992; Sleeman, D., Edwards, P., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1992; pp. 233–240. [Google Scholar]
- Zois, E.N.; Alewijnse, L.; Economou, G. Offline signature verification and quality characterization using poset-oriented grid features. Pattern Recognit. 2016, 54, 162–177. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Maergner, P.; Pondenkandath, V.; Alberti, M.; Liwicki, M.; Riesen, K.; Ingold, R.; Fischer, A. Combining graph edit distance and triplet networks for offline signature verification. Pattern Recognit. Lett. 2019, 125, 527–533. [Google Scholar] [CrossRef]
- Kumar, R.; Sharma, J.D.; Chanda, B. Writer-independent off-line signature verification using surroundedness feature. Pattern Recognit. Lett. 2012, 33, 301–308. [Google Scholar] [CrossRef]
- Liu, L.; Huang, L.; Yin, F.; Chen, Y. Offline signature verification using a region based deep metric learning network. Pattern Recognit. 2021, 118, 108009. [Google Scholar] [CrossRef]
- Zhu, Y.; Lai, S.; Li, Z.; Jin, L. Point-to-Set Similarity Based Deep Metric Learning for Offline Signature Verification. In Proceedings of the 2020 17th International Conference on Frontiers in Handwriting Recognition (ICFHR), Dortmund, Germany, 8–10 September 2020; pp. 282–287. [Google Scholar]
- Soleimani, A.; Araabi, B.N.; Fouladi, K. Deep Multitask Metric Learning for Offline Signature Verification. Pattern Recognit. Lett. 2016, 80, 84–90. [Google Scholar] [CrossRef]
- Hamadene, A.; Chibani, Y. One-Class Writer-Independent Offline Signature Verification Using Feature Dissimilarity Thresholding. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1226–1238. [Google Scholar] [CrossRef]
- Zheng, L.; Zhao, X.; Xu, S.; Ren, Y.; Zheng, Y. Learning discriminative representations by a Canonical Correlation Analysis-based Siamese Network for offline signature verification. Eng. Appl. Artif. Intell. 2025, 139, 109640. [Google Scholar] [CrossRef]





| Type of Measure | |
|---|---|
| AIRM: | |
| Stein: | |
| Jeffrey: | X |
| Notation | |||||
|---|---|---|---|---|---|
| 55 | 75 | 300 | 100 | 160 | |
| 28 | 38 | 150 | 50 | 80 | |
| & | 24/24 | 15/15 | 24/30 | 24/30 | 24/30 |
| & | 17 | 10 | 17/21 | 17/21 | 17/21 |
| & | 7 | 5 | 7/9 | 7/9 | 7/9 |
| & | 3808 | 1710 | 3808 | 3808 | 3808 |
| & | 588 | 380 | 3150 | 1050 | 1680 |
| Design Params. | SPD Measures AIRM, Stein, Jeffrey | Formation (100%RF, 0%RF) | or DSC-BFS | ||||
|---|---|---|---|---|---|---|---|
| Label of Experiment | A | S | J | 0 | 100 | SVM | DSC-BFS |
| Example: Local pole: LFW1 | |||||||
| ✓ | × | × | × | ✓ | ✓ | × | |
| × | ✓ | × | ✓ | × | × | ✓ | |
| Example: Common pole: LFW1 | |||||||
| ✓ | × | × | × | ✓ | ✓ | × | |
| × | ✓ | × | ✓ | × | × | ✓ | |
| Example: Local pole: LFW2 | |||||||
| × | × | ✓ | ✓ | × | × | ✓ | |
| ✓ | × | × | × | ✓ | ✓ | × | |
| Example: Common pole: LFW2 | |||||||
| ✓ | × | × | × | ✓ | ✓ | × | |
| × | ✓ | × | ✓ | × | × | ✓ | |
| Experiment Label | Average EER per Signature Dataset | ||||
|---|---|---|---|---|---|
| CEDAR | MCYT | GPDS300 | BANGLA | HINDI | |
| 0.278 | 1.867 | 1.073 | 0.383 | 0.416 | |
| 0.208 | 2.094 | 0.883 | 0.635 | 0.811 | |
| 1.992 | 2.193 | 4.183 | 0.441 | 1.207 | |
| 1.240 | 2.340 | 2.140 | 0.543 | 1.262 | |
| 0.206 | 1.198 | 0.736 | 0.353 | 0.440 | |
| 0.261 | 2.268 | 1.043 | 0.473 | 0.811 | |
| 0.385 | 1.563 | 1.096 | 0.241 | 0.632 | |
| 0.799 | 2.165 | 1.484 | 0.459 | 1.307 | |
| Common pole—LFW1, a = 8 | |||||
| 0.199 | 1.368 | 0.439 | 0.301 | 0.466 | |
| 0.224 | 1.264 | 0.589 | 0.313 | 1.144 | |
| 0.384 | 1.217 | 0.601 | 0.316 | 0.739 | |
| 0.489 | 1.304 | 0.859 | 0.242 | 1.2096 | |
| Experiment Label | Average EER per Signature Dataset | ||||
|---|---|---|---|---|---|
| CEDAR | MCYT | GPDS300 | BANGLA | HINDI | |
| 0.295 | 2.267 | 1.251 | 0.838 | 0.436 | |
| 0.244 | 2.052 | 0.929 | 1.041 | 0.779 | |
| 2.229 | 2.220 | 4.698 | 0.602 | 1.371 | |
| 1.376 | 2.461 | 2.379 | 0.676 | 1.291 | |
| 0.466 | 1.044 | 1.224 | 0.602 | 0.691 | |
| 0.635 | 2.022 | 1.591 | 0.720 | 1.278 | |
| 0.618 | 1.227 | 1.679 | 0.447 | 0.960 | |
| 1.393 | 1.988 | 2.458 | 0.642 | 1.837 | |
| Common pole—LFW1, a = 8 | |||||
| 0.432 | 1.368 | 0.894 | 0.458 | 1.047 | |
| 0.614 | 1.504 | 1.096 | 0.607 | 1.752 | |
| 0.551 | 1.368 | 1.196 | 0.379 | 1.127 | |
| 0.786 | 1.326 | 1.709 | 0.546 | 2.137 | |
| Experiment Label | Average EER per Signature Dataset | ||||
|---|---|---|---|---|---|
| CEDAR | MCYT | GPDS300 | BANGLA | HINDI | |
| 0.249 | 2.177 | 1.362 | 0.687 | 0.448 | |
| 0.225 | 2.265 | 1.049 | 0.964 | 0.835 | |
| 2.190 | 2.170 | 3.576 | 0.635 | 1.472 | |
| 2.021 | 2.534 | 2.290 | 0.709 | 1.420 | |
| 0.531 | 3.957 | 2.108 | 0.531 | 0.972 | |
| 0.973 | 4.048 | 1.800 | 0.888 | 1.493 | |
| 1.064 | 2.586 | 3.444 | 0.995 | 1.668 | |
| 2.123 | 3.735 | 2.671 | 2.210 | 2.534 | |
| Common pole—LFW1, a = 8 | |||||
| 0.864 | 4.037 | 1.861 | 0.885 | 1.544 | |
| 0.846 | 2.991 | 1.171 | 0.790 | 2.721 | |
| 1.115 | 3.536 | 2.064 | 0.853 | 1.767 | |
| 1.775 | 2.603 | 1.638 | 0.718 | 2.578 | |
| Testing Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CEDAR | MCYT | GPDS300 | BENGALI | HINDI | ||||||
| Learning Dataset | SVM | DSC | SVM | DSC | SVM | DSC | SVM | DSC | SVM | DSC |
| CEDAR | - | 6.49 | 6.07 | 1.02 | 0.95 | 2.15 | 1.93 | 3.87 | 3.65 | |
| MCYT | 1.38 | 2.58 | - | 3.68 | 6.06 | 0.34 | 0.50 | 1.16 | 1.36 | |
| GPDS300 | 0.47 | 0.44 | 2.69 | 2.63 | - | 1.67 | 1.32 | 3.25 | 3.45 | |
| BENGALI | 49.9 | 50.0 | 49.9 | 50.0 | 50.0 | 50.0 | - | 1.26 | 1.44 | |
| HINDI | 2.04 | 2.87 | 2.86 | 2.82 | 3.31 | 4.74 | 0.80 | 0.89 | - | |
| Comparison against | , | |||||||||
| CEDAR | - | 1.18 | 1.26 | 0.47 | 0.42 | 0.41 | 0.43 | 1.04 | 1.20 | |
| MCYT | 0.66 | 0.70 | - | 0.93 | 0.96 | 0.43 | 0.47 | 1.50 | 1.87 | |
| GPDS300 | 0.28 | 0.25 | 1.41 | 1.36 | - | 0.47 | 0.48 | 1.34 | 1.61 | |
| BENGALI | 27.4 | 37.8 | 28.4 | 41.1 | 0.70 | 0.78 | - | 0.90 | 1.24 | |
| HINDI | 0.54 | 0.59 | 1.38 | 1.63 | 1.36 | 1.47 | 0.28 | 0.50 | - | |
| Testing Dataset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CEDAR | MCYT | GPDS300 | BENGALI | HINDI | ||||||
| Learning Dataset | SVM | DSC | SVM | DSC | SVM | DSC | SVM | DSC | SVM | DSC |
| CEDAR | - | 1.92 | 2.20 | 1.11 | 1.14 | 0.45 | 0.47 | 1.27 | 1.38 | |
| MCYT | 0.71 | 0.90 | - | 1.32 | 1.51 | 0.45 | 0.50 | 1.24 | 1.47 | |
| GPDS300 | 0.56 | 0.60 | 2.12 | 2.21 | - | 0.84 | 0.72 | 1.45 | 1.52 | |
| BENGALI | 49.9 | 50.0 | 49.9 | 50.0 | 50.0 | 50.0 | - | 0.71 | 0.85 | |
| HINDI | 2.16 | 2.83 | 2.78 | 2.73 | 3.56 | 4.93 | 0.64 | 0.95 | - | |
| Comparison against | ||||||||||
| CEDAR | - | 1.18 | 1.18 | 0.49 | 0.53 | 0.46 | 0.39 | 1.18 | 1.03 | |
| MCYT | 0.49 | 0.53 | - | 0.71 | 0.71 | 0.32 | 0.36 | 1.26 | 1.50 | |
| GPDS300 | 0.34 | 0.30 | 1.17 | 1.12 | - | 0.38 | 0.30 | 0.99 | 1.15 | |
| BENGALI | 17.2 | 26.7 | 18.6 | 28.2 | 1.05 | 1.05 | - | 0.81 | 1.01 | |
| HINDI | 0.75 | 0.75 | 2.11 | 2.39 | 1.37 | 1.37 | 0.24 | 0.40 | - | |
| Method and [Ref] and DC (✓) | Metric | ) | ||||
|---|---|---|---|---|---|---|
| CEDAR | MCYT | GPDS300 | BANGLA | HINDI | ||
| Graph edit distance (MCS) [77] | 5.91(10) | 3.91(10) | ||||
| Surroundedness [78] | 8.33(1) | - | 13.7(1) | - | - | |
| Region Deep Metric (MSDN) [79] | 1.75(10) 1.67(12) | - | - | - | - | |
| Point2Set DML [80] | 5.22(5) | 9.86(5) | - | - | - | |
| DMML(with HOG) [81] | - | 13.4(5) and 9.86(10) | - | - | - | |
| Partially ordered sets [37] ✓ | 2.90(5) | 3.50(5) | 3.06(5) | |||
| DCCM and Feat. Diss. Thresh. [82] | 2.10(5) | - | 18.4(5) | - | - | |
| SURDS [35] | - | - | - | 12.6(8) | 10.5(8) | |
| TransOSV [19] | - | - | - | 9.90(1) 3.56(1) | 3.24(1) | |
| Sim. Dist. Learn. (SPD) [55] ✓ 100%RF, a = 4 () or a = 7 () | 0.37(10) | 0.96(10) | - | 0.26(10) | 0.77(10) | |
| Sim. Dist. Learn. (SPD) [55] ✓ 0%RF, a = 4 () or a = 7 () | 0.38(10) | 1.02(10) | - | 0.25(10) | 0.78(10) | |
| ESC-DPDF [29] | - | - | 17.8(12) | - | - | |
| Siamese Network and CCA [83] | 3.31(12) | - | - | - | - | |
| HTCSigNet [23] | - | - | - | 8.52(12) | 4.63(12) | |
| [30] and (IH) | 3.32(12) | 2.89(10) | 3.47(12) | - | - | |
| Sigmml and ERP (SPD) [56] ✓ 0%RF, a = 1 () | 0.04(10) | 0.03(10) | - | 0.19(10) | 0.17(10) | |
| Proposed (SPD), , a = 8, | 0.38(10) | 1.22(10) | 0.60(10) | 0.32(10) | 0.74(10) | |
| Proposed (SPD), , a = 8, | 0.20(10) | 1.37(10) | 0.44(10) | 0.30(10) | 0.47(10) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilakis, N.; Chorianopoulos, C.; Zois, E.N. A Riemannian Dichotomizer Approach on Symmetric Positive Definite Manifolds for Offline, Writer-Independent Signature Verification. Appl. Sci. 2025, 15, 7015. https://doi.org/10.3390/app15137015
Vasilakis N, Chorianopoulos C, Zois EN. A Riemannian Dichotomizer Approach on Symmetric Positive Definite Manifolds for Offline, Writer-Independent Signature Verification. Applied Sciences. 2025; 15(13):7015. https://doi.org/10.3390/app15137015
Chicago/Turabian StyleVasilakis, Nikolaos, Christos Chorianopoulos, and Elias N. Zois. 2025. "A Riemannian Dichotomizer Approach on Symmetric Positive Definite Manifolds for Offline, Writer-Independent Signature Verification" Applied Sciences 15, no. 13: 7015. https://doi.org/10.3390/app15137015
APA StyleVasilakis, N., Chorianopoulos, C., & Zois, E. N. (2025). A Riemannian Dichotomizer Approach on Symmetric Positive Definite Manifolds for Offline, Writer-Independent Signature Verification. Applied Sciences, 15(13), 7015. https://doi.org/10.3390/app15137015







