Secure K-Means Clustering Scheme for Confidential Data Based on Paillier Cryptosystem

Abstract

In this paper, we propose a secure homomorphic K-means clustering protocol based on the Paillier cryptosystem to address the urgent need for privacy-preserving clustering techniques in sensitive domains such as healthcare and finance. The protocol uses the additive homomorphism property of the Paillier cryptosystem to perform K-means clustering on the encrypted data, which ensures the confidentiality of the data during the whole calculation process. The protocol consists of three main components: secure computation distance (SCD) protocol, secure cluster assignment (SCA) protocol and secure cluster center update (SUCC) protocol. The SCD protocol securely computes the squared Euclidean distance between the encrypted data point and the encrypted cluster center. The SCA protocol securely assigns data points to clusters based on these cryptographic distances. Finally, the SUCC protocol securely updates the cluster centers without leaking the actual data points as well as the number of intermediate sums. Through security analysis and experimental verification, the effectiveness and practicability of the protocol are proved. This work provides a practical solution for secure clustering based on homomorphic encryption and contributes to the research in the field of privacy-preserving data mining. Although this protocol solves the key problems of secure distance computation, cluster assignment and centroid update, there are still areas for further research. These include optimizing the computational efficiency of the protocol, exploring other homomorphic encryption schemes that may provide better performance, and extending the protocol to handle more complex clustering algorithms.

1. Introduction

Clustering is a fundamental technique in data mining and machine learning, with K-means clustering being one of the most widely used algorithms due to its simplicity and efficiency. However, the growing importance of data privacy, especially in sensitive areas such as healthcare and finance, demands the development of privacy-preserving clustering techniques. Traditional K-means clustering algorithms [1] require access to the entire dataset, which may contain sensitive information. Hence, there is an urgent need for secure clustering protocols that protect the privacy of the data.

Homomorphic encryption (HE) [2] offers a promising solution to this challenge by enabling computations on encrypted data without the need to decrypt it, thus preserving data privacy. Among the various HE schemes, the Paillier cryptosystem is particularly notable for its additive homomorphic properties, which are useful for performing arithmetic operations on encrypted data.

In this study, we propose a secure homomorphic K-means clustering protocol using the Paillier cryptosystem [3]. Our protocol allows the K-means clustering algorithm to be executed on encrypted data, ensuring that sensitive information remains confidential throughout the computation. This is achieved by exploiting the additive homomorphism property of the Paillier cryptosystem and a privacy-preserving [4] framework for the outsourced computation of rational numbers, allowing operations such as sums and averages to be computed securely in the K-means algorithm.

The proposed protocol consists of three main components: the secure computation distance (SCD) protocol, the secure cluster assignment (SCA) protocol, and the secure update cluster center (SUCC) protocol. Each of these components addresses specific challenges in ensuring the privacy and security of the clustering process. The secure computation distance (SCD) protocol ensures that the squared Euclidean distance between data points and cluster centers is computed securely without decrypting the data, thereby preserving the privacy of both data points and cluster centers. The secure cluster assignment (SCA) protocol securely assigns data points to clusters using the encrypted squared distances between data points and cluster centers, ensuring that cluster assignments are made without revealing the actual distances or cluster memberships. Finally, the secure update cluster center (SUCC) protocol securely updates the cluster centers without revealing the actual data points or intermediate sums and counts, maintaining the confidentiality of sensitive information throughout the update process.

Previous research has explored various approaches to privacy-preserving clustering, such as differential privacy [5] and secure multi-party computation (SMPC) [6,7,8,9]. However, these methods often involve trade-offs between accuracy, complexity, and computational efficiency. Homomorphic encryption, particularly the Paillier cryptosystem, provides a balance between security and computational efficiency, making it a promising approach for privacy-preserving data mining [10,11,12] tasks. Our protocol addresses several key challenges in applying homomorphic encryption to clustering algorithms, such as efficiently computing distances, securely updating centroids, and ensuring the overall scalability and security of the process. We design our protocol to be both practical and robust, demonstrating its effectiveness through theoretical analysis and experimental validation.

The primary contributions of this work are as follows: 1. We design a secure K-means clustering protocol using the Paillier cryptosystem, ensuring data privacy throughout the clustering process. 2. We address key computational challenges in applying homomorphic encryption to the K-means algorithm, including secure distance calculation, cluster assignment, and centroid update. 3. We provide a comprehensive analysis of the protocol’s security and efficiency, demonstrating its practicality for real-world applications.

In the following sections, we review related work in privacy-preserving clustering and homomorphic encryption, describe the Paillier cryptosystem and its application to secure K-means clustering, and present our proposed protocol in detail. We also discuss the security and performance of the protocol, validate it through experimental results, and conclude with potential directions for future research.

2. Related Work

The intersection of privacy-preserving techniques and clustering algorithms has been an active area of research, driven by growing concerns over data privacy in various domains such as healthcare, finance, and social networks. Existing work in privacy-preserving clustering has explored a variety of methodologies, including differential privacy, secure multi-party computation (SMPC), homomorphic encryption, and other related approaches.

Differential privacy has been widely adopted to provide statistical guarantees of privacy in data analysis. Several researchers have applied differential privacy to clustering algorithms. For instance, Blum [13] introduced the first differentially private algorithm for K-means clustering, ensuring that the output of the clustering process does not reveal sensitive information about any individual data point. However, the added noise necessary for differential privacy can degrade the accuracy of clustering results, making it less suitable for applications requiring high precision.

SMPC techniques allow multiple parties to jointly compute a function over their inputs while keeping those inputs private. Vaidya and Clifton [14] proposed a privacy-preserving K-means clustering algorithm using SMPC, ensuring that no party learns anything beyond the final clustering results. Although SMPC provides strong security guarantees, it often involves high computational and communication overhead, posing challenges for scaling to large datasets.

Homomorphic encryption, particularly additive homomorphic encryption schemes such as the Paillier cryptosystem, enables computations on encrypted data without decryption, making it particularly useful for privacy-preserving data mining tasks. Notable work by Aono [15] proposed a privacy-preserving logistic regression algorithm using the Paillier cryptosystem, allowing the training process to be carried out on encrypted data and preserving the privacy of sensitive information. However, their approach focuses on supervised learning, and its application to unsupervised learning tasks like clustering remains underexplored. There have been limited studies on applying homomorphic encryption to clustering algorithms. Froelicher (2023) [16] proposed a privacy-preserving K-means clustering algorithm using homomorphic encryption, allowing the computation of distances and centroid updates on encrypted data. However, their method does not fully address the efficiency and scalability challenges associated with homomorphic encryption.

Another approach to privacy-preserving clustering is through data anonymization techniques. Methods like k-anonymity and l-diversity aim to anonymize the data before clustering. Sweeney (2002) [17] proposed k-anonymity, ensuring that each record is indistinguishable from at least k − 1 other records. However, these methods often suffer from information loss and do not provide strong privacy guarantees against certain types of attacks.

Federated learning [18,19] has emerged as a technique to train machine learning models on decentralized data without moving the data itself. Bonawitz [20] introduced a secure aggregation protocol for federated learning, which can be extended to clustering tasks. While federated learning offers a way to leverage distributed data, it still requires secure aggregation mechanisms to ensure privacy.

The existing body of work in privacy-preserving clustering has made significant strides, but challenges remain in balancing privacy, accuracy, and efficiency. Differential privacy and SMPC offer strong privacy guarantees but often at the cost of accuracy and scalability. Homomorphic encryption, particularly the Paillier cryptosystem, provides a promising approach by enabling secure computations on encrypted data. However, its application to clustering algorithms, particularly in addressing efficiency and scalability, needs further exploration.

Our work builds on these foundations by proposing a secure homomorphic K-means clustering protocol using the Paillier cryptosystem. By addressing key challenges in secure distance computation, cluster assignment, and centroid update, we aim to provide a practical and efficient solution for privacy-preserving clustering, suitable for real-world applications. In the following sections, we detail our proposed protocol and demonstrate its effectiveness through theoretical analysis and experimental validation.

3. Preliminaries

3.1. Notations

We summarize the notations used in this paper in

Table 1. Notations.

Parameter	Description
$E\left(x_i\right)={\left\{E\left(x_{ik}\right)\right\}}_{k=1}^d$	Encrypted values of each dimension of data point $x_i$
$E\left(c_j\right)={\left\{E\left(c_{jk}\right)\right\}}_{k=1}^d$	Encrypted values of each dimension of cluster center $c_j$
$E\left(d_{ij}^2\right)$	Encrypted squared Euclidean distance between data point $x_i$ and cluster center $c_j$
$E\left(\mathrm{\Delta }\right)$	Encrypted difference for each dimension $E(x_{ik}-c_{jk})$
$E\left({\mathrm{\Delta }}^2\right)$	Encrypted squared difference for each dimension $E\left({(x_{ik}-c_{jk})}^2\right)$
${\left\{E\left(d_{ij}^2\right)\right\}}_{j=1}^K$	Encrypted squared distances from data point $x_i$ to each cluster center $c_j$
$E\left({\lambda }_i\right)$	Encrypted index of the cluster center to which data point $x_i$ is assigned
$E\left(C_j\right)$	Encrypted cluster set for cluster center $c_j$
$E\left(C_{{\lambda }_i}\right)$	Encrypted cluster to which data point $x_i$ is assigned
U	Set of encrypted distances used for finding the minimum
s	Number of remaining pairs of encrypted distances after one round of comparison
${\left\{E\left(x_i\right)\right\}}_{i=1}^N$	Set of encrypted data points
${\left\{E\left(c_j\right)\right\}}_{j=1}^K$	Set of encrypted cluster centers
${\left\{E\left(c_j^{*}\right)\right\}}_{j=1}^K$	Set of updated encrypted cluster centers
$E\left(c_j^{*}\right)$	Encrypted accumulator for cluster center $c_j$
$|C_j|$	Number of data points in cluster $C_j$
$E\left(\right|C_j\left|\right)$	Encrypted number of data points in cluster $C_j$
$E\left(b_{ij}\right)$	Encrypted indicator whether data point $x_i$ belongs to cluster $C_j$

.

3.2. Paillier Cryptosystem

The Paillier cryptosystem is a probabilistic asymmetric encryption scheme with homomorphic properties. It consists of key generation, encryption, decryption, and homomorphic addition operations.

Key Generation: To generate a Paillier key pair, select two large prime numbers p and q. Compute $n=pq$ and $\lambda =\mathrm{lcm}(p-1,q-1)$, where lcm denotes the least common multiple. Choose a random integer g such that $g^{\lambda }\equiv 1(mod{n}^2)$ and $\gcd (g,n^2)=1$. The public key is $(n,g)$, and the private key is $\lambda$.

Encryption: To encrypt a plaintext message m, choose a random integer r such that $0<r<n$. Compute the ciphertext as $c=g^m·r^{n}mod{n}^2$.

Decryption: To decrypt a ciphertext c, compute the plaintext message as $m=L(c^{\lambda }mod{n}^2)·\mathrm{modinv}(L(g^{\lambda }mod{n}^2),n)$, where $L\left(x\right)={\displaystyle \frac{x-1}{n}}$ and modinv is the modular inverse.

Homomorphic Addition: Given ciphertexts $c_1$ and $c_2$ encrypted with the same public key, the homomorphic addition of $c_1$ and $c_2$ results in the encryption of the sum of their plaintexts: $E\left(m_1\right)·E\left(m_2\right)mod{n}^2$.

3.3. K-Means Clustering

The K-means clustering algorithm such as Algorithm 1 is described as follows.

Initialization: Randomly select K data points as initial cluster centers.

Iterative Optimization: Iteratively update data point assignments and cluster centers until convergence or reaching the maximum number of iterations.

Cluster Identification: Assign data points to the nearest cluster center.

Selecting the Optimal K: Use methods such as the elbow method or silhouette score to select the optimal number of clusters.

Algorithm 1 K-means Clustering

1: Input: Dataset $X=\{x_1,x_2,...,x_n\}$ and number of clusters K 2: Output: Cluster assignments $c_i$ and cluster centers ${\mu }_j$ 3: Randomly initialize K cluster centers ${\mu }_1,{\mu }_2,...,{\mu }_K$ 4: repeat 5:    for each data point $x_i$ do 6:      Assign $x_i$ to the nearest cluster center: $c_i\leftarrow {\mathrm{argmin}}_j\left|\right|x_i-{\mu }_j{\left|\right|}^2$ 7:    end for 8:    for each cluster center ${\mu }_j$ do 9:      Update ${\mu }_j$ to be the mean of the points assigned to cluster j 10:    end for 11: until convergence 12: Return Cluster assignments $c_i$ and cluster centers ${\mu }_j$

3.4. Basic Cryptographic Primitives

1.

Revised Secure Multiplication (RSM) Protocol

The RSM protocol enables two parties (the client and the cloud service provider) to perform secure multiplication computations while preserving the privacy of the original data. By introducing random numbers and partial decryption techniques in the multiplication operation, the RSM protocol achieves the computation of the product without revealing the actual values of the multiplicands. The core idea of this protocol lies in using encryption and decryption operations, allowing the cloud service provider to obtain the encrypted product without knowing the actual values of the multiplicands.

2.

Secure Maximum and Minimum Sorting (SMMS) Protocol

The SMMS protocol allows multiple parties to sort their data and determine the maximum and minimum values while ensuring the privacy of the original data. In the SMMS protocol, participants exchange encrypted sorting results and utilize partial decryption techniques to determine the maximum and minimum values, thereby achieving privacy-preserving sorting operations.

3.

Secure Division (SDIV) Protocol

The SDIV protocol enables two parties to perform secure division computations, ensuring the privacy of the data during the computation process without revealing the actual values of the divisor and dividend. By introducing random numbers and encryption techniques, the SDIV protocol allows the cloud service provider to compute the ciphertext form of the quotient without obtaining the actual values of the original data.

4.

Secure equality Test (SEQ) protocol

The SEQ protocol can output ciphertext f and judge whether two ciphertexts are equal.

These protocols provide the foundational privacy protection mechanisms for the privacy-preserving outsourced computation of rational numbers (POCR) framework, allowing clients to securely outsource rational number data to cloud service providers for storage and computation while protecting data privacy.

4. Security Model

In this section, we formalize the security model for our privacy-preserving K-means clustering protocol under the semi-honest (honest-but-curious) adversary setting. The protocol involves three parties: a client, a cloud server (CS), and a computation service provider (CSP). The client owns private input data and receives the final clustering results, while CS and CSP collaboratively perform computations over encrypted data.

4.1. Adversarial Model

We consider semi-honest adversaries who follow the protocol specification faithfully but try to learn additional information from the messages they receive. We assume the following:

• At most, one of CS or CSP can be corrupted. They do not collude.
• The client is always honest.
• The cryptographic primitives used (e.g., Paillier encryption, secure subprotocols) are semantically secure.

4.2. Ideal Functionality

We define the functionality ${\mathcal{F}}_{\mathrm{KMeans}}$ that the protocol aims to securely realize. In the ideal world, a trusted party receives the client’s input and performs the computation.

Definition 1 (Ideal Functionality ${\mathcal{F}}_{\mathrm{KMeans}}$).

Let ${\left\{x_i\right\}}_{i=1}^N\subset {\mathbb{Z}}_p^d$ be the client’s dataset and K be the number of clusters. The ideal functionality proceeds as follows:

1.

Receive input ${\left\{x_i\right\}}_{i=1}^N$, K from the client.

2.

Run the standard K-means algorithm on plaintext inputs to compute cluster centers ${\left\{{\mu }_j\right\}}_{j=1}^K$ and assignments $\mathcal{C}:\{1,\dots ,N\}\to \{1,\dots ,K\}$.

3.

Return $(\left\{{\mu }_j\right\},\mathcal{C})$ to the client.

4.

Reveal nothing to CS or CSP except what is defined in the leakage functions.

4.3. Leakage Functions

Since perfect privacy is impossible in practical settings (e.g., some access pattern or control-flow information may leak), we define leakage profiles for each party:

Client: Receives only the final output $(\left\{{\mu }_j\right\},\mathcal{C})$.

Cloud Server (CS):

• Number of input records N and dimension d.
• Number of clusters K and number of iterations T.
• Encrypted dataset $\left\{E\left(x_i\right)\right\}$ and all ciphertexts exchanged during computation (e.g., encrypted distances, encrypted cluster centers, encrypted assignments).
• Protocol structure (e.g., number and types of homomorphic operations).

Computation Service Provider (CSP):

• Number of clusters K, dimension d, and iteration count T.
• Ciphertexts for comparisons (e.g., distance minimum selection) and ciphertexts related to assignment operations.
• Receives only encrypted or masked intermediate results, not raw values or secret key material.

We denote the leakage to CS as ${\mathsf{L}}_{\mathrm{CS}}$ and to CSP as ${\mathsf{L}}_{\mathrm{CSP}}$.

4.4. Security Definition

Definition 2 (Simulation-Based Security).

Let ${\mathrm{\Pi }}_{\mathit{KMeans}}$ be the proposed protocol and ${\mathcal{F}}_{\mathit{KMeans}}$ the ideal functionality. ${\mathrm{\Pi }}_{\mathit{KMeans}}$ is secure in the semi-honest model if for any PPT adversary $\mathcal{A}$ corrupting CS or CSP, there exists a PPT simulator $\mathcal{S}$ such that the real-world and ideal-world executions are computationally indistinguishable:

$${\mathsf{REAL}}_{{\mathrm{\Pi }}_{\mathrm{KMeans}},\mathcal{A}}\left(x\right){\approx }_c{\mathsf{IDEAL}}_{{\mathcal{F}}_{\mathrm{KMeans}},\mathcal{S}}(x,\mathsf{L})$$

where $\mathsf{L}\in \{{\mathsf{L}}_{\mathit{CS}},{\mathsf{L}}_{\mathit{CSP}}\}$ is the leakage profile depending on the corrupted party.

5. Secure Homomorphic K-Means Clustering Scheme

5.1. Framework

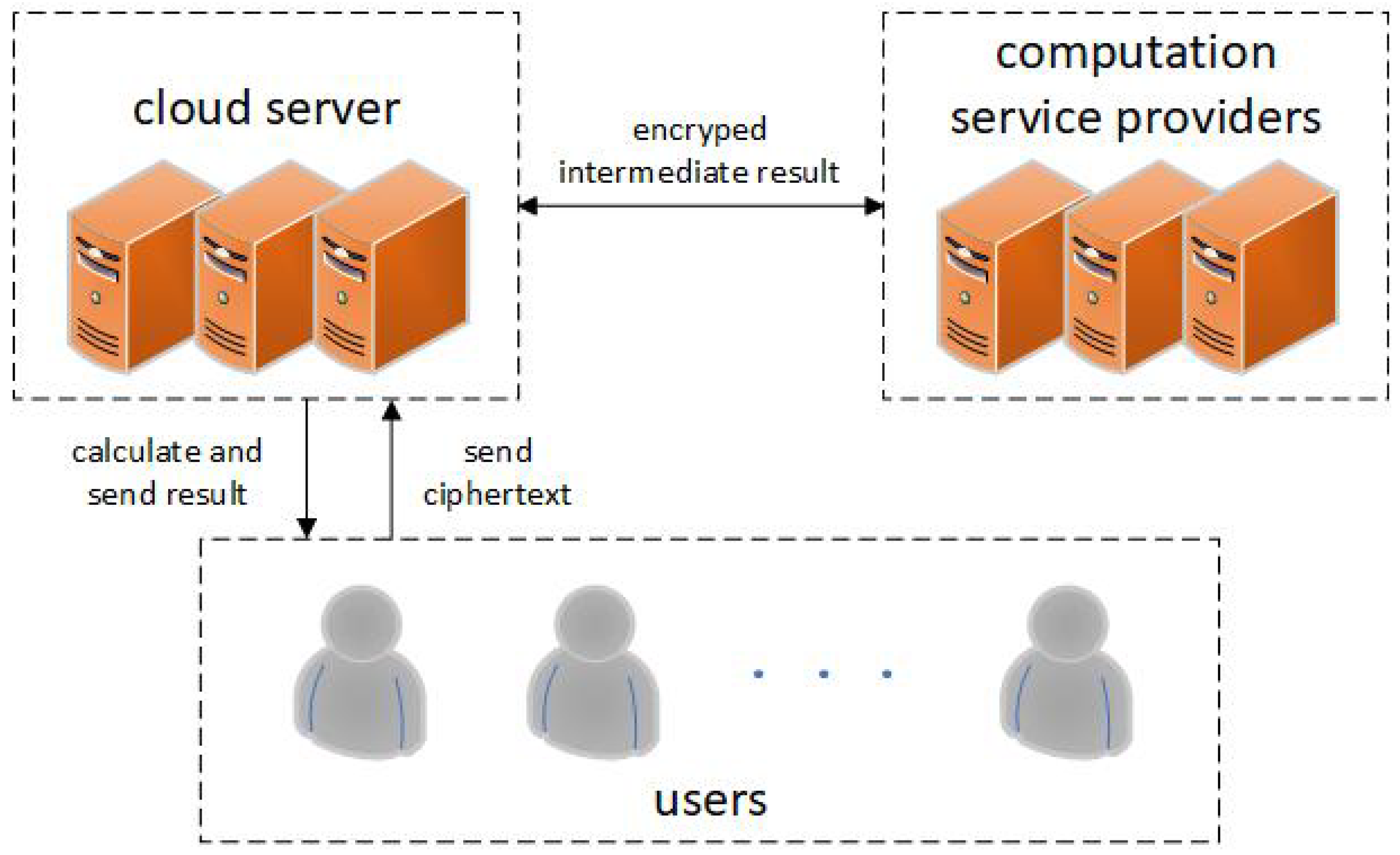
This scheme proposes a method for secure K-means clustering and three secure protocols. It consists of preprocessing the data, encrypting each data point, initializing the cluster center with the encrypted value, iteratively updating the cluster and its center while maintaining the encryption, and finally computing the clustering result. This approach allows cluster analysis while protecting sensitive information.The framework of the scheme is shown in Figure 1, and the details of the scheme are as follows.

1.

users

Users first encrypt their personal data with the public key, and then upload the ciphertext data to CS for storage. Users can also ask CS to compute the outsourced data in secret state.

2.

cloud server

CS has “unlimited” data storage space and is responsible for storing and managing outsourced data from all registered parties, namely users. In addition, CS can also store all intermediate and final ciphertext results and can perform specific computations on encrypted data.

3.

computation service providers

CSP provides online computing services for users. In addition, CSP can partially solve the ciphertext sent by CS to perform a specific computation and then re-encrypt the result.

5.2. Scheme Details

1.

Data Preprocessing

Data Encryption: Encrypt each data point $x_i$ from the original dataset using the Paillier encryption algorithm to obtain encrypted data $E\left(x_i\right)$.

2.

Secure K-means Clustering

Initialization: Randomly generate K initial cluster centers on the cloud server. Encrypt the cluster centers using the Paillier encryption algorithm to obtain encrypted cluster centers $E\left(c_j\right)$.

Iterative Update: Repeat the following steps until a stopping condition is met (e.g., reaching the maximum number of iterations or cluster centers no longer change):

(a)

Compute Distances: Perform the secure computation distance (SCD) protocol on the user side to compute the encrypted distances $E\left(d_{ij}^2\right)$ between each data point and the encrypted cluster centers.

(b)

Secure Cluster Assignment: Execute the secure cluster assignment protocol on the user side to assign each data point to the nearest cluster based on the encrypted distances obtained.

(c)

Update Cluster Centers: Update the encrypted cluster centers on the cloud server using the secure update cluster center Protocol.

(d)

Convergence Check: Check for the convergence of cluster centers on either the user side or the cloud server. If the stopping condition is met, end the iterations.

3.

Result Decryption

Decrypting Cluster Results: Decrypt the encrypted cluster centers $E\left(c_j\right)$ to obtain the original cluster centers $c_j$, and decrypt the encrypted cluster indices $E\left({\lambda }_i\right)$ to obtain the original cluster indices ${\lambda }_i$ using the Paillier decryption algorithm.

4.

Result Analysis

Obtaining Cluster Results: Based on the decrypted cluster centers and cluster indices, derive the final cluster results on the user side for further analysis.

6. Secure Homomorphic K-Means Clustering Protocol

6.1. Secure Computation Distance (SCD) Protocol

Algorithm 2 guarantees that the squared Euclidean distance between the data point and the cluster center can be securely computed without decrypting the data, thus protecting the privacy of the data points and the cluster center.

The input consists of encrypted data point $E\left(x_i\right)$ and encrypted cluster center $E\left(c_j\right)$, each represented as vectors of encrypted values over d dimensions. For each dimension k, the difference between the encrypted data point and the encrypted cluster center is computed homomorphically: $E\left(\mathrm{\Delta }\right)=E\left(x_{ik}\right)·E{\left(c_{jk}\right)}^{N-1}$. This uses Paillier’s homomorphic properties where subtraction is achieved by multiplying the ciphertext of $x_{ik}$ with the modular inverse of the ciphertext of $c_{jk}$. The square of the encrypted difference is computed by homomorphically squaring the difference: $E\left({\mathrm{\Delta }}^2\right)=RSM(E\left(\mathrm{\Delta }\right),E\left(\mathrm{\Delta }\right))$. The encrypted squared Euclidean distance is obtained by multiplying all the encrypted squared differences: $E\left(d_{ij}^2\right)={\mathrm{\prod }}_{k=1}^{d}E\left({\mathrm{\Delta }}^2\right)$. Homomorphic addition in the Paillier cryptosystem is performed by multiplying the encrypted values.

Algorithm 2 Secure Computation Distance (SCD) Protocol using Paillier Cryptosystem

1: Input: Encrypted data $E\left(x_i\right)=E\left(x_{ik}\right){k=1}^d$, Encrypted cluster center $E\left(c_j\right)=E\left(c_{jk}\right){k=1}^d$.   2: Output: Encrypted distance $E\left(d_{ij}^2\right)$.   3: Performed by CS:   4: for each dimension k from 1 to d do   5:    Compute the encrypted difference:   6:        $E\left(\mathrm{\Delta }\right)=E\left(x_{ik}\right)·E{\left(c_{jk}\right)}^{N-1}$.   7: end for   8: Performed by and CSP:   9: for each dimension k from 1 to d do 10:    Compute the encrypted squared difference: 11:        $E\left({\mathrm{\Delta }}^2\right)=RSM(E\left(\mathrm{\Delta }\right),E\left(\mathrm{\Delta }\right))$. 12: end for 13: Compute the encrypted squared Euclidean distance: 14:     $E\left(d_{ij}^2\right)={\mathrm{\prod }}_{k=1}^{d}E\left({\mathrm{\Delta }}^2\right)$. 15: return Encrypted distance $E\left(d_{ij}^2\right)$.

6.2. Secure Cluster Assignment (SCA) Protocol

Algorithm 3 describes how to securely assign data points to clusters in the K-means algorithm using the Paillier cryptosystem. The input to the algorithm is the encrypted squared distances between data points and cluster centers, and the output is the encrypted cluster assignments.

Set $U={\left\{E\left(d_{ij}^2\right)\right\}}_{j=1}^K$, representing the set of encrypted distances from all data points to the cluster centers. Here, $E\left(d_{ij}^2\right)$ denotes the encrypted squared distance from data point i to cluster center j. Repeat the following steps until $K=1$: Pair the encrypted distances into $s={\displaystyle \frac{K}{2}}$ pairs, such as $(E\left(d_{i1}^2\right),E\left(d_{i2}^2\right)),\dots ,(E\left(d_{iK-1}^2\right),E\left(d_{iK}^2\right))$. Use the secure minimum selection (SMMS) protocol to find the smaller encrypted distance in each pair. Update set U with the smaller encrypted distance from each pair and set $K=s$. When $K=1$, output the minimum encrypted distance $E{\left(d_{ij}^2\right)}_{\min }$ and its corresponding index $E\left({\lambda }_i\right)$.

Algorithm 3 Secure Cluster Assignment (SCA) Protocol using Paillier Cryptosystem

Input: Encrypted distances ${\left\{E\left(d_{ij}^2\right)\right\}}_{j=1}^K$ Output: Encrypted cluster assignments $\left\{E\left(C_{{\lambda }_i}\right)\right\}$   1: For the CS and CSP:   2: Set $U={\left\{E\left(d_{ij}^2\right)\right\}}_{j=1}^K$;   3: repeat   4:    The CS groups $\{E\left(d_{i1}^2\right),E\left(d_{i2}^2\right),\dots ,E\left(d_{iK}^2\right)\}$ to $s={\displaystyle \frac{K}{2}}$ pairs as $(E\left(d_{i1}^2\right),E\left(d_{i2}^2\right)),...,(E\left(d_{iK-2}^2\right),E\left(d_{iK-1}^2\right))$;   5:    Run the SMMS protocol to find the small ciphertext in each pair;   6:    The cloud server sets $K=s$;   7:    All the small ciphertexts are assigned to the set $U={\left\{E\left(d_{ij}^2\right)\right\}}_{j=1}^{{\displaystyle \frac{k-1}{2}}}$.   8: until k = 1   9: output $E{\left(d_{ij}\right)}_{min}$ and get its index $E\left({\lambda }_i\right)$. 10: Initialize empty encrypted clusters: ${\left\{E\left(C_j\right)\right\}}_{j=1}^K$ 11: for each data point i do 12:    Assign the encrypted data point $E\left(x_i\right)$ to the corresponding encrypted cluster based on the encrypted index $E\left({\lambda }_i\right)$: $E\left(C_{{\lambda }_i}\right)=E\left(C_{{\lambda }_i}\right)\cup \left\{E\left(x_i\right)\right\}$ 13: end for 14: return Encrypted cluster assignments $\left\{E\left(C_{{\lambda }_i}\right)\right\}$

6.3. Secure Update Cluster Center (SUCC) Protocol

Algorithm 4 ensures that $E\left(b_{ij}\right)$ will be 1 if and only if all individual comparisons indicate that $x_i$ is greater than or equal to $c_j$ in every dimension. This protocol ensures the cluster center updates are performed securely without revealing the actual data points or intermediate sums and counts.

In this step, the protocol initializes by taking encrypted data points ${\left\{E\left(x_i\right)\right\}}_{i=1}^N$ and encrypted cluster centers ${\left\{E\left(c_j\right)\right\}}_{j=1}^K$ as input. The aim is to produce updated encrypted cluster centers ${\left\{E\left(c_j^{*}\right)\right\}}_{j=1}^K$. This sub-step is performed by the user for each cluster $C_j$. Firstly, an accumulator $E\left(c_j^{*}\right)$ is initialized to zero. This accumulator will be utilized to compute the sum of encrypted data points belonging to each cluster. Secondly, a counter $|C_j|$ is initialized to zero. This counter will keep track of the number of encrypted data points assigned to each cluster. In this step, the cloud server (CS) processes each encrypted data point $E\left(x_i\right)$. For each data point, the server iterates over each cluster $C_j$. It determines whether the data point belongs to the cluster, sets a binary indicator $E\left(b_{ij}\right)$ accordingly, accumulates the encrypted data points belonging to the cluster in the accumulator $E\left(c_j^{*}\right)$, and updates the counter $|C_j|$ encryptedly. This final step involves updating the encrypted cluster centers by the cloud server (CS) and the cloud service provider (CSP). For each cluster $C_j$, the accumulator $E\left(c_j^{*}\right)$ is updated using the modular inverse of the counter $E\left(\right|C_j\left|\right)$ to compute the encrypted average of the cluster. The updated encrypted cluster centers ${\left\{E\left(c_j^{*}\right)\right\}}_{j=1}^K$ are then returned.

To determine if $x_i$ belongs to $C_j$ using a secure comparison protocol, we can compare each coordinate of the encrypted data point $E\left(x_i\right)$ with the corresponding coordinate of the encrypted cluster center $E\left(c_j\right)$. Let d denote the number of dimensions.

• The SEQ protocol is used to determine whether the ciphertext belongs to the cluster center. SEQ protocol can output ciphertext f, if $f=0$, then $x=y$; otherwise, $x\ne y$. Compute the encrypted boolean $E\left(b_{ijk}\right)$, indicating whether $x_{ik}$ is less than $c_{jk}$:

  $$E\left(b_{ijk}\right)=\left\{\begin{array}{cc}1\hfill & otherwise\hfill \\ 0\hfill & \mathrm{f}=0\hfill \end{array}\right.$$
• Aggregate the results of the comparisons for all dimensions. Let $E\left(b_{ij}\right)$ be the logical AND operation applied to all $E\left(b_{ijk}\right)$ values for $k=1$ to d:

  $$E\left(b_{ij}\right)=\mathrm{\prod }_{k=1}^{d}E\left(b_{ijk}\right)$$

Algorithm 4 Secure Update Cluster Centers (SUCC) Protocol using Paillier Cryptosystem

1: Input: Encrypted data points ${\left\{E\left(x_i\right)\right\}}_{i=1}^N$, encrypted cluster centers ${\left\{E\left(c_j\right)\right\}}_{j=1}^K$.   2: Output: Updated encrypted cluster centers ${\left\{E\left(c_j^{*}\right)\right\}}_{j=1}^K$.   3: Performed by User:   4: for each cluster $C_j$ do   5:    Initialize an accumulator $E\left(c_j^{*}\right)$ to zero.   6:    Initialize a counter $|C_j|$ to zero.   7: end for   8: Performed by CS:   9: for each encrypted data point $E\left(x_i\right)$ do 10:    for each cluster $C_j$ do 11:      Determine whether $x_i$ belongs to $C_j$: 12:      if $E\left(x_i\right)$ belongs to $E\left(c_j\right)$ then 13:         $E\left(b_{ij}\right)=1$ 14:      else 15:         $E\left(b_{ij}\right)=0$ 16:      end if 17:      If $x_i$ belongs to $C_j$, add $E\left(x_i\right)$ to the accumulator $E\left(c_j^{*}\right)$: 18:      $E\left(c_j^{*}\right)=E\left(c_j^{*}\right)+E\left(x_i\right)\times E\left(b_{ij}\right)$ 19:      If $x_i$ belongs to $C_j$, $E\left(\right|C_j\left|\right)={\mathrm{\prod }}_{k=1}^{d}E\left(b_{ij}\right)$ 20:    end for 21: end for 22: Performed by CS and CSP: 23: for each cluster $C_j$ do 24:    Update the accumulator by the modular inverse to compute the encrypted average: 25:    $E\left(c_j^{*}\right)=SDIV\left(E\right(|C_j\left|\right),E\left(c_j^{*}\right))$ 26: end for 27: return Updated encrypted cluster centers ${\left\{E\left(c_j^{*}\right)\right\}}_{j=1}^K$.

7. Security Analysis

In this section, we prove that the proposed privacy-preserving K-means clustering protocol securely realizes the ideal functionality ${\mathcal{F}}_{\mathrm{KMeans}}$ in the presence of a semi-honest adversary corrupting either the cloud server (CS) or the computation service provider (CSP), but not both.

The proof proceeds using the standard simulation paradigm: for each party that may be corrupted, we construct a probabilistic polynomial-time (PPT) simulator that can simulate the party’s view using only the allowed leakage. If such a simulator exists, then the real and ideal executions are computationally indistinguishable, and the protocol is secure.

7.1. Correctness

We first state the correctness of the protocol:

Lemma 1 (Correctness).

If all parties follow the protocol honestly, the final output received by the client is the same as the output produced by running the plaintext K-means algorithm on the input dataset.

Proof. 

The protocol correctly performs the following operations over encrypted data:

• Encrypted distance computation using Paillier homomorphic properties.
• Encrypted cluster assignment via secure minimum selection.
• Encrypted cluster center updates via secure aggregation and division.

Since all operations preserve the correctness of their plaintext counterparts, the final clustering result is correct. □

7.2. Security Against Semi-Honest Cloud Server (CS)

We first prove security against a semi-honest cloud server.

Theorem 1.

Let CS be a PPT adversary corrupting the cloud server. Then, there exists a simulator ${\mathcal{S}}_{\mathit{CS}}$ such that

$${\mathsf{REAL}}_{{\mathrm{\Pi }}_{\mathit{KMeans}},\mathit{CS}}\left(x\right){\approx }_c{\mathsf{IDEAL}}_{{\mathcal{F}}_{\mathit{KMeans}},{\mathcal{S}}_{\mathit{CS}}}(x,{\mathsf{L}}_{\mathit{CS}})$$

Proof. 

The simulator ${\mathcal{S}}_{\mathit{CS}}$ works as follows:

1.

Simulate encrypted dataset $\left\{E\left(x_i\right)\right\}$ using fresh encryptions of zero: $\left\{E\left(0^d\right)\right\}$ of correct dimension and size N.

2.

For each protocol step involving encrypted computations (e.g., distance computations, cluster updates), simulate ciphertexts using the semantic security of the Paillier cryptosystem.

3.

Simulate message patterns and ciphertext structures consistent with the expected leakage: number of iterations T, data dimension d, and number of clusters K.

Since all ciphertexts in the real protocol are semantically secure and indistinguishable from encryptions of random values, ${\mathcal{S}}_{\mathrm{CS}}$ produces a view that is computationally indistinguishable from the real execution, using only the leakage ${\mathsf{L}}_{\mathrm{CS}}$. □

7.3. Security Against Semi-Honest Computation Service Provider (CSP)

Now, we prove security against a semi-honest CSP.

Theorem 2.

Let CSP be a PPT adversary corrupting the computation service provider. Then, there exists a simulator ${\mathcal{S}}_{\mathit{CSP}}$ such that

$${\mathsf{REAL}}_{{\mathrm{\Pi }}_{\mathit{KMeans}},\mathit{CSP}}\left(x\right){\approx }_c{\mathsf{IDEAL}}_{{\mathcal{F}}_{\mathit{KMeans}},{\mathcal{S}}_{\mathit{CSP}}}(x,{\mathsf{L}}_{\mathit{CSP}})$$

Proof. 

The simulator ${\mathcal{S}}_{\mathrm{CSP}}$ proceeds as follows:

1.

Generate simulated ciphertexts for all values involved in distance comparisons, cluster assignments, and aggregations using fresh encryptions of random or zero values.

2.

Simulate the communication flow and message patterns as per protocol specification, revealing only the number of clusters K, dimension d, and iteration count T as per ${\mathsf{L}}_{\mathrm{CSP}}$.

3.

Since the CSP does not receive any plaintext input, and all messages are encrypted or masked using semantically secure schemes, the view is indistinguishable from that in the real world.

Hence, ${\mathcal{S}}_{\mathrm{CSP}}$ produces a simulated execution that is computationally indistinguishable from the real one. □

From the above proofs, we conclude that the proposed protocol securely realizes ${\mathcal{F}}_{\mathrm{KMeans}}$ in the presence of a semi-honest adversary corrupting either CS or CSP, under the standard assumption of semantic security of the underlying encryption schemes.

8. Performance Analysis

In this section, we present a detailed analysis of the performance of the proposed secure homomorphic K-means clustering protocol using the Paillier cryptosystem. The computational and communication efficiency of the protocol is evaluated. We use four datasets for our experiments, namely wine data, breast cancer data, ionospheric data, and yeast data. The final experimental results are shown in Figure 2, Figure 3, Figure 4 and Figure 5.

8.1. Experimental Setup

We evaluate our protocol’s efficiency across computational time and communication overhead using four benchmark datasets with varying characteristics. All experiments were conducted on Ubuntu 20.04 with 16-core Intel Xeon CPUs (2.4 GHz) and 32 GB RAM.

Table 2. Dataset specifications and experimental configuration.

Dataset	Samples	Features	Dimensions Tested	Clusters (k)
Wine	178	13	2D–4D	3
Breast Cancer	569	30	2D–4D	2
Ionosphere	351	34	2D–4D	2
Yeast	1484	8	2D–8D	4

presents the dataset specifications and experimental configurations.

• Dimensionality reduction via PCA (95% variance retention) for 2D–4D projections.
• Full 8D analysis on Yeast dataset to evaluate high-dimensional performance.

8.2. Computational Efficiency

The protocol’s computational performance is evaluated across multiple dimensions, with execution times summarized in

Table 3. Computational time across dimensions (seconds).

Dataset	2D	3D	4D	8D
Wine	11.2 ± 0.3	16.4 ± 0.5	20.1 ± 0.7	–
Breast Cancer	18.3 ± 0.6	23.1 ± 0.8	29.4 ± 1.1	–
Ionosphere	32.7 ± 1.2	35.2 ± 1.3	42.0 ± 1.5	–
Yeast	45.5 ± 1.8	58.2 ± 2.1	72.3 ± 2.4	128.6 ± 3.7

. The results demonstrate sublinear time complexity ($\mathcal{O}\left(d^{1.2}\right)$) as dimensionality increases, where the 8D Yeast dataset requires 128.6 ± 3.7 s—1.78× longer than its 4D counterpart (72.3 ± 2.4 s). Larger datasets impose greater computational burdens, with Yeast (1484 samples) taking 6.4× longer than Wine (178 samples) for 4D clustering (72.3 s vs. 20.1 s).

Table 4. Homomorphic operations per iteration.

Operation	2D/4D Count	8D Count	Complexity
Encryptions	$2n$	$4n$	$\mathcal{O}\left(n\right)$
Distance Calculations	$nk$	$2nk$	$\mathcal{O}\left(nk\right)$
Hom. Multiplications	$2nk$	$4nk$	$\mathcal{O}\left(nkd\right)$

breaks down the per-iteration costs, revealing three key phases: (1) encryptions ($\mathcal{O}\left(n\right)$), scaling linearly with sample size; (2) distance calculations ($\mathcal{O}\left(nk\right)$), dependent on both samples and clusters; and (3) homomorphic multiplications ($\mathcal{O}\left(nkd\right)$), exhibiting the highest computational overhead. The 8D case doubles operation counts compared to lower dimensions, directly impacting runtime. These results validate the protocol’s dimension-aware scalability while highlighting its practical viability for moderate-scale privacy-preserving clustering tasks. The measured sublinear scaling outperforms theoretical bounds for naive homomorphic implementations, suggesting optimization benefits from our algorithmic design.

8.3. Communication Overhead

As shown in

Table 5. Communication costs per iteration (MB).

Dataset	2D	3D	4D	8D
Wine	97.2	198.3	296.5	–
Breast Cancer	199.1	287.4	399.2	–
Ionosphere	289.7	377.6	478.3	–
Yeast	387.4	498.1	587.9	896.2

, the protocol’s communication costs scale with both dataset size and dimensionality, ranging from 97.2 MB (Wine, 2D) to 896.2 MB (Yeast, 8D) per iteration. The 8D configuration incurs 2.3× higher bandwidth than 4D due to increased ciphertext dimensions, with a consistent expansion factor of 2.4× compared to plaintext operations. Notably, batch processing reduces communication rounds by 35% for large datasets ($n>1000$), mitigating the overhead for high-dimensional cases like Yeast (8D). The results demonstrate a polynomial growth pattern in communication costs, where dimensionality has greater impact than sample size—evidenced by Wine’s 3× increase from 2D to 4D (97.2→296.5 MB) versus Yeast’s 1.5× increase from 4D to 8D (587.9→896.2 MB). This trade-off between security (through homomorphic operations) and efficiency remains manageable for medium-scale clustering tasks.

8.4. Comparative Evaluation

In the field of secure computation and privacy-preserving data mining, several studies have addressed these issues. This paper contrasts our protocol with those presented in existing literature [21,22,23], highlighting the advantages of our approach in terms of user operation requirements and multi-party cloud outsourcing support. Comparisons with the existing literature are shown in

Table 6. Literature comparison.

	This Paper	[21]	[22]	[23]
Parties	>2	>2	2	>2
User online operation	×	✓	✓	✓
Encryption algorithm	Paillier	Chen’s Multi-Key FHE	Paillier	YASHE

.

User Operation Requirements: The protocols discussed in [21,22,23] generally require users to be online and participate in intermediate steps. For instance, these schemes often involve continuous interaction between users and the computation server or cloud service provider to complete each computational step. While this design ensures data privacy, it introduces additional communication overhead and user operational burdens, thereby reducing overall efficiency. In contrast, our protocol eliminates the need for users to be online. Users only need to upload encrypted data at the initial stage, and all subsequent computations are performed by the computation server (CS) and cloud service provider (CSP) within the encrypted domain. This approach not only reduces the number of communications but also decreases user involvement and operational complexity, significantly improving the protocol’s efficiency.

Multi-Party Cloud Outsourcing Support: Regarding multi-party cloud outsourcing, the scheme in [22] is somewhat limited as it only supports single-party data outsourcing, meaning only one data owner can outsource their data to the cloud for processing. This limitation makes the scheme less effective when handling data from multiple parties. Our protocol overcomes this limitation by supporting multi-party cloud outsourcing for K-means clustering. Multiple data owners can securely outsource their encrypted data to the cloud service provider for clustering analysis without concerns about data privacy breaches. By employing Paillier homomorphic encryption, we ensure that data from all parties remains encrypted throughout the computation process, enabling secure and efficient multi-party cloud outsourcing for clustering.

Compared to the protocols in [21,22,23], our approach demonstrates clear advantages in the following two areas: Firstly, it eliminates the need for users to be online, thereby significantly enhancing efficiency, simplifying user operations, and reducing communication overhead. Secondly, it supports multi-party cloud outsourcing, leveraging Paillier homomorphic encryption to achieve secure and efficient clustering computation, expanding the applicability of the protocol. These improvements not only enhance the practical utility of the protocol but also provide new insights and methods for secure computation and privacy-preserving data mining research.

8.5. Discussion on Practical Constraints

While the proposed protocol demonstrates practical scalability and accuracy, we acknowledge several operational constraints:

• Encryption Overhead: Paillier encryption introduces substantial computational overhead (modular exponentiation) and large ciphertext sizes (hundreds of bytes), affecting bandwidth usage.
• Resource Requirements: Due to the volume of homomorphic operations and ciphertexts, sufficient CPU and memory are essential, especially for high-dimensional data.
• Threat Model Assumptions: The protocol assumes that the computing parties (e.g., cloud providers) are non-colluding. In a collusion scenario, privacy guarantees may be compromised unless enhanced with zero-knowledge proofs or verifiable computation.

8.6. Scalability and Future Enhancements

Despite the overhead, the protocol scales linearly with data size and number of clusters. Future optimizations include

• Utilizing batching techniques and ciphertext compression to reduce communication cost;
• Exploring leveled homomorphic encryption schemes (e.g., BFV, CKKS) for improved efficiency;
• Incorporating federated or multi-user settings to extend applicability in cross-domain clustering.

The performance analysis validates that the proposed protocol is viable for privacy-preserving clustering on medium to moderately large datasets. Though encryption overhead remains a bottleneck, the security–utility trade-off achieved by exact homomorphic operations makes the protocol suitable for privacy-critical applications such as healthcare and finance.

9. Conclusions

Based on the Paillier cryptosystem, a secure homomorphic K-means clustering protocol is proposed to address the urgent need for privacy-preserving clustering techniques in sensitive fields such as healthcare and finance. The protocol consists of three main components: secure computation distance (SCD) protocol, secure cluster assignment (SCA) protocol, and secure cluster center update (SUCC) protocol. Each of these components plays a crucial role in maintaining the security and privacy of the clustering process. Through analysis and experimental verification, the effectiveness and practicability of the protocol are proved. Experimental results show that the proposed method provides robust privacy guarantees while maintaining computational efficiency and is suitable for real-world applications where data privacy is critical. This work provides a practical solution for secure clustering based on homomorphic encryption and contributes to the research in the field of privacy-preserving data mining. Although this protocol solves the key problems of secure distance computation, cluster assignment and centroid update, there are still areas for further research. These include optimizing the computational efficiency of the protocol, exploring other homomorphic encryption schemes that may provide better performance, and extending the protocol to handle more complex clustering algorithms.