Evaluating the Effectiveness of Natural Carbon Sinks Through a Temperature-Dependent Model
Abstract
1. Introduction
Outline of the Article
2. Materials and Methods
2.1. The Top-Down Carbon Sink Model from the Continuity Equation
2.1.1. Finding the Appropriate Data Resolution
2.1.2. The Extended Linear Sink Model
2.1.3. Other Approaches That Relate Temperature to Sink Effect
2.2. Separating Absorptions and Natural Emissions
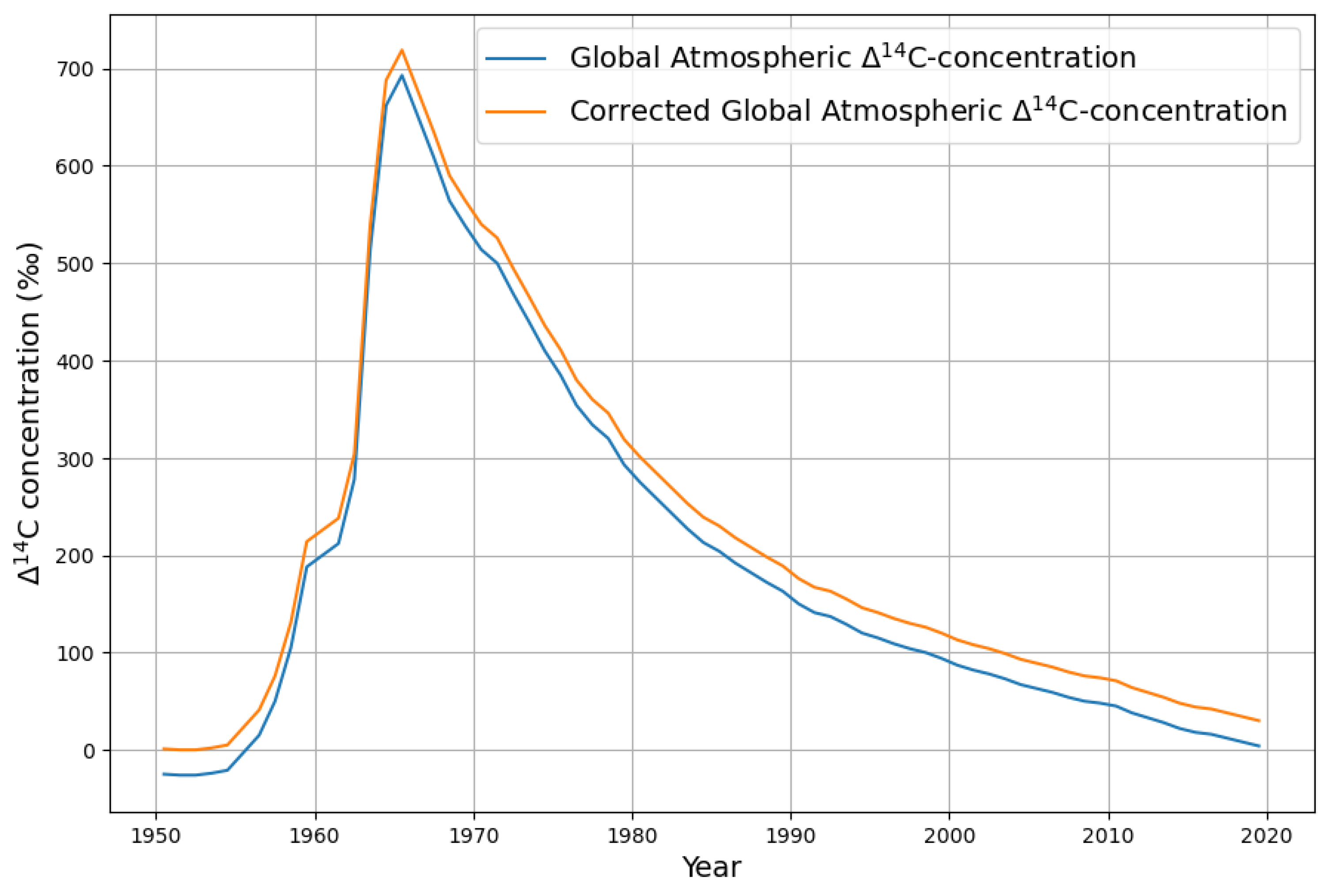
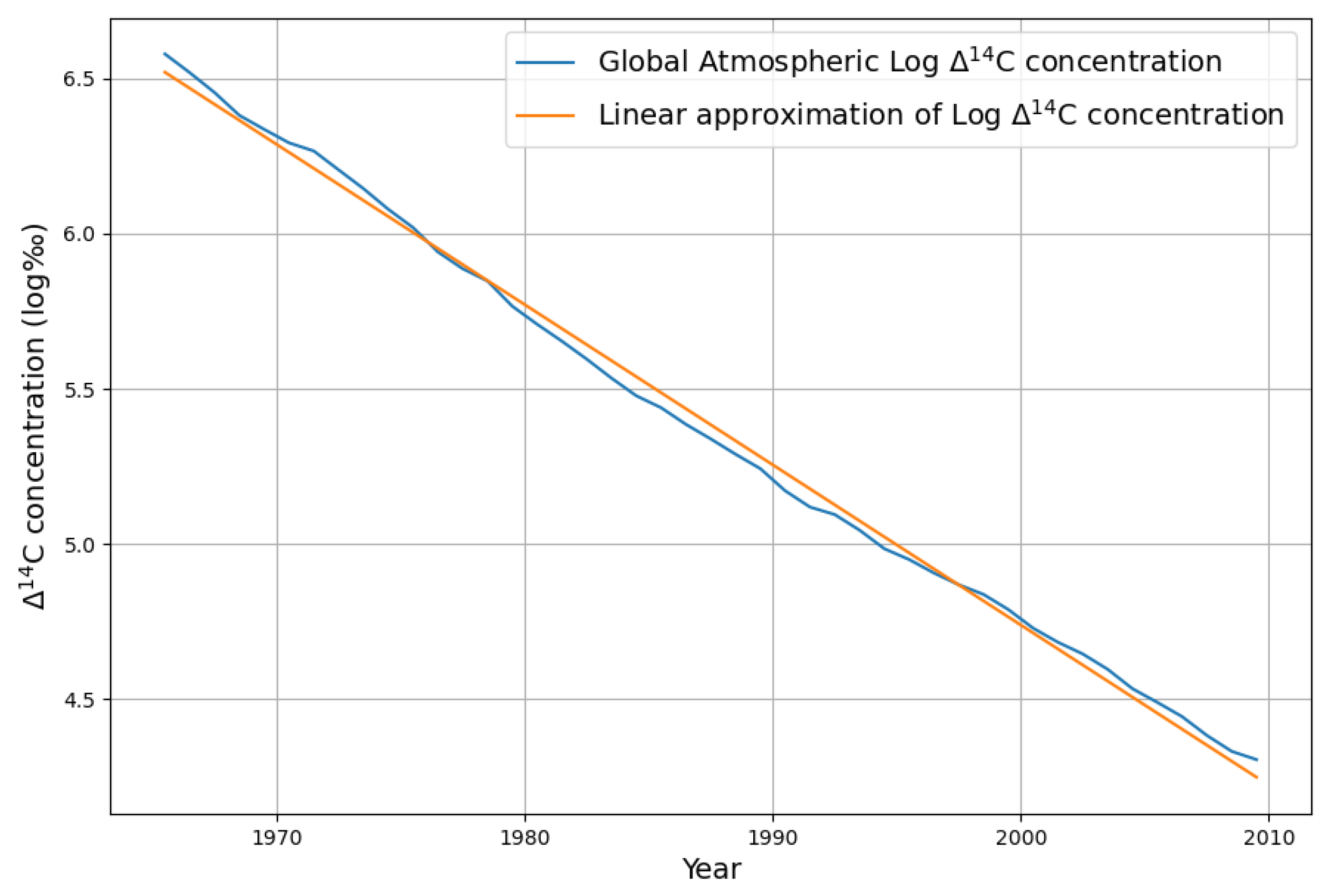
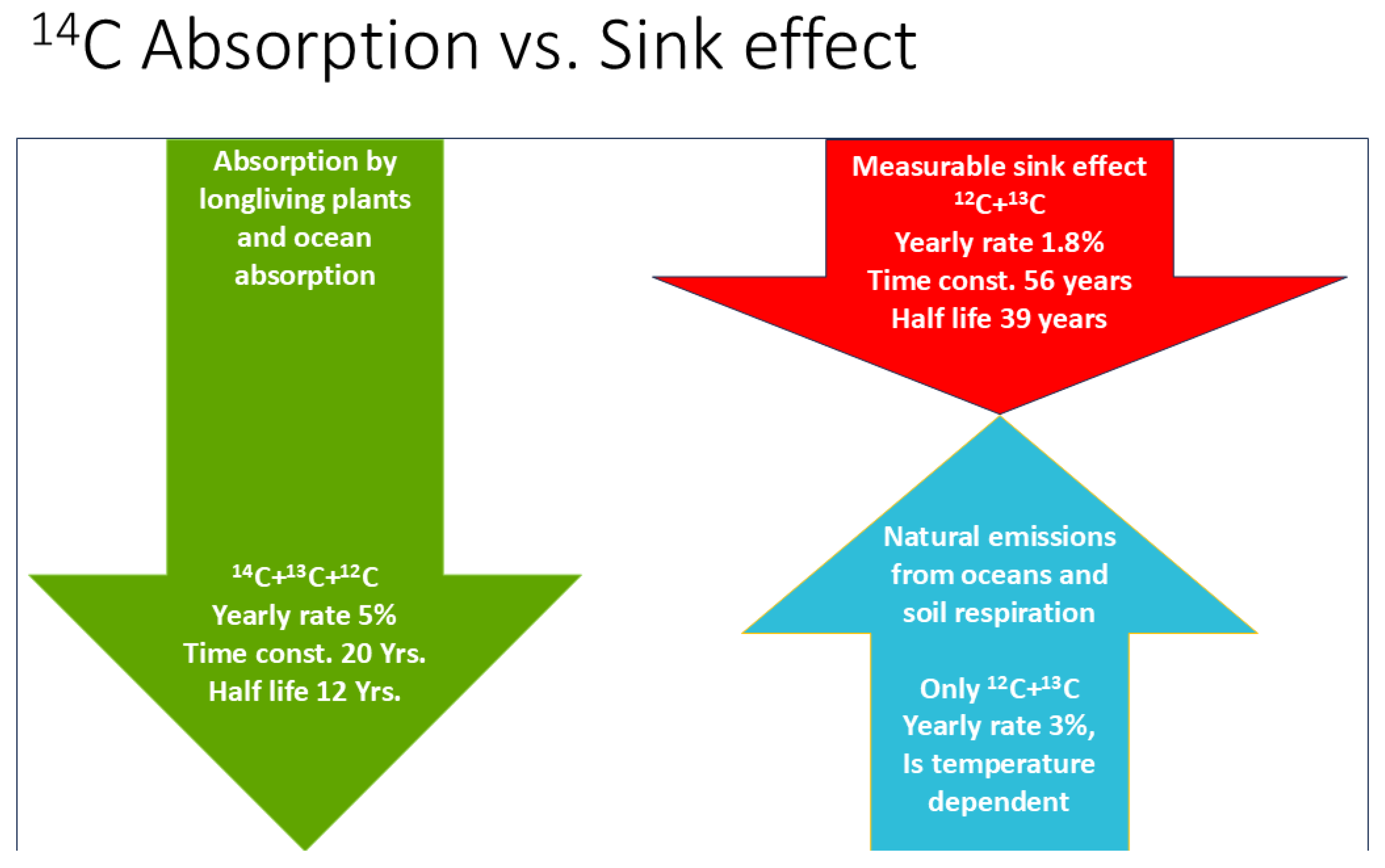
2.2.1. Estimating CO2 Absorption by Means of the Bomb Test Data
2.2.2. Estimating the Temperature Effect on Natural Emissions from Land Plants and Oceans
3. Results and Discussion
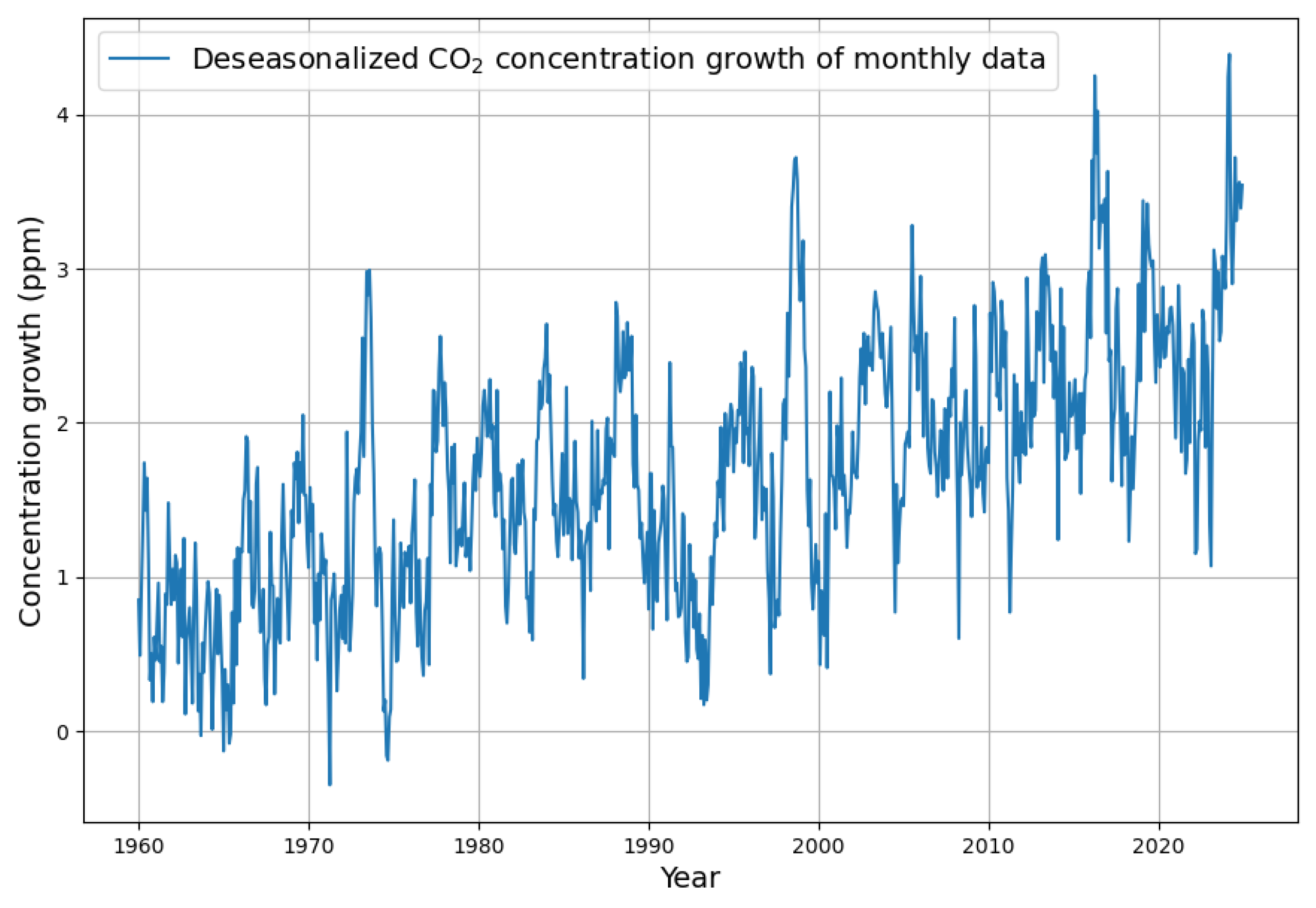
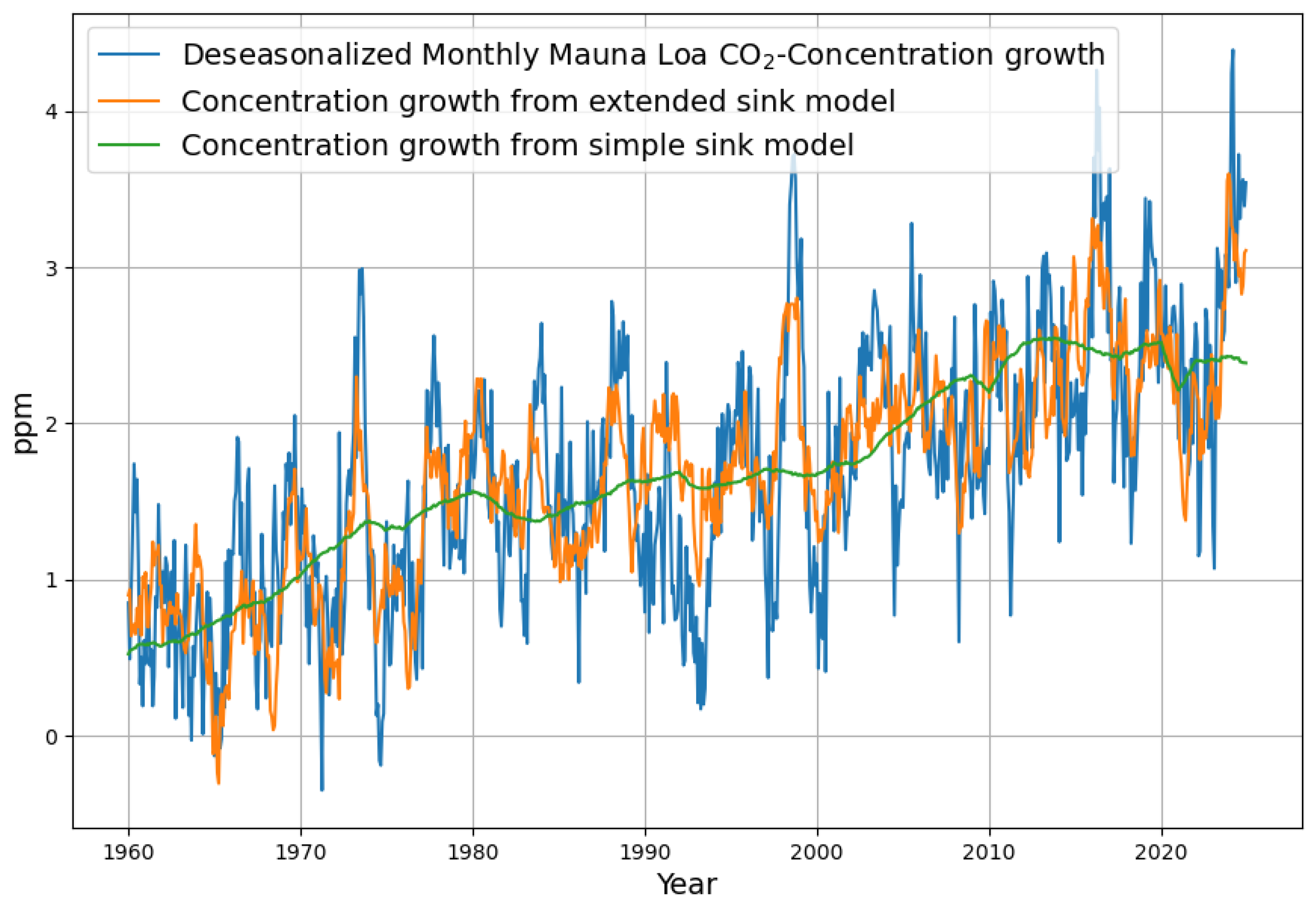
3.1. Formation and Analysis of the Monthly Increase in Concentration
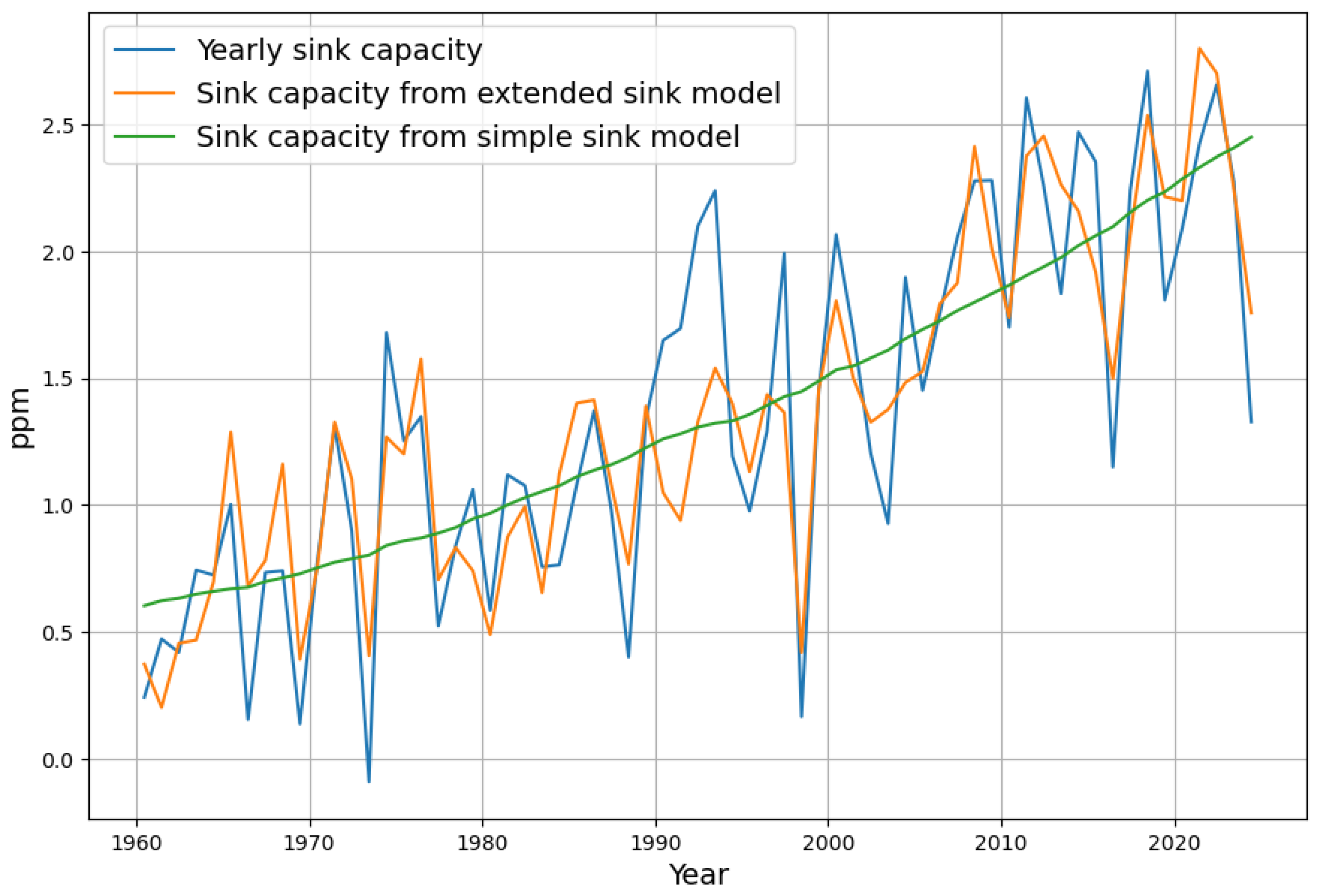
3.2. Evaluation of the Two Sink Models
3.2.1. Evaluation with the Simple Concentration-Dependent Sink Model
3.2.2. Evaluation with the Extended Concentration and Temperature-Dependent Sink Model
3.3. Comparing the Absorption Rate of the Extended Sink Model with the Decay Rate of the Bomb Test Data
3.4. Comparing the Temperature Coefficient of the Extended Model with the Empirical Natural Emissions
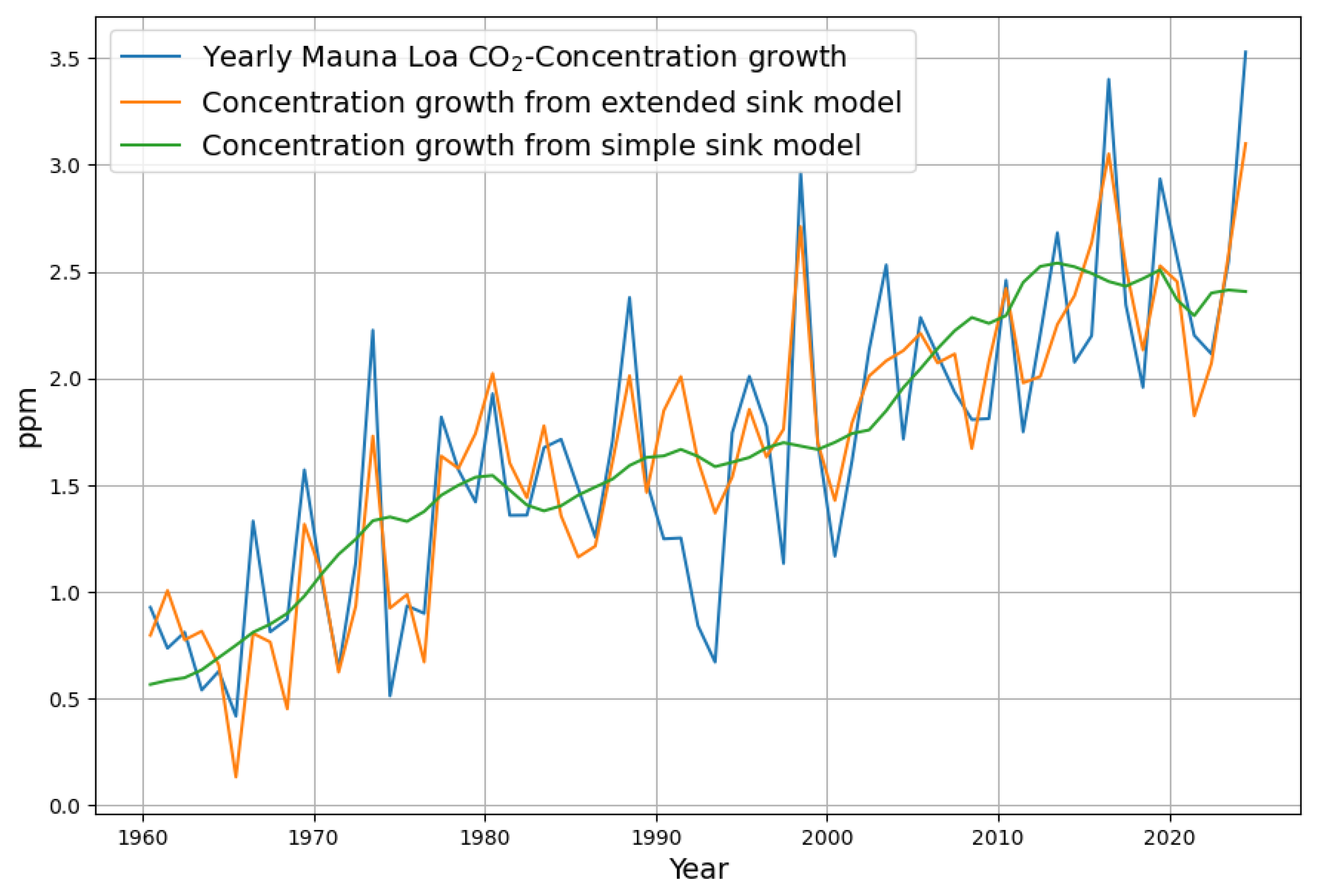
3.5. Reconstruction of the Concentration Growth from Both Sink Models
4. Conclusions
- The most obvious is the argument of some climate skeptics that anthropogenic emissions have no effect because they are apparently “drowned” in the huge natural carbon cycle. The fact is that anthropogenic emissions are a direct cause of concentration growth. Nature behaves as a strict net sink. This is obvious from Figure 7. Both models ended up with a significant, consistent net sink effect for the last 70 years when reliable data were available. Therefore, anthropogenic emissions must have significantly contributed to the total concentration growth. The extended model can hypothetically switch off the variability of natural emissions by setting the parameter for the temperature to 0. Alternatively, the anthropogenic emissions can be set to an arbitrary constant value so that only the temperature-controlled natural emissions control the concentration growth.
- Natural emissions by gardens, animals, and even agriculture, in general, are increasingly becoming a political target. As discussed, increasing natural emissions from biota are almost always a secondary consequence of a previous increase in photosynthesis and, therefore, NPP. But they are only a fraction of NPP. Therefore, extreme care has to be taken not to create more harm than good by carbon-related political interference with biota or agriculture. Mechanical agriculture and chemical contributions to agriculture are already accounted for by the measured anthropogenic emissions. It is, therefore, not legitimate to count them twice by attaching their effect to the biological product.
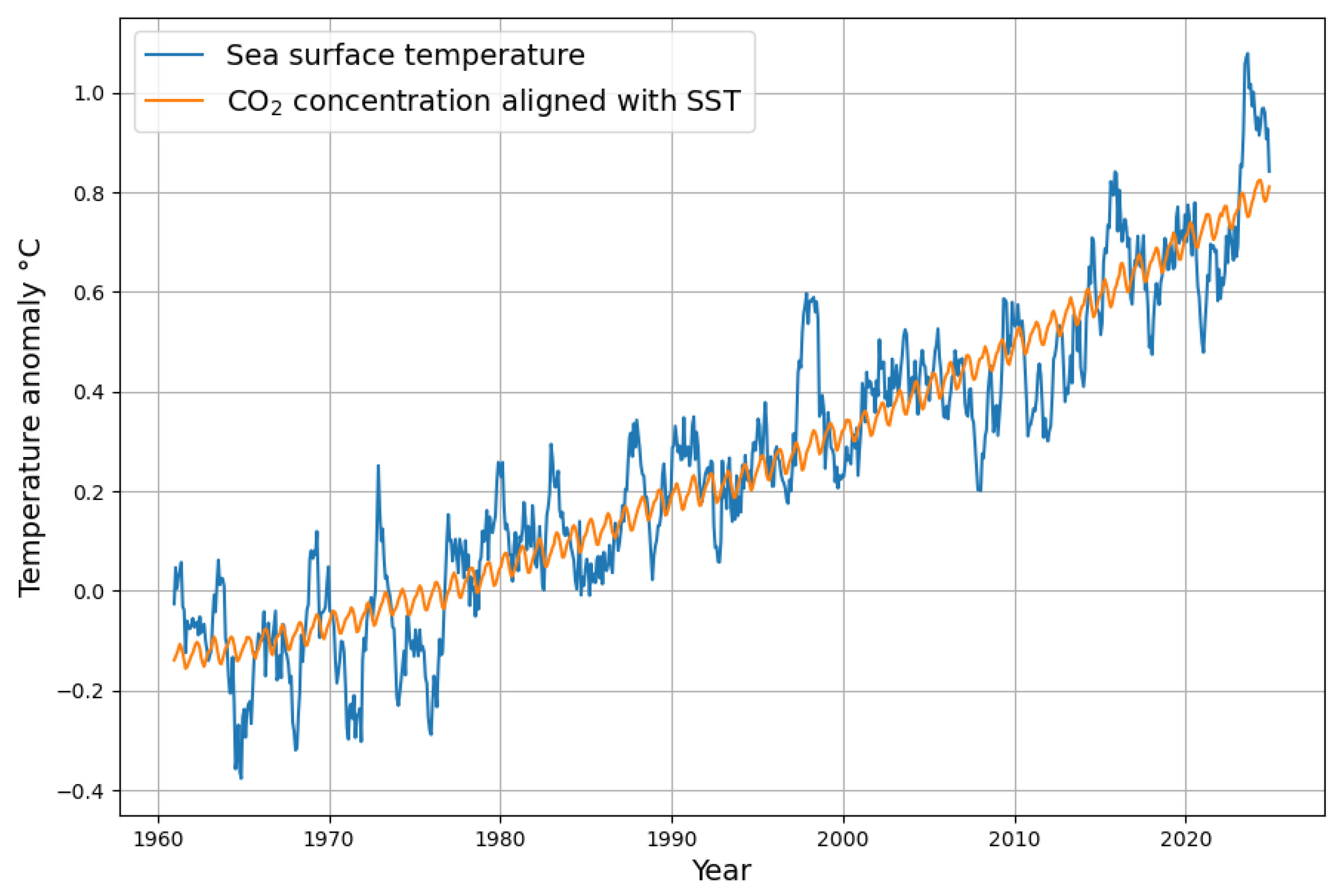
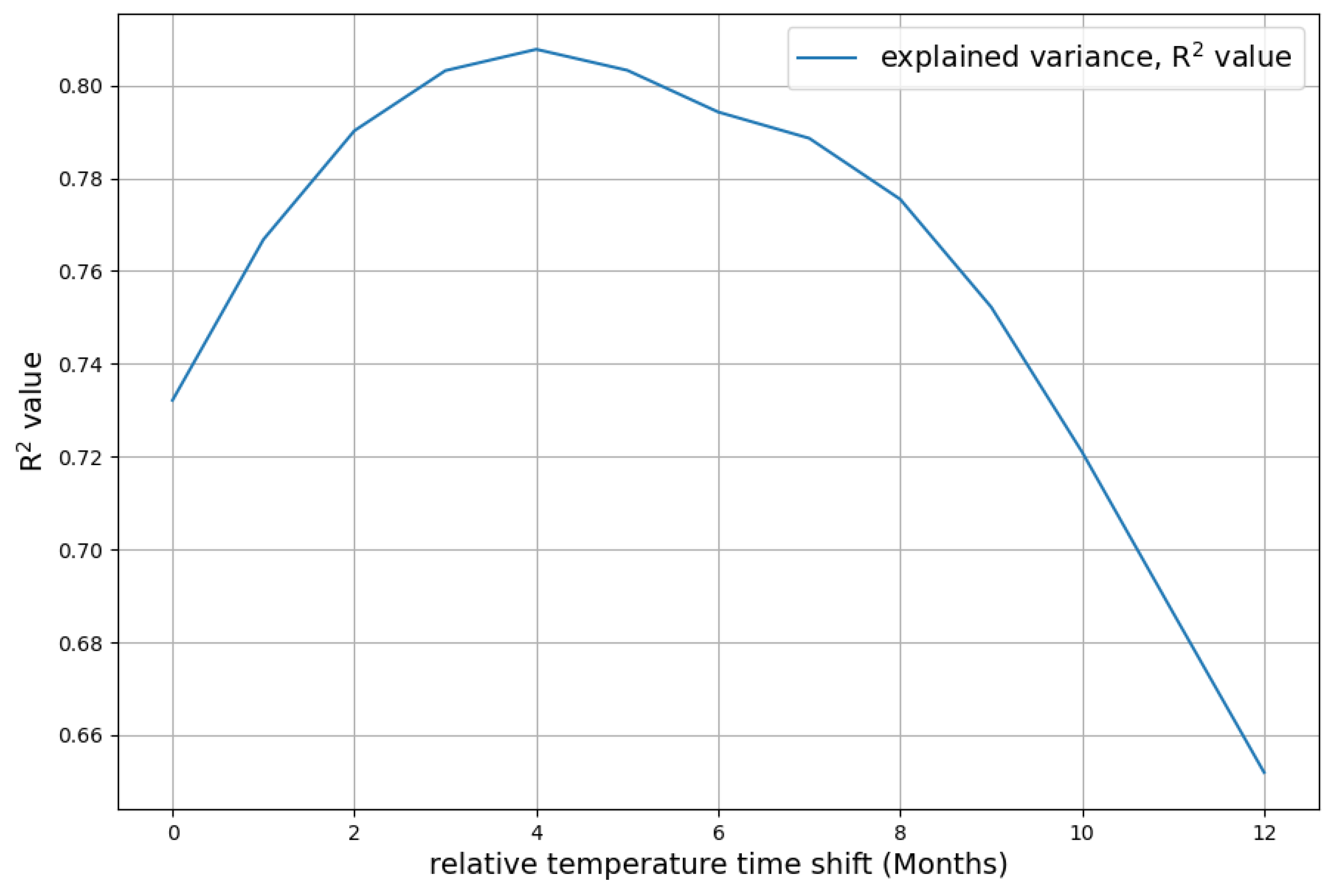
- The necessary time shift, where temperature change precedes changes in concentration change, is a clear statement of causality that, to a certain degree, concentration change follows temperature. Climate models should include this causality and honestly face the consequences. The most dramatic is that it leads in a natural way to a much higher absorption rate of the sink system than the currently accepted value.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NPP | Net Primary Production |
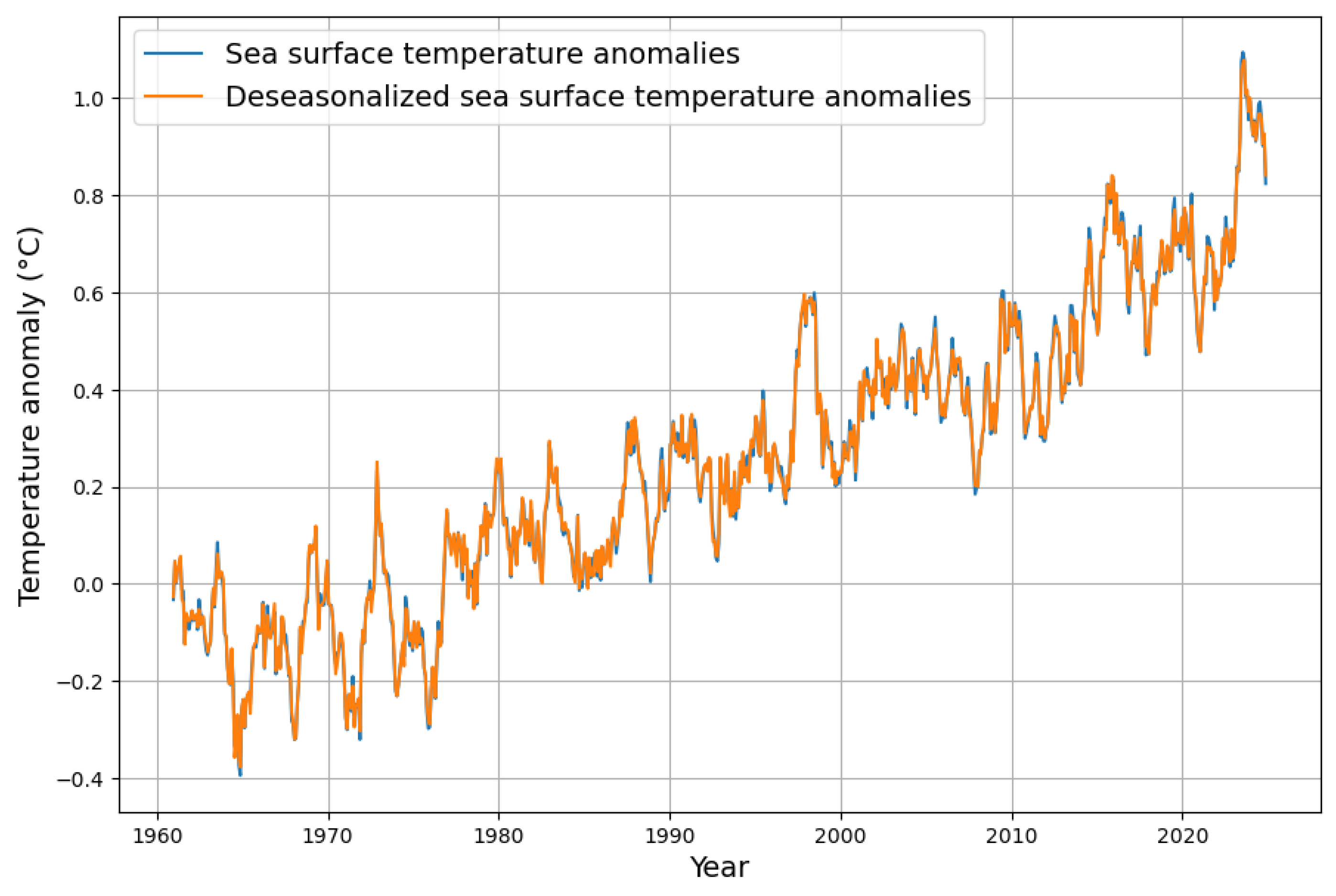
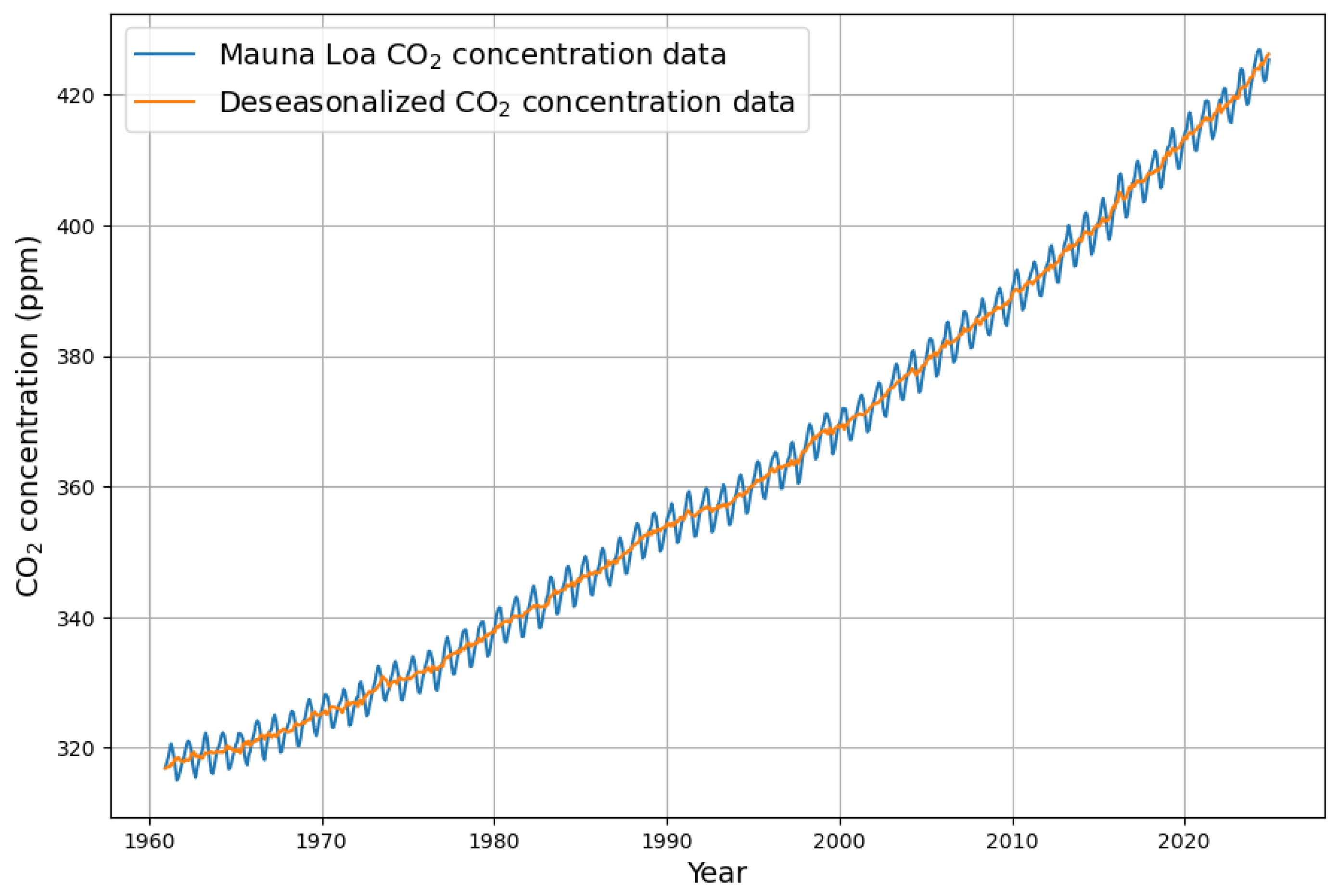
Appendix A. Computation Details of Deseasonalization
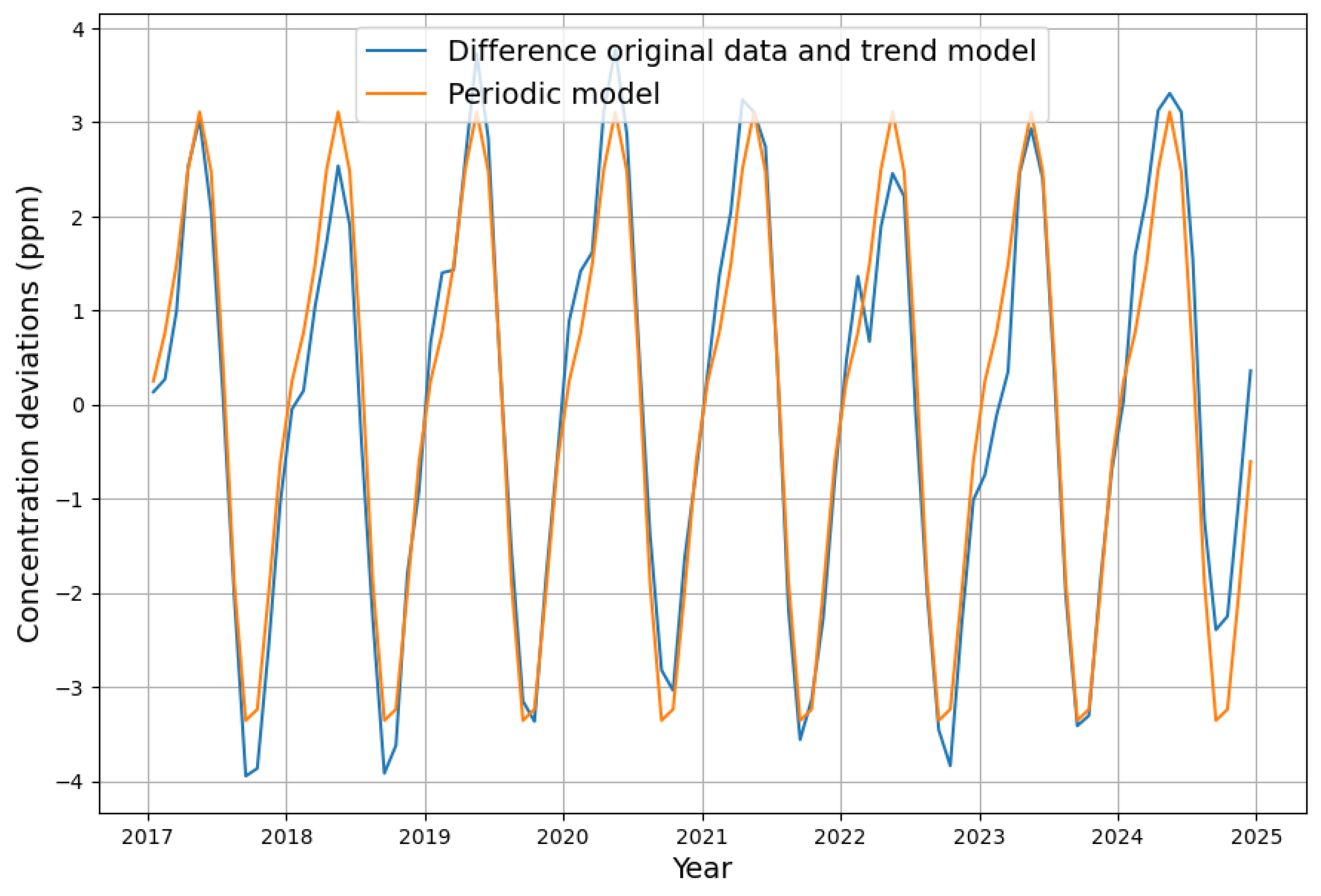

Appendix B. Deseasonalization of Concentration Growth

References
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Bakker, D.C.E.; Hauck, J.; Landschützer, P.; Le Quéré, C.; Luijkx, I.T.; Peters, G.P.; et al. Global Carbon Budget 2024. Earth Syst. Sci. Data Discuss. 2024, 2024, 1–133. [Google Scholar] [CrossRef]
- Ke, P.; Ciais, P.; Sitch, S.; Li, W.; Bastos, A.; Liu, Z.; Xu, Y.; Gui, X.; Bian, J.; Goll, D.S.; et al. Low latency carbon budget analysis reveals a large decline of the land carbon sink in 2023. Natl. Sci. Rev. 2024, 11, nwae367. [Google Scholar] [CrossRef] [PubMed]
- Bunsen, F.; Nissen, C.; Hauck, J. The Impact of Recent Climate Change on the Global Ocean Carbon Sink. Geophys. Res. Lett. 2024, 51, e2023GL107030. [Google Scholar] [CrossRef]
- Ruehr, S.; Keenan, T.F.; Williams, C.; Zhou, Y.; Lu, X.; Bastos, A.; Canadell, J.G.; Prentice, I.C.; Sitch, S.; Terrer, C. Evidence and attribution of the enhanced land carbon sink. Nat. Rev. Earth Environ. 2023, 4, 518–534. [Google Scholar] [CrossRef]
- Arora, V.K.; Katavouta, A.; Williams, R.G.; Jones, C.D.; Brovkin, V.; Friedlingstein, P.; Schwinger, J.; Bopp, L.; Boucher, O.; Cadule, P.; et al. Carbon-concentration and carbon-climate feedbacks in CMIP6 models and their comparison to CMIP5 models. Biogeosciences 2020, 17, 4173–4222. [Google Scholar] [CrossRef]
- Lai, J.; Kooijmans, L.M.J.; Sun, W.; Cho, A.; Xu, L.; Vesala, T.; Krol, M.C.; van der Laan-Luijkx, I.T.; Keronen, P.; Wofsy, S.C.; et al. Terrestrial photosynthesis inferred from plant carbonyl sulfide uptake. Nature 2024, 634, 855–861. [Google Scholar] [CrossRef] [PubMed]
- Spencer, R.W. ENSO Impact on the Declining CO2 Sink Rate. J. Mar. Sci. Res. Oceanogr. 2023, 6, 163–170. [Google Scholar] [CrossRef]
- Engelbeen, F.; Hannon, R.; Burton, D. The Human Contribution to Atmospheric Carbon Dioxide. 2024. Available online: https://co2coalition.org/wp-content/uploads/2024/12/Human-Contribution-to-Atmospheric-CO2-digital-compressed.pdf (accessed on 15 June 2025).
- Engelbeen, F. The Origin of the Increase of CO2 in the Atmosphere. 2022. Available online: http://www.ferdinand-engelbeen.be/klimaat/co2_origin.html (accessed on 15 June 2025).
- Dengler, J. Improvements and Extension of the Linear Carbon Sink Model. Atmosphere 2024, 15, 743. [Google Scholar] [CrossRef]
- NOAA. Trends in Atmospheric Carbon Dioxide (CO2). 2023. Available online: https://gml.noaa.gov/ccgg/trends/data.html (accessed on 15 June 2025).
- Kennedy, J.J.; Rayner, N.A.; Atkinson, C.P.; Killick, R.E. An ensemble data set of sea-surface temperature change from 1850: The Met Office1 Hadley Centre HadSST.4.0.0.0 data set. J. Geophys. Res. Atmos. 2019, 124, 7719–7763. [Google Scholar] [CrossRef]
- Hua, Q.; Turnbull, J.C.; Santos, G.M.; Rakowski, A.Z.; Ancapichun, S.; De Pol-Holz, R.; Hammer, S.; Lehman, S.J.; Levin, I.; Miller, J.B.; et al. Atmospheric Radiocarbon for the Period 1950–2019. Radiocarbon 2022, 64, 723–745. [Google Scholar] [CrossRef]
- Dengler, J.; Reid, J. Emissions and CO2 Concentration—An Evidence Based Approach. Atmosphere 2023, 14, 566. [Google Scholar] [CrossRef]
- Dietze, P. Carbon Model Calculations. 2001. Available online: https://web.archive.org/web/20250305084230/http://www.john-daly.com/dietze/cmodcalc.htm (accessed on 15 June 2025).
- Halparin, A. Simple Equation of Multi-Decadal Atmospheric Carbon Concentration Change. 2015. Available online: https://defyccc.com/docs/se/MDACC-Halperin.pdf (accessed on 15 June 2025).
- Dübal, H.; Vahrenholt, F. Oceans’ surface pH-value as an example of a reversible natural response to an anthropogenic perturbation. Ann. Mar. Sci. 2023, 7, 034–039. [Google Scholar] [CrossRef]
- Vollmer, M.; Eberhardt, W. A simple model for the prediction of CO2 concentrations in the atmosphere, depending on global CO2 emissions. Eur. J. Phys. 2024, 45, 025803. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Meacham-Hensold, K. The Difference Between C3 and C4 Plants. 2020. Available online: https://ripe.illinois.edu/blog/difference-between-c3-and-c4-plants (accessed on 15 June 2025).
- Haverd, V.; Smith, B.; Canadell, J.G.; Cuntz, M.; Mikaloff-Fletcher, S.; Farquhar, G.; Woodgate, W.; Briggs, P.R.; Trudinger, C.M. Higher than expected CO2 fertilization inferred from leaf to global observations. Glob. Change Biol. 2020, 26, 2390–2402. [Google Scholar] [CrossRef]
- Humlum, O.; Stordahl, K.; Solheim, J.E. The phase relation between atmospheric carbon dioxide and global temperature. Glob. Planet. Change 2013, 100, 51–69. [Google Scholar] [CrossRef]
- Richardson, M. Comment on “The phase relation between atmospheric carbon dioxide and global temperature” by Humlum, Stordahl and Solheim. Glob. Planet. Change 2013, 107, 226–228. [Google Scholar] [CrossRef]
- Wolter, K.; Timlin, M.S. El Nio/Southern Oscillation behaviour since 1871 as diagnosed in an extended multivariate ENSO index (MEI.ext). Int. J. Climatol. 2011, 31, 1074–1087. [Google Scholar] [CrossRef]
- Suess, H.E. Radiocarbon Concentration in Modern Wood. Science 1955, 122, 415–417. [Google Scholar] [CrossRef]
- Levin, I.; Kromer, B.; Schoch-Fischer, H.; Bruns, M.; Münnich, M.; Berdau, D.; Vogel, J.C.; Münnich, K.O. 25 Years of Tropospheric 14C Observations in Central Europe. Radiocarbon 1985, 27, 1–19. [Google Scholar] [CrossRef]
- Stuiver, M.; Polach, H.A. Discussion Reporting of 14C Data. Radiocarbon 1977, 19, 355–363. [Google Scholar] [CrossRef]
- Stuiver, M.; Quay, P. Atmospheric14C changes resulting from fossil fuel CO2 release and cosmic ray flux variability. Earth Planet. Sci. Lett. 1981, 53, 349–362. [Google Scholar] [CrossRef]
- Burton, D.A. Comment on Stallinga, P. (2023), Residence Time vs. Adjustment Time of Carbon Dioxide in the Atmosphere. 2024. Available online: https://osf.io/preprints/osf/brdq9_v2 (accessed on 15 June 2025).
- Graven, H.; Keeling, R.F.; Rogelj, J. Changes to Carbon Isotopes in Atmospheric CO2 Over the Industrial Era and Into the Future. Glob. Biogeochem. Cycles 2020, 34, e2019GB006170. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-Driven Increases in Global Terrestrial Net Primary Production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-Induced Reduction in Global Terrestrial Net Primary Production from 2000 Through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Bond-Lamberty, B.; Thomson, A. Temperature-associated increases in the global soil respiration record. Nature 2010, 464, 579–582. [Google Scholar] [CrossRef]
- Hashimoto, S.; Carvalhais, N.; Ito, A.; Migliavacca, M.; Nishina, K.; Reichstein, M. Global spatiotemporal distribution of soil respiration modeled using a global database. Biogeosciences 2015, 12, 4121–4132. [Google Scholar] [CrossRef]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef]
- Takahashi, T.; Olafsson, J.; Goddard, J.G.; Chipman, D.W.; Sutherland, S.C. Seasonal variation of CO2 and nutrients in the high-latitude surface oceans: A comparative study. Glob. Biogeochem. Cycles 1993, 7, 843–878. [Google Scholar] [CrossRef]
- Brownlee, J. How to Identify and Remove Seasonality from Time Series Data with Python. 2020. Available online: https://machinelearningmastery.com/time-series-seasonality-with-python/ (accessed on 15 June 2025).


| Metric | Shift | |||||||
|---|---|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| 0.5880 | 0.5886 | 0.5890 | 0.5895 | 0.5896 | 0.5897 | 0.5896 | 0.5895 | |
| 0.0175 | 0.0176 | 0.0176 | 0.0176 | 0.0176 | 0.0177 | 0.0177 | 0.0177 | |
| n | −4.93 | −4.94 | −4.95 | −4.96 | −4.97 | −4.97 | −4.98 | −4.99 |
| 282.2 | 282.7 | 283.2 | 283.7 | 284.1 | 284.5 | 284.9 | 285.2 | |
| Metric | Shift | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0.7321 | 0.7668 | 0.7902 | 0.8032 | 0.8078 | 0.8033 | 0.7943 | 0.7886 | 0.7755 | |
| a | 0.0456 | 0.0484 | 0.0497 | 0.0500 | 0.0497 | 0.0492 | 0.0485 | 0.0481 | 0.0475 |
| b | −3.12 | −3.45 | −3.61 | −3.66 | −3.63 | −3.59 | −3.51 | −3.49 | −3.42 |
| c | −14.20 | −15.13 | −15.58 | −15.69 | −15.57 | −15.42 | −15.18 | −15.07 | −14.85 |
| 311.8 | 312.9 | 313.5 | 313.6 | 313.5 | 313.4 | 313.2 | 313.1 | 312.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dengler, J. Evaluating the Effectiveness of Natural Carbon Sinks Through a Temperature-Dependent Model. Appl. Sci. 2025, 15, 6907. https://doi.org/10.3390/app15126907
Dengler J. Evaluating the Effectiveness of Natural Carbon Sinks Through a Temperature-Dependent Model. Applied Sciences. 2025; 15(12):6907. https://doi.org/10.3390/app15126907
Chicago/Turabian StyleDengler, Joachim. 2025. "Evaluating the Effectiveness of Natural Carbon Sinks Through a Temperature-Dependent Model" Applied Sciences 15, no. 12: 6907. https://doi.org/10.3390/app15126907
APA StyleDengler, J. (2025). Evaluating the Effectiveness of Natural Carbon Sinks Through a Temperature-Dependent Model. Applied Sciences, 15(12), 6907. https://doi.org/10.3390/app15126907