Abstract
This report analyzes the different standard methods of quantity measurement, which, when applied in the processes of receiving and transferring fuel quantities, lead to discrepancies and accounting losses. Three main factors contribute to these discrepancies: unavoidable errors of measuring devices (calibration uncertainty ranging from 0.1 to 0.5% at best), systematic errors due to non-applied corrections during transactions, and systematic errors due to different regulations, which result in inconsistent conversion rules applied throughout the entire purchase-production-sales chain. Modeling of air buoyancy effects showed that neglecting buoyancy correction can lead to measurable and economically significant discrepancies, especially in large-scale operations. The mass of light petroleum products can be underestimated by up to 0.15%, potentially resulting in approximately $3 million in annual financial losses for a medium-sized refinery processing 10,000 tonnes per day. These findings underscore the necessity of applying buoyancy corrections for conventional weighing, especially for liquid petroleum products (LPP) measured in open systems. Conversely, for LPG weighed in closed, pressurized containers, a constant correction factor (0.99985) applies, but its economic impact is negligible. Therefore, the study recommends omitting this LPG correction unless contractually required, to streamline processes and reduce complexity. Achieving result comparability throughout the entire petroleum supply chain requires implementing uniform quantity calculation provisions using calibrated instruments and standardized methods under different conditions. This necessitates that all measurement results are traceable to reference conditions (mass in vacuum, volume at +15 °C). The proposed algorithms for oil mass and volume measurement and recalculation highlight the need for unified international regulations and a robust system.
1. Introduction
The fuel industry is fundamentally dependent on the uniform interpretation and application of mass and volume measurement methods. This uniformity is not only a technical aspect; it is essential to ensure fair transactions and transparent pricing, which in turn promotes trust between companies, regulators, and investors and fosters a stable and reliable market [1]. In essence, accurate metrology is the foundation for economic equilibrium in the oil sector [2]. Research has continuously addressed this need by improving oil metering methods to increase accuracy [3] and by utilizing advanced data analysis to provide better insights into fuel consumption patterns, trends, and optimization opportunities [4]. Referenced articles delineate best practices for accurately determining true volume or mass values in commercial transactions [5], while other researchers emphasize the critical need for conformity assessment [6] and strategies to mitigate erroneous assessments during petroleum product transfer [7]. However, a significant gap remains in the comprehensive analysis of strategies to reduce accounting losses directly attributable to fundamental differences in measurement methods [5,8]. Our study addresses this gap.
In standard fuel quantity acceptance and transfer processes, quantity is evaluated using volumetric, gravimetric, and geometric methods. The constant recalculations between volume and mass, driven by available equipment or software, introduce complexity. Each measurement instrument category possesses distinct and variable error characteristics, and while instruments comply with legal requirements, their inherent accuracy differences, especially between static and dynamic modes (e.g., dynamic mass systems ranging from 0.2 to 2% [9]), create an environment ripe for discrepancies. This variability and the resulting measurement errors directly disrupt the economic symmetry of transactions. Even seemingly small errors, when applied to the large volumes common in the petroleum industry, can create a significant asymmetry where one party experiences a financial gain solely due to measurement inaccuracy, while the other incurs a corresponding loss. To illustrate, consider a company producing 100,000 barrels per day. A seemingly minor 0.1% measurement error translates to 100 barrels. At an oil price of $80 per barrel, this represents a $8000 daily loss. In large-scale transactions involving tankers or pipelines, even small measurement errors can lead to losses of thousands of dollars.
Ongoing efforts across various international organizations on standardization, accreditation, and metrology aim to overcome hurdles and achieve greater consistency in fuel measurement practices [10]. By creating international (ISO) and European (CEN) standards, these organizations work to ensure uniform quality and safety in petroleum processes and products [11]. The International Organization of Legal Metrology (OIML), the European Committee for Standardization (CEN), the European Cooperation in Legal Metrology (WELMEC), and the European Association of National Metrology Institutes (EURAMET) develop and harmonize metrology guidelines. These guidelines cover issues related to the selection and testing of measuring instruments and encompass the assessment of oil and petroleum product quantities using various methods [12]. Specialized international and national institutions, such as the American Society for Testing and Materials (ASTM), the American Petroleum Institute (API), the Energy Institute (EI) in London, the National Measurement Institute of Australia (NMIA), and others, play an important role in this regulation process [13,14]. ASTM is the leading organization working in the oil industry [15]. A practical example of implementing ASTM D1250 in the oil industry is its use in converting the volume of crude oil and petroleum products to standardized conditions [16]. For instance, when a refinery or storage facility measures crude oil at a high ambient temperature, they use ASTM D1250 tables to adjust the observed volume to a standard reference temperature of 60 °F (15.6 °C) [16]. For consistent operations, uniform measurement methods and instruments of consistent accuracy must be applied, along with unified metrological supervision. However, while the application of standardized measurement methods and instruments is vital, it does not inherently resolve the challenge of method selection and application across the entire supply chain, especially in individual stages of oil purchase and sale, where methods may differ based on operational needs.
The implementation of international, national standards is not mandatory until it falls within national legal acts (cited standards, standard identification number, name provided) or international agreements are signed for their implementation [17,18].
Despite ongoing efforts by international standardization organizations and specialized bodies to harmonize metrology guidelines, national legislation often lacks consistent [19], clear requirements for mass in air or vacuum, as well as clear guidelines for conversion of calculations and presentation of results when using different measurement principles [20,21].
In Europe, the standard pressure and temperature reference conditions for measuring petroleum products, oils, greases, and gases are 101.325 kPa and 15 °C [22,23,24]. In Canada and Australia, however, different standard pressures may be used when measuring petroleum products [25,26]. Norway sets the accuracy with which mass or volume must be measured and regulates when corrections must be made; for instance, a correction is required if the deviation exceeds 0.02% of the total volume [27]. Legal requirements for expressing measurement results aren’t always consistent or logically justified. For example, accounting rules [28] might demand converting liquefied petroleum gas (LPG) mass to volume at ambient temperature, even when LPG excise duties [29] are based on tonnes. This creates unnecessary recalculations and potential discrepancies. An analysis of measurement result protocols and applicable oil volume regulations at a specific company, conducted during a particular project, revealed an issue: mass isn’t consistently converted to volume at ambient temperature, despite this being a requirement of petroleum product accounting rules [30]. These discrepancies can lead to inaccurate inventory management, erroneous financial reporting, and potential regulatory compliance issues.
Regulatory and methodological uncertainty at the national level is also a shortcoming of current practice, preventing full transparency and comparability throughout the oil supply chain.
Figure 1 illustrates a typical, generalized oil processing workflow for a medium-sized regional oil refinery. In Stage 1, the raw material is received through pipelines (where mass is determined using a volumetric method) as well as via rail and trucks (where mass is weighed, and volume is not calculated). Stage 2 involves processing activities, resulting in the production of fuel oil, diesel, LPG, and bitumen, which are then stored in tanks. The internal processes within Stage 2 use the volumetric method to measure volume. Some measuring instruments provide volume measurements, while others quantify in kilograms or tonnes (with a summary provided in tonnes). In Stage 3, petroleum products, LPG, and bitumen are sold by weight, which is determined through weighing. The volume of light petroleum is measured and then converted into mass for final sale and transport in tank trucks. As evident from this workflow, various measurement methods and expressions of quantity are employed. Therefore, it is crucial for all involved parties to reach a consensus on the measurement of quantity, submission of results, and the conversion between mass and volume.
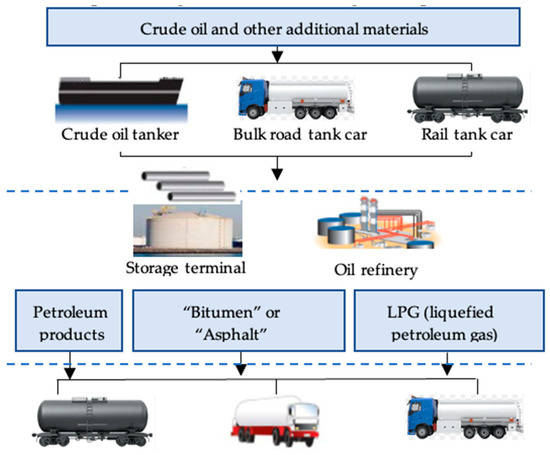
Figure 1.
An example crude oil processing workflow.
This report aims to ensure consistent mass and volume measurement and conversion in oil refining processes. We’ll achieve this by conducting a comparative analysis of standardized weighing, volumetric, and geometric measurement methods used in these operations. To reach our goal, we’ll identify the need to assess instrument corrections, including those for buoyancy, temperature, and other factors dependent on the instrument, method, and measurement conditions. To this end, we’ll develop consistent algorithms for evaluating results and provide proposals for expressing them, thereby ensuring comparability of results throughout the oil supply chain. Through situational modeling, we’ll identify loss reduction trends and offer recommendations for minimizing losses. The analysis of these methods will be linked to measuring instruments and systems employed in oil refining processes, as well as to materials of various densities, including:
- -
- LPP (such as gasoline, diesel, kerosene, etc.) is widely used as fuel in vehicles, industry, and heating.
- -
- LPG, primarily composed of propane and butane, is used as fuel for cars, residential heating, cooking, and industrial applications.
- -
- Liquid-phase bitumen, a viscous, black, and sticky material derived from oil refining, is widely used in road construction, roofing, and waterproofing.
This report focuses on single transfers between distinct loading/unloading points, not on repeated measurements, mass monitoring, or complex flow system analyses that would involve indirect measurements. We believe that the single measurement result is most influenced by the equipment used and its errors. Other systematic errors due to environmental conditions must be managed.
2. Principles of Mass and Volume Evaluation in the Petroleum Industry
Physical principles of volume and mass estimation are presented in Figure 2. The fundamental physical principles governing volume and mass estimation are as follows:

Figure 2.
Physical principles of volume and mass evaluation [31].
- -
- Temperature dependence: Mass remains invariant with temperature variations, while volume and density are subject to change. Specifically, an elevation in temperature typically results in an increase in volume and a decrease in density; conversely, a reduction in temperature leads to a decrease in volume and an increase in density. Critically, the intrinsic mass of the substance remains constant throughout these temperature-induced fluctuations.
- -
- Mass measurement in vacuum: The mass of a substance measured in vacuum at a given temperature can be approximated by calculating the product of its volume and density at that temperature. The main reason for any discrepancy between this calculated mass and the measured mass is the accuracy of the instruments used in each measurement method.
To compare quantities measured under different conditions (temperature, pressure, and density), these factors must be corrected for the reference temperature (15 °C, 15.6 °C, and 20 °C) according to the requirements of international standardization and the oil industry, as well as national legislation, with reference to ASTM D1250 [16].
Generally, the following methods are employed to estimate product quantity:
- -
- The weighing method, considered the primary (direct) mass determination method, is the most utilized [9,32]. The method is preferred when high accuracy is essential. Weighing instruments directly measure apparent mass.
- -
- The volumetric method is considered a secondary, indirect method [12]. This method employs various meters and volume measures. Mass is evaluated indirectly. Typically, the volumetric flow rate or total volume of a liquid passing through devices, along with temperature and density, is measured and then converted to a mass value.
- -
- The geometric volume measurement allows for the indirect determination of mass, particularly when fill level, tank geometric parameters, fluid temperature, and density are known. This method is recommended for the calibration, verification, or volume measurement of liquid products in underground or aboveground, horizontal or vertical storage tanks [33,34,35,36,37], as it enables accurate and consistent volume determination without direct weighing. This approach is especially advantageous for large storage tanks where direct mass measurement is impractical.
Principles for the Loading and Unloading of Raw Materials and Products: Measurement Peculiarities Within the Company
Raw material or product quantities are measured using three commonly employed methods, as detailed in Table 1.

Table 1.
Methods used and corrections made: mass, volumetric, and geometric methods.
Using the weighing method, the gross mass (vehicle and fuel) and the empty vehicle mass are measured. The net mass is calculated as the difference between the full and empty container weights. The fuel mass is then expressed in metric tonnes (in air and vacuum) and recorded in the weighing programs of railway and road tankers, including weighing reports and acceptance documents (acceptance certificates). Measuring instruments used in dynamic and static modes are detailed in Table 2, where d represents the scale division value, e the verification scale division value, and Max the maximum weighing capacity.

Table 2.
Typical weighing instruments and their characteristics.
Volume flow measured by meters is multiplied by density and a volumetric temperature coefficient to calculate mass. For the implementation of this method, the measuring instruments employed for the determination of volume, density, and temperature are presented in Table 3.

Table 3.
Measuring instruments for the volumetric and geometric mass estimation method.
The geometric method is implemented by calculating the volume of a tank based on its geometric parameters. Subsequently, the mass is derived by multiplying the volume by the density and temperature coefficient. The quantity is measured before and after loading the tank, and the difference in quantities is calculated. The following data are recorded: mass (in metric tonnes) in air and vacuum, gross mass (including impurities) and net mass (excluding impurities), US barrels at 60 °F, m3 at 15 °C and 20 °C, oil density at 15 °C and 20 °C, and oil temperature. The measuring instruments used are presented in Table 3. Oil density is measured using the method described in ASTM D5002-16 [39].
All measuring instruments correspond to the modern, improved-accuracy equipment held by a typical medium-sized fuel processing company today. For further analysis, we assume that all measuring instruments have been verified or calibrated. Their calibration results (systematic error plus uncertainty) comply with the ISO 17025 [40] standard’s decision rule, meaning they fall within the permissible error limits specified in Table 2 and Table 3.
3. Mass Evaluation of Petroleum Products Using Weighing Methods
During the mass measurement of petroleum products, specifically when weighing them, the terms “mass in vacuum” and “mass in air” are used. When a product is weighed under normal conditions, the weighing process fails to consider that the product displaces air, leading to a measured mass value that is lower than the actual mass (mass in air). This “mass in air,” also referred to as conventional mass, is the value indicated by the weighing instrument.
3.1. Mass Measurement of LPP
The mass of LPP and LPG is obtained by weighing them in the tank, whose mass is known. The mass of LPP is calculated as the difference between the filled tank and empty tank masses:
Mass (Gross) = Empty (Tare) mass + Contents mass (Net),
Contents mass (Net) = Mass (Gross) − Empty (Tare) mass or
where m is the mass of LPP (Net), kg, mgross is the gross mass (weight indicated by the weighing instrument: tare + product), kg, and mt is the empty (Tare) mass, kg.
Because the weighing instrument indicates a value that is proportional to the gravitational force on the object reduced by the buoyancy in air, the instrument’s indication in general has to be corrected for the buoyancy effect [41]. The value of this correction depends on the density of the object (petroleum product) and the density of air [42].
When evaluating a product’s mass in vacuum value, there is a need to convert the mass of liquid petroleum indicated on a weighing instrument to mass in vacuum, in which case air buoyancy corrections shall be made according to the equation [41]:
where mvac is the mass in vacuum value of LPP, kg, and C is the buoyancy correction coefficient. Coefficient C, is given by the equation:
where ρa is the reference density of air value—equal to 1.2 kg/m3, ρr is the reference density of calibration weight—8000 kg/m3 (according to [41]), ρv is the density of gas or vapor that is displaced when the container/vessel/tank is filled, ρ is the density of the LPP. Since the density of air (which has a relatively large value of about 1.2 kg/m3) can change due to pressure, temperature, or humidity, it may be necessary to consider those factors.
When a liquid product is weighed in an open container/vessel/tank, then the gas displaced can be air, and then ρv will be equal to ρa, thus Equation (3) can be expressed as:
Buoyancy corrections are adjustments made to account for the effect of air buoyancy when measuring the mass of an object in air. These corrections convert the conventional mass indicated by a weighing instrument to the mass in vacuum, where no buoyant force from the air is present. This process compensates for the reduction in weight due to the displacement of air by the object and ensures that the measured mass accurately reflects the object’s mass without external buoyant influences.
As mentioned before, product density depends on the temperature. For buoyancy correction, the density of the product at the observed temperature should be used, but usually the density from the product quality certificate, where it is given at +15 °C temperature, is used. To determine the influence of the density dependence on temperature on the result (i.e., mass in vacuum), we assume that the density of petrol ranges from 740 kg/m3 (at 15 °C) up to 745 kg/m3 (at 10 °C) [43]. This density change, due to the temperature change of 5 °C, influences the result by only 0.001%. This can be considered an extremely small value. If the density is measured at a factual temperature, it can be corrected to the density at 15 °C using ASTM Tables 53 [44]. According to the OIML G19 [45], the density is defined as the ratio of product mass (mass in vacuum) and its volume. Thus, we consider that the density specified in the certificates (determined by any method) is the density in vacuum. The diagram for direct product mass evaluation by weighing is given in Figure 3.
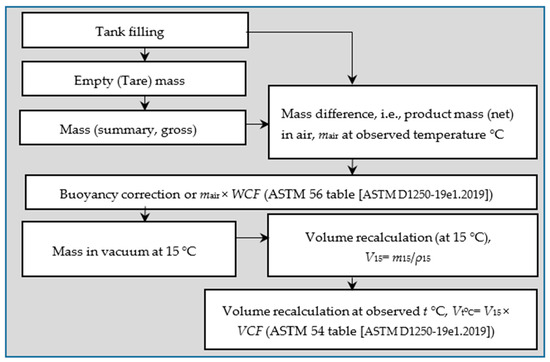
Figure 3.
Diagram of LPP mass evaluation (volume recalculation) using weighing method, where mair—product mass (net) in air at observed temperature; WCF—weight correction factor; V15—recalculated volume (at 15 °C), m15—product mass at 15 °C; ρ15—product density at 15 °C; Vt °C—recalculated volume at observed temperature; VCF—volumetric correction factor; ASTM D1250-19e1.2019—[16].
Considering that mass evaluation is performed using wide-range weighing instruments, let’s discuss a scenario where the scale error is e = ±10 kg at approximately 10 tonnes (corresponding to the tare mass of a rail tank car) and e = ±50 kg at 100 tonnes (corresponding to the gross mass of a full fuel rail tank car). Other data used: petroleum product density 740 kg/m3, air density 1.2 kg/m3, reference weight density 8000 kg/m. The scenario is chosen according to the significant measurement range presented in Table 2. Using the root sum squared (RSS) method, we can calculate the combined standard uncertainty for the net mass estimation from formula (1).
The standard uncertainty for the net mass is approximately 0.1%. The corrected mass in vacuum, where C is 1.00147, is equal to The expanded uncertainty is calculated by multiplying the combined standard uncertainty by the coverage factor k, which corresponds to a rectangular distribution with a 95% coverage probability:
This indicates that the scale error is dominant for the weighing method. The correction does not increase the error; it simply increases the calculated mass in vacuum. As the net mass decreases to 20 t, the standard uncertainty for the net mass increases, and when considering the mass in vacuum, it rises by approximately 4%.
Although the scale error is larger than this specific impact of air density change, the buoyancy correction algorithm removes a fundamental physical influence that consistently affects mass measurements in air. The algorithm allows for the conversion of ‘mass in the air’ to ‘mass in vacuum’, regardless of the initial weighing instrument’s precision. This process is critical for obtaining an accurate and standardized mass evaluation, which is subsequently used for volume recalculation.
3.2. Mass Measurement of LPG
In the case of LPG, a closed hermetic tank (pressure vessel) is weighed. Measured mass comprises the mass of both liquid product and vapours inside. The resultant mass of LPG is calculated as difference between filled tank and empty tank masses as shown in Equation (1). A closed tank that is filled with LPG has a stable mass despite temperature or liquid and saturated gaseous phase changes [46]. With a temperature change, the liquid gas will expand or contract, and thus the amount of saturated gas in the tank will change; however, the total amount of energy will remain the same. This means that the measured mass will not change. Considering OIML R 125 [47], in a closed tank (e.g., LPG weighing case) ρv = 0 as no vapor is displaced. Then, the above-mentioned Equation (2) can be expressed as:
A correction factor of 0.99985 is used to estimate the mass of LPG under vacuum in a closed container. The indication of the weighing instrument without correction in this case is the conventional mass [47], which is determined by the characteristics of the weighing instrument and the ambient conditions. Correction coefficient 0.99985 is universal and it does not depend on the type of used weighing instrument, cargo mass, product composition or measurement units. When LPG is weighed, then its amount has to be converted into liters using density ρ15°C, LPG factual temperature T °C and coefficient VCFT:
where VT°C—LPG volume at factual temperature, m—LPG mass, VCF—LPG volume recalculation, from factual temperature to the +15 °C, coefficient, ρ15°C—LPG density at +15 °C (from LPG quality certificate or measured in laboratory). A diagram of the volumetric correction factor (VCF) dependency on change of density and temperature is presented in Figure 4.
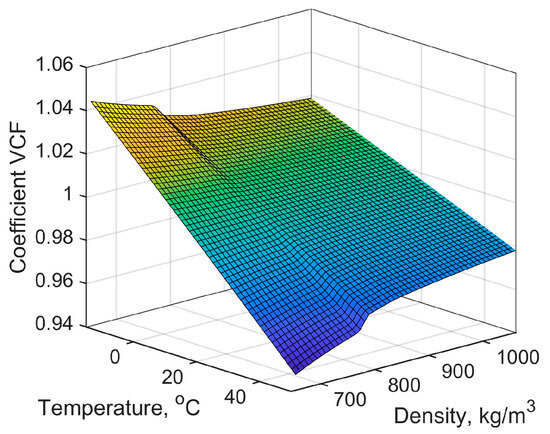
Figure 4.
VCF coefficient variation dependency on change of density and temperature.
VCF coefficient is equal to the ratio of density at factual temperature and density at reference (+15 °C) temperature . Its variation is calculated according to ASTM 54B tables (for petroleum products) [16] and the following conditions: density range 653–1075 kg/m3; temperature range −15–50 °C.
According to the Figure 4 VCF varies with the density of the petroleum product. As density changes (due to product type or composition), the VCF adjusts to account for how much the volume shifts under temperature changes. Temperature fluctuations directly impact the VCF. As temperature increases or decreases, the VCF changes to reflect the corresponding expansion or contraction of the petroleum product volume. This adjustment is critical for accurate volume measurement, as temperature-induced expansion or contraction can lead to significant variations in perceived volume. Figure 4 thus provides insight into the sensitivity of the VCF to different densities and temperatures, emphasizing the importance of applying accurate VCF adjustments in petroleum measurement to ensure reliable data across varying operational conditions.
3.3. Mass Measurement of Bitumen
The mass of liquid bitumen indicated on a weighing instrument has to be converted to the buoyancy-corrected mass using Equation (2). Buoyancy factor C is calculated using Equation (4). Values of volume correction factor for bitumen mass recalculation to the volume are given in the short table of ASTM D 4311 standard [48].
4. Measurement of Petroleum Product Quantity Using Volumetric and Geometric Volume Measurement Method
When evaluating product mass by volumetric and geometric volume measurement methods, mass is calculated using the results from several direct measurements. Using the volumetric and geometric volume measurement method, mass m of LPP in the tank is calculated using the following equation:
where V is measured product volume, l, ρ is measured product density, kg/L.
When using the geometric method, the LPP volume in stationary tanks is determined by using level measurements together with the tank graduation tables [31]. For the volumetric method, the meter is used for the volume flow (debit) measurement. In addition, temperature and density are measured, and then mass is calculated [49,50].
A model for mass recalculation that evaluates the influence of volume, density, and temperature is given below [12,51]:
where tm is the temperature of LPP, V is product’s volume at temperature tm, ρ is measured product’s density at temperature tm, α is the coefficient of cubical thermal expansion, t is reference temperature. Under the conditions, when the assumed standard temperature is +15 °C, every 5 °C deviation from the standard temperature causes about 0.5% mass change, and respectively, each 10 °C deviation causes—0.95% mass change. This is a significant influence on the measurement result. In all applicable standards and recommendations main temperature correction aspects are discussed [52,53].
Petroleum products quantification stages, using the volumetric/geometric method, are presented in Figure 5. A systematic review of the volumetric/geometric approach is presented here, highlighting the importance of accurate environmental corrections for accurate estimation in the petroleum industry. The main steps of this method are initial volume measurement, temperature and pressure regulation, density determination, and volume-to-mass conversion.
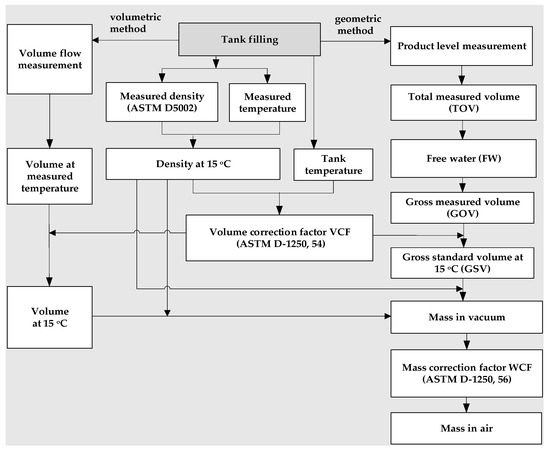
Figure 5.
Petroleum products quantification stages, using a volumetric/geometric method, where ASTM D-1250, 54—[16]; ASTM D-1250, 56—[16].
The product volume at 15 °C temperature can be determined according to ASTM Table 54, using tank graduation table and correcting measured temperature to the reference temperature (usually 15 °C). Tank graduation tables are used to convert level measurement (in millimeters) to volume (in liters). Measured product density is also recalculated to the reference temperature. For this purpose, ASTM Table 53 may be used [44].
According to Equation (7), the calculated mass is called the product mass in vacuum. To calculate product mass in air, a weight correction factor (WCF) is used, which is selected from ASTM Table 56 [12,54]. The weight correction factor can be calculated if the density in the vacuum and the density in the air are known [31]:
where: ρa is product density in air, kg/L, ρvac is product density in vacuum, kg/L.
Let’s consider two methods, volumetric (flow) and geometric, discussing the instruments used, their errors, and the effectiveness of the proposed algorithm. Assume the following instruments and their accuracies are used to implement the volumetric method: the rotary chamber volume meter with an accuracy of ±0.3%; the temperature sensor with an accuracy of ±0.1 °C; and the density meter with an accuracy of ±0.5 kg/m3 (with a density of 0.820 g/cm3). The volume range is 25 m3 to 125 m3, and the cubical thermal expansion coefficient for petroleum products is 950 × 10−6 1/°C. Applying the root sum squared (RSS) method, we can derive the expanded uncertainty for mass estimation based on formula (10). The expanded uncertainty is calculated by multiplying the combined standard uncertainty by the coverage factor k for a rectangular distribution at a 95% confidence level:
In this context, the relative influence coefficients for each constituent are equal to 1, and , .
The following data is used in the error analysis of the geometric method: the volume measurement error (using the graduation tables) is ±0.2%; the product volume ranges widely from 0 to 56,000 m3; the temperature sensor accuracy is ±0.5 °C; the density meter accuracy is ±0.6 kg/m3, with an average density of 850 kg/m3. The expanded uncertainty for mass estimation using the geometric method is calculated according to formula (12) and is equal to: .
Using specific measuring instruments, the volumetric and geometric methods allow for the determination of mass with an expanded uncertainty of less than or equal to 0.5%, which is acceptable by OIML R 117 [55]. Despite the temperature sensor’s accuracy, the petroleum product’s thermal expansion coefficient of 950 × 10−6 1/°C means that even relatively small temperature deviations from the reference temperature cause a significant volume/mass change (approximately 0.5% for a 5 °C change). The algorithm effectively manages this correction.
The algorithm consistently converts mass measured in air to a final mass, even when initial measurements are performed with different instruments and under varying environmental conditions. This is crucial for ensuring the accuracy and comparability of reports.
5. Modeling of Existing Processes and Situations. Results and Discussion
5.1. Simulation of Changes in Air Buoyancy Coefficient C
Buoyancy is a force acting on a body that is in a gaseous or liquid medium, directed opposite to the force of gravity, the latter arising due to Earth’s gravity. In mass measurements, the effect of buoyancy is equal to the mass of the displaced medium corresponding to the volume occupied by the weighed body. The buoyancy coefficient, provided in formulas (3) and (4), reflects this change in body mass, taking into account the buoyancy of the steel reference weights used during the calibration of scales in the air. The influence of individual components on the buoyancy coefficient C was analyzed through modeling: when weighing oil or oil products in an unsealed container and applying formula (4) for buoyancy evaluation, the effects of air density ρa, weight density ρr, and the density of the oil product ρ were modeled.
5.1.1. Negligible Effect of Steel Standard Weight Density
Due to a very large difference in the density of steel standard weight and air, the influence of standard weight density, which is assumed to be 8000 kg/m3 [37,56], is negligible. This assumption is based on a simulated density range of (7000–9000) kg/m3. Since the influence of this component is negligible and can be ignored, for further simulation, it was constant and equal to 8000 kg/m3 [57].
5.1.2. Air Density Variability with Temperature, Pressure, and Humidity
Air density due to temperature, pressure, and relative humidity can vary within the following limits: 0.88 kg/m3 at 35 °C, pressure 80 kPa, relative air humidity from 100% to 1.50 kg/m3; at −30 °C, pressure 105 kPa at any relative humidity. The simulation incorporates a range of air densities from 0.8 to 1.6 kg/m3 to capture these potential variations.
5.1.3. Density Range of Oil and Petroleum Products
Company’s production and raw material range determine the density of the oil or petroleum product. During the simulation over the total product density range, which can vary from light oil to heavy oil, the overlap was analyzed for the range of (600–1000) kg/m3.
5.1.4. Buoyancy Coefficient Dependency on Air and Petroleum Product Density
Figure 6a shows the dependency of the buoyancy coefficient in air on the density of air and petroleum products. Figure 6b shows two sections of this plane.
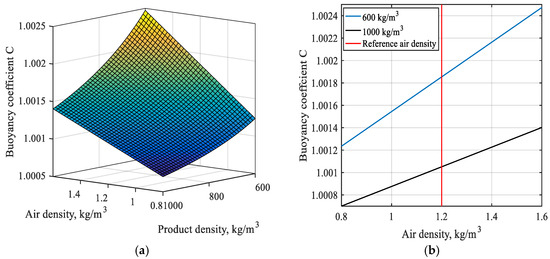
Figure 6.
(a) Simulation of changes in air buoyancy coefficient C, (b) Simulation of changes in air buoyancy coefficient C: individual cases.
The presented graphs highlight these facts:
- The dependency of the buoyancy coefficient on air density is linear, whereas this dependency on the density of the product is non-linear.
- Range of the buoyancy coefficient values is: 1.0007–1.0025 or (0.07–0.25) %.
- The lighter the product is (i.e., the lower its density) and the higher the density of air, the greater the buoyancy effect.
5.1.5. Maximum Buoyancy Effect
The following conclusion can be drawn when air density is the highest (1.6 kg/m3, −30 °C, 105 kPa) and petroleum product is the lightest (600 kg/m3), the maximum buoyancy effect will be 0.25%. Under the real operating conditions, buoyancy correction will be approximately 0.15% (for light oil). Therefore, mass of the product, when m = 100 t is weighed in air, after correction will be: , where mD is the mass value, taking into account the maximum correction for air buoyancy, CD is the maximum air buoyancy correction coefficient, CR is the real (typical) correction for air buoyancy, mR is the mass value when the real (typical) correction for air buoyancy is estimated.
5.2. Analysis of Measurement and Conversion of Quantity at Different Stages of Purchase-Production-Sale
5.2.1. Mass Discrepancies in Air Versus Vacuum Conditions
Assuming a constant air density of 1.2 kg/m3, buoyancy correction decreases as the density of the product increases. This means that the difference between the same mass in air and in a vacuum is smaller. If the change in mass for light oil is 0.15%, at a density of 1000 kg/m3 and higher, the change in mass is 0.1% or smaller. These changes, resulting from the introduction of buoyancy corrections, can be regarded as significant in the same order of magnitude as the errors of the measuring instruments used (0.1–0.5)%. Correcting for these variations is essential in reporting and financial transactions to prevent unintended discrepancies.
5.2.2. Economic Implications of Buoyancy Corrections in Petroleum Sales
When calculating mass without buoyancy adjustments, the resulting mass in air is lower than the mass in a vacuum, leading to potential financial losses for suppliers. This discrepancy implies that sellers may be transferring more product weight than is compensated for, particularly in large-scale transactions.
Figure 7 shows the dependency of mass change on production volumes. For the simulation, products of different densities were selected, namely light oil, heavy oil, and bitumen, with densities of 600 kg/m3, 1000 kg/m3, and 1500 kg/m3, respectively.
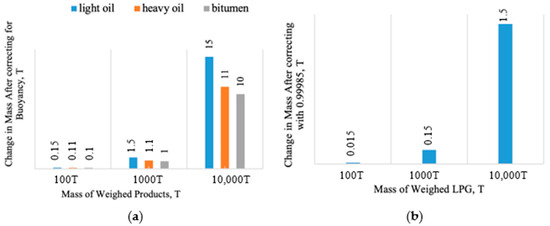
Figure 7.
Changes in mass resulting from air buoyancy correction (supplier loss) (a) and correction factor of 0.99985 for LPG (client loss) (b).
Quantities of these products. The interval from 100 tonnes to 10,000 tonnes is selected for analysis. The results at the top of Figure 7 show that the compensated mass depends on the properties of the product being weighed and the quantity of the product. The lower the density of the product, the greater the losses can be. When weighing small quantities of any product, smaller losses are obtained. When the quantities weighed are from 100 tonnes to 10,000 tonnes, losses can increase from 0.15 tonnes to 150 tonnes. The results presented at the bottom of Figure 7 show how the compensated mass can change with varying quantities of LPG. This means that without inputting the correction factor of 0.99985 for LPG, the client’s losses can increase from 0.015 tons to 1.5 tonnes as the weighed quantity of LPG increases from 100 tonnes to 10,000 tonnes.
5.2.3. Specific Mass Changes Due to Buoyancy Corrections
The mass variations due to buoyancy corrections are as follows:
- For light and heavy oils: Changes range from 110 to 150 kg per 100 tonnes (mass corresponds to one-day measurement with one type of measuring instrument), from 1.1 t to 1.5 t per 1000 tonnes, and 11 t to 15 t per 10,000 tonnes.
- For bitumen: Mass changes are about 100 kg per 100 tonnes and 10 t per 10,000 tonnes.
These mass changes have direct implications for pricing and customer satisfaction. Variations in measured mass can lead to pricing inconsistencies, affecting both the profitability for suppliers and the perceived fairness for customers, particularly in high-volume transactions. Addressing these variations through standardized correction protocols could enhance customer confidence and satisfaction while promoting fair pricing practices across markets.
5.2.4. Specific Corrections for LPG Mass Measurements
After applying a correction factor of 0.99985 [47] when weighing LPG, the mass under vacuum is smaller than the measured value. Figure 7 shows the resulting mass changes due to this correction factor. During LPG weighing, if the specified correction factor is not entered, it turns out to be overweight. This overage translates to 15 kg in 100 tonnes, 150 kg in 1000 tonnes, and 1.5 t in 10,000 tonnes.
By correcting the weight of LPG by a factor of 0.99985, a smaller mass is obtained. If the correction factor isn’t applied, the customer might pay for excess weight, resulting in a potential financial loss. The significance of these adjustments fluctuates based on the volume of transactions, and companies must evaluate the impact based on monthly, seasonal, or annual purchase-sales volumes. The company itself must consider not only the volume of production but also the price and make the final decision on the significance of the loss.
5.2.5. Impacts on Raw Material Purchases and Sales of Petroleum Products
Corrections that are applied at different stages of the purchase-production-sell process are discussed (Figure 8). When purchasing raw materials or selling products, it is important to follow the general rules for the calculation of the same quantity (Section 2) throughout the purchasing and production chain. Otherwise, any conversions will result in systematic errors, which will accumulate depending on the number of conversions. Specific situations are analyzed by the features of these steps. A negative balance arises when raw materials are purchased based on their mass in a vacuum, while sales are determined by their apparent mass in air. If the mass in air is converted to volume at the same temperature without applying the buoyancy correction, it results in a volume error of 0.14%.
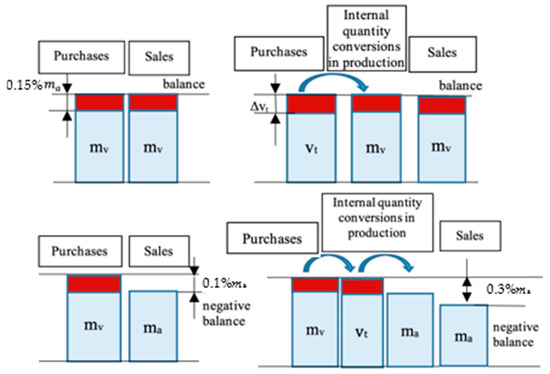
Figure 8.
Balance of products obtained by weighing LPP products or using a volumetric method to estimate mass at different stages of the purchase-production-sell.
This error can be eliminated by converting the mass in vacuum at a specific temperature to volume at the same temperature.
5.2.6. Factors Contributing to Measurement Discrepancies
Three main factors contribute to discrepancies when measuring liquid petroleum product quantities. First, measuring instrument errors are simply unavoidable; however, the company chooses the most accurate and practical measurement methods available. Second, systematic errors from unapplied corrections pop up when essential corrections aren’t made during the buying or selling of liquid petroleum products. Finally, systematic errors from differing regulations happen because of inconsistent rules about applying or not applying corrections and coefficients for presenting measurement results and for converting mass to volume and vice versa throughout the company’s entire purchase, production, and sales process.
5.2.7. Importance of Consistent Reference Conditions in Mass and Volume Calculations
For each goods movement, mass and/or volume should be calculated under reference conditions, considering observed (measured) density and temperature values. This mass and volume calculation method enables clearly defined rules and a basis for price and fee determination, ensuring that “everybody” accepts the stated amount of petroleum product. Volume calculation under reference conditions is achieved using mass in vacuum using the weight correction factor (WCF). Calculation under reference conditions ensures the universally accepted and stated quantity of the petroleum product, aiding in fair and accurate transactions across the entire supply chain.
5.2.8. Practical Potential Implications of Recommendations
Key recommendations include mandating consistent buoyancy correction coefficients and uniform reference conditions for temperature and pressure across the industry. Companies should integrate buoyancy correction protocols, train staff in proper adjustments, and use precise instruments, especially in high-volume transactions. Consistent corrections minimize financial errors, enhance transparency, and prevent losses. Standardized corrections ensure fairness, align with regulations, and promote confidence in trade, benefiting the entire supply chain. A detailed financial analysis of implementing standardized correction protocols could further underscore their importance.
6. Conclusions
This report highlights that comparing quantities measured under diverse environmental conditions (like air temperature, pressure, and density) and with different instruments necessitates establishing normative conditions, especially for temperature. This must align with international and oil industry standards, as well as national regulations. To ensure accurate comparisons, quantitative measurement results (lithe ke volume and weight) require adjustment using specific correction factors. Physically, we can directly compare mass measured by instruments and converted to mass in a vacuum at a reference temperature with mass indirectly calculated from volume and density at the same standard temperature. Any disparities between these masses primarily arise from the precision of the various measuring instruments used for each method. Our proposed consistent result evaluation sequences and result expression methods, based on standardized approaches, ensure the comparability of results obtained through different means and methods. Crucially, all these conclusions hold only when the instruments used meet the characteristics outlined in the standards [9,38,55] and their performance is confirmed through calibration or, if required by legal metrology, through verification procedures.
The simulation of the air buoyancy correction coefficient and its impact on measurement outcomes indicates that buoyancy has a more pronounced effect on the measurement of light petroleum than on heavy petroleum. As a result, the mass in a vacuum rises by 0.15% for light petroleum and by 0.1% for heavy petroleum. These changes are notable, especially in relation to the measurement errors of the instruments used, which range between 0.1% and 0.5%. This implies potential losses between 11 and 15 tonnes per ten thousand tonnes when weighing light and heavy petroleum. Therefore, we acknowledge the significant effect of buoyancy correction on the measurement results of LPP and recommend that any weighing result be corrected by calculating the mass in vacuum. Ultimately, the decision to incorporate buoyancy corrections for weighing petroleum products should be made by the company itself, taking into consideration the actual losses incurred in the broader context of income and costs. The potential financial losses due to neglecting buoyancy correction in a medium-sized refinery can be substantial, reaching approximately $3 million per year in this scenario. Assume that the refinery processes 10,000 tonnes of petroleum products daily, and the average petroleum price for both light and heavy petroleum is $650 per tonne. This highlights the importance of implementing buoyancy correction for accurate mass determination and accounting.
Based on this study, the buoyancy factor is not applicable when weighing LPG in a closed pressure vessel. This is due to the specific properties of the liquid mixture, saturated vapor, and the weighing method used. However, a correction factor of 0.99985 must be applied to the measured result, known as the conventional mass. This correction factor remains constant and does not vary with the type of measuring instrument, the weight of the load, the product composition, or the units of measurement used in the calculation. Consequently, the calculated mass in vacuum in the case of LPG weighing will be lower by approximately 0.015% of the measured value, equivalent to 1.5 tonnes per 10,000 tonnes in favor of the LPG supplier. Its financial impact on a medium-sized refinery is relatively small, approximately $130,000 per year in this scenario. Given that this correction factor is not legally mandated in many countries, and its impact is minor compared to other potential sources of error and loss in the petroleum industry, we recommend against applying it for LPG weighing. This simplifies measurement processes and avoids unnecessary adjustments, especially considering the potential for confusion and disputes that could arise from applying a non-mandatory correction. However, it is crucial for companies to be aware of this potential discrepancy and to have clear contractual agreements with suppliers and customers regarding the measurement and reporting of LPG quantities. Transparency and consistency in measurement practices are essential for maintaining trust and fairness in the petroleum trade.
Although we acknowledge that the buoyancy coefficient does not affect the mass value of LPG in closed tanks, this does not apply to corrections related to the calibration or adjustment of weighing instruments. Therefore, a company’s loss management strategy should include investments in higher-precision measuring instruments (e.g., static weighing scales for cars and wagons with a verification scale division value of 20 kg, and 0.2% dynamic weighing scales for wagons). Additionally, regular maintenance of these instruments is crucial. Measurement errors can be reduced by applying known corrections to individual measurement results through calibration and verification protocols. If there are systematic positive or negative deviations in measuring instruments, or if the weighing errors exceed their verification scale interval, a correction may be applied to the measurement results. The results may be uncorrectable if average weighing errors are smaller than the verification scale interval. Ideally, weighing errors should be randomly distributed within the permissible error range for individual measurements. For all operations where applicable, it is advisable to use scales of the same accuracy class, with the same verification scale division value and weighing mode [58,59].
To eliminate inconsistencies arising from the application of air buoyancy corrections and to ensure consistent mass-to-volume conversions in petroleum transactions, it is recommended to establish clear and unequivocal requirements for measurement protocols and the reporting of results. For comparable quantities, only unambiguous results, expressed in consistent units and representing the same physical property, should be compared. When comparing weighing results, direct comparisons (in terms of physical quantities) are valid: (where and represent weighing results in air).
For comparisons between weighing results and volume: , , , ;
For comparisons between volume and weighing results: , , , ;
For comparisons between two volume measurements: , (where , —mass determined by weighing in air, —air buoyancy correction factor, , , —mass of product in vacuum (corrected for air buoyancy), —product density at 15 °C, —volume of product (corrected to reference temperature), , —volume of product at temperature t, , —volume of product corrected to 15 °C, , —volumetric correction factor (used to convert volume at temperature t to volume at 15 °C)).
To ensure the company’s material balance (when purchasing raw materials, in internal production processes, and when selling products) and to minimize losses, it is crucial to adhere to general, uniform quantity calculation provisions throughout the entire purchase-production-sales chain. This means that in all cases, it is necessary to calculate the mass in vacuum and the volume at +15 °C, regardless of whether direct weighing with scales or indirect mass recalculation from volume and density is applied.
This study emphasizes the critical role of precise metrology in the petroleum industry, advocating for standardized measurement protocols and the application of correction factors to minimize accounting losses and enhance trade transparency. It highlights the necessity for stakeholder consensus on measurement methodologies, aligning with international standards and physical principles. To achieve this, investment in high-precision technology and advanced data analytics is recommended. Furthermore, the research underscores the importance of regulatory harmonization to address jurisdictional discrepancies, proposing future investigations into legislative and technological advancements. Ultimately, the implementation of these recommendations will foster a more stable, equitable, and reliable global petroleum market.
Author Contributions
Conceptualization, A.M. and P.K.; methodology, A.M.; validation, E.R. and J.D.; formal analysis, J.D.; investigation, P.K.; data curation, B.G.U.; writing—original draft preparation, B.G.U.; writing—review and editing, E.R. and B.G.U.; visualization, P.K. and E.R.; supervision, A.M.; project administration, J.D.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by economic entity under Contract No. SV9-2823.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
| LPG | Liquefied petroleum gas |
| ISO | International Organization for Standardization |
| OIML | International Organization of Legal Metrology |
| CEN | European Committee for Standardization |
| WELMEC | European Cooperation in Legal Metrology |
| EURAMET | European Association of National Metrology Institutes |
| ASTM | American Society for Testing and Materials |
| API | American Petroleum Institute |
| NMIA | National Measurement Institute of Australia |
| WTO | World Trade Organization |
| LPP | Liquid petroleum products |
References
- Elcio Cruz de Oliveira, A.; Nogueira Frota, M.; de Oliveira Barreto, G. Use of data reconciliation: A strategy for improving the accuracy in gas flow measurements. J. Nat. Gas Sci. Eng. 2015, 22, 313–320. [Google Scholar] [CrossRef]
- Suwaidan, K. Custody measurement best practices. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 10–13 March 2013. [Google Scholar]
- McGlade, C.E. A review of the uncertainties in estimates of global oil resources. Energy 2012, 47, 262–270. [Google Scholar] [CrossRef]
- Sadri, M.; Shariatipour, S.M.; Hunt, A.; Ahmadinia, M. Effect of systematic and random flow measurement errors on history matching: A case study on oil and wet gas reservoirs. J. Pet. Explor. Prod. Technol. 2019, 9, 2853–2862. [Google Scholar] [CrossRef]
- Lincoln de Souza Filho, P.; de Oliveira, E.C.; Aramaki, L.T. Maximum permissible differences in LPG operations for custody transfer measurements. Measurement 2022, 191, 110805. [Google Scholar] [CrossRef]
- de Oliveira, E.C.; Orsay, G.L.; Medeiros, K.A.R. Conformity assessment applied to custody transfer in the oil and gas industry: A brief review. In Proceedings of the Congresso Brasileiro de Metrologia, Itaipava, Brazil, 28–30 November 2023. [Google Scholar]
- de Oliveira, E.C.; Lourenço, F.R. Risk of false conformity assessment applied to automotive fuel analysis: A multiparameter approach. Chemosphere 2021, 263, 128265. [Google Scholar] [CrossRef]
- Samoilenko, O. Mathematical model of the petroleum products mass balancing in their supply network through the detection of excessive losses by the least squares method. Eng. Res. Express 2023, 5, 13. [Google Scholar] [CrossRef]
- OIML R 106: 2024 (E); Automatic Rail-Weighbridges. Part 1: Metrological and Technical Requirements—Tests. TC 9/SC 2 Automatic Weighing Instruments. Bureau International de Métrologie Légale: Paris, France, 2024; p. 79.
- Harmes-Liedtke, U.; Oteiza Di Matteo, J.J. Measurement and performance of Quality Infrastructure a proposal for a global quality infrastructure index. Buenos Aires Duisburg 2019, 1, 19. [Google Scholar] [CrossRef]
- ISO 6578:2017(E); Refrigerated Hydrocarbon Liquids-Static Measurement-Calculation Procedure. ISO/TC 28/SC 5-Measurement of Refrigerated Hydrocarbon and Non-Petroleum Based Liquefied Gaseous Fuels. International Organization for Standardization: Geneva, Switzerland, 2017; p. 25.
- EURAMET. Guidelines on the Determination of Uncertainty in Gravimetric Volume Calibration; EURAMET Calibration Guide No. 19 Version 3.0; EURAMET: Braunschweig, Germany, 2018; p. 26. [Google Scholar]
- Kishore Nadkarni, R.A. Guide to ASTM Test Methods for the Analysis of Petroleum Products and Lubricants, 2nd ed.; ASTM Manual Series; ASTM International: West Conshohocken, PA, USA, 2007; Volume l44-2nd, p. 299. [Google Scholar]
- American Petroleum Institute (API). Petroleum Measurement Manual of Petroleum Measurement Standards; American Petroleum Institute: Washington, DC, USA, 2022; p. 23. [Google Scholar]
- The Global Leader in Additive Manufacturing Standards. ASTM International USA. 2021. [Online]. Available online: https://amcoe.org/wp-content/uploads/2022/05/Additive-Manufacturing-Sector-Overview.pdf (accessed on 12 May 2025).
- ASTM D1250-19e1; Standard Guide for the Use of the Joint API and ASTM Adjunct for Temperature and Pressure Volume Correction Factors for Generalized Crude Oils, Refined Products, and Lubricating Oils: API MPMS Chapter 11.1. ASTM International: West Conshohocken, PA, USA, 2019.
- Whalley, J. World Trade Organization, International Encyclopedia of the Social &Behavioral Sciences; Elsevier: Amsterdam, The Netherlands, 2001; pp. 16613–16616. [Google Scholar]
- Using and Referencing ISO and IEC Standards to Support Public Policy; ISO/IEC: Geneva, Switzerland, 2015; p. 53.
- Bulletin V-10. Volume Correction Factors of Non-Petroleum Products Authorized for Use with Liquid Measuring Meters. Government of Canada, 2008. [Online]. Available online: https://ised-isde.canada.ca/site/measurement-canada/en/laws-and-requirements/v-10-volume-correction-factors-non-petroleum-products-authorized-use-liquid-measuring-meters (accessed on 7 April 2025).
- Directive 017: Measurement Requirements for Oil and Gas Operations. Alberta Energy Regulator, 2022. [Online]. Available online: https://static.aer.ca/prd/documents/directives/Directive017.pdf (accessed on 10 March 2025).
- Guidelines for Submitting Data from Exploration, Development & Production Activities in a Petroleum Right. State of Israel; Ministry of Energy Natural Resources Administration: Jerusalem, Israel, 2018; p. 32.
- NFPA 59A-2019; Standard for the Production, Storage, and Handling of Liquefied Natural Gas (LNG). NFPA: Quincy, MA, USA, 2019; p. 97.
- Mace, P.; Leckie, D.; Gray, L.; Blumenthal, D.; Desgranges, I.; Anthony, D.; Day, J.; Clyde & Co LLP. Oil and Gas Regulation in the UK: Overview, Country Q&A, UK. 2017. [Online]. Available online: https://uk.practicallaw.thomsonreuters.com/w-029-3584?transitionType=Default&contextData=(sc.Default) (accessed on 10 March 2025).
- Repsol. General Terms & Conditions for Sales and Purchases of Crude Oil & Petroleum Products; Repsol: Madrid, Spain, 2017; p. 107, [Online]; Available online: https://www.repsol.es/content/dam/images-ecommerce/empresas/vvdd/bunker-on-shore/general-terms-conditions-sales-purchases-2020_tcm19-176636.pdf (accessed on 10 March 2025).
- Weights and Measures Regulations C.R.C., c. 1605. Weights and Measures Act. Minister of Justice, Government of Canada, 2019. [Online]. Available online: https://laws-lois.justice.gc.ca/eng/regulations/C.R.C.,_c._1605/index.html (accessed on 10 March 2025).
- Australian Taxation Office Legislative Instrument, Instrument ID: 2016/ITX/0038. Excise (Volume of LPG—Temperature and Pressure Correction) Determination 2016 (No. 1). Australian Government, 2016. [Online]. Available online: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://www.ato.gov.au/law/view/pdf%3FDocId%3DESE%252FEDES20162%252F00001%26filename%3Dlaw%252Fview%252Fpdf%252Fese%252Fesed2016-002.pdf%26PiT%3D99991231235958&ved=2ahUKEwjH3LpazPiNAxVVA9sEHXZUJnsQFnoECB0QAQ&usg=AOvVaw2yZvNeAema89eXO2GTnl5s (accessed on 10 March 2025).
- Regulations Relating to Fiscal Measurement in the Petroleum Activities. Norwegian Offshore Directorate (NOD), 2023. [Online]. Available online: https://www.sodir.no/en/regulations/regulations/regulations-relating-to-fiscal-measurement-in-the-petroleum-activities/ (accessed on 10 March 2025).
- Naftos Produktų, Bioproduktų, Kitų Degiųjų Skystų Produktų ir Gamtinių dujų Apskaitos Taisyklės (Accounting Rules for Petroleum Products, Bio Products, Other Flammable Liquid Products and Natural Gas.) Order No. VA-16, 25 January 2011. Valid Summary 03/03/2023. Available online: https://e-seimas.lrs.lt/portal/legalAct/lt/TAD/TAIS.391813/uZGMvawJcv (accessed on 2 May 2025).
- Lietuvos Respublikos Akcizų įstatymas (Republic of Lithuania Law on Excise Duty) No IX-569, 30 October 2001. Valid Summary 12/03/2023. [Online]. Available online: https://e-seimas.lrs.lt/portal/legalAct/lt/TAD/TAIS.154511/asr (accessed on 18 June 2024).
- Prekybos Naftos Produktais Taisyklės (Rules for Trade in Petroleum Products). Order No. 1-41, 2 March 2012. Valid Summary 01/01/2023. [Online]. Available online: https://e-seimas.lrs.lt/portal/legalAct/lt/TAD/TAIS.389288/pOeDenGdkT (accessed on 2 May 2025).
- Capt Rajeev Jassa. Cargo Calculations on Tankers with ASTM Tables: Here Is All You Need to Know. 23 September 2018. [Online]. Available online: https://studylib.net/doc/25760744/cargo-calculations-on-tankers-with-astm-tables (accessed on 10 March 2025).
- ISO EN 45501:2015 (E); Metrological Aspects of Non-Automatic Weighing Instruments. TC IMIN-Measurement Instruments: Brussels, Belgium, 2015; p. 150.
- Sukhinets, Z.A.; Gulin, A.I. Intelligent System for Measuring the Level and Mass of Liquid in Fuel Reservoirs and Tanks During Pitching and Tilting. Meas. Tech. 2021, 64, 200–204. [Google Scholar] [CrossRef]
- OIML R 71: 2008 (E); Fixed Storage Tanks. General Requirements. TC 8/SC 1 Static Volume and Mass Measurement. Bureau International de Métrologie Légale: Paris, France, 2014; p. 20.
- ISO 12917-1:2017(E); Petroleum and Liquid Petroleum Products–Calibration of Horizontal Cylindrical Tanks-Part 1. Manual Methods. ISO/TC 28/SC 2 Measurement of Petroleum and Related Products. ISO: Geneva, Switzerland, 2017; p. 46.
- OIML R 85-1/2: 2008(E); Automatic Level Gauges for Measuring the Level of Liquid in Stationary Storage Tanks. TC 8/SC 1 Static Volume and Mass Measurement. Bureau International de Métrologie Légale: Paris, France, 2008; p. 45.
- Chen, G.; Wan, Y.; Lin, H.; Hu, H.; Liu, G.; Peng, Y. Vertical tank capacity measurement based on Monte Carlo method. PLoS ONE 2021, 16, e0250207. [Google Scholar] [CrossRef] [PubMed]
- OIML R 76-1: 2006(E); Non-Automatic Weighing Instruments. TC 9/SC 1 Non-Automatic Weighing Instruments. Bureau International de Métrologie Légale: Paris, France, 2006; p. 144.
- ASTM D5002-22; Standard Test Method for Density, Relative Density, and API Gravity of Crude Oils by Digital Density Analyzer. ASTM International: West Conshohocken, PA, USA, 2022; p. 7.
- ISO 17025; Testing and Calibration Laboratories. ISO: Geneva, Switzerland. Available online: https://www.iso.org/ISO-IEC-17025-testing-and-calibration-laboratories.html (accessed on 15 June 2025).
- OIML D 28: 2004(E); Conventional Value of the Result of Weighing in Air. TC 9/SC 3 Weights. Bureau International de Métrologie Légale: Paris, France, 2004; p. 11.
- ASTM D1298; Standard Test Method for Density, Relative Density, or API Gravity of Crude Petroleum and Liquid Petroleum Products by Hydrometer Method. ASTM International: West Conshohocken, PA, USA, 2023.
- ASTM D 2598-02; Standard Practice for Calculation of Certain Physical Properties of Liquefied Petroleum (LP) Gases from Compositional Analysis. ASTM International: West Conshohocken, PA, USA, 2021; p. 3.
- API MPMS Chpt. 11.2.4:2007; API MPMS Chapter 11.2.4-2007/GPA Technical Publication TP-27-2007. Temperature Correction for the Volume of NGL and LPG, Tables 23E, 24E, 53E, 54E, 59E, and 60E. American Petroleum Institute (API): Washington, DC, USA, 2019; p. 155.
- OIML G 19 Edition 2017 (E); The Role of Measurement Uncertainty in Conformity Assessment Decisions in Legal Metrology. TC 3/SC 5 Conformity Assessment. Bureau International de Métrologie Légale: Paris, France, 2017; p. 72.
- EN ISO 8973:1999/A1:2020; Liquefied Petroleum Gases-Calculation Method for Density and Vapour Pressure-Amendment 1 (ISO 8973:1997/Amd 1:2020). CEN/TC 19-Petroleum Products, Lubricants and Related Products. European Committee for Standardization: Brussel, Belgium, 2020; p. 7.
- OIML R 125: 1998 (E); Measuring Systems for the Mass of Liquids in Tanks. TC 8/SC 2 Static Mass Measurement. International Committee of Legal Metrology: Paris, France, 1998; p. 32.
- ASTM D 4311–04; Standard Practice for Determining Asphalt Volume Correction to a Base Temperature. ASTM International: West Conshohocken, PA, USA, 2004; p. 11.
- Belyaev, B.M.; Chesnokov, V.I. Estimation of Measurement Errors for the Mass of Commercial Oil and Petroleum Products Using Liquid Counters. Meas. Tech. 2017, 59, 1156–1164. [Google Scholar] [CrossRef]
- Zuda, J. Comparison of volume measurements of mass standards at low pressures and in liquids. Meas. Sci. Technol. 2022, 33, 9. [Google Scholar] [CrossRef]
- ISO 4787: 2010; Laboratory Glassware–Volumetric Instruments–Methods for Testing of Capacity and for Use. ISO: Geneva, Switzerland, 2010; p. 21.
- ASTM D4052-18; Standard Test Method for Density, Relative Density, and API Gravity of Liquids by Digital Density Meter. ASTM International: West Conshohocken, PA, USA, 2018; p. 8.
- API MPMS Chapter 11.2.2M (R2017); Compressibility Factors for Hydrocarbons: 350–637 Kilograms per Cubic Metre Density (15 °C) and –46 °C to 60 °C Metering Temperature. American Petroleum Institute (API): Washington, DC, USA, 2017; p. 264.
- ISO 91:2017; Petroleum and Related Products-Temperature and Pressure Volume Correction Factors (Petroleum Measurement Tables) and Standard Reference Conditions. ISO/TC 28/SC 2 Measurement of Petroleum and Related Products. ISO: Geneva, Switzerland, 2017; p. 14.
- OIML R 117: 2007 (E); Dynamic Measuring Systems for Liquids Other than Water. International Committee of Legal Metrology: Paris, France, 2007; p. 127.
- OIML G 14: 2011(E); Density Measurement. International Committee of Legal Metrology: Paris, France, 2011; p. 29.
- OIML R 111-1: 2004; Weights of Classes E1, E2, F1, F2, M1, M1–2, M2, M2–3 and M3. Part 1: Metrological and Technical Requirements. TC 9/SC 3 Weights. Bureau International de Métrologie Légale: Paris, France, 2004; p. 80.
- Meškuotienė, A.; Kaškonas, P.; Urbonavičius, B.G. Analysis of fuel‘s amount measurement process and its reliability in commercial transaction. Mapan 2020, 36, 175–185. [Google Scholar] [CrossRef]
- Meškuotienė, A.; Kaškonas, P.; Urbonavičius, B.G.; Balčiūnas, G.; Dobilienė, J. Analysis of Liquid Quantity Measurement in Loading/Unloading Processes in Cylindrical Tanks. Computation 2022, 10, 122. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).