BrushGaussian: Brushstroke-Based Stylization for 3D Gaussian Splatting

Abstract

We present a method for enhancing 3D Gaussian Splatting primitives with brushstroke-aware stylization. Previous approaches to 3D style transfer are typically limited to color or texture modifications, lacking an understanding of artistic shape deformation. In contrast, we focus on individual 3D Gaussian primitives, exploring their potential to enable style transfer that incorporates both color- and brushstroke-inspired local geometric stylization. Specifically, we introduce additional texture features for each Gaussian primitive and apply a texture mapping technique to achieve brushstroke-like geometric effects in a rendered scene. Furthermore, we propose an unsupervised clustering algorithm to efficiently prune redundant Gaussians, ensuring that our method seamlessly integrates with existing 3D Gaussian Splatting pipelines. Extensive evaluations demonstrate that our approach outperforms existing baselines by producing brushstroke-aware artistic renderings with richer geometric expressiveness and enhanced visual appeal.

1. Introduction

Style transfer aims to extract artistic style from a reference and apply it to a target object. This technique plays a crucial role in fields like computer-aided design (CAD), where it traditionally requires significant time and expertise to master both artistic skills and specialized software. For instance, mastering 3D modeling often requires at least six months of training in both artistic fundamentals (such as shape, color, and texture) and complex 3D software tools. However, with the advancement of style transfer techniques, individuals with minimal expertise can now generate artistic 3D content, significantly lowering the barrier to digital art creation. As a result, style transfer has become increasingly influential in various visual domains, including games, AR/VR, animation, and digital content creation.

Style transfer can be categorized into two main branches: 2D and 3D style transfer. The 2D image-based approach typically takes a content image (providing semantic structure) and a style image (providing artistic features) as inputs and then synthesizes a stylized 2D image. However, unlike pixel-based representations in 2D images, 3D representations—such as meshes, point clouds, and volumetric data—vary significantly depending on the chosen primitive format. Extending 2D style transfer to 3D introduces several new constraints and challenges. One of the key challenges is choosing an appropriate 3D representation that ensures both accurate geometry and view consistency during style transfer. Previous research has explored various 3D representations, including polygon meshes [1,2,3,4,5], point clouds [6,7,8,9,10,11], and neural radiance fields (NeRFs) [12,13,14,15,16,17]. However, each of these approaches comes with limitations: Meshes require well-defined polygonal connectivity; otherwise, the output may contain undesirable artifacts; point clouds may struggle with geometric accuracy or high memory consumption; NeRF-based approaches often suffer from slow rendering speeds, as they require intensive sampling through deep neural networks.

More importantly, traditional 3D style transfer methods focus primarily on global features, such as texture and color, while neglecting local geometric attributes—such as brushstroke shapes. This contrasts with artistic intuition, as renowned painters, like Van Gogh, are distinguished by their unique brushwork, which imparts a personal and expressive touch to their art. Capturing and transferring such geometric style elements remains an open challenge in 3D style transfer.

To address these limitations, we propose enhancing 3D Gaussian primitives with texture features for efficient and expressive brushstroke-aware 3D style transfer. Our method transforms a photorealistic 3D Gaussian scene, reconstructed from multi-view images, into a stylized sparse 3D Gaussian scene that supports high-quality and view-consistent renderings from novel viewpoints (See Figure 1). Our approach (Figure 2) consists of three key components: (1) Gaussian Pruning for Efficiency: We first apply an unsupervised clustering algorithm to prune dense 3D Gaussians, improving both visibility and rendering efficiency. (2) Projected Area Computation: We compute the 2D projected area of each 3D Gaussian primitive in image space, providing a basis for texture mapping. (3) Texture Mapping for Stylization: We then project a style texture onto the computed Gaussian regions, ensuring that the brushstroke effects are accurately mapped onto the 3D scene. Compared to previous 3D stylization techniques, which often suffer from inaccurate geometry or a lack of fine-grained style details, our method provides structurally meaningful and visually appealing brushstroke-aware stylization.

In summary, our main contributions are as follows:

1.

An efficient Gaussian pruning algorithm that reduces the density of 3D Gaussian scenes while maintaining structural consistency.

2.

A texture mapping technique that enables the projection of arbitrary style textures onto 3D Gaussian primitives, preserving local geometric style elements such as brushstroke effects.

2. Related Works

In this section, we first introduce 2D image style transfer, which serves as the foundation for 3D style transfer. We then extend the discussion to 3D space, covering both 3D representations and their applications in 3D style transfer.

2.1. Two-Dimensional Image Style Transfer

Image style transfer, also known as image stylization, aims to transform an input content image into a stylized version by extracting and recombining the artistic features of a reference style. The key challenge lies in balancing the preservation of semantic content with artistic expressiveness. A failed attempt may result in an image that is too photorealistic with minimal stylization or, conversely, one where the original content is completely lost.

In the early stages, researchers designed hand-engineered filters to generate artistic effects, utilizing low-level operations such as blurring and sharpening [18,19,20,21,22]. These approaches provided fine-grained control over stylization and offered valuable insights into edge enhancement and texture manipulation. However, crafting effective filters was time-consuming and required expert knowledge [23], making it impractical for broader applications. More importantly, these methods struggled to capture the intricate and unique characteristics of an artist’s style. To overcome these limitations, researchers began exploring example-based approaches, which automatically extract and apply artistic style features to arbitrary images.

A significant breakthrough came with Gatys et al. [24], who first introduced a neural style transfer (NST) algorithm using a pre-trained convolutional neural network (VGG16) [25]. They discovered that a pre-trained VGG, originally designed for object recognition, could effectively separate image content from style, enabling its application to image stylization. This pioneering work marked the beginning of a new era in example-based style transfer, leading to a surge of follow-up research aimed at improving speed [26,27,28,29,30], enhancing visual quality [31,32,33,34], ensuring stability for video stylization [35,36], and introducing finer control over brushstrokes [37,38,39]. In general, these methods formulated style transfer as a feature matching problem, requiring a pre-trained neural network to extract and manipulate style features.

An alternative perspective emerged, viewing image stylization as a domain adaptation problem, where the goal was to transform images from one distribution (content) to another (style). This shift in viewpoint led to the adoption of Generative Adversarial Networks (GANs) [40] for style transfer. Isola et al. [41] introduced pix2pix, a conditional GAN that generates stylized outputs based on paired training images. However, the requirement for well-aligned image pairs made training impractical for many real-world tasks. To address this, Zhu et al. [42] proposed CycleGAN, which introduced cycle consistency loss, enabling style transfer on unpaired datasets and significantly expanding the applicability of GAN-based stylization. Subsequent research extended GANs to multi-modal synthesis [43,44], architectural improvements [45,46,47,48,49,50], and style-conditioned generation [51,52], further demonstrating their potential for artistic content creation. These advancements sparked widespread adoption, with numerous artists experimenting with GAN-based stylization, showcasing its power in image synthesis.

Despite its success, GAN-based style transfer suffered from training instability and mode collapse, leading the research community to seek more robust alternatives. This paved the way for diffusion models [53,54], which soon outperformed GANs in both stability and image quality. Rombach et al. [55] introduced latent space diffusion, significantly reducing computational costs while maintaining high-fidelity stylization. Building upon this work, style transfer researchers widely adopted diffusion models, leveraging their capabilities for conditional image generation [56,57], text-to-image synthesis [58,59,60,61], and interactive image editing [62,63,64]. Diffusion models further democratized digital art creation, lowering the barrier for non-professional users to generate high-quality stylized content.

While diffusion-based methods produce high-quality stylized images, 2D style transfer remains inherently limited to image space, lacking awareness of 3D structure, depth, and view consistency. Consequently, relying solely on 2D style transfer techniques is insufficient for 3D stylization. To bridge this gap, it is essential to incorporate 3D representations, enabling spatially consistent and geometrically aware stylization.

2.2. Three-Dimensional Representation and Style Transfer

Three-dimensional style transfer originates from 2D image style transfer and aims to stylize objects or scenes in 3D space. Compared to 2D style transfer, 3D style transfer is a relatively new and challenging task. In addition to balancing content and style, it must ensure view-consistent stylization across different perspectives. This additional requirement makes 3D style transfer inherently more complex and less explored than its 2D counterpart. To address these challenges, researchers have explored various 3D representations, including polygon meshes, point clouds, neural radiance fields (NeRFs), and 3D Gaussian Splatting, to enable view-consistent 3D style transfer.

A polygon mesh is a structured representation of a 3D object composed of vertices, edges, and faces that define its geometric shape. Mesh-based representations naturally separate shape (polygon structure) and color (UV map or texture), making them an intuitive choice for 3D style transfer. Early research primarily focused on texture stylization, leveraging UV mapping to transfer style-related color information onto 3D objects. For example, Chen et al. [65] incorporated physical reflectance effects to achieve realistic style transfer, while Lukas et al. [3] applied style transfer to mesh-based indoor scene reconstructions. Additionally, Richardson et al. [66] introduced a text-guided approach for texture generation, editing, and transfer on meshes. However, researchers sought not only to stylize texture but also to alter geometric shape. To address this, Liu et al. [67] introduced a differentiable rasterizer, allowing users to edit 3D surfaces using off-the-shelf image processing filters. Similarly, Gao et al. [68] proposed a method to automatically deform triangle meshes based on text descriptions. Despite these advancements, mesh-based methods suffer from a fundamental limitation—they rely on strictly connected polygon structures. Large deformations can introduce topological inconsistencies, leading to holes or distortions in the mesh. This constraint prevents mesh-based approaches from achieving sophisticated, stroke-based rendering, limiting their flexibility in artistic style transfer.

A point cloud is a discrete set of data points in 3D space, representing object geometry without explicit connectivity. Similarly to meshes, point clouds contain both spatial (position) and color attributes, making them a promising 3D style transfer representation. Cao et al. [9] introduced a neural style transfer method for colored point clouds, enabling both geometry and color stylization. Huang et al. [6] further refined this approach by modulating style features via linear transformation matrices, capturing finer stylistic details. Mu et al. [7] extended point cloud stylization to single-image inputs, using depth estimation to infer 3D-aware content features and generate stylized novel views. Unlike meshes, point clouds do not require connectivity, making them less prone to topological issues. Consequently, point cloud-based methods often achieve better visual quality than mesh-based approaches. However, they remain sensitive to geometric reconstruction errors, particularly in complex real-world scenes, and suffer from high memory consumption and slow processing speeds. These limitations hinder their application in detailed and high-resolution stylization.

A neural radiance field (NeRF) [69] is an implicit 3D representation that encodes volumetric radiance and density into a deep neural network, allowing for photo-realistic rendering from novel viewpoints. Unlike mesh-based approaches, which rely on UV maps, NeRF stores learned volumetric features, which are then mapped to RGB values during rendering. Several works have demonstrated the potential of NeRF-based style transfer [12,13,14,15,16,17,70]. Zhang et al. [13] introduced a nearest-neighbor feature matching approach, surpassing previous methods in both visual quality and style preservation. Duan et al. [70] further extended NeRF-based techniques by incorporating stroke-based rendering, simulating the progressive painting process using vector strokes. Although NeRF-based representations outperform all previous approaches in rendering quality, they are computationally expensive, requiring extensive sampling via deep neural networks. The slow rendering speed presents a major bottleneck for real-time applications, prompting researchers to explore more efficient alternatives. To overcome NeRF’s computational bottlenecks, researchers have turned to 3D Gaussian Splatting [71], which provides both high-speed and high-quality rendering. Unlike NeRFs, which requires volumetric sampling, 3D Gaussian Splatting represents a scene as a collection of 3D Gaussians, allowing for efficient real-time rendering. As a result, many recent 3D style transfer approaches have adopted 3D Gaussian primitives as their underlying representation [72,73,74,75]. For example, Wang et al. introduced GaussianEditor [75], a method for editing 3D scenes via 3D Gaussians with text-based instructions, enabling intuitive content creation and stylization.

Our work is most closely related to that of Duan et al. [70] and Chao et al. [76]. While Duan et al. introduced stroke-based rendering into NeRFs with a limited set of predefined stroke shapes requiring manual design, our approach enables arbitrary stroke shapes without additional intervention.

Chao et al. aim to improve photorealistic rendering quality by enriching each Gaussian with learnable texture maps (e.g., RGB or alpha), focusing on the faithful reconstruction of real-world appearances. In contrast, our work targets non-photorealistic rendering (NPR), with a strong emphasis on artistic stylization. We introduce a brushstroke-aware texture mapping method that enables not only color transfer but also shape-aware deformation, enabling visually expressive, painterly renderings. Moreover, we incorporate unsupervised clustering and Gaussian pruning mechanisms to enable stylization at different abstraction levels, which is outside the scope of Chao et al. Our pipeline is explicitly designed to support artistic control rather than photorealistic fidelity. While both approaches enhance 3D Gaussian primitives through texture-based representations, the motivations and technical focuses are fundamentally different.

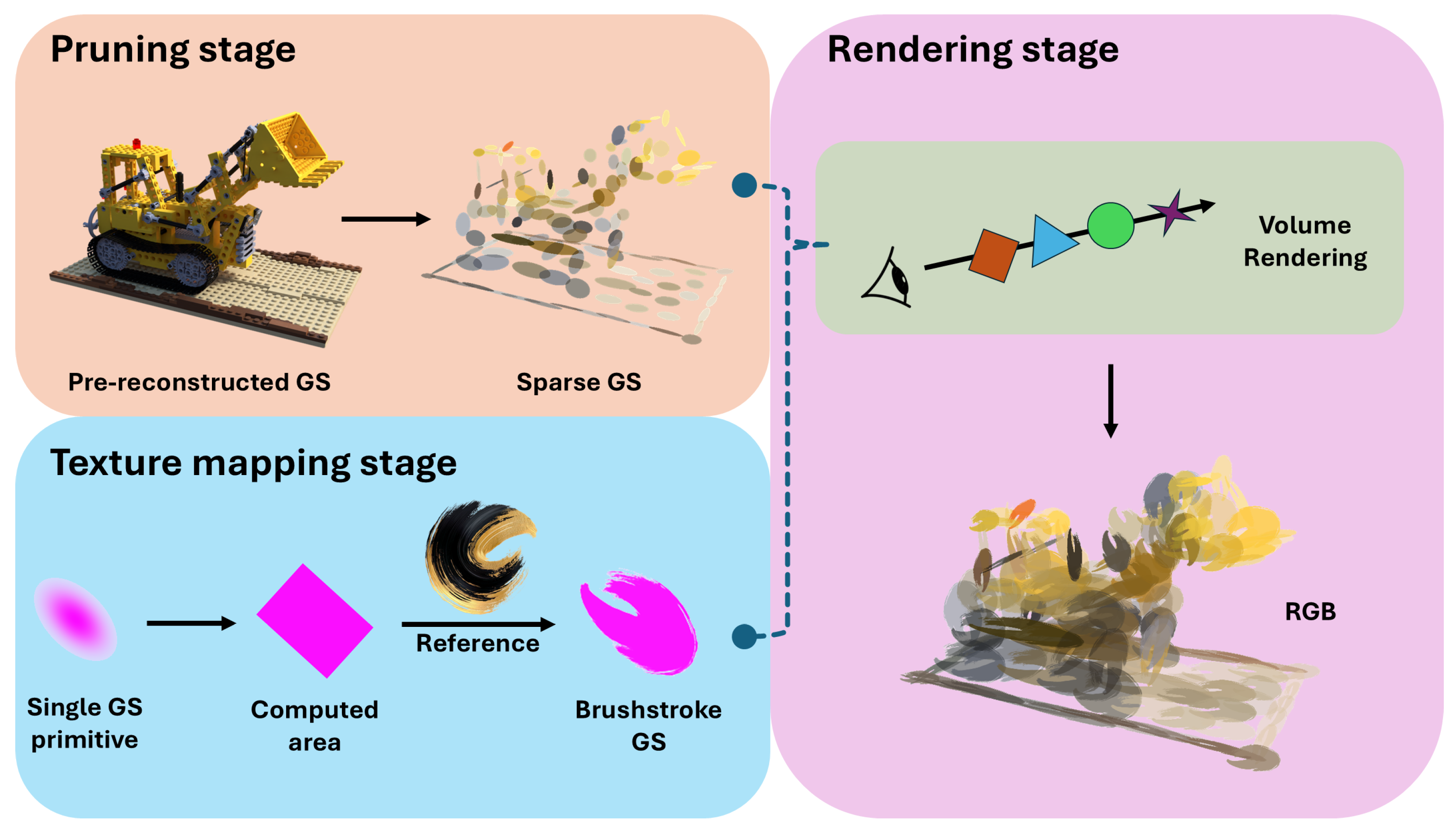
3. Methods

In this section, we present our stroke-based rendering technique in detail. Given a photo-realistic 3D Gaussian Splatting (3DGS) reconstructed from multi-view images of a complex scene, our approach transforms it into an artistic 3DGS by mapping a 2D brushstroke reference to the 3D scene. To achieve this, we treat each 3D Gaussian primitive as an individual brushstroke unit. First, we compute the 2D projection area of each 3D Gaussian primitive (Section 3.1), which naturally forms an elliptical shape in image space. Next, we apply a transformation to convert this elliptical region into a rectangular one (Section 3.3), ensuring alignment with the shape of the given brushstroke reference. Finally, we apply texture mapping (Section 3.4), allowing each Gaussian to inherit the brushstroke shape of the provided texture reference image. However, directly applying this technique to 3DGS produces imperceptible results, as individual Gaussian primitive are too small to be visually distinguishable. To address this, we introduce a pruning and clustering algorithm (Section 3.2) that expands the size of each 3D Gaussian primitive while reducing the overall count by grouping neighboring Gaussian primitives together, ensuring that the stylization effect becomes visually noticeable.

3.1. Three-Dimensional Gaussian Splatting

In 3DGS, each Gaussian primitive is explicitly defined by its 3D covariance matrix $\Sigma \in {\mathbb{R}}^{3\times 3}$, which determines its shape and orientation, and its center $\mu \in {\mathbb{R}}^{3\times 1}$, which defines its position in 3D space. To render a 2D Gaussian ellipse from a 3D Gaussian primitive, the center of the projected 2D Gaussian ellipse is given as follows:

$${\mu }^{\prime }=P\mu ,$$

(1)

where P is the model-view-projection (MVP) matrix, which projects 3D points onto a 2D image plane.

To transform a 3D Gaussian distribution from world coordinates to camera coordinates, we follow the approach introduced by Zwicker et al. [77], which applies a view transformation matrix $V\in {\mathbb{R}}^{3\times 3}$, followed by projection onto a 2D image plane via a local affine transformation $J\in {\mathbb{R}}^{3\times 3}$. The transformed 3D covariance matrix ${\Sigma }^{\prime }$ is computed as follows:

$${\Sigma }^{\prime }=JV\Sigma V^T{J}^T.$$

(2)

Following Zwicker et al. [77], we obtain an approximate 2D covariance matrix by removing the third row and third column of ${\Sigma }^{\prime }$. This $2\times 2$ symmetric matrix consists of three elements, ${\sigma }_x$, ${\sigma }_{xy}$, and ${\sigma }_y$, which correspond to the variances and covariance of the projected Gaussian distribution in the image plane. These elements define the shape and orientation of the projected 2D Gaussian ellipse.

For color rendering, 3DGS adopts a volume rendering approach similar to NeRF-style volumetric rendering. The final pixel color is computed by accumulating colors from $\mathcal{N}$ Gaussian primitives, blending them from front to back according to the conventional volume rendering equation:

$$C=\sum _{i\in \mathcal{N}}{c}_i{\alpha }_i\prod _{j=1}^{i-1}(1-{\alpha }_j),$$

(3)

where $c_i$ is the color of each Gaussian, and ${\alpha }_i$ is the opacity computed using the 2D covariance matrix ${\Sigma }^{\prime }$ and a learned per-point opacity parameter $o_i$.

Specifically, ${\alpha }_i$ is given by the following:

$${\alpha }_i=o_i{e}^{-\frac{1}{2}{x}_i^T{\Sigma }^{\prime -1}{x}_i},$$

(4)

where $x_i$ represents the offset vector between the current pixel position and the center of the 2D Gaussian ellipse ${\mu }_i$, measuring the pixel’s spatial distance from the Gaussian center in the image space.

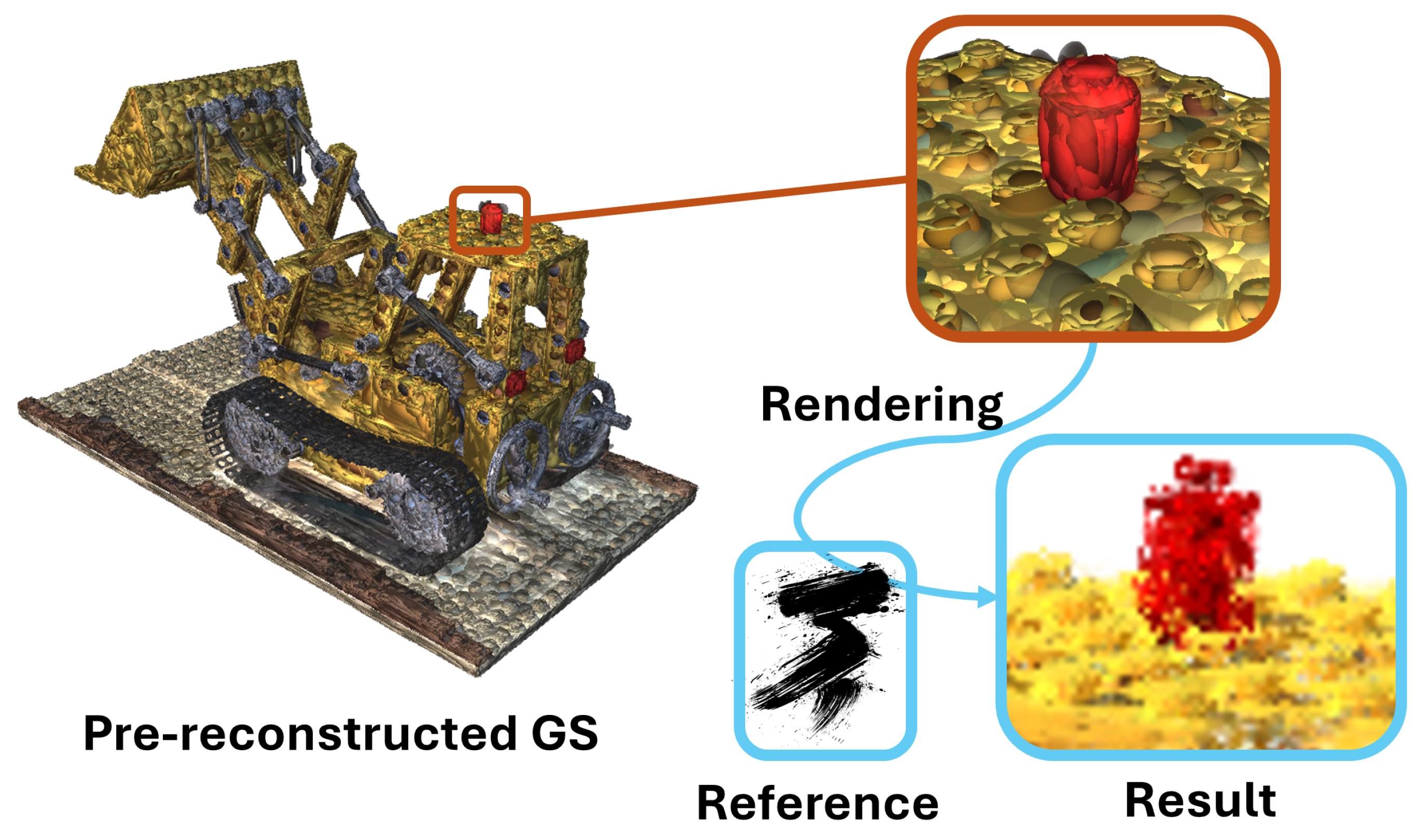
3.2. Gaussian Pruning and Expansion

In general, 3DGS excels at representing highly detailed and complex scenes. However, it is not directly suitable for our task, as we treat each Gaussian primitive as a brushstroke unit. In most cases, a single Gaussian primitive in a pre-trained 3DGS covers only a few pixels, making it imperceptible in the final rendering, as illustrated in Figure 3. Moreover, given the growing popularity of 3DGS, numerous pre-trained models have been shared within the community. To leverage existing pre-trained 3DGS and enhance accessibility, we build our method on pre-trained 3DGS models rather than training from scratch.

We propose an unsupervised pruning and clustering algorithm (see Algorithm A1) that transforms a dense pre-trained 3DGS into a sparser representation, where each Gaussian primitive is larger and more visually distinguishable. This is achieved through a two-step process: (1) clustering 3DGS to reduce their total number and determine new positions and (2) adjusting their scales to ensure that each new Gaussian remains perceptually significant.

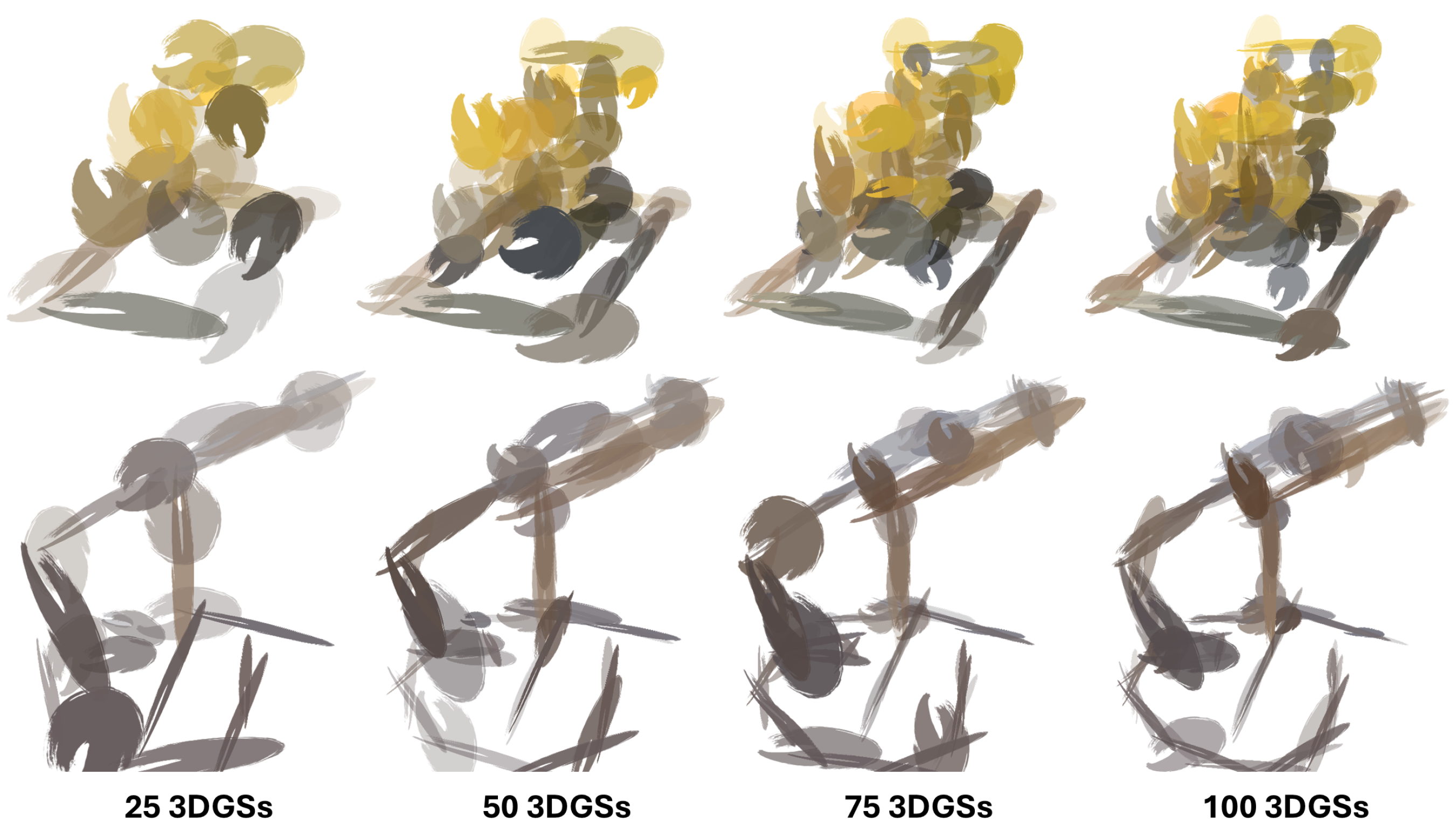
3.2.1. Clustering for 3DGS Reduction

Each Gaussian primitive in 3DGS is defined by its position $\mu$, scale S, rotation R, opacity o, and spherical harmonics $sh$. To enhance the quality of clustering, we first compute the intensity I for each Gaussian primitive and filter out those with low contributions. The intensity is defined as follows:

$$I=o\times Tr(\Sigma )\times l,$$

(5)

where o denotes the opacity, $\Sigma$ is the 3D covariance matrix, and l is the luminance of the Gaussian primitive’s color. The luminance l is calculated from the RGB color converted from the spherical harmonics coefficient $sh$ by the following:

$$l=0.2126R+0.7152G+0.0722B,$$

(6)

where R, G, and B are the respective color channels after clamping to the range $[0,1]$.

Gaussians with importance scores below a certain threshold are pruned to remove floating noise and redundant primitives.

After the filtering step, we perform clustering over the remaining Gaussians to aggregate them into n clusters, aiming to obtain a compact and efficient representation.

Considering the large number of primitives typically involved, we adopt MiniBatchKMeans instead of standard KMeans to reduce memory consumption and accelerate the clustering process, without significantly compromising the clustering quality. Each Gaussian is encoded as a feature vector that concatenates its 3D position, scaling parameters, and RGB color. Clustering is performed based on these feature vectors.

For each resulting cluster, we compute the mean values of the positions, opacities, scaling factors, rotations, and spherical harmonics coefficients of its assigned Gaussians. This aggregation effectively preserves both the geometric structure and appearance information of the original 3D Gaussian distribution while substantially reducing the number of primitives.

3.2.2. Adaptive Scaling of Gaussian Primitives

A straightforward approach would compute the new scale $S^{\prime }$ as the mean of all Gaussians in the cluster. However, this often results in small and barely visible Gaussians, which are not suitable for stroke-based rendering.

To address this issue, we adaptively scale each Gaussian primitive by introducing a scaling factor $\sqrt[3]{N}$, where N represents the number of Gaussians within the cluster. The new scale $S^{\prime }$ is computed as follows:

$$S^{\prime }=S·\sqrt[3]{N},$$

(7)

where S is the average scale of the original Gaussians in the cluster. This approach ensures that larger clusters produce proportionally larger Gaussians, enhancing perceptibility while maintaining geometric consistency within the sparse 3DGS.

3.3. Computing the 2D Projection Area

After pruning (i.e., removing redundant or insignificant Gaussian primitives), each remaining Gaussian primitive can be treated as a brushstroke unit that is ready for use in the style transfer process. In this section, we describe how to compute the bounding box of the projected 2D Gaussian primitive in the image plane. This process is crucial for ensuring that the 2D Gaussian is mapped accurately with the texture, as the bounding box defines the spatial region where the Gaussian will contribute to the rendered texture.

Equations (1) and (2) show how to compute the mean and covariance of the 2D Gaussian after applying the projection. The mean represents the center of the Gaussian distribution, and the covariance matrix characterizes the spread or orientation of the Gaussian, defining how the Gaussian is distributed in 2D space.

The next step is to convert the 2D Gaussian’s elliptical shape into a rectangular bounding box for the convenience of texture mapping (Figure 4), as rectangular boxes are easier to handle and align within the 2D image space when placing textures. To achieve this, we first compute the major axis (the longest axis) and minor axis (the shortest axis) of the 2D Gaussian ellipse, which together define the size of the ellipse in 2D space. The axis can be computed using the following formulas:

$$Axis=\sqrt{mid\pm \sqrt{max(0.1,mi{d}^2-det)}},$$

(8)

where $mid$ and $det$ are defined as follows:

$$\begin{array}{cc}mid& ={\displaystyle \frac{{\sigma }_x^2+{\sigma }_y^2}{2}}\hfill \\ \hfill det& ={\sigma }_x^2·{\sigma }_y^2-{\sigma }_{xy}^2.\hfill \end{array}$$

(9)

Here, $mid$ represents the average of the diagonal elements of the 2D covariance matrix, which corresponds to the mean scale of the ellipse. The determinant ($det$) represents the area of the ellipse and provides information about the spread or “flattening” of the Gaussian. A higher determinant means a larger spread, while a smaller determinant indicates a more concentrated Gaussian distribution.

Now, the computed rectangle area needs to be further aligned with the original ellipse area by applying a rotation. This rotation ensures that the major and minor axes of the rectangle match the orientation of the ellipse in the image space.

The rotation can be computed as follows:

$$R\left(\theta \right)=\left(\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}x-{\mu }_x^{\prime }\\ y-{\mu }_y^{\prime }\end{array}\right),$$

(10)

where $\theta$ can be computed as follows:

$$\theta ={\displaystyle \frac{atan2(2{\sigma }_{xy}^2,{\sigma }_x^2-{\sigma }_y^2)}{2}}.$$

(11)

3.4. Texture Mapping

After computing the projected 2D bounding box and aligning it with the original elliptical Gaussian region, the next step is to apply texture mapping (see Algorithm A2). This allows each Gaussian primitive to inherit the shape and detail of a brushstroke texture, enhancing the artistic expressiveness of the rendering.

To ensure smooth texture mapping, we use bilinear interpolation, a technique that blends texture values from neighboring pixels to create a smooth transition, avoiding sharp edges and aliasing artifacts. We assign $UV$ coordinates to the four corners of the bounding box, which determine how the texture image is mapped onto the Gaussian primitive. Given a texture image of width W and height H, the normalized $UV$ coordinates $(u,v)$ are mapped to discrete texture space as follows:

$$\begin{array}{cc}\hfill x& =u·(W-1)\hfill \\ \hfill y& =v·(H-1),\hfill \end{array}$$

(12)

where u and v are computed using the spatial relationships between the projected Gaussian region and the texture’s coordinate system:

$$\begin{array}{cc}\hfill u& ={\displaystyle \frac{1}{2}}(1+{\displaystyle \frac{R{\left(\theta \right)}_x}{Axi{s}_x}})\hfill \\ \hfill v& ={\displaystyle \frac{1}{2}}(1+{\displaystyle \frac{R{\left(\theta \right)}_y}{Axi{s}_y}}).\hfill \end{array}$$

(13)

However, since x and y may not align exactly with integer pixel positions, direct sampling could cause aliasing or sharp edges in the rendered texture. To prevent this, we apply bilinear interpolation, which blends values from nearby pixels to achieve a smooth transition between them. The interpolated texture value is calculated by blending the texture values from the four neighboring pixels as follows:

$$\begin{array}{cc}\hfill V=& (1-w_x)(1-w_y)V_{00}+w_x(1-w_y)V_{01}\hfill \\ \hfill & +(1-w_x)w_y{V}_{10}+w_x{w}_y{V}_{11},\hfill \end{array}$$

(14)

where $V_{ij}$ represents the texture values at the four neighboring pixels, and $w_x$ and $w_y$ are the interpolation weights based on the distance between the target sampling point and the pixels’ positions.

Texture mapping, combined with bilinear interpolation, allows for the seamless application of brushstroke textures onto Gaussian primitives. This approach effectively prevents artifacts such as sharp edges or aliasing, enhancing rendering quality and transforming simple Gaussian primitives into expressive artistic elements that reflect the characteristics of the brushstroke style.

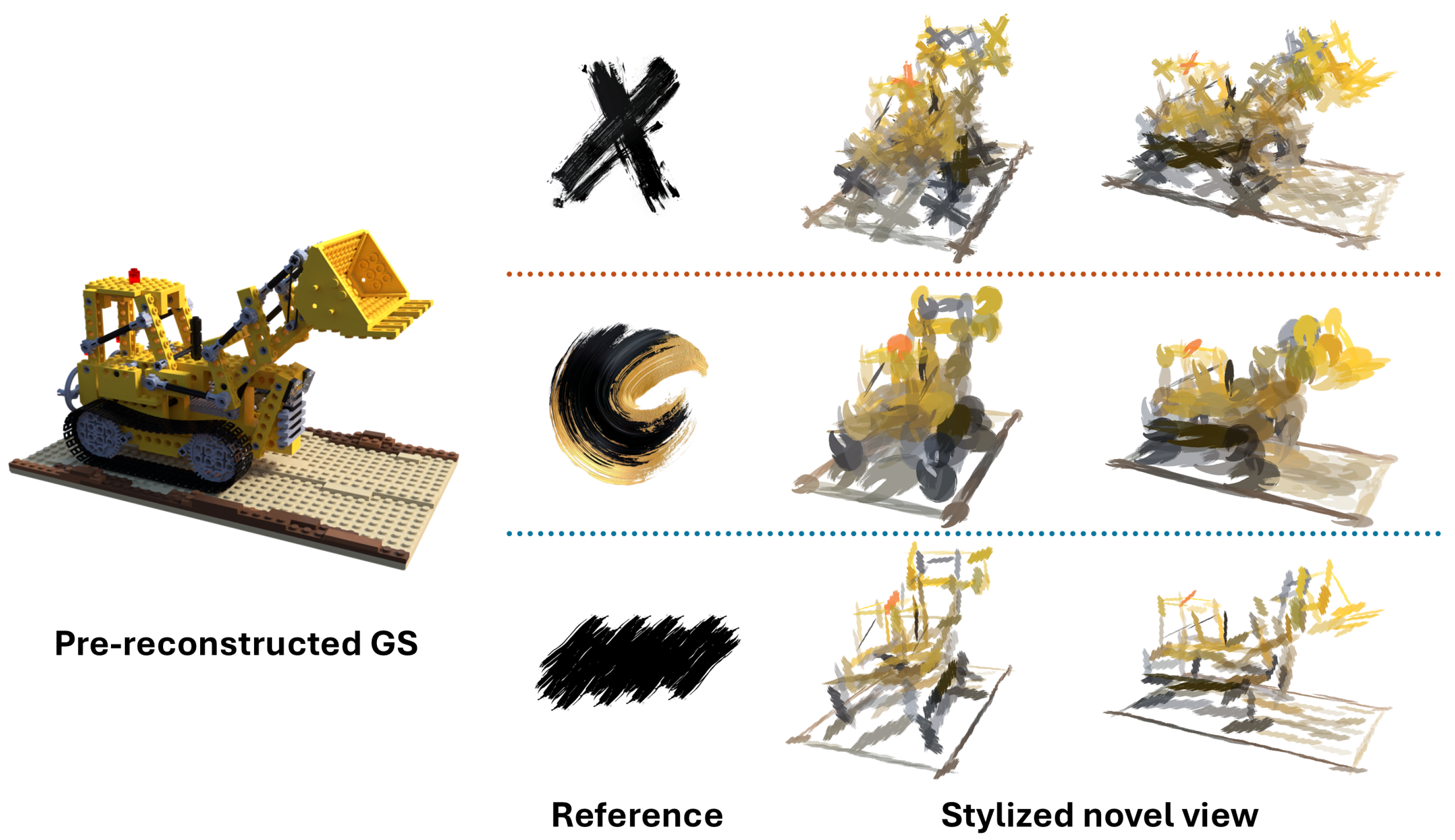
4. Experiments

In this section, we present stylized results using various types of brushstrokes and compare the performance of our method against other state-of-the-art 3D style transfer techniques. We conduct experiments on the NeRF Synthetic [69] and Tanks and Temples (TnT) [71] datasets, both of which provide dozens to hundreds of multi-view images with known camera poses. Finally, we present ablation studies to evaluate the contribution of each component in our method.

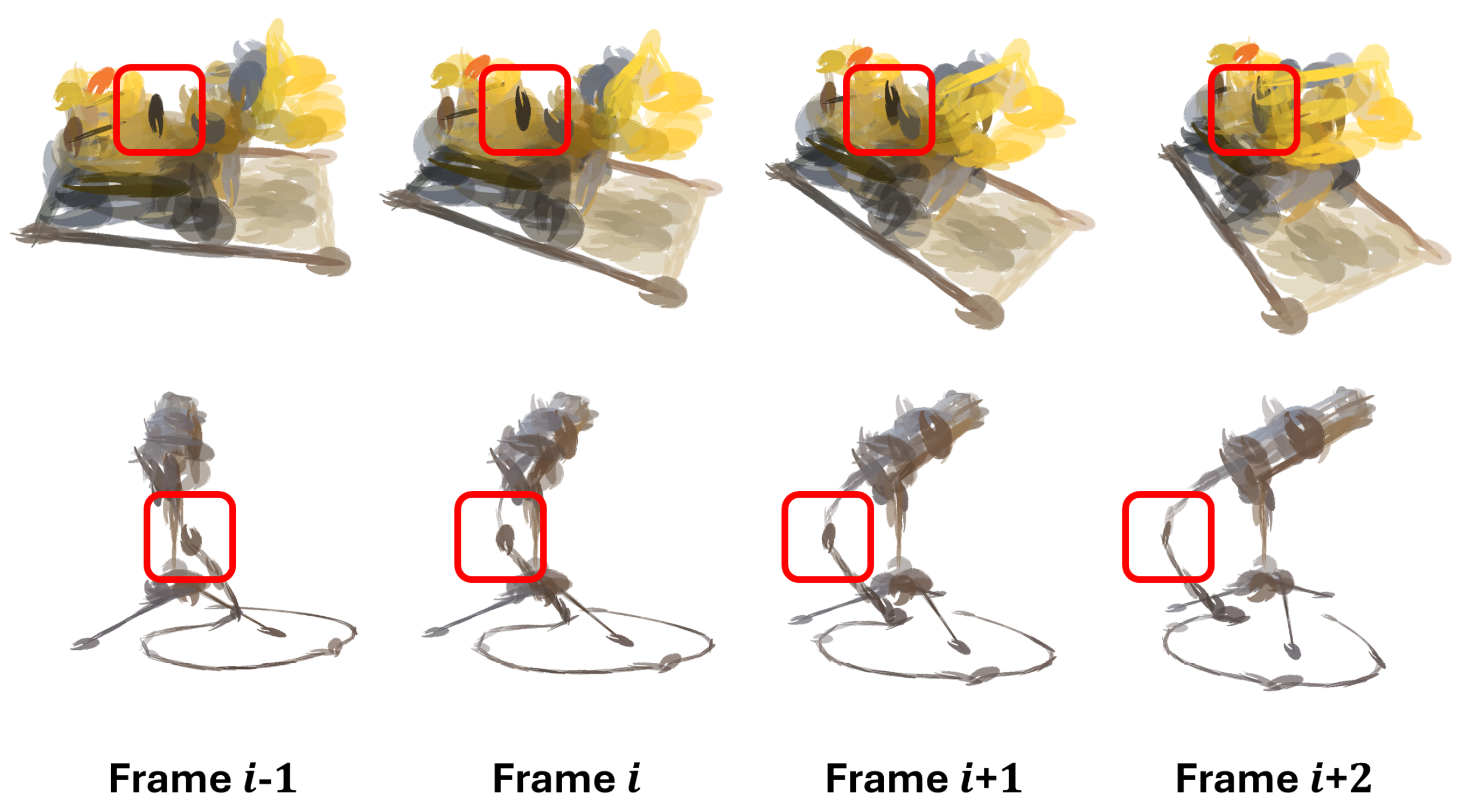
4.1. Stroke-Based Rendering

Figure 5 presents stylized 3D synthetic scenes rendered using our method, with a variety of brushstroke shapes. In this example, we apply several brushstroke types, including moon, swirl, and flower shapes, among others. These results demonstrate the versatility and effectiveness of our method across different brushstroke shapes.

A key hyperparameter in our method is the number of clusters used after the clustering process. In our experiments, we fixed the number of clusters to 150 for the Lego dataset, as all scenes in this dataset are relatively simple, typically containing a single object and lacking complex backgrounds. This value was chosen empirically, as we found, through extensive experiments, that 150 achieves a good balance between preserving semantic meaning and providing an abstract stylization effect.

For more complex scenes such as those in the Tanks and Temples (TnT) dataset, which contain both foreground and background elements, we set the number of clusters to 10% of the total number of pretrained 3D Gaussian primitives. This setting was also determined empirically and offers a reasonable trade-off between preserving detailed structures and achieving abstract stylization. Furthermore, we allow users to adjust this hyperparameter: a smaller number of clusters leads to a more abstract rendering, while a larger number results in a more realistic and detailed appearance, giving users flexible control over the stylization level.

Figure 6 illustrates the transition from abstract to detailed painting results by varying the number of 3D Gaussian primitives used to reconstruct the scene. We observe that a lower number of strokes captures a strong shape-related geometric style, while increasing the number of strokes results in reconstructions with higher fidelity and finer details.

4.2. Comparison with Other Methods

We provide a visual comparison with state-of-the-art 3D style transfer methods [13,14]. Specifically, Zhang et al. [13] introduce a nearest-neighbor-based loss, which is highly effective in capturing style details while maintaining multi-view consistency, replacing the traditional Gram matrix-based VGG loss. Liu et al. [14] propose StyleRF, which restores high-fidelity 3D geometry and enables zero-shot style transfer through a reference-style feature grid. It introduces two innovations: sampling-invariant content transformation for multi-view consistency and deferred style transformation to reduce memory usage. For both methods, we use the released code and train the models from scratch. We choose to carry out comparisons with image reference-based 3D stylization methods rather than text-based methods [16,75], as they offer a more intuitive and fair comparison for our brushstroke-based approach.

Visually, we observe that our results provide a more accurate brushstroke shape (Figure 7) representation based on the provided image reference compared to the baselines. For example, in the chair scene shown in Figure 8, we use a brushstroke reference that features a “splatting” style. Our method not only preserves this splatter-like appearance, creating a truly “Gaussian Splatting”, but also accurately converts the object’s shape, demonstrating both geometric fidelity and artistic expressiveness. In contrast, the baseline methods of ARF [13] and StyleRF [14] leave the pre-reconstructed density field unchanged, focusing only on stylizing surface color and texture. As a result, their outputs appear less vivid.

To show that our method transfers brush-stroke style without sacrificing scene semantics, we conduct a qualitative study with CLIP [78]. For every stylized rendering, we compute the cosine similarity between its CLIP image embedding and the text prompt <This is an image of #.>, where # is replaced by the NeRF-scene label (chair, ficus, hotdog, lego, materials, and mic).

Table 1. Preservation of scene semantics: CLIP similarity ↑ comparison.

	Scene	Chair	Ficus	Hotdog	Lego	Materials	Mic	Mean
Style
Ground truth		99.95	99.61	99.07	99.32	95.46	93.51	97.82
StyleRF (swirl)		69.71	2.54	2.09	60.74	34.1	15.14	30.72
ARF (swirl)		99.02	98.73	23.36	99.46	32.89	99.51	75.49
Ours (swirl)		99.61	96.78	96.88	68.16	60.83	64.45	81.11

lists the CLIP similarity scores for our approach and the baselines under several brush-stroke styles. Higher values indicate the better preservation of the underlying semantic content. As shown in Table 1, our method attains the highest average CLIP similarity among all compared methods, demonstrating its effectiveness in maintaining the original scene’s semantics during 3D style transfer.

4.3. Limitations

Although our method yields promising results, it still has several limitations.

First, while our Gaussian Splatting pruning approach can be applied to complex datasets such as Tanks and Temples (TnT), it requires manual adjustment of the number of clusters. Different cluster settings can significantly affect the rendered artistic style—larger clusters tend to produce coarser, more abstract results, whereas smaller clusters preserve finer details. An automatic method for determining an appropriate number of clusters would further improve usability and consistency.

Second, because Gaussian Splatting primitives inherently treat the left–right and up–down directions symmetrically, our texture mapping may produce inverted or inconsistent details in some rendered frames, leading to minor artifacts in video sequences. We show the results of such inconsistencies in Figure 9, presenting four consecutive frames from $i-1$ to $i+2$. The red rectangular area highlights an individual GS primitive that flips upside down, while most of the surrounding primitives remain stable. This issue only occurs when the affected primitive is aligned perfectly horizontally or vertically, making it sensitive to directional ambiguity during projection. A potential solution is to track the orientation of each 3DGS primitive across consecutive frames during rendering and use the orientation from the previous frame as a temporal constraint to correct inconsistencies in subsequent frames. This can help mitigate abrupt flipping or directional artifacts by ensuring the consistent projection of texture and stroke direction over time.

Finally, our method does not yet support text-based editing, a functionality that many artists find essential for enabling more flexible and creative workflows.

5. Conclusions

We presented a method for reconstructing artistic 3D Gaussian Splatting (3DGS) from photorealistic 3DGS, guided by user-specified brushstroke references. By bridging the gap between color-based and stroke-based stylization, our approach emphasizes the geometry of brushstrokes—capturing the distinctive local structures that define an artist’s personal style, much like the expressive swirls of Van Gogh. In contrast to traditional methods that focus mainly on global texture and color, our method aligns more closely with artistic intuition, recognizing brushwork as a central component of artistic expression.

A key to our method’s success is the coarse-to-fine pruning algorithm for reducing the number of 3DGS primitives, combined with a texture mapping strategy, rather than relying on perceptual losses used in prior works. The experimental results demonstrate that our stroke-based rendering not only preserves the semantic structure of the scene but also faithfully replicates expressive, localized brushstroke characteristics, achieving superior results in 3D stroke-based stylization.