Towards a Digital Twin Approach for Structural Stiffness Assessment: A Case Study on the Cho’ponota L1 Bridge
Abstract
1. Introduction
2. Testing the Cho’ponota L1 Bridge
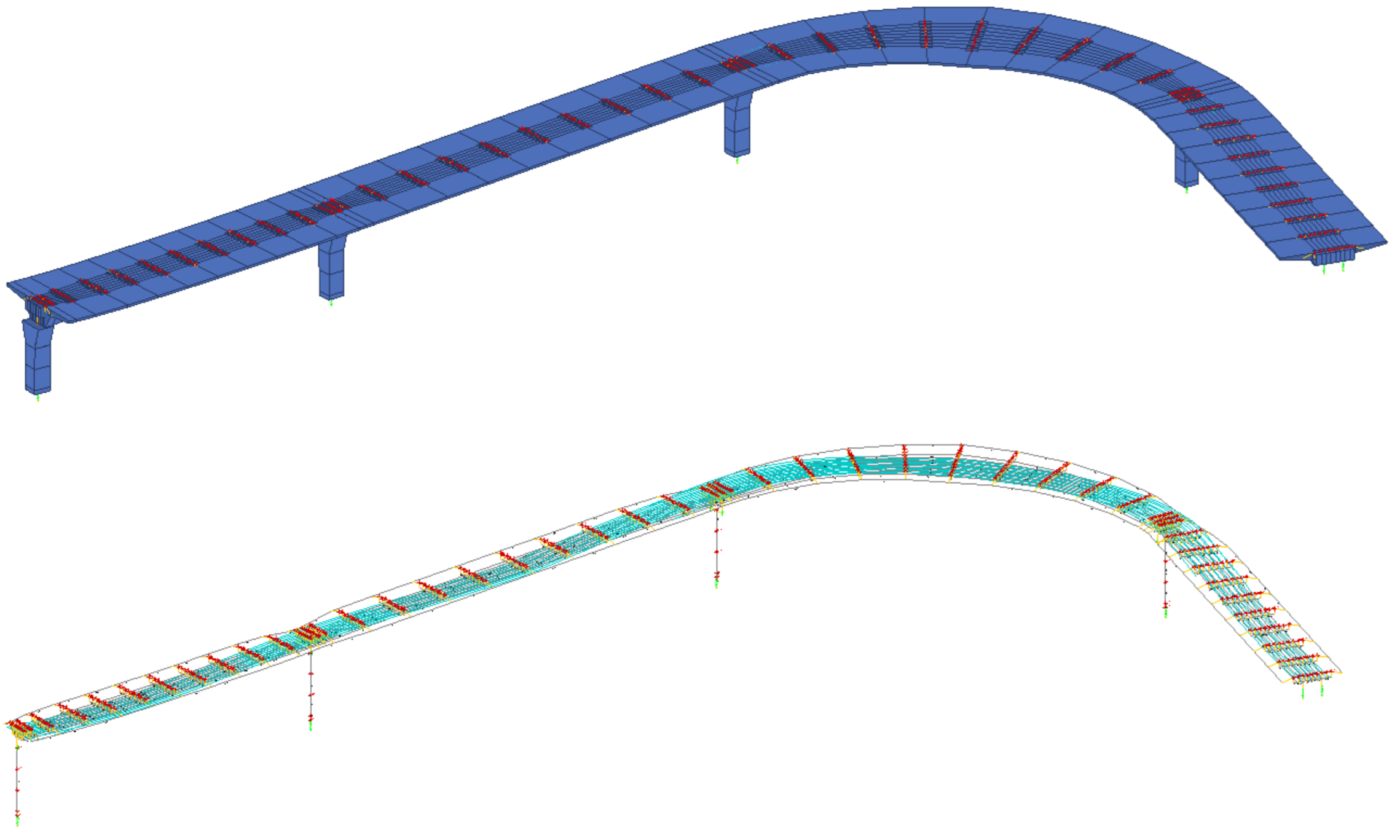
2.1. Description of the Cho’ponota L1 Bridge
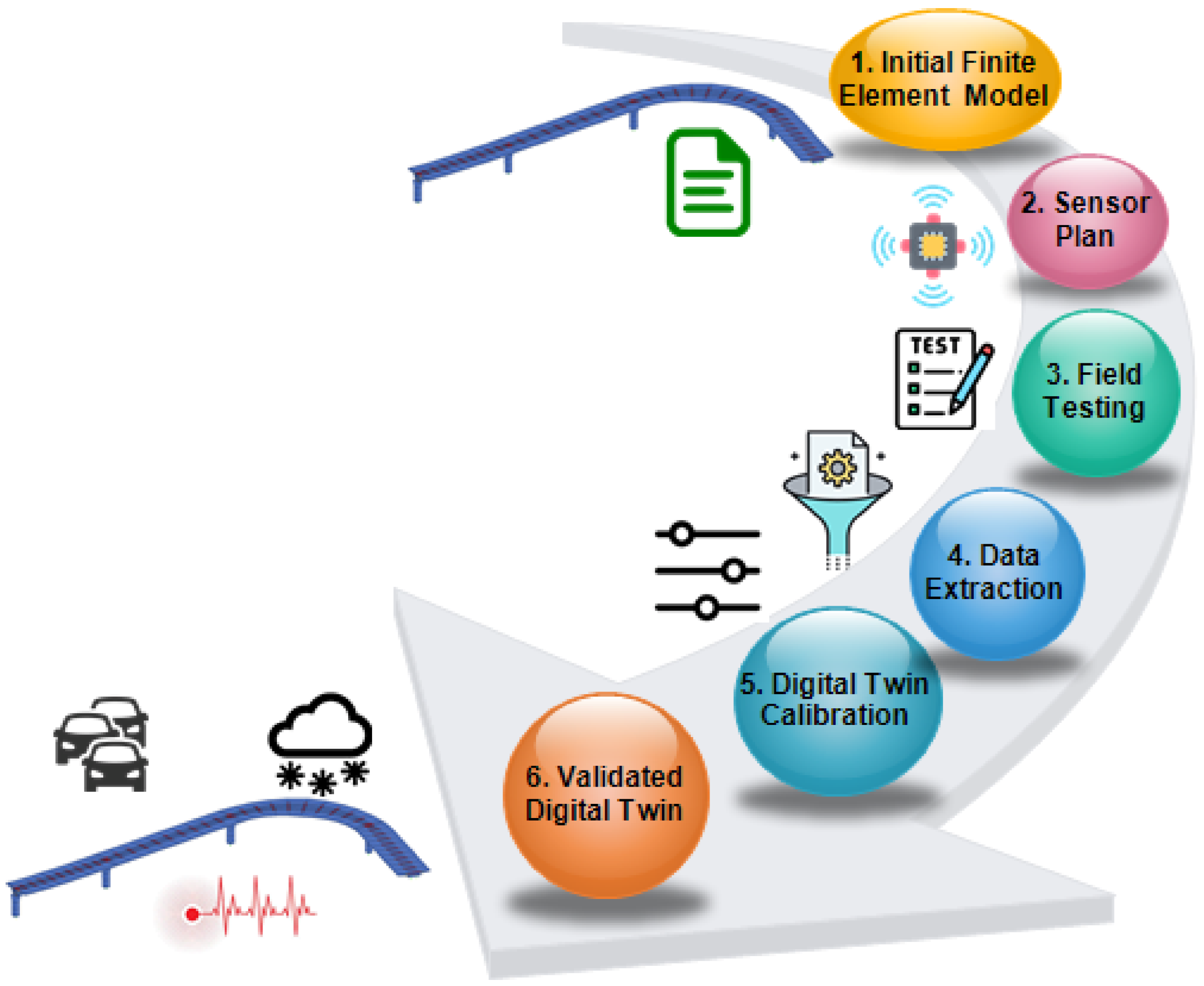
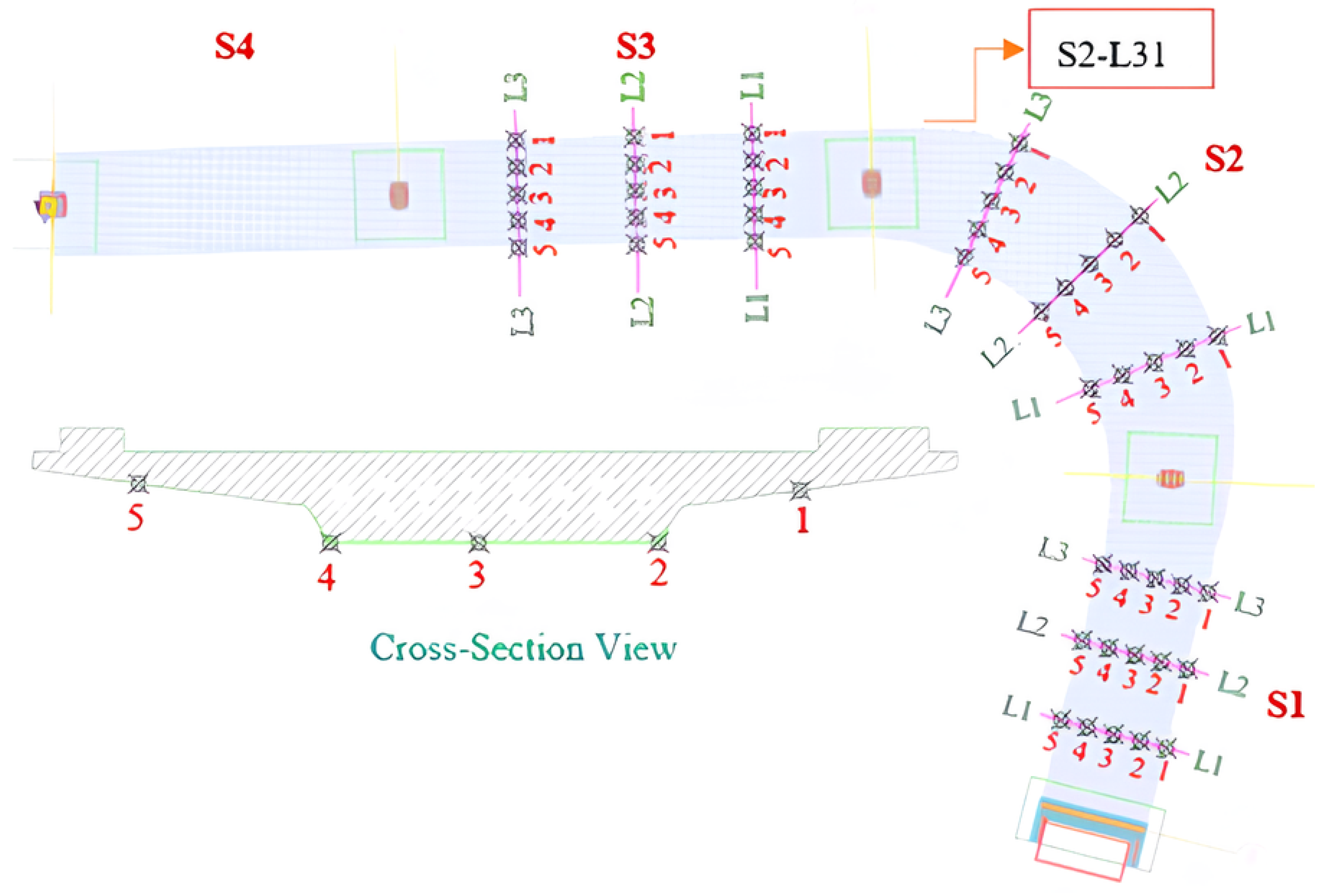
2.2. Digital Twin Construction: Experimental Setup, Field Instrumentation, and Modeling Interface
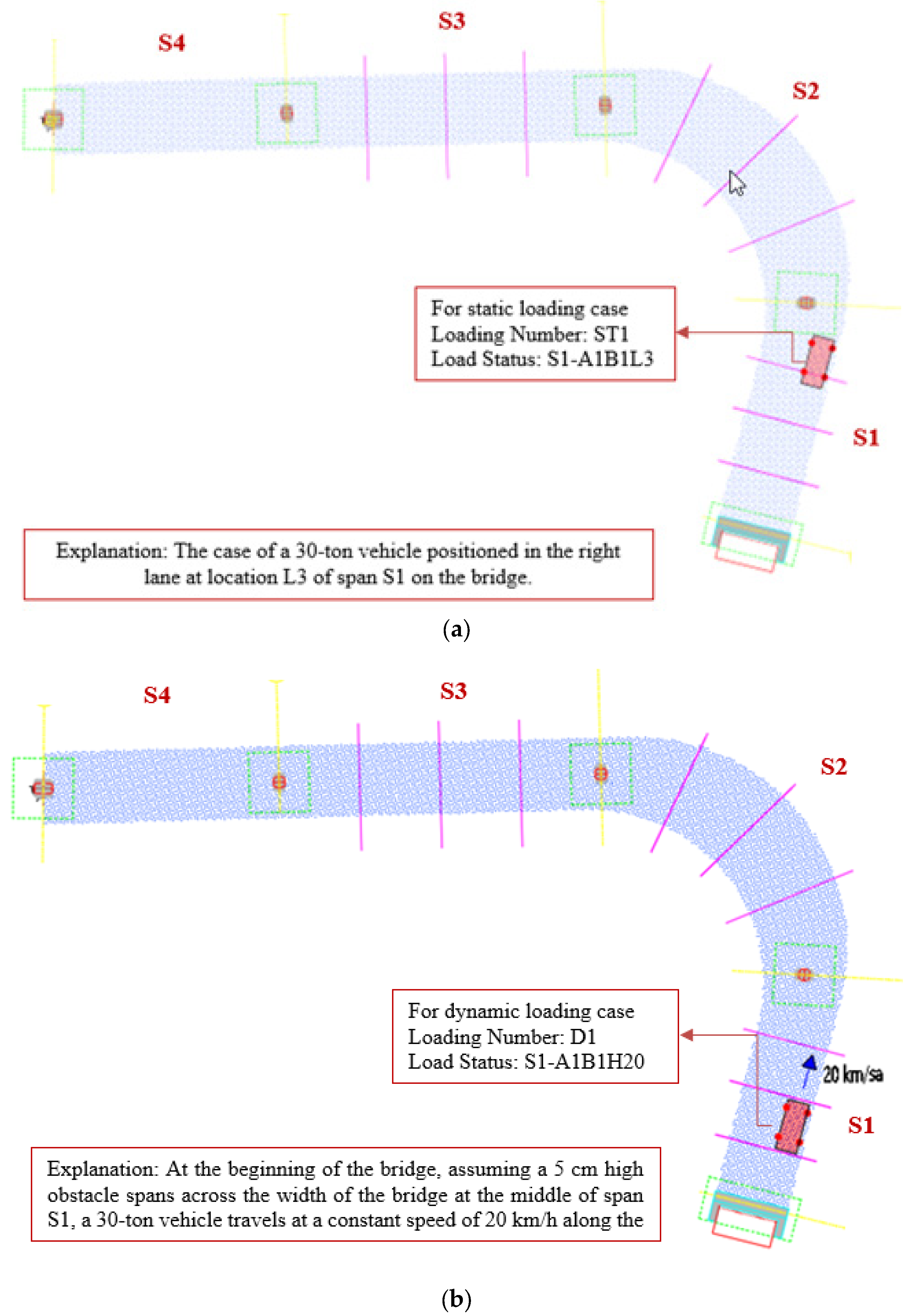
2.3. Static Vehicle Loading Test
2.4. Dynamic Vehicle Loading Test
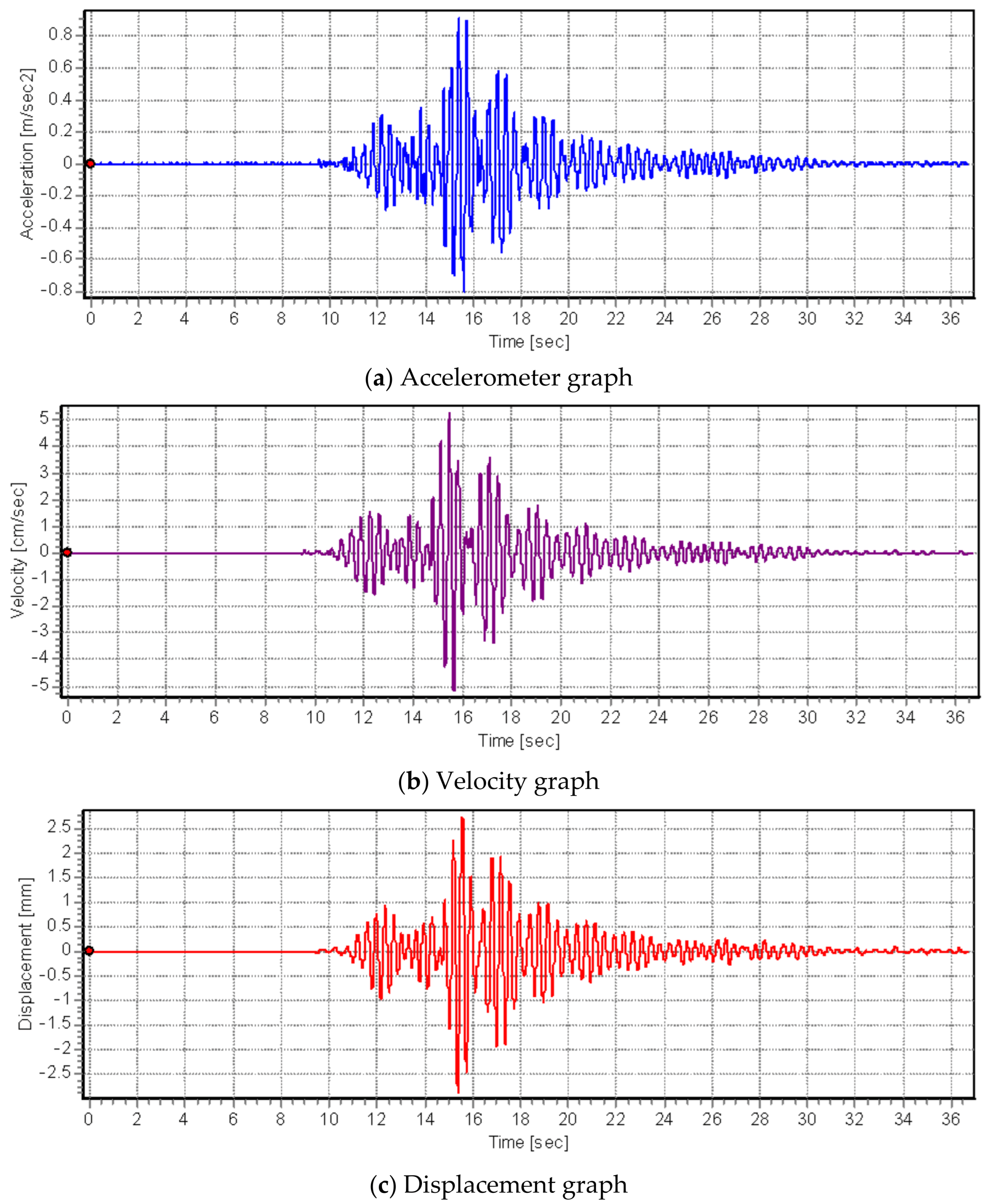
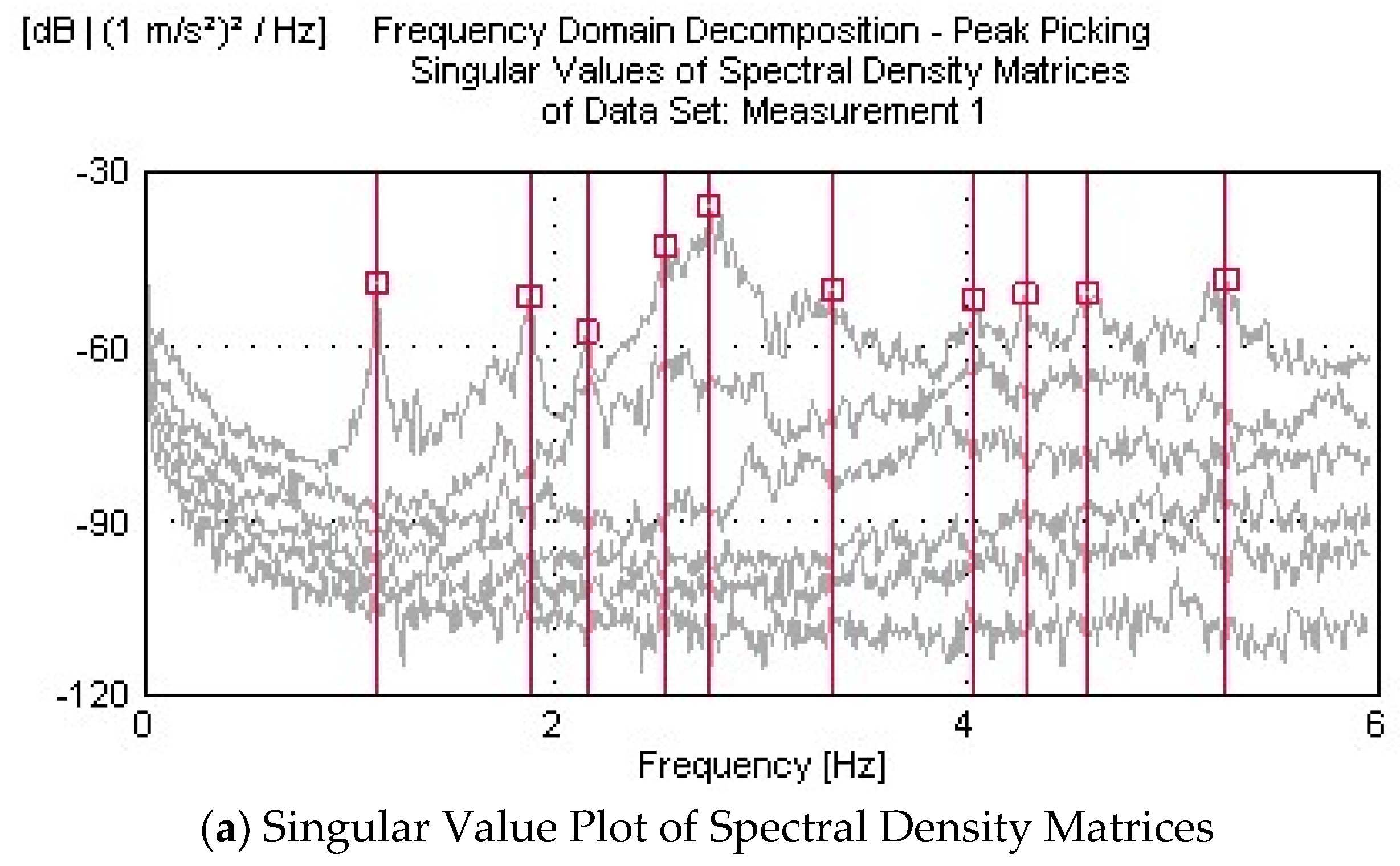
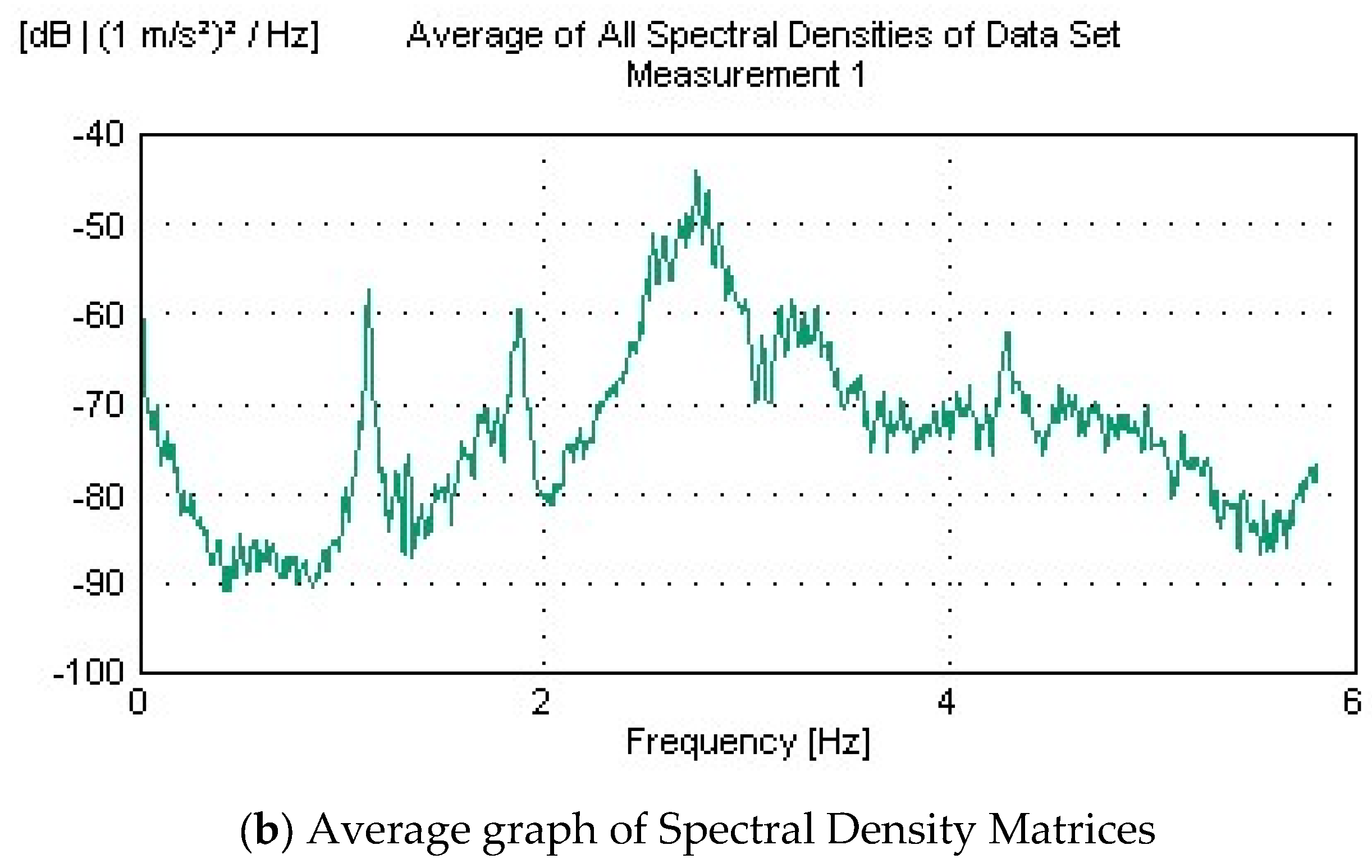
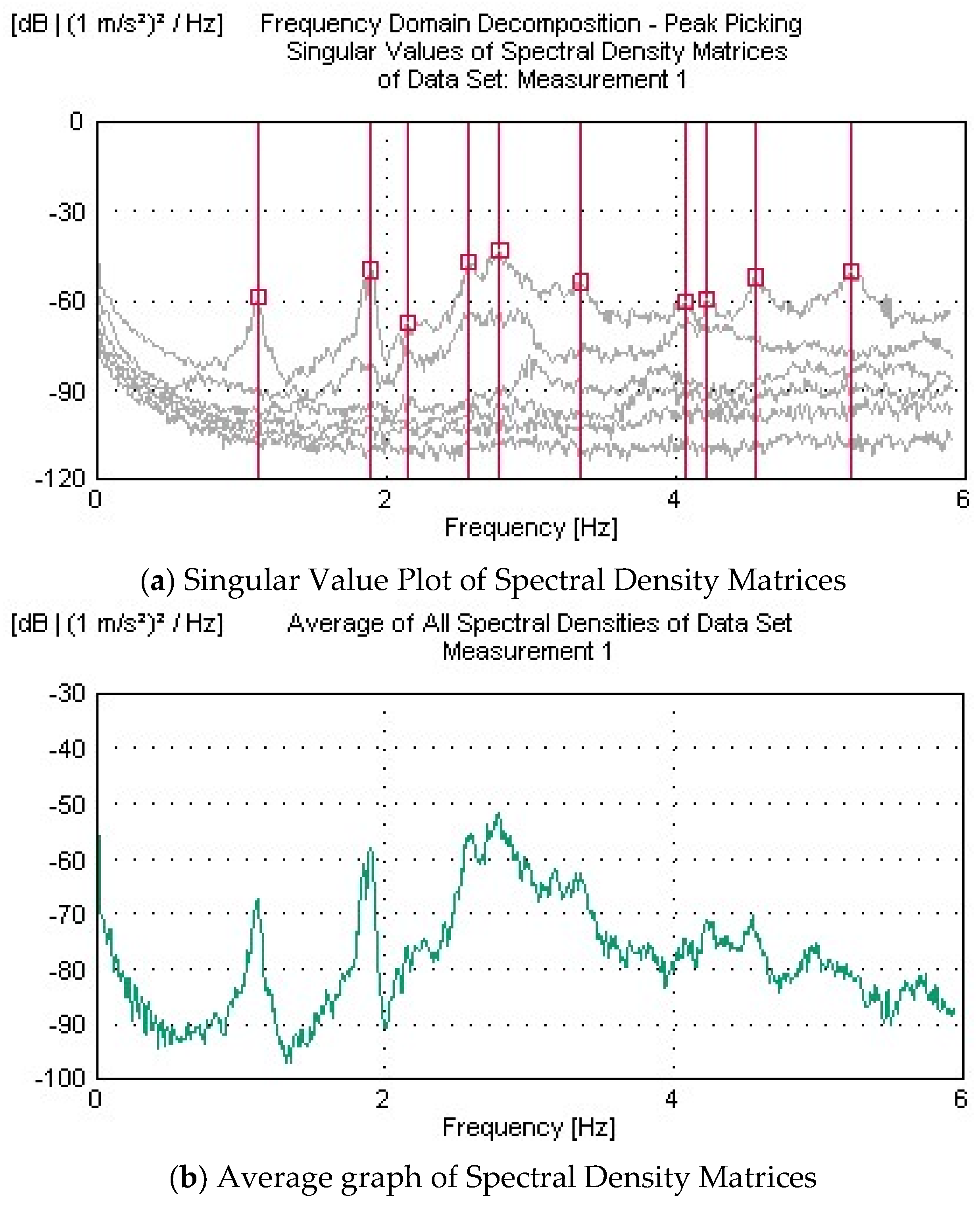
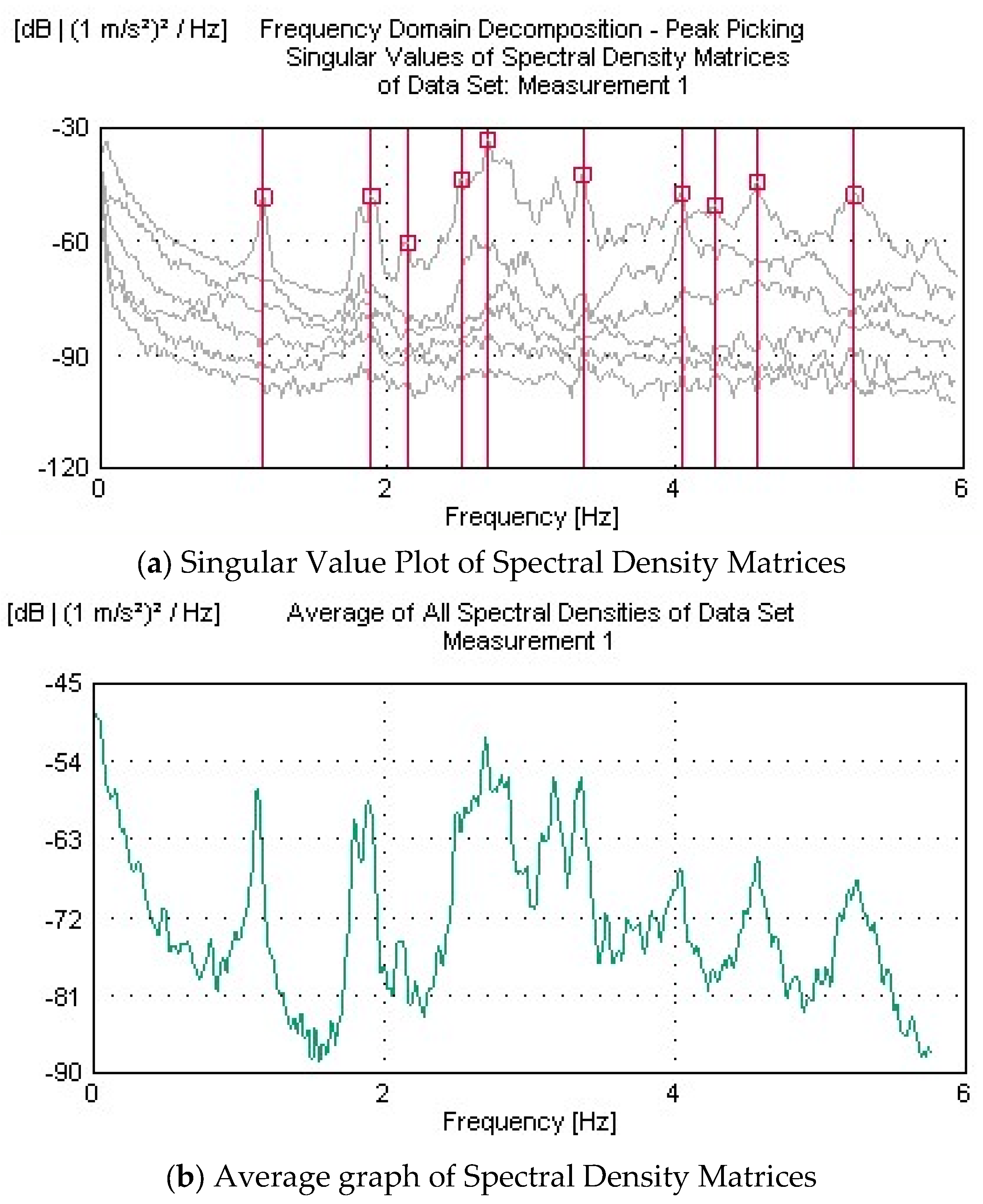
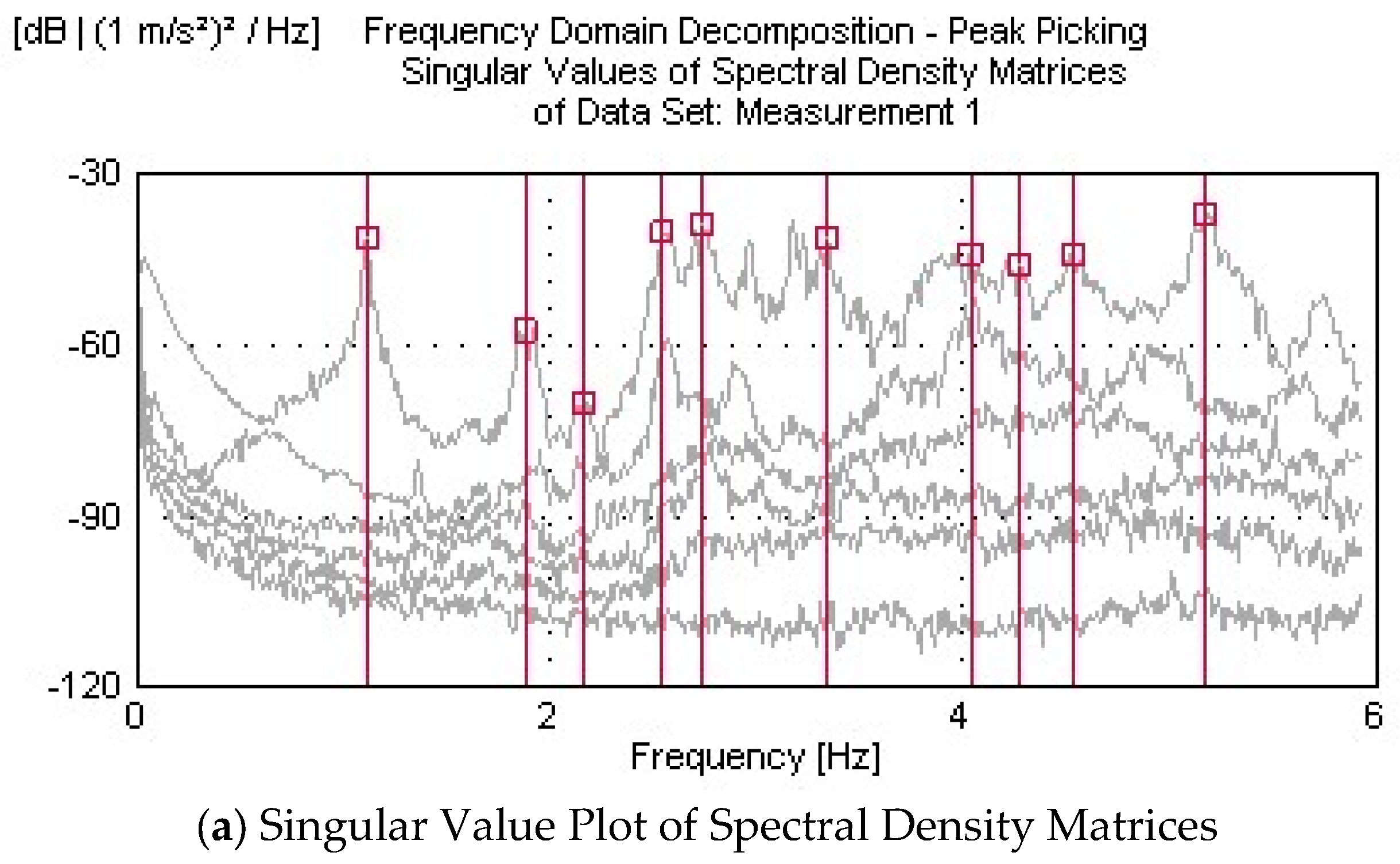
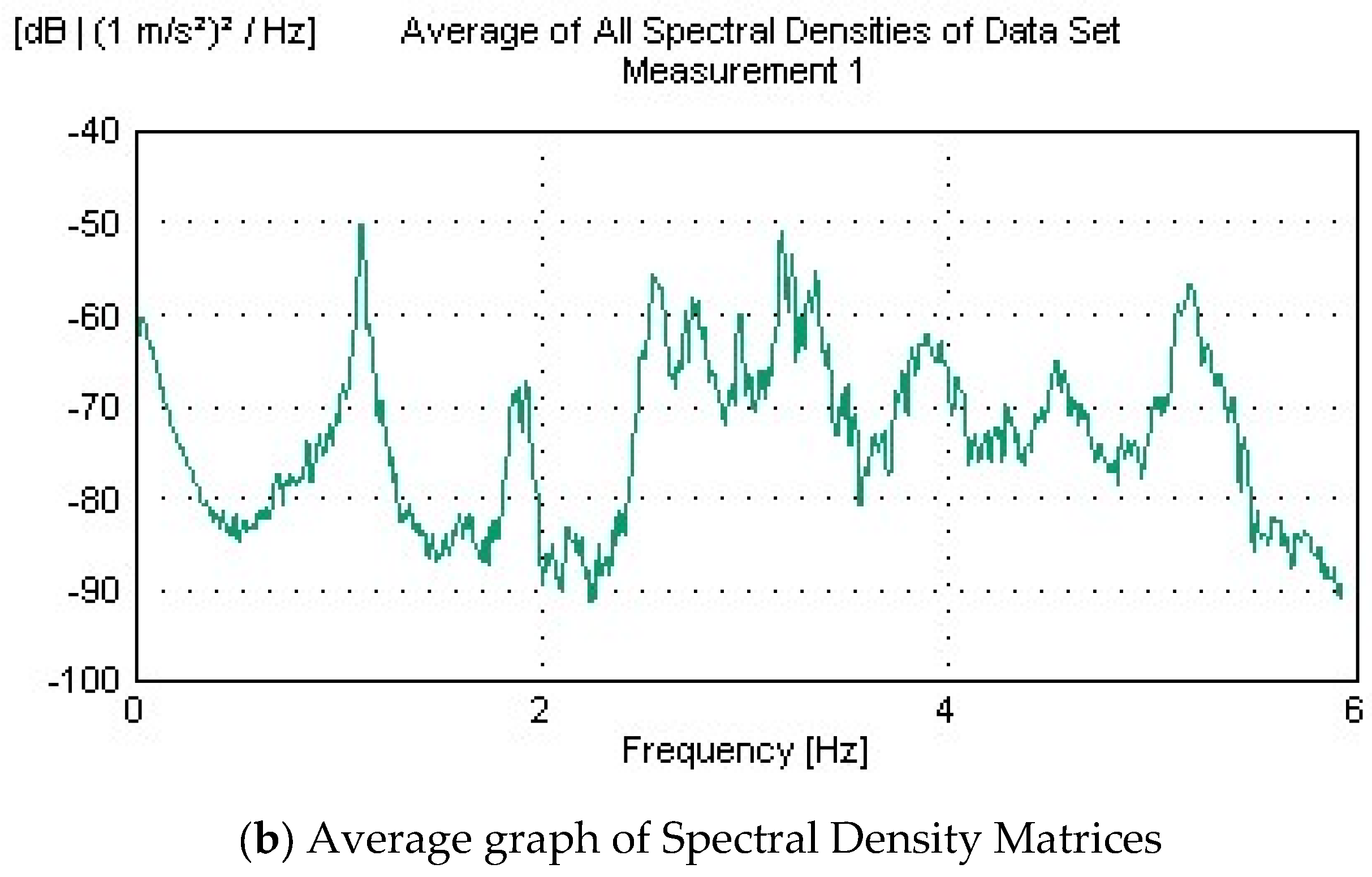
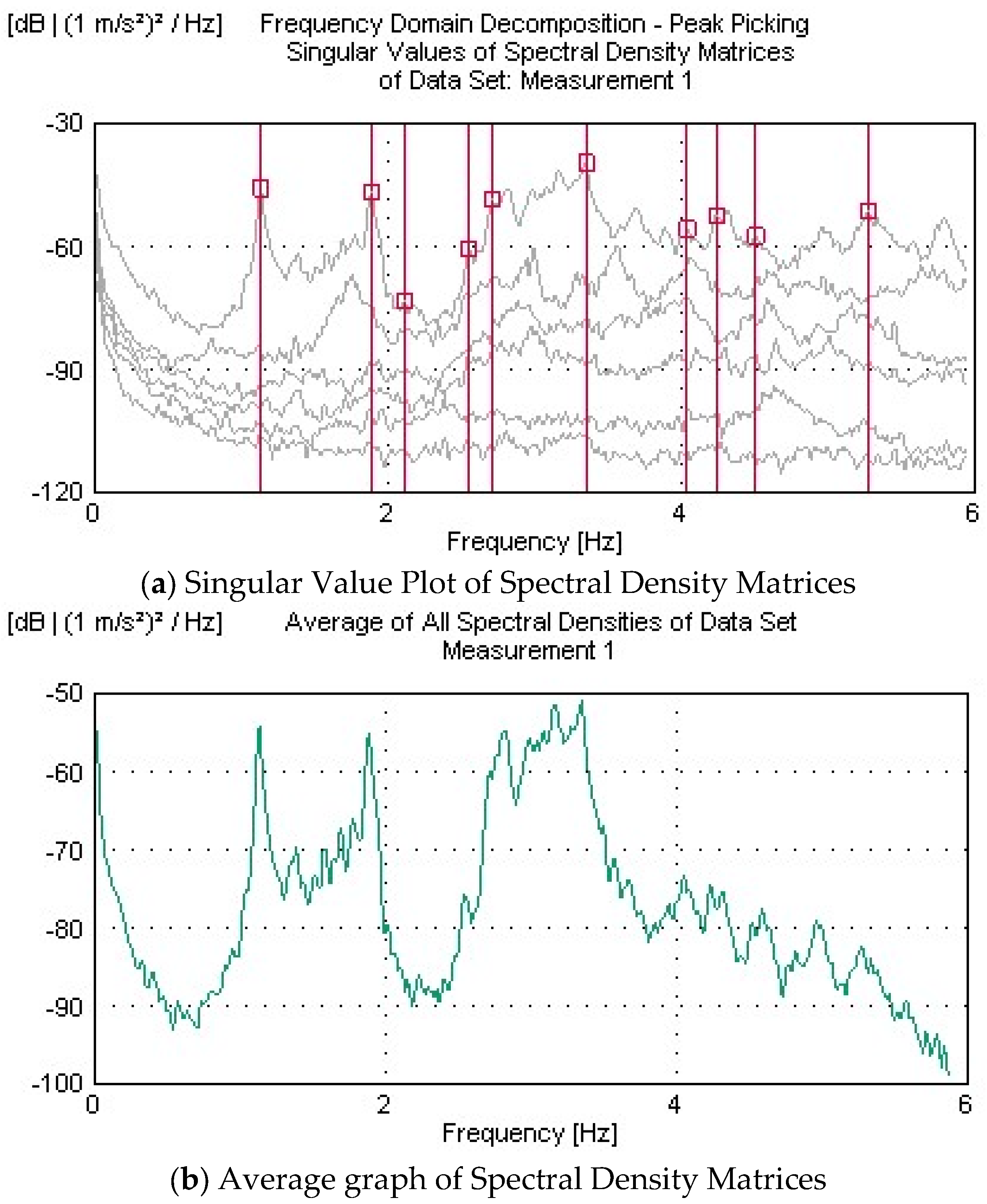
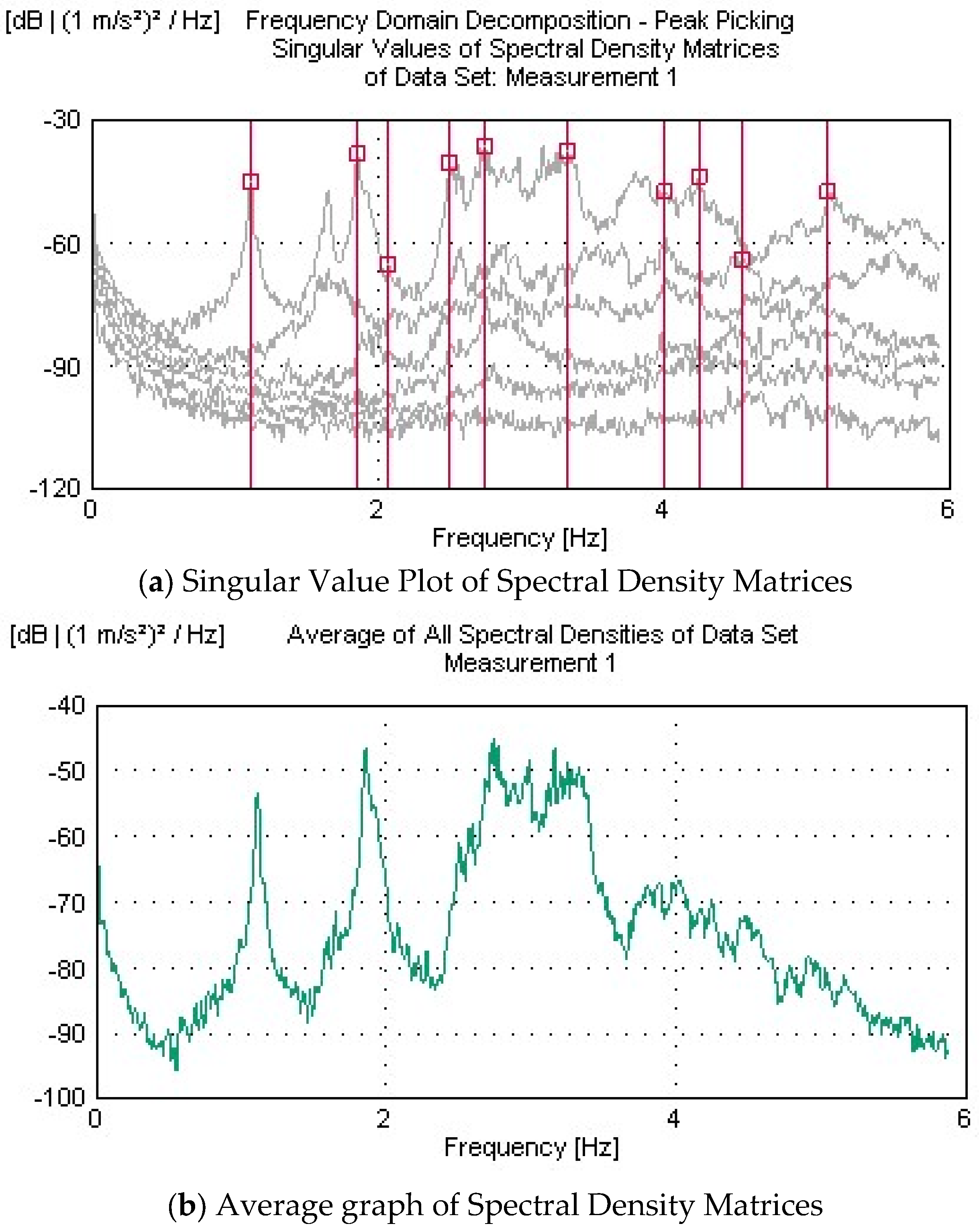
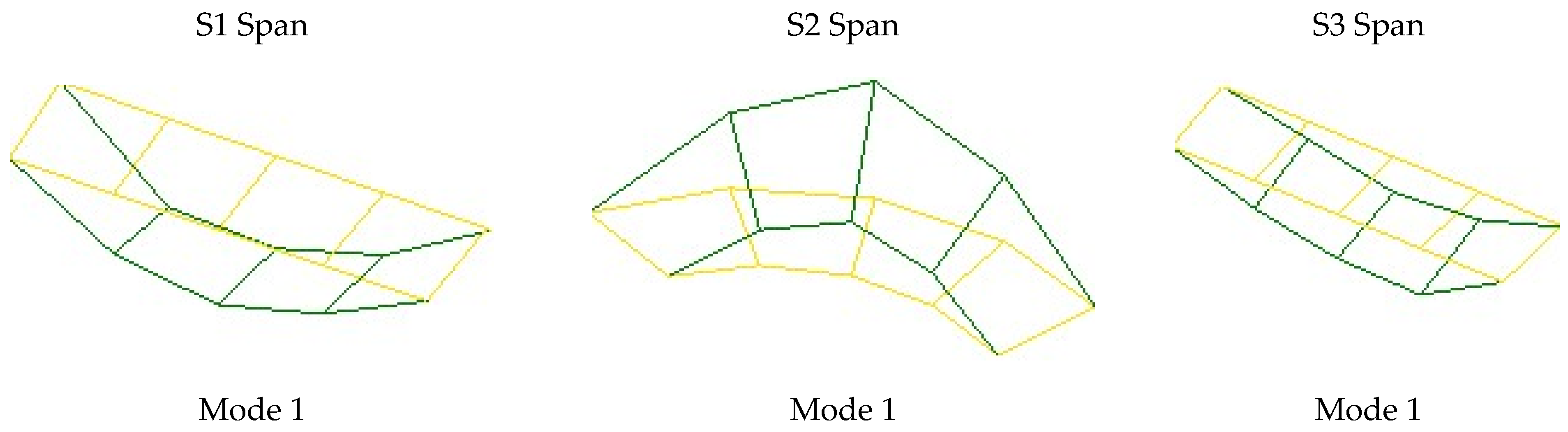
2.5. Operational Modal Analysis Tests
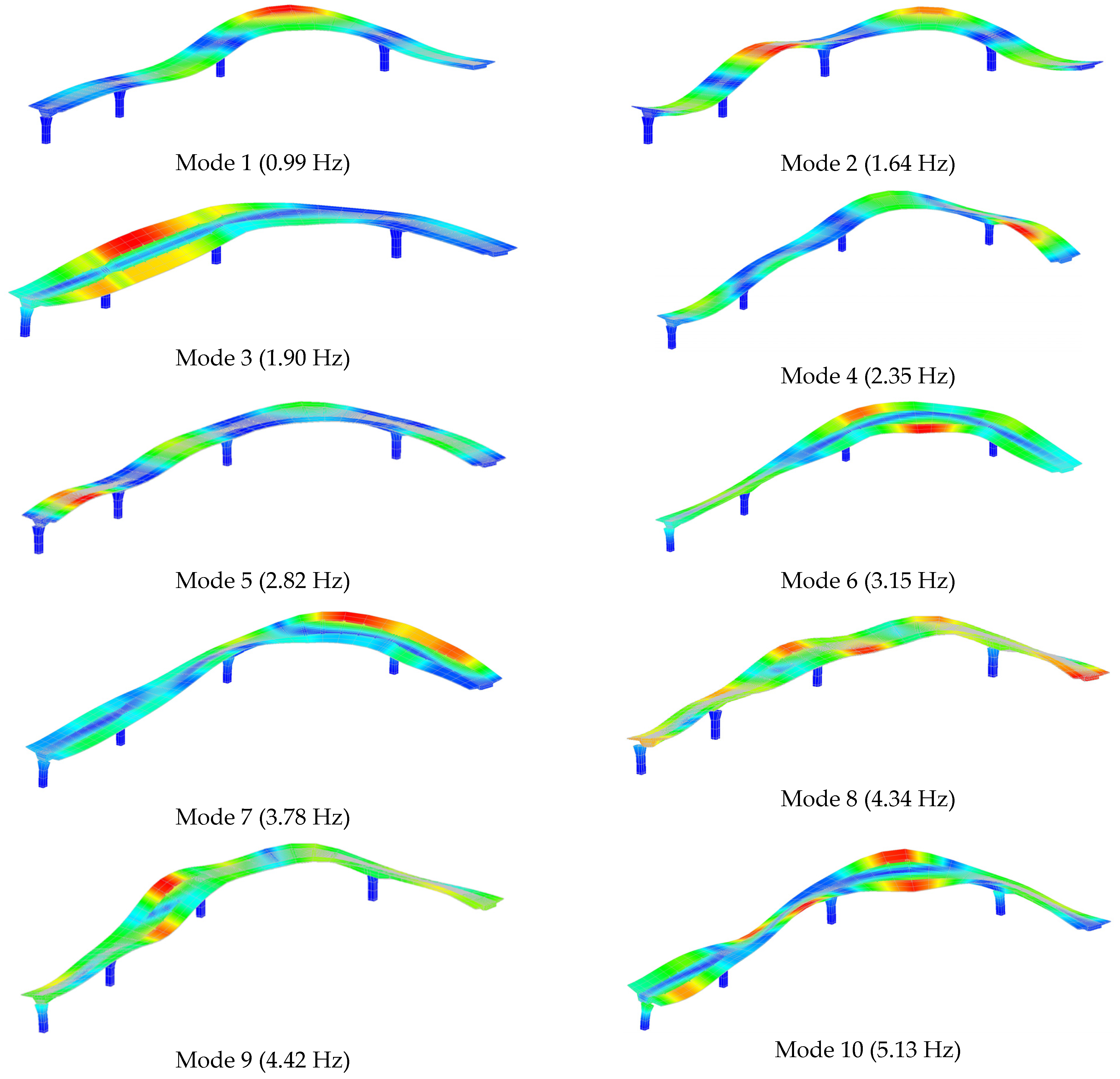
3. Digital Twin Calibration and Validation
4. Evaluation of Test Results
4.1. Static Deformation Data
4.2. Dynamic Deformation Data
4.3. Linearity Control
4.4. Current Situation Assessment
5. Digital Twin Implementation Scope and Limitations
6. Conclusions
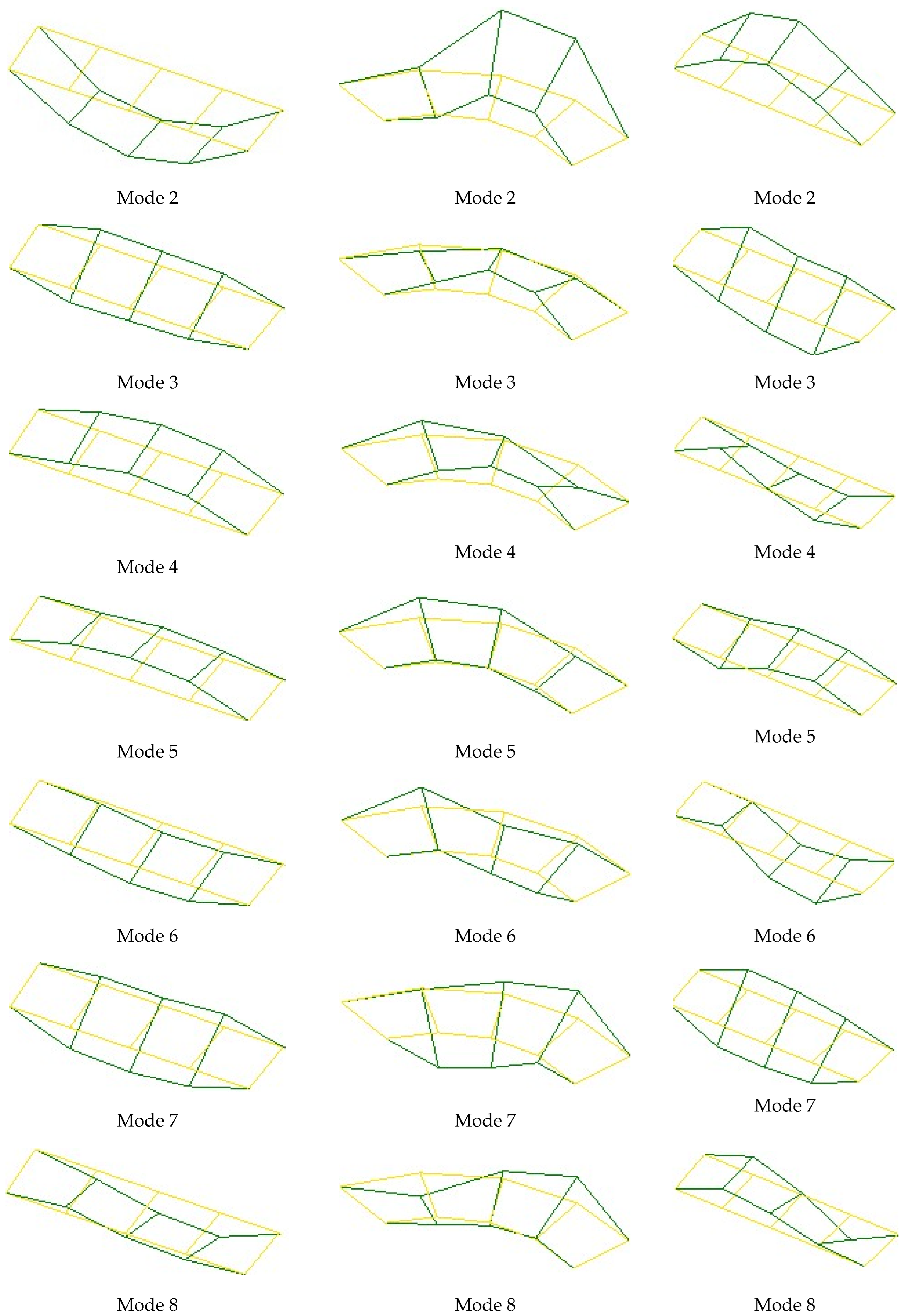
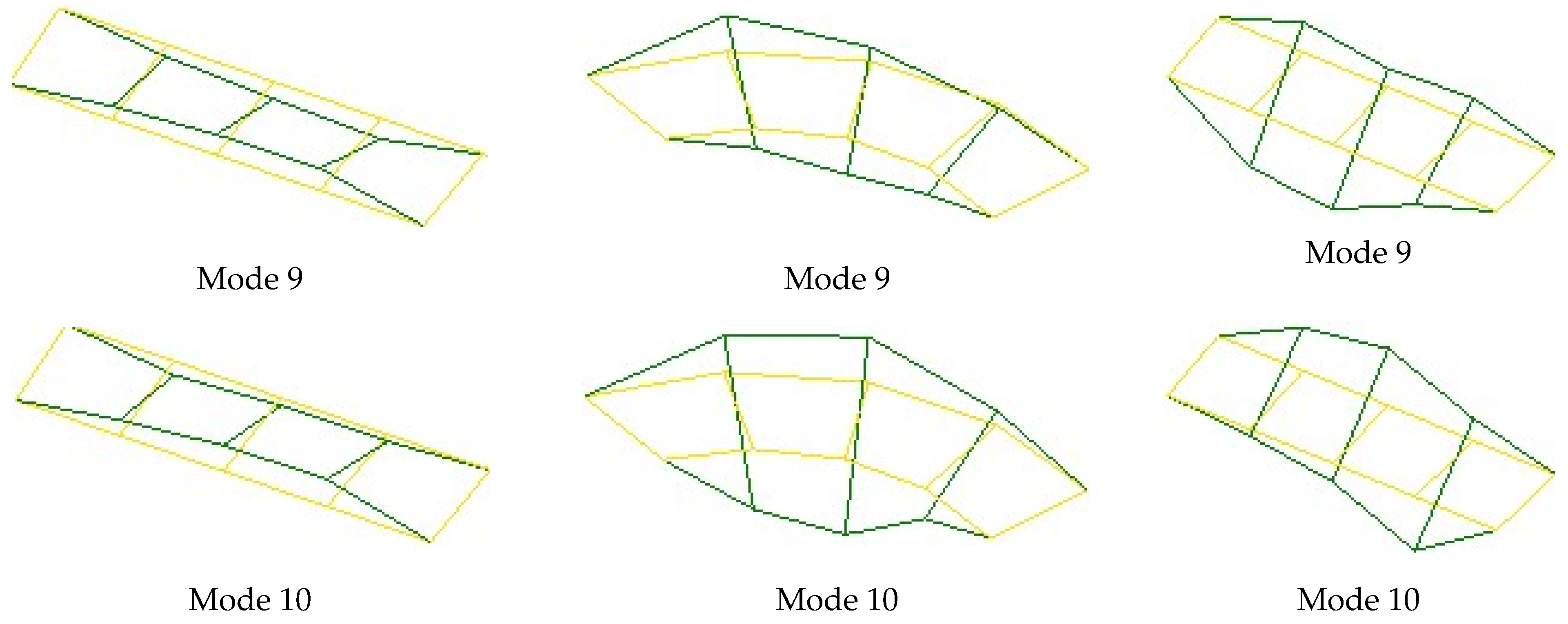
- The initial finite-element model of the bridge was calibrated using the dynamic characteristics (frequencies and mode shapes) obtained from OMA. Differences between the experimental and numerical results, initially as high as 13.22%, were reduced to below 5% through iterative updates to the concrete material properties. This model refinement validated the accuracy of the numerical representation and established a reliable digital twin capable of simulating the actual behavior of the structure.
- Static load tests were performed using 30-ton and 50-ton vehicles under 28 different loading conditions on spans S1, S2, and S3. The displacement values recorded via -the total station were compared to the results of the updated finite-element model. The high degree of agreement between measured and simulated values confirmed the model’s validity. Furthermore, the updated digital twin predicted a displacement of 41.8 mm under the design 100-ton load case, well within the 56.25 mm limit, demonstrating that the bridge operates safely under service loads.
- Dynamic vehicle load tests were conducted across 24 different scenarios using obstacle-induced excitation and two vehicle speeds (20 km/h and 30 km/h). The Dynamic Amplification Factor calculated from accelerometer data complied with the AASHTO LRFD 2017 allowable limit of 33% at 95.6% of the measurement points, indicating that the bridge exhibits stable dynamic behavior under operational loads.
- The linearity of structural response was verified through proportional displacement increases between 30-ton and 50-ton load cases, indicating that the bridge behaves linearly under normal service conditions. Post-test visual inspections revealed no signs of cracking or damage, confirming the structural integrity of the bridge during and after loading.
- In addition to the structural findings, the digital twin constructed in this study offers a validated and test-driven numerical model that can be reused for future decision-making processes. Although it does not operate in real time, the digital twin integrates high-quality field data into a calibrated simulation environment that reflects the actual performance of the bridge. It enables engineers to conduct scenario analyses, predict the impact of different load cases, and plan rehabilitation or strengthening strategies more effectively.
- The test-assisted digital twin approach implemented here bridges the gap between conventional finite-element model updating and real-time monitoring-based digital twin systems. It offers a scalable and economical solution for infrastructure assessment, particularly in contexts where continuous monitoring is not feasible due to budgetary or logistical constraints.
- Unlike predictive digital twin frameworks requiring continuous monitoring and adaptive AI-based modeling throughout the structure’s service life, the presented test-assisted digital twin approach relies on carefully designed field tests combined with finite-element model updating to achieve high model fidelity. This pragmatic strategy enables infrastructure owners to obtain reliable stiffness assessments and digital twin models of existing bridges even without permanent sensing infrastructure, thus making digital twin technologies more accessible and applicable in a broader range of practical scenarios.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Erdal, H.İ. Inspection and Maintenance Management at Bridges. Master’s Thesis, İstanbul University, İstanbul, Türkiye, 2005. [Google Scholar]
- Abudayyeh, O.; Al Bataineh, M.; Abdel-Qader, I. An imaging data model for concrete bridge inspection. Adv. Eng. Softw. 2004, 35, 473–480. [Google Scholar] [CrossRef]
- Kawamura, K.; Miyamoto, A. Condition state evaluation of existing reinforced concrete bridges using neuro-fuzzy hybrid system. Comput. Struct. 2003, 81, 1931–1940. [Google Scholar] [CrossRef]
- Unjoh, S.; Terayama, T.; Adachi, Y.; Hoshikuma, J. Seismic retrofit of existing highway bridges in Japan. Cem. Concr. Compos. 2000, 22, 1–16. [Google Scholar] [CrossRef]
- Grimes, T.C.; Gauntt, F.M.; Davidson, J.S. Local Roads Bridge Replacement Prioritization Database (UTCA Report No.: 00219); UTCA: Tuscaloosa, AL, USA, 2001. [Google Scholar]
- Whelan, M.J.; Gangone, M.V.; Janoyan, K.D.; Jha, R. Real-time wireless vibration monitoring for operational modal analysis of an integral abutment highway bridge. Eng. Struct. 2009, 31, 2224–2235. [Google Scholar] [CrossRef]
- Koo, K.Y.; Brownjohn, J.M.W.; List, D.I.; Cole, R. Structural health monitoring of the Tamar suspension bridge. Struct. Control Health Monit. 2013, 20, 609–625. [Google Scholar] [CrossRef]
- Zhang, J.; Prader, J.; Grimmelsman, K.A.; Moon, F.; Aktan, A.E.; Shama, A. Experimental vibration analysis for structural identification of a long-span suspension bridge. J. Eng. Mech. 2013, 139, 748–759. [Google Scholar] [CrossRef]
- Hao, J. Natural vibration analysis of long-span suspension bridges. In Proceedings of the 2nd International Conference on Civil, Transportation and Environmental Engineering, Shenzhen, China, 10–11 May 2017; Atlantis Press: Dordrecht, The Netherlands, 2017; pp. 193–196. [Google Scholar]
- Zhou, G.D.; Yi, T.H.; Chen, B. Innovative design of a health-monitoring system and its implementation in a complicated long-span arch bridge. J. Aerosp. Eng. 2017, 30, B4016006. [Google Scholar] [CrossRef]
- Sunca, F.; Ergun, M.; Altunışık, A.C.; Günaydın, M.; Okur, F.Y. Modal identification and fatigue behavior of Eynel steel arch highway bridge with calibrated models. J. Civ. Struct. Health Monit. 2021, 11, 1337–1354. [Google Scholar] [CrossRef]
- Günaydın, M.; Sunca, F.; Altunışık, A.C.; Ergun, M.; Okur, F.Y. Nondestructive experimental measurement, model updating, and fatigue life assessment of Çarşamba suspension bridge. J. Bridge Eng. 2022, 27, 05021017. [Google Scholar] [CrossRef]
- Altunışık, A.C.; Sunca, F.; Sevim, B. Ambient vibration-based seismic evaluation of long-span prestressed concrete box-girder bridges under long-duration, near-fault, and far-fault ground motions. J. Earthq. Tsunami 2024, 18, 2450019. [Google Scholar] [CrossRef]
- Doornink, J.D.; Phares, B.M.; Wipf, T.J.; Wood, D.L. Damage detection in bridges through fiber optic structural health monitoring. Proc. SPIE 2006, 6371, 637102. [Google Scholar] [CrossRef]
- Li, S.; Hu, W.; Yang, Y.; Liu, F.; Gan, W. Research of FOG-based measurement technique for continuous curve modes of long-span bridge. Bridge Constr. 2014, 44, 69–74. [Google Scholar]
- Li, L.; Tang, J.; Gan, W.; Hu, W.; Yang, M. The continuous line-shape measurement of bridge based on tri-axis fiber optic gyro. In Proceedings of the 25th International Conference on Optical Fiber Sensors, Jeju, Republic of Korea, 24–28 April 2017; pp. 1–6. [Google Scholar]
- Moughty, J.J.; Casas, J.R. A state of the art review of modal-based damage detection in bridges: Development, challenges, and solutions. Appl. Sci. 2017, 7, 510. [Google Scholar] [CrossRef]
- Li, S.; Zuo, X.; Li, Z.; Wang, H. Applying deep learning to continuous bridge deflection detected by fiber optic gyroscope for damage detection. Opt. Sens. Struct. Health Monit. 2020, 20, 911. [Google Scholar] [CrossRef]
- Biliszczuk, J.; Howiacki, T.; Zuziak, K. Heightened sensitivities: Fibre optic sensing-based insight into crack-width changes on Polish link. Bridge Des. Eng. 2022, 109, 70–71. [Google Scholar]
- Sienko, R.; Bednarski, L.; Howiacki, T. University bridge in Bydgoszcz: Distributed fibre optic measurements (DFOS) of steel anchorages during their renovation. In Proceedings of the 30th International Conference on Structural Failures, Miedzyzdroje, Poland, 23–27 May 2022. [Google Scholar]
- Howiacki, T.; Sienko, R.; Bednarski, L.; Katarzyna, Z. Structural monitoring of concrete, steel, and composite bridges in Poland with distributed fibre optic sensors. Struct. Infrastruct. Eng. 2024, 20, 1213–1229. [Google Scholar] [CrossRef]
- Chen, S.E.; Venkatappa, S.; Moody, J.; Petro, S.; GangaRao, H. A novel damage detection technique using scanning laser vibrometry and a strain energy distribution method. Mater. Eval. 2000, 58, 1389–1394. [Google Scholar]
- Castellini, P.; Revel, G.M.; Tomasini, E.P. Diagnostic of composite materials by laser techniques: Application on panels with different structures and shapes. In Proceedings of the 19th International Modal Analysis Conference, Orlando, FL, USA, 5–8 February 2001; pp. 710–716. [Google Scholar]
- Schmieder, M.; Taylor-Noonan, A.; Heere, R.; Chen, S.E. Laser vibrometry for bridge post-repair investigation. In Dynamics of Bridges, Conference Proceedings of the Society for Experimental Mechanics Series; Springer: New York, NY, USA, 2011; Volume 5. [Google Scholar]
- Xing, W.; Yuan, J.; Szydlowski, M.; Schwingshackl, C. Full-field measurement of lightweight nonlinear structures using three-dimensional scanning laser Doppler vibrometry. AIAA J. 2024, 63, 1523–1540. [Google Scholar] [CrossRef]
- McLaskey, G.C.; Glaser, S.D.; Grosse, C.U. Acoustic emission beamforming for enhanced damage detection. In Proceedings of the Conference on Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, USA, 10–13 March 2008; Volume 6932, p. 693239. [Google Scholar] [CrossRef]
- Tan, A.C.C.; Kaphle, M.; Thambiratnam, D. Structural health monitoring of bridges using acoustic emission technology. In Proceedings of the 8th International Conference on Reliability, Maintainability and Safety (ICRMS 2009), Chengdu, China, 20–24 July 2009; pp. 839–843. [Google Scholar] [CrossRef]
- Tonelli, D.; Rossi, F.; Luchetta, M.; Caspani, V.; Zonta, D.; Migliorino, P.; Selleri, A.; Valeri, E.; Marchiondelli, A.; Ascari, G. Structural health monitoring based on acoustic emissions: Validation on a prestressed concrete bridge tested to failure. Sensors 2020, 20, 7272. [Google Scholar] [CrossRef]
- Ferraro, C.C.; Boyd, A.J.; Hamilton, H.R. Detection and assessment of structural flaws in concrete bridges with NDT methods. Res. Nondestruct. Eval. 2007, 18, 179–192. [Google Scholar] [CrossRef]
- An, Y.K.; Song, H.; Sohn, H. Wireless ultrasonic wavefield imaging via laser for hidden damage detection inside a steel box girder bridge. Smart Mater. Struct. 2014, 23, 095019. [Google Scholar] [CrossRef]
- Cobb, A.C.; Duffer, C.E.; Light, G.M. Evaluation of the feasibility for detecting hidden corrosion damage in multi-layer gusset plates using multiple inspection techniques. In Proceedings of the 10th International Conference on Barkhausen and Micro-Magnetics (ICBM), Baltimore, MD, USA, 21–26 July 2014; pp. 872–879. [Google Scholar]
- Li, B.B.; Liu, B.; Xu, F.; Liu, Y.; Wang, W.T.; Yang, T. Compressive sampling-based ultrasonic computerized tomography technique for damage detection in concrete-filled steel tube in a bridge. Int. J. Distrib. Sens. Netw. 2021, 17, 1550147720986113. [Google Scholar] [CrossRef]
- Kaewsawang, S.; Chaisiriniran, W.; Kaewngam, P.; Chotickai, P. Monitoring damage in PC slabs by modal and ultrasonic tests. Eng. J.-Thail. 2023, 27, 17–27. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the 26th Annual Conference on Neural Information Processing Systems (NIPS 2012), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Zhang, L.; Zhou, G.; Han, Y.; Lin, H.; Wu, Y. Application of Internet of Things technology and convolutional neural network model in bridge crack detection. IEEE Access 2018, 6, 39442–39451. [Google Scholar] [CrossRef]
- Beckman, G.H.; Polyzois, D.; Cha, Y. Deep learning-based automatic volumetric damage quantification using depth camera. Autom. Constr. 2019, 99, 114–124. [Google Scholar] [CrossRef]
- Montaggioli, G.; Puliti, M.; Sabato, A. Automated damage detection of bridges sub-surface defects from infrared images using machine learning. In Proceedings of the Health Monitoring of Structural and Biological Systems XV, Online, USA, 22–26 March 2021; Volume 11593. [Google Scholar] [CrossRef]
- Sevim, B.; Atamturktur, S.; Altunışık, A.C.; Bayraktar, A. Ambient vibration testing and seismic behavior of historical arch bridges under near and far fault ground motions. Bull. Earthq. Eng. 2016, 14, 241–259. [Google Scholar] [CrossRef]
- Altunışık, A.C.; Kalkan, E.; Okur, F.Y.; Karahasan, O.Ş.; Özgan, K. Finite-element model updating and dynamic responses of reconstructed historical timber bridges using ambient vibration test results. J. Perform. Constr. Facil. 2020, 34, 04019085. [Google Scholar] [CrossRef]
- Kocaman, İ.; Kazaz, İ.; Özkaya, S.G. Determination of material properties in masonry arch bridges with non-destructive methods. Dokuz Eylül Univ. Fac. Eng. J. Sci. Eng. 2020, 22, 671–680. [Google Scholar]
- Grieves, M.; Vickers, J. Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems. In Transdisciplinary Perspectives on Complex Systems: New Findings and Approaches; Springer: Cham, Switzerland, 2017; pp. 85–113. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y. Digital twin in industry: State-of-the-art. IEEE Trans. Ind. Inform. 2018, 15, 2405–2415. [Google Scholar] [CrossRef]
- Boschert, S.; Rosen, R. Digital Twin—The Simulation Aspect. In Mechatronic Futures; Springer: Cham, Switzerland, 2018; pp. 59–74. [Google Scholar] [CrossRef]
- Negri, E.; Fumagalli, L.; Macchi, M. A review of the roles of Digital Twin in CPS-based production systems. Procedia Manuf. 2017, 11, 939–948. [Google Scholar] [CrossRef]
- Yuqian, L.; Liu, C.; Kevin, I.; Wang, K.; Huang, H.; Xu, X. Digital Twin-driven smart manufacturing: Connotation, reference model, applications and research issues. Robot. Comput.-Integr. Manuf. 2020, 61, 101837. [Google Scholar] [CrossRef]
- Singh, M.; Fuenmayor, E.; Hinchy, E.P.; Qiao, Y.; Murray, N.; Devine, D. Digital twin: Origin to future. Appl. Syst. Innov. 2021, 4, 36. [Google Scholar] [CrossRef]
- Alam, K.M.; El Saddik, A. C2PS: A digital twin architecture reference model for the cloud-based cyber-physical systems. IEEE Access 2017, 5, 2050–2062. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, C.; Wang, J.; Wang, S.; Lv, D.; Qin, F. Research on digital twin driven rolling bearing model-data fusion life prediction method. IEEE Access 2023, 11, 48611–48627. [Google Scholar] [CrossRef]
- Qin, L.F.; Ren, W.X.; Guo, C.R. A Physics-data hybrid framework to develop bridge digital twin model in structural health monitoring. Int. J. Struct. Stab. Dyn. 2023, 23, 2340037. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, Y.; Lin, Q.; Yu, W.; Pan, W.; Su, A.; Zhao, Y. A digital twin-based assembly model for multi-source variation fusion on vision transformer. J. Manuf. Syst. 2024, 76, 478–501. [Google Scholar] [CrossRef]
- Sun, Z.; Liang, B.; Liu, S.; Liu, Z. Data and Knowledge-Driven Bridge Digital Twin Modeling for Smart Operation and Maintenance. Appl. Sci. 2024, 15, 231. [Google Scholar] [CrossRef]
- Rios, A.J.; Plevris, V.; Nogal, M. Bridge management through digital twin-based anomaly detection systems: A systematic review. Front. Built Environ. 2023, 9, 1176621. [Google Scholar]
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite-element model calibration of a railway vehicle based on experimental modal parameters. Veh. Syst. Dyn. 2013, 51, 821–856. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, M.; Wan, N.; Deng, Z.; He, Z.; Luo, J. Missing measurement data recovery methods in structural health monitoring: The state, challenges and case study. Measurement 2024, 231, 114528. [Google Scholar] [CrossRef]
- Schacht, G.; Krontal, M.; Marx, S.; Bolle, G.; Wismar, H. Loading tests of existing concrete structures: Historical development and present practise. In Proceedings of the Fib Symposium, Prague, Czech Republic, 8–10 June 2011; pp. 8–10. [Google Scholar]
- Moussa, A.I.; Shahawy, M.A. Dynamic and Static Tests of Prestressed Concrete Girder Bridges in Florida; Florida Department of Transportation: Tallahassee, FL, USA, 1993.
- Gatti, M. Structural health monitoring of an operational bridge: A case study. Eng. Struct. 2019, 195, 200–209. [Google Scholar] [CrossRef]
- Hernandez, W.; Viviescas, A.; Riveros-Jerez, C.A. Vehicle bump testing parameters influencing modal identification of long-span segmental prestressed concrete bridges. Sensors 2022, 22, 1219. [Google Scholar] [CrossRef] [PubMed]
- Hassan, M.; Burdet, O.; Favre, R. Analysis and evaluation of bridge behavior under static load testing leading to better design and judgment criteria. In Proceedings of the Fourth Bridge Engineering Conference, San Francisco, CA, USA, 28–30 August 1995; Transportation Research Board (TRB): San Francisco, CA, USA, 1995; pp. 28–30. [Google Scholar]
- Fang, I.K.; Chen, C.R.; Chang, I.S. Field static load test on Kao-Ping-Hsi cable-stayed bridge. J. Bridge Eng. 2004, 9, 531–540. [Google Scholar] [CrossRef]
- Galati, N.; Casadei, P.; Nanni, A. In-Situ Load Testing of Bridge A6101 Lexington, MO; Center for Infrastructure Engineering Studies: Washington, DC, USA, 2005. [Google Scholar]
- Ren, W.X.; Lin, Y.Q.; Peng, X.L. Field load tests and numerical analysis of Qingzhou cable-stayed bridge. J. Bridge Eng. 2007, 12, 261–270. [Google Scholar] [CrossRef]
- Cao, W.J.; Koh, C.G.; Smith, I.F.C. Enhancing static-load-test identification of bridges using dynamic data. Eng. Struct. 2019, 186, 410–420. [Google Scholar] [CrossRef]
- Sun, Z.; Siringoringo, D.M.; Fujino, Y. Load-carrying capacity evaluation of girder bridge using moving vehicle. Eng. Struct. 2021, 229, 111645. [Google Scholar] [CrossRef]
- Meixedo, A.; Ribeiro, D.; Santos, J.; Calçada, R.; Todd, M. Progressive numerical model validation of a bowstring-arch railway bridge based on a structural health monitoring system. J. Civ. Struct. Health Monit. 2021, 11, 421–449. [Google Scholar] [CrossRef]
- Zheng, X.; Du, H.; Zhang, R.; Ma, Q.; Gao, H. Static load test of RC T-beam bridge flexural strengthening with externally bonded steel plates. IOP Conf. Ser. Earth Environ. Sci. 2021, 791, 012018. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Wang, H.; Ning, Y.; Huang, K.; Wang, W. Performance evaluation of a long-span cable-stayed bridge using non-destructive field loading tests. Appl. Sci. 2022, 12, 2367. [Google Scholar] [CrossRef]
- De Angelis, A.; Pecce, M.R. Model assessment of a bridge by load and dynamic tests. Eng. Struct. 2023, 275, 115282. [Google Scholar] [CrossRef]
- Xiao, F.; Mao, Y.; Sun, H.; Chen, G.S.; Tian, G. Stiffness Separation Method for Reducing Calculation Time of Truss Structure Damage Identification. Struct. Control Health Monit. 2024, 2024, 5171542. [Google Scholar] [CrossRef]
- Xiao, F.; Mao, Y.; Tian, G.; Chen, G.S. Partial-Model-Based Damage Identification of Long-Span Steel Truss Bridge Based on Stiffness Separation Method. Struct. Control Health Monit. 2024, 2024, 5530300. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The current development of structural health monitoring for bridges: A review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Bottani, E.; Ciarapica, F.E.; Costantino, F.; Di Donato, L.; Ferraro, A.; Mazzuto, G.; Monteriù, A.; Nardini, G.; Ortenzi, M.; et al. Digital twin reference model development to prevent operators’ risk in process plants. Sustainability 2020, 12, 1088. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, T. Finite Element Model Calibration with Surrogate Model-Based Bayesian Updating: A Case Study of Motor FEM Model. Innov. Appl. Eng. Technol. 2024, 3, 1–13. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, J.; Hu, J.; Ye, Z.; Deng, Z.; Wan, N. Nonlinear modeling of temperature-induced bearing displacement of long-span single-pier rigid frame bridge based on DCNN-LSTM. Case Stud. Therm. Eng. 2024, 53, 103897. [Google Scholar] [CrossRef]
- Vuoto, A.; Funari, M.F.; Lourenço, P.B. On the use of the digital twin concept for the structural integrity protection of architectural heritage. Infrastructures 2023, 8, 86. [Google Scholar] [CrossRef]
- Vuoto, A.; Funari, M.F.; Lourenço, P.B. Shaping digital twin concept for built cultural heritage conservation: A systematic literature review. Int. J. Archit. Herit. 2024, 18, 1762–1795. [Google Scholar] [CrossRef]
- ISO 23247-2; Digital Twin Framework for Manufacturing—Part 2: Reference Architecture. ISO: Geneva, Switzerland, 2021.
- Aheleroff, S.; Xu, X.; Zhong, R.Y.; Lu, Y. Digital twin as a service (DTaaS) in industry 4.0: An architecture reference model. Adv. Eng. Inform. 2021, 47, 101225. [Google Scholar] [CrossRef]
- Kalyon Ulaştırma Mühendislik ve Müşavirlik A.Ş. Structural Analysis Report: Cho’ponota Bridge; Kalyon Ulaştırma Mühendislik ve Müşavirlik A.Ş: Ankara, Türkiye, 2020. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications; AASHTO: Washington, DC, USA, 2017. [Google Scholar]
- PULSE. Computer Software. Bruel and Kjaer, Release 11.2; PULSE: Nærum, Denmark, 2006.
- Dynamic Modal. Dynamic Modal Identification Software, Release 1.0; Dynamic Academy: Trabzon, Türkiye, 2018.
- OMA. Computer Software. Structural Vibration Solution, Release 4.0; OMA: Aalborg, Denmark, 2006.
- Günaydin, M.; Adanur, S.; Altunişik, A.C. Experimental investigation on acceptable difference value in modal parameters for model updating using RC building models. Struct. Eng. Int. 2019, 29, 150–159. [Google Scholar] [CrossRef]



| No. | Element | Material Class |
|---|---|---|
| 1 | Pile | C25/30 |
| 2 | Foundation | C25/30 |
| 3 | Column | C30/35 |
| 4 | Slab | C50/60 |
| Bridge Span | Static Loading Test | Dynamic Loading Test | ||
|---|---|---|---|---|
| Loading Number | Load Status | Loading Number | Load Status | |
| S1 | ST1 | S1-A1B1L3 | D1 | S1-A1B1H20 |
| ST2 | S1-A1B1L2 | D2 | S1-A1B2H20 | |
| ST3 | S1-A1B2L3 | D3 | S1-A1B1H30 | |
| ST4 | S1-A1B2L2 | D4 | S1-A1B2H30 | |
| ST5 | S1-A2B1L3 | D5 | S1-A2B1H20 | |
| ST6 | S1-A2B1L2 | D6 | S1-A2B2H20 | |
| ST7 | S1-A2B2L3 | D7 | S1-A2B1H30 | |
| ST8 | S1-A2B2L2 | D8 | S1-A2B2H30 | |
| S2 | ST9 | S2-A1B1L1 | D9 | S2-A1B1H20 |
| ST10 | S2-A1B1L2 | D10 | S2-A1B2H20 | |
| ST11 | S2-A1B1L3 | D11 | S2-A1B1H30 | |
| ST12 | S2-A1B2L1 | D12 | S2-A1B2H30 | |
| ST13 | S2-A1B2L2 | D13 | S2-A2B1H20 | |
| ST14 | S2-A1B2L3 | D14 | S2-A2B2H20 | |
| ST15 | S2-A2B1L1 | D15 | S2-A2B1H30 | |
| ST16 | S2-A2B1L2 | D16 | S2-A2B2H30 | |
| ST17 | S2-A2B1L3 | ---- | ---- | |
| ST18 | S2-A2B2L1 | ---- | ---- | |
| ST19 | S2-A2B2L2 | ---- | ---- | |
| ST20 | S2-A2B2L3 | ---- | ---- | |
| S3 | ST21 | S3-A1B1L1 | D17 | S3-A1B1H20 |
| ST22 | S3-A1B1L2 | D18 | S3-A1B2H20 | |
| ST23 | S3-A1B2L1 | D19 | S3-A1B1H30 | |
| ST24 | S3-A1B2L2 | D20 | S3-A1B2H30 | |
| ST25 | S3-A2B1L1 | D21 | S3-A2B1H20 | |
| ST26 | S3-A2B1L2 | D22 | S3-A2B2H20 | |
| ST27 | S3-A2B2L1 | D23 | S3-A2B1H30 | |
| ST28 | S3-A2B2L2 | D24 | S3-A2B2H30 | |
| Bridge Span | Measurement No. | X (m) | Y (m) | Z (m) |
|---|---|---|---|---|
| S1 | S1-L11 | 19,804.621 | 69,512.946 | 422.621 |
| S1-L13 | 19,805.154 | 69,509.487 | 421.790 | |
| S1-L15 | 19,805.679 | 69,506.027 | 422.522 | |
| S1-L21 | 19,796.466 | 69,511.709 | 423.096 | |
| S1-L23 | 19,796.993 | 69,508.247 | 422.281 | |
| S1-L25 | 19,797.515 | 69,504.791 | 423.011 | |
| S1-L31 | 19,788.310 | 69,510.475 | 423.525 | |
| S1-L33 | 19,788.832 | 69,507.011 | 422.711 | |
| S1-L35 | 19,789.362 | 69,503.558 | 423.443 | |
| S2 | S2-L11 | 19,768.148 | 69,503.033 | 423.978 |
| S2-L13 | 19,771.272 | 69,499.468 | 423.406 | |
| S2-L15 | 19,774.519 | 69,495.767 | 424.000 | |
| S2-L21 | 19,760.482 | 69,491.887 | 424.003 | |
| S2-L23 | 19,765.012 | 69,490.213 | 423.469 | |
| S2-L25 | 19,769.731 | 69,488.464 | 424.115 | |
| S2-L31 | 19,758.939 | 69,479.325 | 424.100 | |
| S2-L33 | 19,763.121 | 69,479.207 | 423.540 | |
| S2-L35 | 19,767.639 | 69,479.081 | 424.125 | |
| S3 | S3-L11 | 19,767.618 | 69,456.812 | 423.793 |
| S3-L13 | 19,770.541 | 69,458.130 | 423.051 | |
| S3-L15 | 19,773.634 | 69,459.519 | 423.825 | |
| S3-L21 | 19,772.235 | 69,446.555 | 423.302 | |
| S3-L23 | 19,775.165 | 69,447.874 | 422.572 | |
| S3-L25 | 19,778.256 | 69,449.268 | 423.408 | |
| S3-L31 | 19,776.851 | 69,436.301 | 422.772 | |
| S3-L33 | 19,779.783 | 69,437.615 | 422.049 | |
| S3-L35 | 19,782.872 | 69,439.006 | 422.886 |
| Bridge Span | Loading Status | L11 | L13 | L15 | L21 | L23 | L25 | L31 | L33 | L35 |
|---|---|---|---|---|---|---|---|---|---|---|
| S1 | ST1 | −2 | −1 | −1 | −3 | −2 | −2 | −2 | −1 | 0 |
| ST2 | −3 | −2 | −2 | −5 | −4 | −4 | −2 | −2 | −1 | |
| ST3 | −1 | −1 | −2 | −2 | −2 | −3 | −2 | −2 | −1 | |
| ST4 | −2 | −2 | −3 | −3 | −4 | −5 | −2 | −2 | −2 | |
| ST5 | −3 | −2 | −2 | −5 | −4 | −4 | −4 | −3 | −2 | |
| ST6 | −5 | −4 | −3 | −8 | −6 | −6 | −5 | −4 | −2 | |
| ST7 | −2 | −2 | −3 | −4 | −4 | −5 | −3 | −3 | −3 | |
| ST8 | −3 | −4 | −5 | −5 | −6 | −7 | −3 | −4 | −4 | |
| S2 | ST9 | −7 | −5 | 1 | −11 | −6 | 1 | −5 | −2 | 1 |
| ST10 | −8 | −5 | 0 | −16 | −10 | −1 | −9 | −5 | −1 | |
| ST11 | −4 | −3 | 2 | −10 | −6 | 1 | −8 | −4 | 0 | |
| ST12 | −4 | −3 | 1 | −8 | −4 | 2 | −4 | −1 | 2 | |
| ST13 | −5 | −4 | 0 | −11 | −6 | 0 | −6 | −3 | 0 | |
| ST14 | −3 | −2 | 2 | −8 | −4 | 3 | −5 | −2 | 1 | |
| ST15 | −11 | −7 | 1 | −16 | −9 | 0 | −8 | −3 | 1 | |
| ST16 | −15 | −10 | −3 | −27 | −17 | −5 | −16 | −9 | −3 | |
| ST17 | −9 | −6 | 1 | −20 | −12 | −1 | −15 | −9 | −2 | |
| ST18 | −8 | −6 | −1 | −13 | −8 | 0 | −7 | −3 | 1 | |
| ST19 | −11 | −8 | −3 | −19 | −13 | −5 | −12 | −8 | −3 | |
| ST20 | −9 | −5 | 0 | −16 | −10 | −1 | −11 | −7 | −3 | |
| S3 | ST21 | −5 | −5 | −4 | −5 | −4 | −4 | −3 | −2 | −1 |
| ST22 | −5 | −4 | −4 | −7 | −5 | −6 | −5 | −3 | −2 | |
| ST23 | −4 | −5 | −6 | −4 | −5 | −6 | −2 | −2 | −3 | |
| ST24 | −3 | −5 | −6 | −5 | −6 | −9 | −4 | −4 | −6 | |
| ST25 | −7 | −7 | −6 | −7 | −6 | −5 | −5 | −3 | −2 | |
| ST26 | −8 | −7 | −7 | −12 | −10 | −10 | −8 | −6 | −5 | |
| ST27 | −6 | −8 | −10 | −7 | −8 | −10 | −4 | −4 | −5 | |
| ST28 | −7 | −9 | −10 | −10 | −12 | −16 | −6 | −7 | −10 |
| Bridge Span | Loading Status | L11 | L21 | L31 | L15 | L25 | L35 |
|---|---|---|---|---|---|---|---|
| S1 | D1 | 2.86 | 3.8 | 2.09 | 3.29 | 3.91 | 2.16 |
| D2 | 2.21 | 2.89 | 1.59 | 2.36 | 2.82 | 1.6 | |
| D3 | 0.45 | 0.88 | 0.47 | 0.69 | 0.79 | 0.55 | |
| D4 | 0.52 | 0.71 | 0.4 | 0.57 | 0.7 | 0.43 | |
| D5 | 1.25 | 1.6 | 0.95 | 1.39 | 1.63 | 0.97 | |
| D6 | 1.33 | 1.71 | 1.09 | 1.23 | 1.4 | 0.47 | |
| D7 | 0.57 | 0.69 | 0.39 | 0.83 | 0.9 | 0.55 | |
| D8 | 0.95 | 1.43 | 0.92 | 1.01 | 1.31 | 0.66 | |
| S2 | D9 | 1.35 | 2.39 | 1.47 | 0.64 | 1.09 | 0.88 |
| D10 | 1.34 | 2.19 | 1.6 | 1.35 | 1.89 | 1.27 | |
| D11 | 1.13 | 1.19 | 0.91 | 0.49 | 0.75 | 0.46 | |
| D12 | 1.07 | 1.57 | 1 | 0.93 | 1.57 | 1.18 | |
| D13 | 1.58 | 2.32 | 1.75 | 0.61 | 0.79 | 0.74 | |
| D14 | 1.59 | 2.38 | 1.62 | 1.52 | 2.34 | 1.57 | |
| D15 | 1.62 | 1.79 | 1.49 | 0.78 | 0.91 | 0.59 | |
| D16 | 1.21 | 2.05 | 1.56 | 1.39 | 1.99 | 1.41 | |
| S3 | D17 | 1.19 | 1.79 | 0.99 | 0.94 | 1.85 | 0.99 |
| D18 | 1.52 | 1.87 | 1.1 | 1.31 | 1.76 | 1.12 | |
| D19 | 0.88 | 1.43 | 1.32 | 0.93 | 1.16 | 0.84 | |
| D20 | 0.99 | 1.63 | 1.2 | 1.06 | 1.58 | 1.2 | |
| D21 | 1.17 | 1.81 | 1.33 | 1.53 | 1.76 | 1.08 | |
| D22 | 1.49 | 1.84 | 1.13 | 1.17 | 1.71 | 1.21 | |
| D23 | 1.12 | 1.75 | 1.31 | 1.06 | 1.52 | 0.88 | |
| D24 | 1.34 | 2.49 | 1.91 | 1.45 | 2.52 | 1.53 |
| Mode No. | Frequency Values for S1, S2, and S3 Spans (Hz) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 Span | Diff. (%) | S2 Span | Diff. (%) | S3 Span | Diff. (%) | ||||
| Before Loading | After Loading | Before Loading | After | Before | After | ||||
| 1 | 1.12 | 1.11 | 0.89 | 1.12 | 1.11 | 0.89 | 1.12 | 1.11 | 0.89 |
| 2 | 1.87 | 1.89 | 1.07 | 1.89 | 1.88 | 0.53 | 1.89 | 1.86 | 1.59 |
| 3 | 2.12 | 2.12 | 0.00 | 2.13 | 2.13 | 0.00 | 2.12 | 2.07 | 2.36 |
| 4 | 2.53 | 2.57 | 1.58 | 2.51 | 2.54 | 1.20 | 2.56 | 2.51 | 1.95 |
| 5 | 2.75 | 2.78 | 1.09 | 2.75 | 2.75 | 0.00 | 2.74 | 2.75 | 0.36 |
| 6 | 3.34 | 3.35 | 0.30 | 3.35 | 3.34 | 0.30 | 3.35 | 3.34 | 0.30 |
| 7 | 4.03 | 4.07 | 0.99 | 4.04 | 4.03 | 0.25 | 4.04 | 4.02 | 0.50 |
| 8 | 4.28 | 4.25 | 0.70 | 4.28 | 4.25 | 0.70 | 4.25 | 4.25 | 0.00 |
| 9 | 4.58 | 4.55 | 0.66 | 4.57 | 4.53 | 0.88 | 4.55 | 4.55 | 0.00 |
| 10 | 5.26 | 5.23 | 0.57 | 5.25 | 5.23 | 0.38 | 5.28 | 5.23 | 0.95 |
| Mode No. | Frequency Values for S1, S2, and S3 Spans (Hz) | |||||||
|---|---|---|---|---|---|---|---|---|
| Initial FEM | S1 | S2 | S3 | Max. Diff. (%) | ||||
| Before Loading | After Loading | Before Loading | After Loading | Before Loading | After Loading | |||
| 1 | 0.99 | 1.12 | 1.11 | 1.12 | 1.11 | 1.12 | 1.11 | 11.61 |
| 2 | 1.64 | 1.87 | 1.89 | 1.89 | 1.88 | 1.89 | 1.86 | 13.22 |
| 3 | 1.90 | 2.12 | 2.12 | 2.13 | 2.13 | 2.12 | 2.07 | 10.80 |
| 4 | 2.35 | 2.53 | 2.57 | 2.51 | 2.54 | 2.56 | 2.51 | 8.56 |
| 5 | 2.82 | 2.75 | 2.78 | 2.75 | 2.75 | 2.74 | 2.75 | 2.48 |
| 6 | 3.15 | 3.34 | 3.35 | 3.35 | 3.34 | 3.35 | 3.34 | 5.97 |
| 7 | 3.78 | 4.03 | 4.07 | 4.04 | 4.03 | 4.04 | 4.02 | 7.13 |
| 8 | 4.34 | 4.28 | 4.25 | 4.28 | 4.25 | 4.25 | 4.25 | 1.40 |
| 9 | 4.42 | 4.58 | 4.55 | 4.57 | 4.53 | 4.55 | 4.55 | 3.49 |
| 10 | 5.13 | 5.26 | 5.23 | 5.25 | 5.23 | 5.28 | 5.23 | 2.84 |
| Mode No. | Frequency Values for S1, S2, and S3 Spans (Hz) | |||||||
|---|---|---|---|---|---|---|---|---|
| Updated FEM | S1 | S2 | S3 | Max. Diff. (%) | ||||
| Before Loading | After Loading | Before Loading | After Loading | Before Loading | After Loading | |||
| 1 | 1.08 | 1.12 | 1.11 | 1.12 | 1.11 | 1.12 | 1.11 | 4.17 |
| 2 | 1.80 | 1.87 | 1.89 | 1.89 | 1.88 | 1.89 | 1.86 | 5.00 |
| 3 | 2.03 | 2.12 | 2.12 | 2.13 | 2.13 | 2.12 | 2.07 | 4.93 |
| 4 | 2.57 | 2.53 | 2.57 | 2.51 | 2.54 | 2.56 | 2.51 | 2.33 |
| 5 | 2.88 | 2.75 | 2.78 | 2.75 | 2.75 | 2.74 | 2.75 | 4.86 |
| 6 | 3.41 | 3.34 | 3.35 | 3.35 | 3.34 | 3.35 | 3.34 | 2.05 |
| 7 | 4.07 | 4.03 | 4.07 | 4.04 | 4.03 | 4.04 | 4.02 | 1.23 |
| 8 | 4.70 | 4.28 | 4.25 | 4.28 | 4.25 | 4.25 | 4.25 | 9.57 |
| 9 | 4.79 | 4.58 | 4.55 | 4.57 | 4.53 | 4.55 | 4.55 | 5.01 |
| 10 | 5.50 | 5.26 | 5.23 | 5.25 | 5.23 | 5.28 | 5.23 | 4.91 |
| Bridge Span | Loading Status | Displacement Results Obtained from Test and FEM (mm) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L11 | L13 | L15 | L21 | L23 | L25 | L31 | L33 | L35 | |||||||||||
| Test | FEM | Test | FEM | Test | FEM | Test | FEM | Test | FEM | Test | FEM | Test | FEM | Test | FEM | Test | FEM | ||
| S1 | ST1 | −2 | −2.28 | −1 | −1.87 | −1 | −1.46 | −3 | −3.77 | −2 | −3.00 | −2 | −2.22 | −2 | −3.53 | −1 | −2.53 | 0 | −1.43 |
| ST2 | −3 | −3.79 | −2 | −3.20 | −2 | −2.62 | −5 | −5.56 | −4 | −4.66 | −4 | −3.62 | −2 | −3.62 | −2 | −2.96 | −1 | −2.28 | |
| ST3 | −1 | −1.62 | −1 | −2.08 | −2 | −2.56 | −2 | −2.36 | −2 | −3.25 | −3 | −4.12 | −2 | −1.13 | −2 | −2.38 | −1 | −2.48 | |
| ST4 | −2 | −2.64 | −2 | −3.40 | −3 | −4.16 | −3 | −3.54 | −4 | −4.89 | −5 | −6.12 | −2 | −1.78 | −2 | −2.92 | −2 | −3.03 | |
| ST5 | −3 | −3.80 | −2 | −3.11 | −2 | −2.43 | −5 | −6.29 | −4 | −4.95 | −4 | −3.71 | −4 | −5.89 | −3 | −4.22 | −2 | −2.39 | |
| ST6 | −5 | −6.32 | −4 | −5.35 | −3 | −4.36 | −8 | −9.27 | −6 | −7.76 | −6 | −6.04 | −5 | −6.05 | −4 | −4.93 | −2 | −3.80 | |
| ST7 | −2 | −2.69 | −2 | −3.48 | −3 | −4.27 | −4 | −3.94 | −4 | −5.42 | −5 | −6.88 | −3 | −1.87 | −3 | −3.97 | −3 | −5.89 | |
| ST8 | −3 | −4.40 | −4 | −5.67 | −5 | −6.93 | −5 | −5.90 | −6 | −8.16 | −7 | −10.20 | −3 | −2.96 | −4 | −4.85 | −4 | −5.42 | |
| S2 | ST9 | −7 | −8.30 | −5 | −5.72 | 1 | −3.05 | −11 | −10.31 | −6 | −6.92 | 1 | −3.62 | −5 | −4.93 | −2 | −3.44 | 1 | −1.94 |
| ST10 | −8 | −8.77 | −5 | −6.48 | 0 | −4.26 | −16 | −16.54 | −10 | −10.25 | −1 | −6.09 | −9 | −10.34 | −5 | −7.32 | −1 | −4.29 | |
| ST11 | −4 | −4.38 | −3 | −3.16 | 2 | −1.91 | −10 | −10.32 | −6 | −6.82 | 1 | −3.30 | −8 | −9.92 | −4 | −6.85 | 0 | −2.97 | |
| ST12 | −4 | −3.20 | −3 | −3.68 | 1 | −3.94 | −8 | −4.45 | −4 | −4.34 | 2 | −4.67 | −4 | −2.55 | −1 | −2.15 | 2 | −2.35 | |
| ST13 | −5 | −4.53 | −4 | −4.46 | 0 | −4.35 | −11 | −8.51 | −6 | −7.06 | 0 | −6.75 | −6 | −6.27 | −3 | −4.74 | 0 | −4.33 | |
| ST14 | −3 | −2.04 | −2 | −2.19 | 2 | −2.34 | −8 | −4.62 | −4 | −4.40 | 3 | −4.21 | −5 | −3.95 | −2 | −3.64 | 1 | −3.92 | |
| ST15 | −11 | −13.85 | −7 | −9.53 | 1 | −5.08 | −16 | −17.18 | −9 | −10.85 | 0 | −6.04 | −8 | −8.20 | −3 | −5.74 | 1 | −3.23 | |
| ST16 | −15 | −14.61 | −10 | −10.88 | −3 | −7.10 | −27 | −27.57 | −17 | −18.91 | −5 | −10.15 | −16 | −17.23 | −9 | −12.19 | −3 | −7.14 | |
| ST17 | −9 | −9.18 | −6 | −5.26 | 1 | −3.19 | −20 | −17.21 | −12 | −11.36 | −1 | −5.51 | −15 | −17.79 | −9 | −11.42 | −2 | −4.95 | |
| ST18 | −8 | −6.40 | −6 | −6.14 | −1 | −6.56 | −13 | −9.41 | −8 | −7.67 | 0 | −7.79 | −7 | −4.25 | −3 | −3.58 | 1 | −3.91 | |
| ST19 | −11 | −9.59 | −8 | −7.42 | −3 | −7.24 | −19 | −18.17 | −13 | −12.96 | −5 | −11.25 | −12 | −8.53 | −8 | −7.90 | −3 | −7.22 | |
| ST20 | −9 | −4.45 | −5 | −3.65 | 0 | −3.90 | −16 | −7.72 | −10 | −7.34 | −1 | −7.03 | −11 | −5.24 | −7 | −6.07 | −3 | −6.52 | |
| S3 | ST21 | −5 | −6.36 | −5 | −3.98 | −4 | −1.72 | −5 | −6.49 | −4 | −4.40 | −4 | −2.32 | −3 | −3.88 | −2 | −2.24 | −1 | −0.61 |
| ST22 | −5 | −6.09 | −4 | −4.55 | −4 | −3.05 | −7 | −9.39 | −5 | −7.09 | −6 | −4.63 | −5 | −6.19 | −3 | −4.19 | −2 | −2.17 | |
| ST23 | −4 | −0.98 | −5 | −4.52 | −6 | −8.22 | −4 | −2.16 | −5 | −5.45 | −6 | −8.75 | −2 | −0.25 | −2 | −2.82 | −3 | −5.40 | |
| ST24 | −3 | −1.55 | −5 | −4.98 | −6 | −8.40 | −5 | −3.51 | −6 | −7.90 | −9 | −12.14 | −4 | −1.08 | −4 | −4.62 | −6 | −7.16 | |
| ST25 | −7 | −10.60 | −7 | −6.63 | −6 | −2.87 | −7 | −10.81 | −6 | −7.33 | −5 | −3.88 | −5 | −6.47 | −3 | −3.73 | −2 | −1.02 | |
| ST26 | −8 | −10.17 | −7 | −7.59 | −7 | −5.01 | −12 | −15.65 | −10 | −11.81 | −10 | −7.71 | −8 | −10.32 | −6 | −6.98 | −5 | −3.62 | |
| ST27 | −6 | −1.62 | −8 | −7.54 | −10 | −13.71 | −7 | −3.61 | −8 | −9.09 | −10 | −14.59 | −4 | −0.82 | −4 | −4.71 | −5 | −9.00 | |
| ST28 | −7 | −2.59 | −9 | −8.30 | −10 | −14.00 | −10 | −5.85 | −12 | −13.17 | −16 | −20.23 | −6 | −1.79 | −7 | −7.71 | −10 | −13.61 | |
| Bridge Span | Loading Status | L11 | L21 | L31 | L15 | L25 | L35 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| St. | Dyna. | DAF (%) | St. | Dyna. | DAF (%) | St. | Dyna. | DAF (%) | St. | Dyna. | DAF (%) | St. | Dyna. | DAF (%) | St. | Dyna. | DAF (%) | ||
| S1 | D1 | 3 | 2.86 | 95.33 | 5 | 3.8 | 76 | 2 | 2.09 | 104.5 | 2 | 3.29 | 164.5 | 4 | 3.91 | 97.75 | 1 | 2.16 | 216 |
| D2 | 3 | 2.21 | 73.67 | 5 | 2.89 | 57.8 | 2 | 1.59 | 79.5 | 2 | 2.36 | 118 | 4 | 2.82 | 70.5 | 1 | 1.6 | 160 | |
| D3 | 2 | 0.45 | 22.5 | 3 | 0.88 | 29.33 | 2 | 0.47 | 23.5 | 3 | 0.69 | 23 | 5 | 0.79 | 15.8 | 2 | 0.55 | 27.5 | |
| D4 | 2 | 0.52 | 26 | 3 | 0.71 | 23.67 | 2 | 0.4 | 20 | 3 | 0.57 | 19 | 5 | 0.7 | 14 | 2 | 0.43 | 21.5 | |
| D5 | 5 | 1.25 | 25 | 8 | 1.6 | 20 | 5 | 0.95 | 19 | 4 | 1.39 | 34.75 | 6 | 1.63 | 27.17 | 2 | 0.97 | 48.5 | |
| D6 | 5 | 1.33 | 26.6 | 8 | 1.71 | 21.38 | 5 | 1.09 | 21.8 | 4 | 1.23 | 30.75 | 6 | 1.4 | 23.33 | 2 | 0.47 | 23.5 | |
| D7 | 3 | 0.57 | 19 | 5 | 0.69 | 13.8 | 3 | 0.39 | 13 | 5 | 0.83 | 16.6 | 7 | 0.9 | 12.86 | 4 | 0.55 | 13.75 | |
| D8 | 3 | 0.95 | 31.67 | 5 | 1.43 | 28.6 | 3 | 0.92 | 30.67 | 5 | 1.01 | 20.2 | 7 | 1.31 | 18.71 | 4 | 0.66 | 16.5 | |
| S2 | D9 | 8 | 1.35 | 16.88 | 16 | 2.39 | 14.94 | 9 | 1.47 | 16.33 | 0 | 0.64 | - | 1 | 1.09 | 109 | 1 | 0.88 | 88 |
| D10 | 8 | 1.34 | 16.75 | 16 | 2.19 | 13.69 | 9 | 1.6 | 17.78 | 0 | 1.35 | - | 1 | 1.89 | 189 | 1 | 1.27 | 127 | |
| D11 | 5 | 1.13 | 22.6 | 11 | 1.19 | 10.82 | 6 | 0.91 | 15.17 | 0 | 0.49 | - | 0 | 0.75 | - | 1 | 0.46 | 46 | |
| D12 | 5 | 1.07 | 21.4 | 11 | 1.57 | 14.27 | 6 | 1 | 16.67 | 0 | 0.93 | - | 0 | 1.57 | - | 1 | 1.18 | 118 | |
| D13 | 15 | 1.58 | 10.53 | 27 | 2.32 | 8.59 | 16 | 1.75 | 10.94 | 3 | 0.61 | 20.33 | 5 | 0.79 | 15.8 | 0 | 0.74 | - | |
| D14 | 15 | 1.59 | 10.6 | 27 | 2.38 | 8.81 | 16 | 1.62 | 10.13 | 3 | 1.52 | 50.67 | 5 | 2.34 | 46.8 | 0 | 1.57 | - | |
| D15 | 11 | 1.62 | 14.73 | 19 | 1.79 | 9.42 | 12 | 1.49 | 12.42 | 3 | 0.78 | 26 | 5 | 0.91 | 18.2 | 3 | 0.59 | 19.67 | |
| D16 | 11 | 1.21 | 11 | 19 | 2.05 | 10.79 | 12 | 1.56 | 13 | 3 | 1.39 | 46.33 | 5 | 1.99 | 39.8 | 3 | 1.41 | 47 | |
| S3 | D17 | 5 | 1.19 | 23.8 | 7 | 1.79 | 25.57 | 5 | 0.99 | 19.8 | 4 | 0.94 | 23.5 | 5 | 1.85 | 37 | 2 | 0.99 | 49.5 |
| D18 | 5 | 1.52 | 30.4 | 7 | 1.87 | 26.71 | 5 | 1.1 | 22 | 4 | 1.31 | 32.75 | 5 | 1.76 | 35.2 | 2 | 1.12 | 56 | |
| D19 | 3 | 0.88 | 29.33 | 5 | 1.43 | 28.6 | 4 | 1.32 | 33 | 6 | 0.93 | 15.5 | 9 | 1.16 | 12.89 | 6 | 0.84 | 14 | |
| D20 | 3 | 0.99 | 33 | 5 | 1.63 | 32.6 | 4 | 1.2 | 30 | 6 | 1.06 | 17.67 | 9 | 1.58 | 17.56 | 6 | 1.2 | 20 | |
| D21 | 8 | 1.17 | 14.63 | 12 | 1.81 | 15.08 | 8 | 1.33 | 16.63 | 7 | 1.53 | 21.86 | 10 | 1.76 | 17.6 | 5 | 1.08 | 21.6 | |
| D22 | 8 | 1.49 | 18.63 | 12 | 1.84 | 15.33 | 8 | 1.13 | 14.13 | 7 | 1.17 | 16.71 | 10 | 1.71 | 17.1 | 5 | 1.21 | 24.2 | |
| D23 | 7 | 1.12 | 16 | 10 | 1.75 | 17.5 | 6 | 1.31 | 21.83 | 10 | 1.06 | 10.6 | 16 | 1.52 | 9.5 | 10 | 0.88 | 8.8 | |
| D24 | 7 | 1.34 | 19.14 | 10 | 2.49 | 24.9 | 6 | 1.91 | 31.83 | 10 | 1.45 | 14.5 | 16 | 2.52 | 15.75 | 10 | 1.53 | 15.3 | |
| Bridge Span | Loading Status | Vehicle Load (KN) | Load Ratio | L23 | Displacement Ratio |
|---|---|---|---|---|---|
| S1 | ST2 | 300 | 1.67 | −4 | 1.50 |
| ST6 | 500 | −6 | |||
| ST4 | 300 | 1.67 | −4 | 1.50 | |
| ST8 | 500 | −6 | |||
| S2 | ST10 | 300 | 1.67 | −10 | 1.70 |
| ST16 | 500 | −17 | |||
| ST13 | 300 | 1.67 | −6 | 2.17 | |
| ST19 | 500 | −13 | |||
| S3 | ST22 | 300 | 1.67 | −5 | 2.00 |
| ST26 | 500 | −10 | |||
| ST24 | 300 | 1.67 | −6 | 2.00 | |
| ST28 | 500 | −12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okur, F.Y. Towards a Digital Twin Approach for Structural Stiffness Assessment: A Case Study on the Cho’ponota L1 Bridge. Appl. Sci. 2025, 15, 6854. https://doi.org/10.3390/app15126854
Okur FY. Towards a Digital Twin Approach for Structural Stiffness Assessment: A Case Study on the Cho’ponota L1 Bridge. Applied Sciences. 2025; 15(12):6854. https://doi.org/10.3390/app15126854
Chicago/Turabian StyleOkur, Fatih Yesevi. 2025. "Towards a Digital Twin Approach for Structural Stiffness Assessment: A Case Study on the Cho’ponota L1 Bridge" Applied Sciences 15, no. 12: 6854. https://doi.org/10.3390/app15126854
APA StyleOkur, F. Y. (2025). Towards a Digital Twin Approach for Structural Stiffness Assessment: A Case Study on the Cho’ponota L1 Bridge. Applied Sciences, 15(12), 6854. https://doi.org/10.3390/app15126854






