Short-Term Energy Consumption Forecasting Analysis Using Different Optimization and Activation Functions with Deep Learning Models
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
- Data will be organized.
- 4 different architectures will be used.
- To The effect of epoch numbers on the study will be examined.
- 6 different methods will be used as activation functions.
- 11 different methods will be used as optimization functions.
3.1. Data Analysis
3.1.1. Data
3.1.2. Exploratory Data Analysis
Descriptive Statistics, Data Organization, and Time Plot
Seasonal Plots
3.2. Deep Learning Study
- SEED = 123
- batch_size = 128
- return_sequence = True
- target = ‘PJME_MW’ *
- n_hours = 24 **
- train_size = 0.8 ***
- cols_to_analyze = [“PJME_MW”, “year”, “month”, “week”, “day”, “hour”]
- model = Sequential ()
- model.add (Dense (1))
- model.compile (optimizer = ‘adam’, loss = ‘mse’, metrics = [‘accuracy’])
3.3. Creating the Program Interface
4. Working
4.1. Analysis of Consumption Forecast Using 11 Different Optimizer Methods on Four Different Models
4.2. 4 Analysis of Consumption Forecast Using 10 Epochs, 50 Epochs, and 100 Epochs Using 11 Different Optimizer Methods on Four Different Models
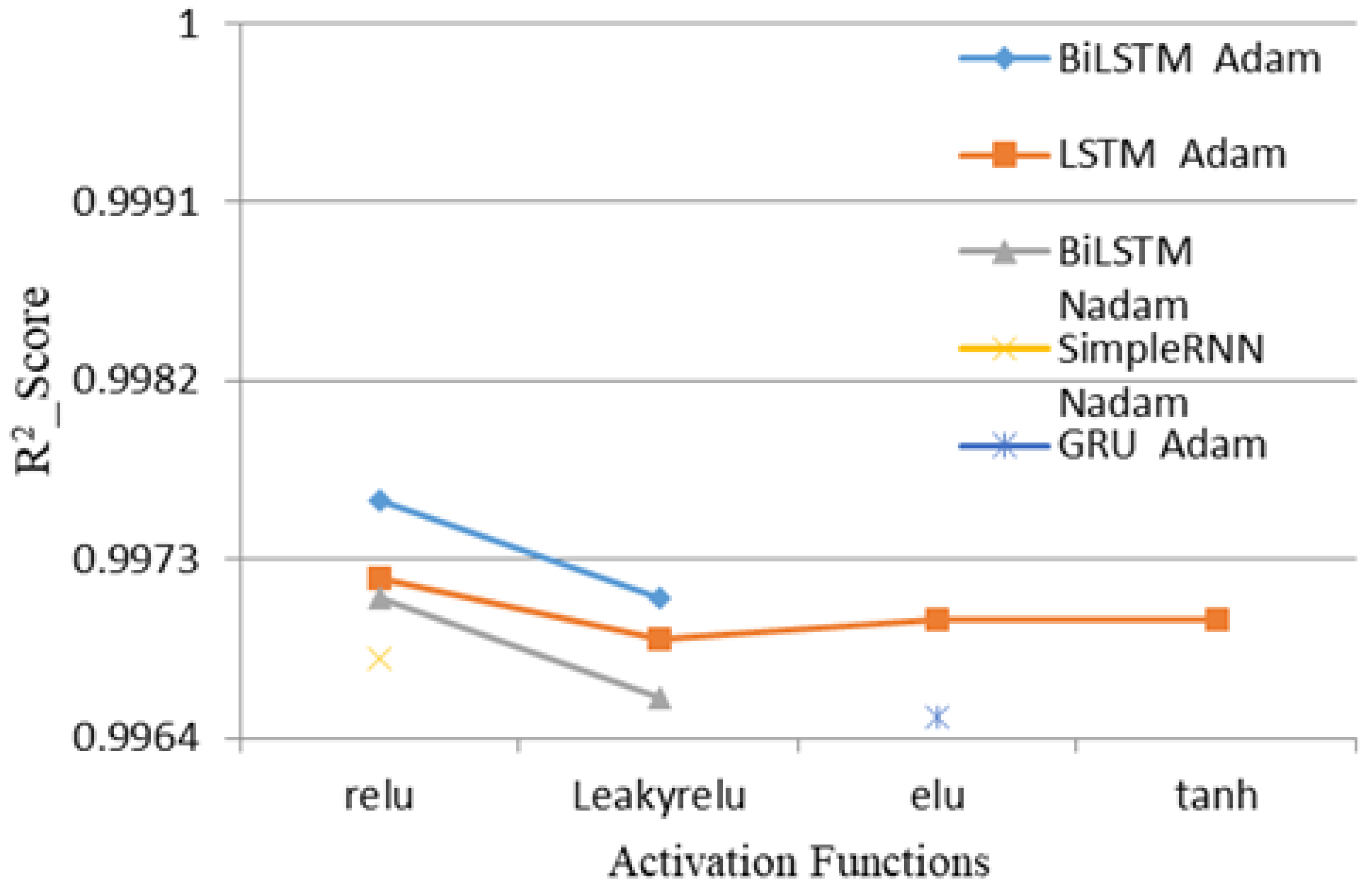
4.3. Analysis of Consumption Forecast Using Four Different Models, Six Different Activation Functions, and 11 Different Optimization Methods
5. Results of the Study
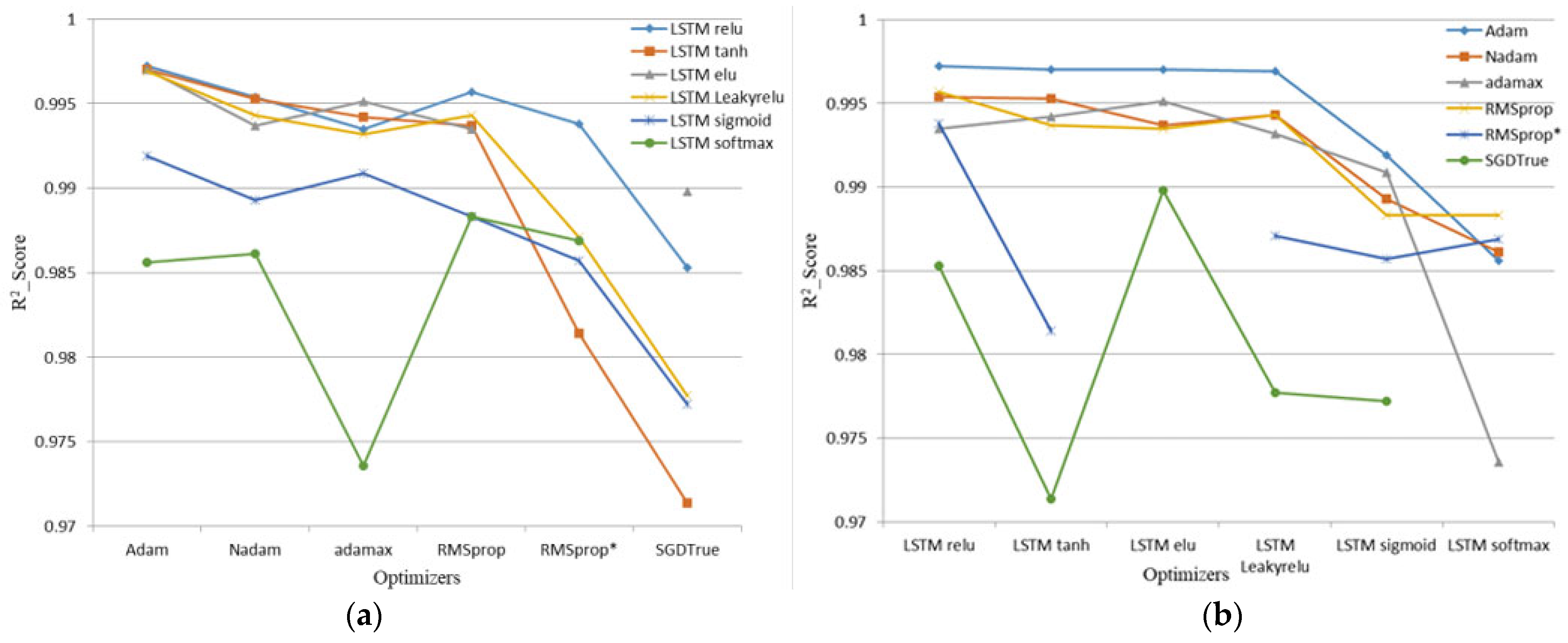
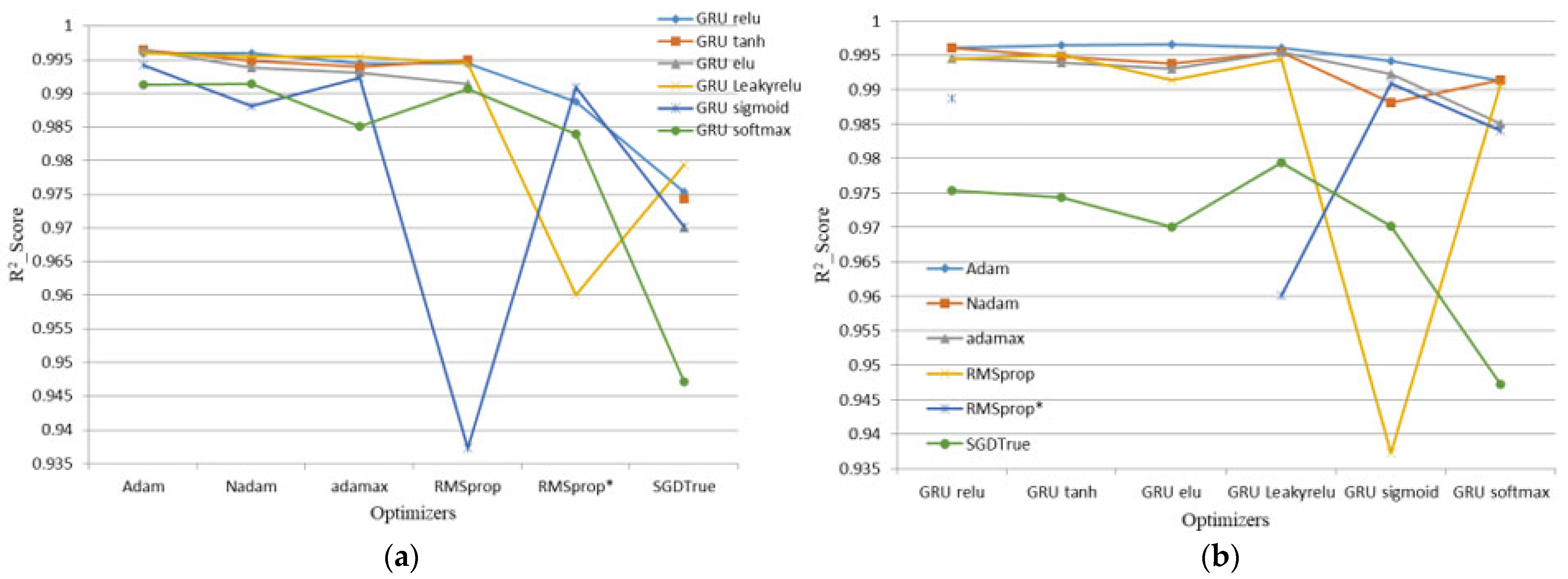
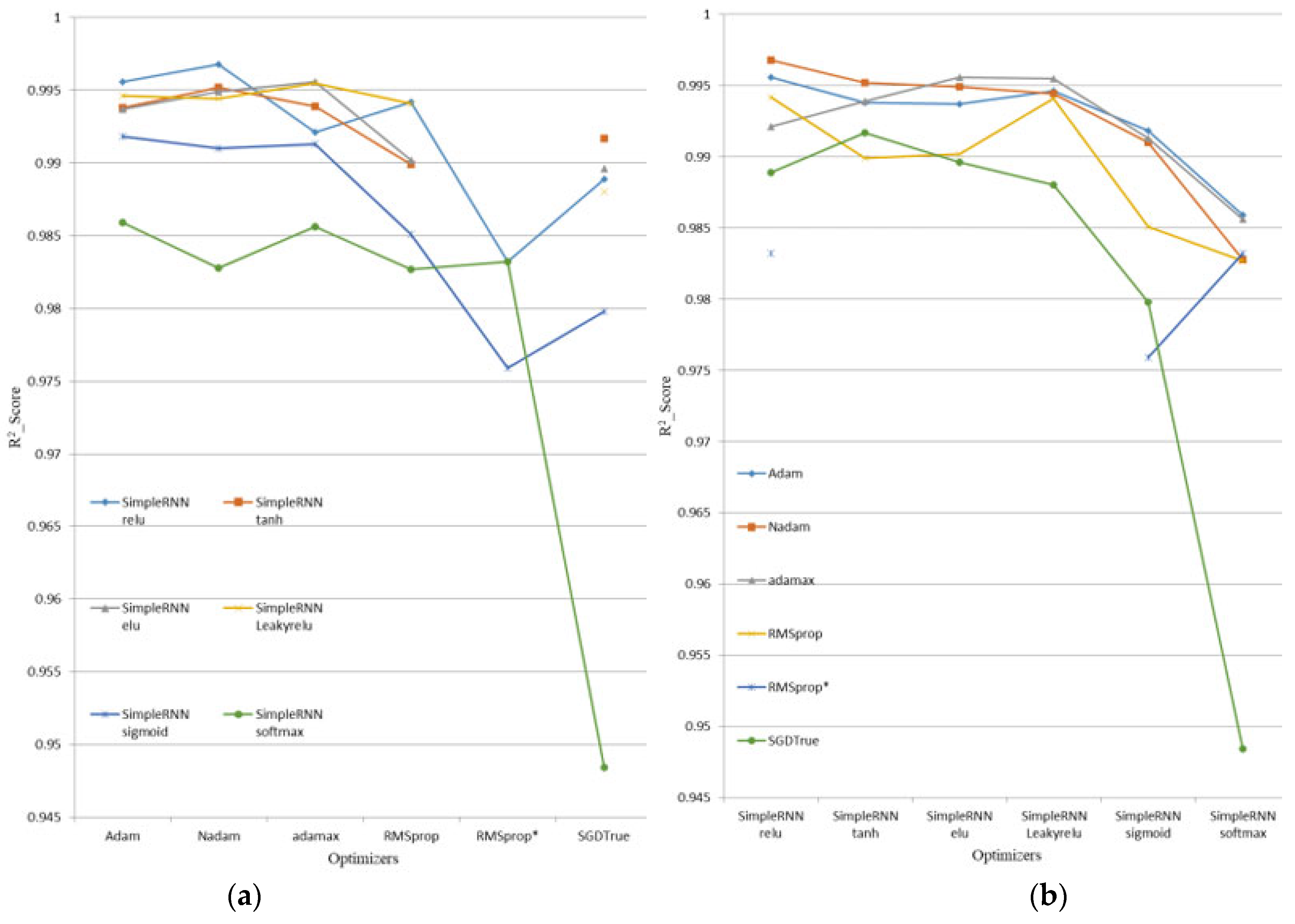
5.1. Results of the Estimation Made Using Four Different Models and 11 Different Optimization Methods
5.2. Results of the Study Using Four Different Models, 11 Different Optimizers, and 10–50–100 Epochs
5.3. Results of the Study Using Four Different Models, Six Different Activation Functions, and 11 Different Optimizers
5.4. Best Results Achieved
6. Discussion, and Conclusions
- Emphasizing the importance of electricity consumption estimation in smart grid energy systems.
- Showing that more accurate data will be obtained with data editing EDA.
- Showing that there are actually many successful options and models, even though single options are usually offered in similar studies.
- Showing the success of the proposed models in estimating energy consumption correctly. Also, obtaining different models and successful results with different variations.
- Outlining statistical metrics with RMSE, MAE, and R2 to evaluate model performances.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, M.; Khan, D.M.; Alshanbari, H.M.; El-Bagoury, A.A.-A.H. Prediction of Complex Stock Market Data Using an Improved Hybrid EMD-LSTM Model. Appl. Sci. 2023, 13, 1429. [Google Scholar] [CrossRef]
- Mndawe, S.T.; Paul, B.S.; Doorsamy, W. Development of a Stock Price Prediction Framework for Intelligent Media and Technical Analysis. Appl. Sci. 2022, 12, 719. [Google Scholar] [CrossRef]
- Jarrah, M.; Derbali, M. Predicting Saudi Stock Market Index by Using Multivariate Time Series Based on Deep Learning. Appl. Sci. 2023, 13, 8356. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, Q.; Wen, Z.; Hu, M.; Xu, W. Research on a Time Series Data Prediction Model Based on Causal Feature Weight Adjustment. Appl. Sci. 2023, 13, 10782. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Chen, Y.-S. Fundamental Analysis of Stock Trading Systems using Classification Techniques. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; pp. 1377–1382. [Google Scholar]
- Vargas, M.R.; de Lima, B.S.L.P.; Evsukoff, A.G. Deep Learning for Stock Market Prediction from Financial News Articles. In Proceedings of the 2017 IEEE International Conference on Computational Intelligence and Virtual Environments for Measurement Systems and Applications (CIVEMSA), Annecy, France, 26–28 June 2017; pp. 60–65. [Google Scholar] [CrossRef]
- Li, C.; Zhao, M.; Liu, Y.; Xu, F. Air Temperature Forecasting using Traditional and Deep Learning Algorithms. In Proceedings of the 7th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 18–20 December 2020; pp. 189–194. [Google Scholar] [CrossRef]
- Escalona-Llaguno, M.I.; Solís-Sánchez, L.O.; Castañeda-Miranda, C.L.; Olvera-Olvera, C.A.; Martinez-Blanco, M.d.R.; Guerrero-Osuna, H.A.; Castañeda-Miranda, R.; Díaz-Flórez, G.; Ornelas-Vargas, G. Comparative Analysis of Solar Radiation Forecasting Techniques in Zacatecas, Mexico. Appl. Sci. 2024, 14, 7449. [Google Scholar] [CrossRef]
- Lyu, C.; Eftekharnejad, S. Probabilistic Solar Generation Forecasting for Rapidly Changing Weather Conditions. IEEE Access 2024, 12, 79091–79103. [Google Scholar] [CrossRef]
- Wu, D.; Jia, Z.; Zhang, Y.; Wang, J. Predicting Temperature and Humidity in Roadway with Water Trickling Using Principal Component Analysis-Long Short-Term Memory-Genetic Algorithm Method. Appl. Sci. 2023, 13, 13343. [Google Scholar] [CrossRef]
- Rosca, C.-M.; Carbureanu, M.; Stancu, A. Data-Driven Approaches for Predicting and Forecasting Air Quality in Urban Areas. Appl. Sci. 2025, 15, 4390. [Google Scholar] [CrossRef]
- Swain, D.; Kumar, M.; Nour, A.; Patel, K.; Bhatt, A.; Acharya, B.; Bostani, A. Remaining Useful Life Predictor for EV Batteries Using Machine Learning. IEEE Access 2024, 12, 134418–134426. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Jiang, G.; Li, J.; Wang, Y. Early fault detection of wind turbines based on operational condition clustering and optimized deep belief network modeling. Energies 2019, 12, 984. [Google Scholar] [CrossRef]
- Zou, Y.; Sun, W.; Wang, H.; Xu, T.; Wang, B. Research on Bearing Remaining Useful Life Prediction Method Based on Double Bidirectional Long Short-Term Memory. Appl. Sci. 2025, 15, 4441. [Google Scholar] [CrossRef]
- Wu, M.; Yue, C.; Zhang, F.; Sun, R.; Tang, J.; Hu, S.; Zhao, N.; Wang, J. State of Health Estimation and Remaining Useful Life Prediction of Lithium-Ion Batteries by Charging Feature Extraction and Ridge Regression. Appl. Sci. 2024, 14, 3153. [Google Scholar] [CrossRef]
- Alsmadi, L.; Lei, G.; Li, L. Forecasting Day-Ahead Electricity Demand in Australia Using a CNN-LSTM Model with an Attention Mechanism. Appl. Sci. 2025, 15, 3829. [Google Scholar] [CrossRef]
- Mukhtar, M.; Oluwasanmi, A.; Yimen, N.; Qinxiu, Z.; Ukwuoma, C.C.; Ezurike, B.; Bamisile, O. Development and Comparison of Two Novel Hybrid Neural Network Models for Hourly Solar Radiation Prediction. Appl. Sci. 2022, 12, 1435. [Google Scholar] [CrossRef]
- Ayaz Atalan, Y.; Atalan, A. Testing the Wind Energy Data Based on Environmental Factors Predicted by Machine Learning with Analysis of Variance. Appl. Sci. 2025, 15, 241. [Google Scholar] [CrossRef]
- Energy Forecasting. A Blog by Dr. Tao Hong. Available online: http://blog.drhongtao.com/2014/10/very-short-short-medium-long-term-load-forecasting.html (accessed on 29 May 2025).
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Tan, Z.; Zhang, J.; Wang, J.; Xu, J. Day-ahead electricity price forecasting using wavelet transform combined with ARIMA and GARCH models. Appl. Energy 2010, 87, 3606–3610. [Google Scholar] [CrossRef]
- Esener, I.I.; Yüksel, T.; Kurban, M. Artificial Intelligence Based Hybrid Structures for Short-Term Load Forecasting Without Temperature Data. In Proceedings of the 11th International Conference on Machine Learning and Applications, Boca Raton, FL, USA, 12–15 December 2012; pp. 457–462. [Google Scholar] [CrossRef]
- Zhang, X.M.; Grolinger, K.; Capretz, M.A.M. Forecasting Residential Energy Consumption Using Support Vector Regressions. In Proceedings of the IEEE International Conference on Machine Learning and Applications, Orlando, FL, USA, 17–20 December 2018; pp. 110–117. [Google Scholar]
- Yang, M.; Li, W.; Zhang, H.; Wang, H. Parameters Optimization Improvement of SVM on Load Forecasting. In Proceedings of the 8th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 27–28 August 2016; IEEE: New York, NY, USA, 2016; pp. 257–260. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, W.; Hu, T.; Xu, X. Evolutionary double attention-based long short-term memory model for building energy prediction: Case study of a green building. Appl. Energy 2021, 288, 116660. [Google Scholar] [CrossRef]
- Fan, C.; Sun, Y.; Zhao, Y.; Song, M.; Wang, J. Deep learning-based feature engineering methods for improved building energy prediction. Appl. Energy 2019, 240, 35–45. [Google Scholar] [CrossRef]
- Zhu, T.; Ran, Y.; Zhou, X.; Wen, Y. A Survey of Predictive Maintenance: Systems, Purposes and Approaches. arXiv 2024, arXiv:1912.07383v2. [Google Scholar] [CrossRef]
- Fan, C.; Wang, J.; Gang, W.; Li, S. Assessment of deep recurrent neural network-based strategies for short-term building energy predictions. Appl. Energy 2019, 236, 700–710. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Muzaffar, S.; Afshari, A. Short-Term Load Forecasts Using LSTM Networks. Energy Procedia 2019, 158, 2922–2927. [Google Scholar] [CrossRef]
- Wang, C.; Yan, Z.; Li, Q.; Zhu, Z.; Zhang, C. Energy Consumption Prediction for Drilling Pumps Based on a Long Short-Term Memory Attention Method. Appl. Sci. 2024, 14, 10750. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A Comparison of ARIMA and LSTM in Forecasting Time Series. In Proceedings of the 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar] [CrossRef]
- IDahlan, A.; Ariateja, D.; Hamami, F.; Heryanto. The Implementation of Building Intelligent Smart Energy using LSTM Neural Network. In Proceedings of the 2021 International Conference on Artificial Intelligence and Mechatronics Systems (AIMS), Bandung, Indonesia, 28–30 April 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Wang, J.Q.; Du, Y.; Wang, J. LSTM-based long-term energy consumption prediction with periodicity. Energy 2020, 197, 117197. [Google Scholar] [CrossRef]
- Ungureanu, S.; Topa, V.; Cziker, A.C. Deep Learning for Short-Term Load Forecasting—Industrial Consumer Case Study. Appl. Sci. 2021, 11, 10126. [Google Scholar] [CrossRef]
- Almalki, A.J.; Wocjan, P. Forecasting Method based upon GRU-based Deep Learning Model. In Proceedings of the 2020 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 16–18 December 2020; pp. 534–538. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H. Insights Into LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2019, 7, 67718–67725. [Google Scholar] [CrossRef]
- Yang, S.; Yu, X.; Zhou, Y. LSTM and GRU Neural Network Performance Comparison Study: Taking Yelp Review Dataset as an Example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 1–4 June 2020; pp. 98–101. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The Performance of LSTM and BiLSTM in Forecasting Time Series. In Proceedings of the IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar] [CrossRef]
- Xu, J.; Zeng, P. Short-term Load Forecasting by BiLSTM Model Based on Multidimensional Time-domain Feature. In Proceedings of the 4th International Conference on Neural Networks, Information and Communication Engineering (NNICE), Guangzhou, China, 19–21 January 2024; pp. 1526–1530. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. Predictions for COVID-19 with deep learning models of LSTM, GRU, and Bi-LSTM. Chaos Solitons Fractals 2020, 140, 110212. [Google Scholar] [CrossRef]
- Şişmanoğlu, G.; Koçer, F.; Önde, M.A.; Sahingoz, O.K. Price Forecasting in Stock Exchange with Deep Learning Methods. BEU J. Sci. 2020, 9, 434–445. [Google Scholar] [CrossRef][Green Version]
- Irfan, M.; Shaf, A.; Ali, T.; Zafar, M.; Rahman, S.; Mursal, S.N.F.; AlThobiani, F.; Almas, M.A.; Attar, H.M.; Abdussamiee, N.; et al. Multi-region electricity demand prediction with ensemble deep neural networks. PLoS ONE 2023, 18, e0285456. [Google Scholar] [CrossRef] [PubMed]
- Alıoghlı, A.A.; Yıldırım Okay, F. IoT-Based Energy Consumption Prediction Using Transformers. Gazi Univ. J. Sci. Part A Eng. Innov. 2024, 11, 304–323. [Google Scholar] [CrossRef]
- Khan, Z.A.; Ullah, A.; Haq, I.U.; Hamdy, M.; Mauro, G.M.; Muhammad, K.; Hijji, M.; Baik, S.W. Efficient Short-Term Electricity Load Forecasting for Effective Energy Management. Sustain. Energy Technol. Assess. 2022, 53 Part A, 102337. [Google Scholar] [CrossRef]
- Energy Consumption Dataset, Kaggle. Available online: https://www.kaggle.com/datasets/raminhuseyn/energy-consumption-dataset/data (accessed on 29 May 2025).
- Time Series Forecasting: Exploratory Data Analysis, Kaggle. Available online: https://www.kaggle.com/code/raminhuseyn/time-series-forecasting-exploratory-data-analysis (accessed on 29 May 2025).
- Time Series Forecasting: A Practical Guide to Exploratory Data Analysis, Towards Data Science. Available online: https://towardsdatascience.com/time-series-forecasting-a-practical-guide-to-exploratory-data-analysis-a101dc5f85b1/ (accessed on 29 May 2025).
- Mellit, A.; Pavan, A.M.; Lughi, V. Deep learning neural networks for short-term photovoltaic power forecasting. Renew. Energy 2021, 172, 276–288. [Google Scholar] [CrossRef]
- Alizadegan, H.; Rashidi Malki, B.; Radmehr, A.; Karimi, H.; Ilani, M.A. Comparative study of long short-term memory (LSTM), bidirectional LSTM, and traditional machine learning approaches for energy consumption prediction. Energy Explor. Exploit. 2024, 43, 281–301. [Google Scholar] [CrossRef]
- Torres, J.F.; Martínez-Álvarez, F.; Troncoso, A. A deep LSTM network for the Spanish electricity consumption forecasting. Neural Comput. Applic 2022, 34, 10533–10545. [Google Scholar] [CrossRef]
- Alsharekh, M.F.; Habib, S.; Dewi, D.A.; Albattah, W.; Islam, M.; Albahli, S. Improving the Efficiency of Multistep Short-Term Electricity Load Forecasting via R-CNN with ML-LSTM. Sensors 2022, 22, 6913. [Google Scholar] [CrossRef] [PubMed]
- Ali, A.N.; Etem, T. Hourly energy consumption forecasting by LSTM and ARIMA methods. J. Comput. Electr. Electron. Eng. Sci. 2025, 3, 14–20. [Google Scholar] [CrossRef]
- Khalil, M.; McGough, A.S.; Pourmirza, Z.; Pazhoohesh, M.; Walker, S. Machine Learning, Deep Learning and Statistical Analysis for forecasting building energy consumption—A systematic review. Eng. Appl. Artif. Intell. 2022, 115, 105287. [Google Scholar] [CrossRef]
- Liu, J.; Ahmad, F.A.; Samsudin, K.; Hashim, F.; Kadir, M.Z.A.A. Performance Evaluation of Activation Functions in Deep Residual Networks for Short-Term Load Forecasting. IEEE Access 2025, 13, 78618–78633. [Google Scholar] [CrossRef]
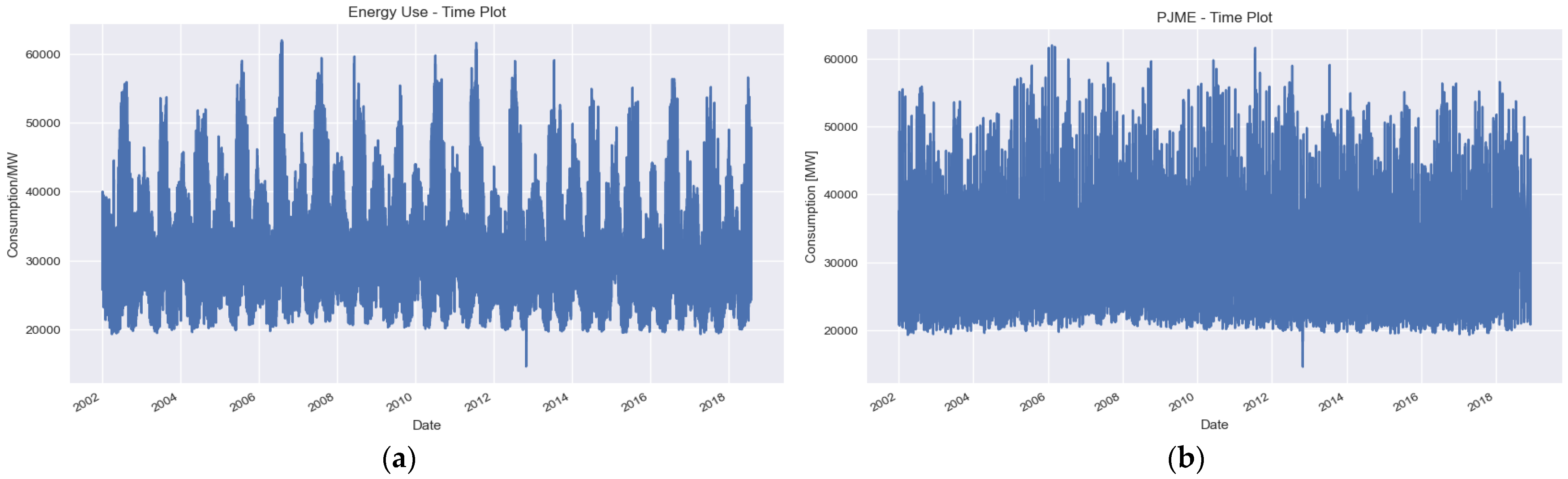













| (a) | (b) | ||||
|---|---|---|---|---|---|
| Line No | Date Time | PJME_MW | Line No | Date Time | PJME_MW |
| 1 | 2002.12.31 01:00 | 26,498.0 | 1 | 1.01.2002 01:00 | 30,393.0 |
| 2 | 2002.12.31 02:00 | 25,147.0 | 2 | 1.01.2002 02:00 | 29,265.0 |
| 3 | 2002.12.31 03:00 | 24,574.0 | 3 | 1.01.2002 03:00 | 28,357.0 |
| 4 | 2002.12.31 04:00 | 24,393.0 | 4 | 1.01.2002 04:00 | 27,899.0 |
| 5 | 2002.12.31 05:00 | 24,860.0 | 5 | 1.01.2002 05:00 | 28,057.0 |
| 145362 | 2018.01.1 20:00 | 44,284.0 | 145388 | 2.08.2018 20:00 | 44,057.0 |
| 145363 | 2018.01.1 21:00 | 43,751.0 | 145389 | 2.08.2018 21:00 | 43,256.0 |
| 145364 | 2018.01.1 22:00 | 42,402.0 | 145390 | 2.08.2018 22:00 | 41,552.0 |
| 145365 | 2018.01.1 23:00 | 40,164.0 | 145391 | 2.08.2018 23:00 | 38,500.0 |
| 145366 | 2018.01.2 00:00 | 38,608.0 | 145392 | 3.08.2018 00:00 | 35,486.0 |
| Date Time | PJME_MW | Year | Month | Week | Hour | Day | day_str | Year_Month |
|---|---|---|---|---|---|---|---|---|
| 1.01.2002 01:00 | 30,393.0 | 2002 | 1 | 1 | 01:00:00 | 1 | Tue | 2002_1 |
| 1.01.2002 02:00 | 29,265.0 | 2002 | 1 | 1 | 02:00:00 | 1 | Tue | 2002_1 |
| 1.01.2002 03:00 | 28,357.0 | 2002 | 1 | 1 | 03:00:00 | 1 | Tue | 2002_1 |
| 1.01.2002 04:00 | 27,899.0 | 2002 | 1 | 1 | 04:00:00 | 1 | Tue | 2002_1 |
| 1.01.2002 05:00 | 28,057.0 | 2002 | 1 | 1 | 05:00:00 | 1 | Tue | 2002_1 |
| Method | How to Use in the Program |
|---|---|
| RMSprop* | optimizer = tf.keras.optimizers.RMSprop (learning_rate = 0.01, rho = 0.9) |
| SGDTrue | optimizer = tf.keras.optimizers.SGD (lr = 0.01, decay = 1 × 10−5, momentum = 0.9, nesterov = True) |
| SGDFalse | optimizer = tf.keras.optimizers.SGD (lr = 0.001, decay = 1 × 10−5, momentum = 1.0, nesterov = False) |
| Model | Optimizer | test_rmse | test-mae | test_R2 | Model | Optimizer | test_rmse | test-mae | test_R2 |
|---|---|---|---|---|---|---|---|---|---|
| LSTM(50, activation = ‘relu’ | Adam | 339.33 | 242.54 | 0.9972 | SimpleRNN(50, activation = ‘relu’ | Nadam | 368.15 | 265.96 | 0.9968 |
| Nadam | 428.91 | 321.56 | 0.9954 | Adam | 425.05 | 307.47 | 0.9956 | ||
| RMSprop | 420.57 | 288.89 | 0.9957 | RMSprop | 486.2 | 357.39 | 0.9942 | ||
| RMSprop* | 500.28 | 376.88 | 0.9938 | adamax | 567.34 | 440.71 | 0.9921 | ||
| adamax | 517.6 | 406.57 | 0.9935 | SGDTrue | 667.51 | 503.7 | 0.9889 | ||
| SGDTrue | 768.55 | 586.43 | 0.9853 | RMSprop* | 812.6 | 664.71 | 0.9832 | ||
| SGD | 1602.39 | 1284.1 | 0.9294 | SGD | 904.34 | 684.67 | 0.9792 | ||
| adagrad | 2278.76 | 1838.13 | 0.8518 | adagrad | 1857.1 | 1488.04 | 0.9031 | ||
| Ftrl | 5526.37 | 4603.25 | −5.2028 | Ftrl | 3173.83 | 2492.14 | 0.4742 | ||
| adadelta | 6749.2 | 5649.35 | −5.44 | adadelta | 5071.94 | 4243.3 | −0.5113 | ||
| SGDFalse | 13,125.06 | 11,938.01 | −1 × 1013 | SGDFalse | 17,577.15 | 16,466.97 | −2 × 1012 | ||
| GRU(50, activation = ‘relu’ | Adam | 412.18 | 296.07 | 0.996 | Bidirectional(LSTM(50, activation = ‘relu’ | Adam | 313.04 | 223.66 | 0.9976 |
| Nadam | 404.5 | 296.4 | 0.996 | Nadam | 345.03 | 255.65 | 0.9971 | ||
| adamax | 481.16 | 366.41 | 0.9945 | adamax | 458.3 | 342.28 | 0.9948 | ||
| RMSprop | 474.57 | 347.39 | 0.9944 | RMSprop | 564.17 | 458.31 | 0.9923 | ||
| RMSprop* | 659.23 | 537.33 | 0.9887 | RMSprop* | 655.86 | 518.52 | 0.989 | ||
| SGDTrue | 961.56 | 721.47 | 0.9754 | SGDTrue | 831.81 | 635.59 | 0.9829 | ||
| SGD | 1336.02 | 1082.17 | 0.9546 | SGD | 1480.73 | 1165.06 | 0.9419 | ||
| adagrad | 1935.03 | 1535.2 | 0.8824 | adagrad | 2212.38 | 1727.57 | 0.865 | ||
| Ftrl | 4800.64 | 3921.81 | −1.7584 | Ftrl | 4940.55 | 4151.66 | −2.66 | ||
| adadelta | 6497.18 | 5390.8 | −5.6841 | adadelta | 6296.76 | 5378.12 | −8.6355 | ||
| SGDFalse | 12,246.21 | 10,396.46 | −4 × 1013 | SGDFalse | 11,978.96 | 10,797.69 | 0 |
| Epochs | 10 Epochs | 50 Epochs | 100 Epochs | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | Optimizer | test rmse | test mae | test_R2 | test rmse | test mae | test_R2 | test rmse | test mae | test_R2 |
| LSTM(50, activation = ‘relu’ | Adam | 571 | 448 | 0.9918 | 339 | 243 | 0.9972 | 289 | 208 | 0.9979 |
| Nadam | 660 | 515 | 0.9885 | 429 | 322 | 0.9954 | 311 | 229 | 0.9976 | |
| RMSprop | 810 | 653 | 0.9838 | 421 | 289 | 0.9957 | 536 | 430 | 0.9931 | |
| RMSprop* | 828 | 691 | 0.9819 | 500 | 377 | 0.9938 | 2602 | 2198 | 0.7719 | |
| adamax | 1282 | 985 | 0.9542 | 518 | 407 | 0.9935 | 345 | 256 | 0.9971 | |
| SGDTrue | 1727 | 1348 | 0.9095 | 769 | 586 | 0.9853 | 607 | 448 | 0.9909 | |
| SGD | 2219 | 1792 | 0.8494 | 1602 | 1284 | 0.9294 | 965 | 753 | 0.9761 | |
| adagrad | 4293 | 3464 | −0.6808 | 2279 | 1838 | 0.8518 | 2076 | 1678 | 0.8796 | |
| Ftrl | 6401 | 5272 | −8.7777 | 5526 | 4603 | −5.2028 | 4754 | 3896 | −1.4893 | |
| adadelta | 9462 | 7775 | −2.6307 | 6749 | 5649 | −5.44 | 4214 | 3415 | −0.5044 | |
| SGDFalse | 6851 | 6365 | −0.2154 | 13,125 | 11,938 | −1 × 1013 | 33,342 | 32,704 | −7.4604 | |
| GRU(50, activation = ‘relu’ | Adam | 601 | 472 | 0.991 | 412 | 296 | 0.996 | 339 | 237 | 0.9972 |
| Nadam | 643 | 488 | 0.9896 | 405 | 296 | 0.996 | 358 | 266 | 0.9969 | |
| adamax | 908 | 707 | 0.9787 | 481 | 366 | 0.9945 | 418 | 308 | 0.9959 | |
| RMSprop | 729 | 587 | 0.9868 | 475 | 347 | 0.9944 | 538 | 431 | 0.993 | |
| RMSprop* | 826 | 625 | 0.9809 | 659 | 537 | 0.9887 | 690 | 564 | 0.9873 | |
| SGDTrue | 1328 | 1033 | 0.9534 | 962 | 721 | 0.9754 | 733 | 546 | 0.9862 | |
| SGD | 1725 | 1378 | 0.9207 | 1336 | 1082 | 0.9546 | 1173 | 942 | 0.965 | |
| adagrad | 3868 | 3063 | −0.3151 | 1935 | 1535 | 0.8824 | 1713 | 1386 | 0.9248 | |
| Ftrl | 6174 | 5109 | −9.9445 | 4801 | 3922 | −1.7584 | 3567 | 2837 | 0.1859 | |
| adadelta | 7176 | 5724 | −4.2308 | 6497 | 5391 | −5.6841 | 4605 | 3768 | −1.6678 | |
| SGDFalse | 12,883 | 11,131 | −4 × 1013 | 12,246 | 10,396 | −4 × 1013 | 47,910 | 47,468 | −3 × 1014 | |
| SimpleRNN(50, activation = ‘relu’ | Nadam | 583 | 444 | 0.9912 | 368 | 266 | 0.9968 | 397 | 300 | 0.9962 |
| Adam | 765 | 592 | 0.985 | 425 | 307 | 0.9956 | 396 | 275 | 0.9962 | |
| RMSprop | 926 | 786 | 0.9783 | 486 | 357 | 0.9942 | 440 | 306 | 0.9953 | |
| adamax | 789 | 602 | 0.9844 | 567 | 441 | 0.9921 | 416 | 310 | 0.9958 | |
| SGDTrue | 930 | 716 | 0.9779 | 668 | 504 | 0.9889 | 615 | 457 | 0.9906 | |
| RMSprop* | 832 | 615 | 0.9814 | 813 | 665 | 0.9832 | 1150 | 941 | 0.963 | |
| SGD | 1640 | 1300 | 0.9215 | 904 | 685 | 0.9792 | 744 | 555 | 0.9861 | |
| adagrad | 2566 | 2035 | 0.7921 | 1857 | 1488 | 0.9031 | 1550 | 1242 | 0.9355 | |
| Ftrl | 5403 | 4469 | −3.4172 | 3174 | 2492 | 0.4742 | 1673 | 1350 | 0.9184 | |
| adadelta | 9941 | 8009 | −0.7133 | 5072 | 4243 | −0.5113 | 2686 | 2132 | 0.7625 | |
| SGDFalse | 14,965 | 13,796 | −4 × 1015 | 17,577 | 16,467 | −2 × 1012 | 19,404 | 18,287 | 0 | |
| Epochs | 10 Epochs | 50 Epochs | 70 Epochs | |||||||
| Bidirectional(LSTM(50, activation = ‘relu’ | Adam | 532 | 404 | 0.9929 | 313 | 224 | 0.9976 | 321 | 228 | 0.9975 |
| Nadam | 563 | 438 | 0.992 | 345 | 256 | 0.9971 | 337 | 253 | 0.9972 | |
| adamax | 749 | 614 | 0.9855 | 458 | 342 | 0.9948 | 432 | 320 | 0.9954 | |
| RMSprop | 748 | 597 | 0.9857 | 564 | 458 | 0.9923 | 486 | 344 | 0.9943 | |
| RMSprop* | 893 | 754 | 0.9796 | 656 | 519 | 0.989 | error | error | error | |
| SGDTrue | 1381 | 1071 | 0.9479 | 832 | 636 | 0.9829 | 718 | 544 | 0.9873 | |
| SGD | 2036 | 1568 | 0.8873 | 1481 | 1165 | 0.9419 | 1357 | 1072 | 0.9515 | |
| adagrad | 3599 | 2861 | 0.0957 | 2212 | 1728 | 0.8649 | 2117 | 1649 | 0.8806 | |
| Ftrl | 6267 | 5193 | −9.7917 | 4941 | 4152 | −2.66 | 4371 | 3639 | −0.8450 | |
| adadelta | 10,693 | 8918 | −3.7992 | 6297 | 5378 | −8.6355 | 4993 | 4202 | −2.7761 | |
| SGDFalse | 10,526 | 9370 | −7 × 1015 | 11,979 | 10,798 | 0 | 18,981 | 17,837 | −4 × 1014 | |
| Model | Optimizer | test rmse | test mae | test_R2 | Model | Optimizer | test rmse | test mae | test_R2 |
|---|---|---|---|---|---|---|---|---|---|
| LSTM(50, activation = ‘relu’ | Adam | 339 | 243 | 0.9972 | LSTM(50, activation = ‘tanh’ | Adam | 348 | 248 | 0.997 |
| Nadam | 429 | 322 | 0.9954 | Nadam | 438 | 327 | 0.9953 | ||
| RMSprop | 421 | 289 | 0.9957 | adamax | 487 | 378 | 0.9942 | ||
| RMSprop* | 500 | 377 | 0.9938 | RMSprop | 512 | 381 | 0.9937 | ||
| adamax | 518 | 407 | 0.9935 | RMSprop* | 855 | 723 | 0.9814 | ||
| SGDTrue | 769 | 586 | 0.9853 | SGDTrue | 1039 | 801 | 0.9714 | ||
| SGD | 1602 | 1284 | 0.9294 | SGD | 1781 | 1437 | 0.9119 | ||
| adagrad | 2279 | 1838 | 0.8518 | adagrad | 2341 | 1879 | 0.8342 | ||
| Ftrl | 5526 | 4603 | −5.2028 | adadelta | 4415 | 3535 | −1.1026 | ||
| adadelta | 6749 | 5649 | −5.44 | Ftrl | 5196 | 4283 | −34704 | ||
| SGDFalse | 13,125 | 11,938 | −1 × 1013 | SGDFalse | 9368 | 8245 | −6 × 1012 | ||
| LSTM(50, activation = ‘elu’ | Adam | 345 | 249 | 0.997 | LSTM(50, model.add(LeakyReLU (alpha = 0.05)) model.add(Dense(1)) model.add(LeakyReLU (alpha = 0.05)) | Adam | 356 | 258 | 0.9969 |
| adamax | 444 | 341 | 0.9951 | RMSprop | 476 | 361 | 0.9943 | ||
| Nadam | 503 | 394 | 0.9937 | Nadam | 480 | 373 | 0.9943 | ||
| RMSprop | 515 | 387 | 0.9935 | adamax | 527 | 415 | 0.9932 | ||
| SGDTrue | 640 | 473 | 0.9898 | RMSprop* | 735 | 612 | 0.9871 | ||
| SGD | 1722 | 1386 | 0.9179 | SGDTrue | 931 | 706 | 0.9777 | ||
| adagrad | 2337 | 1879 | 0.8366 | SGD | 1854 | 1502 | 0.8977 | ||
| RMSprop* | 1,963,629 | 166,538 | −0.0027 | adagrad | 2497 | 1982 | 0.7888 | ||
| adadelta | 4540 | 3641 | −1,4515 | adadelta | 5582 | 4530 | −10.04 | ||
| Ftrl | 5233 | 4319 | −3,6805 | Ftrl | 5595 | 4650 | −6.63 | ||
| SGDFalse | 27,722 | 26,952 | −5 × 1013 | SGDFalse | 19644 | 18541 | −2 × 109 | ||
| LSTM(50, activation = ‘sigmoid’ | Adam | 572 | 425 | 0.9919 | LSTM(50, activation = ‘softmax’ | RMSprop | 674 | 514 | 0.9883 |
| adamax | 604 | 478 | 0.9909 | RMSprop* | 707 | 582 | 0.9869 | ||
| Nadam | 651 | 528 | 0.9893 | Nadam | 738 | 551 | 0.9861 | ||
| RMSprop | 677 | 555 | 0.9883 | Adam | 750 | 576 | 0.9856 | ||
| RMSprop* | 735 | 603 | 0.9857 | adamax | 1010 | 804 | 0.9736 | ||
| SGDTrue | 954 | 742 | 0.9772 | SGDFalse | 7976 | 7769 | −1.0162 | ||
| SGD | 1311 | 1040 | 0.9514 | SGDTrue | 7285 | 6206 | −1506.18 | ||
| adagrad | 4911 | 3931 | −4.5018 | adagrad | 6478 | 5000 | −6 × 104 | ||
| adadelta | 6292 | 5116 | −87.23 | SGD | 6547 | 5237 | −2 × 105 | ||
| Ftrl | 6314 | 5103 | −219.58 | adadelta | 11096 | 9103 | −2 × 105 | ||
| SGDFalse | 7131 | 5998 | −3 × 108 | Ftrl | 6484 | 5017 | −2 × 105 | ||
| GRU(50, activation = ‘relu’ | Adam | 412 | 296 | 0.996 | GRU(50, activation = ‘tanh’ | Adam | 385 | 291 | 0.9964 |
| Nadam | 405 | 296 | 0.996 | RMSprop | 457 | 339 | 0.995 | ||
| adamax | 481 | 366 | 0.9945 | Nadam | 454 | 355 | 0.9948 | ||
| RMSprop | 475 | 347 | 0.9944 | adamax | 504 | 393 | 0.9939 | ||
| RMSprop* | 659 | 537 | 0.9887 | SGDTrue | 988 | 747 | 0.9743 | ||
| SGDTrue | 962 | 721 | 0.9754 | SGD | 1304 | 1059 | 0.9563 | ||
| SGD | 1336 | 1082 | 0.9546 | SGDFalse | 1354 | 1105 | 0.953 | ||
| adagrad | 1935 | 1535 | 0.8824 | adagrad | 1772 | 1445 | 0.9156 | ||
| Ftrl | 4801 | 3922 | −1.7584 | adadelta | 4080 | 3355 | −0.4021 | ||
| adadelta | 6497 | 5391 | −5.6841 | RMSprop* | 5444 | 4511 | −0.5166 | ||
| SGDFalse | 12,246 | 10,396 | −4 × 1013 | Ftrl | 4342 | 3477 | −0.6307 | ||
| GRU(50, activation = ‘elu’ | Adam | 373 | 276 | 0.9965 | GRU(50, model.add(LeakyReLU(alpha = 0.05)) model.add(Dense(1)) model.add(LeakyReLU(alpha = 0.05)) | Adam | 407 | 313 | 0.996 |
| Nadam | 492 | 379 | 0.9938 | adamax | 434 | 330 | 0.9954 | ||
| adamax | 535 | 417 | 0.993 | Nadam | 435 | 337 | 0.9954 | ||
| RMSprop | 593 | 483 | 0.9914 | RMSprop | 485 | 365 | 0.9944 | ||
| SGDTrue | 1064 | 815 | 0.9701 | SGDTrue | 889 | 664 | 0.9794 | ||
| SGD | 1316 | 1070 | 0.9559 | RMSprop* | 1181 | 1045 | 0.9601 | ||
| adagrad | 1809 | 1471 | 0.9117 | SGD | 1349 | 1098 | 0.9531 | ||
| Ftrl | 4373 | 3503 | −0.6797 | adagrad | 1995 | 1606 | 0.8833 | ||
| adadelta | 4296 | 3513 | −0.8821 | Ftrl | 4923 | 4032 | −2.1815 | ||
| RMSprop* | 38,569 | 38,093 | −19.488 | adadelta | 5488 | 4556 | −3.2035 | ||
| SGDFalse | error | error | error | SGDFalse | 34,730 | 34,118 | 0 | ||
| GRU(50, activation = ‘sigmoid’ | Adam | 486 | 365 | 0.9942 | GRU(50, activation = ‘softmax’ | Nadam | 580 | 427 | 0.9914 |
| adamax | 557 | 404 | 0.9923 | Adam | 582 | 437 | 0.9913 | ||
| RMSprop* | 586 | 473 | 0.9909 | RMSprop | 605 | 480 | 0.9907 | ||
| Nadam | 684 | 563 | 0.9881 | adamax | 760 | 588 | 0.9851 | ||
| SGDTrue | 1099 | 875 | 0.9702 | RMSprop* | 772 | 590 | 0.984 | ||
| RMSprop | 1566 | 1440 | 0.9373 | SGDTrue | 1467 | 1163 | 0.9472 | ||
| SGD | 1729 | 1373 | 0.9118 | adagrad | 6507 | 5231 | −589.92 | ||
| adagrad | 5009 | 3992 | −4.7411 | SGD | 6418 | 5136 | −1050.57 | ||
| adadelta | 6401 | 5206 | −25.411 | adadelta | 9056 | 6966 | −1384.89 | ||
| Ftrl | 5875 | 4734 | −28.589 | Ftrl | 6550 | 5234 | −3 × 1012 | ||
| SGDFalse | 17,976 | 16,764 | −3 × 1014 | SGDFalse | 16,742 | 15,610 | −2 × 1013 | ||
| SimpleRNN(50, activation = ‘relu’ | Nadam | 368 | 266 | 0.9968 | SimpleRNN(50, activation = ‘tanh’ | Nadam | 444 | 332 | 0.9952 |
| Adam | 425 | 307 | 0.9956 | adamax | 499 | 391 | 0.9939 | ||
| RMSprop | 486 | 357 | 0.9942 | Adam | 504 | 381 | 0.9938 | ||
| adamax | 567 | 441 | 0.9921 | SGDTrue | 579 | 430 | 0.9917 | ||
| SGDTrue | 668 | 504 | 0.9889 | RMSprop | 637 | 511 | 0.9899 | ||
| RMSprop* | 813 | 665 | 0.9832 | SGD | 988 | 743 | 0.9748 | ||
| SGD | 904 | 685 | 0.9792 | adagrad | 1818 | 1385 | 0.911 | ||
| adagrad | 1857 | 1488 | 0.9031 | Ftrl | 2619 | 2056 | 0.6899 | ||
| Ftrl | 3174 | 2492 | 0.4742 | adadelta | 3752 | 2969 | 0.295 | ||
| adadelta | 5072 | 4243 | −0.5113 | RMSprop* | 8553 | 7295 | −9.0302 | ||
| SGDFalse | 17,577 | 16,467 | −2 × 1012 | SGDFalse | 16,187 | 15,041 | 0 | ||
| SimpleRNN(50, activation = ‘elu’ | adamax | 430 | 329 | 0.9956 | SimpleRNN(50, model.add(LeakyReLU(alpha = 0.05)) model.add(Dense(1)) model.add(LeakyReLU(alpha = 0.05)) | adamax | 434 | 330 | 0.9955 |
| Nadam | 454 | 348 | 0.9949 | Adam | 472 | 370 | 0.9946 | ||
| Adam | 504 | 391 | 0.9937 | Nadam | 481 | 365 | 0.9944 | ||
| RMSprop | 627 | 487 | 0.9902 | RMSprop | 496 | 355 | 0.9941 | ||
| SGDTrue | 637 | 474 | 0.9896 | SGDTrue | 702 | 549 | 0.988 | ||
| SGD | 903 | 684 | 0.9789 | SGD | 1147 | 881 | 0.966 | ||
| adagrad | 1771 | 1351 | 0.9182 | adagrad | 2053 | 1611 | 0.8802 | ||
| Ftrl | 2352 | 1839 | 0.7707 | RMSprop* | 3541 | 3189 | 0.4623 | ||
| adadelta | 3982 | 3055 | 0.5751 | adadelta | 4410 | 3462 | 0.0894 | ||
| RMSprop* | error | error | error | Ftrl | 4199 | 3377 | −0.3491 | ||
| SGDFalse | error | error | error | SGDFalse | 47,858 | 47,417 | −2 × 1015 | ||
| SimpleRNN(50, activation = ‘sigmoid’ | Adam | 575 | 430 | 0.9918 | SimpleRNN(50, activation = ‘softmax’ | Adam | 744 | 568 | 0.9859 |
| adamax | 587 | 436 | 0.9913 | adamax | 759 | 595 | 0.9856 | ||
| Nadam | 603 | 462 | 0.991 | RMSprop* | 802 | 626 | 0.9832 | ||
| RMSprop | 767 | 622 | 0.9851 | Nadam | 822 | 637 | 0.9828 | ||
| SGDTrue | 907 | 718 | 0.9798 | RMSprop | 836 | 649 | 0.9827 | ||
| RMSprop* | 981 | 849 | 0.9759 | SGDTrue | 1469 | 1174 | 0.9484 | ||
| SGD | 1407 | 1123 | 0.9477 | SGD | 6319 | 5068 | −280.15 | ||
| adagrad | 4848 | 3833 | −3.4409 | adagrad | 6492 | 5215 | −363.93 | ||
| Ftrl | 5448 | 4472 | −11.308 | adadelta | 9207 | 7114 | −957.72 | ||
| adadelta | 6623 | 5303 | −16.200 | SGDFalse | 6535 | 5203 | −1 × 1012 | ||
| SGDFalse | 8772 | 6677 | −2 × 1013 | Ftrl | 6550 | 5234 | −2 × 1013 | ||
| Bidirectional(LSTM(50, activation = ‘relu’ | Adam | 313 | 224 | 0.9976 | Bidirectional(LSTM(50, activation = ‘tanh’ | Adam | 449 | 327 | 0.9953 |
| Nadam | 345 | 256 | 0.9971 | adamax | 469 | 356 | 0.9947 | ||
| adamax | 458 | 342 | 0.9948 | Nadam | 486 | 385 | 0.9942 | ||
| RMSprop | 564 | 458 | 0.9923 | RMSprop | 547 | 421 | 0.9927 | ||
| RMSprop* | 656 | 519 | 0.989 | RMSprop* | 759 | 650 | 0.9854 | ||
| SGDTrue | 832 | 636 | 0.9829 | SGDTrue | 1114 | 847 | 0.9678 | ||
| SGD | 1481 | 1165 | 0.9419 | SGD | 1521 | 1182 | 0.9395 | ||
| adagrad | 2212 | 1728 | 0.8649 | adagrad | 2135 | 1653 | 0.8748 | ||
| Ftrl | 4941 | 4152 | −2.66 | adadelta | 3372 | 2585 | 0.3352 | ||
| adadelta | 6297 | 5378 | −8.6355 | Ftrl | 4398 | 3642 | −0.8918 | ||
| SGDFalse | 11,979 | 10,798 | 0 | SGDFalse | 26,463 | 25,656 | −3 × 1015 | ||
| Bidirectional(LSTM(50, activation = ‘elu’ | adamax | 407 | 310 | 0.996 | Bidirectional(LSTM(50, model.add(LeakyReLU(alpha = 0.05)) model.add(Dense(1)) model.add(LeakyReLU(alpha = 0.05)) | Adam | 346 | 255 | 0.9971 |
| Adam | 409 | 295 | 0.996 | Nadam | 376 | 275 | 0.9966 | ||
| Nadam | 457 | 361 | 0.9949 | adamax | 423 | 320 | 0.9956 | ||
| RMSprop | 490 | 368 | 0.9941 | RMSprop | 569 | 443 | 0.9923 | ||
| SGDTrue | 788 | 604 | 0.9844 | SGDTrue | 1044 | 781 | 0.9706 | ||
| adagrad | 2147 | 1657 | 0.8749 | SGD | 1617 | 1272 | 0.9252 | ||
| SGD | 1479 | 1148 | 0.9423 | adagrad | 2356 | 1826 | 0.8345 | ||
| adadelta | 3501 | 2709 | 0.1778 | RMSprop* | 4743 | 3693 | −1.185 | ||
| Ftrl | 4475 | 3706 | −1.0879 | adadelta | 4762 | 3745 | −2.6703 | ||
| SGDFalse | 25,001 | 24,144 | −3 × 1014 | Ftrl | 5080 | 4236 | −3.9808 | ||
| RMSprop* | error | error | error | SGDFalse | 36,371 | 35,825 | −14357 | ||
| Bidirectional(LSTM(50, activation = ‘sigmoid’ | Adam | 533 | 386 | 0.9929 | Bidirectional(LSTM(50, activation = ‘softmax’ | Nadam | 584 | 422 | 0.9914 |
| adamax | 551 | 395 | 0.9924 | RMSprop | 625 | 495 | 0.9901 | ||
| Nadam | 583 | 475 | 0.9914 | Adam | 660 | 479 | 0.9889 | ||
| RMSprop | 648 | 484 | 0.9893 | RMSprop* | 669 | 524 | 0.9882 | ||
| RMSprop* | 718 | 601 | 0.9868 | adamax | 1082 | 839 | 0.97 | ||
| SGDTrue | 942 | 742 | 0.9783 | SGDTrue | 7147 | 6101 | −323.77 | ||
| SGD | 1796 | 1359 | 0.8969 | adagrad | 6490 | 5150 | −19493 | ||
| adagrad | 4410 | 3545 | −0.9066 | SGD | 6525 | 5222 | −20221 | ||
| adadelta | 5906 | 4933 | −14.449 | Ftrl | 6525 | 5189 | −3 × 105 | ||
| Ftrl | 5809 | 4697 | −25.309 | adadelta | 9916 | 7837 | −77048 | ||
| SGDFalse | 32,292 | 31,633 | −7 × 1013 | SGDFalse | 18,930 | 18,878 | −7.3997 |
| Model | Layers | Activatör | Optimizer | Epochs | test_rmse | test-mae | test_R2 |
|---|---|---|---|---|---|---|---|
| BiLSTM | 50 | relu | Adam | 50 | 313.04 | 223.66 | 0.9976 |
| LSTM | 50 | relu | Adam | 50 | 339.33 | 242.54 | 0.9972 |
| BiLSTM | 50 | relu | Nadam | 50 | 345.03 | 255.65 | 0.9971 |
| BiLSTM | 50 | Leakyrelu | Adam | 50 | 345.7 | 255.37 | 0.9971 |
| LSTM | 50 | elu | Adam | 50 | 345.19 | 249 | 0.997 |
| LSTM | 50 | tanh | Adam | 50 | 348.22 | 248.38 | 0.997 |
| LSTM | 50 | Leakyrelu | Adam | 50 | 356.31 | 257.81 | 0.9969 |
| SimpleRNN | 50 | relu | Nadam | 50 | 368.15 | 265.96 | 0.9968 |
| BiLSTM | 50 | Leakyrelu | Nadam | 50 | 375.89 | 275.41 | 0.9966 |
| GRU | 50 | elu | Adam | 50 | 373.14 | 275.81 | 0.9965 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ucar, M.T.; Kaygusuz, A. Short-Term Energy Consumption Forecasting Analysis Using Different Optimization and Activation Functions with Deep Learning Models. Appl. Sci. 2025, 15, 6839. https://doi.org/10.3390/app15126839
Ucar MT, Kaygusuz A. Short-Term Energy Consumption Forecasting Analysis Using Different Optimization and Activation Functions with Deep Learning Models. Applied Sciences. 2025; 15(12):6839. https://doi.org/10.3390/app15126839
Chicago/Turabian StyleUcar, Mehmet Tahir, and Asim Kaygusuz. 2025. "Short-Term Energy Consumption Forecasting Analysis Using Different Optimization and Activation Functions with Deep Learning Models" Applied Sciences 15, no. 12: 6839. https://doi.org/10.3390/app15126839
APA StyleUcar, M. T., & Kaygusuz, A. (2025). Short-Term Energy Consumption Forecasting Analysis Using Different Optimization and Activation Functions with Deep Learning Models. Applied Sciences, 15(12), 6839. https://doi.org/10.3390/app15126839







