Investigating the Secondary Thermal Neutron Intensity of Neutron Capture-Enhanced Proton Therapy

Featured Application

In proton-beam therapy using neutron capture enhancement (NCEPT), we observed that thermal neutron fluence depends on the proton-beam energy and the number of irradiated particles. As the proton beam’s energy increased, the thermal neutron fluence within the target increased, while the depth difference between the Bragg peak of the proton beam and the peak of the thermal neutron fluence became larger. These data are essential for optimizing the beam angle to maximize dose enhancement within the target in the clinical application of NCEPT.

Abstract

This study aimed to investigate the distribution of thermal neutron fluence generated during proton-beam therapy (PBT) scanning, focusing on neutrons produced within the body using Monte Carlo simulations (MCSs). MCSs used the Particle and Heavy Ion Treatment Code System to define a 35 × 35 × 35 cm³ water phantom, and proton-beam energies ranging from 70.2 to 228.7 MeV were investigated. The MCS results were compared with neutron fluence measurements obtained from gold activation analysis, showing good agreement with a difference of 3.54%. The internal thermal neutron distribution generated by PBT was isotropic around the proton-beam axis, with the Bragg peak depth varying between 3.45 and 31.9 cm, while the thermal neutron peak depth ranged from 5.41 to 15.9 cm. Thermal neutron generation depended on proton-beam energy, irradiated particle count, and depth. Particularly, the peak of the thermal neutron fluence did not occur within the treatment target volume but in a location outside the target, closer to the source. This discrepancy between the Bragg peak and the thermal neutron fluence peak is a key finding of this study. These data are crucial for optimizing beam angles to maximize dose enhancement within the target during clinical applications of neutron capture-enhanced particle therapy.

1. Introduction

Proton-beam therapy (PBT), first proposed by Robert R. Wilson, is used to treat various diseases [1]. Charged particles, such as protons, have a unique physical property where the energy lost is inversely proportional to the square of their velocity, resulting in a peak energy release called the Bragg peak immediately before cessation [2]. This property enables a high dose to be focused on the tumor while minimizing the integral dose to the surrounding healthy tissues compared with conventional radiation therapy. However, this property also makes PBT more susceptible to anatomical variations between and within the treatment fractions than photon-based radiation therapy [3]. PBT is characterized by radiation with relatively high linear energy transfer (LET); however, its effectiveness against radioresistant tumors may be limited compared with that of high-LET radiation, which is effective in destroying such tumors [4]. To address this, neutron capture-enhanced particle therapy (NCEPT) has been developed. NCEPT is a therapeutic approach that utilizes alpha particles produced from nuclear interactions between thermal neutrons generated by PBT and tumor-specific agents for dose enhancement and is expected to increase the biological dose contrast between tumors and normal tissues [5,6,7].

In PBT, the energy of the neutrons generated in the body is typically <1 MeV, and most are thermal neutrons [8,9]. When thermal neutrons interact with water, they mainly capture hydrogen and emit high-energy gamma rays. However, their interaction with 10B, which has a large cross-section for neutrons (3840 barns), produces high-energy charged particles (alpha particles and recoiling lithium 7 nuclei) [10]. In NCEPT, a drug containing 10B is administered to the patient before PBT, and the target dose is increased by the 10B(n,α)7Li capture reaction (boron neutron capture reactions: BNCRs) induced by the thermal neutrons generated during PBT. The ranges of the alpha particles and recoiled lithium 7 nuclei emitted by the BNCRs range between approximately 9 μm and 4 μm, respectively, corresponding to the size of a single cell. Theoretically, this enables the selective destruction of cancer cells that have taken up 10B, sparing the surrounding healthy cells.

This allows NCEPT to enhance the dose via BNCRs in tumor cells in addition to the dose from PBT. Compared to PBT alone, this approach offers geometric and biochemical advantages, potentially enabling more precise cancer control. Moreover, while the secondary neutrons produced by PBT may generally induce adverse effects such as secondary cancers [11], NCEPT offers the potential benefit of repurposing these effects to enhance therapeutic outcomes.

However, to achieve sufficient dose enhancement, appropriate intracellular boron concentrations and thermal neutron fields are required to induce the BNCR [12]. Research on these matters remains insufficient. Therefore, this study aimed to elucidate, using Monte Carlo simulations (MCSs), the relationship between the proton-beam energy and the fluence distribution of secondary thermal neutrons generated within the target under clinically relevant conditions to promote the clinical application of NCEPT.

2. Materials and Methods

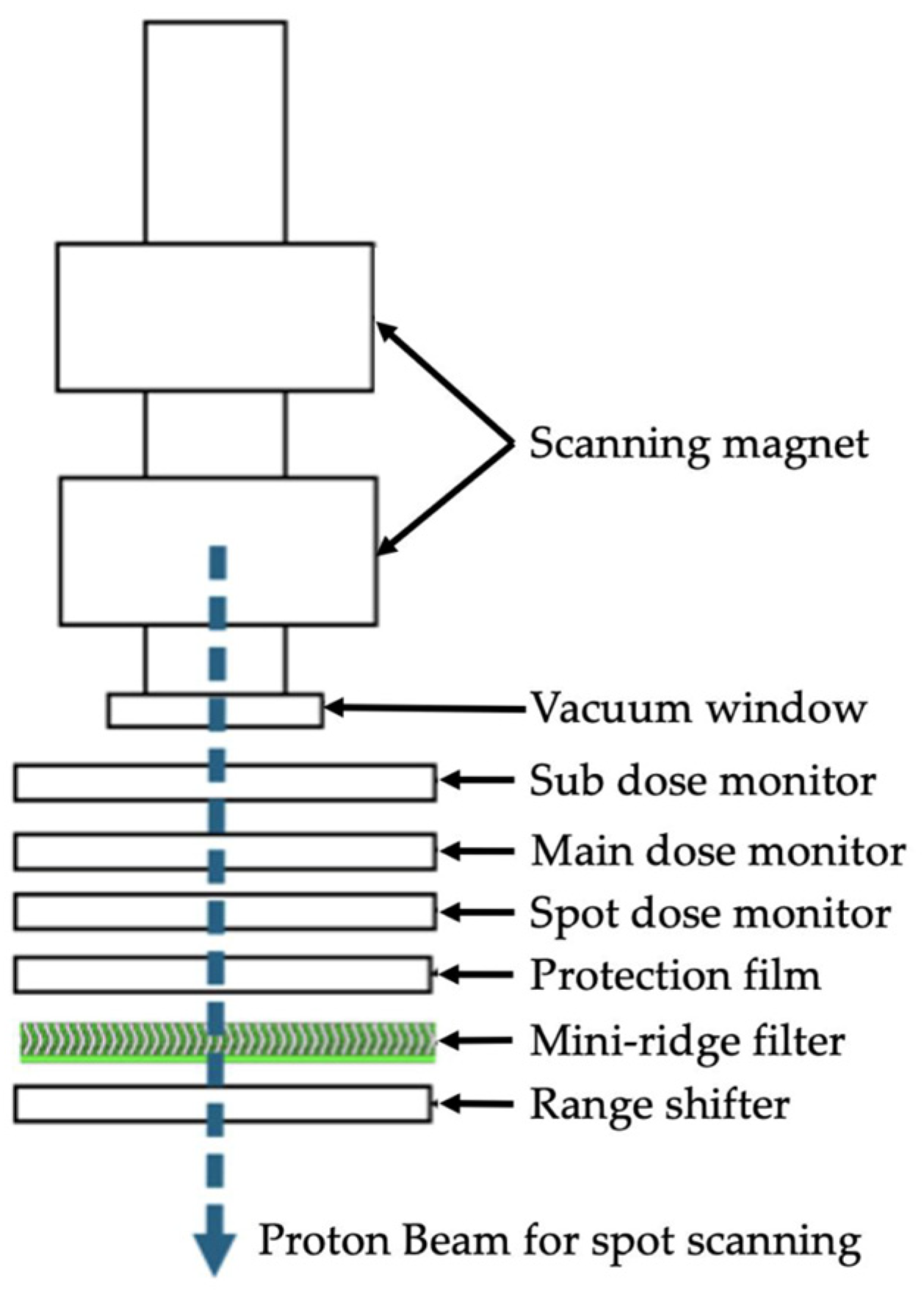
2.1. Monte Carlo Simulation

The nozzle of a HITACHI PROBEAT M1 at our facility was modeled to generate the proton beam (Figure 1). This PBT device enables irradiation with 71 proton-beam energies ranging from 70.2 MeV to 228.7 MeV. Previous studies have reported MCSs using the proton-beam model of our PBT system [13].

Our MCS was conducted using the Particle and Heavy Ion Treatment Code System (PHITS) version 3.31 [14]. We used the Japanese Evaluated Nuclear Data Library 4.0 (JENDL 4.0) developed by the Japan Atomic Energy Agency [15]. The PHITS intranuclear cascade physics model uses the Liège Intranuclear Cascade Model version 4.6, and the Generalized Evaporation Model version 1 is used for de-excitation (Set nevap to 3 and ngem to 1). The γ decay of residual nuclei was calculated using the Evaluated Nuclear Structure Data File-Based Isomeric Transition and Isomer Production Model (set igamma to 2), and parameters were selected to account for energy straggling (set nedisp to 1) in the deceleration process of charged particles other than electrons and positrons. Additionally, the Coulomb scattering of charged particles other than electrons and positrons was adjusted using Lynch’s equation based on the Moliere theory [16] (set nspred to 2), and the settings were configured to ensure proper tabulation of high-energy neutron doses (set e-mode to 2). In the MCS used in this study, the number of histories was determined to keep the statistical error in the simulation <0.1%.

Secondary neutrons used in particle therapy can be classified into internal and external neutrons. External neutrons are generated by the interactions between the proton beam and beamline equipment outside the patient’s body. However, internal neutrons are generated inside the patient’s body. The number of external neutrons varies with the irradiation technique and is lower for the scanning-beam method than for the passive-beam method. However, a study reported no significant difference between the scanning-beam and the passive-beam methods regarding internal neutrons [17]. In this study, the absorbed dose distribution of the proton beam and the internal thermal neutron fluence generated within the phantom by the proton beam were analyzed. The thermal neutrons were defined as those with an energy of ≤0.5 eV [13,15,18].

2.2. Neutron Fluence Measurement

The neutron fluence from proton irradiation was measured using thin gold wire activation analysis [19,20,21]. A 13.6 cm water-equivalent phantom (RW3, PTW) was used, with a multi-well plate placed beneath it. The cells in the multi-well plate contained 1.0 mL of water and one thin gold wire (diameter 0.25 mm; length 10 mm; 99.95% purity; The Nilaco Corporation, Tokyo, Japan) positioned at the isocenter depth (Figure 2).

The well that contained the gold wire was centered and irradiated with a dose of 120.0 Gy with a 4.0 × 4.0 cm² irradiation field and a 6.0 cm Spread-out Bragg Peak (SOBP). The activity of the gold wire was measured using a high-purity germanium spectrometer LVis version 3.3.57.0 (ORTEC, AMETEK GmbH, Germany), and the reaction rate (RR) was calculated using the following equation:

$$\mathrm{R}\mathrm{R}={\displaystyle \frac{\mathsf{\lambda }\mathrm{C}}{\mathcal{E}\mathsf{\gamma }{\mathrm{N}}_0{\mathrm{e}}^{-{\mathsf{\lambda }\mathrm{t}}_{\mathrm{c}}}(1-{\mathrm{e}}^{-{\mathsf{\lambda }\mathrm{t}}_{\mathrm{m}}}){\sum }_{\mathrm{i}=1}^{\mathrm{n}}(\frac{{\mathrm{Q}}_{\mathrm{i}}}{∆\mathrm{t}}\left(1-{\mathrm{e}}^{-\mathsf{\lambda }∆\mathrm{t}}\right){\mathrm{e}}^{-\mathsf{\lambda }\left(\mathrm{n}-\mathrm{i}\right)\mathsf{\Delta }\mathrm{t}})}}$$

(1)

where $\mathcal{E}$ is the detector efficiency for gamma rays emitted from ¹⁹⁸Au,$\mathsf{\gamma }$ is the gamma emission rate due to the decay of ¹⁹⁸Au, λ is the decay constant of ¹⁹⁸Au, t_c is the time from the end of irradiation to the start of measurement, t_m is the measurement time, C is the peak count of gamma rays from ¹⁹⁸Au measured by the detector, and Q_i represents the charge delivered to the target at each interval Δt. Assuming a constant charge during irradiation, the RR was determined using the following modified equation:

$$\mathrm{R}\mathrm{R}={\displaystyle \frac{\mathsf{\lambda }\mathrm{C}}{\mathcal{E}\mathsf{\gamma }{\mathrm{N}}_0{\mathrm{e}}^{-\mathsf{\lambda }{\mathrm{t}}_{\mathrm{c}}}(1-{\mathrm{e}}^{-\mathsf{\lambda }{\mathrm{t}}_{\mathrm{m}}})\left(1-{\mathrm{e}}^{-\mathsf{\lambda }{t}_b}\right)}}$$

(2)

where $t_b$ is the irradiation time.

The thermal neutron fluence ${\mathsf{\varphi }}_{th}$ in the water phantom was subsequently calculated from the RR data using the following equation:

$${\mathsf{\varphi }}_{th}=\mathrm{R}\mathrm{R}∕{\overline{\mathsf{\sigma }}}_{act}\mathrm{f}$$

(3)

where ${\overline{\mathsf{\sigma }}}_{act}$ is the average activation cross-section for thermal neutrons in gold (85.35 barns), and $\mathrm{f}$ represents the self-shielding factor for thermal neutrons (0.87). The measured value primarily indicates the thermal neutron fluence, owing to the predominance of thermal neutrons in the neutron spectrum generated through proton irradiation, as confirmed by prior studies using PHITS simulations [9].

2.3. Energy Influence Assessment

MCS was performed for each proton energy level, and the neutron fluence distribution in a 35 × 35 × 35 cm³ water phantom was measured. The water phantom was positioned with the isocenter aligned to the surface of the water. The neutron fluence peaks for each energy level were compared by detecting the maximum value that satisfied the following conditions:

$${\mathrm{x}}_i>{\mathrm{x}}_{(i+j)} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{j}=-\mathrm{k},-\mathrm{k}+1,\dots ,-1,1,\dots ,\mathrm{k}-1,\mathrm{k}$$

(4)

where ${\mathrm{x}}_i$ is an arbitrary point and ${\mathrm{x}}_{(i+j)}$ denotes its k neighboring elements.

2.4. Depth Influence Assessment

The effect of target depth on proton energy simulations was evaluated by performing MCSs at different target depths in a phantom. Targets of 5 × 5 × 5 cm³ were placed at depths centered at 5.5, 10.5, 15.5, 20.5, and 25.5 cm along the beam axis in a water phantom. Single-field uniform dose plans [22,23] with 5 mm and 3.5% margins were created for each target depth, and the SOBP and neutron fluence distributions in the phantom were compared.

3. Results

3.1. RR and Neutron Fluence Measurement

The treatment plan for a 6.0 cm SOBP centered on a thin gold wire used proton energies between 130.2 MeV and 165.5 MeV. The RR calculated from the gold wire activity was 1.774 × 10⁻¹⁷ Bq. The thermal neutron fluence calculated from the RR using Equation (3) was 1.95 × 10⁶ cm⁻²/source/Gy with a 1 − σ uncertainty of 6.92%. The MCS results for the same geometry indicated a thermal neutron fluence of 2.02 × 10⁶ cm⁻²/source/Gy near the gold wire. The difference between the thermal neutron fluence measured on a thin gold wire and the MCS results was 3.54%.

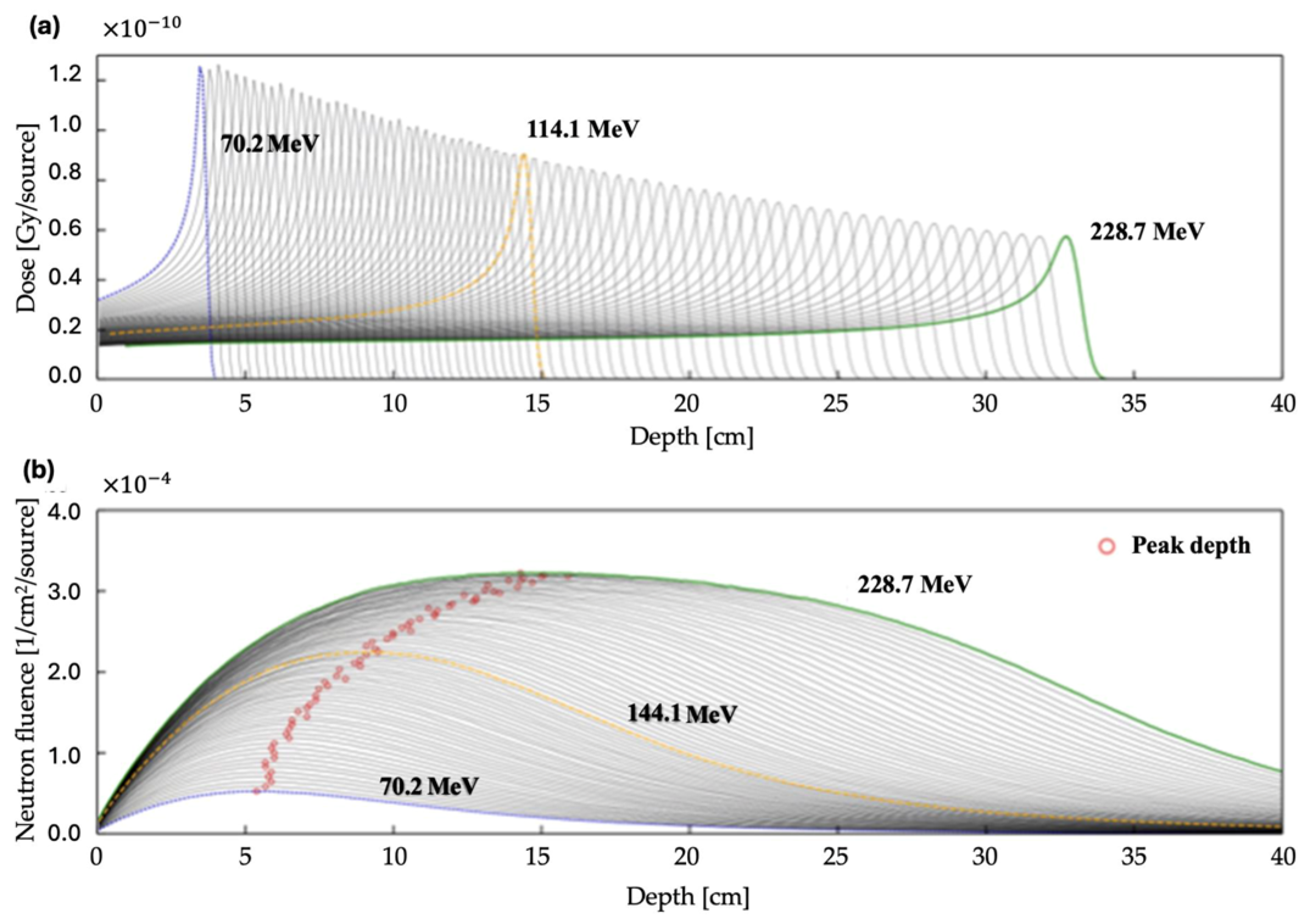
3.2. Proton Energy Simulations

Figure 3 shows the integrated depth dose and thermal neutron distributions for each proton energy level. The Bragg peak depth ranged from 3.45 to 31.9 cm. The peak thermal neutron fluence increased with proton energy, with peak depths ranging from 5.41 to 15.9 cm. The fluence distribution of thermal neutrons was generated isotropically around the proton-beam axis (Figure 4).

3.3. Effect of Target Depth

Table 1. Number of protons and average thermal neutron fluence at varying depths under the same dose.

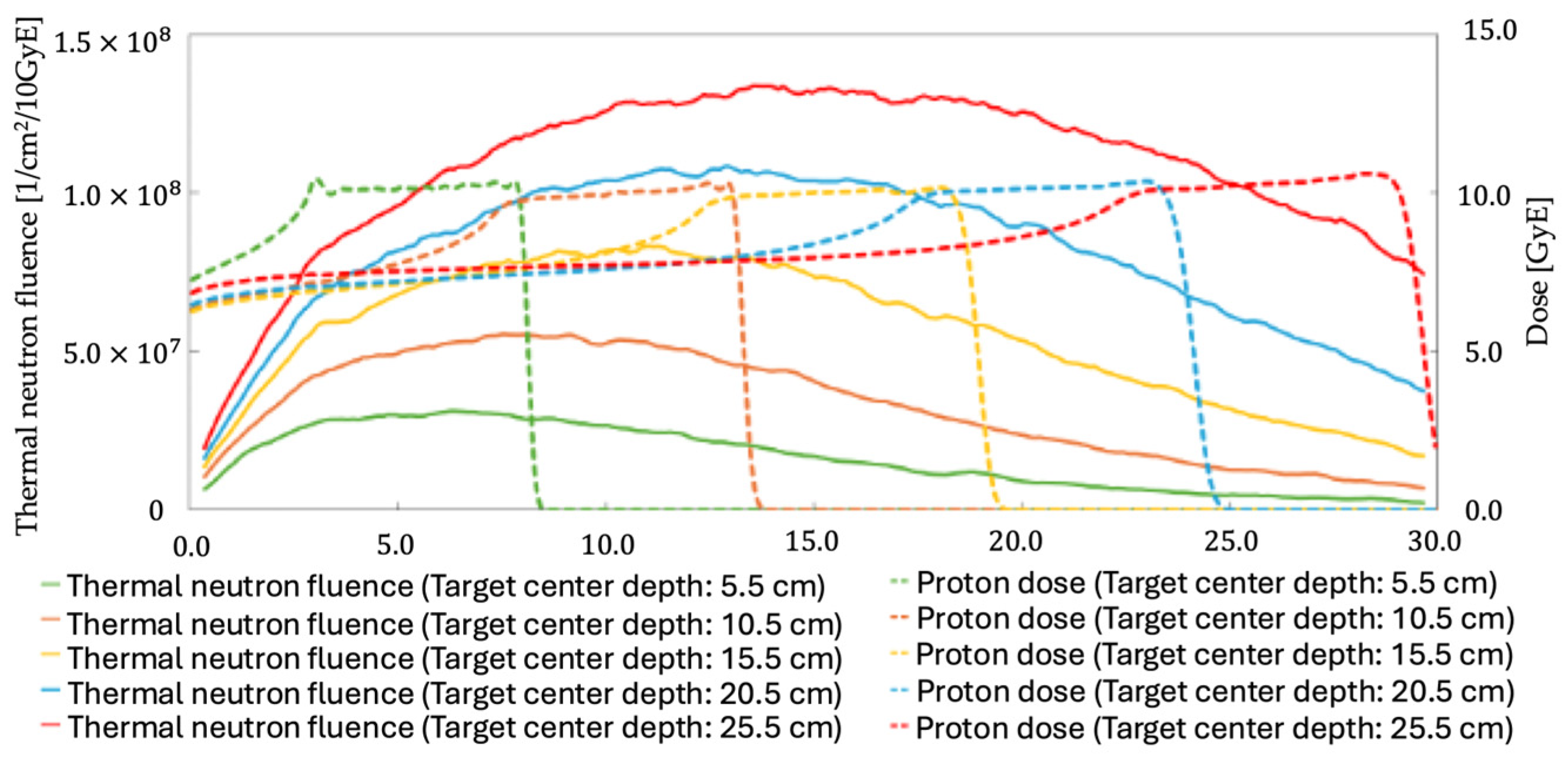
Target Center Depth [cm]	Number of Proton-Beam Particles [n]	Average Thermal Neutron Fluence Within the Target [1/cm2/Gy]
5.5	3.39 × 1011	2.98 × 107
10.5	3.45 × 1011	5.23 × 107
15.5	3.86 × 1011	7.14 × 107
20.5	4.35 × 1011	8.70 × 107
25.5	4.91 × 1011	1.01 × 108

presents the number of irradiated protons and the average number of thermal neutrons from the MCS when the same dose was administered to targets at different depths. Figure 5 shows the results of this MCS. A proportional relationship was observed between the target depth and the obtained thermal neutron fluence. However, the peak thermal neutron fluence was observed on the proximal side of the beam source when the target was deeper than the one centered at 10.5 cm. This effect became more pronounced at higher proton-beam energies.

Next, we investigated the energy spectrum of neutrons generated per absorbed dose (Gy) delivered by each beam during irradiation. The energy spectrum of neutrons generated within the phantom as a side effect of proton-beam therapy showed differences in the low-energy neutron region below 0.1 eV. Regardless of target depth, more than 94.0% of the thermal neutrons generated across the entire beam were neutrons with energies below 0.1 eV. The thermal neutron fluence was highly dependent on the proton-beam energy and the number of irradiated particles.

4. Discussion

For the clinical application of NCEPT, it is essential to develop drugs that increase intracellular boron concentration and understand the behavior of secondary neutrons generated in the body. In this study, we focused on the neutrons generated within the body during scanning PBT and investigated their impact on the thermal neutron fluence distribution using MCSs. The accuracy of the MCS beam model was verified by comparing the calculated thermal neutron fluence with measurements obtained through the activation analysis of a gold wire. The results showed good agreement, confirming that our beam model was generally accurate. Based on the MCS results, the internal thermal neutron distribution generated by PBT was found to be isotropic around the proton-beam axis, and it was evident that the fluence was highly dependent on the proton-beam energy and the number of irradiated protons. Notably, the thermal neutron fluence varied in intensity with depth, peaking not within the treatment target volume but at a location proximal to the source, outside of the target volume. This result is the divergence between the proton-beam Bragg peak and the peak of the thermal neutron fluence increasing as the proton-beam energy level rises. This effect was particularly pronounced in the low-energy neutron region below 1.0 eV; these findings highlight the importance of considering unexpected BNCRs due to thermal neutron peaks occurring outside the target volume.

The 3.54% discrepancy observed between the thermal neutron fluence measured using gold wire activation analysis and the fluence obtained from MCS results may be attributed to the simplifications in modeling the materials within the beam nozzle. Other possible causes include the nuclear reaction cross-sections used in MCSs, the suppression of secondary particle transport other than protons, and the definition of the thermal neutron energy range. However, since this discrepancy was sufficiently small compared to the typical uncertainty range in neutron measurements, we concluded that our MCS results were within the acceptable range.

Previous studies have investigated thermal neutron generation and distribution in PBT. El-Asery et al. emphasized that most secondary neutrons produced during PBT were thermal neutrons, consistent with our PHITS simulation analysis [9]. These results validate our assumption that the measured neutron fluence primarily comprises thermal neutrons. Yanai et al. observed that heavy ions produced forward-directed and knockout neutrons with significant angular dependence, whereas the neutron dose from proton radiation therapy showed minimal angular dependence [24]. These findings suggest that the neutrons generated by PBT are produced isotopically, and our study confirmed these findings. This is attributed to thermal neutrons produced during proton irradiation becoming isotropic as they result from evaporation processes and undergo scattering, leading to a characteristic 1/En energy distribution.

Safavi-Naeini et al. reported that proton irradiation generated thermal neutrons in the order of 10⁸ per Gy, which could significantly enhance therapeutic efficacy with a realistic neutron capture agent concentration [6]. In contrast, in our study, we found a thermal neutron fluence in the order of 10⁷ per Gy, which was approximately lower than that reported by Safavi-Naeini et al. This result may be attributed to differences in the energy range of the neutrons generated or factors related to the spot size and energy of the proton beam. However, since alpha particles produced from neutron capture have high radiation weighting factors (approximately 20-fold) and LET characteristics, an increase in the biological dose remains promising. Figure 5 shows that target depth influences thermal neutron fluence, with deeper targets producing more thermal neutrons. However, this displacement increased with the proton energy as the neutron peak shifted away from the proton Bragg peak, and a difference of 15.9 cm was observed at the maximum energy of 228.7 MeV. SOBP and thermal neutron peak alignment are crucial for an optimal NCEPT. In our study, when the proton energy was 90.8 MeV, the depths of the Bragg and thermal neutron fluence peaks were most closely aligned, with a depth of 6.5 cm. To deliver the same dose to targets deeper than this region, a higher proton energy and a larger number of protons are required. However, in such cases, the peak of the thermal neutron fluence could occur outside the target region. This issue can be addressed by adjusting the direction of the proton beam and modifying the proton-beam path length using a bolus material. Specifically, the bolus extends the path length, which in turn increases the proton energy used, leading to a separation between the SOBP and the secondary thermal neutron peak. This minimizes unexpected BNCRs in at-risk organs and creates the dose distribution to incorporate the thermal neutron intensity required for sensitization at the target position. Our findings are critical in developing a treatment plan that achieves the desired thermal neutron distribution and maximizes the dose enhancement effects in NCEPT. These findings underscore the need for caution in clinical applications, particularly regarding areas outside the target volume.

This study has several limitations. First, this study is a phantom study, and the results may differ from actual patient treatment. Second, in current boron neutron capture therapy applications, boron-containing compounds such as boronophenylalanine are used to selectively deliver boron to tumor cells [25]. Although boronophenylalanine demonstrates relatively high uptake efficiency in tumor cells, the development of more effective and selective agents for boron delivery is crucial for improving treatment outcomes [26]. This challenge is equally relevant in NCEPT; however, it was not addressed in this study as the focus was solely on thermal neutrons. Research focused on drug development, and achieving a high thermal neutron field will likely be crucial for the successful implementation of NCEPT. Finally, conventional proton therapy typically involves approximately 20 fractionated sessions, necessitating technologies and drugs to maintain high intracellular boron levels throughout these treatments. With proton FLASH therapy exploring the application of significantly fewer fractions [27,28], the possibility of integrating NCEPT into such protocols is anticipated. These techniques and further research could enable the selective killing of cancer cells while protecting tumor stromal cells and the microenvironment to some extent; however, additional studies are required.

5. Conclusions

In this study, we demonstrated that in NCEPT for PBT, thermal neutron fluence depends on the proton-beam energy and the number of irradiated particles. We observed that while the thermal neutron fluence within the target increases with higher proton-beam energy, the greater the discrepancy in depth between the Bragg peak of the proton beam and the peak of the thermal neutron fluence, the higher the energy. These data are crucial for optimizing beam angles to maximize dose enhancement within the target during clinical applications of NCEPT and provide important insights for improving both safety and efficacy.