Simulation-Based Determination of Angular Differential Cross Sections of (n,el) Scattering via Evaluated Interaction Potentials
Abstract
1. Introduction
- To design experimental systems tailored to specific research objectives,
- To compare experimental results with simulations to determine error margins and assess the accuracy of the analysis,
- To test the validity and reliability of existing theoretical models.
- Binding energy per nucleon;
- Nuclear density.
2. Materials and Methods
2.1. Skyrme–Hartree–Fock Model
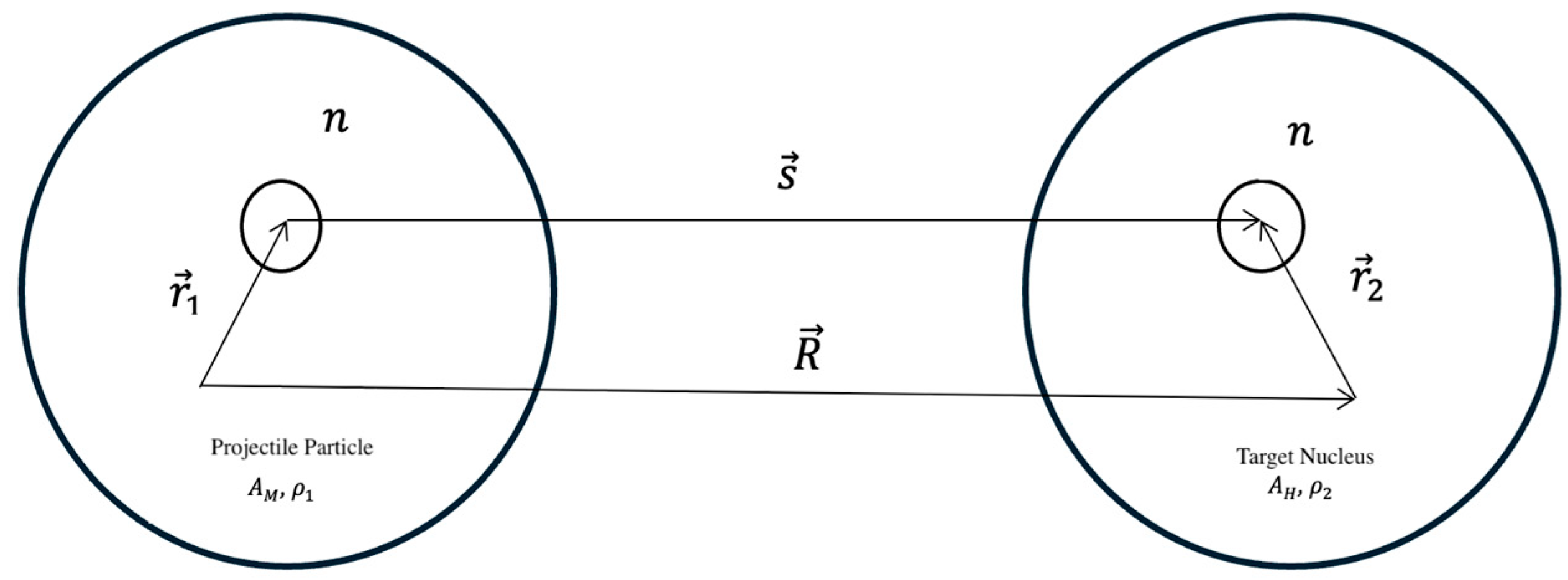
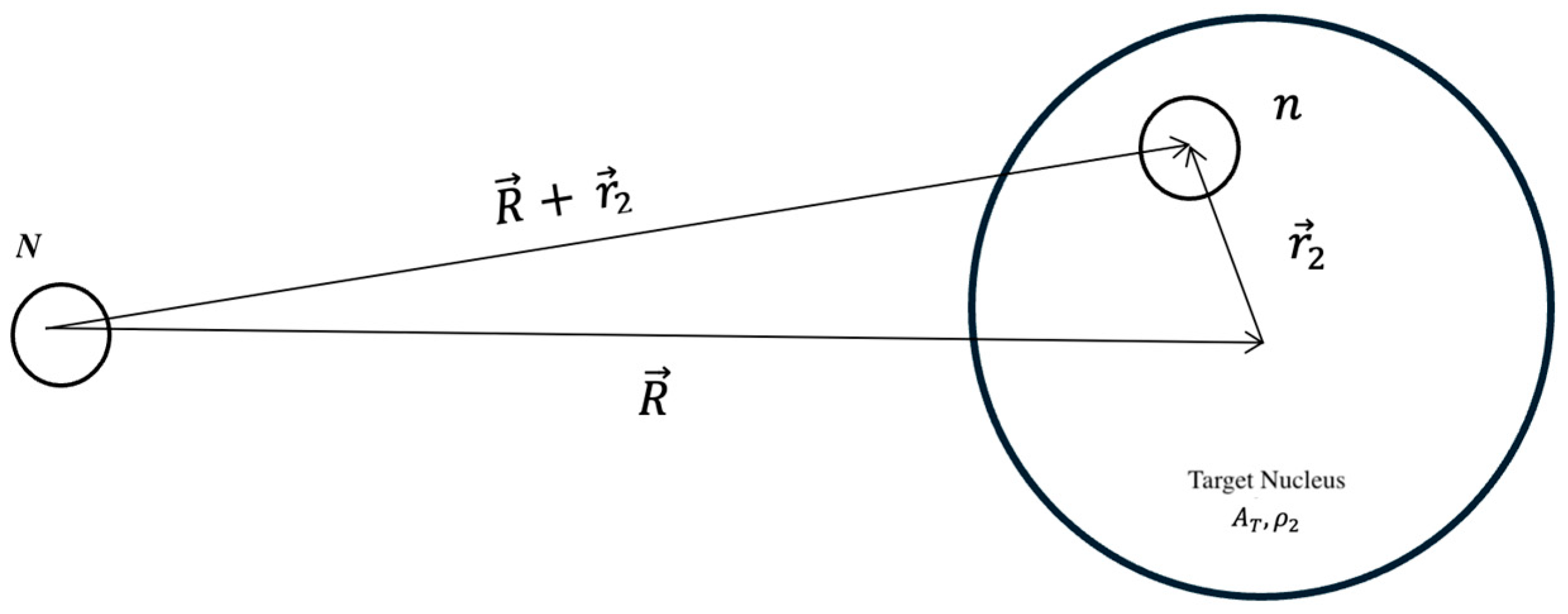
2.2. Folding Potential
Single Folding Potential
2.3. TALYS 1.96
2.4. The Numerical Calculations
- The nucleon densities, , are calculated using the SHF-WS model.
- The interaction potential, , is constructed via the folding integral.
- The Schrödinger equation is solved numerically.
- The scattering amplitude, , and the differential cross section, , are computed.
- Results are compared with experimental data.
2.4.1. Generation of the Folding Potential
2.4.2. Incorporation of the OMP into the Schrödinger Equation
2.4.3. Calculation of the Cross Section via Partial Wave Expansion
2.4.4. Use of TALYS 1.96 Software
2.4.5. Neutron Densities and Folded Potential for W Isotopes
2.4.6. Calculation and Comparison of Results
3. Results
4. Discussion
- 182W(n,el) Scattering Reaction (Figure 4)
- For low-energy neutrons between 1.5 and 3.4 MeV: The observed scattering cross sections are relatively flat, with few minima and maxima. This can be explained by the long neutron wavelength interacting with the entire nucleus, resulting in limited angular resolution. The SHF-WS + SF + TALYS 1.96 model successfully reproduces this flat pattern.
- At 4.87 and 6 MeV: A pronounced minimum around ~50° is observed in the experimental data, which is also clearly seen in the SHF-WS + SF calculations. This indicates that the model can capture fine angular structures due to the interaction potentials derived from the density distributions.
- At 14 MeV: The scattering structure becomes more complex with more peaks and valleys at higher energy. This arises from the dominance of nucleon-level interactions due to the shorter wavelength. The simulation model reproduces this pattern quite well.
- 183W(n,el) Reaction (Figure 5)
- Comparison between 3.4 MeV and 14 MeV: At lower energy, wider angular scattering is dominant, whereas at 14 MeV, distinct angular modulations and more peak/trough structures emerge. The model performs successfully in capturing both the general trend and the proximity to experimental data at both energies.
- 184W(n,el) Reaction (Figure 6)
- At 4.84 and 6 MeV energy levels: Especially at 6 MeV, a distinct oscillation is observed in the experimental data, which the SHF-WS + SF approach largely reproduces. This result, showing higher sensitivity than the Koning and Delaroche model, suggests a theoretical framework better aligned with the experimental diffraction patterns.
- 186W(n,el) Reaction (Figure 7)
- Generally flatter scattering curves with fewer structural variations: The more stable nature of this isotope may contribute to fewer structural features in the scattering spectrum. However, angular differentiations are still observed at 14 MeV, and the model successfully predicts these trends.
4.1. Comparison of the Global OM by Koning and Delaroche [43] and the Microscopic Approach Proposed in This Study Is Presented
4.2. The Distinction and Contribution of This Study in the Literature
- Original Methodological Approach and Application ScopeThis study advances beyond traditional methods in determining angular differential cross sections for (n,el) elastic scattering reactions by integrating nucleon densities computed using the Skyrme-interaction-based HF model with a WS potential (SHF-WS), the SF model, and implementing them within the TALYS 1.96 nuclear reaction simulation code. This tripartite approach—SHF-WS + SF + TALYS 1.96—has not been widely adopted in the existing literature.
- Use of Density-Based Realistic Potentials in Calculations:Whereas studies such as Koning and Delaroche utilize global OM parameters, this work generates interaction potentials by microscopically calculating nucleon densities through SHF-WS and compares these with the realistic interaction surfaces. This enables the use of more physically grounded potentials that are directly relatable to experimental data.
- Comprehensive Surface Analysis Across EnergiesThe study evaluates angular differential cross sections for the isotopes 182,183,184,186W across various energy ranges (1.5–14 MeV), providing separate comparisons for each energy point. This broader energy interval and multi-isotope analysis go beyond many previous studies, which were often limited to a narrow set of energies and isotopes.
- High Agreement of Simulation Results with Experimental DataWhen compared with experimental results from the EXFOR database, the study produced highly consistent outcomes, particularly at forward scattering angles and in intermediate energy ranges. This consistency demonstrates the accuracy and validity of the employed model and indicates that it yields more reliable results than traditional models such as that of Koning and Delaroche [43].
- Filling a Gap in the LiteratureThe contributions of this study stand out in the following ways:
- To date, an integrated approach combining nucleon densities calculated using the SHF-WS model for tungsten isotopes, folded into potentials via the SF method, and subsequently used in (n,el) scattering simulations with TALYS 1.96, has not been applied in the literature.
- This method goes beyond theoretical modeling by enabling direct comparison with experimental data, thereby enhancing the reliability of the simulations.
- In this regard, the study serves as an interdisciplinary example that bridges theoretical nuclear physics with applied simulation technologies.
5. Conclusions
- Nuclei near shell closures,
- Resonance structures,
- Spin-parity dependent transitions.
- Spin effects in single nuclei such as 183W,
- Collective vibrations in open-shell nuclei like 182,184W,
- Resonance damping in more rigid nuclei such as 186W.
- The goal of the global model is broad applicability across wide mass (A) and energy (E) ranges.
- Since the shell structure differs for each isotope, a separate parameterization would be required for each.
- Such a detailed approach would compromise the “global” nature of the model.
- The model attempts to represent shell effects by incorporating variations within its parameters.
- However, this approach is insufficient to explain abrupt structural changes around, for example, magic numbers.
- Example of 183W (single neutron)
- The 183W isotope contains a single neutron, so the spin–orbit splitting affects the angular distribution of scattering.
- Shell model: The placement of this neutron in a specific orbital (e.g., 2f7/2) creates resonances during scattering.
- OMP: The spin–orbit potential is fixed, and individual orbitals are not considered deviations occur at large angles.
- 182,184W (open shell)
- These isotopes may exhibit collective behaviors from the shell model perspective (e.g., surface vibrations).
- Shell model: These collective modes cause oscillations or resonance structures in the angular distribution.
- OMP: Does not include these effects → fine structures in angular distributions cannot be explained, only average behavior is captured.
- 186W (near closed shell)
- This isotope has a “stiffer” potential, with less absorption and smoother scattering.
- Shell model: Surface collective effects are weak, and transitions between levels are limited.
- OMP: The average parameterization generally fits better here, but shell closure effects at low energies can still make a difference.
- 186W (near closed shell)
- This isotope has a “stiffer” potential, with less absorption and smoother scattering.
- Shell model: Surface collective effects are weak, and transitions between levels are limited.
- OMP: The average parameterization generally fits better here, but shell closure effects at low energies can still make a difference.
- They are geometrical parameters
- These parameters directly characterize the global structure of the nucleus: the total volume and surface thickness.
- Especially in heavy nuclei (e.g., 182W to 186W), the nuclear volume and surface properties are relatively independent of shell structure, thus they can be accurately represented by an average effect.
- Regions where the OMP achieves the most accurate fit
- The most significant contribution in scattering data is related to the overall size of the nucleus, which directly correlates with .
- The surface potential diffuseness affects the spread of the potential and the total cross section; effectively controls this.
- Therefore, the general shape of the angular distribution can be well fitted using these two parameters.
- Assumes nucleons occupy discrete energy levels in specific orbitals. This level structure mainly affects the internal nuclear structure and transition phenomena (resonances, spin splitting, etc.).
- and represent an average geometrical distribution of nucleon placement.
- Shell effects only cause minor deviations in this average density distribution.
- In other words, shell model details primarily influence reaction dynamics (resonances, fine structures, spin effects), rather than the overall potential shape.
- In other words, shell model details primarily influence reaction dynamics (resonances, fine structures, spin effects), rather than the overall potential shape.
- Geometrical parameters like and are relatively independent of the shell model.
- Therefore, the absence of shell model details in the OMP does not prevent these parameters from aligning well with experimental data.
- Proliferation of energy-dependent diffraction structuresThe increasing number of peaks and valleys observed at higher energies can be attributed to the shortening of the wavelength. This suggests that scattering occurs not over the entire nucleus but rather on individual nucleons, thereby enhancing the visibility of nuclear shell effects.
- Discrepancies in backward scatteringAlthough the model generally preserves the overall shape of the distribution, it fails to fully reproduce certain peak structures around 150°. This indicates that there is still room for improvement in the model, particularly in better accounting for spin–orbit effects and many-body correlations.
- The angular resolution is particularly high at medium to high energies.
- The positions and numbers of the diffraction-like structures observed experimentally are largely well reproduced.
- Some minima and maxima at backward scattering angles have been overlooked.
- This may be due to the model’s current exclusion of additional effects such as spin–orbit forces or channel coupling.
Regression Analysis
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SHF | Skyrme–Hartree–Fock |
| HF | Hartree–Fock |
| WS | Woods–Saxon |
| SF | Single Folding |
| DF | Double Folding |
| ENDF | Evaluated Nuclear Data File |
| (n,el) | Neutron, Elastik |
| OMP | optical model potential |
| OM | optical model |
| Nucleon–nucleus | Nn |
| Nucleon–nucleon | NN |
| Nucleus–nucleus | Nn |
References
- Charity, R.J.; Sobotka, L.G.; Dickhoff, W.H. Dispersive-optical-model analysis of the asymmetry dependence of correlations in Ca isotopes. Phys. Rev. C 2007, 76, 044314. [Google Scholar] [CrossRef]
- Dickhoff, W.H.; Charity, R.J. Recent developments for the dispersive optical model. Prog. Part. Nucl. Phys. 2019, 105, 252–299. [Google Scholar] [CrossRef]
- Hagen, G.; Hjorth-Jensen, M.; Jansen, G.R.; Machleidt, R.; Papenbrock, T. Continuum effects and three-nucleon forces in neutron-rich oxygen isotopes. Phys. Rev. Lett. 2012, 109, 032502. [Google Scholar] [CrossRef]
- Abu-Ibrahim, B.; Kohama, A.; Suzuki, Y. Reaction cross sections of oxygen isotopes. Phys. Rev. C 2008, 77, 034607. [Google Scholar] [CrossRef]
- Barbagallo, M.; Mastromarco, M.; Colonna, N.; Altstadt, S.; Andrzejewski, J.; Audouin, L.; Bécares, V.; Bečvář, F.; Belloni, F.; Berthoumieux, E.; et al. Neutron cross-sections for advanced nuclear systems: The n_TOF project at CERN. EPJ Web Conf. 2014, 79, 01003. [Google Scholar] [CrossRef]
- Delaroche, J.P.; Haouat, G.; Lachkar, J.; Patin, Y.; Sigaud, J. Deformations, Moments, and Radii of 182,183,184,186W from Fast Neutron Scattering. Phys. Rev. C 1981, 23, 136. [Google Scholar] [CrossRef]
- Nobre, G.P.A.; Palumbo, A.; Herman, M.; Brown, D.; Hoblit, S.; Dietrich, F.S. Derivation of an optical potential for statically deformed rare-earth nuclei from a global spherical potential. Phys. Rev. C 2015, 91, 024618. [Google Scholar] [CrossRef]
- Watanabe, S.; Furumoto, T.; Horiuchi, W.; Suhara, T.; Taniguchi, Y. Investigation of deformation parameters using high-energy heavy-ion scattering. Phys. Rev. C 2024, 110, 024604. [Google Scholar] [CrossRef]
- Gkatis, G.; Diakaki, M.; Noguere, G.; Nyman, M.; Oprea, A.; Paradela Dobarro, C.; Pirovano, E.; Plompen, A. Cross section measurements of neutron elastic and inelastic scattering on 54Fe. Phys. Rev. C 2024, 109, 034612. [Google Scholar] [CrossRef]
- Yang, G.H.; Kuang, Y.; Yang, Z.X.; Li, Z.P. Extracting neutron skin from elastic proton-nucleus scattering with deep neural network. Phys. Lett. B 2025, 862, 139301. [Google Scholar] [CrossRef]
- Catacora-Rios, M.; Lovell, A.E.; Nunes, F.M.; Thompson, I.J. Statistical tools for a better optical model. Phys. Rev. C 2021, 104, 064611. [Google Scholar] [CrossRef]
- Otuka, N.; Ganesan, S.; Zhuang, Y.; Suzuki, R.; Ge, Z.; Tao, X.; Dupont, E.; Tárkányi, F.; Katō, K.; Yang, S.; et al. Towards a More Complete and Accurate Experimental Nuclear Reaction Data Library (EXFOR): International Collaboration Between Nuclear Reaction Data Centers (NRDC). Nucl. Data Sheets 2014, 120, 272–276. [Google Scholar] [CrossRef]
- Harwood, J. Evaluated Nuclear Data File (ENDF). Available online: https://www-nds.iaea.org/exfor/endf.htm (accessed on 20 March 2025).
- Koning, A.; Rochman, D.; Sublet, J.-C.; Dzysiuk, N.; Fleming, M.; van der Marck, S. TENDL: Complete Nuclear Data Library for Innovative Nuclear Science and Technology. Nucl. Data Sheets 2019, 155, 1–55. [Google Scholar] [CrossRef]
- Koning, A.; Hilaire, S.; Goriely, S. TALYS-1.95. Available online: http://www.talys.eu (accessed on 15 March 2025).
- Herman, M.; Capote, R.; Sin, M.; Obložinský, P.; Trkov, A.; Wienke, H.; Zerkin, V.; Carlson, B. EMPIRE: Nuclear Reaction Model Code System for Data Evaluation. Nucl. Data Sheets 2007, 108, 2655–2715. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. The Effective Nuclear Potential. Nucl. Phys. 1959, 9, 615–634. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. The Nuclear Surface. Philos. Mag. 1956, 1, 1043–1054. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 1972, 5, 626. [Google Scholar] [CrossRef]
- Warburton, E.K.; Brown, B.A. Effective Interactions for the 0p1s0d Nuclear Shell-Model Space. Phys. Rev. C 1992, 46, 923. [Google Scholar] [CrossRef]
- Brown, B.A.; Richter, W.A. New “USD” Hamiltonians for the sd Shell. Phys. Rev. C 2006, 74, 034315. [Google Scholar] [CrossRef]
- Stone, J.R.; Reinhard, P.-G. The Skyrme Interaction in Finite Nuclei and Nuclear Matter. Phys. Rep. 2007, 58, 587–657. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.V.; Lalazissis, G.A.; Ring, P. Relativistic Hartree–Bogoliubov Theory: Static and Dynamic Aspects of Exotic Nuclear Structure. Phys. Rep. 2005, 409, 101–259. [Google Scholar] [CrossRef]
- Meng, J. (Ed.) Relativistic Density Functional for Nuclear Structure; International Review of Nuclear Physics: Volume 10; World Scientific: Singapore, 2016; pp. 1–716. [Google Scholar] [CrossRef]
- Liu, Z.X.; Lam, Y.H.; Lu, N.; Ring, P. The Optimized Point-Coupling Interaction for the Relativistic Energy Density Functional of Hartree–Bogoliubov Approach Quantifying the Nuclear Bulk Properties. Phys. Lett. B 2023, 842, 137946. [Google Scholar] [CrossRef]
- Dechargé, J.; Gogny, D. Hartree-Fock-Bogolyubov Calculations with the D1 Effective Interaction on Spherical Nuclei. Phys. Rev. C 1980, 21, 1568–1593. [Google Scholar] [CrossRef]
- Chappert, F.; Pillet, N.; Girod, M.; Berger, J.-F. Gogny Force with a Finite-Range Density Dependence. Phys. Rev. C 2015, 91, 034312. [Google Scholar] [CrossRef]
- Bertsch, G.; Borysowicz, J.; McManus, H.; Love, W.G. Interactions for Inelastic Scattering Derived from Realistic Potentials. Nucl. Phys. A 1977, 284, 399–419. [Google Scholar] [CrossRef]
- Beiner, M.; Flocard, H.; Van Giai, N.; Quentin, P. Nuclear Ground-State Properties and Self-Consistent Calculations with the Skyrme Interaction: (I). Spherical Description. Nucl. Phys. A 1975, 238, 29–69. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme Parametrization from Subnuclear to Neutron Star Densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Love, W.G.; Satchler, G.R. Exchange Effects with a Realistic Interaction for Elastic Scattering. Nucl. Phys. A 1970, 159, 1–44. [Google Scholar] [CrossRef]
- Khoa, D.T.; von Oertzen, W.; Bohlen, H.G.; Loc, B.X. Nuclear matter incompressibility and density-dependent M3Y interaction. Phys. Rev. C 2007, 76, 014603. [Google Scholar] [CrossRef]
- Khoa, D.T.; von Oertzen, W. Nuclear matter saturation properties from density dependent M3Y interaction. Phys. Lett. B 1993, 304, 8–12. [Google Scholar] [CrossRef]
- Khoa, D.T.; Satchler, G.R.; von Oertzen, W. Folding model analysis of elastic and inelastic scattering using density-dependent M3Y interaction. Phys. Rev. C 1997, 56, 954–965. [Google Scholar] [CrossRef]
- Seif, W. Nuclear matter equation of state using density-dependent M3Y nucleon–nucleon interactions. J. Phys. G Nucl. Part. Phys. 2011, 38, 035102. [Google Scholar] [CrossRef]
- Khoa, D.T.; Satchler, G.R. Generalized folding model for elastic and inelastic nucleus–nucleus scattering using realistic density dependent nucleon–nucleon interaction. Nucl. Phys. A 2000, 668, 3–41. [Google Scholar] [CrossRef]
- Bethe, H. Theory of Disintegration of Nuclei by Neutrons. Nature 1935, 47, 747. [Google Scholar] [CrossRef]
- Bohr, N. Neutron Capture and Nuclear Constitution. Nature 1936, 137, 344. [Google Scholar] [CrossRef]
- Fernbach, S.; Serber, R.; Taylor, T.B. The Scattering of High Energy Neutrons by Nuclei. Phys. Rev. 1949, 75, 1352. [Google Scholar] [CrossRef]
- Ostrofsky, M.; Breit, G.; Johnson, D.P. The Excitation Function of Lithium under Proton Bombardment. Phys. Rev. 1936, 49, 22. [Google Scholar] [CrossRef]
- Feshbach, H.; Porter, C.E.; Weisskopf, V.F. Model for Nuclear Reactions with Neutrons. Phys. Rev. 1954, 96, 448–464. [Google Scholar] [CrossRef]
- Le Levier, R.E.; Saxon, D.S. An Optical Model for Nucleon-Nuclei Scattering. Phys. Rev. 1952, 87, 40. [Google Scholar] [CrossRef]
- Koning, A.J.; Delaroche, J.P. Local and Global Nucleon Optical Models from 1 keV to 200 MeV. Nucl. Phys. A 2003, 713, 231–310. [Google Scholar] [CrossRef]
- Arnould, M.; Goriely, S. Astronuclear Physics: A Tale of the Atomic Nuclei in the Skies. Prog. Part. Nucl. Phys. 2020, 112, 103766. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus within the Optical Model Used in Nuclear and Particle Physics. J. Phys. G Nucl. Part. Phys. 2023, 50, 035101. [Google Scholar] [CrossRef]
- Satchler, G.R.; Love, W.G. Folding Model Potentials from Realistic Interactions for Heavy-Ion Scattering. Phys. Rep. 1979, 55, 183–254. [Google Scholar] [CrossRef]
- Satchler, G.R. Direct Nuclear Reactions; Oxford University Press: New York, NY, USA, 1983. [Google Scholar]
- Greenlees, G.W.; Pyle, G.J.; Tang, Y.C. Nuclear-Matter Radii from a Reformulated Optical Model. Phys. Rev. 1968, 171, 1115. [Google Scholar] [CrossRef]
- Karpov, A.V.; Denikin, A.S.; Naumenko, M.A.; Alekseev, A.P.; Rachkov, V.A.; Samarin, V.V.; Zagrebaev, V.I. NRV Web Knowledge Base on Low-Energy Nuclear Physics. Nucl. Instrum. Methods Phys. Res. A 2017, 859, 112–124. [Google Scholar] [CrossRef]
- Zagrebaev, V.I.; Denikin, A.S.; Karpov, A.V.; Alekseev, A.P.; Naumenko, M.A.; Rachkov, V.A.; Samarin, V.V.; Saiko, V.V. NRV Web Knowledge Base on Low-Energy Nuclear Physics. Available online: https://nrv2.jinr.ru (accessed on 30 May 2025).
- Karpov, A.V.; Denikin, A.S.; Alekseev, A.P.; Zagrebaev, V.I.; Rachkov, V.A.; Naumenko, M.A.; Saiko, V.V. NRV Web Knowledge Base on Low-Energy Nuclear Physics. Phys. At. Nucl. 2016, 79, 749–761. [Google Scholar] [CrossRef]
- Woods, R.D.; Saxon, D.S. Diffuse Surface Optical Model for Nucleon-Nuclei Scattering. Phys. Rev. 1954, 95, 577. [Google Scholar] [CrossRef]
- Takigawa, N.; Washiyama, K. Fundamentals of Nuclear Physics; Springer: Tokyo, Japan, 2017. [Google Scholar]
- Hartree, D.R. The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Proc. Camb. Philos. Soc. 1928, 24, 89–110. [Google Scholar] [CrossRef]
- Adamson, R.D. Novel Methods for Large Molecules in Quantum Chemistry. Ph.D. Thesis, University of Cambridge, Cambridgeshire, UK, 1998. [Google Scholar]
- Fock, V. Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Phys. 1930, 61, 126–148. [Google Scholar] [CrossRef]
- Johnson, C.W. SKHAFO.FOR: Skyrme Hartree-Fock Program. Louisiana State University, 1990. Available online: https://ntrs.nasa.gov/api/citations/19920020758/downloads/19920020758.pdf (accessed on 30 May 2025).
- Köhler, H. Skyrme force and the mass formula. Nucl. Phys. A 1976, 258, 301–316. [Google Scholar] [CrossRef]
- Liu, G.-Q. A systematic study of nuclear properties with Skyrme forces. J. Phys. G Nucl. Part. Phys. 1991, 17, 1–34. [Google Scholar] [CrossRef]
- Bartel, J.; Quentin, P.; Brack, M.; Guet, C.; Hakansson, H. Towards a better parametrisation of Skyrme-like effective forces: A critical study of the SKM force. Nucl. Phys. A 1982, 386, 79–100. [Google Scholar] [CrossRef]
- Giai, N.V.; Sagawa, H. Spin-isospin excitations with effective Skyrme interactions. Phys. Lett. B 1981, 106, 379–382. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Part II: Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Chabanat, E. Interactions Effectives Pour des Conditions Extrêmes D’isospin. Ph.D. Thesis, Université Claude Bernard Lyon 1, Lyon, France, 1995. [Google Scholar]
- Love, W.G.; Owen, L.W. Exchange Effects from Realistic Interactions in the Reformulated Optical Model. Nucl. Phys. A 1975, 239, 74–82. [Google Scholar] [CrossRef]
- Love, W. Density-Dependent Interactions and the Folding Model for Heavy-Ion Potentials. Phys. Lett. B 1977, 72, 4–6. [Google Scholar] [CrossRef]
- Petrovich, F.; Stanley, D.; Bevelacqua, J. Density Dependent Interactions and the Consistency of Folding Estimates of Nucleon-Nuclei and Nuclei-Nuclei Potentials. Phys. Lett. B 1977, 71, 259–262. [Google Scholar] [CrossRef]
- Reinhard, P.; Flocard, H. Nuclear Effective Forces and Isotope Shifts. Nucl. Phys. A 1995, 584, 467–488. [Google Scholar] [CrossRef]
- Guenther, P.T.; Smith, A.B.; Whalen, J.F. Fast-Neutron Total and Scattering Cross Sections of 182W, 184W and 186W. Phys. Rev. C 1982, 26, 2433. [Google Scholar] [CrossRef]
- Annand, J.R.M.; Finlay, R.W. Direct Neutron Scattering from 182W and 184W. Nucl. Phys. A 1985, 442, 234–252. [Google Scholar] [CrossRef]






| Ska | −1602.78 | 570.88 | −67.70 | 8000 | 125 | −0.02 | 0 | 0 | −0.286 | 1/3 |
| GS6 | −1012 | 209 | −76.3 | 10,619 | 105 | 0.139 | 0 | 0 | 1 | 1 |
| SKM* | −2645 | 410 | −135.0 | 15,595.0 | 130 | 0.09 | 0 | 0 | 0 | 1/6 |
| SGII | −2645 | 340 | −41.9 | 15,595 | 105 | 0.09 | −0.0588 | 1.425 | 0.06044 | 1/6 |
| SLy4 | −2488.91 | 486.82 | −546.39 | 13,777 | 123 | 0.834 | −0.344 | −1 | 1.354 | 1/6 |
| SLy5 | −2483.45 | 484.23 | −556.69 | 13,757 | 125 | 0.776 | −0.317 | −1 | 1.263 | 1/6 |
| SLy6 | −2479.50 | 462.18 | −448.61 | 13,673 | 122 | 0.825 | −0.465 | −1 | 1.355 | 1/6 |
| SLy7 | −2480.8 | 461.29 | −433.93 | 13,669 | 125 | 0.848 | −0.492 | −1 | 1.393 | 1/6 |
| SLy8 | −2481.41 | 480.78 | −538.34 | 13,731 | 125 | 0.8024 | −0.3424 | −1 | 1.3061 | 1/6 |
| SLy9 | −2511.13 | 510.6 | −429.8 | 13,716 | 110 | 0.7998 | −0.6213 | −1 | 1.3727 | 1/6 |
| SLy10 | −2506.77 | 430.98 | −304.95 | 13,826.41 | 105 | 1.0398 | −0.6745 | −1 | 1.6833 | 1/6 |
| 182W | 1.2324 | 0.6507 |
| 183W | 1.2325 | 0.6506 |
| 184W | 1.2326 | 0.6504 |
| 186W | 1.2329 | 0.6501 |
| Reaction | Energy (MeV) | Experimental (MeV) | Koning and Delaroche (MeV) | SHF-WS (MeV) |
|---|---|---|---|---|
| 182W | 1.5 | 49.5 [68] | −48.234 | −47.7239 |
| 2.5 | 49.0 [68] | −47.893 | −47.5772 | |
| 3.4 | 50.1 [6] | −47.588 | −47.4452 | |
| 4.87 | 50.3 [69] | −47.092 | −47.2297 | |
| 6 | 50.3 [69] | −46.713 | −47.0640 | |
| 14 | NA | −44.090 | −45.8927 | |
| 183W | 3.4 | 49.0 [6] | −47.488 | −47.3332 |
| 14 | NA | −43.998 | −45.7878 | |
| 184W | 1.5 | 49.5 [68] | −48.032 | −47.4708 |
| 2.5 | 49.0 [68] | −47.693 | −47.3254 | |
| 3.4 | 50.1 [6] | −47.389 | −47.1947 | |
| 4.84 | 50.3 [69] | −46.895 | −46.9812 | |
| 6 | 50.3 [69] | −46.518 | −46.8171 | |
| 14 | NA | −43.907 | −45.6567 | |
| 186W | 1.5 | 49.5 [68] | −47.834 | −47.1878 |
| 2.5 | 49.0 [68] | −47.496 | −47.0439 | |
| 3.4 | 50.1 [6] | −47.194 | −46.9144 | |
| 14 | NA | −43.727 | −45.391 |
| Feature | Koning and Delaroche [43] | The Microscopic Approach Proposed in This Study (SHF-WS) |
|---|---|---|
| Method | Parametric global OMP | Microscopic: SHF + SF |
| Physical foundation | Systematic fit based on experimental data | Skyrme NN interaction + potential derived from density |
| Scope of application | Fast and broad (wide mass number and energy range) | Specific nuclei (182W–186W), detailed resolution |
| Computational approach | Fitted parametric functions | Numerical integration from densities (folding) |
| Level of innovation | Innovation lies in scope and parametrization, not method | Methodological detail and microscopic foundation |
| Isotope—Energy (MeV) | R2 Koning and Delaroche [43] | R2 The Microscopic Approach Proposed in This Study (SHF-WS) |
|---|---|---|
| 182W—1.5 | 0.9768 | 0.5479 |
| 182W—2.5 | 0.4525 | 0.4586 |
| 182W—3.4 | 0.9935 | 0.9874 |
| 182W—4.87 | 0.9951 | 0.9967 |
| 182W—6.0 | 0.9969 | 0.9992 |
| 183W—3.4 | 0.9895 | 0.9839 |
| 184W—1.5 | 0.9798 | 0.9940 |
| 184W—2.5 | 0.2950 | 0.2935 |
| 184W—3.4 | 0.9934 | 0.9978 |
| 184W—4.84 | 0.9964 | 0.9991 |
| 184W—6.0 | 0.9980 | 0.9982 |
| 186W—1.5 | 0.9848 | 0.9958 |
| 186W—2.5 | 0.1502 | 0.1540 |
| 186W—3.4 | 0.9918 | 0.9992 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akdeniz, F.; Sarpun, I.H. Simulation-Based Determination of Angular Differential Cross Sections of (n,el) Scattering via Evaluated Interaction Potentials. Appl. Sci. 2025, 15, 6831. https://doi.org/10.3390/app15126831
Akdeniz F, Sarpun IH. Simulation-Based Determination of Angular Differential Cross Sections of (n,el) Scattering via Evaluated Interaction Potentials. Applied Sciences. 2025; 15(12):6831. https://doi.org/10.3390/app15126831
Chicago/Turabian StyleAkdeniz, Ferhan, and Ismail Hakki Sarpun. 2025. "Simulation-Based Determination of Angular Differential Cross Sections of (n,el) Scattering via Evaluated Interaction Potentials" Applied Sciences 15, no. 12: 6831. https://doi.org/10.3390/app15126831
APA StyleAkdeniz, F., & Sarpun, I. H. (2025). Simulation-Based Determination of Angular Differential Cross Sections of (n,el) Scattering via Evaluated Interaction Potentials. Applied Sciences, 15(12), 6831. https://doi.org/10.3390/app15126831






