Asymmetric Magnetohydrodynamic Propulsion for Oil–Water Core Annular Flow Through Elbow
Abstract
1. Introduction
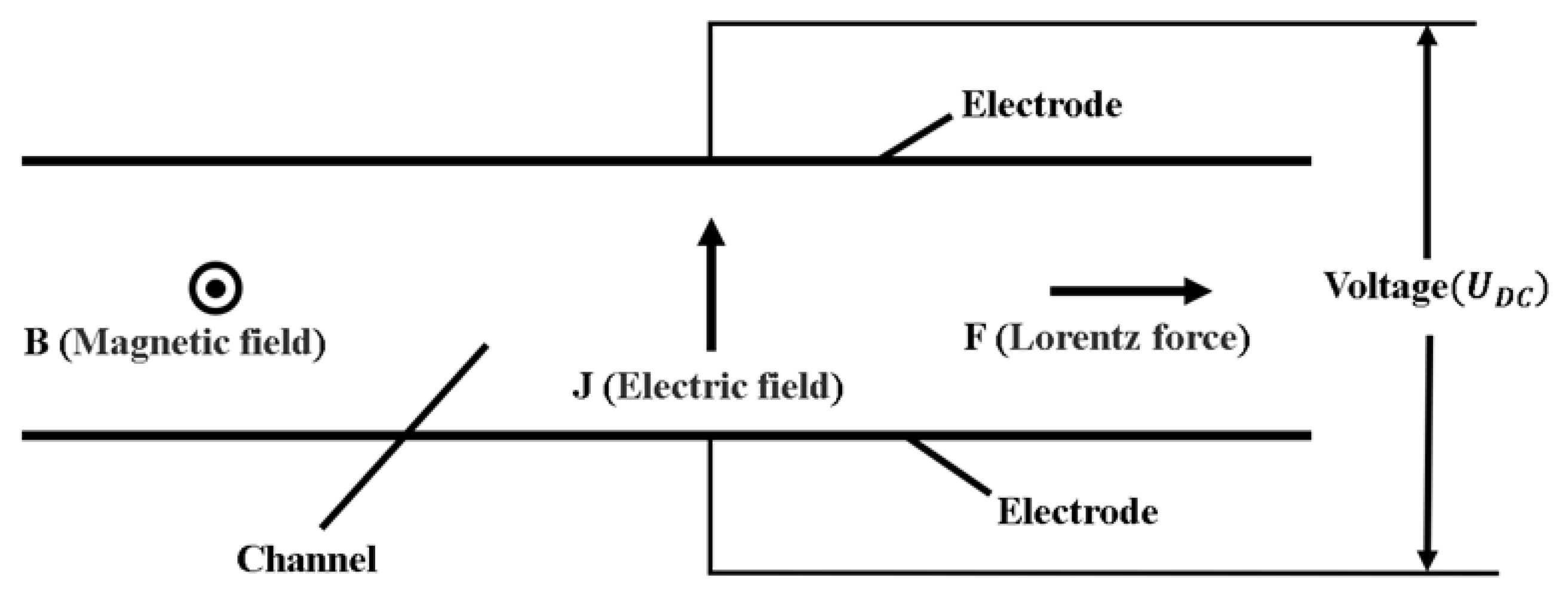
2. Magnetohydrodynamic Principles
3. Simulation Establishment
3.1. Model Design
3.2. Related Parameter Settings
- Parameter setting of heavy oil and electrolyte (water) solution: Oil core length 60 mm, dynamic viscosity 0.2 Pa·s, density 960 kg∙m−3, input initial velocity 0.1 m∙s−1; dynamic viscosity of electrolyte (water) solution 0.001 Pa·s, conductivity 5 m·s−1, density 1000 kg∙m−3, relative dielectric constant 81, input initial velocity 0.05 m·s−1.
- Selection of pipe: The pipe wall conditions are chosen as no slip, the direction of gravity is along the negative path of the Y-axis, the reference pressure level is 1 atm, the temperature is 293.15 K, and the acceleration of gravity is g.
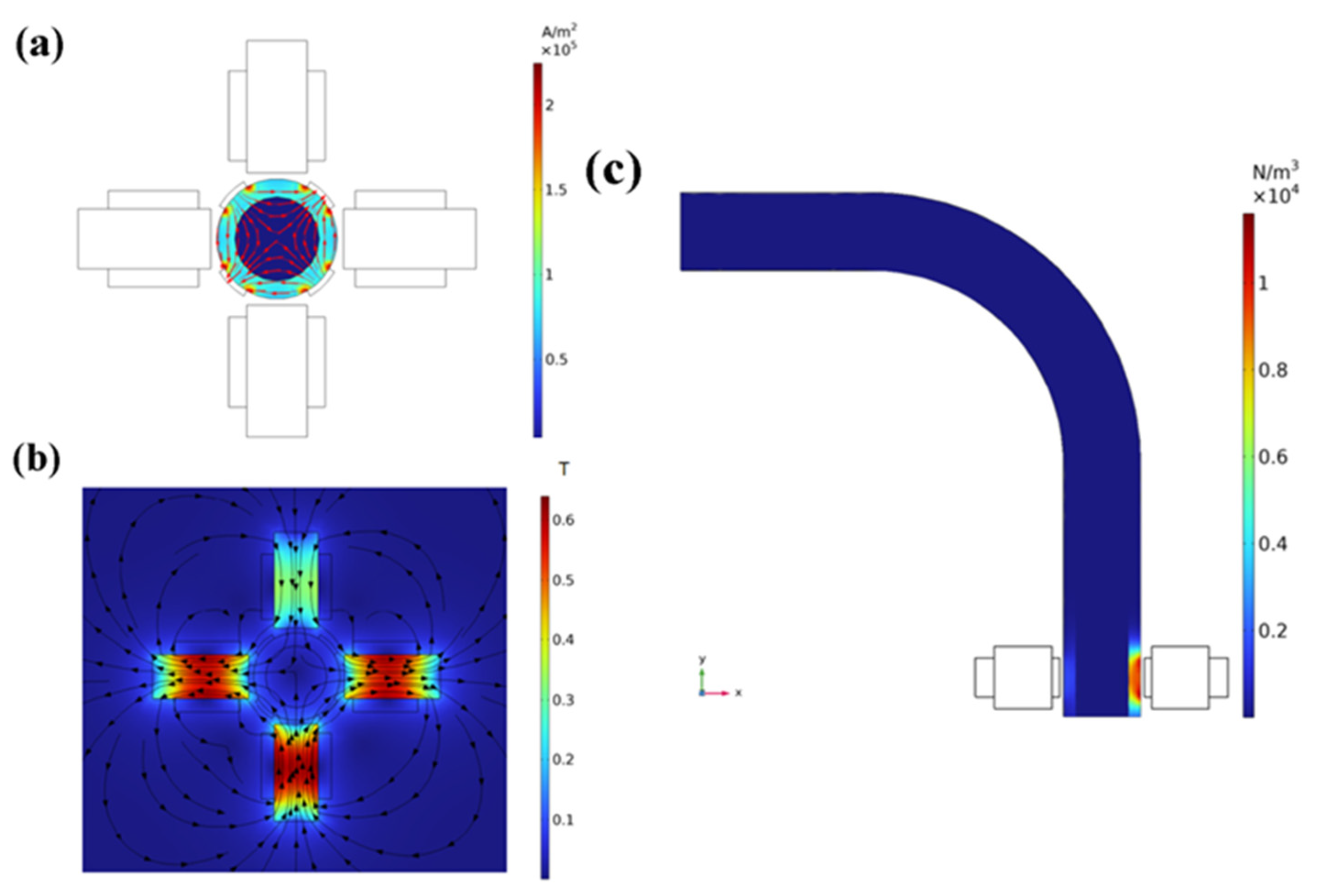
- Magnetic field parameter setting: The magnetic field action range consists of all domains including air, and the relative permeability and electrical conductivity of relevant materials are selected in COMSOL Multiphysics® [59] software’ material library. Coil excitation is current, the current is set to 8 A, the number of coil turns is 100, and the coil wire conductivity is S·m−1.
- Electric field parameter setting: The electric field acts on four electrode plates as well as the water and oil phases, the voltage is set to 220 V, and the same parameter is set relative to two electrode plates, one pair of which is 220 V and the other pair of which is set to 0 V, which constitutes the positive and negative poles to provide current for the fluid.
- Condition setting at the entrance and exit of the pipe: The boundary conditions at both the entrances and exits are set to fully developed flow, the average air pressure at the outlets is 0 kPa, and the hydrostatic pressure compensation is turned on.
4. Discussion
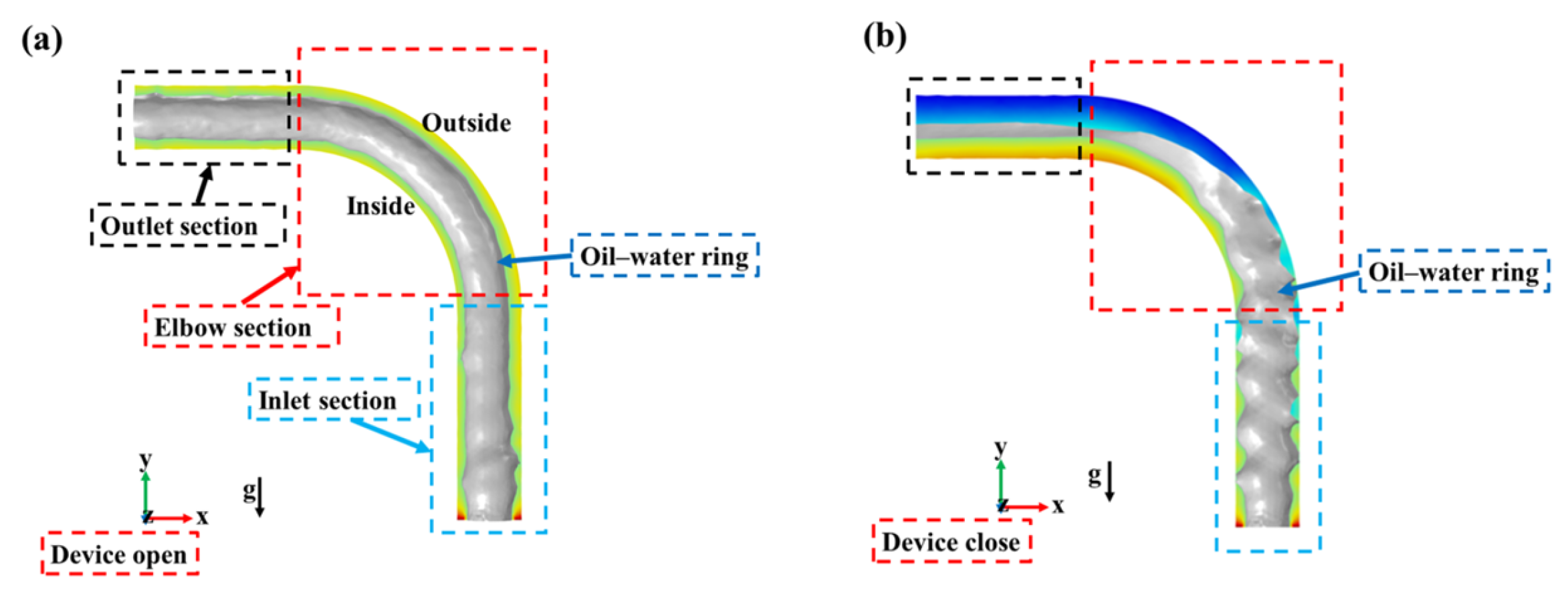
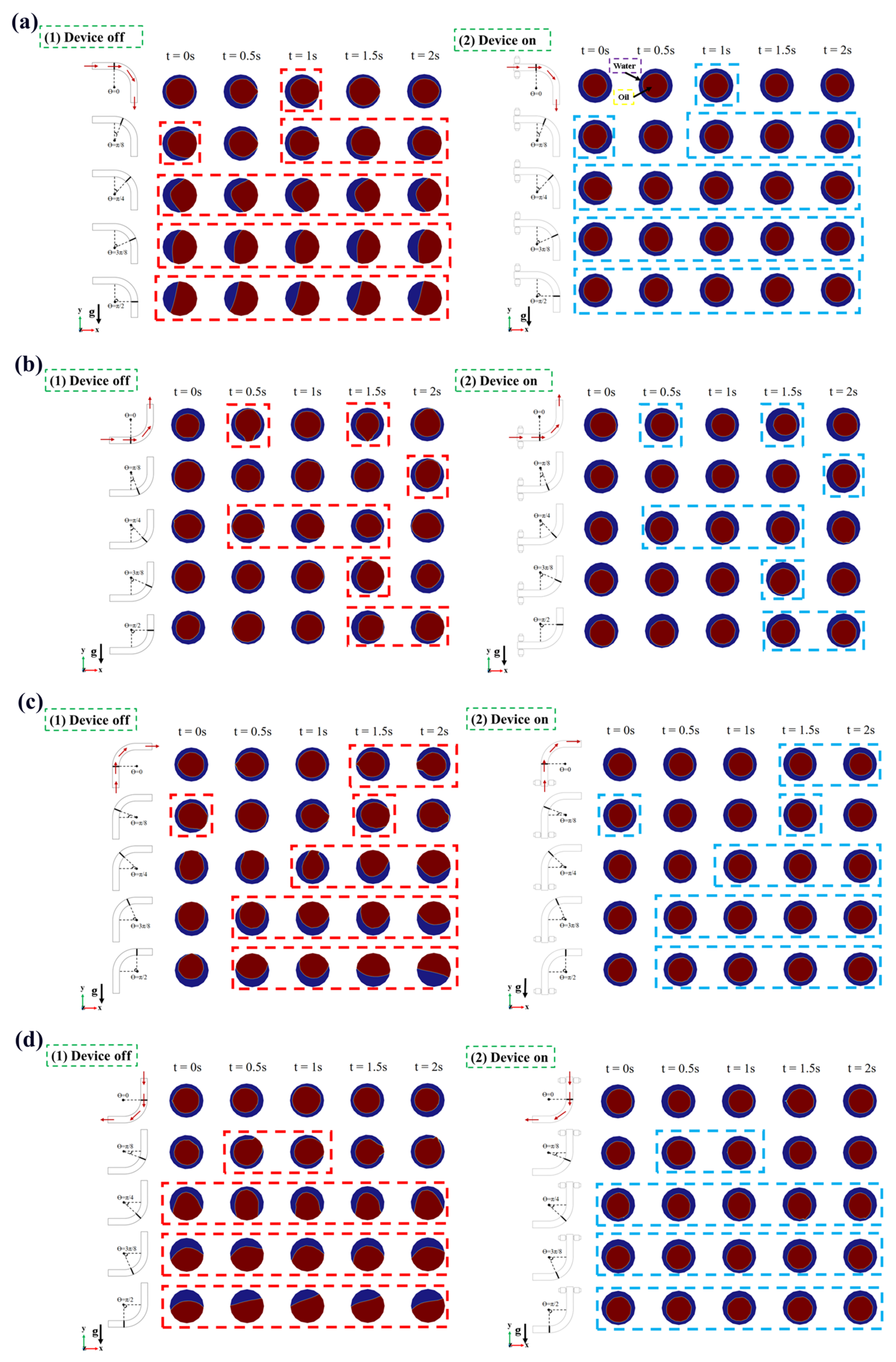
4.1. Oil–Water Interface Evolution
4.2. Electromagnetic Field
4.3. Flow Field
4.4. Regulatory Factors
4.5. Gravitational Action Effects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MHD | Magnetohydrodynamics |
| CFD | Computational fluid dynamics |
| CAF | Core annular flow |
References
- He, M.; Pu, W.; Wu, T.; Yang, X.; Li, X.; Liu, R.; Li, S.; Chen, Y. Investigation on the mechanism of heating effect influencing emulsifying ability of crude oil: Experimental and molecular dynamics simulation. Colloids Surf. A Physicochem. Eng. Asp. 2023, 671, 131654. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, D.; Diao, B.; Tan, L.; Zhang, W.; Liu, K. Comparative performance of electric heater vs. RF heating for heavy oil recovery. Appl. Therm. Eng. 2019, 160, 114105. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Ding, M.; Mao, D.; Chen, M.; Han, Y.; Liu, Y.; Xue, X. Effects of viscosification, ultra-low interfacial tension, and emulsification on heavy oil recovery by combination flooding. J. Mol. Liq. 2023, 380, 121698. [Google Scholar] [CrossRef]
- Wu, R.; Yan, Y.; Li, X.; Tan, Y. Preparation and controllable heavy oil viscosity reduction performance of pH-responsive star block copolymers. J. Mol. Liq. 2023, 389, 122925. [Google Scholar] [CrossRef]
- Santos, R.; Filho, E.; Dourado, R.; Santos, A.; Borges, G.; Dariva, C.; Santana, C.; Franceschi, E.; Santos, D. Study on the use of aprotic ionic liquids as potential additives for crude oil upgrading, emulsion inhibition, and demulsification. Fluid Phase Equilib. 2019, 489, 8–15. [Google Scholar] [CrossRef]
- Isaac, J.; Speed, J. Method of Piping Fluids. U.S. Patent No. 759374, 10 May 1904. [Google Scholar]
- Abraham, S.; Clack, A.F. Method of Pumping Viscous Petroleum. U.S. Patent No. 2533878, 10 January 1950. [Google Scholar]
- Ghosh, S.; Mandal, T.; Das, G.; Das, P. Review of oil water core annular flow. Renew. Sust. Energ. Rev. 2009, 13, 1957–1965. [Google Scholar] [CrossRef]
- Prada, J.; Bannwart, A. Modeling of vertical core-annular flows and application to heavy oil production. J. Energy. Resour. Technol. 2001, 123, 194–199. [Google Scholar] [CrossRef]
- Coelho, N.; Taqueda, M.; Souza, N.; Paiva, J.; Santos, A.; Lia, L.; Moraes, M.; Júnior, D. Energy Savings on Heavy Oil Transportation through Core Annular Flow Pattern: An Experimental Approach. Int. J. Multiph. Flow 2020, 122, 103127. [Google Scholar] [CrossRef]
- Rodriguez, O.; Bannwart, A.; Carvalho, C. Pressure loss in core-annular flow: Modeling, experimental investigation and full-scale experiments. J. Pet. Sci. Eng. 2009, 65, 67–75. [Google Scholar] [CrossRef]
- Shi, J.; Lao, L.Y.; Yeung, H. Water-lubricated transport of high-viscosity oil in horizontal pipes: The water holdup and pressure gradient. Int. J. Multiph. Flow 2017, 96, 70–85. [Google Scholar] [CrossRef]
- Franchi, R.A.; Carraretto, I.M.; Chiarenza, G.; Sotgia, G.; Colombo, L. Effect of the down-slope on the structure and the pressure loss of an oil–water stream. Int. J. Multiph. Flow 2023, 165, 104483. [Google Scholar] [CrossRef]
- Shi, J.; Gourma, M.; Yeung, H. CFD simulation of horizontal oil–water flow with matched density and medium viscosity ratio in different flow regimes. J. Pet. Sci. Eng. 2017, 151, 373–383. [Google Scholar] [CrossRef]
- Rodriguez, O.; Bannwart, C. Stability analysis of core-annular flow and neutral stability wave number. AIChE J. 2007, 54, 20–31. [Google Scholar] [CrossRef]
- Ingen Housz, E.M.R.M.; Ooms, G.; Henkes, R.A.W.M.; Pourquie, M.J.B.M.; Kidess, A.; Radhakrishnan, R. A comparison between numerical predictions and experimental results for horizontal core-annular flow with a turbulent annulus. Int. J. Multiph. Flow 2017, 95, 271–282. [Google Scholar] [CrossRef]
- Colombo, L.; Guilizzoni, M.; Sotgia, G.; Marzorati, D. Influence of sudden contractions on in situ volume fractions for oil–water flows in horizontal pipes. Int. J. Heat Fluid Flow 2015, 53, 91–97. [Google Scholar] [CrossRef]
- Cavicchio, C.; Biazussi, J.; Castro, M.; Bannwart, A.; Rodriguez, O.; Carvalho, C. Experimental study of viscosity effects on heavy crude oil–water core-annular flow pattern. Exp. Therm. Fluid Sci. 2018, 92, 270–285. [Google Scholar] [CrossRef]
- Dehkordi, P.; Colombo, L.; Mohammadian, E.; Azdarpour, A.; Sotgia, G. The influence of abruptly variable cross-section on oil core eccentricity and flow characteristics during viscous oil–water horizontal flow. Exp. Therm. Fluid. Sci. 2019, 105, 261–277. [Google Scholar] [CrossRef]
- Sun, J.; Guo, L.; Fu, J.; Jing, J.; Yin, X.; Lu, Y.; Ullmann, A.; Brauner, N. A new model for viscous oil–water eccentric core annular flow in horizontal pipes. Int. J. Multiph. Flow 2022, 147, 103892. [Google Scholar] [CrossRef]
- Sayeed, R.; Gazder, U.; Qureshi, H.; Arifuzzaman, M. Advanced Machine Learning Applications to Viscous Oil–Water Multi-Phase Flow. Appl. Sci. 2022, 12, 4871. [Google Scholar]
- Sun, J.; Jing, J.; Jing, P.; Duan, N.; Wu, C.; Tan, J. Experimental study on drag reduction of aqueous foam on heavy oil flow boundary layer in an upward vertical pipe. J. Pet. Sci. Eng. 2016, 146, 409–417. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, H.; Zhang, J.; Feng, N.; Cheng, S. Transient pressure analysis of polymer flooding fractured wells with oil–water two-phase flow. Pet. Explor. Dev. 2023, 50, 175–182. [Google Scholar] [CrossRef]
- Hu, H.; Jing, J.; Tan, J.; Yeoh, G. Flow patterns and pressure gradient correlation for oil–water core-annular flow in horizontal pipes. Exp. Comput. Multiph. Flow 2020, 2, 99–108. [Google Scholar] [CrossRef]
- Fan, J.; Li, H.; Pourquié, M.; Ooms, G.; Henkes, R. Simulation of the hydrodynamics in the onset of fouling for oil–water core-annular flow in a horizontal pipe. J. Pet. Sci. Eng. 2021, 207, 109084. [Google Scholar]
- Yang, J.; Li, P.; Zhang, X.; Lu, X.; Li, Q.; Mi, L. Experimental investigation of oil–water flow in the horizontal and vertical sections of a continuous transportation pipe. Sci. Rep. 2021, 11, 20092. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Wang, Y.; Ou, J.; Chen, C. Numerical Simulation of Oil–Water Core Annular Flow in a U-Bend Based on the Eulerian Model. Chem. Eng. Technol. 2014, 37, 659–666. [Google Scholar] [CrossRef]
- Silva, A.; Moraes, D.; Arni, S.; Solisio, C.; Converti, A.; Oliveira, R.; Vianna, A. Large-Eddy Simulation of Oil–Water Annular Flow in Eccentric Vertical Pipes. Chem. Eng. Technol. 2020, 44, 104–113. [Google Scholar] [CrossRef]
- Zhang, H.; Umehara, Y.; Yoshida, H.; Mor, S. Prediction of interfacial shear stress and pressure drop in vertical two-phase annular flow. Int. J. Heat Mass Transf. 2023, 218, 124750. [Google Scholar] [CrossRef]
- Liu, H.; Duan, J.; Li, J.; Gu, K.; Lin, K.; Wang, J.; Yan, H.; Guan, L.; Li, C. Numerical quasi-three dimensional modeling of stratified oil–water flow in horizontal circular pipe. Ocean Eng. 2022, 251, 111172. [Google Scholar] [CrossRef]
- Ayegba, P.; Edomwonyi-Otu, L.; Abubakar, A.; Yusuf, N. Flow pattern and pressure drop for oil–water flows in and around 180° bends. SN Appl. Sci. 2021, 10, 3. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, W.; Liu, Y.; He, Y.; Chen, J.; Qiao, L.; Wang, T. Study on hydrodynamic characteristics of oil–water annular flow in 90° elbow. Chem. Eng. Res. Des. 2020, 153, 443–451. [Google Scholar] [CrossRef]
- Jiang, F.; Chang, J.; Huang, H.; Huang, J. A Study of the Interface Fluctuation and Energy Saving of Oil–Water Annular Flow. Energies 2022, 15, 2123. [Google Scholar] [CrossRef]
- Gupta, R.; Turangan, C.; Manica, R. Oil–water core-annular flow in vertical pipes: A CFD study. Can. J. Chem. Eng. 2016, 94, 980–987. [Google Scholar] [CrossRef]
- Ogilvie, G. Introduction to Modern Magnetohydrodynamics. Phys. Today 2017, 70, 54–55. [Google Scholar] [CrossRef]
- Hotta, H.; Rempel, M.; Yokoyama, T. Large-scale magnetic fields at high Reynolds numbers in magnetohydrodynamic simulations. Science 2016, 351, 1427–1430. [Google Scholar] [CrossRef]
- Dong, C.; Wang, L.; Huang, Y.; Comisso, L.; Sandstrom, T.; Bhattacharjee, A. Reconnection-driven energy cascade in magnetohydrodynamic turbulence. Sci. Adv. 2022, 8, eabn7627. [Google Scholar] [CrossRef]
- Lebedev, S.; Frank, A.; Ryutov, D. Exploring astrophysics-relevant magnetohydrodynamics with pulsed-power laboratory facilities. Rev. Mod. Phys. 2019, 91, 025002. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, J.; Chen, H.; Yong, H.; Wu, Z. A Soft Reconfigurable Circulator Enabled by Magnetic Liquid Metal Droplet for Multifunctional Control of Soft Robots. Adv. Sci. 2023, 10, 2300935. [Google Scholar] [CrossRef]
- Chiolerio, A.; Quadrelli, M. Smart Fluid Systems: The Advent of Autonomous Liquid Robotics. Adv. Sci. 2017, 4, 1700036. [Google Scholar] [CrossRef]
- Fan, X.; Dong, X.; Karacakol, A.; Xie, H.; Sitti, M. Reconfigurable multifunctional ferrofluid droplet robots. Proc. Natl. Acad. Sci. USA 2020, 117, 27916–27926. [Google Scholar] [CrossRef]
- Fan, X.; Sun, M.; Sun, L.; Xie, H. Ferrofluid Droplets as Liquid Microrobots with Multiple Deformabilities. Adv. Funct. Mater. 2020, 30, 2000138. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, Y.; Zhao, J.; Zhang, T.; Zhang, X.; Song, W.; Wang, L.; Li, T. Amoeba-Inspired Magnetic Venom Microrobots. Small 2023, 19, 2207360. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, N.; Anwari, M.; Kondo, J.; Harada, N. Three-dimensional numerical analyses on magnetohydrodynamic accelerator. Energy Convers. Manag. 2007, 48, 2407–2415. [Google Scholar] [CrossRef]
- Subramaniam, V.; Raja, L. Magnetohydrodynamic simulation study of plasma jets and plasma-surface contact in coaxial plasma accelerators. Phys. Plasmas 2017, 24, 062507. [Google Scholar] [CrossRef]
- Anwari, M.; Sakamoto, N.; Hardianto, T.; Kondo, J.; Harada, N. Numerical analysis of magnetohydrodynamic accelerator performance with diagonal electrode connection. Energy Convers. Manag. 2005, 47, 1857–1867. [Google Scholar] [CrossRef]
- Shipley, G.; Awe, T. Three-dimensional magnetohydrodynamic modeling of auto-magnetizing liner implosions on the Z accelerator. Phys. Plasmas 2023, 30, 102707. [Google Scholar] [CrossRef]
- Frolova, V.; Nokhrina, E.; Pashchenko, I. Synchrotron intensity plots from a relativistic stratified jet. Mon. Notices Royal Astron. Soc. 2023, 523, 887–906. [Google Scholar] [CrossRef]
- Gregory, T.S.; Cheng, R.; Tang, G.; Mao, L.; Tse, Z.T.H. The Magnetohydrodynamic Effect and Its Associated Material Designs for Biomedical Applications: A State-of-the-Art Review. Adv. Funct. Mater. 2016, 26, 3942–3952. [Google Scholar] [CrossRef]
- Al-Habahbeh, O.M.; Al-Saqqa, M.; Safi, M.; Abo Khater, T. Review of magnetohydrodynamic pump applications. Alex. Eng. J. 2016, 55, 1347–1358. [Google Scholar] [CrossRef]
- Salinas, G.; Lozon, C.; Kuhn, A. Unconventional applications of the magnetohydrodynamic effect in electrochemical systems. Curr. Opin. Electrochem. 2023, 38, 101220. [Google Scholar] [CrossRef]
- Wu, Q.; Li, Y. Magneto-Hydrodynamics; National University of Defense Technology Press: Changsha, China, 2007. [Google Scholar]
- Sheikholeslami, M.; Ganji, D. Magnetohydrodynamic and ferrohydrodynamic. In External Magnetic Field Effects on Hydrothermal Treatment of Nanofluid; Elsevier: Amsterdam, The Netherlands, 2016; pp. 1–47. [Google Scholar]
- Davidson, P. An Introduction to Magnetohydrodynamics (Cambridge Texts in Applied Mathematics); Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Senel, P. MHD Flow between Electromagnetically Coupled Concentric Cylinders with Slipping Walls. Eur. J. Mech. B Fluids 2022, 93, 101–116. [Google Scholar] [CrossRef]
- Barcelos, R.; Dujić, D. Direct Current Transformer Impact on the DC Power Distribution Networks. IEEE Trans. Smart Grid 2022, 13, 2547–2556. [Google Scholar] [CrossRef]
- Perumal, A.; Fröbel, M.; Gorantla, S.; Gemming, T.; Lüssem, B.; Eckert, J.; Leo, K. Novel Approach for Alternating Current (AC)-Driven Organic Light-Emitting Devices. Adv. Funct. Mater. 2012, 22, 210–217. [Google Scholar] [CrossRef]
- Belyaev, V.; Rodionova, V.; Grunin, A.; Inoue, M.; Fedyanin, A. Magnetic field sensor based on magnetoplasmonic crystal. Sci. Rep. 2020, 10, 7133. [Google Scholar] [CrossRef] [PubMed]
- COMSOL Multiphysics®; Version 6.0; cn.comsol.com; COMSOL AB: Stockholm, Sweden, 2024.
- Griffiths, D.J. Introduction to Electrodynamics, 4th ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]



| Pipe diameter—D (mm) | 20 mm |
| Oil inlet diameter—d (mm) | 14 mm |
| Vertical pipe length—L1 (mm) | 65 mm |
| Inner radius of elbow—r (mm) | 50 mm |
| Outside radius of elbow—R (mm) | 70 mm |
| Horizontal pipe section length—L2 (mm) | 50 mm |
| Electromagnetic Coil | Turns | The Diameter of the Wire (mm) | Material |
| 100 | 0.75 | Copper | |
| Iron core | Column height (mm) | Column width (mm) | Material |
| 22 | 10 | Iron | |
| Electrode plate (slightly curved shape to match the pipe wall) | Plate thickness (mm) | Plate length (mm) | Material |
| 2.5 | 16 | Copper |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Jia, Z.; Yang, L.; Xu, Y.; Zhao, J.; Jiao, S.; Ma, H.; Shen, R.; Liang, E.; Zhang, W.; et al. Asymmetric Magnetohydrodynamic Propulsion for Oil–Water Core Annular Flow Through Elbow. Appl. Sci. 2025, 15, 6828. https://doi.org/10.3390/app15126828
Wang C, Jia Z, Yang L, Xu Y, Zhao J, Jiao S, Ma H, Shen R, Liang E, Zhang W, et al. Asymmetric Magnetohydrodynamic Propulsion for Oil–Water Core Annular Flow Through Elbow. Applied Sciences. 2025; 15(12):6828. https://doi.org/10.3390/app15126828
Chicago/Turabian StyleWang, Chengming, Zezhong Jia, Lei Yang, Yongqi Xu, Jinhao Zhao, Shihui Jiao, Hao Ma, Ruofan Shen, Erjun Liang, Weiwei Zhang, and et al. 2025. "Asymmetric Magnetohydrodynamic Propulsion for Oil–Water Core Annular Flow Through Elbow" Applied Sciences 15, no. 12: 6828. https://doi.org/10.3390/app15126828
APA StyleWang, C., Jia, Z., Yang, L., Xu, Y., Zhao, J., Jiao, S., Ma, H., Shen, R., Liang, E., Zhang, W., Liu, Y., & Li, B. (2025). Asymmetric Magnetohydrodynamic Propulsion for Oil–Water Core Annular Flow Through Elbow. Applied Sciences, 15(12), 6828. https://doi.org/10.3390/app15126828







