Braking Performance and Response Analysis of Trains on Bridges Under Seismic Excitation
Abstract
1. Introduction
2. Materials and Methods
2.1. Vehicle Model
2.2. Subway-Bridge Coupled Systems
2.3. Deceleration Model
2.4. Simulation of Incentives
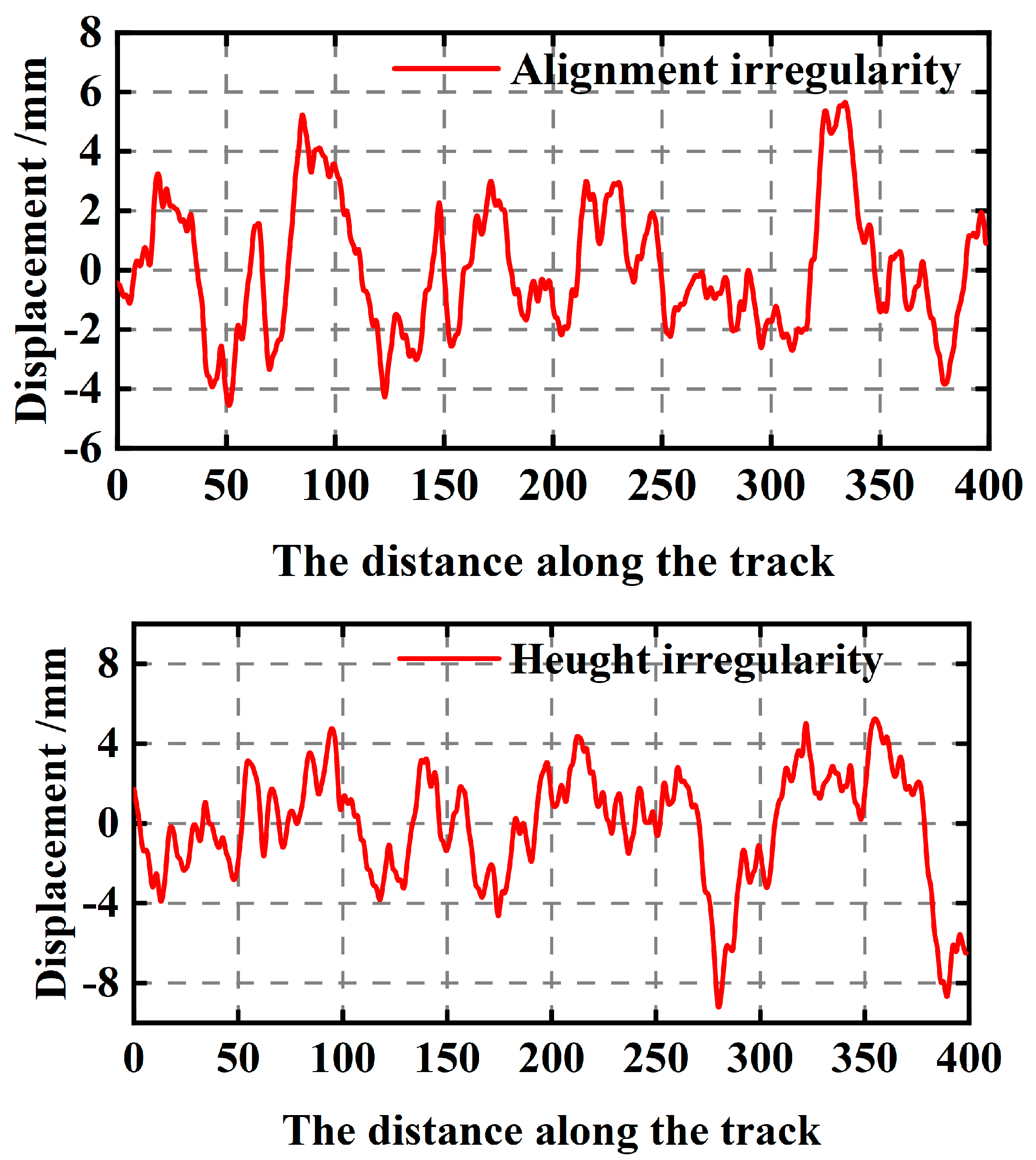
2.4.1. Simulation of Track Irregularities
2.4.2. Earthquake Simulation
3. Calculation and Analysis of Emergency Braking of Subway on Bridge During Earthquake
3.1. Calculation of Working Conditions
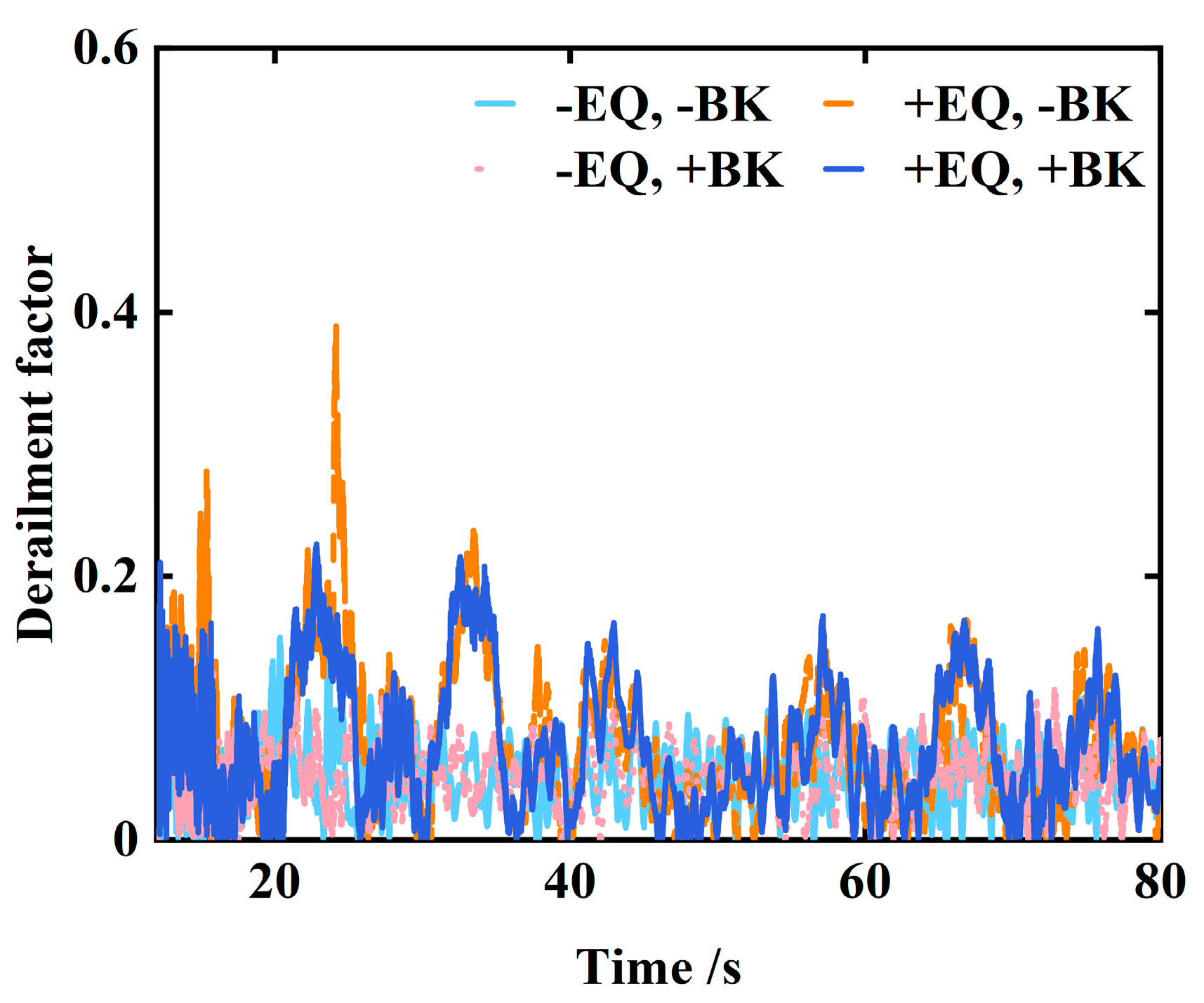
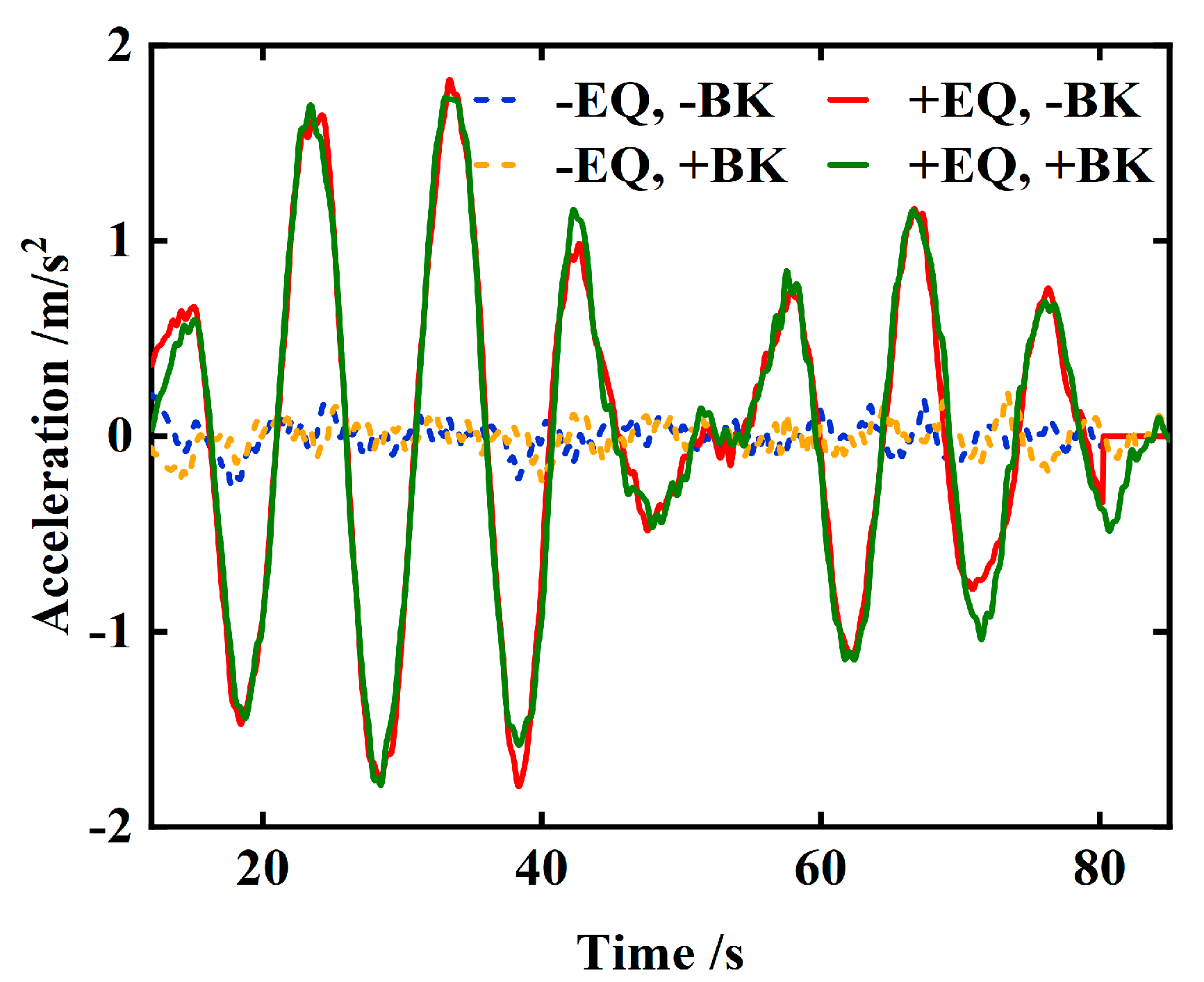
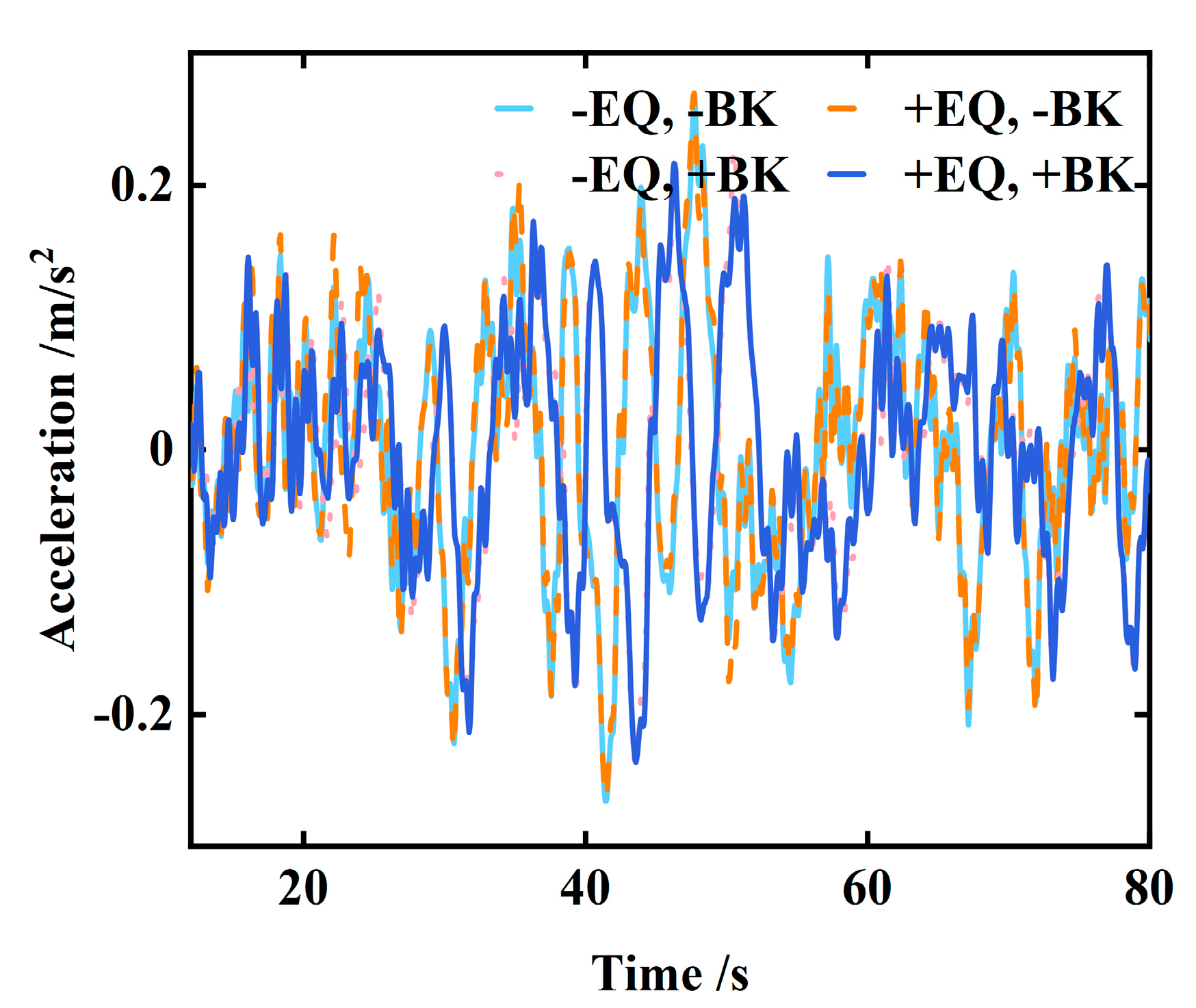
3.2. Analysis of Calculation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, S.; Fang, X.; Lin, F.; Yang, Z.; Wang, X. Reliability of rail transit traction drive system-A review. Microelectron. Reliab. 2018, 88–90, 1281–1285. [Google Scholar] [CrossRef]
- Spiryagin, M. Vehicle-track coupled dynamics: Theory and applications. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2021, 235, 1048–1049. [Google Scholar] [CrossRef]
- Zhai, W.; Han, Z.; Chen, Z.; Ling, L.; Zhu, S. Train-track-bridge dynamic interaction: A state-of-the-art review. Veh. Syst. Dyn. 2019, 57, 984–1027. [Google Scholar] [CrossRef]
- Xiang, P.; Ma, H.K.; Zhao, H.; Jiang, L.Z.; Xu, S.P.; Liu, X. Safety analysis of train-track-bridge coupled braking system under earthquake. Structures 2023, 53, 1519–1529. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, W.B.; Jiang, L.Z.; Yan, W.; Liu, X. Design seismic track irregularity for high-speed railways. Earthq. Eng. Struct. Dyn. 2023, 52, 4865–4883. [Google Scholar] [CrossRef]
- Chen, L.-K.; Liu, P.; Zhu, L.-M.; Ding, J.-B.; Feng, Y.-L.; Moreu, F. A simplified iterative approach for testing the pulse derailment of light rail vehicles across a viaduct to near-fault earthquake scenarios. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2021, 235, 1172–1188. [Google Scholar] [CrossRef]
- Chen, L.-K.; Qin, H.-X.; Jiang, L.-Z.; Xu, L. A vertical near-fault scenario earthquakes-based generic simulation framework for elastoplastic seismic analysis of light rail vehicle-viaduct system. Veh. Syst. Dyn. 2021, 59, 949–973. [Google Scholar] [CrossRef]
- Chen, L.-K.; Kurtulus, A.; Dong, Y.-F.; Taciroglu, E.; Jiang, L.-Z. Velocity pulse effects of near-fault earthquakes on a high-speed railway vehicle-ballastless track-benchmark bridge system. Veh. Syst. Dyn. 2022, 60, 2963–2987. [Google Scholar] [CrossRef]
- Zeng, Q.; Dimitrakopoulos, E.G. Seismic response analysis of an interacting curved bridge-train system under frequent earthquakes. Earthq. Eng. Struct. Dyn. 2016, 45, 1129–1148. [Google Scholar] [CrossRef]
- Zeng, Q.; Dimitrakopoulos, E.G. Vehicle-bridge interaction analysis modeling derailment during earthquakes. Nonlinear Dyn. 2018, 93, 2315–2337. [Google Scholar] [CrossRef]
- Guo, P.; Zhao, H.; Xiang, P.; Liu, X.; Tan, J.; Jiang, L. Probabilistic analysis of high-speed train safety on bridges under stochastic near-fault pulse-type ground motions. Probabilistic Eng. Mech. 2023, 74, 103527. [Google Scholar] [CrossRef]
- Dimitrakopoulos, E.G.; Zeng, Q. A three-dimensional dynamic analysis scheme for the interaction between trains and curved railway bridges. Comput. Struct. 2015, 149, 43–60. [Google Scholar] [CrossRef]
- Li, H.Y.; Yu, Z.W.; Mao, J.F.; Spencer, B.F. Effect of seismic isolation on random seismic response of High-Speed railway bridge based on probability density evolution method. Structures 2021, 29, 1032–1046. [Google Scholar] [CrossRef]
- Li, H.; Yu, Z.; Mao, J.; Jiang, L. Nonlinear random seismic analysis of 3D high-speed railway track-bridge system based on OpenSEES. Structures 2020, 24, 87–98. [Google Scholar] [CrossRef]
- Zhao, H.; Wei, B.; Jiang, L.; Xiang, P.; Zhang, X.; Ma, H.; Xu, S.; Wang, L.; Wu, H.; Xie, X. A velocity-related running safety assessment index in seismic design for railway bridge. Mech. Syst. Signal Process. 2023, 198, 110305. [Google Scholar] [CrossRef]
- Wei, B.; Chen, M.; Jiang, L.; Yu, Y.; Xiao, B.; Zheng, X.; Chen, Y.; Lu, A.; Chen, J. Research on modeling method for connectors in the train-track-bridge system based on multi-timestep explicit-implicit co-simulation. Eng. Struct. 2025, 322, 119100. [Google Scholar] [CrossRef]
- Truong, T.T.; Lee, J.; Nguyen-Thoi, T. Multi-objective optimization of multi-directional functionally graded beams using an effective deep feedforward neural network-SMPSO algorithm. Struct. Multidiscip. Optim. 2021, 63, 2889–2918. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Carvalho, H.; Ribeiro, D.; Calcada, R.; Tokunaga, M.; Tanabe, M.; Zhai, W.M. Assessment of train running safety on bridges: A literature review. Eng. Struct. 2021, 241, 112425. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Calcada, R.; Pouca, N.V.; Tanabe, M. Running safety assessment of trains moving over bridges subjected to moderate earthquakes. Earthq. Eng. Struct. Dyn. 2016, 45, 483–504. [Google Scholar] [CrossRef]
- Xiang, P.; Xu, S.; Zhao, H.; Jiang, L.; Ma, H.; Liu, X. Running safety analysis of a train-bridge coupled system under near-fault ground motions considering rupture directivity effects. Structures 2023, 58, 105382. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Z.; Chen, S.; Zheng, J.; Buyukozturk, O.; Sun, H. Deep long short-term memory networks for nonlinear structural seismic response prediction. Comput. Struct. 2019, 220, 55–68. [Google Scholar] [CrossRef]
- Li, H.; Wang, T.; Wu, G. Probabilistic safety analysis of coupled train-bridge system using deep learning based surrogate model. Struct. Infrastruct. Eng. 2023, 19, 1138–1157. [Google Scholar] [CrossRef]
- Guo, W.W.; Xia, H.; De Roeck, G.; Liu, K. Integral model for train-track-bridge interaction on the Sesia viaduct: Dynamic simulation and critical assessment. Comput. Struct. 2012, 112, 205–216. [Google Scholar] [CrossRef]
- Zhao, H.; Wei, B.; Guo, P.; Tan, J.; Xiang, P.; Jiang, L.; Fu, W.; Liu, X. Random analysis of train-bridge coupled system under non-uniform ground motion. Adv. Struct. Eng. 2023, 26, 1847–1865. [Google Scholar] [CrossRef]
- Wei, B.; Zheng, X.; Jiang, L.; Lai, Z.; Zhang, R.; Chen, J.; Yang, Z. Seismic response prediction and fragility assessment of high-speed railway bridges using machine learning technology. Structures 2024, 66, 106845. [Google Scholar] [CrossRef]
- Wei, B.; Tan, H.; Jiang, L.; Xiao, B.; Lu, A. Shaking table test of the seismic performance for railway simply-supported girder bridge isolated by self-centering bearing. Eng. Struct. 2024, 300, 117249. [Google Scholar] [CrossRef]
- Han, X.; Xiang, H.; Li, Y.; Wang, Y. Predictions of vertical train-bridge response using artificial neural network-based surrogate model. Adv. Struct. Eng. 2019, 22, 2712–2723. [Google Scholar] [CrossRef]
- Zoumb, P.A.W.; Li, X.; Wang, M. Effects of Earthquake-Induced Hydrodynamic Force on Train-Bridge Interactions. J. Bridge Eng. 2022, 27, 04022010. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, X.; Tang, S.; Zhao, H.; Shi, X.; Wang, L.; Wu, H.; Xiang, P. High-speed railway seismic response prediction using CNN-LSTM hybrid neural network. J. Civ. Struct. Health Monit. 2024, 14, 1125–1139. [Google Scholar] [CrossRef]
- Zhang, X.B.; Chen, B.K.; Zheng, Z.Z.; Liu, X.C.; Chen, Z.Z.; Cao, J.; Zhang, T.Y.; Xie, X.N.; Gao, B.W.; Xiang, P. Strain distribution prediction in UHPC beams using deep learning model. Struct. Concr. 2024, 26, 643–657. [Google Scholar] [CrossRef]
- Zhao, H.; Wei, B.; Zhang, P.; Guo, P.D.; Shao, Z.J.; Xu, S.P.; Jiang, L.Z.; Hu, H.F.; Zeng, Y.Y.; Xiang, P. Safety analysis of high-speed trains on bridges under earthquakes using a LSTM-RNN-based surrogate model. Comput. Struct. 2024, 294, 107274. [Google Scholar] [CrossRef]
- Wei, B.; Yang, Z.; Fu, Y.; Chen, J.; Jiang, L.; Chen, M.; Zheng, X. Decoupled Calculation and Case Study Analysis of Friction Pendulum Bearing Considering the Jumping-Off Effect. Int. J. Struct. Stab. Dyn. 2024, 0, 2550195. [Google Scholar] [CrossRef]
- Xiao, B.; Wei, B.; Zhao, H.; Zheng, X.; Zhang, R.; Chen, J.; Jiang, L. Effect of seismic isolation parameters on component damage and running safety performance of high-speed railway bridge-track system under near-fault earthquakes. Eng. Struct. 2025, 328, 119712. [Google Scholar] [CrossRef]
- Zhang, P.; Zhao, H.; Shao, Z.; Xie, X.; Hu, H.; Zeng, Y.; Jiang, L.; Xiang, P. Enhanced multi-scenario running safety assessment of railway bridges based on graph neural networks with self-evolutionary capability. Eng. Struct. 2024, 319, 118785. [Google Scholar] [CrossRef]


| Project | Numerical Value | Unit |
|---|---|---|
| Body mass | 21,920 | kg |
| Frame quality | 2550 | kg |
| Wheelset mass | 1420 | kg |
| Nodal moment of inertia of wheelset | 97 | |
| Frame nodding moment of inertia | 1750 | |
| Body nodding moment of inertia | 617,310 | |
| Axle weight | 14 | t |
| Crew | 240 | people |
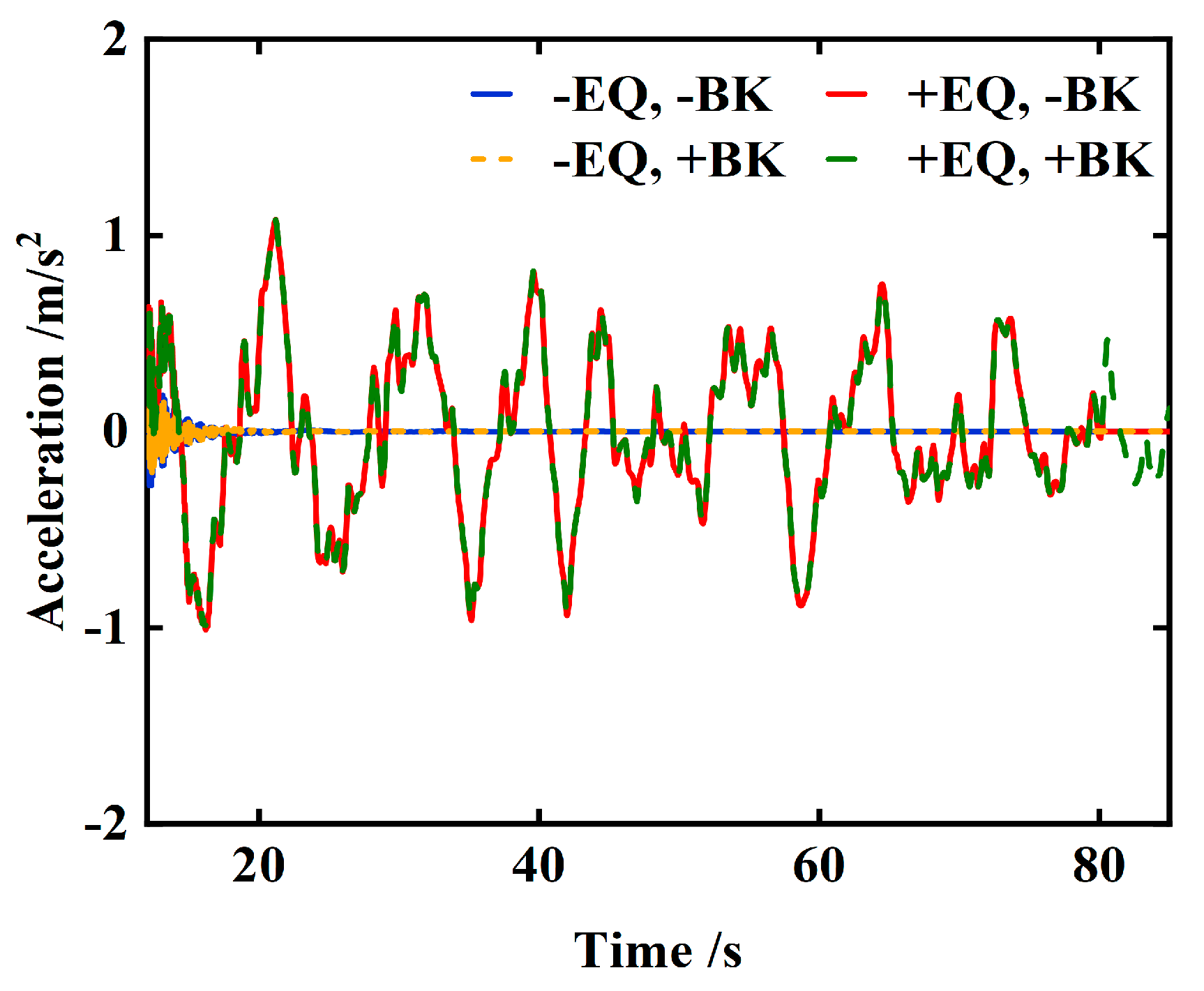
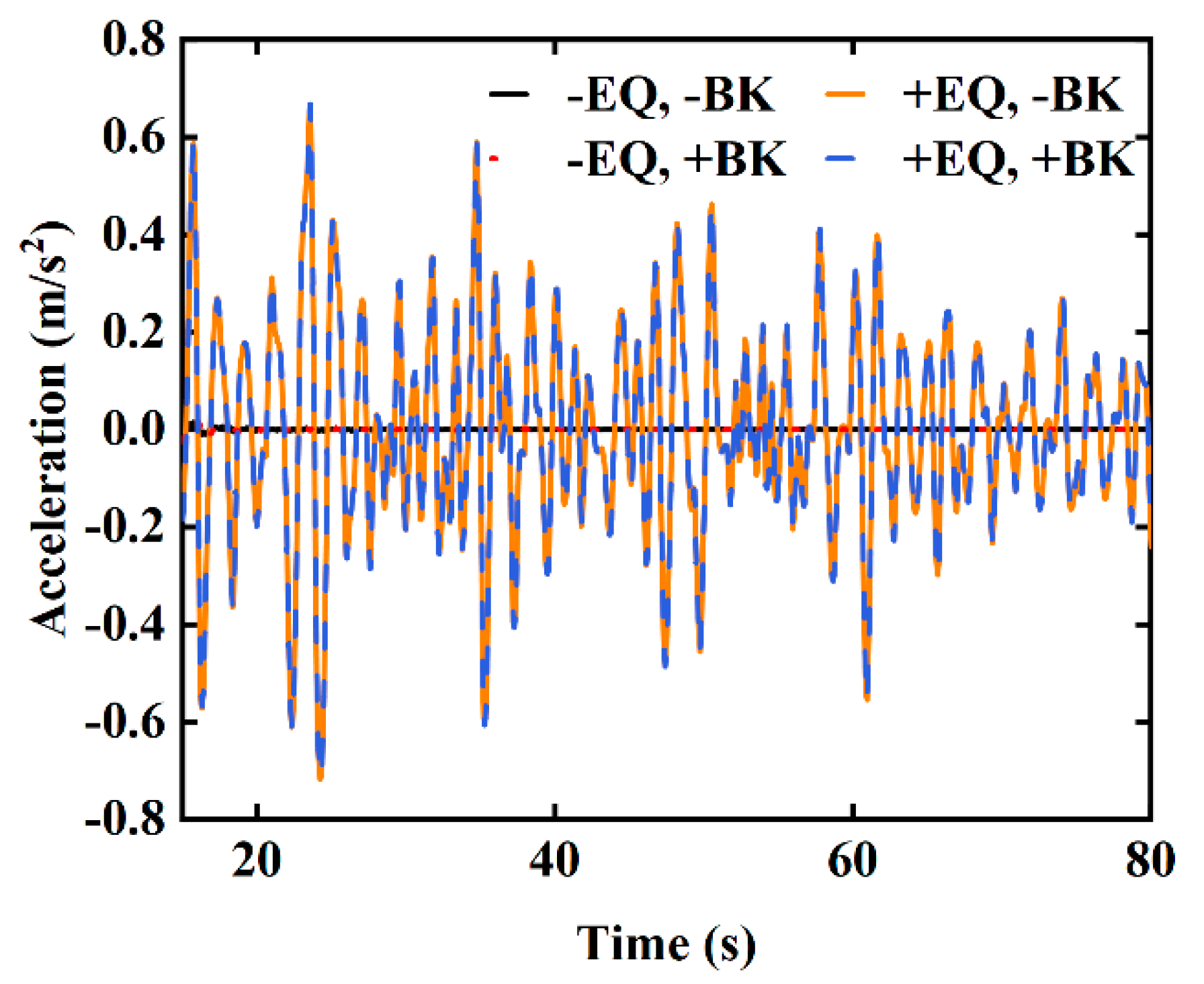
| Operating Condition | Peak Lateral Bridge Acc. (m/s2) | Reduction vs. +EQ, −BK | Peak Vertical Bridge Acc. (m/s2) | Reduction vs. +EQ, −BK | Peak Derailment Coefficient | Reduction vs. +EQ, −BK |
|---|---|---|---|---|---|---|
| −EQ, −BK (no earthquake, constant speed) | 0.05 | — | 0.05 | — | 0.05 | — |
| −EQ, +BK (no earthquake, braking) | 0.05 | — | 0.05 | — | 0.04 | — |
| +EQ, −BK (earthquake, constant speed) | 1.80 | — | 0.75 | — | 0.46 | — |
| +EQ, +BK (earthquake, braking) | 1.40 | −22% | 0.72 | −4% | 0.37 | −19% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Xie, X.; Ma, H.; Xiang, P. Braking Performance and Response Analysis of Trains on Bridges Under Seismic Excitation. Appl. Sci. 2025, 15, 6799. https://doi.org/10.3390/app15126799
Lu Y, Xie X, Ma H, Xiang P. Braking Performance and Response Analysis of Trains on Bridges Under Seismic Excitation. Applied Sciences. 2025; 15(12):6799. https://doi.org/10.3390/app15126799
Chicago/Turabian StyleLu, Yuanqing, Xiaonan Xie, Hongkai Ma, and Ping Xiang. 2025. "Braking Performance and Response Analysis of Trains on Bridges Under Seismic Excitation" Applied Sciences 15, no. 12: 6799. https://doi.org/10.3390/app15126799
APA StyleLu, Y., Xie, X., Ma, H., & Xiang, P. (2025). Braking Performance and Response Analysis of Trains on Bridges Under Seismic Excitation. Applied Sciences, 15(12), 6799. https://doi.org/10.3390/app15126799







