Abstract
To enhance the oxidative stability of aging diesel fuel stored in nuclear power emergency systems, we propose a novel hybrid optimization framework that integrates a Genetic Algorithm (GA), State-Space Network (SSN) modeling, and Computational Fluid Dynamics (CFD) simulation. Unlike previous studies that address treatment efficiency, flow optimization, or simulation separately, our method achieves real-time, simulation-informed optimization by embedding CFD-based performance evaluation directly into the GA fitness function. The SSN is employed to construct a comprehensive superstructure of feasible conditioning paths, which are dynamically explored and optimized by the GA under flow and boundary constraints. The CFD model, implemented via Ansys Fluent, accurately simulates the antioxidant mixing process in the tank and provides feedback on concentration uniformity at key monitoring points. The results demonstrate that the proposed framework reduces the conditioning time by 5.38% and significantly enhances the additive distribution uniformity. This work offers a generalizable approach for intelligent diesel upgrading in high-reliability energy systems and contributes a structured pathway for integrating data-driven optimization with physical process simulation.
1. Introduction
Nuclear power plants play a critical role in the global energy system due to their high power output and low carbon emissions. To ensure safe operation, emergency backup power systems are essential for handling unexpected power outages or equipment failures. Among these, emergency diesel generator systems are widely deployed owing to their rapid response time and high reliability [1]. However, diesel fuel stored in emergency tanks for long periods tends to degrade in quality due to environmental exposure. Studies have shown that prolonged storage leads to moisture absorption from the air, chemical reactions with tank materials, and accumulation of solid impurities and oxidation products [2]. These contaminants adversely affect combustion efficiency and contribute to the wear and blockage of fuel supply systems, ultimately reducing the operational reliability and service life of the generator units [3]. For instance, Heryana et al. found that metal ions released from corrosion significantly reduced the oxidative stability of diesel fuel, lowering the oxidation induction time to nearly zero [4]. Thus, regular quality monitoring and treatment of stored diesel are vital for maintaining emergency power reliability in nuclear facilities.
Oxidative degradation is one of the most significant forms of diesel deterioration during long-term storage. Oxidation reactions generate peroxides, acids, and insoluble gum-like substances, which alter the chemical properties of the fuel and can lead to filter clogging and injector fouling [5]. Extensive studies have shown that diesel’s oxidative stability decreases with storage time, posing increased risks to system performance. For example, Pullen et al. demonstrated that contact between metal ions and biodiesel–diesel blends reduced the oxidation induction period from compliant levels to as low as 0.05 h, revealing the catalytic role of metals in accelerating oxidative degradation [6]. As a result, improving the oxidative stability of stored diesel is essential for ensuring the functionality and safety of backup power systems in nuclear power plants [7].
Adding antioxidants is a widely used method for enhancing diesel oxidative stability. Antioxidants function by scavenging free radicals and decomposing peroxides, thereby interrupting the chain reaction of oxidation and prolonging the shelf life of fuels [7,8]. Numerous studies have reviewed the selection and effectiveness of various antioxidant additives across different fuel types. For instance, He Xuyao et al. [9] investigated a composite additive containing tetraethylenepentamine (TEPA) and tert-butylhydroquinone (TBHQ), which increased the oxidation induction time of Jatropha biodiesel from 4.24 h to 7.83 h, significantly enhancing fuel stability. Both synthetic and natural antioxidant systems are under active investigation. However, there is no universal solution, as different diesel compositions require customized antioxidant formulations. Further research is needed to understand the mechanisms and compatibility of antioxidant additives with various diesel systems.
Genetic Algorithms (GAs), known for their global search capabilities and flexibility in handling nonlinear, non-convex, and discrete problems, have been extensively applied in industrial process optimization [10]. GAs mimic natural evolution to iteratively improve candidate solutions, making it ideal for solving complex scheduling and parameter tuning problems [11]. In the context of diesel treatment, Zhang et al. used a GA to optimize the configuration of filtration modules, reducing treatment time and improving throughput efficiency [12]. GAs have proven effective in the multi-objective optimization of process configurations, especially when integrated with simulation models [13].
In this study, Genetic Algorithms (GAs) were selected as the core optimization tool due to their proven effectiveness in solving discrete combinatorial problems, such as the inlet–outlet configuration optimization presented here. GAs offer strong global search capabilities and are particularly suited for problems involving binary or categorical variables.
Compared with Particle Swarm Optimization (PSO) [14,15], which is better adapted to continuous variable spaces, GAs are generally more robust in exploring complex discrete search spaces and avoiding premature convergence to local optima. Additionally, while NSGA-II is widely used in multi-objective optimization [16,17,18], the problem addressed in this study is single-objective in nature—minimizing diesel conditioning time. Therefore, GAs were deemed sufficient and computationally efficient for the current framework.
Computational Fluid Dynamics (CFD) offers a powerful tool for simulating the complex fluid flow and mixing behavior inside treatment tanks. CFD is widely used in chemical and energy engineering to visualize and quantify velocity fields, pressure distributions, and species concentration gradients [12]. In fuel blending and homogenization processes, CFD enables the evaluation of mixing efficiency and design parameters. For instance, Karuana et al. applied CFD to analyze the mixing of B30 biodiesel blends with additives, and their simulations closely matched experimental density data, demonstrating high model reliability [19]. CFD-guided optimization helps determine appropriate flow rates, nozzle configurations, and residence times to ensure uniform additive distribution [20].
State-Space Network (SSN) modeling is a modern approach to process design that captures the flow of materials between unit operations in a directed graph structure. It is particularly suitable for complex systems involving multiple stages and parallel paths. Compared with traditional modular design or superstructure-based methods, SSN provides greater flexibility and computational efficiency in process synthesis and scheduling [12]. For example, Zhang et al. demonstrated that integrating SSN with a GA can optimize parallel filtration paths and pumping sequences, resulting in significant time savings [12]. While SSN excels in visual clarity and scalability, its application to large-scale systems requires careful complexity management to ensure computational feasibility.
To address this concern, we have revised the Introduction Section to more clearly emphasize the methodological novelty, practical significance, and potential for broader application. We also clarified how our framework contributes to bridging optimization theory and real-world process engineering.
In summary, emergency diesel storage systems in nuclear power plants face challenges related to long-term fuel degradation, including oxidative instability and contaminant accumulation. These issues threaten the reliability of emergency power supply systems. The integration of antioxidant-based conditioning, Genetic Algorithm optimization, and CFD simulation has emerged as a promising direction for improving fuel quality and treatment efficiency. Previous studies have explored each aspect independently, including degradation mechanisms, additive strategies, optimization algorithms, and simulation models [2,9,12,19]. However, a comprehensive, integrated approach tailored to nuclear emergency diesel systems remains underexplored. This work aims to fill that gap by developing a hybrid optimization framework that combines State-Space Network modeling, GA optimization, and CFD simulation for enhancing diesel treatment processes in nuclear facilities.
2. State-Space Network (SSN) Superstructure for Diesel Conditioning Pathways
The State-Space Network (SSN) method represents complex process systems by decomposing them into task nodes (representing processing operations) and state nodes (representing material conditions), connected by directed flows. In the context of emergency diesel conditioning, the SSN superstructure explicitly enumerates all feasible fuel flow paths—for example, from an Initial-State (raw diesel) through pumps and conditioning units to a Final-State (treated diesel). This graphical representation allows engineers to visualize and adjust alternative process routes more clearly [21]. Compared to traditional superstructure methods, SSNs significantly reduce computational complexity and improve modeling flexibility. When combined with modern optimization techniques (e.g., Genetic Algorithms), designers can efficiently explore various conditioning strategies and rapidly identify optimal solutions.
As illustrated in Figure 1, each processing unit in the SSN—such as a pump, conditioning unit, or pipeline—is modeled as a task that links an input state to an output state (e.g., transitions in fuel quality or pressure). For example, a pump task connects a “low-pressure diesel” state to a “high-pressure diesel” state, while a conditioning task converts “untreated diesel” into “conditioned diesel.” The SSN allows multiple units of the same type to appear in parallel or in series. For instance, different pumps with varying capacities can feed into a common downstream route, or the diesel may bypass one conditioning unit and follow an alternative treatment path. By modeling these units as nodes, the SSN captures all feasible combinations of operations [12].
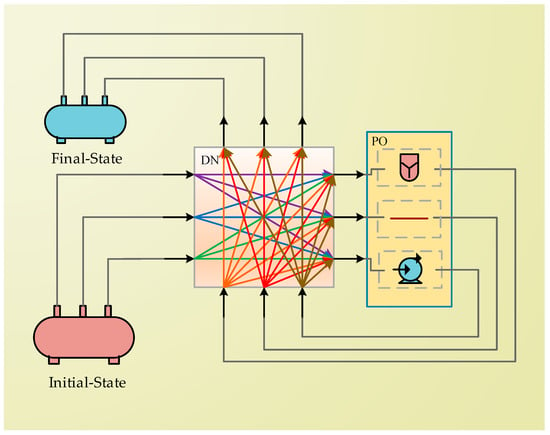
Figure 1.
State-space network (SSN) superstructure for diesel conditioning pathway optimization. The system links initial and final diesel states via transport and processing routes. DN: decision nodes for inlet–outlet configurations; PO: process modules. The colored arrows represent candidate flow paths evaluated by the algorithm.
Path Definition: In an SSN, a path is defined as a sequence of connected tasks leading from an initial material state to a final treated state. In emergency diesel conditioning systems, a typical path might begin at the raw diesel tank, proceed through one or more pumps and conditioning units, and ultimately deliver fuel to a usable diesel state. The SSN framework enforces interface constraints, ensuring that fuel only flows through physically compatible connections—for example, fuel exiting a high-pressure state must enter tasks that accept high-pressure input. Common assumptions include steady-state operation (constant flow through each path, with no accumulation) and pump capacity limits (maximum allowable flow for each pump). All flows must also be balanced at each state node to ensure fuel conservation. These assumptions simplify the model while accurately representing normal operating conditions in emergency systems.
Optimization Objectives: The SSN superstructure is embedded within an optimization framework to achieve operational objectives. In emergency diesel conditioning, the primary goals are to minimize total conditioning time and maximize fuel quality, under safety and reliability constraints. Zhang et al. demonstrated that optimizing SSN paths can significantly enhance system performance—for example, achieving a 7.9% reduction in processing time while improving output quality. The SSN framework naturally supports multi-objective optimization, such as minimizing energy consumption (e.g., pump work), minimizing total residence time, or minimizing residual impurity levels. Because the SSN enumerates all feasible configurations, the optimizer can evaluate trade-offs between different routing strategies such as a slower single-pass path versus a faster recirculating scheme to meet target criteria. In emergency applications, system reliability is also an implicit objective, and the SSN helps identify and preserve critical paths that must remain functional under all conditions.
To enable structured and stable design of the conditioning paths in this study, the following assumptions are made:
- Steady-State Operation: The diesel conditioning paths are assumed to operate under steady-state conditions, without dynamic adjustments over time or in response to changes in oxidant concentration in the storage tank. This simplifies operation and ensures model stability.
- Focus on Oxidative Stability: The primary degradation concern is assumed to be excessive oxidative instability. The conditioning process is therefore designed specifically to improve this property, while other factors affecting fuel quality are neglected.
- Uniform Additive Distribution: It is assumed that the diesel entering the system already contains antioxidants at a constant and homogeneously distributed volume fraction. This assumption simplifies the modeling and analysis of additive effectiveness.
- Pump Capacity Limit: The maximum flow rate of each transport pump is fixed. The total feed flow rate is constrained to remain below the pump’s capacity to avoid overloading and ensure safe operation.
- One-Way Interface Constraints: Each inlet or outlet of a diesel tank can function either as a feed port or a discharge port, but not both simultaneously. This assumption ensures directional clarity and avoids flow ambiguity.
- Minimum Equipment Availability: At least one feed port, one discharge port, and one conditioning unit must be present to ensure that the system is operable and the conditioning process can proceed successfully.
- Steady, Incompressible, Single-Phase Flow: The diesel–antioxidant mixture is assumed to behave as a steady-state, incompressible, single-phase liquid. Multiphase effects such as evaporation, gas entrainment, or cavitation are not considered. As a result, fluid density is treated as constant, and mass conservation is equivalently expressed as a balance of volumetric flow rates, which simplifies the modeling process and enhances numerical stability.
In conclusion, the SSN superstructure for emergency diesel conditioning enumerates all valid flow paths among pumps, conditioning units, and pipelines, based on steady-state assumptions. It enables the optimization of conditioning scheduling (minimizing time, maximizing quality) and provides a structured, flexible framework for enhancing both the reliability and efficiency of critical emergency fuel systems. Leveraging recent SSN-based optimization developments, the proposed approach offers a robust solution for improving emergency diesel treatment performance in nuclear and other high-stakes applications.
3. CFD Numerical Simulation Setup
3.1. CFD Model
As shown in Figure 2, the simulation model is based on the emergency diesel storage tank of a representative nuclear power plant. The geometric complexity of internal components was simplified by retaining only the main tank structure. A 1:125 scale physical model was constructed using SolidWorks 2021 3D modeling software. Three monitoring points (A, B, and C) were selected to evaluate flow behavior and additive concentration during the simulation. The model consists of three identical nozzles on the tank top (each capable of functioning as either an inlet or outlet), a sealed tank body, and two internal baffles. All components are made of aluminum alloy. Except for the baffles, the rest of the internal space is defined as a fluid domain available for diesel storage and circulation.
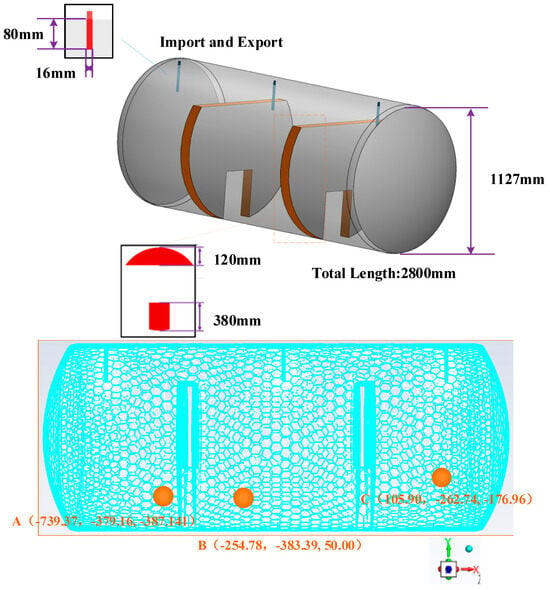
Figure 2.
Physical model and monitoring point locations of the diesel storage tank (unit: mm).
Although the tank geometry is symmetric, the presence of internal baffles and the need for the Genetic Algorithm to explore asymmetric inlet–outlet configurations may lead the final optimal solution to deviate from symmetry. Therefore, the full-domain model was retained in this study.
As illustrated in Figure 3, the meshing of the 3D tank geometry was performed in Fluent-Mesh, using polyhedral elements. Local mesh refinement was applied near the inlets and outlets to enhance computational accuracy.
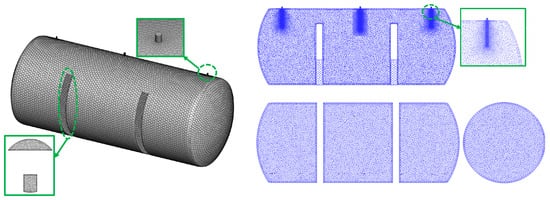
Figure 3.
External view and three-section mesh profile of the diesel tank.
In this study, we employed a primary mesh containing approximately 124,936 cells, with three inflation layers applied to all wall surfaces. The boundary layer parameters included a growth rate of 1.2 and a transition ratio of 0.272, which ensured adequate resolution of velocity gradients and species transport near the walls. With this setup, y+ values were maintained below 30 across all critical regions, satisfying the requirements of the turbulence model used. To evaluate mesh independence, we tested five mesh resolutions: 58,660; approximately 25,000; 57,500; 124,936; and approximately 210,000 cells. The comparison showed that the deviation in conditioning time between the 57,500-cell and 124,936-cell meshes was within a single time step (i.e., 600 s). Furthermore, the difference between the 124,936-cell and ~210,000-cell meshes was negligible, with key performance indicators varying by less than 2%. These results confirm that the chosen mesh resolution achieves sufficient numerical convergence and robustness.
The input data used in our simulation were obtained from an ongoing nuclear engineering project focused on diesel conditioning system optimization. Specifically, the inlet velocity corresponds to the rated flow rate of the pump under standard operating conditions (measured at 20 °C), and the physical properties of the diesel–antioxidant mixture were derived from laboratory analyses conducted on-site using actual fluid samples.
3.2. Boundary Conditions
The simulation is based on a compositional transport model, in which diesel and the antioxidant additive are the only two chemical species. The antioxidant is represented by butylated hydroxytoluene (BHT, C15H24O) [22], with material properties sourced from the Fluent built-in database. The k-epsilon realizable turbulence model was employed to simulate diesel flow. All three nozzles were defined as velocity inlets. The inlet velocity, as well as the multiphase parameters of diesel and antioxidants, was imported from external data. The nozzle flow direction is determined as follows: a positive velocity denotes an inlet, a negative velocity indicates an outlet, and zero velocity defines a sealed wall. The domain was initialized such that only diesel exists inside the tank at the beginning, conforming to real operating conditions. A User-Defined Function (UDF) was applied to monitor the volume fraction of antioxidants at the three sensor points, acting as a termination criterion: the simulation halts once all monitoring points fall below the specified concentration threshold, and the final residence time is recorded. The input data used in our simulation were obtained from an ongoing nuclear engineering project focused on diesel conditioning system optimization. Specifically, the inlet velocity corresponds to the rated flow rate of the pump under standard operating conditions (measured at 20 °C), and the physical properties of the diesel–antioxidant mixture were derived from laboratory analyses conducted on-site using actual fluid samples. The fluid used in this study was a homogeneous diesel–antioxidant mixture, treated as a single-phase, incompressible liquid. Its physical properties (e.g., density and viscosity) were assumed to be constant and were derived from experimental measurements conducted under standard operating conditions. No phase change or compressibility effects were considered in this simulation.
4. Mathematical Model and Optimization Framework CFD Numerical Simulation Setup
4.1. Conditioning Path Design
In this study, the conditioning path is designed by integrating the State-Space Network (SSN) framework with a Genetic Algorithm (GA) [23] to explore the optimal path configuration.
- (a)
- Each individual in the GA population encodes two sets of parameters (A, B, and C and A1, B1, and C1), totaling six genes per individual.
- (b)
- A, B, and C represent the velocity at each of the three tank nozzles (in m/s). The mapping rule is defined as
- ○
- Positive value → inlet with corresponding velocity;
- ○
- Negative value → outlet with absolute value as flow rate;
- ○
- Zero → sealed wall.
PM refers to the maximum delivery velocity of the pump, constrained by nozzle diameter.
- (c)
- A1, B1, and C1 define the configuration of diesel with antioxidant additives. Their constraint condition is
The sign() function ensures each port acts only as an inlet or an outlet, not both, ensuring the feasibility of the conditioning path.
Each configuration parameter (e.g., A1) is further linked to a conditioning state value (A11), with the following logic:
- A11 = −1: diesel outlet (data recorded);
- A11 = 0: sealed boundary;
- A11 = 1: inlet with additive (conditioned diesel);
- A11 = 2: inlet without additive (recycled diesel with same concentration as recorded at outlet);
- B11 and C11 follow the same logic for their respective ports.
4.2. Genetic Algorithm Design
The Genetic Algorithm used in this study incorporates selection, crossover, mutation, generation gap, and elitism strategies.
Selection is performed via the roulette wheel method, where the selection probability of individual i is
Cumulative probability is computed as
Random numbers rk ~ U(0, 1) are used to select individuals satisfying
- Crossover uses a two-point strategy, randomly selecting two positions, q1 and q2, in the chromosome and exchanging the gene segments between them to generate new offspring.
- Mutation introduces random perturbations into selected genes to maintain population diversity and avoid premature convergence. The mutation probability decreases over generations, enhancing stability and convergence speed.
- Generation gap is applied to preserve population diversity.
- Elitism guarantees the best-performing individual of each generation is directly carried into the next generation without undergoing genetic operations, ensuring optimal solutions are retained.
4.3. Optimization Workflow
As illustrated in Figure 4, the proposed diesel conditioning optimization framework proceeds as follows:
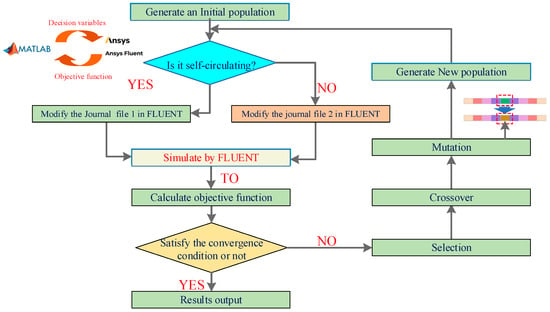
Figure 4.
Schematic of the optimization design process integrating MATLAB and ANSYS Fluent 2022R1. The workflow includes population generation, circulation check, journal file modification, CFD simulation, fitness evaluation, and genetic operations until convergence.
- Initial Population Generation: A random population satisfying path and parameter constraints is generated using MATLAB R2023a-GA. The conditioning parameters are embedded into Fluent journal files.
- CFD Simulation: The journal files are executed in a pre-configured Fluent case to simulate flow and mixing [24].
- Fitness Evaluation: The simulation results are parsed, and the performance of each individual is evaluated based on conditioning effectiveness.
- Convergence Check: If the convergence criterion is met, the optimal result is recorded. If not, the population is updated via selection, crossover, mutation, generation gap, and elitism.
- Population Update: New individuals are translated into journal files, and the simulation is repeated.
- Iterative Optimization: Steps 2–5 are repeated until the termination condition is satisfied and the global optimum is found.
5. Case Study
5.1. Case Configuration
As illustrated by the CFD model in Figure 2, this case study is based on the emergency diesel storage tank of a nuclear power plant, focusing on the design and optimization of the diesel conditioning process. The selected diesel pump is model 65YHC3-25 (The manufacturer is Botou Hengyun Oil Pump Manufacturing Factory, located in Botou City, China), with key specifications listed in Table 1. The rated flow rate of the pump is 25 m3/h, and each nozzle of the storage tank has an actual diameter of 800 mm. After comprehensive evaluation, the pump’s maximum inlet velocity is set to PM = 0.014 m/s. The key quality parameters of standard diesel are shown in Table 2.

Table 1.
Specifications of 65YHC3-25 diesel pump.

Table 2.
Property specifications.
A tested sample of aged diesel exhibited an oxidation stability value of 3.0, exceeding the acceptable limit of 2.5. To address this, a specific antioxidant was selected. Experimental data indicated that each 1 ppm increase in antioxidant concentration improves the oxidation stability by 0.001 units. To achieve a target oxidation stability of 2.0, a final antioxidant mass fraction of 1000 mg/kg is required [19]. Based on this, the target volume fraction threshold for the antioxidant at all three monitoring points is set to 0.0698%. When all sensors detect concentrations at or above this threshold, the fuel in the tank is considered to meet the conditioning criteria.
5.2. Genetic Algorithm Optimization Analysis
The optimization process was conducted on a PC equipped with an Intel Core i7-13700 CPU (16 cores, up to 5.20 GHz) and 16 GB of RAM. Using the mesh with approximately 1,231,434 cells as a reference, the physical simulation time for each case was about 31,800 s, with a fixed time step of 600 s. Depending on the configuration and convergence behavior, the total wall-clock computation time typically ranged from 3.5 to 4.5 h per simulation. A second-order implicit time integration scheme was used throughout, with a maximum of 200 inner iterations per time step. Convergence within each step was determined by monitoring residuals for continuity, momentum, and species transport equations, all of which were required to fall below 1 × 10−4. In addition to residuals, we also tracked the evolution of antioxidant concentration at key monitoring points to ensure the physical reliability of the solution. After six generations of GA evolution, the optimization yielded the following results:
As illustrated in Figure 5,the optimization results show that the best fitness value rapidly decreases in early generations, from 33,609 s in generation 0 to 31,800 s in generation 3, and then stabilizes. This indicates effective convergence due to selection and crossover operations, concentrating the population near optimal regions. The average fitness also improves from 39,937 s to 36,840 s, reflecting overall population quality enhancement.
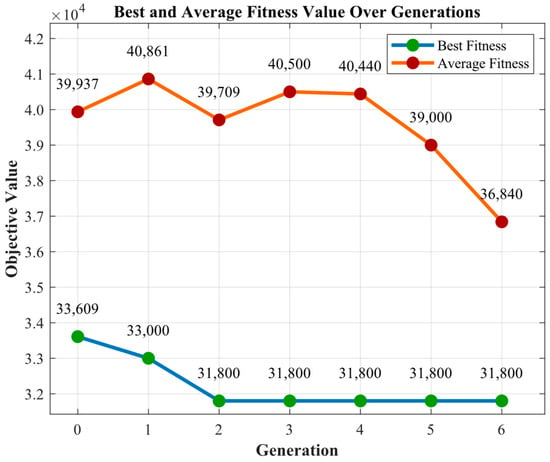
Figure 5.
Evolution of best and average fitness values across generations.
As illustrated in Figure 6,early generations (e.g., generation 0) exhibited broad diversity in inlet velocity values, ranging from approximately −0.01 to 0.015. As evolution proceeds, this range narrows significantly. By generation 6, most values cluster around zero, suggesting convergence and reduced diversity. Velocity distributions become increasingly focused over time. In the early stages, individuals exhibit varied combinations with a wide spread in fitness. In later stages, high-performing individuals tend to cluster around specific velocity ranges, indicating that the GA has identified effective combinations for optimal performance.
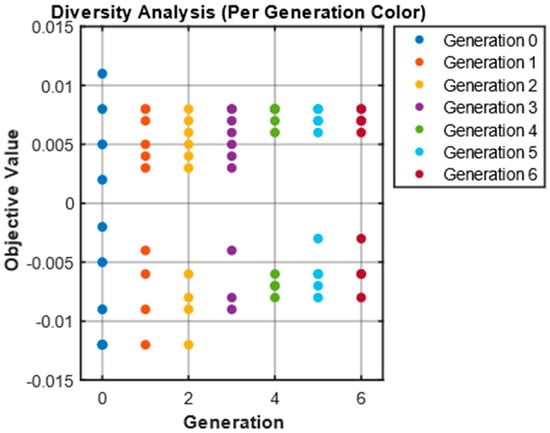
Figure 6.
Diversity analysis of inlet parameters.
A similar trend is observed in the conditioning state parameters. Initially (generations 0–1), the combinations are scattered. By generation 5 and 6, the population converges on a narrow range of effective configurations, showing that the algorithm favors specific conditioning state patterns linked to higher performance. Less effective combinations are gradually eliminated through evolutionary operations.
5.3. SSN-Based Structural Optimization and CFD Validation
The optimal solution identified by the GA is the individual [−0.006, −0.008, 0.014, −1, −1, 1] with the best fitness value, 31,800 s. This indicates that nozzle 1 and nozzle 2 are used as outlets (condition −1), while nozzle 3 serves as an inlet with an antioxidant additive (condition 1). The corresponding SSN configuration is shown in Figure 7.
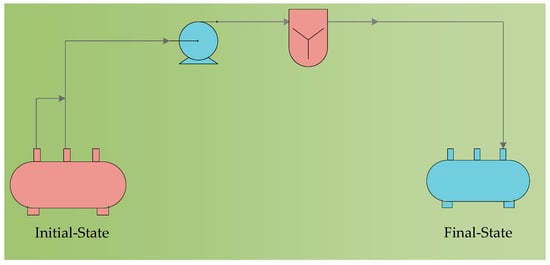
Figure 7.
Optimal diesel conditioning path based on SSN structure.
Based on the optimal flow distribution, CFD simulations were conducted to observe the mixing behavior of the antioxidant additive. Figure 8 presents snapshots of antioxidant distribution at various time intervals.
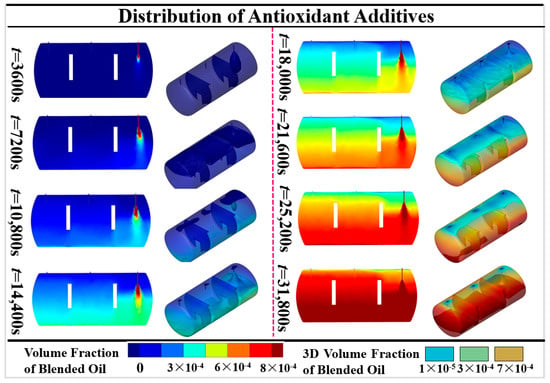
Figure 8.
Temporal evolution of antioxidant distribution inside the tank.
The corresponding volume fraction curves of the antioxidant at the three monitoring points are shown in Figure 9.
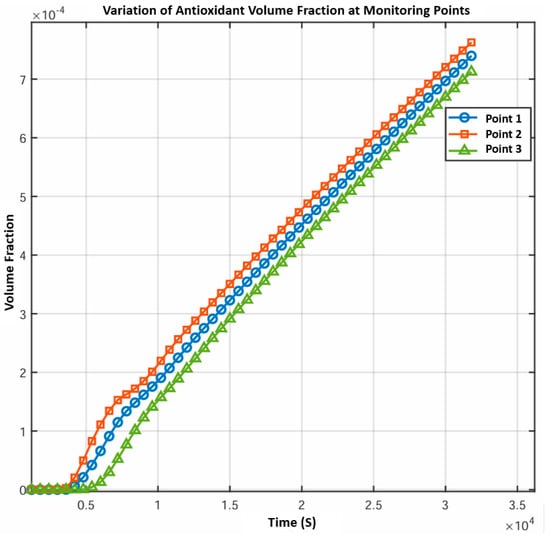
Figure 9.
Time-dependent antioxidant volume fraction at monitoring points.
As seen in Figure 8 and Figure 9, the antioxidant becomes increasingly uniform over time. In early stages (e.g., 3600 s and 7200 s), concentration gradients are evident. By 25,200 s to 31,800 s, the distribution becomes nearly homogeneous, indicating effective mixing. Both 2D and 3D views show diminishing gradients along axial and radial directions. The curves in Figure 9 further confirm this trend: initially, growth rates vary among points (with sensor 2 closest to the injection region), but later, all curves converge, indicating successful homogenization of the antioxidant throughout the tank.
6. Discussion
This study presents a hybrid optimization framework that integrates a Genetic Algorithm (GA), State-Space Network (SSN) modeling, and Computational Fluid Dynamics (CFD) simulation to address the degradation of oxidative stability in emergency diesel fuel used in nuclear power facilities. The proposed method enabled the automatic identification of efficient diesel conditioning pathways through GA-guided structural configuration searches, validated by physically grounded CFD results. The optimization process successfully reduced conditioning time by 5.38%—from 33,609 s to 31,800 s—while ensuring that the antioxidant volume fraction reached the required 0.0698% at all critical monitoring points. The CFD analysis provided insights into the dynamic evolution of mixing efficiency and additive distribution. Notably, under the optimized design, the system exhibited non-symmetric inlet–outlet configurations, which would have been excluded under symmetry-based modeling assumptions. The SSN configuration also offered a modular abstraction for describing multi-port flow pathways, clarifying the distinct roles of the tank nozzles. For example, nozzles 1 and 2 functioned as outlets for untreated diesel, while nozzle 3 served as the key inlet for antioxidant-enriched flow. These results not only demonstrate the technical viability of the proposed framework but also its practical value in improving diesel storage management.
However, it is important to note that this study is based on a single case study. While this provides valuable insights into the diesel conditioning process, future research will benefit from testing additional scenarios, including different tank geometries, inlet/outlet configurations, and operating conditions. This would allow for the generalization of the findings and provide a more comprehensive understanding of the optimization framework’s robustness across different contexts.
Due to stringent safety and regulatory restrictions, in situ experimental validation in actual nuclear facilities was not feasible. However, the use of measured physical properties and equipment-rated flow data helped ensure the realism and credibility of the simulation inputs. Future work should explore the applicability of this method in dynamic scenarios, multicomponent conditioning schemes, or integration with additional processes such as filtration or dewatering. Furthermore, a formal sensitivity analysis on key parameters (e.g., inlet velocity, antioxidant concentration) will be conducted in subsequent studies to evaluate the robustness of the optimization framework and its response to varying operational conditions.
Finally, we recognize the importance of real-time applicability and computational efficiency. Although the current framework requires several hours of computation for each simulation, future work will focus on developing reduced-order models (ROMs) or surrogate models to improve real-time optimization and feedback capabilities. These models could significantly accelerate the process and enable real-time adjustment for operational optimization in real-world applications.
7. Conclusions
An integrated GA–SSN–CFD framework was developed to optimize the conditioning process of aged diesel fuel stored in nuclear emergency tanks. The framework enabled automatic structural exploration and simulation-based evaluation of candidate configurations, with the goal of reducing conditioning time and improving additive uniformity. The proposed method achieved a 5.38% reduction in conditioning time and ensured compliance with oxidative stability thresholds across all flow monitoring points. These results confirm the effectiveness of the approach in enhancing system performance and reliability. This research provides a scalable, modular, and computationally efficient methodology for optimizing emergency diesel conditioning systems. It offers a foundation for further development of real-time, closed-loop optimization solutions applicable to critical energy infrastructure.
Author Contributions
L.Z. and Q.M. conceptualized the study. The methodology was developed by F.L., X.C., and H.Y. Validation was conducted by L.Z. and X.C. The investigation was performed by F.L. and X.C. Resources were provided by L.Z. and Q.M. Data curation was carried out by Q.M. and H.L. H.L. prepared the original draft, while L.Z. and H.Y. were responsible for review and editing. Visualization was completed by H.Y. Supervision was provided by L.Z. and project administration was managed by Q.M. All authors have read and agreed to the published version of the manuscript.
Funding
Supported by the National Natural Science Foundation of China, 52204208.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in this article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Langqi Zhang and Hao Li were employed by China Nuclear Power Operations Co., Ltd. Authors Xiangnan Chu and Qi Ma were employed by Yangjiang Nuclear Power Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GA | Genetic Algorithm |
| SSN | State-Space Network |
| CFD | Computational Fluid Dynamics |
| BHT | Butylated hydroxytoluene (antioxidant additive) |
| PM | Maximum pump velocity |
| A, B, C | Inlet/outlet velocity variables (for each nozzle) |
| A1, B1, C1 | Nozzle configuration state variables |
| A11, B11, C11 | Discrete state values for each nozzle (e.g., −1: outlet, 0: closed, 1: inlet) |
| y+ | Non-dimensional wall distance for near-wall mesh quality |
| η (eta) | Pump efficiency |
| ρ (rho) | Density of diesel–antioxidant mixture |
| μ (mu) | Dynamic viscosity of fluid |
| Q | Volumetric flow rate |
| t | Conditioning time |
| Ca | Antioxidant concentration |
References
- Liu, L.; Guo, H.; Dai, L.; Liu, M.; Xiao, Y.; Cong, T.; Gu, H. The Role of Nuclear Energy in the Carbon Neutrality Goal. Prog. Nucl. Energy 2023, 162, 104772. [Google Scholar] [CrossRef]
- David, E.; Kopac, J. Survey on Antioxidants Used as Additives to Improve Biodiesel’s Stability to Degradation through Oxidation. Molecules 2023, 28, 7765. [Google Scholar] [CrossRef] [PubMed]
- Arole, K.; Velhal, M.; Tajedini, M.; Xavier, P.G.; Bardasz, E.; Green, M.J.; Liang, H. Impacts of Particles Released from Vehicles on Environment and Health. Tribol. Int. 2023, 184, 108417. [Google Scholar] [CrossRef]
- Heryana, Y.; Pamungkas, A.; Romelan, R.; Solikhah, M.D.; Matheofani; Barus, B.R.; Wibowo, C.S.; Supriyadi, F.; Thahar, A.; Wibowo, E.; et al. Evaluation of Corrosion Effects in Diesel-Biodiesel and Diesel-Biodiesel-HVO Blends on Metals for Fuel Storage Systems. Corros. Sci. Technol. 2024, 23, 352–364. [Google Scholar] [CrossRef]
- Kumar, N. Oxidative Stability of Biodiesel: Causes, Effects and Prevention. Fuel 2017, 190, 328–350. [Google Scholar] [CrossRef]
- Pullen, J.; Saeed, K. An Overview of Biodiesel Oxidation Stability. Renew. Sustain. Energy Rev. 2012, 16, 5924–5950. [Google Scholar] [CrossRef]
- Bello, U.; Adamu, H.; Samsuri, S.; Ibrahim, H.; Qamar, M. Improving Biodiesel Oxidative Stability Using Antioxidants: An Insight into the Research Trends and Future Prospects from a Bibliometric Approach. Results Eng. 2025, 26, 105185. [Google Scholar] [CrossRef]
- Hosseinzadeh-Bandbafha, H.; Kumar, D.; Singh, B.; Shahbeig, H.; Lam, S.S.; Aghbashlo, M.; Tabatabaei, M. Biodiesel Antioxidants and Their Impact on the Behavior of Diesel Engines: A Comprehensive Review. Fuel Process. Technol. 2022, 232, 107264. [Google Scholar] [CrossRef]
- He, X.; Chen, R.; Liu, M.; Li, H.; Li, F.; Zhang, H. Effect of TEPA/TBHQ Combination on Oxidative Stability-Corrosion of Biodiesel. Huagong Jinzhan/Chem. Ind. Eng. Prog. 2023, 42, 5661–5668. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Elsayed, S.M.; Sarker, R.A.; Essam, D.L. A New Genetic Algorithm for Solving Optimization Problems. Eng. Appl. Artif. Intell. 2014, 27, 57–69. [Google Scholar] [CrossRef]
- Zhang, L.; He, Y.; Zhou, Y.; Jiang, G.; Chu, X.; Ma, Q.; Liu, F.; Ye, H. A Comprehensive Optimization Framework for Diesel Filtration in Nuclear Emergency Systems: Integrating Genetic Algorithms, State-Space Networks, and Computational Fluid Dynamics. Processes 2025, 13, 648. [Google Scholar] [CrossRef]
- Wang, J.; Xu, L.; Sun, S.; Ma, Y.; Yu, G. Multi-Objective Optimization Using Improved NSGA-II for Integrated Process Planning and Scheduling Problems in a Machining Job Shop for Large-Size Valve. PLoS ONE 2024, 19, e0306024. [Google Scholar] [CrossRef]
- Pektaş, A.; Hacıbeyoğlu, M.; İnan, O. Hybridization of the Snake Optimizer and Particle Swarm Optimization for Continuous Optimization Problems. Eng. Sci. Technol. Int. J. 2025, 67, 102077. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Li, H.; Pan, X.; Jiang, Y.; Zhou, X. Optimising and Analysis of the Hydraulic Performance of a Water Dispersion Needle Sprinkler Using RF-NSGA II and CFD. Biosyst. Eng. 2025, 254, 104113. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Y.; Zhou, W.; Fu, Q. Multi-Objective Optimization of Heat Pump Drying Process Using NSGA-II and Response Surface Methodology: A Case Study of Sludge. Case Stud. Therm. Eng. 2025, 72, 106257. [Google Scholar] [CrossRef]
- Sadni, F.E.; Salhi, I.; Belhora, F.; Hajjaji, A. Multi-Objective Optimization of Energy and Exergy Efficiencies in ORC Configurations Using NSGA-II and TOPSIS. Therm. Sci. Eng. Prog. 2025, 63, 103606. [Google Scholar] [CrossRef]
- Karuana, F.; Ghazidin, H.; Suyatno; Wimada, A.R.; Helios, M.P.; Sutriyanto, H.; Solikhah, M.D. Homogeneity Analysis of B30 Mixing Results with Additives in Mixing Tanks Using Computational Fluid Dynamics (CFD). In Proceedings of the Materials Today: Proceedings; Elsevier Ltd.: Amsterdam, The Netherlands, 2023; Volume 87, pp. 141–146. [Google Scholar]
- Zhang, S.; Tao, X.; Lu, J.; Wang, X.; Zeng, Z. Design, Optimization and CFD Simulation of a Nozzle for Industrial Cleaning Processes Based on High-Pressure Water Jets. Fluid Dyn. Mater. Process. 2015, 11, 143–155. [Google Scholar] [CrossRef]
- Mencarelli, L.; Chen, Q.; Pagot, A.; Grossmann, I.E. A Review on Superstructure Optimization Approaches in Process System Engineering. Comput. Chem. Eng. 2020, 136, 106808. [Google Scholar] [CrossRef]
- Marqusee, J.; Jenket, D. Reliability of Emergency and Standby Diesel Generators: Impact on Energy Resiliency Solutions. Appl. Energy 2020, 268, 114918. [Google Scholar] [CrossRef]
- Lira, J.O.B.; Riella, H.G.; Padoin, N.; Soares, C. Computational Fluid Dynamics (CFD), Artificial Neural Network (ANN) and Genetic Algorithm (GA) as a Hybrid Method for the Analysis and Optimization of Micro-Photocatalytic Reactors: NOx Abatement as a Case Study. Chem. Eng. J. 2022, 431, 133771. [Google Scholar] [CrossRef]
- Heydar Rajaee Shooshtari, S.; Honoré Walther, J.; Wen, C. Combination of Genetic Algorithm and CFD Modelling to Develop a New Model for Reliable Prediction of Normal Shock Wave in Supersonic Flows Contributing to Carbon Capture. Sep. Purif. Technol. 2023, 309, 122878. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).