A Planer Moving Microphone Array for Sound Source Localization
Abstract
1. Introduction
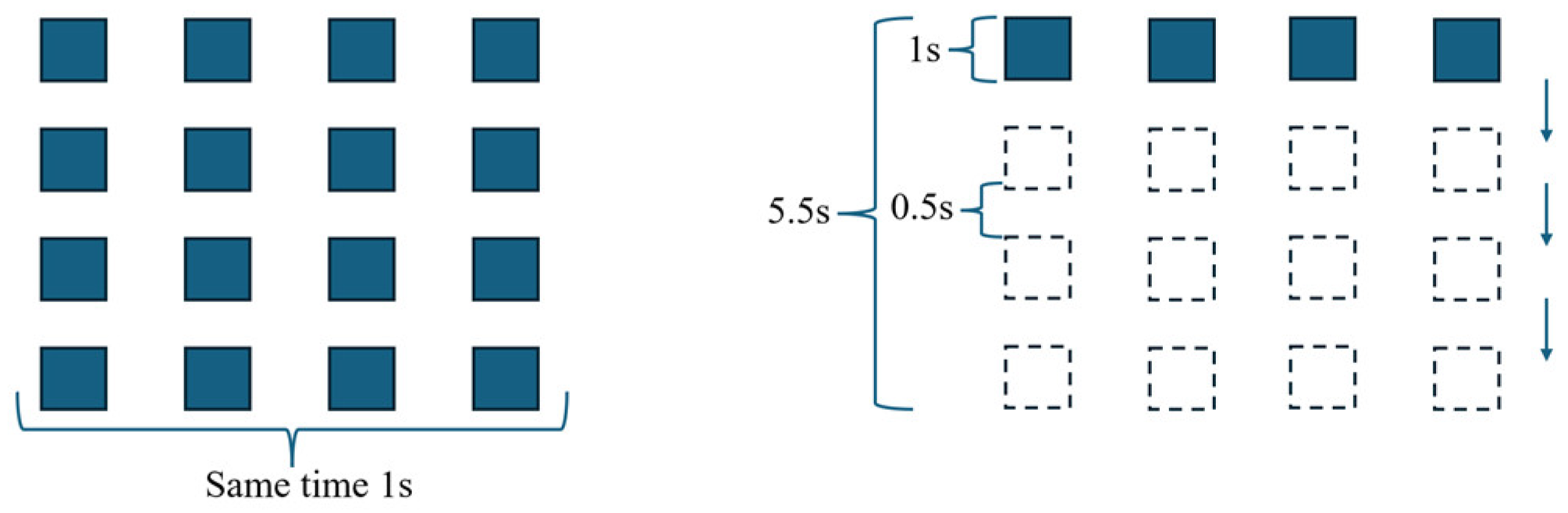
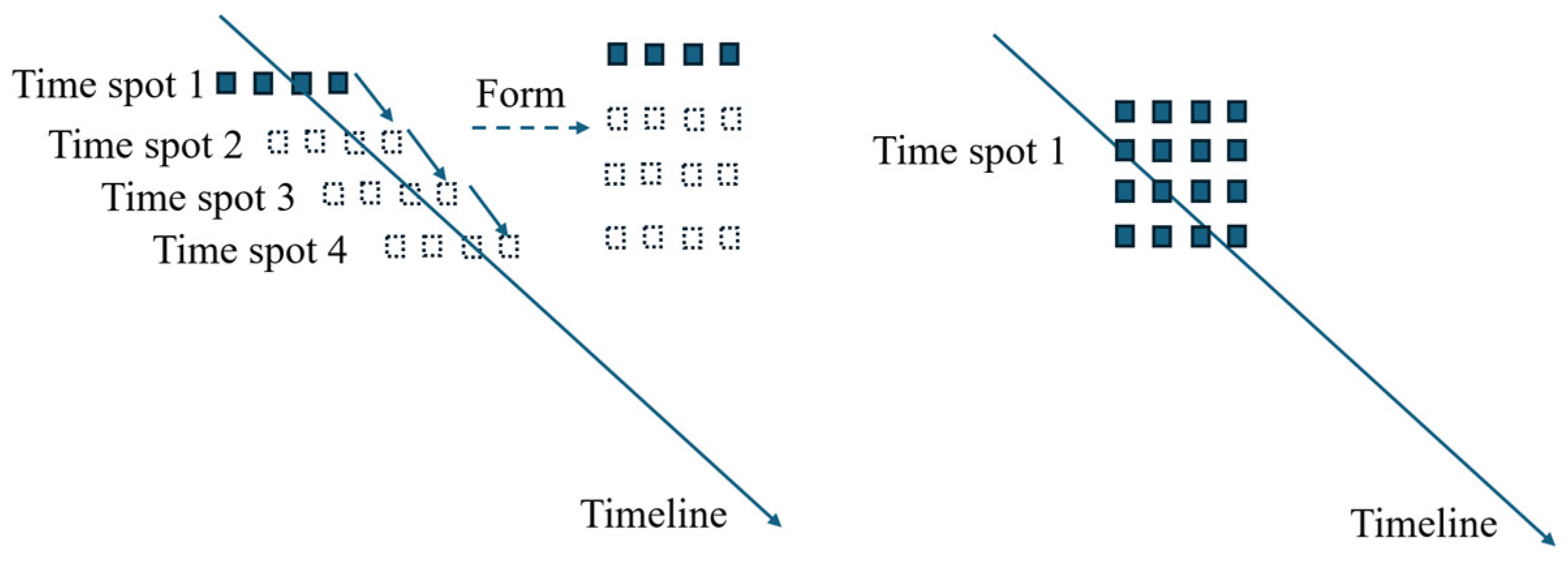
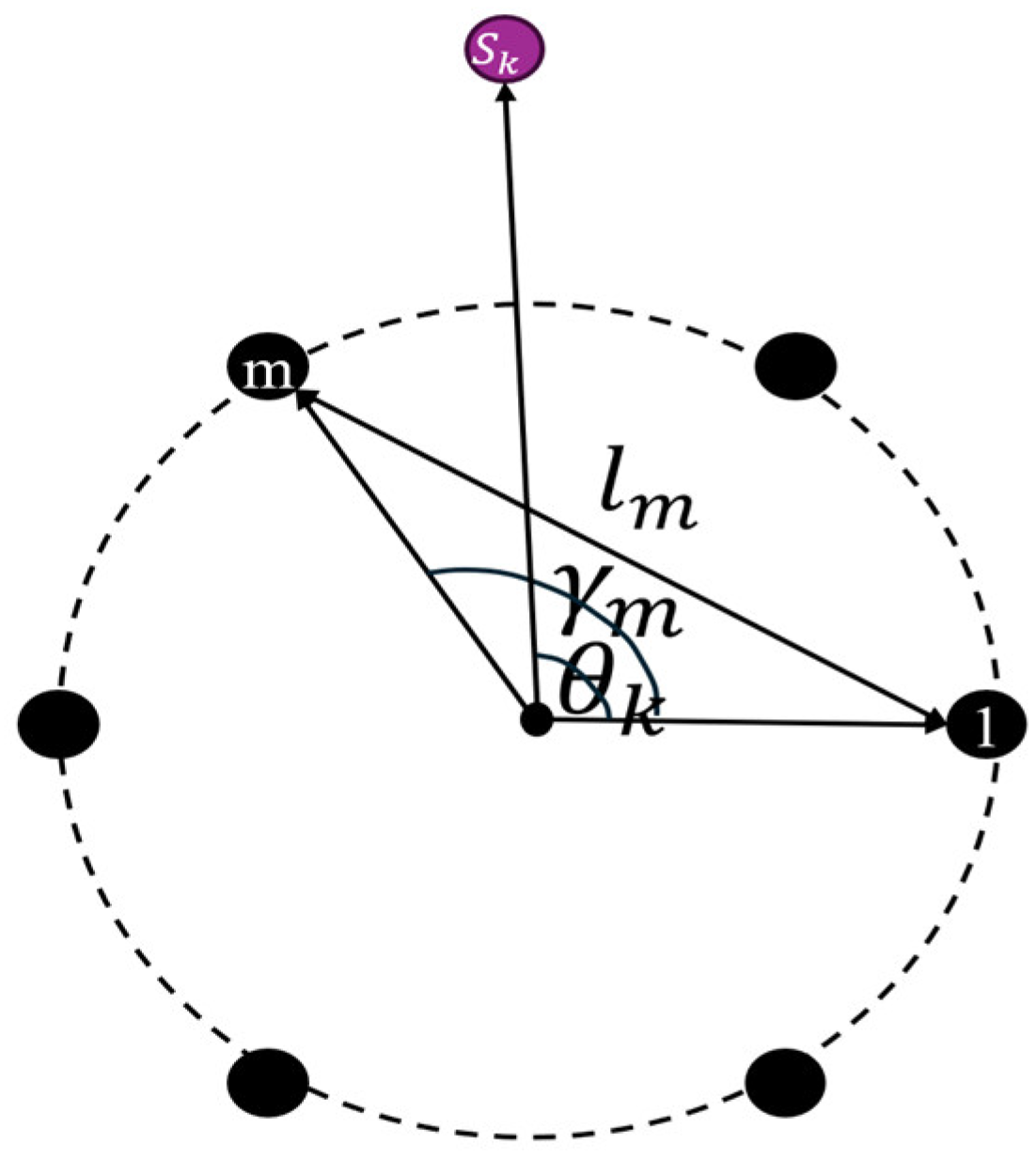
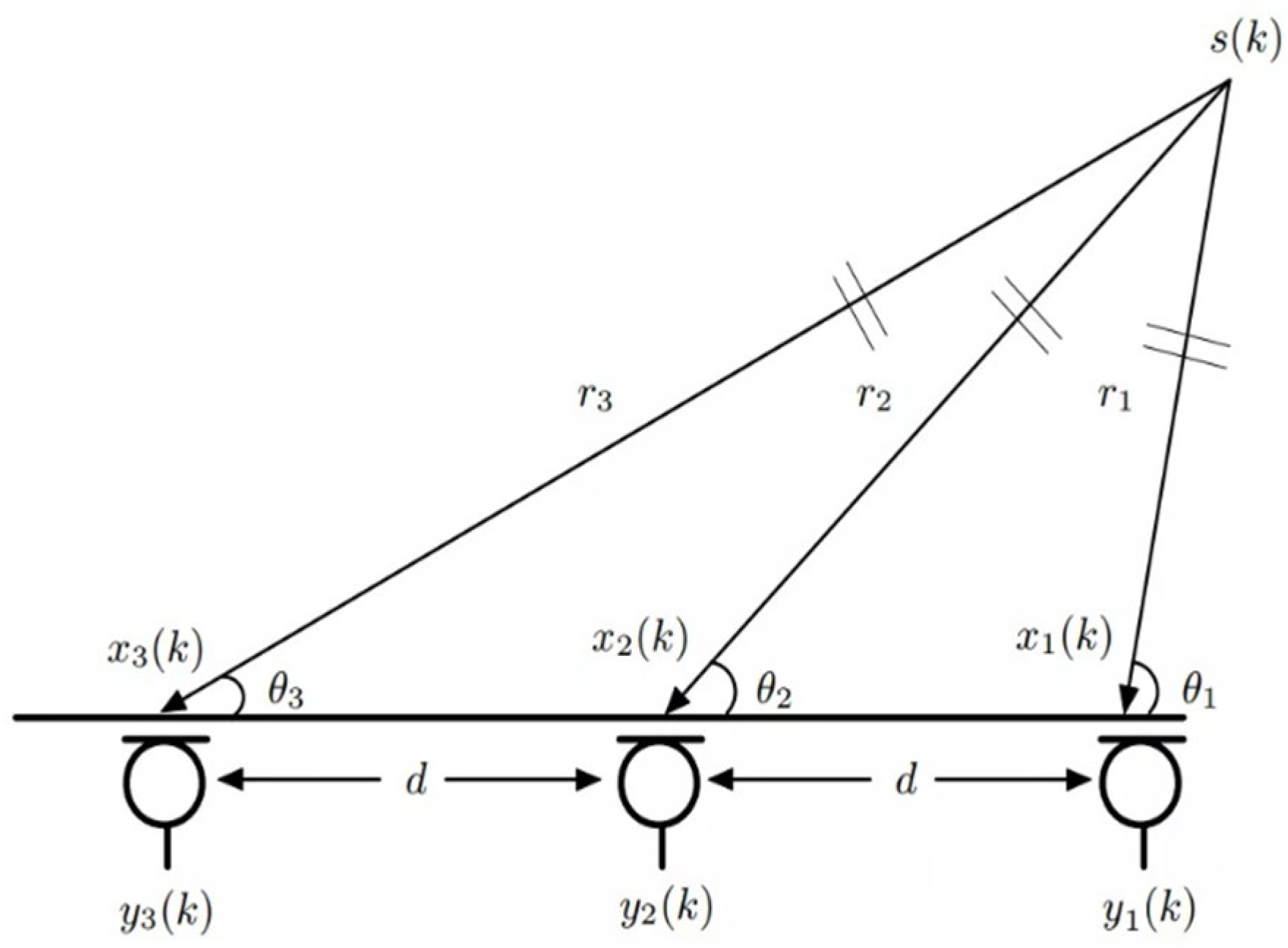
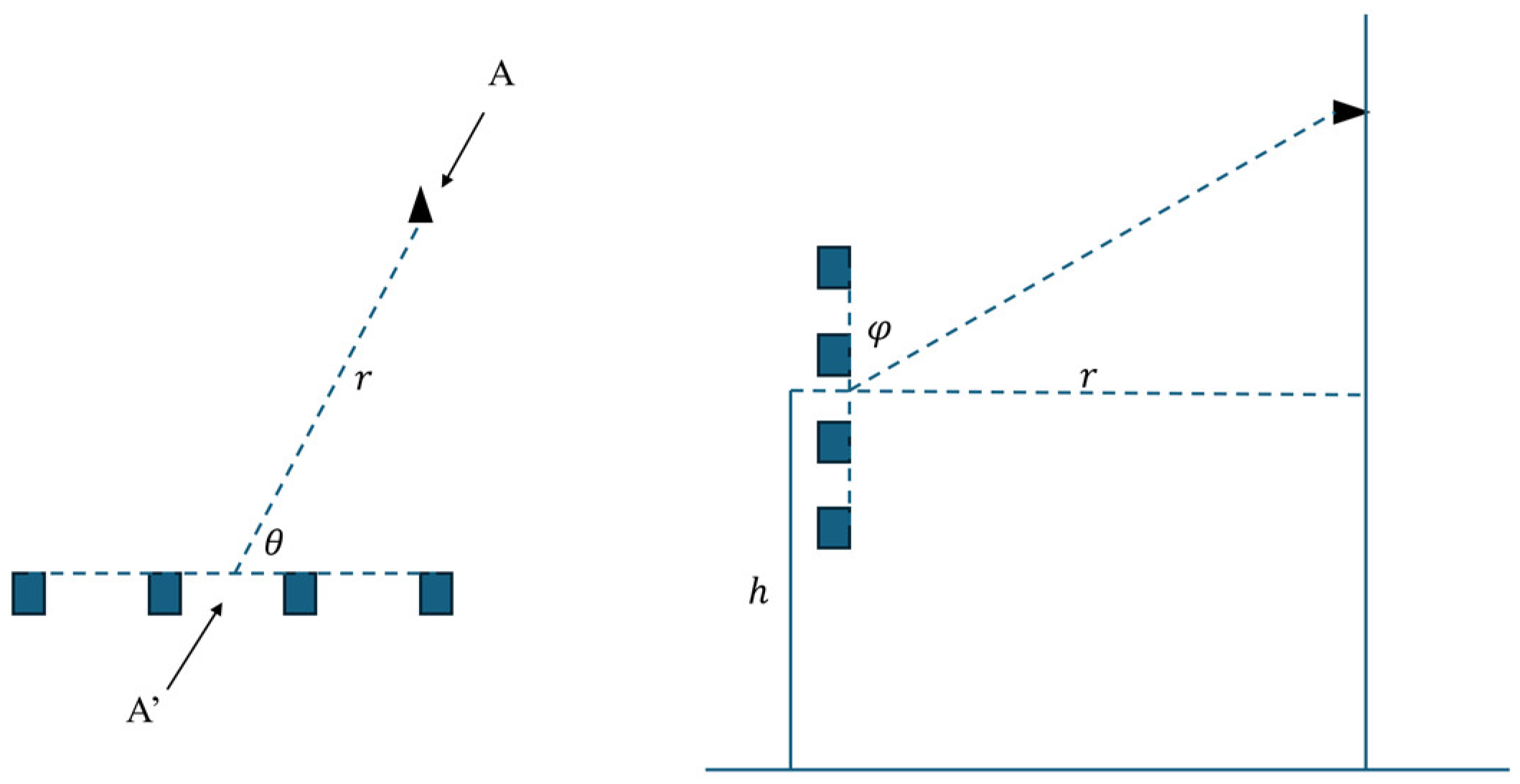
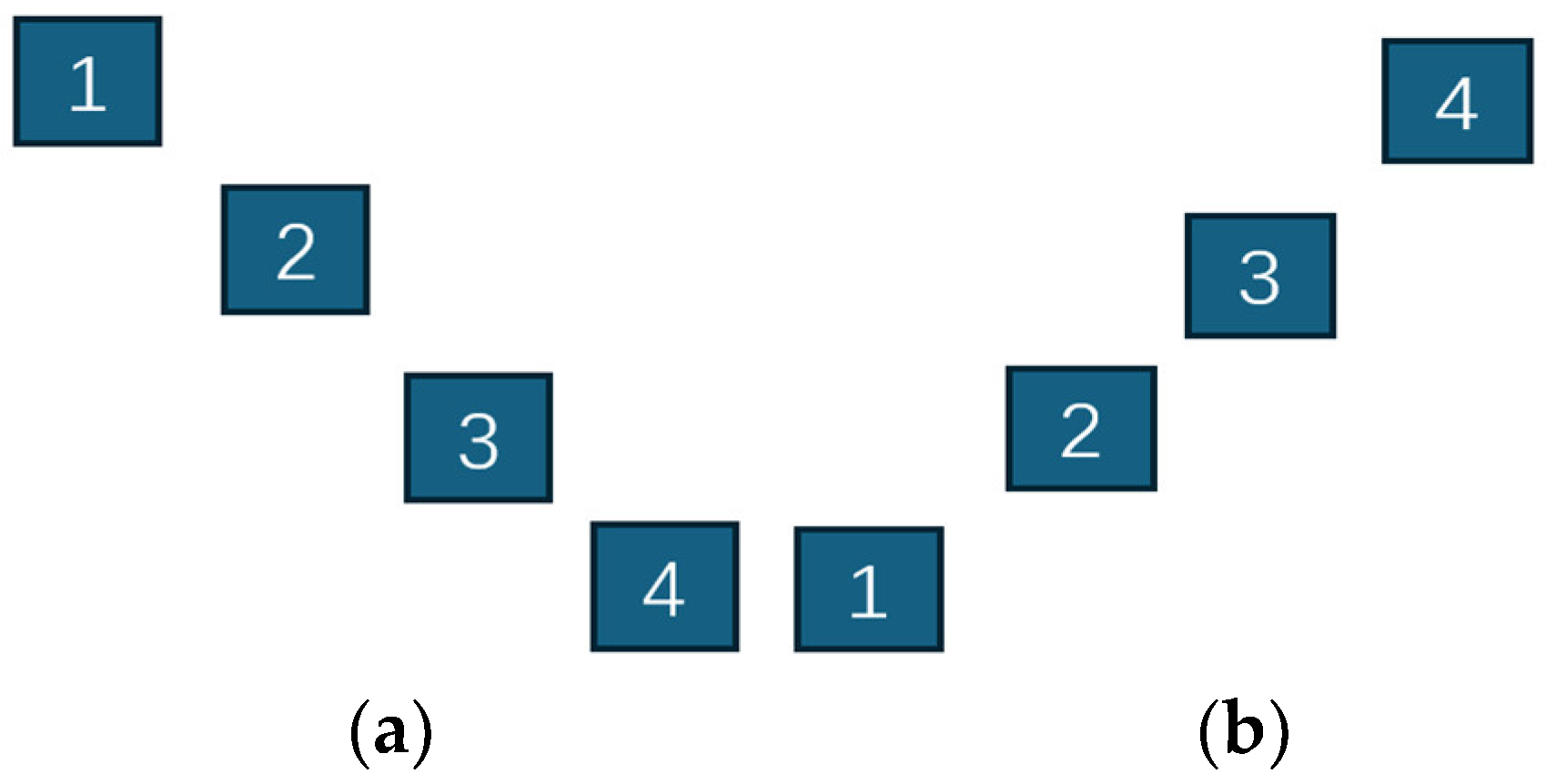
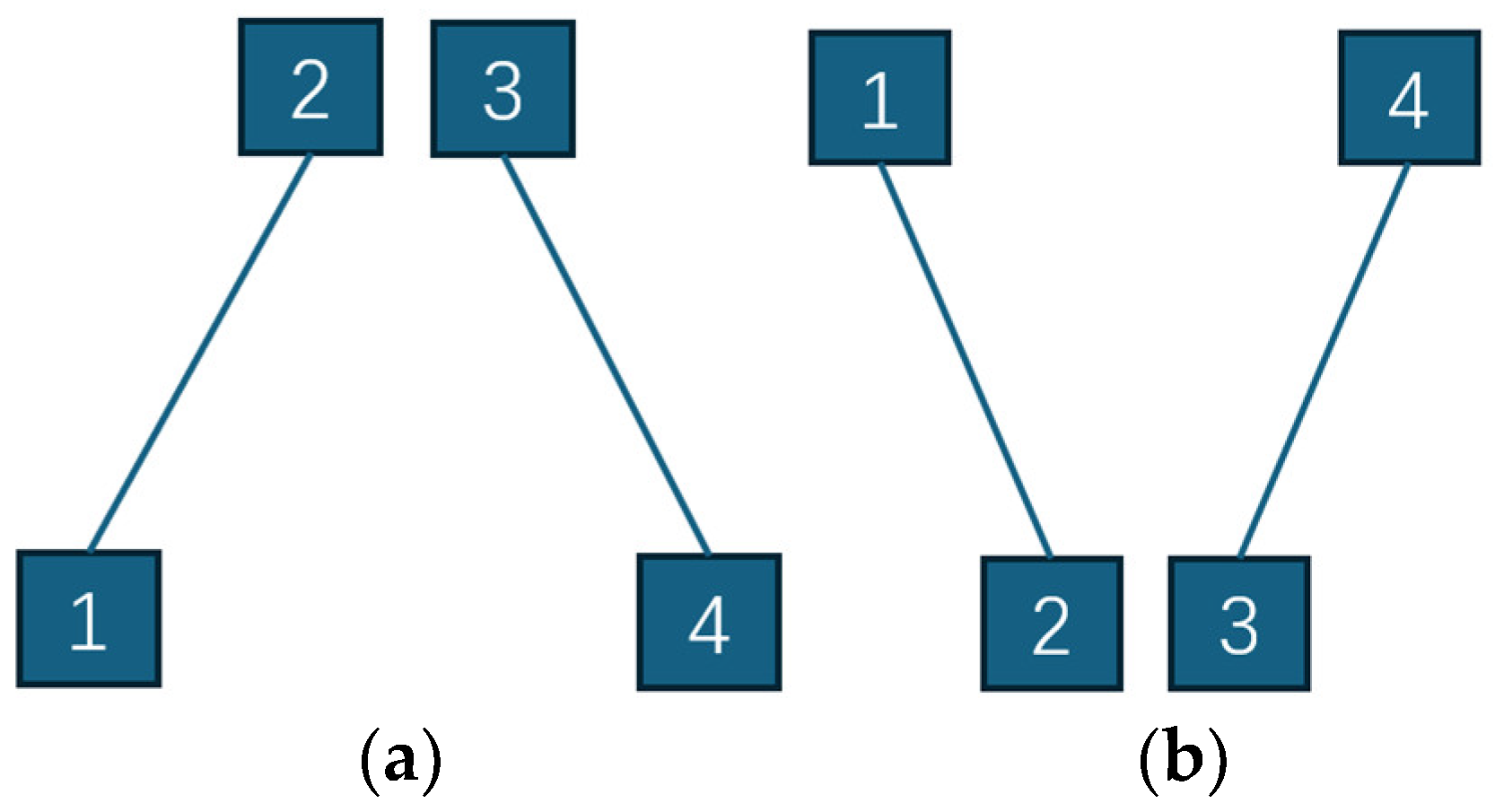
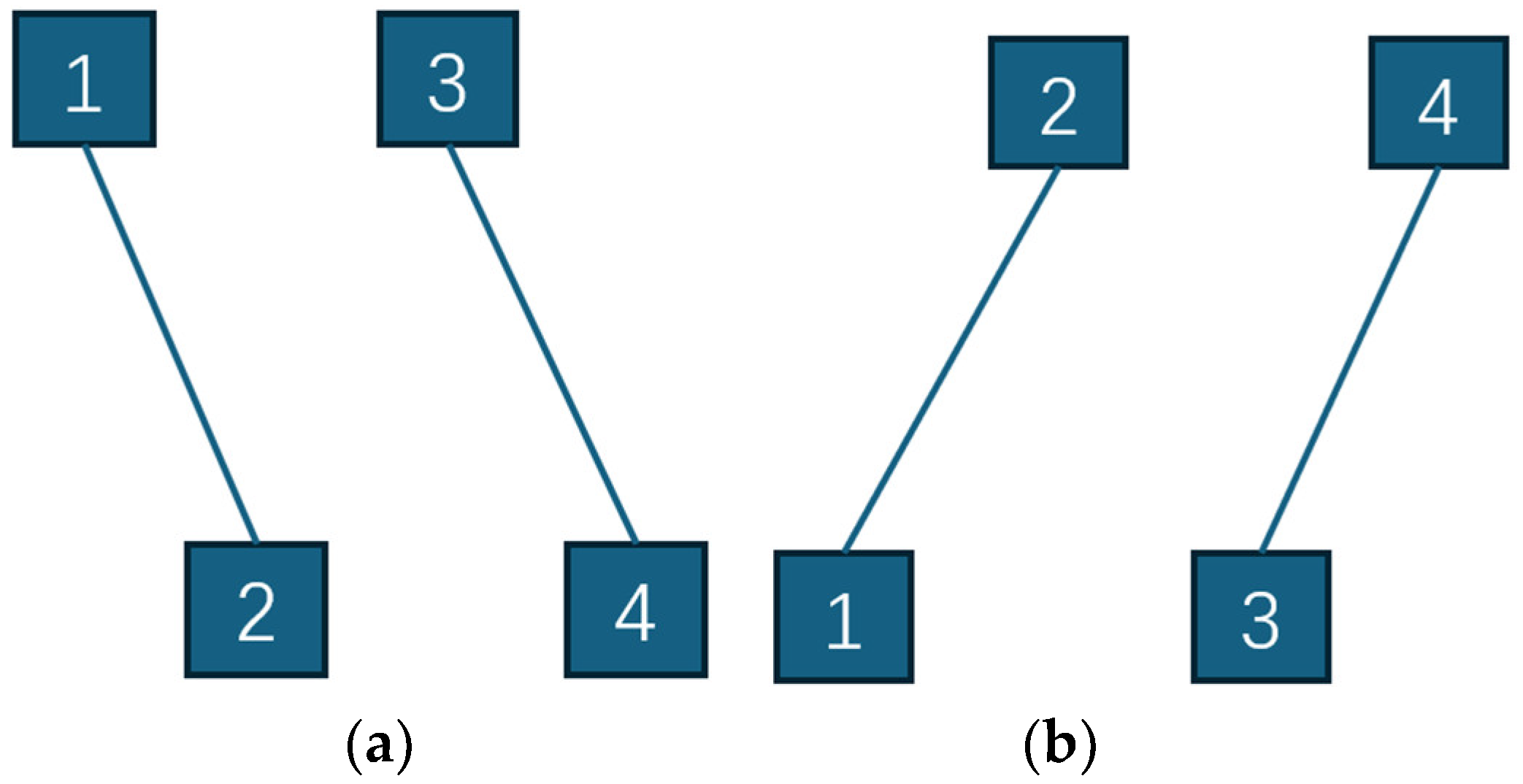
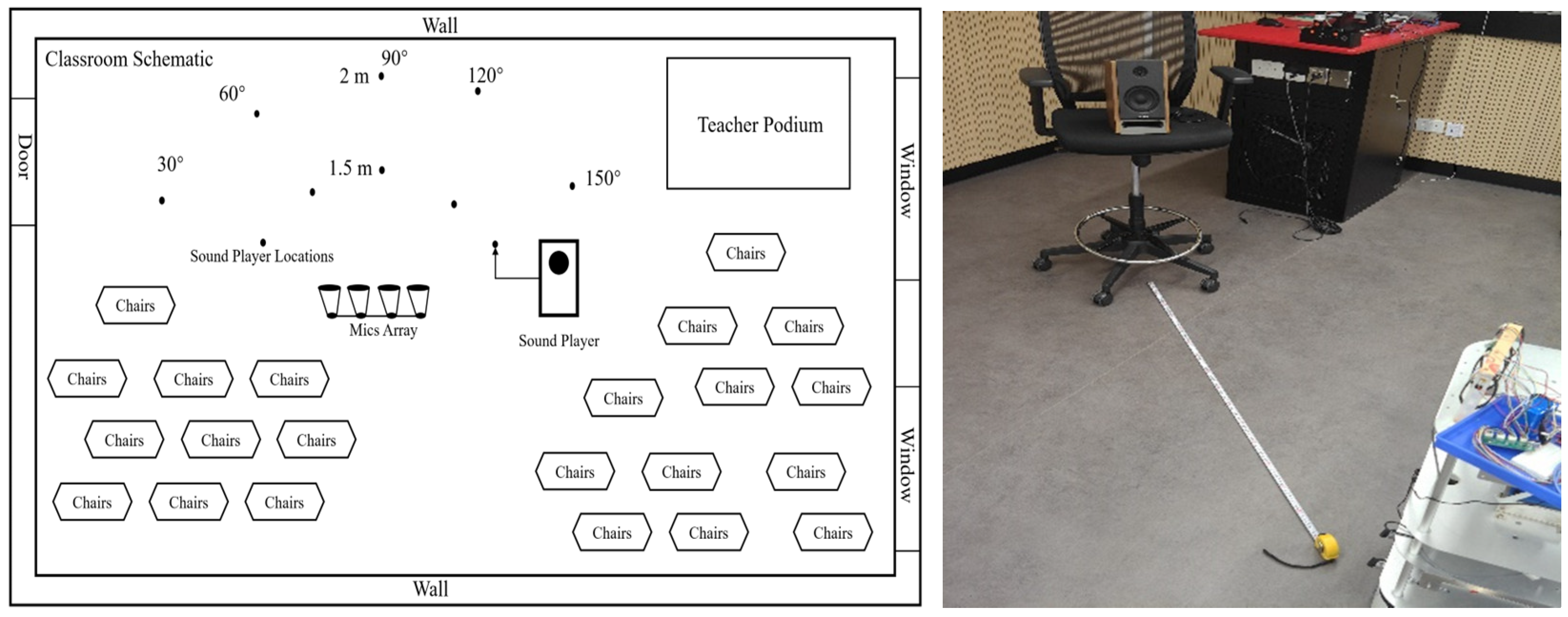
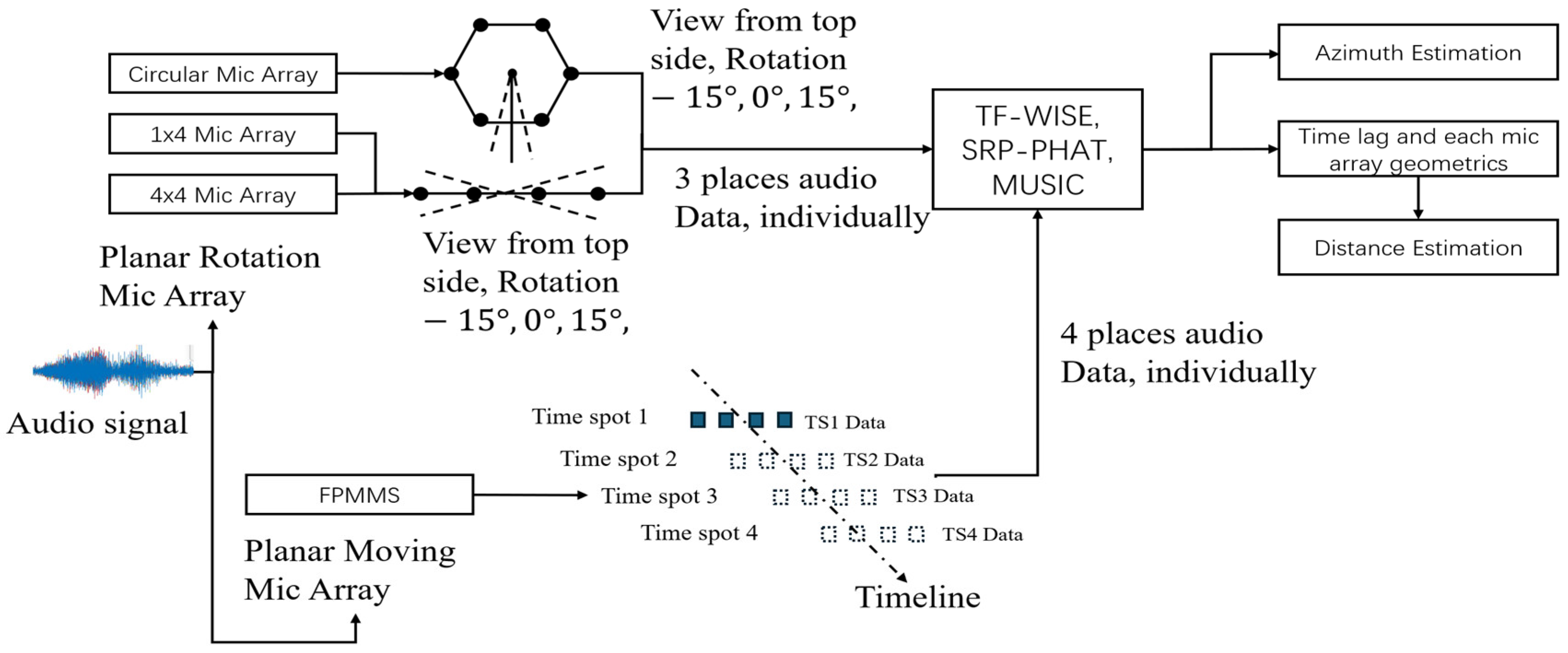
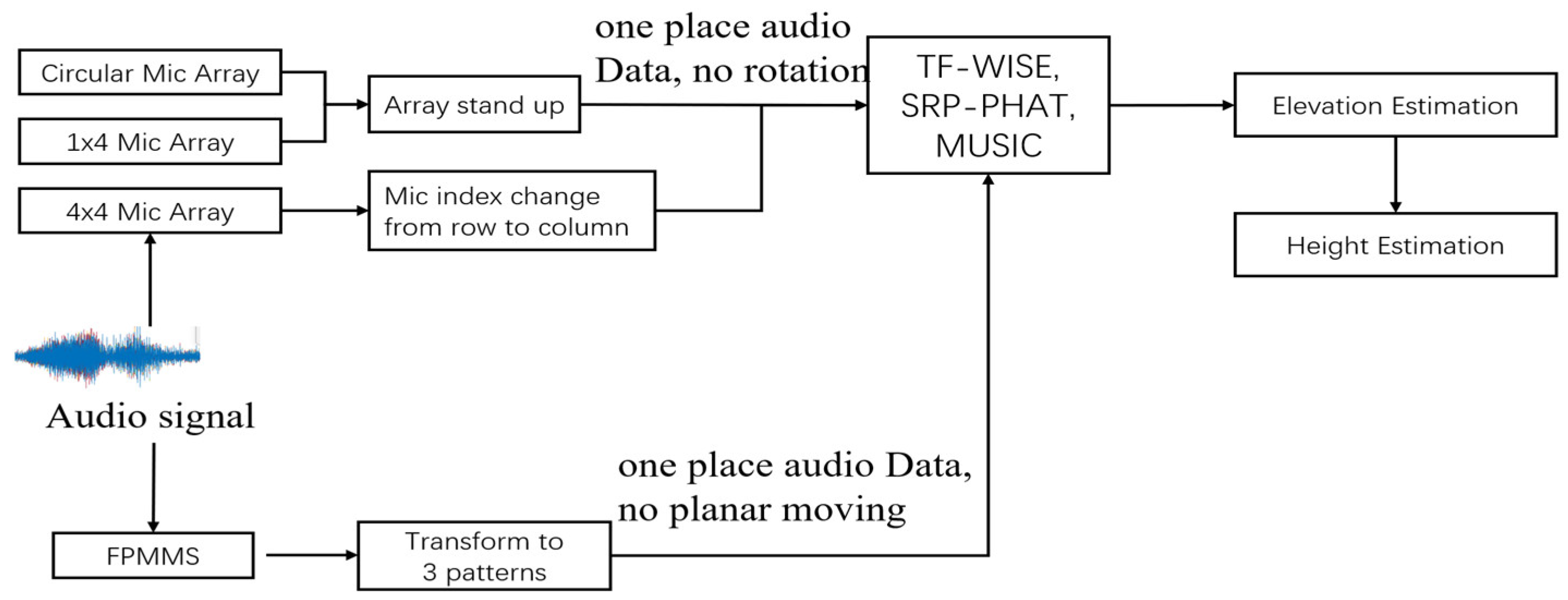
2. Introduction to the FPMMS and Building Procedure
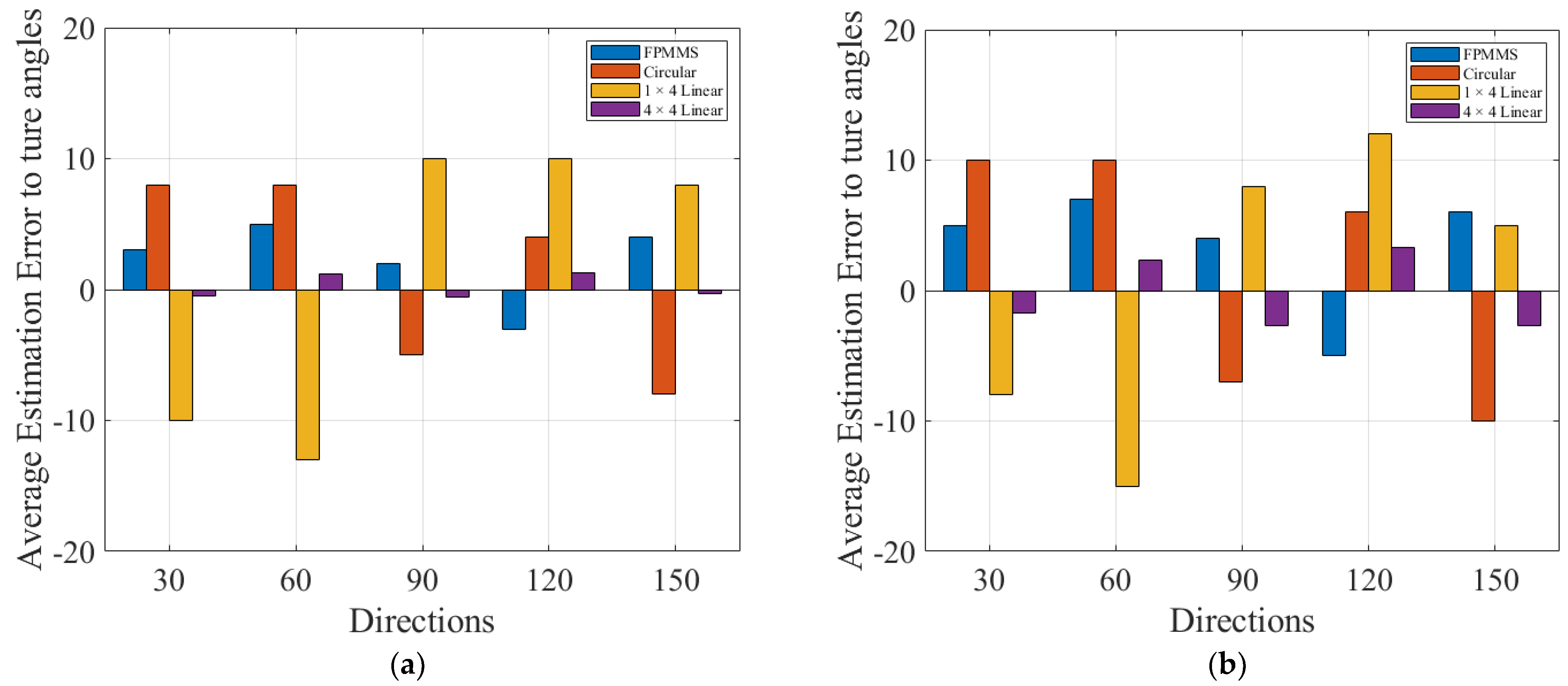
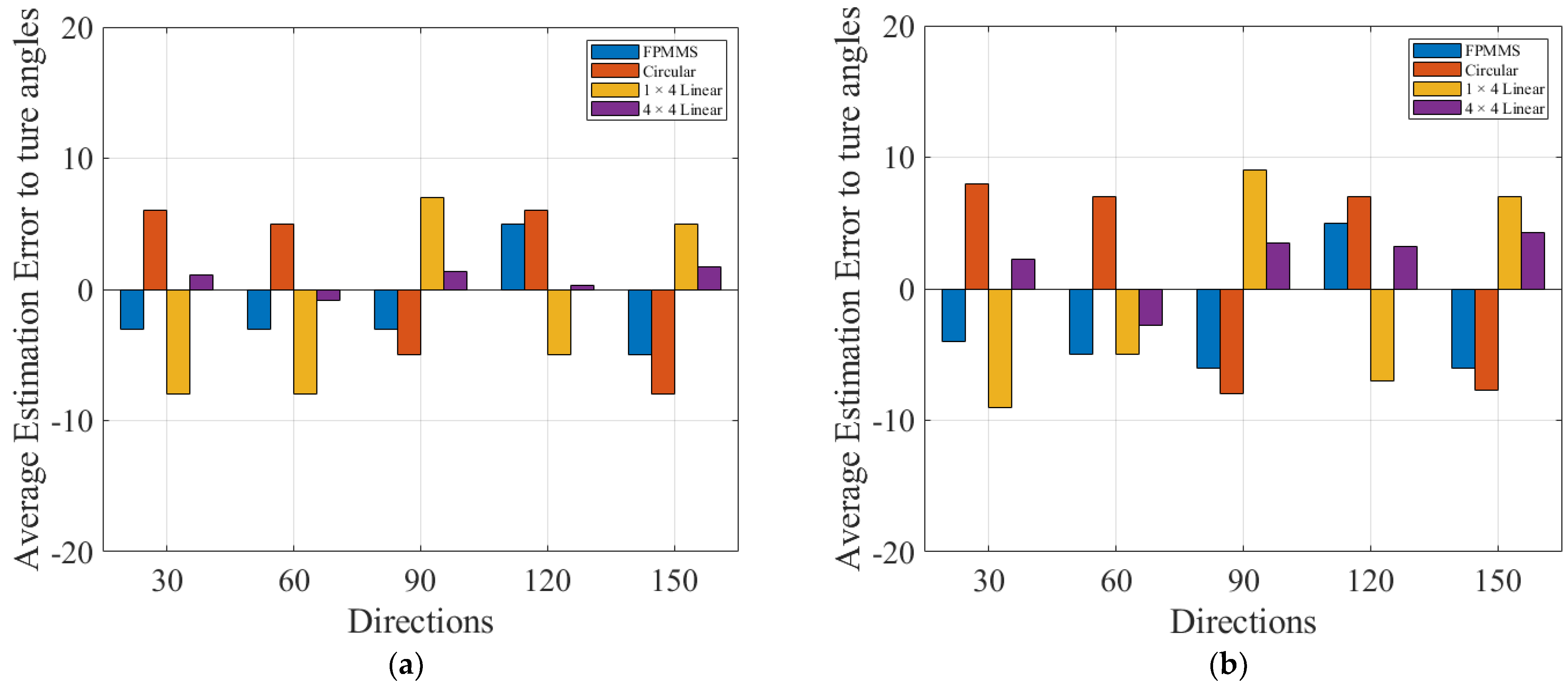
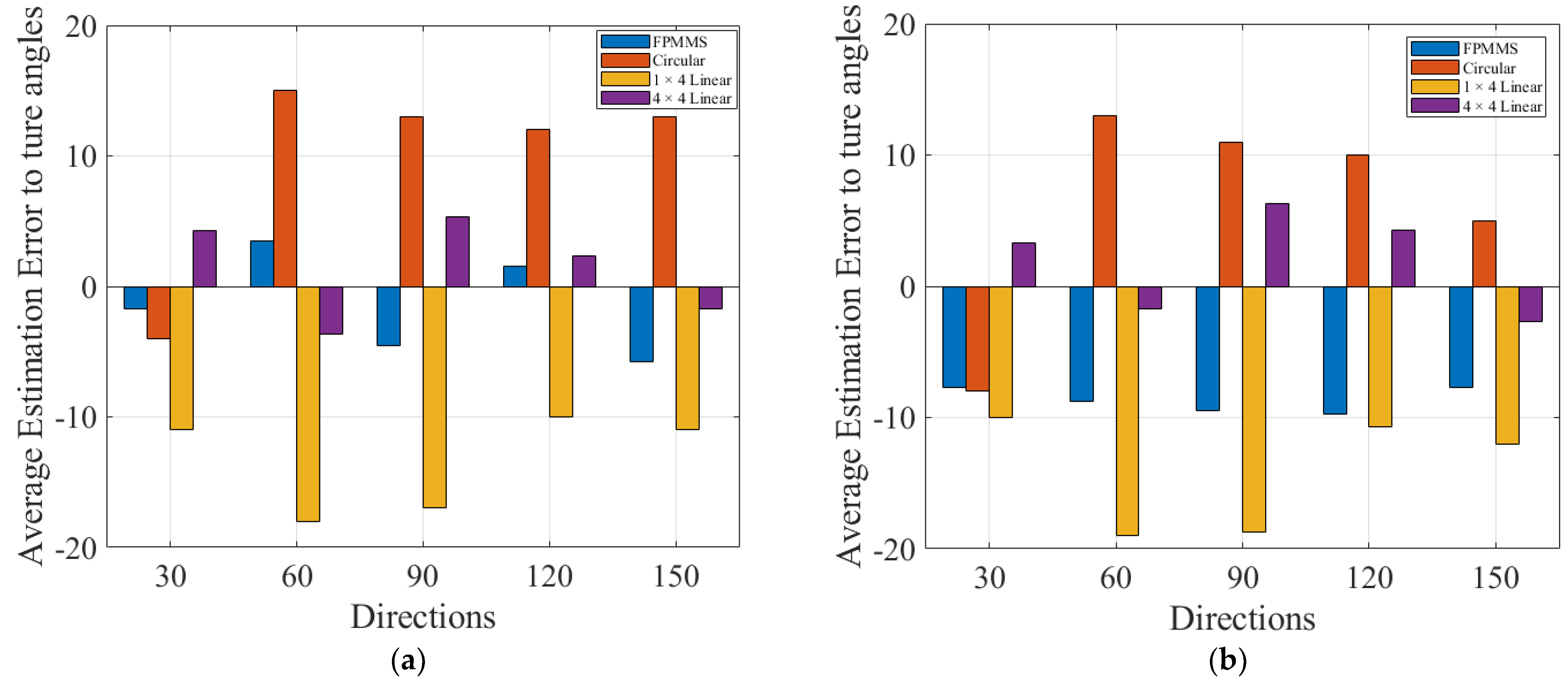
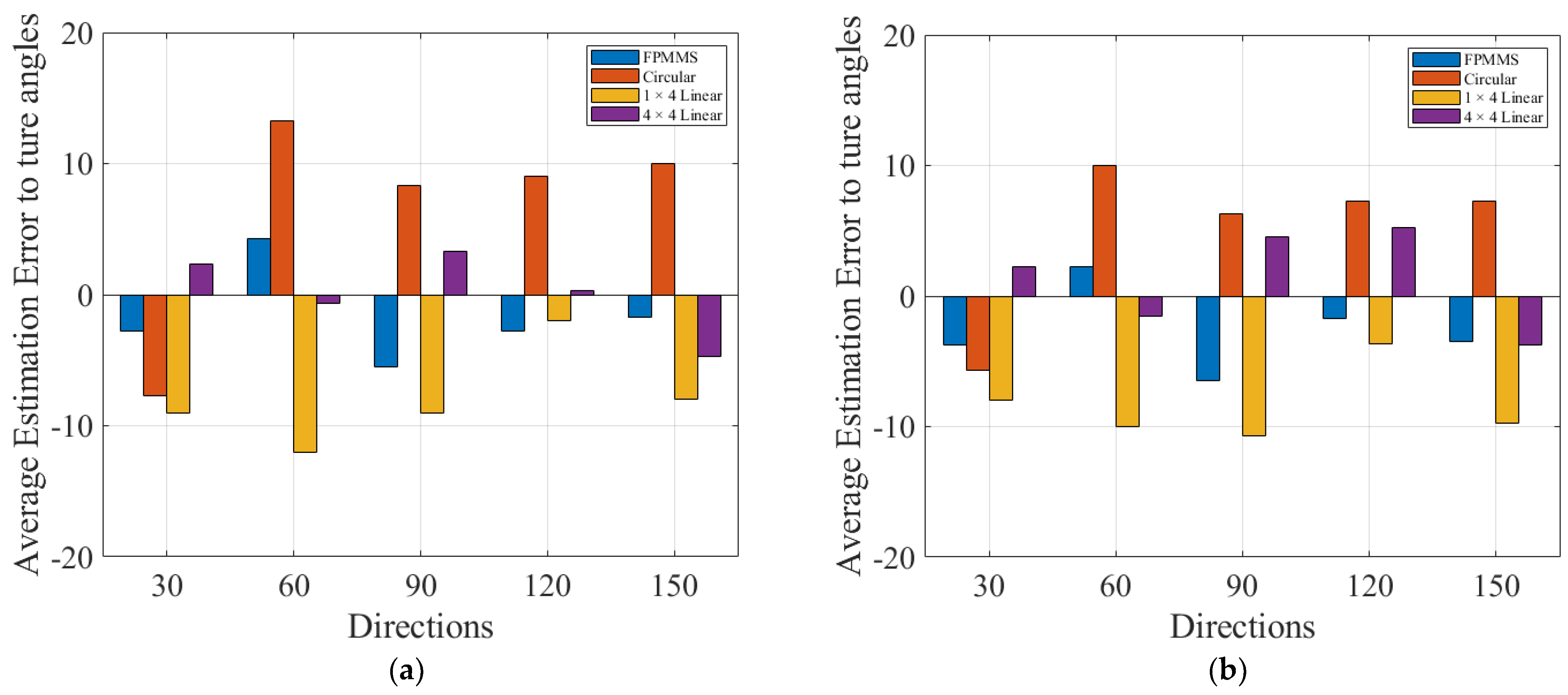
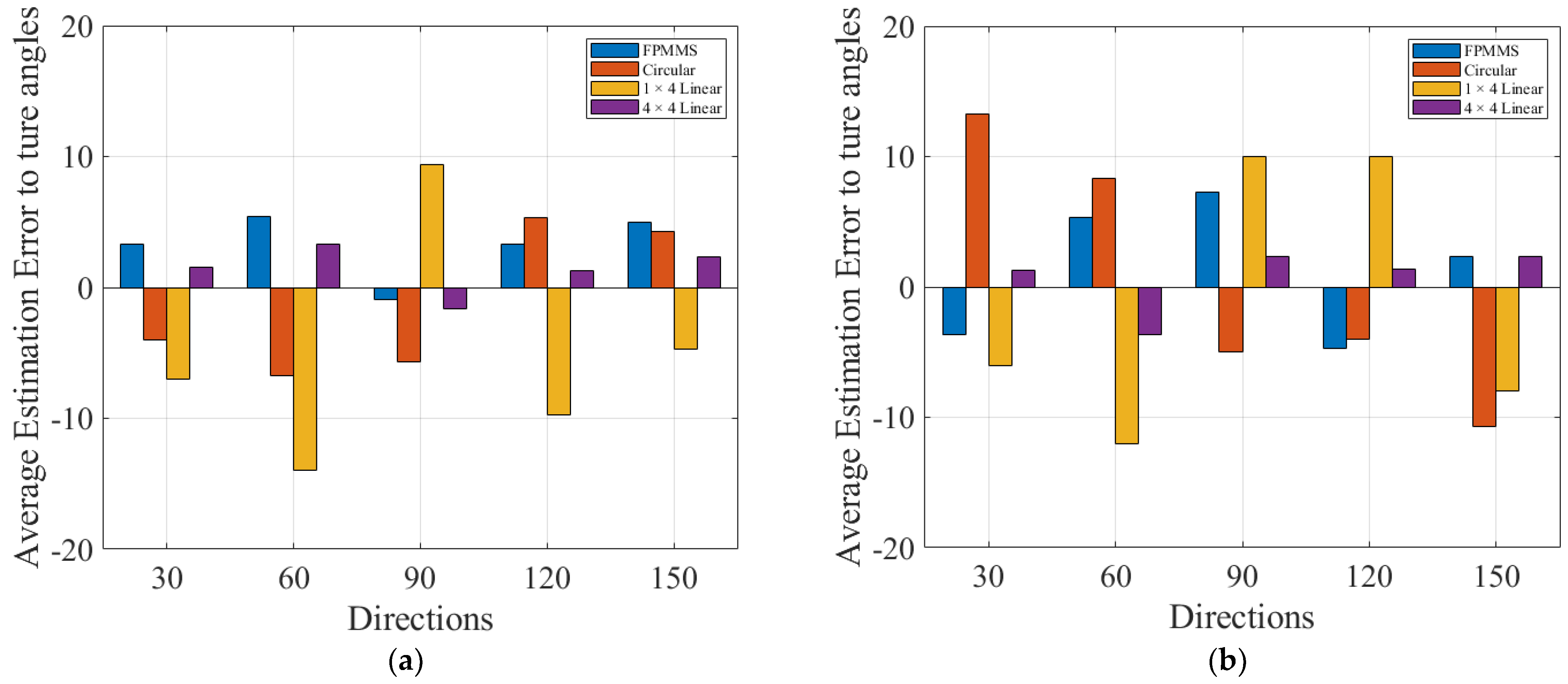
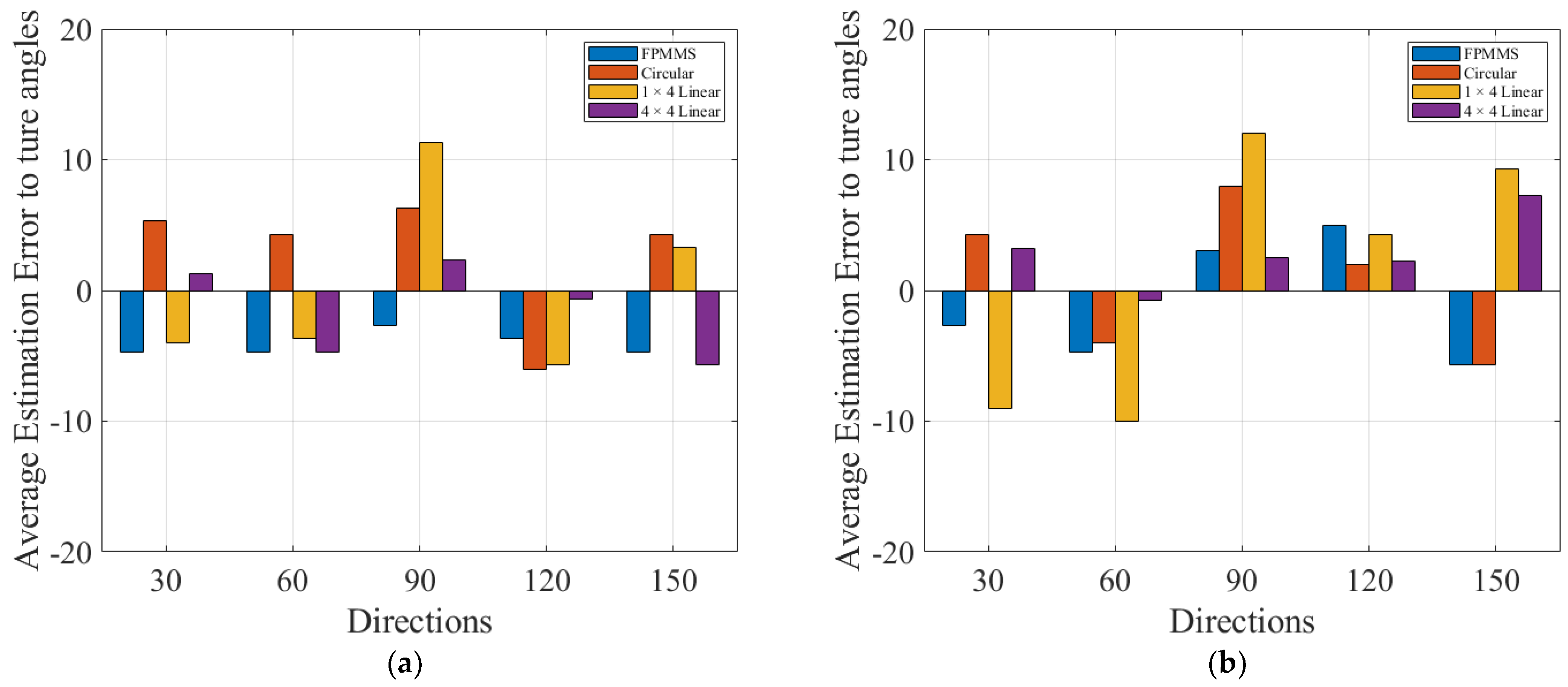
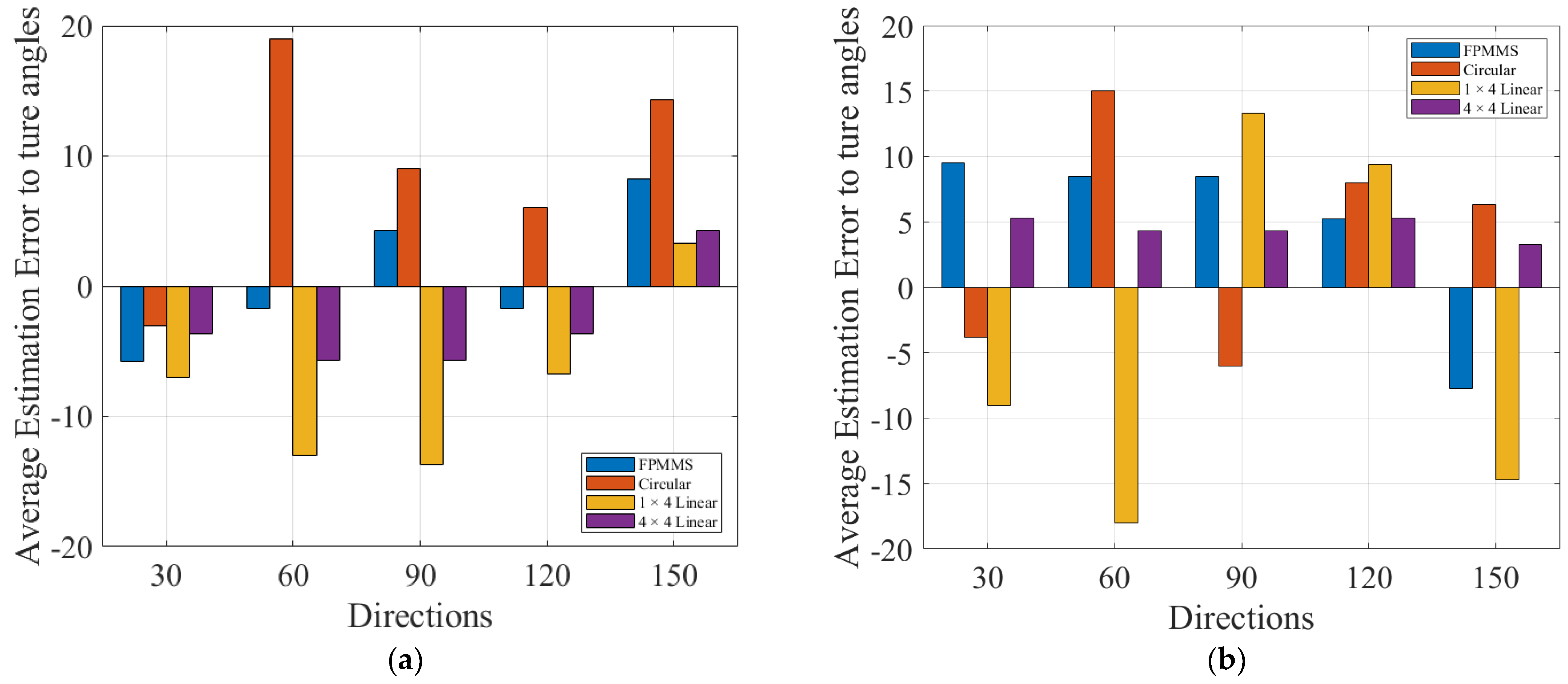
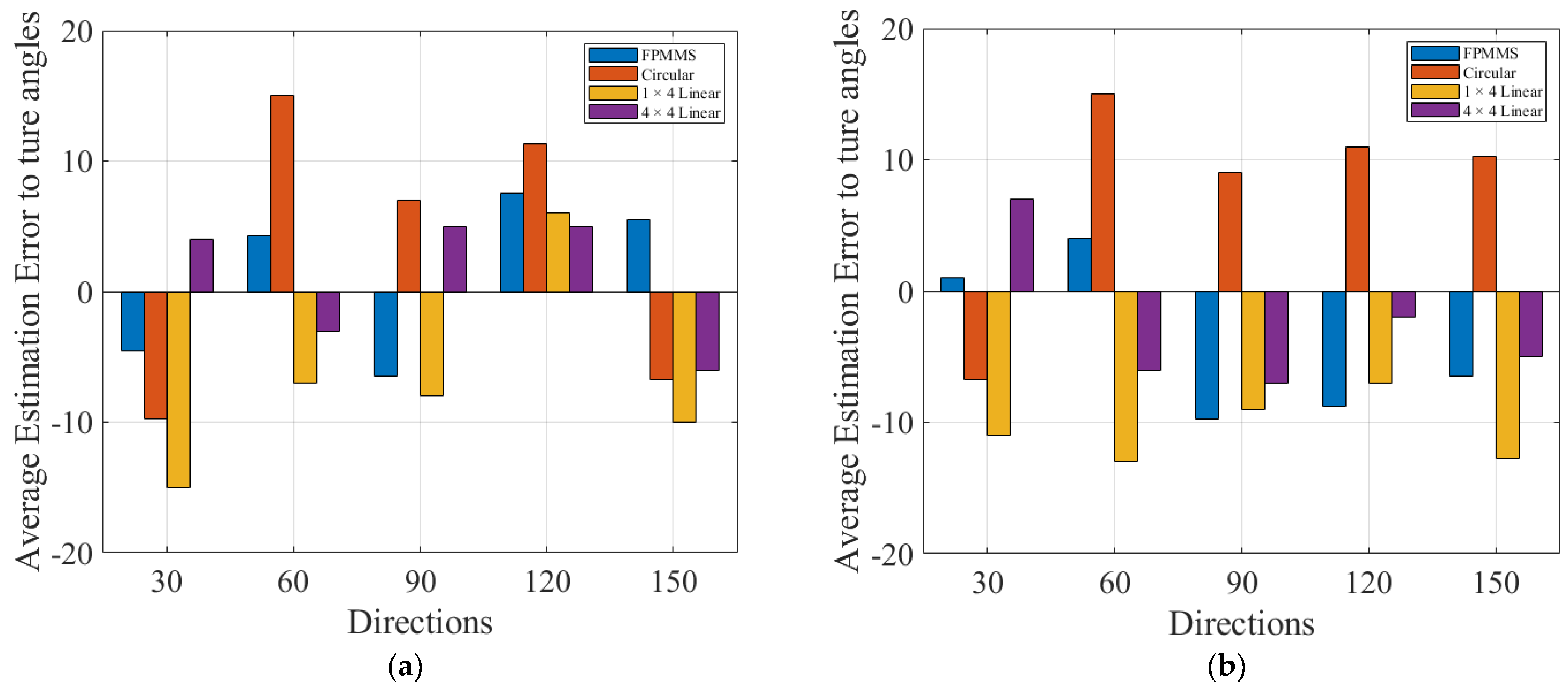
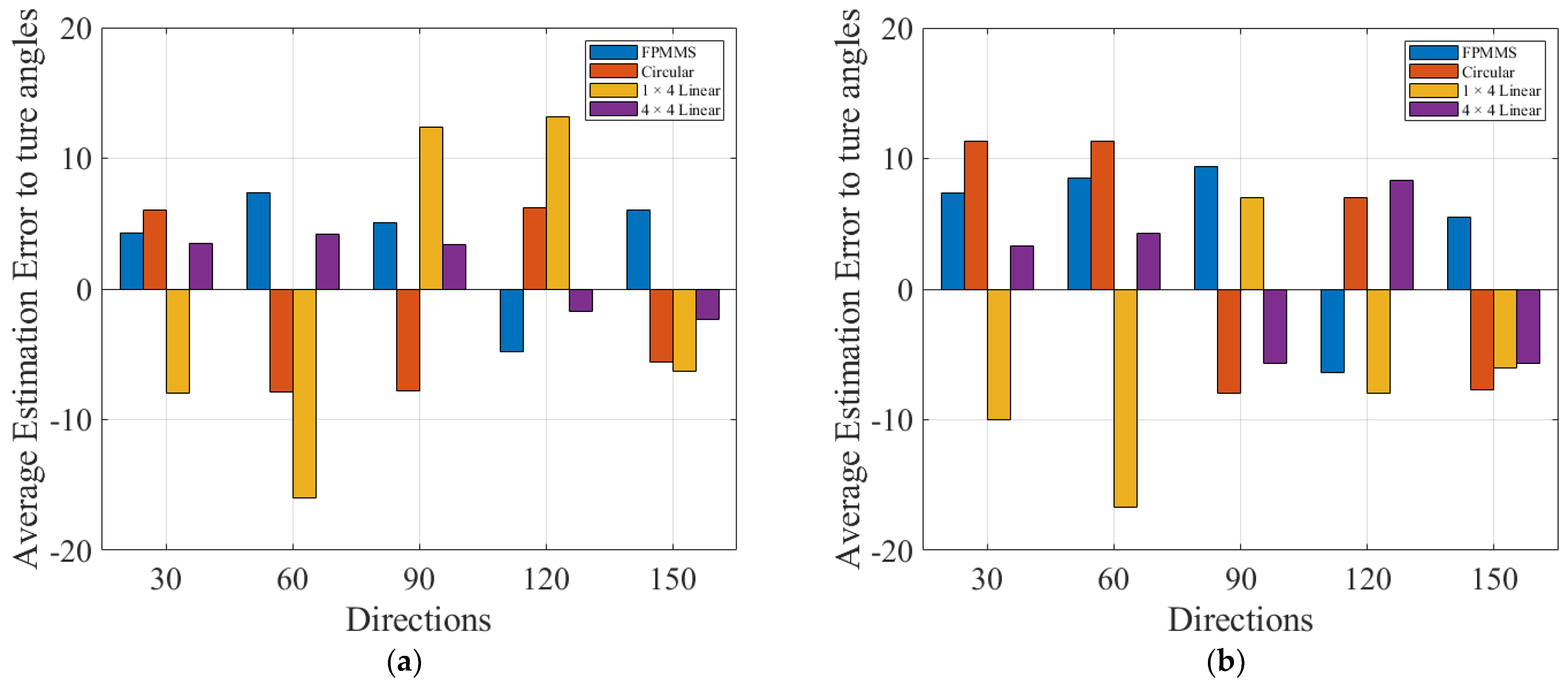
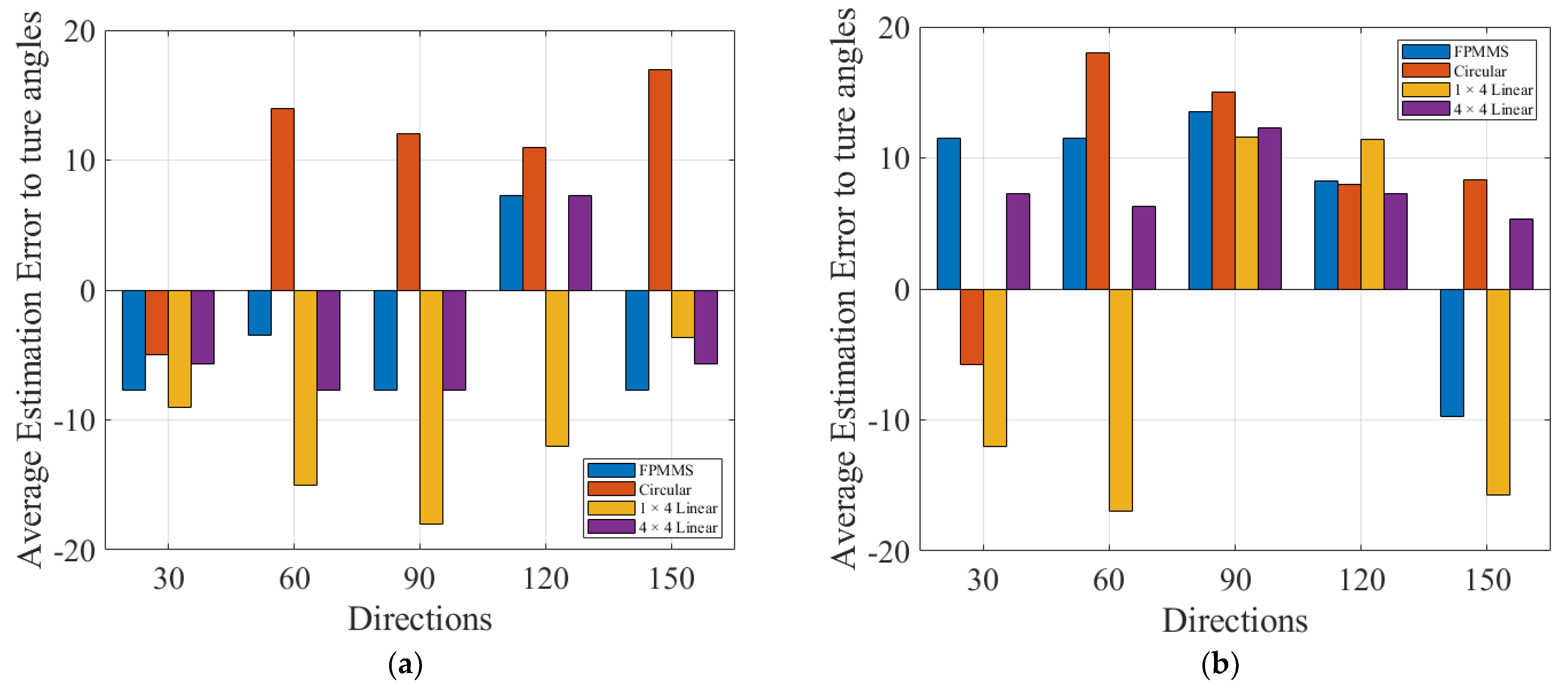
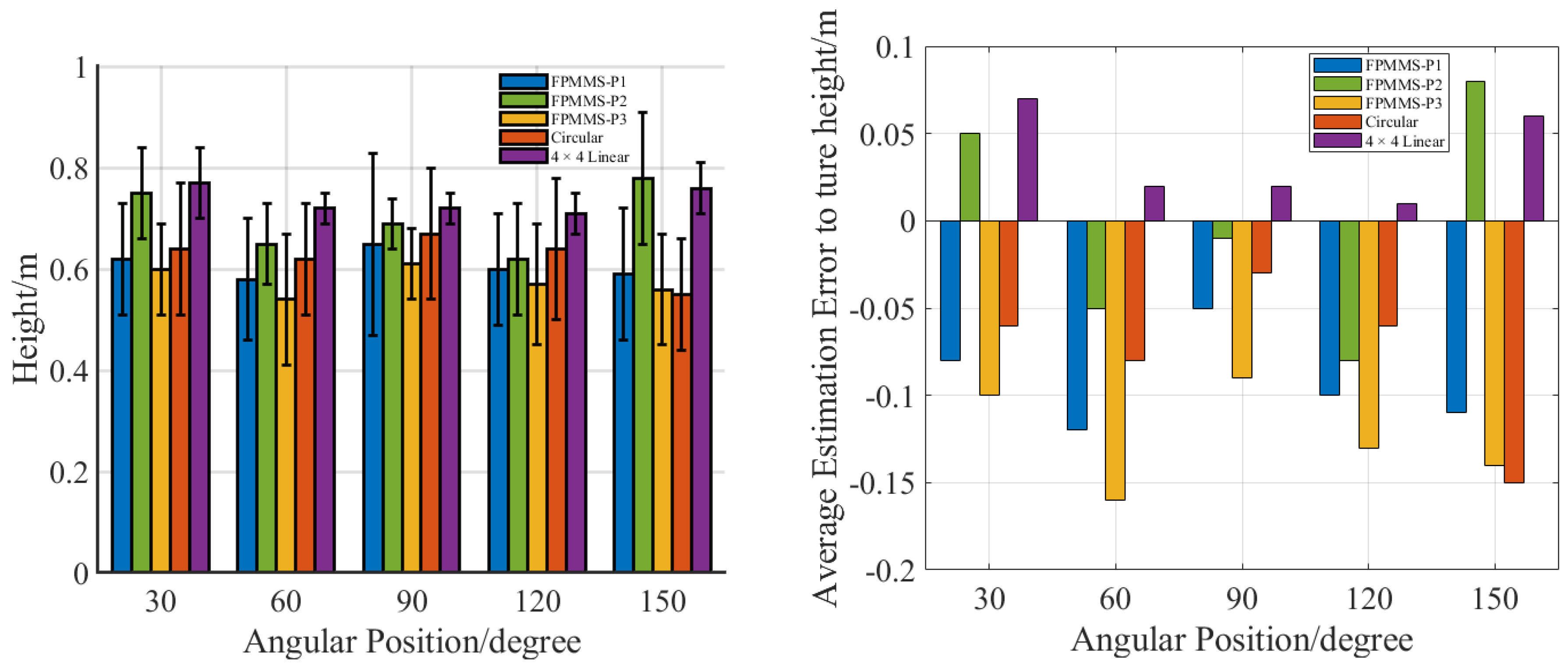
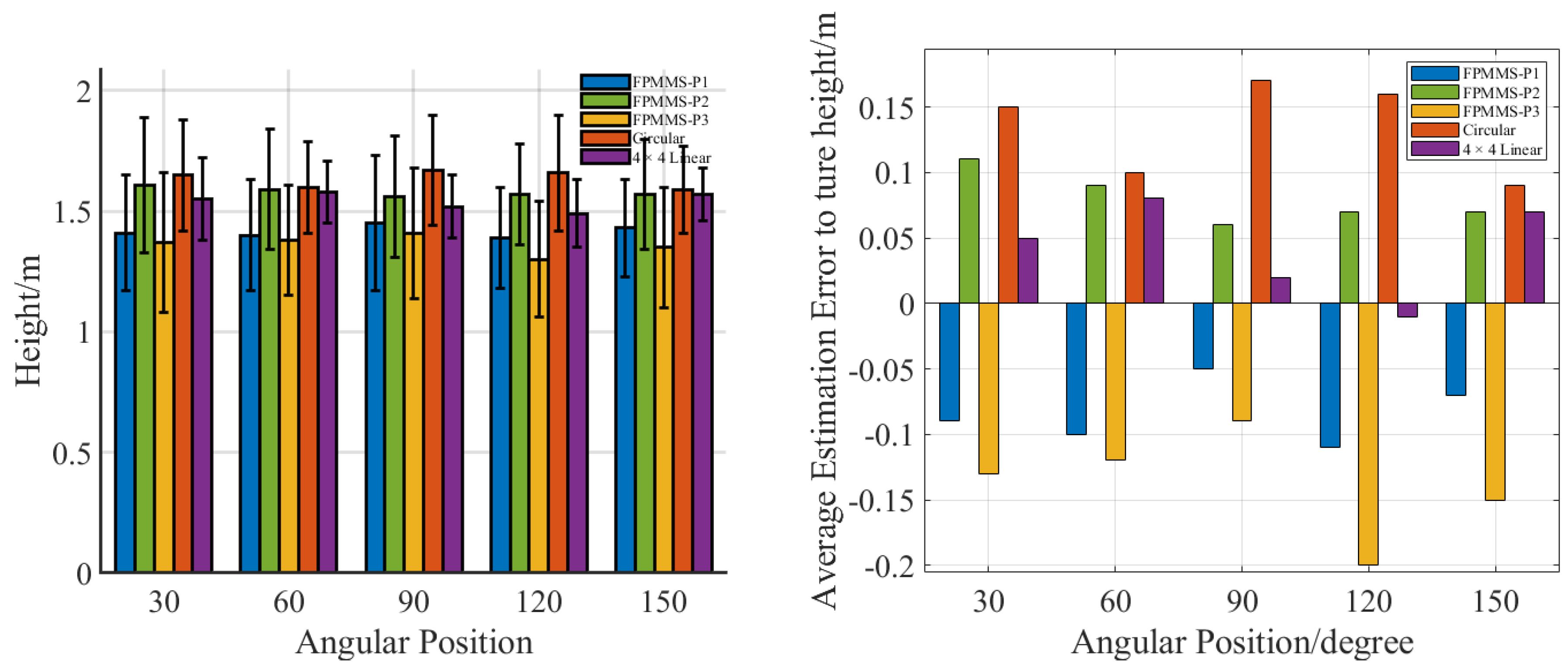
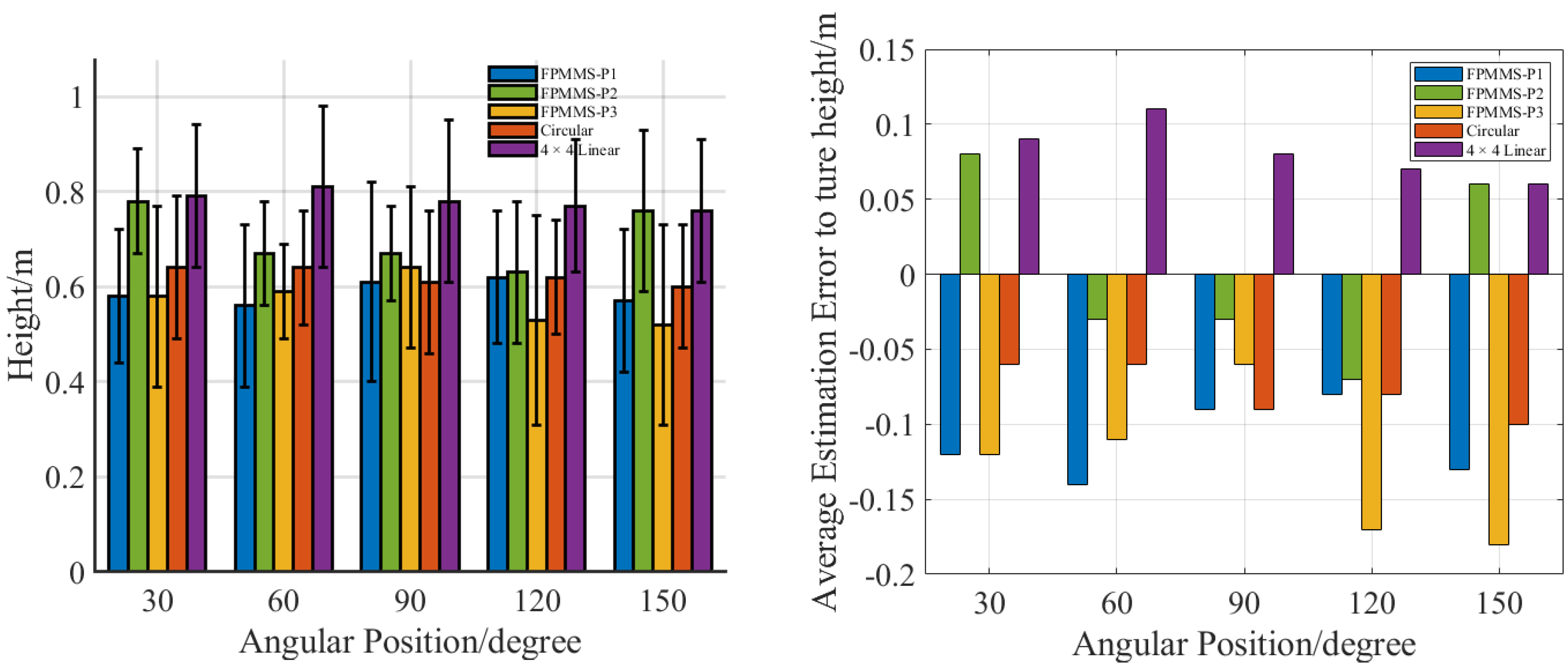
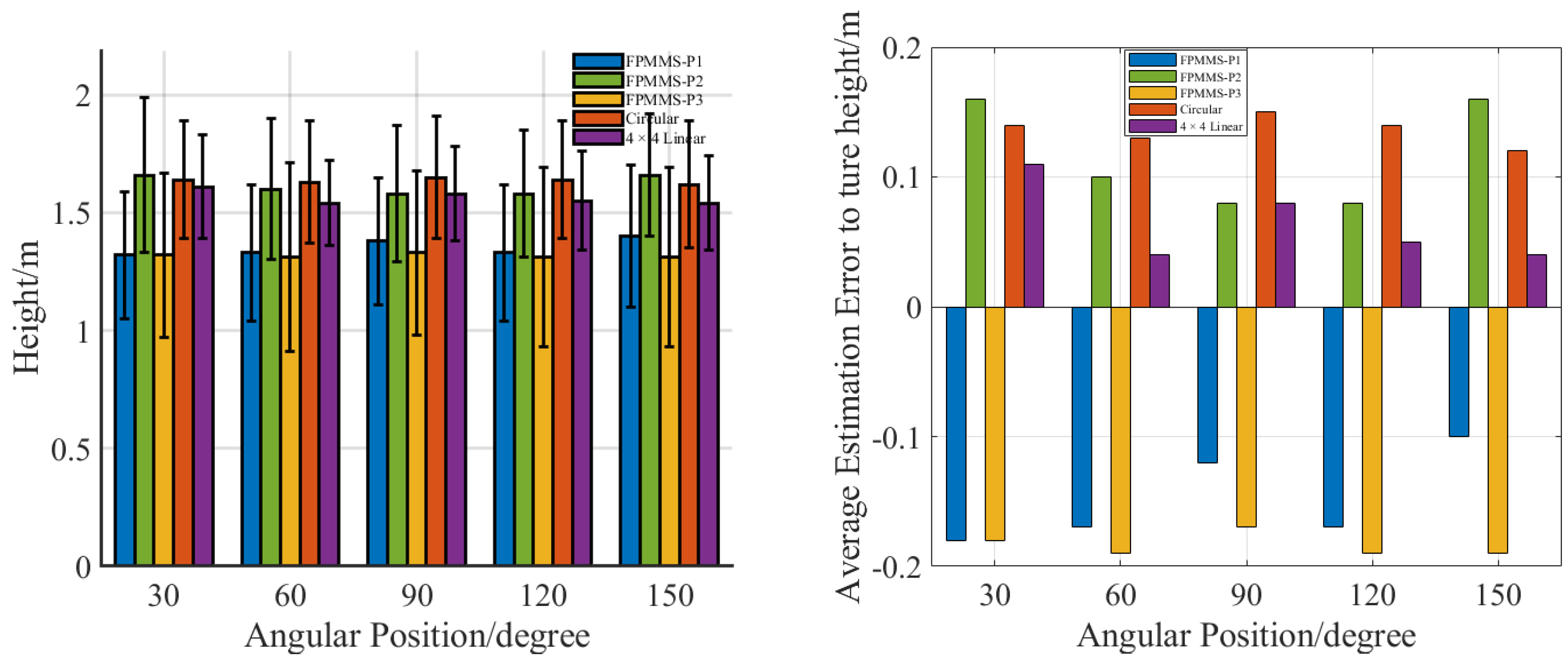
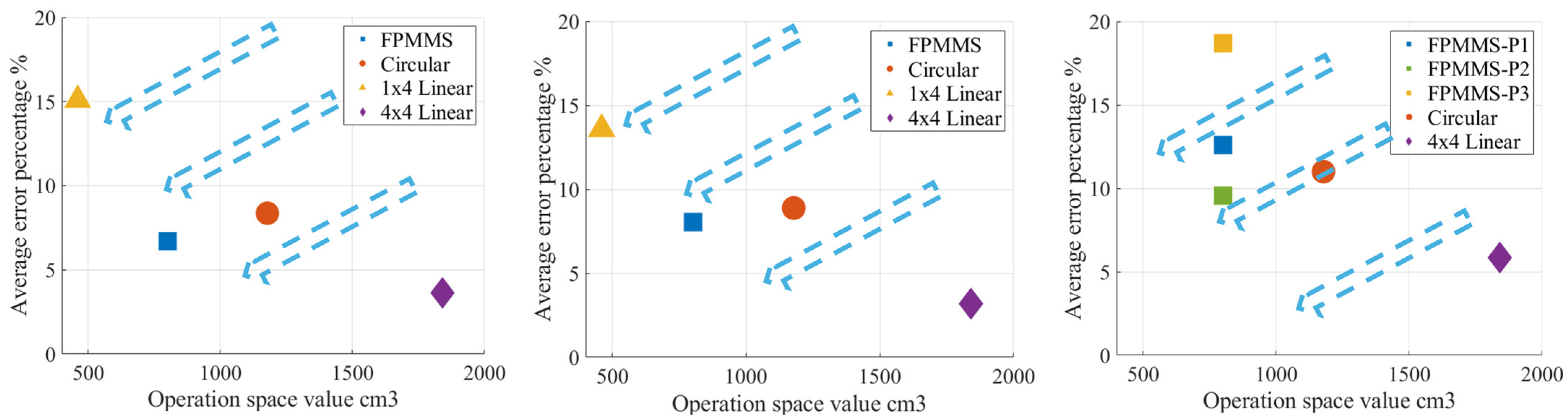
3. Experiment and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, S.; Yang, Y.; Chen, C.; Zhang, X.; Leng, Q.; Zhao, X. Deep learning-based multimodal emotion recognition from audio, visual, and text modalities: A systematic review of recent advancements and future prospects. Expert Syst. Appl. 2024, 237, 121692. [Google Scholar] [CrossRef]
- Zahorik, P. Direct-to-reverberant energy ratio sensitivity. J. Acoust. Soc. Am. 2002, 112, 2110–2117. [Google Scholar] [CrossRef] [PubMed]
- Zahorik, P.; Brungart, D.S.; Bronkhorst, A.W. Auditory distance perception in humans: A summary of past and present research. ACTA Acust. United Acust. 2005, 91, 409–420. [Google Scholar]
- Rafaely, B. Analysis and design of spherical microphone arrays. IEEE Trans. Speech Audio Process. 2005, 13, 135–143. [Google Scholar] [CrossRef]
- Azaria, M.; Hertz, D. Time delay estimation by generalized cross correlation methods. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 280–285. [Google Scholar] [CrossRef]
- Schwarz, A.; Kellermann, W. Coherent-to-Diffuse Power Ratio Estimation for Dereverberation. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 1006–1018. [Google Scholar] [CrossRef]
- Do, H.; Silverman, H.F. SRP-PHAT methods of locating simultaneous multiple talkers using a frame of microphone array data. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 125–128. [Google Scholar]
- Do, H.; Silverman, H.F.; Yu, Y. A real-time SRP-PHAT source location implementation using stochastic region contraction (SRC) on a large-aperture microphone array. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ’07, Honolulu, HI, USA, 15–20 April 2007; pp. 121–124. [Google Scholar]
- Hogg, A.O.T.; Neo, V.W.; Weiss, S.; Evers, C.; Naylor, P.A. A polynomial eigenvalue decomposition music approach for broadband sound source localization. In Proceedings of the 2021 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 17–20 October 2021; pp. 326–330. [Google Scholar]
- Wei, L.; Choy, Y.S.; Cheung, C.S.; Chu, H.K. Comparison of tribology performance, particle emissions and brake squeal noise between Cu-containing and Cu-free brake materials. Wear 2021, 466–467, 203577. [Google Scholar] [CrossRef]
- Choy, Y.S.; Huang, L. Drum silencer with shallow cavity filled with helium. J. Acoust. Soc. Am. 2003, 114, 1477–1486. [Google Scholar] [CrossRef]
- Yang, C.; Sun, L.; Guo, H.; Wang, Y.; Shao, Y. A fast 3D MUSIC method for near-field sound source localization based on the bat algorithm. Int. J. Aeroacoustics 2022, 21, 98–114. [Google Scholar] [CrossRef]
- Zhen, H.S.; Cheung, C.S.; Leung, C.W.; Choy, Y.S. A comparison of the emission and impingement heat transfer of LPG-H2 and CH4-H2 premixed. Int. J. Hydrog. Energy 2012, 37, 10947–10955. [Google Scholar] [CrossRef]
- Choy, Y.S.; Huang, L.; Wang, C. Sound propagation in and low frequency noise absorption by helium-filled porous material. J. Acoust. Soc. Am. 2009, 126, 3008–3019. [Google Scholar] [CrossRef] [PubMed]
- Salvati, D.; Drioli, C.; Foresti, G.L. Acoustic source localization using a geometrically sampled grid SRP-PHAT algorithm with max pooling operation. IEEE Signal Process. Lett. 2022, 29, 1828–1832. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Zhao, Q.; Swami, A. A Survey of Dynamic Spectrum Access: Signal Processing and Networking Perspectives. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ‘07, Honolulu, HI, USA, 15–20 April 2007; pp. IV-1349–IV-1352. [Google Scholar] [CrossRef]
- Kwong, T.C.; Yuan, H.L.; Mung, S.W.Y.; Chu, H.K.; Lai, Y.Y.C.; Chan, C.C.H.; Choy, Y.S. Intervention technology of aural perception controllable headset for children with autism spectrum disorder. Sci. Rep. 2025, 15, 5356. [Google Scholar] [CrossRef]
- Kwong, T.C.; Yuan, H.-L.; Mung, S.W.Y.; Chu, H.K.H.; Chan, C.C.H.; Lun, D.P.K.; Yu, H.M.; Cheng, L.; Choy, Y.S. Healthcare headset with tuneable auditory characteristics control for children with Autism spectrum disorder. Appl. Acoust. 2024, 218, 109876. [Google Scholar] [CrossRef]
- Chen, H.; Huang, X.; Zou, H.; Lu, J. Research on the Robustness of Active Headrest with Virtual Microphones to Human Head Rotation. Appl. Sci. 2022, 12, 11506. [Google Scholar] [CrossRef]
- Gao, K.; Kuai, H.; Jiang, W. Localization of acoustical sources rotating in the cylindrical duct using a sparse nonuniform microphone array. J. Sound Vib. 2025, 596, 118699. [Google Scholar] [CrossRef]
- Ma, W.; Bao, H.; Zhang, C.; Liu, X. Beamforming of phased microphone array for rotating sound source localization. J. Sound Vib. 2020, 467, 115064. [Google Scholar] [CrossRef]
- Ning, F.; Zheng, W.; Hou, H.; Wang, Y. Separation of rotating and stationary sound sources based on robust principal component analysis. Chin. J. Aeronaut. 2025. In Press. [Google Scholar] [CrossRef]
- Heydari, M.; Sadat, H.; Singh, R. A Computational Study on the Aeroacoustics of a Multi-Rotor Unmanned Aerial System. Appl. Sci. 2021, 11, 9732. [Google Scholar] [CrossRef]
- Wakabayashi, Y.; Yamaoka, K.; Ono, N. Rotation-Robust Beamforming Based on Sound Field Interpolation with Regularly Circular Microphone Array. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 771–775. [Google Scholar] [CrossRef]
- Gala, D.; Lindsay, N.; Sun, L. Multi-Sound-Source Localization Using Machine Learning for Small Autonomous Unmanned Vehicles with a Self-Rotating Bi-Microphone Array. J. Intell. Robot. Syst. 2021, 103, 52. [Google Scholar] [CrossRef]
- Zhong, X.; Sun, L.; Yost, W. Active binaural localization of multiple sound sources. Robot. Auton. Syst. 2016, 85, 83–92. [Google Scholar] [CrossRef]
- Moore, A.H.; Lightburn, L.; Xue, W.; Naylor, P.A.; Brookes, M. Binaural Mask-Informed Speech Enhancement for Hearing AIDS with Head Tracking. In Proceedings of the 2018 16th International Workshop on Acoustic Signal Enhancement (IWAENC), Tokyo, Japan, 17–20 September 2018; pp. 461–465. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, W.; Su, H.; Guo, Y.; Li, D. Multiple Sound Source Localization Exploiting Robot Motion and Approaching Control. IEEE Trans. Instrum. Meas. 2023, 72, 7505316. [Google Scholar] [CrossRef]
- An, I.; Son, M.; Manocha, D.; Yoon, S.-E. Reflection-Aware Sound Source Localization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 66–73. [Google Scholar] [CrossRef]
- Sesyuk, A.; Ioannou, S.; Raspopoulos, M. A Survey of 3D Indoor Localization Systems and Technologies. Sensors 2022, 22, 9380. [Google Scholar] [CrossRef]
- Mandal, A.; Lopes, C.V.; Givargis, T.; Haghighat, A.; Jurdak, R.; Baldi, P. Beep: 3D indoor positioning using audible sound. In Proceedings of the Second IEEE Consumer Communications and Networking Conference, 2005, CCNC, Las Vegas, NV, USA, 6 January 2005; pp. 348–353. [Google Scholar] [CrossRef]
- Potamianos, G.; Neti, C.; Luettin, J.; Matthews, I. Audio-visual automatic speech recognition: An overview. Issues Vis. Audio-Vis. Speech Process. 2004, 22, 23. [Google Scholar]
- Afouras, T.; Chung, J.S.; Senior, A.; Vinyals, O.; Zisserman, A. Deep Audio-Visual Speech Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 8717–8727. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.A.; Jing, X.; Eldaly, A.B.M.; Choy, Y. 3-DOF X-structured piezoelectric harvesters for multidirectional low-frequency vibration energy harvesting. Mech. Syst. Signal Process. 2023, 200, 110616. [Google Scholar] [CrossRef]
- Huang, L.; Choy, Y.S.; So, R.M.C.; Chong, T.L. Experimental studies on sound propagation in a flexible duct. J. Acoust. Soc. Am. 2000, 108, 624–631. [Google Scholar] [CrossRef]
- Kumar, L.; Hegde, R.M. Near-Field Acoustic Source Localization and Beamforming in Spherical Harmonics Domain. IEEE Trans. Signal Process. 2016, 64, 3351–3361. [Google Scholar] [CrossRef]
- Shu, T.; He, J.; Dakulagi, V. 3-D Near-Field Source Localization Using a Spatially Spread Acoustic Vector Sensor. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 180–188. [Google Scholar] [CrossRef]
- Yang, B.; Liu, H.; Pang, C.; Li, X. Multiple Sound Source Counting and Localization Based on TF-Wise Spatial Spectrum Clustering. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 1241–1255. [Google Scholar] [CrossRef]
- Behar, V.; Kabakchiev, H.; Garvanov, I. Sound source localization in a security system using a microphone array. In Proceedings of the Second International Conference on Telecommunications and Remote Sensing—Volume 1: ICTRS, Virtual, 5–6 October 2020; pp. 85–94, ISBN 978-989-8565-57-0. [Google Scholar] [CrossRef]
- Sun, X.; Feng, J.; Zhong, L.; Lu, H.; Han, W.; Zhang, F.; Akimoto, R.; Zeng, H. Silicon nitride based polarization-independent 4 × 4 optical matrix switch. Opt. Laser Technol. 2019, 119, 105641. [Google Scholar] [CrossRef]
- Panayotov, V.; Chen, G.; Povey, D.; Khudanpur, S. LibriSpeech: An ASR corpus based on public domain audio books. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 5206–5210. [Google Scholar] [CrossRef]
- Rashid, J.; Teh, Y.W.; Memon, N.A.; Mujtaba, G.; Zareei, M.; Ishtiaq, U.; Akhtar, M.Z.; Ali, I. Text-Independent Speaker Identification Through Feature Fusion and Deep Neural Network. IEEE Access 2020, 8, 32187–32202. [Google Scholar] [CrossRef]
- Saleem, N.; Gunawan, T.S.; Kartiwi, M.; Nugroho, B.S.; Wijayanto, I. NSE-CATNet: Deep Neural Speech Enhancement Using Convolutional Attention Transformer Network. IEEE Access 2023, 11, 66979–66994. [Google Scholar] [CrossRef]
- Saleem, N.; Gunawan, T.S.; Shafi, M.; Bourouis, S.; Trigui, A. Multi-Attention Bottleneck for Gated Convolutional Encoder-Decoder-Based Speech Enhancement. IEEE Access 2023, 11, 114172–114186. [Google Scholar] [CrossRef]
- Hong, Q.-B.; Wu, C.-H.; Wang, H.-M. Decomposition and Reorganization of Phonetic Information for Speaker Embedding Learning. IEEE/ACM Trans. Audio Speech Lang. Process. 2023, 31, 1745–1757. [Google Scholar] [CrossRef]



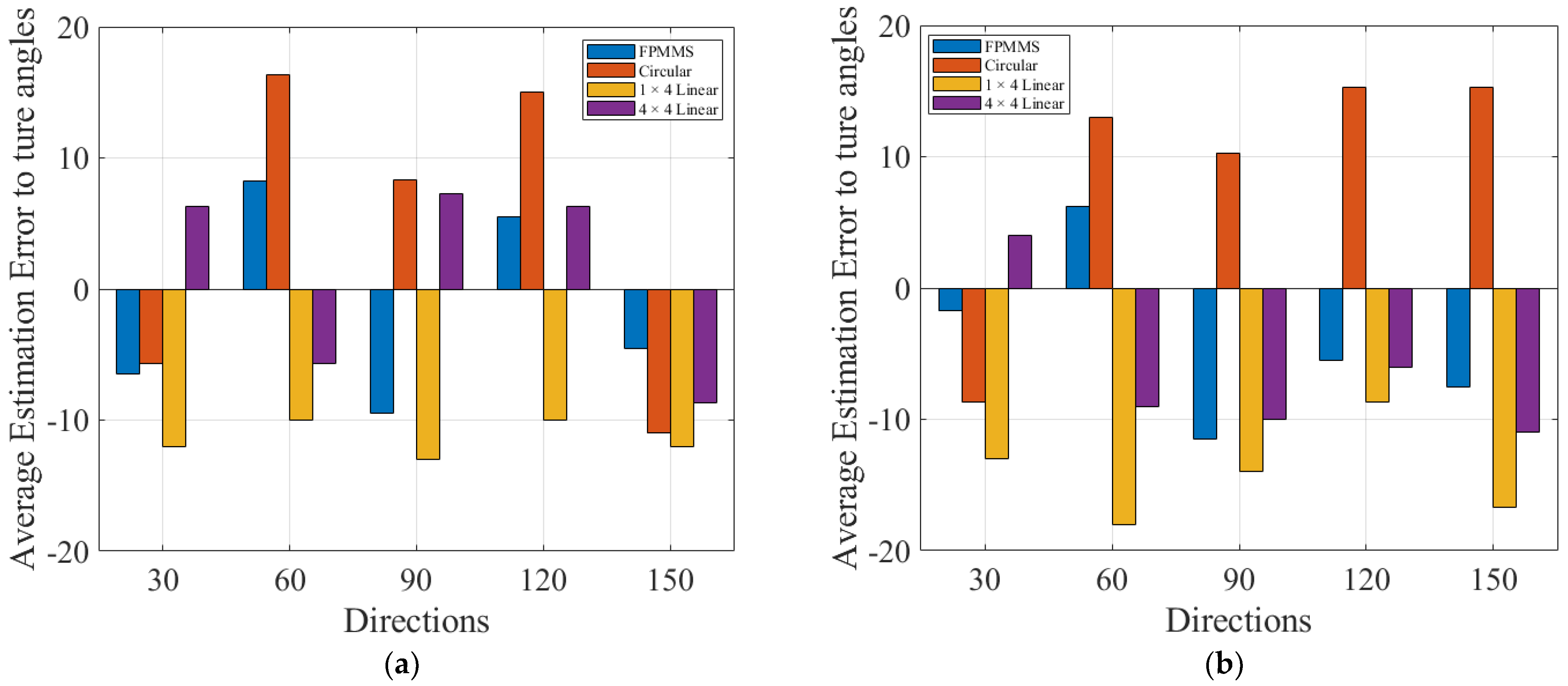
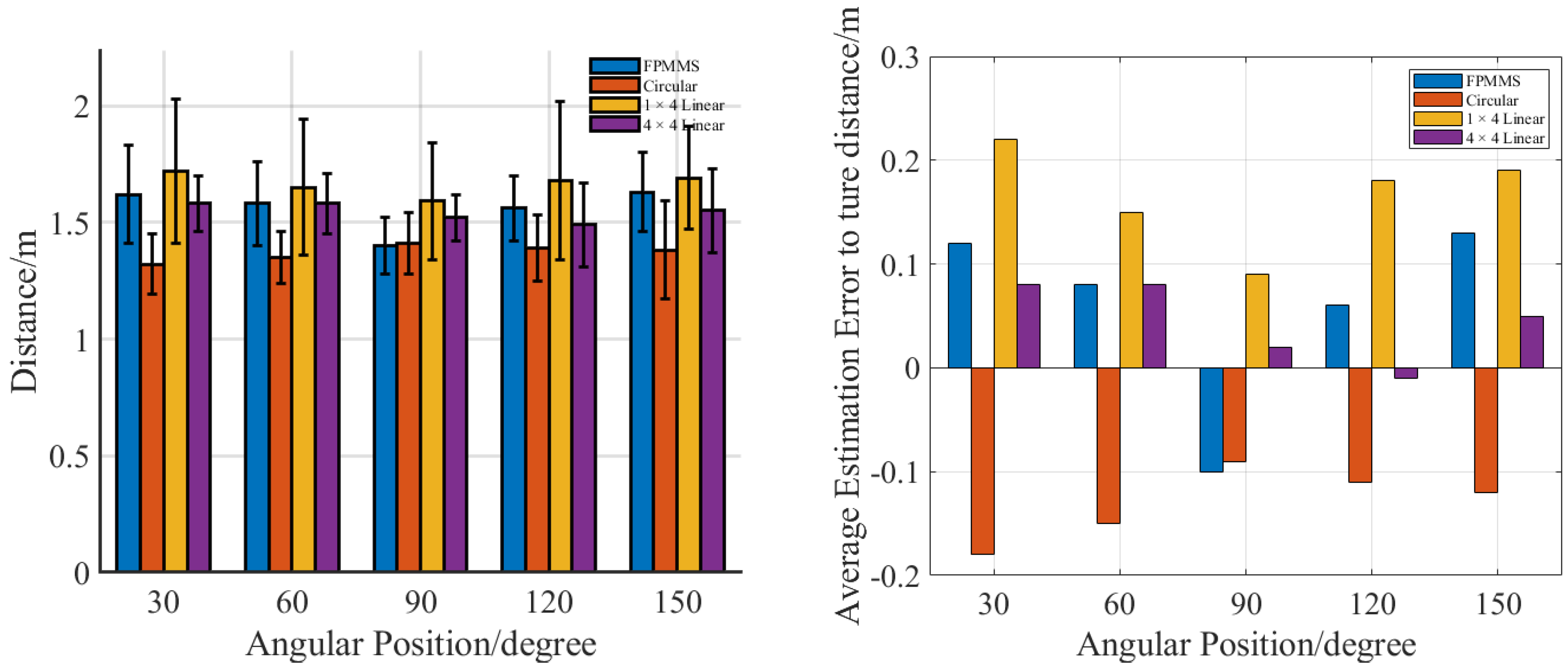
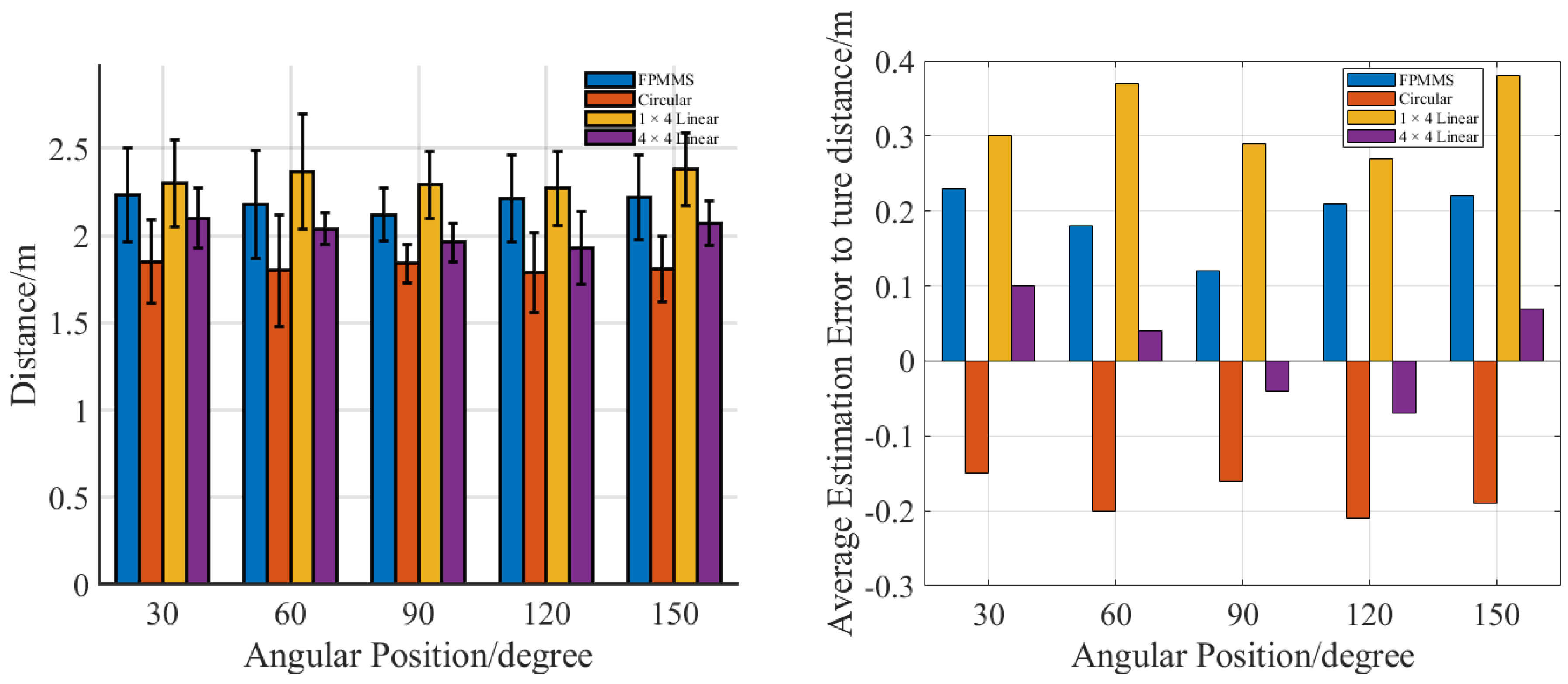
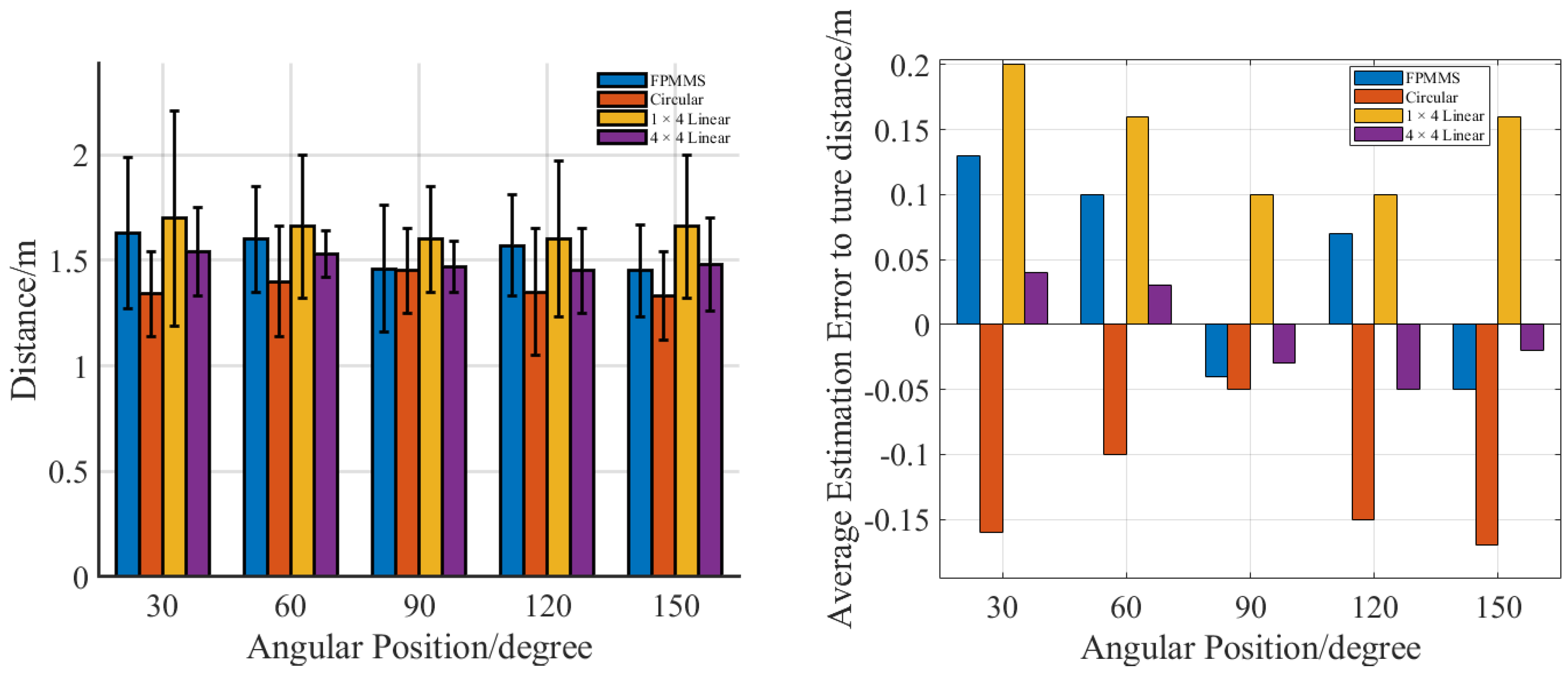
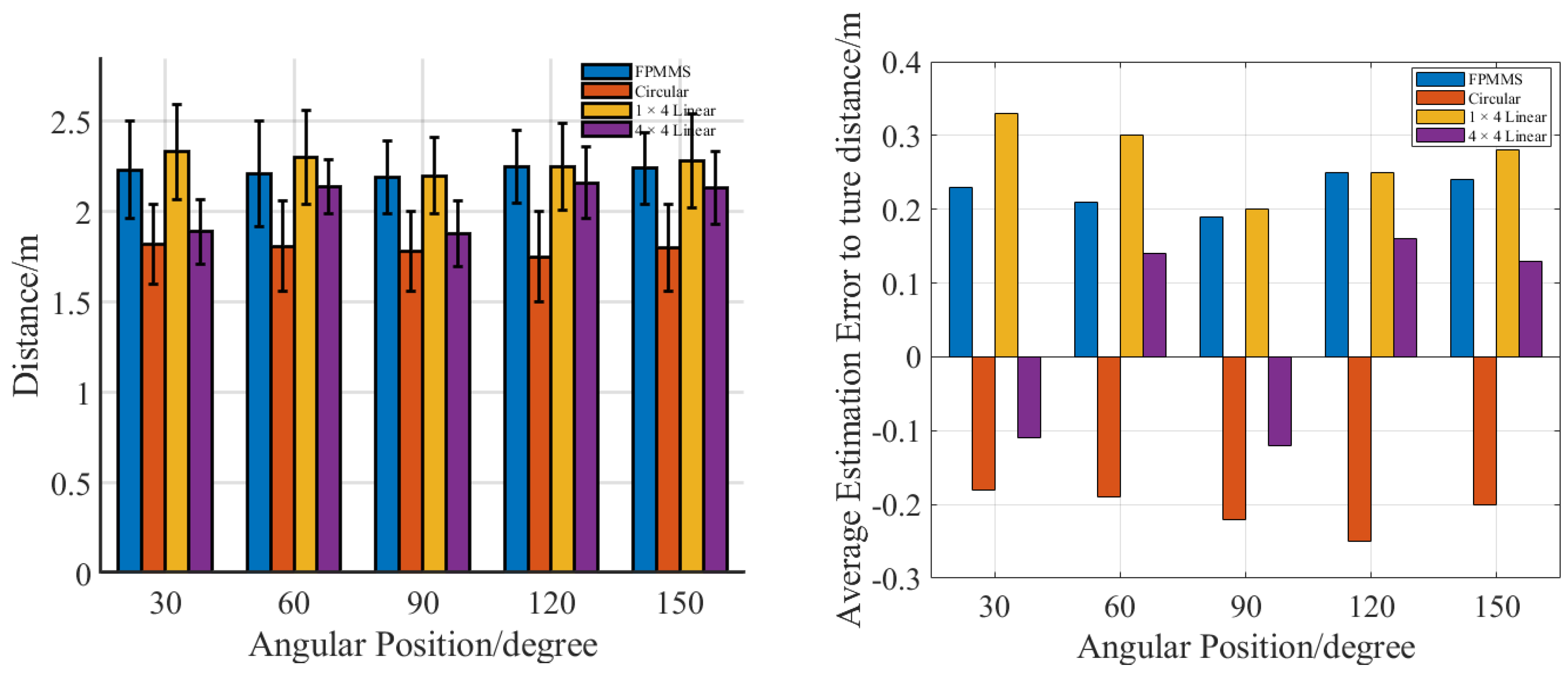
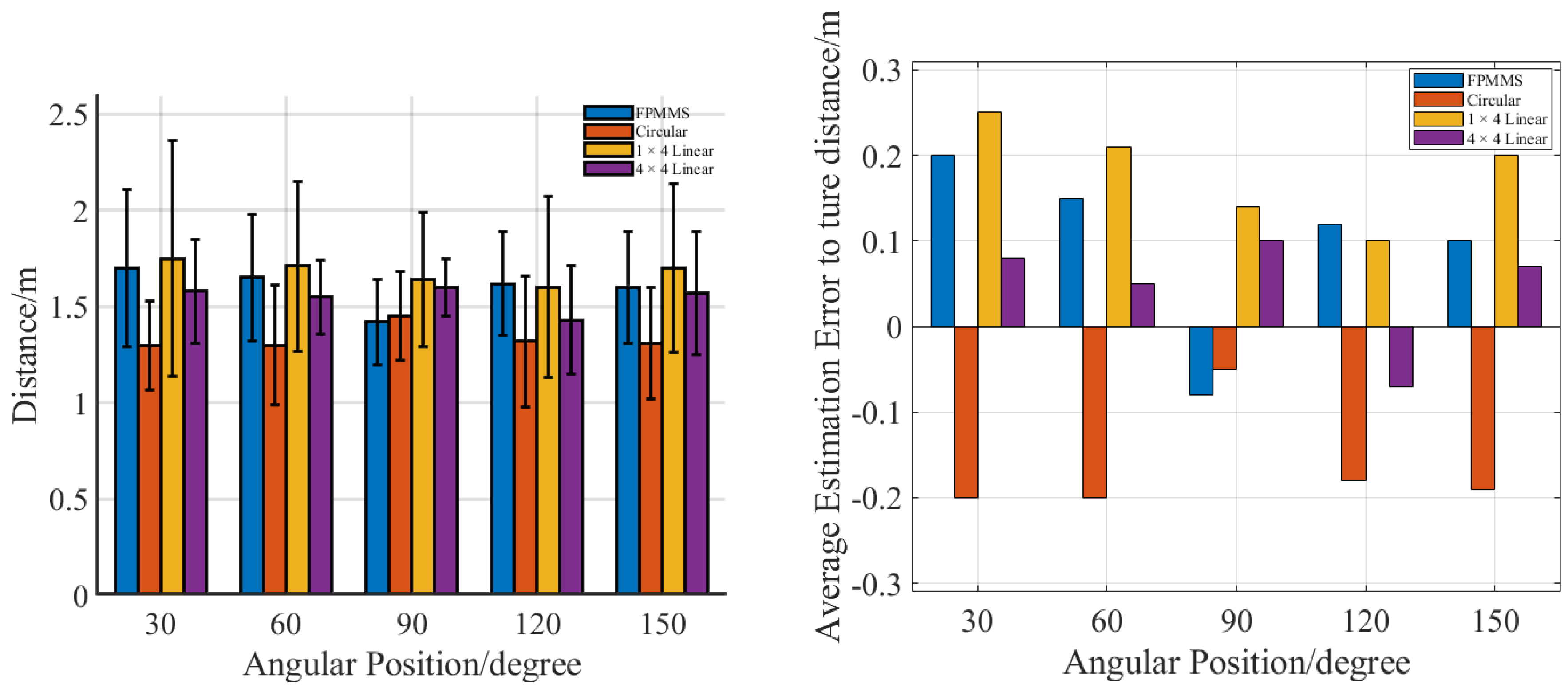
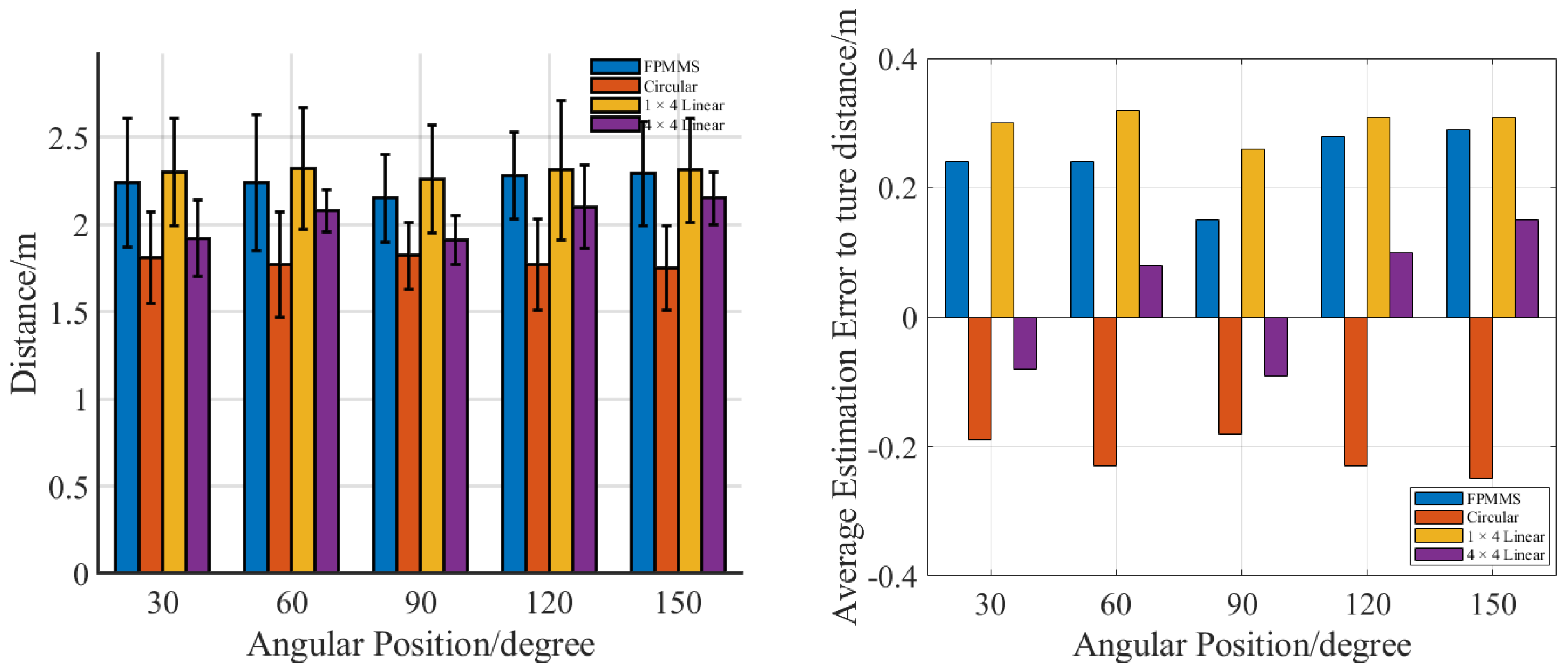


| Target Number = 3 | TF-WISE | MUSIC | SRP-PHAT |
|---|---|---|---|
| FPMMS | 98% | 95% | 93% |
| Circular Array | 100% | 100% | 100% |
| 1 × 4 Microphone Array | 90% | 86% | 88% |
| Target Number = 4 | TF-WISE | MUSIC | SRP-PHAT |
|---|---|---|---|
| FPMMS | 86% | 78% | 80% |
| Circular Array | 98% | 95% | 94% |
| 1 × 4 Microphone Array | 78% | 68% | 72% |
| Target Number = 5 | TF-WISE | MUSIC | SRP-PHAT |
|---|---|---|---|
| FPMMS | 75% | 70% | 71% |
| Circular Array | 85% | 80% | 78% |
| 1 × 4 Microphone Array | 64% | 63% | 62% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chu, K.; Choy, Y. A Planer Moving Microphone Array for Sound Source Localization. Appl. Sci. 2025, 15, 6777. https://doi.org/10.3390/app15126777
Wang C, Chu K, Choy Y. A Planer Moving Microphone Array for Sound Source Localization. Applied Sciences. 2025; 15(12):6777. https://doi.org/10.3390/app15126777
Chicago/Turabian StyleWang, Chuyang, Karhang Chu, and Yatsze Choy. 2025. "A Planer Moving Microphone Array for Sound Source Localization" Applied Sciences 15, no. 12: 6777. https://doi.org/10.3390/app15126777
APA StyleWang, C., Chu, K., & Choy, Y. (2025). A Planer Moving Microphone Array for Sound Source Localization. Applied Sciences, 15(12), 6777. https://doi.org/10.3390/app15126777







