A Combined Method for Localizing Two Overlapping Acoustic Sources Based on Deep Learning

Abstract

Deep learning approaches for multi-source sound localization face significant challenges, particularly the need for extensive training datasets encompassing diverse spatial configurations to achieve robust generalization. This requirement leads to substantial computational demands, which are further exacerbated when localizing overlapping sources in complex acoustic environments with reverberation and noise. In this paper, a new methodology is proposed for simultaneous localization of two overlapping sound sources in the time–frequency domain in a closed, reverberant environment with a spatial resolution of ${10}^{°}$ using a small-sized microphone array. The proposed methodology is based on the integration of the sound source separation method with a single-source sound localization model. A hybrid model was proposed to separate the sound source signals received by each microphone in the array. The model was built using a bidirectional long short-term memory (BLSTM) network and trained on a dataset using the ideal binary mask (IBM) as the training target. The modeling results show that the proposed localization methodology is efficient in determining the directions for two overlapping sources simultaneously, with an average localization accuracy of 86.1% for the test dataset containing short-term signals of 500 ms duration with different signal-to-signal ratio values.

1. Introduction

The problem of sound source localization (SSL) involves estimating the direction from which acoustic waves originating from a sound source are received (direction of arrival, DOA). This is typically achieved using a microphone array, which captures acoustic signals. The spatio-temporal information derived from the array is then analyzed to determine the direction of the sound source.

SSL plays a critical role in various engineering and technological applications, including hands-free communication [1], automatic camera tracking for teleconferencing [2], human–robot interaction [3], and remote speech recognition [4]. Knowledge of a sound source’s location enables enhancement of the desired signal by suppressing interfering signals from other directions. In most practical scenarios, the direction of the sound source is unknown and must be estimated. This task is particularly challenging in environments with noise and reverberation. The complexity increases further when multiple active sound sources must be localized simultaneously.

The problem of SSL is currently addressed using two main approaches: traditional signal processing methods and deep learning (DL)-based methods. Traditional methods—including multiple signal classification (MUSIC) [5], time difference of arrival (TDOA) [6], delay-and-sum beamformer (DAS) [7], generalized cross-correlation–phase transform (GCC–PHAT) [8], and steered response power–phase transform (SRP–PHAT) [9]—are typically developed under the free-field propagation assumption. Consequently, their performance significantly deteriorates in enclosed acoustic environments characterized by reverberation and noise [10].

DL-based SSL methods offer a key advantage by incorporating acoustic signal characteristics into the training process. This allows them to adapt to diverse and complex acoustic environments, often achieving greater robustness against noise and reverberation than traditional methods [10].

Much of the current research in DL-based SSL focuses on localizing multiple sound sources by framing the problem as a multi-class classification task. Deep neural networks (DNNs) have been designed using novel architectures, combinations of serial and parallel configurations, hyperparameter tuning, and varied input feature sets [11,12,13].

For example, in [14] a convolutional neural network (CNN) was employed to detect and localize multiple speakers. However, the model’s generalization capability is limited due to training data that do not encompass all possible combinations of acoustic sources. As a result, it cannot effectively localize multiple sources beyond the scenarios represented in the training set.

In [15], another CNN-based model was proposed, using multichannel short-time Fourier transform (STFT) phase spectrograms as input features to estimate the azimuth of one or two sources in a reverberant environment. While this model outperformed SRP–PHAT and MUSIC under the evaluated conditions, it assumes that the two active sources do not overlap in the time–frequency domain, a constraint that limits its applicability in real-world scenarios involving simultaneous overlapping sources.

Under challenging conditions, one proposed solution to improve model performance has been to expand the size of the training dataset [12]. This expansion aims to capture a wide range of possible scenarios, including overlapping acoustic events in time and space, varying source locations within one or more rooms, room impulse responses and dimensions, microphone array placement, varying distances between sound sources and the microphone array center, and different noise and reverberation conditions. However, increasing dataset size to cover these diverse conditions significantly raises computational costs for training.

To mitigate the issue of increased computational demands, it becomes necessary to reduce the dataset size while preserving model performance. Achieving this requires omitting some of the previously mentioned variations. From both theoretical and practical perspectives, the most impactful and manageable reduction is in the number of acoustic sources—this parameter has the greatest influence on dataset size.

In [16], a novel single-source sound localization model was introduced, offering a spatial resolution of ${10}^{°}$. The problem was formulated as a classification task over discrete source directions. The model utilized a combination of sound intensity (SI) features and GCC–PHAT features as input to a convolutional neural network (CNN). It demonstrated 100% prediction accuracy in closed, reverberant environments, outperforming the existing methods.

We propose a novel methodology for efficiently localizing two fully overlapping (100%) active sound sources in the time–frequency domain under challenging acoustic conditions. The approach addresses reverberant, noise-free environments with variable signal-to-signal ratios (SSRs) (2.1–57.4 dB) and limited training data. By integrating sound source separation with the single-source localization model introduced in [16], our method enables robust localization even with constrained training.

Table 1. Comparative analysis of multi-source sound localization methods.

Study	Approach	Strengths	Limitations	Our Advantages
Chen et al. [13]	DNN + 40-mic array	High-resolution separation and localization	Impractical for real-world setups (massive array)	Fewer mics needed (four) + BLSTM separation improves overlap handling
He et al. [14]	DNN for multi-speaker localization	Real-time, noise-robust	Fails for 100% overlapping sources	Separation-first pipeline resolves full overlap
Chakrabarty and Habets [15]	CNN–DOA (noise-trained)	Generalizable to noisy environments	Limited to partial overlap scenarios	End-to-end overlap handling via BLSTM + localization
Our Method	BLSTM separation + single-source DOA	100% overlap-compatible, computationally efficient (vs. large arrays and large dataset)	Higher latency due to separation step	Novelty: Unified separation- localization

presents a comparative analysis of multi-source sound localization methods, highlighting their respective strengths and limitations while demonstrating the improvements offered by the proposed method.

2. Materials and Methods

We assume that the problem of localizing two overlapping sound sources is solved in a closed environment (for example, in a room). It is assumed that a planar orthogonal microphone array consists of four omnidirectional microphones located in the room, as shown in Figure 1:

The microphones $M_1$ and $M_3$ are located along the x-axis orthogonal to the microphones $M_2$ and $M_4$ along the y-axis; d = $\overline{M_1{M}_3}$ = $\overline{M_2{M}_4}$ represents the size of the microphone array, and O is the center of the array. A far-field propagation model is used [17], where the directions of the two acoustic sources are represented by angles ${\theta }_1$ and ${\theta }_2$ defined with respect to the positive x-axis: that is, ${\theta }_1,{\theta }_2\in [-{180}^{°},{180}^{°})$.

Microphone signals are represented by Formulas (1) and (2) as follows:

$$x_i\left(t\right)=a_i{,}_1\left(t\right)\ast s_1\left(t\right)+a_i{,}_2\left(t\right)\ast s_2\left(t\right)+n_i\left(t\right),$$

(1)

$$x_i\left(t\right)=\sum _{\tau =0}^{T-1}{a}_i{,}_1\left(\tau \right)s_1(t-\tau )+\sum _{\tau =0}^{T-1}{a}_i{,}_2\left(\tau \right)s_2(t-\tau )+n_i\left(t\right),$$

(2)

where $x_i\left(t\right)$ denotes the signal of two overlapping sources received by microphone i, $s_1\left(t\right)$ and $s_2\left(t\right)$ are the signals of the first and second acoustic source, respectively, $a_i{,}_1\left(t\right)$ and $a_i{,}_2\left(t\right)$ are the room impulse responses (RIRs) [18] between microphone i and the first and second sources, respectively, $n_i\left(t\right)$ is background noise and possibly microphone noise, and ∗ denotes convolution. The signals are digital; therefore, t and T are discrete time indices, and T is the effective length of the RIRs.

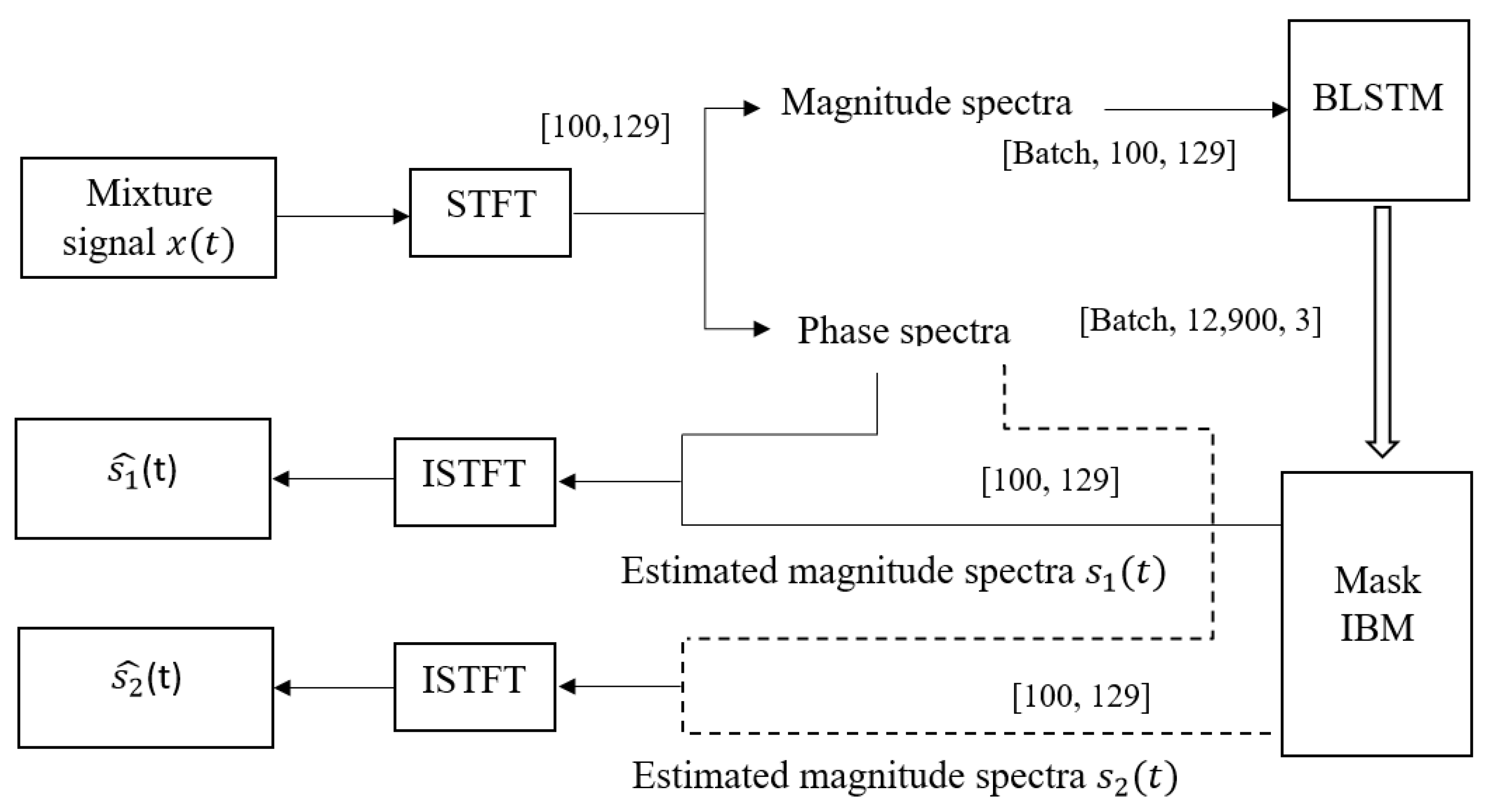
The methodology for localizing two overlapping sound sources is shown schematically in Figure 2:

Each microphone signal from the array is subjected to an acoustic source separation method implemented using an appropriate model. The output of this model is the separated signals from the sound sources. The signals of the first source obtained by the separation method are the raw input to the single SSL model, which, in turn, estimates the direction of the first source, whereas the signals of the second source obtained by the separation method are the raw input to the localization model, which, in turn, estimates the direction of the second source.

3. Sound Source Separation

3.1. General Principle of Sound Source Separation Based on Deep Learning Methods

The task of the sound source separation method is to reconstruct signals from two individual acoustic sources from the mixed signal $x\left(t\right)$ obtained using a microphone array. The proposed source separation model based on DL methods is schematically shown in Figure 3:

Recurrent neural networks (RNNs) have demonstrated superior performance in modeling time-varying functions, predicting sequential data, and solving sound source separation problems. Bidirectional long short-term memory (BLSTM), a recurrent network designed to solve the vanishing gradient problem, has shown good performance in sound source separation, acoustic echo suppression, and quality enhancement [19].

STFT is applied to the mixed microphone signal. The amplitudes of STFT are the input features for network BLSTM. In sound source separation tasks, the ideal binary mask (IBM) is one of the most widely used masks as a training target for DNNs. Using this mask, the signal spectrum of the two sources can be estimated. Using the phase of the microphone signal spectrum and the estimated amplitude of the signal spectrum of each source, the signals are reconstructed using the inverse short-time Fourier transform (ISTFT).

3.2. Signals Reconstruction

IBM is defined as [19]

$$IBM=\left\{\begin{array}{cc}1\hfill & if{\displaystyle \frac{S_1(t,f)}{S_2(t,f)}}>1\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.,$$

(3)

where $S_1(t,f)$ and $S_2(t,f)$ are the spectrograms of $s_1\left(t\right)$ and $s_2\left(t\right)$, respectively.

Using IBM, the spectrogram of the signals of both sources can be reconstructed using relations (4) and (5) [20]:

$$S_1=IBM\odot X,$$

(4)

$$S_2=(1-IBM)\odot X,$$

(5)

where the operator ⊙ represents element-wise multiplication, and where X is the spectrogram of the microphone signal, which can be expressed as follows:

$$X=S_1+S_2.$$

(6)

Based on the obtained spectrograms $S_1(t,f)$ and $S_2(t,f)$, the signals from both sources can then be reconstructed using ISTFT.

3.3. Data Preparation and Feature Extraction

To illustrate the data preparation and feature extraction process for the source separation problem, we present a specific example. The separation task was considered in a closed acoustic environment, a room with dimensions of $15\times 9\times 4$${\mathrm{m}}^3$. An orthogonal microphone array was positioned at point (7.5, 4.5, 1.5) m, with an array size of $d=0.2$ m. The acoustic sources were placed 2 m from the array center and were positioned at the same height as the array (1.5 m).

To train the source separation model, signals from each microphone were used to simulate a wide range of possible source locations within the room. A total of 6000 directions were randomly and uniformly sampled from the range $[-{180}^{°},{180}^{°})$. For data synthesis, 300 audio files—each 500 ms long and sampled at 16 kHz—were randomly selected from the training portion (4620 files) of the TIMIT database [19]. Each audio file was assigned to 20 different randomly generated directions. These audio signals were treated as sound sources and were convolved with the corresponding room impulse responses (RIRs) to produce 6000 direction-specific audio files for each of the four microphones. Next, 3000 random pairs of audio files were selected, each representing two independent sources. These paired files were mixed to simulate overlapping source signals, resulting in 3000 mixed audio files (raw data) per microphone.

The RIRs between each source and microphone were generated using the RIR Generator software https://github.com/ehabets/RIR-Generator (accessed on 5 September 2024) [21], which is based on the image source method [22]. Assuming an RIR length of 4096 samples and a reverberation time RT60 = 0.36 s (the time it takes for the sound energy to decay by 60 dB), the software automatically determines the maximum order of reflections. Small rooms are less reverberant while bigger rooms are more reverberant. To achieve this, the RT60 follows linearly the volume as stated by Sabine’s formula [23].

Feature extraction was performed by applying STFT, using a Hanning window of 256 points, corresponding to a 16 ms window length and yielding 129 frequency bins. To augment the dataset, a 25% overlap between consecutive temporal segments was introduced.

The resulting spectrograms of the microphone signals were segmented into fixed-size blocks of $100\times 129$ (time frames × frequency bins), ensuring consistent input dimensions for the neural network. Additionally, the spectrograms of the two individual sources were extracted to compute the ideal binary mask (IBM), which was used to calculate the loss function during model training. The final training dataset consisted of 23,040 samples, each with dimensions $100\times 129$.

3.4. Structure of the Proposed Source Separation Model

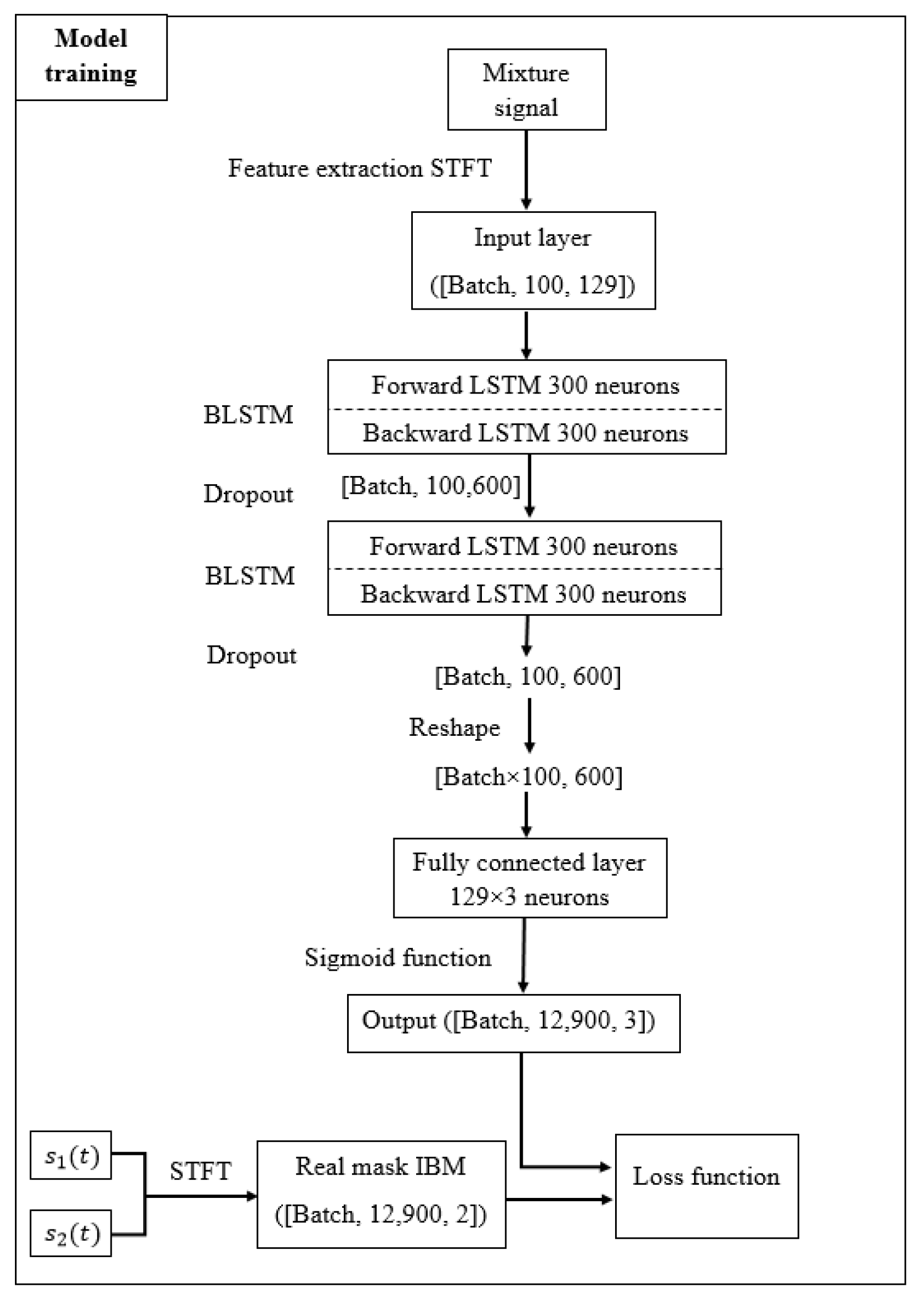
Figure 4 shows the structure of the proposed source separation model at the training stage:

The STFT features with dimension [Batch, 100, 129] represent the input layer that was fed into the BLSTM network. The BLSTM network had two layers; each layer contained two LSTM recurrent networks with 300 neurons, one of which processed the signal in the forward direction and the other in the backward direction. After each BLSTM layer, the dropout regularization procedure was used to avoid overfitting [24]. The output layer was a fully connected layer (FC) with 129 × 3 neurons and a size–weight matrix [600, 129 × 3]. The activation function of the output layer was a sigmoid function, which, in turn, produced output samples with values ranging from 0 to 1. After the fully connected layer, the normalization $L_2$ was used for regularization [25].

The final output samples could be represented as a matrix $V\in {\Re }^{12900\times 3}$, which allowed deep clustering to be applied to them later at the testing stage. The Adam learning algorithm was chosen to train the model with an initial learning rate of 0.01. The model was trained to minimize the difference between the estimated affinity matrix $V{V}^T$ and the target affinity matrix $Y{Y}^T$, where $V\in {\Re }^{12900\times 2}$ represented the true IBM. The loss function was calculated using the following formulas:

$$\pounds ={∥\begin{array}{c}V{V}^T-Y{Y}^T\end{array}∥}_F,$$

(7)

$$\pounds ={∥\begin{array}{c}{V}^{T}V\end{array}∥}_F^2-2{∥\begin{array}{c}{V}^{T}Y\end{array}∥}_F^2+{∥\begin{array}{c}{Y}^{T}Y\end{array}∥}_F^2,$$

(8)

where F denotes the Frobenius norm of the matrix.

The number of training epochs was chosen to be 50 and the batch size to be 64 samples. Figure 5 shows the model testing scheme.

During testing, the model processes extracted features from microphone signals (test data) to generate an output matrix of size (12,900, 3), where each row represented a point in 3D space. These points were clustered into two classes using the K-Means algorithm, producing binary labels (0/1) that were subsequently reshaped into the estimated IBM.

4. Results and Discussion

Following training of the proposed source separation model, we integrated it with the single-source localization model developed in [16] (which achieves ${10}^{°}$ spatial resolution). In order to evaluate the effectiveness of the two-source localization model, the prediction accuracy (localization accuracy) metric was used as a performance measure, which is defined as follows [16]:

$$PA={\displaystyle \frac{N_p}{N_s}}\times 100(\%),$$

(9)

where $N_s$ represents the total number of source directions being evaluated and $N_p$ is the number of source directions correctly recognized. The direction of the source is considered to be correctly recognized if the predicted direction is within the spatial resolution of the model: that is, the deviation of the predicted direction from the actual direction is within $\mp {\theta }_0$ for the spatial resolution ${\theta }_0$ [26].

The total number of candidate source directions was $K=36$, which were uniformly distributed in the range $[-{180}^{°},{180}^{°})$ with a step of ${10}^{°}$.

To synthesize the test data, 36 audio files with a duration of 500 ms and a sampling frequency of 16 kHz were randomly selected from the TIMIT test set without repetition, each audio file corresponding to one of the 36 directions. The audio files associated with the directions represented the acoustic sources, which were convolved with the corresponding RIRs to form a set of 36 samples (each sample contained a signal corresponding to each of the four microphones). This set was randomly divided into pairs; then, the signals corresponding to each microphone were mixed to form a single sample containing the mixed signals of the four microphones.

Thus, the final size of the raw test data set (mixed signals) was 18 samples, which was equal to the number of pairs in the original samples. Each of these mixed signals in each sample represented the raw input to the source separation model. The separated signals representing the first source were raw input to a single SSL model, as were the separated signals representing the second source, which were also raw input to a similar model.

The generalization ability of the model is validated by forming the test samples in such a way that all possible directions of the sound source within the range $[-{180}^{°},{180}^{°})$ are covered, where each direction corresponded to a different sound source signal, and the mixed signals had variable SSR.

The data preprocessing pipeline, including raw data preparation and feature extraction, was implemented in MATLAB R2020a. The machine learning model was subsequently developed using Python 3.* within the Google Colab cloud computing environment. This hybrid implementation approach leveraged MATLAB’s robust signal processing capabilities for feature engineering while utilizing Python’s extensive deep learning ecosystem for model development.

Table 2. Values of metric PA for each test sample containing source signals with different SSR values.

Sample No.	${\mathit{\theta }}_1$	$\widehat{{\mathit{\theta }}_1}$	${\mathit{\theta }}_2$	$\widehat{{\mathit{\theta }}_2}$	SSR (dB)	PA (%)
1	100	100	80	80	16.9	100
2	250	250	90	250	17.8	50
3	240	230	320	320	9.4	100
4	0	0	230	230	10.6	100
5	30	30	160	160	19.2	100
6	280	280	270	280	57.4	100
7	110	140	220	220	6.9	50
8	40	40	60	60	3.4	100
9	180	180	190	190	15.4	100
10	150	150	120	120	15	100
11	260	130	130	130	2.1	50
12	20	20	10	10	13	100
13	210	210	350	210	49.2	50
14	300	300	70	70	9.9	100
15	200	200	140	200	9.8	50
16	340	340	310	310	2.7	100
17	170	170	50	50	10.3	100
18	330	330	290	290	7.4	100

shows the true values (${\theta }_1$ and ${\theta }_2$) and predicted values ($\widehat{{\theta }_1}$ and $\widehat{{\theta }_2}$) of the directions of each of the two sources, the SSR, and the values of the prediction accuracy metric (PA) for each of the test samples.

The SSR was calculated using the following formula:

$$SSR=10lo{g}_{10}\left({\displaystyle \frac{E\left[s_1^2\left(t\right)\right]}{E\left[s_2^2\left(t\right)\right]}}\right),$$

(10)

where E is the average value.

The prediction accuracy for each test sample was considered 100% when the model correctly estimated the directions of both sound sources. If only one direction was correctly predicted while the other was incorrect, the accuracy for that sample was set at 50%.

The proposed localization methodology demonstrated high effectiveness in simultaneously estimating the directions of two overlapping sources, achieving an average localization accuracy of 86.1% on the test dataset, which included source signals with varying SSRs.

The simulation results presented in Table 2 show that for certain samples (e.g., samples 2, 11, 13, and 15), the model predicted the same direction for both sources. In these cases, the predicted direction matched that of one of the actual sources, resulting in a correct prediction for one source and an incorrect one for the other. This type of error can be attributed to the relatively small size of the microphone array, which limits the discernible differences in amplitude and time delay between signals from different sources. As a result, applying the separation model to mixed source signals can impair the model’s sensitivity to distinguishing between features associated with each individual source.

The geometry of the microphone array plays a crucial role in resolving phase differences. Different configurations influence the array’s ability to differentiate between signals arriving at various angles or with distinct phase shifts. While larger arrays and more complex geometries combined with beamforming preprocessing can lead to improved signal characterization and separation accuracy, our research was constrained by limitations in adapting large-scale microphone arrays to work in conjunction with the single-source localization model.

In [26], it was shown that the size of the array has a similar effect on all the localization methods used, including the proposed method based on using the features of SI as input data, so that the localization performance deteriorates when the array size is either too small or too large. One reason is that the SI features are based on the finite difference of the acoustic pressure signals to approximate the particle velocity using an orthogonal microphone array. As a result, as the size of the array increases, the approximation error will increase accordingly, thus leading to poor SI estimation. On the other hand, if the array size is too small, the microphone array will exhibit poor noise sensitivity, especially at low frequencies [27]. It was also shown that the optimal range of array sizes for the proposed method is 2–5.5 cm. The GCC–PHAT–CNN approach, which utilizes GCC–PHAT features as input, showed significantly worse performance than comparable methods when using small arrays, but outperformed them with larger array sizes (approximately 40 cm). To maintain consistency with our method’s requirements while ensuring good localization accuracy, we selected an intermediate array size of 20 cm for the final implementation.

The features were extracted using STFT, which divides the audio signal into fixed-length time windows, treating each segment as a time-invariant signal. Due to its computational efficiency and straightforward implementation, STFT is widely adopted in audio signal processing. However, a key limitation is its fixed window size, which cannot optimally resolve all frequency components simultaneously. In contrast, the wavelet transform addresses this issue by employing variable time scales—inversely proportional to frequency—to better analyze different spectral components. While this adaptability improves frequency resolution, it comes at the cost of higher computational complexity. The integration of wavelet transform-based feature extraction with time-frequency masking targets (e.g., ideal ratio mask (IRM)) could improve the performance of the proposed approach.

The source separation model was trained on 500 ms short-term signals to align with the raw audio length used in the single SSL model. In real-time scenarios where sources may move within the room, applying the localization model to short audio segments ensures timely updates to source directions, maintaining accuracy as positions change.

5. Conclusions

This paper presents a novel approach for simultaneous localization of two overlapping sound sources with a spatial resolution of ${10}^{°}$ in a reverberant environment using a small-sized orthogonal microphone array. The proposed methodology is based on the integration of the sound source separation method with the single SSL model.

A hybrid model was proposed to separate the sound source signals received by each microphone in the array. The model was built using a BLSTM network and trained on a dataset using the IBM as the training target. The raw data was first generated from the TIMIT training set, and then the features were extracted by applying STFT. The K-Means algorithm was applied to the output samples of the trained model; then, the IBM mask was estimated and the source signals were reconstructed.

The proposed methodology for simultaneous localization of two overlapping sound sources represents a significant advancement in multi-source localization. By enabling the separation of concurrent sound sources, this work extends the scope of existing approaches and lays the foundation for future research in this direction.