A New Look at the Stress State Across the Bohai Strait, China
Abstract
1. Introduction
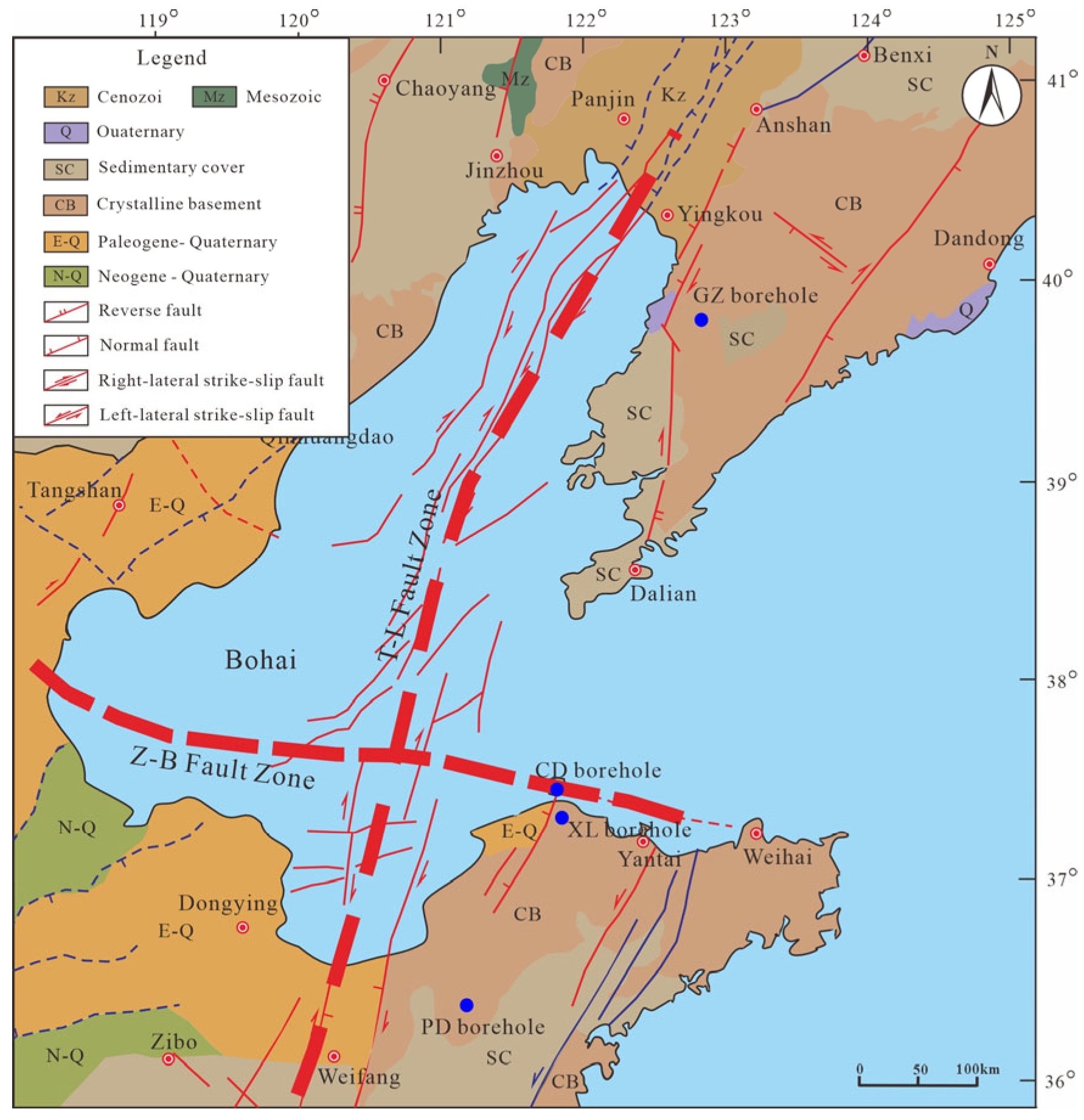
2. Geological Setting
3. Materials and Methods
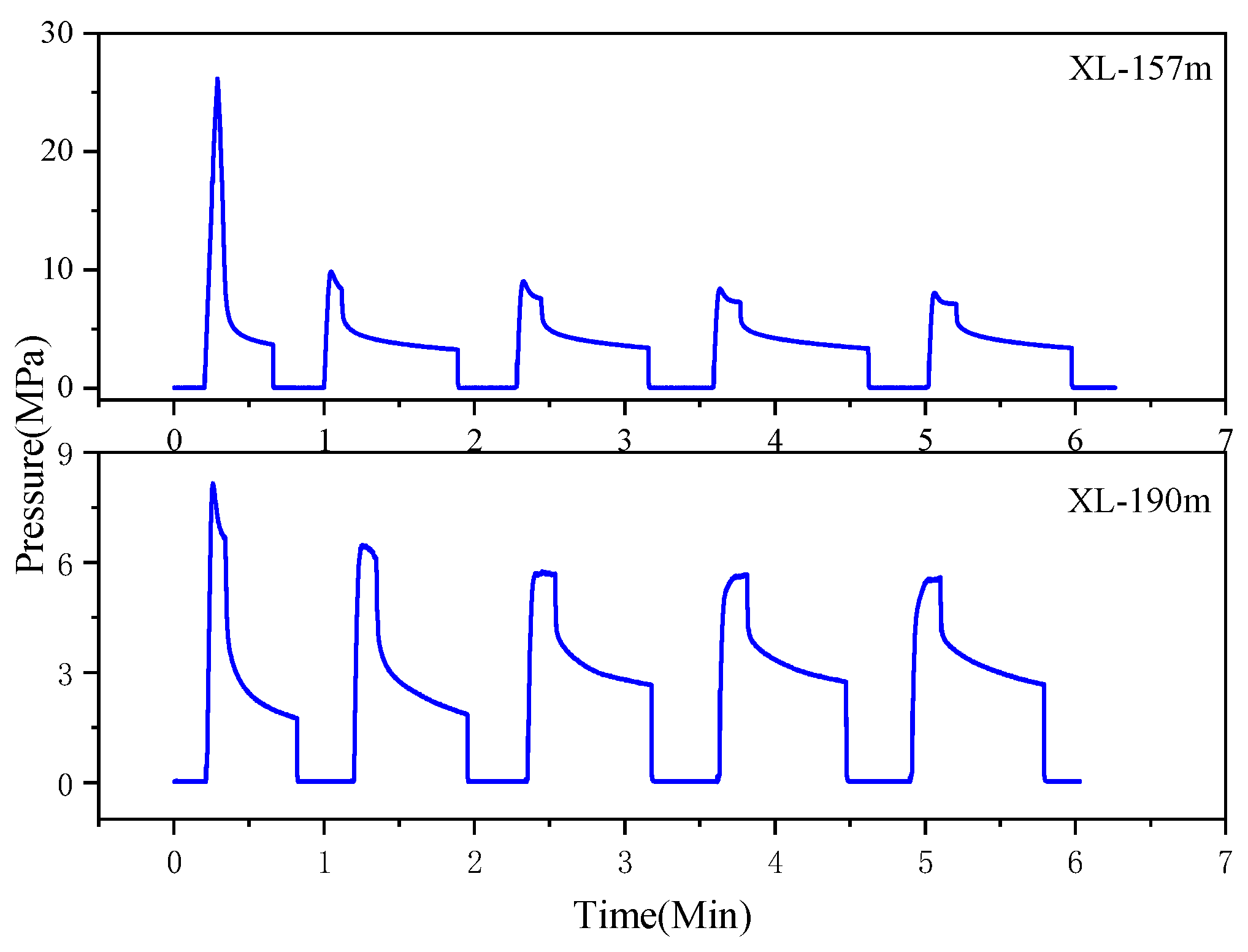
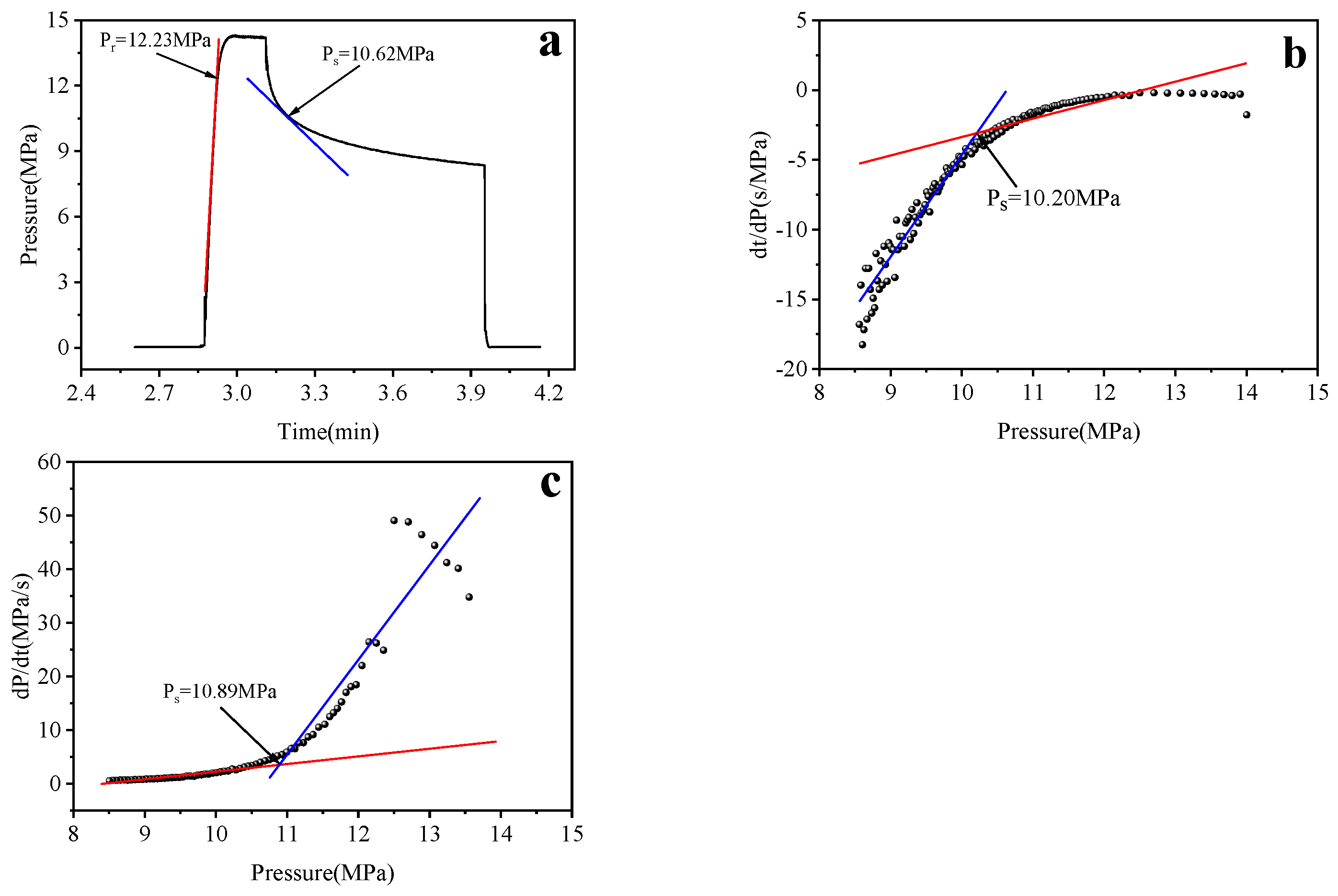
3.1. Hydraulic Fracturing
3.2. HF Measurements in Xiangli and Changdao
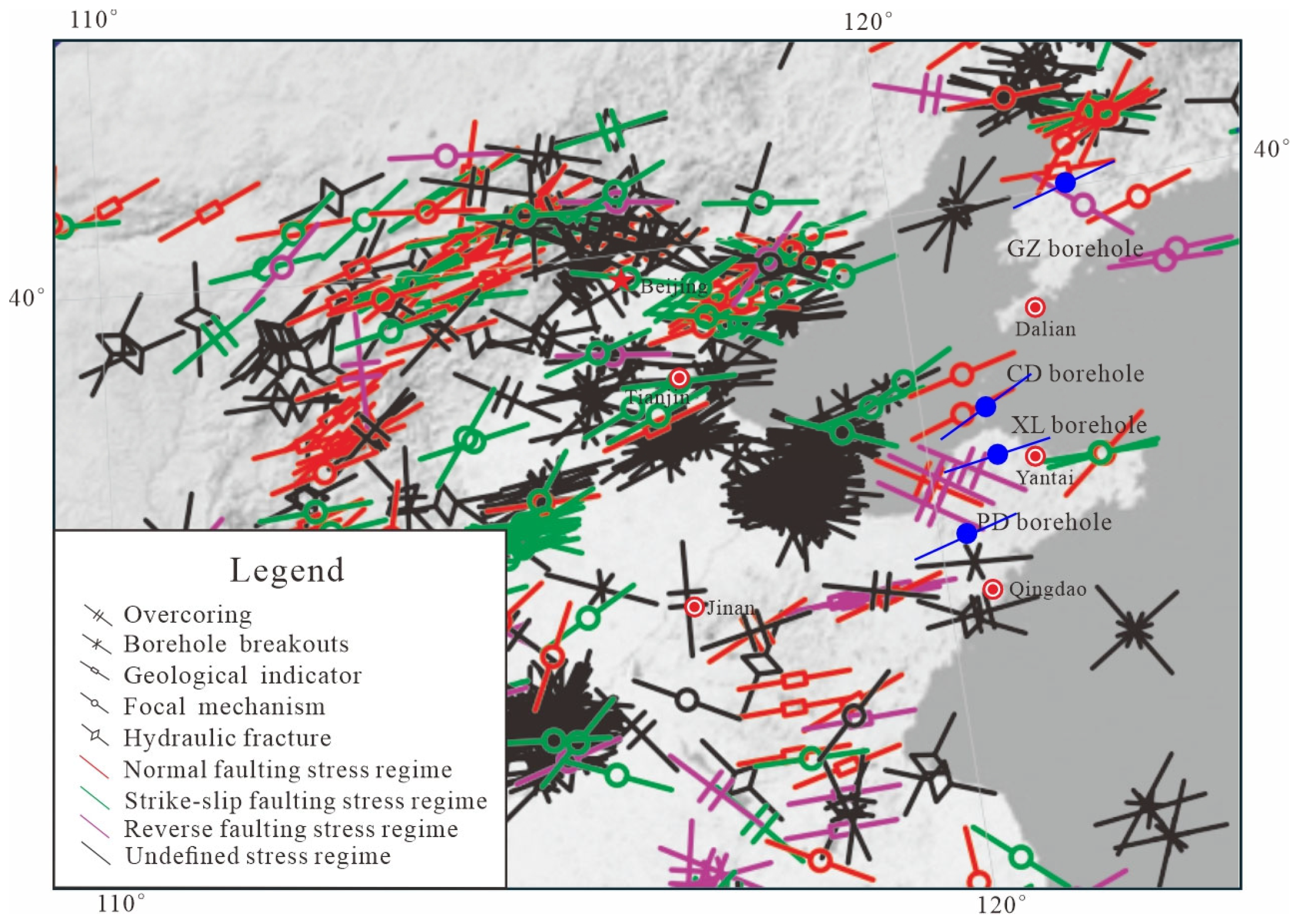
3.3. In-Situ Stress Data Compilation
4. Results
4.1. Stress Magnitudes
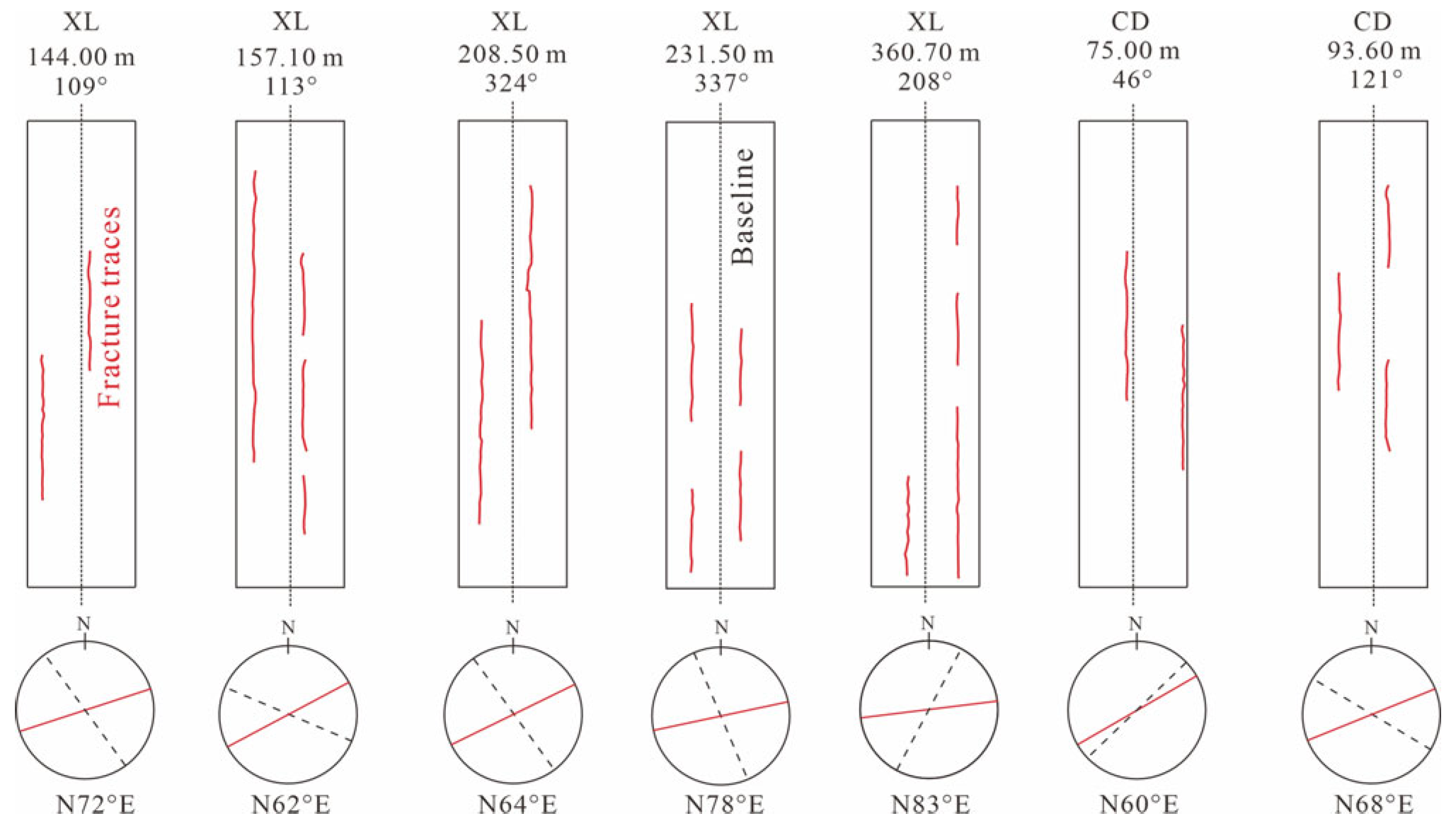
4.2. Stress Orientations
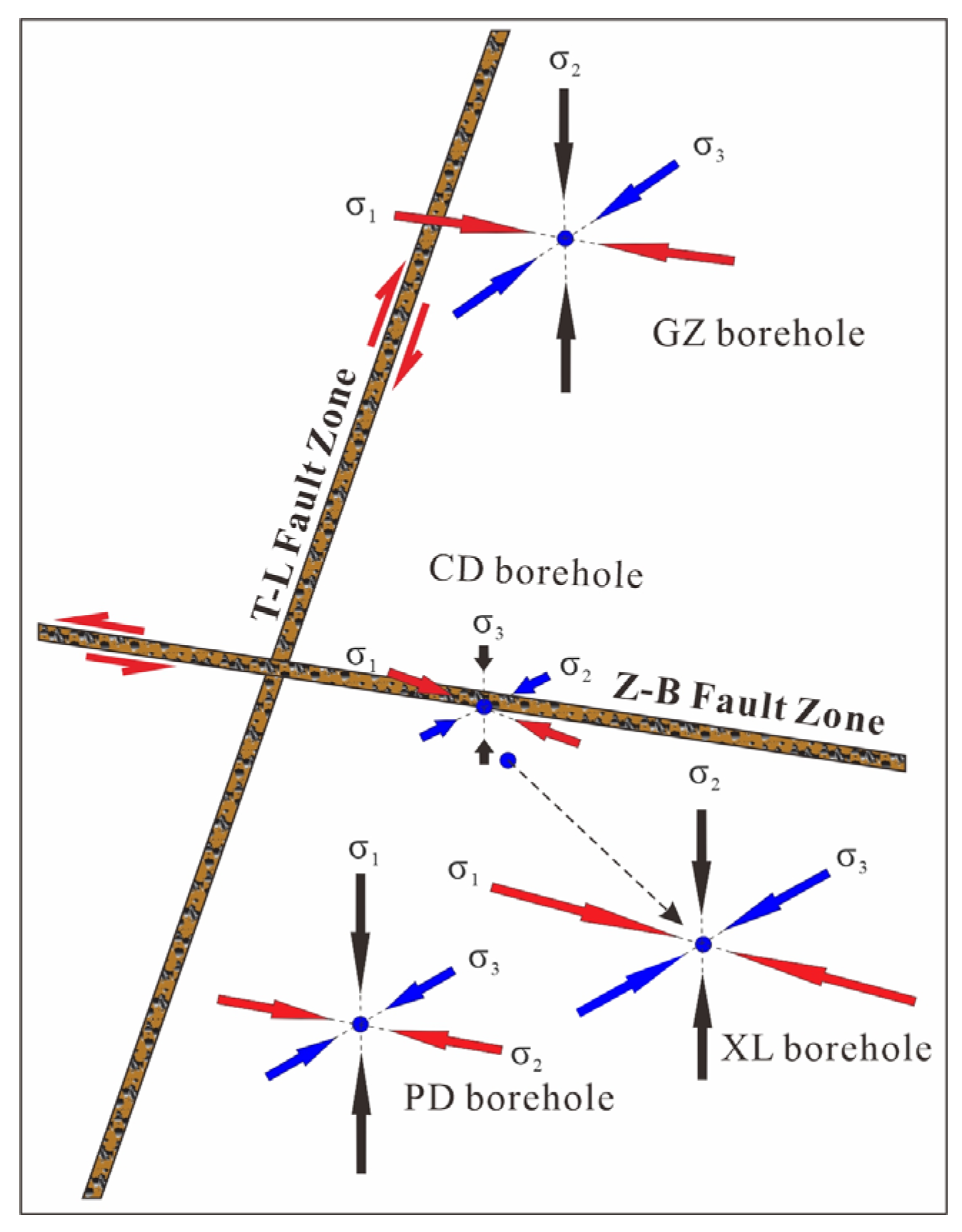
4.3. Stress Regimes
5. Discussion
5.1. Relationship Between the Stress State and Tectonic Feature
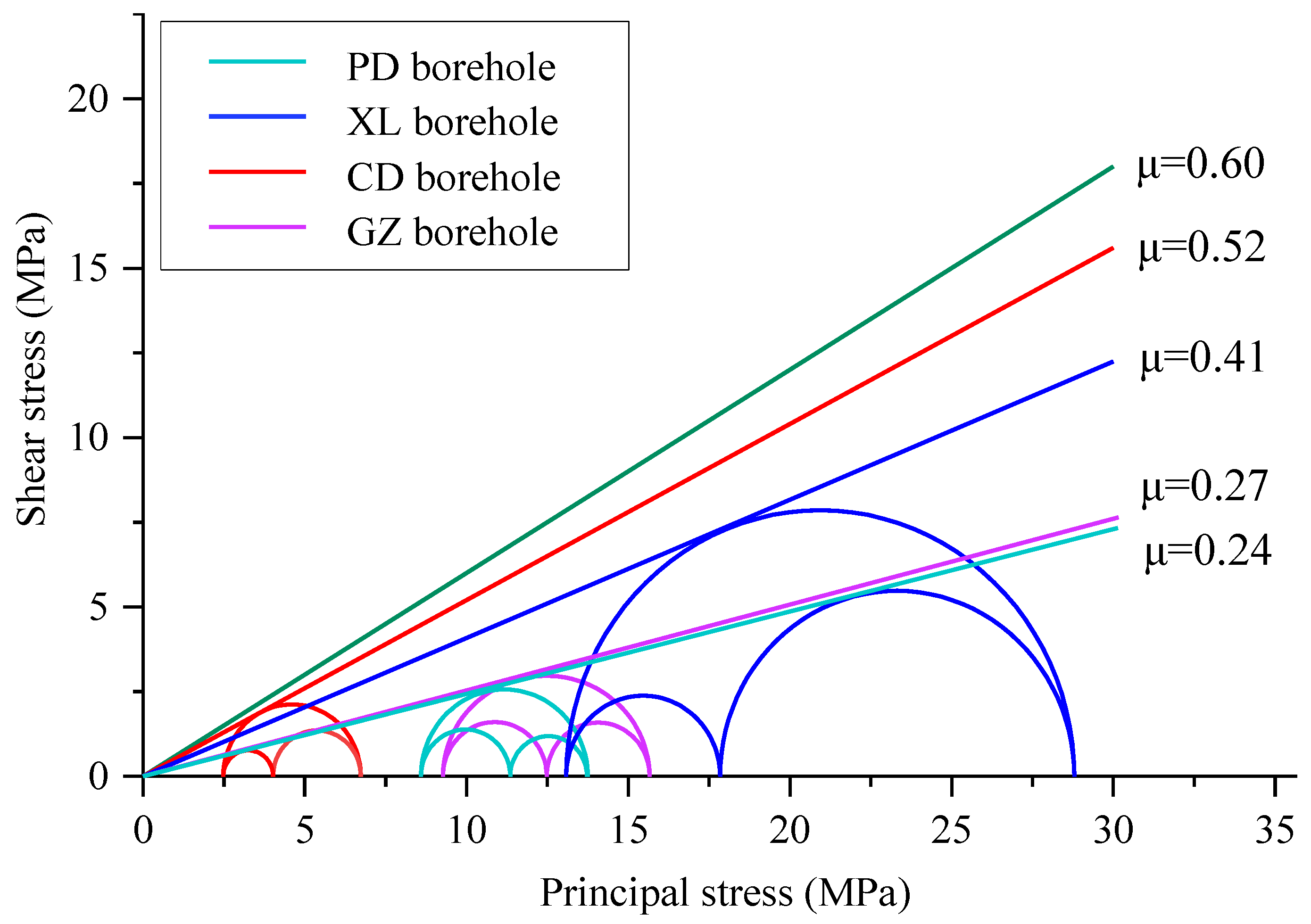
5.2. Implications for Fault Reactivation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Townend, J.; Zoback, M.D. How Faulting Keeps the Crust Strong. Geology 2000, 28, 399–402. [Google Scholar] [CrossRef]
- Heidbach, O.; Rajabi, M.; Cui, X.F.; Ziegler, M.O.; Reiter, K. The World Stress Map Database Release 2016: Crustal Stress Pattern Across Scales. Tectonophysics 2018, 744, 484–498. [Google Scholar] [CrossRef]
- Zang, A.; Stephansson, O. Stress Field of the Earth’s Crust; Springer: Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Hoek, E. Practical Rock Engineering; Rocscience: Toronto, ON, Canada, 2007; Available online: https://www.rocscience.com (accessed on 15 April 2025).
- Wang, J. On area-specific underground research laboratory for geological disposal of high-level radioactive waste in China. J. Rock Mech. Geotech. Eng. 2014, 6, 99–104. [Google Scholar] [CrossRef]
- Tobin, H.J.; Saffer, D.M.; Castillo, D.A.; Hirose, T. Direct Constraints on In Situ Stress State from Deep Drilling into the Nankai Subduction Zone, Japan. Geology 2022, 50, 1229–1233. [Google Scholar] [CrossRef]
- Zoback, M.D. Reservoir Geomechanics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Zhang, C.Y.; Xu, J.D.; Wang, H.J.; Li, X. Evaluating In-Situ Stress State and Stress Heterogeneity by Hydraulic Fracturing and Image Logging in Changcun Coalbed Methane Area, North China. Rock Mech. Rock Eng. 2025, 58, 1723–1738. [Google Scholar] [CrossRef]
- Shang, Y.J.; Park, H.D.; Shi, Y.Y.; Yuan, G.X.; Sun, Y.C. Some large values of in-situ stress and related engineering geological problems in China. Geosci. J. 2010, 14, 135–153. [Google Scholar] [CrossRef]
- Tapponnier, P.; Xu, Z.; Roger, F.; Meyer, B.; Arnaud, N. Oblique stepwise rise and growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef]
- Clair, J.S.; Moon, S.; Holbrook, W.S.; Perron, J.T.; Riebe, C.S.; Martel, S.J.; Carr, B.; Harman, C.; Singha, K.; Richter, D.B. Geophysical imaging reveals topographic stress control of bedrock weathering. Science 2015, 350, 534–538. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Guo, Q.; Cai, M. Contemporary stress field in and around a gold mine area adjacent to the Bohai Sea, China, and its seismological implications. Bull. Eng. Geol. Environ. 2022, 81, 86. [Google Scholar] [CrossRef]
- Sai, M.; Chu, H.X.; Dong, L.Y.; Fang, Z.H.; Li, P.F.; Zhang, F.F. Influencing factors and evaluation application of regional crustal stability in the Bohai Strait. China Geol. 2019, 2, 354–363. [Google Scholar] [CrossRef]
- Wang, P.T.; Wang, Y.C.; Wang, Z.C.; Gao, Y.; Sun, L.; Li, H.; Shi, J. Tsunami free oscillations excited by potential local earthquake sources in Bohai Sea, China. Ocean Eng. 2022, 266, 112949. [Google Scholar] [CrossRef]
- Wang, J.; Main, I.G. Strong historical earthquakes and their relationships with the Tan-Lu fault system and modern seismicity in eastern China. Nat. Hazards 2023, 115, 539–564. [Google Scholar] [CrossRef]
- Sun, Q.S.; Bai, L.S.; Wang, L.; Wang, J.Y.; Yang, S.C.; Li, E.L. Fault structures of the Haichenghe fault zone in Liaoning, China from high-precision location based on dense array observation. J. Seismol. 2024, 28, 1293–1307. [Google Scholar] [CrossRef]
- Chen, F.C.; Guo, L.Q.; Zheng, Z.J. Research on activity of Zhangjiakou-Bohai fault zone based on GPS observations. Seismol. Geol. 2020, 42, 95–108. [Google Scholar]
- Li, X.R.; Wang, J.; Zeng, Z.X.; Dai, Q. Spatial variations of current tectonic stress field and its relationship to the structure and rheology of lithosphere around the Bohai Sea, North China. J. Asian Earth Sci. 2016, 139, 83–94. [Google Scholar] [CrossRef]
- Xue, Y.G.; Qu, C.Q.; Su, M.X.; Qiu, D.H.; Li, X.; Ma, X. Comprehensive and quantitative evaluation of subsea tunnel route selection: A case study on Bohai Strait. KSCE J. Civ. Eng. 2025, 25, 3540–3555. [Google Scholar] [CrossRef]
- Qi, J.F.; Zhou, X.H.; Deng, R.J.; Zhang, K.X. Structural characteristics of the Tan-Lu fault zone in Cenozoic basins offshore the Bohai Sea. Sci. China Ser. D Earth Sci. 2008, 51, 20–31. [Google Scholar] [CrossRef]
- Zheng, H.X.; Zhang, X.H.; Zhao, T.H.; Qi, J. In-situ stress field and geological analysis of Bohai Trait. Period. Ocean Univ. China 2015, 45, 81–91. [Google Scholar] [CrossRef]
- Zhang, P.; Qin, X.H.; Feng, C.; Sun, W.F.; Tan, C.X. In-Situ Stress Measurement of Deep Borehole in Shandong Segment of Tan-Lu Fracture Belt and Analysis of Its Activity. Rock Soil Mech. 2013, 34, 2329–2336. [Google Scholar]
- Zhang, P.; Feng, C.; Sun, W.; Tan, C. In-Situ Stress Measurement of Deep Borehole in North Segment of Jinzhou Fracture Belt and Analysis on Its Activity. Earth Sci. 2014, 39, 1295–1306. [Google Scholar] [CrossRef]
- Li, B.; Ding, L.F.; Wang, J.X.; Hou, Y.H.; Xie, F.R. The state of the in-situ stress and fault stability evaluation of the Penglai coast. J. Geomech. 2022, 25, 459–466. [Google Scholar] [CrossRef]
- Feng, C.J.; Zhang, P.; Meng, J.; Qi, B.S.; Qin, X.H.; Niu, L.L.; Sun, D.S.; Sun, W.F.; Tan, C.X.; Chen, Q.C. Recent tectonic stress field at the shallow Earth’s crust near the Tan-Lu Fault Zone. Geosciences 2017, 3, 45–58. [Google Scholar]
- Wang, J.S.; Peng, H. Measurement of 3D In-Situ Stress in the Sea Area of Trans-Bohai Strait Passage Engineering Region. Rock Soil Mech. 2024, 45, 245–256. [Google Scholar] [CrossRef]
- Peng, J.S.; Wei, A.J.; Sun, Z.; Chen, X.L.; Zhao, D.J. Sinistral strike slip of the Zhangjiakou-Penglai Fault and its control on hydrocarbon accumulation in the northeast of Shaleitian Bulge, Bohai Bay Basin, East China. Pet. Explor. Dev. 2018, 45, 215–226. [Google Scholar] [CrossRef]
- Jia, N.; Liu, C.Y.; Wang, J.Q.; Fu, X.F.; Huang, L.; Yang, H.F.; Wang, H.X.; Ma, J.H.; Li, D. New insights into Cenozoic evolution of the Shijiutuo uplift, Bohai Bay basin, China: Constraints from apatite fission track analysis and seismic data. Mar. Pet. Geol. 2024, 164, 106808. [Google Scholar] [CrossRef]
- Meng, W.; Chen, Q.C.; Zhao, Z.; Li, S.; Zhang, Y. Characteristics and Implications of the Stress State in the Longmen Shan Fault Zone, Eastern Margin of the Tibetan Plateau. Tectonophysics 2015, 656, 1–19. [Google Scholar] [CrossRef]
- Editorial Board for Lithospheric Dynamics Atlas of China; State Seismological Bureau. Lithospheric Dynamics Atlas of China; China Cartographic Publishing House: Beijing, China, 1989. (In Chinese)
- Xue, Y.D.; Lyu, D.Y.; Hu, Z.W.; Huang, J.B.; Ren, J. Tectonic development of subtle faults and exploration in mature areas in Bohai Sea, East China. Pet. Explor. Dev. 2021, 48, 269–285. [Google Scholar] [CrossRef]
- Chen, A.L.; Chen, X.H. Origin of the Bohai Sea Basin, North China Craton, and implications for bidirectional back-arc extension in the East Asian continental margin. Solid Earth 2025, 16, 63–80. [Google Scholar] [CrossRef]
- Qi, J.; Yang, Q. Cenozoic structural deformation and dynamic processes of the Bohai Bay basin province, China. Mar. Pet. Geol. 2010, 27, 757–771. [Google Scholar] [CrossRef]
- Li, S.Z.; Suo, Y.H.; Dai, L.M.; Liu, L.P.; Jiao, Q. Development of the Bohai Bay Basin and destruction of the North China Craton. Earth Sci. Front. 2010, 17, 64–89. [Google Scholar]
- Liu, C.; Li, P.; Sun, J.; Hou, F.; Chu, H.; Qi, J.; Yang, Y.; Chen, S. High-resolution seismic sequence characteristics and its paleoenvironmental evolution in the Bohai Straits. Prog. Geophys. 2020, 35, 2373–2383. [Google Scholar] [CrossRef]
- Ding, D. Natural conditions of the Trans-Bohai Strait Passage. Mar. Geol. Dyn. 1994, 2, 4–6. [Google Scholar]
- Guo, L.; Li, S.; Suo, Y.; Ji, Y.; Dai, L.; Yu, S.; Somerville, I.D. Experimental study and active tectonics on the Zhangjiakou-Penglai fault zone across North China. J. Asian Earth Sci. 2015, 114, 18–27. [Google Scholar] [CrossRef]
- Zhao, R.; Zheng, J.; Cui, H.; Ji, D. Analysis on the Seismogenic Mechanism of Changdao Earthquake Swarm in Shandong Province. In Advances in Civil Engineering: Structural Seismic Resistance, Monitoring and Detection; CRC Press: Boca Raton, FL, USA, 2022; pp. 727–734. [Google Scholar]
- Zhang, J.D.; Hao, T.Y.; Dong, S.W.; Chen, X.H.; Cui, J.J.; Yang, X.Y.; Liu, C.Z.; Li, T.J.; Xu, Y.; Huang, S.; et al. The structural and tectonic relationships of the major fault systems of the Tan-Lu fault zone, with a focus on the segments within the North China region. Asian Earth Sci. 2015, 110, 85–100. [Google Scholar] [CrossRef]
- Li, W.; Li, J.; Wu, W.Q.; Zhang, T.J.; Chen, X.P.; Meng, M.F.; Cao, M.Y.; Zhang, Q. Time limit of dextral strike-slip in Cenozoic of Liaodong Bay section of Tan-Lu Fault Zone. Earth Sci. 2024, 49, 2071–2084. [Google Scholar] [CrossRef]
- Zhu, G.; Hu, W.; Song, L.H.; Liu, B. Quaternary activity along the Tan-Lu Fault Zone in the Bohai Bay, East China: Evidence from seismic profiles. Asian Earth Sci. 2015, 114, 5–17. [Google Scholar] [CrossRef]
- Qu, J.H.; Yang, Y.Y.; Liu, Y.G. Causative structure of the 2013 Laizhou earthquake sequence. China Earthq. Eng. J. 2015, 37, 546–552. [Google Scholar]
- Wang, D.M.; Hu, J.M.; Zhang, Z.G.; Yan, J.Y.; Hu, Y. Kinematic history of the Tan-Lu fault zone constrained by the Late Mesozoic-Cenozoic tectono-sedimentary evolution of basins in the Luxi Block, eastern North China Craton. J. Asian Earth Sci. 2022, 225, 105041. [Google Scholar] [CrossRef]
- Yuan, H.W.; Dai, K.; Zhang, C.; Liu, L.; Jing, T.; Li, J.; Zhao, W.; Chen, F. Cenozoic sedimentary archives of a strike-slip fault zone in the Tanhai Region, Bohai Bay Basin, Northeastern China. J. Struct. Geol. 2024, 186, 105203. [Google Scholar] [CrossRef]
- Fu, Z.X.; Liu, J.; Liu, G.P. On the long-term seismic hazard analysis in the Zhangjiakou–Penglai seismotectonic zone, China. Tectonophysics 2004, 390, 75–83. [Google Scholar] [CrossRef]
- Scholz, C.H. The critical slip distance for seismic faulting. Nature 1988, 336, 761–763. [Google Scholar] [CrossRef]
- Li, S.Z.; Zhao, G.C.; Dai, L.M.; Zhou, L.H.; Liu, X.; Suo, Y.H.; Santosh, M. Cenozoic faulting of the Bohai Bay Basin and its bearing on the destruction of the eastern North China Craton. J. Asian Earth Sci. 2012, 47, 80–93. [Google Scholar] [CrossRef]
- Tao, Y.; Chen, A.Q.; Hou, M.C.; Niu, C.M.; Wang, Q.B. Characteristic of the Bodong segment of the Tanlu Fault Zone, Bohai Sea Area, Eastern China: Implications for hydrocarbon exploration and regional tectonic evolution. J. Pet. Sci. Eng. 2021, 201, 108478. [Google Scholar] [CrossRef]
- Amadei, B.; Stephansson, O. Rock Stress and Its Measurement; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Haimson, B.C.; Cornet, F.H. ISRM Suggested Methods for Rock Stress Estimation—Part 3: Hydraulic Fracturing (HF) and/or Hydraulic Testing of Pre-existing Fractures (HTPF). Int. Rock Mech. Min. Sci. 2003, 40, 1011–1020. [Google Scholar] [CrossRef]
- Ljunggren, C.; Chang, Y.; Janson, T.; Christiansson, R. An Overview of Rock Stress Measurement Methods. Int. Rock Mech. Min. Sci. 2003, 40, 975–989. [Google Scholar] [CrossRef]
- Schmitt, D.R.; Currie, C.A.; Zhang, L. Crustal stress determination from boreholes and rock cores: Fundamental principles. Tectonophysics 2012, 580, 1–26. [Google Scholar] [CrossRef]
- Huenges, E.; Erzinger, J.; Kuck, J.; Engeser, B.; Kessels, W. The permeable crust: Geohydraulic properties down to 9101 m depth. J. Geophys. Res. 1997, 102, 18255–18265. [Google Scholar] [CrossRef]
- Coyle, B.J.; Zoback, M.D. In situ permeability and fluid pressure measurements at approximately 2-km in the Cajon Pass research well. Geophys. Res. Lett. 1988, 15, 1029–1032. [Google Scholar] [CrossRef]
- Desroches, J.; Peyret, E.; Gisolf, A.; Wilcox, A.; Di Giovanni, M.; Schram de Jong, A.; Sepehri, S.; Garrard, R.; Giger, S. Stress measurement campaign in scientific deep boreholes: Focus on tool and methods. In Proceedings of the SPWLA 62nd Annual Logging Symposium, Virtual Event, 19–23 June 2021. Paper ID SPWLA-2021-0056. [Google Scholar] [CrossRef]
- Qin, X.H.; Zhao, X.G.; Zhang, C.Y.; Li, P.F.; Chen, Q.C.; Wang, J. Measurement and assessment of the in-situ stress of the Shazaoyuan rock block, a candidate site for HLW disposal in northwest China. Rock Mech. Rock Eng. 2024, 57, 4011–4031. [Google Scholar] [CrossRef]
- Gronseth, J.M.; Kry, P.R. Instantaneous Shut-in Pressure and Its Relationship to the Minimum In-Situ Stress. In Hydraulic Fracturing Stress Measurements; National Academy Press: Washington, DC, USA, 1983; pp. 55–60. [Google Scholar]
- Hayashi, K.; Haimson, B.C. Characteristics of Shut-in Curves in Hydraulic Fracturing Stress Measurements and Determination of In Situ Minimum Compressive Stress. Geophys. Res. Solid Earth 1991, 96, 18311–19321. [Google Scholar] [CrossRef]
- Lee, M.Y.; Haimson, B.C. Statistical Evaluation of Hydraulic Fracturing Stress Measurement Parameters. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 447–456. [Google Scholar] [CrossRef]
- Brown, E.T.; Hoek, E. Trends in Relationship Between Measured In-Situ Stresses and Depth. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 211–215. [Google Scholar] [CrossRef]
- Yang, S.X.; Yao, R.; Cui, X.F.; Chen, Q.C.; Huang, L.Y. Analysis of the characteristics of measured stress in Chinese mainland and its active blocks and North-South seismic belt. Chin. J. Geophys. 2012, 55, 708–718. [Google Scholar] [CrossRef]
- Xie, F.R. Recent Tectonic Stress Map of China and Its Adjacent Areas; Sinomaps Press: Nanjing, China, 2015. (In Chinese) [Google Scholar]
- Anderson, E.M. The Dynamics of Faulting and Dyke Formation with Application to Britain; Oliver and Boyd: Edinburgh, UK, 1951. [Google Scholar]
- Bott, M.H.P.; Kusznir, N.J. The origin of tectonic stress in the lithosphere. Tectonophysics 1984, 105, 1–13. [Google Scholar] [CrossRef]
- Sagaseta, C. Mechanics of jointed and faulted rock: Rossmanith, HP (Ed.): Proceedings of the International Conference, Vienna, April 1990. AA Balkeme, Rotterdam. Rock Mech. Rock Eng. 1992, 25, 63. [Google Scholar]
- Magnenet, V.; Cornet, F.H.; Fond, C. A nontectonic origin for the present-day stress field in the Paris Basin (France). J. Geophys. Res. Solid Earth 2017, 122, 9313–9327. [Google Scholar] [CrossRef]
- Heidbach, O.; Iaffaldano, G.; Bunge, H.P. Topography growth drives stress rotation in the central Andes: Observation and models. Geophys. Res. Lett. 2008, 35, L08301. [Google Scholar] [CrossRef]
- Oliva, S.J.; Ebinger, C.J.; Rivalta, E.; Williams, C.A.; Wauthier, C.; Currie, C.A. State of stress and stress rotations: Quantifying the role of surface topography and subsurface density contrasts in magmatic rift zone (Eastern Rift, Africa). Earth Planet. Sci. Lett. 2022, 584, 117478. [Google Scholar] [CrossRef]
- Su, S.R.; Zhu, H.H.; Wang, S.T.; Stephansson, O. The effect of fracture properties on stress field in the vicinity of a fracture. Northwest Univ. (Nat. Sci. Ed.) 2002, 32, 655–658. [Google Scholar]
- Rajabi, M.; Tingay, M.; King, R.; Heidbach, O. Present-day stress orientation in the Clarence-Moreton Basin of New South Wales, Australia: A new high density dataset reveals local stress rotations. Basin Res. 2017, 29, 622–640. [Google Scholar] [CrossRef]
- Reiter, K. Stress rotation-impact and interaction of rock stiffness and faults. Solid Earth 2021, 12, 1287–1307. [Google Scholar] [CrossRef]
- Su, S.R.; Zhu, H.H.; Wang, S.T.; Stephansson, O. Effect of physical and mechanical properties of rocks on stress field in the vicinity of fractures. Chin. J. Rock Mech. Eng. 2003, 24 (Suppl. 2), 2431–2436. [Google Scholar] [CrossRef]
- Roche, V.; van der Baan, M. Modeling of the in situ stress state in elastic layered rock subject to stress and strain-driven tectonic forces. Solid Earth 2017, 8, 479–498. [Google Scholar] [CrossRef]
- Harper, T. Dependence of stress state on the histories of burial, erosion, mechanical properties, pore pressure, and faulting. Int. J. Rock Mech. Min. Sci. 2020, 136, 104523. [Google Scholar] [CrossRef]
- Tan, C.X.; Wang, R.J.; Sun, Y.; Lei, W.; Wu, S.; Yang, M.; Sun, W. Numerical modeling estimation of the ‘tectonic stress plane’ (TSP) beneath topography with quasi-U-shaped valleys. Int. J. Rock Mech. Min. Sci. 2004, 41, 303–310. [Google Scholar] [CrossRef]
- Hou, G.T.; Ye, L.X.; Du, Q.E. Tectonic mechanism and geological significance of the Bozhang fault zone. Chin. Geol. 1999, 34, 123–135. [Google Scholar]
- Xu, J.; Song, C.Q.; Chu, Q.Z. Primary study of the seismotectonic characteristics of the Zhangjiakou-Penglai fault zone. Seismol. Geol. 1998, 20, 146–154. [Google Scholar]
- Wang, R.B.; Gu, G.H.; Xu, J. Discussion on characteristics of crustal deformation along the Zhangjiakou-Bohai seismotectonic zone. Seismol. Geol. 2004, 26, 456–468. [Google Scholar]
- Huang, L.; Liu, C.Y.; Kusky, T.M. Cenozoic evolution of the Tan-Lu Fault Zone (East China)—Constraints from seismic data. Gondwana Res. 2015, 28, 1079–1095. [Google Scholar] [CrossRef]
- Feng, C.J.; Zhang, P.; Qin, X.H.; Meng, W.; Tan, C.X.; Chen, Q.C. Near-surface stress measurements in the Longmenshan fault belt after the 2008 Wenchuan Ms 8.0 earthquake. Int. J. Rock Mech. Min. Sci. 2015, 77, 358–377. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Peng, X.M.; Zhao, T.H.; Sun, J. Fault activity and characteristics of earthquake distribution in the engineering area of Bohai Strait cross-sea channel. Geosciences 2017, 31, 860–868. [Google Scholar] [CrossRef]
- Zoback, M.D.; Townend, J. Implications of hydrostatic pore pressures and high crustal strength for the deformation of intraplate lithosphere. Tectonophysics 2001, 336, 19–30. [Google Scholar] [CrossRef]
- Barton, C.A.; Zoback, M.D.; Moos, D. Fluid flow along potentially active faults in crystalline rock. Geology 1995, 23, 683–686. [Google Scholar] [CrossRef]
- Byerlee, J.D. Friction of rocks. Pure Appl. Geophys. 1978, 116, 615–626. [Google Scholar] [CrossRef]
- Byerlee, J. Friction, overpressure and fault normal compression. Geophys. Res. Lett. 1990, 17, 2109–2112. [Google Scholar] [CrossRef]
- Carpenter, B.M.; Marone, C.; Saffer, D.M. Weakness of the San Andreas Fault revealed by samples from the active fault zone. Nat. Geosci. 2011, 4, 251–254. [Google Scholar] [CrossRef]
- Zhang, L.; He, C. Frictional properties of natural gouges from Longmenshan fault zone ruptured during the Wenchuan Mw7.9 earthquake. Tectonophysics 2013, 594, 149–164. [Google Scholar] [CrossRef]
- Hergert, T.; Heidbach, O.; Reiter, K.; Giger, S.B.; Marschall, P. Stress field sensitivity analysis in a sedimentary sequence of the Alpine foreland, north Switzerland. Solid Earth 2015, 6, 533–552. [Google Scholar] [CrossRef]
- Röckel, L.; Ahlers, S.; Müller, B.; Reiter, K.; Heidbach, O.; Henk, A.; Hergert, T.; Schilling, F. The analysis of slip tendency of major tectonic faults in Germany. Solid Earth 2022, 13, 1087–1105. [Google Scholar] [CrossRef]
- Zaccagnino, D.; Doglioni, C. Fault slip vs shear stress gradient. Geosyst. Geoenviron. 2023, 2, 10021. [Google Scholar] [CrossRef]
- Qin, X.H.; Chen, Q.C.; Tan, C.X.; An, Q.M.; Wu, M.L.; Feng, C.J. Analysis of current geostress state and seismic risk in southwest segment of Longmenshan fracture belt. Chin. J. Rock Mech. Eng. 2013, 32, 2870–2876. [Google Scholar]
- Lin, W.R.; Conin, M.; Moore, J.C.; Chester, F.M.; Nakamura, Y.; Mori, J.J.; Anderson, L. Stress state in the largest displacement area of the 2011 Tohoku-Oki earthquake. Science 2013, 339, 687–690. [Google Scholar] [CrossRef] [PubMed]
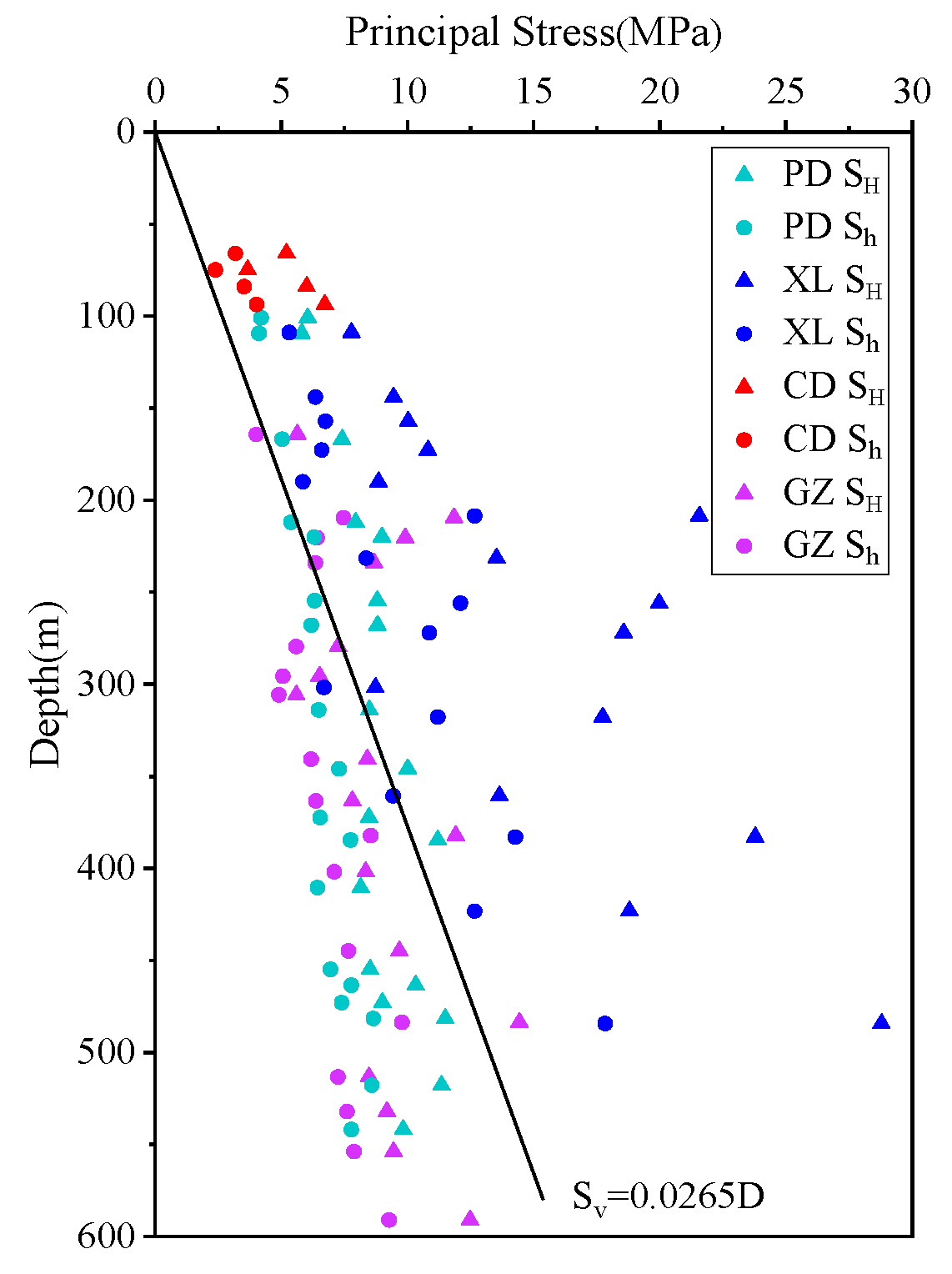
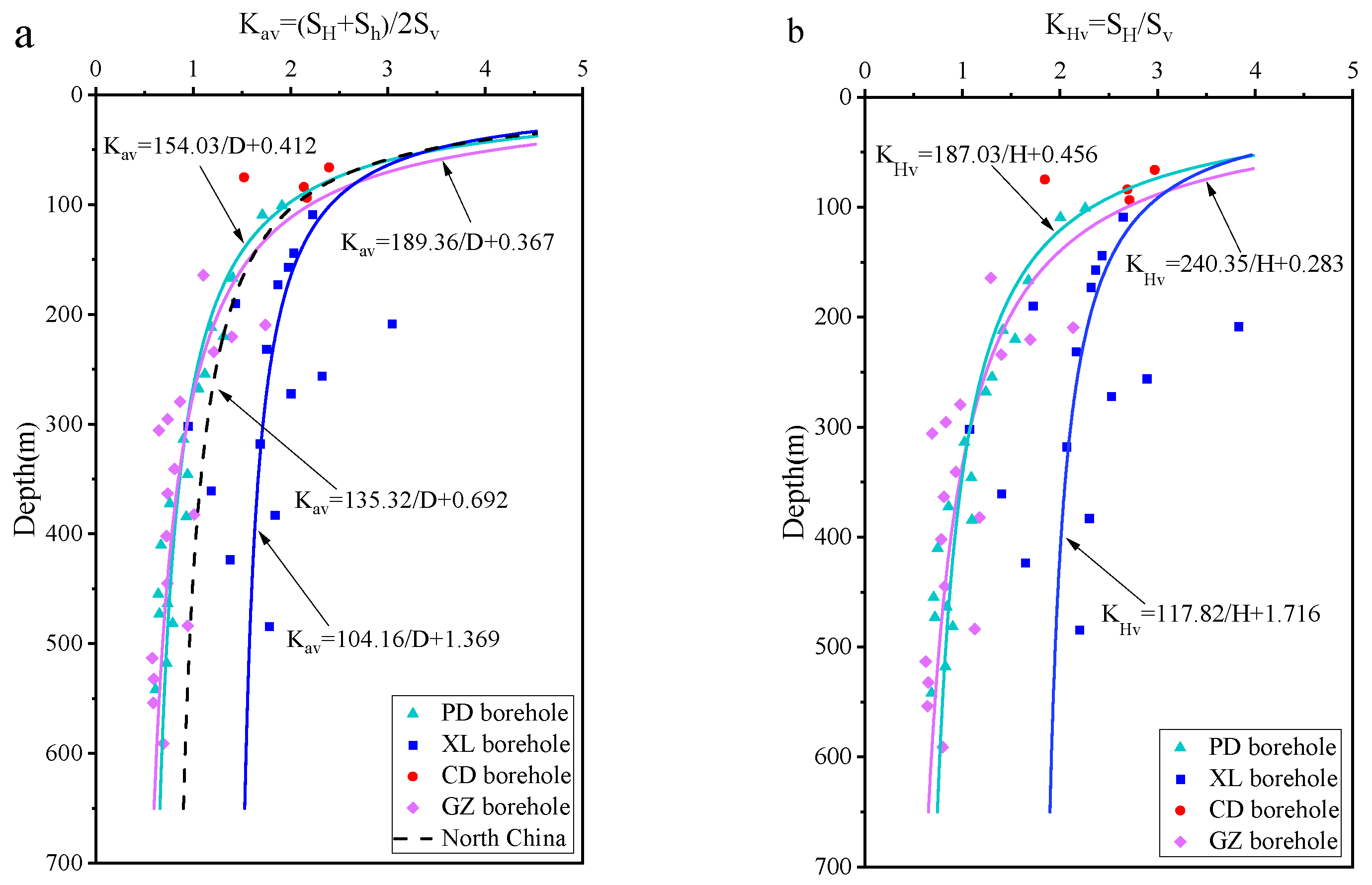
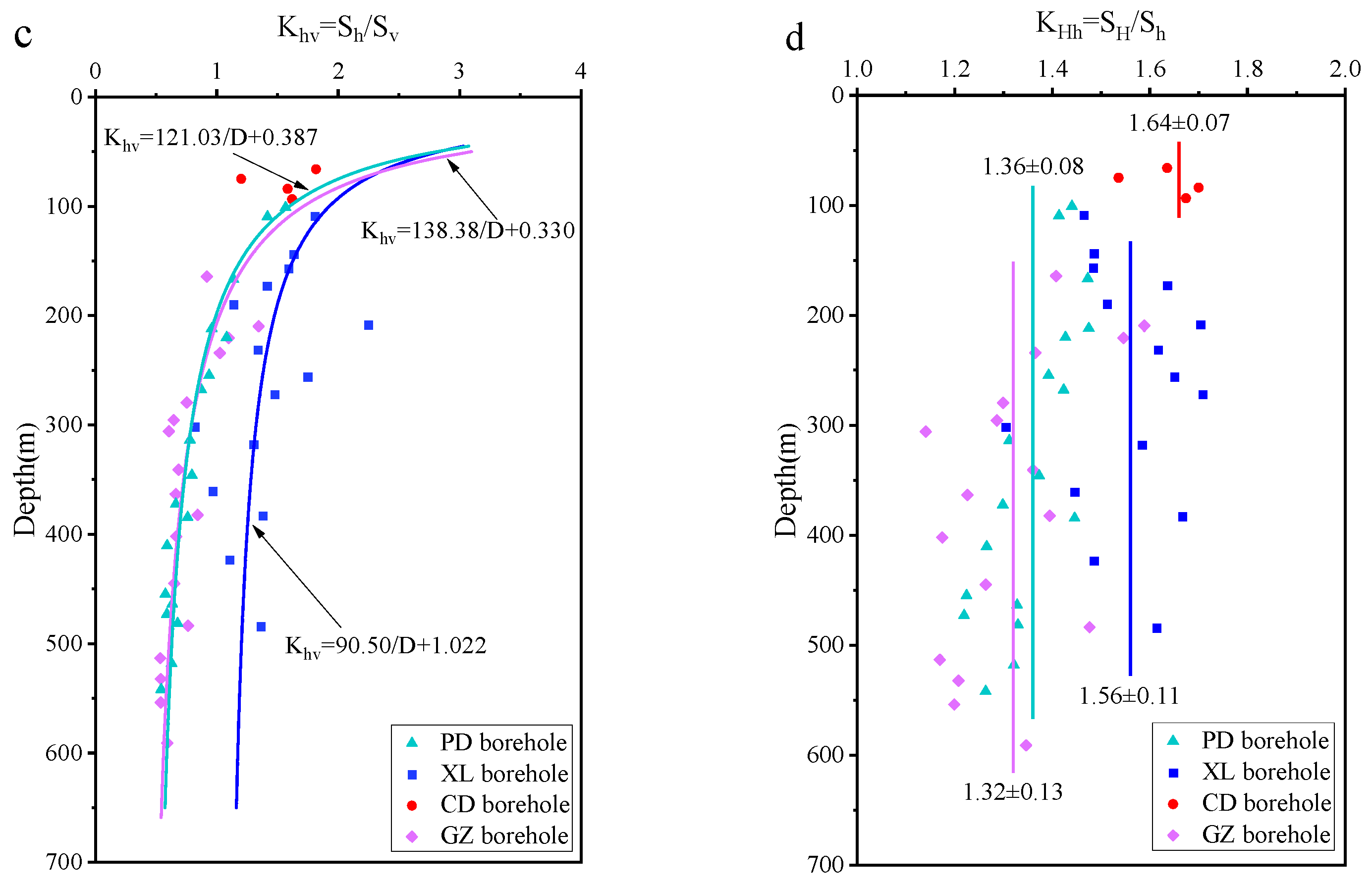
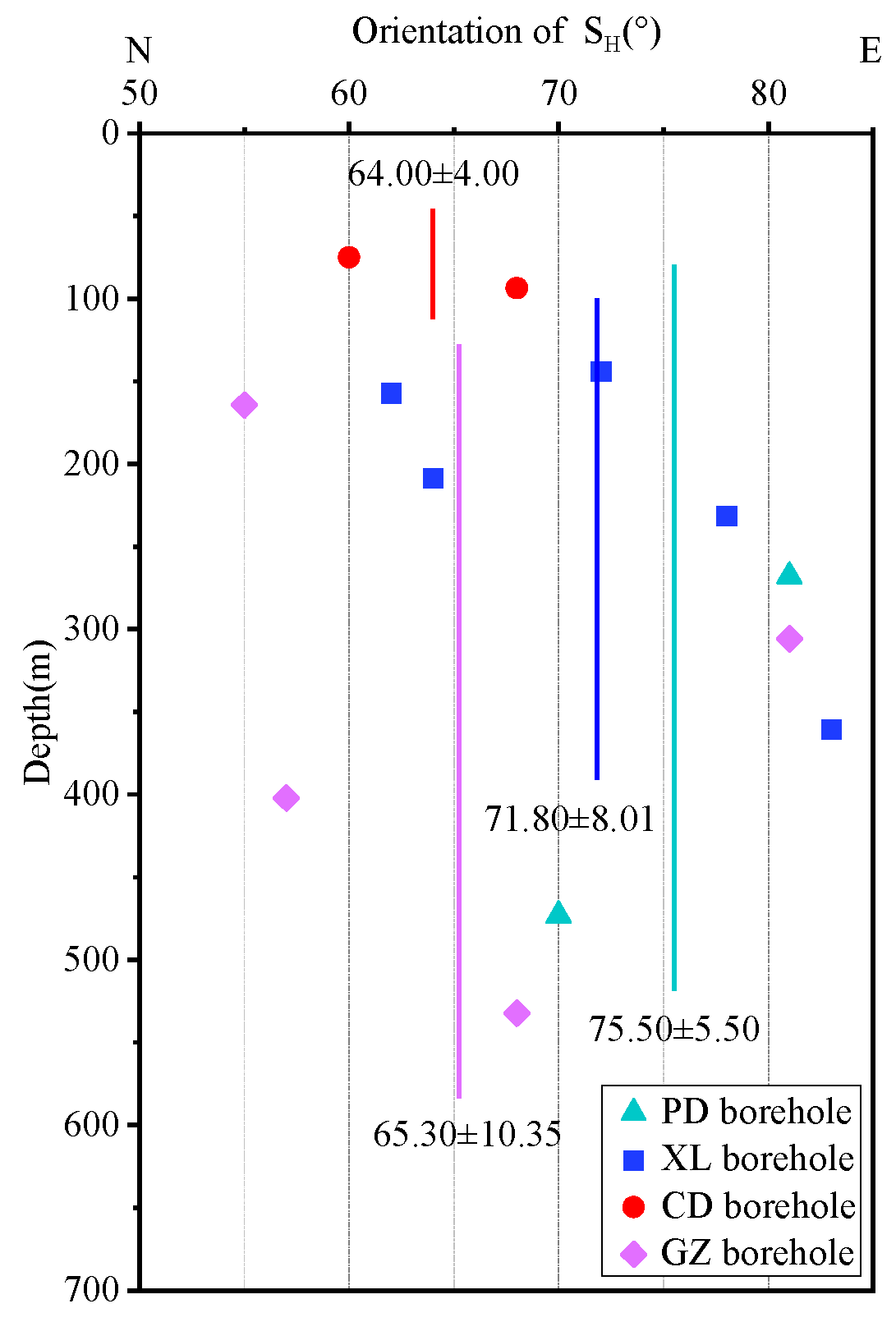

| Borehole | Depth (m) | Pb (MPa) | Pr (MPa) | Ps (MPa) | P0 (MPa) | SH (MPa) | Sh (MPa) | Sv (MPa) | Kav | KHv | Khv | KHh | SH Azimuth |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PD [22] | 101.00 | 0.91 | 5.57 | 4.2 | 13.7 | 6.05 | 4.20 | 2.68 | 1.91 | 2.26 | 1.57 | 1.44 | N80° W |
| 109.40 | 0.99 | 5.64 | 4.11 | 7.62 | 5.81 | 4.11 | 2.90 | 1.71 | 2.00 | 1.42 | 1.41 | ||
| 166.80 | 1.57 | 6.02 | 5 | 11.79 | 7.41 | 5.03 | 4.42 | 1.41 | 1.68 | 1.14 | 1.47 | N87° W | |
| 212.00 | 2.02 | 6.2 | 5.39 | 14.43 | 7.95 | 5.39 | 5.62 | 1.19 | 1.42 | 0.96 | 1.47 | ||
| 220.10 | 2.10 | 7.81 | 6.3 | 10.42 | 8.99 | 6.3 | 5.83 | 1.31 | 1.54 | 1.08 | 1.43 | ||
| 254.60 | 2.45 | 7.71 | 6.32 | 11.81 | 8.8 | 6.32 | 6.75 | 1.12 | 1.30 | 0.94 | 1.39 | ||
| 268.00 | 2.58 | 7.18 | 6.19 | 11.95 | 8.81 | 6.19 | 7.10 | 1.06 | 1.24 | 0.87 | 1.42 | N81° E | |
| 314.00 | 3.04 | 8.1 | 6.48 | 10.68 | 8.5 | 6.48 | 8.32 | 0.90 | 1.02 | 0.78 | 1.31 | ||
| 346.00 | 3.36 | 8.5 | 7.29 | 11.37 | 10.01 | 7.29 | 9.17 | 0.94 | 1.09 | 0.80 | 1.37 | ||
| 372.50 | 3.63 | 7.48 | 6.53 | 11.17 | 8.48 | 6.53 | 9.87 | 0.76 | 0.86 | 0.66 | 1.30 | ||
| 384.60 | 3.75 | 8.28 | 7.74 | 9.4 | 11.19 | 7.74 | 10.19 | 0.93 | 1.10 | 0.76 | 1.45 | ||
| 410.40 | 4 | 7.15 | 6.43 | 14.36 | 8.14 | 6.43 | 10.88 | 0.67 | 0.75 | 0.59 | 1.27 | ||
| 454.90 | 4.45 | 7.89 | 6.95 | 13.77 | 8.51 | 6.95 | 12.05 | 0.64 | 0.71 | 0.58 | 1.22 | ||
| 463.50 | 4.54 | 8.47 | 7.78 | 12.56 | 10.33 | 7.78 | 12.28 | 0.74 | 0.84 | 0.63 | 1.33 | ||
| 473.00 | 4.63 | 8.53 | 7.39 | 16.82 | 9.01 | 7.39 | 12.53 | 0.65 | 0.72 | 0.59 | 1.22 | N70° E | |
| 481.60 | 4.72 | 9.71 | 8.64 | 15.05 | 11.49 | 8.64 | 12.76 | 0.79 | 0.90 | 0.68 | 1.33 | ||
| 517.90 | 5.08 | 9.34 | 8.59 | 14.56 | 11.35 | 8.59 | 13.72 | 0.73 | 0.83 | 0.63 | 1.32 | ||
| 542.00 | 5.32 | 8.19 | 7.78 | 15.17 | 9.83 | 7.78 | 14.36 | 0.61 | 0.68 | 0.54 | 1.26 | ||
| XL | 108.90 | 11.83 | 7.06 | 5.31 | 1.09 | 7.78 | 5.31 | 2.89 | 2.27 | 2.70 | 1.84 | 1.47 | |
| 144.00 | 17.15 | 8.19 | 6.36 | 1.44 | 9.45 | 6.36 | 3.82 | 2.07 | 2.48 | 1.67 | 1.49 | N72° E | |
| 157.10 | 27.71 | 8.66 | 6.75 | 1.57 | 10.02 | 6.75 | 4.16 | 2.01 | 2.41 | 1.62 | 1.48 | N62° E | |
| 172.80 | 13.38 | 7.29 | 6.61 | 1.73 | 10.81 | 6.61 | 4.58 | 1.90 | 2.36 | 1.44 | 1.64 | ||
| 190.00 | 10.06 | 6.80 | 5.85 | 1.90 | 8.85 | 5.85 | 5.04 | 1.46 | 1.76 | 1.16 | 1.51 | ||
| 208.50 | 19.25 | 14.32 | 12.66 | 2.09 | 21.57 | 12.66 | 5.53 | 3.10 | 3.90 | 2.29 | 1.70 | N64° E | |
| 231.50 | 13.63 | 9.26 | 8.37 | 2.32 | 13.53 | 8.37 | 6.13 | 1.78 | 2.21 | 1.36 | 1.62 | N78° E | |
| 256.00 | 16.52 | 13.77 | 12.10 | 2.56 | 19.97 | 12.10 | 6.78 | 2.36 | 2.94 | 1.78 | 1.65 | ||
| 272.10 | 15.08 | 11.32 | 10.87 | 2.72 | 18.57 | 10.87 | 7.21 | 2.04 | 2.58 | 1.51 | 1.71 | ||
| 301.80 | 12.24 | 8.32 | 6.69 | 3.02 | 8.73 | 6.69 | 8.00 | 0.96 | 1.09 | 0.84 | 1.30 | ||
| 317.90 | 17.88 | 12.68 | 11.20 | 3.18 | 17.74 | 11.20 | 8.42 | 1.72 | 2.11 | 1.33 | 1.58 | ||
| 360.70 | 16.42 | 11.06 | 9.44 | 3.61 | 13.65 | 9.44 | 9.56 | 1.21 | 1.43 | 0.99 | 1.45 | N83° E | |
| 383.00 | 17.59 | 15.20 | 14.27 | 3.83 | 23.78 | 14.27 | 10.15 | 1.87 | 2.34 | 1.41 | 1.67 | ||
| 423.30 | 18.14 | 14.94 | 12.66 | 4.23 | 18.81 | 12.66 | 11.22 | 1.40 | 1.68 | 1.13 | 1.49 | ||
| 484.40 | 25.58 | 19.89 | 17.84 | 4.84 | 28.79 | 17.84 | 12.84 | 1.82 | 2.24 | 1.39 | 1.61 | ||
| CD | 66.00 | 7.94 | 3.70 | 3.18 | 0.64 | 5.20 | 3.18 | 1.75 | 2.40 | 2.97 | 1.82 | 1.64 | |
| 75.00 | 5.68 | 2.77 | 2.39 | 0.73 | 3.67 | 2.39 | 1.99 | 1.52 | 1.85 | 1.20 | 1.54 | N60° E | |
| 84.00 | 5.49 | 3.77 | 3.53 | 0.82 | 6.00 | 3.53 | 2.23 | 2.14 | 2.70 | 1.59 | 1.70 | ||
| 93.60 | 7.54 | 4.41 | 4.02 | 0.92 | 6.73 | 4.02 | 2.48 | 2.17 | 2.71 | 1.62 | 1.67 | N68° E | |
| GZ [23] | 164.35 | 13.05 | 4.73 | 4.00 | 1.64 | 5.63 | 4.00 | 4.36 | 1.11 | 1.29 | 0.92 | 1.41 | N55° E |
| 209.60 | 18.69 | 8.43 | 7.46 | 2.10 | 11.85 | 7.46 | 5.55 | 1.74 | 2.13 | 1.34 | 1.59 | ||
| 220.45 | 12.05 | 7.12 | 6.41 | 2.20 | 9.91 | 6.41 | 5.84 | 1.40 | 1.70 | 1.10 | 1.55 | ||
| 234.13 | 15.34 | 8.04 | 6.35 | 2.34 | 8.67 | 6.35 | 6.20 | 1.21 | 1.40 | 1.02 | 1.37 | ||
| 279.60 | 15.77 | 6.69 | 5.58 | 2.80 | 7.25 | 5.58 | 7.41 | 0.87 | 0.98 | 0.75 | 1.30 | ||
| 295.65 | 12.60 | 5.71 | 5.06 | 2.96 | 6.51 | 5.06 | 7.83 | 0.74 | 0.83 | 0.65 | 1.29 | ||
| 305.81 | 17.38 | 6.05 | 4.90 | 3.06 | 5.59 | 4.90 | 8.10 | 0.65 | 0.69 | 0.60 | 1.14 | N81° E | |
| 340.73 | 15.87 | 6.72 | 6.18 | 3.41 | 8.41 | 6.18 | 9.03 | 0.81 | 0.93 | 0.68 | 1.36 | ||
| 363.40 | 14.77 | 7.67 | 6.37 | 3.63 | 7.81 | 6.37 | 9.63 | 0.74 | 0.81 | 0.66 | 1.23 | ||
| 382.20 | 21.89 | 9.89 | 8.54 | 3.82 | 11.91 | 8.54 | 10.13 | 1.01 | 1.18 | 0.84 | 1.39 | ||
| 402.00 | 17.16 | 8.94 | 7.10 | 4.02 | 8.34 | 7.10 | 10.65 | 0.72 | 0.78 | 0.67 | 1.17 | N57° E | |
| 444.90 | 16.29 | 8.85 | 7.66 | 4.45 | 9.68 | 7.66 | 11.79 | 0.74 | 0.82 | 0.65 | 1.26 | ||
| 483.71 | 22.25 | 10.06 | 9.78 | 4.84 | 14.44 | 9.78 | 12.82 | 0.94 | 1.13 | 0.76 | 1.48 | ||
| 513.27 | 13.00 | 8.14 | 7.25 | 5.13 | 8.48 | 7.25 | 13.60 | 0.58 | 0.62 | 0.53 | 1.17 | ||
| 532.20 | 17.90 | 8.30 | 7.60 | 5.32 | 9.18 | 7.60 | 14.10 | 0.59 | 0.65 | 0.54 | 1.21 | N68° E | |
| 553.90 | 17.82 | 8.65 | 7.88 | 5.54 | 9.45 | 7.88 | 14.68 | 0.59 | 0.64 | 0.54 | 1.20 | ||
| 591.00 | 15.56 | 9.42 | 9.27 | 5.91 | 12.48 | 9.27 | 15.66 | 0.69 | 0.80 | 0.59 | 1.35 |
| Borehole | SH | R2 | Sh | R2 | SV |
|---|---|---|---|---|---|
| Gaizhou | SH = 0.0115D + 4.67 | 0.4448 | Sh = 0.0101D + 3.03 | 0.7237 | Sv = 0.0265D |
| Changdao | SH = 0.0758D − 0.64 | 0.4689 | Sh = 0.0401D + 0.08 | 0.4807 | Sv = 0.0265D |
| Xiangli | SH = 0.0429D + 4.00 | 0.5447 | Sh = 0.0270D + 2.58 | 0.6479 | Sv = 0.0265D |
| Pingdu | SH = 0.0090D + 5.89 | 0.6051 | Sh = 0.0087D + 3.67 | 0.8302 | Sv = 0.0265D |
| North China Block | SH = 0.0229D + 4.00 | Sh = 0.0170D + 2.58 | Sv = 0.0272D |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Qin, X.; Yang, G.; Zhao, Y.; Gao, Z.; Chen, Y.; Zhang, C. A New Look at the Stress State Across the Bohai Strait, China. Appl. Sci. 2025, 15, 6708. https://doi.org/10.3390/app15126708
Liang Z, Qin X, Yang G, Zhao Y, Gao Z, Chen Y, Zhang C. A New Look at the Stress State Across the Bohai Strait, China. Applied Sciences. 2025; 15(12):6708. https://doi.org/10.3390/app15126708
Chicago/Turabian StyleLiang, Zhihao, Xianghui Qin, Guoxiang Yang, Yiran Zhao, Zixuan Gao, Yifan Chen, and Chongyuan Zhang. 2025. "A New Look at the Stress State Across the Bohai Strait, China" Applied Sciences 15, no. 12: 6708. https://doi.org/10.3390/app15126708
APA StyleLiang, Z., Qin, X., Yang, G., Zhao, Y., Gao, Z., Chen, Y., & Zhang, C. (2025). A New Look at the Stress State Across the Bohai Strait, China. Applied Sciences, 15(12), 6708. https://doi.org/10.3390/app15126708







