Effect of Soft Interlayer Dip Angle on the Attenuation and Prediction of Blast-Induced Vibrations in Rock Slopes: An Experimental Study
Abstract
1. Introduction
2. Background and Overview of Slope Engineering and Blasting Engineering
3. On-Site Blasting In Situ Experiment and Testing Analysis
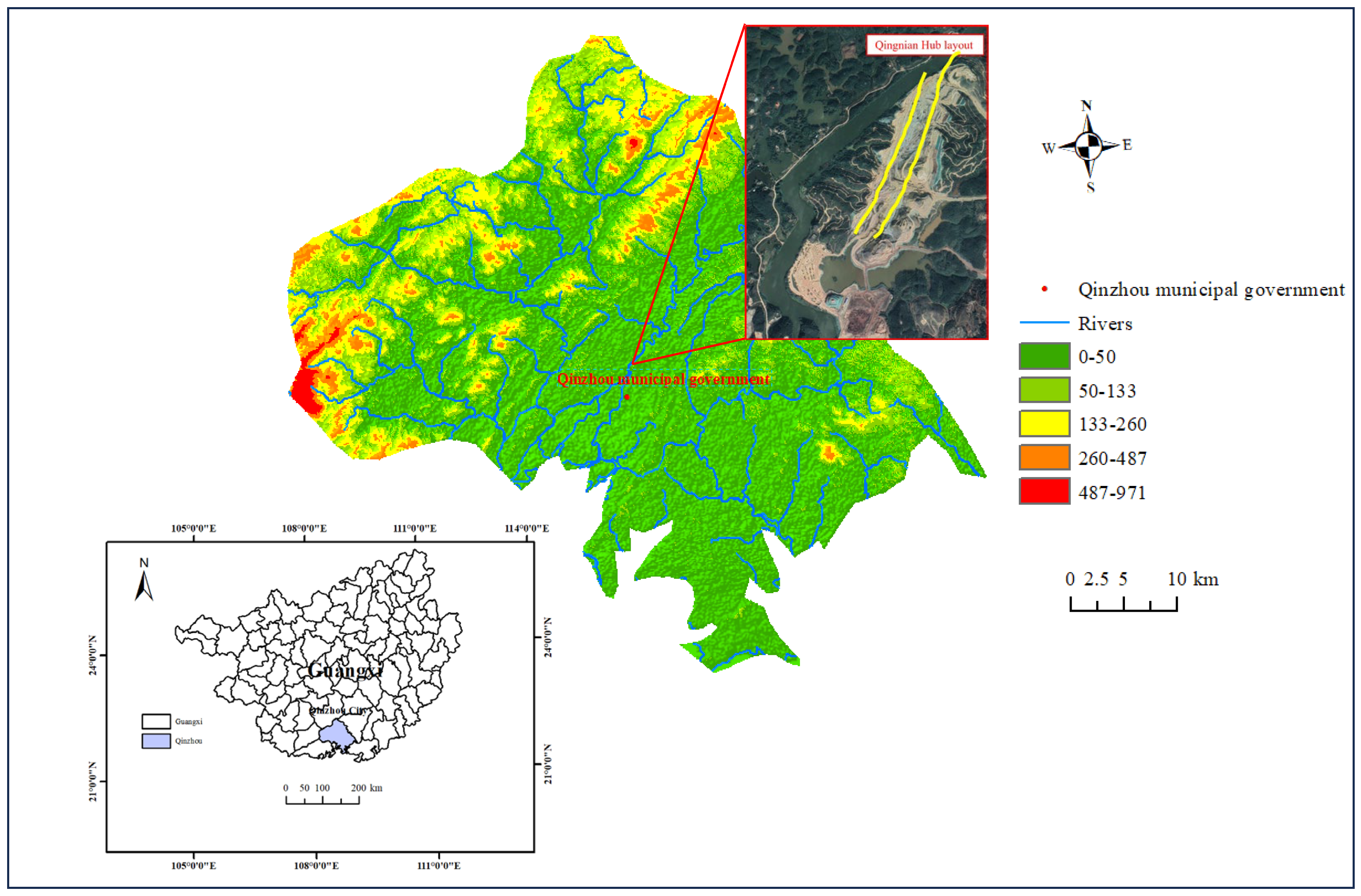
3.1. Field Test
3.2. Analysis of Test Results
4. Establishment of a New Prediction Model for Blasting Vibration Attenuation
4.1. Conventional Model for Predicting Blasting Vibration Attenuation
4.2. Prediction Model for Blast Vibration Attenuation, Taking Elevation Effect into Account
4.3. Prediction Model for Blast Vibration Attenuation Taking into Account the Angle of Inclination of the Layer
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| PPV | peak particle velocity |
References
- Liu, X.; Liu, Y.; Lu, Y.; Li, X.; Li, P. Numerical analysis of evaluation methods and influencing factors for dynamic stability of bedding rock slope. J. Vibroeng. 2017, 19, 1937–1961. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, H.; Xia, X.; Liu, B.; Zuo, H.; Jiang, J. Blast-induced rock damage control in Fangchenggang nuclear power station, China. J. Rock Mech. Geotech. Eng. 2018, 10, 914–923. [Google Scholar] [CrossRef]
- Wu, C. Study on the Influence of Bedding Orientation on Blasting Vibration in Tunnel Construction. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2017. [Google Scholar]
- Matidza, M.I.; Zhang, J.; Huang, G.; Mwangi, A.D. Assessment of blast-induced ground vibration at Jinduicheng molybdenum open pit mine. Nat. Resour. Res. 2020, 29, 831–841. [Google Scholar] [CrossRef]
- Gao, J.; Huang, C.; Huang, X.; Ren, J.J.; Wang, N. A Study of Blast Vibration Propagation Law under Negative Altitude Terrains. Math. Probl. Eng. 2022, 2022, 4289057. [Google Scholar] [CrossRef]
- Ma, H.Y. Attenuation and time-frequency characteristics of explosion ground vibration of shallow buried OD1422-X80 mm12 MPa pipeline based on prototype experiment. J. Perform. Constr. Fac. 2019, 34, 04019092. [Google Scholar]
- Wu, T.Y. Experimental and numerical investigations on damage assessment of high-density polyethylene pipe subjected to blast loads. Eng. Fail. Anal. 2022, 131, 105856. [Google Scholar] [CrossRef]
- Liang, Q.; An, Y.; Zhao, L. Comparative Study on Calculation Methods of Blasting Vibration Velocity. Rock Mech. Rock Eng. 2011, 44, 93–101. [Google Scholar] [CrossRef]
- Ak, H.; Iphar, M.; Yavuz, M.; Konuk, A. Evaluation of ground vibration effect of blasting operations in a magnesite mine. Soil Dyn. Earthq. Eng. 2009, 29, 669–676. [Google Scholar] [CrossRef]
- Wu, X.G.; Zhu, D.; Lu, H.; Li, L. Simulation research on blasting of an open pit mine slope considering elevation conditions and slope shape factors. Front. Earth Sci. 2024, 12, 1417895. [Google Scholar] [CrossRef]
- Qu, Y.; Xu, B.; Li, J.; Song, H.; Zuo, S. Influence of the elevation effect of slope blasting on the vibration velocity of existing buried steel pipes. Sci. Rep. 2024, 14, 23476. [Google Scholar] [CrossRef]
- Su, H.; Ma, S. Study on the stability of high and steep slopes under deep bench blasting vibration in open-pit mines. Front. Earth Sci. 2022, 10, 990012. [Google Scholar] [CrossRef]
- Azarfar, B.; Ahmadvand, S.; Sattarvand, J. Stability Analysis of Rock Structure in Large Slopes and Open-Pit Mine: Numerical and Experimental Fault Modeling. Rock Mech. Rock Eng. 2019, 52, 4889–4905. [Google Scholar] [CrossRef]
- Yan, B.; Liu, M.; Meng, Q.; Li, Y.; Deng, S.; Liu, T. Study on the Vibration Variation of Rock Slope Based on Numerical Simulation and Fitting Analysis. Appl. Sci. 2022, 12, 4208. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, C. Study on dynamic response and safety control of reinforced concrete rigid frame structure under foundation pit blasting. Int. J. Prot. Struct. 2022, 14, 549–570. [Google Scholar] [CrossRef]
- Wang, G. Stability analysis of steep and high bedding rock slopes under the action of underground blasting vibration. J. China Foreign Highw. 2018, 2018, 24–28. [Google Scholar]
- Wu, T.; Zhou, C.; Jiang, N.; Xia, Y.; Zhang, Y. Stability analysis for high-steep slope subjected to repeated blasting vibration. Arab. J. Geosci. 2020, 13, 828. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, W.; Wu, X.; Liu, M.; Li, P. Numerical and experimental investigation of blasting damage control of a high rock slope in a deep valley. Eng. Geol. 2018, 237, 12–20. [Google Scholar] [CrossRef]
- Yin, Z.Q.; Hu, Z.X.; Wei, Z.D.; Zhao, G.M.; Hai-feng, M.; Zhang, Z.; Feng, R.M. Assessment of Blasting-Induced Ground Vibration in an Open-Pit Mine under Different Rock Properties. Adv. Civ. Eng. 2018, 2018, 4603687. [Google Scholar] [CrossRef]
- Li, Q.; Dai, B.; Long, L.; Zhang, D.; Liang, F. Response Characteristics of Slope Subjected to Blasting: A Case Study in Manaoke Open-pit Gold Mine. Geotech. Geol. Eng. 2022, 40, 3957–3971. [Google Scholar] [CrossRef]
- Jiang, N.; Zhou, C.; Lu, S.; Zhang, Z. Propagation and prediction of blasting vibration on slope in an open pit during underground mining. Tunn. Undergr. Space Technol. 2017, 70, 409–421. [Google Scholar] [CrossRef]
- Chen, M.; Lu, W.B.; Li, P.; Liu, M.; Zhou, C.B.; Zhao, G. Elevation amplification effect of blasting vibration velocity in rock slope. Chin. J. Rock Mech. Eng. 2011, 30, 2189–2195. (In Chinese) [Google Scholar]
- Jiang, N.; Zhou, C.B.; Ping, W.; Xu, X.; Lu, S.W. Altitude effect of blasting vibration velocity in rock slopes. J. Cent. South Univ. (Sci. Technol.) 2014, 45, 237–243. [Google Scholar]
- Wu, X.; Wang, M.; Lu, H.; Zhang, Y.; Nie, W. Modified Sadowski formula-based model for the slope shape amplification effect under multistage slope blasting vibration. Int. J. Min. Sci. Technol. 2024, 34, 631–641. [Google Scholar] [CrossRef]
- Tian, L.; Zhu, L.; Yang, Z.; Hu, Y.; Li, P.; Liu, M.; Zhao, G. Prediction formula of blasting vibration under complex terrain based on dimensional analysis. Adv. Comput. Eng. Technol. Res. 2024, 1, 380–386. [Google Scholar] [CrossRef]
- Gao, Y.; Fu, H.; Rong, X.; Paneiro, G. Ground-Borne Vibration Model in the near Field of Tunnel Blasting. Appl. Sci. 2023, 13, 87. [Google Scholar] [CrossRef]
- Shi, J.-J.; Guo, S.-C.; Zhang, W. Expansion of Blast Vibration Attenuation Equations for Deeply Buried Small Clearance Tunnels Based on Dimensional Analysis. Front. Earth Sci. 2022, 10, 889504. [Google Scholar] [CrossRef]







| Name | Natural Density | Saturation Density | Coefficient of Water Saturation | Uniaxial Compression | Young’s Modulus | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| sandstone | 2.64 g·cm−3 | 2.70 g·cm−3 | 0.51% | 30.66 MPa | 13.35 Gpa | 0.30 |
| mudstone | 2.63 g·cm−3 | / | 2.91% | 3.93 MPa | 7.1 Gpa | 0.34 |
| Test Sequence | Numbering | High Displacement/m | PPV/cm·s−1 | Blasting Distance/m | Charge/kg | ||
|---|---|---|---|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | |||||
| I | V1 | 0.10 | 37.72 | 16.38 | 35.20 | 12.80 | 48 |
| 36.92 | 16.42 | 34.56 | 8.23 | 42 | |||
| 36.37 | 32.77 | 33.22 | 4.39 | 36 | |||
| V2 | 20.13 | 1.26 | 43.10 | 48 | |||
| 0.86 | 39.80 | 42 | |||||
| 1.02 | 36.20 | 36 | |||||
| V3 | 50.50 | 0.57 | 1.15 | 1.25 | 81.20 | 48 | |
| 0.35 | 0.63 | 0.66 | 78.90 | 42 | |||
| 0.38 | 0.74 | 0.71 | 75.10 | 36 | |||
| II | V4 | 0.13 | 6.85 | 12.70 | 34.41 | 14.20 | 48 |
| 9.55 | 13.53 | 28.73 | 10.10 | 42 | |||
| 15.29 | 27.91 | 37.36 | 6.30 | 36 | |||
| V5 | 14.01 | 2.36 | 1.50 | 2.83 | 36.00 | 48 | |
| 0.16 | 0.50 | 1.32 | 32.30 | 42 | |||
| 2.30 | 0.72 | 2.70 | 28.80 | 36 | |||
| V6 | 33.65 | 0.68 | 0.61 | 67.40 | 48 | ||
| 0.50 | 0.48 | 63.40 | 42 | ||||
| 0.46 | 0.45 | 60.60 | 36 | ||||
| III | V7 | 0.11 | 12.24 | 16.40 | 35.20 | 13.40 | 48 |
| 13.40 | 16.84 | 34.12 | 9.90 | 42 | |||
| 18.36 | 22.63 | 38.54 | 6.10 | 36 | |||
| V8 | 9.40 | 7.04 | 6.14 | 10.07 | 23.30 | 48 | |
| 4.09 | 4.06 | 3.93 | 19.60 | 42 | |||
| 7.54 | 9.45 | 10.2 | 16.30 | 36 | |||
| V9 | 52.63 | 0.67 | 3.02 | 73.30 | 48 | ||
| 0.16 | 0.80 | 70.70 | 42 | ||||
| 0.42 | 2.74 | 68.10 | 36 | ||||
| Test Sequence | Direction | The Fitting Results of the Sadowsky Formula | Coefficient of Determination (r2) |
|---|---|---|---|
| I | X-direction | 0.720 | |
| Y-direction | 0.965 | ||
| Z-direction | 0.722 | ||
| II | X-direction | 0.975 | |
| Y-direction | 0.967 | ||
| Z-direction | 0.719 | ||
| III | X-direction | 0.929 | |
| Y-direction | 0.817 | ||
| Z-direction | 0.772 |
| Test Sequence | Direction | Fitting Results Considering Elevation Effect Correction | Coefficient of Determination (r2) |
|---|---|---|---|
| I | X-direction | 0.974 | |
| Y-direction | 0.968 | ||
| Z-direction | 0.997 | ||
| II | X-direction | 0.981 | |
| Y-direction | 0.982 | ||
| Z-direction | 0.965 | ||
| III | X-direction | 0.929 | |
| Y-direction | 0.910 | ||
| Z-direction | 0.976 |
| Variable Type | Sign | Paraphrase | Dimension |
|---|---|---|---|
| Dependent variable | μ | Displacement of particle vibration | L |
| v | Peak velocity of particle vibration | LT−1 | |
| a | Acceleration of particle vibration | LT−2 | |
| f | Frequency of particle vibration | T−1 | |
| Independent variable | Q | Explosive quality | M |
| R | The distance between the source of the explosion and the particle | L | |
| H | Difference in elevation between the explosion source and the particles | L | |
| ρ | Density of rocks | ML−3 | |
| c | Vibration wave speed of propagation | LT−1 | |
| t | Detonation time | T | |
| θ | Inclination angle | / |
| Test Sequence | Direction | Fitting Results Considering Elevation Effect Correction | Coefficient of Determination (r2) |
|---|---|---|---|
| I/II/III | X-direction | 0.9928 | |
| Y-direction | 0.9862 | ||
| Z-direction | 0.9946 |
| Blasting Vibration Attenuation Prediction Model Equations | Direction | The Fitting Results of Equations (1) and (2) | Coefficient of Determination (r2) |
| Traditional blasting vibration attenuation prediction model | X-direction | 0.848 | |
| Y-direction | 0.875 | ||
| Z-direction | 0.847 | ||
| Prediction model of blasting vibration attenuation considering elevation effect | X-direction | 0.859 | |
| Y-direction | 0.885 | ||
| Z-direction | 0.902 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Jiang, N.; Sun, Y.; Pan, J.; He, L.; Guo, J.; Zhang, J.; Zhang, Z. Effect of Soft Interlayer Dip Angle on the Attenuation and Prediction of Blast-Induced Vibrations in Rock Slopes: An Experimental Study. Appl. Sci. 2025, 15, 6683. https://doi.org/10.3390/app15126683
Chen S, Jiang N, Sun Y, Pan J, He L, Guo J, Zhang J, Zhang Z. Effect of Soft Interlayer Dip Angle on the Attenuation and Prediction of Blast-Induced Vibrations in Rock Slopes: An Experimental Study. Applied Sciences. 2025; 15(12):6683. https://doi.org/10.3390/app15126683
Chicago/Turabian StyleChen, Sheng, Nan Jiang, Ying Sun, Jian Pan, Liping He, Jianxiong Guo, Jikui Zhang, and Zicheng Zhang. 2025. "Effect of Soft Interlayer Dip Angle on the Attenuation and Prediction of Blast-Induced Vibrations in Rock Slopes: An Experimental Study" Applied Sciences 15, no. 12: 6683. https://doi.org/10.3390/app15126683
APA StyleChen, S., Jiang, N., Sun, Y., Pan, J., He, L., Guo, J., Zhang, J., & Zhang, Z. (2025). Effect of Soft Interlayer Dip Angle on the Attenuation and Prediction of Blast-Induced Vibrations in Rock Slopes: An Experimental Study. Applied Sciences, 15(12), 6683. https://doi.org/10.3390/app15126683






