Abstract
Accurate temperature prediction is critical for ensuring mechanical stability and operational safety during complex operating conditions and long-term operation of rolling bearings. This study proposes a digital twin (DT) system for bearing thermal analysis and a digital twin-driven virtual–real hybrid framework, achieving thermal prediction from low-risk behaviors (low-speed/light-load) to high-risk behaviors (high-speed/heavy-load). To address the time-varying and ambiguous parameters, an efficient Nutcracker Optimization Algorithm (NOA)-based identification mechanism is introduced to dynamically calibrate the virtual thermal model, overcoming the limitations of static modeling and data isolation inherent in conventional thermal analysis methods. The Euclidean distance and uncertainty analysis between real temperature and predicted temperature demonstrate the highly reliable predictive ability of the proposed framework in terms of bearing thermal, especially under variable speed conditions. The proposed framework has certain guiding significance for enhancing thermal safety and fault early-warning capabilities of bearings during long-term operation.
1. Introduction
Rolling bearings constitute critical mechanical connectors between rotating and stationary components in transmission systems. The transient thermal characteristics of bearings are directly governed by multiple operational parameters, including rotational speed, applied load, lubricant performance, and external heat transfer/dissipation conditions. The evolving thermal states throughout the service life present significant challenges to bearing safety. Failure to accurately predict and control temperature surges caused by intrinsic degradation mechanisms (e.g., grease deterioration and mechanical wear) in conjunction with heat influx from adjacent overheating equipment during long-term operation or computational modeling scenarios may induce critical failures such as bearing instability and functional breakdown. These thermal-induced anomalies ultimately damage the operational stability and safety reliability of mechanical systems [,].
On the other hand, there is an indirect correlation between bearing failure and temperature. Extensive research identifies an abnormal increase in bearing vibration acceleration as a key indicator of both incipient failure and approaching end-of-life, a phenomenon typically observed as bearings near the imposed life time []. The root cause lies in the reduction of lubrication performance or excessive mechanical friction induced by prolonged exposure to high temperatures. Under high-intensity operation involving significant speed and load, combined with excessive heat transfer from adjacent components, the temperature of bearing components gradually rises. Prolonged exposure to these elevated temperatures causes degradation of the grease’s performance. Consequently, the degree of mechanical friction between the bearing’s inner/outer rings and the rolling elements increases. When the bearing’s vibration level exceeds a critical threshold, warnings and eventual failure occur.
1.1. Research Background
Within the background of evaluating equipment health status and service life through behavioral analysis of mechanical systems, DT technology has emerged as an innovative solution. This advanced methodology employs multisensory data acquisition to capture physical parameters from real-world operations, which are subsequently mapped to virtual mathematical models via data interaction and integration protocols. Such implementations enable the simulation of latent risks undetectable in physical domains and extreme operational scenarios that defy conventional monitoring, achieving cost-effective acquisition of equivalent or superior information compared to physical prototypes [,]. Current applications of vibration signal-based DT implementations have been extensively deployed in bearing fault diagnosis [], online monitoring [], health management [], and full lifecycle prognosis []. The thermally driven behavioral prediction methodologies derived from DT frameworks have been innovatively extended to diverse domains, including architectural structures [], thermal power generation [], power electronics modules [], lithium-ion batteries [], and electric vehicles []. These approaches demonstrate superior prediction accuracy, enhanced robustness, and low parametric dependency, positioning DT as an interdisciplinary research frontier with significant developmental potential.
The current literature demonstrates limited exploration in predictive methodologies for bearing thermal behaviors. Yuan et al. [] implemented temperature correction models to recalibrate thermal boundaries, achieving digital twin-enabled real-time monitoring of thermal characteristics and health status in motorized spindle bearings. Present research predominantly focuses on refining pure thermal models (virtual layer) through enhanced analytical/numerical approaches for superior temperature computation, exemplified by lumped parameter thermal network (LPTN) [], finite element (FE), and computational fluid dynamics (CFD) [,]. Notably, CFD implementations employing finite volume methods require extensive preprocessing time for 3D model construction and mesh generation. Furthermore, the dynamic phase variations of multiphase media (such as oil–air mixtures in oil lubrication or grease–oil–air mixtures in grease lubrication) within the bearing chamber cavity necessitate advanced techniques like dynamic meshing and user-defined functions (UDFs) for accurate cooling-state simulation and thermal fluid domain analysis. However, the long convergence time during iterative computations remains a critical bottleneck, hindering real-time thermal monitoring and estimation in bearing systems [,]. Consequently, the LPTN model approaches persist as conventional tools for bearing thermal analysis, particularly under transient operational conditions. Ma et al. [] established mathematical models and numerical solutions for heat generation rates in grease-lubricated spherical roller bearings using local heat source analysis. Ai et al. [] developed thermal network models for grease-lubricated bearings through analysis of load distribution and kinematic parameters in high-speed railway double-row tapered roller bearings. Zheng et al. [] systematically compared enhanced thermal node configuration schemes under different lubrication states and proposed an optimized hybrid LPTN model integrating seven-node and multi-node configurations to investigate thermal disparities in oil–air lubricated angular contact bearings.
While these advancements have significantly contributed to virtual modeling frameworks and thermal distribution pattern elucidation, persistent challenges remain in existing thermal models regarding long-term durability analysis.
1.2. Problem Description
(1) The necessity of thermal behaviors prediction: Addressing the demands of predictive maintenance in industrial equipment and thermal failure risks under extreme operating conditions, this study focuses on grease-lubricated rolling bearings for high-speed railway traction motors. Due to the frequent start-stop operational patterns inherent to railway systems, these bearings endure full-lifecycle service characterized by multi-stage acceleration–deceleration dynamics and frequent switching between light and heavy loads. Such operational complexities result in differences in grease degradation states and bearing microscale surface, both critically influencing bearing temperature evolution. Conventional thermal models exhibit limited capability in resolving transient heat transfer characteristics across these dynamically shifting operational stages.
As illustrated in Figure 1, the deep groove ball bearings for the traction motors of high-speed trains were subjected to a multi-stage discontinuous long-term durability test spanning 2778 h. During each stage, the bearing speed was ramped from 0 to 5600 rpm while maintaining a constant radial load of 2650 N, simulating actual operating conditions of traction motors. Post-experimental analysis revealed grease carbonization phenomena in both internal bearing components and chamber surface, induced by sustained frictional heating during testing. The surface morphology characterization of bearing assemblies demonstrated burning marks on the cage and ball surfaces, accompanied by a microscopic crack in the ball surface structure. These observations confirm the critical temperature-dependent degradation mechanisms affecting both bearing surface integrity (particularly smoothness) and lubricant performance. The identified microscopic crack in the final stage implies potential mechanical risks, including abnormal vibration spectra, should the bearing continue operating under such thermally compromised conditions. Conversely, a comparative analysis of temperature rise characteristics on the inner surface of the inner ring and outer surface of the outer ring during the initial, mid, and final stages reveals that the degradation of metal surface smoothness and lubricant effectiveness dynamically alters the frictional heat generation and bearing cooling efficiency. This thermal phenomenon manifests as significant fluctuations in the temperature curves of both surfaces during the final stage, deviating from their theoretically stable thermal progression. The initial stage exhibited higher temperatures compared to the mid-stage, attributable to incomplete grease homogenization. This demonstrates that transient comparisons of bearing temperature rise across different operational stages can effectively reflect both the grease lubrication status and the surface topographical characteristics of bearing components. Consequently, in order to avoid various problems caused by mechanical thermal failures, implementing real-time thermal monitoring and conducting predictive studies on bearing thermal behaviors are essential during long-term durability operation.
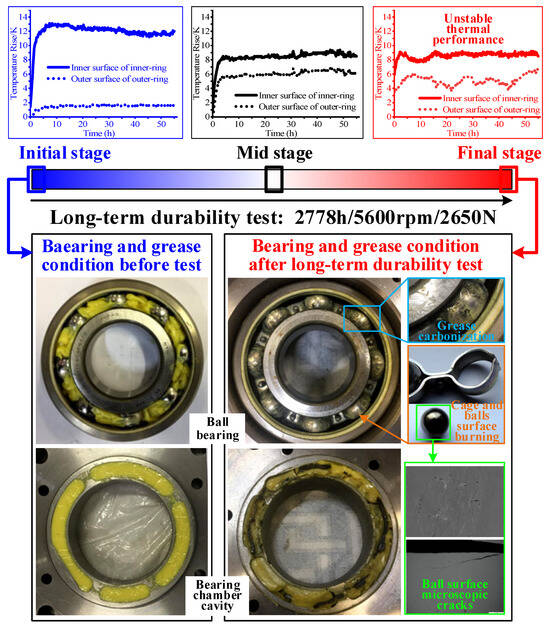
Figure 1.
Comparison of temperature, grease state, and surface morphology of traction motor bearings during long-term durability operation.
(2) The application conditions relying solely on the thermal modeling of the Virtual Model Layer (VML) are limited. Traditional thermal modeling methodologies struggle to obtain accurate computational parameters throughout the entire lifecycle due to variations in grease properties and mechanical wear. Precise bearing thermal modeling relies on calculations of heat sources, thermal resistances (TRs), and heat capacity, particularly real-time varying contact TRs and internal convective TRs dependent on rotational speed and applied loads. Although certain TRs equivalent methods demonstrate satisfactory computational accuracy and simulation efficacy [,], thermal calculations require continuous support from extensive oil–air mixture state data and material property parameters (including viscosity, diffusion coefficient, and Prandtl number of oil–air mixtures) [] (see Section 3). As shown in Figure 1, most of these parameters are environment-dependent variables across operational stages. Sensor limitations in precision and application conditions prevent real-time acquisition of these time-varying physical quantities. Consequently, VML models constructed using initial-stage grease parameters may exhibit deviations between calculated bearing temperatures and actual measurements, rendering them insufficiently accurate for real-time bearing temperature estimation.
Furthermore, from the perspective of the solving process, traditional thermal models adopt a forward-solving approach from physical infrastructure to simulation models to temperature rise results. Consequently, the calculation of thermal capacities, TRs, and heat sources inherently depends on dimensional and material parameters of bearing components [,]. However, in most practical applications, only bearing type and basic model data are available. Critical manufacturing parameters such as detailed cage dimensions, raceway diameters of inner/outer rings, material properties, and lubrication conditions are either partially missing or entirely unknown, introducing significant uncertainties and complexities in thermal model construction. Although parameter ambiguity can be mitigated through high-precision metrology or inverse-solving approaches, the multi-objective optimization-based inverse calculation method for convective heat transfer coefficients proposed in []—which derives optimized parameters from limited experimental data—is currently restricted to steady-state temperature rise analysis under single constant-speed conditions. Its applicability throughout the entire lifecycle requires further investigation.
Parameter identification, as a high-precision method for determining ambiguous numerical values, integrates theoretical models with experimental data for predictive applications. This technique has been widely implemented across multiple domains, such as motor control [], aerospace systems [], power transmission lines [], and chemical engineering [], addressing the identification of electromagnetic properties, modal parameters, vibration characteristics, and gas concentrations. In thermal parameter identification, Feng et al. [] developed a model-optimized automatic parameter identification scheme for lithium-ion batteries to mitigate thermal runaway in battery materials. Zhang et al. [] proposed a thermal model and parameter identification method for calculating axial conductor temperatures of overhead lines in laboratory environments. Sýkora et al. [] established an advanced inverse thermal tomography strategy based solely on boundary-layer thermographic measurements. Cheng et al. [] designed a modified particle filter algorithm with adaptive prediction time windows to identify time-varying parameters in HVAC spatial thermal models. Cao et al. [] introduced an online prediction method for electromagnetic-thermal behaviors in permanent magnet motors using improved lumped-parameter thermal networks with global parameter identification. When thermal model parameters exhibit uncertainties or time-dependent characteristics, constructing simplified mathematical frameworks with dedicated data transfer protocols to determine invariant parameters from partial sampled data becomes critically significant for developing reliable virtual layer mathematical models.
In summary, while DT technology has garnered significant attention in industrial applications in recent years, its implementation for bearing thermal prediction remains in its nascent stages. Compared to conventional pure VML physical modeling approaches, the methodology leveraging DT technology to achieve dynamic parameter updates through physical-virtual interactions has not been extensively explored in bearing thermal management. This technical pathway demonstrates breakthrough potential in scenarios requiring real-time performance and multi-physics coupling. When grease-lubricated bearings operate long-term under extreme conditions such as high-speed, heavy-load, and high-disturbance environments, the thermal behaviors of bearing systems exhibit pronounced nonlinear and time-varying characteristics. Traditional thermal analysis methods confined to VML frameworks face challenges in meeting high-precision real-time monitoring demands due to inherent limitations such as model rigidity and parameter hysteresis.
1.3. Research Contribution
This study leverages the high reliability and fidelity of DT technology to establish a virtual–real hybrid framework based on the key thermal parameter identification, enabling thermal prediction from low-risk behaviors (low-speed, light-load) to high-risk behaviors (high-speed, heavy-load) in bearing thermal analysis. The core innovation lies in overcoming the limitations of static modeling and data isolation inherent in conventional thermal analysis methods, providing real-time and adaptive solutions for bearing thermal behavior analysis under complex operating conditions. This approach significantly enhances thermal safety and fault early-warning capabilities during long-term durability operation.
Unlike some studies on bearing health monitoring or remaining useful life prediction based on vibration signals, the temperature prediction method in this research relies on traditional physical models, adopting a semi-physical and semi-data fusion approach. The training data does not serve machine learning purposes but rather refines the conventional physical model through parameter identification.
The principal contributions, potential application domains, and manuscript structure are outlined as follows:
- Principal contributions
(1) A DT system for bearing thermal characteristics and a digital twin-driven virtual–real hybrid framework are proposed to achieve bearing thermal prediction under complex operating and long-term operation. (2) A key thermal parameter identification mechanism is introduced to dynamically calibrate the virtual thermal model, effectively addressing time-varying and ambiguous thermal parameter characteristics caused by material degradation and grease property evolution during thermal prediction. (3) An NOA-based optimization method is developed to enhance the efficiency of parameter identification processes.
- Potential application domains
The primary research focus of this study is the traction motor bearings of high-speed trains. The proposed thermal prediction methodology enables precise determination of grease service lifecycles and provides risk warning capabilities for thermal faults under high-risk operational scenarios. In analogous industrial applications, this virtual–real framework can leverage digital twin-derived thermal predictions to reverse-optimize physical system control parameters (e.g., lubricant flow rates, cooling fan speeds), thereby advancing preventive maintenance and intelligent control strategies for industrial bearings.
- Manuscript structure
Section 2 introduces the DT system for bearing thermal analysis and the virtual–real hybrid framework for thermal prediction, as well as the influence of input parameters on bearing temperature. Section 3 describes the construction of the LPTN model in VML. Section 4 introduces the NOA-based thermal parameter identification strategy. Section 5 presents the results and discussion of bearing thermal parameter identification and temperature prediction.
2. Methodology
2.1. DT System
The DT system for bearing thermal analysis comprises four components: the Physical Entity Layer (PEL), the Data Acquisition Layer (DAL), the VML, and the Data Mapping Part (DMP), as illustrated in Figure 2.
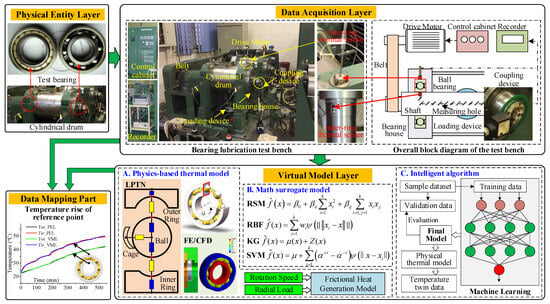
Figure 2.
DT system for bearing thermal analysis.
The PEL constitutes the tangible objects reflecting research characteristics and the physical manifestation of the twin model. The deep groove ball bearing and cylindrical roller bearing, serving as the physical entities of the DT system, are assembled within a cylindrical drum for transient experimental testing under diverse operating conditions.
Based on the bearing lubrication test bench, the DAL employs high-precision sensors and recording instruments to capture high-fidelity real-time data and feature labels during bearing rotational operation. In this study, a monitoring system composed of a control cabinet, inductive coupling device, thermal sensors, and a data recorder measures the surface temperatures of deep groove ball bearings in real time. The control cabinet governs experimental condition loading, including runtime parameterization, load application, and rotational speed regulation. As shown in the overall block diagram of test bench, the outer ring thermal sensor (PT100 platinum resistance thermometer) is inserted into the measuring hole inside the bearing house, and the probe directly contacts the outer surface of the outer ring to measure its temperature. The inner ring thermal sensor (PT100 platinum resistance thermometer, NTN (China) Investment Corporation, Shanghai, China) is embedded within the measuring hole of the shaft, with its probe contacting the inner surface of the bearing inner ring. The lead of the thermal sensor is connected to a non-contact inductive coupling device on the shaft. This arrangement allows the electrical signals to be transmitted from the shaft to the external system. After being processed by the recorder, the temperature measurement of the inner surface of the bearing inner ring is achieved.
The VML can be implemented through three distinct methodologies—physics-based thermal model, mathematical surrogate model, or intelligent algorithm—depending on model category requirements and bearing specifications. The selection among these approaches is governed by engineering constraints, including the clarity of thermal parameters, sensor placement configurations, and measurement accuracy.
- A.
- Physics-based thermal model
When insufficient thermal sensors are available in practical applications, the VML must be constructed exclusively through numerical methods based on thermal models (LPTN/FE/CFD). However, this methodology imposes stringent requirements: precise knowledge of bearing geometric dimensions, grease material properties, and a comprehensive understanding of parameter variation mechanisms during long-term operation. Specifically, all thermal calculation parameters must be fully defined without ambiguity that could compromise result validity. Figure 2 illustrates a simplified 2D-LPTN model with multi-node topology for grease-lubricated traction motor bearings, featuring a deep groove ball bearing operating under pure radial load at rotational speeds. This model has evolved from an initial three-node configuration to a sophisticated multi-node structure incorporating lubricant rheological behavior, thermal expansion effects, and cage interactions [,]. Critical factors in LPTN modeling include node network design, heat source quantification, and TR calculations.
- B.
- Mathematical surrogate model
Surrogate models constitute mathematical frameworks that simulate complex behaviors in black-box systems, originally developed for engineering design scenarios requiring simulated experiments to evaluate objectives and optimize computational processes. These models are constructed through the design of experiments (DOE) to approximate high-fidelity computational systems while reducing experimental costs []. Common surrogate modeling techniques include Response Surface Methodology (RSM), Radial Basis Functions (RBF), Kriging Models (KG), Support Vector Machines (SVM), and Kalman Filters (KF) []. In DT implementations for bearing thermal analysis, mathematical surrogate models can effectively replace conventional thermal modeling approaches when sufficient sensor coverage and data density are achieved, coupled with low degrees of freedom in physical modeling. This substitution significantly reduces both the demand for time-varying parameter characterization and the computational overhead associated with solving numerical governing equations.
- C.
- Intelligent algorithm
In recent years, advancements in sensing technologies and computational capabilities have established machine learning-driven intelligent algorithms as pivotal components within DT structures. Intelligent algorithm-based twin systems leverage extensive historical datasets to generate novel samples for thermal analysis through sequential workflows encompassing data preprocessing, model training, and result validation []. This methodology explores the inherent laws between data patterns and thermal behaviors, circumventing limitations posed by parameter ambiguity and physical modeling constraints. However, its application to bearing thermal analysis necessitates temperature datasets comparable to or exceeding the scale required by the surrogate modeling approaches.
The DMP serves as the functional bridge connecting the bearing physical entity and virtual space, with node temperatures acting as mapping references. When operational constraints prevent the PEL from operating under specific or extreme conditions, the required datasets can be generated by the VML and reflected through the DMP. When the physics-based thermal model is employed in the VML for predictive analysis, the DMP provides validation evidence for the final computational framework. Correspondingly, when the mathematical surrogate models or intelligent algorithms are implemented to construct thermal twins of bearing systems, the DMP’s temperature datasets facilitate model calibration and predictive accuracy enhancement.
The present study employs only two thermal sensors for monitoring the deep groove ball bearings of traction motor, with reference nodes positioned at the inner surface of inner ring and outer surface of outer ring, as shown in Figure 1. This sensor configuration fails to meet the data requirements for constructing the mathematical surrogate model or intelligent algorithm-based VML twin structure. Consequently, a hybrid virtual–real framework driven by the DT thermal system is established, leveraging an LPTN thermal model to achieve thermal prediction transitions from low-risk behaviors (low-speed, light-load) to high-risk behaviors (high-speed, heavy-load) in bearing thermal analysis.
2.2. Digital Twin-Driven Virtual-Real Hybrid Framework
The proposed hybrid virtual–real framework for bearing thermal prediction integrates temperature datasets physically acquired from the real part, with the digital twin-driven virtual part, as detailed in the flowchart of Figure 3.
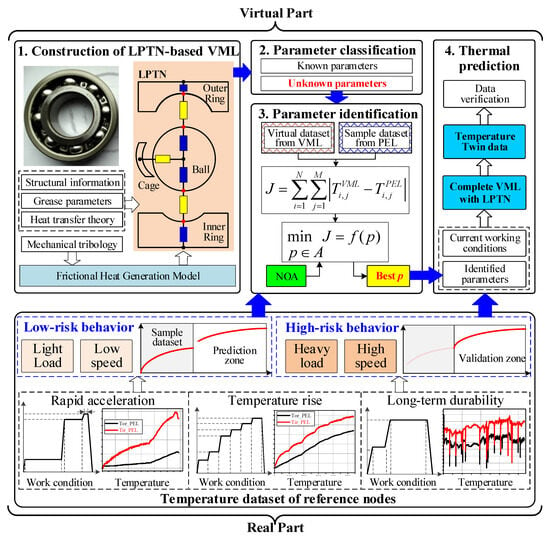
Figure 3.
Flowchart of digital twin-driven virtual–real hybrid framework for bearing thermal prediction.
- A.
- Real part
Within the real part, temperature datasets for the VML reference nodes are generated through multi-category bearing tests simulating actual operating conditions of high-speed electric multiple unit (EMU) traction motors, including rapid acceleration, temperature rise, and long-term durability tests. Given the correlation between steady-state bearing temperatures and operational parameters (radial loads and rotational speeds), bearings under heavy-load/high-speed conditions exhibit significantly higher temperatures compared to light-load/low-speed conditions. Consequently, the temperature datasets are partitioned into two categories: sample data for parameter identification under low-risk behaviors (light load/low speed) and validation data for testing identification accuracy and prediction results under high-risk behaviors (heavy load/high speed).
It is noteworthy that all datasets in this study consist of offline data collected under diverse operating conditions of the bearing, specifically to validate the predictive efficacy of the proposed hybrid virtual–real framework. When deployed for online thermal fault early-warning applications, the framework exclusively acquires temperature data from low-risk behaviors to identify unknown parameters, thereby refining the VML twin structure. High-risk behaviors in this context correspond to extreme operating conditions where bearings are prone to abnormal temperature excursions and incipient thermal faults during service. Real-time thermal anomaly alerts generated by this framework, based on predictive results and historical data correlations, will be demonstrated in future research.
- B.
- Virtual part
The virtual part, grounded in the DT system, is systematically executed through four sequential phases: Construction of LPTN-based VML, parameter classification, parameter identification, and thermal prediction.
- Step 1:
- Construction of LPTN-based VML
An LPTN model is established based on the structural dimensions of the investigated deep groove ball bearing, grease property parameters, and heat transfer theory. Concurrently, a frictional heat generation model for bearing surfaces is developed using tribological principles. These dual models collectively constitute the thermal analysis VML space.
- Step 2:
- Parameter classification
All parameters involved in heat source quantification and TRs calculation within the LPTN model are classified into constant parameters and time-varying/ambiguous parameters (e.g., convective TRs). The intrinsic relationships between these unknown parameters and operational variables (time, rotational speed, and applied loads) are analytically derived to simplify heat source/resistance formulations, thereby defining parameters that need to be identified for subsequent step.
- Step 3:
- Parameter identification
Treating all parameters that need to be identified as independent variables, a fitness function is formulated by aggregating cumulative errors between virtual datasets from the VML and sample datasets from the PEL. This transforms the identification task into a minimization problem seeking optimal parameter values that maximize virtual and sample datasets’ congruence. To accelerate convergence, the Nutcracker Optimizer Algorithm (NOA) is implemented for fitness function optimization.
- Step 4:
- Thermal prediction
Post-identification, the refined LPTN-based VML twin structure is completed. Under current working conditions, thermal twin data are generated, with virtual temperature predictions under high-risk behaviors rigorously validated against data validation.
This completes the digital twin-driven virtual–real hybrid framework for bearing thermal prediction. Subsequent chapters provide a detailed explanation of the constituent models and methods involved in each step.
2.3. Influence of Input Parameters on Bearing Temperature
The selection of the datasets is critical for implementing the proposed temperature prediction framework. Furthermore, determining input parameters for the bearing thermal model necessitates physical analysis of temperature-influencing factors. Leveraging the DT system for bearing temperature monitoring, we conducted multi-condition transient thermal tests using bearing lubrication test bench within the PEL and DAL. The resultant temperature variations at reference nodes—outer surface temperature (Tor)of the outer ring and inner surface temperature (Tir) of the inner ring—versus operational inputs (rotational speeds and radial loads) are presented in Figure 4.
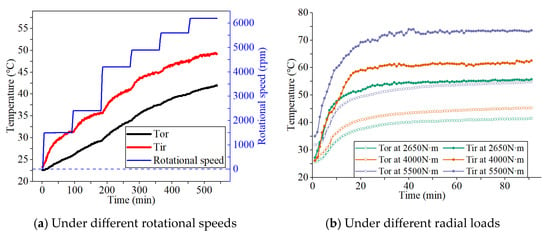
Figure 4.
Influence of input parameters on bearing temperature of reference nodes.
In Figure 4a, the radial load on the bearing is set at 2650 N·m. When the rotational speed is held constant for specific durations, the temperature at the reference node exhibits a continuous rise over time under each constant speed. Furthermore, each switch to a higher speed resulted in a further temperature increase. The bearing consistently failed to reach thermally stable state under unchanged heat dissipation conditions, indicating intensified frictional losses. This demonstrates that rotational speed is one of the factors influencing bearing temperature.
In Figure 4b, the bearing rotational speed is fixed at 6000 rpm. Higher radial load leads to increased bearing temperatures. Notably, when the radial load applied to double (5500 N·m), the steady-state temperatures on the inner surface of the inner ring and the outer surface of the outer ring increased by nearly 20 °C and 15 °C, respectively, compared to the 2650 N·m condition. This demonstrates that radial load is also one of the factors influencing bearing temperature.
The above physical analysis clarified the influencing factors of bearing temperature and determined the input parameters of the bearing thermal model.
3. Construction of LPTN-Based VML
3.1. Bearing LPTN Model
The time it takes for a bearing to roll for one cycle is much shorter than the time it takes for heat to diffuse along the circumferential direction of the raceway. Therefore, assuming that the transient temperature of the bearing is symmetrically distributed along the axis, the 3D heat transfer problem is transformed into a 2D problem []. The selection of nodes, calculation of heat sources, and TRs are key conditions for constructing the LPTN model, which has evolved from the initial simple three-node model to a multi-node thermal model that considers the rheological properties of lubricants, thermal expansion, and the influence of retaining frames []. Under the lumped mass assumption, the LPTN model for the traction motor’s deep groove ball bearing and its house is configured with 14 nodes, as illustrated in Figure 5, with detailed node description provided in Table 1.
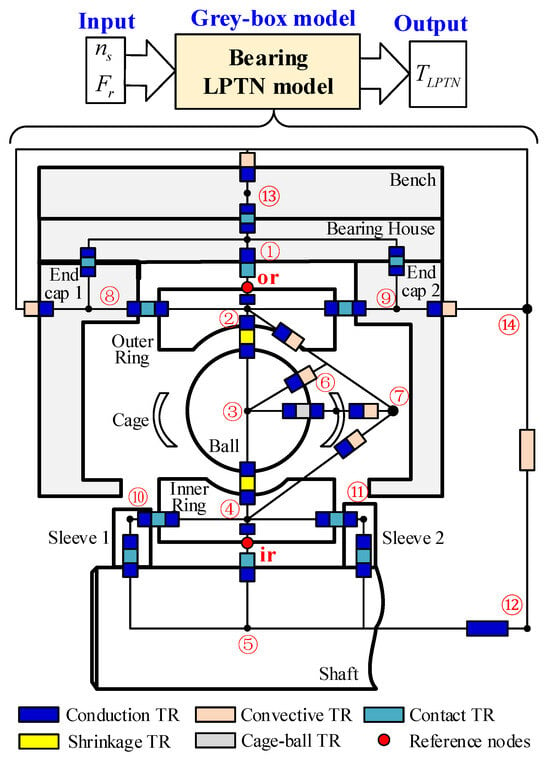
Figure 5.
LPTN model for the traction motor’s deep groove ball bearing and its house.

Table 1.
Description of nodes.
In order to solve the LPTN model, it is necessary to set initial and boundary conditions. In this study, the initial temperature of the T1~T13 temperature nodes was set to 22.6 °C to match the experimental environment. The T14 temperature node is set as a boundary condition, i.e., the temperature of the surrounding environment, ignoring its changes over time, and is also set to 22.6 °C. The time step for solving is set to 60 s.
Critical analysis reveals that the investigated bearing, primarily subjected to radial loads, generates heat dominantly through three mechanisms: frictional heating at rolling/stationary component interfaces, viscous power dissipation within the lubricant, and auxiliary frictional losses from other elements. During thermal transients, non-uniform thermal expansion of solid materials, induced by temperature gradients and geometric constraints, alters initial interference fits and introduces thermally induced loads []. Concurrently, temperature-dependent variations in grease kinematic viscosity induce time-varying friction torque fluctuations at contact interfaces, thereby modifying global heat generation patterns. Notably, certain parameters in heat source calculations derived from empirical formulations exhibit strong dependencies on bearing type, operational loads, rotational speeds, and initial conditions. While the existing literature provides nominal value ranges for these parameters [], their precise quantification under transient operational states remains unresolved.
Furthermore, heat transfer between nodes primarily occurs through contact conduction and convective heat transfer mechanisms []. Temperature variations exhibit negligible influence on the thermal conductivity of solid materials, while thermal expansion effects on conduction TRs related to bearing dimensions are considered insignificant. Consequently, conduction TRs of solid components remain essentially invariant and are categorized as constant TRs. Conversely, Hertzian contact TRs within bearing clearances and ball/roller-cage gaps, as well as TRs induced by grease–oil–air mixtures, demonstrate strong dependencies on rotational speeds and applied loads []. Additionally, grease’s physical properties (e.g., kinematic viscosity, thermal conductivity, and density) exhibit working conditions-dependent behavioral patterns [], classifying these resistances as variable TRs. The precise quantification of such resistances necessitates complex computational procedures involving initialization protocols and nonlinear problem-solving, where calculation accuracy directly governs the fidelity of thermal analysis and temperature prediction results.
As established in Section 1.2, the investigated bearing undergoes multi-stage operational states characterized by dynamic speed transients and frequent load switching throughout its lifecycle. For analytical tractability, we posit that within any given operational stage, microstructural bearing morphology, lubricant characteristics, and convective conditions remain invariant. Under this stage, thermal parameters (heat sources, TRs) exhibit exclusive dependence on instantaneous operating conditions (rotational speed and radial load).
Conceptualizing the integrated thermal model of the bearing assembly as a system, the given inputs are defined as rotational speed and radial load, with node temperatures constituting system outputs. This framework constitutes a gray-box model [] where precisely calculable parameters derive from material properties and geometric specifications, while empirically estimated parameters require iterative calibration via experimental measurements. Obviously, all variable parameters within the LPTN model demonstrate strong correlations with rotational speed and radial load. The subsequent analysis provides rigorous mathematical formulations for heat source quantification and TRs classification.
3.2. Fractional Heat Generation Model
Palmgren’s analytical method for heat generation rate calculation, derived from extensive experimental measurements and empirical formulations, has been validated across numerous studies under moderate loads, medium rotational speeds, and optimal lubrication conditions []. This method establishes that for deep groove ball bearings subjected exclusively to radial loads, the heat generation rate is calculated as the product of total frictional torque and bearing rotational speed. To explicitly characterize the intrinsic relationship between unknown parameters in thermal loss calculations and system inputs (rotational speed and radial load ), the formulation is expressed as a function of these operational parameters:
where and are the friction torque related to the radial load and thermally induced preload on the bearing, calculated according to the following formula, respectively.
In the formula, is the coefficient related to the type of bearing and the load it is subjected to. For the deep groove ball bearings under only radial load conditions, its value is . and are, respectively, the equivalent static load and rated static load, obtained from the product design manual of the bearing.
The frictional torque determined by bearing type, rotational speed, and grease properties, is calculated as follows:
In the formula, is the coefficient related to the type of bearing and lubrication method. For grease-lubricated deep groove ball bearings, the value is 1.5~3.5, which is used as the unknown parameter to be identified. The relationship between the kinematic viscosity of lubricating grease base oil and working temperature is as follows [].
In the formula, is the viscosity–temperature coefficient of the lubricant, and and are the working temperature and initial temperature, respectively, and is the viscosity of the lubricant at the initial temperature.
describes the total heat generation of the bearing components. When solving the LPTN model, the total heat generation is distributed to the outer ring, rolling elements, and inner ring in a ratio of 1:2:1 [], namely nodes ②, ③, and ④ in Figure 5.
3.3. Calculation and Classification of TRs
To determine the parameters requiring identification in the LPTN model, all TRs in the LPTN model (Figure 5) are systematically calculated and classified. This process aims to establish intrinsic relationships between time-varying/ambiguous TRs and operational variables (rotational speed and radial load ), ultimately deriving simplified mathematical expressions for parameter identification.
3.3.1. Constant TRs
The constant TRs in the bearing LPTN model primarily include the radial conduction TRs of the inner/outer rings, conduction TRs of rolling elements, conduction TRs of the rotating shaft and bearing chamber, and contact TRs at solid–solid interfaces. Due to the negligible influence of external loads on contact TRs, these terms are omitted from computational considerations. Additionally, the natural convection heat transfer coefficient between the bearing chamber’s outer surface and ambient air is treated as a constant. Mathematical formulations for these constant TRs are summarized in Table 2 [].

Table 2.
Calculation of constant TRs.
3.3.2. Variable TRs
Applied radial loads and rotational speeds induce variations in specific TRs, which mainly include the thermal shrinkage TRs between the inner/outer race raceway and the rolling elements, and the convective TRs between the oil–grease–air mixture inside the bearing cavity and rolling elements (including cage), as well as inner/outer ring surface.
- Shrinkage TRs
The contact heat transfer between the inner/outer ring raceways and rolling elements is related to the moving heat source. Considering factors such as contact area and pressure, the mathematical expression of the shrinkage TRs model proposed by Muzychka et al. [] based on Hertz contact theory is as follows:
where is the thermal conductivity of the medium and is the Peclet number. and are the diffusion coefficient and the linear velocity of the contact area, respectively. and are the semi-major and semi-minor axes of the elliptical, respectively, which can be expressed by the following formula.
where and are the dimensionless quantities obtained from the lookup table. , , and are, respectively, the elastic modulus and Poisson’s ratio of the two contact materials. and are the curvature and normal contact load at the contact point. In the deep groove ball bearings that only bear radial loads, the normal contact load is proportional to the radial load. Assuming that the size and physical parameters of the bearing material remain basically unchanged during the temperature rise process, substituting Equation (6) into Equation (5), the contact TRs is related to the radial load and rotational speed of the bearing as follows:
Let the proportional coefficient of the contact TRs in the bearing contact area be and , respectively. Then, the simple expression is
In the formula, and are related to the size and physical parameters of each bearing component. When the influence of temperature rise on these parameters is ignored, the proportional coefficient is approximately constant and set as the parameter to be identified.
- Convective TRs
The bearing cavity is filled with a mixture of grease, precipitated lubricating oil, and air (the vast majority). As the bearing rotates, the oil–grease–air mixture undergoes convective heat transfer with the inner/outer rings, cage, and rolling elements at all times. According to the expression of convective TRs []
where , , and represent the characteristic length, fluid thermal conductivity, heat dissipation area, and Nusselt coefficient, respectively. The first three parameters remain basically unchanged, and the calculation of the Nusselt coefficient requires approximating each part of the bearing as a typical heat transfer model [].
According to the calculation method summarized in [], the convection model of balls and oil–grease–air mixture is equivalent to a roller immersed in an infinite medium, such as 3–6 in Figure 4. In the case, for the Nusselt number during convection between balls and oil–grease–air mixture, there are
where , , , and represent the density, viscosity pressure, viscosity coefficient, dynamic viscosity of the oil–grease–air mixture, and balls diameter, respectively. These parameters remain relatively constant during the stage operation. is the race linear velocity of the rolling element, which is positively correlated with the speed of the bearing. Let the parameters to be identified as , , , where the physical meaning of can be regarded as the natural convection heat transfer coefficient when the speed is 0. The simple relationship between the Nusselt number of rolling elements and the bearing speed can be expressed as:
Such as the node pair 2–7 in Figure 4, the Nusselt number for convection between the outer ring and the oil–grease–air mixture is equivalent in the form of two concentric rotating cylinders and calculated using the following equation:
The Nusselt number in the above equation is also related to the bearing speed, and the simplified calculation formula for the convective Nusselt number of the inner/outer rings can also be used in a similar way to Equation (11)
For the node pairs 4–7 and 6–7 in Figure 4, we simplify it into a convection model of a rotating disk and a shaft end to calculate the Nusselt number between inner ring/cage and oil–grease–air mixture using Equation (15).
Similarly, the Nusselt number in this equation is also related to the rotational speed and is expressed in a similar form as:
Based on the above analysis, 15 unknown parameters that need to be identified are stored in the set as follows:
4. Parameter Identification
4.1. State Space Representation and Discretization
To enhance the utility of the LPTN model within the VML for parameter identification, the LPTN framework is first reformulated into a continuous state-space representation. Concurrently, the governing state equations are discretized to align with implementation requirements. Given that bearing losses and certain TR calculations are inherently linked to radial load and rotational speed , a loss vector is defined encompassing all heat sources within the LPTN model. Let and denote matrices of known and unknown TRs, respectively. Under steady-state conditions, the node temperatures are formulated as:
For transient analysis, time parameters are explicitly incorporated into the governing equations. The heat transfer dynamics adhere to the energy conservation principle: the net heat flux at any node equals the internal energy accumulation within the corresponding component volume []. This relationship is mathematically expressed as:
where , and , respectively, represent the vectors formed by the specific heat capacity, density of the material, and component volume. is the temperature change vector in a time period , and is the temperature vector at the current time. Write the above formula as the state space form as:
In the formula, and are the system matrix and input matrix composed of TRs and heat capacity, respectively. and , respectively, are system input variables and output variables, where is related to bearing loss and ambient temperature. represents the reference node temperatures corresponding to the sample datasets (real parameters) obtained from the PEL during identification, that is, the inner surface temperature of the inner ring and the outer surface temperature of the outer ring in this paper, which can be obtained by the temperature of adjacent nodes.
To enable the identification of unknown parameters and real-time processing in thermal modeling, the continuous state-space equations require discretization. Employing the Euler discretization method with a fixed sampling period , and assuming the input matrix remains constant during each sampling period, the discretized state-space representation is formulated as []:
where the superscript and represent the two moments before and after the discrete time, respectively.
4.2. NOA
The NOA is a metaheuristic algorithm inspired by the food-searching behavior of nutcracker birds. It employs distinct local and global search operators to address diverse optimization challenges. Compared to classical algorithms such as Particle Swarm Optimization (PSO), Slap Swarm Algorithm (SSA), and Whale Optimization Algorithm (WOA), the NOA demonstrates advantages including ease of implementation and rapid convergence rates [].
The NOA-based thermal parameter identification process for bearings is illustrated in Figure 6. Referring to Figure 6, the implementation process of the NOA can be divided into Parameter Setup, Initialization, Loop Process, and Accuracy Judgment. The detailed description of each step is as follows.
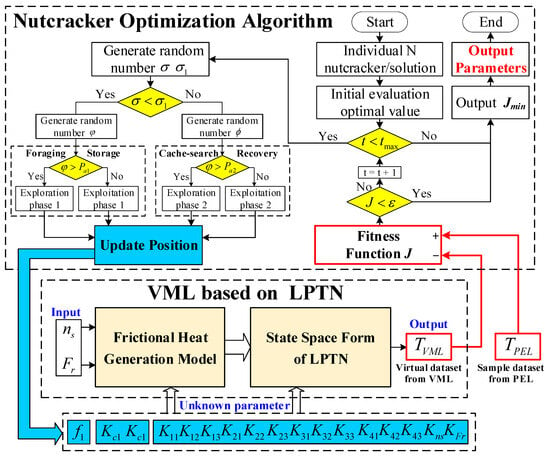
Figure 6.
Process of the NOA-based thermal parameter identification.
- Step 1:
- Parameter Setup
Set the necessary basic parameters for the NOA program, including population size, upper and lower limits, the current and maximum number of iterations, and accuracy of requirements.
- Step 2:
- Initialization
During program execution, initialization is first required based on the value ranges of thermal parameters, i.e.,
where is the j-th position of the i-th nutcracker in the current generation t. and are upper and lower boundaries constructed from the maximum and minimum values within the range of D-dimensional thermal parameters. is a random vector within the range of [0, 1].
- Step 3:
- Loop Process
In the loop process, the NOA operates through two core strategies: Foraging and Storage Strategy/Cache-Search and Recovery Strategy. To mitigate accidental behaviors and local optima entrapment, the NOA employs stochastic selection between these two strategies through generating random numbers, each governed by distinct mathematical formulations and variable update mechanisms. Both strategies include two phases, the exploration phase and the exploitation phase. The selection of two stages is determined by random values between 0 and 1 and probability values between 1 and 0.
- Strategy 1:
- Foraging and Storage Strategy
At the exploration phase 1 in this strategy, the nutcracker adopts a location update strategy to determine whether a good seed is being found and bring it into the storage area. Each candidate solution represents a potential parameter set. New-generation solutions are generated through nutcracker-inspired behavioral rules and positional inheritance from predecessor solutions. The variable update mechanism at the exploration phase 1 is mathematically expressed as:
where is the new position of the i-th nutcracker in the current generation. is the j-th position of the nutcracker in the current generation. is a number generated based on Lévy-flight. is the j-th dimension of the best solution obtained even now.// are randomly selected from three different indices. /// are random variables ranging from 0 to 1. is the mean of the jth dimensions of all solutions of the current population in the iteration. is a randomly generated comparison number based on normal distribution, Lévy-flight and 0~1.
At exploitation phase 1 in this strategy, the nutcracker transporting the seeds to temporary storage location and store them. The variable update mechanism at exploitation phase 1 is mathematically expressed as:
where is the new location of the nutcracker storage area in the current generation t. is the highest function quality of the current generation. is a number generated based on Lévy-flight. // are random variables ranging from 0 to 1. is a linearly decreasing factor from 1 to 0 introduced in the NOA development behavior to avoid falling into local optima.
- Strategy 2:
- Cache-Search and Recovery Strategy
This strategy simulates the behavior of nutcrackers searching for food in winter, using spatial memory methods to locate the location of their seeds. The nutcracker should consider all possibilities encountered when searching for its cache. The detailed variable update mechanism of this strategy can be found in Reference []. The performance of each candidate solution is evaluated by comparing the fitness function values of newly generated solutions with their predecessors. If a new-generation solution exhibits superior fitness quality, the parameter sets updated accordingly. Otherwise, the original solution is retained. This selection mechanism is mathematically defined as:
- Step 4:
- Accuracy Judgment
The convergence criterion is determined by evaluating whether the fitness function value satisfies the accuracy of requirements, indicating successful localization of the global minimum solution. The current position corresponding to the output minimum value is designated as the optimal parameters. If this requirement is not met, return to step 3.
This is the basic optimization process of NOA, and the next section will briefly explain the parameter identification method based on NOA.
4.3. Parameter Identification Strategy
The critical challenge involves establishing precise mappings between the state-space model, thermal network model, and optimization algorithm—translating the thermal parameter identification problem into a multidimensional optimization framework. In this strategy, thermal parameters requiring identification are stored in set , which is equivalent to candidate solutions . During each generational iteration, updated parameters are propagated into the LPTN model within the VML through the NOA’s positional update mechanisms.
The LPTN model is expressed in state-space form with input (time-varying rotational speed and radial load) and output temperature . For the transient-state or high thermal gradient conditions, outputs correspond to real-time temperatures at reference nodes. Under the steady-state or low thermal gradient conditions, outputs represent domain-averaged temperatures. As shown in the Equation (19), inputs and outputs of the LPTN model directly map to the state-space model’s and , respectively. The system matrix and input matrix embed unknown parameters , which are treated as optimization variables in the NOA. This equivalence allows NOA’s “food location” search mechanism to correspond to parameter identification, where identifying unknown thermal parameters is analogous to seeking the best position in the algorithm’s logic. To accelerate NOA convergence and improve results’ accuracy, the MATLAB R2021a implementation employs parallel computing techniques leveraging multi-core processors, significantly reducing computational time while maintaining solution accuracy. Owing to the nonlinear characteristics of bearing contact TRs and the complexity of convective heat transfer within the bearing chamber, recursive formulations designed for linear systems, such as least squares and maximum likelihood methods, yield suboptimal identification performance. To address this limitation, a fitness function based on cumulative temperature error aggregation is adopted for solution quality evaluation, expressed as:
where and are the reference node temperatures for the virtual datasets and sample datasets, respectively, while and refer to the total number of sample data and reference nodes, respectively. Through key thermal parameter identification, the most accurate thermal parameters are ultimately obtained, ensuring that the virtual temperature datasets at all reference nodes closely approximate the experimental temperature datasets. This process achieves determination of unknown parameters within the LPTN in the VML, thereby enabling high-fidelity thermal prediction for bearing systems under complex operational conditions.
5. Results and Analysis
5.1. Comparison of Parameter Identification Results
To evaluate the efficacy and applicability of the NOA-based thermal parameter identification method, a simplified LPTN model is designed as shown in Figure 7. The model comprises five temperature nodes and seven TRs, where Node ⑤ represents ambient temperature. A linear heat source is applied in a 1:1 ratio to Node ② and Node ③. TRs ,, and are predefined constants, while and are unknown constant TRs. To emulate the nonlinear exponential characteristics of thermal parameters in full-scale bearing LPTN models, is formulated as a time-varying TR expressed through a power law function with unknown coefficients. Mathematical expressions for all unknown parameters are provided below:
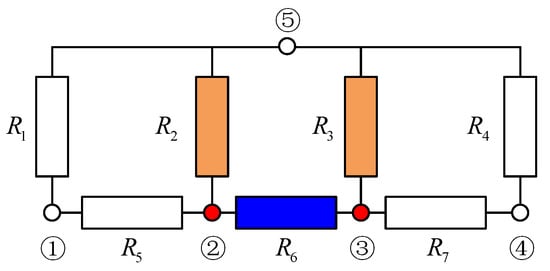
Figure 7.
Simple LPTN model.
From this, it can be inferred that the set of thermal parameters that need to be identified is .
The model inputs are defined as the bearing’s rotational speed and radial load , with outputs corresponding to real-time temperatures at reference Nodes ① and Node ②. The experimental procedure is initiated by giving predetermined target thermal parameters , followed by forward-solving the LPTN model to generate a benchmark dataset under these target parameters. This dataset, combined with a predefined range for thermal parameter values, is then imported into the NOA-based identification framework for unknown parameter identification. Throughout the identification process, the convergence process of each parameter relative to its target value is illustrated in Figure 8.
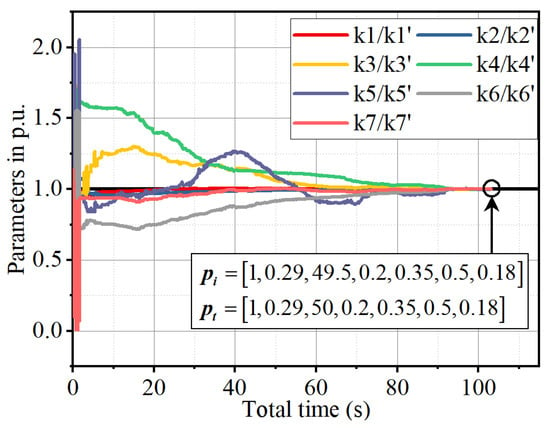
Figure 8.
Comparison of convergence process and results of identification value relative to target value .
As illustrated in Figure 8, the per-unit values of all parameters progressively approach unity as the identification process iterates, indicating that the identified values converge toward their target values. Ultimately, the identified parameters exhibit near-complete agreement with the target values, conclusively demonstrating the feasibility of the NOA-based identification method in resolving time-varying and nonlinear unknown parameters within the LPTN model.
To evaluate the efficiency of the NOA-based identification strategy, a comparative analysis was conducted under identical computational resource allocations, search space dimensions, and maximum iteration constraints. The PSO algorithm was applied to identify unknown parameters in the simplified LPTN model, with comparative results detailed in Figure 9. Parameter served as the benchmark metric: the NOA-based method achieved the required accuracy threshold within 103 s, whereas the PSO-based approach required 1045 s to meet convergence criteria, demonstrating a tenfold disparity in identification efficiency.
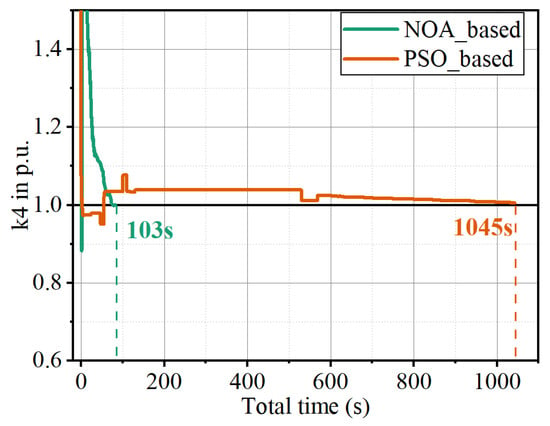
Figure 9.
Comparison of identification speed between NOA-based and PSO-based.
These findings conclusively demonstrate the superior identification efficacy and convergence performance of the NOA-based method. The integration of this approach with the proposed digital twin-driven hybrid virtual–real framework enables the systematic exploration of parameter identification capabilities and thermal prediction accuracy for deep groove ball bearings in traction motor applications.
It is critical to note that the experimental datasets in the bearing test rig play a pivotal role in accurately identifying unknown parameters within the LPTN model. The selection of an appropriate sample dataset must account for comprehensive bearing operation, steady-state thermal equilibrium, and environmental variations. However, the hydraulic loading system in the test platform exhibits inherent pressure hysteresis, limiting rapid load control during transient operations. To mitigate the influence of equipment limitations on bearing temperature responses, this study adopts a single-variable control strategy: system inputs are constrained to individual variables (either fixed radial load with variable rotational speed or fixed speed with variable radial load), enabling systematic investigation of thermal parameter identification capabilities and thermal prediction performance under both variable-speed and variable-load conditions using the proposed digital twin-driven virtual–real hybrid framework.
5.2. Thermal Prediction Under Variable Speed Conditions
5.2.1. Comparison of Predicted and Real Temperature
The case study employs a 6311 deep groove ball bearing, with fundamental dimensions detailed in Table 3 and material parameters detailed in Table 4. Under a fixed radial load (2650 N), rotational speed is utilized as the input variable for thermal parameter identification. During the temperature rise test, six operational speed conditions are defined: 1500 rpm, 2400 rpm, 4200 rpm, 4900 rpm, 5600 rpm, and 6200 rpm. Each speed condition is maintained for designated durations to acquire comprehensive temperature datasets across the entire operational range. Reference nodes are defined as the inner surface temperature of the inner ring and the outer surface temperature of the outer ring of the deep groove ball bearing.

Table 3.
Bearing fundamental dimensions.

Table 4.
Material parameters.
As illustrated in Figure 10, temperature comparisons at reference nodes obtained through the proposed digital twin-driven virtual–real hybrid framework are presented and the identified values of unknown parameters are showed in Equation (27)
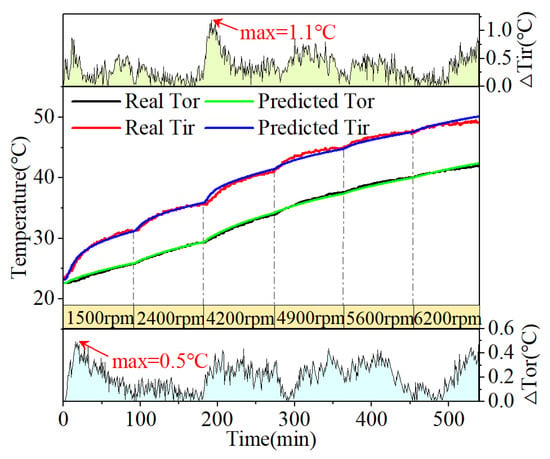
Figure 10.
Temperature and errors comparison of reference nodes under variable speed conditions (Real Tor/Real Tir: real measured temperature acquired from the PEL. Predicted Tor/Predicted Tir: Predicted temperature generated by the bearing LPTN model from the VML).
The predicted temperature generated by the VML exhibit strong congruence with the real temperature acquired from the PEL, as shown in Figure 10. The temperature discrepancies at the inner surface of the inner ring and outer surface of the outer ring are plotted in the upper and lower subplots, respectively, with maximum errors of approximately 1.2 °C and 0.5 °C. This empirically confirms the accuracy of the proposed methodology in identifying bearing thermal parameters. Due to sensor number limitations, experimental validation data for non-reference nodes are unavailable. Consequently, the parameter identified in Figure 10 was integrated into the VML twin structure to generate twin temperature datasets for all bearing nodes, as illustrated in Figure 11. The thermal distribution reveals significantly elevated temperatures at the inner ring and shaft sleeve compared to other components. The bench’s large-volume components exhibit enhanced heat dissipation capacity due to their substantial surface area, resulting in minimal temperature rise. This thermal gradient aligns with empirical observations, confirming the physical plausibility of all the temperature nodes results.
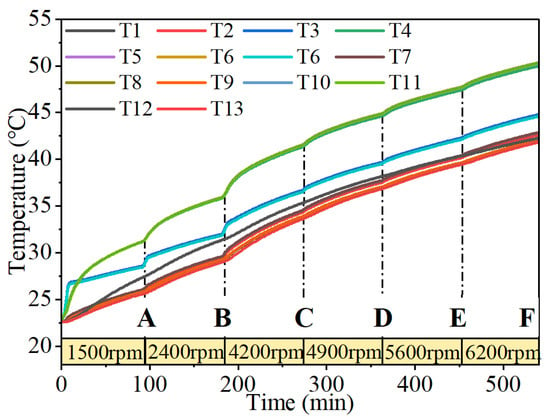
Figure 11.
Twin temperature data of all temperature nodes.
Uncertainty analysis plays a critical role in verifying prediction model accuracy and systematically evaluating uncertainty and aleatory variability inherent. To further validate the thermal prediction accuracy of the digital twin-driven hybrid virtual–real framework, the identified parameters shown in Equation (26) are imported into the LPTN model of the bearing, and the predicted temperature of the reference nodes is compared with the real temperature measured under the condition of rapid acceleration test. The temperature comparison and uncertainty analysis results are shown in Figure 12.
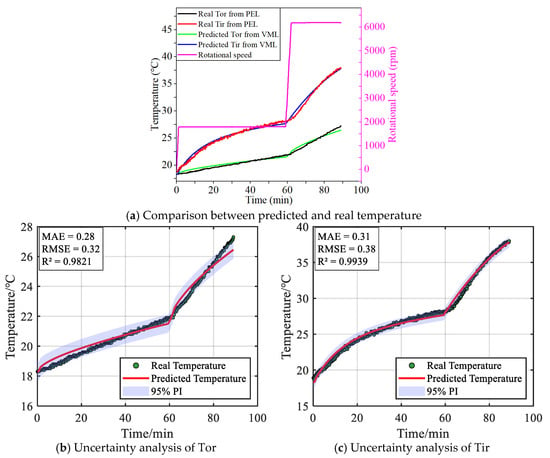
Figure 12.
Temperature prediction results and uncertainty analysis in rapid acceleration test (Tor: temperature of outer surface of the outer ring; Tir: temperature of inner surface of the inner ring).
From Figure 12a, it can be seen that the predicted temperature of the reference node is basically consistent with the real measured temperature. Figure 12b,c present the uncertainty analysis results for the real and predicted temperatures at the reference node, respectively. As shown, the R2 values for the temperature curves at the reference node are 0.9821 and 0.9939, indicating high accuracy of the thermal prediction model under varying rotational speed conditions. Uncertainty is quantified using prediction intervals (PI). Both subfigures exhibit relatively wide PI, with nearly all real temperature data points falling within the 95% PI of the predicted temperatures, confirming the robust predictive capability of the implemented framework.
5.2.2. Influence on Prediction Efficacy of Sample Size and Reference Node Numbers
In the prediction model, the number of samples and reference nodes are the key factors determining the prediction accuracy. To analyze the influence on prediction efficacy of sample size and reference node numbers, real temperature datasets from the PEL are partitioned into two subsets: sample dataset simulating low-speed under low-risk behaviors and validation dataset representing high-speed under high-risk behaviors. The framework’s predictive capability was evaluated by comparing validation temperatures against predictive temperatures of reference nodes across varying sample sizes, as depicted in Figure 13. Detailed scheme specifications and maximum temperature errors at reference nodes are quantitatively contrasted in Table 5 and Table 6.
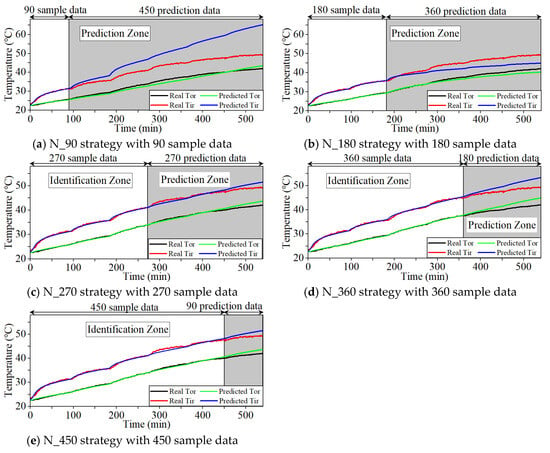
Figure 13.
Temperature comparison reference node under different sample sizes.

Table 5.
Detailed scheme specifications under varying sample sizes.

Table 6.
Comparison of predicted and validated data under varying sample sizes.
The digital twin-driven hybrid virtual–real framework was evaluated using five strategies: N_90, N_180, N_270, N_360, and N_450, corresponding to 90, 180, 270, 360, and 450 temperature sample data size, respectively. The N_90 strategy exclusively utilized temperature samples from the low-speed 1500 rpm, resulting in significant prediction deviations with maximum errors of 3.7 °C and 3.0 °C at reference nodes. In contrast, other strategies incorporating multi-speed operation demonstrated improved predictive accuracy, highlighting the necessity of diverse speed-range samples for accurate thermal parameter identification.
Notably, while increased sample size (e.g., N_360 and N_450) theoretically enhances data density, their prediction temperature in the prediction zone exhibited suboptimal alignment with validation temperatures. Conversely, the N_270 strategy achieved superior accuracy despite a moderate sample size, yielding maximum reference node errors of 0.6 °C and 1.3 °C. This conclusively demonstrates that the selection of sample data sizes significantly impacts the thermal prediction outcomes of the proposed framework. In practical implementations, priority should be given to datasets encompassing diverse speed-range operational conditions to ensure robust parameter identification and prediction accuracy.
To comprehensively analyze the thermal prediction performance of the proposed framework, a Euclidean distance-based similarity assessment method [] was employed to quantify the discrepancy between twin temperature datasets encompassing all nodes and the aforementioned predicted temperatures, as illustrated in Figure 14.
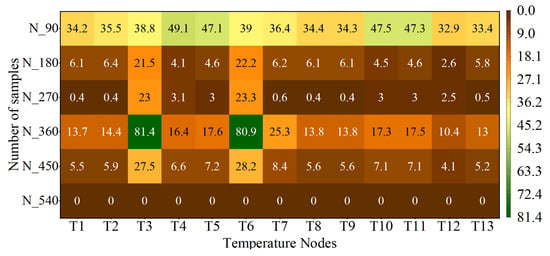
Figure 14.
Similarity of temperature nodes with different sample sizes.
In Figure 14, numerical values and color gradients represent similarity levels, where smaller values or brown-dominated hues indicate higher congruence between predicted temperatures and twin temperatures , signifying superior predictive accuracy. Table 6 quantifies the average Euclidean distances across all nodes for each scheme. Analysis of the numerical trends and color distributions across nodes T1~T13 reveals that the N_270 scheme achieves the lowest Euclidean distances at all nodes except T3 and T6, with the minimum value 0.5 K observed at node T13. This aligns with the conclusions drawn from Figure 11, demonstrating that the digital twin-driven hybrid framework utilizing 270 sample data sizes yields parameters with the best predictive validity during the temperature rise test. This is further corroborated by the N_270 scheme’s globally minimal average Euclidean distance of 4.9 K across all nodes, as detailed in Table 6. Notably, the elevated Euclidean distances at nodes T3 and T6 may stem from the selected reference nodes (/), as the framework prioritizes minimizing discrepancies at these reference points during thermal prediction. To investigate this hypothesis, the proposed framework was re-evaluated using 180 sample data sizes while varying the number of reference nodes. Comparative results of temperature similarity and average Euclidean distances for these schemes are systematically presented in Figure 15 and Table 7.
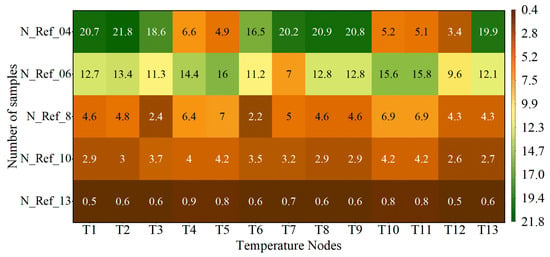
Figure 15.
Similarity of temperature nodes with different numbers of reference nodes.

Table 7.
Detailed scheme specifications and average Euclidean distances.
As illustrated in Figure 15, while the N_Ref_4 scheme, which utilizes four temperature reference nodes exhibits the smaller Euclidean distances between predicted and twin temperatures at specific nodes, the maximum Euclidean distance reaches 21.8 at node T2, and the average Euclidean distance of all nodes reaches 13.7, that indicates the lower prediction accuracy for this scheme. In contrast, the N_Ref_6, N_Ref_8, and N_Ref_10 schemes demonstrate localized improvements in similarity. For instance, the Euclidean distance at node T3 under N_Ref_8 scheme is 2.4, lower than 3.7 of N_Ref_10 scheme, yet this does not signify global superiority, as other nodes within N_Ref_8 exhibit higher deviations.
A comprehensive analysis of average Euclidean distances reveals a monotonic reduction from 13.7 (N_Ref_4) to 0.7 (N_Ref_10) as the number of reference nodes increases. This trend empirically validates that augmenting the number of reference nodes enhances the congruence between predicted and twin temperature datasets. Specifically, when the proposed digital twin-driven virtual–real hybrid framework employs a low-speed sample dataset under low-risk behavior for thermal prediction, adopting more reference nodes can improve the accuracy of parameter identification within the LPTN model, thereby accurately predicting bearing temperature of high speed under high-risk behavior.
5.3. Thermal Prediction Under Variable Radial Load Conditions
The proposed digital twin-driven virtual–real hybrid framework is applied to predict high-risk thermal behaviors under heavy loads for a 6016 deep groove ball bearing (dimensional specifications in Table 3). Under constant rotational speed (5800 rpm), reference node temperatures acquired from the PEL under light-load (2650 N) conditions are utilized to identify unknown parameters in the LPTN. These identified parameters are subsequently imported into the VML to generate twin temperature predictions under heavy-load conditions (4000 N and 5500 N), which are rigorously validated against experimental measurements. The unknown parameter values extracted during the identification process are
Figure 16 and Table 8 present the temperature transient variations under variable radial load conditions and the maximum prediction errors relative to experimental temperatures, respectively. As depicted in Figure 16, in the parameter identification process with the 2650 N light-load sample data, the maximum temperature differences at reference nodes during the rise phase are 1.6 °C and 1.2 °C, whereas these differences reduce to 0.6 °C and 0.4 °C at the stabilization stage. The steady-state temperature errors are 1.1% and 1.0%, respectively.
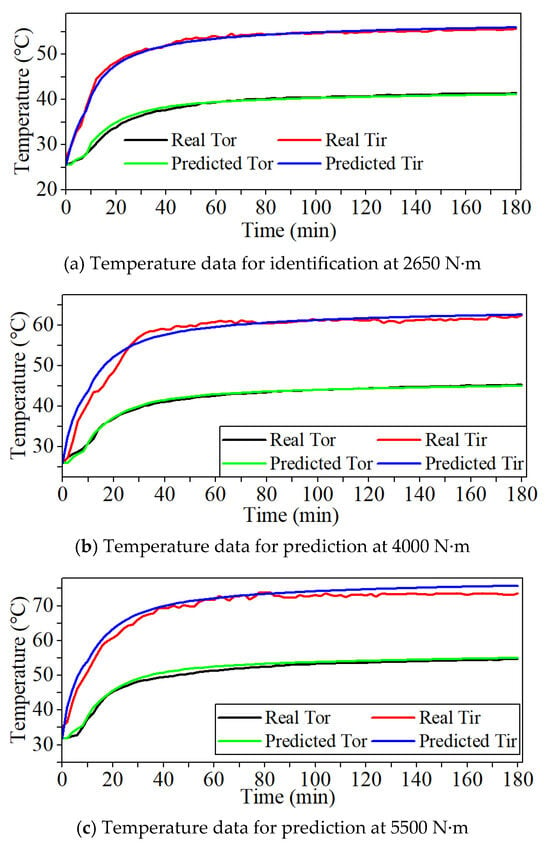
Figure 16.
Temperature comparison under variable radial load conditions.

Table 8.
Maximum prediction differences and errors relative to the experimental temperatures.
For the heavy-load conditions of 4000 N and 5500 N, the temperature curves generated by the digital twin-driven virtual–real hybrid framework exhibit strong congruence with experimental measurements. Under 4000 N radial load of the 6016 deep groove ball bearing, maximum temperature differences at reference nodes during the rise stage are 5.4 °C (inner ring) and 1.1 °C (outer ring). These differences reduce to 1.4 °C and 0.3 °C at the stabilization stage. Similarly, under 5500 N radial load, maximum transient differences are 4.3 °C and 1.8 °C, stabilizing to 2.6 °C and 0.6 °C at the stabilization stage. In this case, it can be seen that the temperature difference on the inner surface of the inner ring is consistently greater than that on the outer surface of the outer ring during thermal prediction. Thermal equilibrium attenuates these discrepancies, yet elevated loads exacerbate these differences. Critically, the proposed framework achieves robust predictive accuracy under extreme loading, with stabilization stage errors ≤ 3.5% even at 5500 N, validating its applicability for thermal prediction under high-risk behaviors with variable radial load conditions.
To further verify the transient accuracy of the thermal prediction model under variable radial load conditions, uncertainty analysis is conducted on the predicted and real temperatures of the reference nodes at 4000 N·m and 5500 N·m, as shown in Figure 17.
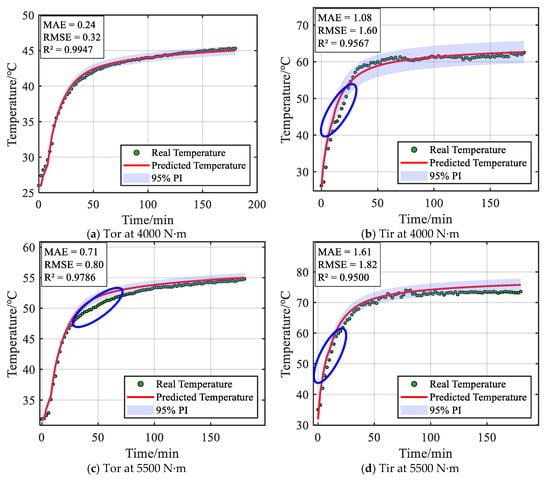
Figure 17.
Uncertainty analysis results under variable radial load conditions.
Based on Figure 17a, it can be observed that under a radial load of 4000 N·m, the transient predicted temperature on the outer surface of the outer ring shows a high goodness-of-fit with the real temperature (R2 = 0.9947), with real temperature data points largely falling within the 95% prediction intervals. However, in the other three subfigures, the goodness-of-fit decreases to 0.9567, 0.9786, and 0.95, respectively, indicating reduced prediction accuracy under these conditions. Real temperature points also intermittently fall outside the 95% prediction intervals (marked by blue circulars). These results suggest that the proposed prediction framework requires further enhancement in accuracy under variable load conditions. Additionally, the real temperature data exhibits minor fluctuations under high-load conditions, which may be related to sensor performance. The reliability of sample data remains a critical factor for ensuring accurate parameter identification and early-warning results.
6. Discussion
Building upon the innovative pathways and research Results of this study, our subsequent efforts will focus on implementing the proposed digital twin-driven virtual–real hybrid framework for online monitoring and thermal fault warning. Furthermore, detailed applications of surrogate model- and intelligent algorithm-enhanced DT frameworks for bearing thermal analysis will be thoroughly investigated. These advancements aim to establish a unified DT ecosystem for predictive maintenance and thermal safety management in next-generation rotating machinery systems.
7. Conclusions
Leveraging high-reliability and high-precision DT technology, this study proposes a virtual–real hybrid framework for bearing thermal prediction under complex operating conditions and long-term operation. The framework employs an NOA-based identification method to determine key thermal parameters in the LPTN model within the VML, addressing the time-varying and ambiguous characteristics of unknown parameters. This enables thermal prediction transitions from low-risk behaviors (low-speed, light-load) to high-risk behaviors (high-speed, heavy-load) in bearing systems. A comprehensive analysis of comparative results yields the following conclusions:
- (1)
- The NOA-based identification mechanism achieves near-perfect alignment between identified and target values for time-varying and ambiguous parameters, with convergence speeds 10 times faster than the PSO-based.
- (2)
- Under variable-speed conditions, the proposed framework exhibits maximum temperature errors of 1.2 °C and 0.5 °C at reference nodes during identification. With 270 samples, the average Euclidean distance between twin and validation temperatures reaches a minimum of 4.9 K. Expanding the number of reference nodes from 4 to 13 reduces the average Euclidean distance from 13.7 K to 0.4 K, validating its capability for thermal prediction from low-speed to high-speed and highlighting the benefits of multi-speed-range samples. The uncertainty analysis of the rapid acceleration test shows that all real temperature data points fall within the 95% prediction intervals of the predicted temperatures, confirming the robust predictive capability of the implemented framework.
- (3)
- Under variable radial load conditions, steady-state temperature errors at reference nodes are 0.6 °C and 0.4 °C for 2650 N light-load identification. When predicting the temperature of heavy-load conditions (4000 N and 5500 N), maximum differences remain below 2.6 °C, and stabilization stage errors ≤ 3.5% even at 5500 N. But uncertainty analysis shows that real temperature points intermittently fall outside the 95% prediction intervals; the proposed prediction framework requires further enhancement in accuracy under variable load conditions.
Author Contributions
Conceptualization, J.C. (Junci Cao); methodology, Y.W.; software, Y.W.; validation, J.C. (Jiang Cao), Q.T.; formal analysis, L.Y.; investigation, L.Y.; resources, Q.T.; data curation, J.C. (Jiang Cao); writing—original draft preparation, Y.W.; writing—review and editing, Y.W.; visualization, Q.T.; supervision, J.C. (Junci Cao); project administration, L.Y.; funding acquisition, J.C. (Junci Cao). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China, grant number 2022YFB2502600, and the Science and Technology Research and Development Joint Fund of Henan Province, grant number 225101610002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are not publicly available due to confidentiality requirements of the project.
Conflicts of Interest
Author Luqiang Yang was employed by the company Luoyang Bearing Research Institute Co., Ltd. Author Jiang Cao was employed by the company CRRC Qingdao Sifang Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DT | Digital Twin |
| NOA | Nutcracker Optimization Algorithm |
| LPTN | Lumped parameter thermal network |
| FE | Finite Element |
| CFD | Computational Fluid Dynamics |
| UDFs | User-defined functions |
| TRs | Thermal resistances |
| PEL | Physical Entity Layer |
| VML | Virtual Model Layer |
| DAL | Data Acquisition Layer |
| DMP | Data Mapping Part |
| CI | Confidence Intervals |
| PI | Prediction Intervals |
References
- Wang, Y.; Cao, J.; Tong, Q.; An, G.; Liu, R.; Zhang, Y.; Yan, H. Study on the Thermal Performance and Temperature Distribution of Ball Bearings in the Traction Motor of a High-Speed EMU. Appl. Sci. 2020, 10, 4373. [Google Scholar] [CrossRef]
- Chang, Z.; Hou, L.; Chen, Y. Nonlinear dynamics and thermal bidirectional coupling characteristics of a rotor-ball bearing system. Appl. Math. Model. 2023, 119, 513–533. [Google Scholar] [CrossRef]
- Shao, H.; Xia, M.; Han, G.; Zhang, Y.; Wan, J. Intelligent Fault Diagnosis of Rotor-Bearing System Under Varying Working Conditions With Modified Transfer Convolutional Neural Network and Thermal Images. IEEE Trans. Ind. Inform. 2021, 17, 3488–3496. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Z.; Yang, Y.; Xiao, J.; Chen, J. A Dynamic Monitoring Method of Temperature Distribution for Cable Joints Based on Thermal Knowledge and Conditional Generative Adversarial Network. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Aguilera, J.J.; Padullés, R.; Meesenburg, W.; Markussen, W.B.; Zühlsdorf, B.; Elmegaard, B. Operation optimization in large-scale heat pump systems: A scheduling framework integrating digital twin modelling, demand forecasting, and MILP. Appl. Energy 2024, 376, 124259. [Google Scholar] [CrossRef]
- Li, S.; Jiang, Q.; Xu, Y.; Feng, K.; Zhao, Z.; Sun, B.; Huang, G.Q. Digital twin-assisted interpretable transfer learning: A novel wavelet-based framework for intelligent fault diagnostics from simulated domain to real industrial domain. Adv. Eng. Inform. 2024, 62, 102681. [Google Scholar] [CrossRef]
- Hu, H.-X.; Feng, Y.; Hu, Q.; Zhang, Y. A Masked One-Dimensional Convolutional Autoencoder for Bearing Fault Diagnosis Based on Digital Twin Enabled Industrial Internet of Things. IEEE J. Sel. Areas Commun. 2023, 41, 3242–3253. [Google Scholar] [CrossRef]
- Cui, L.; Wang, X.; Liu, D.; Wang, H. An Adaptive Sparse Graph Learning Method Based on Digital Twin Dictionary for Remaining Useful Life Prediction of Rolling Element Bearings. IEEE Trans. Ind. Inform. 2024, 20, 10892–10900. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, C.; Wang, J.; Wang, S.; Lv, D.; Qin, F. Research on Digital Twin Driven Rolling Bearing Model-Data Fusion Life Prediction Method. IEEE Access 2023, 11, 48611–48627. [Google Scholar] [CrossRef]
- Abdelrahman, M.M.; Chong, A.; Miller, C. Personal thermal comfort models using digital twins: Preference prediction with BIM-extracted spatial–temporal proximity data from Build2Vec. Build. Environ. 2022, 207, 108532. [Google Scholar] [CrossRef]
- Lei, Z.; Zhou, H.; Hu, W.; Liu, G.-P.; Guan, S.; Feng, X. Toward a Web-Based Digital Twin Thermal Power Plant. IEEE Trans. Ind. Inform. 2022, 18, 1716–1725. [Google Scholar] [CrossRef]
- Kuprat, J.; Debbadi, K.; Schaumburg, J.; Liserre, M.; Langwasser, M. Thermal Digital Twin of Power Electronics Modules for Online Thermal Parameter Identification. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 1020–1029. [Google Scholar] [CrossRef]
- Yi, Y.; Xia, C.; Feng, C.; Zhang, W.; Fu, C.; Qian, L.; Chen, S. Digital twin-long short-term memory (LSTM) neural network based real-time temperature prediction and degradation model analysis for lithium-ion battery. J. Energy Storage 2023, 64, 107203. [Google Scholar] [CrossRef]
- Shi, J.; Wang, X.; Zhang, Z.; Zhang, C.; Chen, J. Optimization of energy flow in thermal management of electric vehicles based on real vehicle testing and digital twin simulation. Case Stud. Therm. Eng. 2024, 60, 104607. [Google Scholar] [CrossRef]
- Yuan, Y.; Fan, K. Digital twin-driven life health monitoring for motorized spindle. J. Manuf. Process. 2024, 113, 373–387. [Google Scholar] [CrossRef]
- Than, V.-T.; Huang, J.H. Nonlinear thermal effects on high-speed spindle bearings subjected to preload. Tribol. Int. 2016, 96, 361–372. [Google Scholar] [CrossRef]
- Truong, D.S.; Kim, B.-S.; Ro, S.-K. An analysis of a thermally affected high-speed spindle with angular contact ball bearings. Tribol. Int. 2021, 157, 106881. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z. A simulation investigation of lubricating characteristics for a cylindrical roller bearing of a high-power gearbox. Tribol. Int. 2022, 167, 107373. [Google Scholar] [CrossRef]
- Nategh, S.; Zhang, H.; Wallmark, O.; Boglietti, A.; Nassen, T.; Bazant, M. Transient Thermal Modeling and Analysis of Railway Traction Motors. IEEE Trans. Ind. Electron. 2019, 66, 79–89. [Google Scholar] [CrossRef]
- Nategh, S.; Huang, Z.; Krings, A.; Wallmark, O.; Leksell, M. Thermal Modeling of Directly Cooled Electric Machines Using Lumped Parameter and Limited CFD Analysis. IEEE Trans. Energy Convers. 2013, 28, 979–990. [Google Scholar] [CrossRef]
- Ma, F.; Li, Z.; Qiu, S.; Wu, B.; An, Q. Transient thermal analysis of grease-lubricated spherical roller bearings. Tribol. Int. 2016, 93, 115–123. [Google Scholar] [CrossRef]
- Ai, S.; Wang, W.; Wang, Y.; Zhao, Z. Temperature rise of double-row tapered roller bearings analyzed with the thermal network method. Tribol. Int. 2015, 87, 11–22. [Google Scholar] [CrossRef]
- Zhen, D.; Chen, W.; Li, M. An optimized thermal network model to estimate thermal performances on a pair of angular contact ball bearings under oil-air lubrication. Appl. Therm. Eng. 2018, 131, 328–339. [Google Scholar]
- Hao, J.; Li, C.; Song, W.; Yao, Z.; Miao, H.; Xu, M.; Gong, X.; Lu, H.; Liu, Z. Thermal-mechanical dynamic interaction in high-speed motorized spindle considering nonlinear vibration. Int. J. Mech. Sci. 2023, 240, 107959. [Google Scholar] [CrossRef]
- Zheng, D.; Chen, W.; Zheng, D. An enhanced estimation on heat generation of angular contact ball bearings with vibration effect. Int. J. Therm. Sci. 2021, 159, 106610. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, H.; Hao, X.; Liao, X.; Han, Q. Investigation on thermal behavior and temperature distribution of bearing inner and outer rings. Tribol. Int. 2019, 130, 289–298. [Google Scholar] [CrossRef]
- Zheng, D.; Chen, W. Thermal performances on angular contact ball bearing of high-speed spindle considering structural constraints under oil-air lubrication. Tribol. Int. 2017, 109, 593–601. [Google Scholar] [CrossRef]
- Yan, K.; Wang, N.; Zhai, Q.; Zhu, Y.; Zhang, J.; Niu, Q. Theoretical and experimental investigation on the thermal characteristics of double-row tapered roller bearings of high speed locomotive. Int. J. Heat Mass Transf. 2015, 84, 1119–1130. [Google Scholar] [CrossRef]
- Yan, B.; Yan, K.; Luo, T.; Zhu, Y.; Li, B.Q.; Hong, J. Thermal coefficients modification of high speed ball bearing by multi-object optimization method. Int. J. Therm. Sci. 2019, 137, 313–324. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, W.; Huang, S.; Zhang, J.; Yang, M.; Li, C.; Huang, S. A Robust DPCC for IPMSM Based on a Full Parameter Identification Method. IEEE Trans. Ind. Electron. 2023, 70, 7695–7705. [Google Scholar] [CrossRef]
- Wu, W.; Chen, R. An improved online system identification method for tiltrotor aircraft. Aerosp. Sci. Technol. 2021, 110, 106491. [Google Scholar] [CrossRef]
- Liu, X.; Chen, L.; Wu, C.; Ye, Z.; Zhang, B.; Tao, Y. Research on parameter identification of transmission line galloping model under different degrees of freedom. Appl. Math. Model. 2025, 140, 106491. [Google Scholar] [CrossRef]
- Ibarrola-Chamizo, J.; Agirre-Olabide, I.; Merino, M.; Aginaga, J. Modal Complexity Factors as indexes for modal parameter identification in Operational Modal Analysis of coupled dynamic systems. J. Sound Vib. 2025, 600, 118860. [Google Scholar] [CrossRef]
- Feng, X.; Wong, S.K.; Chen, T.; Ouyang, M. An automatic identification method of thermal physical parameter for lithium-ion batteries suffering from thermal runaway. J. Energy Storage 2024, 83, 110358. [Google Scholar] [CrossRef]
- Zhang, X.; Ying, Z.; Chen, Y.; Chen, X. A thermal model for calculating axial temperature distribution of overhead conductor under laboratory conditions. Electr. Power Syst. Res. 2019, 166, 223–231. [Google Scholar] [CrossRef]
- Sýkora, J.; Havelka, J. Sparse polynomial chaos expansions for uncertainty quantification in thermal tomography. J. Comput. Appl. Math. 2024, 436, 115406. [Google Scholar] [CrossRef]
- Cheng, D.; Zhang, W.; Liu, J. Window-Varying Particle Filter for Parameter Identification of Space Thermal Model. IEEE Trans. Instrum. Meas. 2017, 66, 165–176. [Google Scholar] [CrossRef]
- Cao, L.; Fan, X.; Li, D.; Kong, W.; Qu, R.; Liu, Z. Improved LPTN-Based Online Temperature Prediction of Permanent Magnet Machines by Global Parameter Identification. IEEE Trans. Ind. Electron. 2023, 70, 8830–8841. [Google Scholar] [CrossRef]
- Su, C.; Chen, W. Thermal behavior on motorized spindle considering bearing thermal deformation under oil-air lubrication. J. Manuf. Process. 2021, 72, 483–499. [Google Scholar] [CrossRef]
- Tan, F.; Wang, L.; Yin, M.; Yin, G. Obtaining more accurate convective heat transfer coefficients in thermal analysis of spindle using surrogate assisted differential evolution method. Appl. Therm. Eng. 2019, 149, 1335–1344. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. Recent advances and applications of surrogate models for finite element method computations: A review. Soft Comput. 2022, 26, 13709–13733. [Google Scholar] [CrossRef]
- Song, H.; Song, M.; Liu, X. Online autonomous calibration of digital twins using machine learning with application to nuclear power plants. Appl. Energy 2022, 326, 119995. [Google Scholar] [CrossRef]
- Tarawneh, C.M.; Cole, K.D.; Wilson, B.M.; Alnaimat, F. Experiments and models for the thermal response of railroad tapered-roller bearings. Int. J. Heat Mass Transf. 2008, 51, 5794–5803. [Google Scholar] [CrossRef]
- Gao, P.; Chen, Y.; Hou, L. Nonlinear thermal behaviors of the inter-shaft bearing in a dual-rotor system subjected to the dynamic load. Nonlinear Dyn. 2020, 101, 191–209. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.H.; Hong, J.; Yan, K.; Li, S. Uneven heat generation and thermal performance of spindle bearings. Tribol. Int. 2018, 126, 324–335. [Google Scholar] [CrossRef]
- Liu, J.; Ma, C.; Wang, S.; Wang, S.; Yang, B. Thermal contact resistance between bearing inner ring and shaft journal. Int. J. Therm. Sci. 2019, 138, 521–535. [Google Scholar] [CrossRef]
- Hao, X.; Zhai, J.; Liang, J.; Chen, Y.; Han, Q. Time-varying stiffness characteristics of roller bearing influenced by thermal behavior due to surface frictions and different lubricant oil temperatures. Tribol. Int. 2020, 144, 106125. [Google Scholar] [CrossRef]
- Wallscheid, O.; Bocker, J. Global Identification of a Low-Order Lumped-Parameter Thermal Network for Permanent Magnet Synchronous Motors. IEEE Trans. Energy Convers. 2016, 31, 354–365. [Google Scholar] [CrossRef]
- Palmgren, A. Ball and Roller Bearing Engineering, 3rd ed.; SKF Industries Inc.: Philadelphia, PA, USA, 1959. [Google Scholar]
- Muzychka, Y.S.; Yonanovich, M.M. Thermal resistance models for non-circular moving heat sources on a half space. J. Heat Transf.-Trans. ASME 2001, 123, 624–632. [Google Scholar] [CrossRef]
- Sciascera, C.; Giangrande, P.; Papini, L.; Gerada, C.; Galea, M. Analytical Thermal Model for Fast Stator Winding Temperature Prediction. IEEE Trans. Ind. Electron. 2017, 64, 6116–6126. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl.-Based Syst. 2023, 262, 110248. [Google Scholar] [CrossRef]
- Merigó, J.M.; Casanovas, M. Induced aggregation operators in the Euclidean distance and its application in financial decision making. Expert Syst. Appl. 2011, 38, 7603–7608. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).