A Bidirectional Cross Spatiotemporal Fusion Network with Spectral Restoration for Remote Sensing Imagery
Abstract
1. Introduction
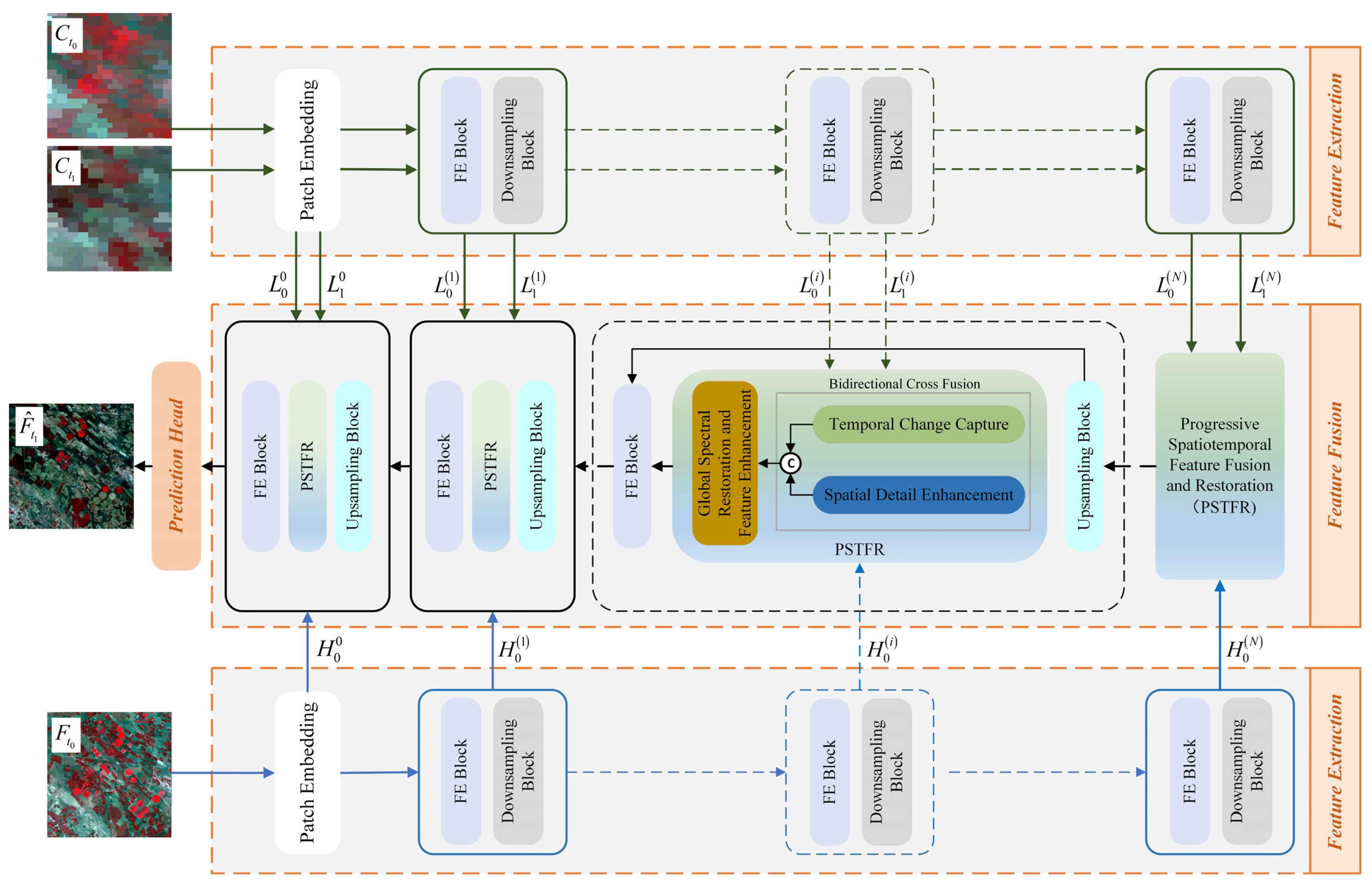
- An end-to-end BCSR-STF model is proposed. The PSTFR module within BCSR-STF employs multi-scale iterative optimization, enabling effective exchange between high-level and low-level information. The design enhances the model’s capability to address variations in object scale within input images, thereby improving the accuracy of spatiotemporal fusion.
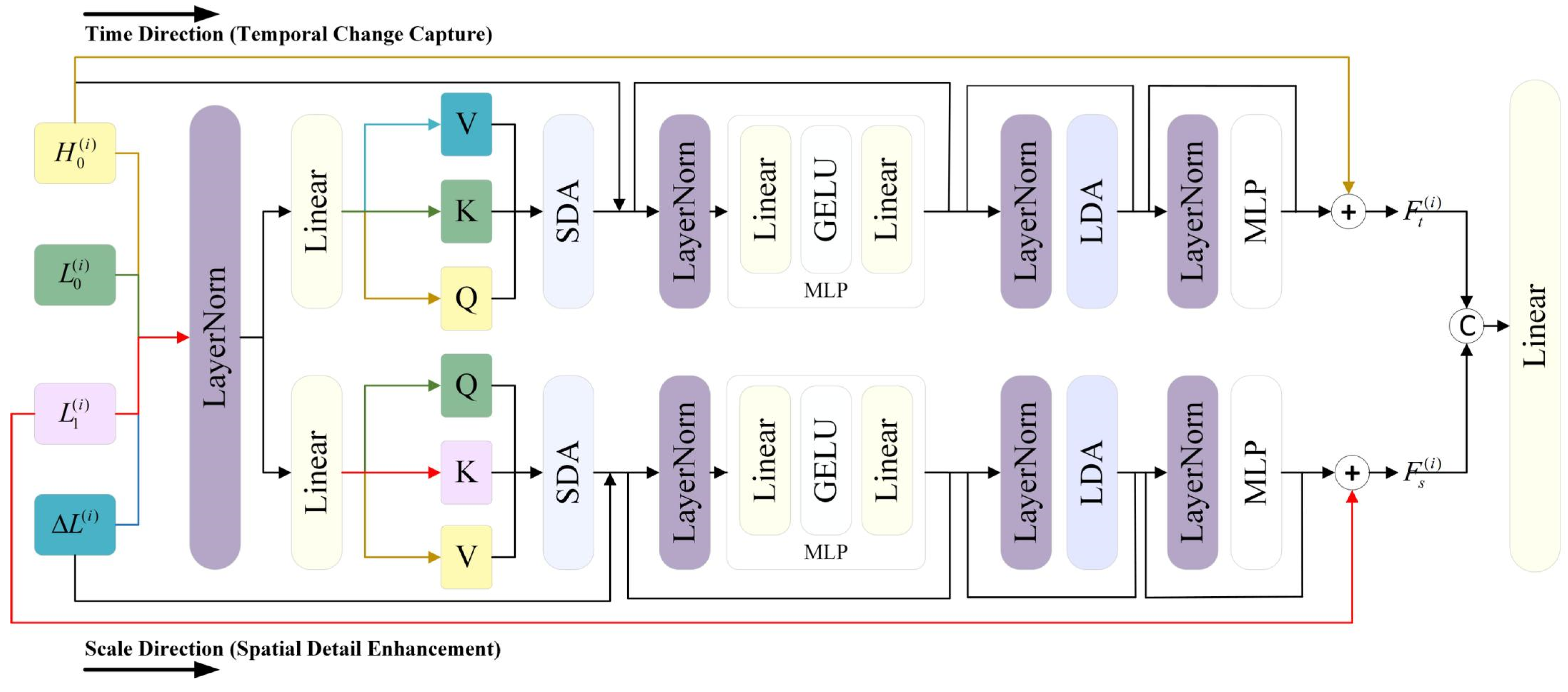
- A Bidirectional Cross Fusion (BCF) module is designed to leverage the advantages and mitigate the limitations of temporal and scale directions. This module simultaneously considers temporal variations and scale differences, utilizing short-range and long-range attention mechanisms based on the Vision Transformer to enhance interactions between temporal and spatial information, thereby improving fusion accuracy.
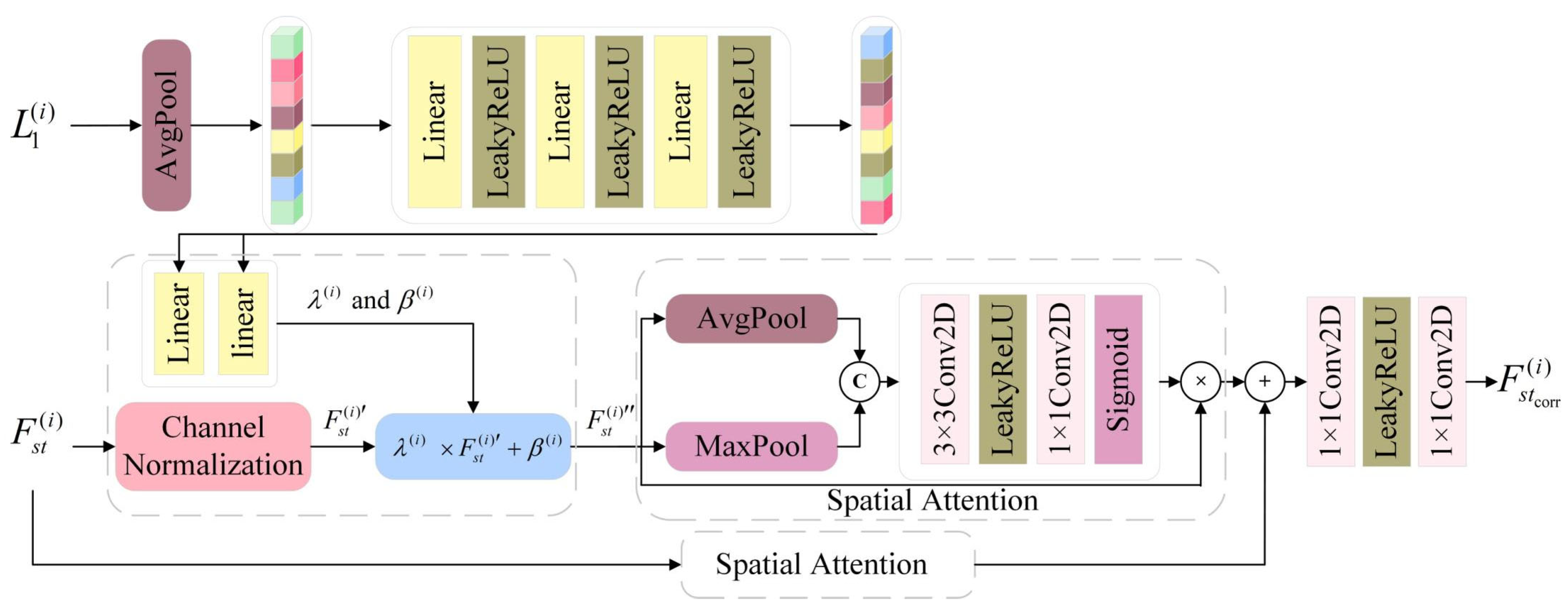
- The Global Spectral Restoration and Feature Enhancement (GSRFE) module is introduced to restore and enhance spectral information often overlooked in coarse images. By incorporating Adaptive Instance Normalization (AdaIN) and spatial attention mechanisms, GSRFE adaptively adjusts spectral distributions and enhances the quality of spatiotemporal fusion through feature enhancement.
2. Methodology
2.1. Network Architecture
2.2. Bidirectional Cross Fusion
2.2.1. Time Direction
2.2.2. Scale Direction
2.3. Global Spectral Restoration and Feature Enhancement
2.4. Loss Function
3. Experimental Results
3.1. Study Areas and Datasets
3.2. Experiment Design and Evaluation
3.3. Experimental Results for CIA
3.4. Experimental Results for LGC
3.5. Experimental Results for Wuhan
4. Discussion
4.1. Ablation Studies
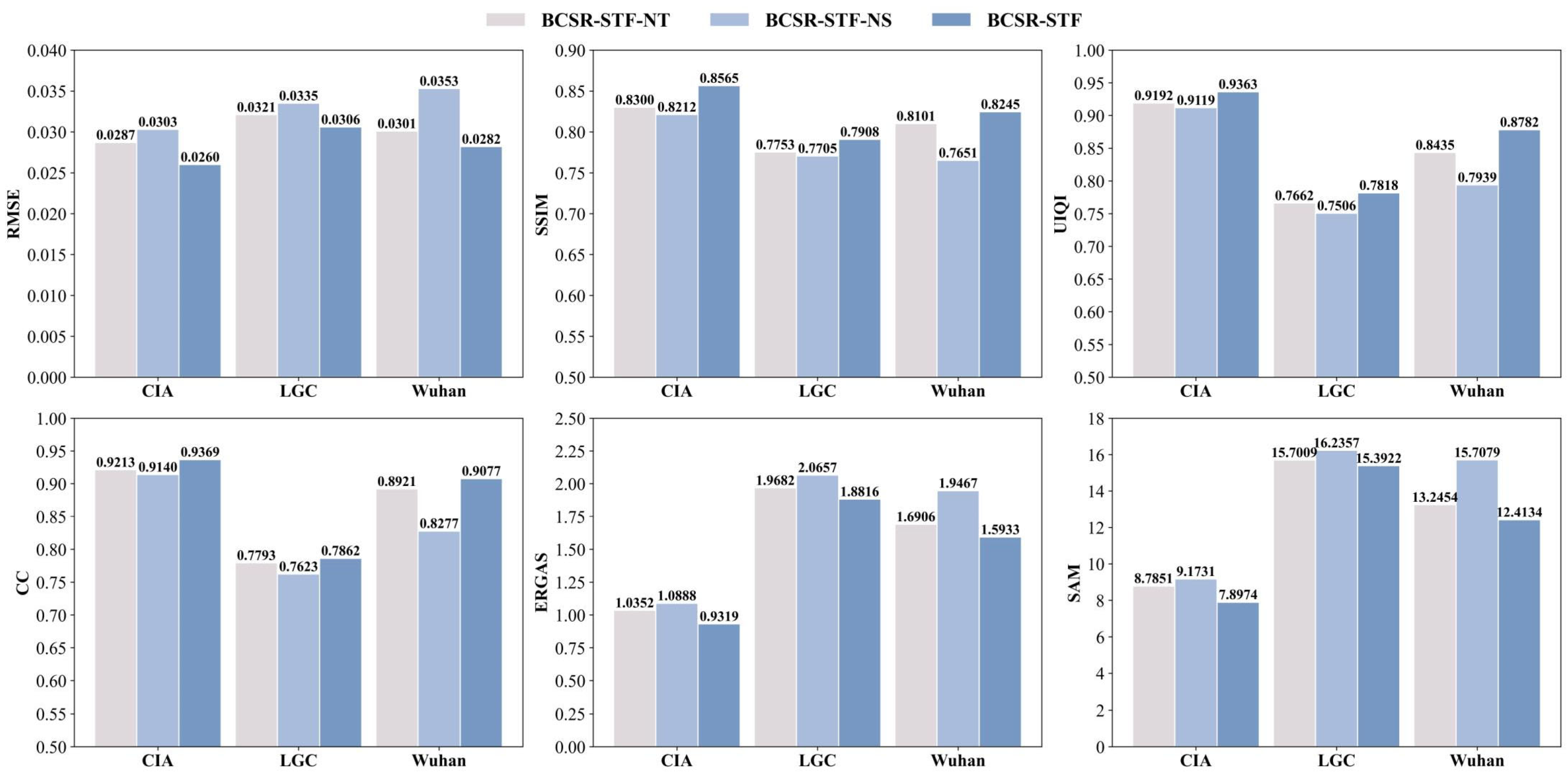
4.1.1. Progressive Spatiotemporal Feature Fusion and Restoration
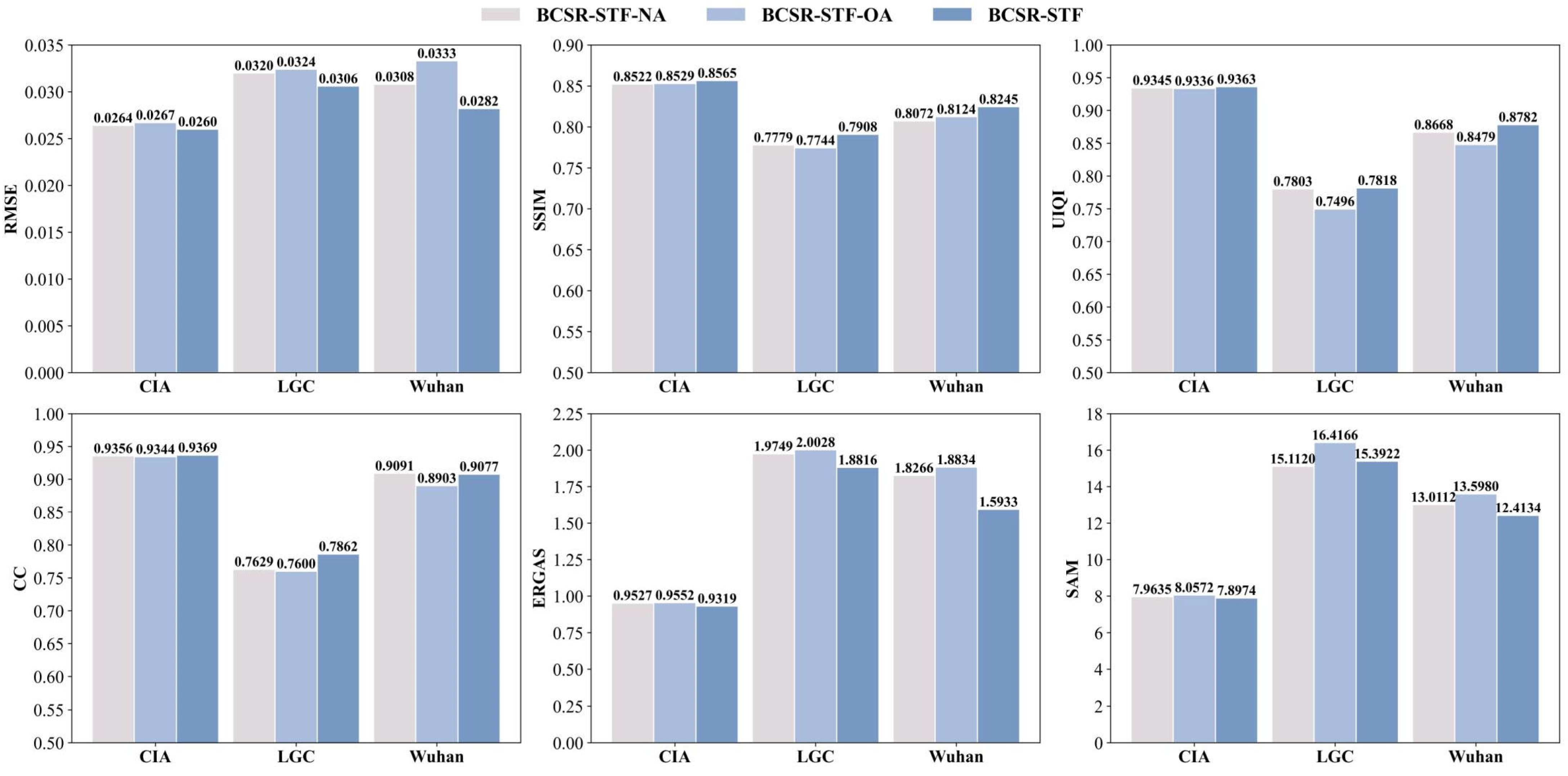
4.1.2. Bidirectional Cross Fusion
4.1.3. Global Spectral Restoration and Feature Enhancement
4.2. Computation Load
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STF | Spatiotemporal fusion |
| DL | Deep learning |
| CNN | Convolutional neural network |
| GAN | Generative adversarial network |
| SR | Super-resolution |
| NDVI | Normalized difference vegetation index |
| PSTFR | Progressive Spatiotemporal Feature Fusion and Restoration |
| BCF | Bidirectional Cross Fusion |
| GSRFE | Global Spectral Restoration and Feature Enhancement |
| AdaIN | Adaptive Instance Normalization |
| SDA | Short-distance attention |
| LDA | Long-distance attention |
| MLP | Multi-layer perceptron |
| CIA | Coleambally Irrigation Area |
| LGC | Lower Gwydir Catchment |
| RMSE | Root Mean Square Error |
| SSIM | Structure Similarity Index |
| UIQI | Universal Image Quality Index |
| CC | Correlation Coefficient |
| SAM | Spectral Angle Mapper |
| ERGAS | Erreur Relative Global Adimensionnelle de Synthène |
| AAD | Average Absolute Difference |
| FLOPs | Floating Point Operations per Second |
References
- Zhu, X.; Cai, F.; Tian, J.; Williams, T. Spatiotemporal Fusion of Multisource Remote Sensing Data: Literature Survey, Taxonomy, Principles, Applications, and Future Directions. Remote Sens. 2018, 10, 527. [Google Scholar] [CrossRef]
- Li, J.; Hong, D.; Gao, L.; Yao, J.; Zheng, K.; Zhang, B.; Chanussot, J. Deep Learning in Multimodal Remote Sensing Data Fusion: A Comprehensive Review. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102926. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, Y.; Zhang, Y. Review of Pixel-Level Remote Sensing Image Fusion Based on Deep Learning. Inf. Fusion 2023, 90, 36–58. [Google Scholar] [CrossRef]
- Mbabazi, D.; Mohanty, B.P.; Gaur, N. High Spatio-Temporal Resolution Evapotranspiration Estimates within Large Agricultural Fields by Fusing Eddy Covariance and Landsat Based Data. Agric. For. Meteorol. 2023, 333, 109417. [Google Scholar] [CrossRef]
- Ferreira, T.R.; Maguire, M.S.; da Silva, B.B.; Neale, C.M.U.; Serrão, E.A.O.; Ferreira, J.D.; de Moura, M.S.B.; dos Santos, C.A.C.; Silva, M.T.; Rodrigues, L.N.; et al. Assessment of Water Demands for Irrigation Using Energy Balance and Satellite Data Fusion Models in Cloud Computing: A Study in the Brazilian Semiarid Region. Agric. Water Manag. 2023, 281, 108260. [Google Scholar] [CrossRef]
- Bilotta, G.; Genovese, E.; Citroni, R.; Cotroneo, F.; Meduri, G.M.; Barrile, V. Integration of an Innovative Atmospheric Forecasting Simulator and Remote Sensing Data into a Geographical Information System in the Frame of Agriculture 4.0 Concept. AgriEngineering 2023, 5, 1280–1301. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, T.; Batelaan, O.; Duan, L.; Wang, Y.; Li, X.; Li, M. Spatiotemporal Fusion of Multi-Source Remote Sensing Data for Estimating Aboveground Biomass of Grassland. Ecol. Indic. 2023, 146, 109892. [Google Scholar] [CrossRef]
- Shi, C.; Wang, N.; Zhang, Q.; Liu, Z.; Zhu, X. A Comprehensive Flexible Spatiotemporal DAta Fusion Method (CFSDAF) for Generating High Spatiotemporal Resolution Land Surface Temperature in Urban Area. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9885–9899. [Google Scholar] [CrossRef]
- Pan, L.; Lu, L.; Fu, P.; Nitivattananon, V.; Guo, H.; Li, Q. Understanding Spatiotemporal Evolution of the Surface Urban Heat Island in the Bangkok Metropolitan Region from 2000 to 2020 Using Enhanced Land Surface Temperature. Geomat. Nat. Hazards Risk 2023, 14, 2174904. [Google Scholar] [CrossRef]
- Zhukov, B.; Oertel, D.; Lanzl, F.; Reinhackel, G. Unmixing-Based Multisensor Multiresolution Image Fusion. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1212–1226. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A Flexible Spatiotemporal Method for Fusing Satellite Images with Different Resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, Y.; Li, S.; Huang, W. Spectral Unmixing Based Spatiotemporal Downscaling Fusion Approach. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102054. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the Blending of the Landsat and MODIS Surface Reflectance: Predicting Daily Landsat Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An Enhanced Spatial and Temporal Adaptive Reflectance Fusion Model for Complex Heterogeneous Regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Wang, Q.; Atkinson, P.M. Spatio-Temporal Fusion for Daily Sentinel-2 Images. Remote Sens. Environ. 2018, 204, 31–42. [Google Scholar] [CrossRef]
- Li, A.; Bo, Y.; Zhu, Y.; Guo, P.; Bi, J.; He, Y. Blending Multi-Resolution Satellite Sea Surface Temperature (SST) Products Using Bayesian Maximum Entropy Method. Remote Sens. Environ. 2013, 135, 52–63. [Google Scholar] [CrossRef]
- Liao, L.; Song, J.; Wang, J.; Xiao, Z.; Wang, J. Bayesian Method for Building Frequent Landsat-Like NDVI Datasets by Integrating MODIS and Landsat NDVI. Remote Sens. 2016, 8, 452. [Google Scholar] [CrossRef]
- Huang, B.; Song, H. Spatiotemporal Reflectance Fusion via Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3707–3716. [Google Scholar] [CrossRef]
- Song, H.; Huang, B. Spatiotemporal Satellite Image Fusion Through One-Pair Image Learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1883–1896. [Google Scholar] [CrossRef]
- Tan, Z.; Yue, P.; Di, L.; Tang, J. Deriving High Spatiotemporal Remote Sensing Images Using Deep Convolutional Network. Remote Sens. 2018, 10, 1066. [Google Scholar] [CrossRef]
- Tan, Z.; Di, L.; Zhang, M.; Guo, L.; Gao, M. An Enhanced Deep Convolutional Model for Spatiotemporal Image Fusion. Remote Sens. 2019, 11, 2898. [Google Scholar] [CrossRef]
- Tan, Z.; Gao, M.; Li, X.; Jiang, L. A Flexible Reference-Insensitive Spatiotemporal Fusion Model for Remote Sensing Images Using Conditional Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5601413. [Google Scholar] [CrossRef]
- Song, B.; Liu, P.; Li, J.; Wang, L.; Zhang, L.; He, G.; Chen, L.; Liu, J. MLFF-GAN: A Multilevel Feature Fusion with GAN for Spatiotemporal Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4410816. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need 2017. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Chen, G.; Jiao, P.; Hu, Q.; Xiao, L.; Ye, Z. SwinSTFM: Remote Sensing Spatiotemporal Fusion Using Swin Transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5410618. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV 2021), Montreal, BC, Canada, 11–17 October 2021; IEEE: New York, NY, USA, 2021; pp. 9992–10002. [Google Scholar]
- Benzenati, T.; Kallel, A.; Kessentini, Y. STF-Trans: A Two-Stream Spatiotemporal Fusion Transformer for Very High Resolution Satellites Images. Neurocomputing 2024, 563, 126868. [Google Scholar] [CrossRef]
- Jiang, M.; Shao, H. A CNN-Transformer Combined Remote Sensing Imagery Spatiotemporal Fusion Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 13995–14009. [Google Scholar] [CrossRef]
- Liu, X.; Deng, C.; Chanussot, J.; Hong, D.; Zhao, B. StfNet: A Two-Stream Convolutional Neural Network for Spatiotemporal Image Fusion. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6552–6564. [Google Scholar] [CrossRef]
- Li, W.; Yang, C.; Peng, Y.; Du, J. A Pseudo-Siamese Deep Convolutional Neural Network for Spatiotemporal Satellite Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1205–1220. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, K.; Ge, Y.; Zhou, Y. Spatiotemporal Remote Sensing Image Fusion Using Multiscale Two-Stream Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Peng, Y.; Dong, M. DMNet: A Network Architecture Using Dilated Convolution and Multiscale Mechanisms for Spatiotemporal Fusion of Remote Sensing Images. IEEE Sens. J. 2020, 20, 12190–12202. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Peng, Y.; Dong, M. Spatiotemporal Fusion of Remote Sensing Images Using a Convolutional Neural Network with Attention and Multiscale Mechanisms. Int. J. Remote Sens. 2021, 42, 1973–1993. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Liang, S.; Li, M. A New Spatial–Temporal Depthwise Separable Convolutional Fusion Network for Generating Landsat 8-Day Surface Reflectance Time Series over Forest Regions. Remote Sens. 2022, 14, 2199. [Google Scholar] [CrossRef]
- Liu, Q.; Meng, X.; Shao, F.; Li, S. PSTAF-GAN: Progressive Spatio-Temporal Attention Fusion Method Based on Generative Adversarial Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5408513. [Google Scholar] [CrossRef]
- Song, H.; Liu, Q.; Wang, G.; Hang, R.; Huang, B. Spatiotemporal Satellite Image Fusion Using Deep Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
- Liu, H.; Yang, G.; Deng, F.; Qian, Y.; Fan, Y. MCBAM-GAN: The Gan Spatiotemporal Fusion Model Based on Multiscale and CBAM for Remote Sensing Images. Remote Sens. 2023, 15, 1583. [Google Scholar] [CrossRef]
- Jia, D.; Song, C.; Cheng, C.; Shen, S.; Ning, L.; Hui, C. A Novel Deep Learning-Based Spatiotemporal Fusion Method for Combining Satellite Images with Different Resolutions Using a Two-Stream Convolutional Neural Network. Remote Sens. 2020, 12, 698. [Google Scholar] [CrossRef]
- Jia, D.; Cheng, C.; Shen, S.; Ning, L. Multitask Deep Learning Framework for Spatiotemporal Fusion of NDVI. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5616313. [Google Scholar] [CrossRef]
- Wang, W.; Chen, W.; Qiu, Q.; Chen, L.; Wu, B.; Lin, B.; He, X.; Liu, W. CrossFormer++: A Versatile Vision Transformer Hinging on Cross-Scale Attention. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 3123–3136. [Google Scholar] [CrossRef]
- Emelyanova, I.V.; McVicar, T.R.; Van Niel, T.G.; Li, L.T.; Van Dijk, A.I.J.M. Assessing the Accuracy of Blending Landsat–MODIS Surface Reflectances in Two Landscapes with Contrasting Spatial and Temporal Dynamics: A Framework for Algorithm Selection. Remote Sens. Environ. 2013, 133, 193–209. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, L.; Li, S.; Lei, F.; Cao, L.; Li, X. Wuhan Dataset: A High-Resolution Dataset of Spatiotemporal Fusion for Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2024, 21, 2504305. [Google Scholar] [CrossRef]







| Band | STARFM | FSDAF | Fit-FC | EDCSTFN | GAN-STFM | MLFF-GAN | STF-Trans | CTSTFM | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | 1 | 0.0166 | 0.0161 | 0.0157 | 0.0162 | 0.0126 | 0.0122 | 0.0123 | 0.0133 | 0.0118 |
| 2 | 0.0250 | 0.0234 | 0.0235 | 0.0255 | 0.0180 | 0.0180 | 0.0167 | 0.0173 | 0.0164 | |
| 3 | 0.0399 | 0.0364 | 0.0376 | 0.0436 | 0.0293 | 0.0286 | 0.0267 | 0.0273 | 0.0261 | |
| 4 | 0.0496 | 0.0509 | 0.0472 | 0.0445 | 0.0401 | 0.0395 | 0.0374 | 0.0371 | 0.0370 | |
| 5 | 0.0460 | 0.0459 | 0.0468 | 0.0477 | 0.0396 | 0.0374 | 0.0362 | 0.0375 | 0.0348 | |
| 6 | 0.0379 | 0.0384 | 0.0385 | 0.0398 | 0.0344 | 0.0334 | 0.0324 | 0.0316 | 0.0302 | |
| Avg | 0.0358 | 0.0352 | 0.0349 | 0.0362 | 0.0290 | 0.0282 | 0.0270 | 0.0273 | 0.0260 | |
| SSIM | 1 | 0.8928 | 0.9007 | 0.8939 | 0.8850 | 0.9250 | 0.9286 | 0.9306 | 0.9271 | 0.9359 |
| 2 | 0.8464 | 0.8594 | 0.8536 | 0.8259 | 0.8966 | 0.8956 | 0.9030 | 0.9026 | 0.9084 | |
| 3 | 0.7739 | 0.7910 | 0.7873 | 0.7165 | 0.8413 | 0.8463 | 0.8511 | 0.8543 | 0.8594 | |
| 4 | 0.6811 | 0.6740 | 0.6785 | 0.7147 | 0.7608 | 0.7687 | 0.7710 | 0.7835 | 0.7873 | |
| 5 | 0.7429 | 0.7498 | 0.7462 | 0.7377 | 0.8006 | 0.8056 | 0.8096 | 0.8080 | 0.8160 | |
| 6 | 0.7748 | 0.7800 | 0.7723 | 0.7749 | 0.8178 | 0.8193 | 0.8284 | 0.8265 | 0.8318 | |
| Avg | 0.7853 | 0.7925 | 0.7886 | 0.7758 | 0.8404 | 0.8440 | 0.8489 | 0.8503 | 0.8565 | |
| UIQI | 1 | 0.8140 | 0.8293 | 0.8190 | 0.8152 | 0.8979 | 0.9113 | 0.9201 | 0.9107 | 0.9245 |
| 2 | 0.8152 | 0.8387 | 0.8275 | 0.8023 | 0.9107 | 0.9145 | 0.9279 | 0.9225 | 0.9312 | |
| 3 | 0.8165 | 0.8498 | 0.8400 | 0.7815 | 0.9132 | 0.9178 | 0.9294 | 0.9264 | 0.9336 | |
| 4 | 0.8275 | 0.8262 | 0.8370 | 0.8806 | 0.8976 | 0.9043 | 0.9128 | 0.9178 | 0.9184 | |
| 5 | 0.9222 | 0.9247 | 0.9224 | 0.9174 | 0.9444 | 0.9491 | 0.9551 | 0.9528 | 0.9576 | |
| 6 | 0.9206 | 0.9215 | 0.9193 | 0.9174 | 0.9368 | 0.9408 | 0.9477 | 0.9475 | 0.9521 | |
| Avg | 0.8527 | 0.8650 | 0.8609 | 0.8524 | 0.9168 | 0.9230 | 0.9322 | 0.9296 | 0.9363 | |
| CC | 1 | 0.8320 | 0.8370 | 0.8401 | 0.8331 | 0.9022 | 0.9116 | 0.9230 | 0.9148 | 0.9265 |
| 2 | 0.8369 | 0.8501 | 0.8473 | 0.8234 | 0.9153 | 0.9160 | 0.9292 | 0.9247 | 0.9320 | |
| 3 | 0.8454 | 0.8654 | 0.8551 | 0.8013 | 0.9165 | 0.9198 | 0.9306 | 0.9275 | 0.9345 | |
| 4 | 0.8344 | 0.8281 | 0.8459 | 0.8813 | 0.8994 | 0.9049 | 0.9141 | 0.9187 | 0.9186 | |
| 5 | 0.9222 | 0.9249 | 0.9238 | 0.9180 | 0.9451 | 0.9497 | 0.9554 | 0.9532 | 0.9577 | |
| 6 | 0.9210 | 0.9217 | 0.9198 | 0.9177 | 0.9376 | 0.9412 | 0.9484 | 0.9478 | 0.9523 | |
| Avg | 0.8653 | 0.8712 | 0.8720 | 0.8625 | 0.9194 | 0.9239 | 0.9334 | 0.9311 | 0.9369 | |
| ERGAS | ALL | 1.3146 | 1.2666 | 1.2612 | 1.3488 | 1.0298 | 1.0047 | 0.9640 | 0.9931 | 0.9319 |
| SAM | ALL | 11.1256 | 10.9104 | 10.8326 | 11.4756 | 8.8898 | 8.6679 | 8.0970 | 8.2494 | 7.8974 |
| Band | STARFM | FSDAF | Fit-FC | EDCSTFN | GAN-STFM | MLFF-GAN | STF-Trans | CTSTFM | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | 1 | 0.0143 | 0.0149 | 0.0140 | 0.0151 | 0.0146 | 0.0161 | 0.0142 | 0.0167 | 0.0143 |
| 2 | 0.0200 | 0.0207 | 0.0201 | 0.0200 | 0.0207 | 0.0223 | 0.0203 | 0.0234 | 0.0214 | |
| 3 | 0.0251 | 0.0258 | 0.0251 | 0.0257 | 0.0264 | 0.0269 | 0.0260 | 0.0320 | 0.0256 | |
| 4 | 0.0376 | 0.0397 | 0.0385 | 0.0394 | 0.041 | 0.0400 | 0.0360 | 0.0532 | 0.0351 | |
| 5 | 0.0568 | 0.0621 | 0.0565 | 0.0590 | 0.054 | 0.0533 | 0.0574 | 0.0660 | 0.0503 | |
| 6 | 0.0455 | 0.0515 | 0.0446 | 0.0407 | 0.0399 | 0.0404 | 0.0411 | 0.0476 | 0.0372 | |
| Avg | 0.0332 | 0.0358 | 0.0331 | 0.0333 | 0.0328 | 0.0332 | 0.0325 | 0.0398 | 0.0306 | |
| SSIM | 1 | 0.9132 | 0.9125 | 0.9233 | 0.9228 | 0.9185 | 0.9059 | 0.9217 | 0.9166 | 0.9268 |
| 2 | 0.8730 | 0.8709 | 0.8800 | 0.8897 | 0.8801 | 0.8709 | 0.8856 | 0.8843 | 0.8888 | |
| 3 | 0.8350 | 0.8331 | 0.8438 | 0.8455 | 0.8413 | 0.8356 | 0.8498 | 0.8391 | 0.8562 | |
| 4 | 0.7292 | 0.7294 | 0.7405 | 0.7083 | 0.7037 | 0.7239 | 0.7409 | 0.6910 | 0.7593 | |
| 5 | 0.5697 | 0.5220 | 0.5532 | 0.5513 | 0.5696 | 0.5948 | 0.5797 | 0.5766 | 0.6241 | |
| 6 | 0.6408 | 0.5754 | 0.6274 | 0.6267 | 0.6438 | 0.6533 | 0.6481 | 0.6473 | 0.6895 | |
| Avg | 0.7601 | 0.7405 | 0.7614 | 0.7574 | 0.7595 | 0.7641 | 0.7710 | 0.7591 | 0.7908 | |
| UIQI | 1 | 0.7152 | 0.7062 | 0.7124 | 0.6132 | 0.6844 | 0.6839 | 0.7313 | 0.5813 | 0.7354 |
| 2 | 0.7019 | 0.6890 | 0.6943 | 0.6560 | 0.6807 | 0.7125 | 0.7283 | 0.5637 | 0.7262 | |
| 3 | 0.7072 | 0.6965 | 0.7007 | 0.6573 | 0.696 | 0.7179 | 0.7184 | 0.5366 | 0.7541 | |
| 4 | 0.7857 | 0.7794 | 0.7827 | 0.7431 | 0.766 | 0.7826 | 0.8193 | 0.6991 | 0.8370 | |
| 5 | 0.7531 | 0.7198 | 0.7313 | 0.6645 | 0.7659 | 0.7940 | 0.7663 | 0.7436 | 0.8169 | |
| 6 | 0.7205 | 0.6531 | 0.7021 | 0.7316 | 0.7798 | 0.7918 | 0.7849 | 0.7713 | 0.8215 | |
| Avg | 0.7306 | 0.7073 | 0.7206 | 0.6776 | 0.7288 | 0.7471 | 0.7581 | 0.6493 | 0.7818 | |
| CC | 1 | 0.7158 | 0.7076 | 0.7160 | 0.6582 | 0.6878 | 0.6870 | 0.7322 | 0.6073 | 0.7363 |
| 2 | 0.7071 | 0.6916 | 0.7007 | 0.6958 | 0.6888 | 0.7169 | 0.7283 | 0.5902 | 0.7293 | |
| 3 | 0.7130 | 0.7004 | 0.7086 | 0.6834 | 0.6994 | 0.7192 | 0.7188 | 0.5469 | 0.7564 | |
| 4 | 0.8075 | 0.8011 | 0.8098 | 0.7832 | 0.769 | 0.7871 | 0.8300 | 0.7243 | 0.8375 | |
| 5 | 0.7909 | 0.7666 | 0.7832 | 0.7695 | 0.7864 | 0.7993 | 0.8109 | 0.7750 | 0.8282 | |
| 6 | 0.7873 | 0.7473 | 0.7786 | 0.7871 | 0.7883 | 0.7977 | 0.8153 | 0.7949 | 0.8293 | |
| Avg | 0.7536 | 0.7358 | 0.7495 | 0.7295 | 0.7366 | 0.7512 | 0.7726 | 0.6731 | 0.7862 | |
| ERGAS | ALL | 2.0655 | 2.2230 | 2.0322 | 2.0245 | 1.9837 | 2.0300 | 1.9938 | 2.3816 | 1.8816 |
| SAM | ALL | 16.2826 | 17.0293 | 16.2303 | 16.8170 | 16.7738 | 16.5577 | 15.9620 | 18.0406 | 15.3922 |
| Band | STARFM | FSDAF | Fit-FC | EDCSTFN | GAN-STFM | MLFF-GAN | STF-Trans | CTSTFM | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | 1 | 0.0583 | 0.0574 | 0.0636 | 0.0307 | 0.0257 | 0.0485 | 0.0224 | 0.0223 | 0.0195 |
| 2 | 0.0495 | 0.0478 | 0.0522 | 0.0294 | 0.0341 | 0.0535 | 0.0294 | 0.0288 | 0.0246 | |
| 3 | 0.0459 | 0.0495 | 0.0437 | 0.0334 | 0.0279 | 0.0505 | 0.0363 | 0.0387 | 0.0274 | |
| 4 | 0.0583 | 0.0599 | 0.0515 | 0.0507 | 0.0635 | 0.0568 | 0.0537 | 0.0970 | 0.0413 | |
| Avg | 0.0530 | 0.0536 | 0.0528 | 0.0361 | 0.0378 | 0.0523 | 0.0354 | 0.0467 | 0.0282 | |
| SSIM | 1 | 0.6448 | 0.6396 | 0.6239 | 0.8070 | 0.8433 | 0.6907 | 0.8405 | 0.8634 | 0.8820 |
| 2 | 0.6662 | 0.6437 | 0.6620 | 0.8128 | 0.8068 | 0.6644 | 0.7807 | 0.8093 | 0.8470 | |
| 3 | 0.6838 | 0.6171 | 0.6911 | 0.8029 | 0.8497 | 0.6513 | 0.7604 | 0.7933 | 0.8483 | |
| 4 | 0.5599 | 0.5214 | 0.5844 | 0.7172 | 0.7146 | 0.5634 | 0.6079 | 0.3777 | 0.7207 | |
| Avg | 0.6387 | 0.6054 | 0.6403 | 0.7850 | 0.8036 | 0.6424 | 0.7474 | 0.7109 | 0.8245 | |
| UIQI | 1 | 0.6375 | 0.5972 | 0.5536 | 0.7658 | 0.8159 | 0.6103 | 0.7599 | 0.7275 | 0.8579 |
| 2 | 0.7041 | 0.6336 | 0.6407 | 0.8133 | 0.8183 | 0.6268 | 0.7692 | 0.7562 | 0.8643 | |
| 3 | 0.7969 | 0.7120 | 0.7690 | 0.8464 | 0.8965 | 0.7019 | 0.7994 | 0.7819 | 0.9106 | |
| 4 | 0.7769 | 0.7405 | 0.7800 | 0.8600 | 0.8460 | 0.7586 | 0.8081 | 0.1907 | 0.8802 | |
| Avg | 0.7289 | 0.6708 | 0.6858 | 0.8214 | 0.8442 | 0.6744 | 0.7842 | 0.6141 | 0.8782 | |
| CC | 1 | 0.8106 | 0.7868 | 0.8519 | 0.9129 | 0.8945 | 0.7761 | 0.8572 | 0.8264 | 0.9013 |
| 2 | 0.7930 | 0.7599 | 0.8531 | 0.9139 | 0.8994 | 0.7645 | 0.8655 | 0.8611 | 0.9007 | |
| 3 | 0.8636 | 0.7884 | 0.8845 | 0.9388 | 0.9325 | 0.7874 | 0.8926 | 0.8780 | 0.9235 | |
| 4 | 0.8104 | 0.7810 | 0.8430 | 0.9077 | 0.9033 | 0.7863 | 0.7842 | 0.3400 | 0.8894 | |
| Avg | 0.8194 | 0.7790 | 0.8581 | 0.9183 | 0.9074 | 0.7786 | 0.8699 | 0.7264 | 0.9077 | |
| ERGAS | ALL | 3.7344 | 3.7053 | 3.9652 | 2.1718 | 2.0695 | 3.4732 | 1.9407 | 2.1609 | 1.5933 |
| SAM | ALL | 17.7869 | 19.3630 | 18.8012 | 14.5189 | 13.4744 | 19.3714 | 15.2835 | 17.1857 | 12.4134 |
| MODEL | Param. (M) | FLOPs | |
|---|---|---|---|
| EDCSTFN | 0.28 | 1.86 × 1010 | |
| GAN-STFM | Generator | 0.58 | 3.78 × 1010 |
| Discriminator | 3.67 | 1.03 × 107 | |
| MLFF-GAN | Generator | 5.93 | 1.36 × 1010 |
| Discriminator | 2.78 | 3.77 × 109 | |
| STF-Trans | 23.34 | 1.74 × 1011 | |
| CTSTFM | 6.30 | 3.8 × 1011 | |
| BCSR-STF | 34.80 | 2.71 × 1010 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Wu, K.; Xu, G. A Bidirectional Cross Spatiotemporal Fusion Network with Spectral Restoration for Remote Sensing Imagery. Appl. Sci. 2025, 15, 6649. https://doi.org/10.3390/app15126649
Zhou D, Wu K, Xu G. A Bidirectional Cross Spatiotemporal Fusion Network with Spectral Restoration for Remote Sensing Imagery. Applied Sciences. 2025; 15(12):6649. https://doi.org/10.3390/app15126649
Chicago/Turabian StyleZhou, Dandan, Ke Wu, and Gang Xu. 2025. "A Bidirectional Cross Spatiotemporal Fusion Network with Spectral Restoration for Remote Sensing Imagery" Applied Sciences 15, no. 12: 6649. https://doi.org/10.3390/app15126649
APA StyleZhou, D., Wu, K., & Xu, G. (2025). A Bidirectional Cross Spatiotemporal Fusion Network with Spectral Restoration for Remote Sensing Imagery. Applied Sciences, 15(12), 6649. https://doi.org/10.3390/app15126649







