Improved Liquefaction Hazard Assessment via Deep Feature Extraction and Stacked Ensemble Learning on Microtremor Data
Abstract
1. Introduction
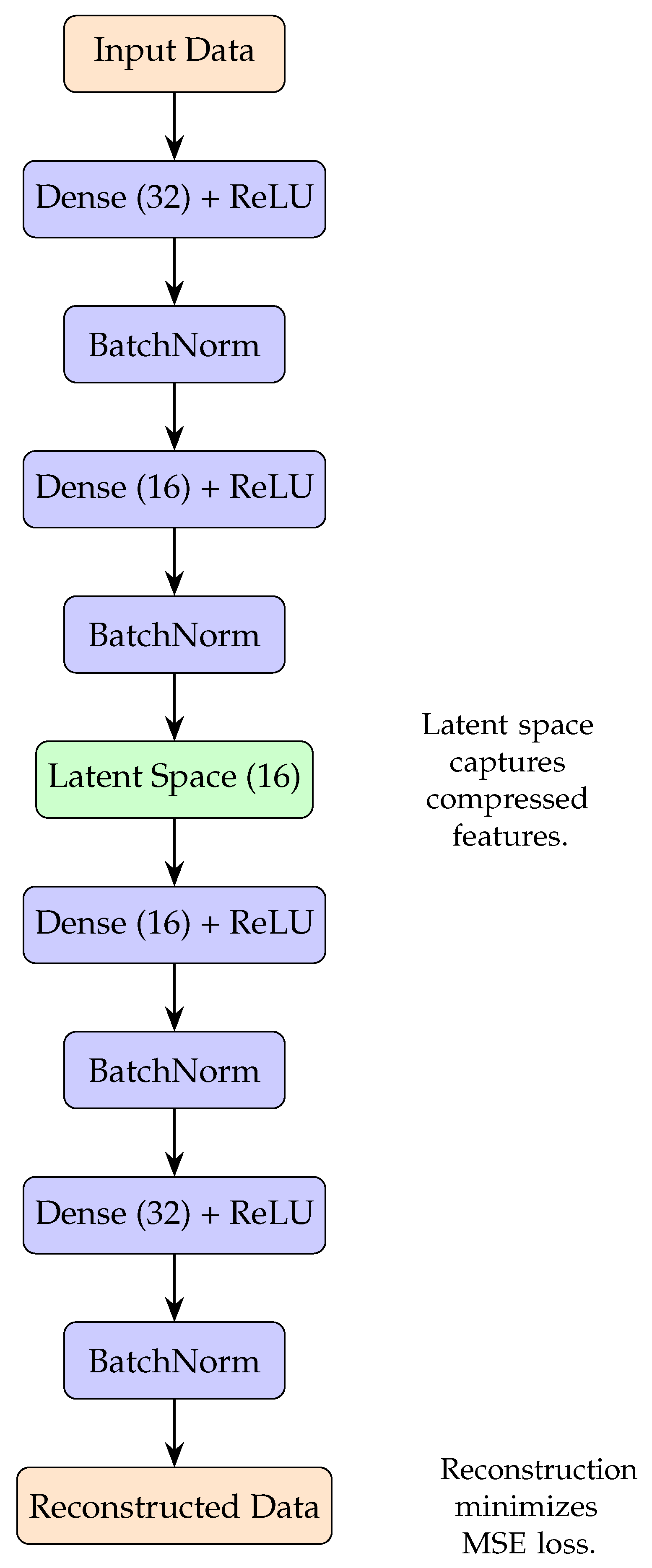
- Feature Extraction with an Autoencoder: An encoder has used ReLU activations to compress complex microtremor data and give more amplitude to the subtle pattern related to liquefaction.
- Robust Learning with Regularization: Batch normalization ascertains that the model will not overfit features, focusing only on the rare signal of liquefaction.
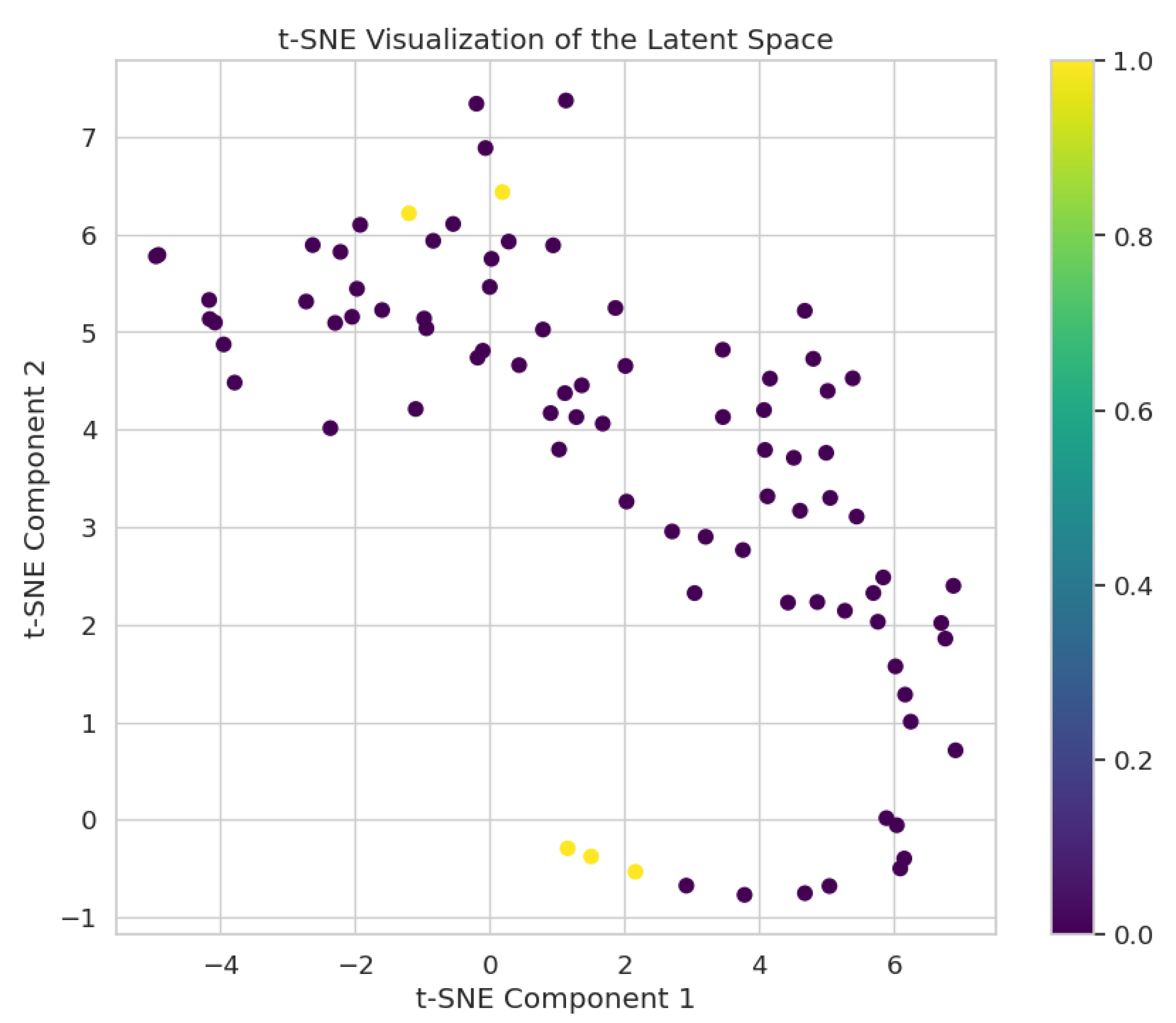
- Latent Space Embeddings: Critical indirect factors of liquefaction are caught by a latent 16-dimensional space, showing inner patterns of data.
- Stacked Classifier Ensemble: A stacked classified enseble combines the complex relationships identified by MLPwith the handling of class imbalance treated using XGBoost to make sure that the diversity within the data is reflected.
- Intelligent Meta-Model Aggregation: The final meta-model of MLP refines base model outputs, providing high priority to the rare events of liquefaction that may be missed in the individual models.
- Bias Mitigation by Representation Learning: The strengths of an autoencoder with embeddings and a stacked classifier are combined to avoid biases in concentrated datasets to represent liquefaction occurrence for rare data distributions.
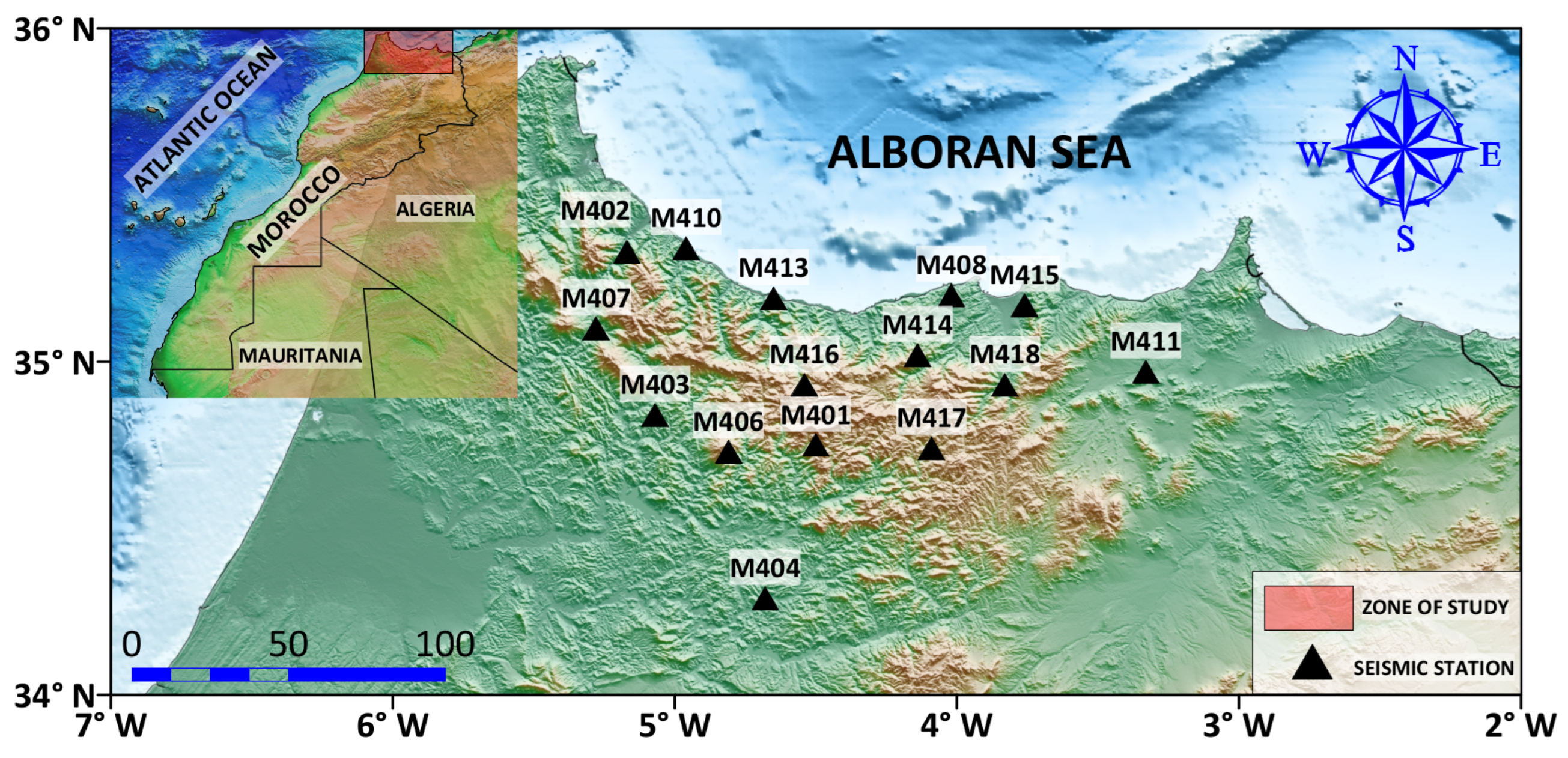
2. Geographical Setting
3. Methodology
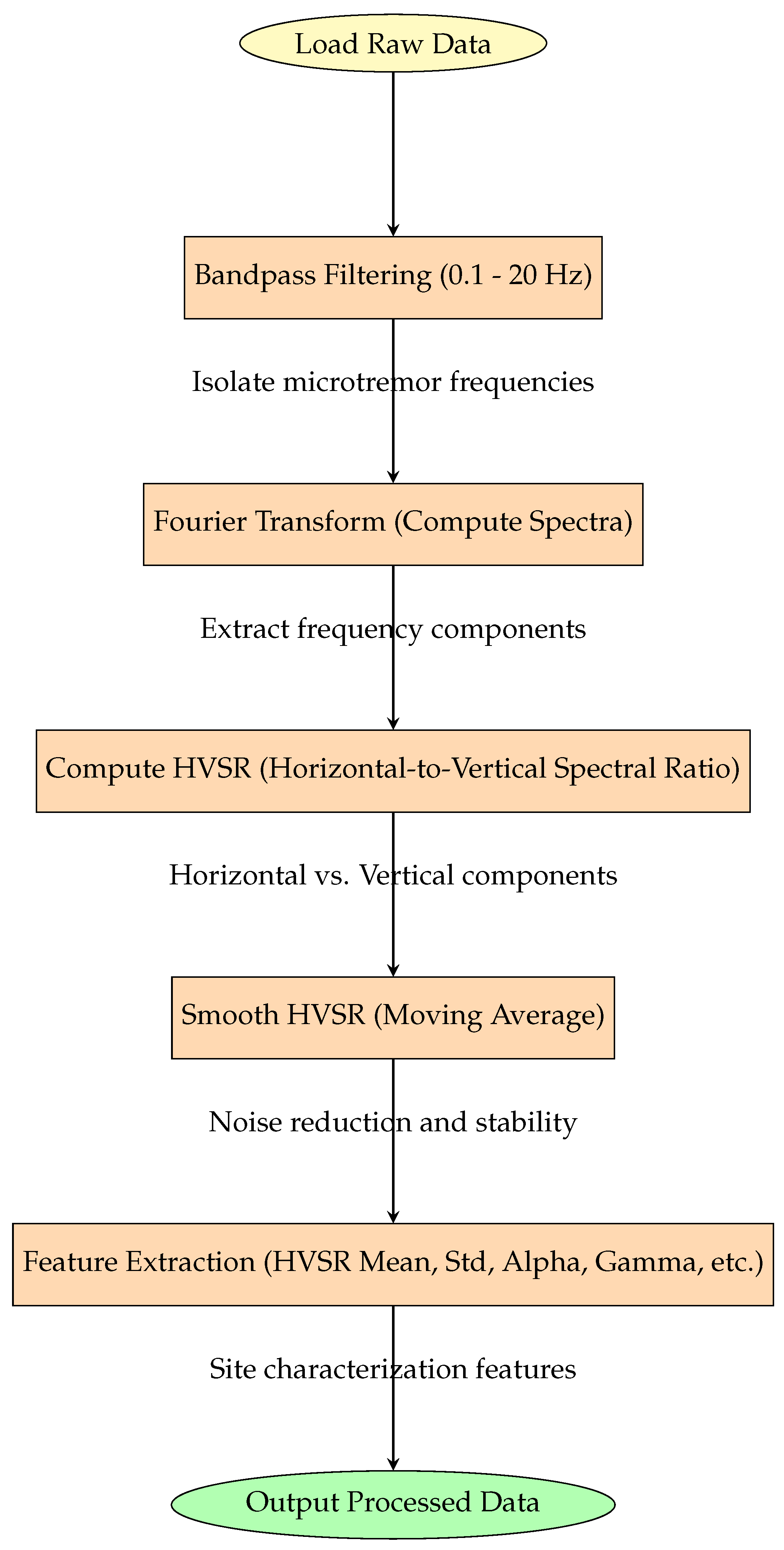
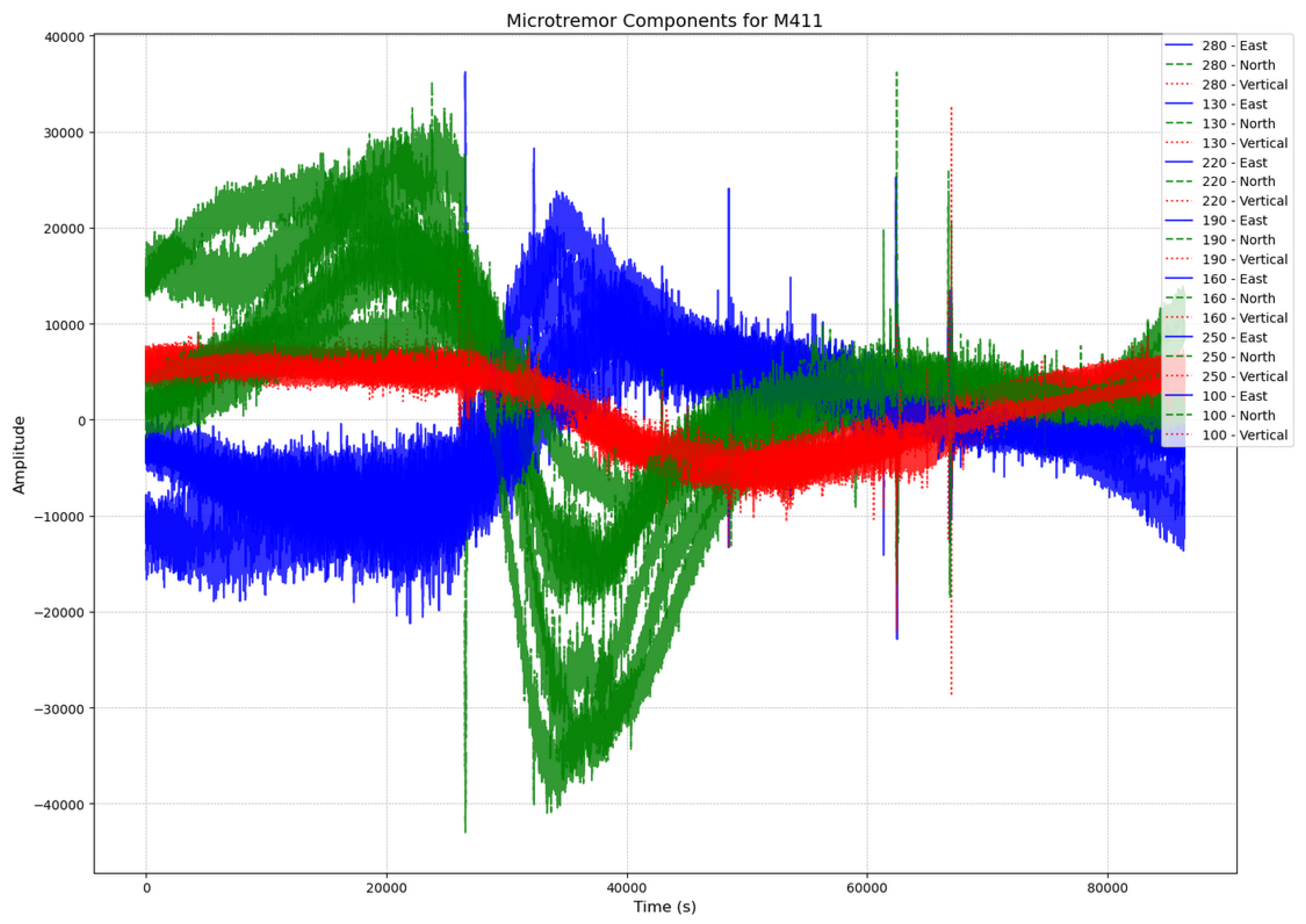
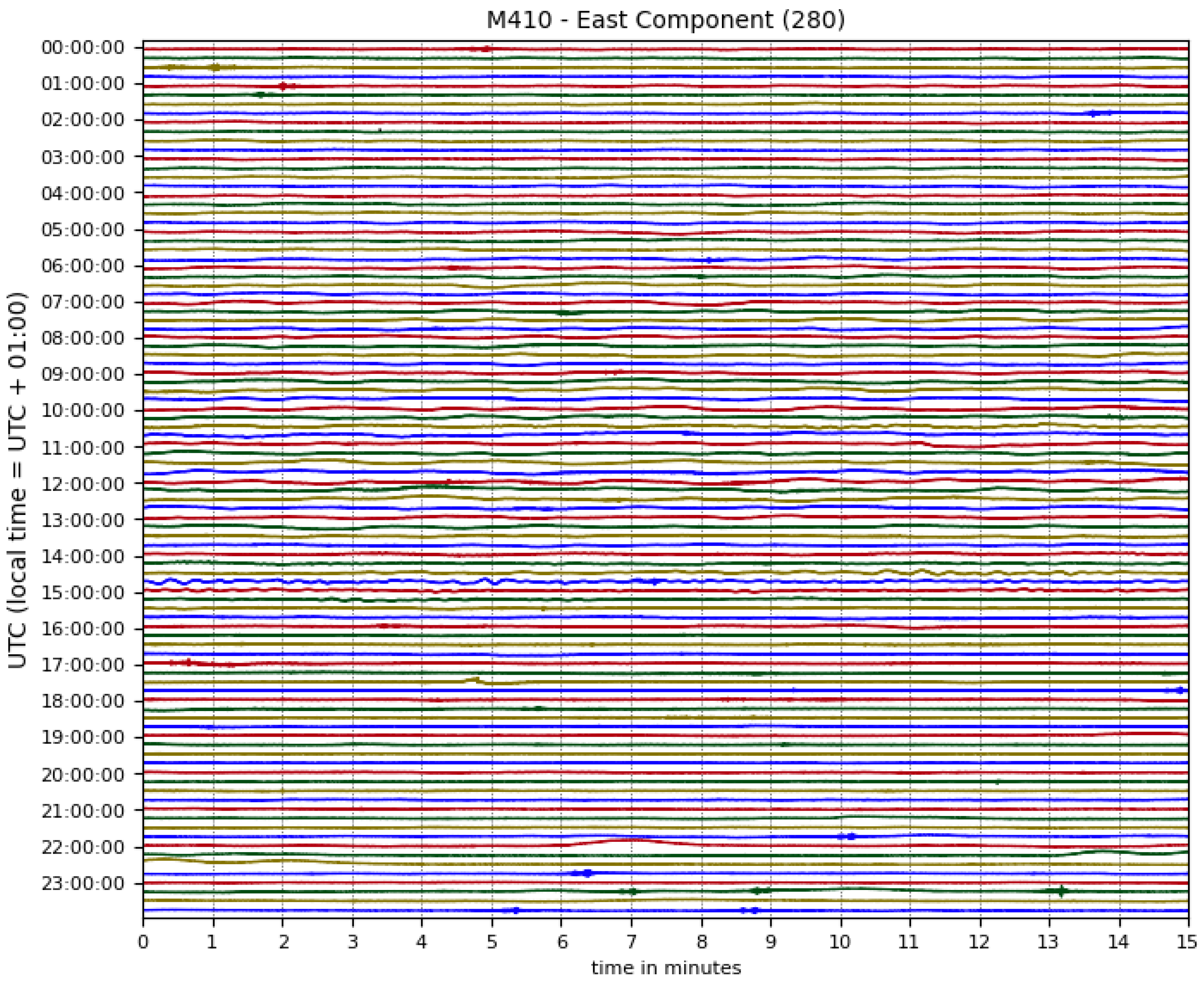
3.1. Data Acquisition and Preprocessing
3.2. Bandpass Filtering
3.3. HVSR Computation
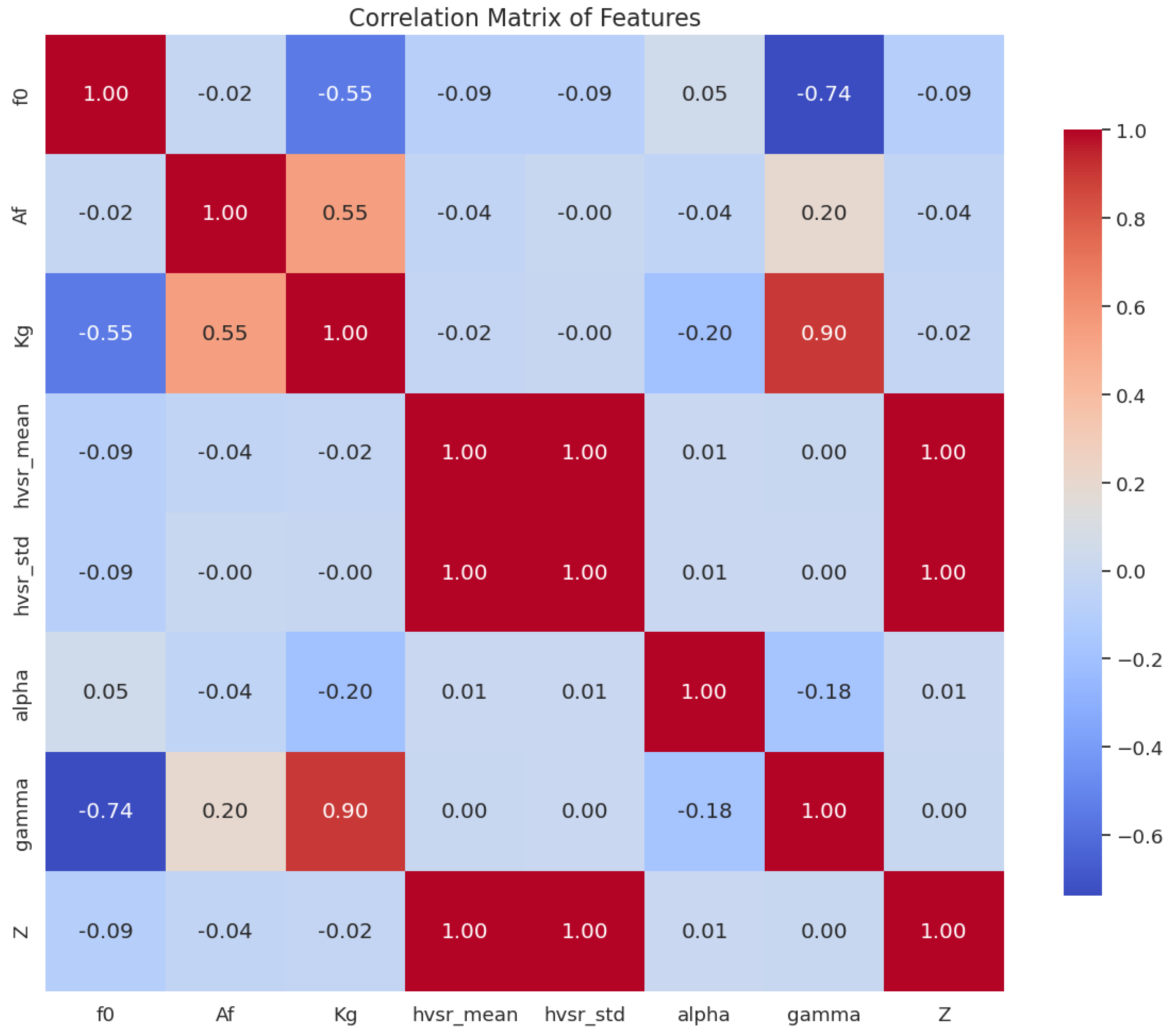
3.4. Feature Extraction
- The amplitude spectra are obtained via Fast Fourier Transform (FFT):
- The HVSR (hvsr_ratio) is the ratio of the horizontal spectral components (East–West and North–South) to the vertical component.where- is the amplitude spectrum of the North–South component;- is the amplitude spectrum of the East–West component;- is the amplitude spectrum of the vertical component.Then, this ratio is smoothed using a moving average with a kernel of size 10:
- Mean and Standard Deviation of HVSR: Shapes and variability in the overall HVSR curve provide critical information on resonance and amplification phenomena of the site.The mean of the smoothed HVSR ratio is expressed as follows:where N is the total number of frequency points.The standard deviation of the smoothed HVSR is expressed as follows:
- Alpha and gamma are parameters derived as the logarithmic and direct ratio, respectively, between the amplification factor and the fundamental frequency of the site; these are important in interpreting the dynamic resonance characteristics of the site.
- Z represents the energy distribution between horizontal and vertical components of microseismic waves to provide an integrated view of wave characteristics.where
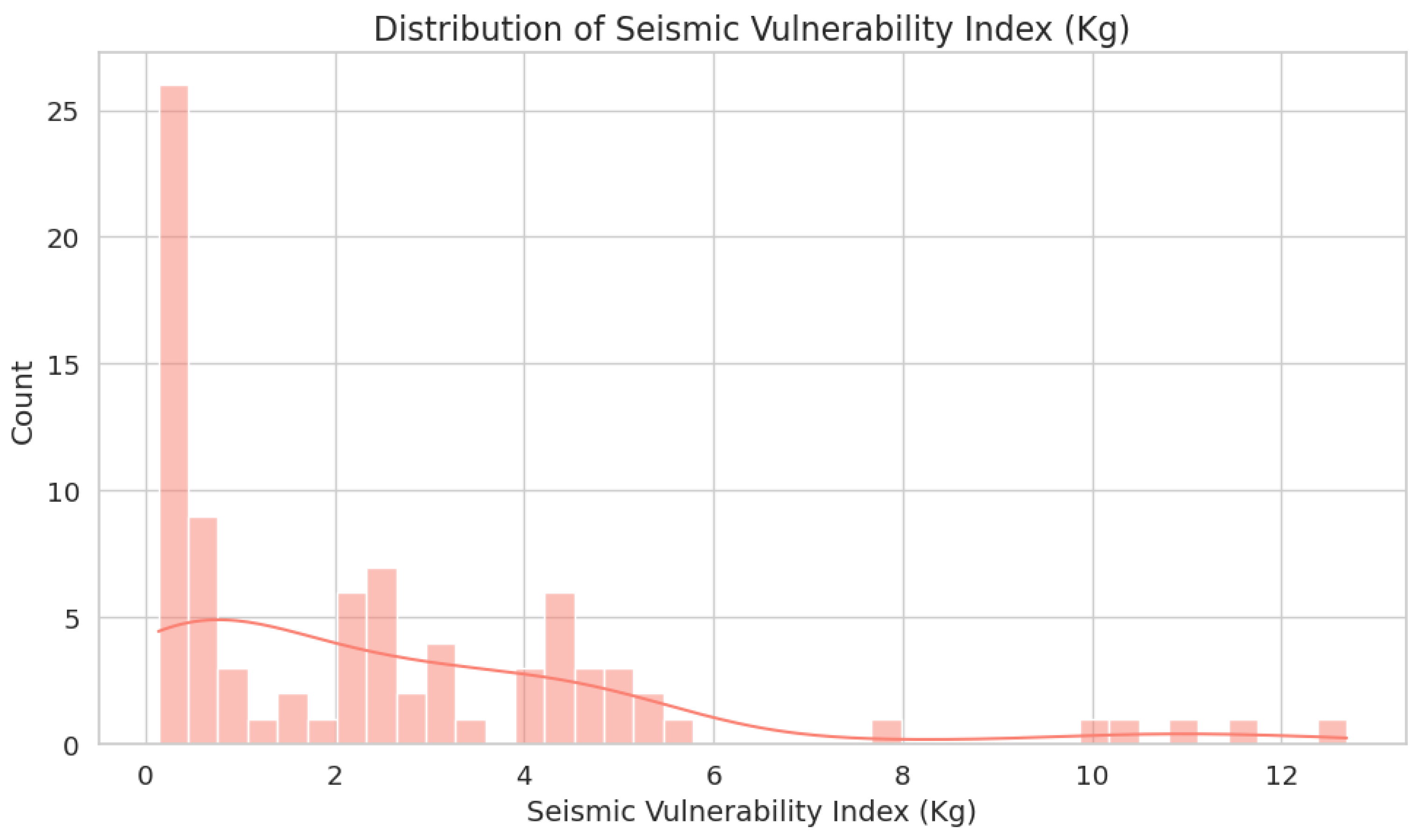
- The vulnerability index () is derived from the amplitude factor () and the resonant frequency (), which provides more detail for the determination of spectral properties of the site.
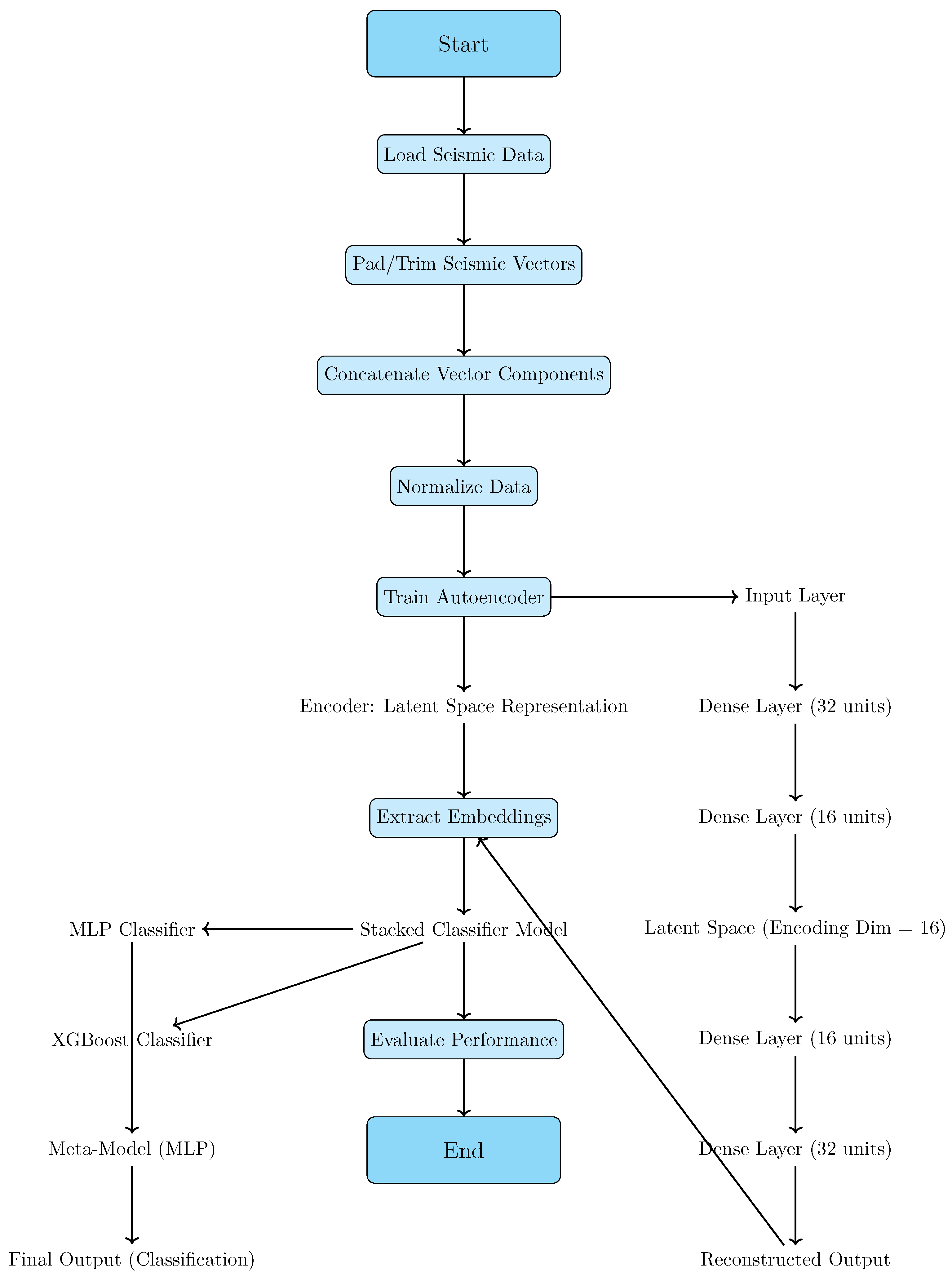
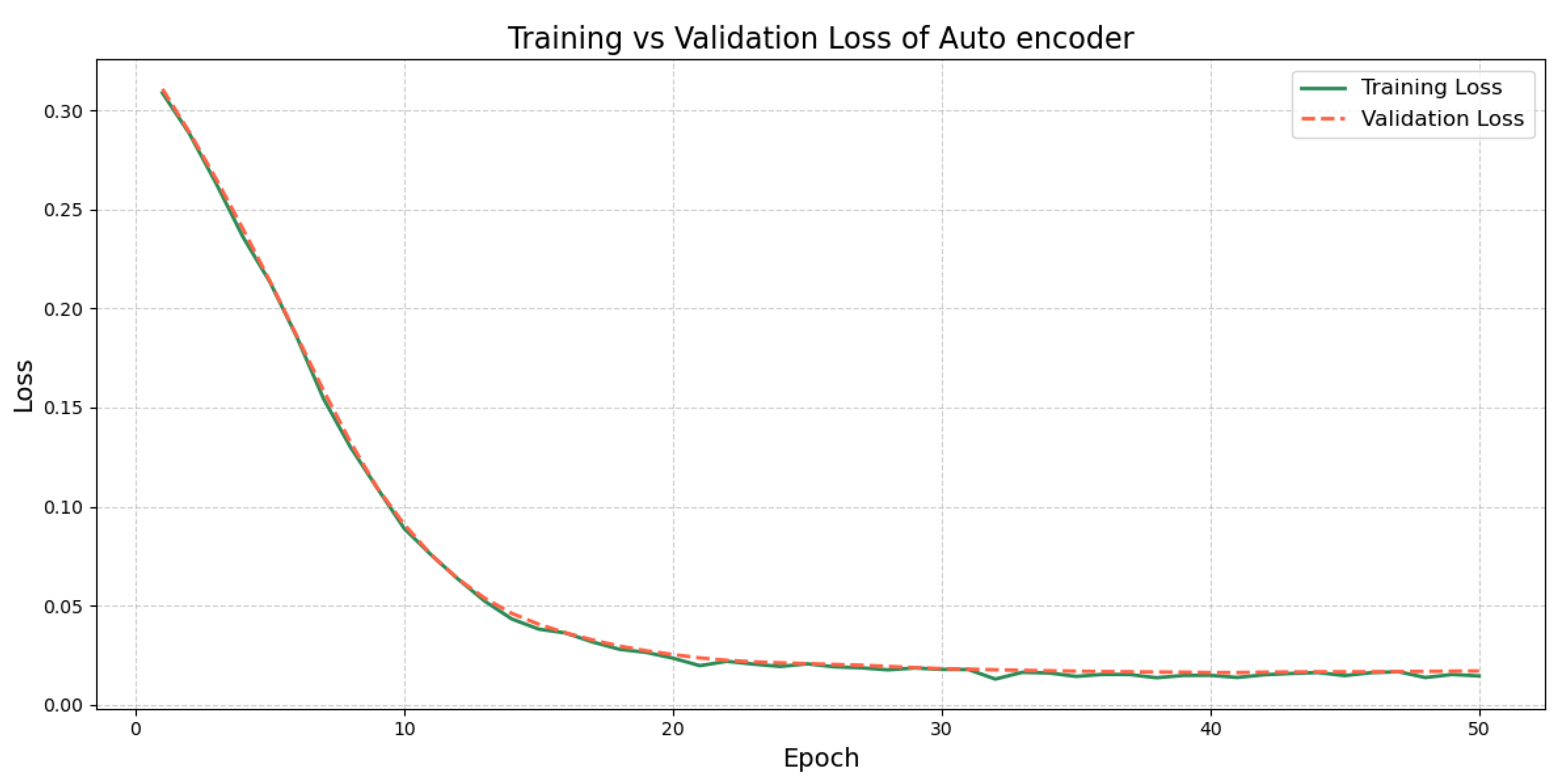
3.5. Model Description
4. Experiments
- Accuracy compares the total accuracy of the model as a ratio of true predictions to the total number of predictions.
- Precision estimates the number of predicted positives that are actually positive:
- Recall estimates how many actual positives were correctly identified by the model:
- The F1 score is the mean of precision and recall, offering a balance between the two metrics:
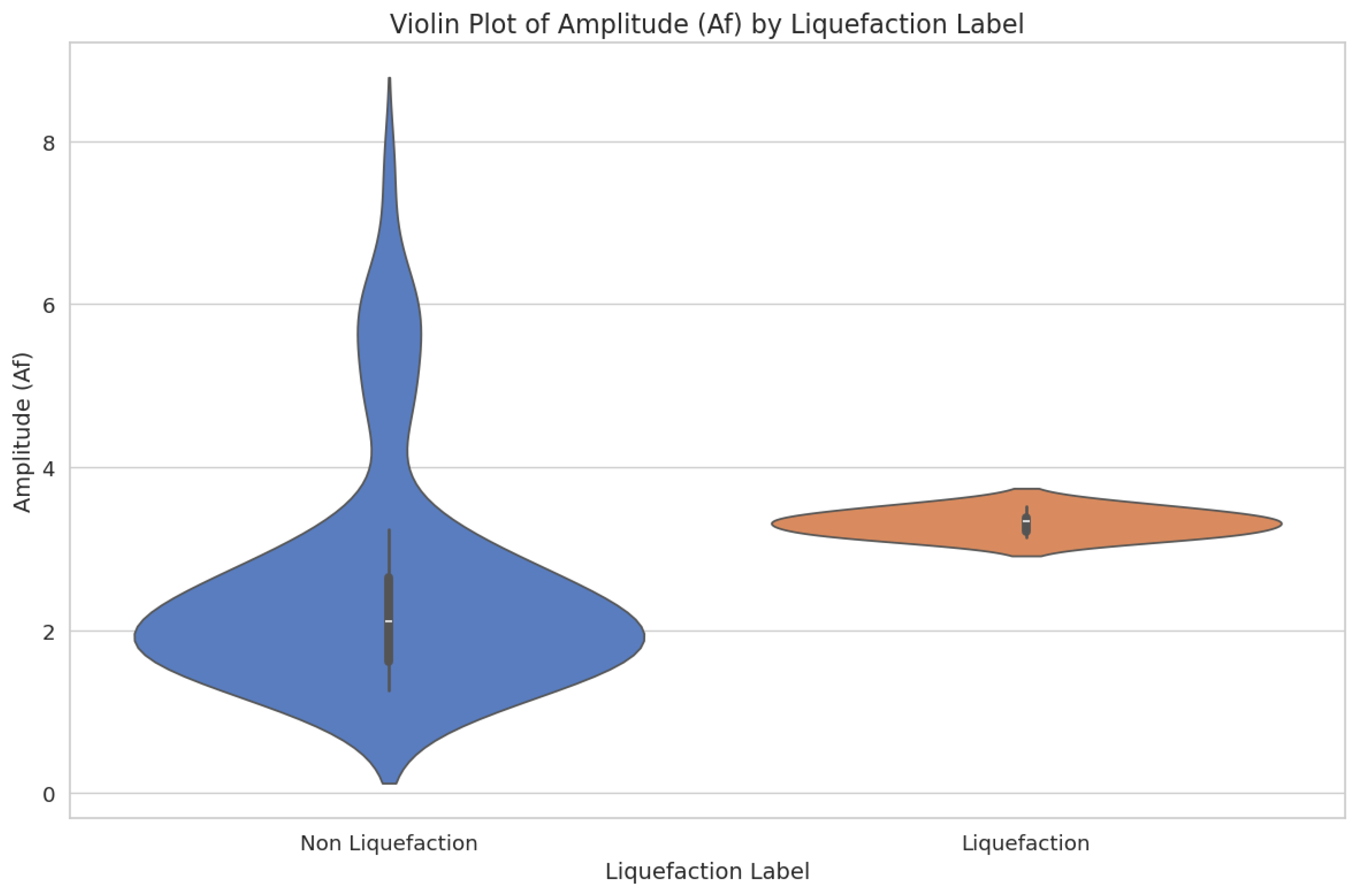
4.1. Data Description
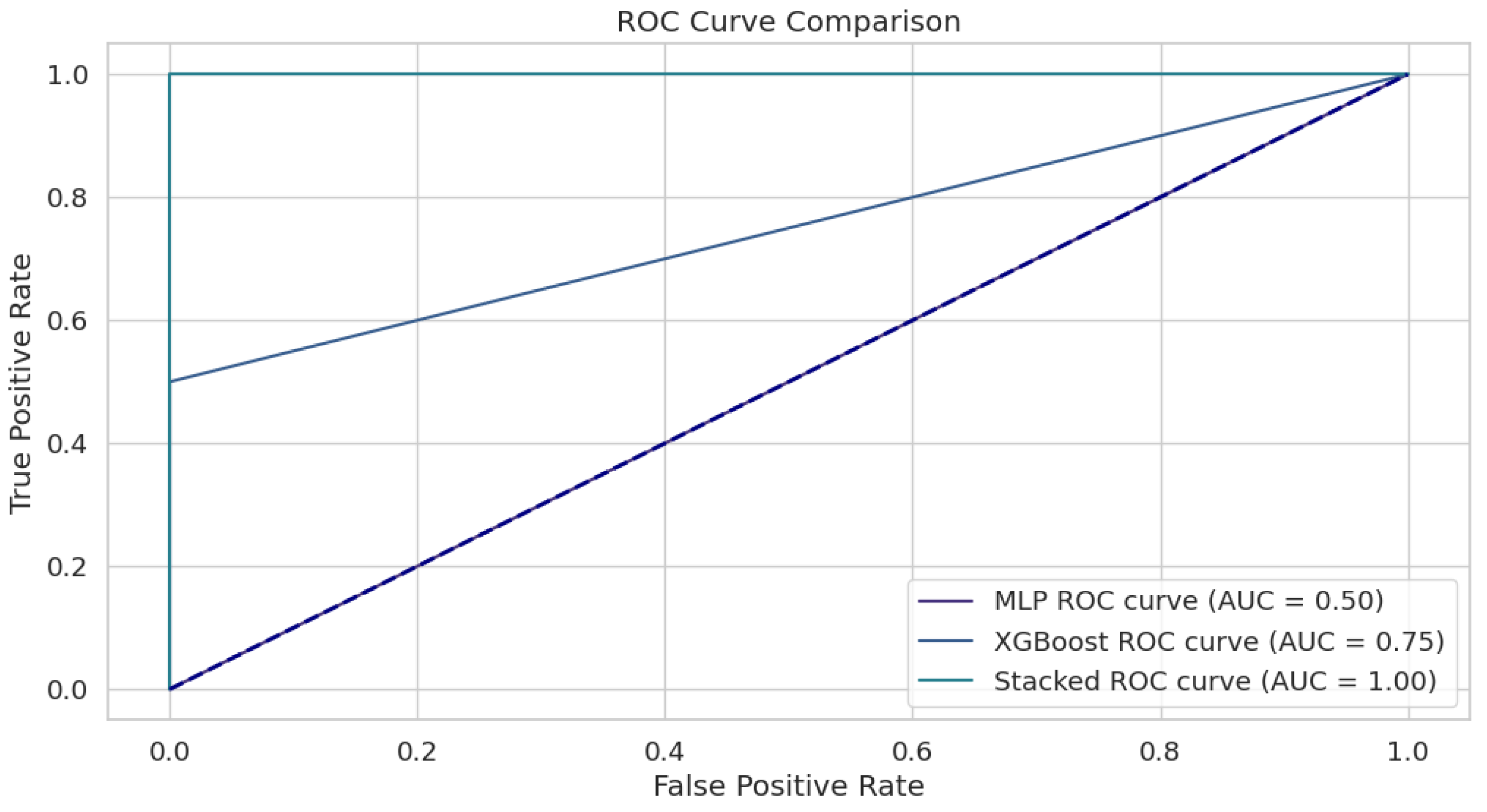
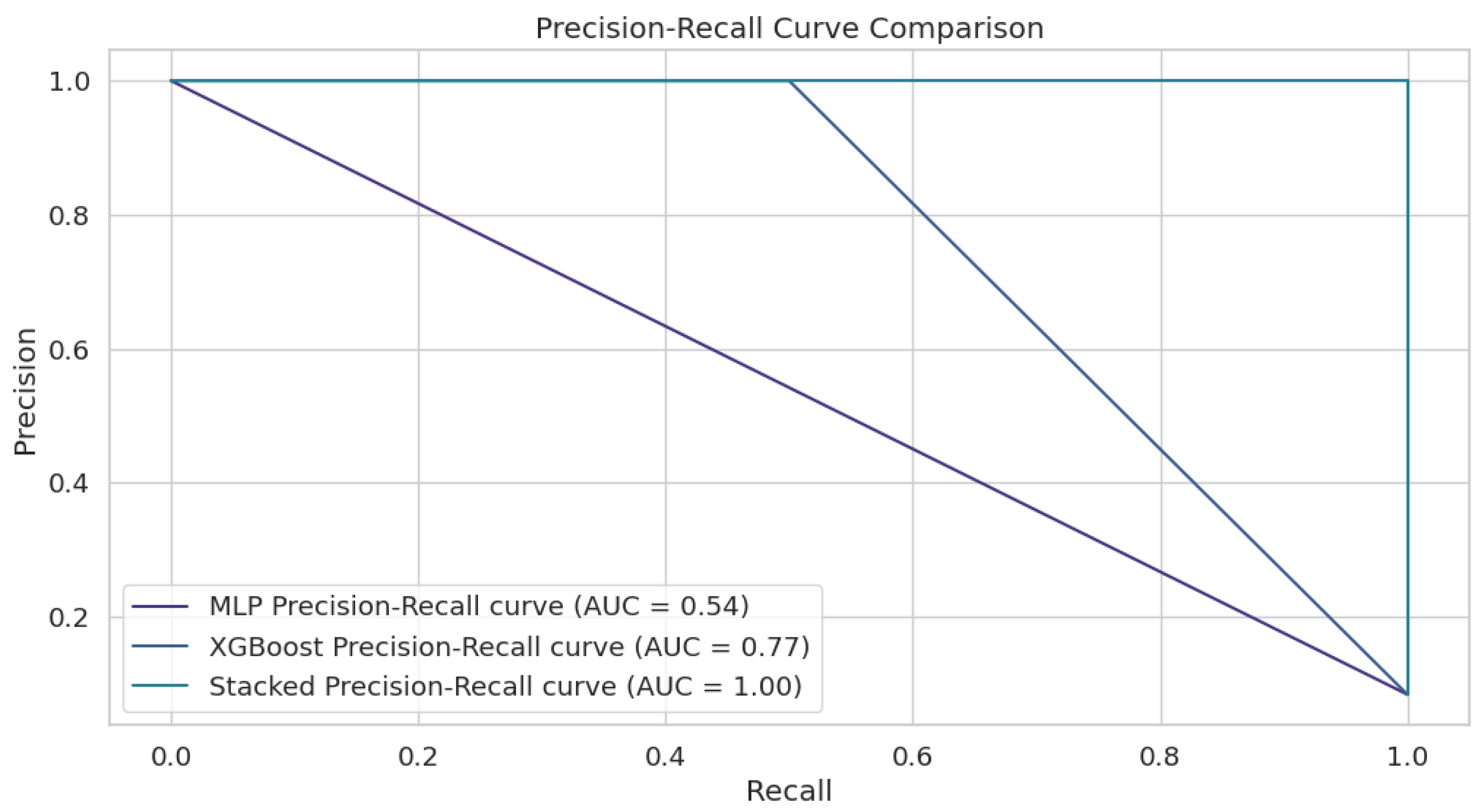
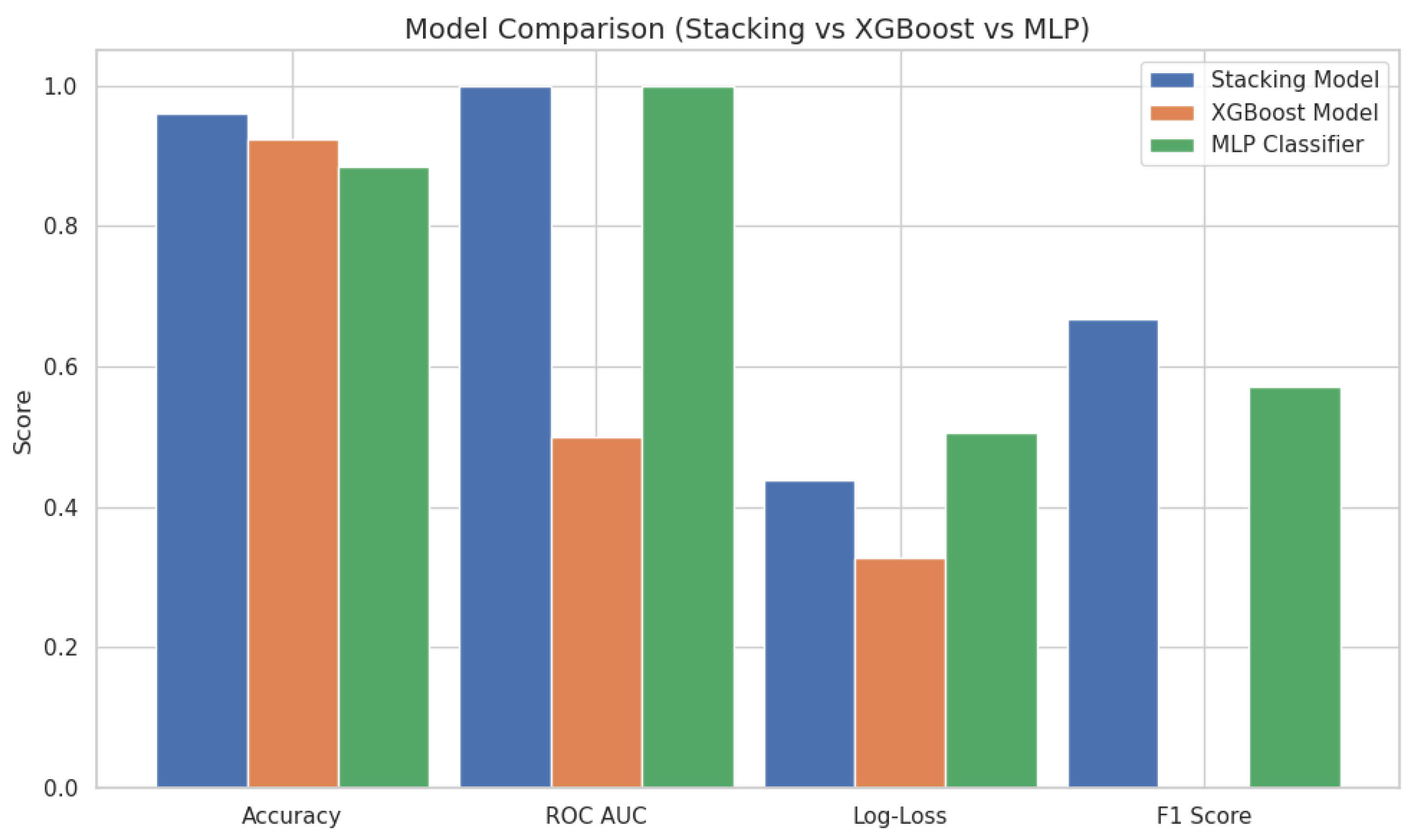
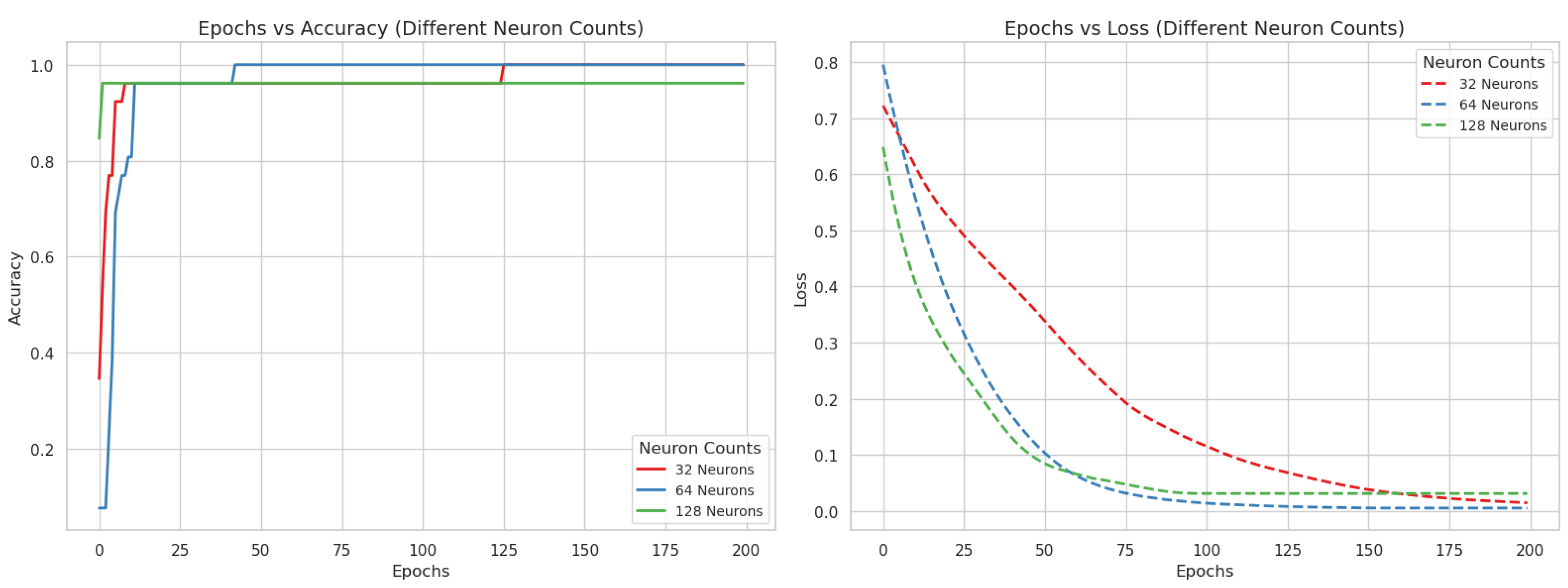
4.2. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marten Caceres, R.; Abrassart, T.; Boano, C. Urban Planning and Natural Hazard Governance; Oxford University Press: Oxford, UK, 2019. [Google Scholar]
- Bird, J.F.; Bommer, J.J. Earthquake losses due to ground failure. Eng. Geol. 2004, 75, 147–179. [Google Scholar] [CrossRef]
- Wani, K.M.N.S.; Mir, B.A.; Naik, T.H.; Farooq, M. Liquefaction mitigation by induced partial saturation: A comprehensive review. J. Struct. Integr. Maint. 2024, 9, 2429471. [Google Scholar] [CrossRef]
- Youd, T.L. Liquefaction-induced damage to bridges. Transp. Res. Rec. 1993, 1411, 35–41. [Google Scholar]
- Turner, B.; Brandenberg, S.J.; Stewart, J.P. Evaluation of collapse and non-collapse of parallel bridges affected by liquefaction and lateral spreading. In Proceedings of the 10th International Conference on Urban Earthquake Engineering, Tokyo, Japan, 1–2 March 2013; Tokyo Institute of Technology: Tokyo, Japan, 2013. [Google Scholar]
- Shafapourtehrany, M.; Batur, M.; Shabani, F.; Pradhan, B.; Kalantar, B.; Özener, H. A comprehensive review of geospatial technology applications in earthquake preparedness, emergency management, and damage assessment. Remote Sens. 2023, 15, 1939. [Google Scholar] [CrossRef]
- Pribadi, K.S.; Abduh, M.; Wirahadikusumah, R.D.; Hanifa, N.R.; Irsyam, M.; Kusumaningrum, P.; Puri, E. Learning from past earthquake disasters: The need for knowledge management system to enhance infrastructure resilience in indonesia. Int. J. Disaster Risk Reduct. 2021, 64, 102424. [Google Scholar] [CrossRef]
- He, X.; Chen, Z.; Yang, Q.; Xu, C. Advances in earthquake and cascading disasters. Nat. Hazards Res. 2025, 5, 421–431. [Google Scholar] [CrossRef]
- Poulos, S.J.; Castro, G.; France, J.W. Liquefaction evaluation procedure. J. Geotech. Eng. 1985, 111, 772–792. [Google Scholar] [CrossRef]
- Youd, T.L.; Perkins, D.M. Mapping liquefaction-induced ground failure potential. J. Geotech. Eng. Div. 1978, 104, 433–446. [Google Scholar] [CrossRef]
- Maurer, B.W.; Sanger, M.D. Why “AI” models for predicting soil liquefaction have been ignored, plus some that shouldn’t be. Earthq. Spectra 2023, 39, 1883–1910. [Google Scholar] [CrossRef]
- Yilmaz, C.; Silva, V.; Weatherill, G. Probabilistic framework for regional loss assessment due to earthquake-induced liquefaction including epistemic uncertainty. Soil Dyn. Earthq. Eng. 2021, 141, 106493. [Google Scholar] [CrossRef]
- Abbasimaedeh, P. Soil liquefaction in seismic events: Pioneering predictive models using machine learning and advanced regression techniques. Environ. Earth Sci. 2024, 83, 189. [Google Scholar] [CrossRef]
- Kim, H.-S. Geospatial data-driven assessment of earthquake-induced liquefaction impact mapping using classifier and cluster ensembles. Appl. Soft Comput. 2023, 140, 110266. [Google Scholar] [CrossRef]
- Phoon, K.-K.; Ching, J.; Shuku, T. Challenges in data-driven site characterization. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 16, 114–126. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Q.; Arduino, P. Data-centric seismic soil liquefaction assessment: Approaches, data, and tools. In Databases for Data-Centric Geotechnics; CRC Press: Boca Raton, FL, USA, 2024; pp. 427–451. [Google Scholar]
- Dieck, R.H. Measurement Uncertainty: Methods and Applications; ISA: Geneva, Switzerland, 2007. [Google Scholar]
- Kumar, D.R.; Samui, P.; Burman, A. Prediction of probability of liquefaction using hybrid ann with optimization techniques. Arab. J. Geosci. 2022, 15, 1587. [Google Scholar] [CrossRef]
- Ghani, S.; Thapa, I.; Kumari, S.; Correia, A.G.; Asteris, P.G. Revealing the nature of soil liquefaction using machine learning. Earth Sci. Inform. 2025, 18, 198. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J.; Zhang, Z.; Liu, H. Continuous-discrete hybrid bayesian network models for predicting earthquake-induced liquefaction based on the vs database. Comput. Geosci. 2022, 169, 105231. [Google Scholar] [CrossRef]
- Jas, K.; Dodagoudar, G.R. Liquefaction potential assessment of soils using machine learning techniques: A state-of-the-art review from 1994–2021. Int. J. Geomech. 2023, 23, 03123002. [Google Scholar] [CrossRef]
- Kurnaz, T.F.; Erden, C.; Kökçam, A.H.; Dağdeviren, U.; Demir, A.S. A hyper parameterized artificial neural network approach for prediction of the factor of safety against liquefaction. Eng. Geol. 2023, 319, 107109. [Google Scholar] [CrossRef]
- Hameed, M.M.; Masood, A.; Srivastava, A.; Abd Rahman, N.; Razalid, S.F.M.; Salem, A.; Elbeltagi, A. Investigating a hybrid extreme learning machine coupled with dingo optimization algorithm for modeling liquefaction triggering in sand-silt mixtures. Sci. Rep. 2024, 14, 10799. [Google Scholar] [CrossRef]
- Alobaidi, M.H.; Meguid, M.A.; Chebana, F. Predicting seismic-induced liquefaction through ensemble learning frameworks. Sci. Rep. 2019, 9, 11786. [Google Scholar] [CrossRef]
- Khatti, J.; Fissha, Y.; Grover, K.S.; Ikeda, H.; Toriya, H.; Adachi, T.; Kawamura, Y. Cone penetration test-based assessment of liquefaction potential using machine and hybrid learning approaches. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 3841–3864. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, W.; Cai, G.; Wu, M.; Liu, S.; Puppala, A.J. Probabilistic capacity energy-based machine learning models for soil liquefaction reliability analysis. Eng. Geol. 2024, 338, 107613. [Google Scholar] [CrossRef]
- Ghani, S.; Kumari, S. Reliability analysis for liquefaction risk assessment for the city of patna, india using hybrid computational modeling. J. Geol. Soc. India 2022, 98, 1395–1406. [Google Scholar] [CrossRef]
- Li, P.; Pei, Y.; Li, J. A comprehensive survey on design and application of autoencoder in deep learning. Appl. Soft Comput. 2023, 138, 110176. [Google Scholar] [CrossRef]
- Riedmiller, M.; Lernen, A. Multi layer perceptron. In Machine Learning Lab Special Lecture; University of Freiburg: Freiburg, Germany, 2014; p. 24. [Google Scholar]
- Chen, T. Xgboost: Extreme Gradient Boosting. In R Package; Version 0.4-2; R Foundation for Statistical Computing: Vienna, Austria, 2015; Volume 1, pp. 1–4. [Google Scholar]
- Pateau, M. From hazard to natural risk: Tangier-tetouan region example (Rif, Morocco). Geo-Eco-Trop 2014, 38, 23–32. [Google Scholar]
- Arab, O.; Fellah, Y.E.; Harnafi, M.; Sebbani, J.; Abd el-aal, A.K. Estimation of the liquefaction potential in the region of Rif, Northern Morocco. Arab. J. Geosci. 2021, 14, 1–13. [Google Scholar] [CrossRef]
- Molnar, S.; Sirohey, A.; Assaf, J.; Bard, P.Y.; Castellaro, S.; Cornou, C.; Cox, B.; Guillier, B.; Hassani, B.; Kawase, H.; et al. A review of the microtremor horizontal-to-vertical spectral ratio (MHVSR) method. J. Seismol. 2022, 26, 653–685. [Google Scholar] [CrossRef]
- Oweiss, K.G. Statistical Signal Processing for Neuroscience and Neurotechnology; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Xu, R.; Wang, L. The horizontal-to-vertical spectral ratio and its applications. EURASIP J. Adv. Signal Process. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- SESAME. Guidelines for the Implementation of the H/V Spectral Ratio Technique on Ambient Vibrations: Measurements, Processing and Interpretation; Technical Report, SESAME European Research Project WP12; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Vivó-Truyols, G.; Schoenmakers, P.J. Automatic selection of optimal savitzky- golay smoothing. Anal. Chem. 2006, 78, 4598–4608. [Google Scholar] [CrossRef] [PubMed]
- Gomez, B.; Kadri, U. Earthquake source characterization by machine learning algorithms applied to acoustic signals. Sci. Rep. 2021, 11, 23062. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.M.; Rahman, M.Z.; Fahim, A.K.F. Earthquake induced liquefaction hazard analysis for chittagong city using machine learning. Geomat. Nat. Hazards Risk 2025, 16, 2451126. [Google Scholar] [CrossRef]
- Ma, Z.; Mei, G. Deep learning for geological hazards analysis: Data, models, applications, and opportunities. Earth-Sci. Rev. 2021, 223, 103858. [Google Scholar] [CrossRef]
- Pilz, M.; Cotton, F.; Kotha, S.R. Data-driven and machine learning identification of seismic reference stations in europe. Geophys. J. Int. 2020, 222, 861–873. [Google Scholar] [CrossRef]
- Gárate, J.; Martin-Davila, J.; Khazaradze, G.; Echeverria, A.; Asensio, E.; Gil, A.J.; De Lacy, M.C.; Armenteros, J.A.; Ruiz, A.M.; Gallastegui, J.; et al. Topo-iberia project: Cgps crustal velocity field in the Iberian Peninsula and Morocco. GPS Solut. 2015, 19, 287–295. [Google Scholar] [CrossRef]
- Liu, R.; Misra, S. Machine learning assisted recovery of subsurface energy: A review. Authorea Prepr. 2022, 16, 6079. [Google Scholar] [CrossRef]
- Ioffe, S. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Vessia, G.; Laurenzano, G.; Pagliaroli, A.; Pilz, M. Seismic site response estimation for microzonation studies promoting the resilience of urban centers. Eng. Geol. 2021, 284, 106031. [Google Scholar] [CrossRef]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond accuracy, f-score and roc: A family of discriminant measures for performance evaluation. In Australasian Joint Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1015–1021. [Google Scholar]
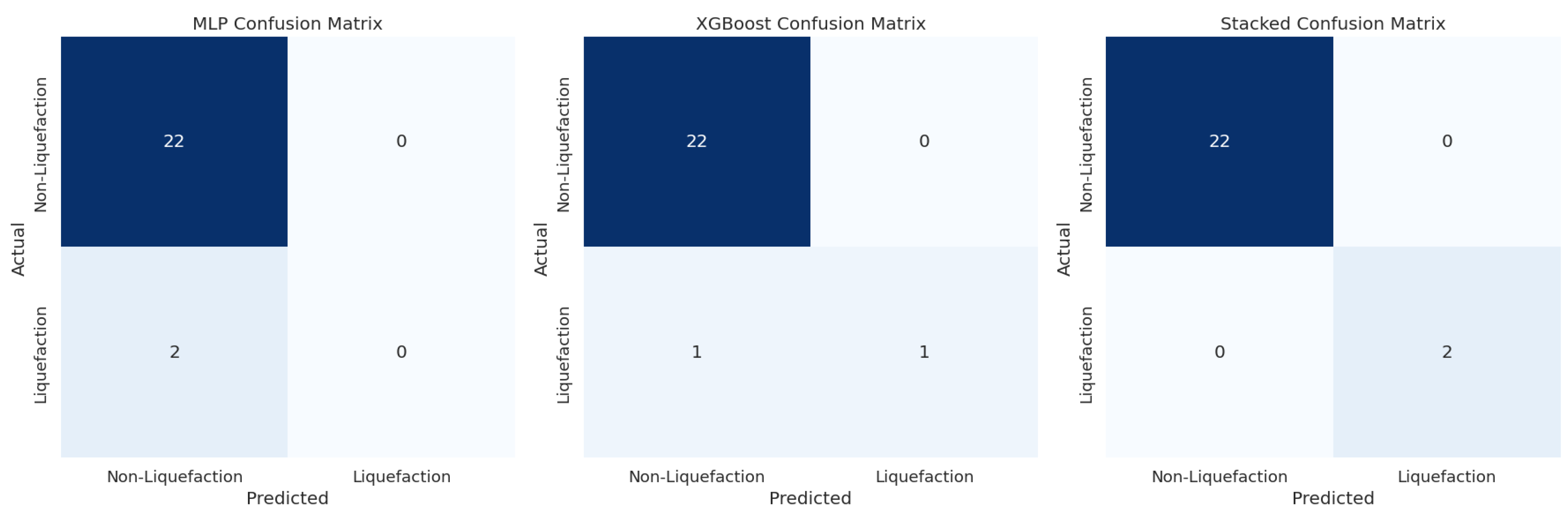
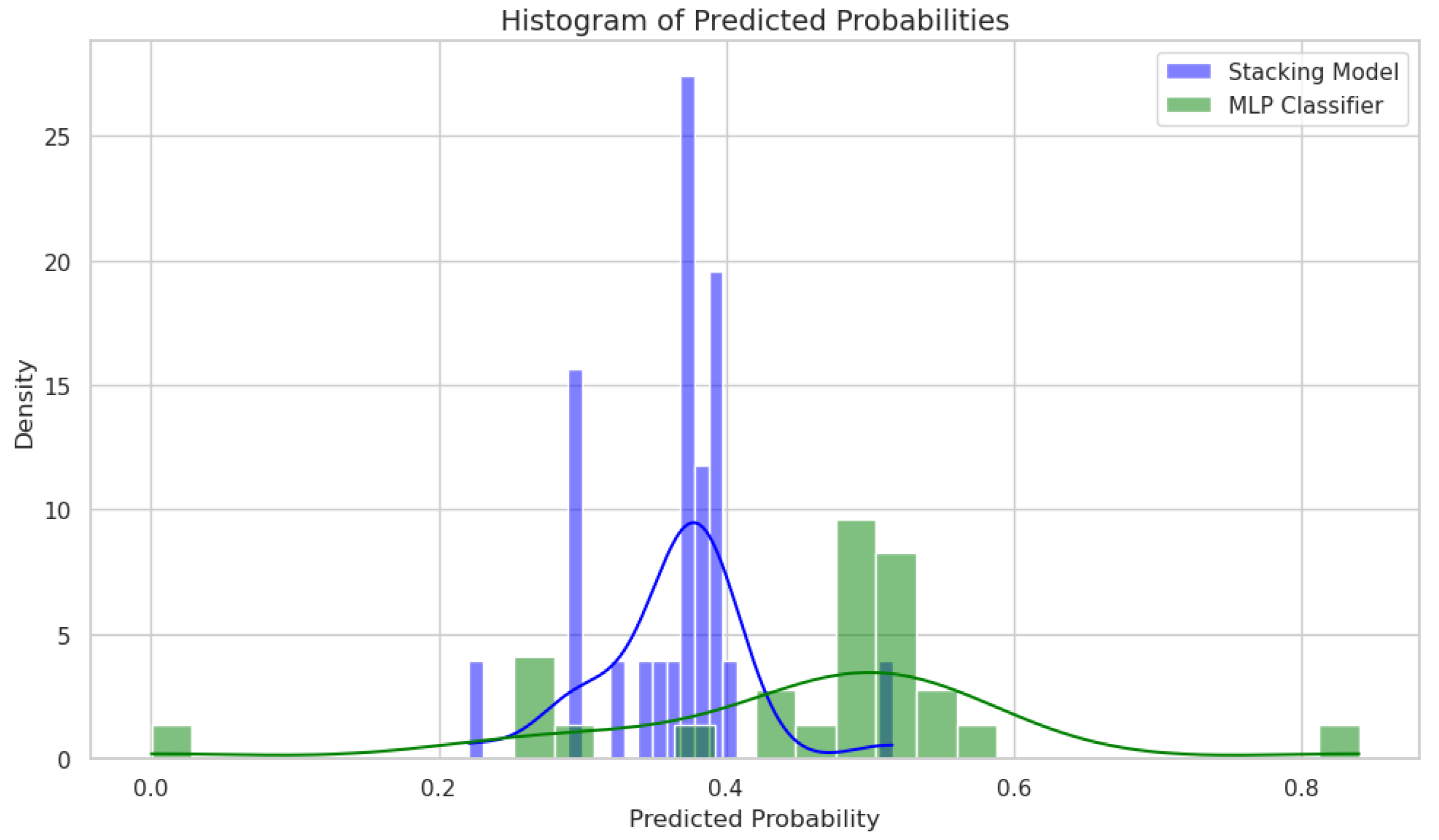


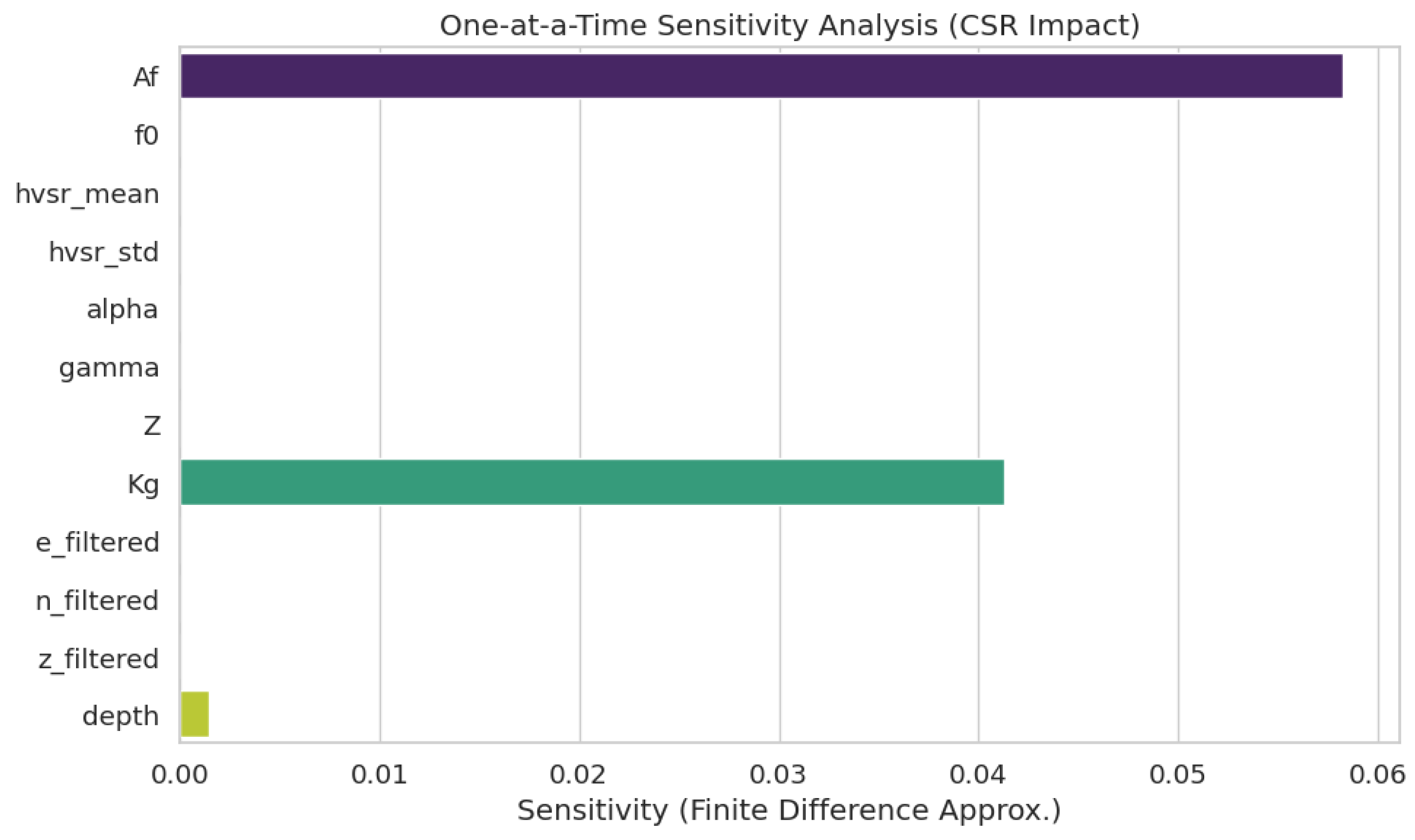
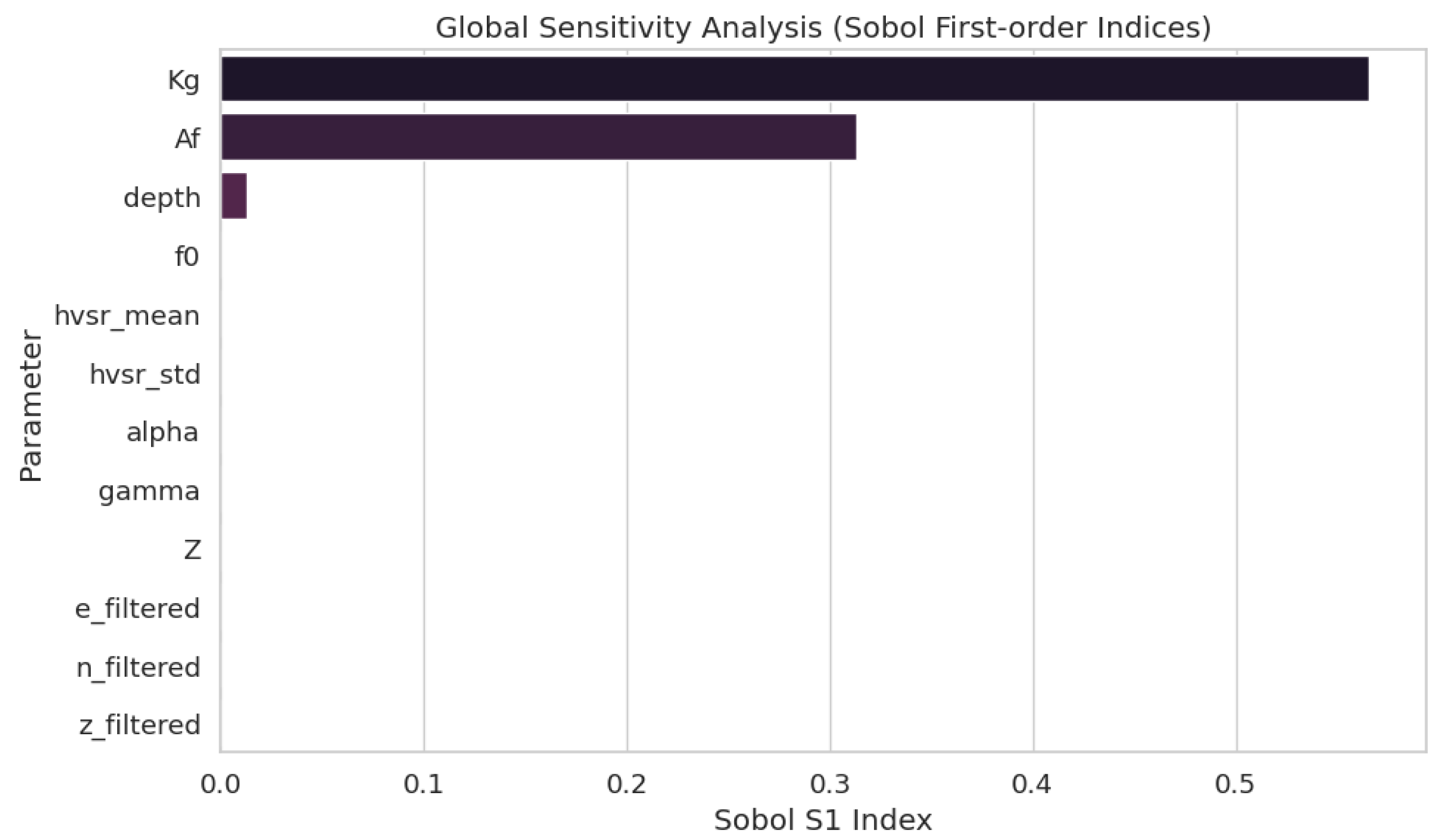
| Model | Class | Precision | Recall | F1 Score | Support |
|---|---|---|---|---|---|
| MLP | 0 | 0.92 | 1.00 | 0.96 | 22 |
| 1 | 0.00 | 0.00 | 0.00 | 2 | |
| Accuracy | 0.92 | 24 | |||
| Macro Avg | 0.46 | 0.50 | 0.48 | 24 | |
| Weighted Avg | 0.84 | 0.92 | 0.88 | 24 | |
| XGBoost | 0 | 0.96 | 1.00 | 0.98 | 22 |
| 1 | 1.00 | 0.50 | 0.67 | 2 | |
| Accuracy | 0.96 | 24 | |||
| Macro Avg | 0.98 | 0.75 | 0.82 | 24 | |
| Weighted Avg | 0.96 | 0.96 | 0.95 | 24 | |
| Stacked Model | 0 | 1.00 | 1.00 | 1.00 | 22 |
| 1 | 1.00 | 1.00 | 1.00 | 2 | |
| Accuracy | 1.00 | 24 | |||
| Macro Avg | 1.00 | 1.00 | 1.00 | 24 | |
| Weighted Avg | 1.00 | 1.00 | 1.00 | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arab, O.; Mekouar, S.; Mastere, M.; Cabieces, R.; Collantes, D.R. Improved Liquefaction Hazard Assessment via Deep Feature Extraction and Stacked Ensemble Learning on Microtremor Data. Appl. Sci. 2025, 15, 6614. https://doi.org/10.3390/app15126614
Arab O, Mekouar S, Mastere M, Cabieces R, Collantes DR. Improved Liquefaction Hazard Assessment via Deep Feature Extraction and Stacked Ensemble Learning on Microtremor Data. Applied Sciences. 2025; 15(12):6614. https://doi.org/10.3390/app15126614
Chicago/Turabian StyleArab, Oussama, Soufiana Mekouar, Mohamed Mastere, Roberto Cabieces, and David Rodríguez Collantes. 2025. "Improved Liquefaction Hazard Assessment via Deep Feature Extraction and Stacked Ensemble Learning on Microtremor Data" Applied Sciences 15, no. 12: 6614. https://doi.org/10.3390/app15126614
APA StyleArab, O., Mekouar, S., Mastere, M., Cabieces, R., & Collantes, D. R. (2025). Improved Liquefaction Hazard Assessment via Deep Feature Extraction and Stacked Ensemble Learning on Microtremor Data. Applied Sciences, 15(12), 6614. https://doi.org/10.3390/app15126614







