Next Article in Journal
Analysis of Tunnel Deformation Using Elastoplastic Stillinger Weber (SW) Potential Embedded Discretized Virtual Internal Bond (DVIB) Method
Previous Article in Journal
Deep Learning-Enhanced Electronic Packaging Defect Detection via Fused Thermal Simulation and Infrared Thermography
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 12
10.3390/app15126593
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Kinematic Analysis of Dynamic Coactivation During Arm Swing at the Shoulder and Elbow Joints

by
Jae Ho Kim
1,
Jaejin Hwang
2,
Myung-Chul Jung
3 and
Seung-Min Mo
4,*
1
Department of Industrial Safety Management, Suncheon Jeil College, 17, Jeildaehak-gil, Suncheon-si 57997, Jeollanam-do, Republic of Korea
2
Department of Industrial and Systems Engineering, Northern Illinois University, DeKalb, IL 60115, USA
3
Department of Industrial Engineering, Ajou University, 206, World cup-ro, Yeongtong-gu, Suwon-si 16499, Gyeonggi-do, Republic of Korea
4
Department of Occupational Safety and Health Management, Osan University, 45 Cheonghak-ro, Osan-si 18119, Gyeonggi-do, Republic of Korea
*
Author to whom correspondence should be addressed.
Appl. Sci. 2025, 15(12), 6593; https://doi.org/10.3390/app15126593
Submission received: 16 April 2025 / Revised: 5 June 2025 / Accepted: 10 June 2025 / Published: 11 June 2025
(This article belongs to the Section Biomedical Engineering)
Browse Figures
Versions Notes

Abstract

This study aimed to investigate the influence of different walking speeds on shoulder and elbow joint kinematics, specifically focusing on range of motion, angular velocity, and angular acceleration during arm swing. The natural rhythm of human gait was studied to develop an effective mechanical interface, particularly with respect to joint impedance and force controllability. The independent variable in this study was walking speed, operationalized at four levels—3.6 km/h (slow), 4.2 km/h (preferred walking speed, PWS), 5.4 km/h (normal), and 7.2 km/h (fast)—and defined as a within-subject factor. The dependent variables consisted of quantitative kinematic parameters, including joint range of motion (ROM, in degrees), peak and minimum joint angular velocity (deg/s), and peak and minimum joint angular acceleration (deg/s2). For each subject, data from twenty gait cycles were extracted for analysis. The kinematic variables of the shoulder and elbow were analyzed, showing increasing trends as the walking speed increased. As walking speed increases, adequate arm swing contributes to gait stability and energy efficiency. Notably, the ROM of shoulder was slightly reduced at the PWS compared to the slowest speed (3.6 km/h), which may reflect more natural and coordinated limb movements at the PWS. Dynamic covariation of torque patterns in the shoulder and elbow joints was observed, reflecting a synergistic coordination between these joints in response to human body movement.

1. Introduction

Recent advancements in exoskeletal technology have focused on amplifying human physical capabilities, including strength, endurance, and mobility [1]. These wearable systems have been increasingly adopted in fields such as physical rehabilitation, elderly support, and industrial operations that require activities like walking, running, repetitive motions, and material handling [2]. Exoskeletons, as integrated mechatronic devices, are specifically designed to mirror human anatomy—either in parallel or in series—with the goal of assisting in load bearing and transmitting force to the ground or other parts of the body [3]. This body–machine interface plays a crucial role in minimizing physical strain by lowering joint resistance, reducing muscular workload, and improving energy efficiency during tasks [4].
The exoskeletal devices continue to face several design and engineering challenges [5]. Effective locomotion requires natural interlimb coordination, which can be disrupted by mechanical constraints introduced by the device [6,7]. Misalignment between the exoskeleton’s joints and the user’s anatomical joints may induce resistance during movement, resulting in discomfort and reduced mobility [1]. Furthermore, the added mass of the device can elevate metabolic demands and restrict range of motion, potentially contributing to premature fatigue during ambulation [8]. Traditionally, wearable robotic systems have focused primarily on sensor-based prediction of user intent to guide robotic actuation, often overlooking the neuromechanical synergy required for coordinated limb movement during arm swing [9,10,11]. Consequently, there remains a gap in the literature regarding the integration of human motor control principles, neural feedback mechanisms, and ergonomic design in exoskeleton development.
To overcome the current limitations in the development of human–machine interfaces, particularly in assistive and wearable robotics, it is imperative to gain a comprehensive understanding of the biomechanical characteristics and neuromuscular control of natural arm swing during gait. From an ergonomics and human factors engineering perspective, effective mechanical integration requires that joint impedance and force controllability be precisely tuned to accommodate the dynamic properties of the upper limbs. Meyns et al. [12] provided critical evidence indicating that arm swing is not merely a passive byproduct of locomotion, but serves an active functional role in maintaining postural stability and restoring dynamic balance following perturbations. This suggests that any ergonomic device interfacing with the upper extremities must support such intrinsic stabilizing functions. Moreover, Kuhtz-Buschbeck and Jing [13], along with Goudriaan et al. [14], demonstrated through musculoskeletal modeling that arm swing encompasses both passive mechanical oscillations and active neuromuscular control, with the contribution of active components increasing significantly at higher walking speeds. This finding underscores the need for adaptive control strategies in robotic systems or exoskeletal devices to accommodate varying task demands and user states. Further insights have been gleaned from clinical gait analyses focusing on upper-limb kinematics, particularly with respect to spatiotemporal parameters and coordination patterns across different walking speeds [15,16,17,18,19]. However, the study by Romkes and Bracht-Schweizer [18], while informative in quantifying joint range of motion in upper-body segments such as the shoulders, trunk, and pelvis, did not capture essential dynamic variables such as angular velocity and angular acceleration. These parameters are critical from an ergonomic standpoint, as they influence momentary joint loading, energy expenditure, and the timing requirements for motor assistance or resistance in wearable technologies. Taken together, these studies highlight the importance of integrating biomechanical fidelity and neuromotor adaptability into the design of mechanical interfaces, ensuring not only alignment with human movement patterns but also real-time responsiveness to dynamic coactivation demands.
Furthermore, most clinical analyses of arm swing have been conducted within the context of rehabilitation or pathological conditions, which may limit their direct applicability to the ergonomic design of exoskeletal systems. For instance, Kim et al. [20] investigated the natural rhythmic coordination between the shoulder and elbow joints at varying walking speeds. However, the generalizability of their findings is constrained by a small sample size, reducing the robustness of their conclusions for broader ergonomic applications. Also, the analysis of dynamic coactivation during arm swing was conducted in a limited scope, focusing primarily on joint-specific kinematic variables rather than inter-joint coordination patterns. A deeper understanding of the intrinsic rhythm and coordination patterns of upper extremity motion during gait is essential for defining functional boundaries such as joint torque profiles and ranges of motion. These parameters are critical to optimizing the mechanical and control design of wearable exoskeletons. Such insight enables the development of systems that better align with human biomechanics, thereby improving limb dynamics and enhancing user comfort—particularly in long-duration or high-repetition applications aimed at augmenting locomotor function [21]. Moreover, integrating interlimb coordination principles into exoskeletal design can facilitate more naturalistic movement patterns. This not only promotes biomechanical efficiency but also allows users to engage in tasks with improved intuitiveness and reduced cognitive and physical load [7,9].
This study aimed to investigate the influence of different walking speeds on shoulder and elbow joint kinematics, specifically focusing on range of motion, angular velocity, and angular acceleration during arm swing. It was hypothesized that joint kinematic patterns would exhibit significant variations depending on walking speed. The findings of this study are anticipated to inform the ergonomic development of upper-limb exoskeletons by enhancing alignment with the natural pattern of arm swing.

2. Materials and Methods

2.1. Subject

To determine the appropriate sample size for the study, a statistical power analysis was conducted using G*Power ver.3.1.9.6 (G*Power, Dusseldorf, Germany). The analysis was based on a repeated-measures ANOVA design (within factors), with an alpha level set at 0.05, 1 group, 4 repeated measurements, and an assumed medium effect size of Cohen’s f = 0.3. These parameters were selected to ensure sufficient power to detect meaningful effects in the experimental conditions [22,23]. Twenty male subjects were recruited for this study. The protocol of this study was reviewed and approved by the Human Research Ethics Committee of Ajou University (IRB approval No. 202102–HS–003) and conducted in accordance with the principles of the Declaration of Helsinki, as revised in 2008. Prior to the experiment, all subjects provided written informed consent and were thoroughly briefed on the experimental procedure. None of the subjects reported any musculoskeletal disorders or injuries within the past 12 months, and all were familiarized with the experimental procedures. The average (standard deviation) age, height, and body weight of the subjects were 24.3 (±3.5) years, 174.2 (±7.7) cm, and 69.4 (±9.5) kg.

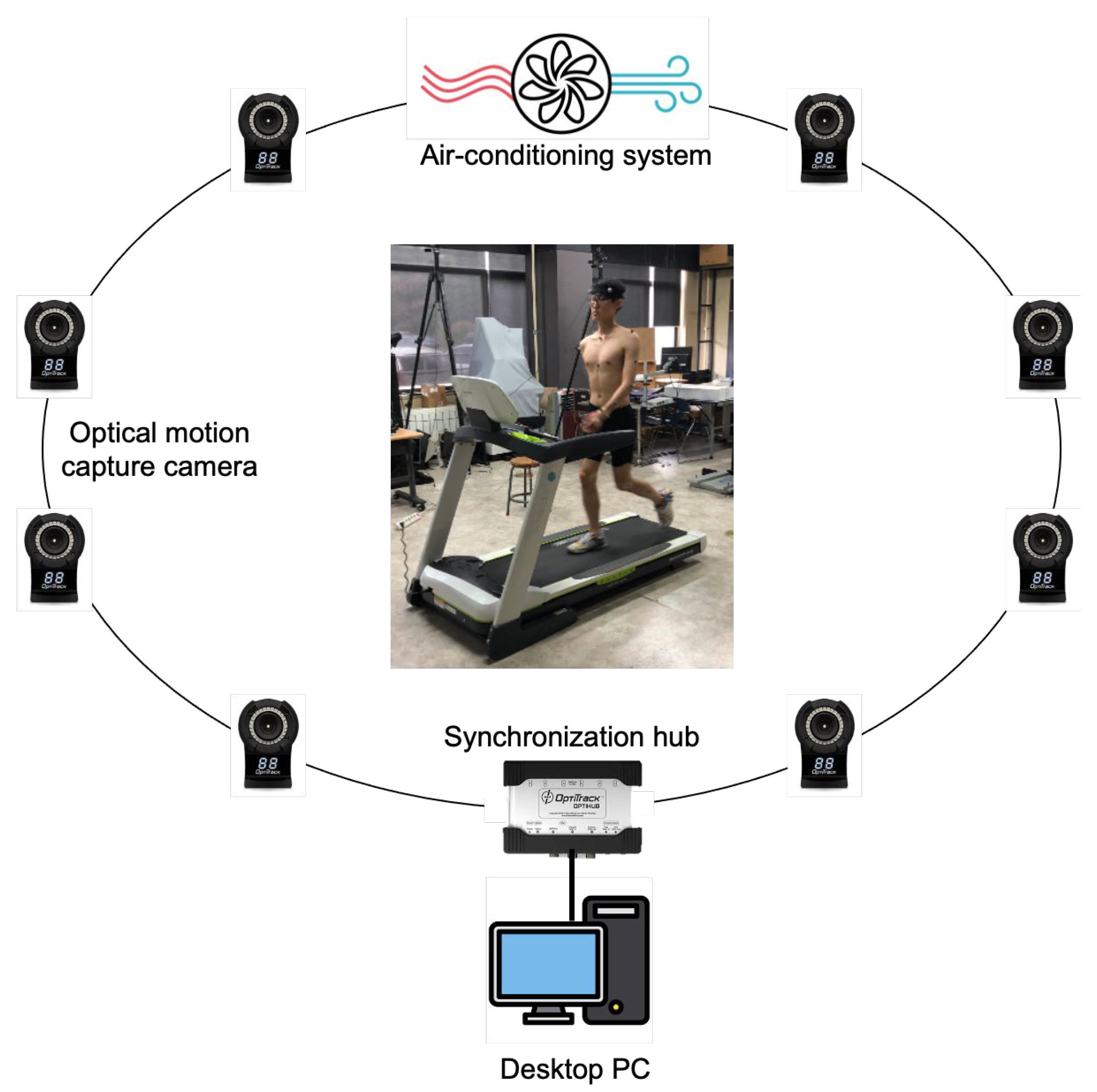
2.2. Apparatus

A controlled walking scenario was simulated using a treadmill system (Bertec Co., Columbus, OH, USA) in the laboratory. The kinematic variables, including joint angles, angular velocity, and angular acceleration, for the shoulder and elbow were taken at various walking speeds. To capture and analyze arm swing kinematics, an optical motion capture system (Optitrack, Natural Point Inc., Corvallis, OR, USA) equipped with 1.3-megapixel eight Flex 13 cameras was utilized, operating at a sampling rate of 100 Hz. Prior to each experimental condition, the motion capture system was calibrated in accordance with the manufacturer’s specifications. As seen in Figure 1, a total of 23 retro-reflective markers, each with a diameter of 14 mm, were attached to the subject’s upper body at specific bony anatomical landmarks, following the Upper-Body Plug-in-Gait model documentation [24].

2.3. Experimental Design

The independent variable in this study was walking speed, operationalized at four levels—3.6 km/h (slow), 5.4 km/h (normal), 7.2 km/h (fast), and each subject’s preferred walking speed (PWS)—defined as a within-subject factor [20]. The dependent variables consisted of quantitative kinematic parameters, including joint range of motion (ROM, in degrees), peak and minimum joint angular velocity (deg/s), and peak and minimum joint angular acceleration (deg/s2). A within-subject repeated-measures experimental design was employed to minimize inter-subject variability, with all walking speed conditions randomized per subject to mitigate potential sequence and learning effects.

2.4. Procedure

Upper-body marker sets were strategically placed on specific anatomical landmarks [24]. To ensure consistency across experimental conditions, all trials were conducted within a controlled indoor laboratory environment. The laboratory was equipped with a centralized air-conditioning system, which maintained a stable temperature of approximately 23 °C and relative humidity of around 28%. Each subject performed walking trials on a treadmill at four speeds, with each trial lasting 120 s (Figure 2).
The PWS was individually determined based on each subject’s comfort level, which reflects their subjective sense of comfort and natural gait under normal conditions [25]. Each subject was instructed to walk at a self-selected, comfortable pace on a treadmill, resulting in an average walking speed of 4.2 (±0.5) km/h. To minimize the potential effects of fatigue, subjects were provided with a minimum 15 min rest period between trials to ensure optimal performance during subsequent conditions.

2.5. Analysis

Kinematic data were collected and analyzed for each walking trial, focusing on a single gait cycle, which was defined as the period from the initial heel contact to the subsequent heel contact with the floor [26]. For each subject, data from twenty gait cycles were extracted for analysis. Post-processing was performed using Motive version 2.1.0 (OptiTrack, Natural Point Inc., Corvallis, OR, USA), and joint angles, angular velocity, and angular acceleration of the shoulder and elbow were calculated using Visual 3D v6 (C–Motion Inc., Germantown, MD, USA). To minimize noise and improve signal accuracy, a low-pass filter with a 6 Hz cut-off frequency was applied. Shoulder kinematics were analyzed in both the sagittal (flexion–extension) and frontal (abduction–adduction) planes, while elbow kinematics were restricted to analysis in the sagittal plane (flexion–extension).
Descriptive statistics and repeated-measures analysis of variance (ANOVA) were performed to identify significant differences among the variables. When significant effects were found, Tukey’s post hoc test was conducted for pairwise comparisons. A significance level of 0.05 was used for all statistical analyses, which were performed using SAS software 9.4 (SAS Institute, Cary, NC, USA).

3. Results

Table 1 presents the ANOVA results for each dependent variable by joint, showing the mean values of kinematic variables based on walking speed.

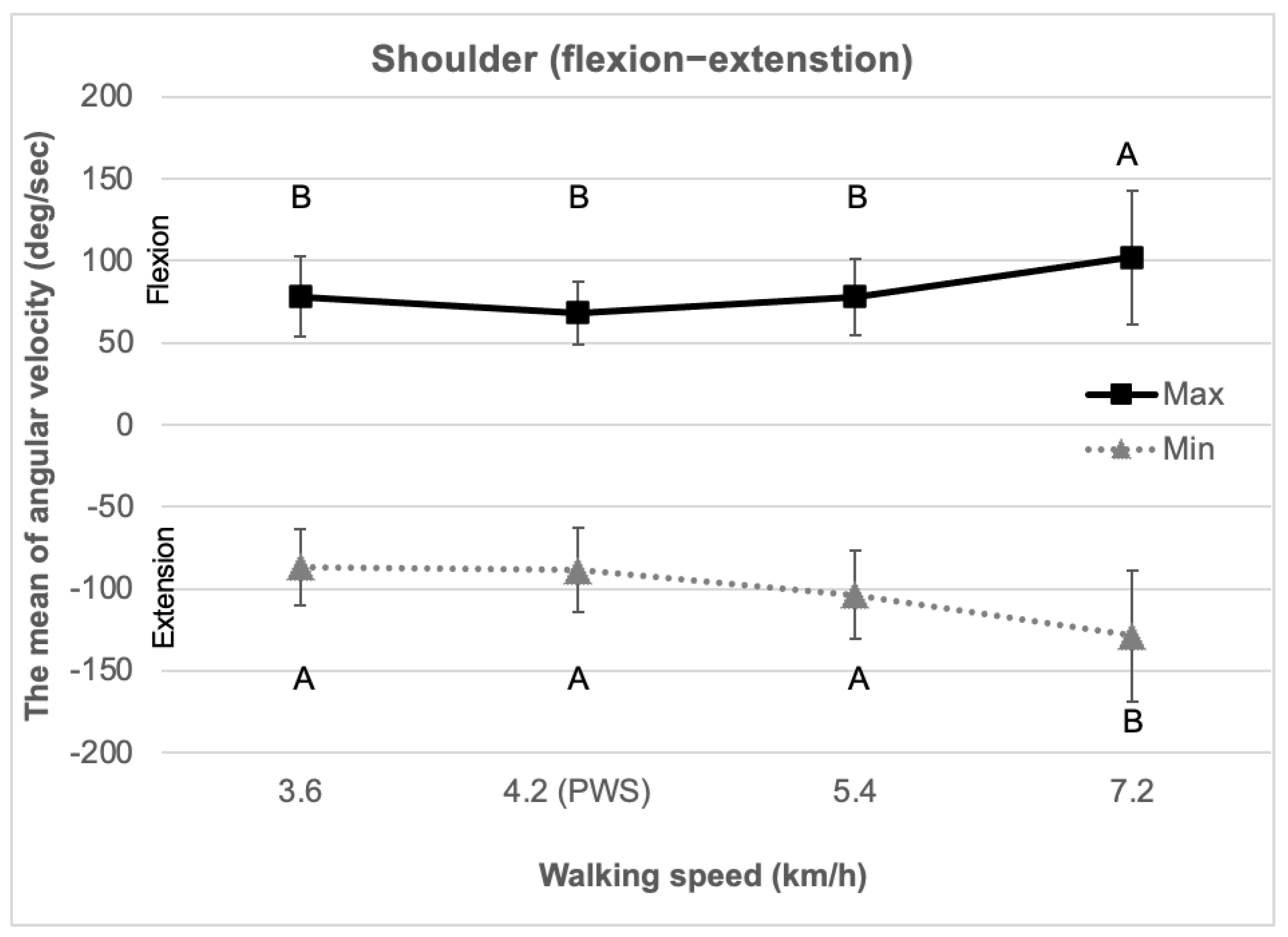
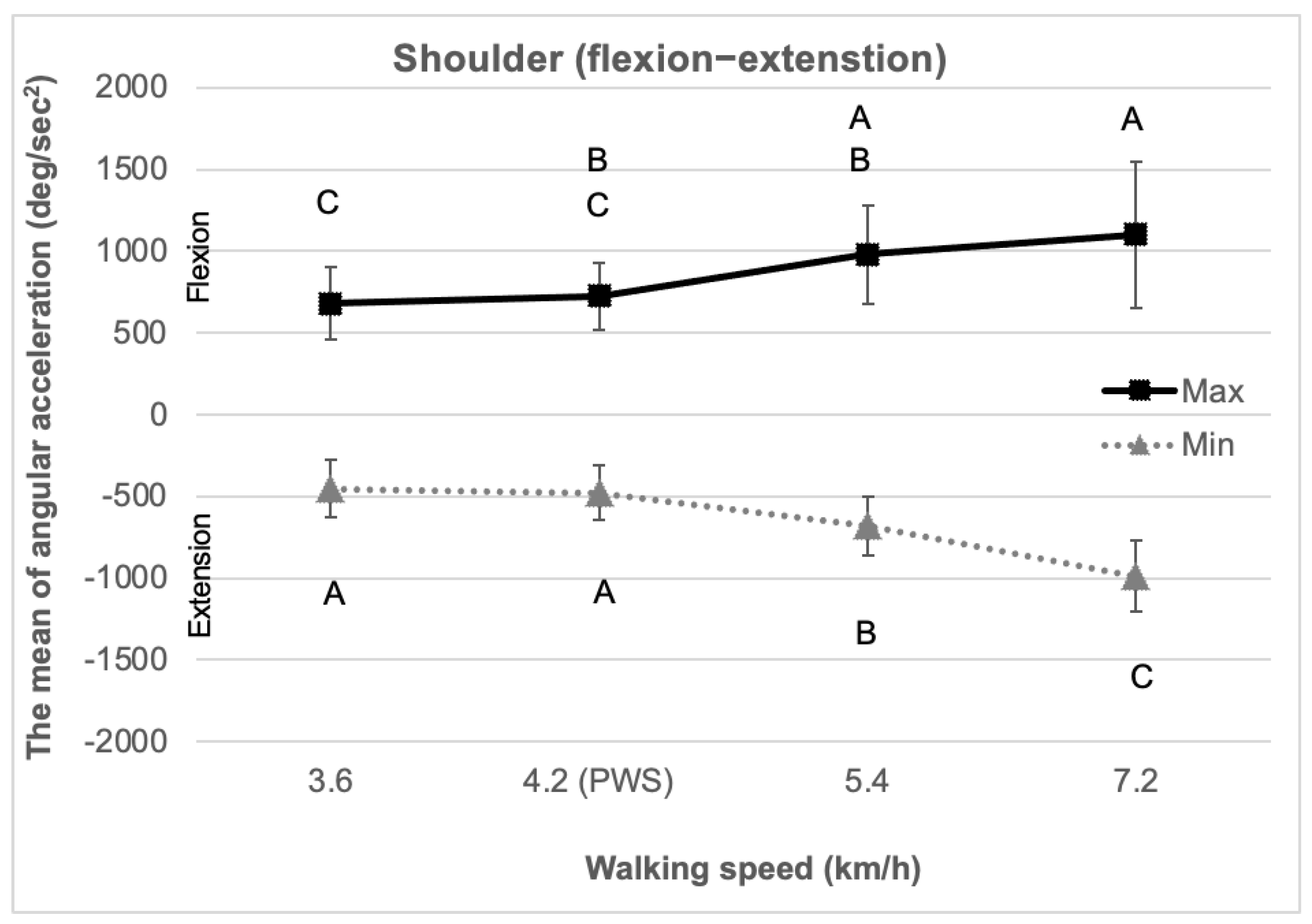
3.1. Shoulder (Flexion–Extension)

According to the ANOVA results, statistically significant differences were observed in all kinematic variables, including ROM, the maximum and minimum joint angular velocities, and the maximum and minimum joint angular accelerations (Table 1).
At the fastest walking speed of 7.2 km/h, the mean ROM for shoulder flexion–extension was significantly greater compared to other walking speeds. However, Tukey’s post hoc test indicated no significant differences in ROM among the walking speeds of 3.6, 5.4, and 7.2 km/h. Notably, the lowest mean ROM was observed at a preferred walking speed (PWS) of 4.2 km/h.
As shown in Figure 3, the mean maximum flexion angular velocity at a walking speed of 7.2 km/h was significantly higher than at other speeds. Similarly, the mean minimum extension angular velocity was lowest at 7.2 km/h. While no significant differences were found among the walking speeds of 3.6, 4.2, and 5.4 km/h, the lowest mean maximum flexion angular velocity occurred at the PWS of 4.2 km/h. Moreover, the highest mean minimum extension angular velocity was observed at this same PWS.
As shown in Figure 4, the mean flexion–extension angular acceleration followed a trend similar to that of angular velocity. Specifically, there was a progressive increase in angular acceleration with walking speed, peaking at 7.2 km/h. Similarly, the mean minimum extension angular acceleration demonstrated a decreasing trend with increasing walking speed, reaching its lowest value at 7.2 km/h.

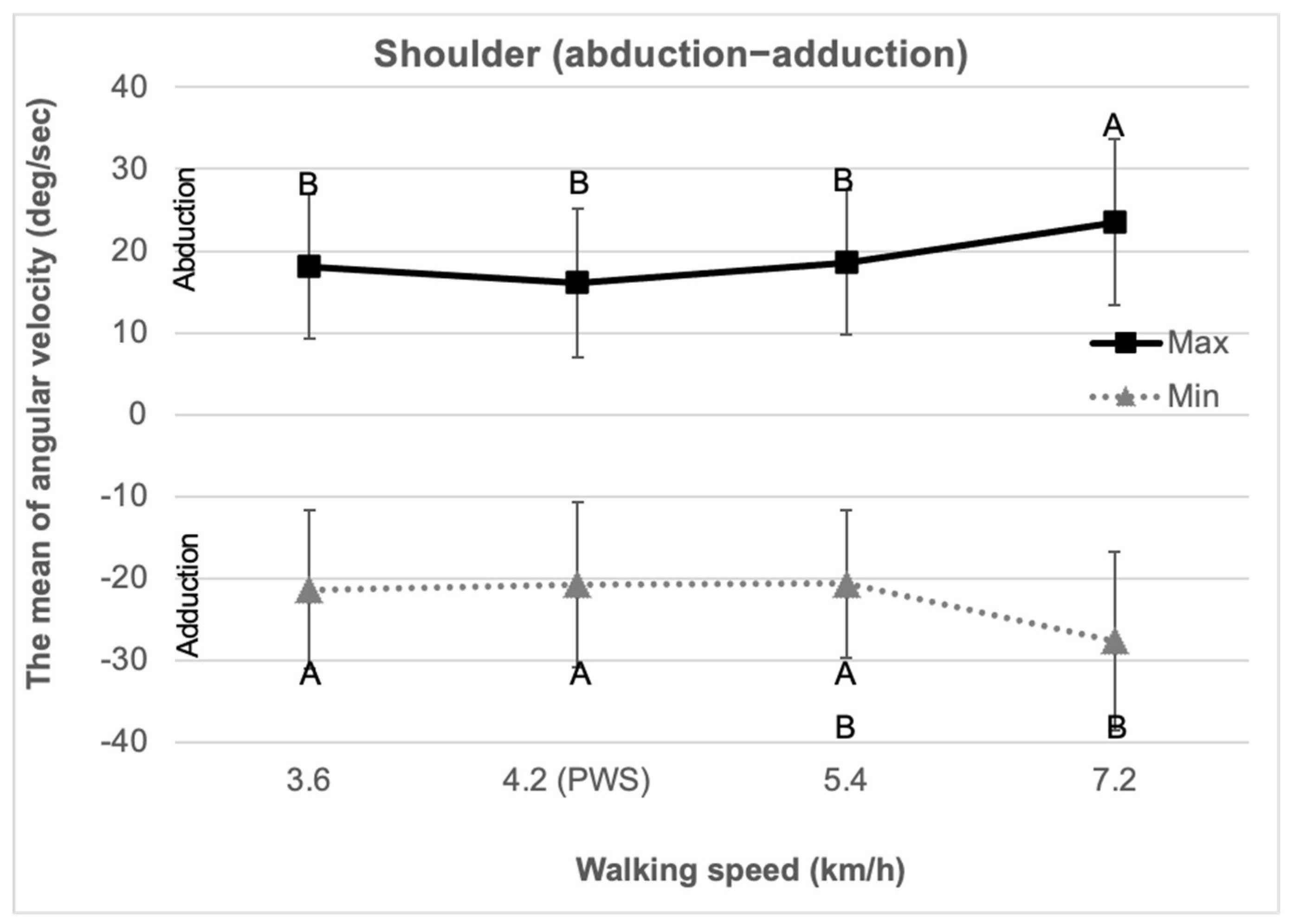
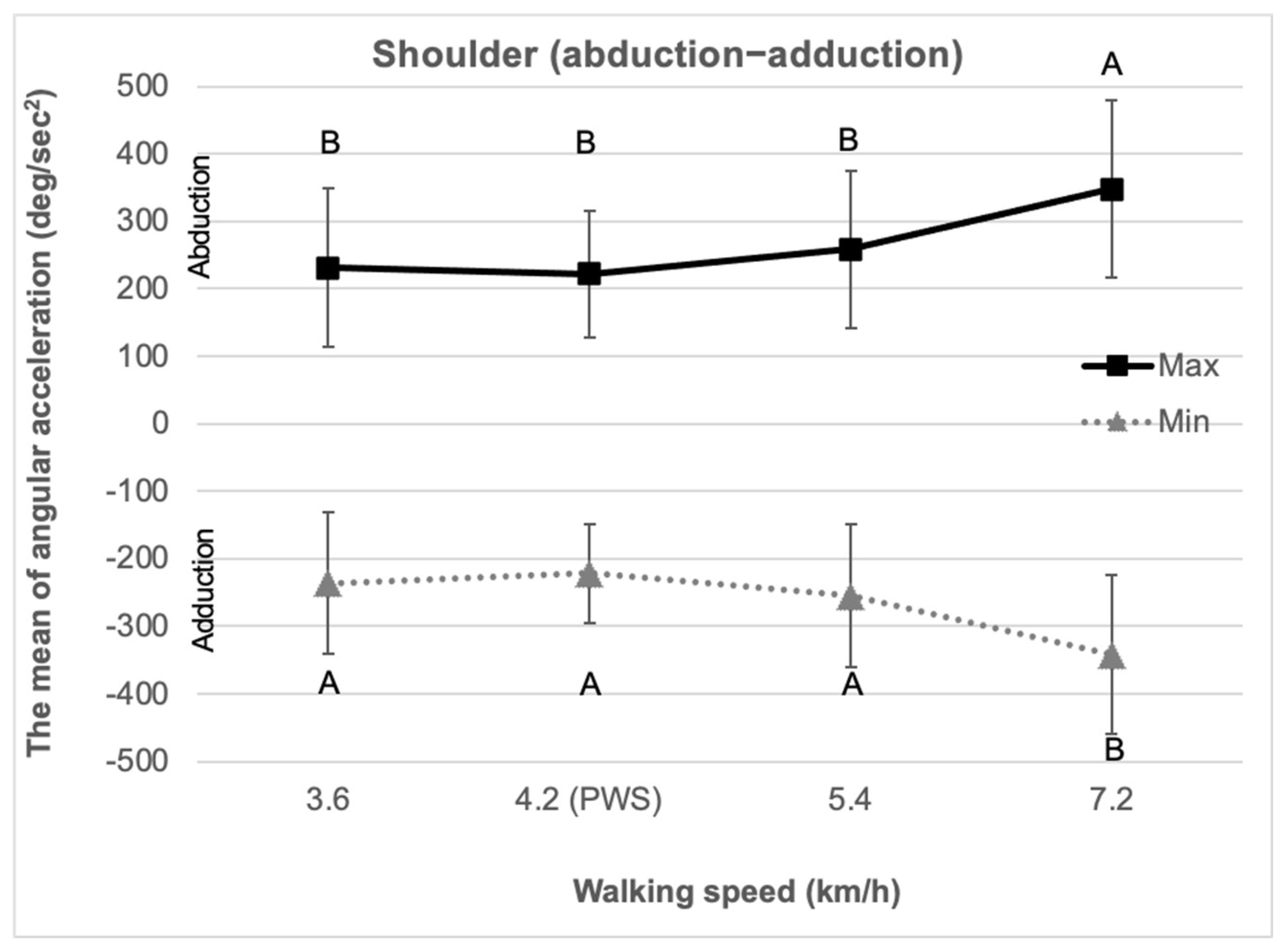
3.2. Shoulder (Abduction–Adduction)

Table 1 presents significant differences in maximum and minimum joint angular velocity as well as in maximum joint angular acceleration. However, no significant differences were found in the ROM.
As shown in Figure 5, the mean maximum abduction angular velocity at a walking speed of 7.2 km/h was significantly higher compared to other walking speeds. Similarly, the mean minimum adduction angular velocity was lowest at 7.2 km/h. No significant differences were found among the walking speeds of 3.6, 4.2, and 5.4 km/h; however, the mean maximum abduction angular velocity was lowest at PWS of 4.2 km/h. Additionally, the mean minimum adduction angular velocity was highest at the same PWS.
As shown in Figure 6, the mean abduction–adduction angular acceleration followed a similar trend to that of angular velocity. The mean maximum abduction angular acceleration at a walking speed of 7.2 km/h was significantly higher than at other walking speeds. Similarly, the mean minimum adduction angular acceleration was lowest at 7.2 km/h. Although no significant differences were observed among the walking speeds of 3.6, 4.2, and 5.4 km/h, the mean maximum abduction angular acceleration was lowest at the PWS. In contrast, the mean minimum adduction angular acceleration was highest at the PWS.

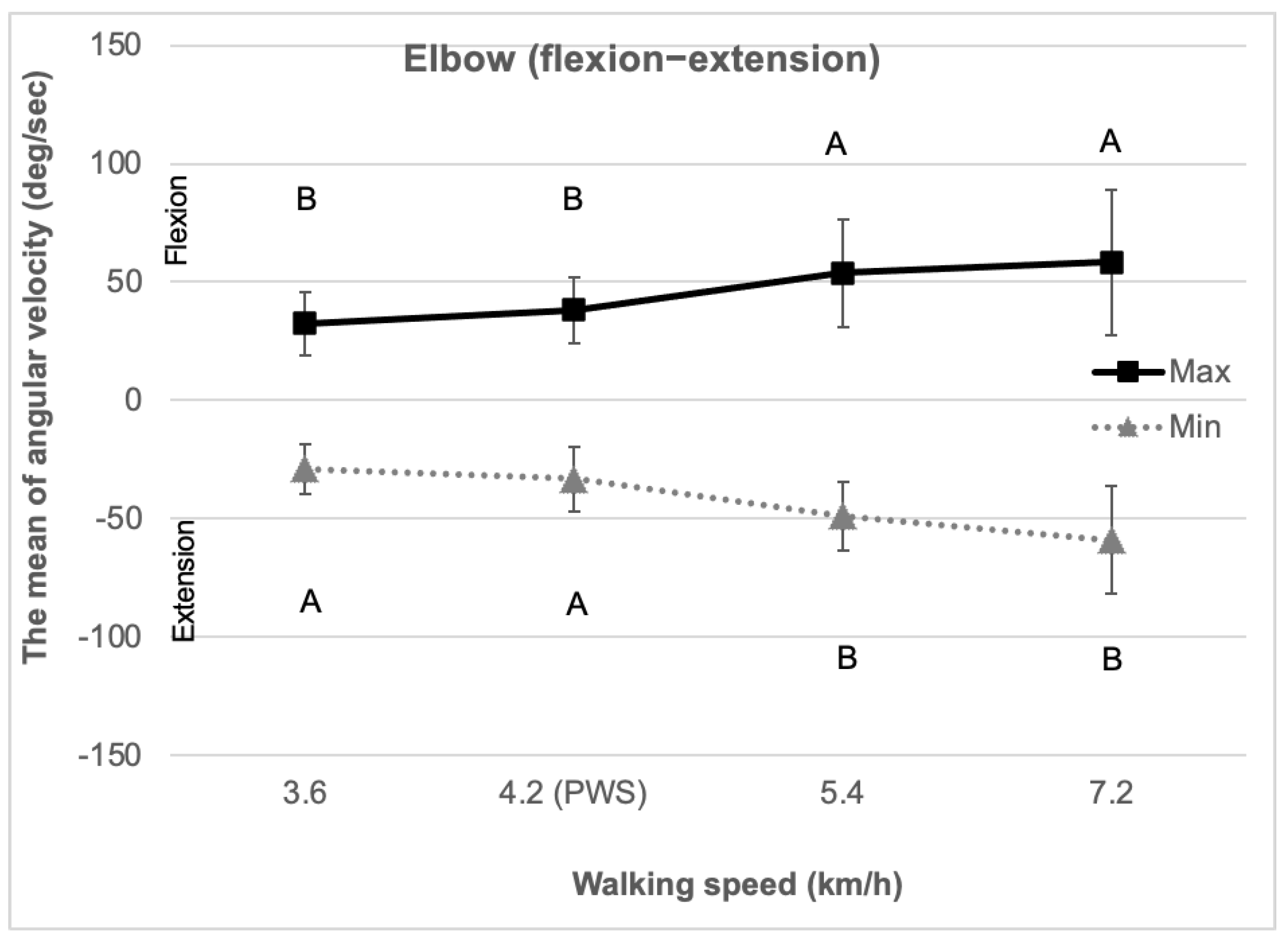
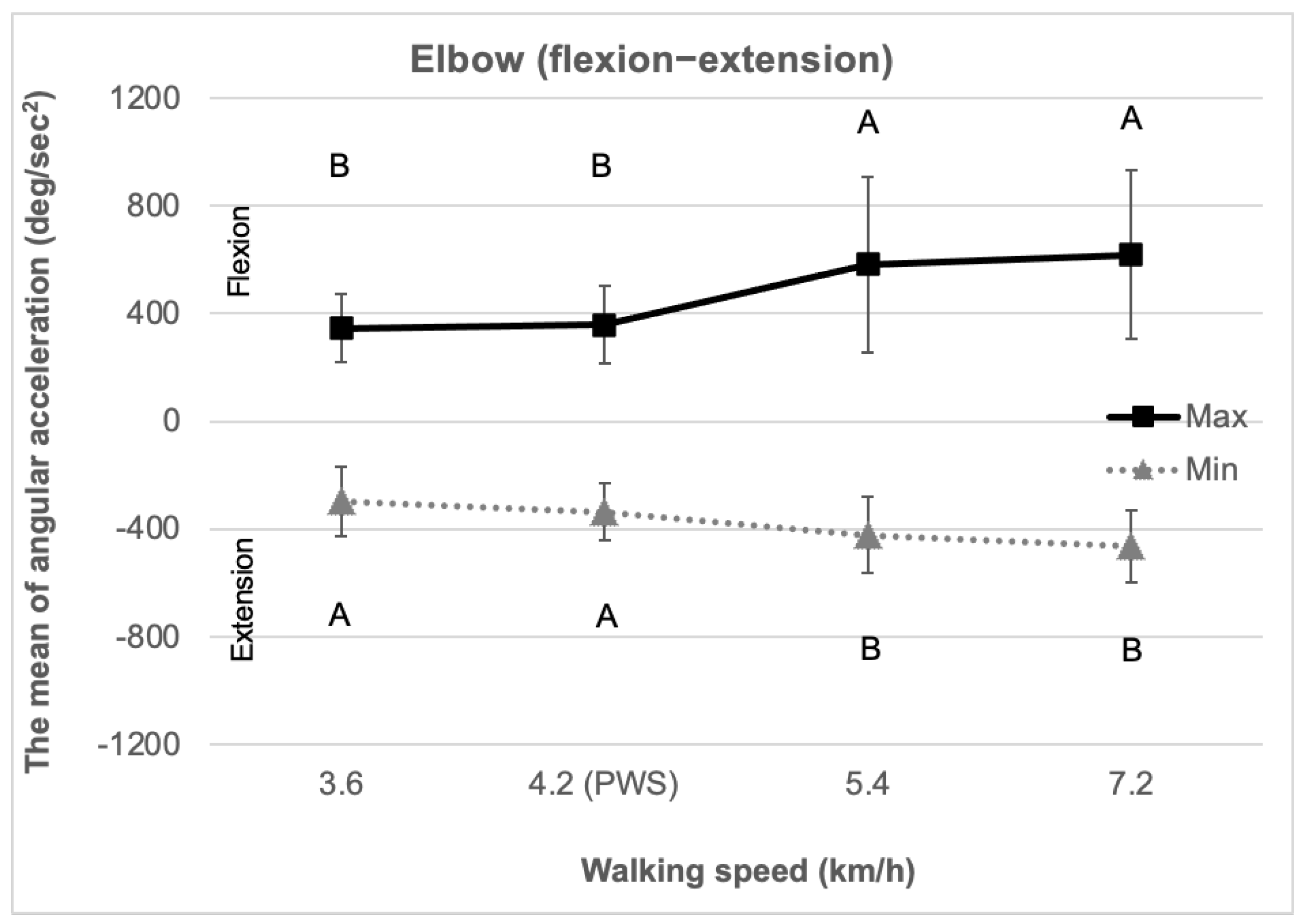
3.3. Elbow (Flexion–Extension)

Table 1 indicates significant differences in ROM, maximum joint angular velocity, minimum joint angular velocity, maximum joint angular acceleration, and minimum joint angular acceleration. However, no significant differences were observed in the minimum joint angle.
At a walking speed of 7.2 km/h, the mean ROM for elbow flexion–extension was significantly higher than at the other walking speeds. An increasing trend in ROM was observed up to a walking speed of 7.2 km/h. Tukey’s test results revealed no significant differences between the walking speeds of 3.6, 4.2, and 5.4 km/h.
As shown in Figure 7, the mean maximum flexion angular velocity at a walking speed of 7.2 km/h was significantly higher than at the other walking speeds. Similarly, the mean minimum extension angular velocity at 7.2 km/h was the lowest. An increasing trend in angular velocity was observed up to the walking speed of 7.2 km/h.
The mean flexion–extension angular acceleration exhibited a pattern similar to that of the flexion–extension angular velocity, as shown in Figure 8. The mean maximum flexion angular acceleration at a walking speed of 7.2 km/h was significantly higher than at the other walking speeds. Similarly, the mean minimum extension angular acceleration at 7.2 km/h was the lowest.

4. Discussion

Most kinematic variables of the shoulder and elbow exhibited an increasing trend as walking speed increased. As shown in Table 1, the maximum joint angle of the shoulder remained consistent across different walking speeds. However, the minimum joint angle of the shoulder significantly decreased with increasing walking speed, indicating that the arm swing becomes more pronounced in the posterior direction relative to the anterior movement at higher speeds. Angular velocity and acceleration demonstrated a consistent increase of approximately 10% as walking speed increased, reflecting a natural augmentation of passive movement as arm swing intensifies [27]. Arm kinematic variables showed a proportional relationship with walking speed increments [15]. Adequate arm swing is essential for maintaining stability and reducing energy expenditure as walking speed increases [28,29,30,31]. Kubo et al. [32] found that arm and trunk movements adjust to changes in walking speed to facilitate coordinated limb motion. Similarly, Romkes and Bracht-Schweizer [33] observed a strong association between arm movement and walking speed, noting that arm swing corresponds to changes in walking speed at the shoulder’s center of rotation. Moreover, Kuhtz-Buschbeck and Jing [13] and Goudriaan et al. [14] evaluated that arm swing is driven by the active contribution of arm muscles during walking. Thus, in the design of exoskeletal devices, it is crucial to account for the rhythmic synchronization of arm movement in relation to walking speed.
The walking speed of 7.2 km/h was designated as the fastest walking speed in this study. At this speed on the treadmill, the duration of the stance and swing phases during a single gait cycle (heel strike–toe off) is significantly reduced. Consequently, the range of motion required for adequate arm swing was constrained [33]. Analyzing upper-limb kinematics under such high-speed conditions is essential for understanding the limits of natural arm–leg coordination and for informing the ergonomic design of assistive technologies, particularly in applications where gait speed may be intentionally increased, such as in exoskeletons or advanced rehabilitation protocols. As a result, kinematic variables were analyzed at their peak values at the 7.2 km/h walking speed. As shown in Figure 8, maximum angular acceleration increased with walking speed, reflecting a rise in the instantaneous velocity of the shoulder joint. This suggests that the mechanical load on the shoulder joint intensifies as walking speed increases. Based on the findings of this study, walking at 7.2 km/h may result in a relatively higher biomechanical load and discomfort in the shoulder joint compared to lower walking speeds. Cavagna and Kaneko [34] reported that as walking speed increases, upper-limb movement also intensifies due to passive muscle recoil, thereby decreasing walking efficiency. The arm functions as a mass damper during walking, leading to higher instantaneous acceleration of the shoulder and elbow joints as walking speed increases, which elevates the risk of injury [35]. In this study, the kinematic variables of the shoulder and elbow were most prominently affected at a walking speed of 7.2 km/h. Furthermore, the observed increase in standard deviation at higher walking speeds (e.g., 7.2 km/h) may reflect a shift toward greater reliance on active motor control rather than passive arm swing dynamics. This transition highlights the critical need to integrate sensor-based feedback and compliant actuation mechanisms into the design of exoskeletal systems to facilitate safe, responsive, and user-centered interaction. Accommodating natural variability in shoulder kinematics is therefore essential not only for enhancing user comfort but also for minimizing neuromuscular fatigue and improving the long-term usability of the assistive device. Based on these findings, we highlight the critical role of adaptive control strategies in exoskeletons that dynamically adjust to variations in gait speed and upper-limb coordination. The observed modulation of arm movement patterns with increasing walking speed supports the use of impedance control models, which can flexibly modulate assistance by interpreting user intent and biomechanical state. Such models reduce resistance during natural arm swings while delivering targeted support during periods of increased load or fatigue. Furthermore, exoskeletal systems intended for dynamic walking environments should integrate multisensory inputs and sophisticated control algorithms capable of real-time assistance adjustment based on walking speed and trunk–arm coordination. By promoting seamless coordination between the upper and lower limbs, these designs can improve gait stability and overall biomechanical efficiency across diverse locomotor conditions. These insights provide valuable guidance for the development of next-generation upper-limb exoskeletons that synchronize effectively with whole-body movement, ultimately enhancing user safety, comfort, and functional performance.
As walking speed increases, the amplitude of the arm swing increases proportionally [29]. However, the ROM of shoulder was slightly lower at PWS (4.2 km/h) compared to the slowest walking speed of 3.6 km/h. This is attributed to an unnatural walking pattern that occurs at deliberately slow walking speeds. Schöner et al. [36] and Jeka et al. [37] have reported a close relationship between arm swing and gait stability at slow walking speeds. Wagenaar and van Emmerik [19] found instability due to changes in arm swing patterns at slow walking speeds ranging from 0.3 to 0.7 m/s. The arm swing has been shown to reduce trunk movement and improve walking stability [18,38,39]. However, excessively slow walking speed could lead to unnatural arm swing, which may decrease walking stability. Therefore, the preferred walking speed induces natural walking patterns of the limbs and improves walking stability.
The kinematic variables of the elbow demonstrated a positive correlation with increasing walking speed. The elbow joint operates as part of a linked segment system, moving in synchrony with the shoulder joint during arm motion [40,41]. Both joints exhibit dynamic covariation in their torque patterns, reflecting the body’s natural biomechanics and generating a linear synergy effect [27,42]. This synergy minimizes the degrees of freedom that the central nervous system must independently control, optimizing coordination and efficiency in limb movement [43]. In addition, a significant increase in the standard deviation of elbow joint angular velocity and acceleration was observed with increasing walking speed. This increased variability reflects not only the heightened neuromuscular demands but also the adaptive strategies employed by the central nervous system to maintain postural stability and dynamic coordination under varying locomotor conditions. From an ergonomics perspective, such variability may be interpreted as an indicator of functional complexity, wherein the arm swing mechanism continuously adjusts to gait perturbations and shifting task demands. The observed increase in kinematic variables at the elbow joint with rising walking speed indicates a growing demand for linear inter-joint synergy, emphasizing the need for enhanced neuromuscular coordination. This finding carries significant implications for the design of wearable robotic systems and upper-limb assistive devices. In particular, the increased variability suggests that exoskeletal systems should employ adaptive control algorithms capable of accounting for both inter-individual and intra-individual differences in upper-limb dynamics across varying gait speeds. Rather than imposing rigid or pre-defined motion trajectories, ergonomically optimized systems should support controlled flexibility and real-time responsiveness, aligning with the natural variability and complexity inherent in human joint behavior. Based on these findings, it is recommended that exoskeletal devices be designed to replicate the natural linkage between the shoulder and elbow joints, enhancing the stability of gait dynamics and improving overall biomechanical efficiency during locomotion.
The coordinated function of the upper and lower limbs forms a linked biomechanical system that contributes significantly to gait stability and facilitates more natural movement patterns during walking [32]. However, a limitation of this study is its exclusive focus on the shoulder and elbow joints, without incorporating the interactions and coordination among lower-limb joints. To develop a more comprehensive understanding of gait dynamics, future studies should examine the co-activation and coordination of kinematic variables across lower extremity joints in response to varying walking speeds. To enhance the generalizability of the findings, further research should include both male and female subjects to account for potential sex-related differences in dynamic coactivation patterns during arm swing. Moreover, including a larger and more demographically diverse sample, particularly one that covers a wider age range, is recommended to improve the statistical reliability and robustness of the experimental results. In addition, it is crucial to assess ergonomic factors such as muscle activity and fatigue during locomotion through electromyographic measurements. The simultaneous collection of lower-limb kinematics and muscle activation data would enable the establishment of a more holistic gait coordination control model. Such a model could serve as a valuable framework for advancing ergonomic assessments and the design of assistive devices tailored to the dynamic interplay between upper and lower limbs.

5. Conclusions

The findings of this study have direct implications for the design of exoskeletal devices, including wearable robots and upper-limb swing assistive devices for rehabilitation. The following conclusions were drawn from this study:
  • Arm swing is essential for maintaining walking stability and minimizing energy expenditure, especially as walking speed increases.
  • Shoulder range of motion (ROM) was slightly lower at the preferred walking speed (PWS) compared to the slowest walking speed (3.6 km/h). The PWS facilitates more natural limb movement, thereby improving walking stability.
  • Dynamic covariation of torque patterns in the shoulder and elbow joints was observed, reflecting a synergistic coordination between these joints in response to human body movement.
The study suggests that arm movement should be rhythmically coordinated based on walking speed. It is recommended that the design of exoskeletal devices focus on enhancing coordination between the upper and lower limbs to optimize stability across various walking speeds.

Author Contributions

Conceptualization, S.-M.M.; methodology, S.-M.M.; software, J.H.K.; validation, M.-C.J.; formal analysis, J.H.; investigation, J.H.K.; resources, J.H.K.; data curation, J.H.; writing—original draft preparation, J.H.; writing—review and editing, J.H.K. and J.H.; visualization, S.-M.M.; supervision, M.-C.J.; project administration, M.-C.J.; funding acquisition, S.-M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This work was carried out with the support of “Cooperative Research Program for Agriculture Science and Technology Development (Project No. PJ01709903)” Rural Development Administration, Republic of Korea.

Institutional Review Board Statement

The experimental protocol was approved by the Ajou IRB (approval No. 202102-HS-003) and was conducted in accordance with the 1964 Helsinki Declaration.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study. Written informed consent has been obtained from the subjects to publish this paper.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Asbeck, A.T.; De Rossi, S.M.M.; Galiana, I.; Ding, Y.; Walsh, C.J. Stronger, smarter, softer: Next-generation wearable robots. IEEE Robot. Autom. Mag. 2014, 21, 22–33. [Google Scholar] [CrossRef]
  2. Low, K.H.; Liu, X.; Goh, C.H.; Yu, H. Locomotive control of a wearable lower exoskeleton for walking enhancement. J. Vib. Control 2006, 12, 1311–1336. [Google Scholar] [CrossRef]
  3. Esquenazi, A.; Talaty, M.; Packel, A.; Saulino, M. The ReWalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury. Am. J. Phys. Med. Rehabil. 2012, 91, 911–921. [Google Scholar] [CrossRef] [PubMed]
  4. Lee, H.; Ho, P.; Rastgaar, M.; Krebs, H.I.; Hogan, N. Multivariable static ankle mechanical impedance with active muscles. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 44–52. [Google Scholar] [CrossRef]
  5. Herr, H. Exoskeletons and orthoses: Classification, design challenges and future directions. J. Neuroeng. Rehabil. 2009, 6, 1–9. [Google Scholar] [CrossRef]
  6. Grillner, S. Control of Locomotion in Bipeds, Tetrapods, and Fish; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
  7. Hassan, M.; Kadone, H.; Ueno, T.; Hada, Y.; Sankai, Y.; Suzuki, K. Feasibility of synergy-based exoskeleton robot control in hemiplegia. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1233–1242. [Google Scholar] [CrossRef]
  8. Browning, R.C.; Modica, J.R.; Kram, R.; Goswami, A. The effects of adding mass to the legs on the energetics and biomechanics of walking. Med. Sci. Sports Exerc. 2007, 39, 515–525. [Google Scholar] [CrossRef]
  9. Moschetti, A.; Cavallo, F.; Esposito, D.; Penders, J.; Di Nuovo, A. Wearable sensors for human–robot walking together. Robotics 2019, 8, 38. [Google Scholar] [CrossRef]
  10. St-Onge, N.; Feldman, A.G. Interjoint coordination in lower limbs during different movements in humans. Exp. Brain Res. 2003, 148, 139–149. [Google Scholar] [CrossRef]
  11. Jacobson, M.; Kantharaju, P.; Jeong, H.; Ryu, J.K.; Park, J.J.; Chung, H.J.; Kim, M. Foot contact forces can be used to personalize a wearable robot during human walking. Sci. Rep. 2022, 12, 10947. [Google Scholar] [CrossRef]
  12. Meyns, P.; Bruijn, S.M.; Duysens, J. The how and why of arm swing during human walking. Gait Posture 2013, 38, 555–562. [Google Scholar] [CrossRef] [PubMed]
  13. Kuhtz-Buschbeck, J.P.; Jing, B. Activity of upper limb muscles during human walking. J. Electromyogr. Kinesiol. 2012, 22, 199–206. [Google Scholar] [CrossRef] [PubMed]
  14. Goudriaan, M.; Jonkers, I.; van Dieen, J.H.; Bruijn, S.M. Arm swing in human walking: What is their drive? Gait Posture 2014, 40, 321–326. [Google Scholar] [CrossRef] [PubMed]
  15. Eke-Okoro, S.T.; Gregoric, M.; Larsson, L.E. Alterations in gait resulting from deliberate changes of arm-swing amplitude and phase. Clin. Biomech. 1997, 12, 516–521. [Google Scholar] [CrossRef]
  16. Meyns, P.; Van Gestel, L.; Bruijn, S.M.; Desloovere, K.; Swinnen, S.; Duysens, J. Is interlimb coordination during walking preserved in children with cerebral palsy? Gait Posture 2012, 36, S25. [Google Scholar] [CrossRef]
  17. Meyns, P.; Van Gestel, L.; Massaad, F.; Desloovere, K.; Molenaers, G.; Duysens, J. Arm swing during walking at different speeds in children with Cerebral Palsy and typically developing children. Res. Dev. Disabil. 2011, 32, 1957–1964. [Google Scholar] [CrossRef]
  18. Romakes, J.; Bracht-Schweizer, K. The effects of walking speed on upper body kinematics during gait in healthy subjects. Gait Posture 2017, 54, 304–310. [Google Scholar] [CrossRef]
  19. Wagenaar, R.C.; van Emmerik, R.E. Resonant frequencies of arms and legs identify different walking patterns. J. Biomech. 2000, 33, 853–861. [Google Scholar] [CrossRef]
  20. Kim, J.H.; Hwang, J.; Jung, M.C.; Mo, S.M. The kinematic evaluation of shoulder and elbow joints for different walking speeds. Int. J. Eng. Technol. 2019, 11, 169–172. [Google Scholar] [CrossRef]
  21. Klaner, T.; Pearcey, G.E.P.; Sun, Y.; Brass, T.S.; Zehr, E.P. Changing coupling between the arms and legs with slow walking speeds alters regulation of somatosensory feedback. Exp. Brain Res. 2020, 238, 1335–1349. [Google Scholar] [CrossRef]
  22. Faul, F.; Erdfelder, E.; Lang, A.-G.; Buchner, A. G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 2007, 39, 175–191. [Google Scholar] [CrossRef] [PubMed]
  23. Faul, F.; Erdfelder, E.; Buchner, A.; Lang, A.-G. Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behav. Res. Methods 2009, 41, 1149–1160. [Google Scholar] [CrossRef] [PubMed]
  24. Upper Body Modeling with Plug-in Gait. Vicon Motion Systems Ltd. UK. Available online: https://help.vicon.com/space/Nexus216/11602259/Upper+body+modeling+with+Plug-in+Gait (accessed on 4 June 2025).
  25. Johnson, R.T.; Hafer, J.F.; Wedge, R.D.; Boyer, K.A. Comparison of measurement protocols to estimate preferred walking speed between sites. Gait Posture 2020, 77, 171–174. [Google Scholar] [CrossRef] [PubMed]
  26. Lythgo, N.; Wilson, C.; Galea, M. Basic gait and symmetry measures for primary school-aged children and young adults. II: Walking at slow, free and fast speed. Gait Posture 2011, 33, 29–35. [Google Scholar] [CrossRef]
  27. Shemmell, J.; Johansson, J.; Portra, V.; Gottlieb, G.L.; Thomas, J.S.; Corcos, D.M. Control of interjoint coordination during the swing phase of normal gait at different speeds. J. Neuroeng. Rehabil. 2007, 4, 1–14. [Google Scholar] [CrossRef]
  28. Bruijn, S.M.; Meijer, E.G.; Beek, P.J.; van Dieën, J.H. The effects of arm swing on human gait stability. J. Exp. Biol. 2010, 213, 3945–3952. [Google Scholar] [CrossRef]
  29. Meyns, P.; Van de Walle, P.; Hoogkamer, W.; Kiekens, C.; Desloovere, K.; Duysens, J. Coordinating arms and legs on a hybrid rehabilitation tricycle: The metabolic benefit of asymmetrical compared to symmetrical arm movements. Eur. J. Appl. Physiol. 2014, 114, 743–750. [Google Scholar] [CrossRef]
  30. Ortega, J.D.; Fehlman, L.A.; Farley, C.T. Effects of aging and arm swing on the metabolic cost of stability in human walking. J. Biomech. 2008, 41, 3303–3308. [Google Scholar] [CrossRef]
  31. Umberger, B.R. Effects of suppressing arm swing on kinematics, kinetics, and energetics of human walking. J. Biomech. 2008, 41, 2575–2580. [Google Scholar] [CrossRef]
  32. Kubo, M.; Wagenaar, R.C.; Saltzman, E.; Holt, K.G. Biomechanical mechanism for transitions in phase and frequency of arm and leg swing during walking. Biol. Cybern. 2004, 91, 91–98. [Google Scholar] [CrossRef]
  33. Punt, M.; Bruijn, S.M.; Wittink, H.; van Dieën, J.H. Effect of arm swing strategy on local dynamic stability of human gait. Gait Posture 2015, 41, 504–509. [Google Scholar] [CrossRef] [PubMed]
  34. Cavagna, G.A.; Kaneko, M. Mechanical work and efficiency in level walking and running. J. Physiol. 1977, 268, 467–481. [Google Scholar] [CrossRef] [PubMed]
  35. Pontzer, H.; Holloway, J.H., 4th; Raichlen, D.A.; Lieberman, D.E. Control and function of arm swing in human walking and running. J. Exp. Biol. 2009, 212, 523–534. [Google Scholar] [CrossRef] [PubMed]
  36. Schöner, G.; Jiang, W.Y.; Kelso, J.A.S. A synergetic theory of quadrupedal gaits and gait transitions. J. Theor. Biol. 1990, 142, 359–391. [Google Scholar] [CrossRef]
  37. Jeka, J.J.; Kelso, J.A.S.; Kiemel, T. Pattern switching in human multilimb coordination dynamics. Bull. Math. Biol. 1993, 55, 829–845. [Google Scholar] [CrossRef]
  38. Delabastita, T.; Desloovere, K.; Meyns, P. Restricted arm swing affects gait stability and increased walking speed alters trunk movements in children with cerebral palsy. Front. Hum. Neurosci. 2016, 15, 1–16. [Google Scholar] [CrossRef]
  39. Tester, N.J.; Howland, D.R.; Day, K.V.; Suter, S.P.; Cantrell, A.; Behrman, A.L. Device use, locomotor training and the presence of arm swing during treadmill walking after spinal cord injury. Spinal Cord. 2011, 49, 451–456. [Google Scholar] [CrossRef]
  40. Galloway, J.; Koshland, G. General coordination of shoulder, elbow and wrist dynamics during multijoint arm movements. Exp. Brain Res. 2002, 142, 163–180. [Google Scholar] [CrossRef]
  41. Gribble, P.L.; Ostry, D.J. Independent coactivation of shoulder and elbow muscles. Exp. Brain Res. 1998, 123, 355–360. [Google Scholar] [CrossRef]
  42. Gottlieb, G.L.; Song, Q.; Hong, D.A.; Almeida, G.L.; Corcos, D. Coordinating movement at two joints: A principle of linear covariance. J. Neurophysiol. 1996, 75, 1760–1764. [Google Scholar] [CrossRef]
  43. Zaal, F.T.; Daigle, K.; Gottlieb, G.L.; Thelen, E. An unlearned principle for controlling natural movements. J. Neurophysiol. 1999, 82, 255–259. [Google Scholar] [CrossRef]
Applsci 15 06593 g001
Figure 1. Marker placement for upper body at bony landmarks.
Figure 1. Marker placement for upper body at bony landmarks.
Applsci 15 06593 g001
Applsci 15 06593 g002
Figure 2. Experimental setup and procedure.
Figure 2. Experimental setup and procedure.
Applsci 15 06593 g002
Applsci 15 06593 g003
Figure 3. The mean and standard deviation of angular velocity of shoulder joint from the sagittal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Figure 3. The mean and standard deviation of angular velocity of shoulder joint from the sagittal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Applsci 15 06593 g003
Applsci 15 06593 g004
Figure 4. The mean and standard deviation of angular acceleration of the shoulder joint from the sagittal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Figure 4. The mean and standard deviation of angular acceleration of the shoulder joint from the sagittal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Applsci 15 06593 g004
Applsci 15 06593 g005
Figure 5. The mean and standard deviation of angular velocity of the shoulder joint from the frontal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Figure 5. The mean and standard deviation of angular velocity of the shoulder joint from the frontal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Applsci 15 06593 g005
Applsci 15 06593 g006
Figure 6. The mean and standard deviation of angular acceleration of the shoulder joint from the frontal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Figure 6. The mean and standard deviation of angular acceleration of the shoulder joint from the frontal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Applsci 15 06593 g006
Applsci 15 06593 g007
Figure 7. The mean and standard deviation of angular velocity of the elbow joint from the sagittal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Figure 7. The mean and standard deviation of angular velocity of the elbow joint from the sagittal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Applsci 15 06593 g007
Applsci 15 06593 g008
Figure 8. The mean and standard deviation of angular acceleration of the elbow joint from the sagittal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Figure 8. The mean and standard deviation of angular acceleration of the elbow joint from the sagittal plane. Different letters in alphabetical order indicate Tukey’s post hoc groupings, where distinct letters denote statistically significant differences between conditions (p < 0.05).
Applsci 15 06593 g008
Table 1. The significant results of analysis of variance and the mean values (±standard deviation) according to walking speed (* p < 0.05, ** p < 0.01).
Table 1. The significant results of analysis of variance and the mean values (±standard deviation) according to walking speed (* p < 0.05, ** p < 0.01).
Joint
(Motion)		Kinematic Variable
(Unit)		Walking Speed (km/h)
3.64.2 (PWS)5.47.2
Shoulder
(flexion–
extension)		Range of motion *
(deg)		27.1 (8.8)24.9 (8.4)28.4 (8.5)30.0 (9.9)
Maximum joint angular velocity **
(deg/s)		78.2 (24.4)68.2 (19.4)77.9 (22.9)102.2 (40.8)
Minimum joint angular velocity *
(deg/s)		−86.9 (23.0)−88.7 (25.5)−104.0 (26.9)−128.9 (40.3)
Maximum joint angular acceleration *
(deg/s2)		680.2 (221.2)723.4 (203.4)979.8 (298.7)1102.8 (447.1)
Minimum joint angular acceleration *
(deg/s2)		−453.9 (174.3)−478.1 (167.6)−681.7 (181.2)−987.9 (217.2)
Shoulder
(abduction–adduction)		Range of motion
(deg)		6.9 (2.7)6.6 (3.1)6.7 (4.2)6.4 (2.3)
Maximum joint angular velocity **
(deg/s)		18.1 (8.8)16.1 (9.0)18.6 (8.9)23.5 (10.1)
Minimum joint angular velocity **
(deg/s)		−21.4 (9.7)−20.8 (10.0)−20.7 (9.0)−27.7 (10.9)
Maximum joint angular acceleration **
(deg/s2)		231.0 (117.2)221.9 (94.0)258.8 (117.0)347.6 (131.8)
Minimum joint angular acceleration **
(deg/s2)		−236.5 (104.8)−221.9 (73.7)−254.8 (106.5)−342.0 (117.4)
Elbow
(flexion–
extension)		Range of motion *
(deg)		13.8 (5.1)14.3 (6.7)15.9 (6.9)17.3 (7.8)
Maximum joint angular velocity **
(deg/s)		32.5 (13.4)38.1 (14.1)53.8 (22.9)58.4 (30.7)
Minimum joint angular velocity **
(deg/s)		−29.0 (10.5)−33.2 (13.6)−48.9 (14.6)−59.0 (22.8)
Maximum joint angular acceleration **
(deg/s2)		345.8 (128.4)358.2 (143.5)581.1 (325.4)618.2 (312.9)
Minimum joint angular acceleration **
(deg/s2)		−297.8 (130.1)−336.5 (106.8)−423.5 (142.1)−462.9 (134.4)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kim, J.H.; Hwang, J.; Jung, M.-C.; Mo, S.-M. Kinematic Analysis of Dynamic Coactivation During Arm Swing at the Shoulder and Elbow Joints. Appl. Sci. 2025, 15, 6593. https://doi.org/10.3390/app15126593

AMA Style

Kim JH, Hwang J, Jung M-C, Mo S-M. Kinematic Analysis of Dynamic Coactivation During Arm Swing at the Shoulder and Elbow Joints. Applied Sciences. 2025; 15(12):6593. https://doi.org/10.3390/app15126593

Chicago/Turabian Style

Kim, Jae Ho, Jaejin Hwang, Myung-Chul Jung, and Seung-Min Mo. 2025. "Kinematic Analysis of Dynamic Coactivation During Arm Swing at the Shoulder and Elbow Joints" Applied Sciences 15, no. 12: 6593. https://doi.org/10.3390/app15126593

APA Style

Kim, J. H., Hwang, J., Jung, M.-C., & Mo, S.-M. (2025). Kinematic Analysis of Dynamic Coactivation During Arm Swing at the Shoulder and Elbow Joints. Applied Sciences, 15(12), 6593. https://doi.org/10.3390/app15126593

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop