Analytical Solution for Thermal Runaway of Li-Ion Battery with Simplified Thermal Decomposition Equation
Abstract
1. Introduction
2. Method
2.1. Model Assumptions
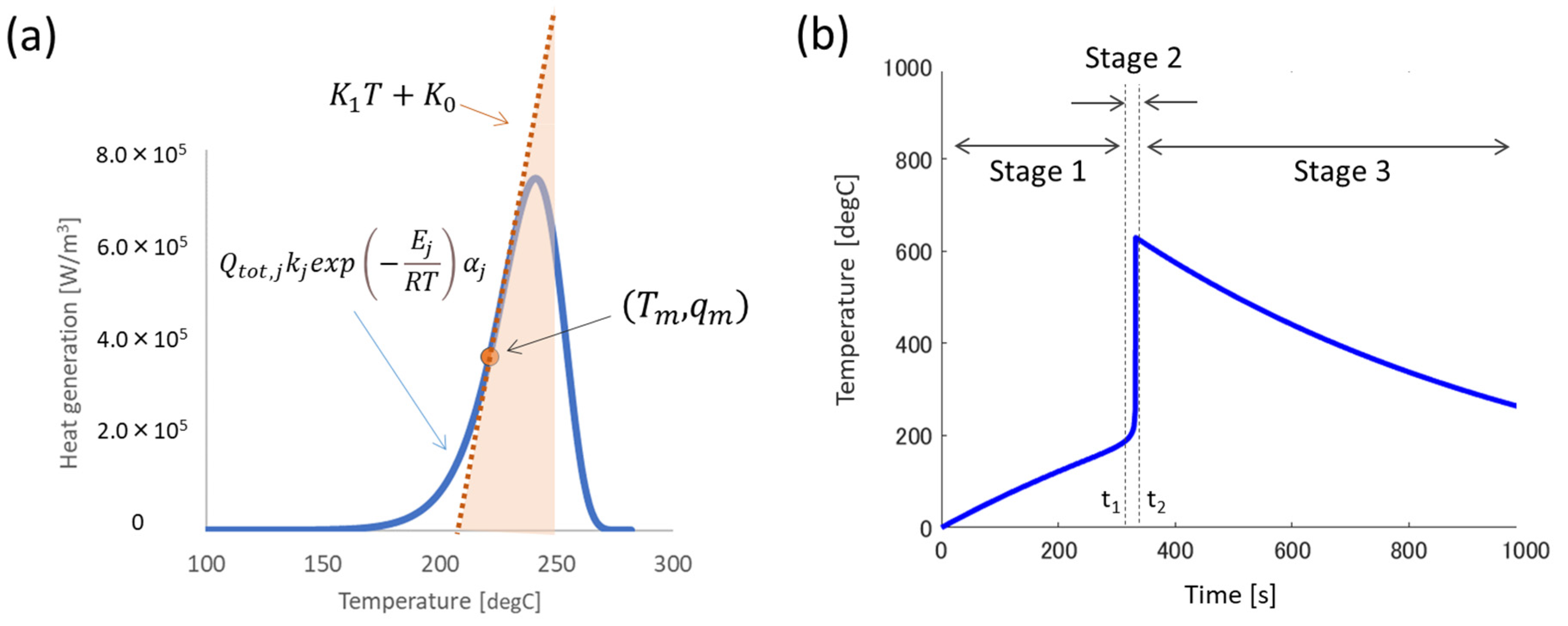
2.2. Linearizing Heat Generation of Battery Cell
2.3. Approximation to Overall Reaction
2.4. Analytical Temperature Profile of Battery Cell
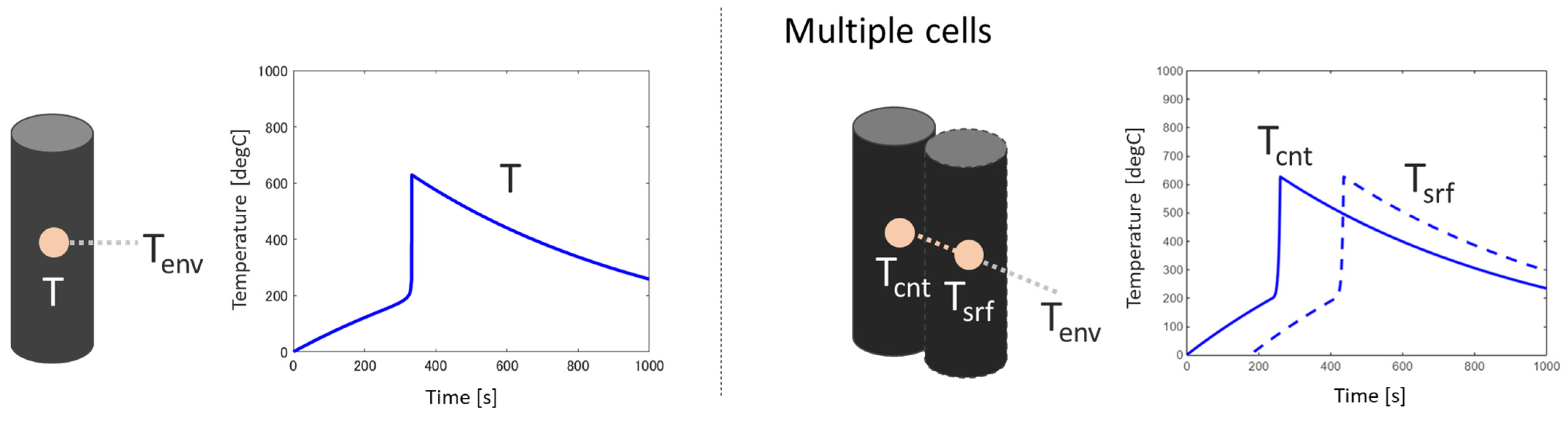
2.5. Temperature Profiles of Multiple Battery Cells
2.6. Simulation Method
3. Results
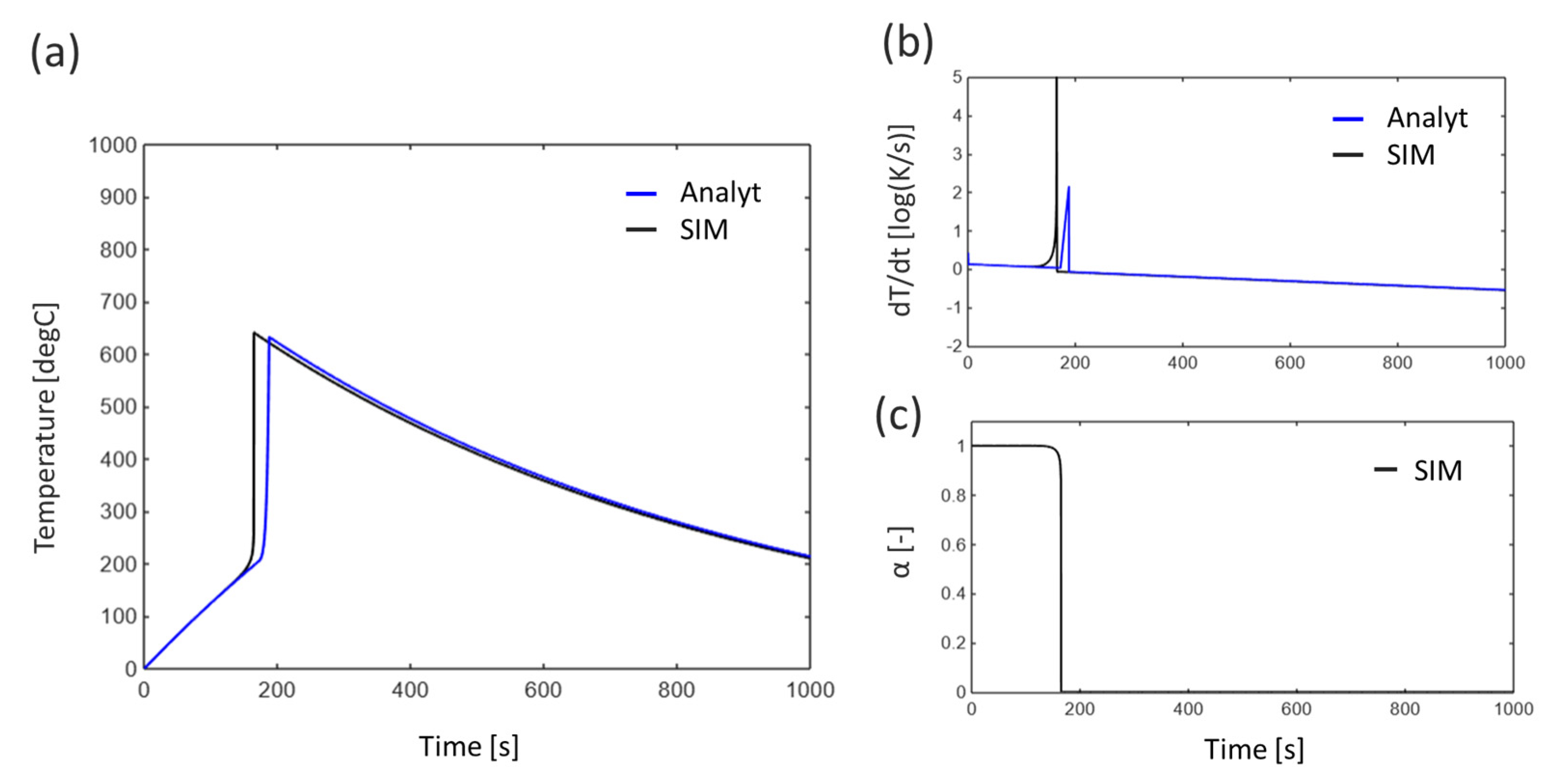
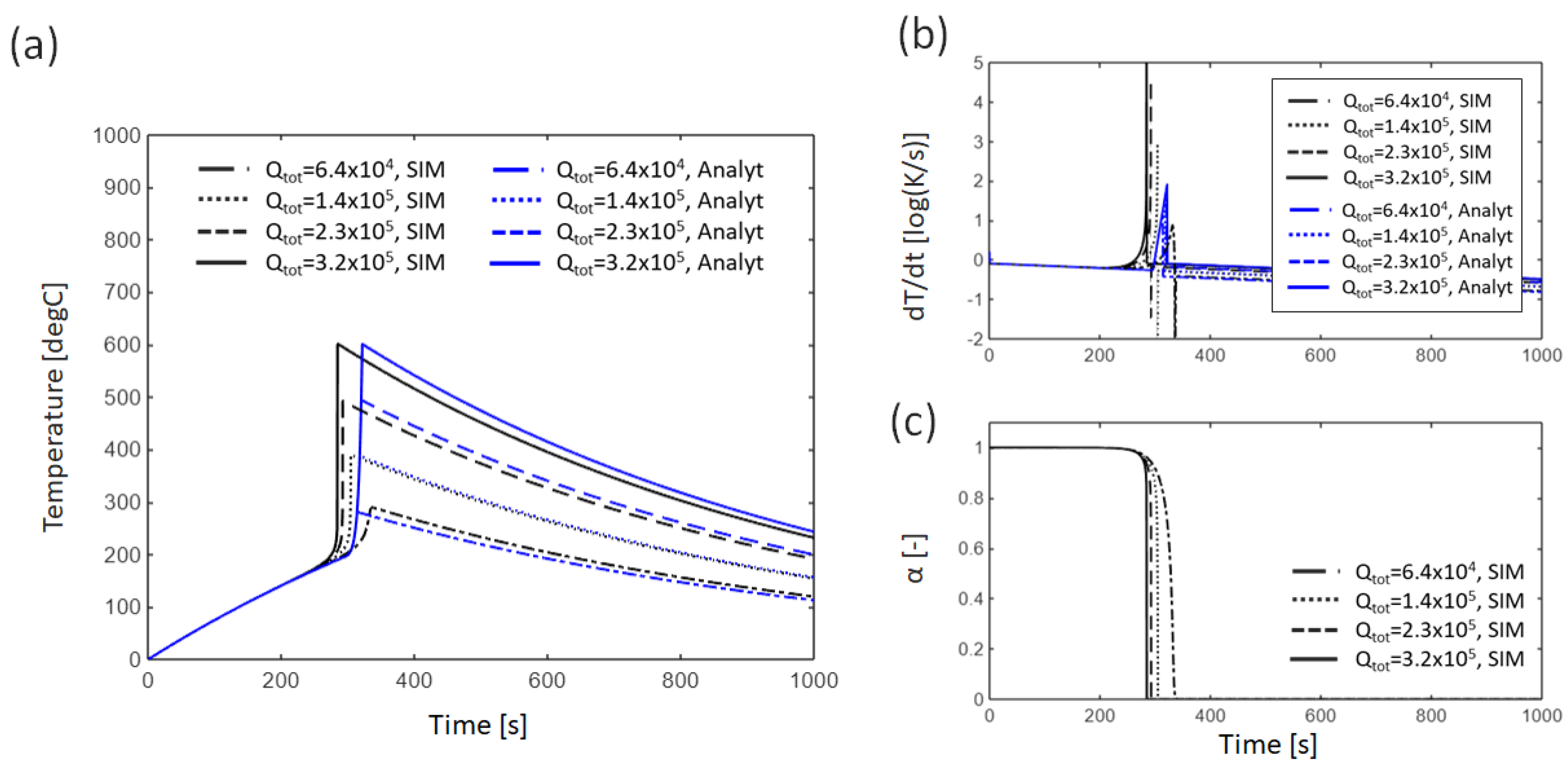
3.1. Single Cell
3.1.1. Baseline Condition
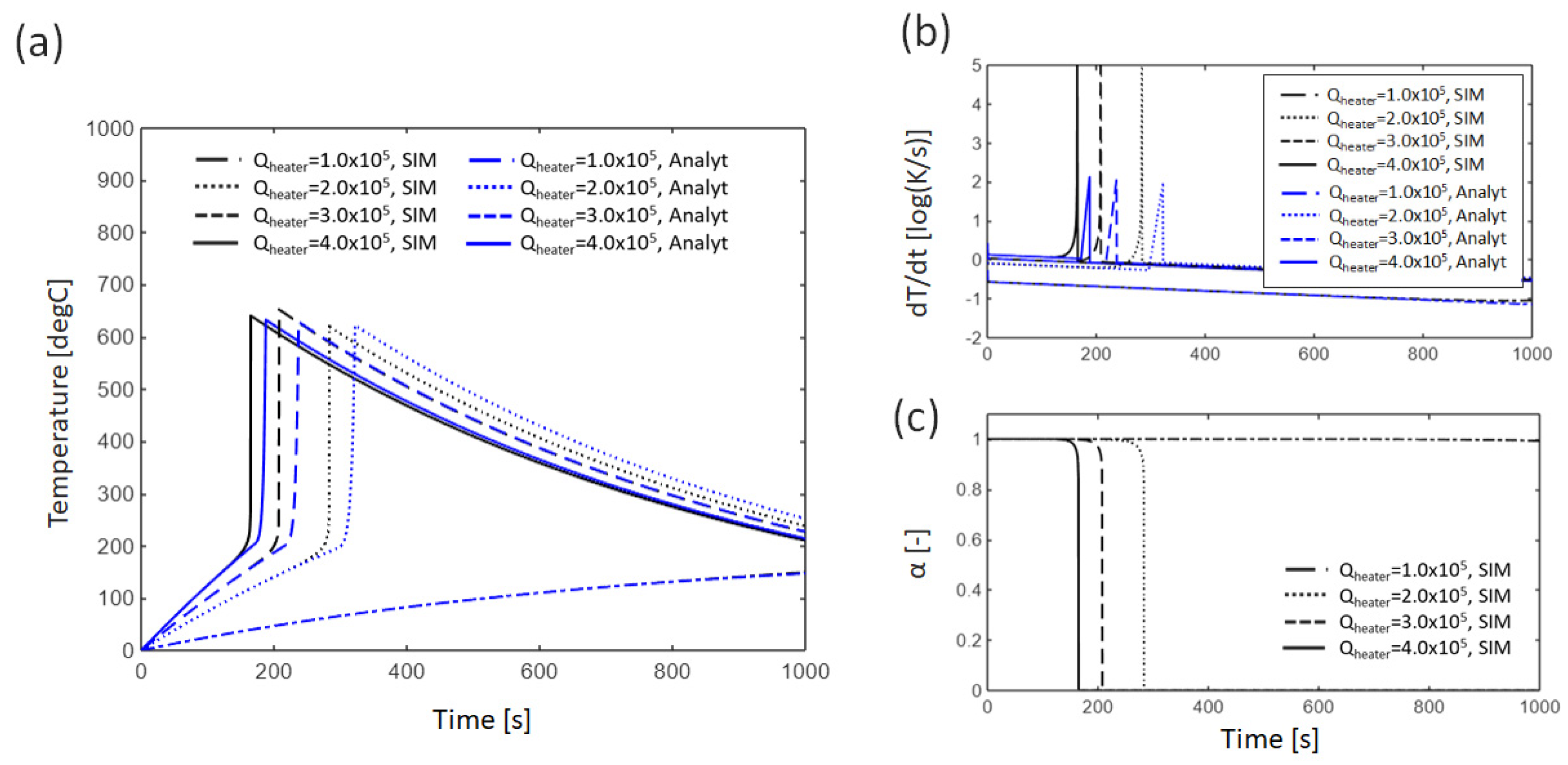
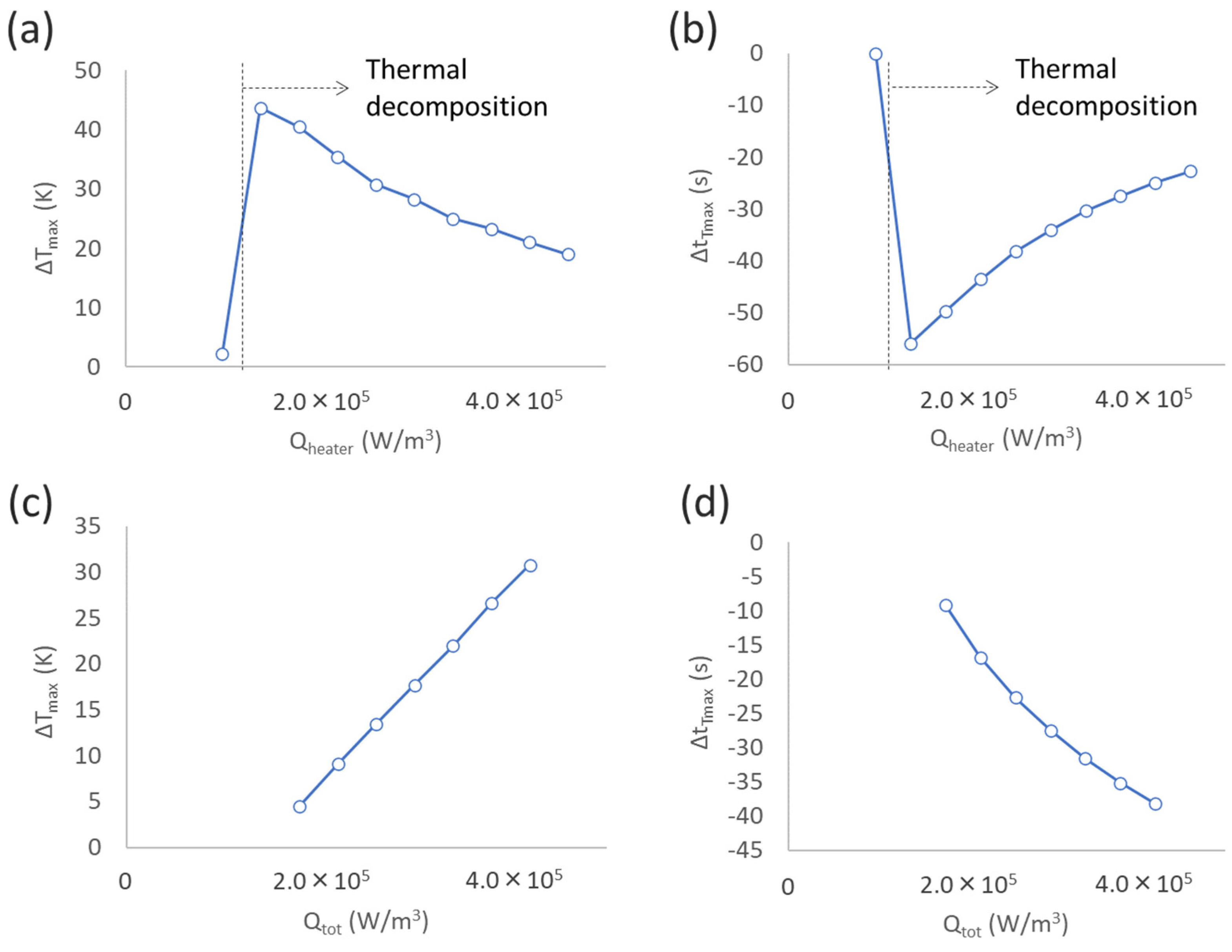
3.1.2. Effect of External Heating
3.1.3. Effect of Latent Heat of Thermal Decomposition Reaction
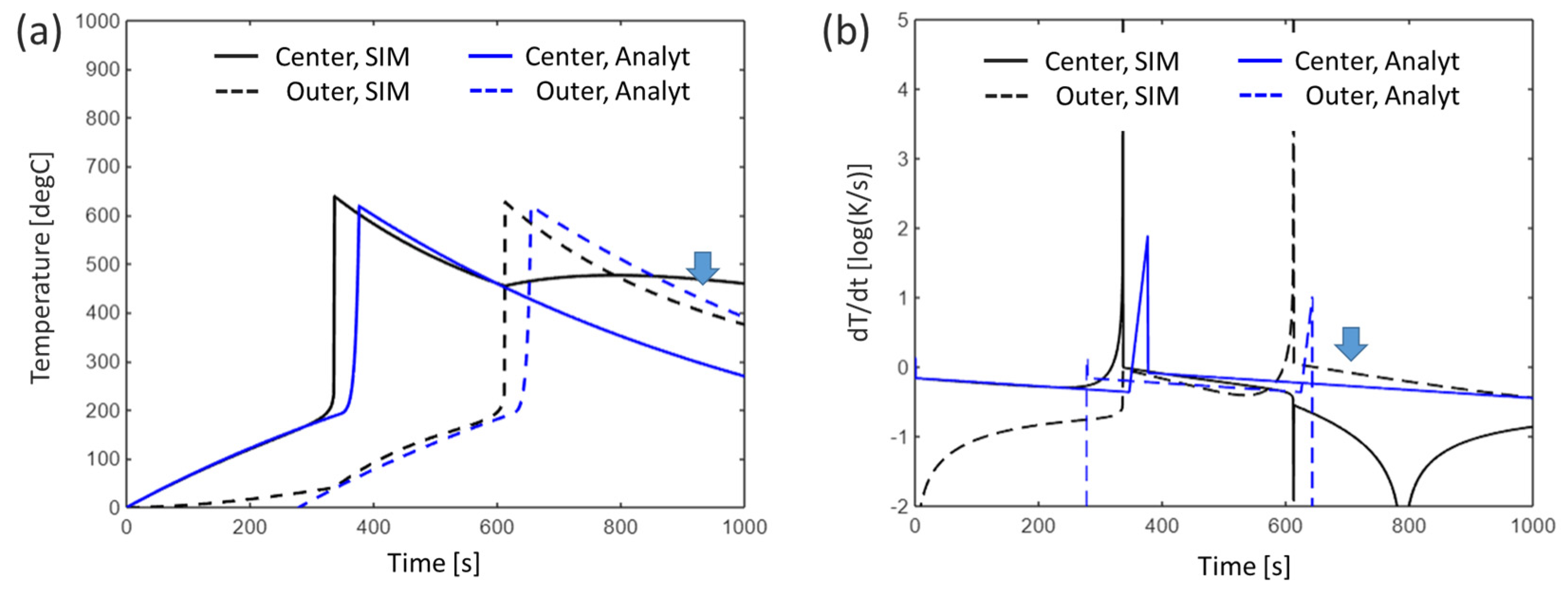
3.2. Multiple Cells
3.2.1. Baseline Condition
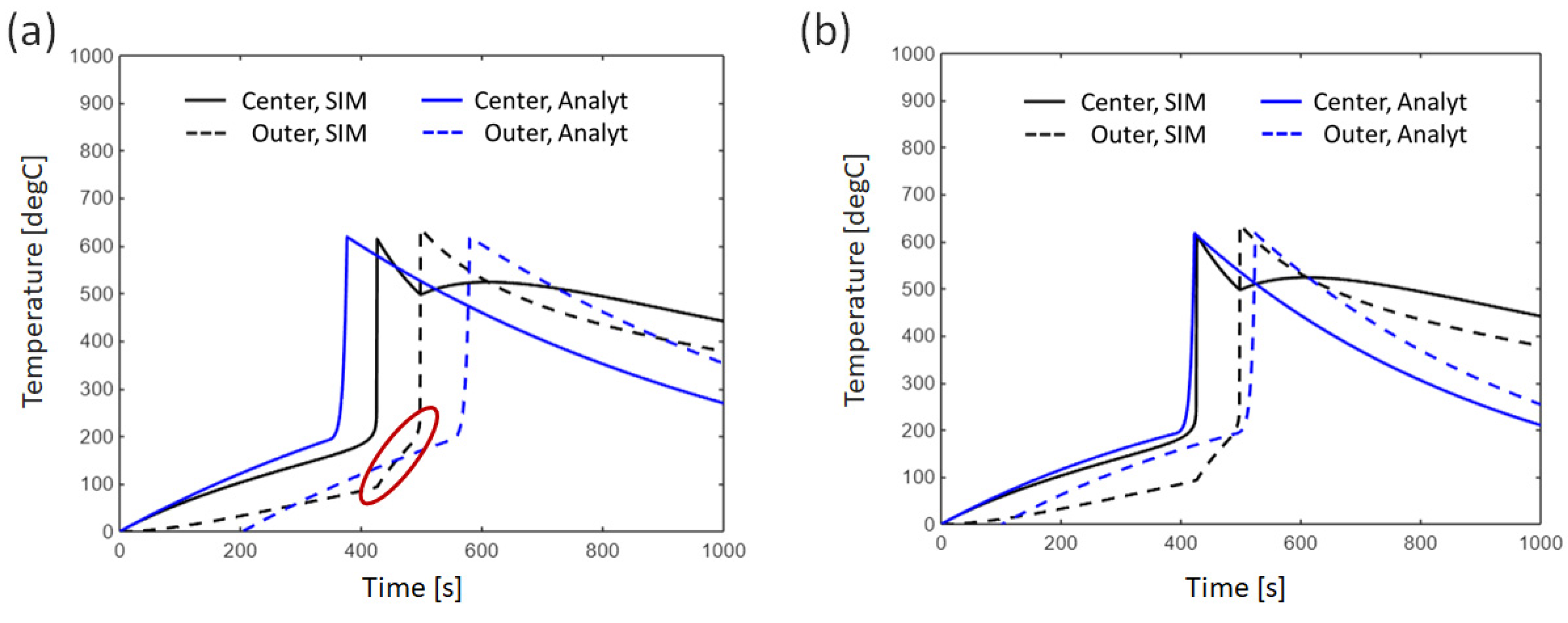
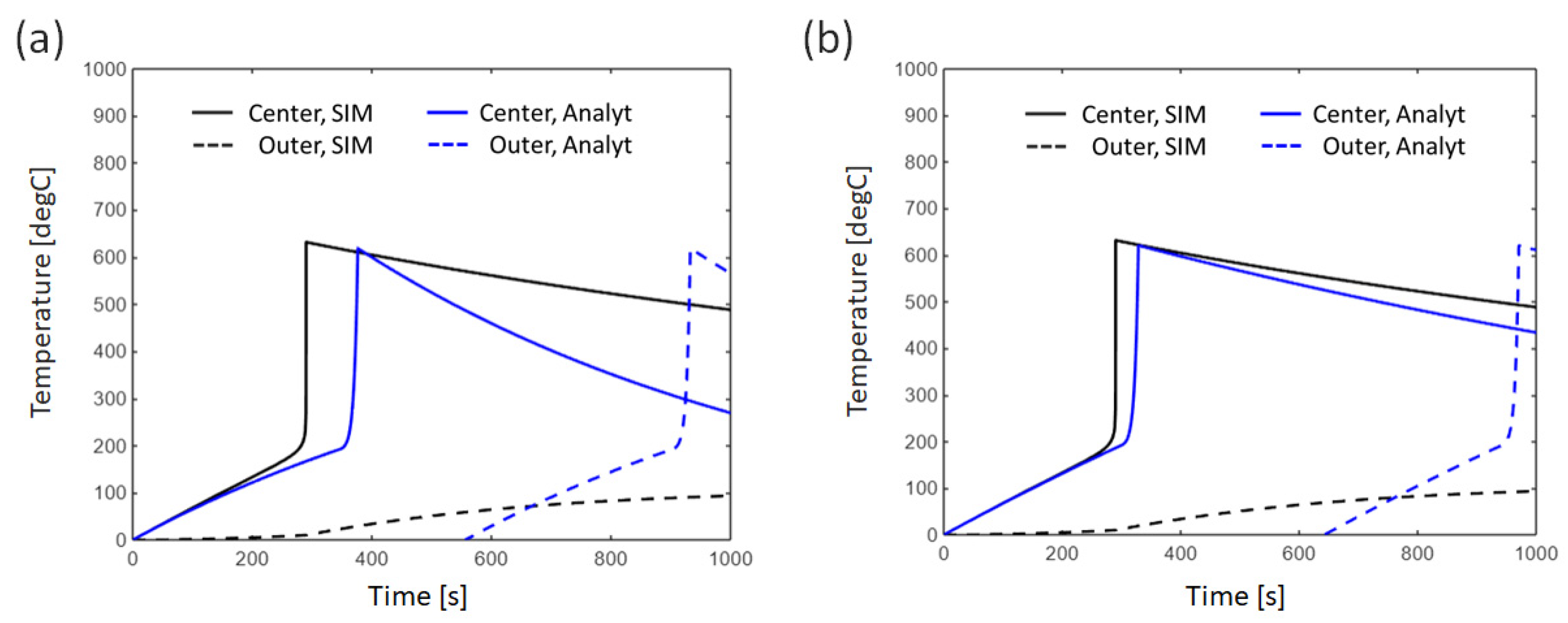
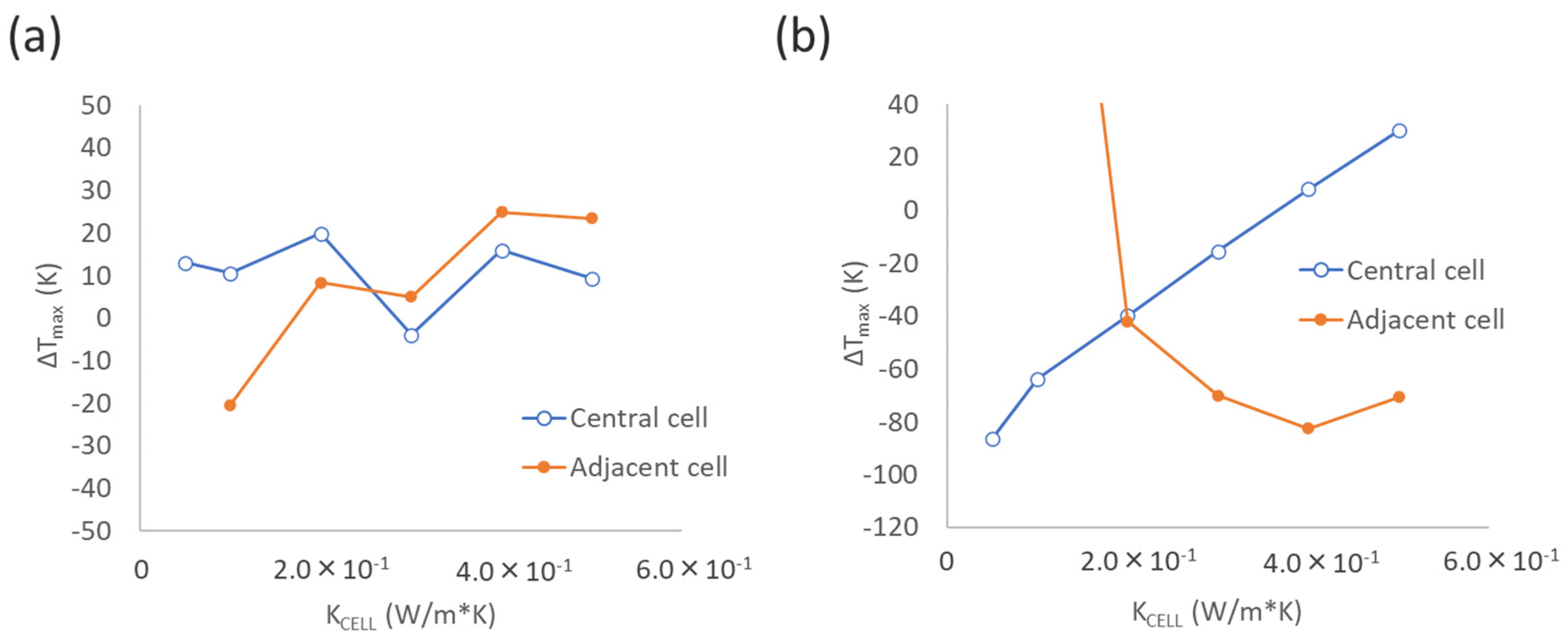
3.2.2. Effect of Thermal Conductivity Between Cells
4. Discussion
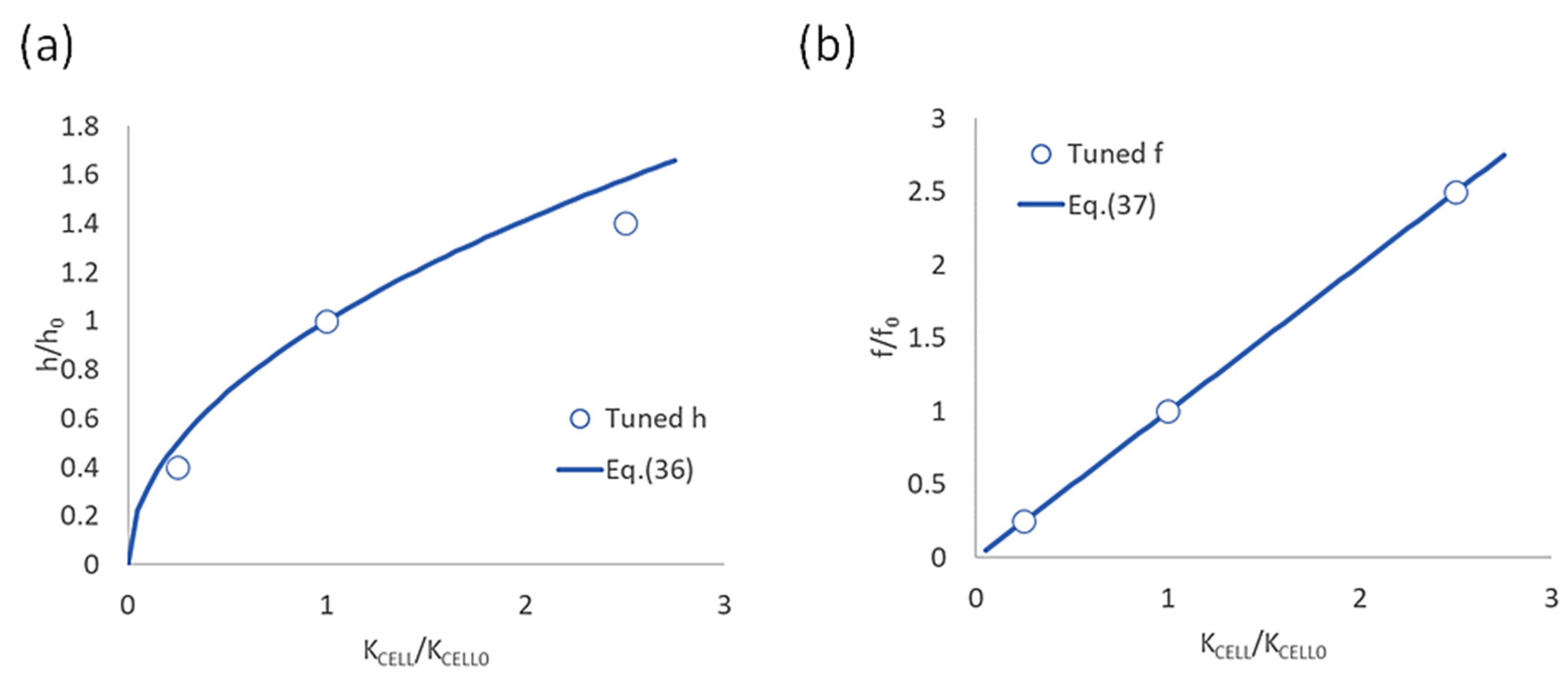
4.1. Error Analysis Between Analytical Solutions and Numerical Simulations
4.2. Applicability and Limitations of the Model
- Examination of representative α value selection: Clarifying the relationship between thermal decomposition reaction parameters (k0, C1, m, n, E) and the representative α;
- Improvement of the thermal decomposition reaction linearization method:
- -
- Representation using two linear functions, including the rising region in addition to the maximum slope;
- -
- Representation using a quadratic function. The energy equation will become Riccati-type equations.
- Creation of an effective parameter database through parametric studies;
- Consideration of the physical meaning and improvement of the estimation accuracy of parameters R, f, and Δt in multiple-cell systems.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Xu, C.; Dai, Q.; Gaines, L.; Hu, M.; Tukker, A.; Steubing, B. Future Material Demand for Automotive Lithium-Based Batteries. Commun. Mater. 2020, 1, 99. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal Runaway Mechanism of Lithium Ion Battery for Electric Vehicles: A Review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Duan, J.; Tang, X.; Dai, H.; Yang, Y.; Wu, W.; Wei, X.; Huang, Y. Building Safe Lithium-Ion Batteries for Electric Vehicles: A Review. Electrochem. Energ. Rev. 2020, 3, 1–42. [Google Scholar] [CrossRef]
- Sun, P.; Bisschop, R.; Niu, H.; Huang, X. A Review of Battery Fires in Electric Vehicles. Fire Technol. 2020, 56, 1361–1410. [Google Scholar] [CrossRef]
- Jaguemont, J.; Bardé, F. A Critical Review of Lithium-Ion Battery Safety Testing and Standards. Appl. Therm. Eng. 2023, 231, 121014. [Google Scholar] [CrossRef]
- Lai, X.; Yao, J.; Jin, C.; Feng, X.; Wang, H.; Xu, C.; Zheng, Y. A Review of Lithium-Ion Battery Failure Hazards: Test Standards, Accident Analysis, and Safety Suggestions. Batteries 2022, 8, 248. [Google Scholar] [CrossRef]
- Svetlík, J.; Tancos, Z.; Tancos, P.; Markova, I.; Slastan, K. Large-Scale Fire Tests of Battery Electric Vehicle (BEV): Slovak Case Study. Appl. Sci. 2024, 14, 4013. [Google Scholar] [CrossRef]
- Chai, Z.; Li, J.; Liu, Z.; Liu, Z.; Jin, X. Experimental Analysis and Safety Assessment of Thermal Runaway Behavior in Lithium Iron Phosphate Batteries under Mechanical Abuse. Sci. Rep. 2024, 14, 8673. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A Review of Lithium-Ion Battery Safety Concerns: The Issues, Strategies, and Testing Standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Mallarapu, A.; Sunderlin, N.; Boovaragavan, V.; Tamashiro, M.; Peabody, C.; Pelloux-gervais, T.; Li, X.X.; Sizikov, G. Effects of Trigger Method on Fire Propagation during the Thermal Runaway Process in Li-Ion Batteries. J. Electrochem. Soc. 2024, 171, 040514. [Google Scholar] [CrossRef]
- Doughty, D.; Roth, E.P. A General Discussion of Li Ion Battery Safety. Electrochem. Soc. Interface 2012, 21, 37. [Google Scholar]
- Comanescu, C. Ensuring Safety and Reliability: An Overview of Lithium-Ion Battery Service Assessment. Batteries 2025, 11, 6. [Google Scholar] [CrossRef]
- Long, T.; Wang, L.; Kan, C.-D. Experimental and Modeling Approaches for Electric Vehicle Battery Safety: A Technical Review. Eng. Res. Express 2024, 6, 032503. [Google Scholar] [CrossRef]
- Abada, S.; Marlair, G.; Lecocq, A.; Petit, M.; Sauvant-Moynot, V.; Huet, F. Safety Focused Modeling of Lithium-Ion Batteries: A Review. J. Power Sources 2016, 306, 178–192. [Google Scholar] [CrossRef]
- Sorensen, A.; Utgikar, V.; Belt, J. A Study of Thermal Runaway Mechanisms in Lithium-Ion Batteries and Predictive Numerical Modeling Techniques. Batteries 2024, 10, 116. [Google Scholar] [CrossRef]
- Hamisi, C.M.; Chombo, P.V.; Laoonual, Y.; Wongwises, S. An Electrothermal Model to Predict Thermal Characteristics of Lithium-Ion Battery under Overcharge Condition. Energies 2022, 15, 2284. [Google Scholar] [CrossRef]
- Li, J.; Sun, D.; Jin, X.; Shi, W.; Sun, C. Lithium-Ion Battery Overcharging Thermal Characteristics Analysis and an Impedance-Based Electro-Thermal Coupled Model Simulation. Appl. Energy 2019, 254, 113574. [Google Scholar] [CrossRef]
- Zavalis, T.G.; Behm, M.; Lindbergh, G. Investigation of Short-Circuit Scenarios in a Lithium-Ion Battery Cell. J. Electrochem. Soc. 2012, 159, A848–A859. [Google Scholar] [CrossRef]
- Yamanaka, T.; Takagishi, Y.; Tozuka, Y.; Yamaue, T. Modeling Lithium Ion Battery Nail Penetration Tests and Quantitative Evaluation of the Degree of Combustion Risk. J. Power Sources 2019, 416, 132. [Google Scholar] [CrossRef]
- Zhang, C.; Santhanagopalan, S.; Sprague, M.A.; Pesaran, A.A. Coupled Mechanical-Electrical-Thermal Modeling for Short-Circuit Prediction in a Lithium-Ion Cell under Mechanical Abuse. J. Power Sources 2015, 290, 102–113. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, X.; Sahraei, E.; Wierzbicki, T. Deformation and Failure Mechanisms of 18650 Battery Cells under Axial Compression. J. Power Sources 2016, 336, 332–340. [Google Scholar] [CrossRef]
- Spotnitz, R.; Franklin, J. Abuse Behavior of High-Power, Lithium-Ion Cells. J. Power Sources 2003, 113, 81–100. [Google Scholar] [CrossRef]
- Mao, B.; Huang, P.; Chen, H.; Wang, Q.; Sun, J. Self-Heating Reaction and Thermal Runaway Criticality of the Lithium Ion Battery. Int. J. Heat. Mass. Transf. 2020, 149, 119178. [Google Scholar] [CrossRef]
- MacNeil, D.D.; Hatchard, T.D.; Dahn, J.R. A Comparison Between the High Temperature Electrode Electrolyte Reactions of LixCoO2 and LixMn2O4. J. Electrochem. Soc. 2001, 148, A663. [Google Scholar] [CrossRef]
- Li, W.; León Quiroga, V.; Crompton, K.R.; Ostanek, J.K. High Resolution 3-D Simulations of Venting in 18650 Lithium-Ion Cells. Front. Energy Res. 2021, 9, 788239. [Google Scholar] [CrossRef]
- Ostanek, J.K.; Parhizi, M.; Li, W.; Kilaz, G.; Crompton, K.R. CFD-Based Thermal Abuse Simulations Including Gas Generation and Venting of an 18650 Li-Ion Battery Cell. J. Electrochem. Soc. 2023, 170, 090512. [Google Scholar] [CrossRef]
- Kim, J.; Mallarapu, A.; Finegan, D.P.; Santhanagopalan, S. Modeling Cell Venting and Gas-Phase Reactions in 18650 Lithium Ion Batteries during Thermal Runaway. J. Power Sources 2021, 489, 229496. [Google Scholar] [CrossRef]
- Takagishi, Y.; Tozuka, Y.; Yamanaka, T.; Yamaue, T. Heating Simulation of a Li-Ion Battery Cylindrical Cell and Module with Consideration of Gas Ejection. Energy Rep. 2022, 8, 3176–3188. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, X.; Qiu, J.; Xu, C.; Wang, Y.; Feng, X. Modeling and Simulation of a Gas-Exhaust Design for Battery Thermal Runaway Propagation in a LiFePO4 Module. Batteries 2024, 10, 176. [Google Scholar] [CrossRef]
- Ye, Z.; Fu, X. Experimental and Simulation Investigation on Suppressing Thermal Runaway in Battery Pack. Sci. Rep. 2024, 14, 12723. [Google Scholar] [CrossRef]
- Choi, Y.; Park, P. Thermal Runaway Diagnosis of Lithium-Ion Cells Using Data-Driven Method. Appl. Sci. 2024, 14, 9107. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Jiang, B.; He, H.; Huang, S.; Wang, C.; Zhang, Y.; Han, X.; Guo, D.; He, G.; et al. Realistic Fault Detection of Li-Ion Battery via Dynamical Deep Learning. Nat. Commun. 2023, 14, 5940. [Google Scholar] [CrossRef] [PubMed]
- Naha, A.; Khandelwal, A.; Agarwal, S.; Tagade, P.; Hariharan, K.S.; Kaushik, A.; Yadu, A.; Kolake, S.M.; Han, S.; Oh, B. Internal Short Circuit Detection in Li-Ion Batteries Using Supervised Machine Learning. Sci. Rep. 2020, 10, 1301. [Google Scholar] [CrossRef] [PubMed]
- Domalanta, M.R.B.; Paraggua, J.A.D.R. A Multiphysics Model Simulating the Electrochemical, Thermal, and Thermal Runaway Behaviors of Lithium Polymer Battery. Energies 2023, 16, 2642. [Google Scholar] [CrossRef]
- Zhang, E.; Dao, M.; Karniadakis, G.E.; Suresh, S. Analyses of Internal Structures and Defects in Materials Using Physics-Informed Neural Networks. Sci. Adv. 2022, 8, eabk0644. [Google Scholar] [CrossRef]
- Zhao, R.; Lai, Z.; Li, W.; Ye, M.; Yu, S. Development of a Coupled Model of Heat Generation and Jet Flow of Lithium-Ion Batteries during Thermal Runaway. J. Energy Storage 2023, 63, 107048. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, F.; Feng, J.; Jin, C.; Wang, H.; Xu, C.; Ouyang, M. Propagation Dynamics of the Thermal Runaway Front in Large-Scale Lithium-Ion Batteries: Theoretical and Experiment Validation. Int. J. Heat. Mass. Transf. 2024, 225, 125393. [Google Scholar] [CrossRef]
- He, T.; Zhang, T.; Gadkari, S.; Wang, Z.; Mao, N.; Cai, Q. An Investigation on Thermal Runaway Behaviour of a Cylindrical Lithium-Ion Battery under Different States of Charge Based on Thermal Tests and a Three-Dimensional Thermal Runaway Model. J. Clean. Prod. 2023, 388, 135980. [Google Scholar] [CrossRef]
- Feng, Y.-F.; Wang, C.; Shen, J.-N.; He, Y.-J. Kinetic Resolution of Thermal Runaway for Lithium-Ion Batteries: A Gaussian Surrogate-Assisted Separate Optimization Approach. Chem. Eng. Sci. 2023, 277, 118875. [Google Scholar] [CrossRef]
- Zhou, H.; Parmananda, M.; Crompton, K.R.; Hladky, M.P.; Dann, M.A.; Ostanek, J.K.; Mukherjee, P.P. Effect of Electrode Crosstalk on Heat Release in Lithium-Ion Batteries under Thermal Abuse Scenarios. Energy Storage Mater. 2022, 44, 326–341. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, H.; Yang, K.; Lu, Y.; Huang, Y. Accelerated Computational Strategies for Multi-Scale Thermal Runaway Prediction Models in Li-Ion Battery. Energy 2024, 305, 132371. [Google Scholar] [CrossRef]
- Peng, R.; Kong, D.; Ping, P.; Wang, G.; Gao, X.; Lv, H.; Zhao, H.; He, X.; Zhang, Y.; Dai, X. Thermal Runaway Modeling of Lithium-Ion Batteries at Different Scales: Recent Advances and Perspectives. Energy Storage Mater. 2024, 69, 103417. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, J.; Yang, K.; Chen, H.; Huang, Y. A 3D Simulation Model of Thermal Runaway in Li-Ion Batteries Coupled Particles Ejection and Jet Flow. J. Power Sources 2023, 580, 233357. [Google Scholar] [CrossRef]
- Liu, Y.; He, C.; Offer, G.; Wang, H.; Huang, X.; Zhao, T. Modelling Thermal Runaway of Cylindrical Battery under Sub-Atmospheric Pressure. J. Power Sources 2025, 633, 236363. [Google Scholar] [CrossRef]
- Wu, X.; Hu, Y.; Wu, T.; Zhuo, Z.; Qiu, H.; Zhu, Y.; Li, X.; Tang, R. Numerical Simulation Study of Thermal Runaway Jet Fire Characteristics of Forced Air-Cooled Cylindrical Battery Module. Case Stud. Therm. Eng. 2025, 66, 105750. [Google Scholar] [CrossRef]
- Semenoff, N. Zur Theorie des Verbrennungsprozesses. Z. Phys. 1928, 48, 571. [Google Scholar] [CrossRef]
- Thomas, P.H. Effect of Reactant Consumption on the Induction Period and Critical Condition for a Thermal Explosion. Proc. R. Soc. Lond. A 1961, 262, 192–206. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, D.A. Diffusion and Heat Exchange in Chemical Kinetics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Padhi, U.P.; Oh, J.; Mehrotra, A.; Lee, Y.; Yoh, J.J. A Predictive Theory on Thermal Runaway of Ultrahigh Capacity Lithium-Ion Batteries. Combust. Flame 2023, 258, 113116. [Google Scholar] [CrossRef]
- An, Z.; Shah, K.; Jia, L.; Ma, Y. Modeling and Analysis of Thermal Runaway in Li-Ion Cell. Appl. Therm. Eng. 2019, 160, 113960. [Google Scholar] [CrossRef]
- Zhao, P.; Liu, L.; Chen, Y.; Ge, H. Theoretical and Numerical Analysis for Thermal Runaway Propagation within a Single Cell. Int. J. Heat Mass Transf. 2021, 181, 121901. [Google Scholar] [CrossRef]
- Huang, P.; Chen, H.; Verma, A.; Wang, Q.; Mukherjee, P.; Sun, J. Non-Dimensional Analysis of the Criticality of Li-Ion Battery Thermal Runaway Behavior. J. Hazard. Mater. 2019, 369, 268–278. [Google Scholar] [CrossRef] [PubMed]
- Larsson, F.; Anderson, J.; Andersson, P.; Mellander, B.-E. Thermal Modelling of Cell-to-Cell Fire Propagation and Cascading Thermal Runaway Failure Effects for Lithium-Ion Battery Cells and Modules Using Fire Walls. J. Electrochem. Soc. 2016, 163, A2854–A2865. [Google Scholar] [CrossRef]
- Ioka, S.; Kubo, S.; Ochi, M.; Hojo, K. Development of inverse analysis method using a plate model for estimation of temperature distribution history of an elbow with thermal stratification. Trans. JSME 2014, 80, 818. [Google Scholar] [CrossRef][Green Version]
- Laloui, L.; Rotta Loria, A.F. Analysis and Design of Energy Geostructures; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
| Parameter | Value | Reference |
|---|---|---|
| Density | 500 (kg/m3) | Assumed *1 |
| Specific heat | 750 (J/kg) | [28] |
| Specific surface area | 10 (1/m) | Assumed *2 |
| Environment temperature, Tenv | 298 (K) | Assumed |
| Heat transfer coefficient, ht | 50 (W/m2·K) | Assumed *3 |
| External heating, qheating (Baseline) | Single cell 4.00 × 105 (W/m3) Multiple cells 3.0 × 105 (W/m3) | Assumed *4 |
| Latent heat, Qtot,i (baseline) | 3.22 × 105 (J/m3) | [19] |
| Frequency factor, kα | 5.00 × 1013 (1/s) | [19] |
| Activation energy, Ei | R × 1.85 × 104 (J/mol) | [19] |
| Constant, m | 1 | [19] |
| Constant, n | 1 | [19] |
| Constant, C | 1.01 | [19] |
| Thermal conductivity between cells, Kcell (baseline) | 0.2 (W/m·K) | Assumed *5 |
| Temperature frequency, f (baseline) | 1/400 (1/s) | Assumed *5 |
| Space between cells, Dcell | 1.8 × 10−3 (m) | Assumed *5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takagishi, Y.; Kitagawa, H.; Yamaue, T. Analytical Solution for Thermal Runaway of Li-Ion Battery with Simplified Thermal Decomposition Equation. Appl. Sci. 2025, 15, 6574. https://doi.org/10.3390/app15126574
Takagishi Y, Kitagawa H, Yamaue T. Analytical Solution for Thermal Runaway of Li-Ion Battery with Simplified Thermal Decomposition Equation. Applied Sciences. 2025; 15(12):6574. https://doi.org/10.3390/app15126574
Chicago/Turabian StyleTakagishi, Yoichi, Hayato Kitagawa, and Tatsuya Yamaue. 2025. "Analytical Solution for Thermal Runaway of Li-Ion Battery with Simplified Thermal Decomposition Equation" Applied Sciences 15, no. 12: 6574. https://doi.org/10.3390/app15126574
APA StyleTakagishi, Y., Kitagawa, H., & Yamaue, T. (2025). Analytical Solution for Thermal Runaway of Li-Ion Battery with Simplified Thermal Decomposition Equation. Applied Sciences, 15(12), 6574. https://doi.org/10.3390/app15126574







