Multi-Scenario Robust Distributed Permutation Flow Shop Scheduling Based on DDQN
Abstract
1. Introduction
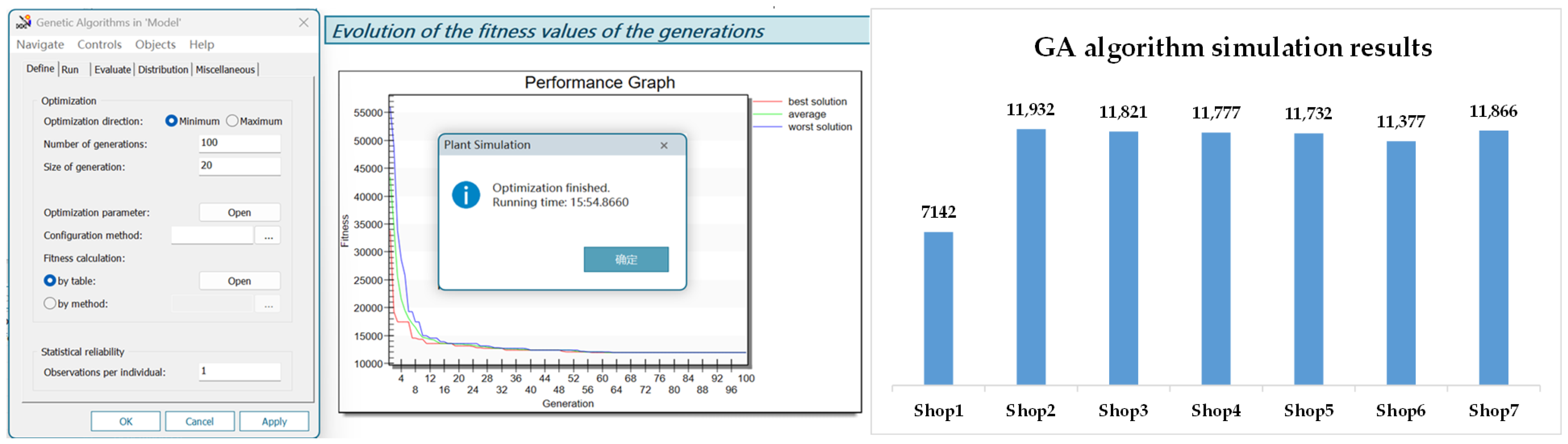
- Siemens Plant Simulation is employed to digitally model the distributed workshop through the definition of operational processes, dynamic events, scheduling rules, and optimization goals. To simulate the complexity of real-world production environments, seven distinct factory types are designed to quantitatively analyze the workshop layout, assembly line design, the state of the workers, robotic arms, AGV vehicles, and other production system parameters. Fault rates are incorporated into the production system to maximize the reproduction of the real production environment. Moreover, GA components are employed to optimize the production process, greatly improving production efficiency.
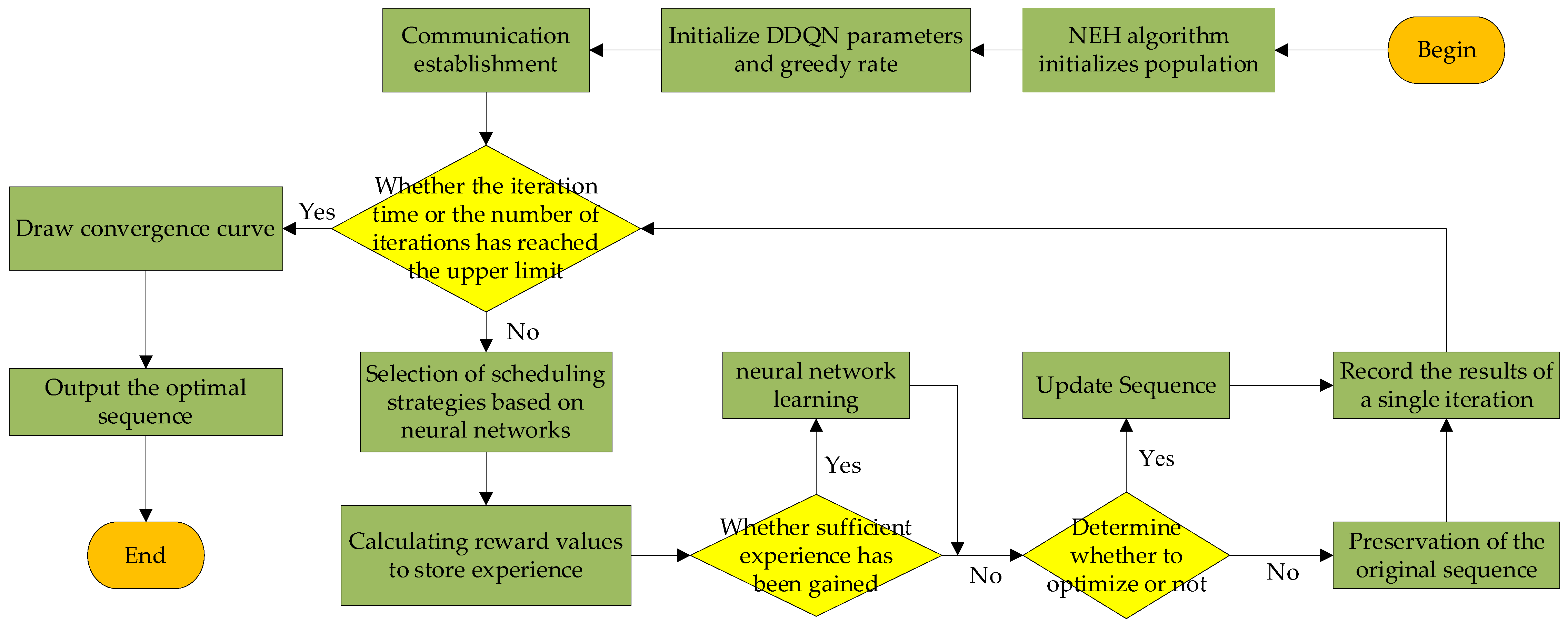
- An approximate optimal solution is generated for the DPFSP using the NEH algorithm and used as the initial solution for MSRDPFSP. Four search strategies are designed, with DQN introduced to minimize the processing time as the target for evaluating Q values. Greedy selection is performed among the four search strategies. The DDQN approach separates the Target Network and the Evaluation Network to mitigate the overestimation of Q-values. Additionally, the allocation information of the workpieces is replaced with the makespan of each workshop as the state information, reducing the training difficulty of the neural network.
- Using the COM interface of Plant Simulation, the models in Plant Simulation are controlled through Pytharm to retrieve simulation results, while calculation and analysis functions in Pytharm are invoked through Plant Simulation. The hybrid DDQN-NEH algorithm is directly integrated into the MSRDPFSP simulation model via DLL, thus completing the entire link from modeling, optimization, to simulation.
2. Related Theory
2.1. The Distributed Replacement Flow Shop Scheduling Problem
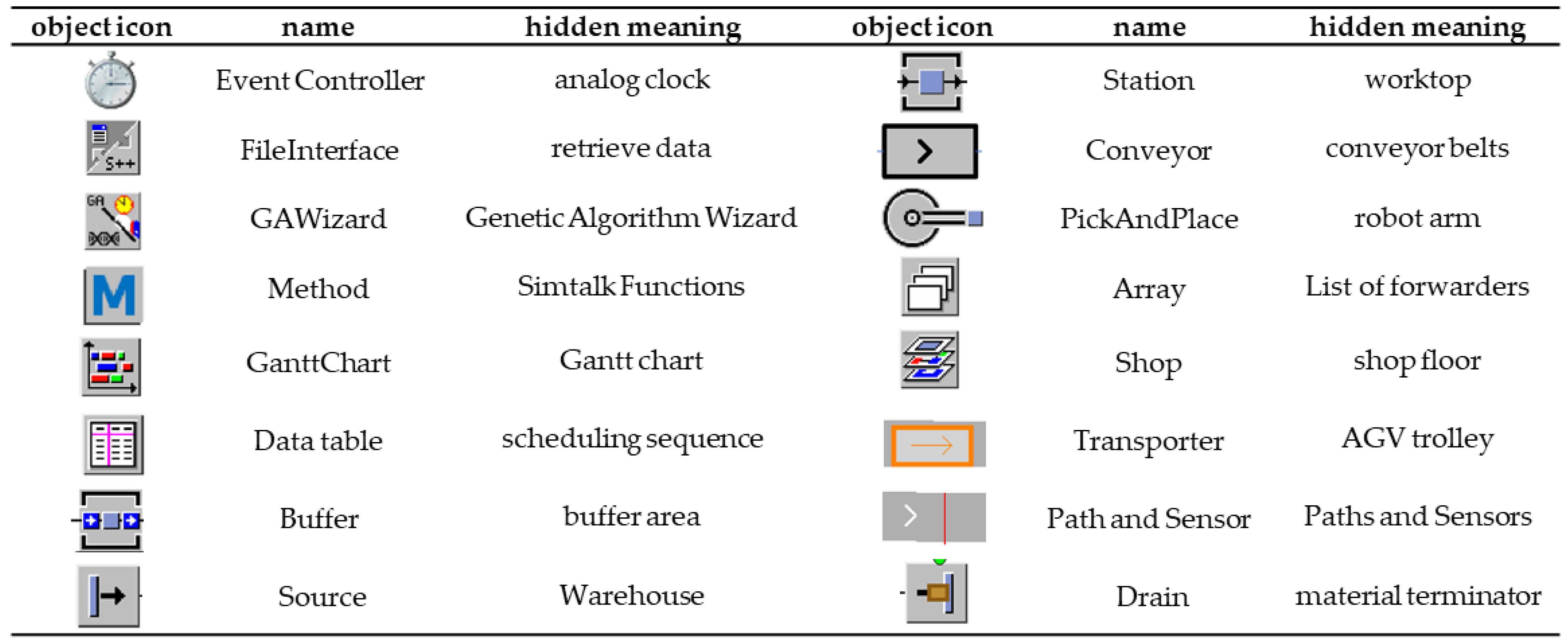
2.2. Computer Simulation Software Plant Simulation
2.3. NEH and DDQN Algorithms
3. Simulation Model
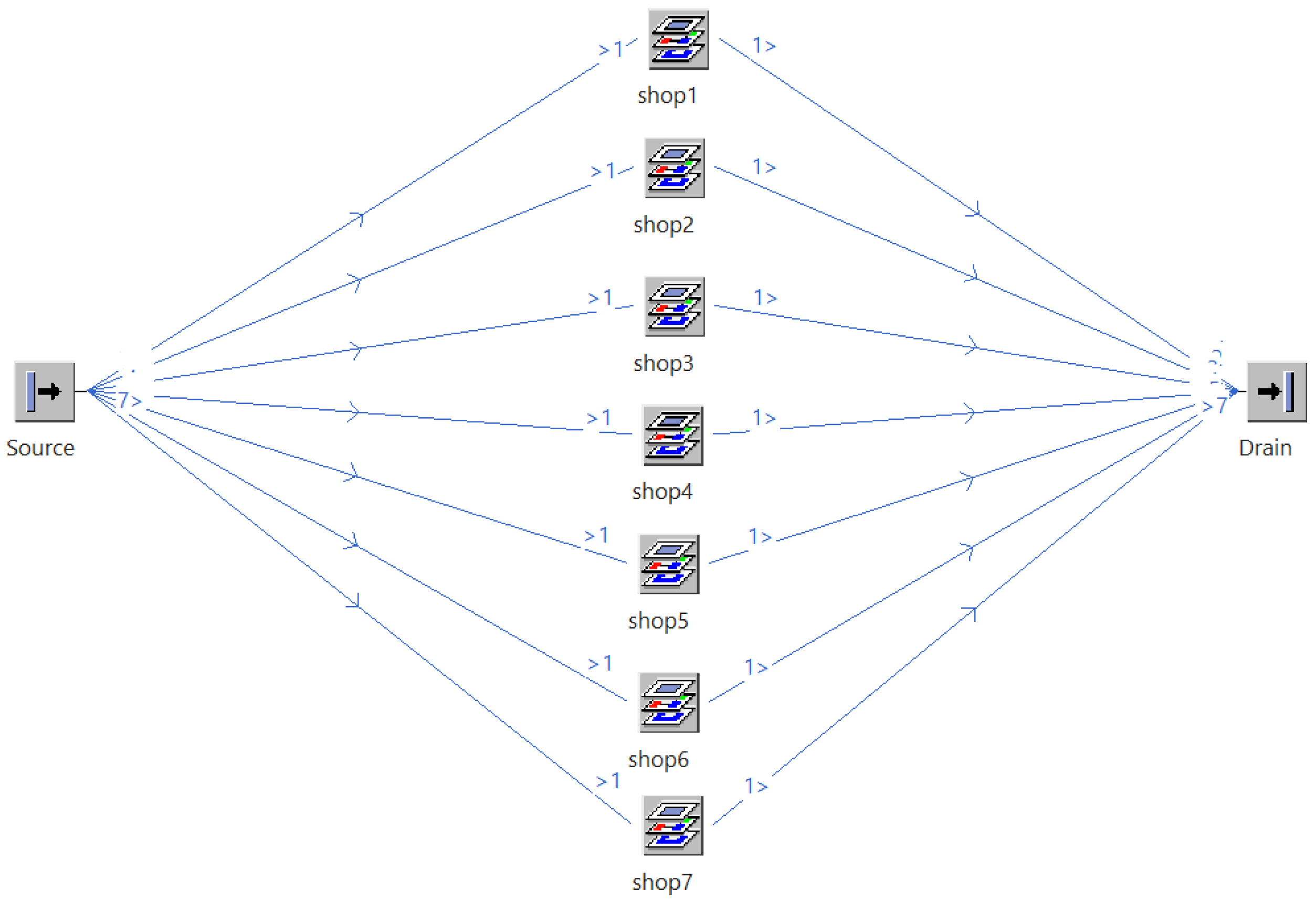
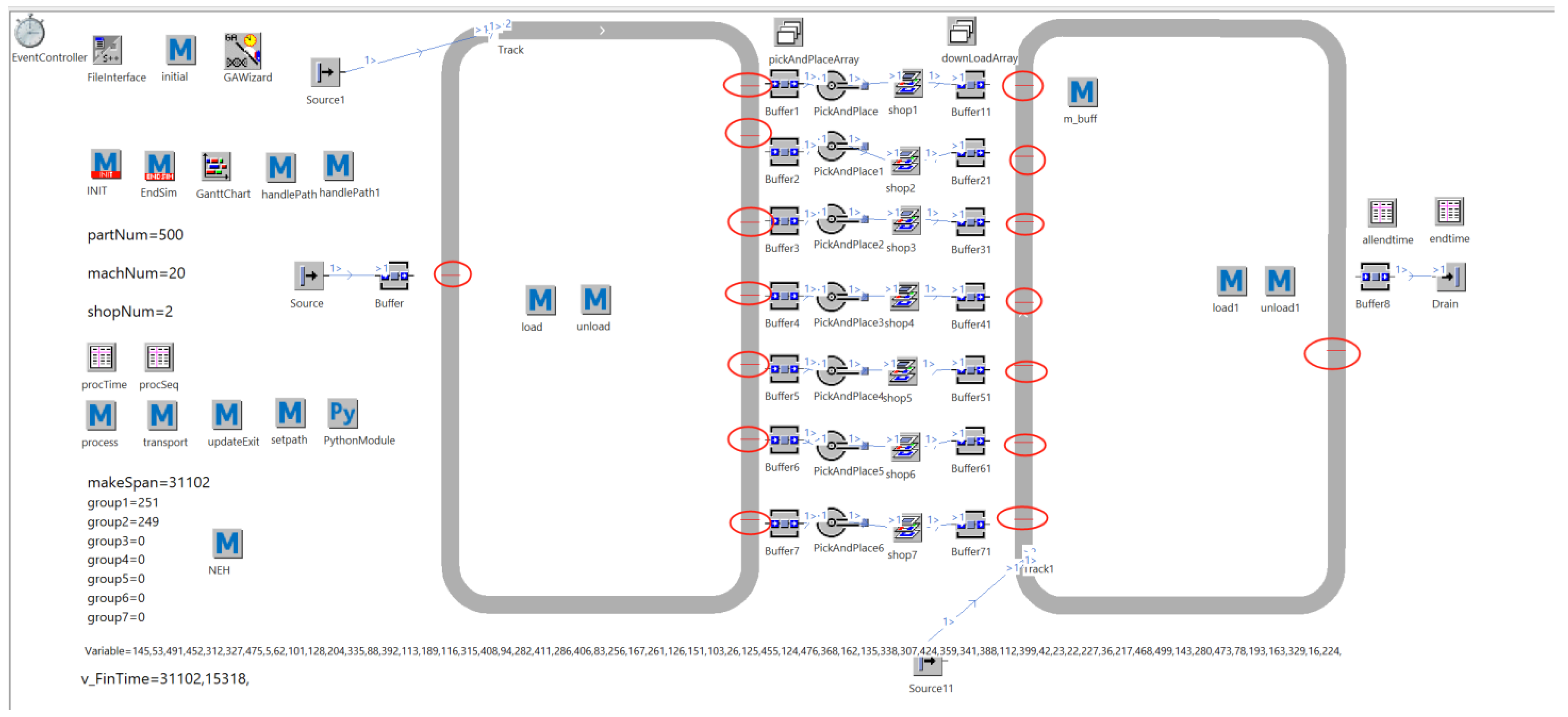
3.1. DPFSP Model Construction
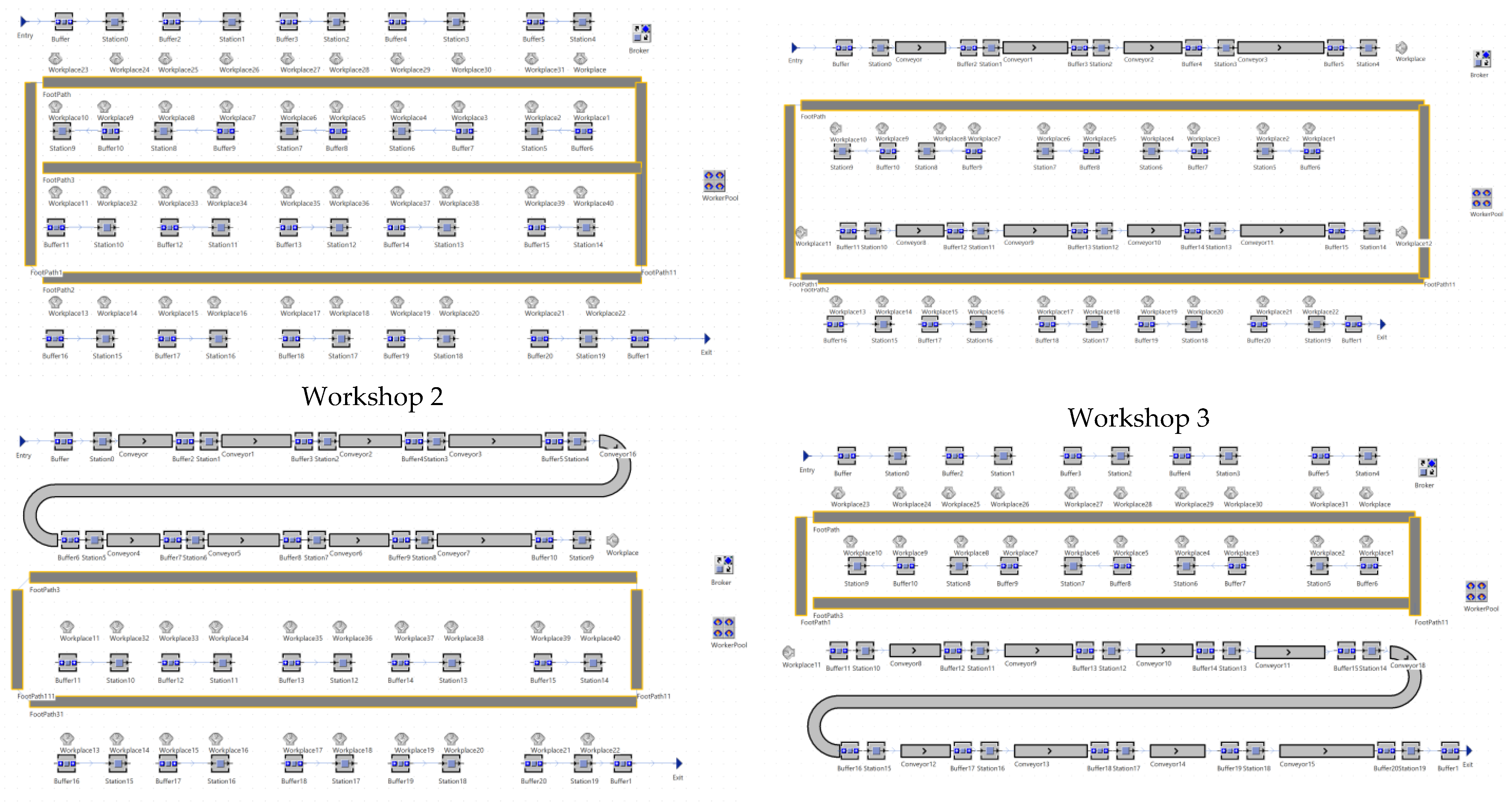
3.2. MSRDPFSP Model Construction
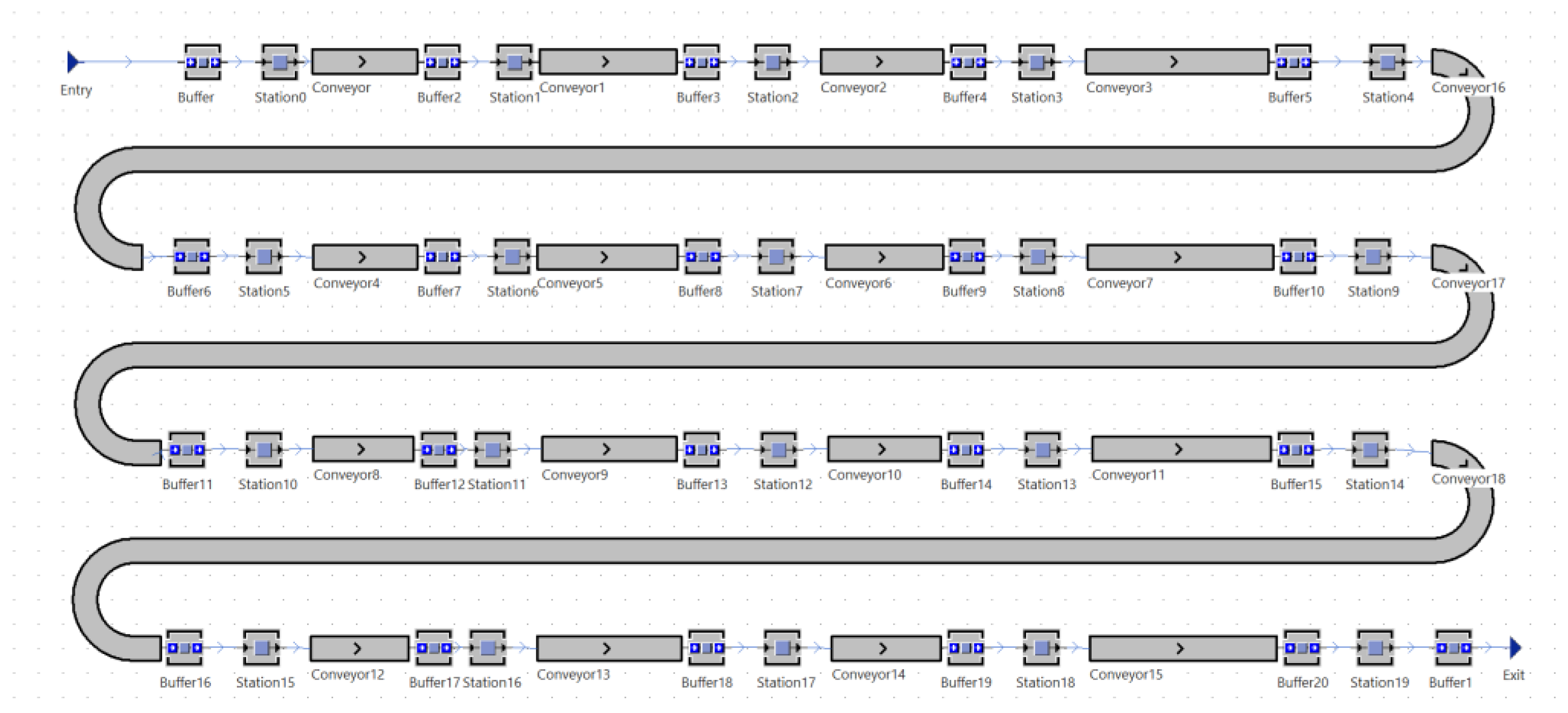
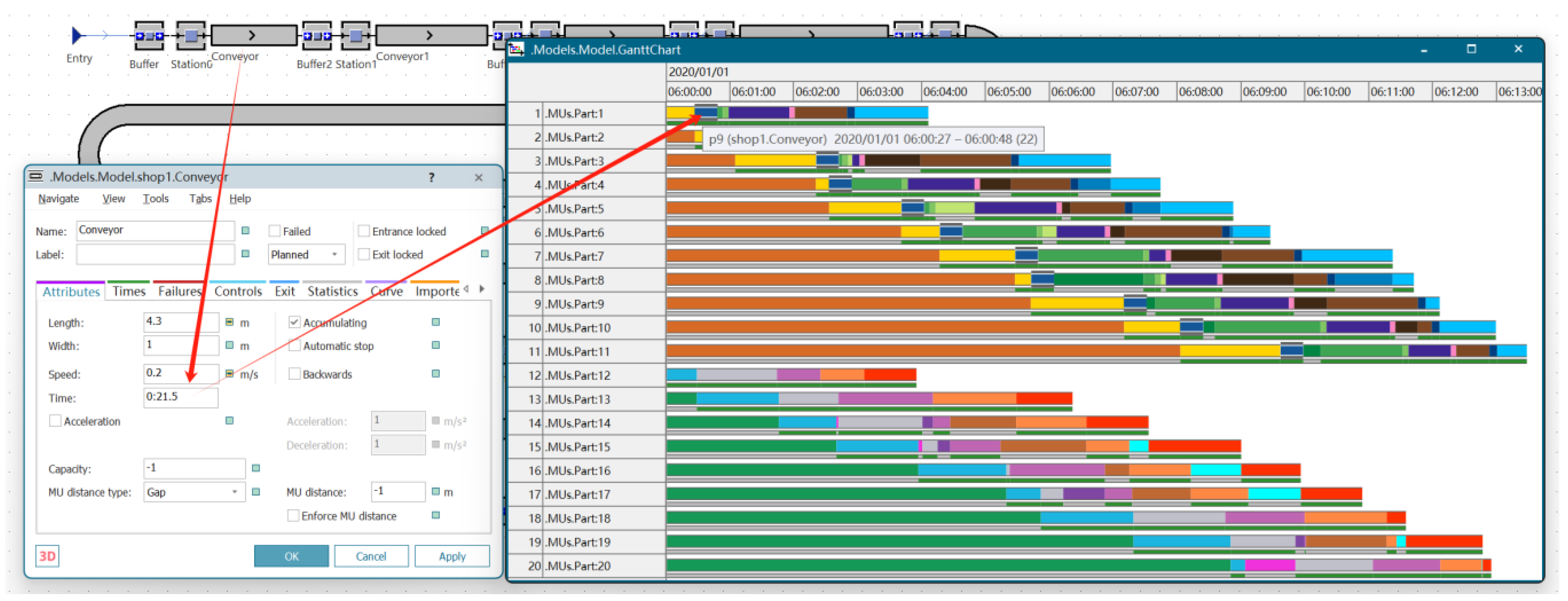
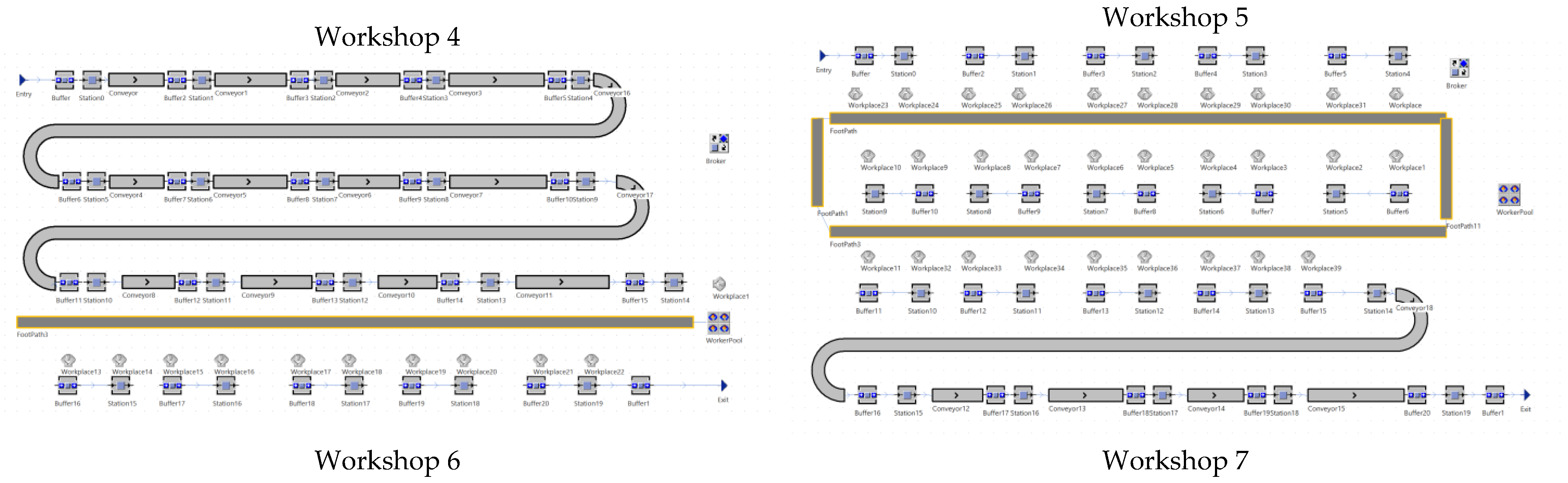
3.2.1. Conveyor Belt Workshop Construction
3.2.2. Workshop Construction for Workers
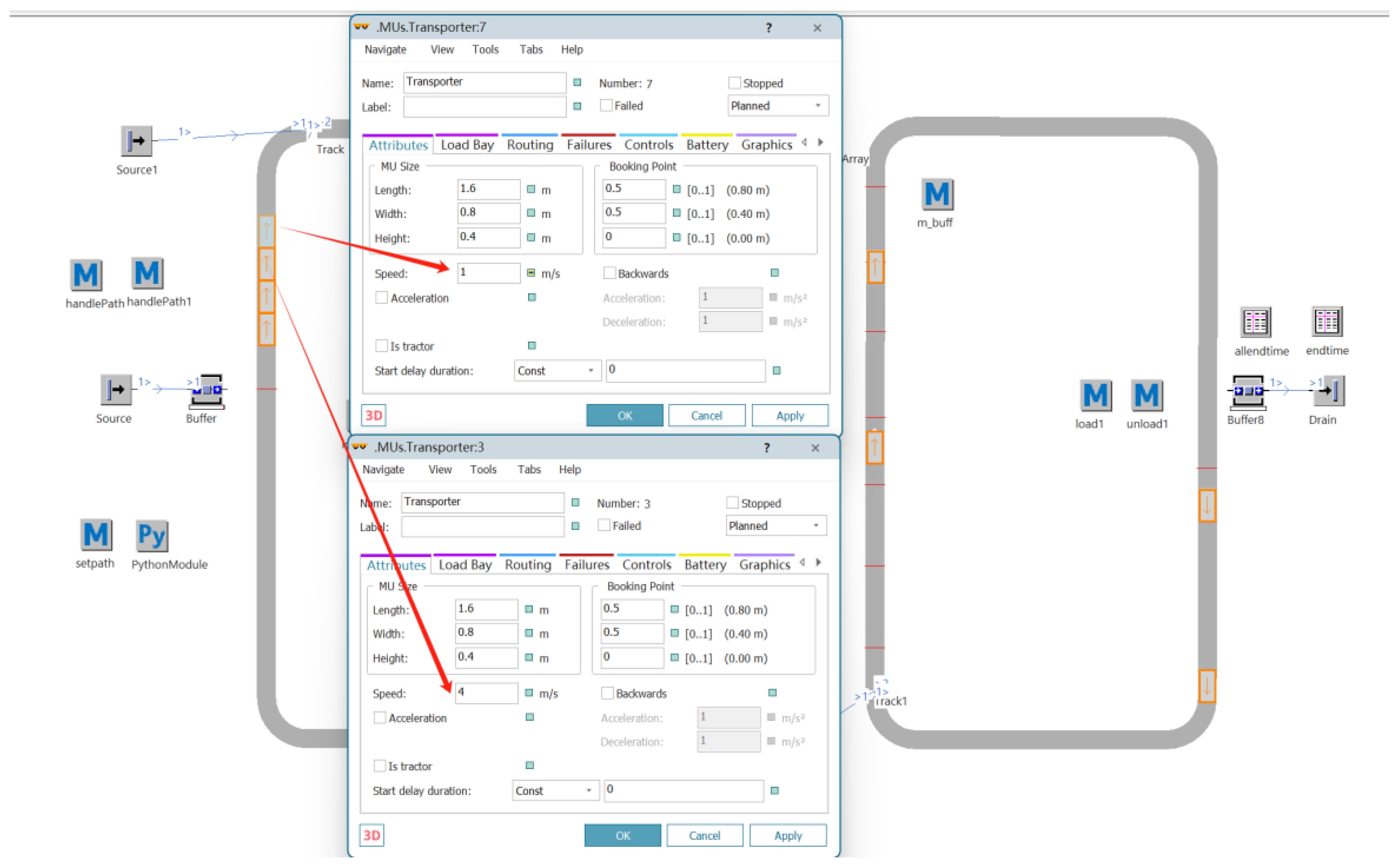
3.2.3. AGV Carts and Robotic Arms and Path Setting
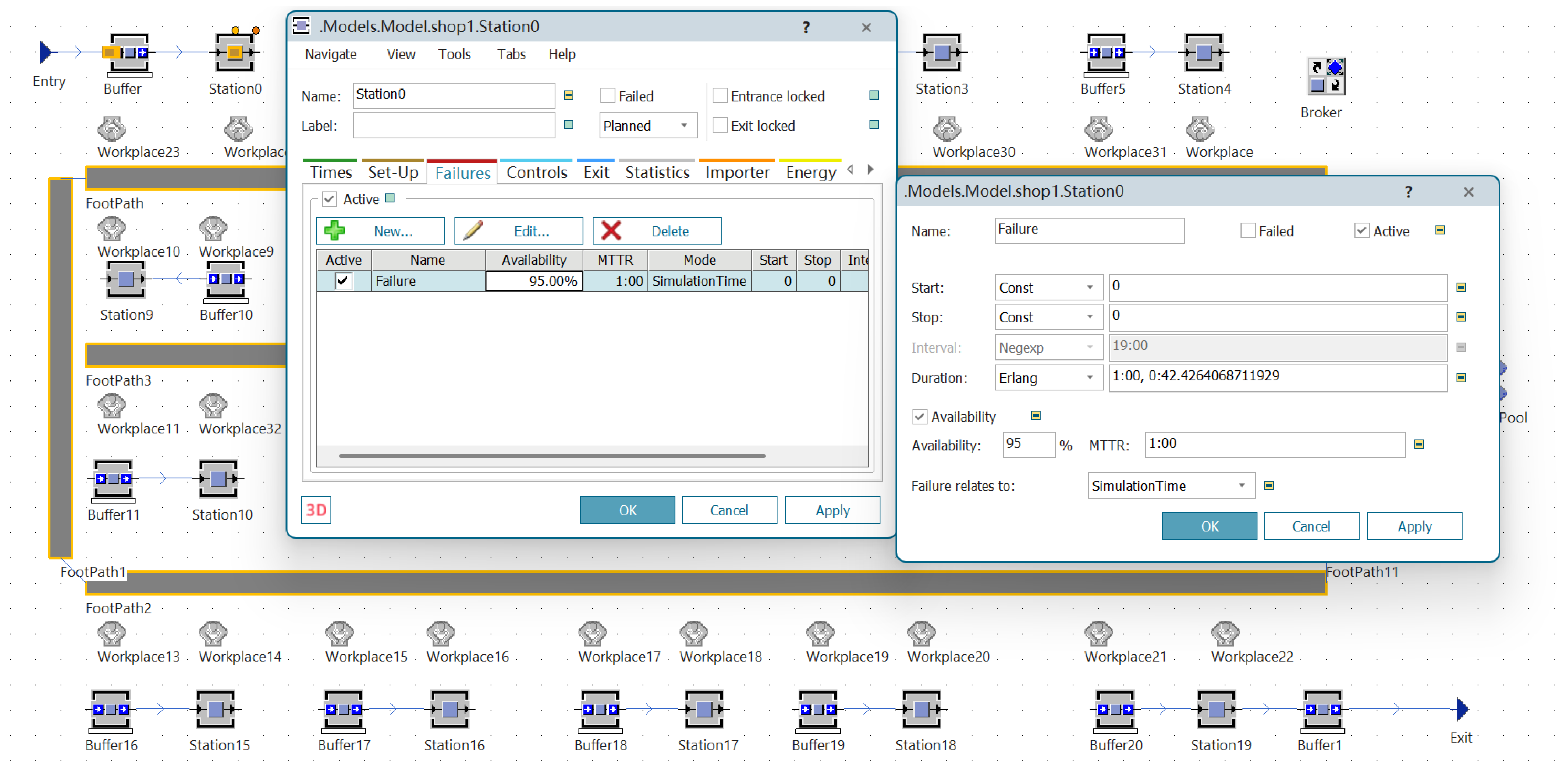
3.2.4. MTTR and Statistics Function Settings
3.2.5. Statistical Modules and Summaries
4. Algorithm Design
4.1. Search Strategy
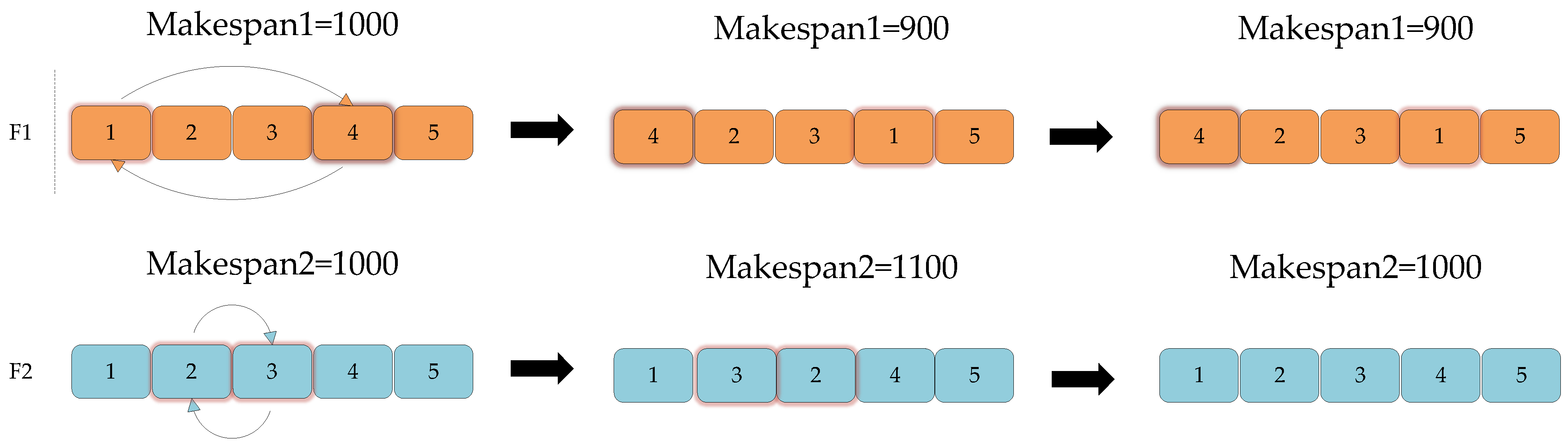
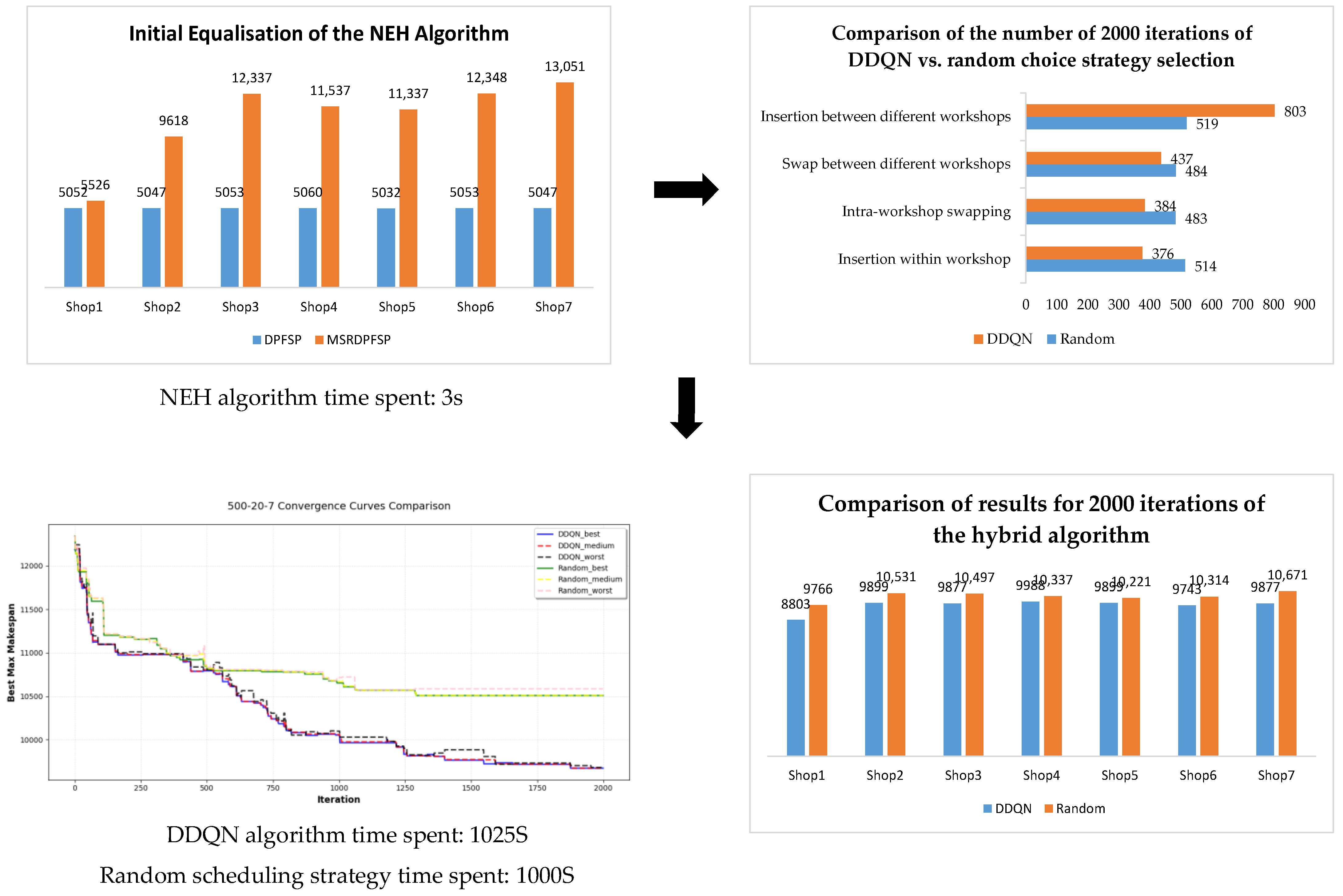
- Insertion within workshop: It is executed for all workshops. A set of consecutive sequences within a workshop are randomly selected and inserted into a random position in that workshop. If there is optimization, the optimized sequences are returned; otherwise, the pre-optimized sequences are returned, as shown in Figure 15 below.
- Intra-workshop swapping: It is executed for all workshops. A set of consecutive sequences within a workshop are randomly selected to recombine their positions, and the optimized sequence is returned if there is an optimization; otherwise, the pre-optimized sequence is returned, as shown in Figure 16 below.
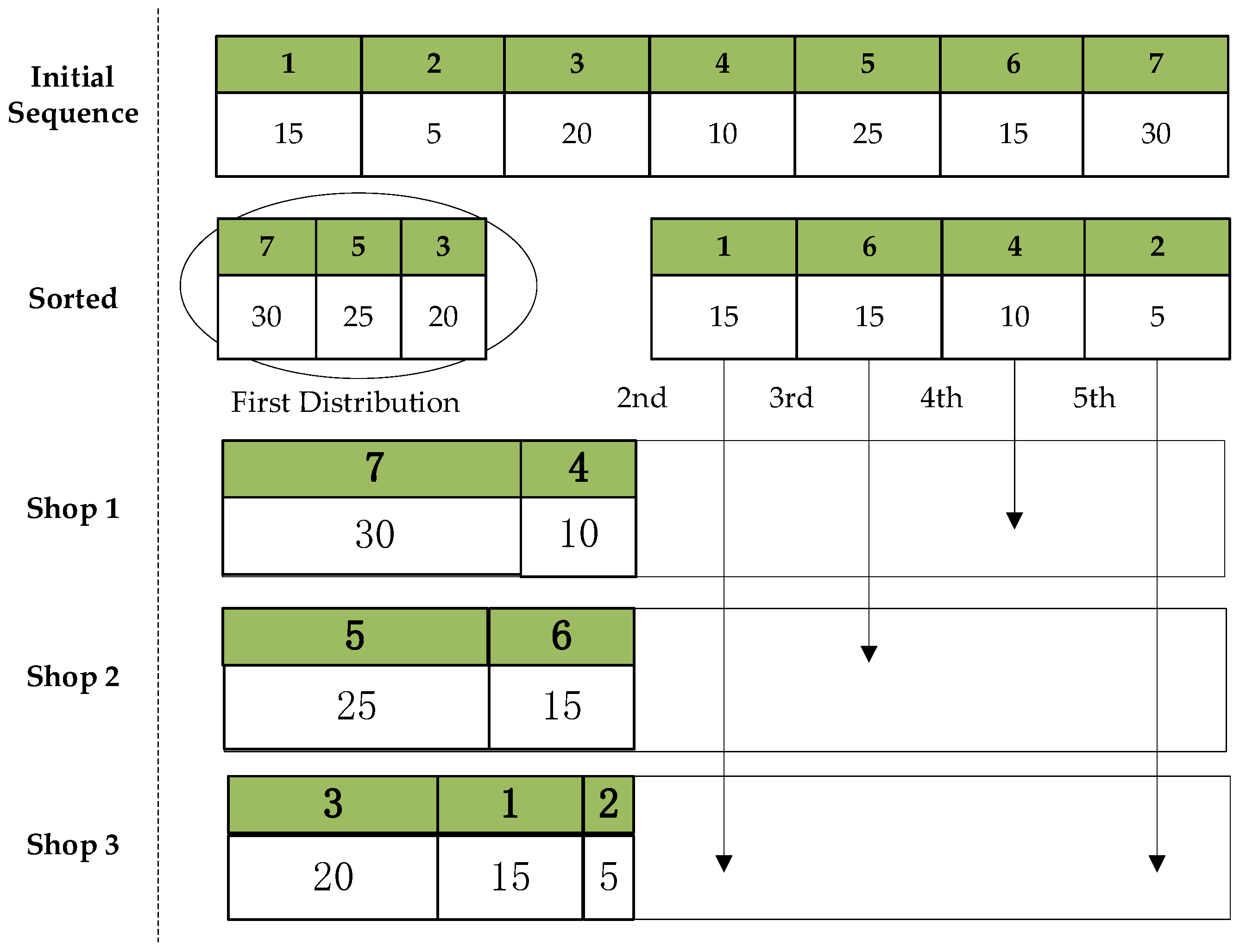
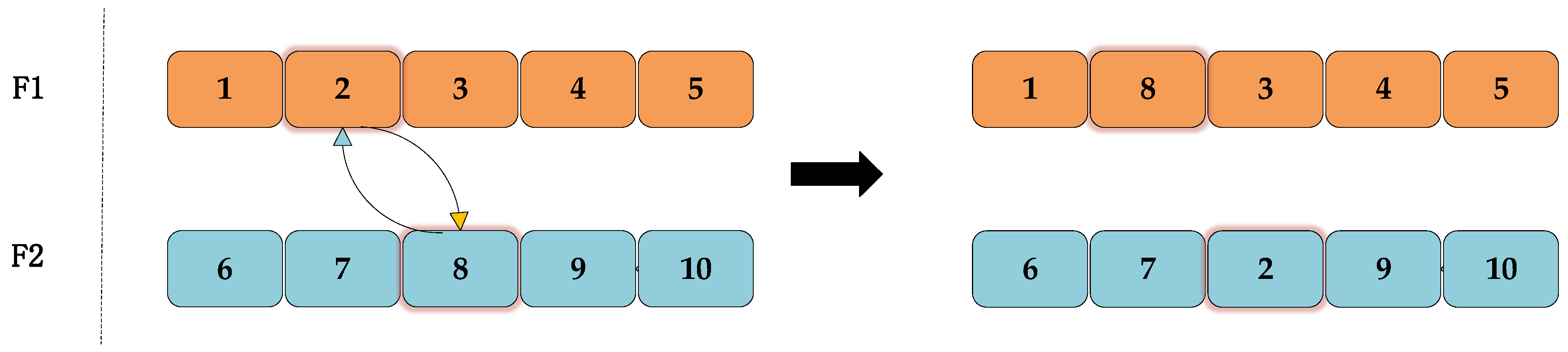
- Swap between different workshops: All workshops are sorted in terms of elapsed time. Specifically, a set of consecutive sequences in the workshop with the longest elapsed time are chosen to be swapped with the same number of consecutive random sequences in another random workshop. If there is an optimization, the optimized sequences are returned; otherwise, the pre-optimized sequences are returned, as shown in Figure 17 below.
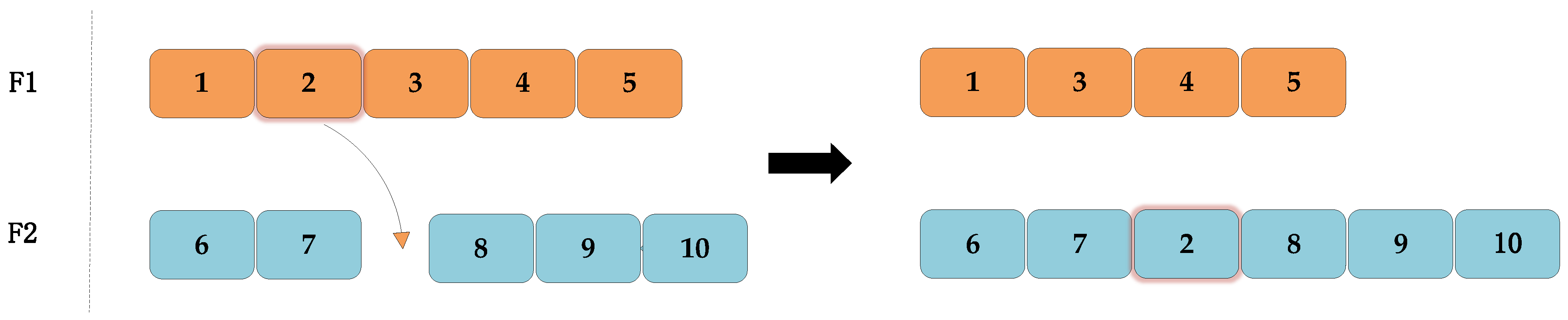
- Insertion between different workshops: All workshops are sorted in terms of elapsed time. Multiple tasks within the workshop taking the longest time are selected and inserted into other workshops with a short elapsed time. If there is an optimization, the optimized sequence is returned; otherwise, the pre-optimized sequence is returned, as shown in Figure 18 below.
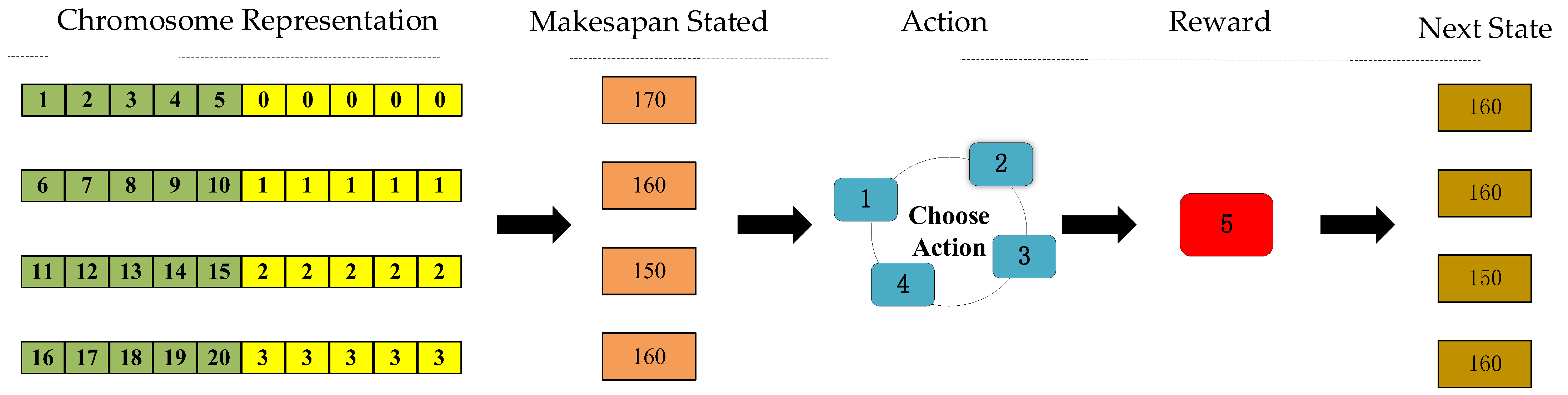
4.2. Reward Function and Update Strategy Design
4.3. DDQN Neural Network Design
4.4. Joint Communications Establishment
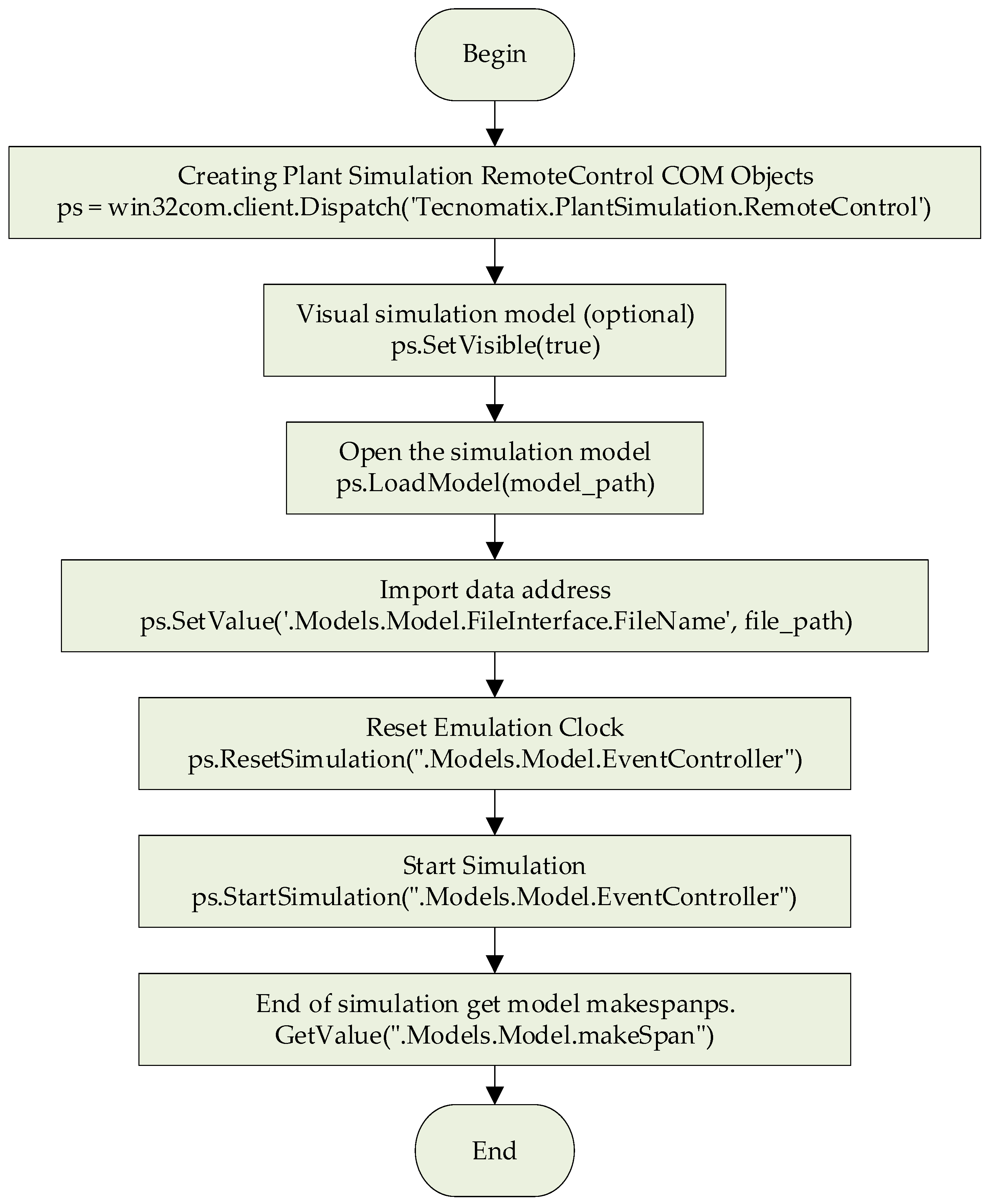
4.4.1. Joint Calls Via COM Interfaces
4.4.2. Joint Calls Via DLL
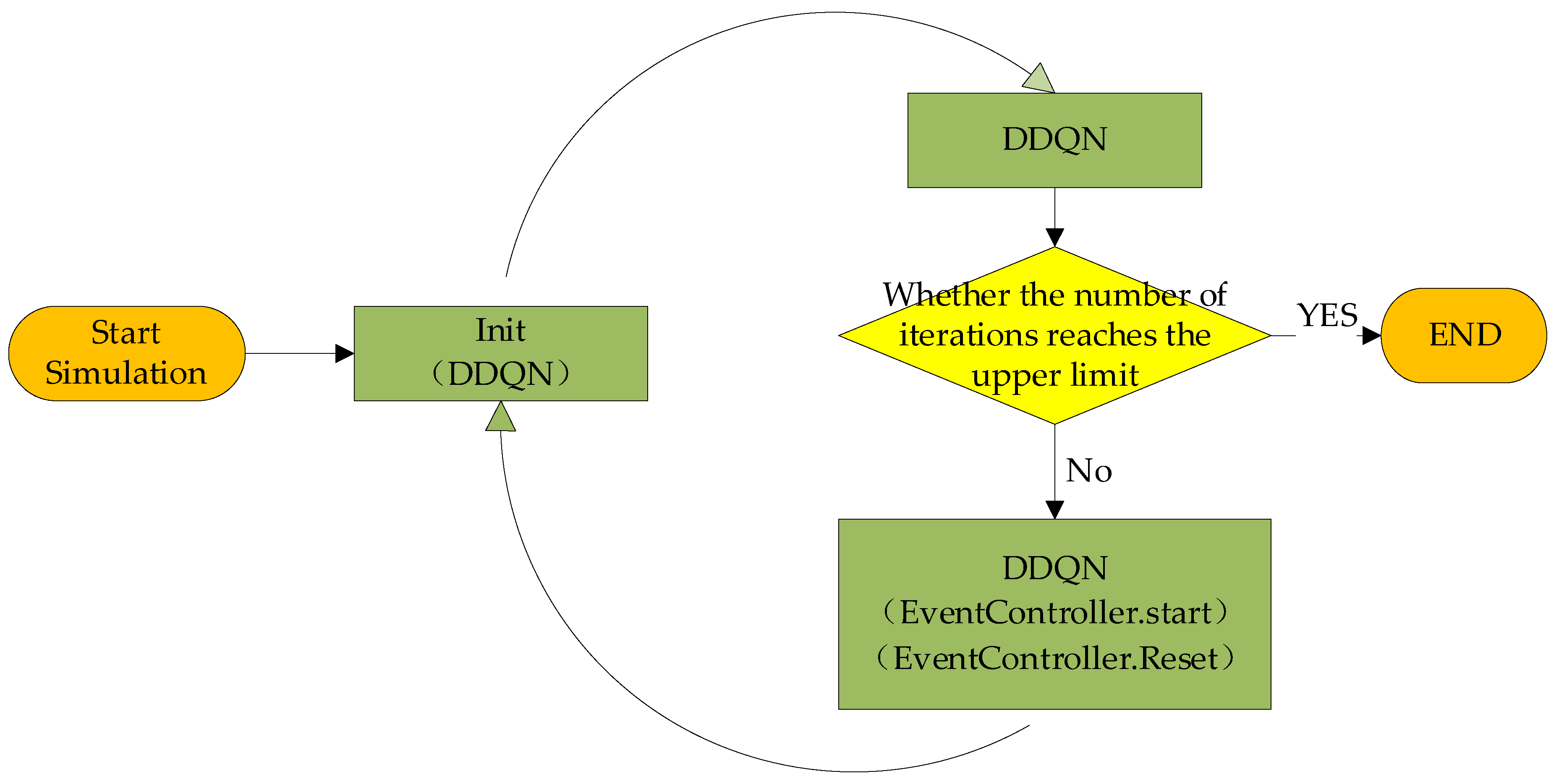
4.5. Algorithm Flow
5. Experiments
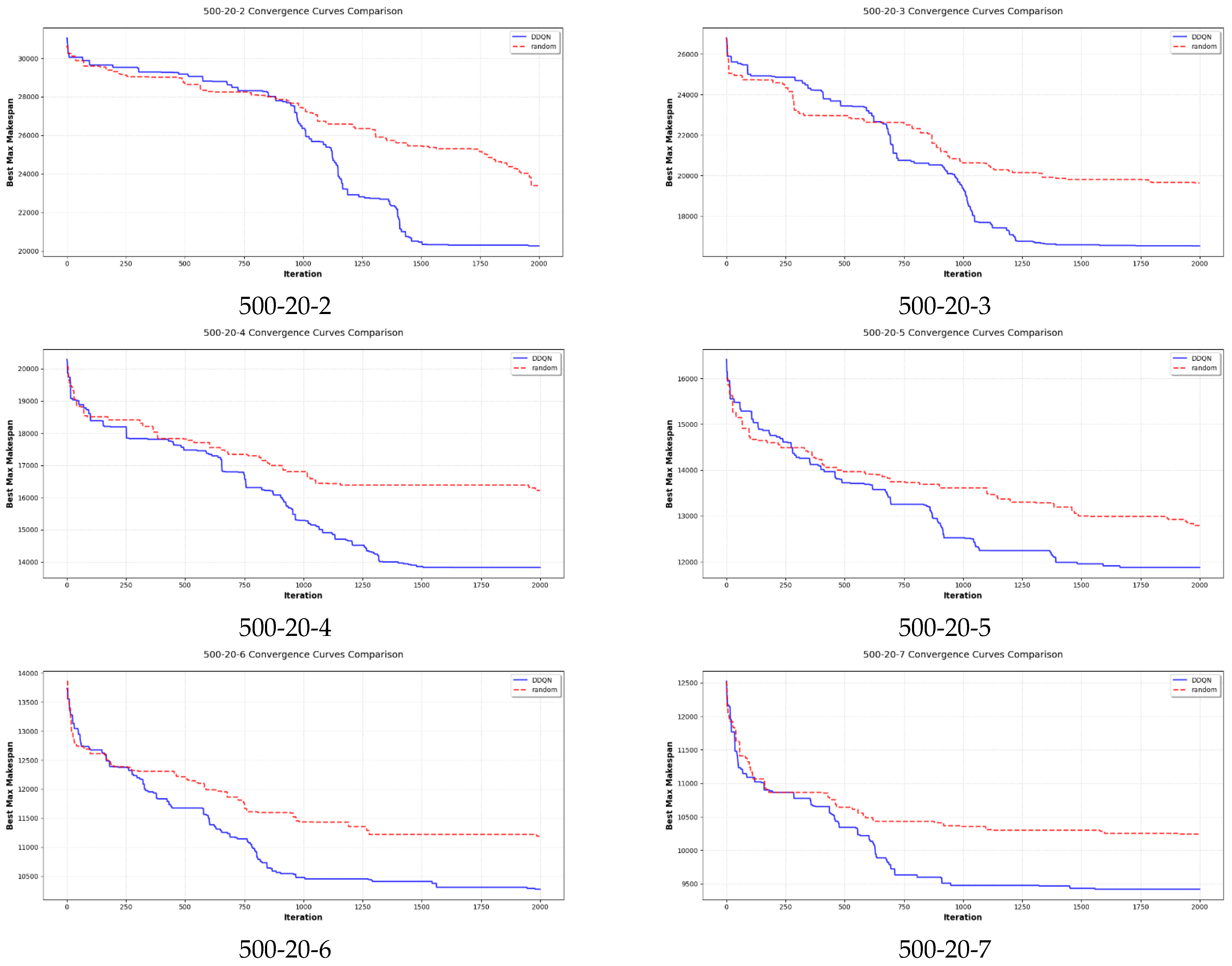
5.1. DDQN Performance Evaluation for DPFSP
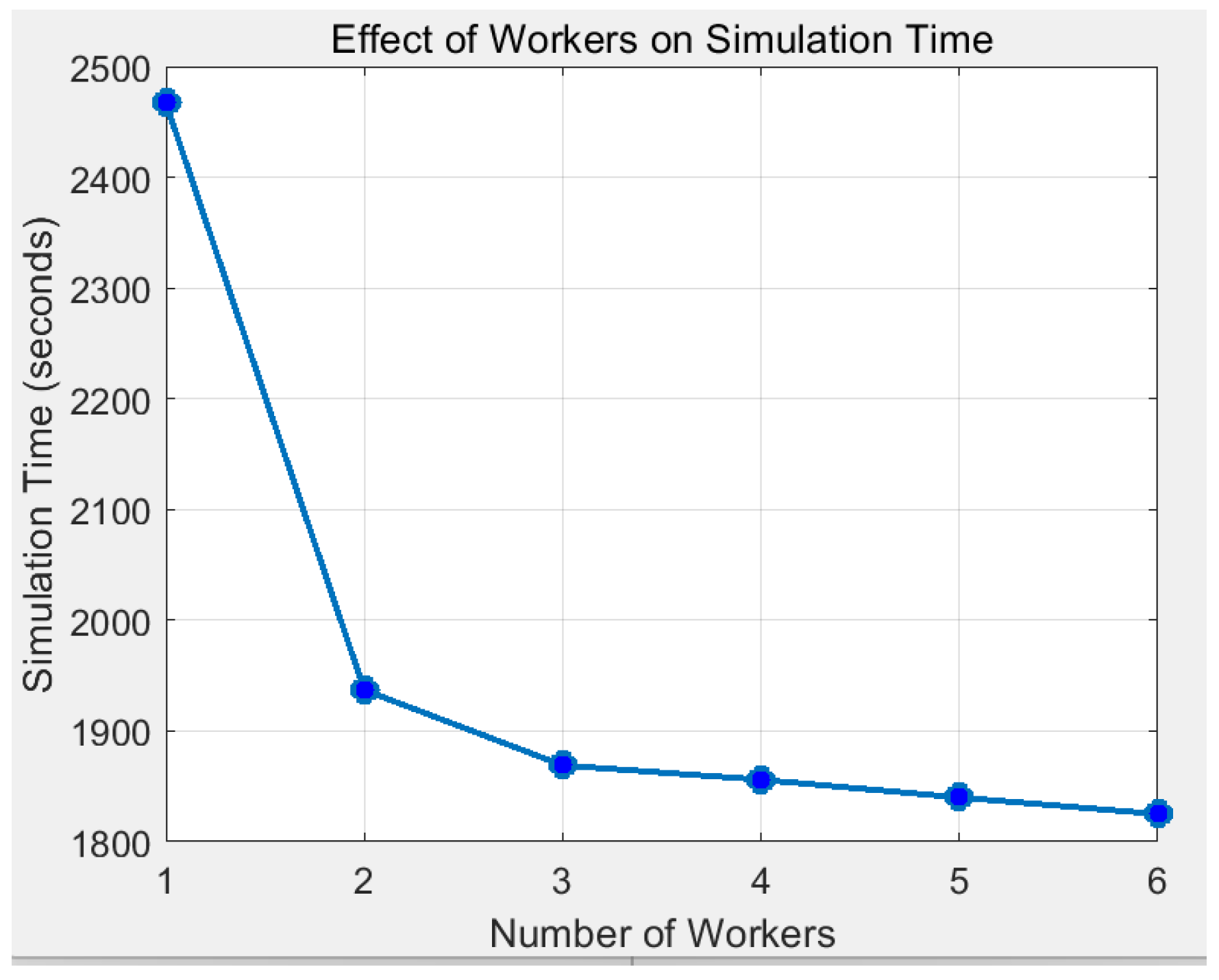
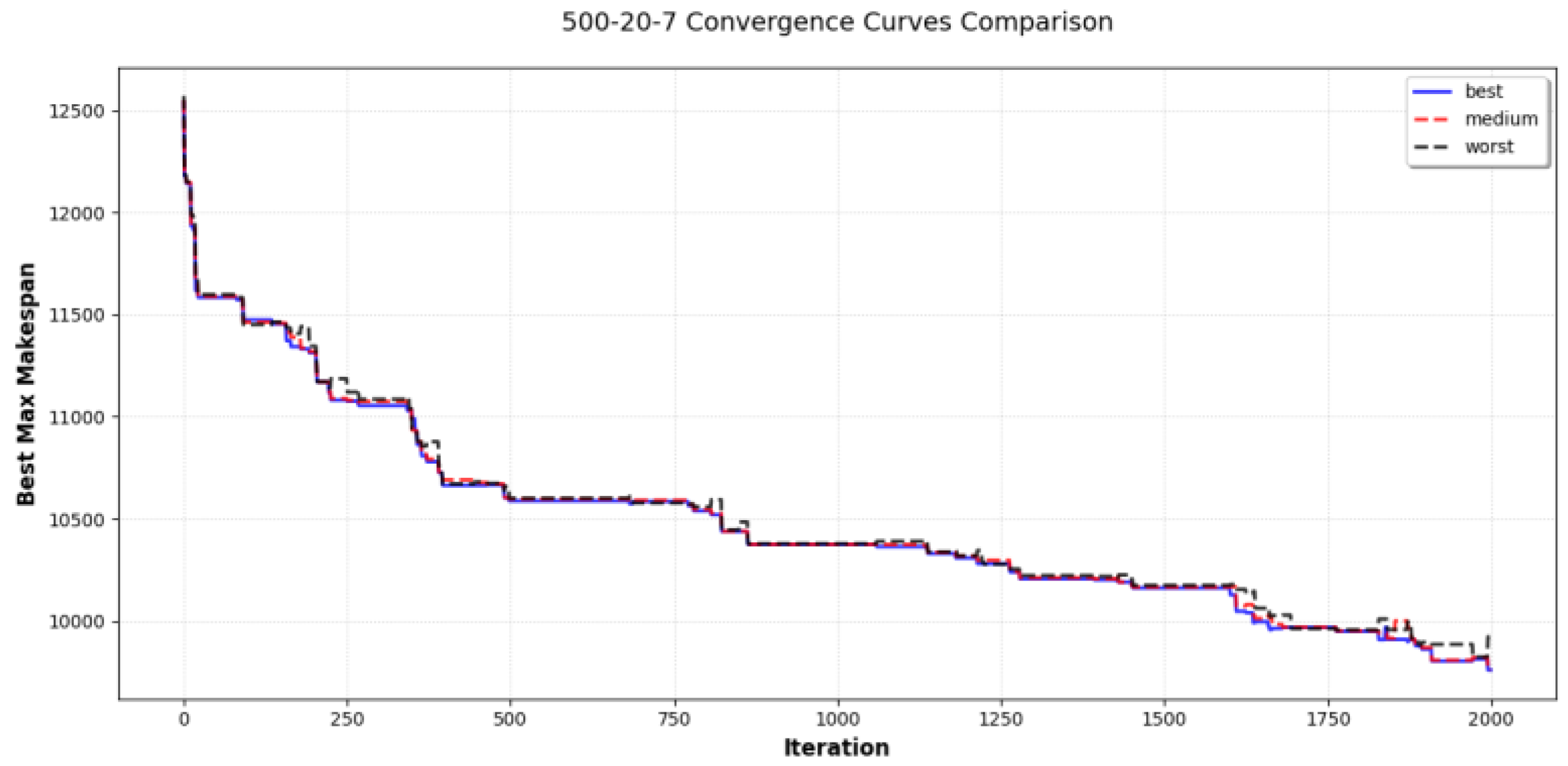
5.2. DDQN Performance Evaluation for MSRDPFSP
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DPFSP | Distributed Replacement Flow Shop Scheduling |
| PFSP | Scheduling problem of replacement flow workshop |
| MAKESPAN | The total completion time |
| MSRDPFSP | Robust Distributed Displacement Flow Shop Scheduling for Multiple Scenarios |
| NEH | A heuristic search method |
| DQN | Deep Reinforcement Learning |
| DDQN | Double Deep Enhanced Learning |
| COM | Component Object Model |
| DLL | Dynamic-link Library |
References
- Ghobakhloo, M. Industry 4.0, digitization, and opportunities for sustainability. J. Clean. Prod. 2020, 252, 119869. [Google Scholar] [CrossRef]
- Zimmermann, A.; Schmidt, R.; Sandkuhl, K.; Wißotzki, M.; Jugel, D.; Möhring, M. Digital enterprise architecture-transformation for the internet of things. In Proceedings of the IEEE 19th International Enterprise Distributed Object Computing Workshop, Adelaide, Australia, 21–25 September 2015; pp. 130–138. [Google Scholar]
- Naderi, B.; Ruiz, R. The distributed permutation flowshop scheduling problem. Comput. Oper. Res. 2010, 37, 754–768. [Google Scholar] [CrossRef]
- Ruiz, R.; Vázquez-Rodríguez, J.A. The hybrid flow shop scheduling problem. Eur. J. Oper. Res. 2010, 205, 1–18. [Google Scholar] [CrossRef]
- Xiong, H.; Fan, H.; Jiang, G.; Li, G. Asimulation-based study of dispatching rules in a dynamic job shop scheduling problem with batch release and extended technical precedence constraints. Eur. J. Oper. Res. 2017, 257, 13–24. [Google Scholar] [CrossRef]
- Deng, J.; Wang, L. A competitive memetic algorithm for multi-objective distributed permutation flow shop scheduling problem. Swarm Evol. Comput. 2017, 32, 121–131. [Google Scholar] [CrossRef]
- Lu, P.H.; Wu, M.C.; Tan, H.; Peng, Y.H.; Chen, C.F. A genetic algorithm embedded with a concise chromosome representation for distributed and flexible job-shop scheduling problems. J. Intell. Manuf. 2018, 29, 19–34. [Google Scholar] [CrossRef]
- Ruiz, R.; Pan, Q.K.; Naderi, B. Iterated Greedy methods for the distributed permutation flowshop scheduling problem. Omega 2019, 83, 213–222. [Google Scholar] [CrossRef]
- Gogos, C. Solving the Distributed Permutation Flow-Shop Scheduling Problem Using Constrained Programming. Appl. Sci. 2023, 13, 12562. [Google Scholar] [CrossRef]
- Li, Q.Y.; Pan, Q.K.; Sang, H.Y.; Jing, X.L.; Framiñán, J.M.; Li, W.M. Self-adaptive population-based iterated greedy algorithm for distributed permutation flowshop scheduling problem with part of jobs subject to a common deadline constraint. Expert Syst. Appl. 2024, 248, 123278. [Google Scholar] [CrossRef]
- Zhao, A.; Liu, P. Q-Learning-Based Priority Dispatching Rule Preference Model for Non-Permutation Flow Shop. J. Adv. Manuf. Syst. 2024, 23, 601–612. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, B.; Hu, R.; Yang, Y.; Chen, W. Deep Reinforcement Learning for Solving Distributed Permutation Flow Shop Scheduling Problem. In Advanced Intelligent Computing Technology and Applications, Proceedings of the 19th International Conference, ICIC 2023, Zhengzhou, China, 10–13 August 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 333–342. [Google Scholar]
- Meng, T.; Pan, Q.K.; Wang, L. A distributed permutation flowshop scheduling problem with the customer order constraint. Knowl.-Based Syst. 2019, 184, 104894. [Google Scholar] [CrossRef]
- Wang, B.; Wang, X.; Lan, F.; Pan, Q. A hybrid local-search algorithm for robust job-shop scheduling under scenarios. Appl. Soft Comput. 2018, 62, 259–271. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, J. A dual-population genetic algorithm with Q-learning for multi-objective distributed hybrid flow shop scheduling problem. Symmetry 2023, 15, 836. [Google Scholar] [CrossRef]
- Zhou, T.; Luo, L.; Ji, S.; He, Y. A reinforcement learning approach to robust scheduling of permutation flow shop. Biomimetics 2023, 8, 478. [Google Scholar] [CrossRef]
- Waubert de Puiseau, C.; Meyes, R.; Meisen, T. On reliability of reinforcement learning based production scheduling systems: A comparative survey. J. Intell. Manuf. 2022, 33, 911–927. [Google Scholar] [CrossRef]
- Souza, R.L.C.; Ghasemi, A.; Saif, A.; Gharaei, A. Robust job-shop scheduling under deterministic and stochastic unavailability constraints due to preventive and corrective maintenance. Comput. Ind. Eng. 2022, 168, 108130. [Google Scholar] [CrossRef]
- Luo, L.; Yan, X. Scheduling of stochastic distributed hybrid flow-shop by hybrid estimation of distribution algorithm and proximal policy optimization. Expert Syst. Appl. 2025, 271, 126523. [Google Scholar] [CrossRef]
- Gu, W.; Liu, S.; Guo, Z.; Yuan, M.; Pei, F. Dynamic scheduling mechanism for intelligent workshop with deep reinforcement learning method based on multi-agent system architecture. Comput. Ind. Eng. 2024, 191, 110155. [Google Scholar] [CrossRef]
- Malega, P.; Daneshjo, N. Increasing the production capacity of business processes using plant simulation. Int. J. Simul. Model. 2024, 23, 41–52. [Google Scholar] [CrossRef]
- Fedorko, G.; Molnár, V.; Strohmandl, J.; Horváthová, P.; Strnad, D.; Cech, V. Research on using the tecnomatix plant simulation for simulation and visualization of traffic processes at the traffic node. Appl. Sci. 2022, 12, 12131. [Google Scholar] [CrossRef]
- Sobrino, D.R.D.; Ružarovský, R.; Václav, Š.; Caganova, D.; Rychtárik, V. Developing simulation approaches: A simple case of emulation for logic validation using tecnomatix plant simulation. J. Phys. Conf. Ser. 2022, 2212, 012011. [Google Scholar] [CrossRef]
- Zhao, W.B.; Hu, J.H.; Tang, Z.Q. Virtual Simulation-Based Optimization for Assembly Flow Shop Scheduling Using Migratory Bird Algorithm. Biomimetics 2024, 9, 571. [Google Scholar] [CrossRef] [PubMed]
- Pekarcikova, M.; Trebuna, P.; Kliment, M.; Schmacher, B.A.K. Milk run testing through Tecnomatix plant simulation software. Int. J. Simul. Model. 2022, 21, 101–112. [Google Scholar] [CrossRef]
- Afizul, N.A.; Selimin, M.A.; Pagan, N.A.; Yinn, N.K. Modelling an assembly line using tecnomatix plant simulation software. Res. Manag. Technol. Bus. 2024, 5, 1048–1055. [Google Scholar]
- Wesch, J.O. An Implementation Strategy for Tecnomatix Plant Simulation Software. Master’s Thesis, North-West University, Potchefstroom, South Africa, 2022. [Google Scholar]
- Komaki, G.M.; Sheikh, S.; Malakooti, B. Flow shop scheduling problems with assembly operations: A review and new trends. Int. J. Prod. Res. 2019, 57, 2926–2955. [Google Scholar] [CrossRef]
- Siderska, J. Application of tecnomatix plant simulation for modeling production and logistics processes. Bus. Manag. Educ. 2016, 14, 64–73. [Google Scholar] [CrossRef]
- Bangsow, S. Tecnomatix Plant Simulation; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Kikolski, M. Identification of production bottlenecks with the use of plant simulation software. Econ. Manag./Ekon. Zarz. 2016, 8, 103–112. [Google Scholar] [CrossRef]
- Gao, J.; Chen, R. An NEH-based heuristic algorithm for distributed permutation flowshop scheduling problems. Sci. Res. Essays 2011, 6, 3094–3100. [Google Scholar]
- del Real Torres, A.; Andreiana, D.S.; Ojeda Roldán, Á.; Bustos, A.H.; Galicia, L.E.A. A review of deep reinforcement learning approaches for smart manufacturing in industry 4.0 and 5.0 framework. Appl. Sci. 2022, 12, 12377. [Google Scholar] [CrossRef]
- Han, B.A.; Yang, J.J. Research on adaptive job shop scheduling problems based on dueling double DQN. IEEE Access 2020, 8, 186474–186495. [Google Scholar] [CrossRef]
- Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent manufacturing in the context of industry 4.0: A review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
- Malega, P.; Gazda, V.; Rudy, V. Optimization of production system in plant simulation. Simulation 2022, 98, 295–306. [Google Scholar] [CrossRef]
- Mraihi, T.; Driss, O.B.; El-Haouzi, H.B. Distributed permutation flow shop scheduling problem with worker flexibility: Review, trends and model proposition. Expert Syst. Appl. 2024, 238, 121947. [Google Scholar] [CrossRef]
- Luo, Q.; Deng, Q.; Gong, G.; Guo, X.; Liu, X. A distributed flexible job shop scheduling problem considering worker arrangement using an improved memetic algorithm. Expert Syst. Appl. 2022, 207, 117984. [Google Scholar] [CrossRef]
- Hu, H.; Jia, X.; He, Q.; Liu, K.; Fu, S. Deep reinforcement learning based AGVs real-time scheduling with mixed rule for flexible shop floor in industry 4.0. Comput. Ind. Eng. 2020, 149, 106749. [Google Scholar] [CrossRef]
- Chen, K.; Bi, L.; Wang, W. Research on integrated scheduling of AGV and machine in flexible job shop. J. Syst. Simul. 2022, 34, 461–469. [Google Scholar]
- Holthaus, O. Scheduling in job shops with machine breakdowns: An experimental study. Comput. Ind. Eng. 1999, 36, 137–162. [Google Scholar] [CrossRef]
- Fernandez -Viagas, V.; Framinan, J.M. NEH-based heuristics for the permutation flowshop scheduling problem to minimise total tardiness. Comput. Oper. Res. 2015, 60, 27–36. [Google Scholar] [CrossRef]
- Salh, A.; Audah, L.; Alhartomi, M.A.; Kim, K.S.; Alsamhi, S.H.; Almalki, F.A. Smart packet transmission scheduling in cognitive IoT systems: DDQN based approach. IEEE Access 2022, 10, 50023–50036. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Li, Q.; He, Y.; Sun, L.; Sun, Y.; Zhao, P.; Jia, L. Research on Application Automation Operations Based on Win32com. In Advances in Artificial Intelligence, Big Data and Algorithms; IOS Press: Amsterdam, The Netherland, 2023; pp. 113–118. [Google Scholar]
- Towers, M.; Kwiatkowski, A.; Terry, J.; Balis, J.U.; De Cola, G.; Deleu, T.; Goulão, M.; Kallinteris, A.; Krimmel, M.; Arjun, K.G.; et al. Gymnasium: A standard interface for reinforcement learning environments. arXiv 2024, arXiv:2407.17032. [Google Scholar]
- Schäfer, G.; Schirl, M.; Rehrl, J.; Huber, S.; Hirlaender, S. Python-Based Reinforcement Learning on Simulink Models. In Proceedings of the International Conference on Soft Methods in Probability and Statistics, Salzburg, Austria, 3–6 September 2024; Springer Nature: Cham, Switzerland, 2024; pp. 449–456. [Google Scholar]




| Number of Workpieces | Number of Machines | Number of Workshops |
|---|---|---|
| 20 | 5, 10, 20 | 2, 3, 4, 5, 6, 7 |
| 50 | 5, 10, 20 | 2, 3, 4, 5, 6, 7 |
| 100 | 5, 10, 20 | 2, 3, 4, 5, 6, 7 |
| 200 | 10, 20 | 2, 3, 4, 5, 6, 7 |
| 500 | 20 | 2, 3, 4, 5, 6, 7 |
| N × M × F | Time | N × M × F | Time |
|---|---|---|---|
| 100 × 5 × 7 | 0.03 s | 100 × 5 × 2 | 0.03 s |
| 100 × 10 × 7 | 0.04 s | 100 × 10 × 2 | 0.04 s |
| 100 × 20 × 7 | 0.04 s | 100 × 20 × 2 | 0.06 s |
| 200 × 10 × 7 | 0.05 s | 200 × 10 × 2 | 0.06 s |
| 200 × 20 × 7 | 0.08 s | 200 × 20 × 2 | 0.11 s |
| 500 × 20 × 7 | 0.18 s | 500 × 20 × 2 | 0.26 s |
| N × M × F | DDQN | NEH | N × M × F | DDQN | NEH |
|---|---|---|---|---|---|
| 100 × 5 × 2 | 0.74 | 7.24 | 200 × 10 × 2 | 0.86 | 6.12 |
| 100 × 5 × 3 | 0.50 | 5.43 | 200 × 10 × 3 | 1.85 | 6.93 |
| 100 × 5 × 4 | 0.38 | 4.41 | 200 × 10 × 4 | 1.91 | 5.82 |
| 100 × 5 × 5 | 1.35 | 7.80 | 200 × 10 × 5 | 1.91 | 5.54 |
| 100 × 5 × 6 | 1.71 | 7.83 | 200 × 10 × 6 | 2.28 | 5.60 |
| 100 × 5 × 7 | 1.32 | 6.24 | 200 × 10 × 7 | 2.60 | 5.11 |
| 100 × 10 × 2 | 0.72 | 5.15 | 200 × 20 × 2 | 0.29 | 5.28 |
| 100 × 10 × 3 | 1.93 | 6.87 | 200 × 20 × 3 | 0.08 | 2.83 |
| 100 × 10 × 4 | 2.14 | 6.31 | 200 × 20 × 4 | 0.08 | 1.84 |
| 100 × 10 × 5 | 1.89 | 5.69 | 200 × 20 × 5 | 1.62 | 8.17 |
| 100 × 10 × 6 | 2.52 | 6.06 | 200 × 20 × 6 | 1.84 | 7.91 |
| 100 × 10 × 7 | 2.34 | 4.95 | 200 × 20 × 7 | 1.23 | 6.26 |
| 100 × 20 × 2 | 0.73 | 6.67 | 500 × 20 × 2 | 0.84 | 6.40 |
| 100 × 20 × 3 | 0.17 | 3.31 | 500 × 20 × 3 | 2.10 | 6.86 |
| 100 × 20 × 4 | 0.19 | 3.89 | 500 × 20 × 4 | 1.81 | 6.03 |
| 100 × 20 × 5 | 1.36 | 7.88 | 500 × 20 × 5 | 1.95 | 5.93 |
| 100 × 20 × 6 | 1.52 | 7.34 | 500 × 20 × 6 | 2.39 | 5.38 |
| 100 × 20 × 7 | 1.26 | 5.67 | 500 × 20 × 7 | 3.03 | 5.13 |
| Parameters | Hidden Meaning | Parameter Value |
|---|---|---|
| lr | Discount rate | 0.005 |
| batch_size | Number of training samples | 32 |
| EPSILON | Initial greedy rate | 1 |
| EPSILON_decay | Decay rate | 0.998 |
| EPSILON_min | Minimum greedy rate | 0.1 |
| GAMMA | Discount rate | 0.9 |
| TARGET_REPLACE_ITER | Synchronization frequency | 16 |
| MEMORY_CAPACITY | Experience pool size | 128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Chen, M. Multi-Scenario Robust Distributed Permutation Flow Shop Scheduling Based on DDQN. Appl. Sci. 2025, 15, 6560. https://doi.org/10.3390/app15126560
Guo S, Chen M. Multi-Scenario Robust Distributed Permutation Flow Shop Scheduling Based on DDQN. Applied Sciences. 2025; 15(12):6560. https://doi.org/10.3390/app15126560
Chicago/Turabian StyleGuo, Shilong, and Ming Chen. 2025. "Multi-Scenario Robust Distributed Permutation Flow Shop Scheduling Based on DDQN" Applied Sciences 15, no. 12: 6560. https://doi.org/10.3390/app15126560
APA StyleGuo, S., & Chen, M. (2025). Multi-Scenario Robust Distributed Permutation Flow Shop Scheduling Based on DDQN. Applied Sciences, 15(12), 6560. https://doi.org/10.3390/app15126560






