Numerical Investigation of Factors Influencing Multiple Hydraulic Fracture Propagation from Directional Long Boreholes in Coal Seam Roofs
Abstract
1. Introduction
2. Methodology
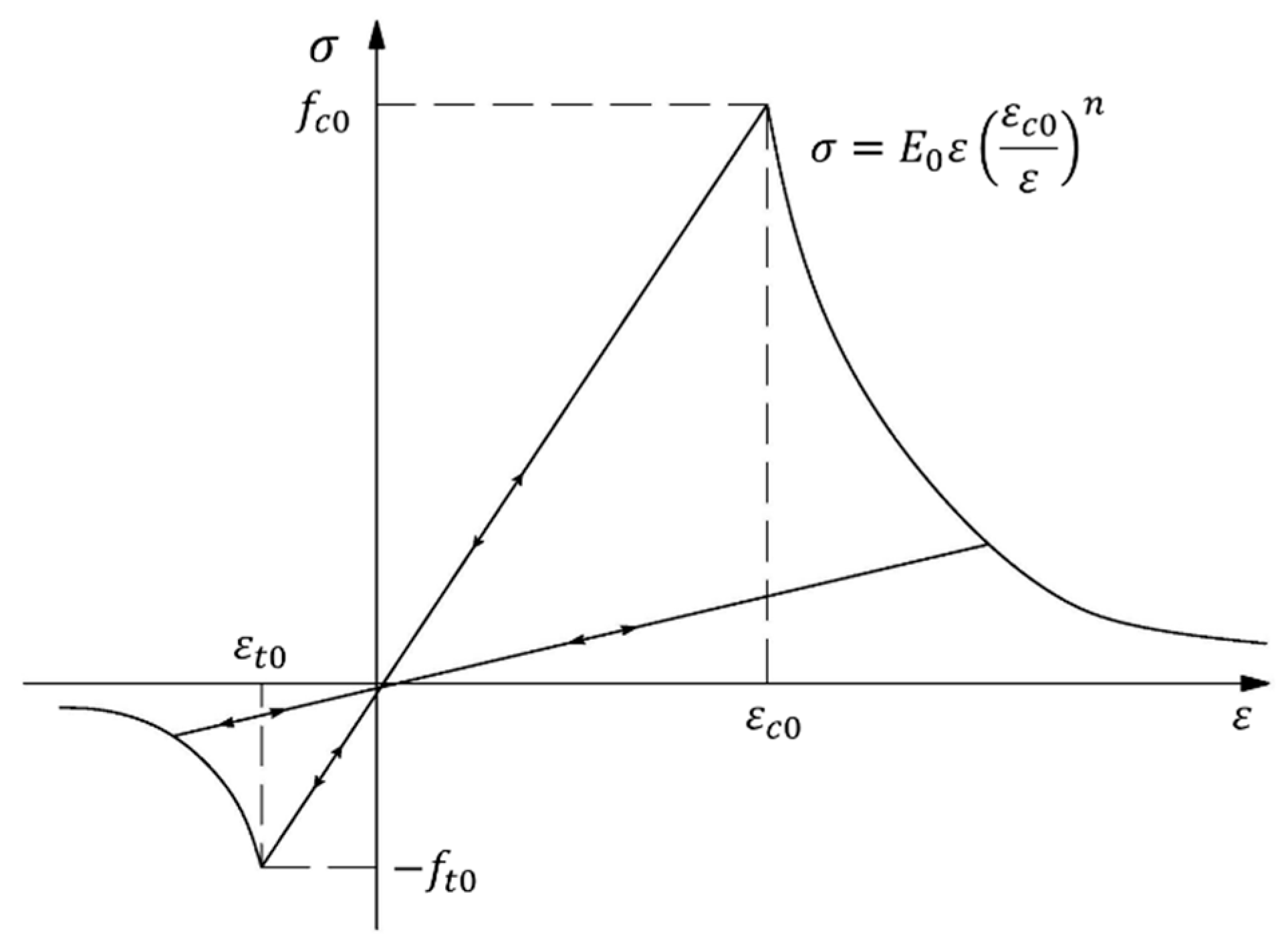
2.1. Governing Equation of Rock Deformation and Damage
2.2. Seepage Equation
2.3. Influence of Damage on Physical Field Parameters
3. Numerical Modelling and Validation
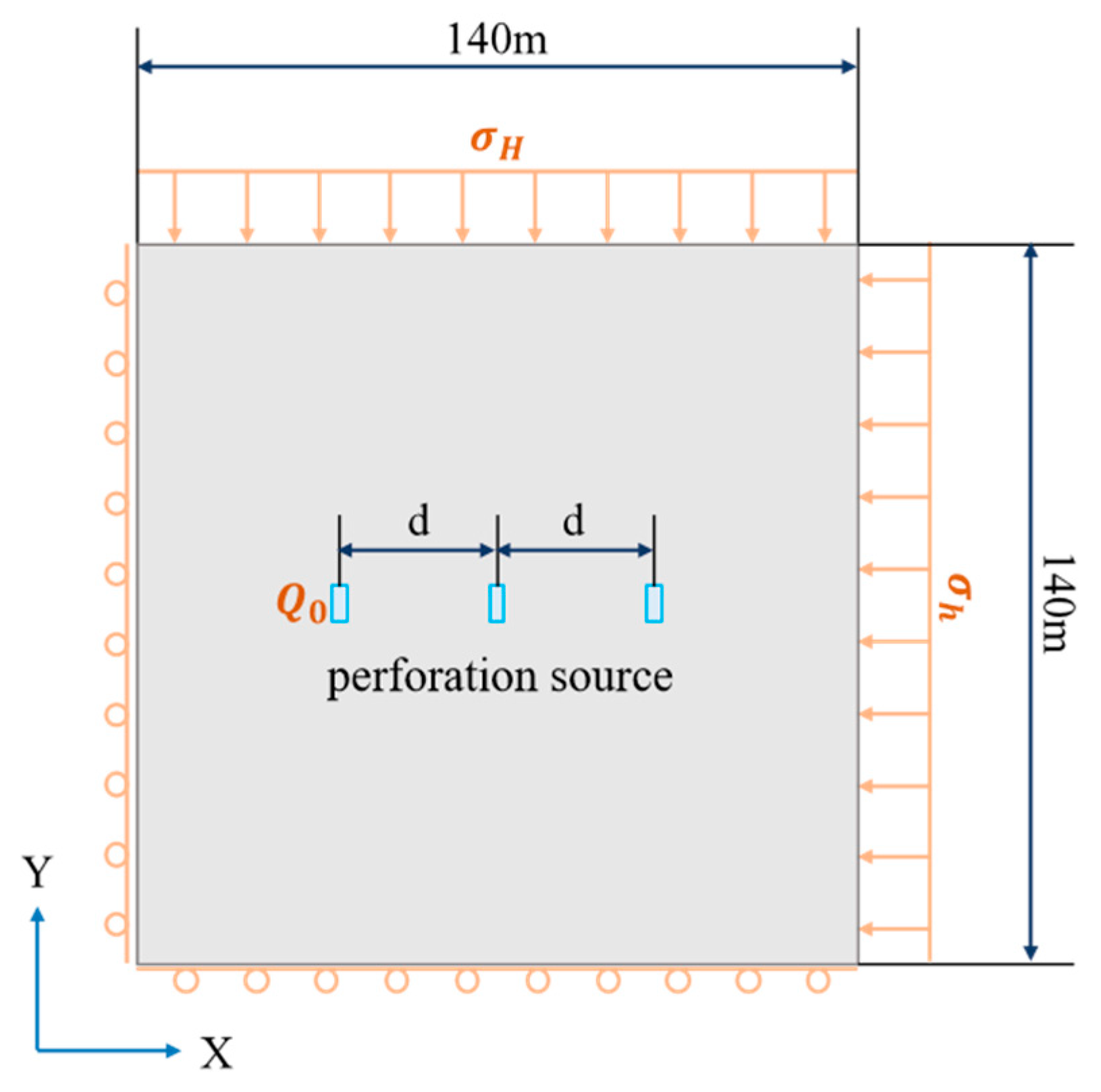
3.1. Numerical Model Establishment
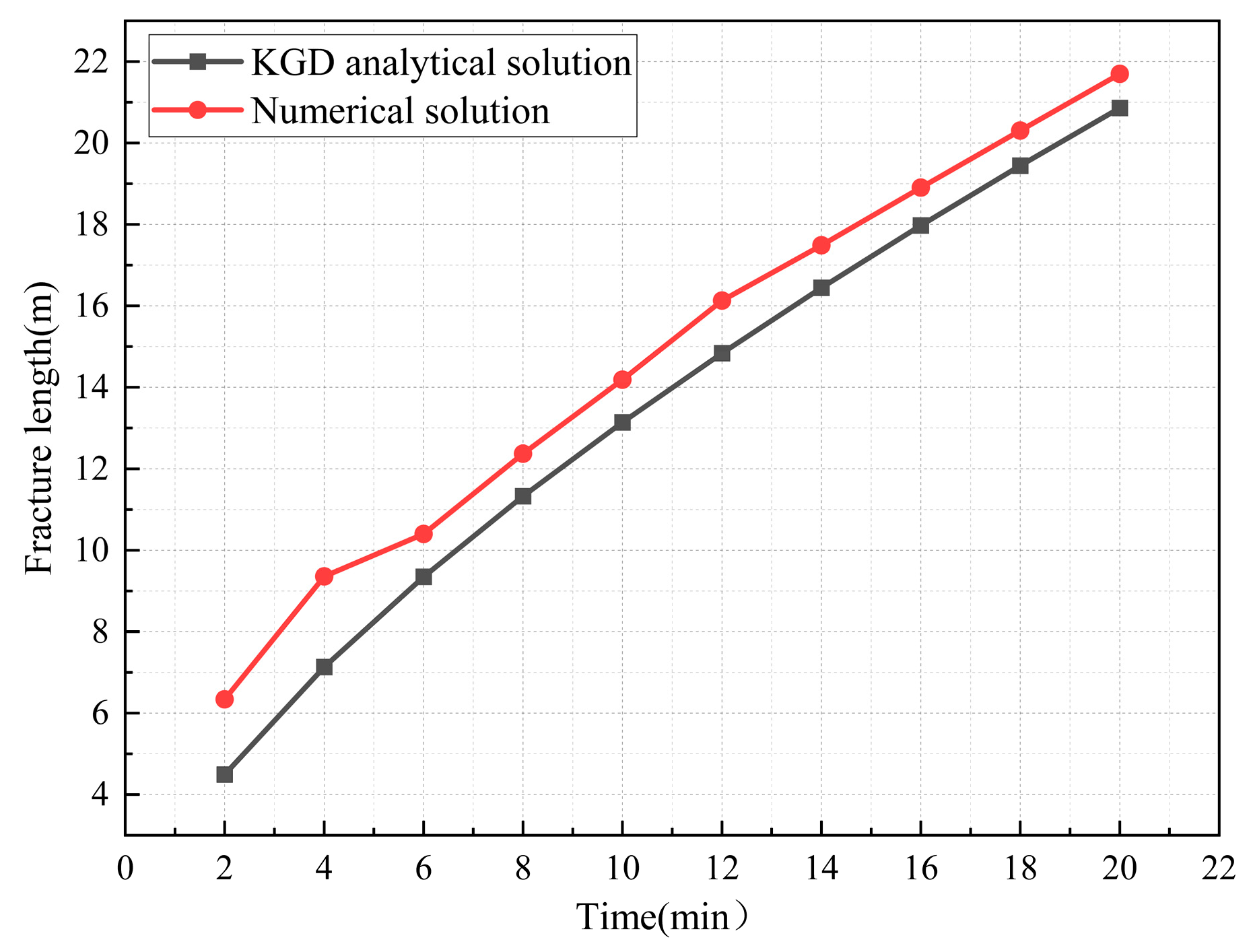
3.2. Model Validation
4. Analysis of Factors Influencing Hydraulic Fracture Propagation Behavior
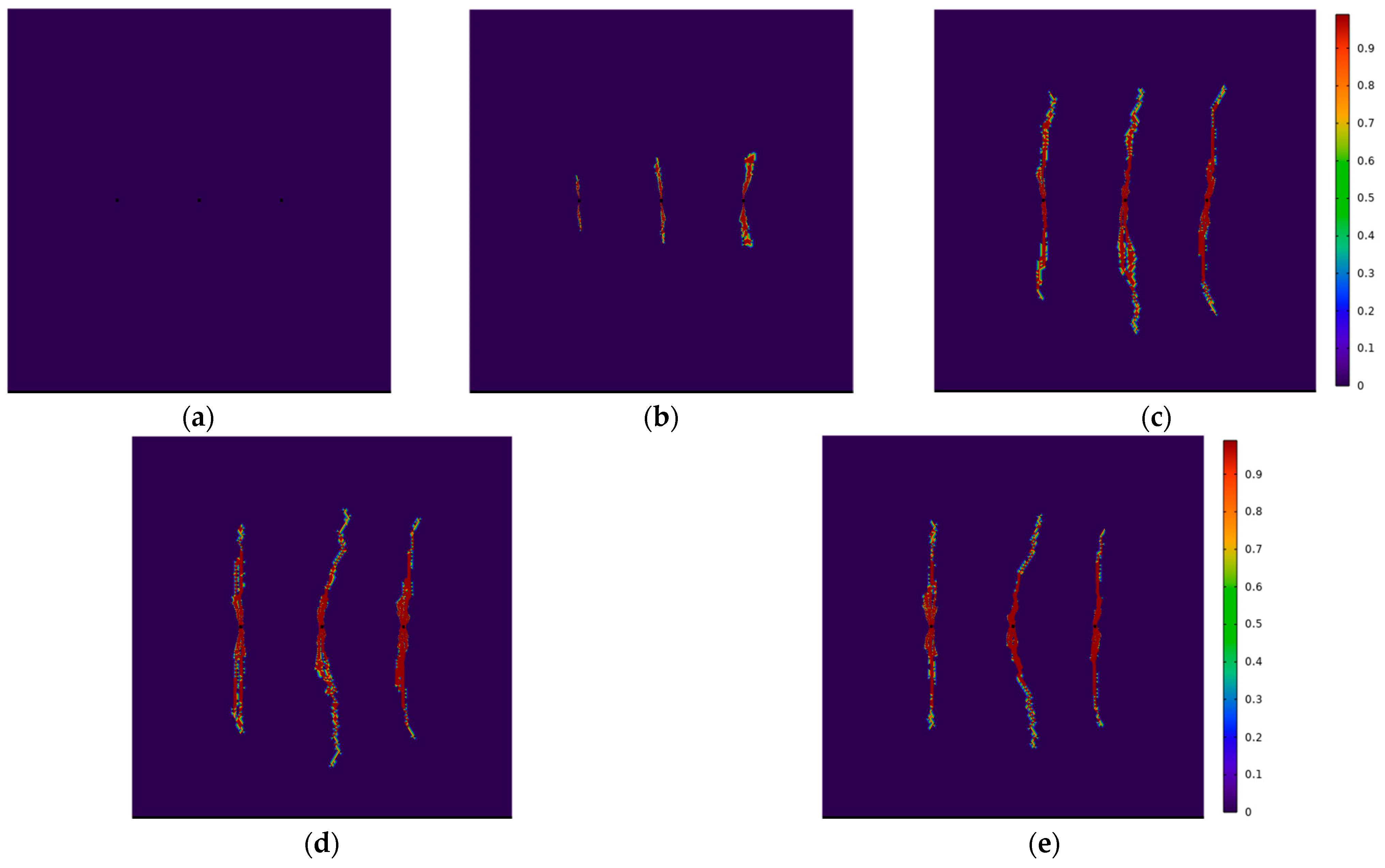
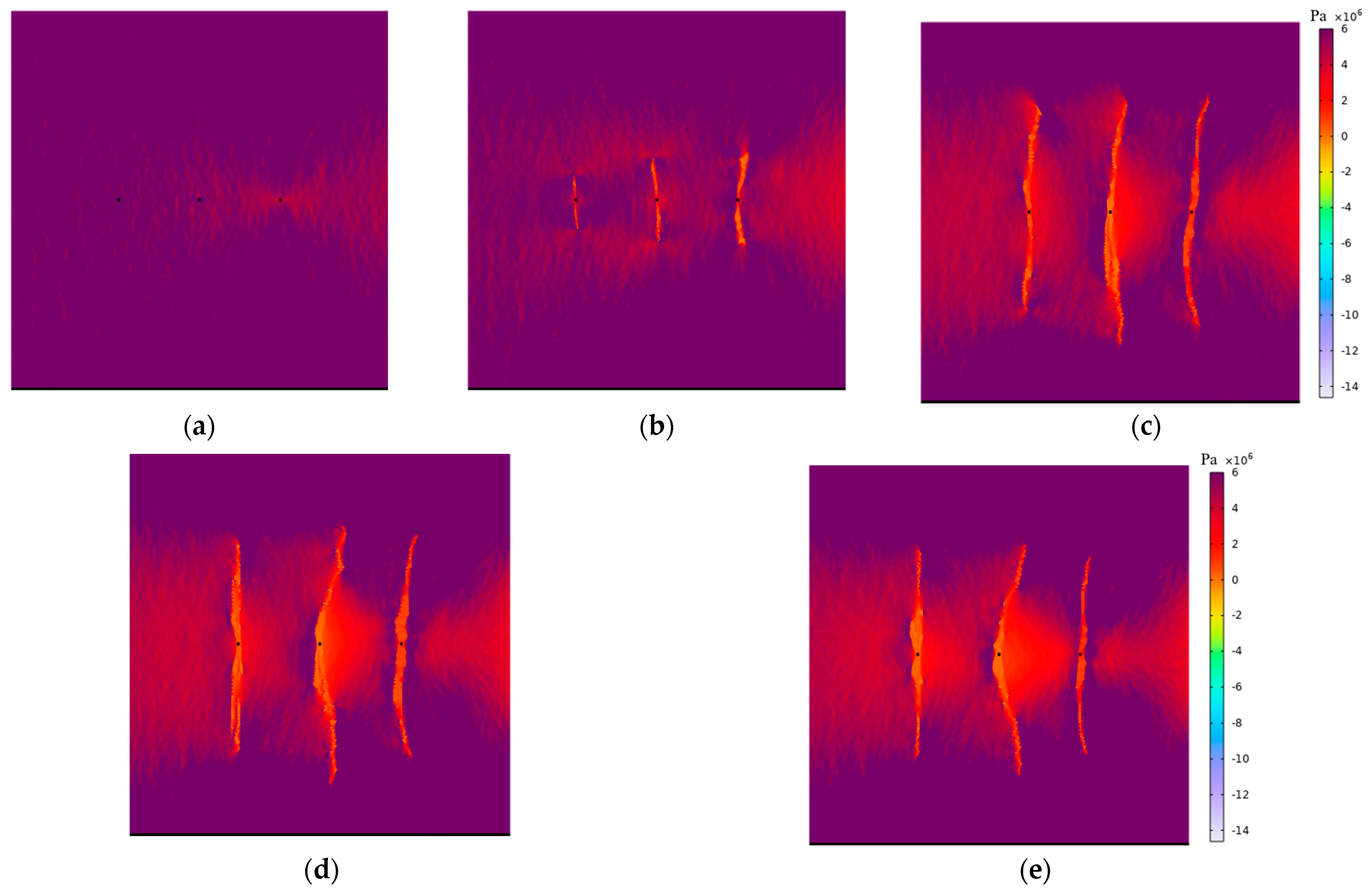
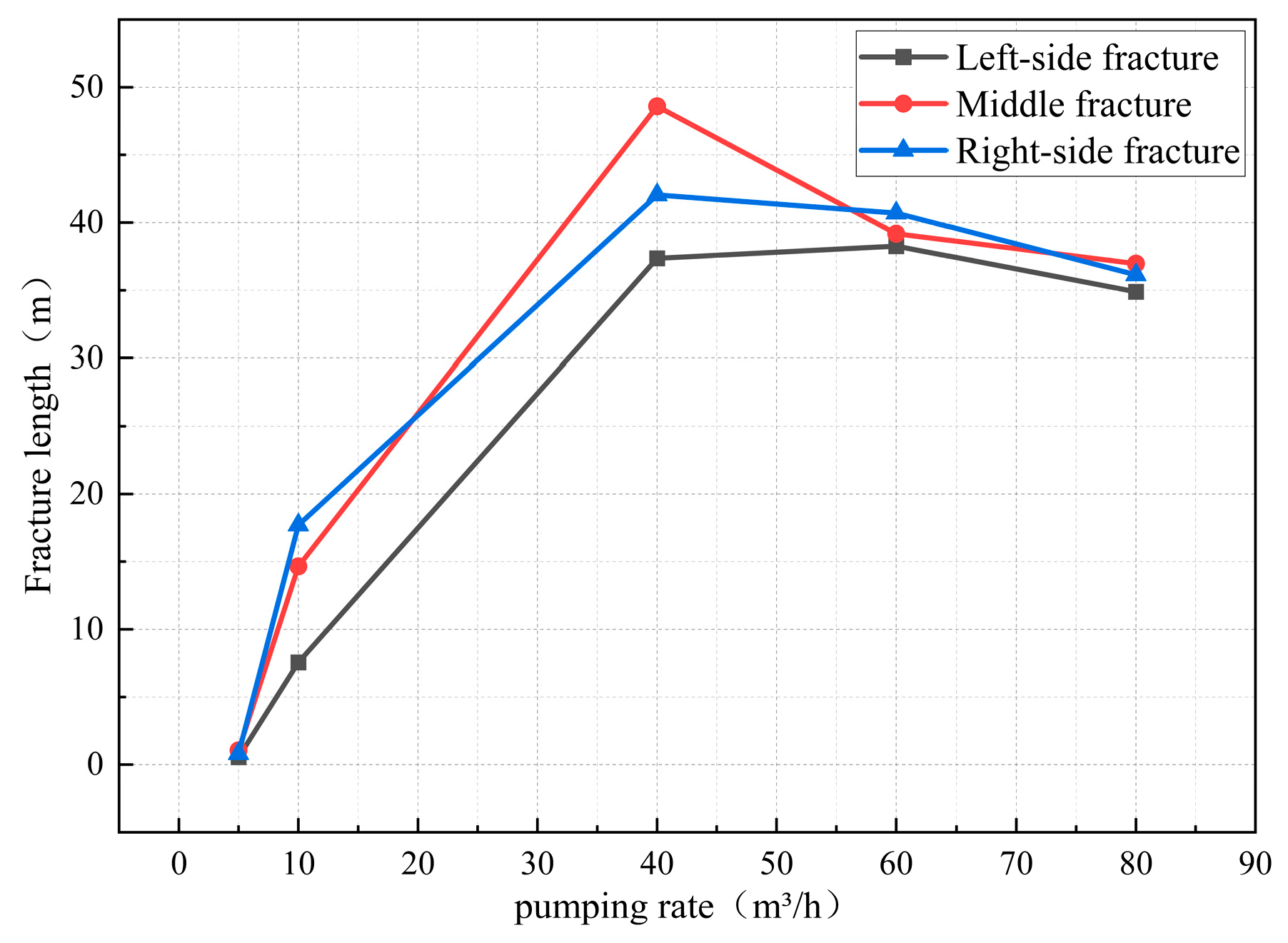
4.1. Influence of Pumping Rate on Multi-Fracture Propagation
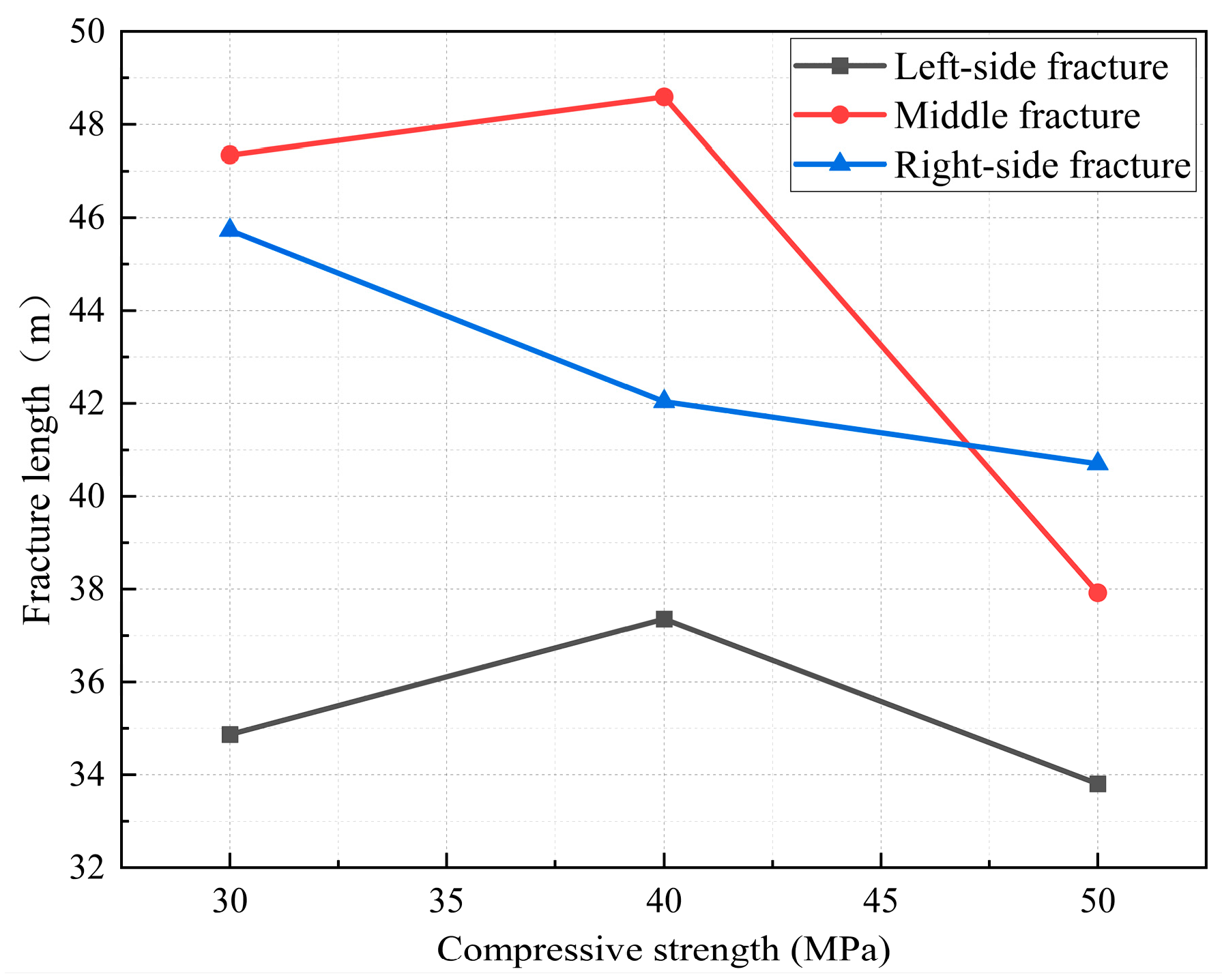
4.2. Influence of Compressive Strength on Multi-Fracture Propagation
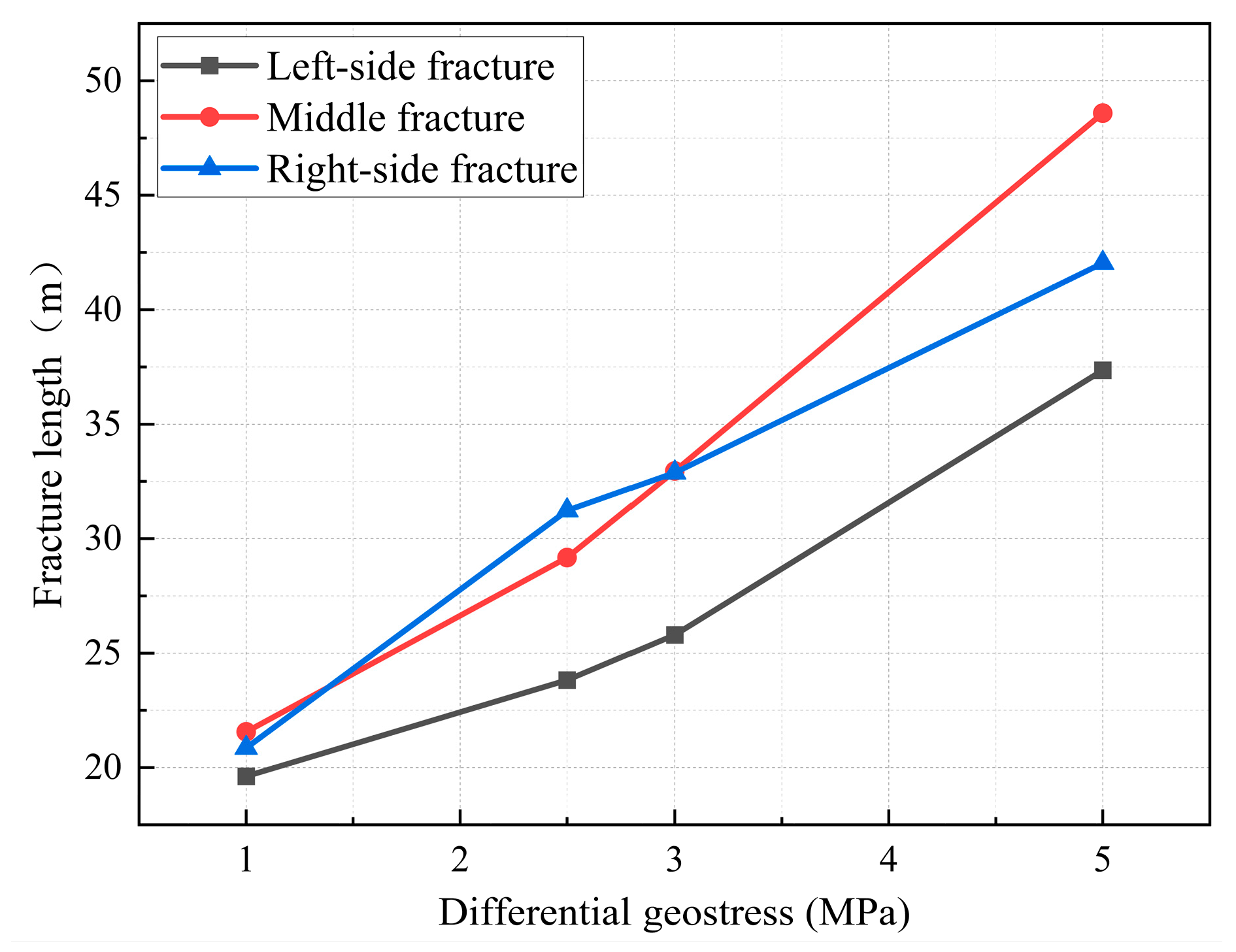
4.3. Influence of In Situ Stress Difference on Multi-Fracture Propagation
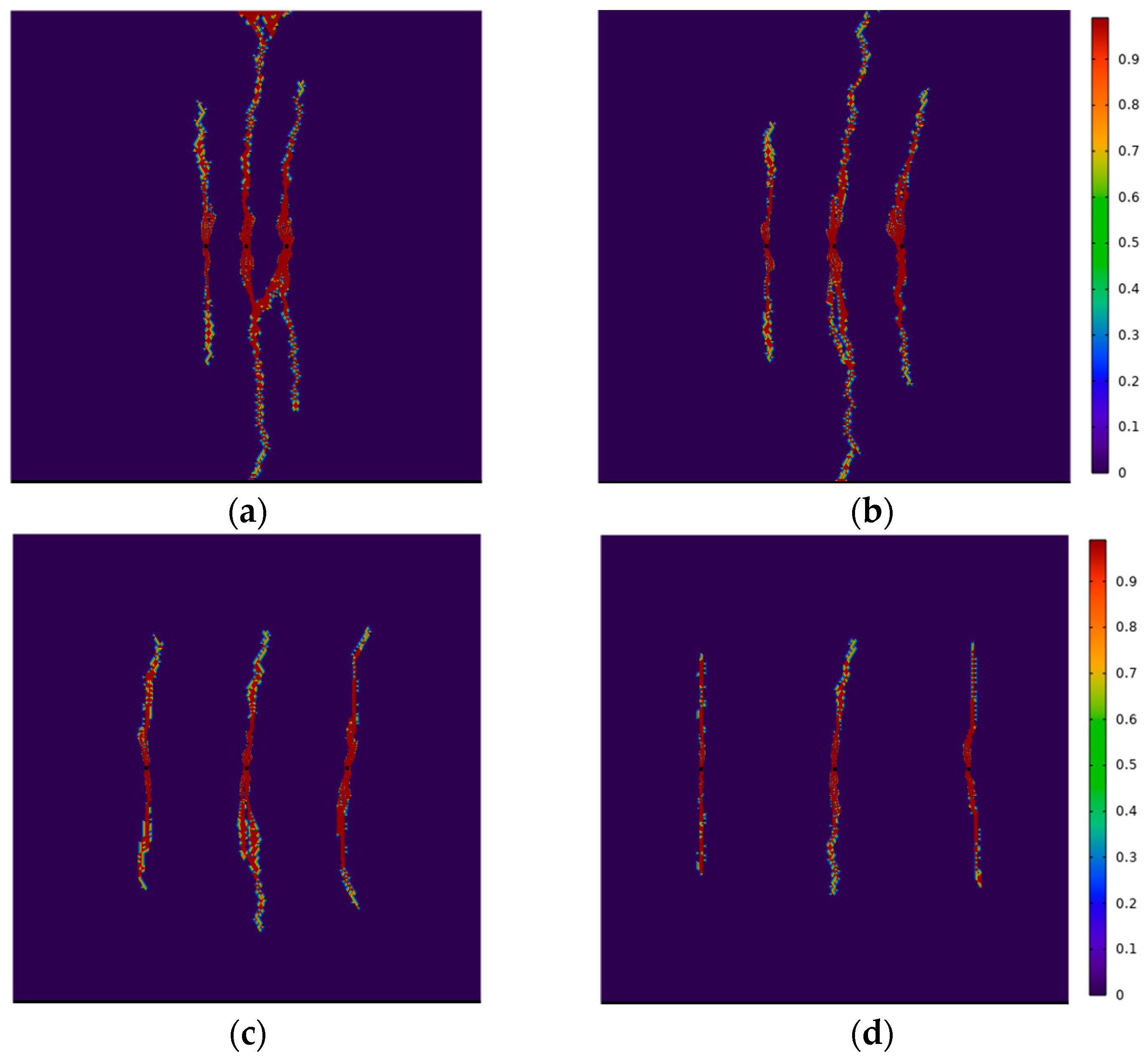
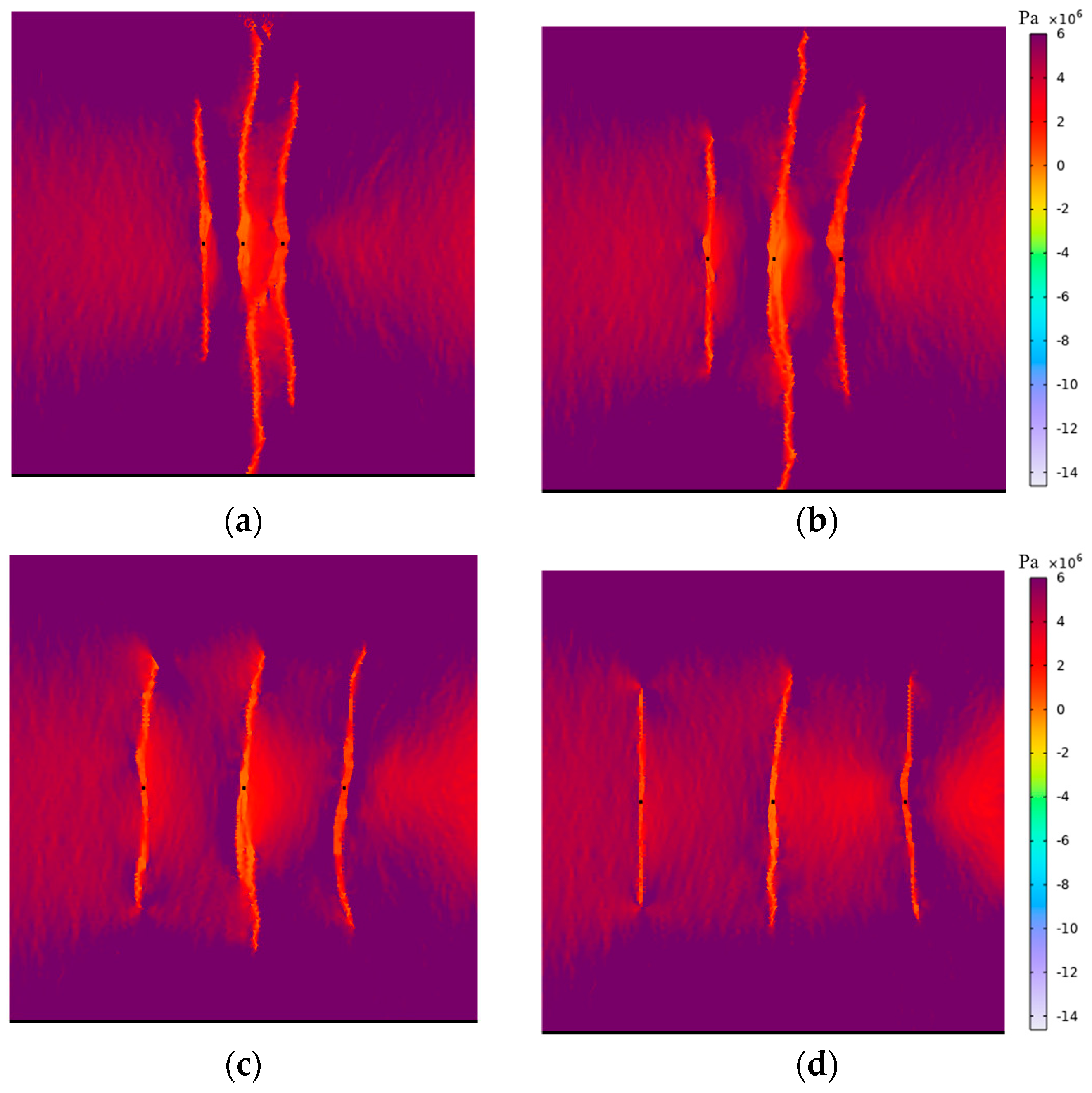
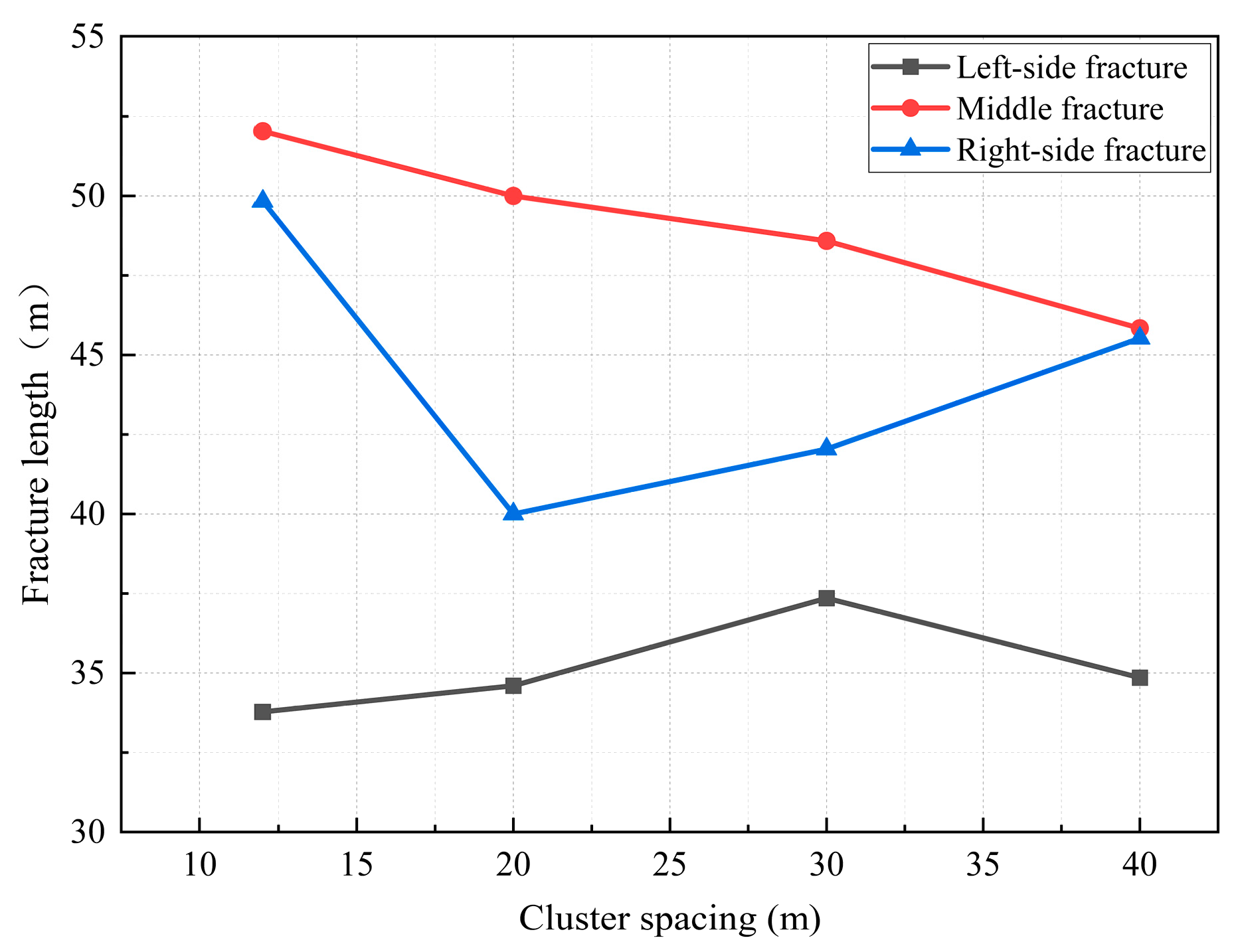
4.4. Influence of Segment Length on Multi-Fracture Propagation
5. Engineering Application
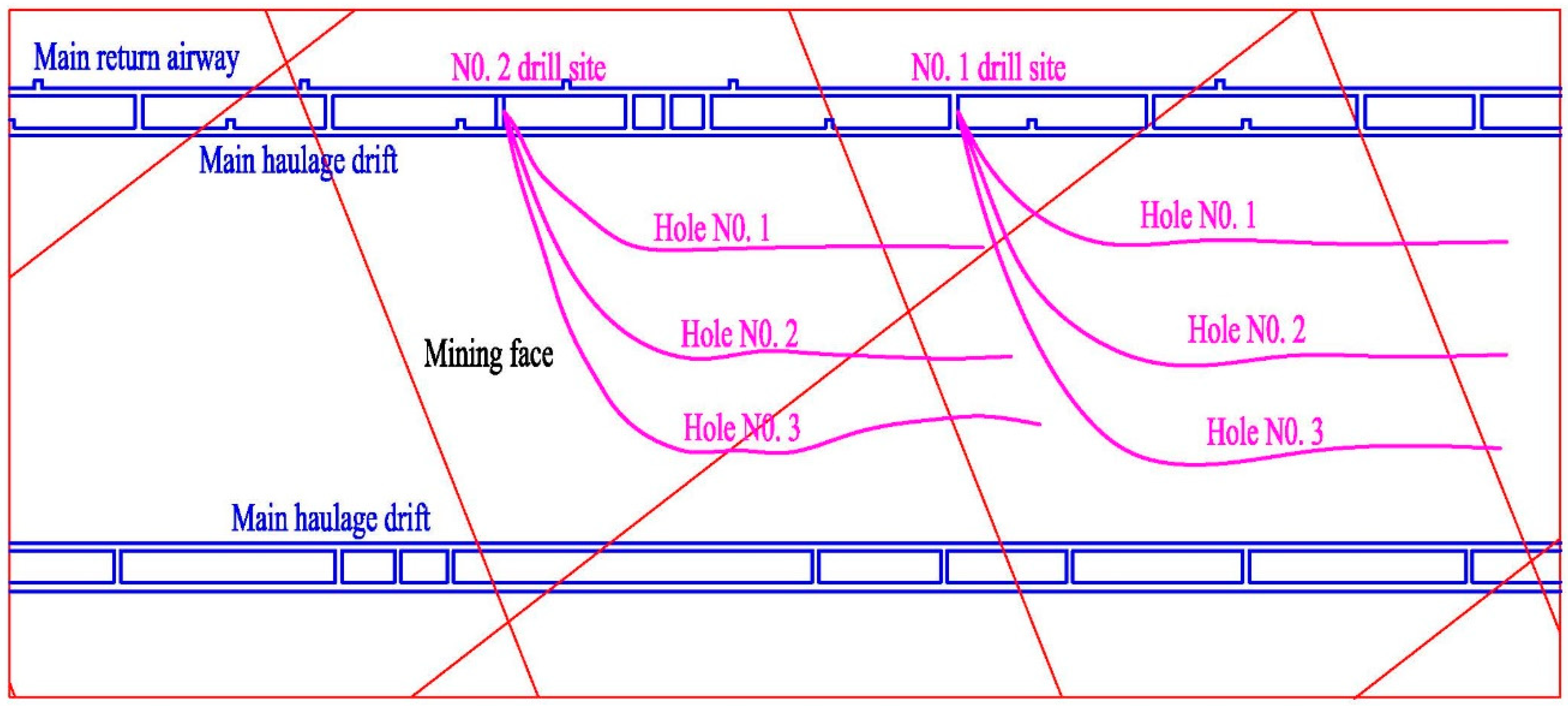
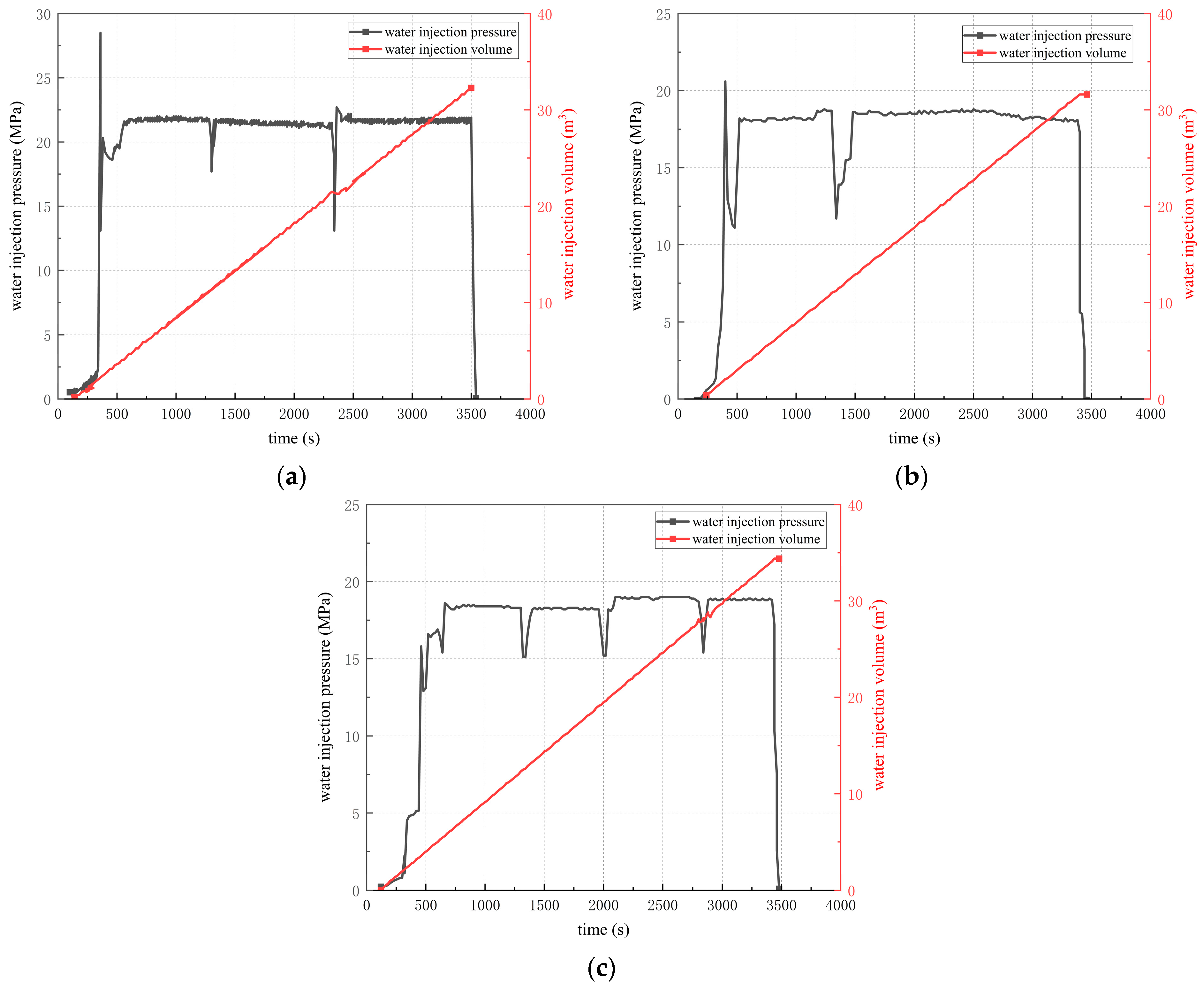
5.1. Fracturing Design and Construction Process
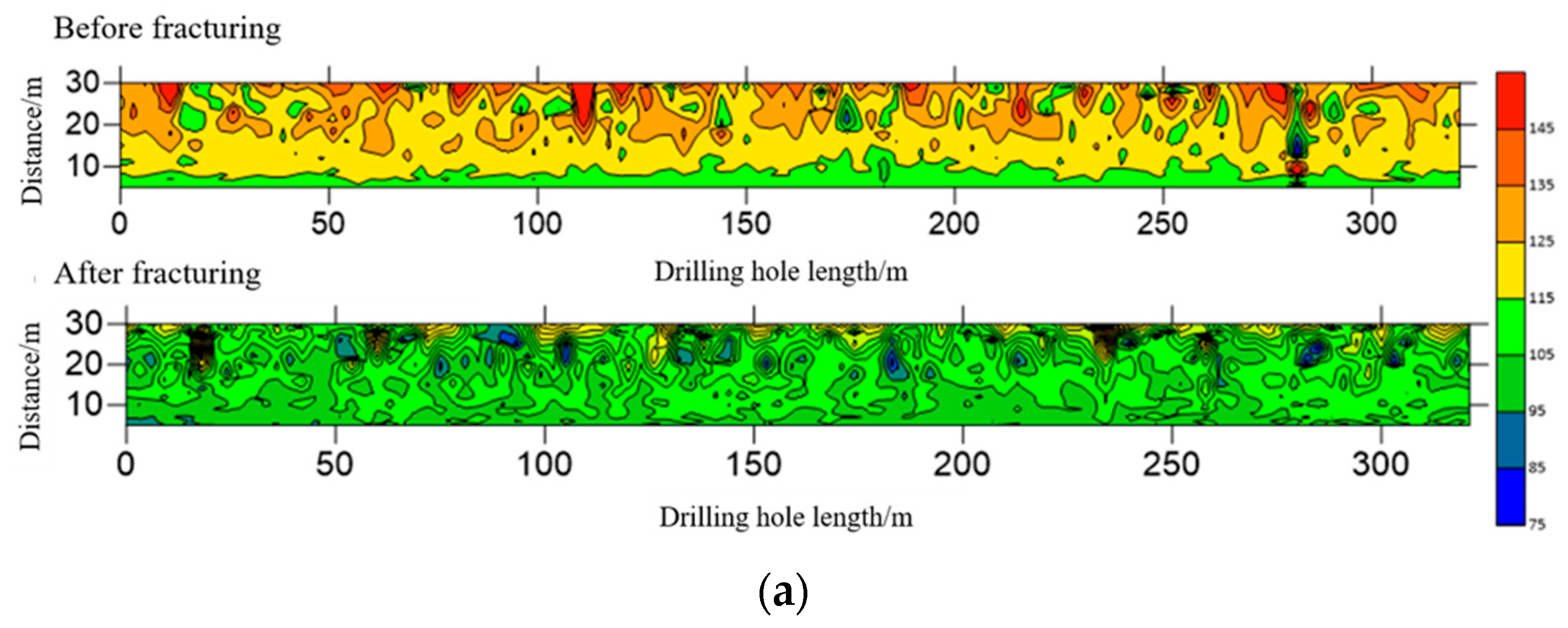
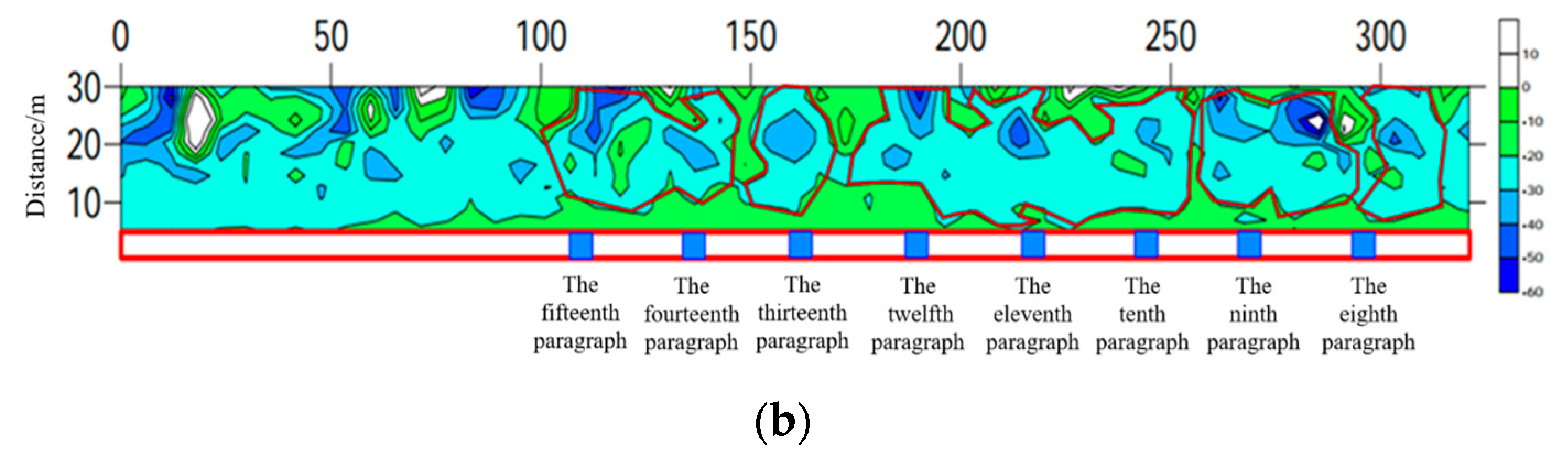
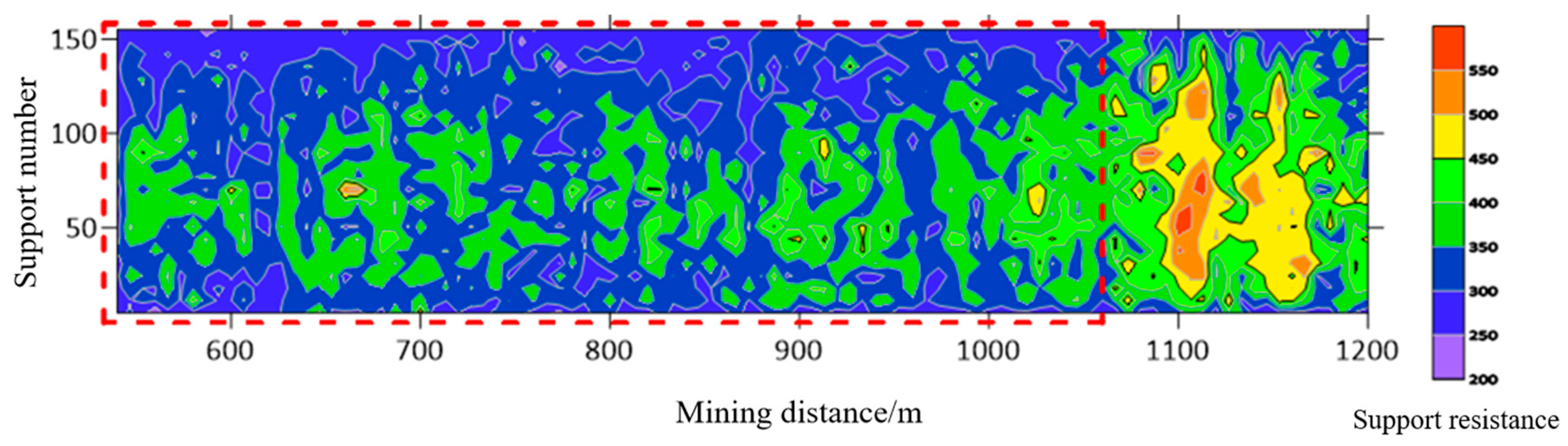
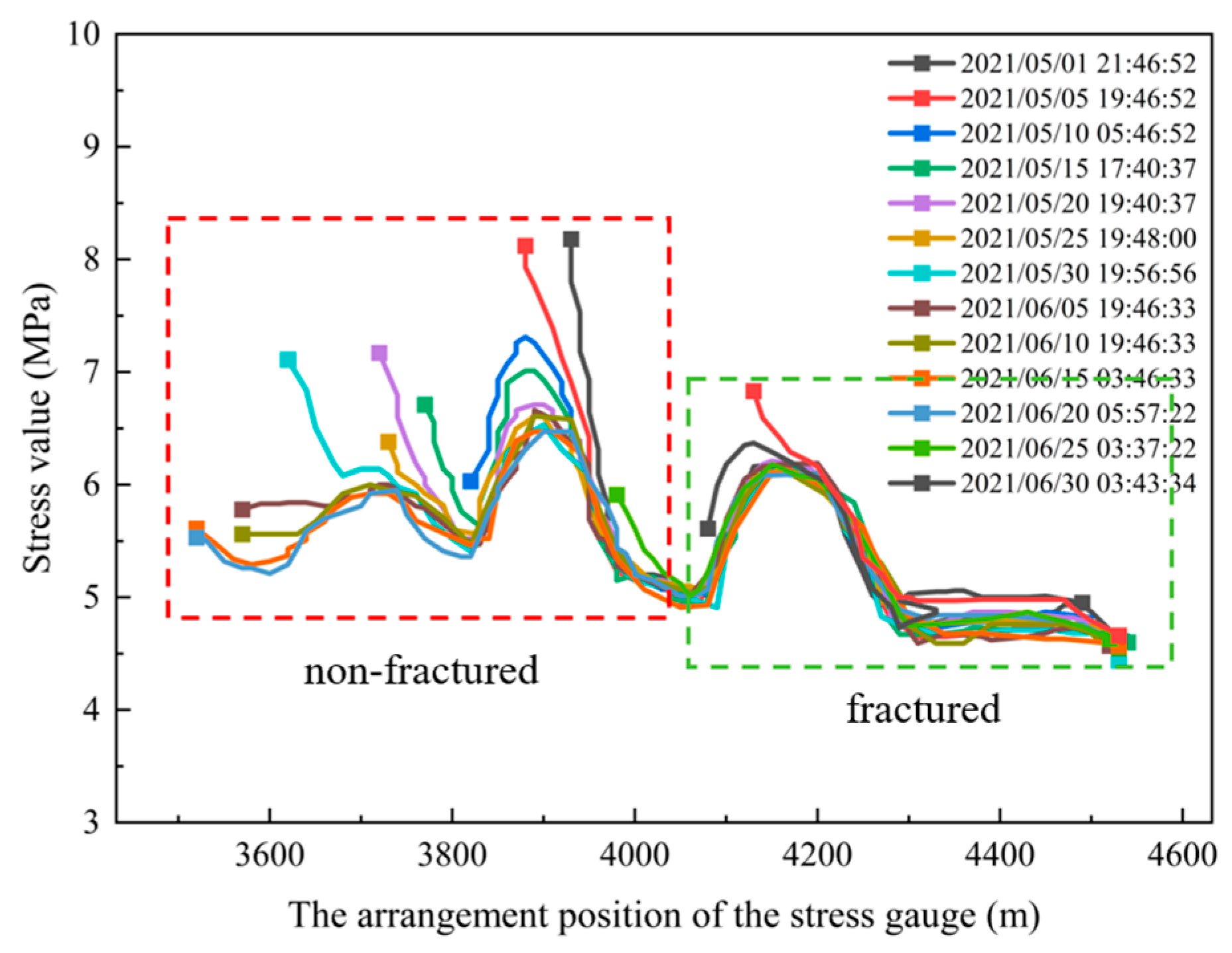
5.2. Fracturing Effect Validation
6. Conclusions
- (1)
- During the process of increasing the segment spacing from 12 m to 40 m, the fracture length decreased by 12%, limiting the overall fracture propagation. However, excessively small segment length can cause fractures to be influenced by the induced stress of adjacent clusters, leading to asymmetric propagation. Therefore, segment length should be optimized based on the specific objectives of the fracturing operation. Considering economic factors and fracture length, this study recommends a segment spacing of 30 m for the field application.
- (2)
- During the progressive increase of pumping rate from 5 to 40 m3/h, a 98% extension in fracture length was observed. However, underground space constraints impose limitations on equipment capacity, including flow rate and pump pressure. Thus, fracturing designs should be tailored to the characteristics of the working face, segment length, and flow parameters. Based on the results of numerical simulations, a pumping rate of 40 m3/h is recommended for the field application.
- (3)
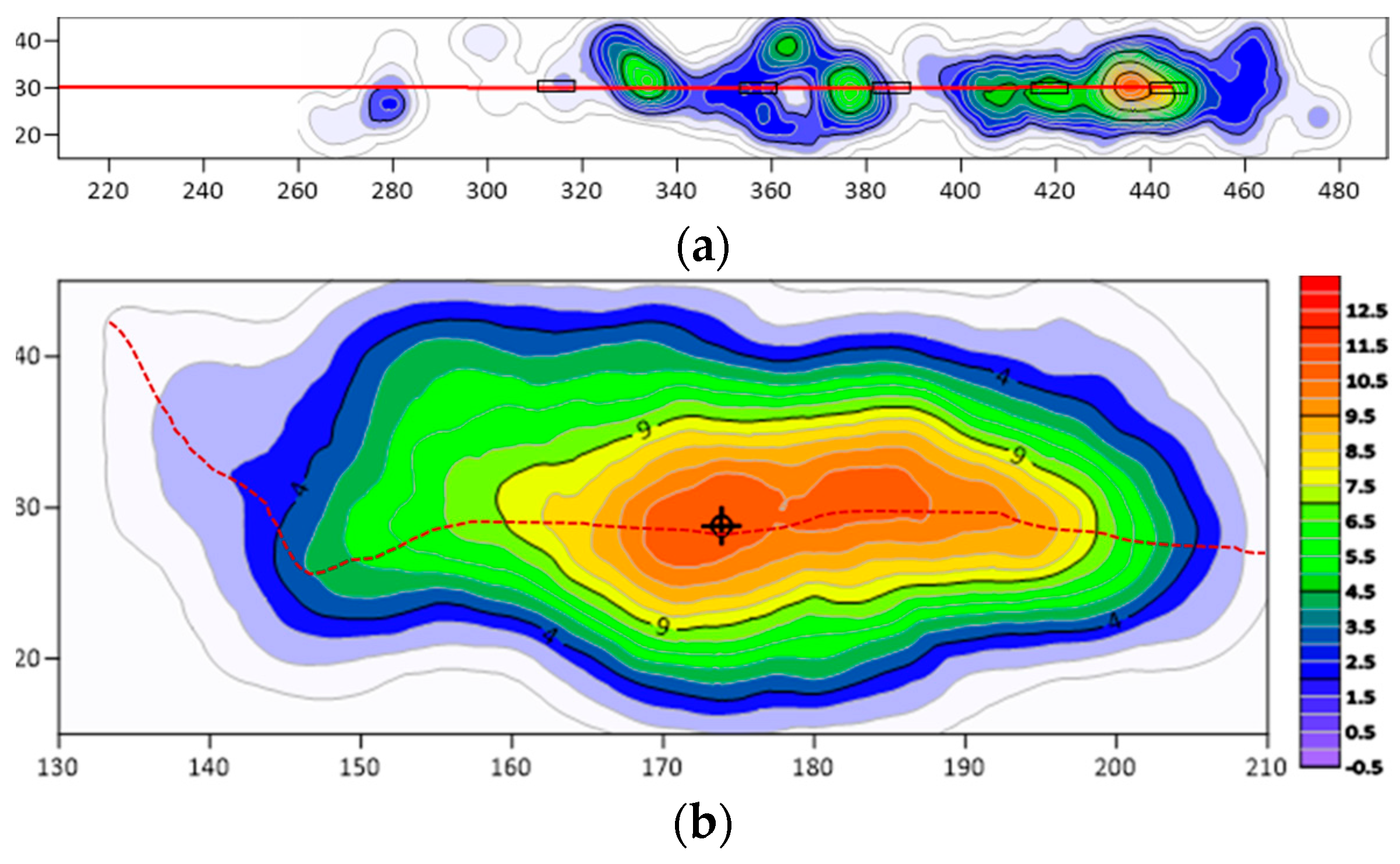
- Segmented hydraulic fracturing in underground directional boreholes exhibits significant responses in resistivity, microseismic activity, and mine pressure variations. The experimental results indicate that this technique effectively weakens hard coal seam roofs and improves mine pressure distribution, facilitating coal mine production planning and management.
- (4)
- The numerical simulation framework developed in this study is flexible and adaptable. By adjusting key geological parameters, it can be extended to assess hydraulic fracturing performance under varying geological conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Li, B.; Zhou, N.; Zhang, Q. Application of solid backfilling to reduce hard-roof caving and longwall coal face burst potential. Int. J. Rock Mech. Min. Sci. 2016, 88, 197–205. [Google Scholar] [CrossRef]
- He, H.; Dou, L.; Fan, J.; Du, T.; Sun, X. Deep-hole directional fracturing of thick hard roof for rockburst prevention. Tunn. Undergr. Space Technol. 2012, 32, 34–43. [Google Scholar] [CrossRef]
- Yu, B.; Gao, R.; Kuang, T.; Huo, B.; Meng, X. Engineering study on fracturing high-level hard rock strata by ground hydraulic action. Tunn. Undergr. Space Technol. 2019, 86, 156–164. [Google Scholar] [CrossRef]
- Sun, T.; Li, Z.; He, Q.; Ma, D.; Liu, B.; Gao, X. Research on Hydraulic Fracturing Technology for Roof Stratigraphic Horizon in Coal Pillar Gob-Side Roadway. Appl. Sci. 2025, 15, 4759. [Google Scholar] [CrossRef]
- Ju, J.; Qi, C.; Li, Z. Effect of Thick–Hard Main Roof Fracturing on the Spatiotemporal Evolution of Overburden Fractures. Appl. Sci. 2024, 14, 10308. [Google Scholar] [CrossRef]
- Lu, J.; Jiang, C.; Jin, Z.; Wang, W.; Zhuang, W.; Yu, H. Three-dimensional physical model experiment of mining-induced deformation and failure characteristics of roof and floor in deep underground coal seams. Process Saf. Environ. Prot. 2021, 150, 400–415. [Google Scholar] [CrossRef]
- Zhu, X.; Zhai, C.; Yu, X.; Sun, Y.; Cong, Y.; Zheng, Y.; Tang, W.; Chen, A. Fracture damage characteristics of hard roof with different bedding angles induced by modified soundless cracking agents. Eng. Fract. Mech. 2023, 289, 109387. [Google Scholar] [CrossRef]
- Yang, L.; Wang, X.; Niu, T. Propagation Characteristics of Multi-Cluster Hydraulic Fracturing in Shale Reservoirs with Natural Fractures. Appl. Sci. 2025, 15, 4418. [Google Scholar] [CrossRef]
- Liu, D.; Deng, J.; Yang, T.; Zhang, J.; Lin, H.; Liu, H.; Sun, J.; Zhang, Y. Research on Disaster Prevention and Control Technology for Directional Hydraulic Fracturing and Roof Plate Unloading. Appl. Sci. 2024, 14, 8733. [Google Scholar] [CrossRef]
- Lu, C.; Liu, Y.; Liu, G.; Zhao, T. Stress evolution caused by hard roof fracturing and associated multi-parameter precursors. Tunn. Undergr. Space Technol. 2019, 84, 295–305. [Google Scholar] [CrossRef]
- Cao, M.; Yang, S.; Du, S.; Li, Y.; Wang, S. Study on fault-slip process and seismic mechanism under dynamic loading of hard roof fracture disturbance. Eng. Fail. Anal. 2024, 163, 108598. [Google Scholar] [CrossRef]
- Dai, H.; Yin, T.; Wu, Y.; Chen, Y.; Ma, J.; Li, X. A study of geothermal hydraulic fracture surface morphology and heat transfer characteristics. Energy 2024, 312, 133527. [Google Scholar] [CrossRef]
- He, Q.; Suorineni, F.T.; Ma, T.; Oh, J. Effect of discontinuity stress shadows on hydraulic fracture re-orientation. Int. J. Rock Mech. Min. Sci. 2017, 91, 179–194. [Google Scholar] [CrossRef]
- Liu, C.; Hu, Y.; Zhang, P.; Deng, E.; Huang, Y.; Nie, Z.; Zhang, X. Experimental study on directional fracturing by slotted hydraulic blasting in underground drilling. Nat. Gas Ind. B 2024, 11, 454–467. [Google Scholar] [CrossRef]
- Bai, Q.; Tu, S.; Wang, F.; Zhang, C. Field and numerical investigations of gateroad system failure induced by hard roofs in a longwall top coal caving face. Int. J. Coal Geol. 2017, 173, 176–199. [Google Scholar] [CrossRef]
- Deng, J.; Song, H. Formulizing relationships between producing area of fracture-controlled unit and productivity of segmented multi-cluster fractured well by delineating water saturation limit. Geoenerg. Sci. Eng. 2025, 244, 213448. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, G.; Geng, Y.; Guo, Y.; Chang, X.; Peng, C.; Ai, C. Laboratory study of the factors affecting hydraulic fracturing effect for inter-salt oil shale layers, Qianjiang Depression, China. Petrol. Sci. 2023, 20, 1690–1706. [Google Scholar] [CrossRef]
- Zhuang, J.; Mu, Z.; Cai, W.; He, H.; Hosking, L.J. Multistage hydraulic fracturing of a horizontal well for hard roof related coal burst control: Insights from numerical modelling to field application. Int. J. Min. Sci. Technol. 2024, 34, 1095–1114. [Google Scholar] [CrossRef]
- Xia, B.; Zhou, Y.; Zhang, X.; Zhou, L.; Ma, Z. Physical and numerical investigations of target stratum selection for ground hydraulic fracturing of multiple hard roofs. Int. J. Min. Sci. Technol. 2024, 34, 699–712. [Google Scholar] [CrossRef]
- Shi, Z.; Li, B.; Li, L.; Wang, N.; Zhang, J. Study on the directional extension law of hydraulic fractures induced by pre-cast slot under tru-triaxial. Theor. Appl. Fract. Mech. 2024, 133, 104546. [Google Scholar] [CrossRef]
- Liu, J.; Liu, C.; Yao, Q.; Si, G. The position of hydraulic fracturing to initiate vertical fractures in hard hanging roof for stress relief. Int. J. Rock Mech. Min. Sci. 2020, 132, 104328. [Google Scholar] [CrossRef]
- Huang, B.; Liu, J.; Zhang, Q. The reasonable breaking location of overhanging hard roof for directional hydraulic fracturing to control strong strata behaviors of gob-side entry. Int. J. Rock Mech. Min. Sci. 2018, 103, 1–11. [Google Scholar] [CrossRef]
- Boone, T.J.; Ingraffea, A.R. A numerical procedure for simulation of hydraulically-driven fracture propagation in poroelastic media. Int. J. Numer. Anal. Meth. Geomech. 1990, 14, 27–47. [Google Scholar] [CrossRef]
- Hunsweck, M.J.; Shen, Y.; Lew, A.J. A finite element approach to the simulation of hydraulic fractures with lag. Int. J. Numer. Anal. Meth. Geomech. 2013, 37, 993–1015. [Google Scholar] [CrossRef]
- Bao, J.Q.; Fathi, E.; Ameri, S. A coupled finite element method for the numerical simulation of hydraulic fracturing with a condensation technique. Eng. Fract. Mech. 2014, 131, 269–281. [Google Scholar] [CrossRef]
- Bao, J.Q.; Fathi, E.; Ameri, S. Uniform investigation of hydraulic fracturing propagation regimes in the plane strain model. Int. J. Numer. Anal. Meth. Geomech. 2015, 39, 507–523. [Google Scholar] [CrossRef]
- Shi, F.; Wang, X.; Liu, C.; Wu, H. An XFEM-based method with reduction technique for modeling hydraulic fracture propagation in formations containing frictional natural fractures. Eng. Fract. Mech. 2017, 173, 64–90. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Meth. Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Gordeliy, E.; Peirce, A. Coupling schemes for modeling hydraulic fracture propagation using the XFEM. Comput. Meth. Appl. Mech. Eng. 2013, 253, 305–322. [Google Scholar] [CrossRef]
- Wang, H.Y. Numerical modeling of non-planar hydraulic fracture propagation in brittle and ductile rocks using XFEM with cohesive zone method. J. Petrol. Sci. Eng. 2015, 135, 127–140. [Google Scholar] [CrossRef]
- Feng, Y.; Gray, K.E. Modeling of curving hydraulic fracture propagation from a wellbore in a poroelastic medium. J. Nat. Gas Sci. Eng. 2018, 53, 83–93. [Google Scholar] [CrossRef]
- Shi, F.; Liu, J. A fully coupled hydromechanical XFEM model for the simulation of 3D non-planar fluid-driven fracture propagation. Comput. Geotech. 2021, 132, 103971. [Google Scholar] [CrossRef]
- Crouch, S.L. Solution of plane elasticity problems by the displacement discontinuity method. I. Infinite body solution. Int. J. Numer. Meth. Eng. 1976, 10, 301–343. [Google Scholar] [CrossRef]
- Skopintsev, A.M.; Dontsov, E.V.; Kovtunenko, P.V.; Baykin, A.N.; Golovin, S.V. The coupling of an enhanced pseudo-3D model for hydraulic fracturing with a proppant transport model. Eng. Fract. Mech. 2020, 236, 107177. [Google Scholar] [CrossRef]
- Dontsov, E.V.; Peirce, A.P. An enhanced pseudo-3D model for hydraulic fracturing accounting for viscous height growth, non-local elasticity, and lateral toughness. Eng. Fract. Mech. 2015, 142, 116–139. [Google Scholar] [CrossRef]
- Dontsov, E.V.; Peirce, A.P. Comparison of toughness propagation criteria for blade-like and pseudo-3D hydraulic fractures. Eng. Fract. Mech. 2016, 160, 238–247. [Google Scholar] [CrossRef]
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Petrol. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Khalil, A.; Khan, Z.; Attom, M.; Khalafalla, O. Evaluation of Ground Improvement with Dynamic Replacement and Rapid Impact Compaction of an Artificial Island in the UAE—A Case Study. Geo-Congress 2024, 351, 116–125. [Google Scholar] [CrossRef]
- Zheng, K.; Wang, L.; Li, B.; Li, Y.; Yang, H.; Yang, S.; Dai, N.; Wang, H.; Wang, Z.; Xi, J. Dynamic disaster evolution mechanism of high mine pressure at hard roof and advance area prevention and control technology. Coal Geol. Explor. 2022, 50, 62–71. [Google Scholar] [CrossRef]
- Zheng, K.; Wang, L.; Wang, Y. Study on advanced regional control technology for strong mine pressure dynamic disaster in hard roof. China Coal 2024, 50, 36–45. [Google Scholar] [CrossRef]


| Parameter Name | Symbol | Value | Unit | Parameter Name | Symbol | Value | Unit |
|---|---|---|---|---|---|---|---|
| Heterogeneity Coefficient | m | 10 | / | Initial Permeability | k0 | 5 × 10−15 | m2 |
| Compressive Strength | fc0 | 40 | MPa | Pumping rate | q | 40 | m3/h |
| Poisson’s Ratio | υ | 0.2 | / | Injection Pressure | p | 25 | Mpa |
| Internal Friction Angle | φ | 40 | ° | Fluid Density | ρw | 1 × 103 | kg/m3 |
| Initial Porosity | Φ0 | 0.1 | / | Maximum Principal Stress | σ1 | 11 | Mpa |
| Residual Porosity | φr | 0.001 | / | Biot Coefficient | α | 0.5 | / |
| Model Length | L | 140 | m | Fluid Viscosity | μw | 1 × 10−3 | Pa·s |
| Model Width | H | 140 | m | Porosity of Matrix Region | nr | 0.1 | / |
| Initial Hydraulic Fracture Length | a | 1 | m | Minimum horizontal stress | σ2 | 6 | Mpa |
| Segment length | d | 30 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Lv, S.; Meng, Y.; Wang, X.; Wang, S.; He, J. Numerical Investigation of Factors Influencing Multiple Hydraulic Fracture Propagation from Directional Long Boreholes in Coal Seam Roofs. Appl. Sci. 2025, 15, 6521. https://doi.org/10.3390/app15126521
Yang M, Lv S, Meng Y, Wang X, Wang S, He J. Numerical Investigation of Factors Influencing Multiple Hydraulic Fracture Propagation from Directional Long Boreholes in Coal Seam Roofs. Applied Sciences. 2025; 15(12):6521. https://doi.org/10.3390/app15126521
Chicago/Turabian StyleYang, Maolin, Shuai Lv, Yu Meng, Xing Wang, Sicheng Wang, and Jiangfu He. 2025. "Numerical Investigation of Factors Influencing Multiple Hydraulic Fracture Propagation from Directional Long Boreholes in Coal Seam Roofs" Applied Sciences 15, no. 12: 6521. https://doi.org/10.3390/app15126521
APA StyleYang, M., Lv, S., Meng, Y., Wang, X., Wang, S., & He, J. (2025). Numerical Investigation of Factors Influencing Multiple Hydraulic Fracture Propagation from Directional Long Boreholes in Coal Seam Roofs. Applied Sciences, 15(12), 6521. https://doi.org/10.3390/app15126521






