Intelligent Recognition of Rock Mass Discontinuities on the Basis of RGB-Enhanced Point Cloud Features

Abstract

Rock slopes, composed of intact rock masses and relatively weak discontinuities, exhibit stability primarily governed by the spatial distribution of these discontinuities. Under the framework of structural control theory, acquiring discontinuity information is a fundamental prerequisite for rock slope stability analysis. However, advancements in measurement methods have significantly enhanced slope modeling precision while paradoxically reducing the efficiency of discontinuity data acquisition. To address this challenge, this study proposes a novel discontinuity identification method on the basis of high-precision UAV (unmanned aerial vehicle) point clouds, integrating principal component analysis (PCA), multi-channel gradient fusion, and cascaded edge detection techniques. Applying this approach, a high-resolution UAV-derived 3D model was constructed, and surface discontinuities were systematically identified for a slope case study in the North Qinling Belt, Shanxi Province, China. Results demonstrate that the proposed method achieves effective discontinuity identification performance, cumulatively detecting 1401 discontinuities. Statistical analysis of the identified discontinuities reveals three dominant orientation groups: I: S085° E/80°, II: S015° W/15°, and III: S005° W/85°.

1. Introduction

Rock slope hazards, including rockfalls and landslides, account for over 70% of natural geological disasters [1,2,3,4]. Rock slopes are composed of intact rock and discontinuities, with the strength of discontinuities being significantly lower than that of intact rock [5]. Consequently, the formation of rock slope hazards is primarily controlled by the strength characteristics and spatial distribution of discontinuities. On the basis of this understanding, numerous scholars have conducted research on rock slope disasters following the structural control theory of rock masses [6,7,8,9].

The rock mass structure control theory involves predicting mechanical behaviors by analyzing the internal structural characteristics. The most fundamental aspect of this approach lies in acquiring information about rock discontinuities. Traditional methods employ geological compasses and survey lines to measure discontinuities within specific observation windows. However, these approaches only capture partial discontinuity information from localized areas of rock slopes, making them incomplete for comprehensive characterization. With advancements in Terrestrial Laser Scanning (TLS) and LiDAR technologies, the interpretation of discontinuity information through 3D point cloud data has become a primary method for its characterization [10]. TLS and LiDAR systems acquire three-dimensional spatial coordinates by uniformly emitting laser beams and capturing reflected signals [11]. Nevertheless, due to topographic constraints and imaging distance limitations, TLS-derived point cloud data typically exhibits centimeter-level spacing [12]. Under the recent framework of multi-scale rock mass structure analysis [13], millimeter-scale discontinuities, though not constituting controlling factors for slope instability, can still reduce rock mass strength and influence slope stability assessments [14]. Consequently, analyzing millimeter-aperture discontinuities becomes essential. However, current TLS and LiDAR methods, constrained by centimeter-level precision, remain inadequate for detecting such fine-scale discontinuities.

Against this backdrop, UAV (unmanned aerial vehicle) low-altitude photogrammetric modeling has gradually emerged as a mainstream method for acquiring discontinuity information in engineering and research applications, owing to its cost-effectiveness and efficient field operations [15]. Notably, Zhang et al. [16] proposed a multi-angle and nap-of-the-object photogrammetric method, enabling millimeter-level precision modeling of rock slopes. This advancement provides a feasible approach for detecting millimeter-aperture discontinuities. However, higher-precision models inevitably generate massive point cloud data and discontinuity information. Relying on traditional manual interpretation methods remains time-consuming and labor-intensive, significantly hindering the efficiency of discontinuity extraction. Consequently, achieving rapid acquisition of discontinuity information from high-precision UAV models has become a critical focus for advancing rock slope hazard analysis.

In recent years, UAV photogrammetry surveys equipped with GNSS antennas and RTK/PPK systems have enabled the generation of 3D models with accuracies of around 3–5 cm. This makes it possible to analyze vertical rock faces with high accuracy and supports both susceptibility assessments and mitigation strategies for rockfalls [17]. UAV-derived models not only provide point cloud data representing 3D spatial information but also integrate RGB color attributes for each point [18]. Field observations indicate that discontinuities often exhibit distinct gray-black coloration, contrasting sharply with surrounding rock surfaces. This chromatic differentiation offers a potential pathway for automated identification and interpretation of discontinuities.

Building on these insights, this study proposes an intelligent discontinuity identification method leveraging RGB information from high-precision UAV models. The approach integrates geometric normalization on the basis of principal component analysis (PCA), multi-channel gradient fusion, and cascaded edge detection to achieve the recognition and segmentation of discontinuity point clouds. By utilizing the 3D spatial information of discontinuity point clouds, the orientations of different discontinuities are subsequently calculated. Following these combined methods, a high-precision UAV model was constructed for a slope in the Qinling Belt of northern Shanxi Province, China, to identify and statistically characterize discontinuities. On the basis of the results, discontinuity sets were grouped and analyzed. The proposed method significantly enhances the efficiency of discontinuity acquisition and analysis in rock slopes, thereby further advancing research on rock slope hazard assessment.

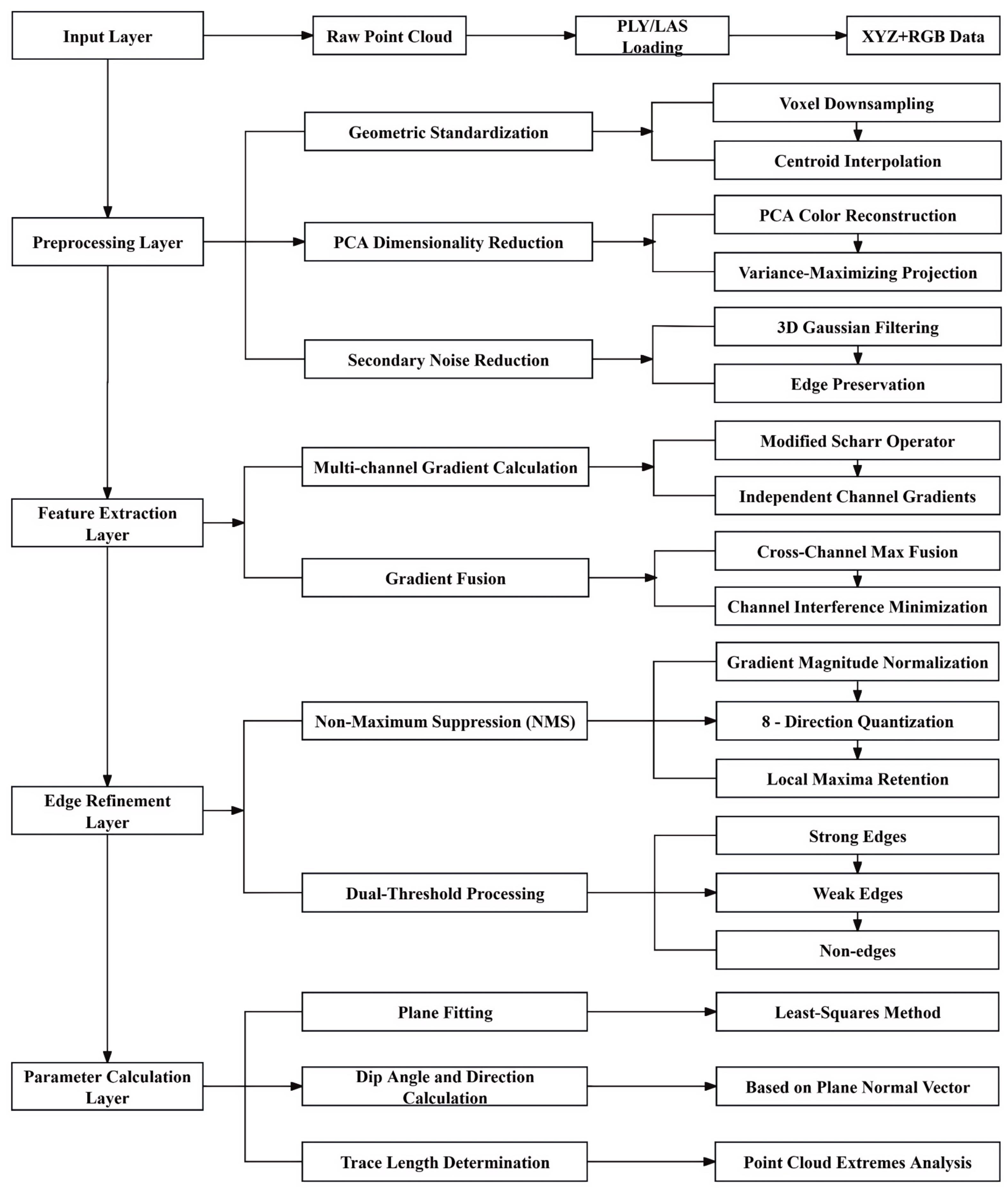
2. Methods

To meet the requirement of the intelligent recognition of rock discontinuities, a new framework for the detection of their edges is proposed in this paper. It combines dimensionality reduction, multichannel gradient analysis, and an adaptive threshold. This automated workflow is optimized for parallel computation by Python 3.10 programming and consists of three core modules: geometric normalization on the basis of principal component analysis (PCA), multi-channel gradient fusion, and cascaded edge detection. Its technical structure is shown and described in Figure 1.

2.1. Geometric Standardization with PCA

Drone-captured 3D point clouds contain spatial coordinates (XYZ) and RGB color information, providing comprehensive geometric and spectral data. However, for edge detection of rock discontinuities, the high-dimensional complexity of 3D point clouds introduces challenges such as noise, redundancy, and illumination sensitivity. Therefore, point cloud preprocessing is essential to enhance edge pixel features and establish the foundation for accurate discontinuity edge identification.

This paper first applies geometric standardization to normalize the spatial distribution of point cloud, ensuring consistent input dimensions to simplify matrix operations and memory management. Additionally, large-scale point clouds contain millions of points, and the time complexity of subsequent operations increases quadratically with point count. Thus, voxel-based downsampling [19] is employed to reduce computational load while preserving structural features. To avoid geometric distortion during downsampling, a centroid-based interpolation method is adopted, which retains critical geometric and color information.

To enhance dominant color variations in point cloud RGB channels while suppressing noise, we employ PCA [20,21] for dimensionality reduction. PCA is applied to the RGB color space of the point cloud to identify the direction of maximum variance in color distribution. By projecting the RGB data onto the principal component via variance-maximizing reconstruction, the algorithm retains dominant color patterns (e.g., salient edges or homogeneous regions) while isolating zero-mean noise. This step amplifies color contrasts critical for discontinuity detection and reduces redundancy across channels.

2.2. Multi-Channel Gradient Fusion

Although PCA reconstruction reduces channel-specific noise, residual high-frequency noise may persist in the point cloud. A secondary denoising step using gradient computation is implemented. First, 3D Gaussian filtering [22] is applied to the RGB channels of the point cloud to suppress noise through weighted averaging on the basis of spatial proximity and color similarity between neighboring points while preserving edge structures.

Next, multi-channel gradient computation is performed on the RGB channels by use of a modified Scharr operator adapted for 3D point clouds. Horizontal and vertical gradients are calculated within the 2D projection plane of the point cloud. Compared with single-channel gradient calculation, multi-channel calculation can capture edge information only existing in specific color channel by analyzing gradient of each channel independently, so as to avoid missed detection caused by relying on single channel. At the same time, the gradient responses of multiple channels are synthesized, the channel information with the least interference is automatically selected, and the maximum values among the channels are fused. The gradient magnitude and direction for each RGB channel are computed independently. To fuse multi-channel gradients, the maximum gradient magnitude across channels is selected at each point, ensuring robust edge preservation under varying lighting and color conditions. This fusion strategy prioritizes the channel with the most significant color contrast, improving detection accuracy in complex scenes.

These preprocessing steps collectively ensure that subsequent edge detection algorithms operate on high-quality and consistent gradient information, laying the foundation for generating precise and continuous edge structures.

2.3. Cascaded Edge Detection

Edge detection is crucial for intelligent rock discontinuity recognition, with high-performance edge detection operators being essential for achieving optimal detection outcomes. At present, the mainstream edge detection methods are mainly on the basis of the principle of differential operation and feature analysis. The representative algorithms include the Roberts operator, Sobel operator, and Prewitt operator on the basis of the first-order differential; the Laplacian operator [23] on the basis of the second-order differential; wavelet transform on the basis of multi-scale analysis; morphological method on the basis of topological features; and the Phase Congruency algorithm [24] combined with phase consistency. Among them, the Canny edge detection operator [25] shows significant advantages due to its unique algorithm design. Building on the principles of the Canny algorithm, we integrate non-maximum suppression, a dual-threshold mechanism, and edge smoothing to identify discontinuity edges from the 2D planes converted from 3D point cloud RGB information. At the same time, parallel computing is adopted to optimize the processing speed of the algorithm, so as to achieve rapid batch processing of massive point cloud data, save data processing time, and improve efficiency.

Non-maximum suppression (NMS) refines edges by comparing the gradient amplitudes of adjacent pixels along the gradient direction, retaining only local maxima and suppressing non-maximum gradient amplitudes. First, gradient magnitudes are normalized to ensure scale consistency across the point cloud. Non-maximum suppression (NMS) is then applied to refine edges by comparing the gradient amplitudes of neighboring points along the gradient direction. Specifically, for each point in the 3D point cloud, NMS checks the two immediate neighbors aligned with its gradient direction (quantized into 8 discrete intervals, e.g., 0°, 45°, 90°, etc.). If the current point’s gradient magnitude is not the maximum among these three points, it is suppressed as a non-edge. This process eliminates spurious edges caused by noise or redundant detections from multi-channel gradient fusion, thereby avoiding artifacts such as “double edges” or blurred boundaries.

To adapt NMS to 3D data, gradient directions are projected onto a 2D plane for quantization, and neighborhood comparisons are performed within this plane. Each quantized direction defines a unique comparison axis (e.g., horizontal, vertical, or diagonal), determining which neighboring points are evaluated. By retaining only local maxima, NMS suppresses amplitude fluctuations induced by sensor noise or minor color variations between RGB channels, ensuring that edges follow the dominant gradient direction with high spatial coherence. Additionally, the quantization of gradient directions standardizes edge topology, enabling the continuous tracing of discontinuities even in geometrically complex regions.

Threshold selection serves as the “quality controller” in edge detection, directly impacting result efficacy by striking a balance between sensitivity (detecting faint edges) and specificity (suppressing noise). A custom dual-threshold mechanism is adopted by use of empirically optimized thresholds to categorize pixels into three classes, as

Table 1. Overview of Threshold Selection List.

Edges Characteristic	Threshold	Detailed Description
Strong edges	M ≥ high threshold	High-confidence edges with significant gradient magnitudes.
Weak edges	low threshold ≤ M < high threshold	High-confidence edges with significant gradient magnitudes.
Non-edges	M < low threshold	Discarded as irrelevant noise.

shows.

This dual-threshold strategy maximizes the retention of genuine weak edges while enhancing edge continuity. Proper threshold settings enable the algorithm to achieve high-precision, low-noise edge extraction in complex geological scenes.

To adapt to large-scale point cloud processing, a parallel architecture distributes sub-regions of the point cloud across CPU cores using ProcessPoolExecutor. Dynamic task allocation minimizes idle cores, achieving near-linear speedup. The design of cascade edge detection can improve the practicability of the algorithm in complex geological scenes while ensuring edge accuracy.

2.4. Geometric Parameter Calculation of Discontinuity

In this study, the optimal plane was fitted via the least-squares method for the identified and segmented discontinuity sets. The fitted plane can be represented by Equation (1), with its normal vector given as [−A, −B, 1].

$$Ax+By-z+C=0$$

(1)

Parameters A, B, and C represent the coefficients of the plane fitted to the same structural discontinuity set using the least-squares method. On the basis of this plane equation, the dip angle α and dip direction β of the discontinuity can be calculated, as expressed by Equations (2) and (3), respectively.

When A = 0,

$$\left\{\begin{array}{l}\alpha =\left|arctan\left(B\right)\right|\\ \beta =\left\{\begin{array}{c}\pi /2,B<0\\ 3\pi /2,B>0\\ \forall ,B=0\end{array}\right.\end{array}\right.$$

(2)

When A ≠ 0,

$$\left\{\begin{array}{c}\alpha =\left|arctan\left(\sqrt{A^2+B^2}\right)\right|\\ \beta =\left\{\begin{array}{c}arctan(B/A),A<0,B\le 0\\ arctan(B/A)+2\pi ,A<0,B>0\\ arctan(B/A)+\pi ,A>0\end{array}\right.\end{array}\right.$$

(3)

The trace length d of the discontinuity is determined by measuring the maximum distance between the two farthest points in the point cloud, calculated via Equation (4):

$$\mathrm{d}=\sqrt{{({\mathrm{x}}_1-{\mathrm{x}}_2)}^2+{({\mathrm{y}}_1-{\mathrm{y}}_2)}^2+{({\mathrm{z}}_1-{\mathrm{z}}_2)}^2}$$

(4)

3. Data Acquisition

3.1. Overview of the Study Slopes

In this study, a slope in the North Qinling Belt of Shanxi Province, China, was selected as a case study in Figure 2. The slope has a height of about 120 m, a dip direction of N009° E, and a gradient of 80°. The lithology of the slope consists of slightly weathered monzonitic granite. Influenced by shear stress associated with regional tectonic evolution, numerous shear joints have developed on the slope surface, including a small fault and several sets of gently dipping discontinuities (S1), ranging in scale from 2 to 60 m. In addition, the slope features a prominent set of steeply dipping discontinuities that are generally aligned with the slope’s orientation and are relatively large in scale (S2). Another set of steeply dipping oblique discontinuities (S3), oriented nearly perpendicular to the slope’s dip direction, is also observed. These multiple sets of discontinuities divide the rock mass into blocky structural units, resulting in a distinctly blocky and discontinuous rock structure.

3.2. Field Work Framework for UAV Operations

To obtain a high-quality 3D model of the slope, this study employed a UAV-based multi-angle nap-of-the-object photogrammetry technique for image acquisition. Building upon conventional photogrammetry, this method integrates the topographic variability of the slope and the spatial distribution of discontinuities, enabling the capture of high-resolution images of complex rock masses.

The process began with oblique terrain-following photogrammetry to acquire the initial topographic data of the slope. The area was then subdivided into several terrain sub-units characterized by relatively gentle relief (Figure 3a). For each sub-unit, multiple close-range flight paths were planned, with priority given to capturing high-resolution images perpendicular to the slope surface (Figure 3b). On the basis of field investigations and preliminary UAV survey results, dominant discontinuity sets were identified. Additional flight paths were subsequently designed for each major set, with the camera orientation adjusted to align as closely as possible with the planes of the discontinuities (Figure 3c). Furthermore, supplementary flights were conducted in shaded or recessed areas to eliminate blind spots and ensure comprehensive high-resolution coverage of all discontinuities (Figure 3d).

According to this strategy, the DJI M300 from DJI company in China, equipped with a Zenmuse P1 camera, is employed to capture images of the slope, with the relevant parameters detailed in

Table 2. Parameters of the DJI PHANTOM 4 RTK and DJI Zenmuse P1.

UAV Platform Parameters
Positioning accuracy	1.5 cm + 1 ppm (vertical), 1 cm + 1 ppm (horizontal)
Maximum speed	14 m/s
Operation temperature Flight duration	0 °C to 40 °C
	30 min
Camera Parameters
Lens	DJI DL 24 mm F2.8 LS ASPH, FOV 84°
Image dimensions	8192 × 5460 with 45 MP effective pixels
Sensor size	35.9 × 24 mm

. The initial topographic survey was conducted at a flight altitude of 255 m, with 80% forward overlap and 60% side overlap. A total of 1245 images were collected, covering an area of approximately 0.3 km². The images were imported into DJI Terra (Mapping Version) software to automatically generate a preliminary digital elevation model (DEM). On the basis of the DEM, the slope was divided into two terrain sub-units, and multi-angle close-range flight paths were planned for each. During this phase, the UAV operated at a speed of 1.5 m/s, with 85% forward overlap and 70% side overlap. A total of 625 high-resolution images were acquired.

4. Results

4.1. The Results of UAV-Based Multi-Angle Nap-of-the-Object Photogrammetry Modeling

High-resolution images acquired from the multi-angle close-range flights enabled the generation of a precise 3D point cloud model measuring 176 × 127 m, with 26.48 million points at an average spacing of 8 mm (Figure 4). The model clearly reveals the textures of discontinuity surfaces, enabling accurate identification of even narrow-aperture features, thus providing a critical data foundation for subsequent structural analysis.

4.2. Discontinuity Identification Results

In the discontinuity identification algorithm, the configuration of numerical parameters plays a decisive role in detection accuracy, noise robustness, and computational efficiency. According to the characteristics of complex lighting conditions and high vegetation coverage in the study area, firstly, the image size of the study area is unified, and the threshold interval of strong edge and weak edge is defined. Then, the image denoised by PCA is filtered by a Gaussian filter with a kernel of 9 × 9. The setting of this parameter can effectively suppress the vegetation texture interference and sensor noise while maintaining the macro continuity of the discontinuity edge. Through repeated experiments, we found that the effect of selecting a low threshold of 150 and a high threshold of 350 to identify the discontinuity on the slope in the study area is better. We identified discontinuities within the entire model of the slope, ultimately obtaining 1401 discontinuity surfaces, as detailed in Figure 5.

4.3. Statistical Characterization of Discontinuities

The orientation of each discontinuity was calculated by use of the method described in Section 2.4. Statistical analysis was performed on the 1401 discontinuities identified in the slope. The 1401 discontinuities were input into the DIPS 7.0 software, which generated a pole density map of the slope’s discontinuities. Three different groups could be identified in the pole density map (Figure 6a). Further classification was carried out and the discontinuity information was visualized through Origin 2024 software, as shown in Figure 6.

The first group (272 discontinuities) corresponds to a high-density cluster in the southern sector of the pole density plot, exhibiting a near E-W strike with a mean dip direction of N095° E and steep dip angle of 80°. These steeply inclined discontinuities display concentrated strike orientations, as evidenced by a pronounced E-W trend in the rose diagram. Probability density function (PDF) analysis indicates their trace lengths follow a log-normal distribution, peaking in the 2~5 m range and dominated by short traces.

The second group (258 discontinuities) forms a low-angle cluster in the southwestern sector, characterized by a dip direction of N195° E and gentle dip angle of 15°, representing subhorizontal features. Their near N-S strike distribution contrasts sharply with Group 1. Although trace lengths similarly adhere to a log-normal distribution, the frequency peak is slightly lower, with short traces (<5 m) predominating and rare occurrences exceeding 20 m.

Group 3 (871 discontinuities), the most prevalent cluster, occupies the highest-density southern zone of the pole density plot. These near-vertical discontinuities (dip direction: N185° E; dip angle: 85°) exhibit trace lengths conforming to a log-normal distribution, with maximum probability density in the 3–6 m range. An extended distribution tail suggests a significant population of long traces (>10 m).

5. Conclusions and Discussion

This study proposes an intelligent discontinuity identification method leveraging RGB information from high-precision UAV models. The specific conclusions are described as follows:

(1)

The algorithm proposed in this paper performs well in the identification of rock discontinuities and can effectively identify structural traces in complex environments and to some extent suppress the influence of interference factors such as illumination, vegetation, and color mutation. However, there is still room for improvement in missed detection, false detection, and trace continuity. Future research can further optimize the algorithm to improve its detection accuracy and robustness under complex conditions.

(2)

All groups of discontinuities in the study slope exhibit log-normal trace length distributions dominated by short traces, with limited long-trace occurrences. The systematic spatial organization and maturity of the discontinuity network strongly imply tectonic controls, consistent with regional structural frameworks. This statistical framework enhances the efficiency of discontinuity characterization while advancing methods for rock slope hazard assessment.

(3)

The occurrence of rock mass discontinuities and their spatial relationship with slope surfaces give rise to two distinct types of discontinuities. One manifests as planar discontinuities approximately parallel to the slope surface, while the other presents as linear structural features formed by intersections with the slope surface, which are commonly referred to as lineation. The technical workflow proposed in this study specifically focuses on lineation that exhibits significant color contrast with slope surfaces. Regarding the identification of planar discontinuities, extensive research has been conducted by numerous scholars, such as Pola et al. [26] and Chen et al. [27]. Both types of discontinuities require consideration in subsequent rock slope hazard assessments. Therefore, the technical framework we propose serves as a supplement to previous research. In practical engineering applications, these two identification methodologies should be employed in combination.