A Hybrid Optimization Algorithm for the Synthesis of Sparse Array Pattern Diagrams
Abstract
1. Introduction
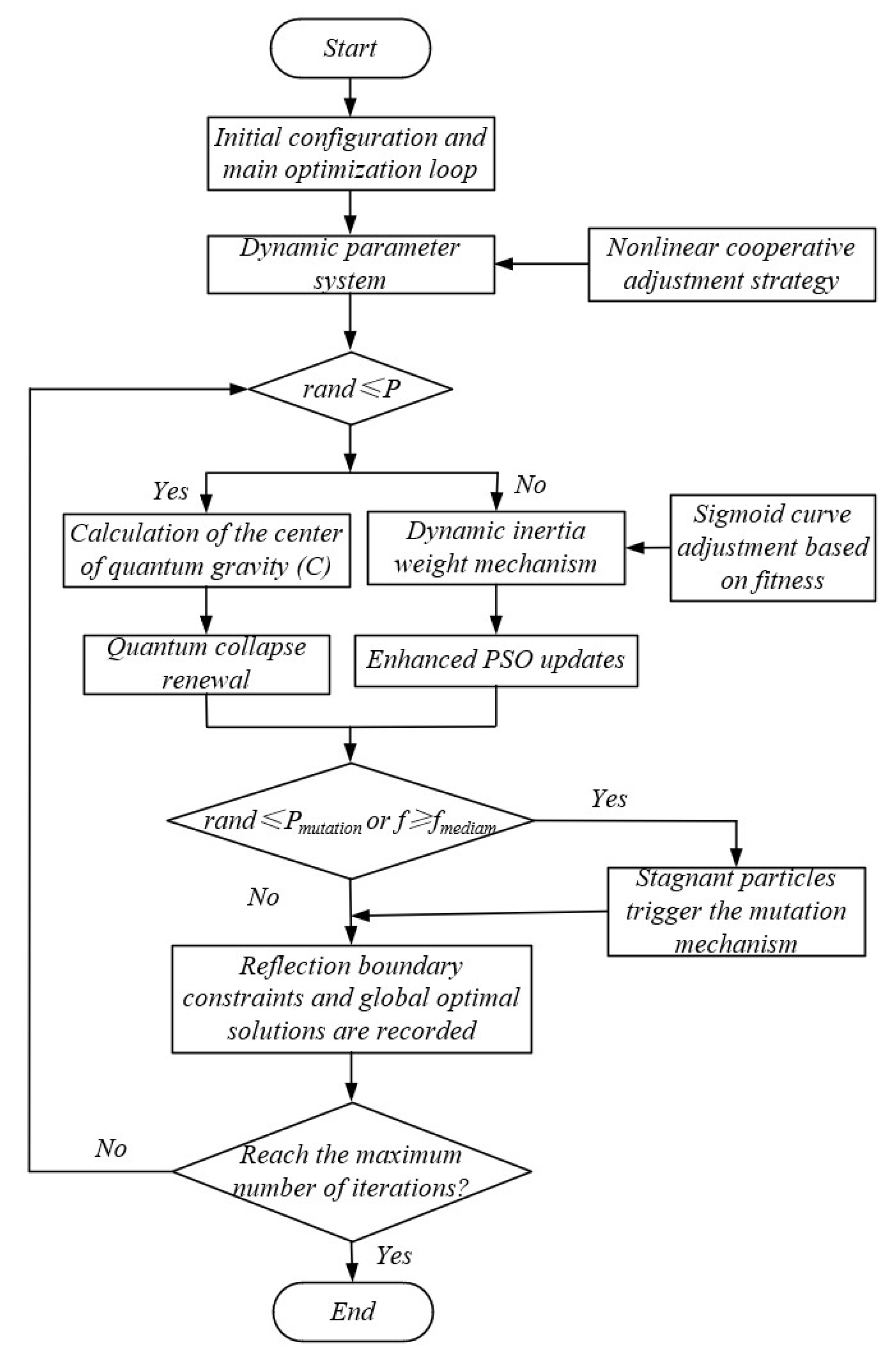
2. Quantum Hybrid Particle Swarm Optimization Algorithm Combined with Quantum Behavior
2.1. Classical Particle Swarm Optimization Algorithm
2.2. Quantum-Behaved Optimization Algorithm
2.3. Quantum-Behaved Particle Swarm Optimization Algorithm
| Algorithm 1 Quantum-behaved Particle Swarm Optimization Algorithm |
| Input: Population size M, maximum generations , search space constraints: , , Initial parameters: , , , , Output: the optimal result Initialization Initialize population: , Initialize personal bests , for to do and , If ( satisfies the first item in Equation (9)) then The quantum gravitational center is calculated by Equation (8), and then by Equations (6), (7), (11) to (13) The update of its particle positions mainly relies on the first term of Equation (9) Else Update the inertia weight and learning factor through (3) to (5) The update of the positions of its particle swarm relies on the second term in Equation (9) If ( satisfies Equation (14)) then The stop particle triggers the mutation operation through Equation (14) The updated particle positions and boundaries are shown in Equations (15) and (16) else Retain the population positions end if Select the best individuals in the population and retain them for the next generation end for return Outputs |
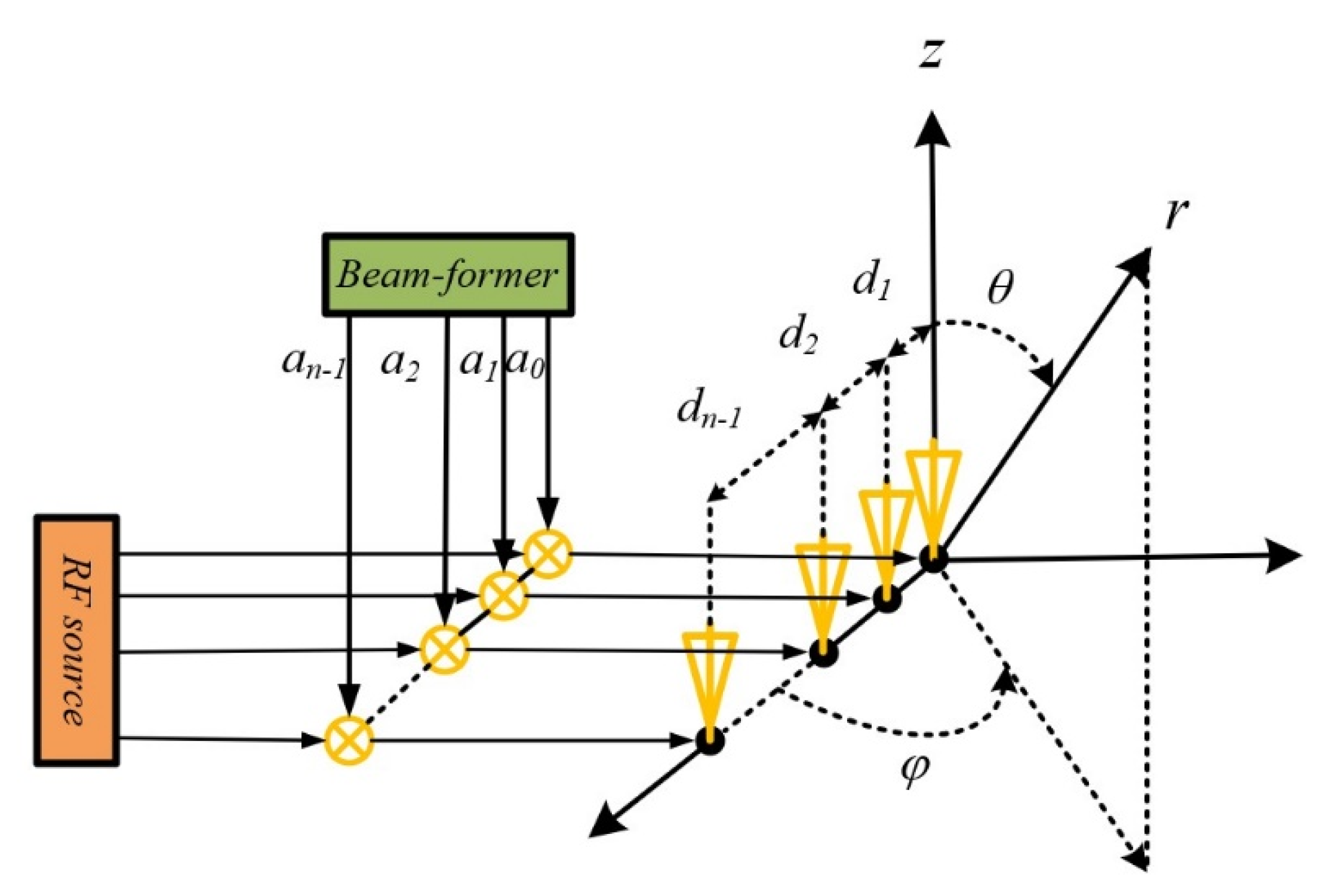
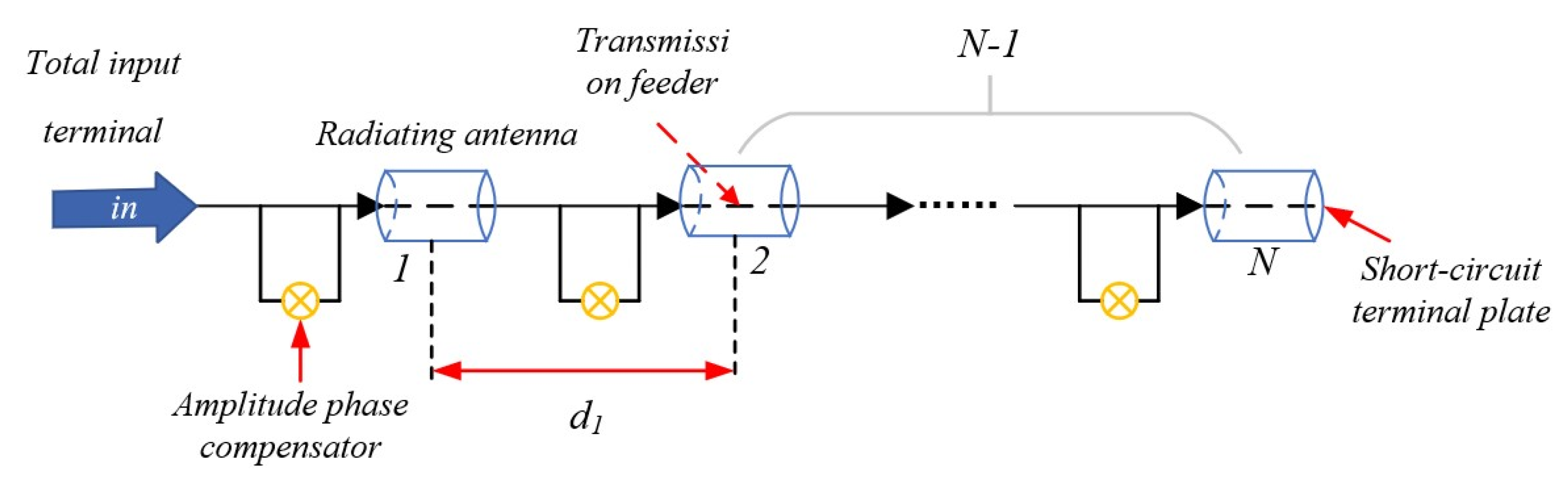
3. Experiments and Analyses
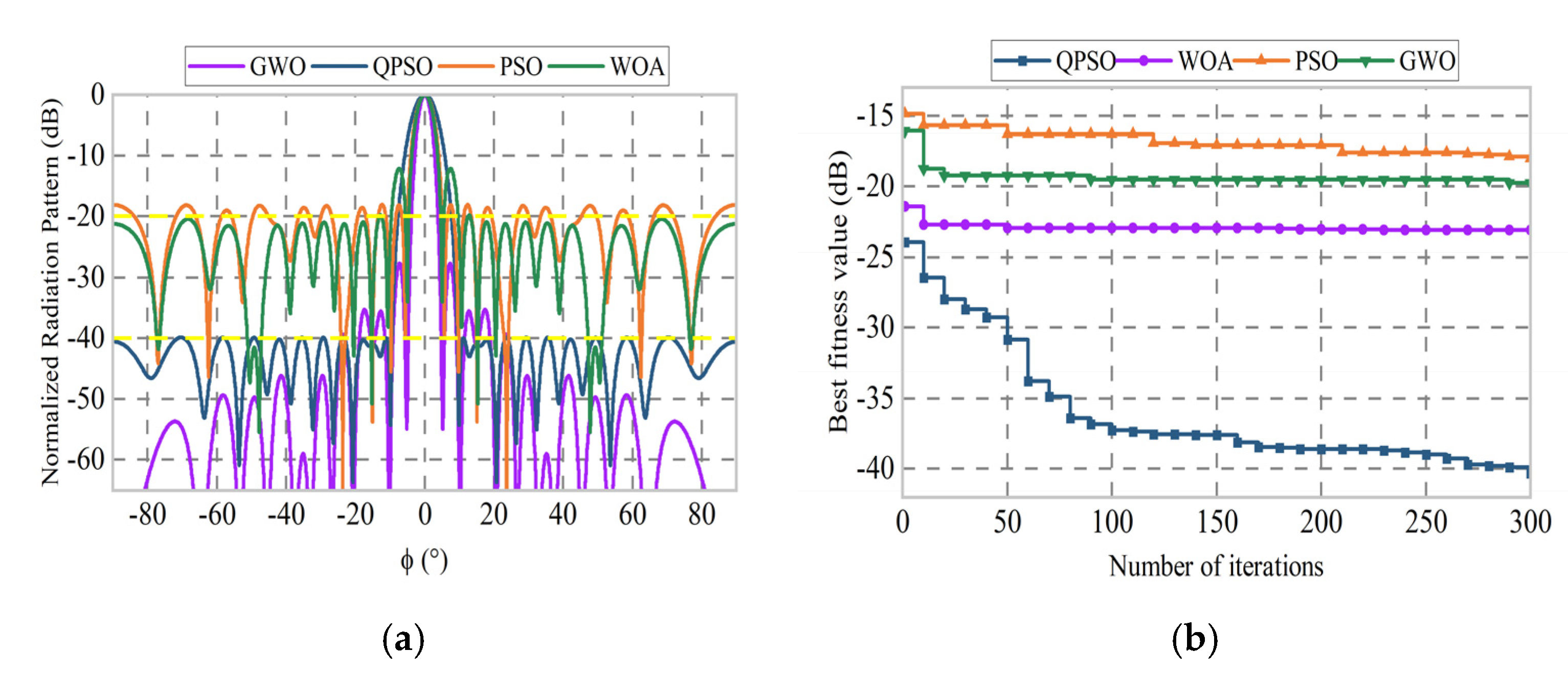
3.1. Sparse Linear Array Simulation Test
3.2. Sparse Matrix Simulation Test
3.3. Sparse Multi-Ring Concentric Circular Array
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QPSO | Quantum-behaved particle swarm optimization algorithm |
| WOA | Whale optimization algorithm |
| LFPSO | Levi’s flying particle swarm optimization |
| PSLL | Peak sidelobe level |
| GWO | Grey wolf optimization algorithm |
| AOA | Arithmetic optimization algorithm |
| CGA | Chaotic genetic algorithm |
| DEA | Differential evolution algorithm |
| ICO | Iterative convex optimization algorithm |
References
- Ma, W.; Zhu, L.; Zhang, R. Multi-beam forming with movable-antenna array. IEEE Commun. Lett. 2024, 28, 697–701. [Google Scholar] [CrossRef]
- Saeed, M.A.; Nwajana, A.O. A review of beamforming microstrip patch antenna array for future 5G/6G networks. Front. Mech. Eng. 2024, 9, 1288171. [Google Scholar] [CrossRef]
- Geyi, W. The method of maximum power transmission efficiency for the design of antenna arrays. IEEE Open J. Antennas Propag. 2021, 2, 412–430. [Google Scholar] [CrossRef]
- Zhang, L.; Marcus, C.; Lin, D.; Mejorado, D.; Schoen, S.J.; Pierce, T.T.; Kumar, V.; Fernandez, S.V.; Hunt, D.; Li, Q.; et al. A conformable phased-array ultrasound patch for bladder volume monitoring. Nat. Electron. 2024, 7, 77–90. [Google Scholar] [CrossRef]
- Ji, L.; Ren, Z.; Chen, Y.; Zeng, H. Large-Scale Sparse Antenna Array Optimization for RCS Reduction with an AM-FCSN. IEEE Sens. J. 2024, 25, 5782–5794. [Google Scholar] [CrossRef]
- Owoola, E.O.; Xia, K.; Wang, T.; Umar, A.; Akindele, R.G. Pattern synthesis of uniform and sparse linear antenna array using mayfly algorithm. IEEE Access 2021, 9, 77954–77975. [Google Scholar] [CrossRef]
- Wu, P.; Liu, Y.-H.; Zhao, Z.-Q.; Liu, Q.-H. Sparse antenna array design methodologies—A review. J. Electron. Sci. Technol. 2024, 22, 100276. [Google Scholar] [CrossRef]
- Shao, W.; Hu, J.; Ji, Y.; Zhang, W.; Fang, G. W-Band FMCW MIMO System for 3-D Imaging Based on Sparse Array. Electronics 2024, 13, 369. [Google Scholar] [CrossRef]
- Chen, D.; Schlegel, A.; Nanzer, J.A. Imageless contraband detection using a millimeter-wave dynamic antenna array via spatial fourier domain sampling. IEEE Access 2024, 12, 149543–149556. [Google Scholar] [CrossRef]
- Yangyu, X.; Weimin, J.; Fenggan, Z. Pattern optimization of thinned linear arrays based on improved cuckoo search algorithm. Mod. Electron. Tech. 2021, 44, 7–12. [Google Scholar]
- Xue, T.; Bin, W.; Jingrui, L. A synthesis method for thinned linear arrays based on improved sparrow search algorithm. J. Microw. 2022, 38, 43–51. [Google Scholar]
- Zhang, S.R.; Zhang, Y.X.; Cui, C.Y. Efficient multiobjective optimization of time-modulated array using a hybrid particle swarm algorithm with convex programming. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1842–1846. [Google Scholar] [CrossRef]
- Tinh, N.D. Optimization of Radiation Pattern for Circular Antenna Array using Genetic Algorithm and Particle Swarm Optimization with Combined Objective Function. IEIE Trans. Smart Process. Comput. 2024, 13, 579–586. [Google Scholar]
- Zang, Z.; Wu, J.; Huang, Q. Design of an Aperiodic Optical Phased Array Based on the Multi-Strategy Enhanced Particle Swarm Optimization Algorithm. Photonics 2025, 12, 210. [Google Scholar] [CrossRef]
- Zhu, T.; Liu, Y.; Li, J.; Zhao, W. Optimization of time modulated array antennas based on improved gray wolf optimizer. AIP Adv. 2025, 15, 025126. [Google Scholar] [CrossRef]
- Bouchachi, I.; Reddaf, A.; Boudjerda, M.; Alhassoon, K.; Babes, B.; Alsunaydih, F.N.; Ali, E.; Alsharef, M.; Alsaleem, F. Design and performances improvement of an UWB antenna with DGS structure using a grey wolf optimization algorithm. Heliyon 2024, 10, e26337. [Google Scholar] [CrossRef] [PubMed]
- Amiriebrahimabadi, M.; Mansouri, N. A comprehensive survey of feature selection techniques based on whale optimization algorithm. Multimed. Tools Appl. 2024, 83, 47775–47846. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R. Multistrategy improved whale optimization algorithm and its application. Comput. Intell. Neurosci. 2022, 2022, 3418269. [Google Scholar] [CrossRef] [PubMed]
- Xu, C. Application of Improved Particle Swarm Optimization in Array Antenna Beamforming. Master’s Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2022. [Google Scholar] [CrossRef]
- Zhang, T.Y. Research on Sparse Array Optimization Based on Intelligent Optimization Algorithms. Ph.D. Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2024. [Google Scholar] [CrossRef]
- Zhao, Y.D.; Fang, Z.H. Particle swarm optimization algorithm with weight function learning factors. J. Comput. Appl. 2013, 33, 2265–2268. [Google Scholar]
- Yang, C.X.; Zhang, J.; Tong, M.S. A hybrid quantum-behaved particle swarm optimization algorithm for solving inverse scattering problems. IEEE Trans. Antennas Propag. 2021, 69, 5861–5869. [Google Scholar] [CrossRef]
- Fahad, S.; Yang, S.; Khan, S.U.; Khan, S.A.; Khan, R.A. A hybrid smart quantum particle swarm optimization for multimodal electromagnetic design problems. IEEE Access 2022, 10, 72339–72347. [Google Scholar] [CrossRef]
- Xue, W. An Improved Particle Swarm Optimization Algorithm with Inertia Weight. Mod. Inf. Technol. 2023, 7, 88–91. [Google Scholar] [CrossRef]
- Zheng, S.; Zhao, X.; Zhang, C.; Li, Y.; Chai, M. Multi-objective optimization of hydraulic performance for low-specific-speed stamping centrifugal pump based on PSO algorithm. Trans. Chin. Soc. Agric. Mach. 2025, 56, 353–360. [Google Scholar]
- Zhao, Z.H.; Yin, Y.F.; Wang, Y.K.; Qin, K.R.; Xue, C.D. Adaptive ECG Signal Denoising Algorithm Based on the Improved Whale Optimization Algorithm. IEEE Sens. J. 2024, 24, 34788–34797. [Google Scholar] [CrossRef]
- He, J.; Hong, Z.; Sun, X.; Deng, Q.; Zhu, M.; Zhu, C.; Liu, K.; Sun, B.; Yao, J. Three-dimensional Image Reconstruction of Breast Tumor by Electrical Impedance Tomography based on Dimensional Grey Wolf Optimization Algorithm. IEEE Trans. Instrum. Meas. 2025, 74, 4504310. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, L.; Li, H.; Sun, C. Dual-Frequency Common-Cable Waveguide Slot Satellite Communication Antenna. Electronics 2025, 14, 1326. [Google Scholar] [CrossRef]
- Liu, J.L.; Wang, X.M. Synthesis of sparse arrays with spacing constraints using an improved particle swarm optimization algorithm. J. Microw. 2010, 26, 7–10. [Google Scholar] [CrossRef]
- Meng, X.M.; Cai, C.C. Synthesis of sparse array antennas based on Lévy flight particle swarm optimization. J. Terahertz Sci. Electron. Inf. Technol. 2021, 19, 90–95. [Google Scholar]
- Qiang, G.; Ye, L.C.; Ni, W.Y.; Wang, Y.; Chernogor, L. Synthesis of sparse planar arrays using an improved arithmetic optimization algorithm. J. Xidian Univ. 2023, 50, 202–212. [Google Scholar] [CrossRef]
- Jiang, W.Q.; Zhang, H.M.; Wang, X.F. Research on two-dimensional planar array based on chaotic genetic algorithm. Appl. Electron. Tech. 2023, 49, 68–72. [Google Scholar] [CrossRef]
- Cheng, D.D.; Li, Y.M.; Wei, J.; Zhang, F. Optimal design of sparse concentric ring arrays. Syst. Eng. Electron. 2018, 40, 739–745. [Google Scholar]
- Aslan, Y.; Roederer, A.; Yarovoy, A. Concentric ring array synthesis for low side lobes: An overview and a tool for optimizing ring radii and angle of rotation. IEEE Access 2021, 9, 120744–120754. [Google Scholar] [CrossRef]


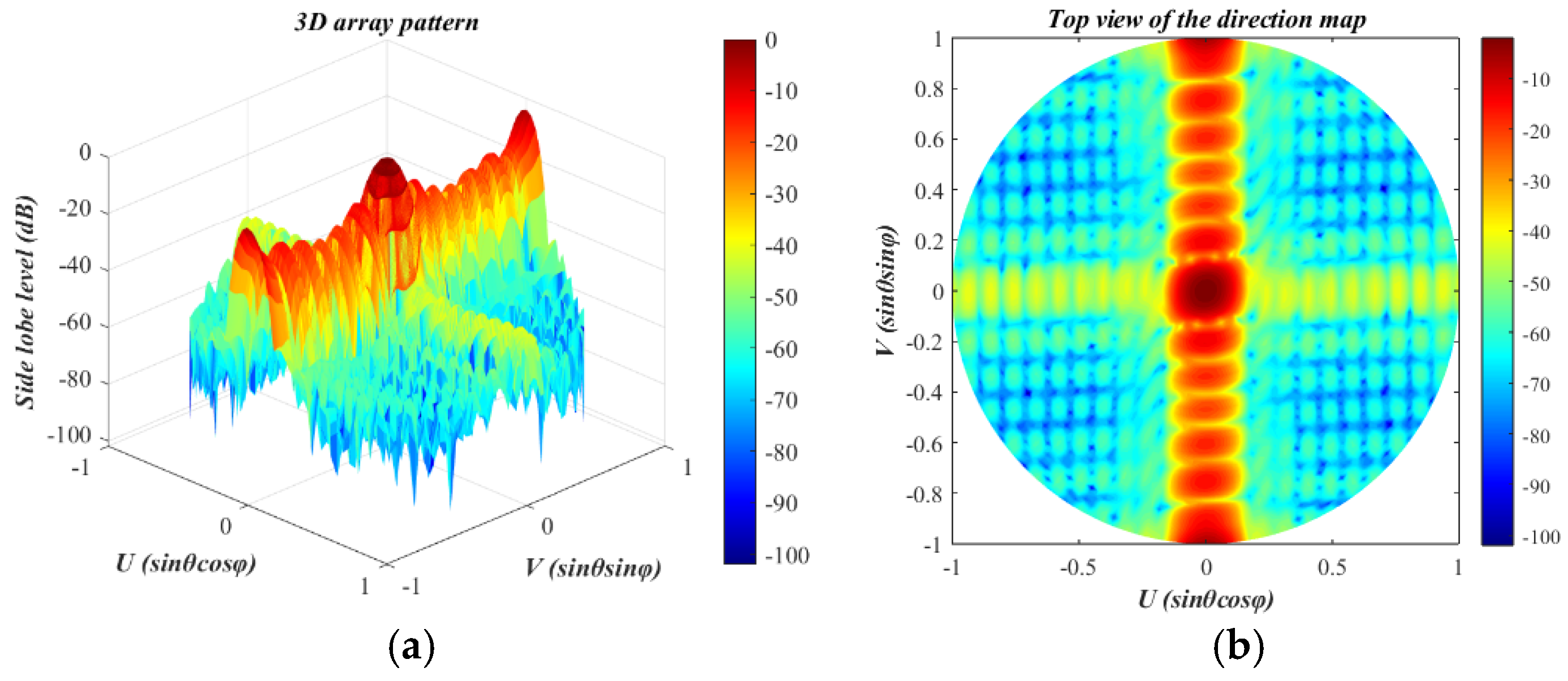
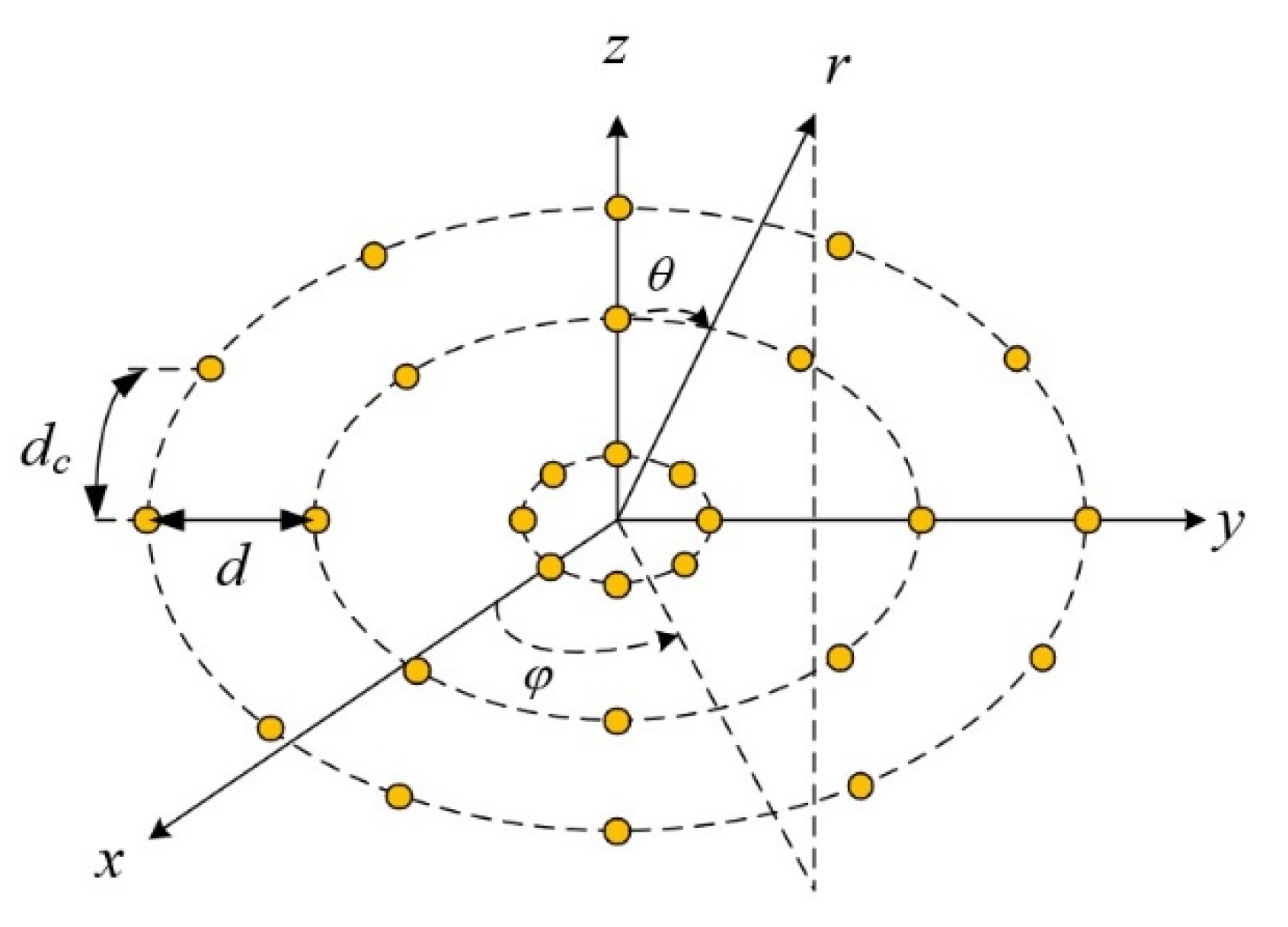
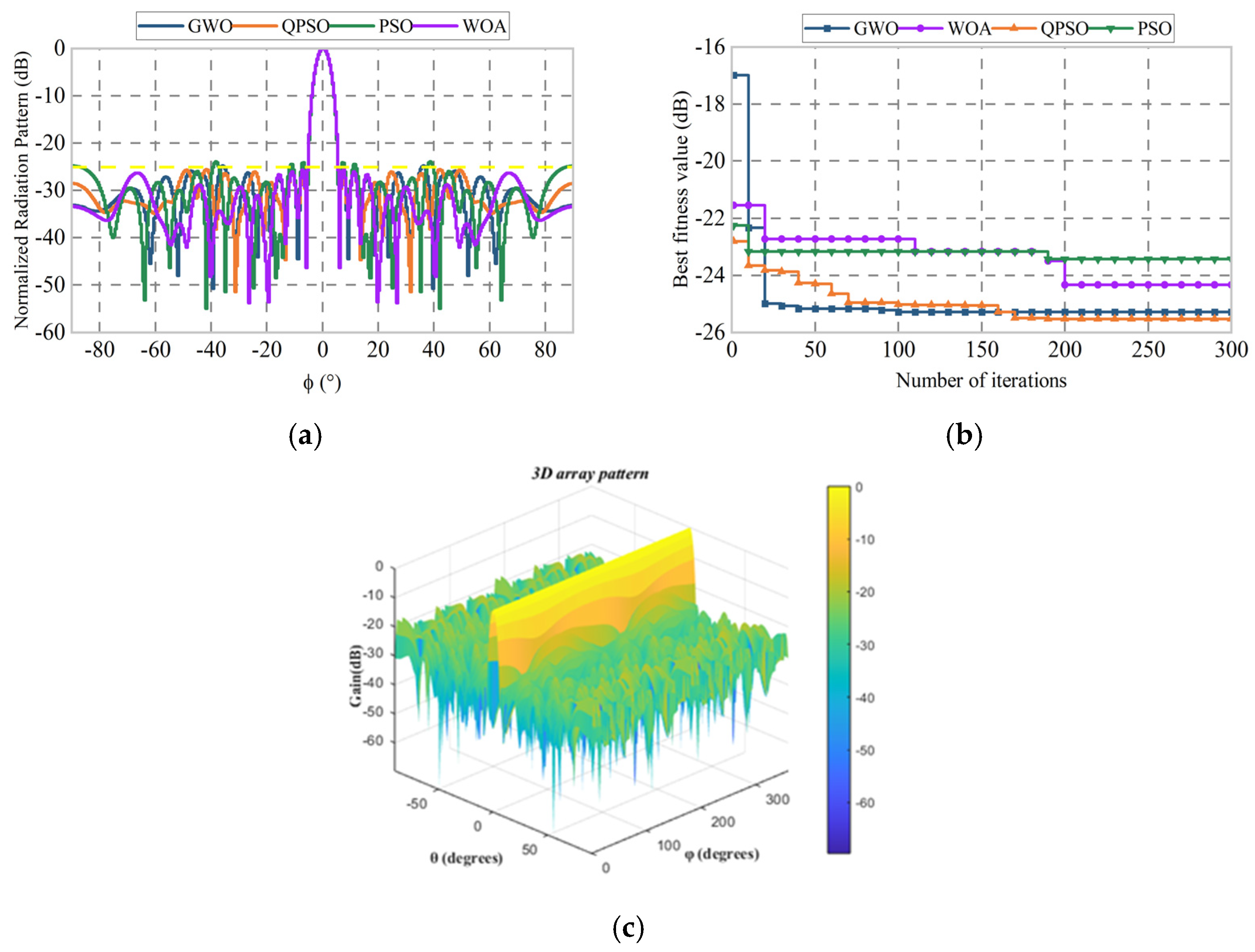
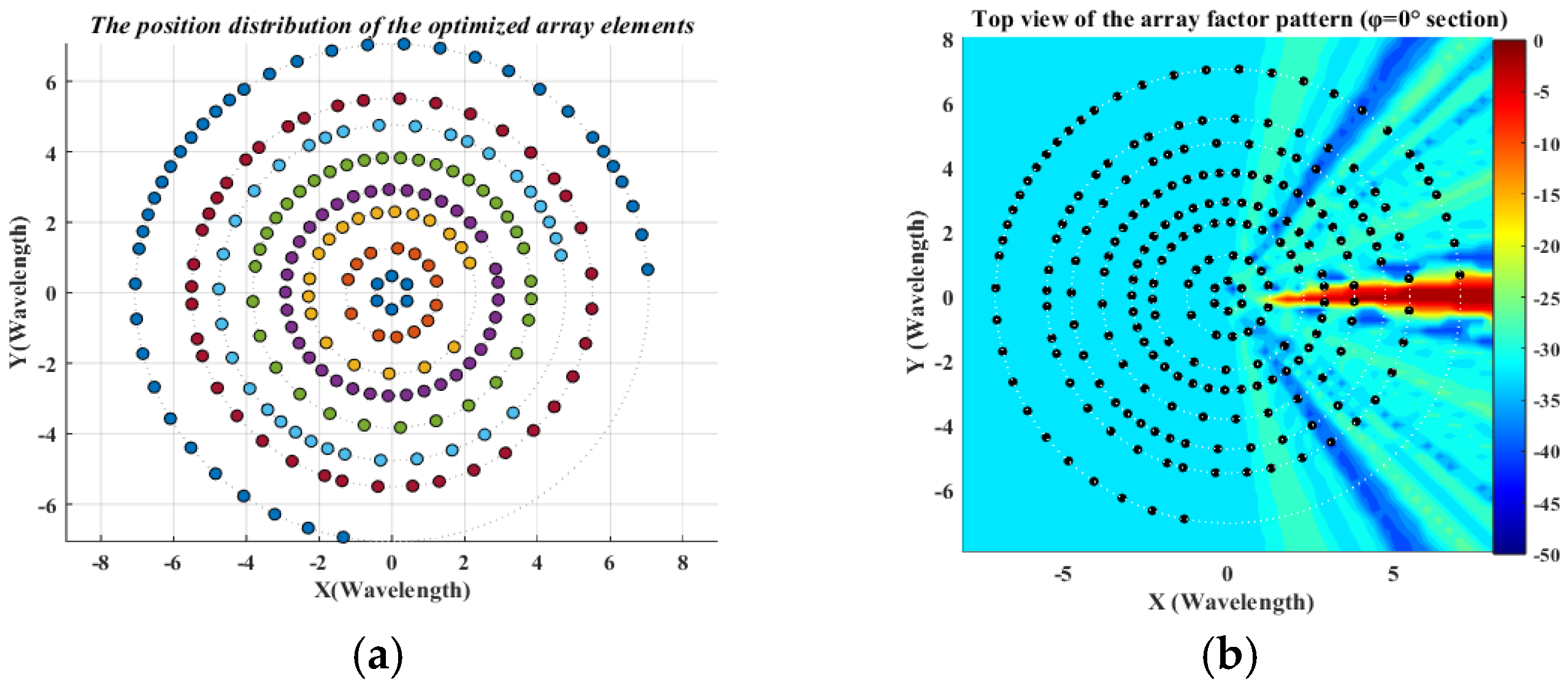
| Elements | Unit Spacing () | Elements | Unit Spacing () |
|---|---|---|---|
| 1-2 | 1 | 9-10 | 0.5000 |
| 2-3 | 0.7597 | 10-11 | 0.5000 |
| 3-4 | 0.7599 | 11-12 | 0.5670 |
| 4-5 | 0.5136 | 12-13 | 0.5683 |
| 5-6 | 0.5000 | 13-14 | 0.7792 |
| 6-7 | 0.5000 | 14-15 | 0.7821 |
| 7-8 | 0.5065 | 15-16 | 0.9157 |
| 8-9 | 0.5000 | 16-17 | 0.7761 |
| Work | Type | Array Elements | Array Type | Iterations | Spacing Requirement | PSLL (dB) |
|---|---|---|---|---|---|---|
| [29] | LFPSO | 17 | Symmetry | 500 | −19.61 | |
| [30] | PSO | 100 | −19.87 | |||
| This work | QPSO | Asymmetry | 300 | −20.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Huang, L.; Xie, X.; Ye, H. A Hybrid Optimization Algorithm for the Synthesis of Sparse Array Pattern Diagrams. Appl. Sci. 2025, 15, 6490. https://doi.org/10.3390/app15126490
Liu Y, Huang L, Xie X, Ye H. A Hybrid Optimization Algorithm for the Synthesis of Sparse Array Pattern Diagrams. Applied Sciences. 2025; 15(12):6490. https://doi.org/10.3390/app15126490
Chicago/Turabian StyleLiu, Youzhi, Linshu Huang, Xu Xie, and Huijuan Ye. 2025. "A Hybrid Optimization Algorithm for the Synthesis of Sparse Array Pattern Diagrams" Applied Sciences 15, no. 12: 6490. https://doi.org/10.3390/app15126490
APA StyleLiu, Y., Huang, L., Xie, X., & Ye, H. (2025). A Hybrid Optimization Algorithm for the Synthesis of Sparse Array Pattern Diagrams. Applied Sciences, 15(12), 6490. https://doi.org/10.3390/app15126490






