Dynamic Node Privacy Feature Decoupling Graph Autoencoder Based on Attention Mechanism
Abstract
1. Introduction
- A novel node privacy ranking algorithm that employs attention mechanisms to dynamically score the privacy features of each node, quantifying their privacy importance. This method mitigates the influence of high-privacy nodes in the embedding while retaining low-privacy nodes to ensure data utility.
- We introduce the use of the Hilbert-Schmidt Independence Criterion (HSIC) to assess the dependency relationship between privacy and non-privacy distribution, which avoids the deviations that occur when using approximate methods by means of hypothesis testing
- A dual-channel privacy graph autoencoder that decouples embedded privacy and utility features of graph data. Freezing parameters during alternating training, prevents gradient interference during backpropagation, enhancing the stability of node privacy importance measurement.
- Comprehensive evaluation on real-world graph datasets using node classification and link prediction. Experimental results show that the proposed method effectively resists inference attacks on private information in node classification. It maintains high utility in link prediction while achieving an optimal privacy-utility trade-off.
2. Related Work
3. Preliminaries
Variational Graph Autoencoder
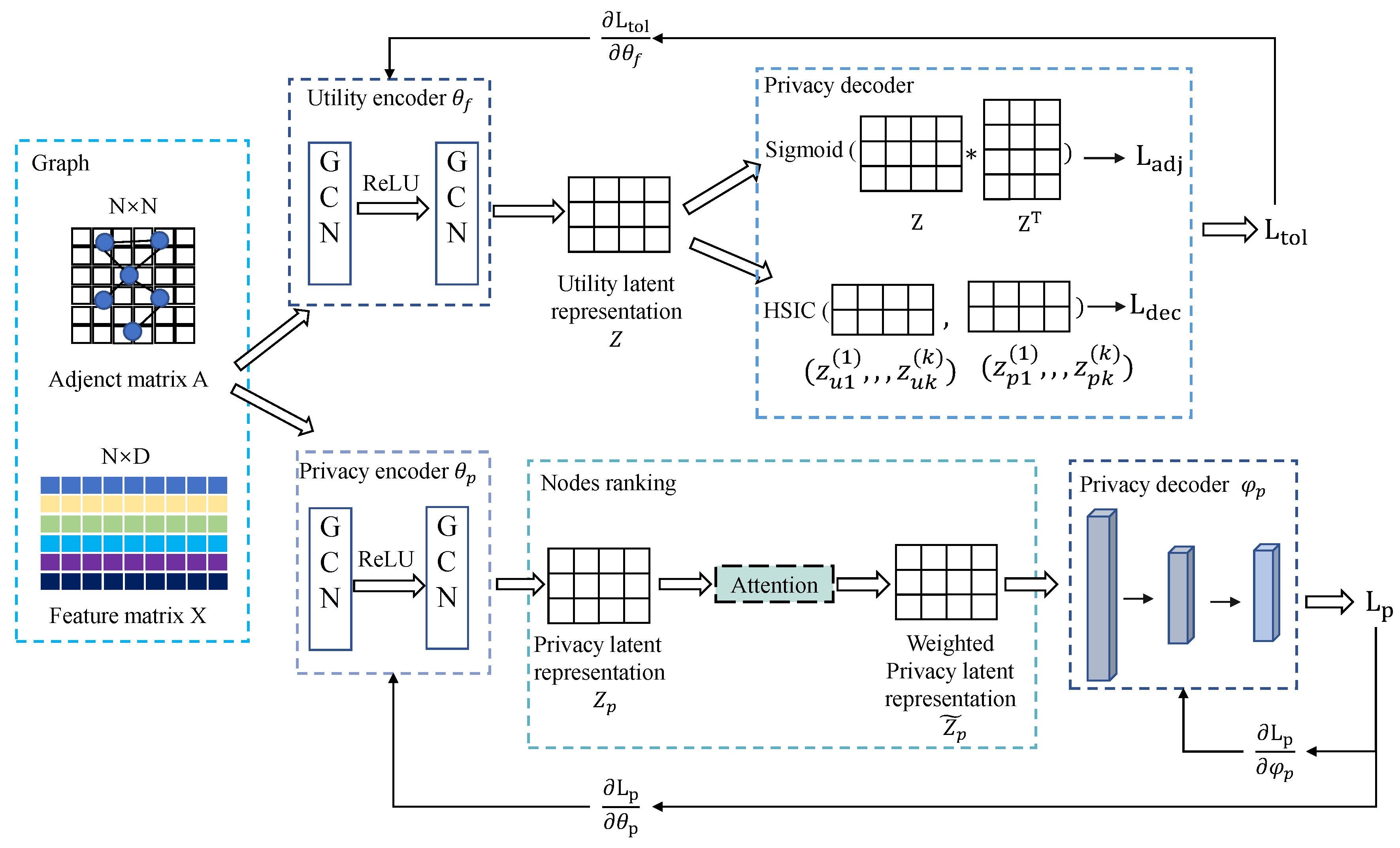
4. System Model
5. Method Details
5.1. Node Privacy Ranking by Attention
| Algorithm 1 Node Privacy Importance Ranking Algorithm |
Input: Adjacency matrix A, node features X, training epochs , learning rate , partial observed privacy information P Output: Node privacy importance matrix 1: Initialize network parameters , , 2: for to do 3: //Generate privacy-preserving latent representation 4: //Generate queries, keys and values through attention layer , , 5: //Normalized attention matrix 6: //Weighted aggregation of neighbor information 7: //Predicted privacy information 8: //Compute loss 9: //Update parameters via gradient descent 10: end for 11: //Compute node privacy importance score 12: return |
5.2. Privacy Decoupling Based on Node Privacy Ranking
5.3. Model Training
| Algorithm 2 Dynamic Privacy Decoupling |
Input: Adjacency matrix A, node features X, utility autoencoder epochs , utility learning rate , privacy autoencoder epochs , selected node count k Output: Publishable privacy-preserving graph embedding 1: Initialize network parameters , , 2: for to do 3: for to do 4: Compute node privacy importance scores via Algorithm 1 5: end for 6: //Generate utility latent representation 7: //Reconstruct adjacency matrix 8: //Compute reconstruction error 9: //Construct the privacy distribution 10: //Construct the non-privacy distribution 11: //Compute privacy decoupling loss 12: //Compute total utility autoencoder loss 13: //Update parameters via gradient descent 14: end for 15: return |
6. Simulation Results
6.1. Dataset and Evaluation Metrics
6.2. Compared Models, Attack Model and Parameter Settings
- (1)
- VGAE [21]: VGAE employs a variational autoencoder architecture that combines graph structure reconstruction loss with KL divergence by enforcing latent representations to fit a prior distribution, effectively achieving distributed learning of graph embeddings. Notably, this model does not incorporate any privacy protection mechanisms, thus providing a fundamental reference for evaluating the privacy protection efficacy of subsequent models.
- (2)
- PVGAE [20]: An enhanced version of the VGAE architecture that introduces a dual-encoder alternating training mechanism. By constructing variational independence constraints, it systematically eliminates privacy-sensitive information from embedded representations. This method achieves targeted privacy stripping while maintaining graph structure representation capabilities.
- (3)
- GAE-MI [24]: Adopts an adversarial training framework to simultaneously optimize utility performance and privacy protection objectives. Innovatively employs mutual information as the metric: by maximizing application utility mutual information while minimizing privacy leakage mutual information, it constructs a dual-objective optimization function. To improve computational efficiency, it uses variational lower bounds for approximation estimation, significantly reducing computational complexity while ensuring model performance.
- (4)
- APGE [25]: Based on the classical graph autoencoder architecture, proposes an extended layer fusion mechanism to encode privacy label information into latent space. Designs a dual-path adversarial training strategy: while minimizing public label prediction error, it maximizes privacy label prediction loss through adversarial optimization, thereby achieving active obfuscation of privacy information in latent space.
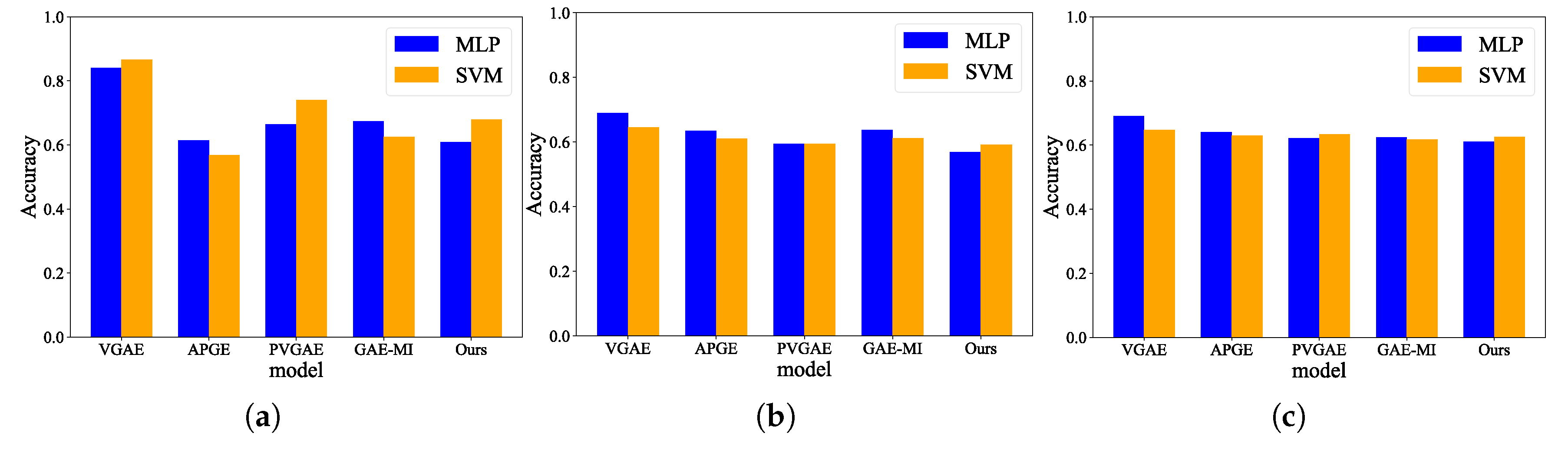
6.3. Overall Utility and Privacy Performance
6.4. The Impect of Attack Model
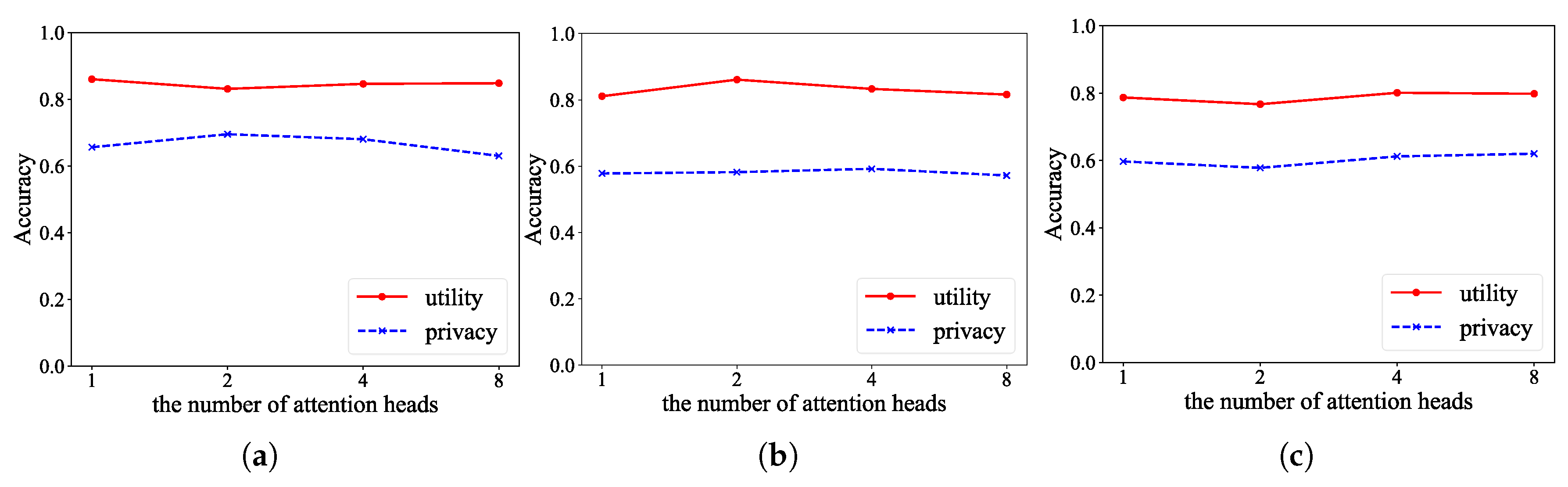
6.5. Sensitive Study
6.6. The Performance of Downstream Tasks
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agarwal, C.; Lakkaraju, H.; Zitnik, M. Towards a unified framework for fair and stable graph representation learning. In Proceedings of the Uncertainty in artificial intelligence, PMLR, Online, 27–30 July 2021; pp. 2114–2124. [Google Scholar]
- Amara, A.; Taieb, M.A.H.; Aouicha, M.B. A multi-view GNN-based network representation learning framework for recommendation systems. Neurocomputing 2025, 619, 129001. [Google Scholar] [CrossRef]
- Sharma, A.; Sharma, A.; Nikashina, P.; Gavrilenko, V.; Tselykh, A.; Bozhenyuk, A.; Masud, M.; Meshref, H. A graph neural network (GNN)-based approach for real-time estimation of traffic speed in sustainable smart cities. Sustainability 2023, 15, 11893. [Google Scholar] [CrossRef]
- Hou, Z.; Liu, X.; Cen, Y.; Dong, Y.; Yang, H.; Wang, C.; Tang, J. Graphmae: Self-supervised masked graph autoencoders. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 594–604. [Google Scholar]
- Wang, K.; Wu, J.; Zhu, T.; Ren, W.; Hong, Y. Defense against membership inference attack in graph neural networks through graph perturbation. Int. J. Inf. Secur. 2023, 22, 497–509. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chen, M.; Backes, M.; Shen, Y.; Zhang, Y. Inference attacks against graph neural networks. In Proceedings of the 31st USENIX Security Symposium (USENIX Security 22), Boston, MA, USA, 10–12 August 2022; pp. 4543–4560. [Google Scholar]
- Wang, T.; Dai, X.; Liu, Y. Learning with Hilbert–Schmidt independence criterion: A review and new perspectives. Knowl.-Based Syst. 2021, 234, 107567. [Google Scholar] [CrossRef]
- Sweeney, L. k-anonymity: A model for protecting privacy. Int. J. Uncertain. Fuzziness- Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Meyerson, A.; Williams, R. On the complexity of optimal k-anonymity. In Proceedings of the Twenty-Third ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Paris, France, 14–16 June 2004; pp. 223–228. [Google Scholar]
- Dwork, C. Differential privacy. In Proceedings of the International Colloquium on Automata, Languages, and Programming, Venice, Italy, 10–14 July 2006; pp. 1–12. [Google Scholar]
- Sajadmanesh, S.; Shamsabadi, A.S.; Bellet, A.; Gatica-Perez, D. {GAP}: Differentially private graph neural networks with aggregation perturbation. In Proceedings of the 32nd USENIX Security Symposium (USENIX Security 23), Anaheim, CA, USA, 9–11 August 2023; pp. 3223–3240. [Google Scholar]
- Mandal, B.; Amariucai, G.; Wei, S. Uncertainty-autoencoder-based privacy and utility preserving data type conscious transformation. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Bose, A.; Hamilton, W. Compositional fairness constraints for graph embeddings. In Proceedings of the International conference on machine learning. PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 715–724. [Google Scholar]
- Dai, E.; Wang, S. Say no to the discrimination: Learning fair graph neural networks with limited sensitive attribute information. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Online, 8–12 March 2021; pp. 680–688. [Google Scholar]
- Liu, J.; Li, Z.; Yao, Y.; Xu, F.; Ma, X.; Xu, M.; Tong, H. Fair representation learning: An alternative to mutual information. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1088–1097. [Google Scholar]
- Oh, C.; Won, H.; So, J.; Kim, T.; Kim, Y.; Choi, H.; Song, K. Learning fair representation via distributional contrastive disentanglement. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1295–1305. [Google Scholar]
- Lin, W.; Lan, H.; Cao, J. Graph privacy funnel: A variational approach for privacy-preserving representation learning on graphs. IEEE Trans. Dependable Secur. Comput. 2024, 22, 967–978. [Google Scholar] [CrossRef]
- Yuan, H.; Xu, J.; Wang, C.; Yang, Z.; Wang, C.; Yin, K.; Yang, Y. Unveiling privacy vulnerabilities: Investigating the role of structure in graph data. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 4059–4070. [Google Scholar]
- Duddu, V.; Boutet, A.; Shejwalkar, V. Quantifying privacy leakage in graph embedding. In Proceedings of the MobiQuitous 2020-17th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services, Darmstadt, Germany, 7–9 December 2020; pp. 76–85. [Google Scholar]
- Hu, Q.; Song, Y. Independent distribution regularization for private graph embedding. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 823–832. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; NIPS: Long Beach, CA, USA, 2017; Volume 30. [Google Scholar]
- Bloch, F.; Jackson, M.O.; Tebaldi, P. Centrality measures in networks. Soc. Choice Welf. 2023, 61, 413–453. [Google Scholar] [CrossRef]
- Wang, B.; Guo, J.; Li, A.; Chen, Y.; Li, H. Privacy-preserving representation learning on graphs: A mutual information perspective. In Proceedings of the 27th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Online, 14–18 August 2021; pp. 1667–1676. [Google Scholar]
- Li, K.; Luo, G.; Ye, Y.; Li, W.; Ji, S.; Cai, Z. Adversarial privacy-preserving graph embedding against inference attack. IEEE Internet Things J. 2020, 8, 6904–6915. [Google Scholar] [CrossRef]



| Nodes | Edges | Features | Attributes | Average Degree | |
|---|---|---|---|---|---|
| Yale | 8578 | 405,450 | 188 | 6 | 94.3 |
| Rochester | 4563 | 167,653 | 236 | 6 | 73.5 |
| Credit defaulter | 30,000 | 1,459,992 | 14 | 14 | 97.3 |
| Dataset | Model | Utility Attribute | Privacy Attribute | ||
|---|---|---|---|---|---|
| ACC | Macro-F1 | ACC | Macro-F1 | ||
| VGAE | |||||
| APGE | |||||
| Yale | PVGAE | ||||
| GAEMI | |||||
| ours | |||||
| VGAE | |||||
| APGE | |||||
| Rochester | PVGAE | ||||
| GAEMI | |||||
| ours | |||||
| VGAE | |||||
| APGE | |||||
| Credit defaulter | PVGAE | ||||
| GAEMI | |||||
| ours | |||||
| Methods | Yale | Rochester | ||
|---|---|---|---|---|
| AP | AUC | AP | AUC | |
| VGAE | ||||
| APGE | ||||
| PVGAE | ||||
| GAE-MI | ||||
| ours | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Tang, J.; Dang, S. Dynamic Node Privacy Feature Decoupling Graph Autoencoder Based on Attention Mechanism. Appl. Sci. 2025, 15, 6489. https://doi.org/10.3390/app15126489
Huang Y, Tang J, Dang S. Dynamic Node Privacy Feature Decoupling Graph Autoencoder Based on Attention Mechanism. Applied Sciences. 2025; 15(12):6489. https://doi.org/10.3390/app15126489
Chicago/Turabian StyleHuang, Yikai, Jinchuan Tang, and Shuping Dang. 2025. "Dynamic Node Privacy Feature Decoupling Graph Autoencoder Based on Attention Mechanism" Applied Sciences 15, no. 12: 6489. https://doi.org/10.3390/app15126489
APA StyleHuang, Y., Tang, J., & Dang, S. (2025). Dynamic Node Privacy Feature Decoupling Graph Autoencoder Based on Attention Mechanism. Applied Sciences, 15(12), 6489. https://doi.org/10.3390/app15126489





