Towards Geodetic Datum Modernization: A Comparative Study of GNSS Solutions in KGD2002 Using GAMIT/GLOBK and Bernese
Abstract
1. Introduction
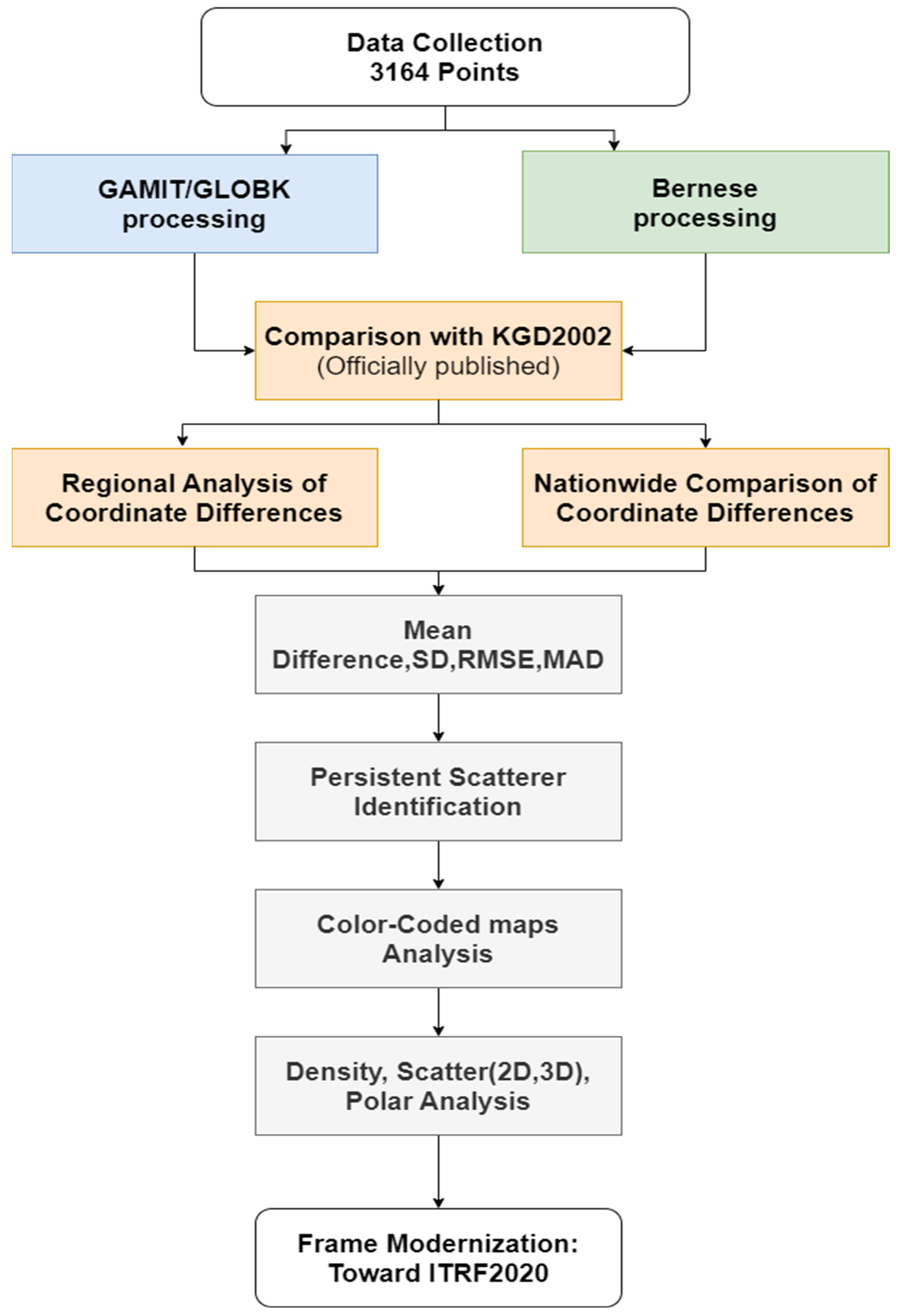
2. Materials and Methods
2.1. Study Areas
2.2. Comparison of GNSS Data Processing Strategies and Software
2.3. Analysis of ΔN/ΔE and Regional Statistics
- Mean difference (MD): The average of ΔN or ΔE across all stations, representing the overall bias or systematic offset of the solution relative to the official KGD2002 coordinates [21].
- Standard deviation (SD): The dispersion of the differences around the mean, indicating the typical magnitude of random error in the coordinate estimates [22].
- Root mean square error (RMSE): A combined measure of bias and scatter, calculated as RMSE = √(Mean2 + SD2). This metric represents the overall positional accuracy of the software-derived coordinates relative to the official KGD2002 values [23].
- Mean absolute deviation (MAD): The mean of the absolute values of ΔN or ΔE, providing a robust measure of typical error magnitude that is less affected by outliers than SD or RMSE [24].
- 95% confidence interval: The range between the 2.5th and 97.5th percentiles of the difference distribution, indicating the interval within which approximately 95% of the coordinate differences fall. Given that the distributions are generally centered near zero, this interval is approximately equivalent to ±1.96 standard deviations under the assumption of normality [25].
2.4. Methodological Strategy for Comparative GNSS Processing
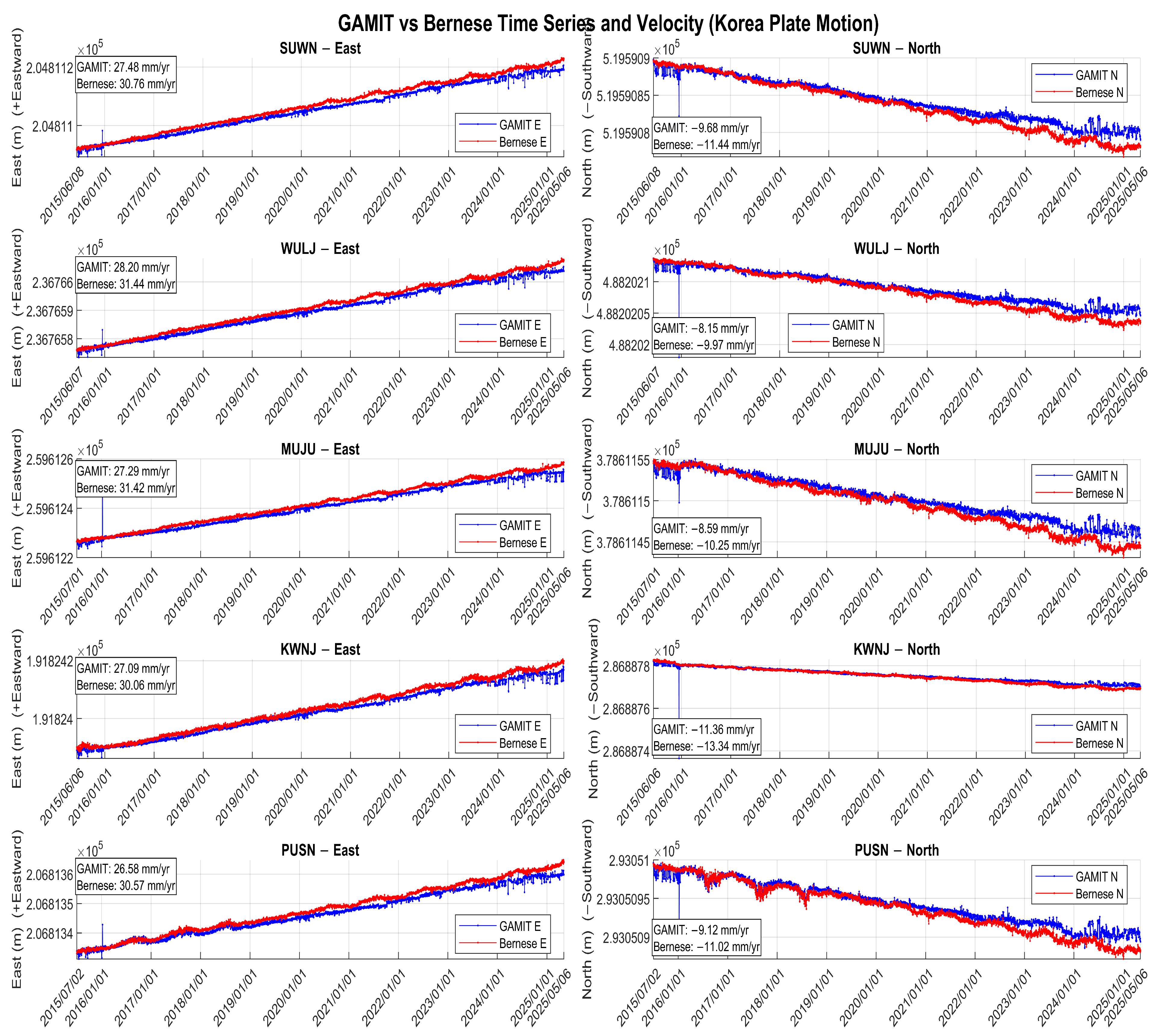
2.5. Long-Term Crustal Velocity Field of the Korean Peninsula: Impact on Static Datum Realization
3. Results
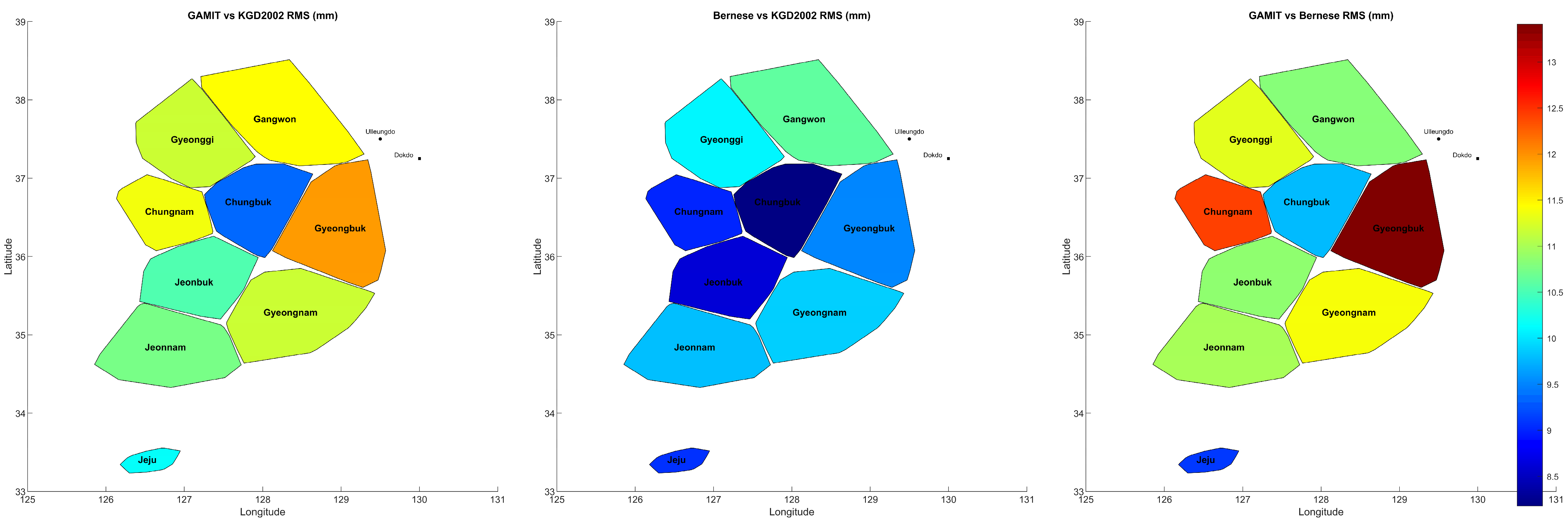
3.1. Regional Analysis of Coordinate Differences
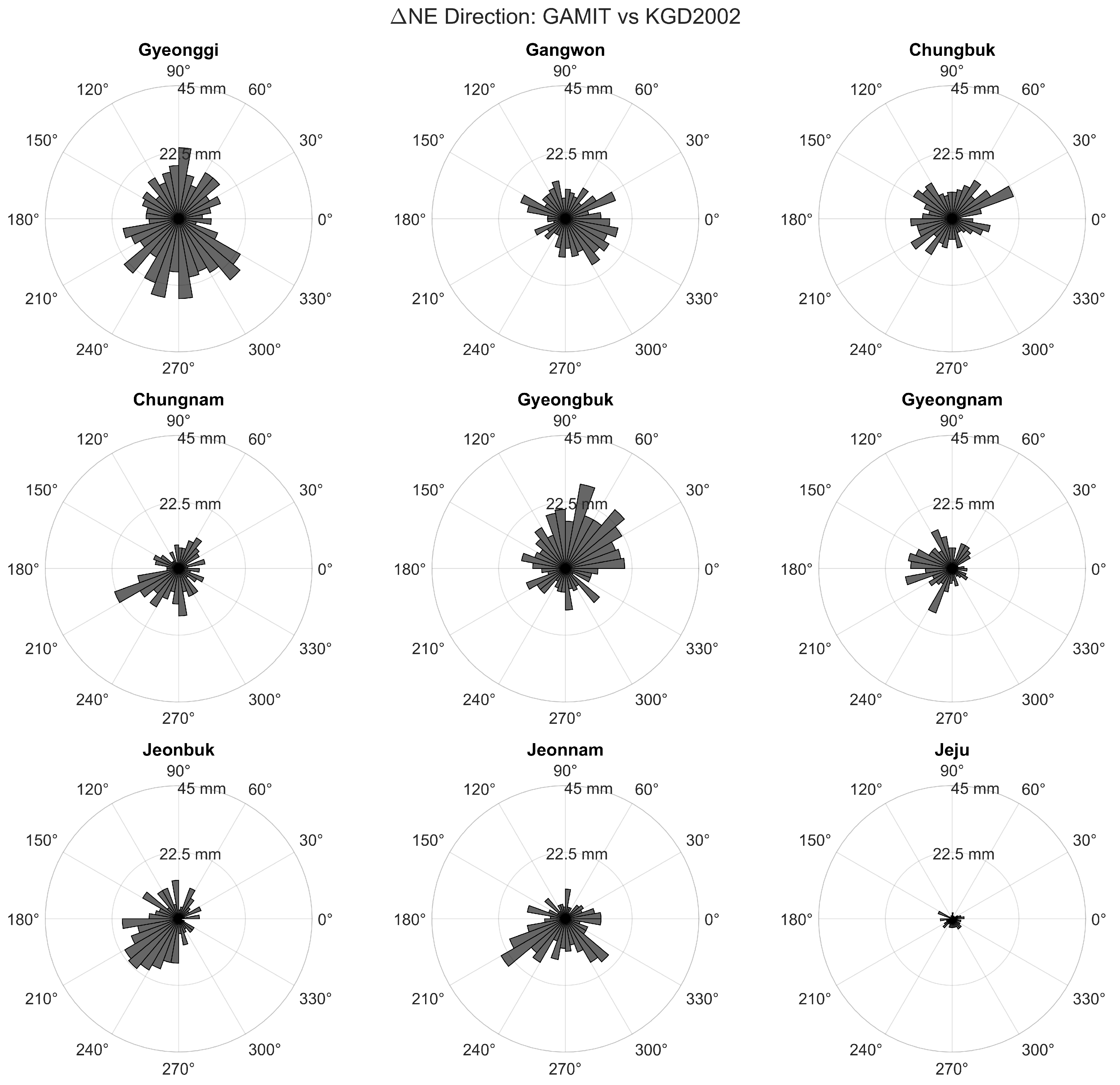
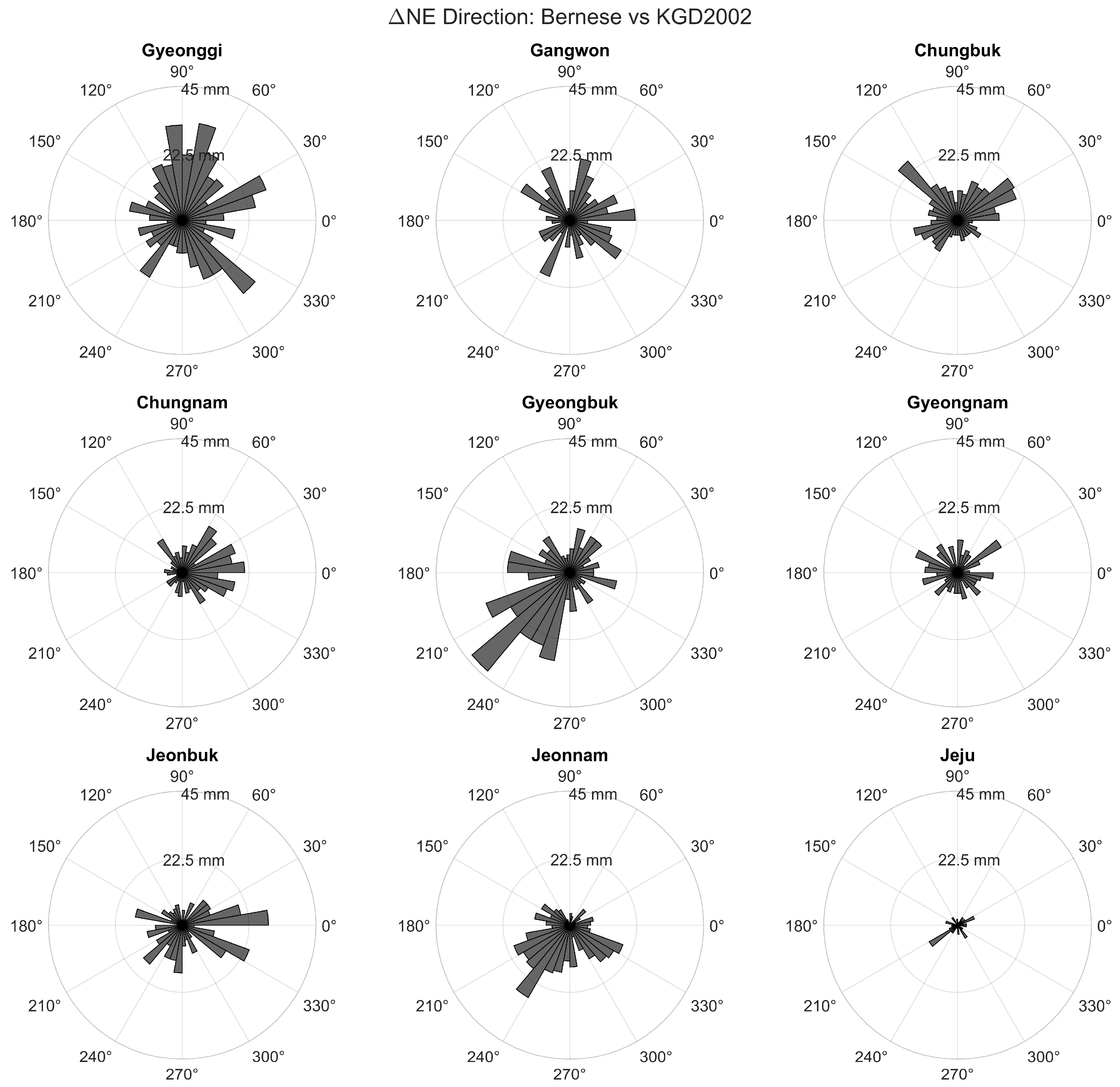
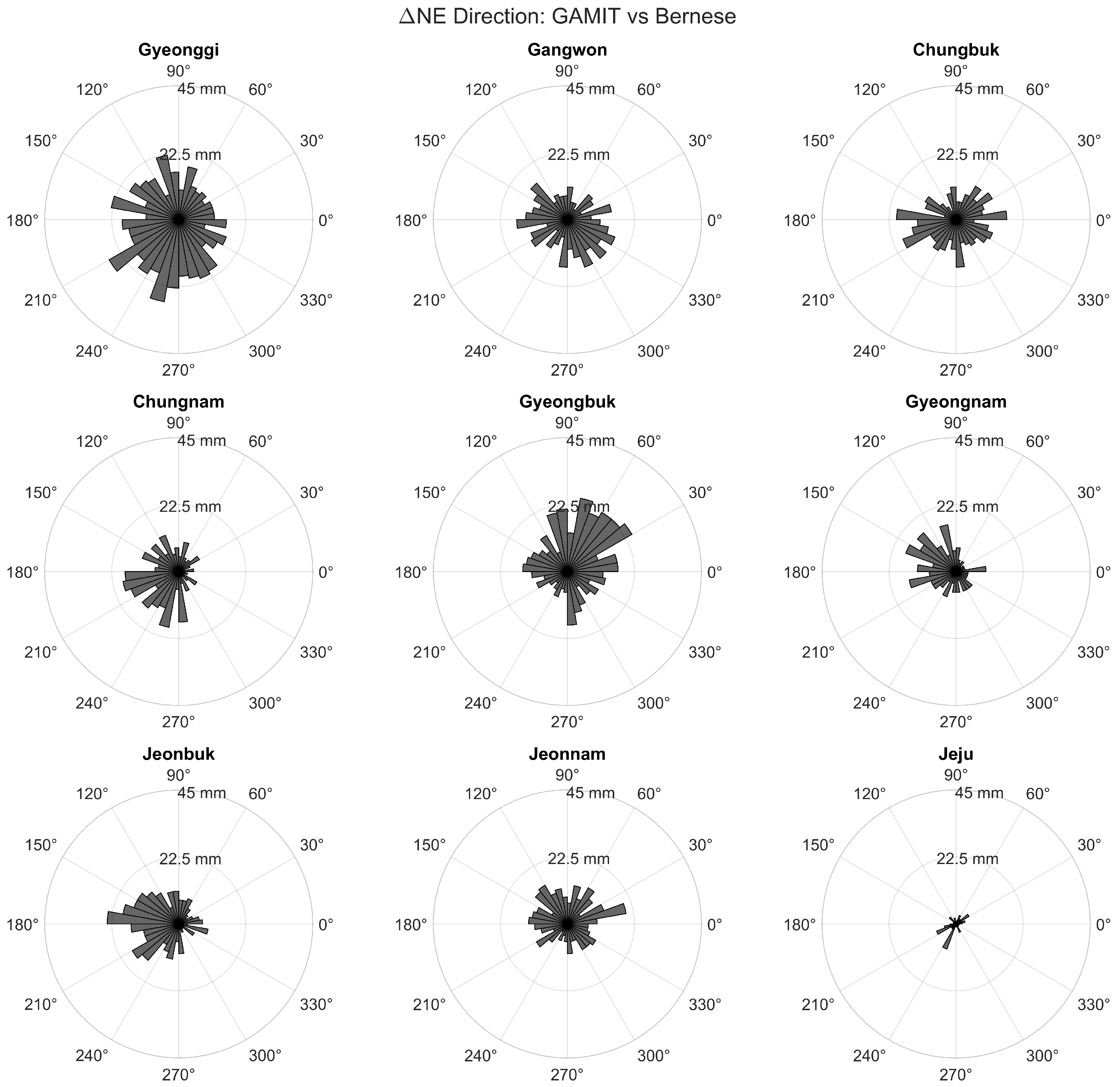
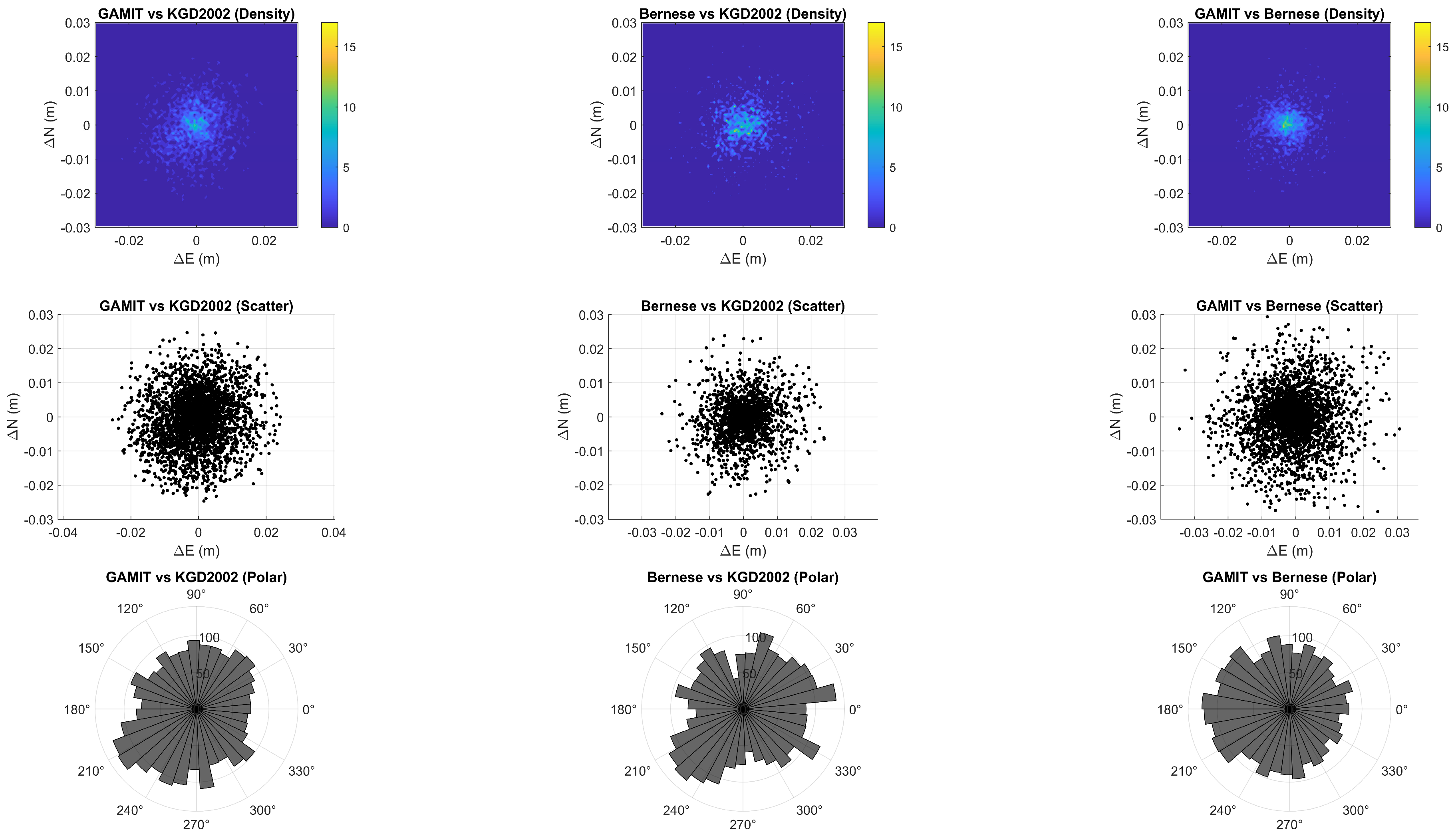
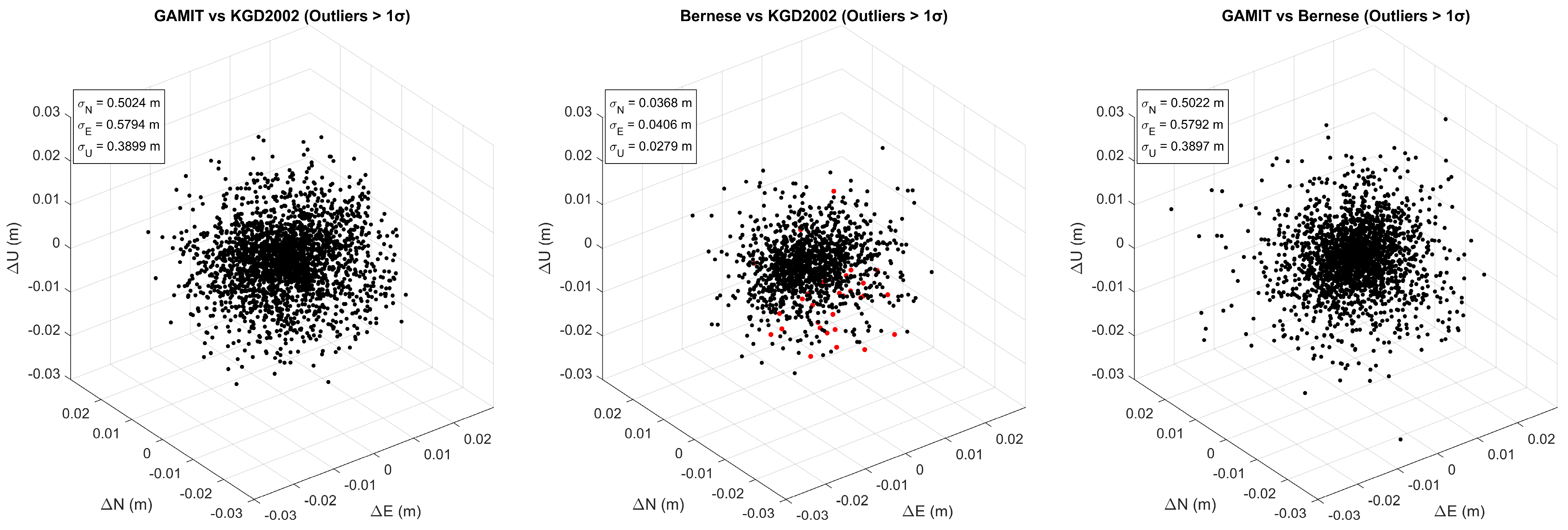
3.2. Analysis of Coordinate Differences
- (1)
- Two-dimensional density maps to show the spatial distribution of the residuals;
- (2)
- Scatter plots to illustrate the spread and concentration of points;
- (3)
- Polar histograms to examine directional tendencies in the horizontal residual vectors.
- GAMIT/GLOBK vs. KGD2002;
- Bernese vs. KGD2002;
- GAMIT/GLOBK vs. Bernese.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A New Release of the International Terrestrial Reference Frame Modeling Nonlinear Station Motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Chen, G.; Wei, N.; Wang, H.; Li, T.; Li, M.; Zhao, Q. Impacts of Non-Linear ITRF2020 on Reference Frame Alignment. Adv. Space Res. 2024, 74, 2569–2582. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Collilieux, X.; Métivier, L.; Chanard, K. ITRF2020: An Augmented Reference Frame Refining the Modeling of Nonlinear Station Motions. J. Geod. 2023, 97, 47. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, C.; Lian, L.; Zhang, S. Assessment of the Improvement in Observation Precision of GNSS, SLR, VLBI, and DORIS Inputs from ITRF2014 to ITRF2020 Using TRF Stacking Methods. Remote Sens. 2024, 16, 1240. [Google Scholar] [CrossRef]
- Rudenko, S.; Esselborn, S.; Schöne, T.; Dettmering, D. Impact of Terrestrial Reference Frame Realizations on Altimetry Satellite Orbit Quality and Global and Regional Sea Level Trends: A Switch from ITRF2008 to ITRF2014. Solid Earth 2019, 10, 293–305. [Google Scholar] [CrossRef]
- Blewitt, G. Terrestrial Reference Frame Requirements for Studies of Geodynamics and Climate Change. In International Association of Geodesy Symposia; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Delva, P.; Altamimi, Z.; Blazquez, A.; Bonnor, J.; Bouquillon, S.; Capitaine, N.; Cécile, L.; Sośnica, K.; Wolf, P. GENESIS: Co-Location of Geodetic Techniques in Space. arXiv 2022, arXiv:2209.15298. [Google Scholar] [CrossRef]
- Snay, R.A.; Soler, T. Evolution of NAD 83 in the United States: Journey from 2D toward 4D. J. Surv. Eng. 2012, 138, 161–171. [Google Scholar] [CrossRef]
- Imakiire, T.; Murakami, M. Establishment of the New Geodetic Reference Frame of Japan (JGD2000). In Proceedings of the IVS 2002 General Meeting, Tsukuba, Japan, 4–7 February 2002; pp. 304–308. Available online: https://ivscc.gsfc.nasa.gov/publications/gm2002/imakiire.pdf (accessed on 17 May 2025).
- Harrison, C.; Brown, N.; Dawson, J.; Fraser, R. Geocentric Datum of Australia 2020: The First Australian Datum Developed from a Rigorous Continental-Scale Adjustment. J. Spat. Sci. 2023, 69, 167–179. [Google Scholar] [CrossRef]
- Altamimi, Z.; Sillard, P.; Boucher, C. ITRF2000: A New Release of the International Terrestrial Reference Frame for Earth Science Applications. J. Geophys. Res. 2002, 107, 2214. [Google Scholar] [CrossRef]
- Lee, Y.-J.; Lee, H.-K.; Jeong, K.-H.; Cha, S.-H. Korean Geodetic Datum 2002 (KGD2002): Nationwide GPS Network Densification. In Proceedings of the FIG Working Week 2008, Stockholm, Sweden, 14–19 June 2008; pp. 1–12. Available online: https://fig.net/resources/proceedings/fig_proceedings/fig2008/papers/ts03a/ts03a_02_lee_etal_2891.pdf (accessed on 17 May 2025).
- Lee, S.-J.; Yun, H.-S. Nationwide Adjustment of Unified Geodetic Control Points for the Modernization of South Korea’s Spatial Reference Frame. Appl. Sci. 2025, 15, 5500. [Google Scholar] [CrossRef]
- Han, J.; Lee, S.J.; Yun, H.S.; Kim, K.B.; Bae, S.W. PyRINEX: A New Multi-Purpose Python Package for GNSS RINEX Data. PeerJ Comput. Sci. 2024, 10, e1800. [Google Scholar] [CrossRef] [PubMed]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to GAMIT/GLOBK; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010; Available online: http://www-gpsg.mit.edu/gg/docs/Intro_GG.pdf (accessed on 15 April 2025).
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual, GPS Analysis at MIT, Release 10.7; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018; Available online: http://www-gpsg.mit.edu/gg/docs/GAMIT_Ref.pdf (accessed on 15 April 2025).
- Herring, T.A.; King, R.W.; McClusky, S.C. GLOBK Reference Manual, Global Kalman Filter VLBI and GPS Analysis Program, Release 10.7; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018; Available online: http://www-gpsg.mit.edu/gg/docs/GLOBK_Ref.pdf (accessed on 15 April 2025).
- King, R.W.; Bock, Y. Documentation for the GAMIT GPS Analysis Software; Massachusetts Institute of Technology: Cambridge, MA, USA, 2003. [Google Scholar]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2—Documentation; Astronomical Institute, University of Bern: Bern, Switzerland, 2015; Available online: https://www.bernese.unibe.ch/docs/DOCU52.pdf (accessed on 13 April 2025).
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Ranacher, P.; Brunauer, R.; Trutschnig, W.; Van der Spek, S.C.; Reich, S. Why GPS Makes Distances Bigger Than They Are. J. Transp. Geogr. 2016, 52, 20–27. [Google Scholar] [CrossRef]
- Qiu, X.; Sun, B.; Li, Y.; Ding, X.; Wang, L. Experimental Study of Accuracy of High-Rate GNSS in Context of Structural Health Monitoring. Remote Sens. 2022, 14, 4989. [Google Scholar] [CrossRef]
- Gillins, D.; Heck, J.; Scott, G.; Jordan, K.; Hippenstiel, R. Accuracy of GNSS Observations from Three Real-Time Networks in Maryland, USA. In Proceedings of the FIG Working Week 2019, Hanoi, Vietnam, 22–26 April 2019; Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2019/papers/ts05e/TS05E_gillins_heck_et_al_10077.pdf (accessed on 17 May 2025).
- Mustafin, M.; Nasrullah, M.; Abboud, M. A Comparative Analysis of GNSS Processing Services for Static Measurements: Evaluating Accuracy and Stability at Different Observation Periods. Int. J. Geoinform. 2024, 20, 112–121. [Google Scholar] [CrossRef]
- Wang, G.; Shen, Z.; Wang, Y. The 95% Confidence Interval for GNSS-Derived Site Velocities. J. Surv. Eng. 2022, 148, 04021033. [Google Scholar] [CrossRef]
- Jivall, L.; Lidberg, M.; Johansson, J.M. Analysis of 20 Years of GPS Data from SWEREF Consolidation Points Using BERNESE and GAMIT-GLOBK Software. J. Geod. 2022, 96, 26. Available online: https://www.lantmateriet.se/globalassets/geodata/gps-och-geodetisk-matning/rapporter/lantmaterirapport-2022-1.pdf (accessed on 17 May 2025).
- Ampatzidis, D.; Rossikopoulos, D.; Papadopoulou, M.; Pikridas, C.; Fotiou, A. The Correlations of the Helmert Transformation Parameters as an Additional Auxiliary Diagnostic Tool for Terrestrial Reference Frames Quality Assessment. Surv. Rev. 2022, 54, 233–247. Available online: https://link.springer.com/chapter/10.1007/1345_2022_164 (accessed on 17 May 2025).
- Tran, T.K.; Dao, H.T.; Nguyen, M.D. Determination of Helmert Transformation Parameters for Continuous GNSS Networks. J. Geod. 2022, 96, 58. [Google Scholar] [CrossRef]
- UNAVCO. GAGE Plate Motion Calculator. Available online: https://www.unavco.org/software/geodetic-utilities/plate-motion-calculator/plate-motion-calculator.html (accessed on 17 May 2025).
- Kreemer, C.; Blewitt, G.; Klein, E.C. A geodetic plate motion and Global Strain Rate Model. Geochem. Geophys. Geosyst. 2014, 15, 3849–3889. [Google Scholar] [CrossRef]
- Drewes, H. The Actual Plate Kinematic and Crustal Deformation Model APKIM2005 as Basis for a Non-Rotating ITRF. In Geodetic Reference Frames, Proceedings of the IAG Symposium, Munich, Germany, 9–14 October 2006; Springer: Berlin/Heidelberg, Germany, 2009; pp. 95–99. [Google Scholar]
- Mitsakaki, C.; Agatza-Balodimou, A.M.; Papazissi, K. Geodetic reference frames transformations. Surv. Rev. 2006, 38, 608–618. [Google Scholar] [CrossRef]
- National Geodetic Survey (NGS). Improving the National Spatial Reference System (NSRS); White Paper from the 2010 Geospatial Summit; NOAA/NOS/NGS: Silver Spring, MD, USA, 2010. Available online: https://geodesy.noaa.gov/2010Summit/Improving_the_NSRS.pdf (accessed on 17 May 2025).
- Rebischung, P.; Altamimi, Z.; Métivier, L.; Collilieux, X.; Gobron, K.; Chanard, K. Analysis of the IGS Contribution to ITRF2020. J. Geod. 2024, 98, 49. [Google Scholar] [CrossRef]
- Azhari, M.; Altamimi, Z.; Azman, G.; Kadir, M.; Simons, W.J.F.; Sohaime, R.; Saiful, A. Semi-Kinematic Geodetic Reference Frame Based on the ITRF2014 for Malaysia. J. Geod. Sci. 2020, 10, 91–109. [Google Scholar] [CrossRef]
- Drewes, H.; Seitz, M.; Sánchez, L. Realisation of the Non-Rotating Terrestrial Reference Frame by an Actual Plate Kinematic and Crustal Deformation Model (APKIM2020). In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2024; pp. 1–9. Available online: https://link.springer.com/chapter/10.1007/1345_2024_276 (accessed on 17 May 2025).
- Donnelly, N. Deformation Models for Dynamic (and Semi-Dynamic) Datums. In Proceedings of theFIG/IAG/UNOOSA Reference Frame in Practice Technical Seminar, Rome, Italy, 4–5 May 2012; Available online: https://www.fig.net/resources/proceedings/2013/2013_reference_frame_in_practice_comm5/2.3_dynamic_datums_donnelly.pdf (accessed on 17 May 2025).

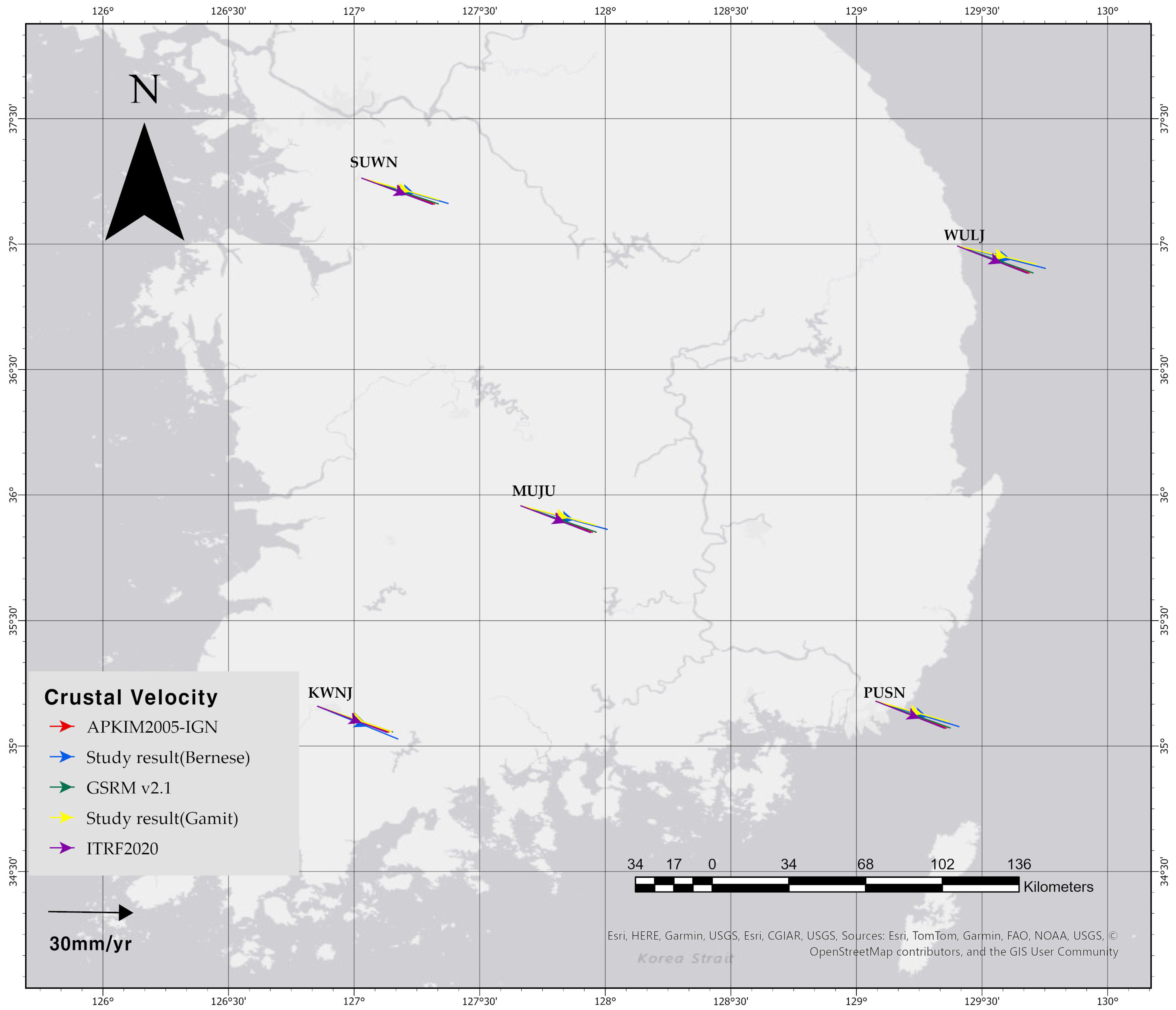

| Region | Bernese | Gamit | ITRF2020 | GSRM v2.1 | APKIM2005-IGN | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Crustal Velocity | Azimuth | Crustal Velocity | Azimuth | Crustal Velocity | Azimuth | Crustal Velocity | Azimuth | Crustal Velocity | Azimuth | |
| SUWN | 32.82 | 110.15° | 29.14 | 109.41° | 27.91 | 114.90° | 29.69 | 112.86° | 28.53 | 114.10° |
| WULJ | 32.98 | 107.63° | 29.35 | 106.12° | 27.86 | 115.98° | 29.65 | 113.98° | 28.5 | 115.26° |
| MUJU | 33.05 | 108.38° | 28.61 | 107.47° | 27.99 | 115.10° | 29.77 | 113.09° | 28.6 | 114.35° |
| KWNJ | 32.89 | 116.4° | 29.38 | 112.75° | 28.07 | 114.67° | 29.85 | 112.66° | 28.65 | 113.91° |
| PUSN | 32.50 | 110.47° | 28.10 | 108.94° | 28.01 | 115.69° | 29.79 | 113.71° | 28.61 | 115.00° |
| Region | Mean ΔN (cm) | Mean ΔE (cm) | RMSE ΔN (cm) | RMSE ΔE (cm) |
|---|---|---|---|---|
| Gyeonggi | −0.18 | 0.01 | 0.86 | 0.72 |
| Gangwon | −0.13 | 0.19 | 0.79 | 0.83 |
| Chungbuk | 0.08 | −0.03 | 0.62 | 0.70 |
| Chungnam | −0.24 | −0.09 | 0.83 | 0.77 |
| Gyeongbuk | 0.30 | 0.15 | 0.87 | 0.81 |
| Gyeongnam | 0.12 | −0.31 | 0.77 | 0.81 |
| Jeonbuk | −0.24 | −0.33 | 0.76 | 0.73 |
| Jeonnam | −0.37 | −0.13 | 2.52 | 1.20 |
| Jeju | −0.28 | −0.14 | 0.70 | 0.73 |
| Region | Mean ΔN (cm) | Mean ΔE (cm) | RMSE ΔN (cm) | RMSE ΔE (cm) |
|---|---|---|---|---|
| Gyeonggi | 0.03 | 0.12 | 0.74 | 0.68 |
| Gangwon | 0.04 | 0.10 | 0.73 | 0.77 |
| Chungbuk | 0.15 | 0.01 | 0.54 | 0.62 |
| Chungnam | 0.04 | 0.28 | 0.62 | 0.65 |
| Gyeongbuk | −0.04 | −0.06 | 0.64 | 0.70 |
| Gyeongnam | 0.05 | −0.05 | 0.64 | 0.75 |
| Jeonbuk | −0.18 | 0.04 | 0.60 | 0.62 |
| Jeonnam | −0.35 | −0.14 | 0.69 | 0.70 |
| Jeju | −0.21 | −0.12 | 0.64 | 0.64 |
| Region | Mean ΔN (cm) | Mean ΔE (cm) | RMSE ΔN (cm) | RMSE ΔE (cm) |
|---|---|---|---|---|
| Gyeonggi | −0.21 | −0.11 | 0.86 | 0.73 |
| Gangwon | −0.17 | 0.09 | 0.75 | 0.77 |
| Chungbuk | −0.07 | −0.05 | 0.63 | 0.75 |
| Chungnam | −0.28 | −0.37 | 0.91 | 0.85 |
| Gyeongbuk | 0.35 | 0.21 | 0.96 | 0.93 |
| Gyeongnam | 0.07 | −0.26 | 0.80 | 0.81 |
| Jeonbuk | −0.06 | −0.37 | 0.70 | 0.83 |
| Jeonnam | −0.02 | 0.01 | 2.55 | 1.22 |
| Jeju | −0.07 | −0.01 | 0.64 | 0.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-J.; Yun, H.-S. Towards Geodetic Datum Modernization: A Comparative Study of GNSS Solutions in KGD2002 Using GAMIT/GLOBK and Bernese. Appl. Sci. 2025, 15, 6460. https://doi.org/10.3390/app15126460
Lee S-J, Yun H-S. Towards Geodetic Datum Modernization: A Comparative Study of GNSS Solutions in KGD2002 Using GAMIT/GLOBK and Bernese. Applied Sciences. 2025; 15(12):6460. https://doi.org/10.3390/app15126460
Chicago/Turabian StyleLee, Seung-Jun, and Hong-Sik Yun. 2025. "Towards Geodetic Datum Modernization: A Comparative Study of GNSS Solutions in KGD2002 Using GAMIT/GLOBK and Bernese" Applied Sciences 15, no. 12: 6460. https://doi.org/10.3390/app15126460
APA StyleLee, S.-J., & Yun, H.-S. (2025). Towards Geodetic Datum Modernization: A Comparative Study of GNSS Solutions in KGD2002 Using GAMIT/GLOBK and Bernese. Applied Sciences, 15(12), 6460. https://doi.org/10.3390/app15126460







