EEMD Energy Spectrum Decoupling: An Efficient Hilbert–Huang Fusion Approach for Intelligent Bearing Fault Diagnosis
Abstract
1. Introduction
- This paper proposes an innovative hybrid approach combining Hilbert envelope demodulation with EEMD to address the limitations of conventional vibration analysis in detecting rolling bearing faults. The method effectively separates fault-related features from non-linear, non-stationary signals while overcoming mode-mixing issues inherent in traditional EMD.
- A novel normalized energy distribution feature vector (ED) is introduced as a quantitative diagnostic indicator. By analyzing the energy distribution patterns of EEMD-derived IMFs, the method distinguishes faulty bearings (non-monotonic ED) from healthy ones (monotonic ED) with high interpretability and computational efficiency.
- The proposed method is rigorously validated on the Case Western Reserve University bearing dataset, achieving 100% fault identification accuracy under varying operational conditions, including different sampling rates (12 kHz/48 kHz) and fault locations (drive end/fan end). This exceptional performance highlights the algorithm’s strong noise immunity and practical applicability.
2. Related Work
2.1. Bearing Diagnostic Methods
2.2. The EMD Method Based on IMF
3. Envelope Demodulation
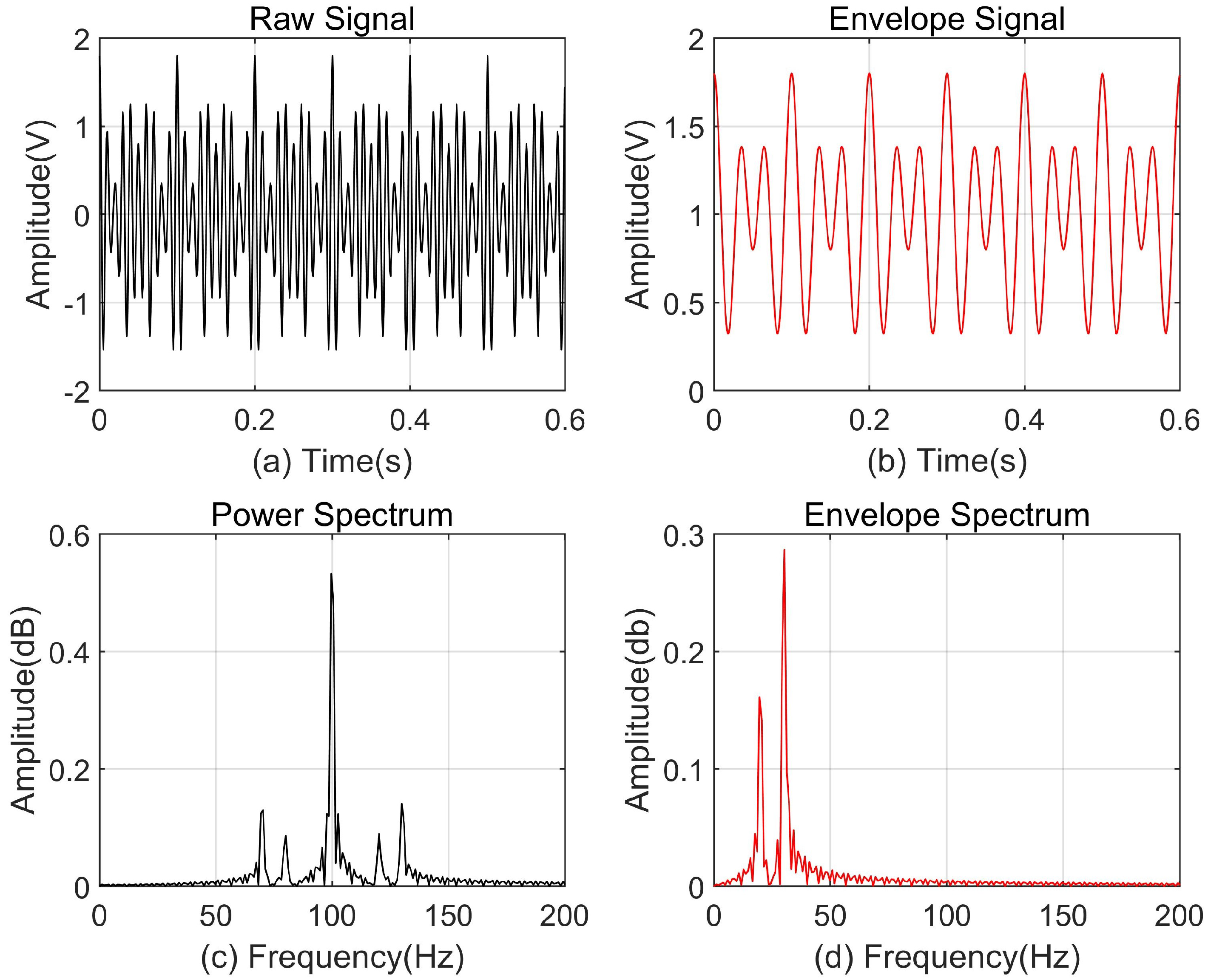
3.1. Verification of Envelope Demodulation
3.2. The Practical Application and Existing Problems of the Envelope Demodulation Algorithm
4. Materials and Methods
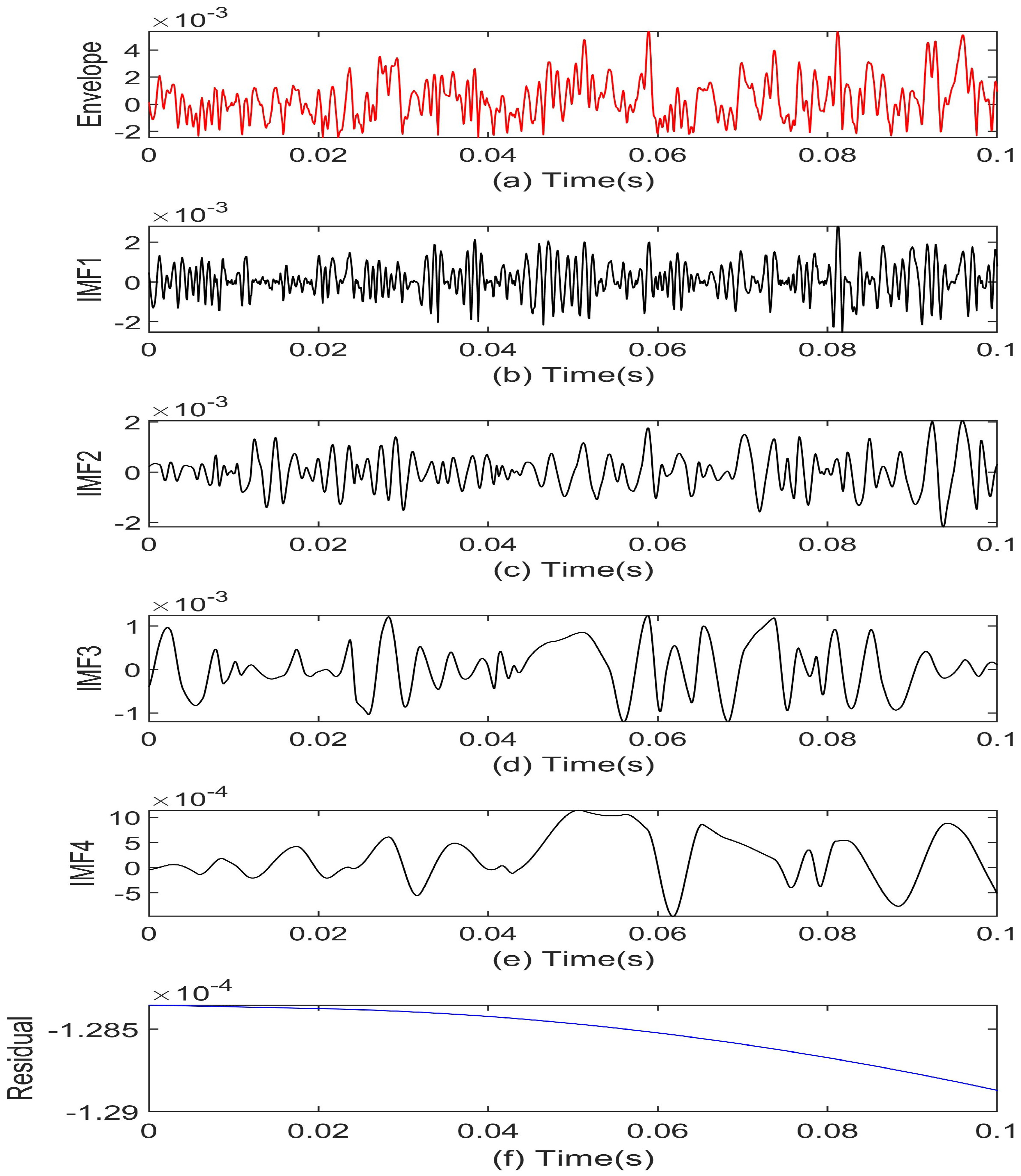
4.1. Signal Decomposition Based on EEMD
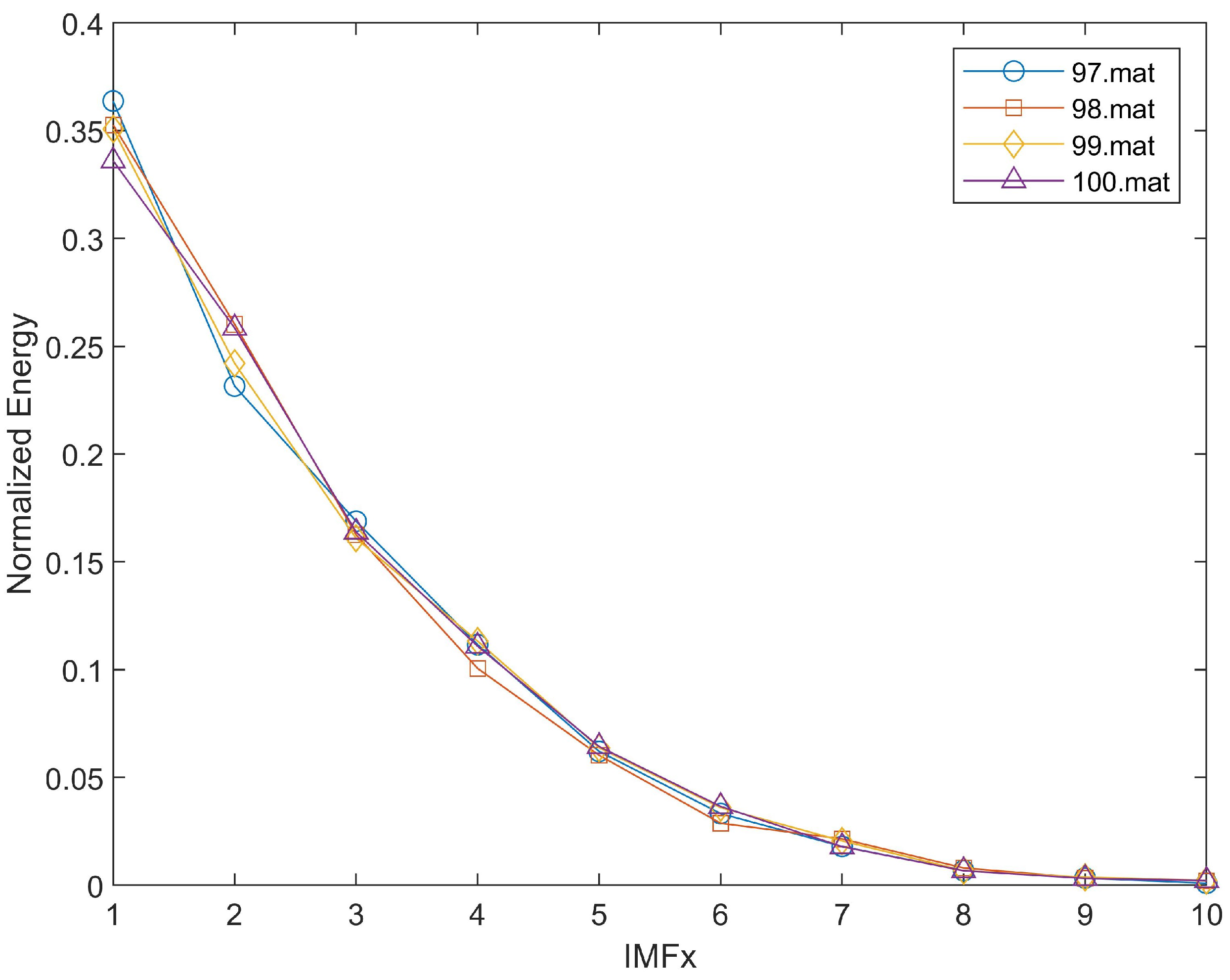
4.2. EEMD-Based Bearing Fault Diagnosis Using Energy Distribution Features of IMFs
5. Results and Discussion
5.1. Introduction to the Experimental Dataset
5.2. Performance Analysis of the Proposed Algorithm
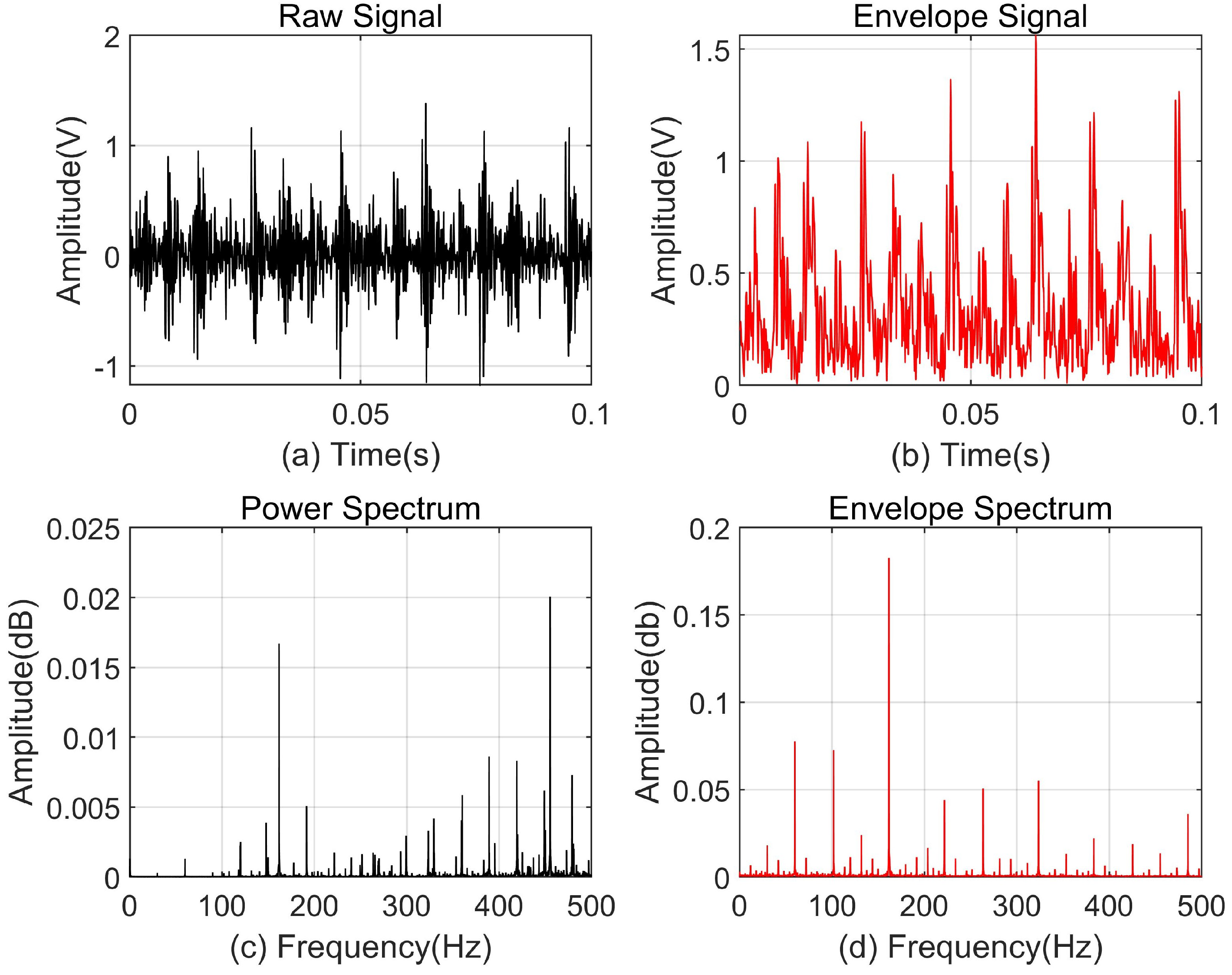
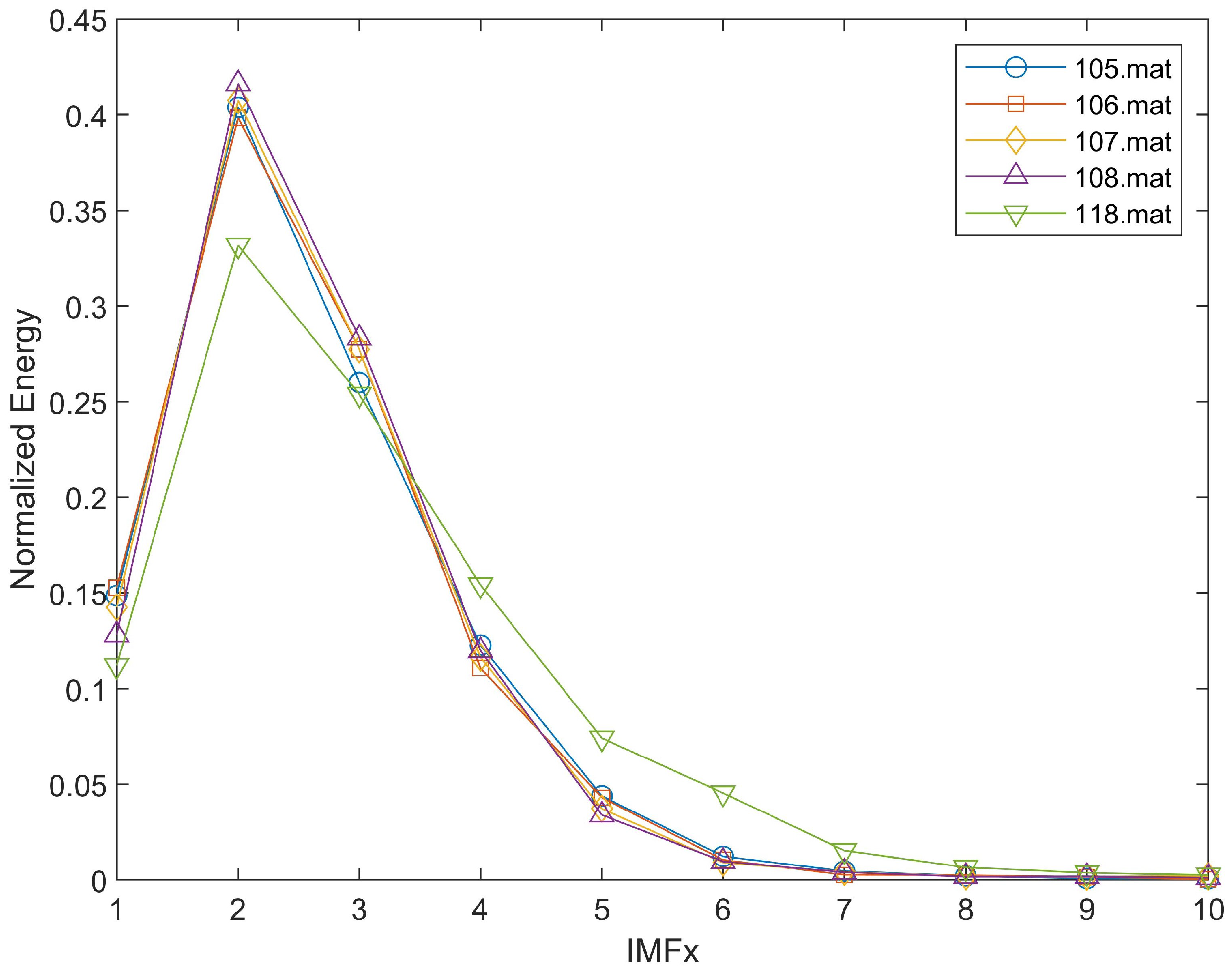
5.2.1. The Normal Condition of the Bearing Without Any Faults
5.2.2. Fault Characteristics Analysis of Bearing
5.3. Performance Comparison of Different Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Wang, H.; Bai, R.; Shi, Y.; Chen, X.; Xu, Q. Enhanced Rolling Bearing Fault Diagnosis Using Multimodal Deep Learning and Singular Spectrum Analysis. Appl. Sci. 2025, 15, 4828. [Google Scholar] [CrossRef]
- Siddique, M.F.; Saleem, F.; Umar, M.; Kim, C.H.; Kim, J.M. A Hybrid Deep Learning Approach for Bearing Fault Diagnosis Using Continuous Wavelet Transform and Attention-Enhanced Spatiotemporal Feature Extraction. Sensors 2025, 25, 2712. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Bobadilla, H.A.; Martin, U. Modern tendencies in vehicle-based condition monitoring of the railway track. IEEE Trans. Instrum. Meas. 2023, 72, 3507344. [Google Scholar] [CrossRef]
- Amarouayache, I.I.E.; Saadi, M.N.; Guersi, N.; Boutasseta, N. Bearing fault diagnostics using EEMD processing and convolutional neural network methods. Int. J. Adv. Manuf. Technol. 2020, 107, 4077–4095. [Google Scholar] [CrossRef]
- Kiakojouri, A.; Wang, L. A Generalized Convolutional Neural Network Model Trained on Simulated Data for Fault Diagnosis in a Wide Range of Bearing Designs. Sensors 2025, 25, 2378. [Google Scholar] [CrossRef]
- Suhas, M.; Abisset-Chavanne, E.; Rey, P.A. Cooperative Hybrid Modelling and Dimensionality Reduction for a Failure Monitoring Application in Industrial Systems. Sensors 2025, 25, 1952. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A review on vibration-based condition monitoring of rotating machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- McInerny, S.A.; Dai, Y. Basic vibration signal processing for bearing fault detection. IEEE Trans. Educ. 2003, 46, 149–156. [Google Scholar] [CrossRef]
- Guo, Y.; Zhou, J.; Dong, Z.; She, H.; Xu, W. Research on bearing fault diagnosis based on novel MRSVD-CWT and improved CNN-LSTM. Meas. Sci. Technol. 2024, 35, 095003. [Google Scholar] [CrossRef]
- Mitra, S.; Koley, C. Real-time robust bearing fault detection using scattergram-driven hybrid CNN-SVM. Electr. Eng. 2024, 106, 3615–3625. [Google Scholar] [CrossRef]
- Yu, M.; Zhang, J.; Liu, L. Rub-impact fault identification based on EMD and stochastic resonance. Int. J. Ind. Syst. Eng. 2024, 46, 509–530. [Google Scholar] [CrossRef]
- Han, Z.; Jin, S.; Greaves, D.; Hann, M.; Shi, H. Study on the energy capture spectrum of a two-body hinged-raft wave energy converter. Energy 2024, 304, 132057. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, X.; Yin, R.; Ma, Z. The feature extraction method based on quadratic wavelet packet energy entropy and t-SNE for bearing fault diagnosis. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2025, 239, 520–531. [Google Scholar] [CrossRef]
- Bouaissi, I.; Rezig, A.; Laib, A.; Djerdir, A.; Guellout, O.; Touati, S.; N’diaye, A. Real-time detection of bearing faults through a hybrid WTMP analysis of frequency-related states. Int. J. Dyn. Control 2024, 12, 3947–3962. [Google Scholar] [CrossRef]
- Santer, P.; Reinhard, J.; Schindler, A.; Graichen, K. Detection of localized bearing faults in PMSMs by means of envelope analysis and wavelet packet transform using motor speed and current signals. Mechatronics 2025, 106, 103294. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, S. Maximum L-Kurtosis deconvolution and frequency-domain filtering algorithm for bearing fault diagnosis. Mech. Syst. Signal Process. 2025, 223, 111916. [Google Scholar] [CrossRef]
- Zhao, F.; Jiang, Y.; Cheng, C.; Wang, S. An improved fault diagnosis method for rolling bearings based on wavelet packet decomposition and network parameter optimization. Meas. Sci. Technol. 2023, 35, 025004. [Google Scholar] [CrossRef]
- Zhang, Q.; Deng, L. An intelligent fault diagnosis method of rolling bearings based on short-time Fourier transform and convolutional neural network. J. Fail. Anal. Prev. 2023, 23, 795–811. [Google Scholar] [CrossRef]
- Han, K.; Wang, W.; Guo, J. Research on a Bearing Fault Diagnosis Method Based on a CNN-LSTM-GRU Model. Machines 2024, 12, 927. [Google Scholar] [CrossRef]
- Luchuan, S.; Zhao, B.; Xutao, K. Rolling Bearing Fault Diagnosis Based on VMD-DWT and HADS-CNN-BiLSTM Hybrid Model. Machines 2025, 13, 423. [Google Scholar]
- Zhu, D.; Liu, Y.; Zhu, Q. Ensemble average of enhanced generalized envelope spectrum for fault detection of rolling element bearings. Int. J. Adapt. Control Signal Process. 2024, 38, 1386–1402. [Google Scholar] [CrossRef]
- Yang, X.; Yang, J.; Jin, Y.; Liu, Z. A New Method for Bearing Fault Diagnosis across Machines Based on Envelope Spectrum and Conditional Metric Learning. Sensors 2024, 24, 2674. [Google Scholar] [CrossRef]
- Li, M.; Li, X.; Liu, B.; Lv, S.; Liu, C. A rolling bearing fault signal denoising algorithm that combines a new adaptive information entropy with a new wavelet threshold function. Eng. Res. Express 2024, 6, 045536. [Google Scholar] [CrossRef]
- Alvarez-Ramirez, J.; Rodriguez, E.; Castro, L. Hurst exponent estimation for short-time series based on singular value decomposition entropy. Fractals 2023, 31, 2350132. [Google Scholar] [CrossRef]
- Ge, Q.; Wang, D.; Sun, K.; Wang, D. Fault Diagnosis of Wind Turbine Bolts based on ICEEMD-SSA-SVM Model. Recent Adv. Electr. Electron. Eng. (Former. Recent Patents Electr. Electron. Eng.) 2024, 17, 269–282. [Google Scholar] [CrossRef]
- Liu, L.; Wei, Y.; Song, X.; Zhang, L. Fault diagnosis of wind turbine bearings based on CEEMDAN-GWO-KELM. Energies 2023, 16, 48. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Fu, Y.; Jia, L.; Qin, Y.; Yang, J.; Fu, D. Fast EEMD based AM-correntropy matrix and its application on roller bearing fault diagnosis. Entropy 2016, 18, 242. [Google Scholar] [CrossRef]





| Reference | Methodology | Advantage | Limitation |
|---|---|---|---|
| Liu et al. (2023) [26] | CEEMDAN + GWO-KELM | Higher diagnosis success rate via optimized extreme learning | Limited interpretability of GWO-KELM |
| Zhang et al. (2023) [18] | STFT-CNN for direct time-frequency analysis | Avoids feature extraction-induced information loss | Sensitive to noise and data quality |
| Zhao et al. (2023) [17] | Wavelet packet decomposition + chaotic sparrow search-optimized DBN | Improved fault diagnosis accuracy through parameter optimization | Complex implementation; risk of overfitting |
| Ge et al. (2024) [25] | ICEEMDAN for fault feature extraction | Superior noise robustness compared to traditional EMD | Computationally expensive |
| Li et al. (2024) [23] | IMF denoising via optimized wavelet threshold + information entropy | Improved diagnostic accuracy in noisy environments | Dependent on IMF quality |
| Han et al. (2024) [12] | EMD-based envelope/energy spectrum analysis | Adaptive decomposition for non-stationary signals | Mode mixing issues in EMD |
| Han et al. (2024) [19] | Hybrid CNN-LSTM-GRU model | Enhanced spatiotemporal feature extraction | High computational complexity; requires large datasets |
| Bouaissi et al. (2024) [14] | CWT and WPT for non-stationary signal reconstruction | Improved fault frequency prominence and detection accuracy | Computationally intensive for real-time applications |
| Lu et al. (2025) [20] | VMD-DWT + HADS-CNN-BiLSTM with hybrid attention | Robust fault diagnosis under noisy conditions | Complex architecture; training inefficiency |
| Xu et al. (2025) [16] | Maximum L-Kurtosis Deconvolution (MLKD) with iterative filtering | Enhanced fault signal deconvolution via L-kurtosis maximization | Requires optimization of filter parameters |
| Santer et al. (2025) [15] | Envelope analysis + WPT with SVM classification | Effective fault type discrimination | Sensitivity to wavelet basis selection; high computational load |
| Cao et al. (2025) [13] | Hybrid QWPEE and t-SNE for feature extraction | Enhanced pattern recognition for bearing faults | Dependency on parameter tuning |
| Author i | Method | Fault Diagnosis Rate (%) |
|---|---|---|
| Zhao et al. [17] | WPD-CSSOA-DBN | 98.24 |
| Han et al. [19] | CNN-LSTM-GRU | >99 |
| Liu et al. [26] | CEEMDAN | 99.42 |
| Luchuan et al. [20] | HADS-CNN-BiLSTM | 99.58 |
| Zhang and Deng [18] | STFT-CNN | 100 |
| The propose method | Hilbert-EEMD | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, L.; Xu, W.; Song, Z. EEMD Energy Spectrum Decoupling: An Efficient Hilbert–Huang Fusion Approach for Intelligent Bearing Fault Diagnosis. Appl. Sci. 2025, 15, 6458. https://doi.org/10.3390/app15126458
Lai L, Xu W, Song Z. EEMD Energy Spectrum Decoupling: An Efficient Hilbert–Huang Fusion Approach for Intelligent Bearing Fault Diagnosis. Applied Sciences. 2025; 15(12):6458. https://doi.org/10.3390/app15126458
Chicago/Turabian StyleLai, Lianyou, Weijian Xu, and Zhongzhe Song. 2025. "EEMD Energy Spectrum Decoupling: An Efficient Hilbert–Huang Fusion Approach for Intelligent Bearing Fault Diagnosis" Applied Sciences 15, no. 12: 6458. https://doi.org/10.3390/app15126458
APA StyleLai, L., Xu, W., & Song, Z. (2025). EEMD Energy Spectrum Decoupling: An Efficient Hilbert–Huang Fusion Approach for Intelligent Bearing Fault Diagnosis. Applied Sciences, 15(12), 6458. https://doi.org/10.3390/app15126458






