Sillcom: A Communication-Efficient Privacy-Preserving Scheme for Indoor Localization
Abstract
1. Introduction
1.1. Our Contributions
- Overall, we propose Sillcom, which combines replicated secret sharing and function secret sharing in the outsourcing model, with the aim of reducing the user’s computational burden and minimizing server online communication cost, thus enabling secure indoor localization with low communication.
- To further enhance performance, we employ a multi-branch tree structure and multi-thread parallelism to optimize both offline phase overhead and online query time.
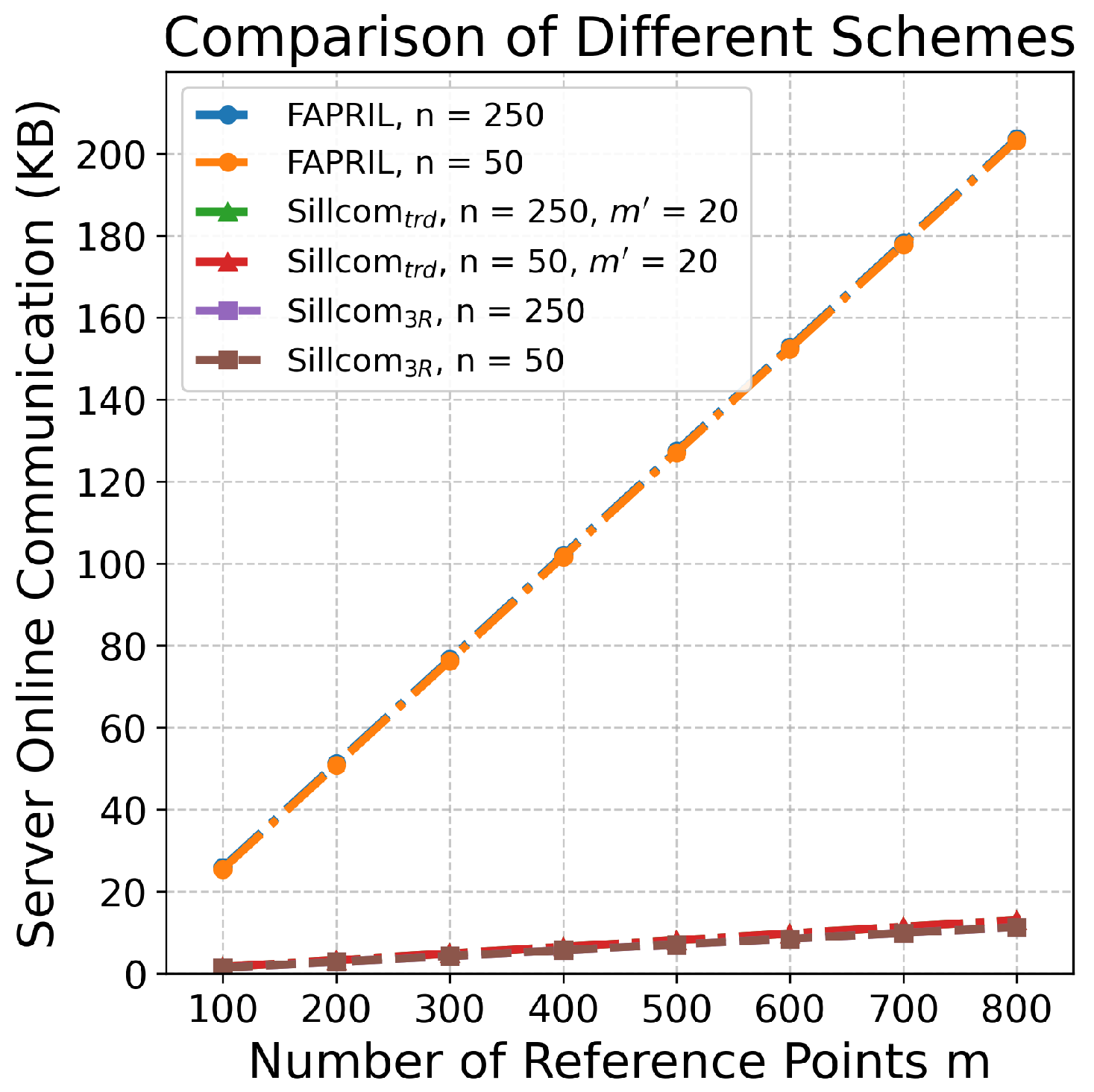
- We validate the performance of Sillcom through extensive experiments. Compared to the state-of-the-art scheme, FAPRIL [14], our improved design provides secure localization services with 1/15 of the online communication and 1/4 of the end-to-end query time.
1.2. Organization
2. Related Works
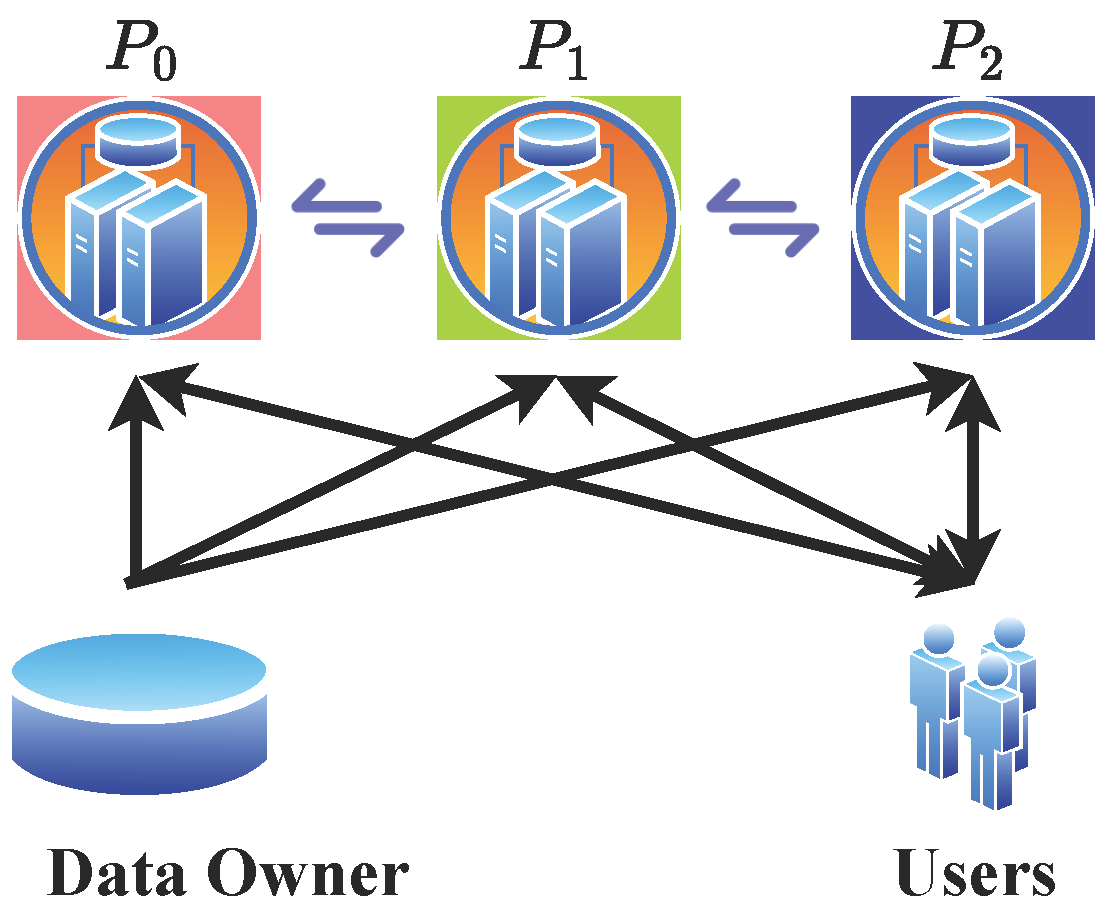
3. Problem Statement
4. Preliminaries
4.1. Notation
4.2. WiFi Fingerprint-Based Localization
4.2.1. Parameter Settings
4.3. Secret Sharing
4.4. Function Secret Sharing
- A PPT key generation algorithm inputs security parameter λ and (description of a function f), then outputs a pair of FSS keys and .
- A polynomial time evaluation algorithm inputs ’s FSS key , , and evaluates on , then outputs a value , which satisfies .
4.4.1. Secure Computation with FSS in the Preprocessing Model
4.4.2. Distributed Comparison Function
5. Sillcom3R: Basic Design with Three Online Rounds
5.1. Overview of Sillcom3R
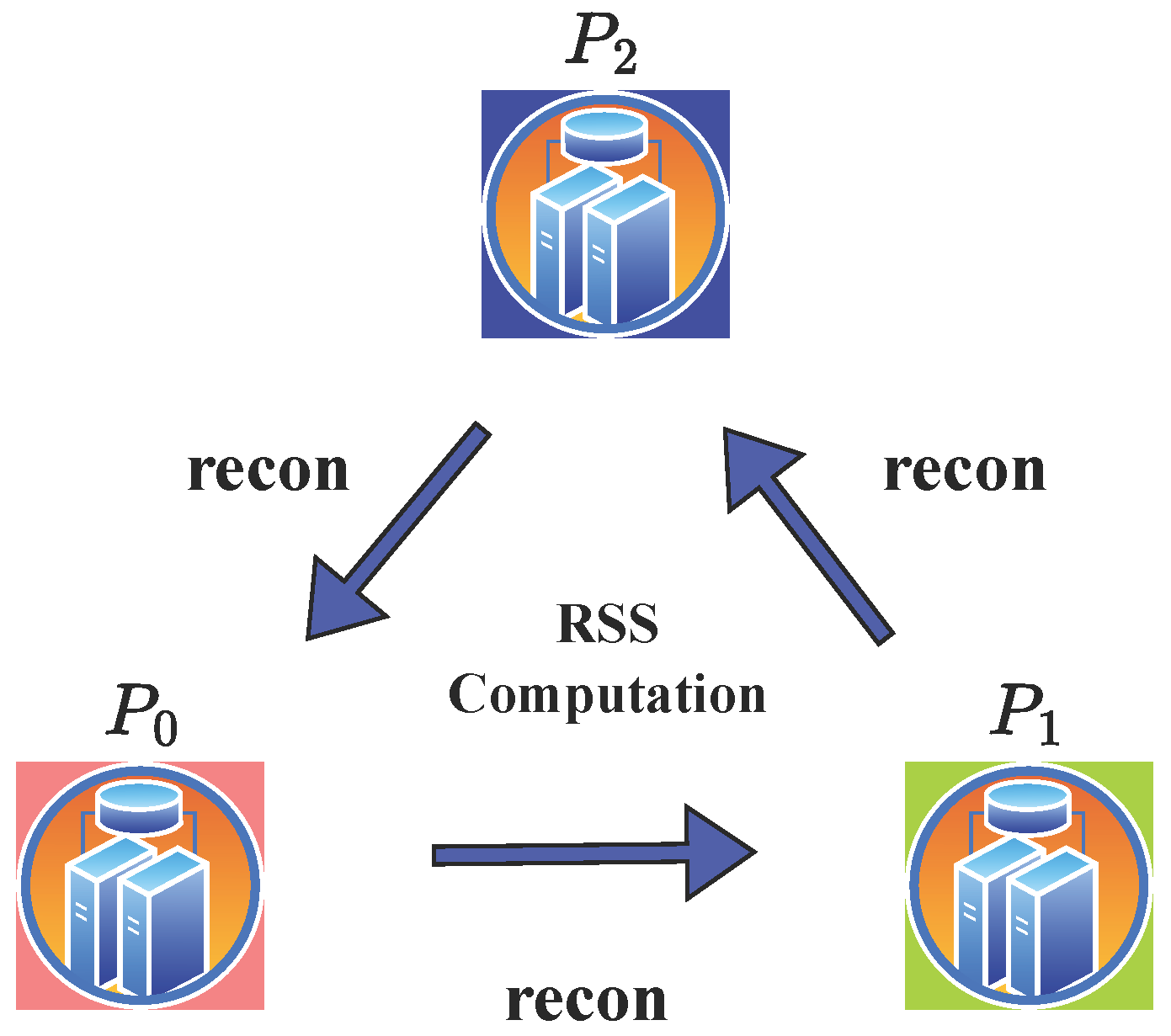
5.2. Communication-Efficient Distance Computation via RSS
| Algorithm 1 Secure square Euclidean distance computation via RSS |
| Input: RSS shared fingerprints of and of client, . Output: RSS shared square Euclidean distance between and . Offline preprocessing: 1: DO RSS share fingerprints to three computing servers , and , . Online computing: 1: Client RSS shares fingerprint to , and . 2: for to m do 3: Server locally computes − , , ,. 4: gets 3P-ASS share of square Euclidean distance between and by locally computing . 5: Servers perform RSS construction with compressed communication in one round. 6: end for |
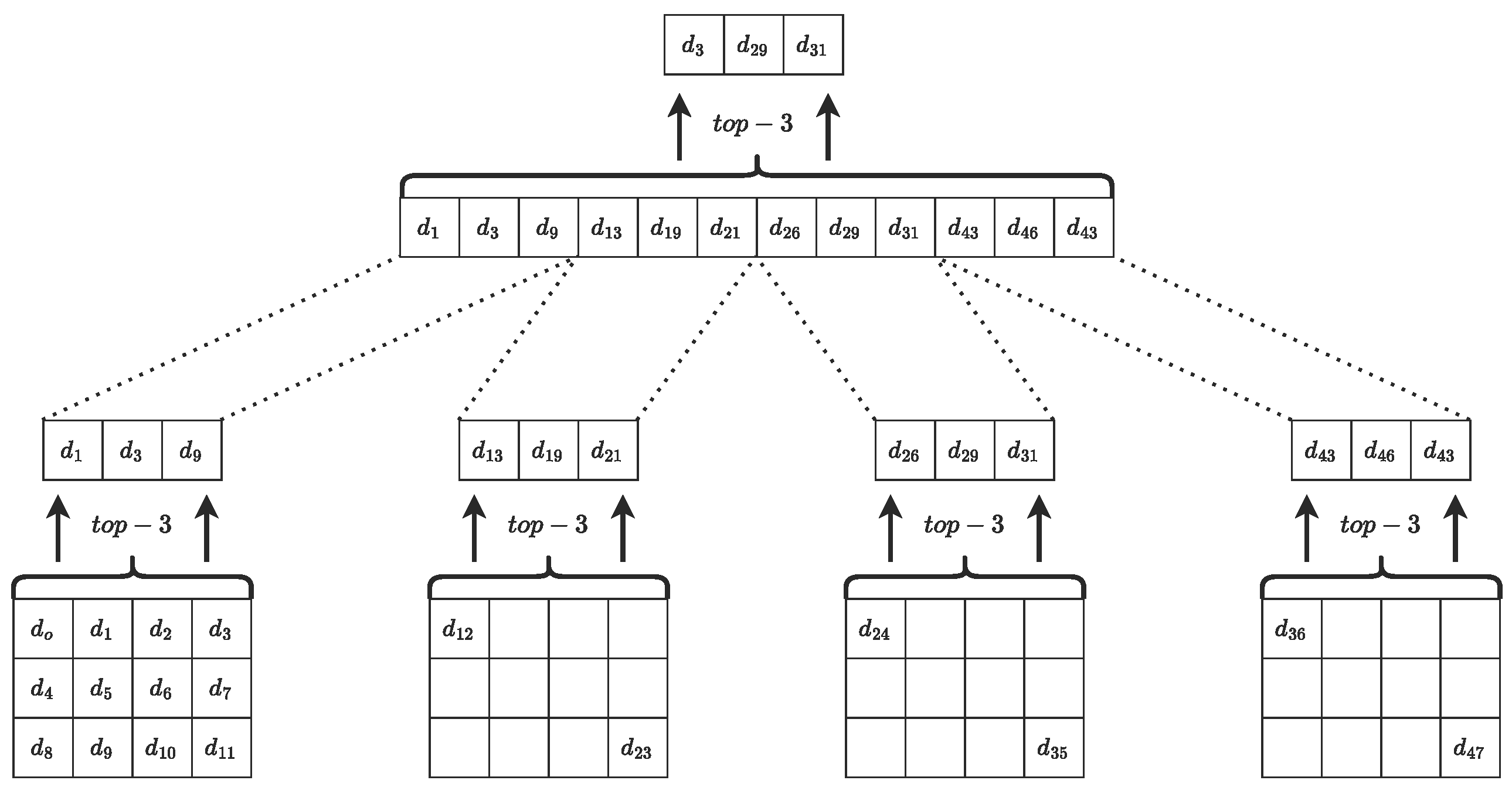
5.3. Round-Efficient Secure Top-k Ranking via FSS
Reducing Communication to
| Algorithm 2 Secure ranking via FSS |
| Input: 2P-ASS shared , holds , , . Output: gets 2P-ASS shared , denotes rank of . Offline preprocessing:
|
5.4. Secure Selection via Secure Shuffle
5.5. Eliminating RSS Reconstruction to Reduce One Round
| Algorithm 3 Share conversion |
| Input: ’s 3P-ASS shared distance vector . Output: and each gets 2P-ASS share of shuffled . Offline preprocessing:
|
5.6. Putting It All Together
| Algorithm 4 Three online round Sillcom3R |
| Input: RSS shared fingerprints of and of client, . Output: Client gets location coordinates. Offline preprocessing:
|
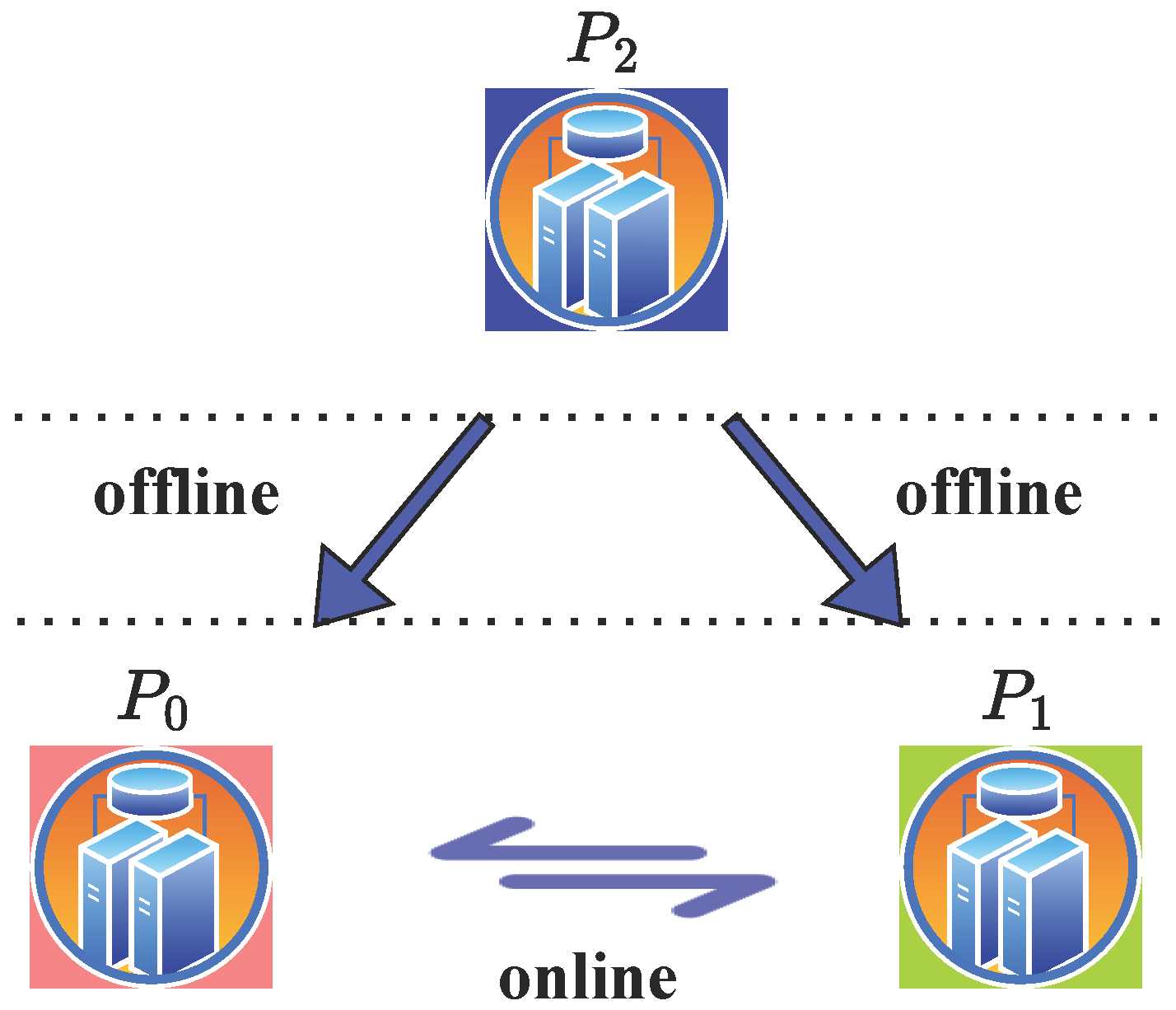
6. Sillcomtrd: Customized Optimization with Computation/Communication Tradeoff
6.1. Optimized Top-k Circuit for Small k
6.2. Accelerating FSS keys Computation via Multi-threads
7. Efficiency and Security Analysis
7.1. Cost Analysis
7.1.1. Communication Cost
7.1.2. Computation Cost
7.2. Security Proof
8. Evaluation Results
8.1. Experiment Setup
8.2. Micro Benchmarks
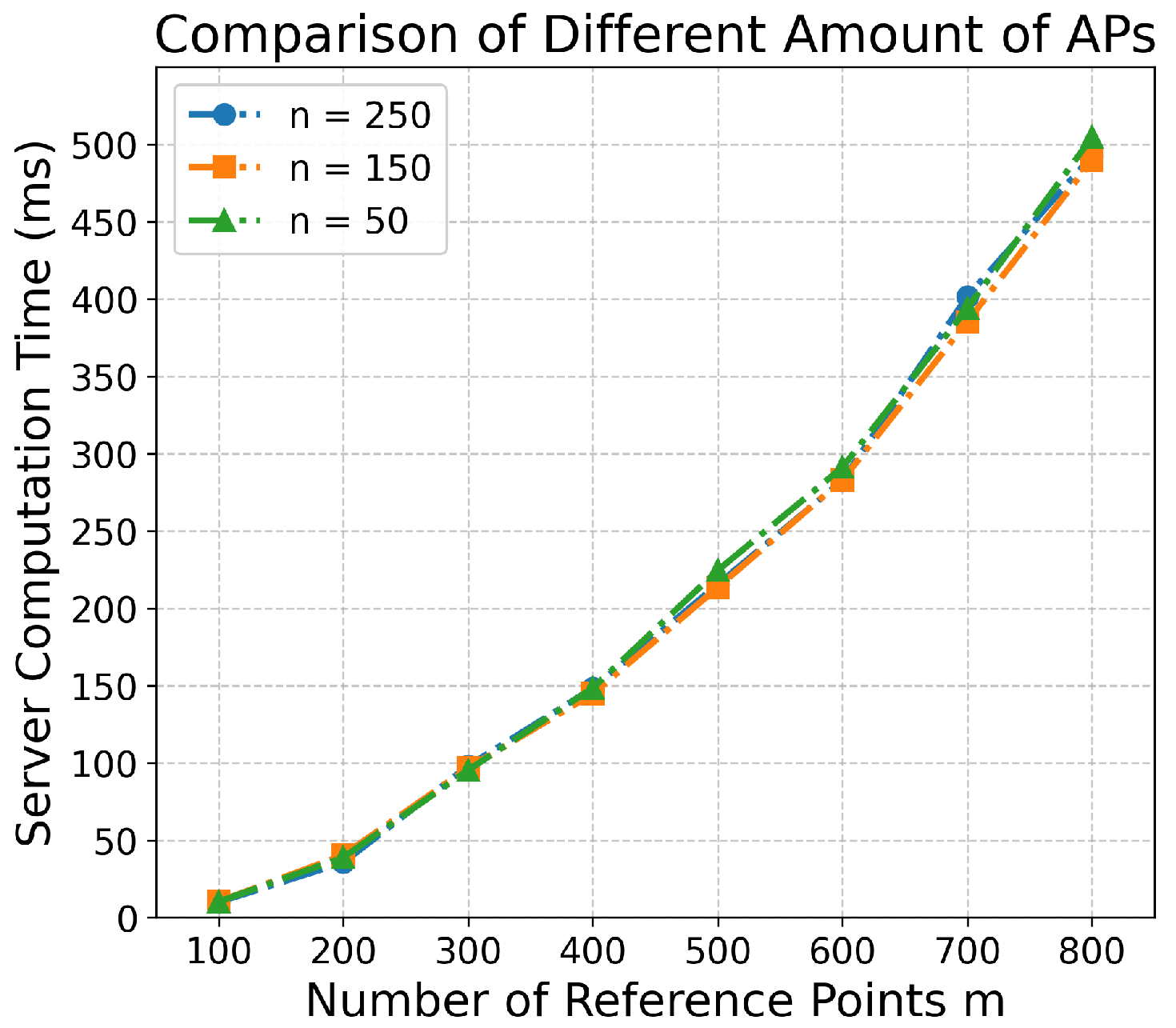
8.2.1. Different Amount of APs
8.2.2. Different Subset Size
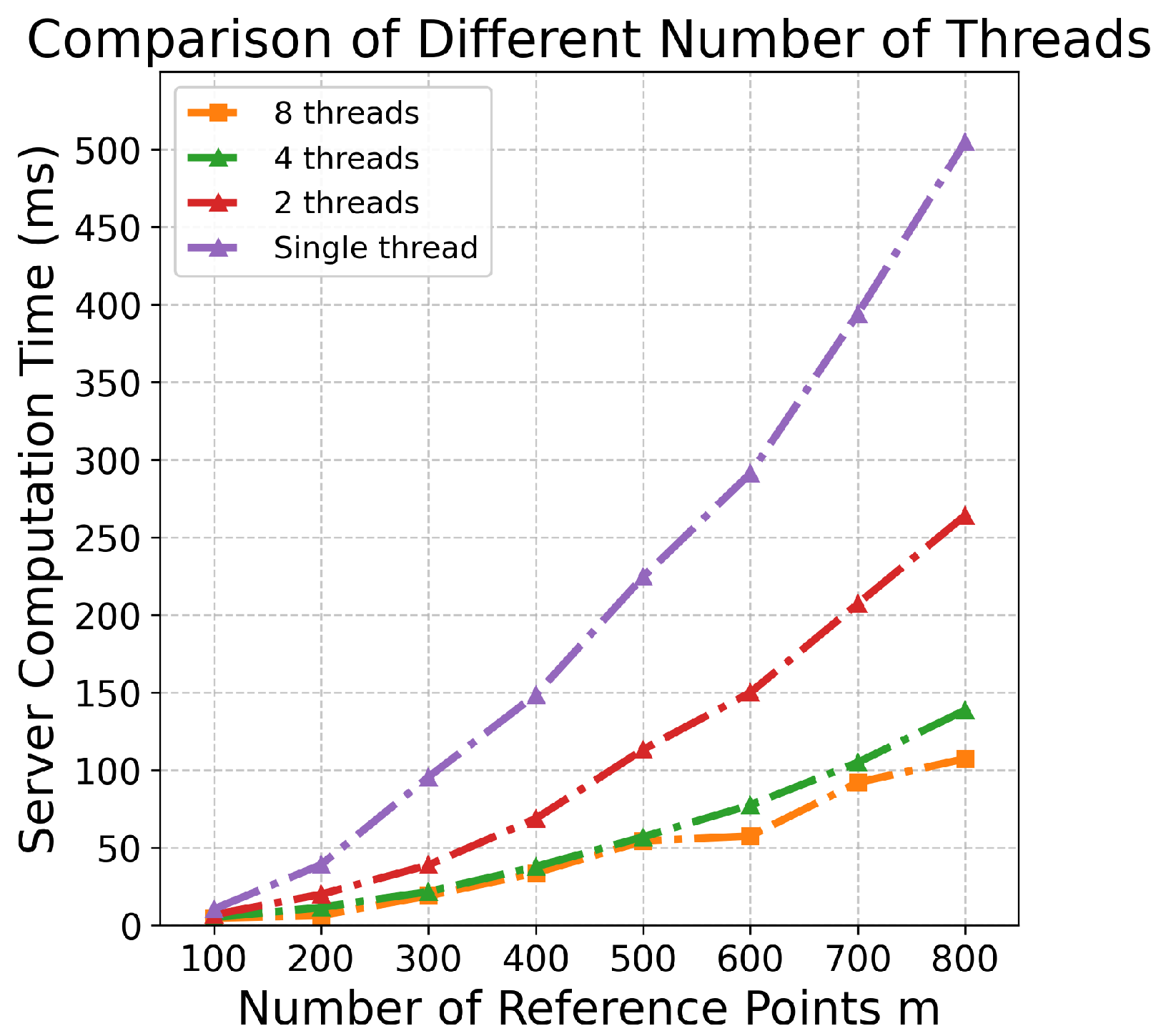
8.2.3. Different Number of Threads
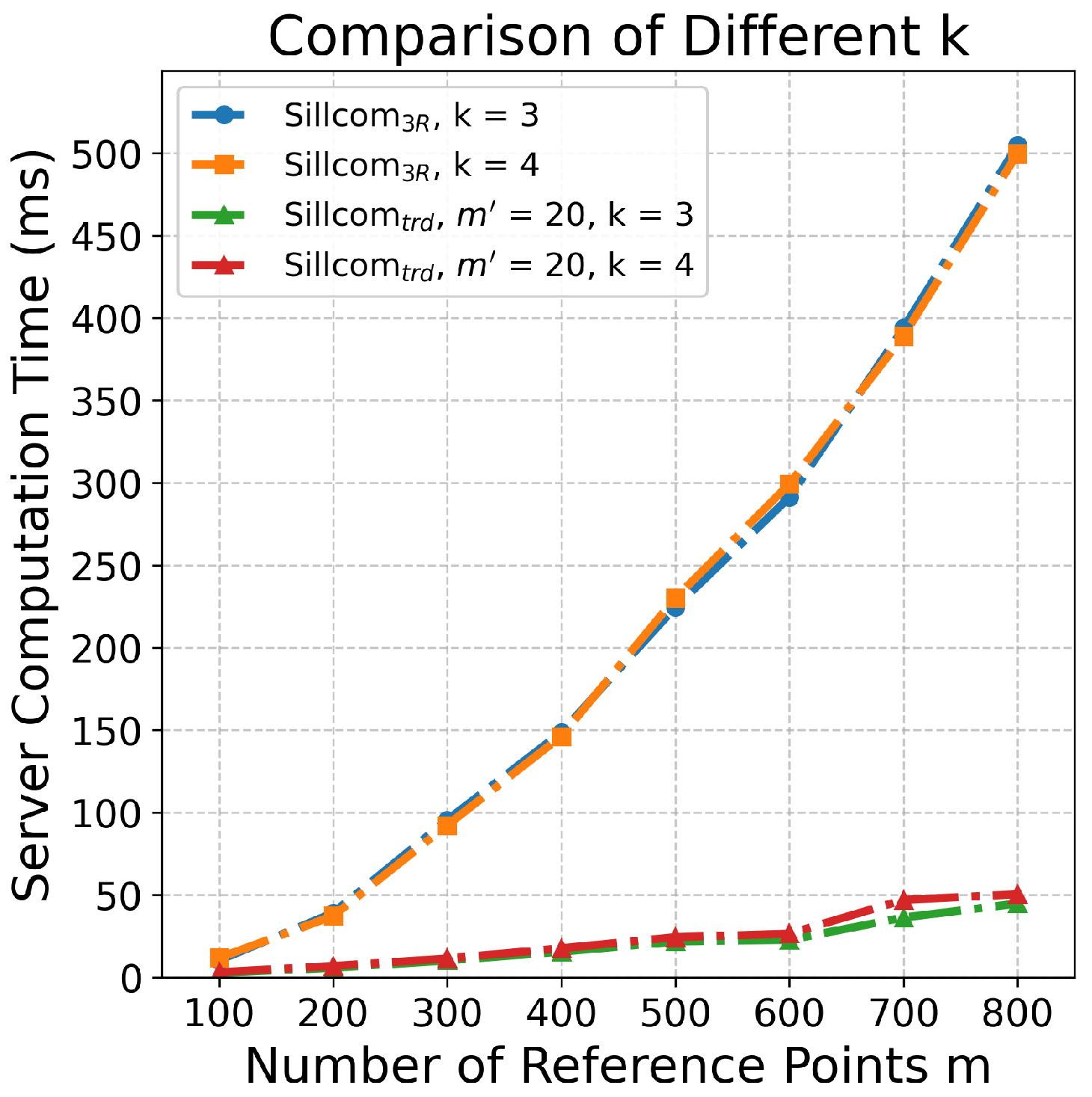
8.2.4. Different k
8.2.5. Runtime Breakdown
8.3. Comparison with FAPRIL [14]
9. Limitation and Future Work
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RSSs | Received Signal Strengths |
| 2P-ASS | 2-party Additive Secret Sharing |
| 3P-ASS | 3-party Additive Secret Sharing |
| RSS | Replicated Secret Sharing |
| FSS | Function Secret Sharing |
| DCF | Distributed Comparison Function |
| DDCF | Dual Distributed Comparison Function |
Appendix A. Detailed Secure Shuffle Protocol
| Algorithm A1 Secure shuffle |
| Input: Vector , holds , . holds random vector and random permutation . Output: gets and , . , . Offline preprocessing:
|
References
- Langlois, C.; Tiku, S.; Pasricha, S. Indoor localization with smartphones: Harnessing the sensor suite in your pocket. IEEE Consum. Electron. Mag. 2017, 6, 70–80. [Google Scholar] [CrossRef]
- Ladd, A.M.; Bekris, K.E.; Rudys, A.; Marceau, G.; Kavraki, L.E.; Wallach, D.S. Robotics-based location sensing using wireless ethernet. In Proceedings of the 8th Annual International Conference on Mobile Computing and Networking, Atlanta, GA, USA, 23–28 September 2002; pp. 227–238. [Google Scholar]
- Haeberlen, A.; Flannery, E.; Ladd, A.M.; Rudys, A.; Wallach, D.S.; Kavraki, L.E. Practical robust localization over large-scale 802.11 wireless networks. In Proceedings of the 10th Annual International Conference on Mobile Computing and Networking, Philadelphia, PA, USA, 26 September–1 October 2004; pp. 70–84. [Google Scholar]
- Chen, L.; Kuusniemi, H.; Chen, Y.; Pei, L.; Kröger, T.; Chen, R. Information filter with speed detection for indoor Bluetooth positioning. In Proceedings of the 2011 International Conference on Localization and GNSS (ICL-GNSS), Tampere, Finland, 29–30 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 47–52. [Google Scholar]
- Chawla, K.; McFarland, C.; Robins, G.; Shope, C. Real-time RFID localization using RSS. In Proceedings of the 2013 International Conference on Localization and GNSS (ICL-GNSS), Turin, Italy, 25–27 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Talvitie, J.; Lohan, E.S. Modeling received signal strength measurements for cellular network based positioning. In Proceedings of the 2013 International Conference on Localization and GNSS (ICL-GNSS), Turin, Italy, 25–27 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Guan, T.; Fang, L.; Dong, W.; Hou, Y.; Qiao, C. Indoor localization with asymmetric grid-based filters in large areas utilizing smartphones. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- He, S.; Lin, W.; Chan, S.H.G. Indoor localization and automatic fingerprint update with altered AP signals. IEEE Trans. Mob. Comput. 2016, 16, 1897–1910. [Google Scholar] [CrossRef]
- Voigt, P.; Von dem Bussche, A. The eu general data protection regulation (gdpr). In A Practical Guide, 1st ed.; Springer International Publishing: Cham, Switzerland, 2017; Volume 10, p. 10-5555. [Google Scholar]
- Li, H.; Sun, L.; Zhu, H.; Lu, X.; Cheng, X. Achieving privacy preservation in WiFi fingerprint-based localization. In Proceedings of the IEEE Infocom 2014-IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2337–2345. [Google Scholar]
- Shu, T.; Chen, Y.; Yang, J.; Williams, A. Multi-lateral privacy-preserving localization in pervasive environments. In Proceedings of the IEEE INFOCOM 2014-IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2319–2327. [Google Scholar]
- Zhang, G.; Zhang, A.; Zhao, P.; Sun, J. Lightweight privacy-preserving scheme in Wi-Fi fingerprint-based indoor localization. IEEE Syst. J. 2020, 14, 4638–4647. [Google Scholar] [CrossRef]
- Järvinen, K.; Leppäkoski, H.; Lohan, E.S.; Richter, P.; Schneider, T.; Tkachenko, O.; Yang, Z. PILOT: Practical privacy-preserving indoor localization using outsourcing. In Proceedings of the 2019 IEEE European Symposium on Security and Privacy (EuroS&P), Stockholm, Sweden, 17–19 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 448–463. [Google Scholar]
- van der Beets, C.; Nieminen, R.; Schneider, T. FAPRIL: Towards faster privacy-preserving fingerprint-based localization. Cryptol. ePrint Arch. 2022. [Google Scholar]
- Quijano, A.; Akkaya, K. Server-side fingerprint-based indoor localization using encrypted sorting. In Proceedings of the 2019 IEEE 16th International Conference on Mobile Ad Hoc and Sensor Systems Workshops (MASSW), Monterey, CA, USA, 4–7 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 53–57. [Google Scholar]
- Nieminen, R.; Järvinen, K. Practical privacy-preserving indoor localization based on secure two-party computation. IEEE Trans. Mob. Comput. 2020, 20, 2877–2890. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Yan, Y.; Ouyang, X.; Zhang, B. Privacy-Preserving WiFi localization based on inner product encryption in a cloud environment. IEEE Internet Things J. 2024, 11, 17264–17282. [Google Scholar] [CrossRef]
- Yang, Z.; Järvinen, K. The death and rebirth of privacy-preserving WiFi fingerprint localization with Paillier encryption. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications, Honolulu, HI, USA, 16–19 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1223–1231. [Google Scholar]
- Richter, P.; Leppakoski, H.; Lohan, E.S.; Yang, Z.; Jarvinen, K.; Tkachenko, O.; Schneider, T. Received signal strength quantization for secure indoor positioning via fingerprinting. In Proceedings of the 2018 8th International Conference on Localization and GNSS (ICL-GNSS), Guimaraes, Portugal, 26–28 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Wang, Z.; Xu, Y.; Yan, Y.; Zhang, Y.; Rao, Z.; Ouyang, X. Privacy-preserving indoor localization based on inner product encryption in a cloud environment. Knowl.-Based Syst. 2022, 239, 108005. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques 1999, Prague, Czech Republic, 2–6 May 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 223–238. [Google Scholar]
- Naor, M.; Pinkas, B. Efficient oblivious transfer protocols. In Proceedings of the SODA 2001, Washington, DC, USA, 7–9 January 2001; Volume 1, pp. 448–457. [Google Scholar]
- Ishai, Y.; Kilian, J.; Nissim, K.; Petrank, E. Extending oblivious transfers efficiently. In Proceedings of the Annual International Cryptology Conference 2003, Santa Barbara, CA, USA, 17–21 August 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 145–161. [Google Scholar]
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (SFCS 1986), Toronto, ON, Canada, 27–29 October 1986; IEEE: Piscataway, NJ, USA, 1986; pp. 162–167. [Google Scholar]
- Kolesnikov, V.; Schneider, T. Improved garbled circuit: Free XOR gates and applications. In Proceedings of the Automata, Languages and Programming: 35th International Colloquium, ICALP 2008, Reykjavik, Iceland, 7–11 July 2008; Proceedings, Part II 35. Springer: Berlin/Heidelberg, Germany, 2008; pp. 486–498. [Google Scholar]
- Damgard, I.; Geisler, M.; Kroigard, M. Homomorphic encryption and secure comparison. Int. J. Appl. Cryptogr. 2008, 1, 22–31. [Google Scholar] [CrossRef]
- Demmler, D.; Schneider, T.; Zohner, M. ABY-A framework for efficient mixed-protocol secure two-party computation. In Proceedings of the NDSS 2015, San Diego, CA, USA, 8–11 February 2015. [Google Scholar]
- Patra, A.; Schneider, T.; Suresh, A.; Yalame, H. {ABY2.0}: Improved {Mixed-Protocol} secure {Two-Party} computation. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Online, 11–13 August 2021; pp. 2165–2182. [Google Scholar]
- Fathalizadeh, A.; Moghtadaiee, V.; Alishahi, M. On the privacy protection of indoor location dataset using anonymization. Comput. Secur. 2022, 117, 102665. [Google Scholar] [CrossRef]
- Sazdar, A.M.; Alikhani, N.; Ghorashi, S.A.; Khonsari, A. Privacy preserving in indoor fingerprint localization and radio map expansion. Peer-to-Peer Netw. Appl. 2021, 14, 121–134. [Google Scholar] [CrossRef]
- Fathalizadeh, A.; Moghtadaiee, V.; Alishahi, M. Indoor geo-indistinguishability: Adopting differential privacy for indoor location data protection. IEEE Trans. Emerg. Top. Comput. 2023, 12, 293–306. [Google Scholar] [CrossRef]
- Hemkumar, D. Preserving location privacy against inference attacks in indoor positioning system. Peer-to-Peer Netw. Appl. 2024, 17, 784–799. [Google Scholar] [CrossRef]
- Varma, P.S.; Anand, V.; Donta, P.K. Federated KNN-based privacy-preserving position recommendation for indoor consumer applications. IEEE Trans. Consum. Electron. 2023, 70, 2738–2745. [Google Scholar] [CrossRef]
- Yan, J.; Cui, Y.; Wang, W. A Three-Level Federated Learning Framework for CSI Fingerprint Based Indoor Localization in Multiple Servers Environment. IEEE Commun. Lett. 2024, 28, 818–822. [Google Scholar] [CrossRef]
- Fathalizadeh, A.; Moghtadaiee, V.; Alishahi, M. Indoor Location Fingerprinting Privacy: A Comprehensive Survey. arXiv 2024, arXiv:2404.07345. [Google Scholar]
- Bahl, P.; Padmanabhan, V.N. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the IEEE INFOCOM 2000. Conference on Computer Communications. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies (Cat. No. 00CH37064), Tel Aviv, Israel, 26–30 March 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 2, pp. 775–784. [Google Scholar]
- Li, B.; Wang, Y.; Lee, H.K.; Dempster, A.; Rizos, C. Method for yielding a database of location fingerprints in WLAN. IEE Proc.-Commun. 2005, 152, 580–586. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the Managing Requirements Knowledge, International Workshop on IEEE Computer Society 1979, New York, NY, USA, 4–7 June 1979; p. 313. [Google Scholar]
- Ito, M.; Saito, A.; Nishizeki, T. Secret sharing scheme realizing general access structure. Electron. Commun. Jpn. (Part III Fundam. Electron. Sci.) 1989, 72, 56–64. [Google Scholar] [CrossRef]
- Araki, T.; Furukawa, J.; Lindell, Y.; Nof, A.; Ohara, K. High-throughput semi-honest secure three-party computation with an honest majority. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 805–817. [Google Scholar]
- Boyle, E.; Gilboa, N.; Ishai, Y. Function secret sharing. In Proceedings of the Advances in Cryptology-EUROCRYPT 2015: 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2015; pp. 337–367. [Google Scholar]
- Boyle, E.; Gilboa, N.; Ishai, Y. Function secret sharing: Improvements and extensions. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 1292–1303. [Google Scholar]
- Gilboa, N.; Ishai, Y. Distributed point functions and their applications. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques 2014, Copenhagen, Denmark, 11–15 May 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 640–658. [Google Scholar]
- Boyle, E.; Gilboa, N.; Ishai, Y. Secure computation with preprocessing via function secret sharing. In Proceedings of the Theory of Cryptography: 17th International Conference, TCC 2019, Nuremberg, Germany, 1–5 December 2019; Proceedings, Part I 17. Springer: Berlin/Heidelberg, Germany, 2019; pp. 341–371. [Google Scholar]
- Boyle, E.; Chandran, N.; Gilboa, N.; Gupta, D.; Ishai, Y.; Kumar, N.; Rathee, M. Function secret sharing for mixed-mode and fixed-point secure computation. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques 2021, Zagreb, Croatia, 17–21 October 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 871–900. [Google Scholar]
- Wagh, S. Pika: Secure computation using function secret sharing over rings. Proc. Priv. Enhancing Technol. 2022, 2022, 351–377. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Chen, R.; Peng, W.; Huang, X. SecRec: A privacy-preserving method for the context-aware recommendation system. IEEE Trans. Dependable Secur. Comput. 2021, 19, 3168–3182. [Google Scholar] [CrossRef]
- Mohassel, P.; Rindal, P. ABY3: A mixed protocol framework for machine learning. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 35–52. [Google Scholar]
- Agarwal, A.; Boyle, E.; Chandran, N.; Gilboa, N.; Gupta, D.; Ishai, Y.; Kelkar, M.; Ma, Y. Secure Sorting and Selection via Function Secret Sharing. In Proceedings of the 2024 on ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2024; pp. 3023–3037. [Google Scholar]
- Chase, M.; Ghosh, E.; Poburinnaya, O. Secret-shared shuffle. In Proceedings of the Advances in Cryptology–ASIACRYPT 2020: 26th International Conference on the Theory and Application of Cryptology and Information Security, Daejeon, Republic of Korea, 7–11 December 2020; Proceedings, Part III 26. Springer: Berlin/Heidelberg, Germany, 2020; pp. 342–372. [Google Scholar]
- Asharov, G.; Hamada, K.; Ikarashi, D.; Kikuchi, R.; Nof, A.; Pinkas, B.; Takahashi, K.; Tomida, J. Efficient secure three-party sorting with applications to data analysis and heavy hitters. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, CA, USA, 7–11 November 2022; pp. 125–138. [Google Scholar]
- Guo, C.; Katz, J.; Wang, X.; Yu, Y. Efficient and secure multiparty computation from fixed-key block ciphers. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 18–21 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 825–841. [Google Scholar]
- Guo, C.; Wang, X.; Xie, X.; Yu, Y. The Multi-user Constrained PRF Security of Generalized GGM Trees for MPC and Hierarchical Wallets. Cryptol. ePrint Arch. 2024. [Google Scholar]
- Ajtai, M.; Komlós, J.; Szemerédi, E. An 0 (n log n) sorting network. In Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing, Boston, MA, USA, 25–27 April 1983; pp. 1–9. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming; Pearson Education: London, UK, 1997; Volume 3. [Google Scholar]
- Li, J.; Huang, Z.; Zhang, M.; Liu, J.; Hong, C.; Wei, T.; Chen, W. PANTHER: Private Approximate Nearest Neighbor Search in the Single Server Setting. Cryptol. ePrint Arch. 2024. [Google Scholar]
- Dong, Y.; Lu, W.; Zheng, Y.; Wu, H.; Zhao, D.; Tan, J.; Huang, Z.; Hong, C.; Wei, T.; Chen, W. Puma: Secure inference of llama-7b in five minutes. arXiv 2023, arXiv:2307.12533. [Google Scholar]
- Kamara, S.; Raykova, M. Secure outsourced computation in a multi-tenant cloud. In Proceedings of the IBM Workshop on Cryptography and Security in Clouds 2011, Zurich, Switzerland, 15–16 March 2011; Volume 6. [Google Scholar]
- Chaudhari, H.; Choudhury, A.; Patra, A.; Suresh, A. Astra: High throughput 3pc over rings with application to secure prediction. In Proceedings of the 2019 ACM SIGSAC Conference on Cloud Computing Security Workshop, London, UK, 11 November 2019; pp. 81–92. [Google Scholar]
- Kushilevitz, E.; Lindell, Y.; Rabin, T. Information-theoretically secure protocols and security under composition. In Proceedings of the Thirty-Eighth Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 21–23 May 2006; pp. 109–118. [Google Scholar]
- Chandran, N.; Gupta, D.; Rastogi, A.; Sharma, R.; Tripathi, S. EzPC: Programmable and efficient secure two-party computation for machine learning. In Proceedings of the 2019 IEEE European Symposium on Security and Privacy (EuroS&P), Stockholm, Sweden, 17–19 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 496–511. [Google Scholar]
- Bai, J.; Song, X.; Zhang, X.; Wang, Q.; Cui, S.; Chang, E.C.; Russello, G. Mostree: Malicious secure private decision tree evaluation with sublinear communication. In Proceedings of the 39th Annual Computer Security Applications Conference, Austin, TX, USA, 4–8 December 2023; pp. 799–813. [Google Scholar]




| Scheme | Technique | Query Time | Communication | Security |
|---|---|---|---|---|
| [10] | Paillier | Slow | Middle | × |
| [11] | Paillier + OT | Middle | Middle | 🗸 |
| [18] | Paillier + GC | N/A | High | 🗸 |
| [19] | Paillier + GC | N/A | High | 🗸 |
| [15] | Paillier + DGK | Slow | Middle | 🗸 |
| [13] | GC + OT | Fast | High | 🗸 |
| [12] | Paillier | Slow | Middle | 🗸 |
| [16] | Paillier + GC | Slow | High | 🗸 |
| [14] | Delta sharing + GC | Fast | High | 🗸 |
| [20] | IPE | Slow | Middle | 🗸 |
| [17] | IPE + LSH | Fast | High | × Access Pattern |
| RSS + FSS | Middle | Low | 🗸 | |
| RSS + FSS | Fast | Low | 🗸 |
| Notations | Descriptions |
|---|---|
| Security parameter, =128 | |
| Computing servers, | |
| n | Number of access points |
| m | Number of reference points |
| Subset size for two-layer | |
| k | Number of nearest neighbors as result |
| Bit-length of | |
| l | Bit-length of in secure computation |
| Bit-length for ranks | |
| Secure protocol | |
| FSS key for comparison |
| Scheme | Module | Rounds | P2 | P0 | P1 |
|---|---|---|---|---|---|
| 0 | 0/0 | 0/0 | 0/0 | ||
| Merged | 0/ | 0/0 | 0/0 | ||
| 2 | /0 | 0/ | 0/ | ||
| 1 | /0 | 0/ | 0/ | ||
| 0 | 0/0 | 0/0 | 0/0 | ||
| Merged | 0/ | 0/0 | 0/0 | ||
| /0 | 0/ | 0/ | |||
| 0/ | 0/ |
| Offline Phase | Online Phase | |||
|---|---|---|---|---|
| Runtime (ms) | Comm. (MB) | Runtime (ms) | Comm. (KB) | |
| , | ||||
| FAPRIL [14] | 2500 | 9.8 | 96 | 129 |
| Sillcom3R | 621.3 | 87.4 | 16 + 221 | 7.2 |
| 451.8 | 87.4 | 16 + 54 | 7.2 | |
| , | 57.9 | 3.7 | 16 + 23 | 8.2 |
| , | 43.3 | 3.7 | 16 + 7 | 8.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Liu, L.; Peng, W. Sillcom: A Communication-Efficient Privacy-Preserving Scheme for Indoor Localization. Appl. Sci. 2025, 15, 6439. https://doi.org/10.3390/app15126439
Song S, Liu L, Peng W. Sillcom: A Communication-Efficient Privacy-Preserving Scheme for Indoor Localization. Applied Sciences. 2025; 15(12):6439. https://doi.org/10.3390/app15126439
Chicago/Turabian StyleSong, Shang, Lin Liu, and Wei Peng. 2025. "Sillcom: A Communication-Efficient Privacy-Preserving Scheme for Indoor Localization" Applied Sciences 15, no. 12: 6439. https://doi.org/10.3390/app15126439
APA StyleSong, S., Liu, L., & Peng, W. (2025). Sillcom: A Communication-Efficient Privacy-Preserving Scheme for Indoor Localization. Applied Sciences, 15(12), 6439. https://doi.org/10.3390/app15126439







