Quantitative Assessment of Bolt Looseness in Beam–Column Joints Using SH-Typed Guided Waves and Deep Neural Network
Abstract
1. Introduction
2. Dispersion Analysis of the I-Shaped Steel Beam
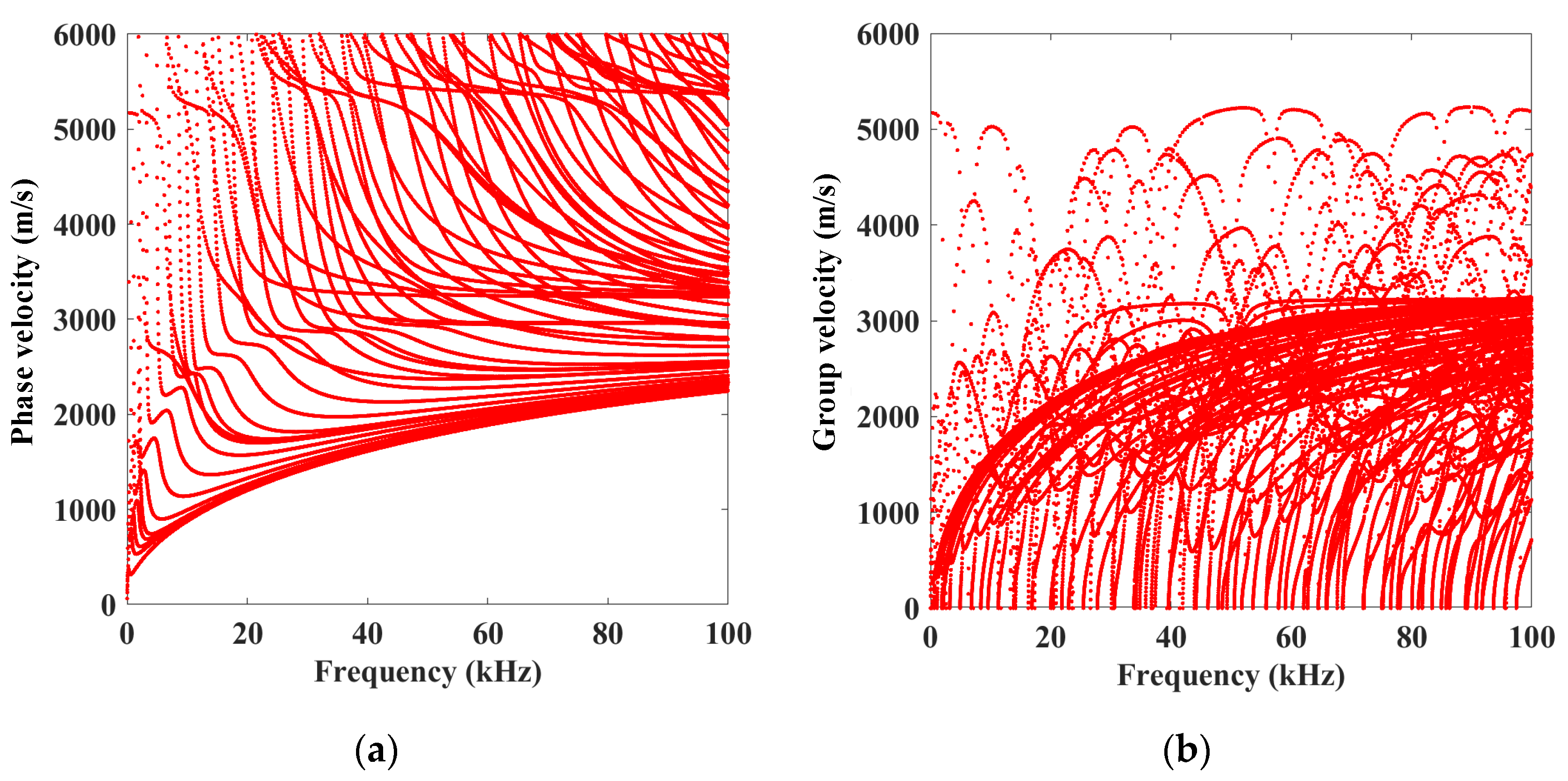
2.1. The SAFE Model
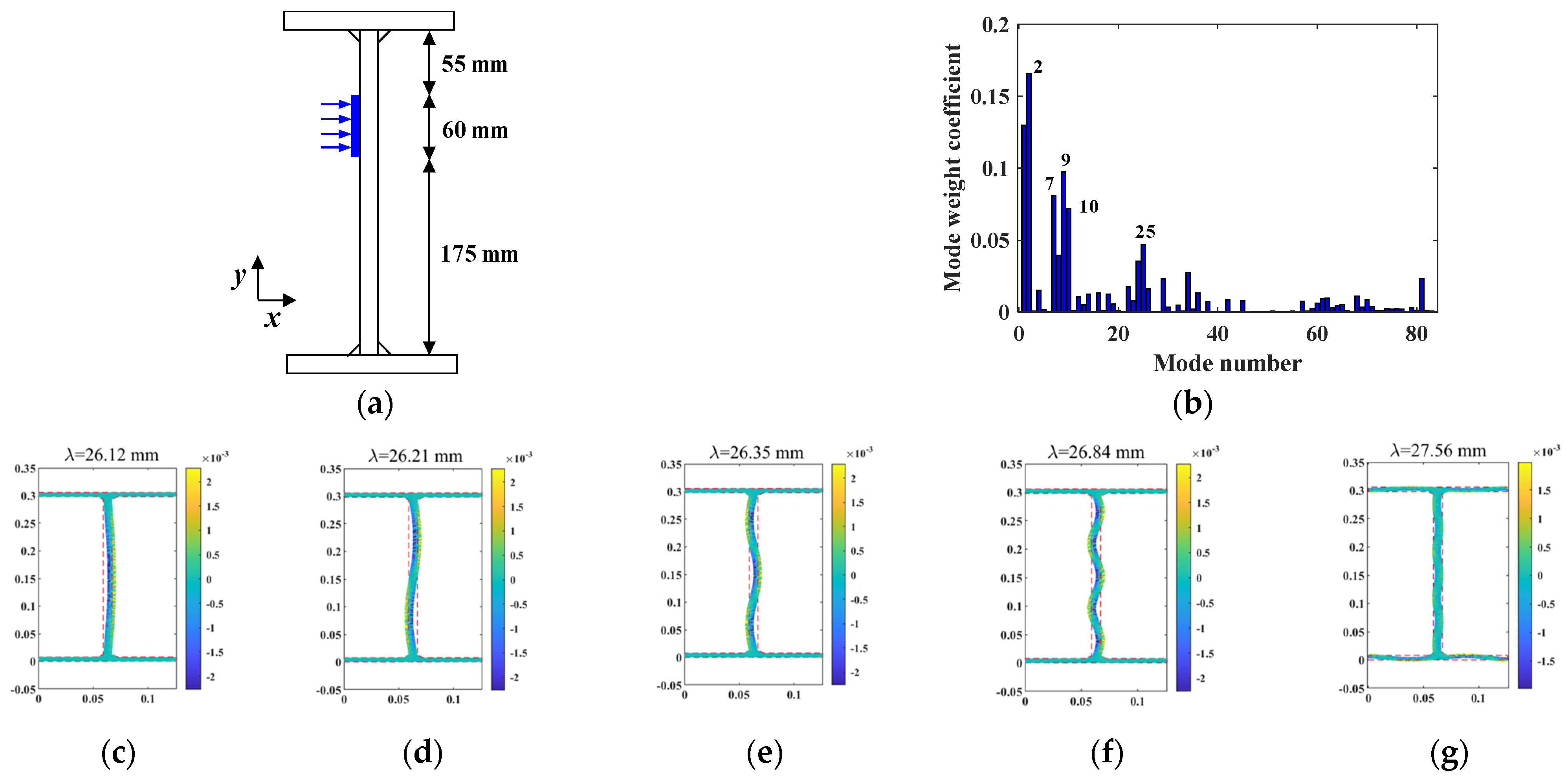
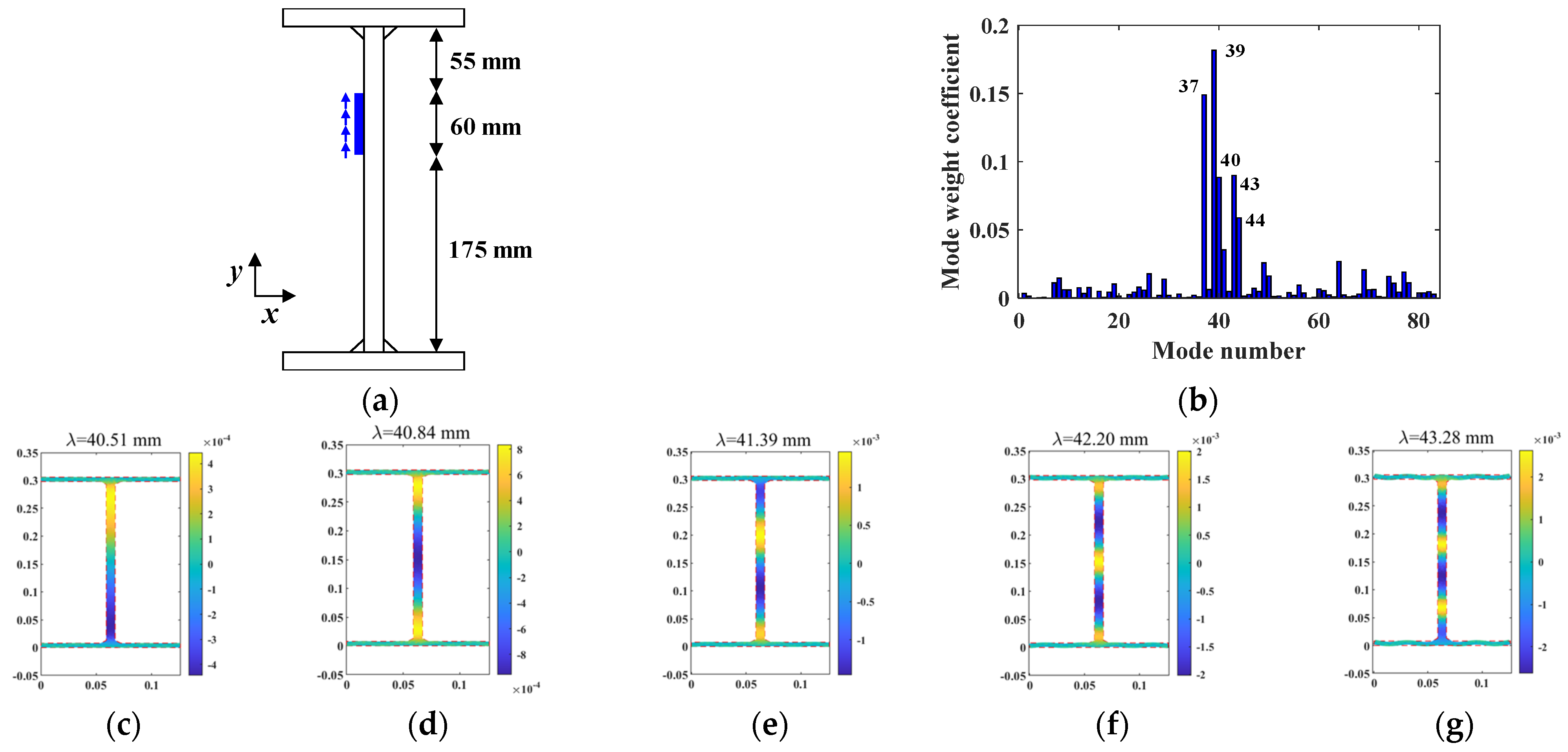
2.2. Wave Mode Analysis Under the External Load
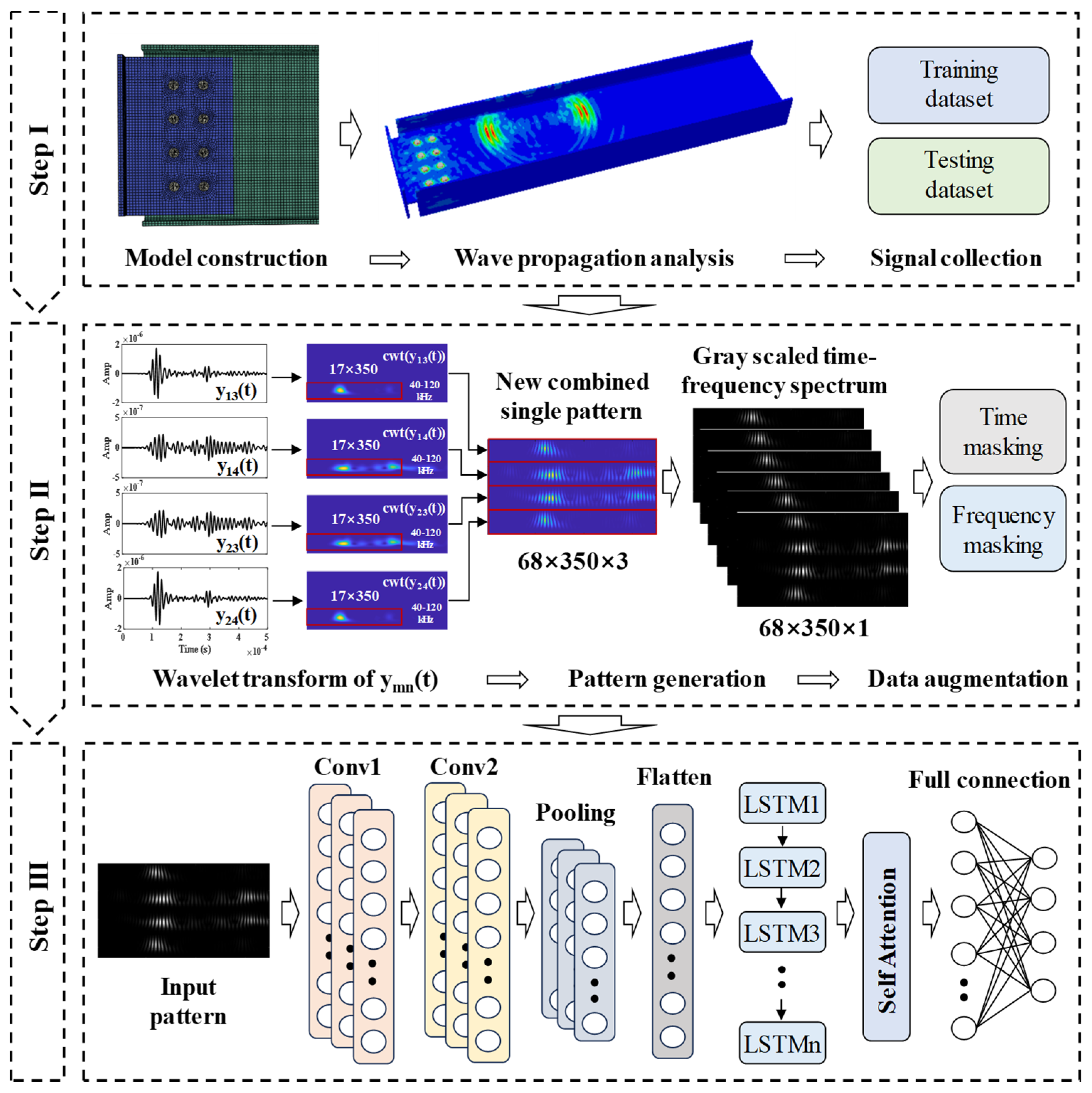
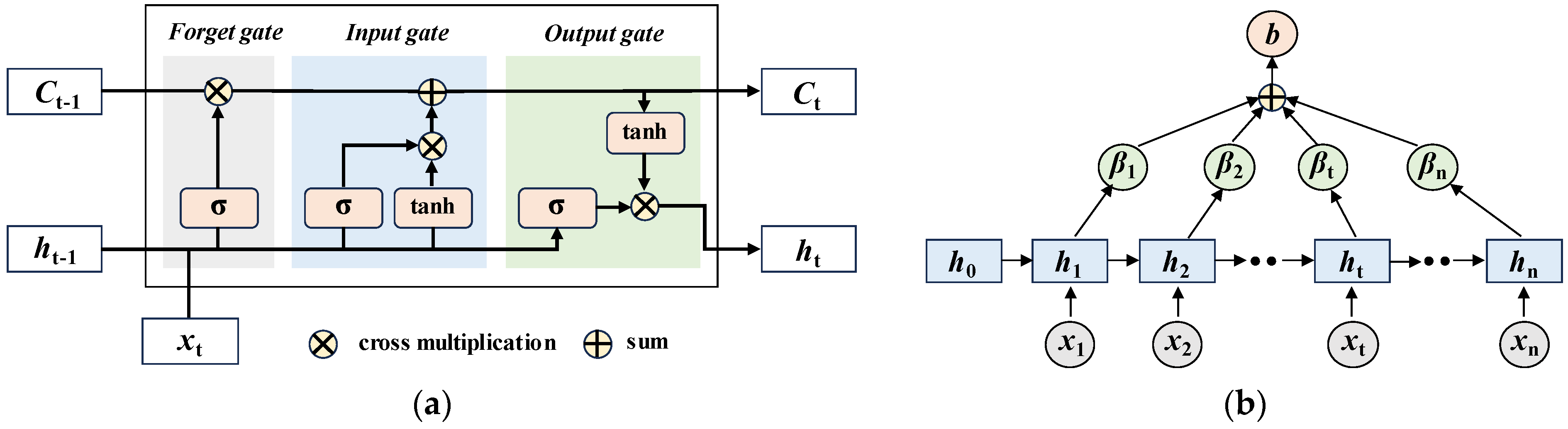
3. CNN-LSTM-MHSA Model-Based Multiple Bolt Looseness Detection
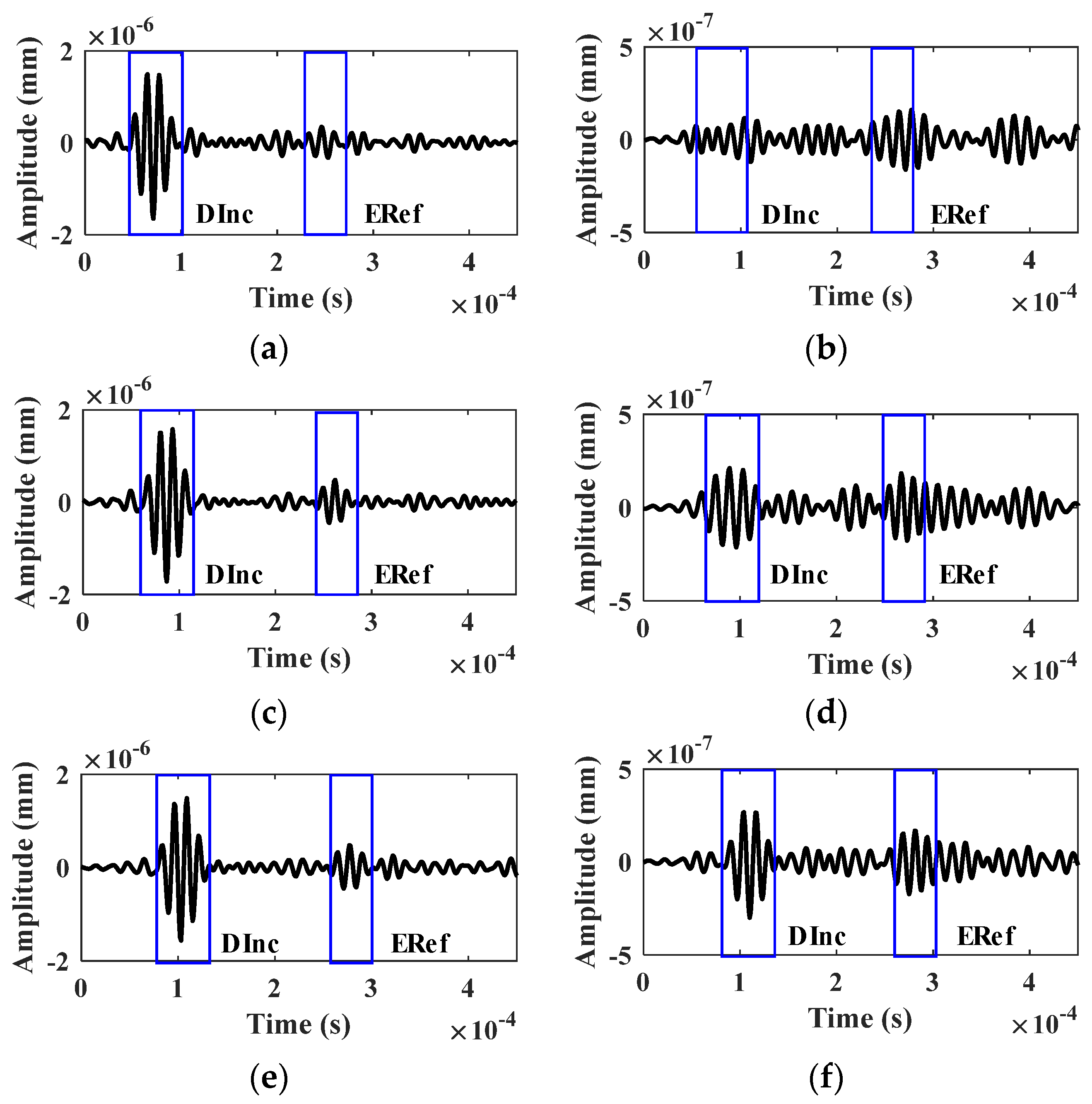
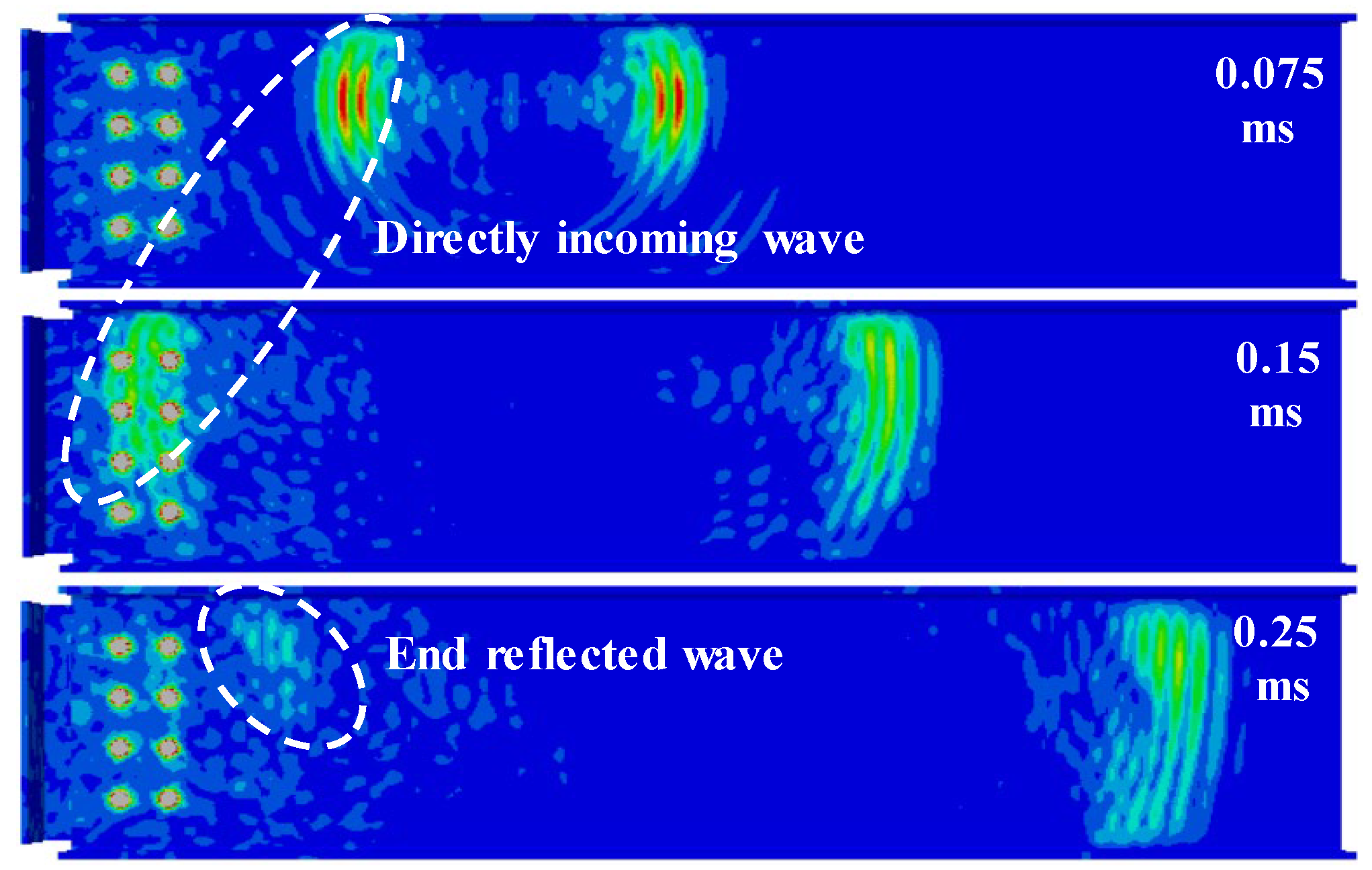
4. Numerical Example
4.1. Modeling of the Beam–Column Joint
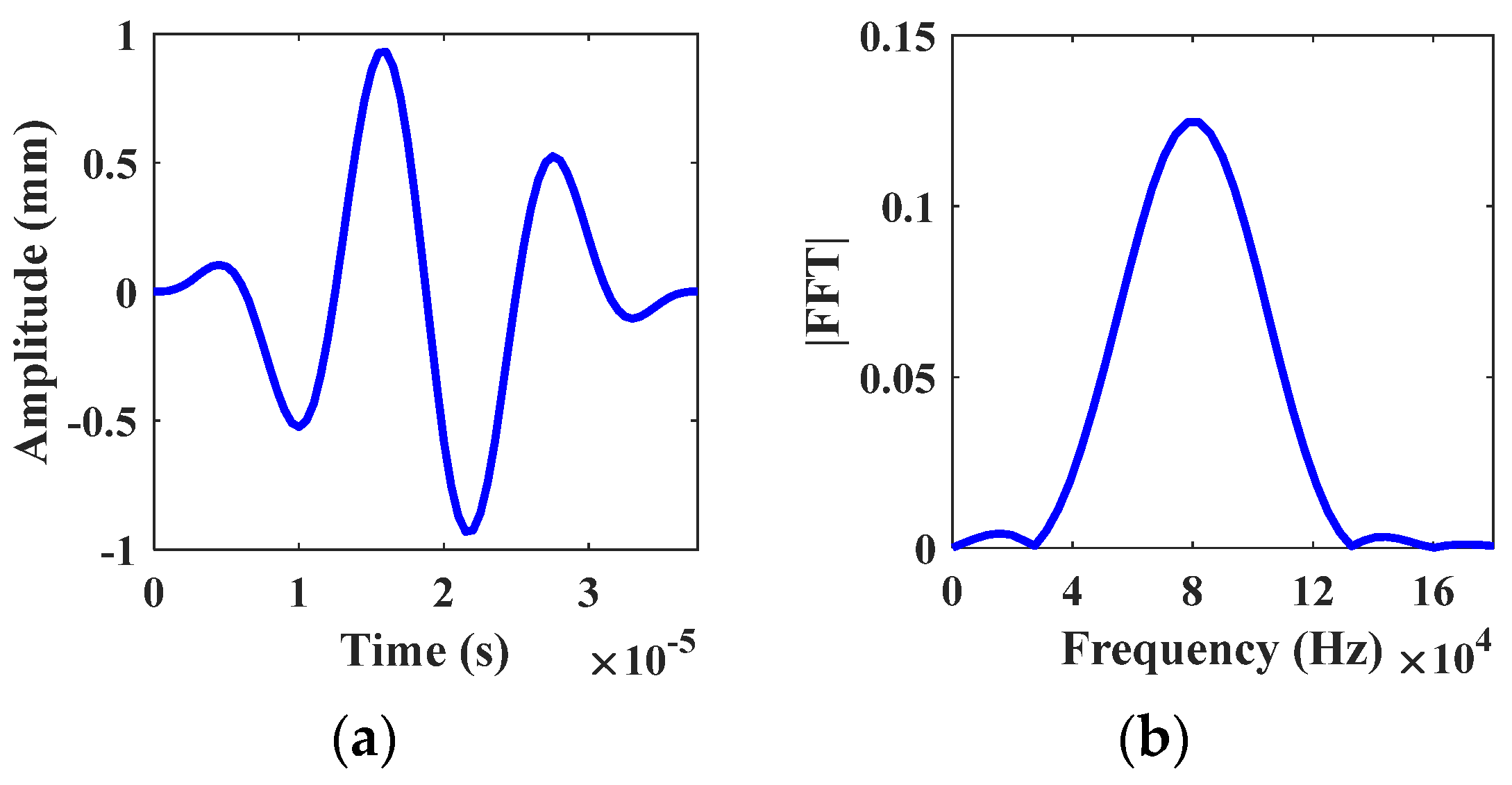
4.2. Simulation of Training and Testing Samples
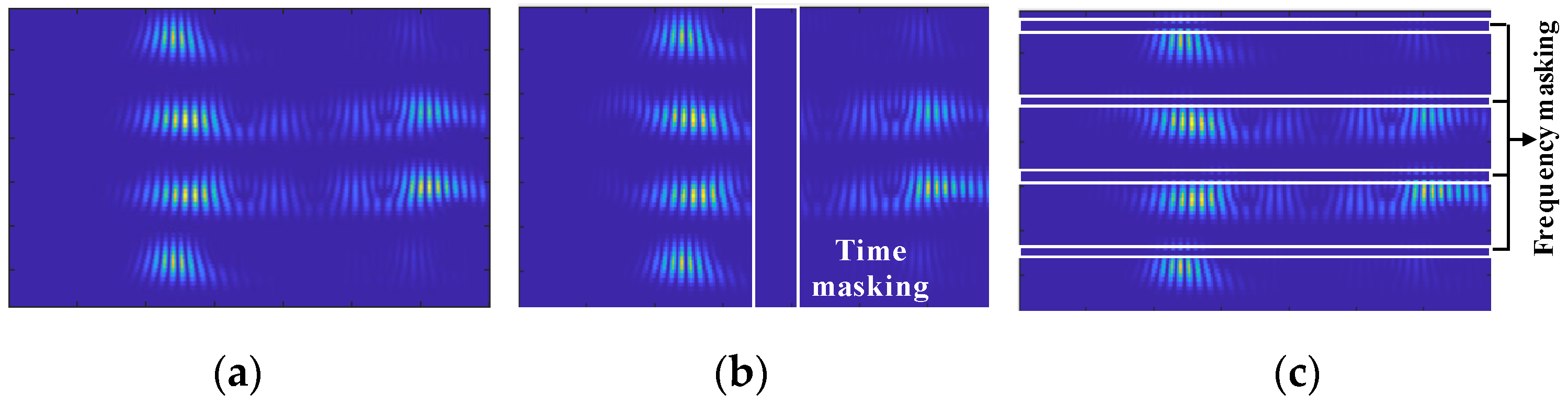
4.3. Data Augmentation
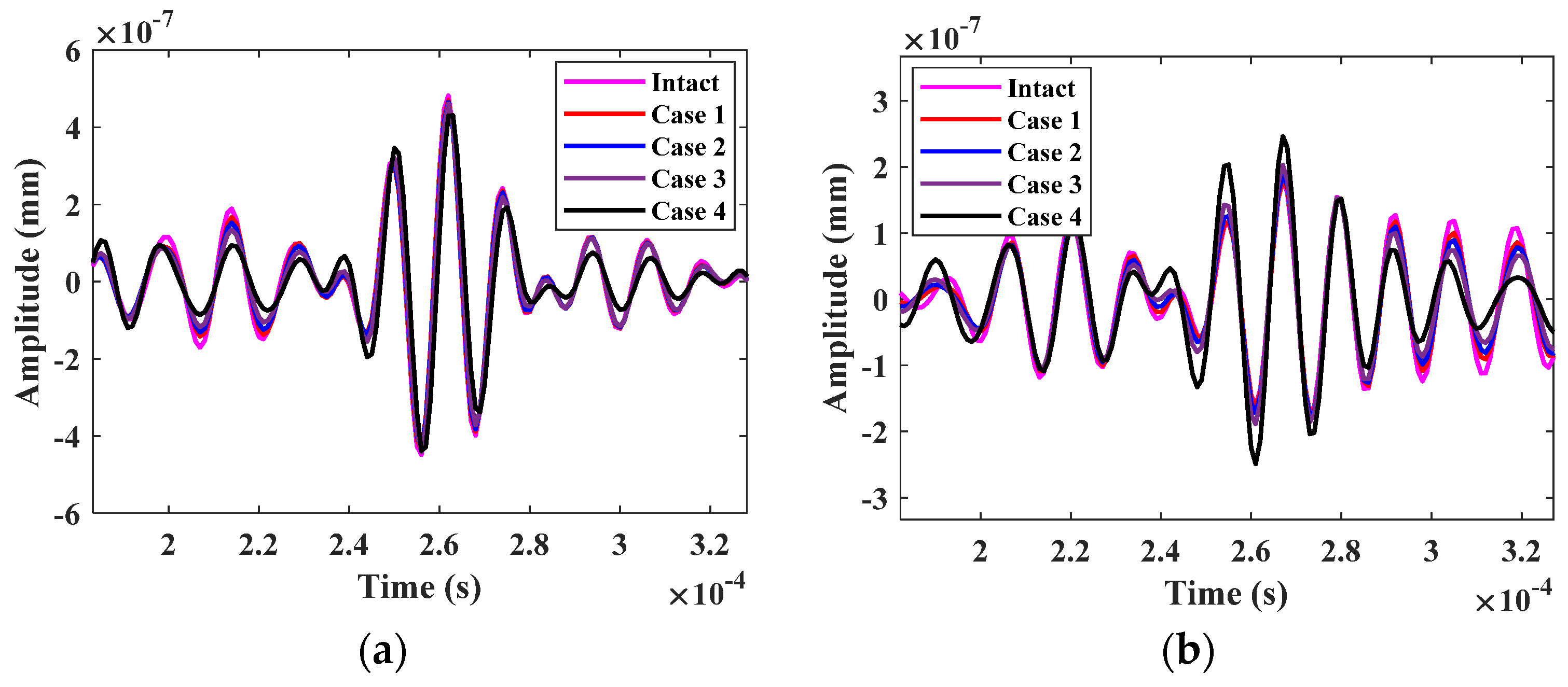
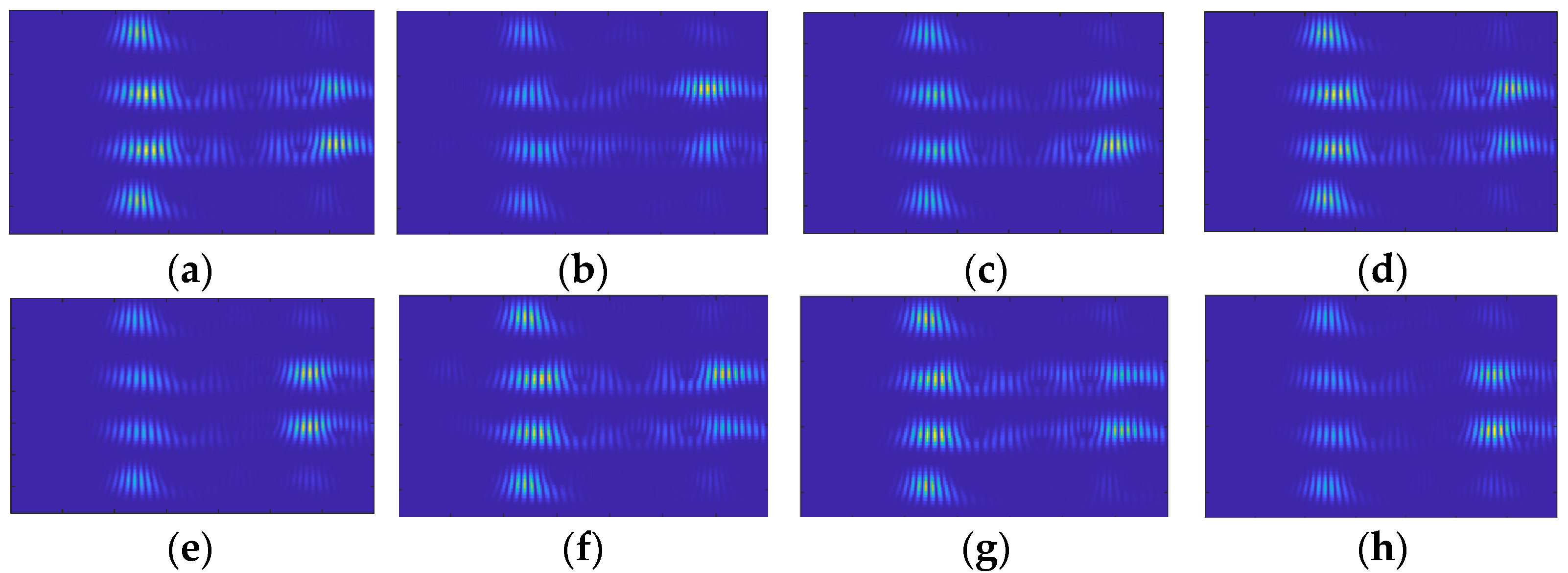
5. Bolt Looseness Detection Results and Discussion
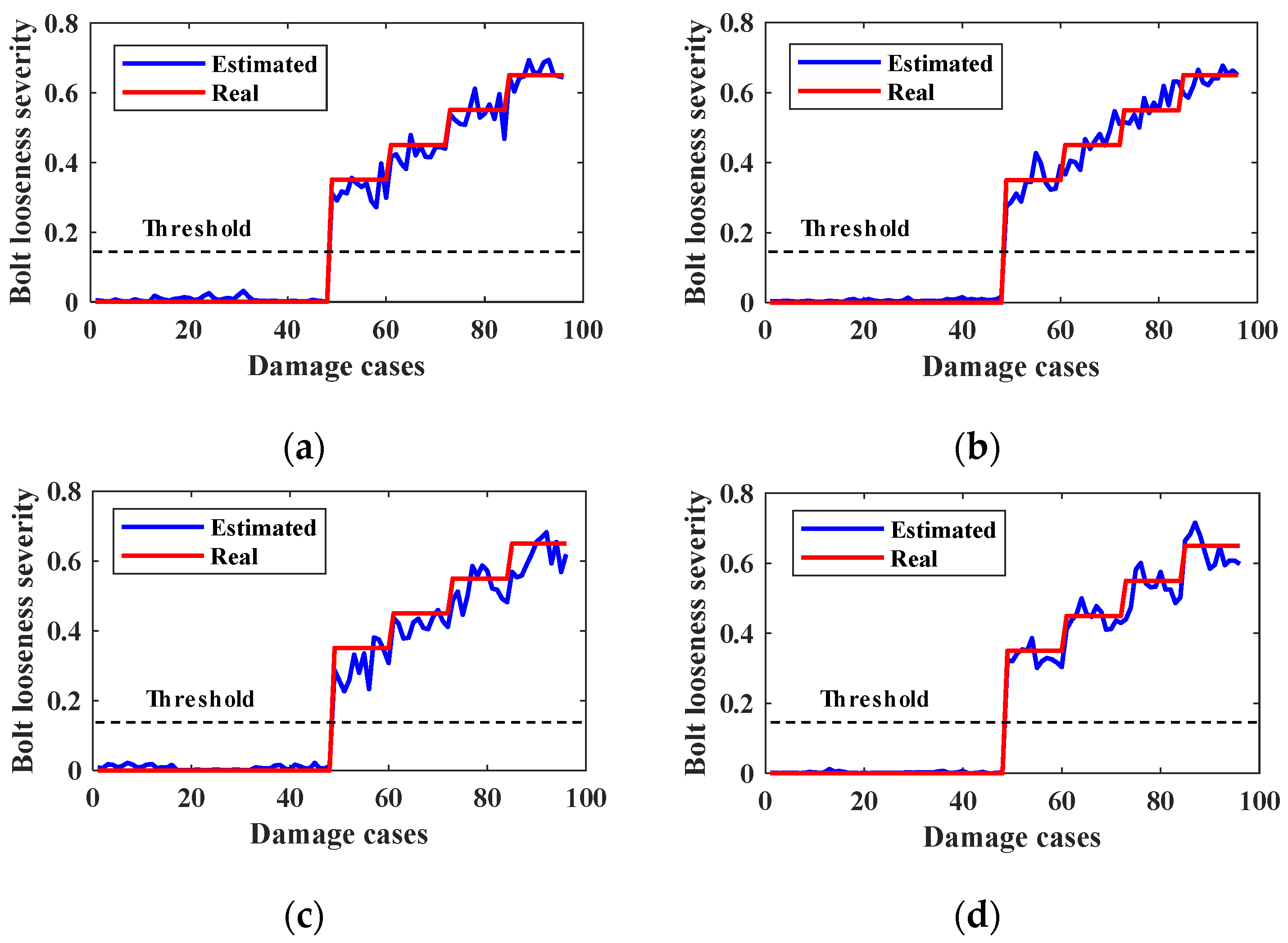
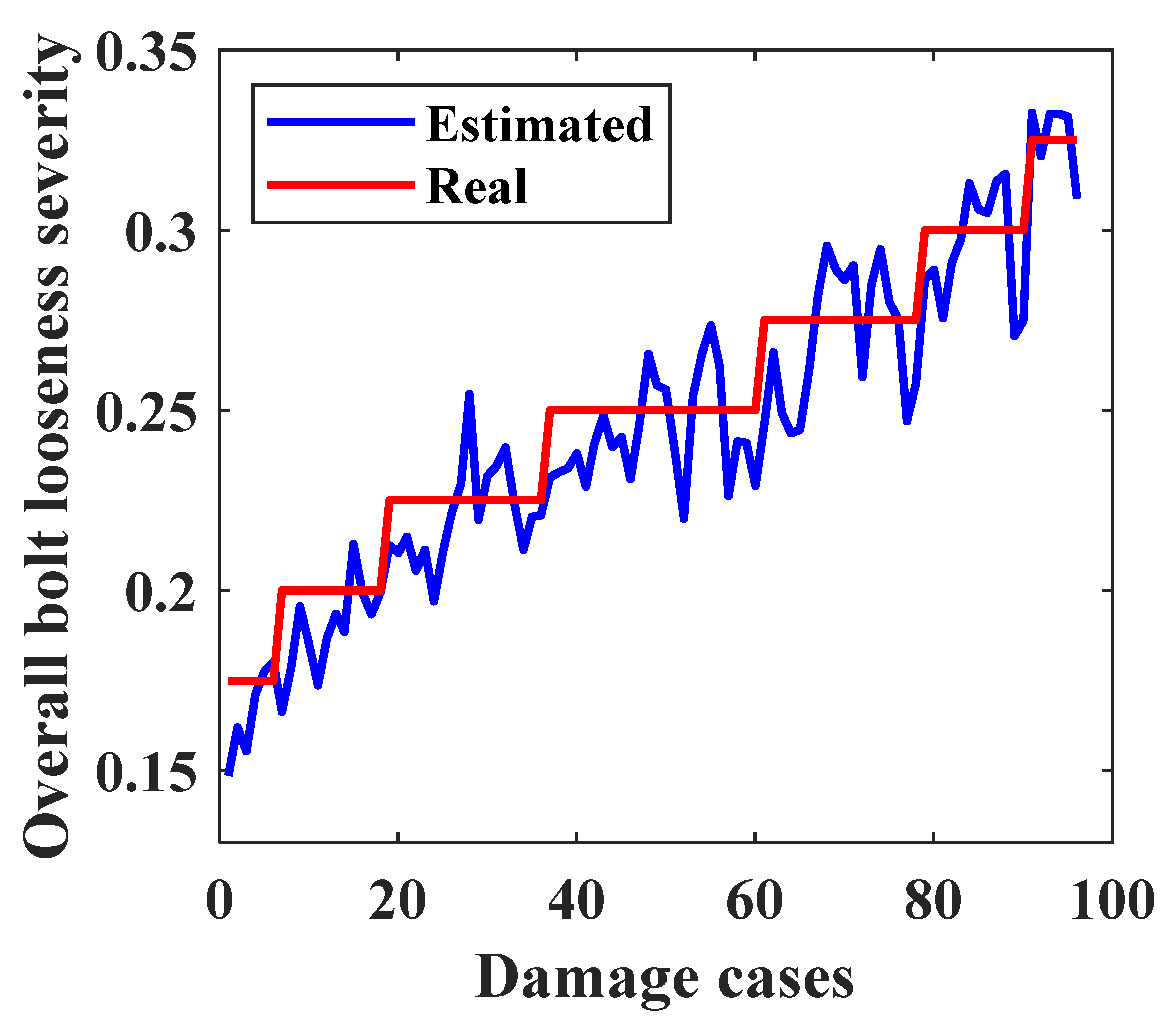
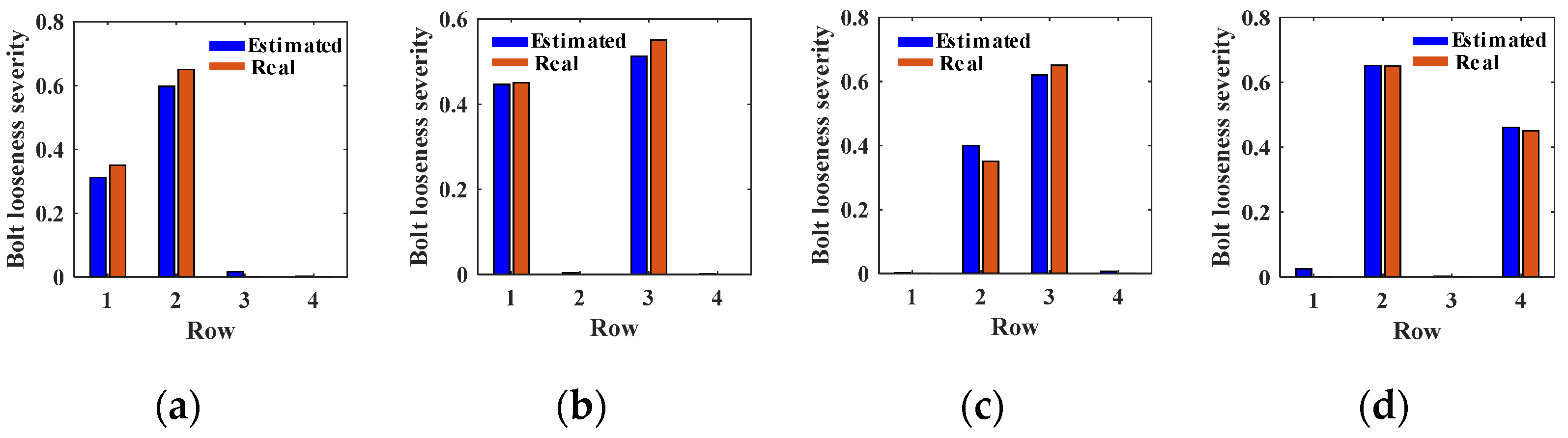
5.1. Training and Testing Results
5.2. Comparison for Different Input Patterns and Other Neural Network Models
5.3. Noise Injection Testing
6. Conclusions
- (1)
- The proposed mode weight coefficient aids in understanding how wave modes are distributed under different external loads for the I-shaped steel beam with complex dispersion properties. This coefficient can also assist in selecting the appropriate mode and position for the excitation signal.
- (2)
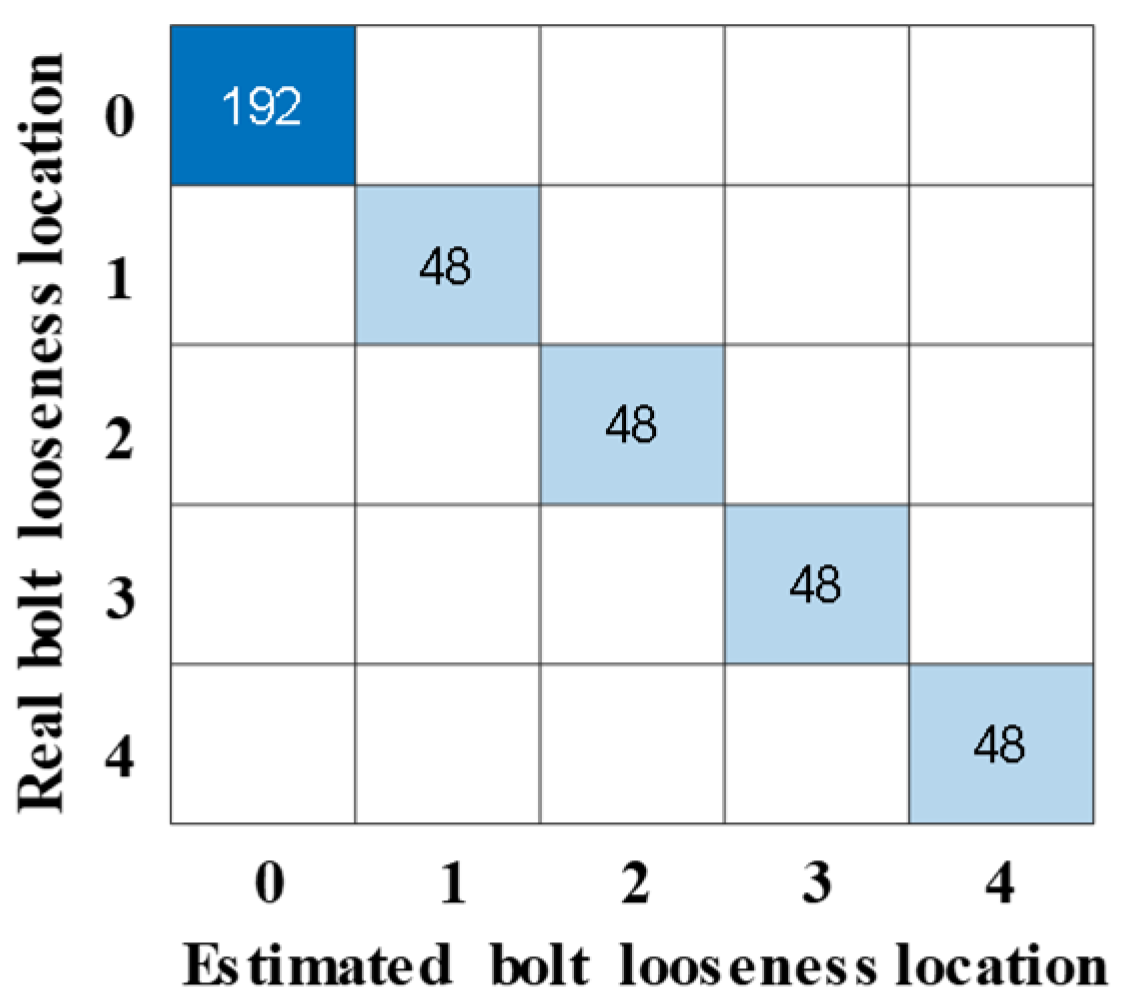
- The looseness conditions of multiple bolts in the beam–column joint were easily detected using the proposed CNN-LSTM-MHSA model. The bolt looseness localization accuracy was 100%, with local and overall severity estimation errors of 3.96% and 2.09%, respectively.
- (3)
- The CNN-LSTM-MHSA model, which integrates the time–frequency spectrum extracted from the guided wave signals, outperformed traditional deep neural networks with inputs of time series data and Fourier amplitude spectra, as well as the wave energy reflection ratio-based method.
- (4)
- White noise levels of 10% and 20% were added to the training and testing samples to simulate the effects of measurement noise. The proposed method maintained good bolt looseness localization accuracy, with values exceeding 93%. The maximum errors for Errorlocal and Erroroverall were 17.24% and 7.57%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, T.T.; Ta, Q.B.; Ho, D.D.; Kim, J.T.; Huynh, T.C. A method for automated bolt-loosening monitoring and assessment using impedance technique and deep learning. Dev. Built Environ. 2023, 14, 100122. [Google Scholar] [CrossRef]
- Chelimilla, N.; Chinthapenta, V.; Kali, N.; Korla, S. Review on recent advances in structural health monitoring paradigm for looseness detection in bolted assemblies. Struct. Health Monit. 2023, 22, 4264–4304. [Google Scholar] [CrossRef]
- Bonab, B.T.; Sadeghi, M.H.; Ettefagh, M.M. Bolt looseness detection in flanged pipes using parametric modeling. J. Pipeline Syst. Eng. Pract. 2024, 16, 04024067. [Google Scholar] [CrossRef]
- Huynh, T.C. Vision-based autonomous bolt-looseness detection method for splice connections: Design, lab-scale evaluation, and field application. Automat. Constr. 2021, 124, 103591. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, S.X.; Ni, Y.Q.; Choy, A.W.H. EMI-GCN: A hybrid model for real-time monitoring of multiple bolt looseness using electromechanical impedance and graph convolutional networks. Smart Mater. Struct. 2021, 30, 035032. [Google Scholar] [CrossRef]
- Chen, D.D.; Li, W.; Dong, Z.Q.; Fu, R.L.; Yu, Q. Multi-bolt looseness monitoring using guided waves: A cross-correlation approach of the wavelet energy envelope. Smart Mater. Struct. 2024, 33, 125019. [Google Scholar] [CrossRef]
- Wang, X.; Yue, Q.R.; Liu, X.G. Bolted lap joint loosening monitoring and damage identification based on acoustic emission and machine learning. Mech. Syst. Signal Process. 2024, 220, 111690. [Google Scholar] [CrossRef]
- Mori, K.; Horibe, T.; Maejima, K. Evaluation of the axial force in an FeCo bolt using the inverse magnetostrictive effect. Measurement 2020, 165, 108131. [Google Scholar] [CrossRef]
- Allen, J.C.P.; Ng, C.T. Nonlinear guided-wave mixing for condition monitoring of bolted joints. Sensors 2021, 21, 5093. [Google Scholar] [CrossRef]
- Zhang, M.R.; Tang, Z.F.; Yun, C.B.; Sui, X.D.; Chen, J.; Duan, Y.F. Bolt looseness detection using SH guided wave and wave energy transmission. Smart Mater. Struct. 2021, 30, 105015. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.H.; Cui, X.S.; Li, D.S. Guided wave-based damage assessment on bolt in precast beam-to-column joints. J. Build. Eng. 2024, 87, 108998. [Google Scholar] [CrossRef]
- Kitazawa, S.; Lee, Y.; Patel, R. Noncontact measurement of bolt axial force in tightening processes using scattered laser ultrasonic waves. NDT E Int. 2023, 137, 102838. [Google Scholar] [CrossRef]
- Du, F.; Wu, S.W.; Sheng, R.Z.; Xu, C.; Gong, H.; Zhang, J. Investigation into the transmission of guided waves across bolt jointed plates. Appl. Acoust. 2022, 196, 108866. [Google Scholar] [CrossRef]
- Wang, T.; Liu, S.P.; Shao, J.H.; Li, Y.R. Health monitoring of bolted joints using the time reversal method and piezoelectric transducers. Smart Mater. Struct. 2016, 25, 025010. [Google Scholar]
- Parvasi, S.M.; Ho, S.C.M.; Kong, Q.; Mousavi, R.; Song, G. Real time bolt preload monitoring using piezoceramic transducers and time reversal technique-a numerical study with experimental verification. Smart Mater. Struct. 2016, 25, 085015. [Google Scholar] [CrossRef]
- Xu, C.; Wu, G.N.; Du, F.; Zhu, W.D.; Mahdavi, S.H. A modified time reversal method for guided wave based bolt loosening monitoring in a lap joint. J. Nondestruct. Eval. 2019, 38, 85. [Google Scholar] [CrossRef]
- Qiu, J.X.; Abbas, S.; Zhu, Y.P.; Abbas, Z. Integrated acoustic-vibration frequency-modulation technology to detect the contact nonlinear features of mechanical structure. Struct. Control Health Monit. 2022, 29, e3057. [Google Scholar] [CrossRef]
- Chen, D.D.; Zhang, N.N.; Huo, L.S.; Song, G.B. Full-range bolt preload monitoring with multi-resolution using the time shifts of the direct wave and coda waves. Struct. Health Monit. 2023, 22, 3871–3890. [Google Scholar] [CrossRef]
- Hayashi, T.; Tamayama, C.; Murase, M. Wave structure analysis of guided waves in a bar with an arbitrary cross-section. Ultrasonics 2006, 44, 17–24. [Google Scholar] [CrossRef]
- Shen, W.; Li, D.S.; Ou, J.P. Dispersion analysis of multiscale wavelet finite element for 2D elastic wave propagation. J. Eng. Mech. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Tu, J.Q.; Tang, Z.F.; Yun, C.B.; Wu, J.J.; Xu, X. Guided wave-based damage assessment on welded steel I-beam under ambient temperature variations. Struct. Control Health Monit. 2021, 28, e2696. [Google Scholar] [CrossRef]
- Daneshyar, A.; Sotoudeh, P.; Ghaemian, M. The scaled boundary finite element method for dispersive wave propagation in higher-order continua. Int. J. Numer. Methods Eng. 2023, 124, 880–927. [Google Scholar] [CrossRef]
- Nemer, R.; Bouchoucha, F.; Arfa, H.; Ichchou, M. Wave propagation in uncertain laminated structure through stochastic wave finite element method. Mech. Res. Commun. 2025, 143, 104350. [Google Scholar] [CrossRef]
- Wu, J.J.; Tang, Z.F.; Lv, F.Z.; Yang, K.J. Ultrasonic guided wave focusing in waveguides with constant irregular cross-sections. Ultrasonics 2018, 89, 1–12. [Google Scholar] [CrossRef]
- Tang, Z.F.; Sui, X.D.; Duan, Y.F.; Zhang, P.F.; Yun, C.B. Guided wave-based cable damage detection using wave energy transmission and reflection. Struct. Control Health Monit. 2021, 28, e2688. [Google Scholar] [CrossRef]
- Li, W.X.; Dwight, R.A.; Zhang, T.L. On the study of vibration of a supported railway rail using the semi-analytical finite element method. J. Sound Vib. 2015, 345, 121–145. [Google Scholar] [CrossRef]
- Mariani, S.; Palermo, A.; Marzani, A. An extended semi-analytical finite element method for modeling guided waves in plates with pillared metasurfaces. J. Sound Vib. 2025, 607, 119030. [Google Scholar] [CrossRef]
- Khurjekar, I.D.; Harley, J.B. Reliability assessment of guided wave damage localization with deep learning uncertainty quantification methods. NDT E Int. 2024, 144, 103099. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Kong, Q.Z.; Song, G.B. Percussion-based bolt looseness monitoring using intrinsic multiscale entropy analysis and BP neural network. Smart Mater. Struct. 2019, 28, 125001. [Google Scholar] [CrossRef]
- Duan, Y.F.; Sui, X.D.; Tang, Z.F.; Yun, C.B. Bolt looseness detection and localization using time reversal signal and neural network techniques. Smart Struct. Syst. 2022, 30, 397–410. [Google Scholar]
- Wang, F.R.; Mobiny, A.; Nguyen, H.V.; Song, G.B. If structure can exclaim: A novel robotic-assisted percussion method for spatial bolt-ball joint looseness detection. Struct. Health Monit. 2021, 20, 1597–1608. [Google Scholar] [CrossRef]
- Chen, Y.X.; Zhu, L.; Gao, Z.N.; Li, W.J.; Wu, J.C. Multi-bolt looseness positioning using multivariate recurrence analytic active sensing method and MHAMCNN model. Struct. Health Monit. 2025, 24, 812–829. [Google Scholar] [CrossRef]
- Sui, X.D.; Zhang, R.; Luo, Y.Z.; Fang, Y. Multiple bolt looseness detection using SH-typed guided waves: Integrating physical mechanism with monitoring data. Ultrasonics 2025, 150, 107601. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.R.; Song, G.B. A novel percussion-based method for multi-bolt looseness detection using one-dimensional memory augmented convolutional long short-term memory networks. Mech. Syst. Signal Process. 2021, 161, 107955. [Google Scholar] [CrossRef]
- Ding, Y.; Ye, X.W.; Su, Y.H. Wind-induced fatigue life prediction of bridge hangers considering the effect of wind direction. Eng. Struct. 2025, 327, 119523. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xia, Y.; Zhao, J.F. Intelligent identification of bolt looseness with one-dimensional deep convolutional neural networks. Signal Image Video Process. 2025, 19, 158. [Google Scholar] [CrossRef]
- Yu, K.; Lin, T.R.; Ma, H.; Li, X.; Li, X. A multi-stage semi-supervised learning approach for intelligent fault diagnosis of rolling bearing using data augmentation and metric learning. Mech. Syst. Signal Process. 2021, 146, 107043. [Google Scholar] [CrossRef]
- Hu, T.H.; Tang, T.; Lin, R.L.; Chen, M.; Han, S.F.; Wu, J. A simple data augmentation algorithm and a self-adaptive convolutional architecture for few-shot fault diagnosis under different working conditions. Measurement 2020, 156, 107539. [Google Scholar] [CrossRef]
- Zayat, A.; Obeed, M.; Chaaban, A. Diversion detection in small-diameter HDPE pipes using guided waves and deep learning. Sensors 2022, 22, 9586. [Google Scholar] [CrossRef]
- Ghazimoghadam, S.; Hosseinzadeh, S.A.A. A novel unsupervised deep learning approach for vibration-based damage diagnosis using a multi-head self-attention LSTM autoencoder. Measurement 2024, 229, 114410. [Google Scholar] [CrossRef]
- Seung, H.M.; Kim, H.W.; Kim, Y.Y. Development of an omni-directional shear-horizontal wave magnetostrictive patch transducer for plates. Ultrasonics 2013, 53, 1304–1308. [Google Scholar] [CrossRef] [PubMed]
- Alam, Z.; Sharma, A.K. Topology optimization of hard-magnetic soft laminates for wide tunable SH wave bandgaps. Compos. Struct. 2025, 366, 119157. [Google Scholar] [CrossRef]
- Sui, X.D.; Zhang, R.; Luo, Y.Z.; Tang, Z.F.; Wang, Z. A Lorentz force-based SH-typed electromagnetic acoustic transducer using flexible circumferential printed circuit. Ultrasonics 2024, 141, 107348. [Google Scholar] [CrossRef] [PubMed]
- Sui, X.D.; Duan, Y.F.; Yun, C.B.; Tang, Z.F.; Chen, J.W.; Shi, D.W.; Hu, G.M. Bolt looseness detection and localization using wave energy transmission ratios and neural network technique. J. Infrastruct. Intell. Resil. 2023, 2, 100025. [Google Scholar] [CrossRef]
- Du, F.; Wu, S.W.; Tian, Z.X.; Qiu, F.; Xu, C.; Su, Z.Q. An improved prototype network and data augmentation algorithm for few-shot structural health monitoring using guided waves. IEEE Sens. J. 2023, 23, 8714–8726. [Google Scholar] [CrossRef]
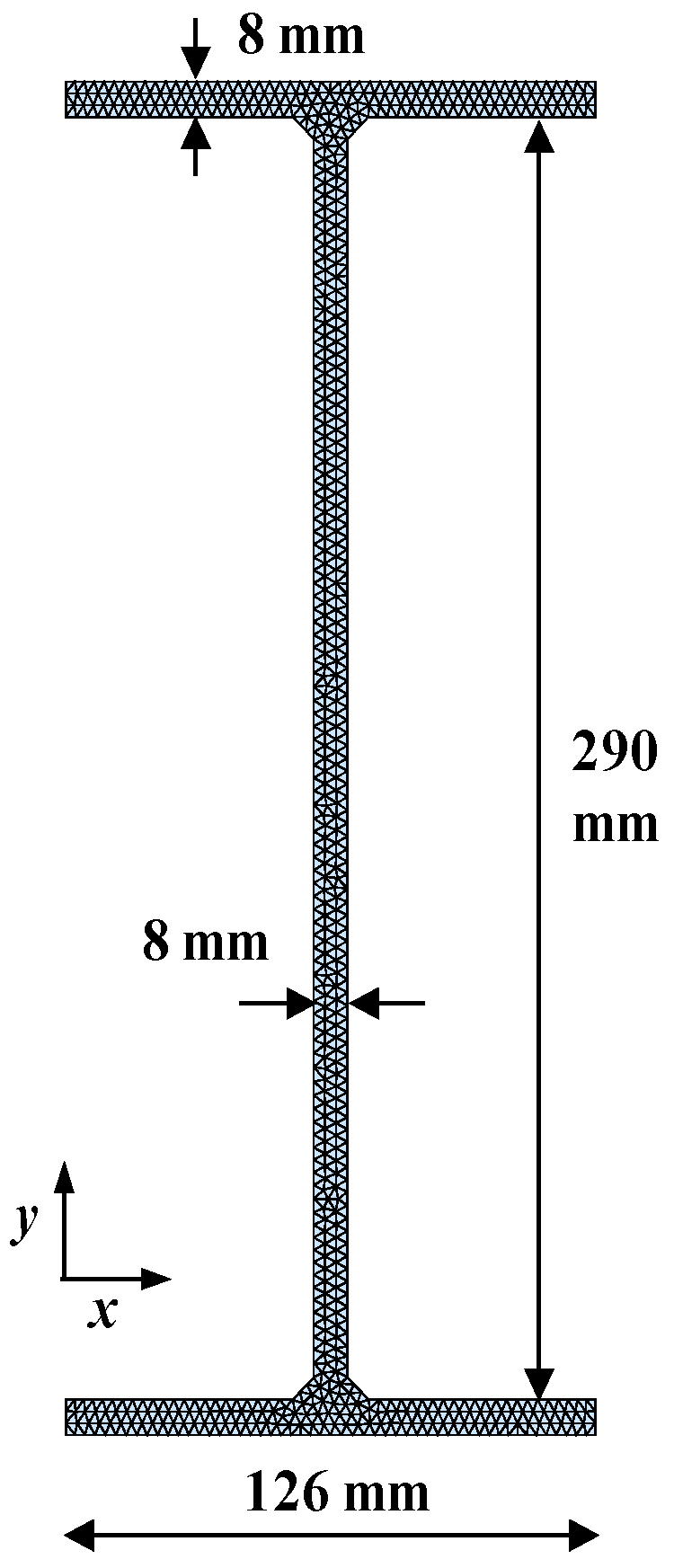
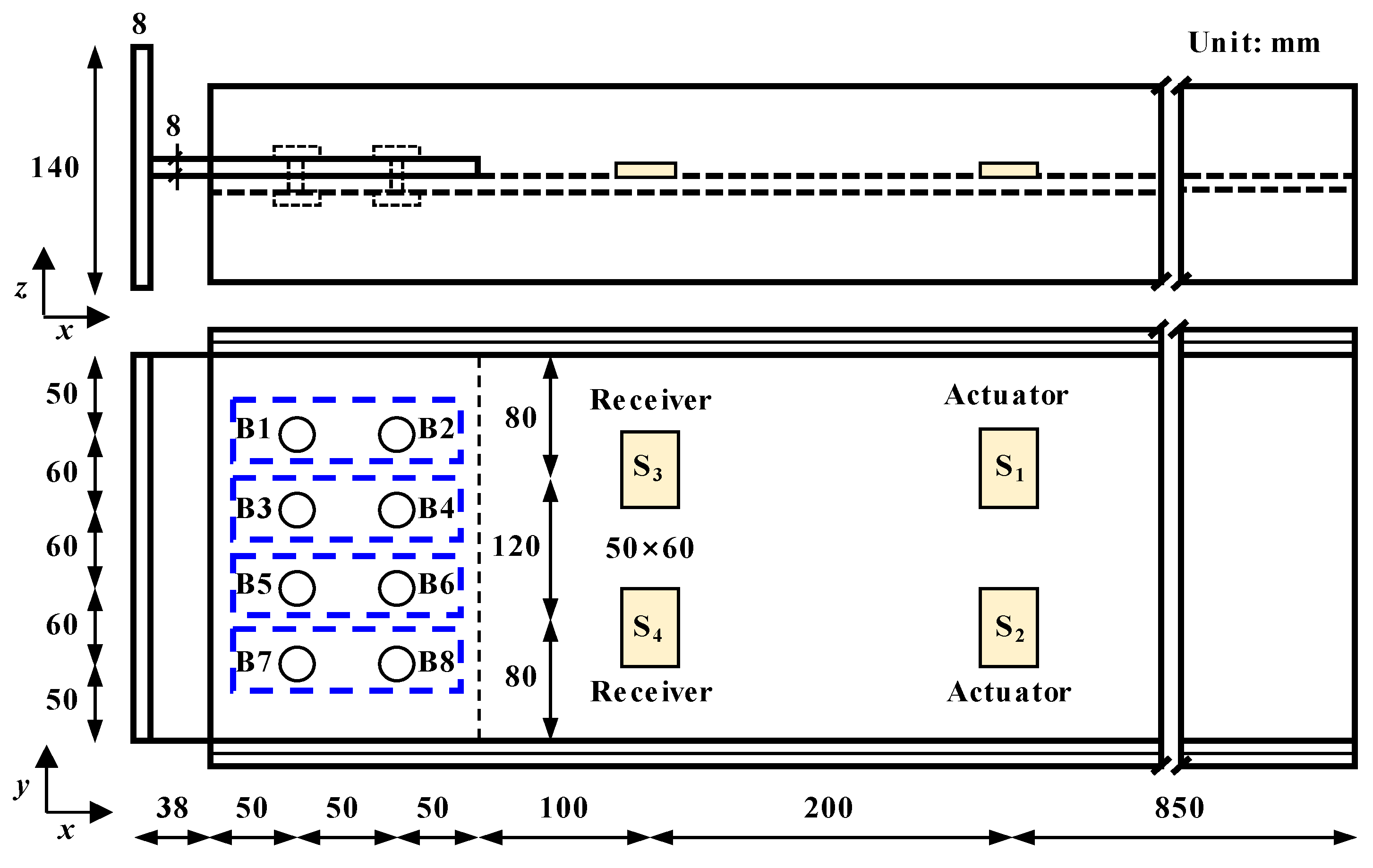
| Young’s Modulus | Density | Poisson Ratio | Width of Flange | Height of Web | Thickness of Flange and Web |
|---|---|---|---|---|---|
| 210 GPa | 7800 kg/m3 | 0.28 | 126 mm | 290 mm | 8 mm |
| Damage Cases | {f} = {f1, f2, f3, f4} |
|---|---|
| Case 1 | {0, 0.3, 0.3, 0} |
| Case 2 | {0, 0.45, 0.45, 0} |
| Case 3 | {0, 0.6, 0.6, 0} |
| Case 4 | {0, 0.75, 0.75, 0} |
| Layer | Active Function | Size | Remarks |
|---|---|---|---|
| Conv1 | ReLU | 16 × [3, 4] | Padding: same |
| Conv2 | ReLU | 32 × [3, 4] | Padding: same |
| Max-pooling | ReLU | [2, 2] | Padding: same Stride: 2 × 2 |
| Flatten | - | - | - |
| LSTM | - | 24 | Number of hidden units |
| MHSA | - | 8 × 24 | - |
| Fully connected1 | ReLU | 128 | - |
| Fully connected2 | Sigmoid | 4 | - |
| Neural Network and Evaluation Index | Time Series | Fourier Amplitude Spectrum | Time–Frequency Spectrum | |
|---|---|---|---|---|
| CNN | Acc | 97.39% | 99.48% | 99.74% |
| Errorlocal | 13.40% | 6.84% | 7.53% | |
| Erroroverall | 7.70% | 5.09% | 3.94% | |
| CNN-LSTM | Acc | 99.74% | 100% | 100% |
| Errorlocal | 7.44% | 5.85% | 4.88% | |
| Erroroverall | 4.44% | 3.27% | 2.50% | |
| CNN-LSTM-MHSA | Acc | 100% | 100% | 100% |
| Errorlocal | 5.96% | 5.98% | 3.96% | |
| Erroroverall | 3.79% | 2.83% | 2.09% | |
| Noise in the Testing Samples | CNN-LSTM-MHSA Trained with 10% Noise | ||
|---|---|---|---|
| Acc | Errorlocal | Erroroverall | |
| No | 99.48% | 8.90% | 5.60% |
| 10% | 97.92% | 12.42% | 6.23% |
| 20% | 93.48% | 17.24% | 7.57% |
| Noise in the Testing Samples | CNN-LSTM-MHSA Trained with 20% Noise | ||
| Acc | Errorlocal | Erroroverall | |
| No | 99.74% | 7.43% | 3.97% |
| 10% | 97.40% | 11.43% | 6.03% |
| 20% | 97.14% | 16.09% | 7.57% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Sui, X.; Duan, Y.; Luo, Y.; Fang, Y.; Miao, R. Quantitative Assessment of Bolt Looseness in Beam–Column Joints Using SH-Typed Guided Waves and Deep Neural Network. Appl. Sci. 2025, 15, 6425. https://doi.org/10.3390/app15126425
Zhang R, Sui X, Duan Y, Luo Y, Fang Y, Miao R. Quantitative Assessment of Bolt Looseness in Beam–Column Joints Using SH-Typed Guided Waves and Deep Neural Network. Applied Sciences. 2025; 15(12):6425. https://doi.org/10.3390/app15126425
Chicago/Turabian StyleZhang, Ru, Xiaodong Sui, Yuanfeng Duan, Yaozhi Luo, Yi Fang, and Rui Miao. 2025. "Quantitative Assessment of Bolt Looseness in Beam–Column Joints Using SH-Typed Guided Waves and Deep Neural Network" Applied Sciences 15, no. 12: 6425. https://doi.org/10.3390/app15126425
APA StyleZhang, R., Sui, X., Duan, Y., Luo, Y., Fang, Y., & Miao, R. (2025). Quantitative Assessment of Bolt Looseness in Beam–Column Joints Using SH-Typed Guided Waves and Deep Neural Network. Applied Sciences, 15(12), 6425. https://doi.org/10.3390/app15126425






