Finite Mixture Model-Based Analysis of Yarn Quality Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Theoretical Background of Poisson Mixture Distribution
2.2.1. EM Algorithm for Poisson Mixture Distribution
2.2.2. The Mean and Variance of the Poisson Mixture Distribution
2.3. Theoretical Background of the Gamma Mixture Distribution
2.3.1. EM Algorithm for Gamma Mixture Distribution
2.3.2. The Mean and Variance of the Gamma Mixture Distribution
2.4. Model Evaluation
3. Results and Discussion
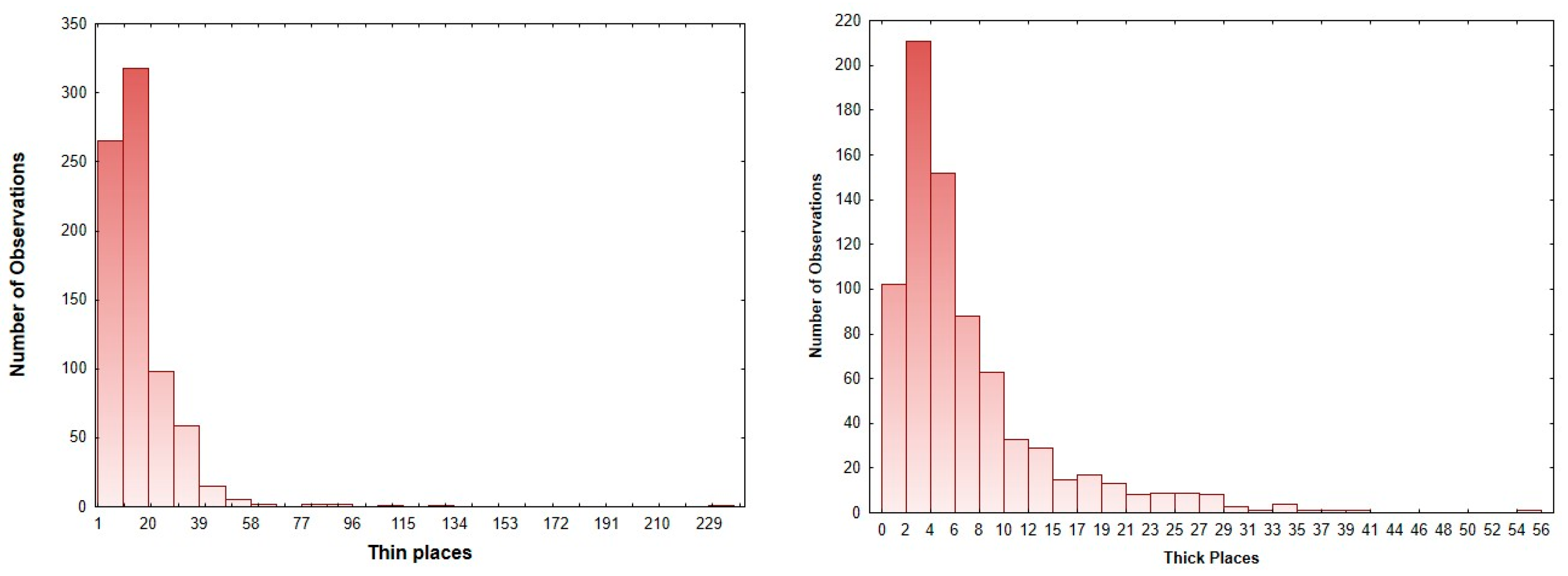
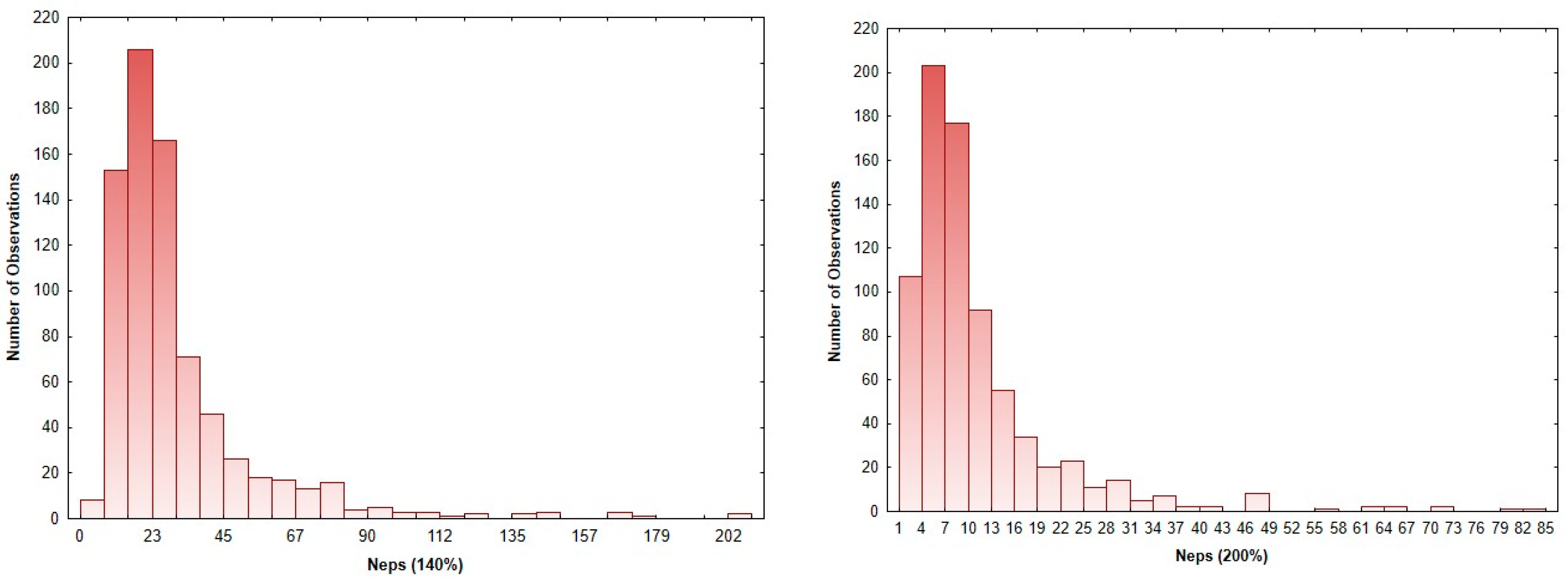
3.1. Distribution Fitting of Yarn Imperfection Parameters
- Thin places: The analysis identifies a high-proportion component (0.79) with a mean of 11.64. This indicates that most thin places are relatively minor deviations, with occasional severe irregularities (mean of 35.68).
- Thick places: The three components represent varying degrees of thickness irregularities, with the largest proportion (0.72) attributed to minor variations. The presence of more extreme thick places (means of 25.76 and 11.80) highlights potential process inefficiencies, potentially attributable to such factors as inappropriate tension settings or irregular fiber feeding.
- Neps: The data indicate that across both the 140% and 200% sensitivity levels for neps, there is a mixture of mild, moderate, and severe instances. The extreme values identified could be indicative of inconsistencies in fiber preparation or during spinning processes. Such irregularities are often linked to fiber contamination or processing errors that can lead to significant adverse effects on the overall fabric quality.
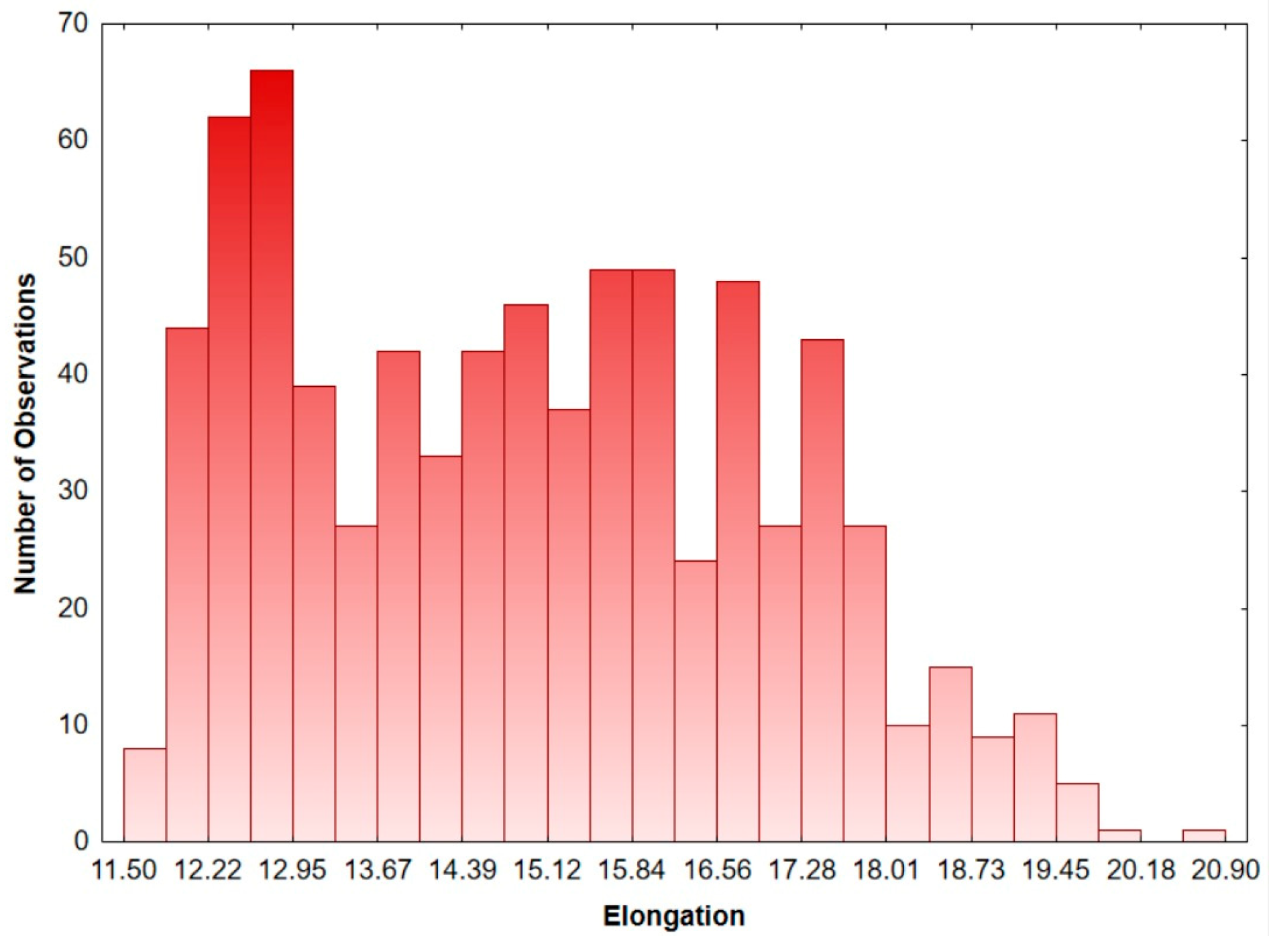
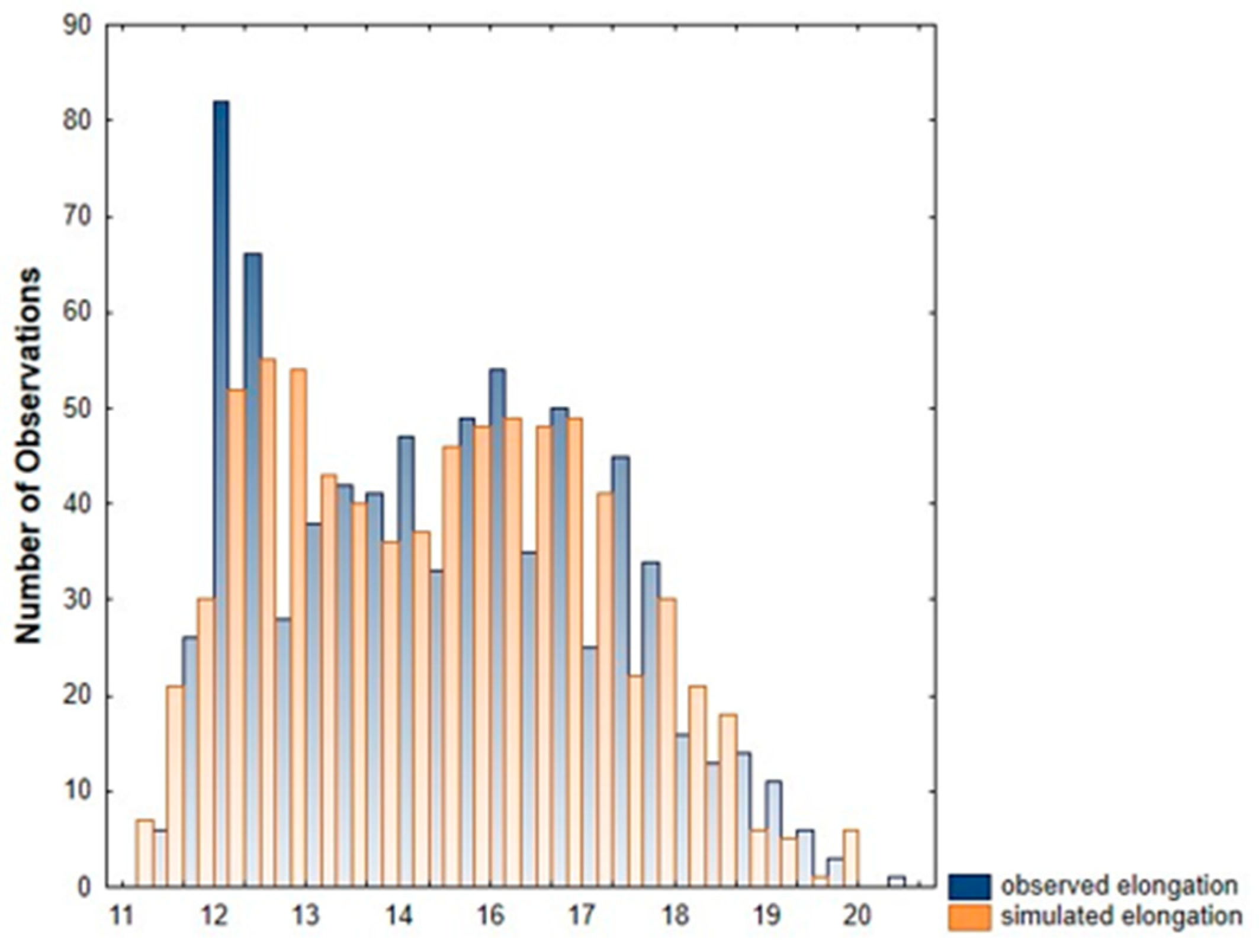
3.2. Distribution Fitting of Yarn Mechanical Properties
- Prediction and control: The obtained probability density functions allow for the prediction of the likelihood of specific parameter values occurring in future yarn production. This predictive capability is crucial for process control, enabling adjustments to maintain desired quality standards. When integrated into real-time quality monitoring systems, this predictive capability enables timely interventions by triggering alerts when the probability of conformance falls below critical thresholds.
- Modeling and simulation: Probability functions can be integrated into more complex models and simulations of textile manufacturing processes. This facilitates virtual experimentation and optimization, reducing reliance on costly and time-consuming physical trials.
- Risk assessment: The obtained probability density functions allow for a more precise evaluation of the risk associated with producing fabrics that do not meet predefined performance specifications. By quantifying the probability of conformance, manufacturers can assess the likelihood of deviation from quality standards in advance. This type of risk assessment is particularly crucial in high-performance applications—such as medical textiles, aerospace composites, or protective fabrics—where yarn failure could lead to severe functional or safety consequences.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FMM | Finite mixture model |
| EM | Expectation–maximization |
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| MLE | Maximum likelihood estimation |
References
- Bouguila, N.; Fan, W. Mixture Models and Applications; Springer: Berlin/Heidelberg, Germany, 2020; Volume 530. [Google Scholar]
- Ng, S.-K. Mixture Modelling for Medical and Health Sciences; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar]
- Yu, J.; Qin, S.J. Multiway Gaussian mixture model based multiphase batch process monitoring. Ind. Eng. Chem. Res. 2009, 48, 8585–8594. [Google Scholar] [CrossRef]
- Hafemeister, C.; Costa, I.G.; Schönhuth, A.; Schliep, A. Classifying short gene expression time-courses with Bayesian estimation of piecewise constant functions. Bioinformatics 2011, 27, 946–952. [Google Scholar] [CrossRef] [PubMed]
- Neema, I.; Böhning, D. Improved methods for surveying and monitoring crimes through likelihood based cluster analysis. Int. J. Criminol. Sociol. Theory 2010, 3, 477–495. [Google Scholar]
- Chambers, S.K.; Ng, S.K.; Baade, P.; Aitken, J.F.; Hyde, M.K.; Wittert, G.; Frydenberg, M.; Dunn, J. Trajectories of quality of life, life satisfaction, and psychological adjustment after prostate cancer. Psycho-Oncology 2017, 26, 1576–1585. [Google Scholar] [CrossRef] [PubMed]
- Wessman, J.; Paunio, T.; Tuulio-Henriksson, A.; Koivisto, M.; Partonen, T.; Suvisaari, J.; Turunen, J.A.; Wedenoja, J.; Hennah, W.; Pietiläinen, O.P. Mixture model clustering of phenotype features reveals evidence for association of DTNBP1 to a specific subtype of schizophrenia. Biol. Psychiatry 2009, 66, 990–996. [Google Scholar] [CrossRef]
- Palardy, G.J.; Vermunt, J.K. Multilevel growth mixture models for classifying groups. J. Educ. Behav. Stat. 2010, 35, 532–565. [Google Scholar] [CrossRef]
- ElMoaqet, H.; Kim, J.; Tilbury, D.; Ramachandran, S.K.; Ryalat, M.; Chu, C.-H. Gaussian mixture models for detecting sleep apnea events using single oronasal airflow record. Appl. Sci. 2020, 10, 7889. [Google Scholar] [CrossRef]
- Fahey, M.T.; Ferrari, P.; Slimani, N.; Vermunt, J.K.; White, I.R.; Hoffmann, K.; Wirfält, E.; Bamia, C.; Touvier, M.; Linseisen, J. Identifying dietary patterns using a normal mixture model: Application to the EPIC study. J. Epidemiol. Community Health 2012, 66, 89–94. [Google Scholar] [CrossRef]
- Ji, Z.; Xia, Y.; Sun, Q.; Chen, Q.; Xia, D.; Feng, D.D. Fuzzy local Gaussian mixture model for brain MR image segmentation. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 339–347. [Google Scholar]
- Tentoni, S.; Astolfi, P.; De Pasquale, A.; Zonta, L.A. Birthweight by gestational age in preterm babies according to a Gaussian mixture model. BJOG Int. J. Obstet. Gynaecol. 2004, 111, 31–37. [Google Scholar] [CrossRef]
- Sun, T.; Wen, Y.; Zhang, X.; Jia, B.; Zhou, M. Gaussian mixture model for marine reverberations. Appl. Sci. 2023, 13, 12063. [Google Scholar] [CrossRef]
- Krifa, M. Fiber length distribution in cotton processing: A finite mixture distribution model. Text. Res. J. 2008, 78, 688–698. [Google Scholar] [CrossRef]
- Cui, X.; Rodgers, J.; Cai, Y.; Li, L.; Belmasrour, R.; Pang, S.-S. Obtaining cotton fiber length distributions from the beard test method Part 1-Theoretical distributions related to the beard method. J. Cotton Sci. 2009, 13, 265–273. [Google Scholar]
- Belmasrour, R.; Li, L.; Cui, X.; Cai, Y.; Rodgers, J. Obtaining cotton fiber length distributions from the beard test method. Part 1—A new approach through PLS Regression. J. Cotton Sci. 2011, 15, 73–79. [Google Scholar]
- Lin, Q.; Xing, M.; Oxenham, W.; Yu, C. Generation of cotton fiber length probability density function with length measures. J. Text. Inst. 2012, 103, 225–230. [Google Scholar] [CrossRef]
- Kuang, X.; Hu, Y.; Yang, J.; Yu, C. Application of finite mixture model in cotton fiber length probability distribution. J. Text. Inst. 2015, 106, 146–151. [Google Scholar] [CrossRef]
- Repon, M.R.; Al Mamun, R.; Reza, S.; Das, M.K.; Islam, T. Effect of spinning parameters on thick, thin places and neps of rotor spun yarn. J. Text. Sci. Technol. 2016, 2, 47–55. [Google Scholar] [CrossRef]
- Mwasıagı, J.; Mırembel, J. Influence of Spinning Parameters on thin and thick Places of rotor spun yarns. Int. J. Comput. Exp. Sci. Eng. 2018, 4, 1–7. [Google Scholar] [CrossRef]
- Ozcelik, G.; Kirtay, E.; Derici, I.M. Examination of fiber neps count during yarn manufacturing. In Proceedings of the Beltwide Cotton Conference, New Orleans, LA, USA, 4–7 January 2005; pp. 2229–2235. [Google Scholar]
- Frydrych, I.; Matusiak, M. Predicting the Nep Number in Cotton Yarn—Determining the Critical Nep Size. Text. Res. J. 2002, 72, 917–923. [Google Scholar] [CrossRef]
- Nath, J.M.; Shukla, S.; Patil, P. Neps in cotton. J. Cotton Res. Dev. 2015, 29, 329–332. [Google Scholar]
- Habib, A.; Olgun, Y.; Babaarslan, O. Development of dual-core spun yarn using different filaments as a core and its impact on denim fabric properties. Text. Leather Rev. 2024, 7, 534–549. [Google Scholar] [CrossRef]
- Kebabcı, M.; Babaarslan, O.; Hacıoğulları, S.Ö.; Telli, A. The effect of drawing ratio and cross-sectional shapes on the properties of polypropylene CF and BCF yarns. Tekst. Mühendis 2015, 22, 46–53. [Google Scholar] [CrossRef]
- Lemmi, T.S.; Barburski, M.; Kabziński, A.; Frukacz, K. Effect of thermal aging on the mechanical properties of high tenacity polyester yarn. Materials 2021, 14, 1666. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Meng, C.; Zhou, J.; Li, Z.; Ding, J.; Liu, F.; Yu, C. Characterization and control of oxidized cellulose in ramie fibers during oxidative degumming. Text. Res. J. 2017, 87, 1828–1840. [Google Scholar] [CrossRef]
- Liu, Y.; Thibodeaux, D.; Gamble, G.; Rodgers, J. Preliminary study of relating cotton fiber tenacity and elongation with crystallinity. Text. Res. J. 2014, 84, 1829–1839. [Google Scholar] [CrossRef]
- Široká, B.; Manian, A.P.; Noisternig, M.F.; Henniges, U.; Kostic, M.; Potthast, A.; Griesser, U.J.; Bechtold, T. Wash–dry cycle induced changes in low-ordered parts of regenerated cellulosic fibers. J. Appl. Polym. Sci. 2012, 126, E397–E408. [Google Scholar] [CrossRef]
- Upreti, M.; Jahan, S. Study the effect of scouring time on Grewia asiatica (Phalsa) fibres properties. J. Appl. Nat. Sci. 2017, 9, 1388. [Google Scholar] [CrossRef]
- Maiti, S.; Islam, M.R.; Uddin, M.A.; Afroj, S.; Eichhorn, S.J.; Karim, N. Sustainable fiber-reinforced composites: A review. Adv. Sustain. Syst. 2022, 6, 2200258. [Google Scholar] [CrossRef]
- Gorjanc, D.S.; Bizjak, M. The influence of constructional parameters on deformability of elastic cotton fabrics. J. Eng. Fibers Fabr. 2014, 9, 155892501400900106. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Ghojogh, B.; Ghojogh, A.; Crowley, M.; Karray, F. Fitting a mixture distribution to data: Tutorial. arXiv 2019, arXiv:1901.06708. [Google Scholar]
- Almhana, J.; Liu, Z.; Choulakian, V.; McGorman, R. A recursive algorithm for gamma mixture models. In Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; pp. 197–202. [Google Scholar]
- Liu, Z.; Almhana, J.; Choulakian, V.; McGorman, R. Traffic modeling with gamma mixtures and dynamical bandwidth provisioning. In Proceedings of the 4th Annual Communication Networks and Services Research Conference (CNSR’06), Moncton, NB, Canada, 24–25 May 2006; pp. 8–130. [Google Scholar]
- Nachar, N. The Mann-Whitney U: A test for assessing whether two independent samples come from the same distribution. Tutor. Quant. Methods Psychol. 2008, 4, 13–20. [Google Scholar] [CrossRef]




| i. Start with initial parameter values of and iterate the following steps until convergence. | |
| ii. E-step: Find the classification probability that the observation comes from the Poisson distribution based on the following estimate: | |
| (13) | |
| where | |
| iii. M-step: Update the Poisson mixture distribution parameters as follows: | |
| (14) | |
| (15) | |
| i. Start with initial parameter values of and iterate the following steps until convergence: | |
| ii. E-step: Find the classification probability that the observation comes from the gamma distribution based on the following estimate: | |
| (43) | |
| where | |
| iii. M-step: Update the gamma mixture distribution parameters as follows: | |
| (44) | |
| (45) | |
| (46) | |
| Data | k | Proportions | Poisson Mixture Distribution Parameters | Selection Criteria | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | LL | ||||||||
| Thin 40% | 2 | 0.79 | 0.21 | - | 11.64 | 35.68 | - | 6934.28 | 6948.21 | −3464.14 |
| Thick 50% | 3 | 0.073 | 0.21 | 0.72 | 25.76 | 11.80 | 4.42 | 4466.874 | 4490.099 | 4634.936 |
| Neps 140% | 3 | 0.71 | 0.23 | 0.06 | 19.31 | 45.89 | 107.06 | 7152.014 | 7175.239 | 7224.290 |
| Neps 200% | 2 | 0.15 | 0.85 | - | 30.80 | 8.25 | - | 5508.402 | 5522.338 | 5550.933 |
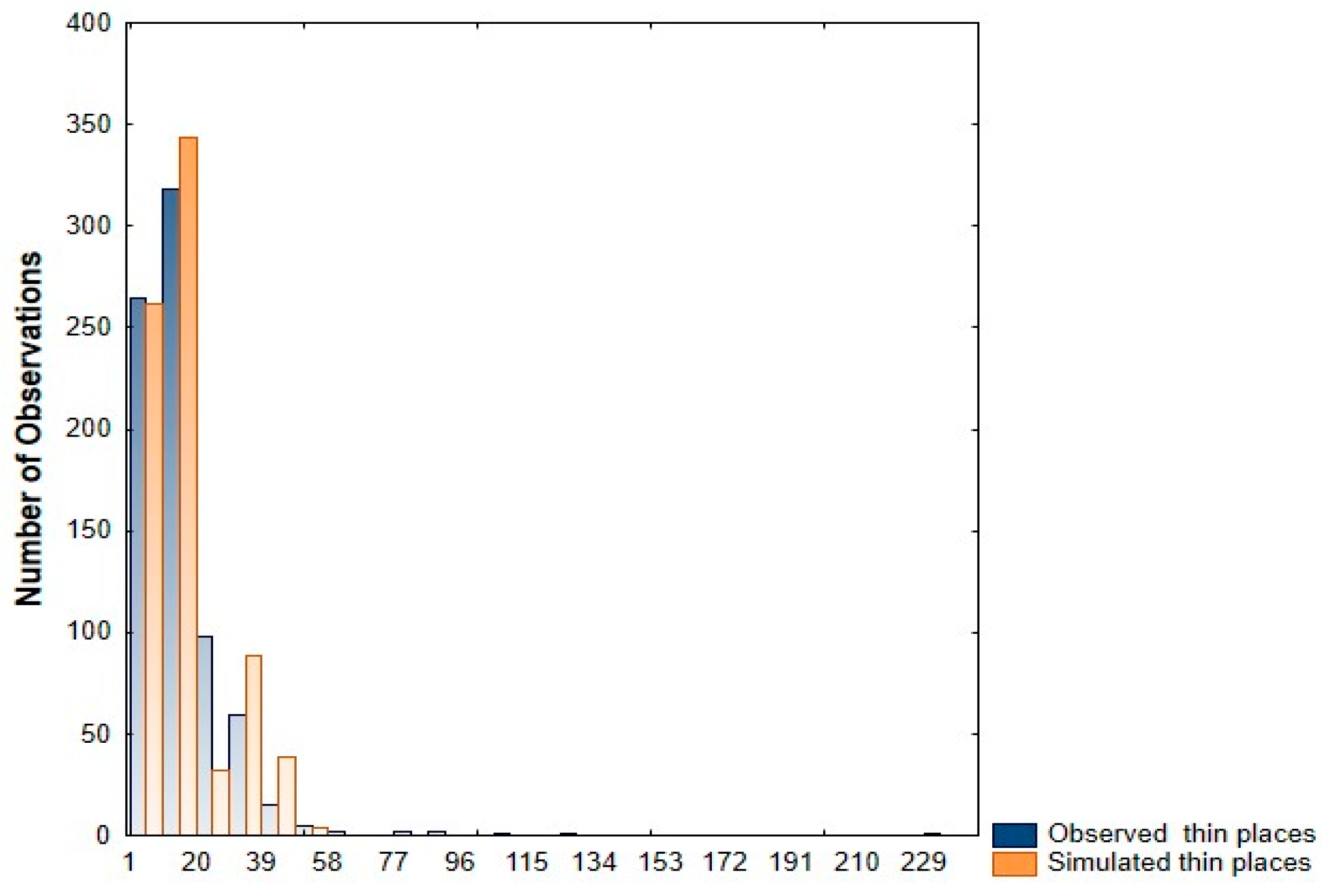
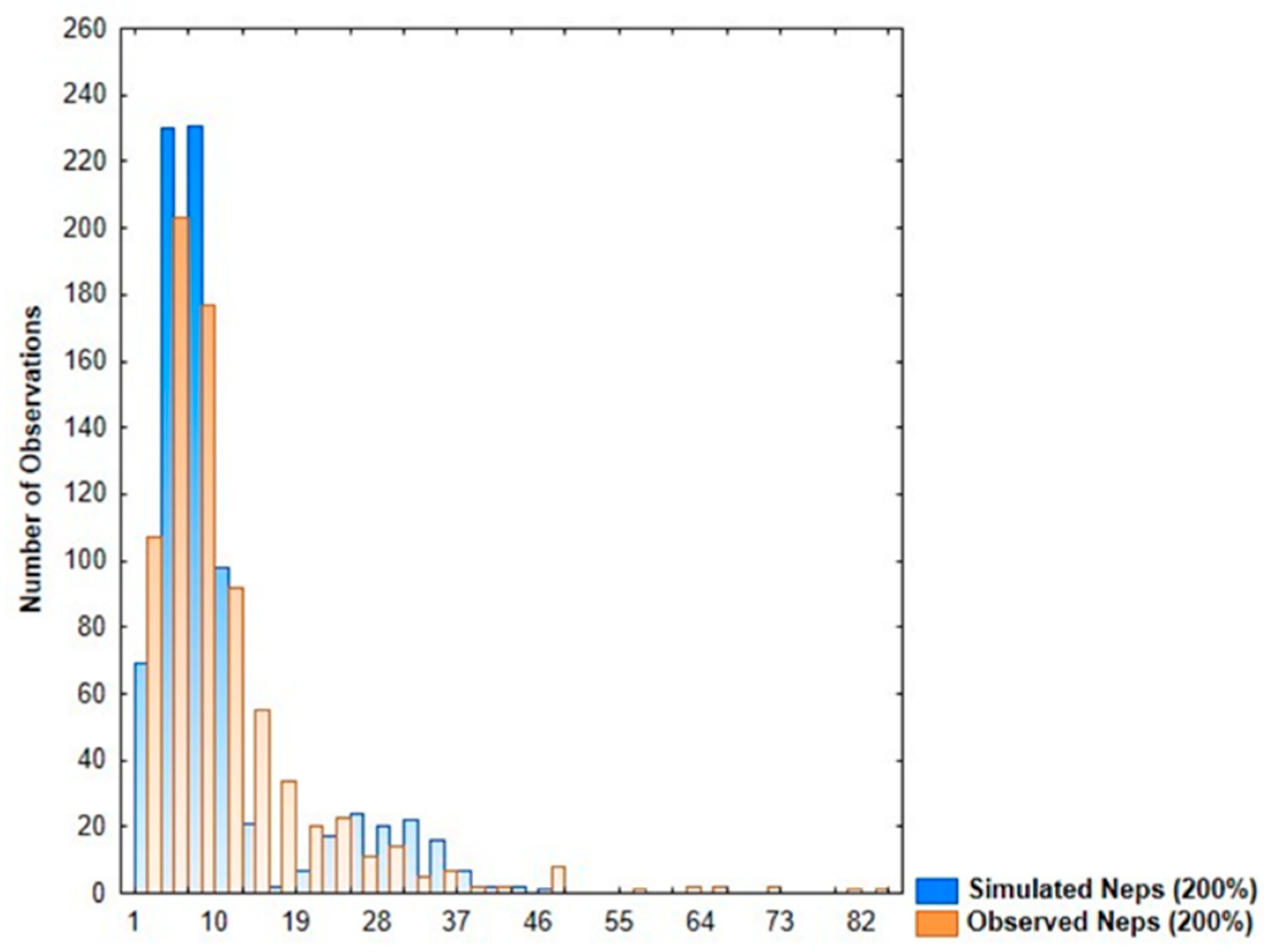
| Quality Parameters | Observed Data | PMM Data | ||
|---|---|---|---|---|
| Mean | Standard Dev. | Mean | Standard Dev. | |
| Thin Places (40%) | 16.63 | 14.83 | 16.68 | 10.60 |
| Thick Places (50%) | 7.52 | 6.67 | 7.54 | 6.51 |
| Neps (140%) | 29.70 | 23.61 | 30.68 | 22.92 |
| Neps (200%) | 11.55 | 9.61 | 11.63 | 8.74 |
| Data | k | Proportions | Gamma Mixture Distribution Parameters | Selection Criteria | ||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | LL | ||||||
| Elongation | 2 | 0.33 | 0.67 | (320, 0.04) | (110, 0.146) | 3121.86 | 3145.06 | −1555.93 |
| Tensile Str. | 2 | 0.52 | 0.48 | (120, 0.17) | (280, 0.09) | 3825.70 | 3848.90 | −1907.85 |
| Quality Parameters | Observed Data | GMM Data | ||
|---|---|---|---|---|
| Mean | Standard Dev. | Mean | Standard Dev. | |
| Elongation | 14.97 | 2.03 | 14.98 | 2.01 |
| Tensile strength | 22.89 | 3.25 | 22.86 | 3.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakaş, E.; Koyuncu, M.; Ükelge, M.Ö. Finite Mixture Model-Based Analysis of Yarn Quality Parameters. Appl. Sci. 2025, 15, 6407. https://doi.org/10.3390/app15126407
Karakaş E, Koyuncu M, Ükelge MÖ. Finite Mixture Model-Based Analysis of Yarn Quality Parameters. Applied Sciences. 2025; 15(12):6407. https://doi.org/10.3390/app15126407
Chicago/Turabian StyleKarakaş, Esra, Melik Koyuncu, and Mülayim Öngün Ükelge. 2025. "Finite Mixture Model-Based Analysis of Yarn Quality Parameters" Applied Sciences 15, no. 12: 6407. https://doi.org/10.3390/app15126407
APA StyleKarakaş, E., Koyuncu, M., & Ükelge, M. Ö. (2025). Finite Mixture Model-Based Analysis of Yarn Quality Parameters. Applied Sciences, 15(12), 6407. https://doi.org/10.3390/app15126407






