Enhanced Prediction of the Remaining Useful Life of Rolling Bearings Under Cross-Working Conditions via an Initial Degradation Detection-Enabled Joint Transfer Metric Network
Abstract
1. Introduction
2. Introduction to Related Theories
2.1. Convolutional Autoencoder Network
2.2. Domain Adaptation Technology
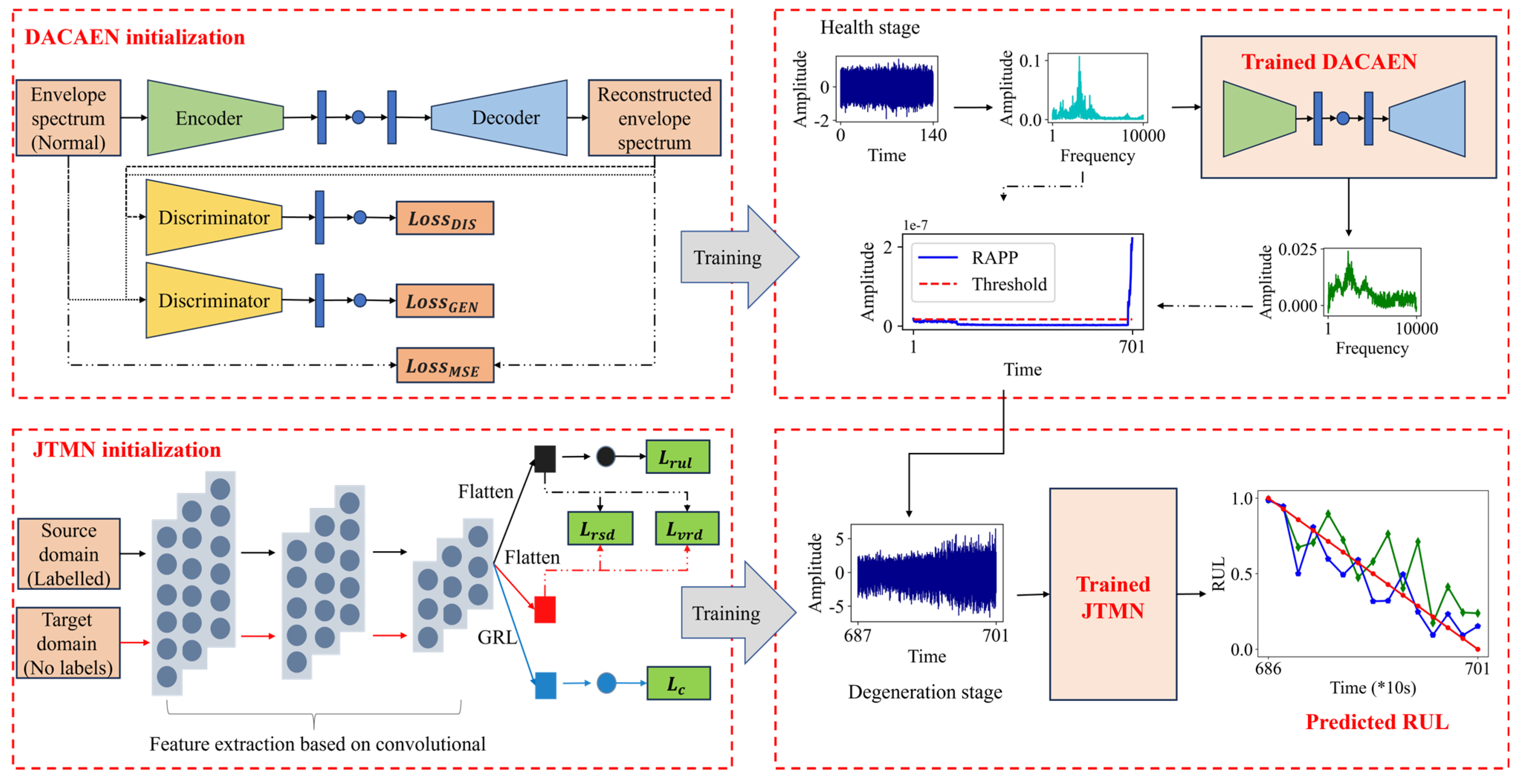
3. Proposed Cross-Working Condition RUL Prediction Method
3.1. RAPP-Based Initial Degradation Detection
3.1.1. DACAEN Model
3.1.2. Construction of RAPP via DACAEN
3.2. JTMN-Based RUL Prediction
3.2.1. Joint Domain Adaptation Loss
3.2.2. Joint Transfer Metric Network for RUL Prediction
3.3. Implementation Procedures
3.3.1. Data Acquisition and Signal Processing
3.3.2. IDD
- The former 20% data of each bearing’s life cycle is selected to construct the training set of the input for DACAEN.
- Build the DACAEN model and initialize its parameters. The model hyperparameters are determined by grid search and cross-validation.
- Train the DACAEN model until it converges, so as to minimize the reconstruction error between the input data and the reconstructed data.
- Send the bearing life cycle data to the trained DACAEN model to build the RAPP health indicator, and combine the health threshold to realize the whole process of IDD.
3.3.3. RUL Prediction
- Set cross-domain prediction tasks according to operating conditions, build the source domain with the labeled training set and the target domain with the unlabeled training set and the target domain test set, and carry out RUL labeling processing on the source domain with the labeled training set.
- Build the JTMN model and initialize its parameters. The model hyperparameters were determined by grid search and cross-validation.
- Use the labeled source domain and unlabeled target domain as training sets to train the JTMN model until it converges, so as to minimize regression errors and distribution differences in the source domain.
- The trained JTMN is directly used for RUL prediction of the test set. The testing process can simulate an online scenario where samples taken chronologically are predicted using JTMN.
- The superior performance of the proposed method is demonstrated using evaluation indicators and analysis of the execution results.
4. Experiment Study
4.1. Dataset Introduction
4.2. Model Building
4.3. Results and Discussion for RUL Prediction
4.3.1. Results and Discussion for Initial Degradation Detection
- (1)
- Results and Discussion
- (2)
- Ablation Study
- (3)
- Comparison with Popular HIs
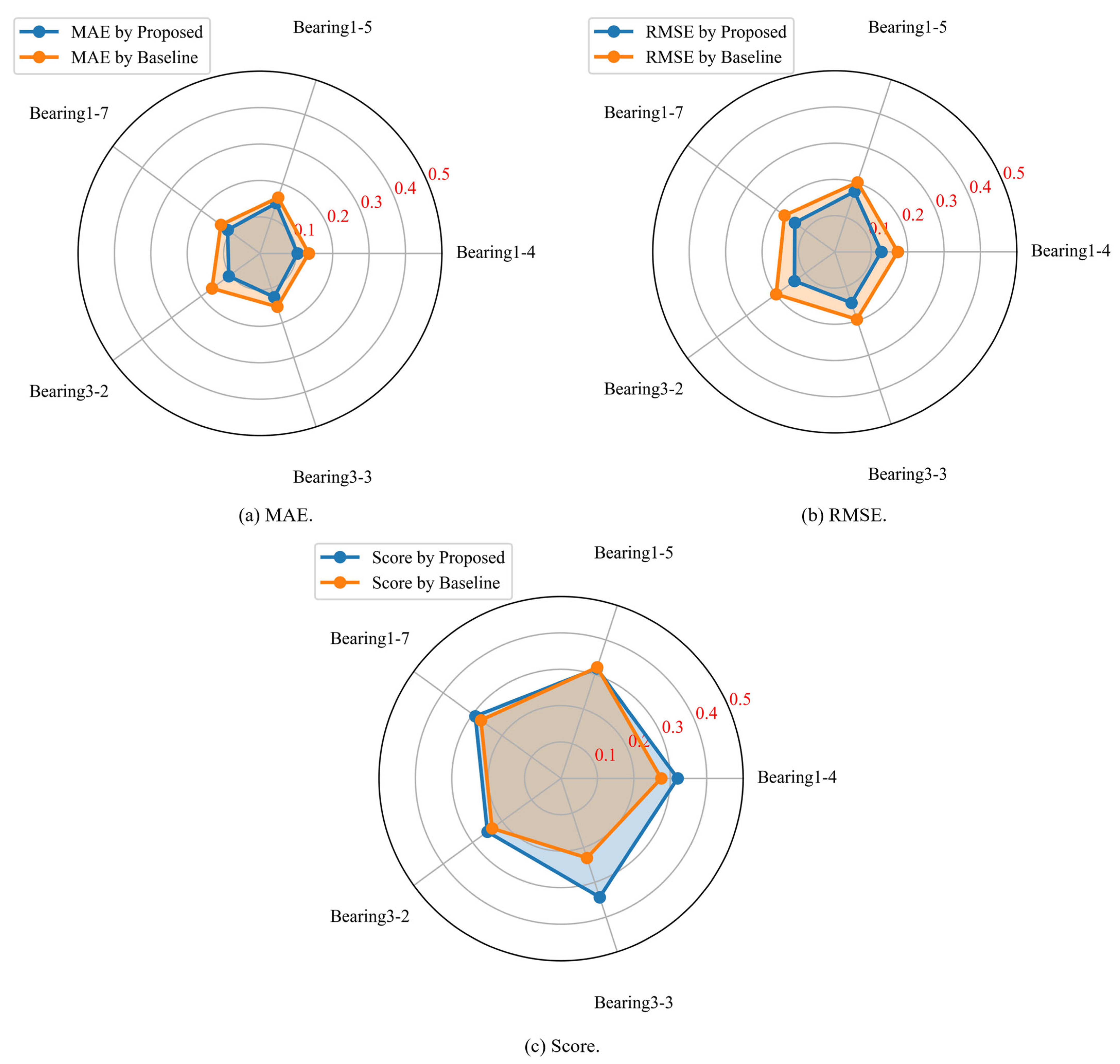
4.3.2. Results and Discussion of Cross-Working Condition RUL Prediction
- (1)
- Evaluation Indicators for Prediction Results
- (2)
- Results and Discussion
- (3)
- Comparison experiment and ablation study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zou, Y.; Sun, W.; Wang, H.; Xu, T.; Wang, B. Research on Bearing Remaining Useful Life Prediction Method Based on Double Bidirectional Long Short-Term Memory. Appl. Sci. 2025, 15, 4441. [Google Scholar] [CrossRef]
- Wu, J.; Hu, K.; Cheng, Y.; Zhu, H.; Shao, X. Temporal Multi-Resolution Hypergraph Attention Network for Remaining Useful Life Prediction of Rolling Bearings. Reliab. Eng. Syst. Saf. 2024, 247, 110123. [Google Scholar] [CrossRef]
- Yu, J.; Shao, J.; Peng, X.; Liu, T.; Yao, Q. Remaining Useful Life of the Rolling Bearings Prediction Method Based on Transfer Learning Integrated with CNN-GRU-MHA. Appl. Sci. 2024, 14, 9039. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, W.; Chen, X.; Li, G. Remaining Useful Life Prediction for Machinery Using Multimodal Interactive Attention Spatial-Temporal Networks with Deep Ensembles. Expert Syst. Appl. 2025, 263, 123456. [Google Scholar] [CrossRef]
- Song, L.Y.; Wang, H.; Zhang, J.; Liu, Z. Advancements in Bearing Remaining Useful Life Prediction Methods: A Comprehensive Review. Meas. Sci. Technol. 2024, 35, 095005. [Google Scholar] [CrossRef]
- Yan, M.; Wang, X.; Wang, B.; Chang, M.; Muhammad, I. Bearing Remaining Useful Life Prediction Using Support Vector Machine and Hybrid Degradation Tracking Model. ISA Trans. 2020, 98, 471–482. [Google Scholar] [CrossRef]
- Zhang, C.; Yao, X.; Zhang, J.; Tang, H. An Optimized Support Vector Regression for Prediction of Bearing Degradation. Appl. Soft Comput. 2021, 113, 107991. [Google Scholar] [CrossRef]
- Hou, W.; Peng, Y. Adaptive Ensemble Gaussian Process Regression-Driven Degradation Prognosis with Applications to Bearing Degradation. Reliab. Eng. Syst. Saf. 2023, 239, 109543. [Google Scholar] [CrossRef]
- Li, H.; Zhao, W.; Zhang, Y.; Zio, E. Remaining Useful Life Prediction Using Multi-Scale Deep Convolutional Neural Network. Appl. Soft Comput. 2020, 89, 106113. [Google Scholar] [CrossRef]
- Wan, S.; Li, X.; Yin, Y.; Hong, J.; Zhang, J. Bearing Remaining Useful Life Prediction with Convolutional Long Short-Term Memory Fusion Networks. Reliab. Eng. Syst. Saf. 2022, 224, 108540. [Google Scholar] [CrossRef]
- Zhang, B.; Li, W.; Hao, J.; Li, X.; Zhang, S. A Hybrid Algorithm for Predicting the Remaining Service Life of Hybrid Bearings Based on Bidirectional Feature Extraction. Measurement 2025, 242, 111234. [Google Scholar] [CrossRef]
- Ding, Y.F.; Jia, M.P. Convolutional Transformer: An Enhanced Attention Mechanism Architecture for Remaining Useful Life Estimation of Bearings. IEEE Trans. Instrum. Meas. 2022, 71, 3515010. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D. Remaining Useful Life Prediction of Bearings with Attention-Awared Graph Convolutional Network. Adv. Eng. Inform. 2023, 58, 102143. [Google Scholar] [CrossRef]
- Hakim, M.; Omran, A.A.B.; Ahmed, A.N.; Al-Waily, M.; Abdellatif, A. A Systematic Review of Rolling Bearing Fault Diagnoses Based on Deep Learning and Transfer Learning: Taxonomy, Overview, Application, Open Challenges, Weaknesses and Recommendations. Ain Shams Eng. J. 2023, 14, 101945. [Google Scholar] [CrossRef]
- Tian, M.; Su, X.; Chen, C.; An, W. A Novel Method for Multistage Degradation Predicting the Remaining Useful Life of Wind Turbine Generator Bearings Based on Domain Adaptation. Appl. Sci. 2023, 13, 12332. [Google Scholar] [CrossRef]
- Lu, X.; Yao, X.; Jiang, Q.; Shen, Y.; Xu, F.; Zhu, Q. Remaining Useful Life Prediction Model of Cross-Domain Rolling Bearing via Dynamic Hybrid Domain Adaptation and Attention Contrastive Learning. Comput. Ind. 2025, 164, 104567. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Xu, L. Deep Transfer Learning Remaining Useful Life Prediction of Different Bearings. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Virtual, 18–22 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–8. [Google Scholar]
- Cheng, H.; Kong, X.; Chen, G.; Wang, Q.; Wang, R. Transferable Convolutional Neural Network Based Remaining Useful Life Prediction of Bearing Under Multiple Failure Behaviors. Measurement 2021, 168, 108286. [Google Scholar] [CrossRef]
- Cao, Y.; Ding, Y.; Jia, M.; Tian, Z. Transfer Learning for Remaining Useful Life Prediction of Multi-Conditions Bearings Based on Bidirectional-GRU Network. Measurement 2021, 178, 109287. [Google Scholar] [CrossRef]
- Shi, H.; Li, X.; Zhao, W.; Liu, Y. Wasserstein Distance Based Multi-Scale Adversarial Domain Adaptation Method for Remaining Useful Life Prediction. Appl. Intell. 2022, 53, 3622–3637. [Google Scholar] [CrossRef]
- Da Costa, P.R.d.O.; Akçay, A.; Zhang, Y.; Kaymak, U. Remaining Useful Lifetime Prediction via Deep Domain Adaptation. Reliab. Eng. Syst. Saf. 2020, 195, 106682. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, B.; Li, H.; Zhang, X. Multistage Convolutional Autoencoder and BCM-LSTM Networks for RUL Prediction of Rolling Bearings. IEEE Trans. Instrum. Meas. 2023, 72, 2527713. [Google Scholar] [CrossRef]
- Gretton, A.; Sriperumbudur, B.; Sejdinovic, D.; Fukumizu, K. Optimal Kernel Choice for Large-Scale Two-Sample Tests. In Advances in Neural Information Processing Systems 25; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1205–1213. [Google Scholar]
- Cheng, H.; Kong, X.; Yang, S.; Wang, R. Remaining Useful Life Prediction Combined Dynamic Model with Transfer Learning Under Insufficient Degradation Data. Reliab. Eng. Syst. Saf. 2023, 236, 109321. [Google Scholar] [CrossRef]
- Qi, J.Y.; Li, C.; Chen, X.; Wang, B. Remaining Useful Life Prediction Combining Advanced Anomaly Detection and Graph Isomorphic Network. IEEE Sens. J. 2024, 24, 38365–38376. [Google Scholar] [CrossRef]
- Shin, S.Y.; Kim, H.-J. Extended Autoencoder for Novelty Detection with Reconstruction along Projection Pathway. Appl. Sci. 2020, 10, 4497. [Google Scholar] [CrossRef]
- González-Muñiz, A.; Díaz, I.; Cuadrado, A.A.; García, D.F. Health Indicator for Machine Condition Monitoring Built in the Latent Space of a Deep Autoencoder. Reliab. Eng. Syst. Saf. 2022, 224, 108541. [Google Scholar] [CrossRef]
- Qian, Q.; Li, H.; Wang, J.; Zhang, Y. Variance Discrepancy Representation: A Vibration Characteristic-Guided Distribution Alignment Metric for Fault Transfer Diagnosis. Mech. Syst. Signal Process. 2024, 217, 111234. [Google Scholar] [CrossRef]
- Qian, Q.; Li, H.; Wang, J.; Zhang, Y. Maximum Subspace Transferability Discriminant Analysis: A New Cross-Domain Similarity Measure for Wind-Turbine Fault Transfer Diagnosis. Comput. Ind. 2025, 164, 104567. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An Experimental Platform for Bearings Accelerated Life Test. In Proceedings of the 2012 IEEE International Conference on Prognostics and Health Management, Spokane, WA, USA, 22–25 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–8. [Google Scholar]
- Zhang, G.; Li, X.; Chen, Y.; Li, H. Health Indicator Based on Signal Probability Distribution Measures for Machinery Condition Monitoring. Mech. Syst. Signal Process. 2023, 198, 110432. [Google Scholar] [CrossRef]












| Operating Conditions | Condition_1 | Condition_2 | Condition_3 |
|---|---|---|---|
| Datasets | Bearing1-1\Bearing1-2\Bearing1-3\Bearing1-4\Bearing1-5\Bearing1-6\Bearing1-7 | Bearing2-1\Bearing2-2\Bearing2-3\Bearing2-4\Bearing2-5\Bearing2-6\Bearing2-7 | Bearing3-1\Bearing3-2\Bearing3-3 |
| Model Name | Module Name | Network Layer | Activation Function | Stride | Size | Number | Output Size |
|---|---|---|---|---|---|---|---|
| DACAEN | Generator | Convolution layer1 + BN | Leaky relu | 1 × 16 | 1 × 64 | 16 | 16 × 80 |
| Convolution layer2 + BN | Leaky relu | 1 × 4 | 1 × 4 | 32 | 32 × 20 | ||
| Convolution layer3 + BN | Leaky relu | 1 × 4 | 1 × 4 | 64 | 64 × 5 | ||
| Average Pooling layer | - | - | - | - | 1 × 64 | ||
| Hidden layer | - | - | - | - | 1 × 1 | ||
| FC layer | - | - | - | - | 1 × 320 | ||
| Translation layer | - | - | - | - | 64 × 5 | ||
| Deconvolution layer3 + BN | Leaky relu | 1 × 4 | 1 × 4 | 32 | 32 × 20 | ||
| Deconvolution layer3 + BN | Leaky relu | 1 × 4 | 1 × 4 | 16 | 16 × 80 | ||
| Reconstruction Layer3 + BN | Leaky relu | 1 × 16 | 1 × 4 | 1 | 1 × 1280 | ||
| Discriminator | Convolution layer1 + BN | Leaky relu | 1 × 16 | 1 × 64 | 16 | 16 × 80 | |
| Convolution layer2 + BN | Leaky relu | 1 × 4 | 1 × 4 | 32 | 32 × 20 | ||
| Convolution layer3 + BN | Leaky relu | 1 × 4 | 1 × 4 | 64 | 64 × 5 | ||
| Average Pooling Layer | - | 1 × 64 | |||||
| FC layer | Softmax | - | 1 × 1 | 1 | 1 × 1 | ||
| JTMN | Feature extractor | Convolution layer1 + BN | Leaky relu | 1 × 10 | 1 × 64 | 16 | 16 × 128 |
| Pooling layer | - | 1 × 4 | 1 × 4 | 16 | 16 × 32 | ||
| Convolution layer2 + BN | Leaky relu | 1 × 1 | 1 × 4 | 32 | 32 × 32 | ||
| Pooling layer | - | 1 × 4 | 1 × 4 | 32 | 32 × 8 | ||
| Convolution layer3 + BN | Leaky relu | 1 × 1 | 1 × 4 | 64 | 64 × 8 | ||
| Pooling layer | - | 1 × 4 | 1 × 4 | 64 | 64 × 2 | ||
| Domain adaptation and regressor | Flatten layer | - | - | - | 1 × 128 | ||
| FC layer 1 | Sigmoid | - | - | 64 | 1 × 64 | ||
| FC layer 2 | Sigmoid | - | - | 1 | 1 × 1 | ||
| Classifier | Gradient reversal layer | - | - | - | - | - | |
| FC layer 1 | Softmax | - | - | 2 | 1 × 2 | ||
| Bearings | Results of IDD | Total Number of Samples | Number of Degraded Samples |
|---|---|---|---|
| Bearing 1-1 | 1451 | 2803 | 1352 |
| Bearing 1-2 | 828 | 871 | 43 |
| Bearing 1-3 | 1267 | 2375 | 1108 |
| Bearing 1-4 | 1087 | 1428 | 341 |
| Bearing 1-5 | 2443 | 2463 | 20 |
| Bearing 1-6 | - | 2448 | - |
| Bearing 1-7 | 2206 | 2259 | 53 |
| Bearing 2-1 | 877 | 911 | 34 |
| Bearing 2-2 | 388 | 797 | 409 |
| Bearing 2-3 | 1946 | 1955 | 9 |
| Bearing 2-4 | - | 751 | -- |
| Bearing 2-5 | - | 2311 | - |
| Bearing 2-6 | 687 | 701 | 14 |
| Bearing 2-7 | 225 | 230 | 5 |
| Bearing 3-1 | 493 | 515 | 22 |
| Bearing 3-2 | 1610 | 1637 | 27 |
| Bearing 3-3 | 420 | 434 | 14 |
| Functions | Model Name | Ablation Name | |
|---|---|---|---|
| Adversarial Mechanism | RAPP | ||
| Reconstruction ability | DCAE | No | No |
| DACAEN | Yes | No | |
| Transfer Condition Setting | Prediction Scenario | Training Bearing | Test Bearing | |
|---|---|---|---|---|
| Source Domain with Label | Source Domain Without Label | |||
| 1→2 and 3 | Scenario A | Bearing 1-2 | Bearing 2-1 | Bearing 2-3/Bearing 2-6/Bearing 2-7 |
| Scenario B | Bearing 3-1 | Bearing 3-2/Bearing 3-3 | ||
| 2→1 and 3 | Scenario C | Bearing 2-1 | Bearing 1-2 | Bearing 1-4/Bearing 1-5/Bearing 1-7 |
| Scenario D | Bearing 3-1 | Bearing 3-2/Bearing 3-3 | ||
| 3→1 and 2 | Scenario E | Bearing 3-1 | Bearing 2-1 | Bearing 2-3 Bearing 2-6/Bearing 2-7 |
| Scenario F | Bearing 1-2 | Bearing 1-4/Bearing 1-5/Bearing 1-7 | ||
| 2→1 | Scenario G | Bearing 2-2 | Bearing 1-1 | Bearing 1-1 |
| Source Domain | Target Domain | Tests | Model Name | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VDR + RSD + CNN | VDR + CNN | MMD + CNN | CNN | |||||||||||
| MAE | RMSE | Score | MAE | RMSE | Score | MAE | RMSE | Score | MAE | RMSE | Score | |||
| Bearing 1-2 | Bearing 2-1 | 2-3 | 0.320 | 0.389 | 0.244 | 0.332 | 0.426 | 0.277 | 0.345 | 0.413 | 0.229 | 0.430 | 0.509 | 0.140 |
| 2-6 | 0.082 | 0.105 | 0.316 | 0.115 | 0.132 | 0.354 | 0.088 | 0.115 | 0.347 | 0.121 | 0.156 | 0.384 | ||
| 2-7 | 0.241 | 0.302 | 0.282 | 0.274 | 0.385 | 0.454 | 0.323 | 0.359 | 0.209 | 0.322 | 0.372 | 0.210 | ||
| AVG | 0.214 | 0.265 | 0.280 | 0.241 | 0.314 | 0.362 | 0.250 | 0.294 | 0.262 | 0.291 | 0.346 | 0.245 | ||
| Bearing 3-1 | 3-2 | 0.115 | 0.150 | 0.373 | 0.081 | 0.105 | 0.375 | 0.111 | 0.131 | 0.312 | 0.159 | 0.183 | 0.173 | |
| 3-3 | 0.082 | 0.103 | 0.477 | 0.141 | 0.173 | 0.341 | 0.134 | 0.163 | 0.304 | 0.111 | 0.145 | 0.304 | ||
| AVG | 0.099 | 0.126 | 0.425 | 0.111 | 0.139 | 0.358 | 0.123 | 0.147 | 0.308 | 0.135 | 0.164 | 0.238 | ||
| Bearing 2-1 | Bearing 1-2 | 1-4 | 0.103 | 0.128 | 0.320 | 0.137 | 0.166 | 0.186 | 0.115 | 0.140 | 0.245 | 0.134 | 0.173 | 0.275 |
| 1-5 | 0.145 | 0.175 | 0.318 | 0.161 | 0.196 | 0.297 | 0.184 | 0.211 | 0.270 | 0.161 | 0.202 | 0.321 | ||
| 1-7 | 0.110 | 0.136 | 0.291 | 0.108 | 0.131 | 0.299 | 0.088 | 0.108 | 0.348 | 0.133 | 0.171 | 0.272 | ||
| AVG | 0.119 | 0.146 | 0.310 | 0.135 | 0.165 | 0.261 | 0.129 | 0.153 | 0.288 | 0.143 | 0.182 | 0.289 | ||
| Bearing 3-1 | 3-2 | 0.106 | 0.137 | 0.250 | 0.117 | 0.137 | 0.278 | 0.164 | 0.197 | 0.218 | 0.163 | 0.199 | 0.234 | |
| 3-3 | 0.126 | 0.148 | 0.343 | 0.147 | 0.170 | 0.262 | 0.132 | 0.159 | 0.211 | 0.154 | 0.196 | 0.230 | ||
| AVG | 0.116 | 0.143 | 0.297 | 0.132 | 0.153 | 0.270 | 0.148 | 0.178 | 0.214 | 0.158 | 0.198 | 0.232 | ||
| Bearing 3-1 | Bearing 1-2 | 1-4 | 0.157 | 0.200 | 0.303 | 0.163 | 0.228 | 0.335 | 0.159 | 0.214 | 0.251 | 0.197 | 0.253 | 0.307 |
| 1-5 | 0.241 | 0.294 | 0.222 | 0.304 | 0.361 | 0.278 | 0.222 | 0.274 | 0.263 | 0.286 | 0.346 | 0.185 | ||
| 1-7 | 0.141 | 0.185 | 0.364 | 0.141 | 0.197 | 0.403 | 0.143 | 0.172 | 0.279 | 0.211 | 0.237 | 0.233 | ||
| AVG | 0.180 | 0.226 | 0.297 | 0.203 | 0.262 | 0.339 | 0.175 | 0.220 | 0.264 | 0.231 | 0.279 | 0.242 | ||
| Bearing 2-1 | 2-3 | 0.204 | 0.278 | 0.355 | 0.269 | 0.336 | 0.310 | 0.279 | 0.390 | 0.219 | 0.320 | 0.377 | 0.267 | |
| 2-6 | 0.178 | 0.232 | 0.379 | 0.180 | 0.243 | 0.330 | 0.168 | 0.232 | 0.392 | 0.202 | 0.259 | 0.362 | ||
| 2-7 | 0.132 | 0.154 | 0.269 | 0.155 | 0.254 | 0.497 | 0.208 | 0.259 | 0.324 | 0.241 | 0.317 | 0.334 | ||
| AVG | 0.171 | 0.221 | 0.334 | 0.201 | 0.278 | 0.379 | 0.219 | 0.294 | 0.312 | 0.254 | 0.318 | 0.321 | ||
| AVG | 0.155 | 0.194 | 0.319 | 0.170 | 0.218 | 0.328 | 0.174 | 0.214 | 0.274 | 0.202 | 0.247 | 0.261 | ||
| Source Domain | Target Domain | Tests | Model Name | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VDR + RSD + CNN | Wasserstein + CNN | CORAL + CNN | CCD + CNN | |||||||||||
| MAE | RMSE | Score | MAE | RMSE | Score | MAE | RMSE | Score | MAE | RMSE | Score | |||
| Bearing 1-2 | Bearing 2-1 | 2-3 | 0.320 | 0.389 | 0.244 | 0.332 | 0.429 | 0.246 | 0.357 | 0.413 | 0.178 | 0.322 | 0.392 | 0.247 |
| 2-6 | 0.082 | 0.105 | 0.316 | 0.122 | 0.145 | 0.226 | 0.087 | 0.108 | 0.342 | 0.112 | 0.138 | 0.329 | ||
| 2-7 | 0.241 | 0.302 | 0.282 | 0.354 | 0.428 | 0.236 | 0.240 | 0.305 | 0.338 | 0.192 | 0.256 | 0.414 | ||
| AVG | 0.214 | 0.265 | 0.280 | 0.269 | 0.334 | 0.236 | 0.228 | 0.275 | 0.286 | 0.208 | 0.262 | 0.330 | ||
| Bearing 3-1 | 3-2 | 0.115 | 0.150 | 0.373 | 0.103 | 0.130 | 0.365 | 0.111 | 0.137 | 0.317 | 0.168 | 0.232 | 0.314 | |
| 3-3 | 0.082 | 0.103 | 0.477 | 0.141 | 0.166 | 0.282 | 0.133 | 0.164 | 0.342 | 0.149 | 0.199 | 0.321 | ||
| AVG | 0.099 | 0.126 | 0.425 | 0.122 | 0.148 | 0.323 | 0.122 | 0.159 | 0.330 | 0.159 | 0.215 | 0.317 | ||
| Bearing 2-1 | Bearing 1-2 | 1-4 | 0.103 | 0.128 | 0.320 | 0.101 | 0.124 | 0.278 | 0.335 | 0.386 | 0.356 | 0.123 | 0.153 | 0.242 |
| 1-5 | 0.145 | 0.175 | 0.318 | 0.139 | 0.173 | 0.297 | 0.117 | 0.222 | 0.110 | 0.156 | 0.204 | 0.337 | ||
| 1-7 | 0.110 | 0.136 | 0.291 | 0.106 | 0.130 | 0.291 | 0.095 | 0.170 | 0.095 | 0.137 | 0.166 | 0.206 | ||
| AVG | 0.119 | 0.146 | 0.310 | 0.115 | 0.142 | 0.289 | 0.120 | 0.150 | 0.359 | 0.139 | 0.175 | 0.262 | ||
| Bearing 3-1 | 3-2 | 0.106 | 0.137 | 0.250 | 0.120 | 0.151 | 0.270 | 0.135 | 0.175 | 0.314 | 0.108 | 0.134 | 0.338 | |
| 3-3 | 0.126 | 0.148 | 0.343 | 0.134 | 0.154 | 0.220 | 0.120 | 0.171 | 0.299 | 0.128 | 0.159 | 0.310 | ||
| AVG | 0.116 | 0.143 | 0.297 | 0.127 | 0.152 | 0.245 | 0.128 | 0.173 | 0.307 | 0.118 | 0.146 | 0.324 | ||
| Bearing 3-1 | Bearing 1-2 | 1-4 | 0.157 | 0.200 | 0.303 | 0.212 | 0.284 | 0.269 | 0.160 | 0.220 | 0.340 | 0.146 | 0.189 | 0.323 |
| 1-5 | 0.241 | 0.294 | 0.222 | 0.207 | 0.277 | 0.307 | 0.279 | 0.303 | 0.191 | 0.206 | 0.261 | 0.270 | ||
| 1-7 | 0.141 | 0.185 | 0.364 | 0.210 | 0.278 | 0.180 | 0.156 | 0.206 | 0.339 | 0.145 | 0.182 | 0.292 | ||
| AVG | 0.180 | 0.226 | 0.297 | 0.209 | 0.280 | 0.252 | 0.199 | 0.243 | 0.290 | 0.166 | 0.211 | 0.295 | ||
| Bearing 2-1 | 2-3 | 0.204 | 0.278 | 0.355 | 0.320 | 0.417 | 0.222 | 0.266 | 0.334 | 0.290 | 0.260 | 0.348 | 0.288 | |
| 2-6 | 0.178 | 0.232 | 0.379 | 0.212 | 0.263 | 0.209 | 0.231 | 0.276 | 0.280 | 0.285 | 0.358 | 0.178 | ||
| 2-7 | 0.132 | 0.154 | 0.269 | 0.281 | 0.311 | 0.213 | 0.234 | 0.281 | 0.208 | 0.227 | 0.282 | 0.273 | ||
| AVG | 0.171 | 0.221 | 0.334 | 0.271 | 0.330 | 0.215 | 0.243 | 0.297 | 0.259 | 0.257 | 0.329 | 0.246 | ||
| AVG | 0.155 | 0.194 | 0.319 | 0.193 | 0.241 | 0.256 | 0.191 | 0.241 | 0.271 | 0.179 | 0.228 | 0.292 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, L.; Pan, J.; Huang, T.; Zhou, Z.; Huang, F. Enhanced Prediction of the Remaining Useful Life of Rolling Bearings Under Cross-Working Conditions via an Initial Degradation Detection-Enabled Joint Transfer Metric Network. Appl. Sci. 2025, 15, 6401. https://doi.org/10.3390/app15126401
Qi L, Pan J, Huang T, Zhou Z, Huang F. Enhanced Prediction of the Remaining Useful Life of Rolling Bearings Under Cross-Working Conditions via an Initial Degradation Detection-Enabled Joint Transfer Metric Network. Applied Sciences. 2025; 15(12):6401. https://doi.org/10.3390/app15126401
Chicago/Turabian StyleQi, Lingfeng, Jiafang Pan, Tianping Huang, Zhenfeng Zhou, and Faguo Huang. 2025. "Enhanced Prediction of the Remaining Useful Life of Rolling Bearings Under Cross-Working Conditions via an Initial Degradation Detection-Enabled Joint Transfer Metric Network" Applied Sciences 15, no. 12: 6401. https://doi.org/10.3390/app15126401
APA StyleQi, L., Pan, J., Huang, T., Zhou, Z., & Huang, F. (2025). Enhanced Prediction of the Remaining Useful Life of Rolling Bearings Under Cross-Working Conditions via an Initial Degradation Detection-Enabled Joint Transfer Metric Network. Applied Sciences, 15(12), 6401. https://doi.org/10.3390/app15126401









