Three-Dimensional Pedalling Kinematics Analysis Through the Development of a New Marker Protocol Specific to Cycling
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
- Participants aged 18 years or older.
- Leg length discrepancy (dysmetria) less than or equal to 5 mm.
- Body size compatible with the test bicycle.
- Intrinsic Q-factor similar to the standard Q-factor of the bicycle.
- Diagnosed locomotor or cardiopulmonary conditions that could interfere with test performance.
- High-performance or professional cyclists.
2.2. Instrumentation
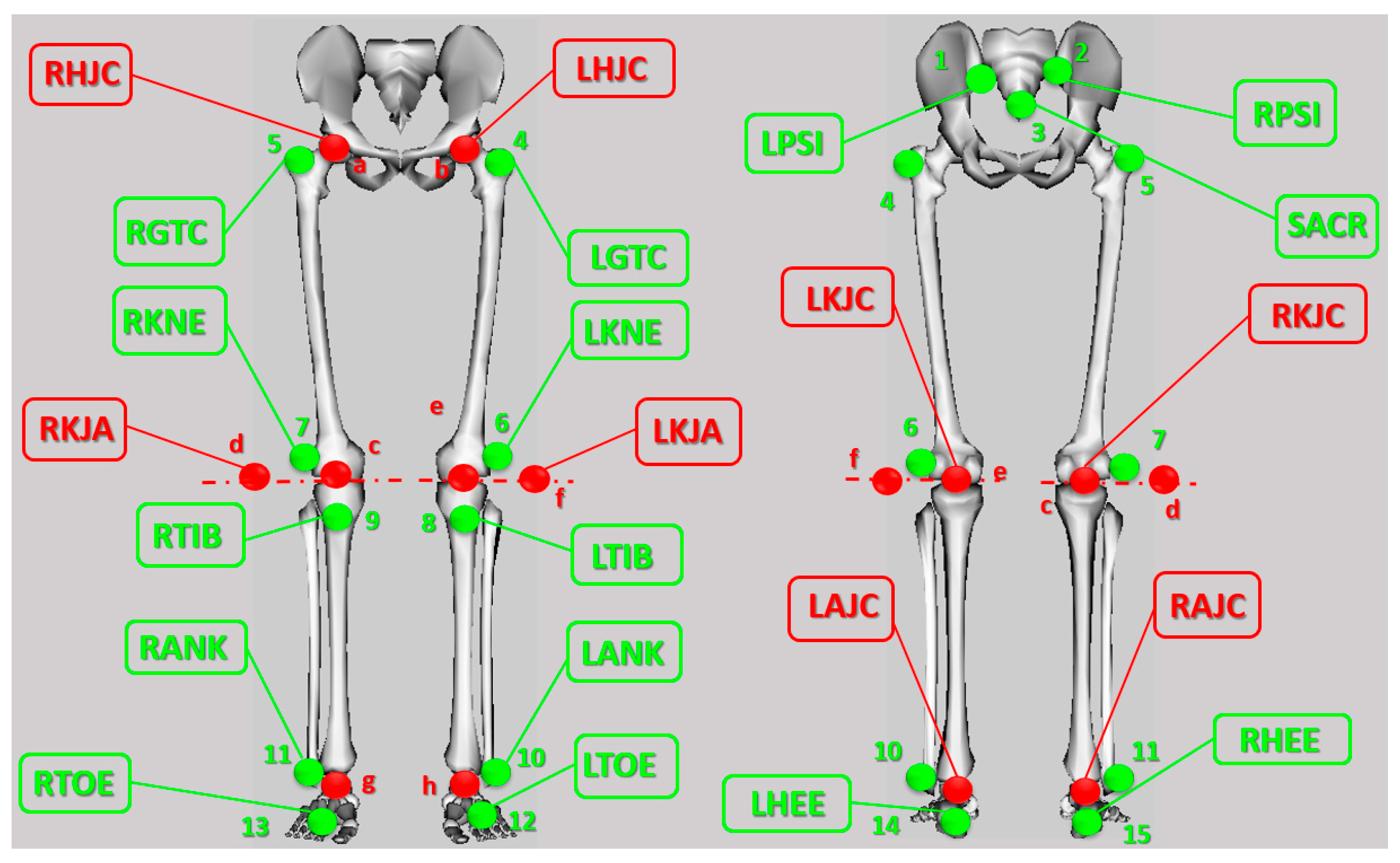
2.3. Marker Protocol
2.4. Body Pose Reconstruction Method
2.5. Test Conditions
2.6. Experimental Data Post-Processing
2.7. Evaluation of the Proposed Protocol
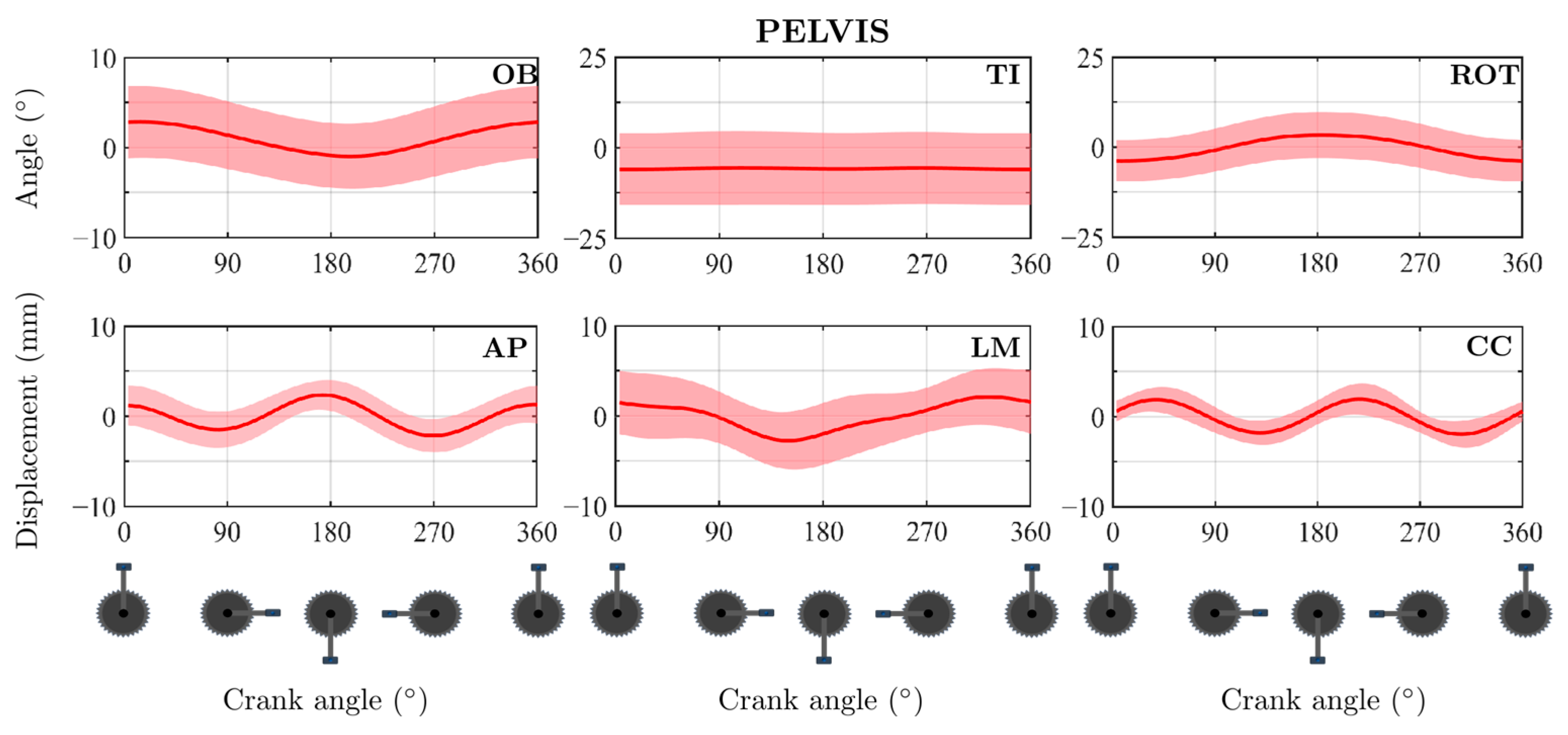
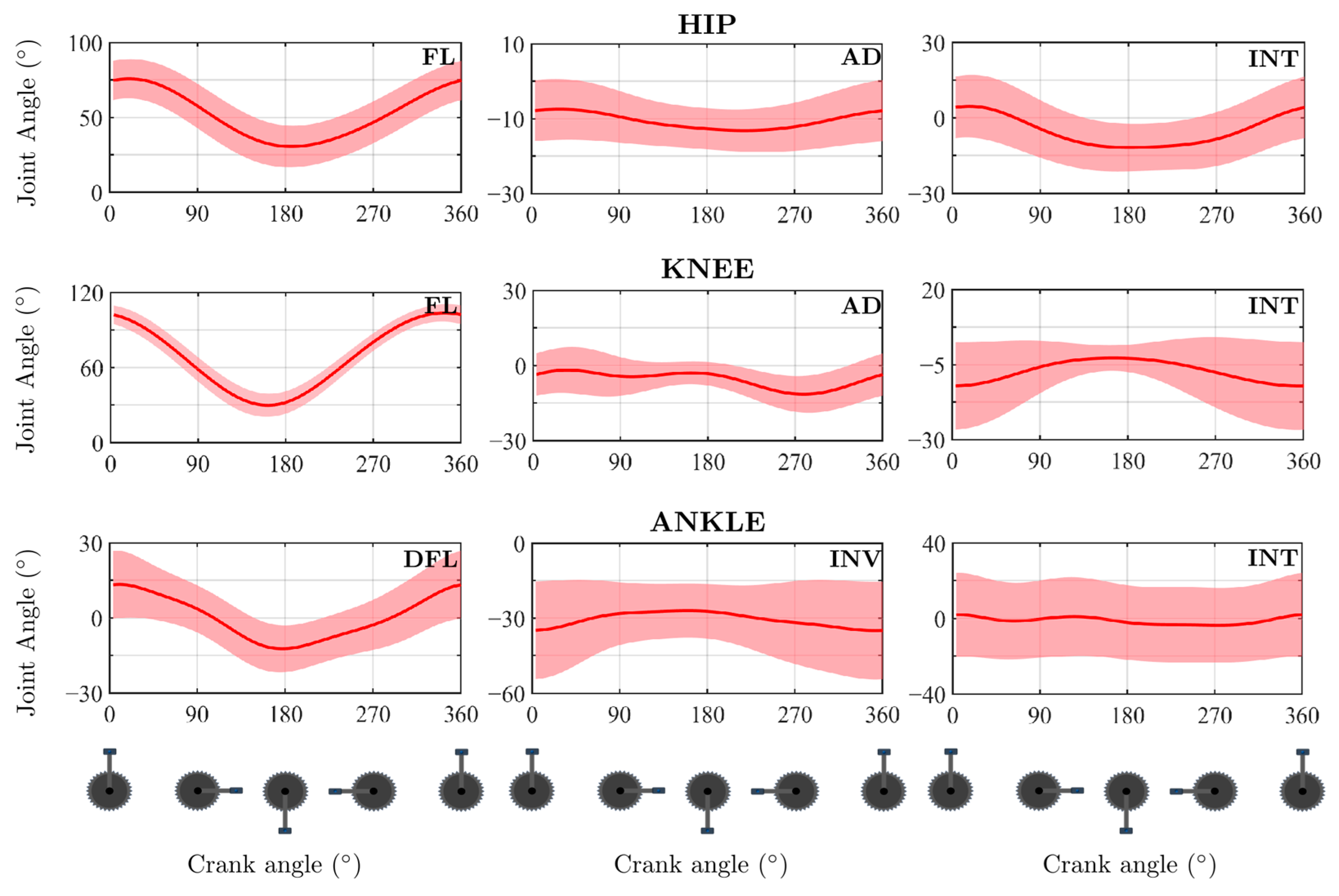
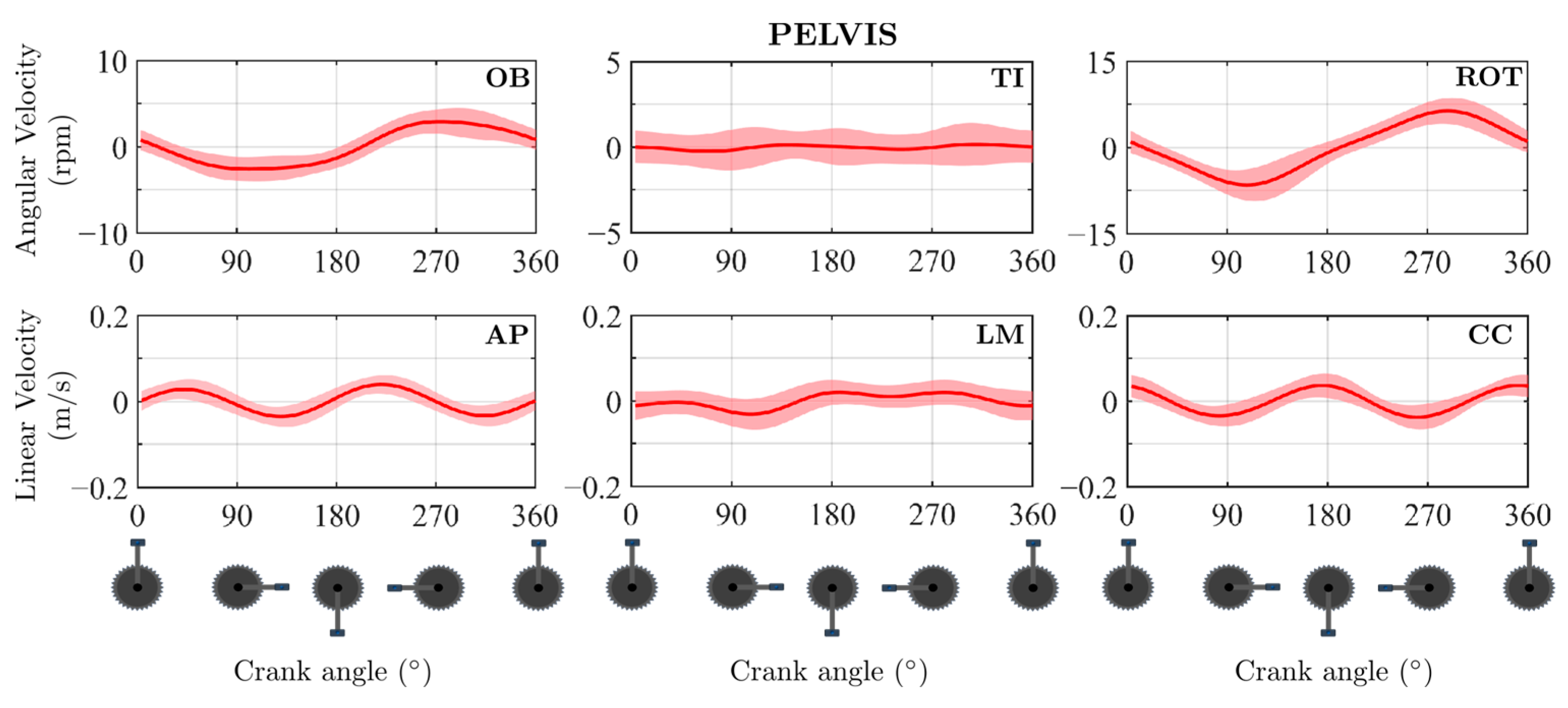
3. Results
4. Discussion
4.1. Proposed Protocol Evaluation
4.2. Position Problem
4.3. Velocity Problem
4.4. Acceleration Problem
4.5. Examples of Protocol Applicability
4.6. Limitations
4.7. Advantages of This Study
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fonda, B.; Sarabon, N.; Li, F. Validity and reliability of different kinematics methods used for bike fitting. J. Sports Sci. 2014, 32, 940–946. [Google Scholar] [CrossRef]
- Ericsson, M.O.; Nissel, R.; Németh, G. Joint Motions of the Lower Limb during Ergometer Cycling. J. Orthop. Sports Phys. Ther. 1988, 9, 273–278. [Google Scholar] [CrossRef]
- Umberger, B.R.; Martin, P.E. Testing the Planar Assumption During Ergometer Cycling. J. Appl. Biomech. 2001, 17, 55–62. [Google Scholar] [CrossRef]
- Vrints, J.; Koninckx, E.; Van Leemputte, M.; Jonkers, I. The Effect of Saddle Position on Maximal Power Output and Moment Generating Capacity of Lower Limb Muscles During Isokinetic Cycling. J. Appl. Biomech. 2011, 27, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Cordillet, S.; Bideau, N.; Bideau, B.; Nicolas, G. Estimation of 3D Knee Joint Angles during Cycling Using Inertial Sensors: Accuracy of a Novel Sensor-to-Segment Calibration Procedure Based on Pedaling Motion. Sensors 2019, 19, 2474. [Google Scholar] [CrossRef]
- Bini, R.R.; Diefenthaeler, F. Kinetics and kinematics analysis of incremental cycling to exhaustion. Sports Biomech. 2010, 9, 223–235. [Google Scholar] [CrossRef] [PubMed]
- Bini, R.R.; Tamborindeguy, A.C.; Mota, C.B. Effects of Saddle Height, Pedaling Cadence, and Workload on Joint Kinetics and Kinematics During Cycling. J. Sport Rehabil. 2010, 19, 301–314. [Google Scholar] [CrossRef]
- Bini, R.R.; Dagnese, F.; Rocha, E.; Silveira, M.C.; Carpes, F.P.; Mota, C.B. Three-dimensional kinematics of competitive and recreational cyclists across different workload during cycling. Eur. J. Sport Sci. 2016, 16, 553–559. [Google Scholar] [CrossRef]
- Sinclair, J.; Hebron, J.; Atkins, S.; Hurst, H.; Taylor, P.J. The influence of 3D kinematic and electromyographical parameters on cycling economy. Acta Bioeng. Biomech. 2014, 16, 89–95. [Google Scholar]
- Sinclair, J.; Hebron, J.; Hurst, H.; Taylor, P.J. The influence of different cardan sequences on three-dimensional cycling kinematics. Hum. Mov. Sci. 2013, 14, 334–339. [Google Scholar] [CrossRef]
- Pouliquen, C.; Nicolas, G.; Bideau, B.; Garo, G.; Megret, A.; Delamarche, P.; Bideau, N. Spatiotemporal analysis of 3D kinematic asymmetry in professional cycling during an incremental test to exhaustion. J. Sports Sci. 2018, 36, 2155–2163. [Google Scholar] [CrossRef] [PubMed]
- Hébert-Losier, K.; Yin, N.S.; Beaven, C.M.; Tee, C.C.L.; Richards, J. Physiological, kinematic, and electromyographic responses to kinesiologytype patella tape in elite cyclists. J. Electromyogr. Kinesiol. 2019, 44, 36–45. [Google Scholar] [CrossRef] [PubMed]
- Thorsen, T.; Strohacker, K.; Weinhandl, J.T.; Zhang, S. Increased Q-Factor increases frontal-plane knee joint loading in stationary cycling. J. Sport Health Sci. 2020, 9, 258–264. [Google Scholar] [CrossRef] [PubMed]
- Millour, G.; Duc, S.; Puel, F.; Bertucci, W. Physiological, Biomechanical and subjective effects of medio-lateral distance between the feet during pedaling for cyclists of different morphologies. J. Sports Sci. 2021, 39, 768–776. [Google Scholar] [CrossRef]
- Galindo-Martínez, A.; López-Valenciano, A.; Albaladejo-García, C.; Vallés-González, J.M.; Elvira, J.L.L. Changes in the Trunk and Lower Extremity Kinematics Due to Fatigue Can Predispose to Chronic Injuries in Cycling. Int. J. Environ. Res. Public Health 2021, 18, 3719. [Google Scholar] [CrossRef]
- Yum, H.; Kim, H.; Lee, T.; Park, M.S.; Lee, S.Y. Cycling kinematics in healthy adults for musculoskeletal rehabilitation guidance. BMC Musculoskelet. Disord. 2021, 22, 1044. [Google Scholar] [CrossRef]
- Pouliquen, C.; Nicolas, G.; Bideau, B.; Bideau, N. Impact of Power Output on Muscle Activation and 3D Kinematics During an Incremental Test to Exhaustion in Professional Cyclists. Front. Sport Act. Living 2021, 2, 516911. [Google Scholar] [CrossRef]
- Ojeda, J.; Martínez-Reina, J.; Mayo, J. A method to evaluate human skeletal models using marker residuals and global optimization. Mech. Mach. Theory 2014, 73, 259–272. [Google Scholar] [CrossRef]
- McLeod, W.D.; Blackburn, T.A. Biomechanics of knee rehabilitation with cycling. Am. J. Sports Med. 1980, 8, 175–180. [Google Scholar] [CrossRef]
- Farrell, K.C.; Reisinger, K.D.; Tillman, M.D. Force and repetition in cycling: Possible implications for iliotibial band friction syndrome. Knee 2003, 10, 103–109. [Google Scholar] [CrossRef]
- Wanich, T.; Hodgkins, C.; Columbier, J.A.; Muraski, E.; Kennedy, J.G. Cycling injuries of the lower extremity. J. Am. Acad. Orthop. Surg. 2007, 15, 748–756. [Google Scholar] [CrossRef] [PubMed]
- Kotler, D.H.; Babu, A.N.; Robidoux, G. Prevention, evaluation, and rehabilitation of cycling-related injury. Curr. Sports Med. Rep. 2016, 15, 199–206. [Google Scholar] [CrossRef]
- Capozzo, A.; Cappello, A.; Della Croce, U.; Pensalfini, F. Surface-Marker Cluster Design Criteria for 3-D Bone Movement Reconstruction. IEEE Trans. Biomed. Eng. 1997, 44, 1165–1174. [Google Scholar] [CrossRef]
- Davis, R.; Ounpuu, S.; Tyburski, D.; Gage, J.R. A gait analysis collection and reduction technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Carpes, F.P.; Rossato, M.; Faria, I.E.; Mota, C.B. Bilateral pedalling asymmetry during a simulated 40 km cycling time-trial. J. Sports Med. Phys. Fit 2007, 47, 51–57. [Google Scholar]
- Martín-Sosa, E.; Chaves, V.; Alvarado, I.; Mayo, J.; Ojeda, J. Design and Validation of a Device Attached to a Conventional Bicycle to Measure the Three-Dimensional Forces Applied to a Pedal. Sensors 2021, 21, 4590. [Google Scholar] [CrossRef]
- Balbinot, A.; Milani, C.; da Nascimento, J.S.B. A new crank arm-based load cell for the 3D analysis of the force applied by a cyclist. Sensors 2014, 14, 22921–22939. [Google Scholar] [CrossRef]
- Bini, R.R.; Carpes, F.P. Biomechanics of Cycling, 1st ed.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Ehrig, R.M.; Taylor, W.R.; Duda, G.N.; Heller, M.O. A survey of formal methods for determining the centre of rotation of ball joints. J. Biomech. 2006, 39, 2798–2809. [Google Scholar] [CrossRef] [PubMed]
- Ehrig, R.M.; Taylor, W.R.; Duda, G.N.; Heller, M.O. A survey of formal methods for determining functional joint axes. J. Biomech. 2007, 40, 2150–2157. [Google Scholar] [CrossRef]
- Wu, G.; Cavanagh, P.R. ISB Recommendation for standardization in the reporting of kinematic data. J. Biomech. 1995, 28, 1257–1261. [Google Scholar] [CrossRef]
- Ojeda, J.; Martínez-Reina, J.; Mayo, J. The effect of kinematic constraints in the inverse dynamics problem in biomechanics. Multibody Syst. Dyn. 2016, 37, 291–309. [Google Scholar] [CrossRef]
- Holmes, J.C.; Pruitt, A.L.; Whalen, N.J. Lower extremity overuse in bicycling. Clin. Sports Med. 1994, 13, 187–205. [Google Scholar] [CrossRef]
- Cyr, A.; Ascher, J. Clinical Applications of Bike Fitting. In Endurance Sports Medicine; Miller, T.L., Ed.; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2009; ISBN 978-0-470-39818-0. [Google Scholar]
- Fang, Y.; Fitzhugh, E.C.; Crouter, S.E.; Gardner, J.K.; Zhang, S. Effects of workloads and cadences on frontal plane knee biomechanics in cycling. Med. Sci. Sports Exerc. 2016, 48, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Gregersen, C.S.; Hull, M.L. Non-driving intersegmental knee moments in cycling computed using a model that includes three-dimensional kinematics of the shank/foot and the effect of simplifying assumptions. J. Biomech. 2003, 36, 803–813. [Google Scholar] [CrossRef]
- Sutherland, D. The evolution on clinical gait analysis Part II: Kinematics. Gait Posture 2002, 16, 159–179. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Caldwell, G. Coefficient of cross correlation and the time domain correspondence. J. Electromyogr. Kinesiol. 1999, 9, 385–389. [Google Scholar] [CrossRef]
- de Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Roja Ruiz, F.J.; Oña Sicilia, A.; Gutiérrez Dávila, M. Evaluation of interindividual and intraindividual variability in basketball jump throws through biomechanical analysis. Biomecánica 1998, 11, 88–97. [Google Scholar]
- Ferrari, A.; Benedetti, M.G.; Pavan, E.; Frigo, C.; Bettinelli, D.; Rabuffetti, M.; Crenna, P.; Leardini, A. Quantitative comparison of five current protocolos in gait analysis. Gait Posture 2008, 28, 207–216. [Google Scholar] [CrossRef]
- Davis, R.B.; DeLuca, P.A. Clinical gait analysis: Current methods and future decision. In Human Motion Analysis: Current Applications and Future Directions; Harris, G.F., Smith, P.A., Eds.; The Institute of Electrical and Electronic Engineers Press: New York, NY, USA, 1996; pp. 17–42. [Google Scholar]
- Ferrer-Roca, V.; Rivero-Palomo, V.; Ogueta-Alday, A.; Rodríguez-Marroyo, J.A.; García-López, J. Acute effects of small changes in crank length on gross efficiency and pedalling technique during submaximal cycling. J. Sports Sci. 2017, 35, 1328–1335. [Google Scholar] [CrossRef]
- Johnston, T.E. Biomechanical considerations for cycling interventions in rehabilitation. Phys. Ther. 2007, 87, 1243–1252. [Google Scholar] [CrossRef] [PubMed]
- Bini, R.; Hume, P.A.; Croft, J.L. Effects of bicycle saddle height on knee injury risk and cycling performance. Sports Med. 2011, 41, 463–476. [Google Scholar] [CrossRef] [PubMed]
- Barton, C.J.; Lack, S.; Malliaras, P.; Morrissey, D. Gluteal muscle activity and patellofemoral pain syndrome: A systematic review. Br. J. Sports Med. 2013, 47, 207–214. [Google Scholar] [CrossRef] [PubMed]
- Vicari, D.S.S.; Patti, A.; Giustino, V.; Figlioli, F.; Zangla, D.; Maksimovic, N.; Drid, P.; Palma, A.; Bianco, A. Saddle pressures distribution at different pedaling intensities in young off-road cyclists: Focus on sex. Ann. Med. 2025, 57, 2495764. [Google Scholar] [CrossRef]
- Potter, J.J.; Sauer, J.L.; Weisshaar, C.L.; Thelen, D.G.; Ploeg, H.L. Gender differences in bicycle saddle pressure distribution during seated cycling. Med. Sci. Sports Exerc. 2008, 40, 1126–1134. [Google Scholar] [CrossRef]


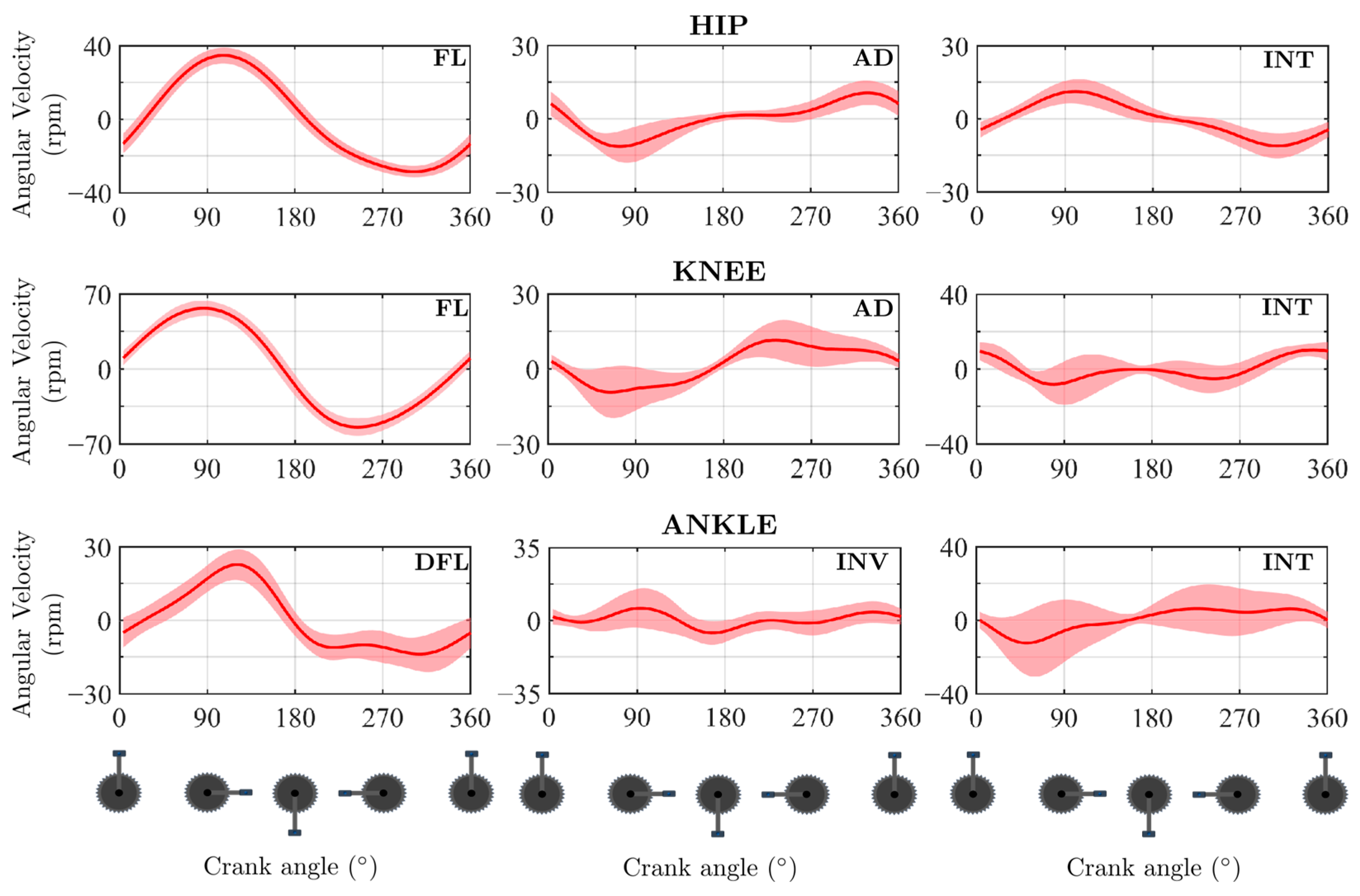
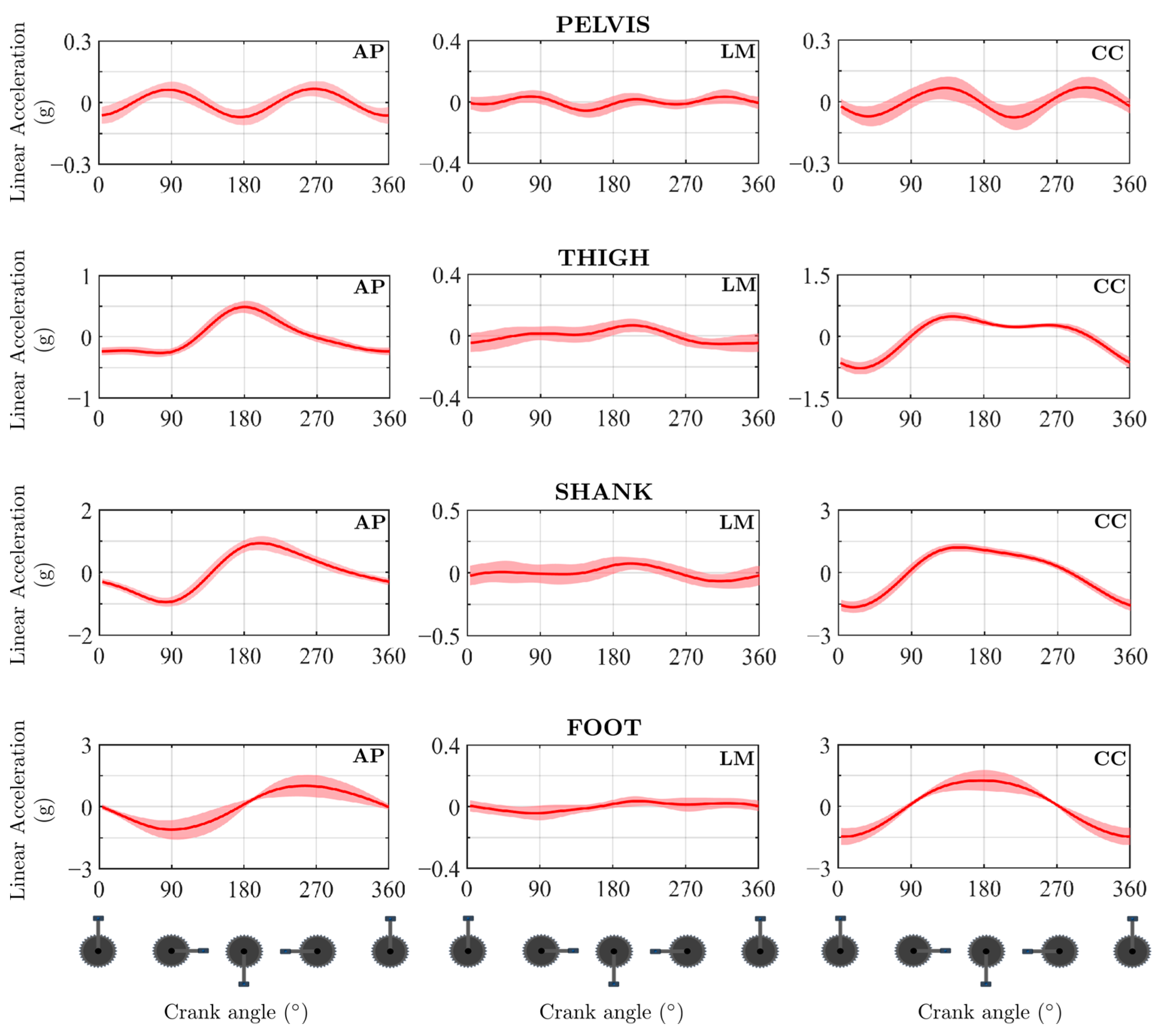
| Joint | Joint Angle | PP vs. CMP | PP vs. PiG | PiG vs. CMP | |||
|---|---|---|---|---|---|---|---|
| CCC | (%) | CCC | (%) | CCC | (%) | ||
| Hip | FL | 0.979 ± 0.006 | 2.4 ± 0.5 | 0.991 ± 0.004 | 0.6 ± 0.5 | 0.991 ± 0.001 | 1.4 ± 0.5 |
| AD | 0.805 ± 0.014 | −1.4 ± 0.5 | 0.914 ± 0.014 | 0 ± 0 | 0.950 ± 0.010 | 0 ± 0.0 | |
| INT | 0.437 ± 0.120 | −28.6 ± 17.3 | 0.533 ± 0.084 | −19.6 ± 18.5 | 0.828 ± 0.022 | −0.2 ± 0.4 | |
| Knee | FL | 0.996 ± 0.001 | −1 ± 0.0 | 0.998 ± 0.000 | 0 ± 0 | 0.994 ± 0.001 | −1 ± 0.0 |
| AD | 0.898 ± 0.016 | −2.6 ± 0.5 | 0.760 ± 0.063 | −4 ± 0.7 | 0.837 ± 0.023 | 0.2 ± 0.4 | |
| INT | 0.741 ± 0.035 | 13.2 ± 0.4 | 0.745 ± 0.014 | 4.8 ± 0.4 | 0.660 ± 0.032 | 6.4 ± 0.5 | |
| Ankle | DFL | 0.883 ± 0.006 | −2 ± 0.0 | 0.991 ± 0.001 | 0 ± 0 | 0.840 ± 0.013 | −2 ± 0.0 |
| INV | 0.750 ± 0.043 | −39.6 ± 1.8 | 0.942 ± 0.015 | −6.2 ± 0.4 | 0.779 ± 0.043 | −33 ± 1.4 | |
| INT | 0.583 ± 0.095 | 9.2 ± 2.3 | 0.967 ± 0.010 | −0.2 ± 0.4 | 0.588 ± 0.094 | 9.6 ± 2.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín-Sosa, E.; Soler-Vizán, E.; Mayo, J.; Ojeda, J. Three-Dimensional Pedalling Kinematics Analysis Through the Development of a New Marker Protocol Specific to Cycling. Appl. Sci. 2025, 15, 6382. https://doi.org/10.3390/app15126382
Martín-Sosa E, Soler-Vizán E, Mayo J, Ojeda J. Three-Dimensional Pedalling Kinematics Analysis Through the Development of a New Marker Protocol Specific to Cycling. Applied Sciences. 2025; 15(12):6382. https://doi.org/10.3390/app15126382
Chicago/Turabian StyleMartín-Sosa, Ezequiel, Elena Soler-Vizán, Juana Mayo, and Joaquín Ojeda. 2025. "Three-Dimensional Pedalling Kinematics Analysis Through the Development of a New Marker Protocol Specific to Cycling" Applied Sciences 15, no. 12: 6382. https://doi.org/10.3390/app15126382
APA StyleMartín-Sosa, E., Soler-Vizán, E., Mayo, J., & Ojeda, J. (2025). Three-Dimensional Pedalling Kinematics Analysis Through the Development of a New Marker Protocol Specific to Cycling. Applied Sciences, 15(12), 6382. https://doi.org/10.3390/app15126382






