A Comparative Study on the Accuracy and Resolution of DAS and DORT-MUSIC Damage Imaging Method Based on Ultrasonic Guided Waves
Abstract
1. Introduction
2. Materials and Methods
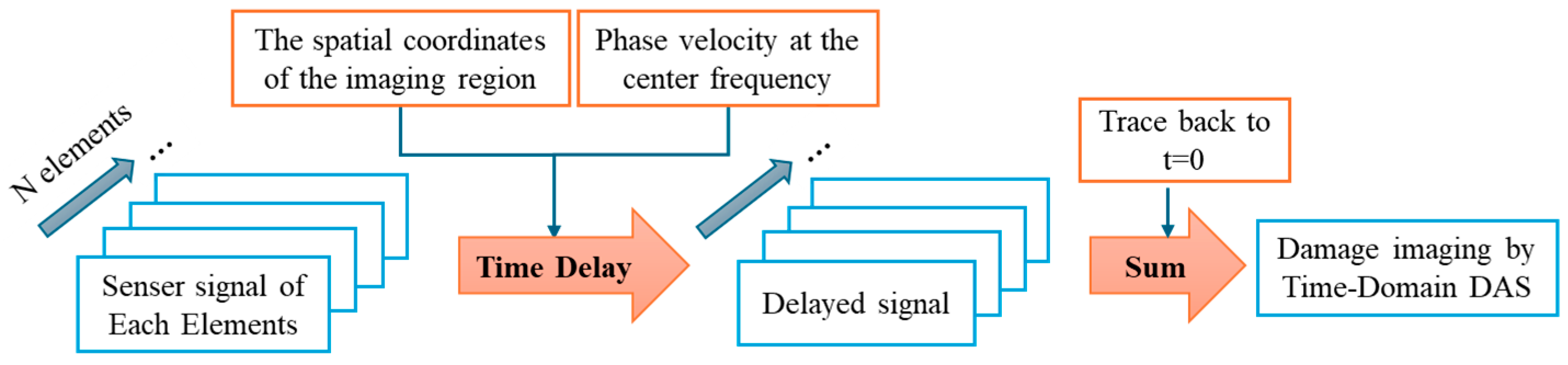
2.1. Time-Domain DAS
2.2. Frequency-Domain DAS
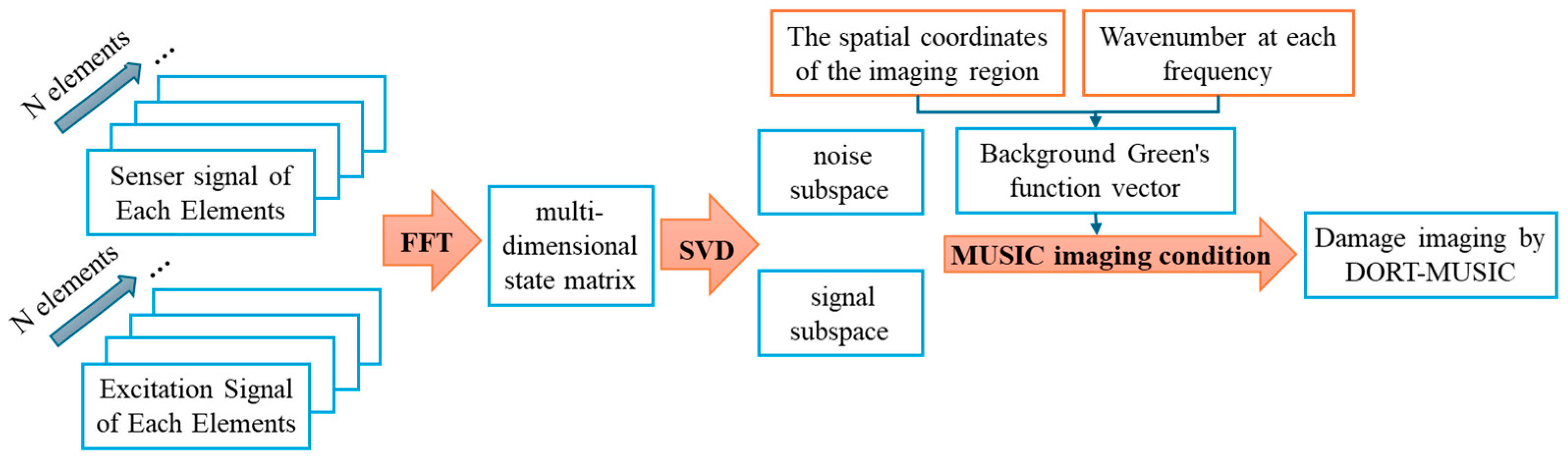
2.3. DORT-MUSIC
2.4. Performance Indicators
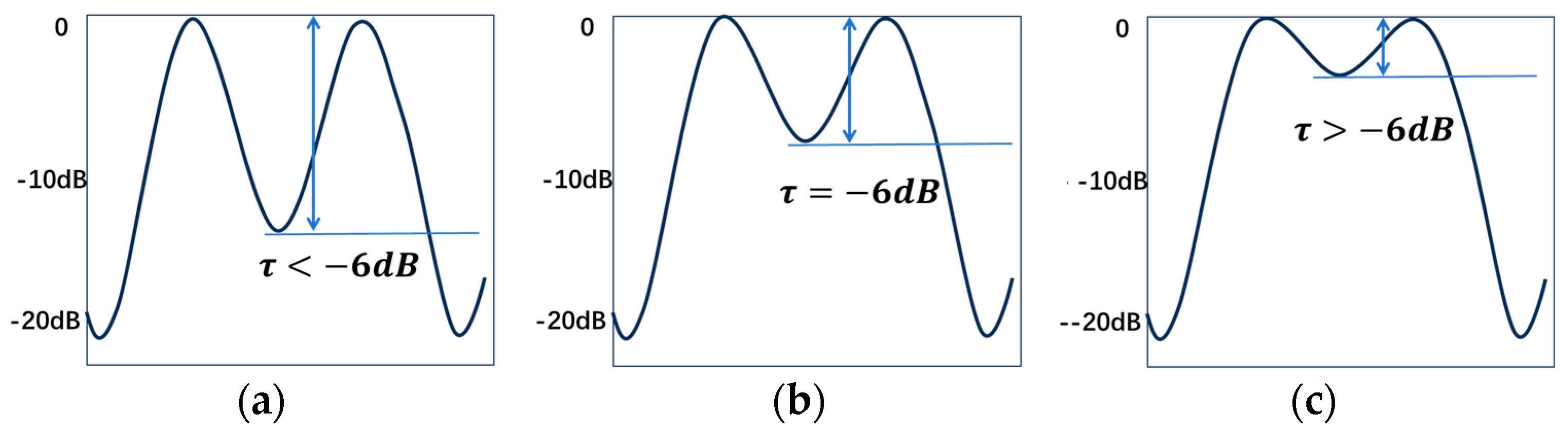
2.5. Rayleigh Diffraction Limit
2.6. Numerical Simulation
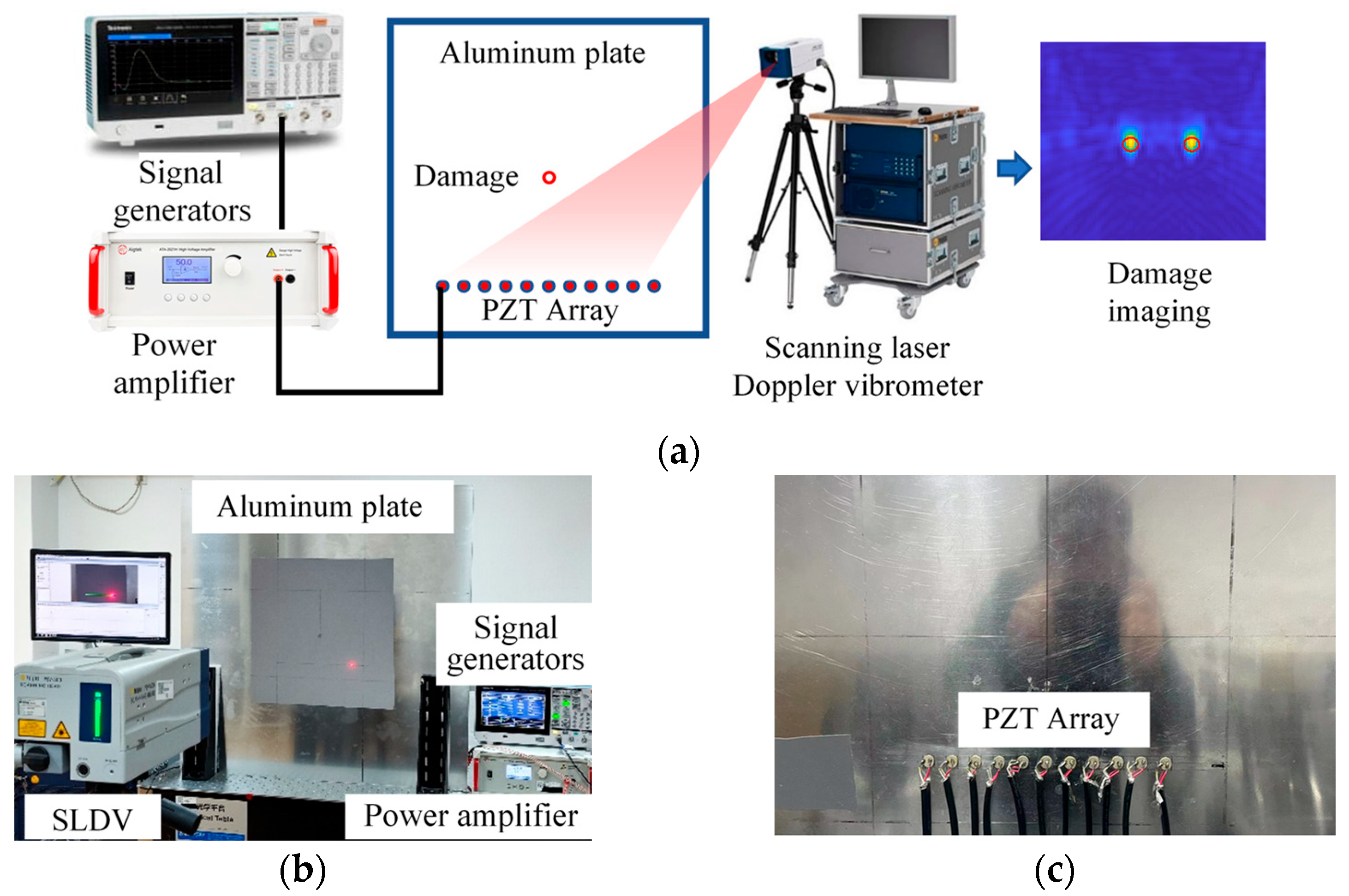
2.7. Experimental Validation
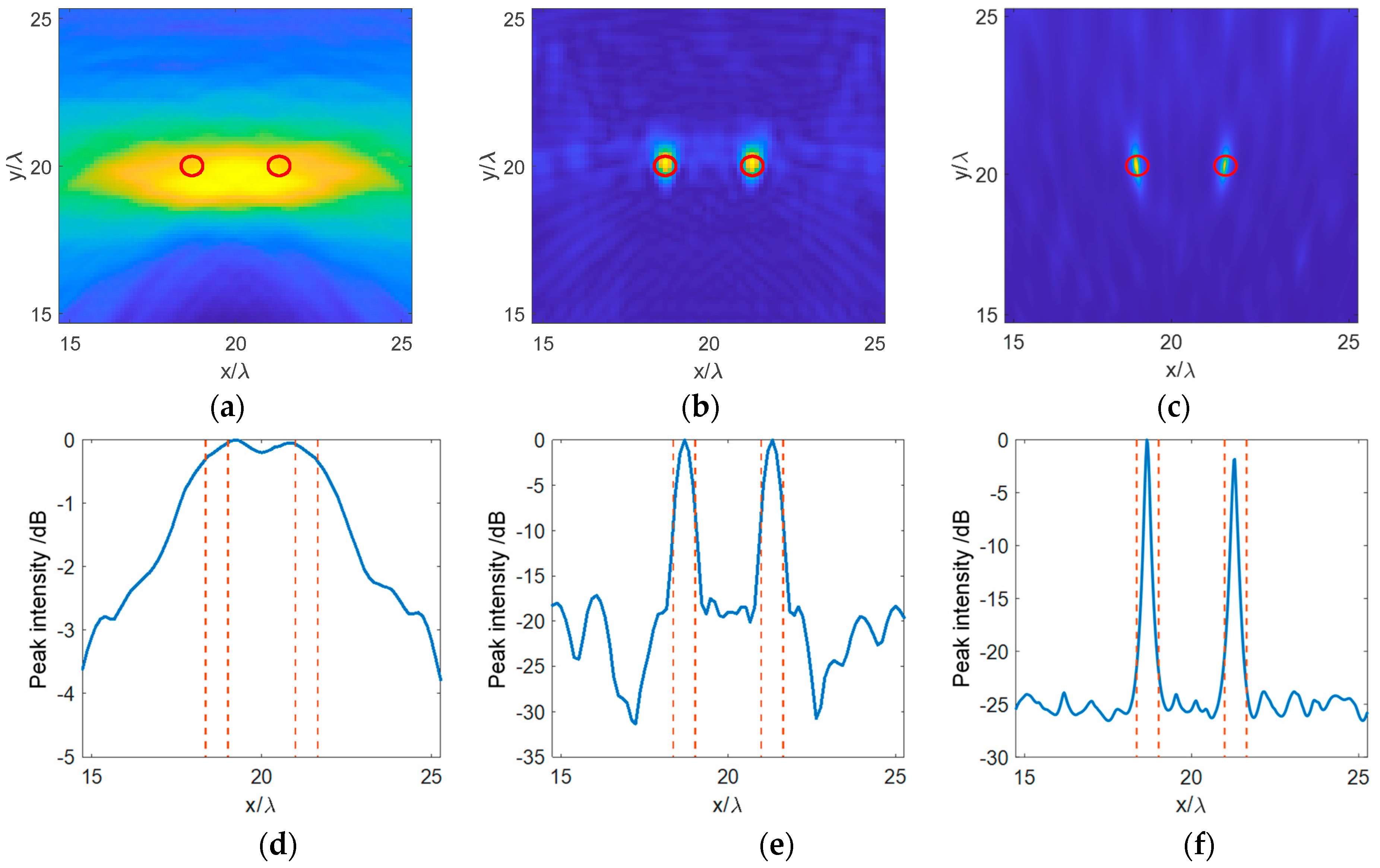
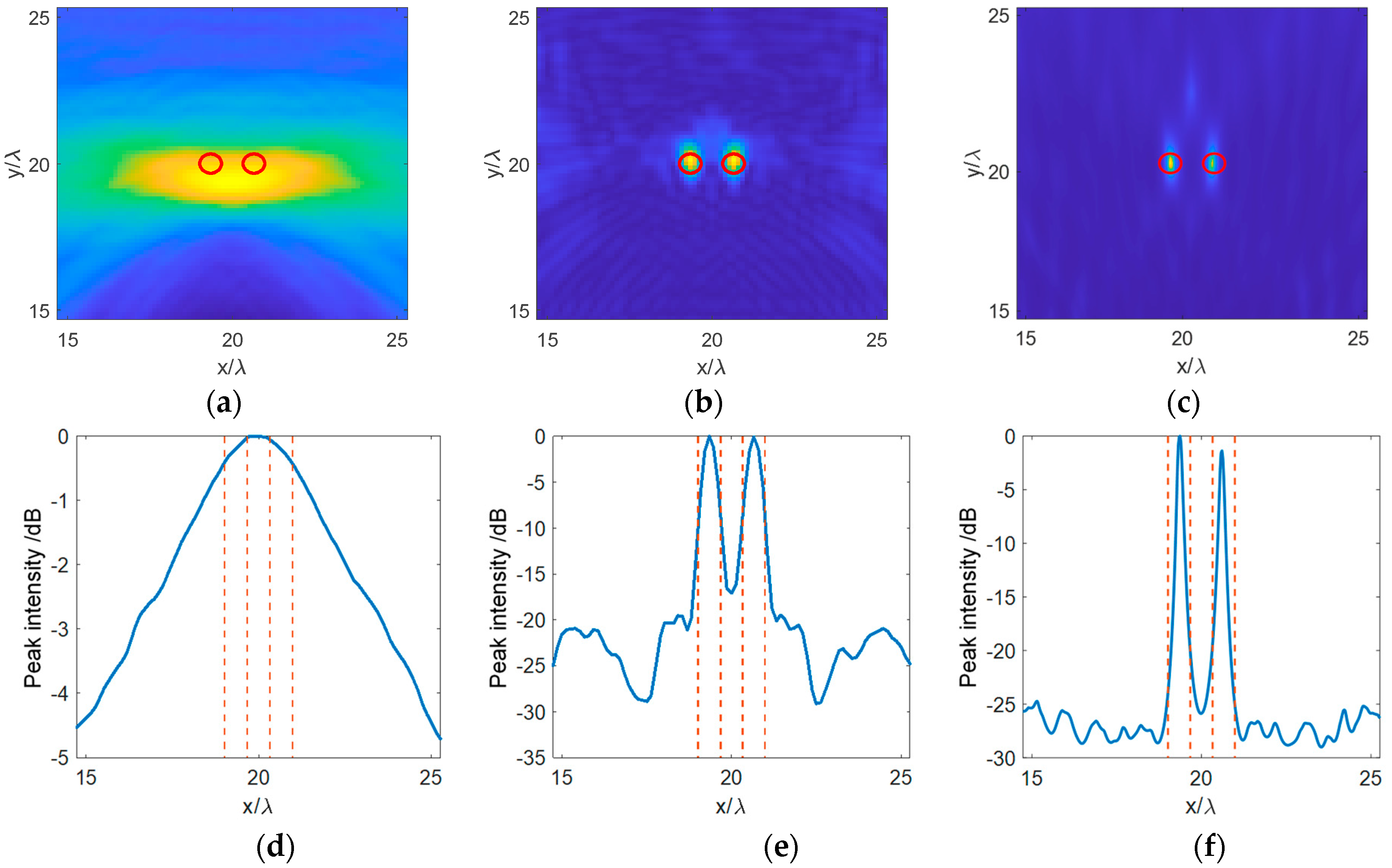
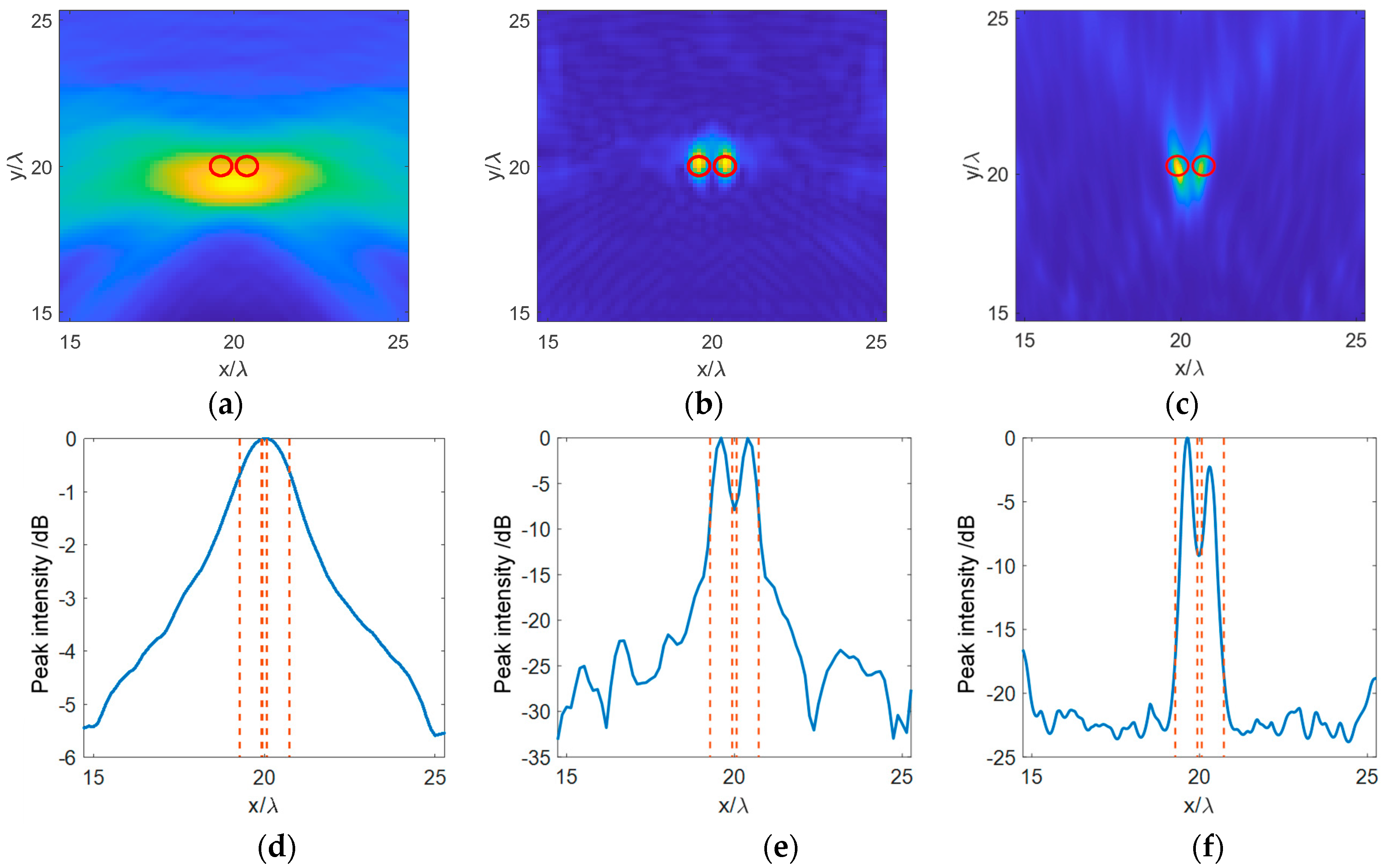
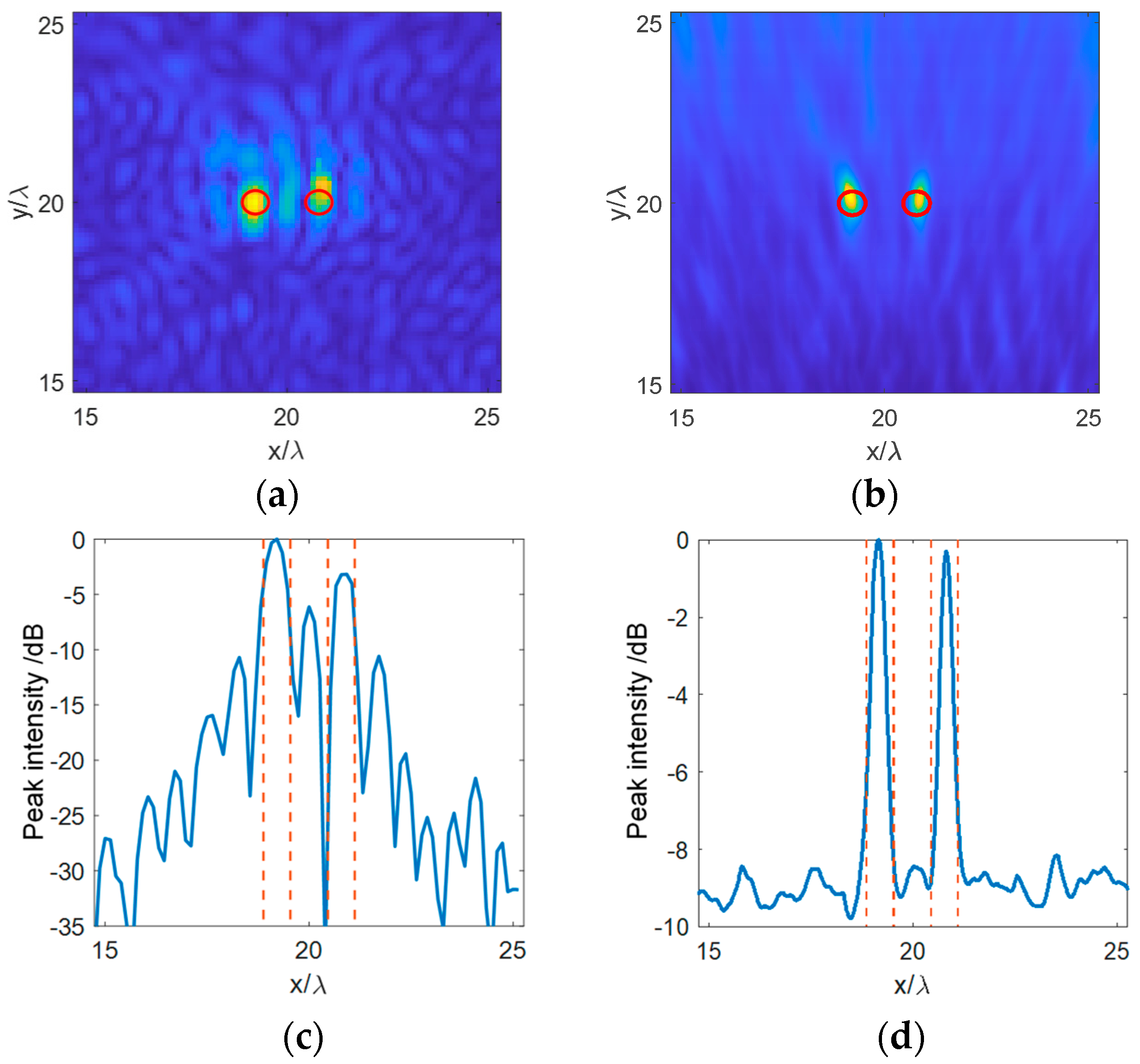
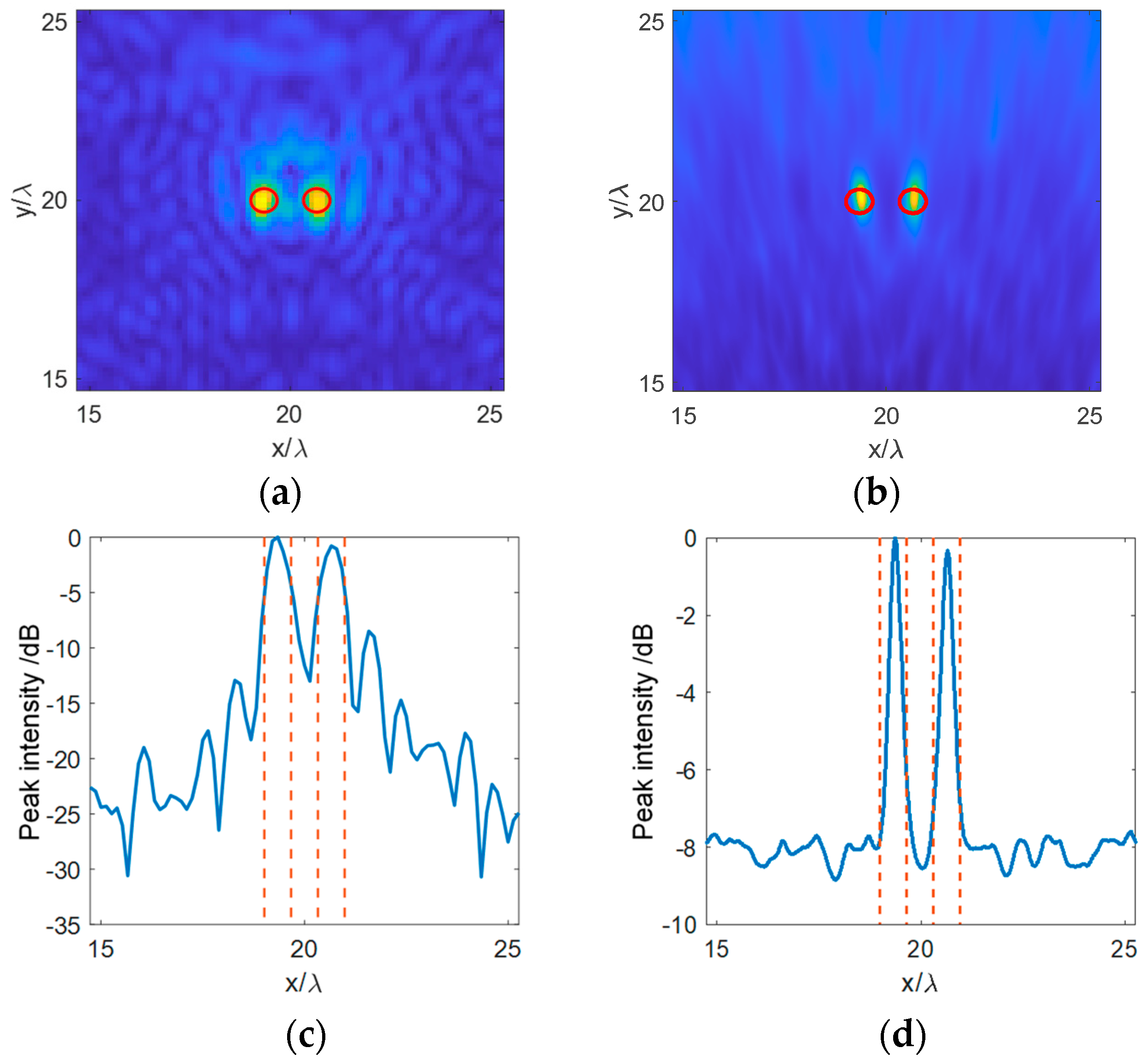
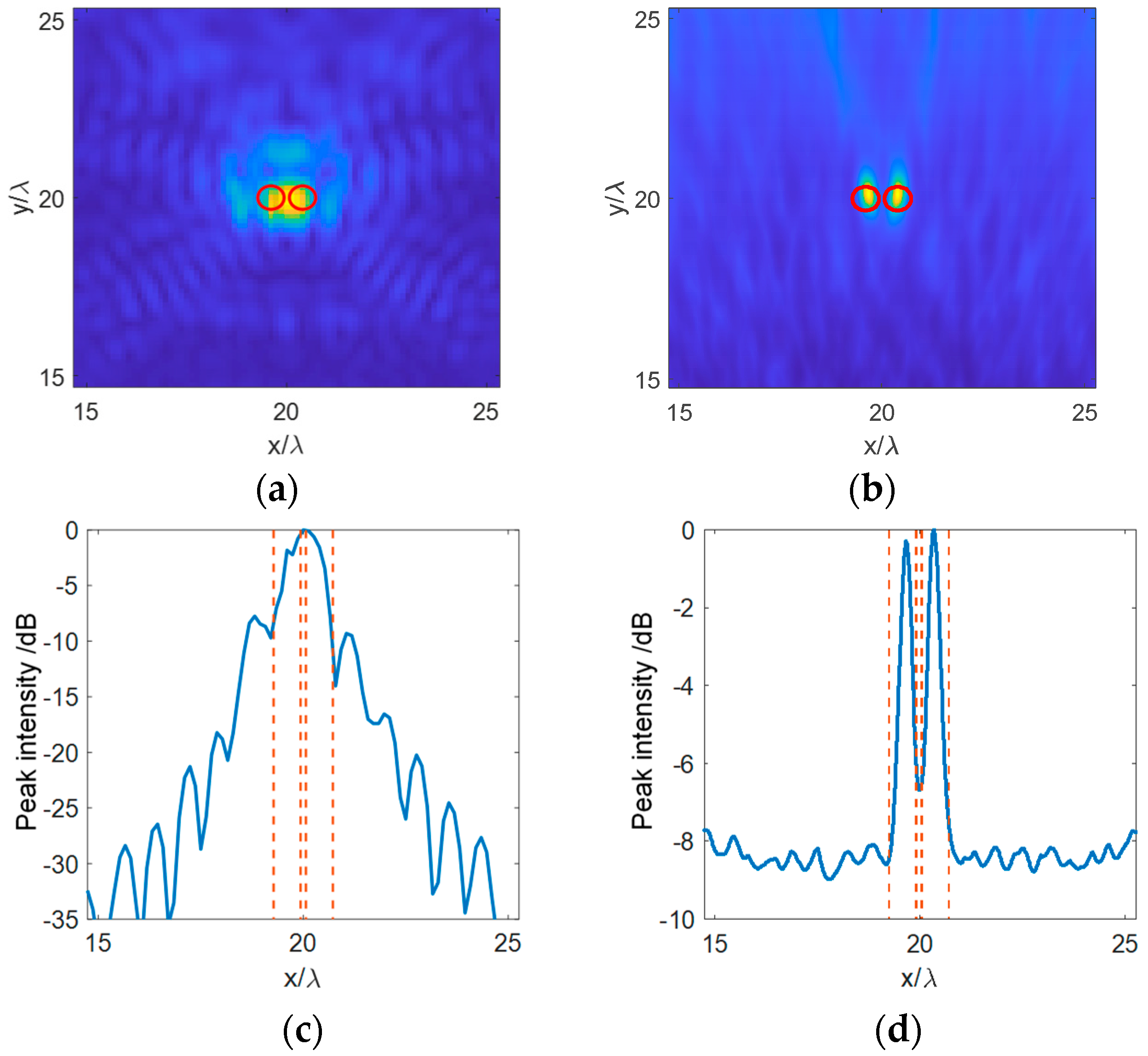
3. Results and Discussion
3.1. Numerical Simulation Results
3.2. Experiment Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giurgiutiu, V. Structural Health Monitoring: With Piezoelectric Wafer Active Sensors; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Di Ianni, T.; De Marchi, L.; Perelli, A.; Marzani, A. Compressive sensing of full wave field data for structural health monitoring applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1373–1383. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Tian, Z.; Leckey, C.A. Crack imaging and quantification in aluminum plates with guided wave wavenumber analysis methods. Ultrasonics 2015, 62, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Lugovtsova, Y.; Bulling, J.; Mesnil, O.; Prager, J.; Gohlke, D.; Boller, C. Damage quantification in an aluminium-CFRP composite structure using guided wave wavenumber mapping: Comparison of instantaneous and local wavenumber analyses. NDT E Int. 2021, 122, 102472. [Google Scholar] [CrossRef]
- Tabjula, J.L.; Kanakambaran, S.; Kalyani, S.; Rajagopal, P.; Srinivasan, B. Outlier analysis for defect detection using sparse sampling in guided wave structural health monitoring. Struct. Control Health Monit. 2021, 28, e2690. [Google Scholar] [CrossRef]
- Shen, R.; Zhou, Z.; Xu, G.; Zhang, S.; Xu, C.; Xu, B.; Luo, Y. Adaptive Weighted Damage Imaging of Lamb Waves Based on Deep Learning. IEEE Access 2024, 12, 128860–128870. [Google Scholar] [CrossRef]
- Shen, R.; Zhou, Z.; Xu, G.; Zhang, S.; Xu, C.; Xu, B.; Luo, Y. Adaptive Beamforming Damage Imaging of Lamb Wave Based on CNN. Appl. Sci. 2025, 15, 3801. [Google Scholar] [CrossRef]
- Sicard, R.; Goyette, J.; Zellouf, D. A SAFT algorithm for lamb wave imaging of isotropic plate-like structures. Ultrasonics 2002, 39, 487–494. [Google Scholar] [CrossRef]
- Gaul, T.; Schubert, L.; Weihnacht, B.; Frankenstein, B. Localization of defects in pipes using guided waves and synthetic aperture focussing technique (SAFT). In Proceedings of the EWSHM-7th European Workshop on Structural Health Monitoring, Nantes, France, 8–11 July 2014. [Google Scholar]
- Sun, X.; Lin, L.; Jin, S. Resolution enhancement in ultrasonic TOFD imaging by combining sparse deconvolution and synthetic aperture focusing technique (Sparse-SAFT). Chin. J. Mech. Eng. 2022, 35, 94. [Google Scholar] [CrossRef]
- Lyu, Y.; Hong, H.; Song, G.; He, C. A Simplified Integration of Multi-Channel Ultrasonic Guided Wave System for Phased Array Detection and Total Focusing Imaging. Int. J. Acoust. Vib. 2021, 26, 104–109. [Google Scholar] [CrossRef]
- Zhang, J.; Drinkwater, B.W.; Wilcox, P.D.; Hunter, A.J. Defect detection using ultrasonic arrays: The multi-mode total focusing method. NDT E Int. 2010, 43, 123–133. [Google Scholar] [CrossRef]
- Shen, P.; Wu, Y.; Luo, Z.; Wu, Z.; Jing, J.; Zhang, H. Advanced orthogonal frequency and phase modulated waveform for ultrasonic phased array tfm detection in cfrp composites. IEEE Trans. Instrum. Meas. 2024, 73, 1–10. [Google Scholar] [CrossRef]
- Li, X.; Xiang, Y.; Liu, L.; Xuan, F.-Z. Ultrasonic guided wave phased array based on reconstructed pulse-echo signals from phase information. J. Phys. Conf. Ser. 2024, 2822, 012111. [Google Scholar] [CrossRef]
- Zhu, W.; Xiang, Y.; Zhang, H.; Zhang, M.; Fan, G.; Zhang, H. Super-resolution ultrasonic Lamb wave imaging based on sign coherence factor and total focusing method. Mech. Syst. Signal Process. 2023, 190, 110121. [Google Scholar] [CrossRef]
- Park, H.W.; Kim, S.B.; Sohn, H. Understanding a time reversal process in Lamb wave propagation. Wave Motion 2009, 46, 451–467. [Google Scholar] [CrossRef]
- Ing, R.K.; Fink, M. Time-reversed Lamb waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 1032–1043. [Google Scholar] [CrossRef]
- He, J.; Yuan, F.-G. Lamb-wave-based two-dimensional areal scan damage imaging using reverse-time migration with a normalized zero-lag cross-correlation imaging condition. Struct. Health Monit. 2017, 16, 444–457. [Google Scholar] [CrossRef]
- Lang, Y.; Yang, Z.; Kong, D.; Zhang, W.; Chen, X. Forward-propagation-free focusing MUSIC algorithm for Lamb waves. Struct. Health Monit. 2023, 22, 3856–3870. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, A.; Sun, H.; Yun, F. A local TR-MUSIC algorithm for damage imaging of aircraft structures. Sensors 2021, 21, 3334. [Google Scholar] [CrossRef]
- Song, H.; Yang, Y. Noncontact super-resolution guided wave array imaging of subwavelength defects using a multiscale deep learning approach. Struct. Health Monit. 2021, 20, 1904–1923. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Bao, J. Embedded-ultrasonics structural radar for nondestructive evaluation of thin-wall structures. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 17–22 November 2002; pp. 333–340. [Google Scholar]
- Yu, L.; Giurgiutiu, V. In situ 2-D piezoelectric wafer active sensors arrays for guided wave damage detection. Ultrasonics 2008, 48, 117–134. [Google Scholar] [CrossRef]
- Yu, L.; Santoni-Bottai, G.; Xu, B.; Liu, W.; Giurgiutiu, V. Piezoelectric wafer active sensors for in situ ultrasonic-guided wave SHM. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 611–628. [Google Scholar] [CrossRef]
- Moulin, E.; Bourasseau, N.; Assaad, J.; Delebarre, C. Lamb-wave beam-steering for integrated health monitoring applications. In Proceedings of the Nondestructive Evaluation and Health Monitoring of Aerospace Materials and Composites II, San Diego, CA, USA, 3–5 March 2003; pp. 124–131. [Google Scholar]
- Yu, L.; Tian, Z. Guided wave phased array beamforming and imaging in composite plates. Ultrasonics 2016, 68, 43–53. [Google Scholar] [CrossRef]
- Wilcox, P.D. Omni-directional guided wave transducer arrays for the rapid inspection of large areas of plate structures. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 699–709. [Google Scholar] [CrossRef]
- Simonetti, F. Multiple scattering: The key to unravel the subwavelength world from the far-field pattern of a scattered wave. Phys. Rev. E 2006, 73, 036619. [Google Scholar] [CrossRef] [PubMed]
- Prada, C.; Wu, F.; Fink, M. The iterative time reversal mirror: A solution to self-focusing in the pulse echo mode. J. Acoust. Soc. Am. 1991, 90, 1119–1129. [Google Scholar] [CrossRef]
- Lehman, S.K.; Devaney, A.J. Transmission mode time-reversal super-resolution imaging. J. Acoust. Soc. Am. 2003, 113, 2742–2753. [Google Scholar] [CrossRef]
- Liu, X.-F.; Wang, B.-Z.; Li, L.-W. Time reversal dort and music methods for extended targets detection and imaging. In Proceedings of the 2013 IEEE International Conference On Microwave Technology & Computational Electromagnetics, Qingdao, China, 25–28 August 2013; pp. 304–307. [Google Scholar]
- He, J.; Yuan, F.-G. Lamb wave-based subwavelength damage imaging using the DORT-MUSIC technique in metallic plates. Struct. Health Monit. 2016, 15, 65–80. [Google Scholar] [CrossRef]
- He, J.; Yuan, F.-G. Lamb waves based fast subwavelength imaging using a DORT-MUSIC algorithm. AIP Conf. Proc. 2016, 1706, 030022. [Google Scholar] [CrossRef]
- Fan, C.; Yu, S.; Gao, B.; Zhao, Y.; Yang, L. Ultrasonic time-reversal-based super resolution imaging for defect localization and characterization. NDT E Int. 2022, 131, 102698. [Google Scholar] [CrossRef]
- Gruber, F.K.; Marengo, E.A.; Devaney, A.J. Time-reversal imaging with multiple signal classification considering multiple scattering between the targets. J. Acoust. Soc. Am. 2004, 115, 3042–3047. [Google Scholar] [CrossRef]
- Devaney, A.J. Super-resolution processing of multi-static data using time reversal and MUSIC. 2000. Available online: http://www.ece.neu.edu/faculty/devaney/ajd/preprints.htm (accessed on 4 May 2025).
- Fan, C.; Caleap, M.; Pan, M.; Drinkwater, B.W. A comparison between ultrasonic array beamforming and super resolution imaging algorithms for non-destructive evaluation. Ultrasonics 2014, 54, 1842–1850. [Google Scholar] [CrossRef] [PubMed]
- Davy, M.; Minonzio, J.-G.; de Rosny, J.; Prada, C.; Fink, M. Influence of noise on subwavelength imaging of two close scatterers using time reversal method: Theory and experiments. Prog. Electromagn. Res. 2009, 98, 333–358. [Google Scholar] [CrossRef]
- Holmes, C.; Drinkwater, B.W.; Wilcox, P.D. Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation. NDT E Int. 2005, 38, 701–711. [Google Scholar] [CrossRef]
- Laroche, N.; Carcreff, E.; Bourguignon, S.; Idier, J.; Duclos, A. An inverse approach for ultrasonic imaging by total focusing point for close reflectors separation. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018; pp. 1–4. [Google Scholar]
- Cicero, T. Signal Processing for Guided Wave Structural Health Monitoring. Ph.D. Thesis, Imperial College London, London, UK, 2009. [Google Scholar]







| Material Parameters | Value |
|---|---|
| Aluminum plate dimensions (mm) | 300 × 300 × 2 |
| Damping absorption boundary width (mm) | 50 |
| Poisson ratio ν | 0.33 |
| Elastic modulus E (GPa) | 70 |
| 1 | |
| (kg/m3) | 2700 |
| Damage Center Distance (mm) | Damage Localization Deviation (mm) | Peak-to-Center Intensity Difference (dB) | Array Performance Indicator (API) | |||
|---|---|---|---|---|---|---|
| f-DAS | DORT-MUSIC | f-DAS | DORT-MUSIC | f-DAS | DORT-MUSIC | |
| 20 | (0, 1) (0, 1) | (−0.2, −1.8) (0.2, −1.8) | −20.7 | −35.4 | 0.848 | 0.185 |
| 10 | (0, 1) (0, 1) | (−0.2, 0.4) (0, 0.4) | −17.1 | −24.6 | 0.796 | 0.21 |
| 8 | (0, 1) (0, 1) | (0.2, −0.6) (0, 1.8) | −16.1 | −22.8 | 0.85 | 0.28 |
| 6 | (0, 1) (0, 1) | (0.6, −0.8) (−0.6, −0.4) | −7.4 | −9.2 | 0.83 | 0.34 |
| Damage Center Distance (mm) | Damage Localization Deviation (mm) | Peak-to-Center Intensity Difference (dB) | Array Performance Indicator (API) | |||
|---|---|---|---|---|---|---|
| f-DAS | DORT-MUSIC | f-DAS | DORT-MUSIC | f-DAS | DORT-MUSIC | |
| 20 | (0, 0) (0, 1) | (0, 0.6) (0, −0.4) | −26.2 | −8.9 | 1.30 | 1.17 |
| 12 | (0, 0) (0, 4) | (−0.6, 1.2) (0.2, 0.8) | −16.0 | −8.5 | 1.17 | 1.17 |
| 10 | (0, −1) (0, −1) | (0.2, 0.8) (−0.2, 0.4) | −12.0 | −8.4 | 1.43 | 1.08 |
| 6 | NA NA | (0.2, 0.6) (−0.2, 0.8) | NA | −6.7 | 1.33 | 0.97 |
| Method | Complexity | Computational Time | Resolution | Noise Sensitivity |
|---|---|---|---|---|
| Time-domain DAS | Low | Fast | Low | Moderate |
| Frequency-domain DAS | Moderate | Moderate | High | Moderate |
| DORT-MUSIC | High | Slow | Extremely High | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Luo, Y.; Xu, G.; Zhang, S.; Xu, B. A Comparative Study on the Accuracy and Resolution of DAS and DORT-MUSIC Damage Imaging Method Based on Ultrasonic Guided Waves. Appl. Sci. 2025, 15, 6380. https://doi.org/10.3390/app15126380
Xu C, Luo Y, Xu G, Zhang S, Xu B. A Comparative Study on the Accuracy and Resolution of DAS and DORT-MUSIC Damage Imaging Method Based on Ultrasonic Guided Waves. Applied Sciences. 2025; 15(12):6380. https://doi.org/10.3390/app15126380
Chicago/Turabian StyleXu, Chenguang, Ying Luo, Guidong Xu, Sai Zhang, and Baiqiang Xu. 2025. "A Comparative Study on the Accuracy and Resolution of DAS and DORT-MUSIC Damage Imaging Method Based on Ultrasonic Guided Waves" Applied Sciences 15, no. 12: 6380. https://doi.org/10.3390/app15126380
APA StyleXu, C., Luo, Y., Xu, G., Zhang, S., & Xu, B. (2025). A Comparative Study on the Accuracy and Resolution of DAS and DORT-MUSIC Damage Imaging Method Based on Ultrasonic Guided Waves. Applied Sciences, 15(12), 6380. https://doi.org/10.3390/app15126380






