EEG-Based Inverse Reinforcement Learning for Safety-Oriented Global Path Planning in Dynamic Environments

Abstract

Recent advancements in lightweight electroencephalogram(EEG) signal classification have enabled real-time human–robot interaction, yet challenges persist in balancing computational efficiency and safety in dynamic path planning. This study proposes an EEG-based inverse reinforcement learning (EIRL) framework to simulate human navigation strategies by decoding neural decision preferences. The method integrates a pruned WNFG-SSCCNet-ADMM classifier for EEG signal mapping, apprenticeship learning for reward function extraction, and Q-learning for policy optimization. Experimental validation in an 8 × 8 FrozenLake-v1 environment demonstrates that EIRL reduces average path risk values by 50% compared with traditional reinforcement learning, achieving expert-level safety ($\Delta$ = 4) while maintaining optimal path lengths. The framework enhances adaptability in unknown environments by embedding human-like risk aversion into robotic planning, offering a robust solution for applications requiring minimal prior environmental knowledge. Results highlight the synergy between neural feedback and computational models, advancing inclusive human–robot collaboration in safety-critical scenarios.

1. Introduction

In recent years, lightweight electroencephalogram (EEG) signal classification technologies have opened new possibilities for real-time human–robot interaction in wearable devices and robotic systems [1,2,3,4]. By integrating pruning algorithms and graph representation methods, researchers can significantly compress neural network parameters, enabling efficient EEG classification in low-computational environments [5,6,7]. Recent advancements in neural network optimization have witnessed significant progress through innovative integration of mathematical optimization and graph theory. A notable example is the WNFG-SSGCNet-ADMM framework developed by Wang et al. [8], which employs the alternating direction method of multipliers (ADMM) to achieve lightweight model design while maintaining performance integrity. The framework addresses critical challenges in model compression through constrained non-convex optimization formulation, demonstrating remarkable tenfold parameter reduction on both Bonn and SSW datasets without compromising classification accuracy. The theoretical underpinnings of the approach are strengthened by rigorous proofs of local convergence under practical assumptions, particularly when employing full-rank operators ($\Omega$), thereby overcoming theoretical limitations inherent in conventional pruning methodologies. The computational architecture is further enhanced through a weighted neighborhood field graph (WNFG) that dramatically reduces graph construction complexity from quadratic $O\left(n^2\right)$ to $O\left(Kn\right)(K\ll n)$, achieving an order-of-magnitude reduction in redundant edges while significantly improving memory efficiency.

Particularly noteworthy is the framework’s frequency-domain sparse graph construction, which demonstrates superior classification accuracy and stability compared with traditional time-domain approaches, especially under aggressive pruning conditions.

Subsequent validation in epileptic EEG recognition tasks has confirmed the framework’s robustness and practical applicability in critical biomedical applications. The Bonn dataset comprises five subsets (A–E), with subset E containing seizure data. Signals are segmented into non-overlapping 256-point windows to form four binary classification tasks (A v.s. E, B v.s. E, C v.s. E, D v.s. E), each containing 3200 samples (1600 epileptic vs non-epileptic) [9]. Experiments demonstrate that SSGCNet with WNFG in the frequency domain outperforms traditional time-domain methods, while ADMM pruning reduces model parameters by 10-fold without performance degradation. These results highlight ADMM’s superiority in balancing lightweight design and precision, paving the way for portable epilepsy monitoring devices [8].

Motor imagery (MI)-based EEG classification, which decodes neural activity patterns generated during imagined movements (e.g., limb motion), has emerged as a critical research direction in human-machine interaction. The PhysioNet MI dataset [10], for example, includes 64-channel EEG signals (sampled at 160 Hz) from 109 subjects performing 14 tasks (e.g., eye opening/closing, fist clenching/relaxing), with over 1500 samples [11]. Traditional classifiers such as support vector machines (SVM) [12] and linear discriminant analysis (LDA) [13] achieve high accuracy but rely on manually designed features, limiting their generalizability. In contrast, deep learning models (e.g., convolutional neural networks (CNN) [3,14]) automatically extract frequency-domain features but suffer from excessive training time and computational costs [15,16].

To address these challenges, lightweight improvement strategies have been proposed. Dropout techniques mitigate overfitting by randomly deactivating neurons [17,18], while magnitude-based pruning removes redundant weights for model compression. However, existing methods often lack theoretical optimization of network sparsity, leading to a trade-off between pruning rates and classification accuracy. Recent studies have demonstrated that hybrid frameworks combining ADMM with masked retraining have effectively solved non-convex sparse optimization problems, showing advantages in convergence and computational efficiency for epileptic EEG classification tasks [7,19].

Meanwhile, reinforcement learning (RL) and inverse reinforcement learning (IRL) have gained traction in robotic path planning. Sichkar [20] compared Q-Learning and Sarsa algorithms, highlighting parameter optimization for safety enhancement in dynamic environments; Wang et al. [21] proposed a globally guided RL framework (G2RL) achieving near-centralized planning efficiency in distributed multi-robot scenarios; and Gao [22] improved trajectory smoothness by integrating path graph preprocessing with Q-Learning. Nevertheless, traditional methods depend on prior environmental knowledge, struggling to adapt to unknown dynamic risks (e.g., random obstacles or terrain variations).

This study introduces an Embodied Intelligence Reinforcement Learning (EIRL) framework that synthesizes safety-conscious global path strategies through computational modeling of human navigation preferences. The methodology initiates with neurocognitive signal translation, where electroencephalogram (EEG) patterns are transformed into robotic control commands using a lightweight classification architecture, generating expert-level navigation trajectories. Building upon these empirical demonstrations, the framework subsequently employs apprenticeship learning to distill essential feature expectations and quantify reward weight distributions inherent in human decision-making processes. These optimized reward functions are then systematically integrated into Q-Learning iterations, enabling dynamic path planning that intrinsically balances exploration efficiency with collision avoidance. Experimental validation in the Frozen Lake V1 benchmark environment reveals the framework’s superior safety performance, achieving over 50% reduction in path risk metrics compared with conventional reinforcement learning and $A^{*}$ search algorithms. This neurocognitive-inspired approach establishes a novel paradigm for developing human-aligned autonomous systems that preserve biological decision-making advantages while addressing the safety-critical requirements of real-world robotic operations.

The main contributions of this study include:

(I)

Providing a physical-operation-free robot control interface for individuals with motor impairments, enhancing human–robot collaboration inclusivity;

(II)

Learning reward functions from EEG-implicit decision preferences via IRL, reducing reliance on prior maps;

(III)

Establishing a synergistic “brain-machine-environment” learning framework by integrating neural feedback with path execution results.

The research progression is structured to systematically bridge critical gaps in EEG-driven path planning. Initial investigations revealed two persistent limitations: conventional reinforcement learning frameworks struggle to decode human-like risk sensitivity from sparse neural signals, while existing EEG classification methods prioritize accuracy over real-time deployability. To address these challenges, our methodology integrates lightweight neural decoding with inverse reward modeling, enabling policy optimization that inherently balances safety and efficiency. This phased approach ensures theoretical rigor while maintaining practicality for real-world robotic applications. Conventional navigation systems rely on explicit environmental models or reactive RL policies, both of which struggle in partially observable, safety-critical scenarios (e.g., disaster rescue). EIRL addresses this gap by integrating EEG as a safety prior—a paradigm shift that enables proactive risk mitigation through human neurocognitive patterns. While traditional baselines (RL/$A^{*}$) are used for benchmarking, their inability to leverage neural data inherently limits comparability, as no prior work combines EEG with IRL for navigation.

2. Problem Modeling and Analysis

This section decomposes the EEG-based inverse reinforcement learning framework for human-like navigation simulation into three interconnected components: neurosignal-driven expert trajectory generation, apprenticeship learning-based reward modeling, and reinforcement learning-optimized global path planning. The methodology initiates with multi-channel EEG signal acquisition, followed by feature classification and pattern recognition to establish deterministic mappings between EEG biomarkers and robotic motion primitives. Target-oriented navigation tasks leverage classified EEG signals to generate movement trajectories while recording complete path histories, from which expert datasets are synthesized by identifying optimal path segments through EEG pattern analysis. Inverse reinforcement learning algorithms then extract spatial–temporal feature expectations and their associated weights from these datasets, enabling the derivation of biomimetic reward functions that are systematically integrated into reinforcement learning architectures for policy optimization. The final policy undergoes rigorous validation in parametrized simulation environments through iterative refinement cycles until achieving deployment readiness criteria.

2.1. EEG Signal Mapping and Expert Data Generation

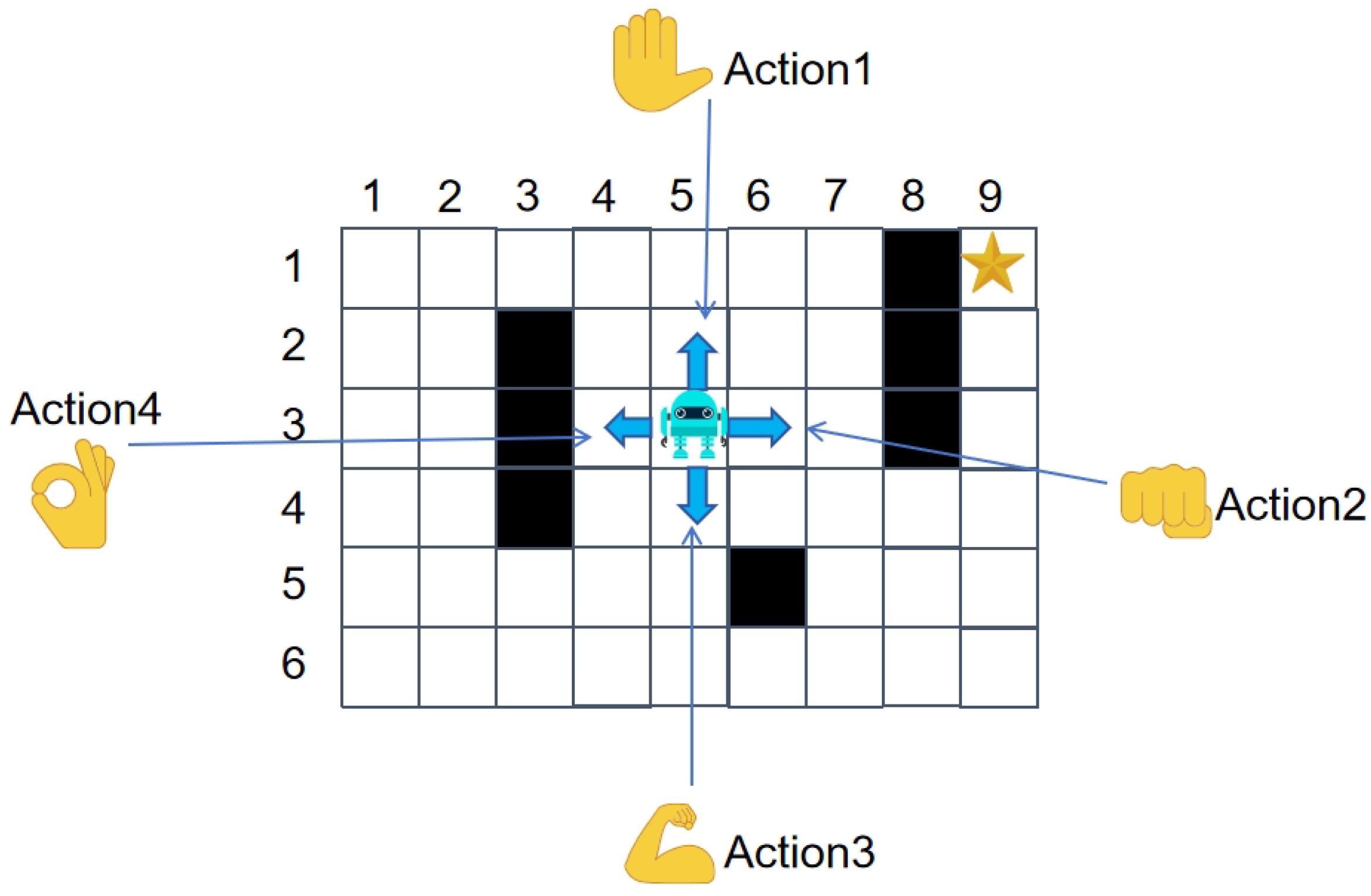
Beyond binary classification, EEG signal categorization can be extended to multi-class paradigms contingent on specific requirements and dataset characteristics. As illustrated in Figure 1, a robot navigating a grid-based environment permits four directional movements (up, down, left, right), necessitating corresponding EEG signal classification into four distinct categories. This alignment enables precise robotic maneuver control through discrete EEG-driven commands.

Following the categorical mapping of EEG signals to specific actions, subjects were tasked with repeated pathfinding attempts in hazardous environments while maintaining cognitive unawareness of test map configurations. Through iterative trials, optimal paths (minimizing traversal time/distance while circumventing hazards) were identified and translated into expert strategies via EEG-controlled robotic navigation.

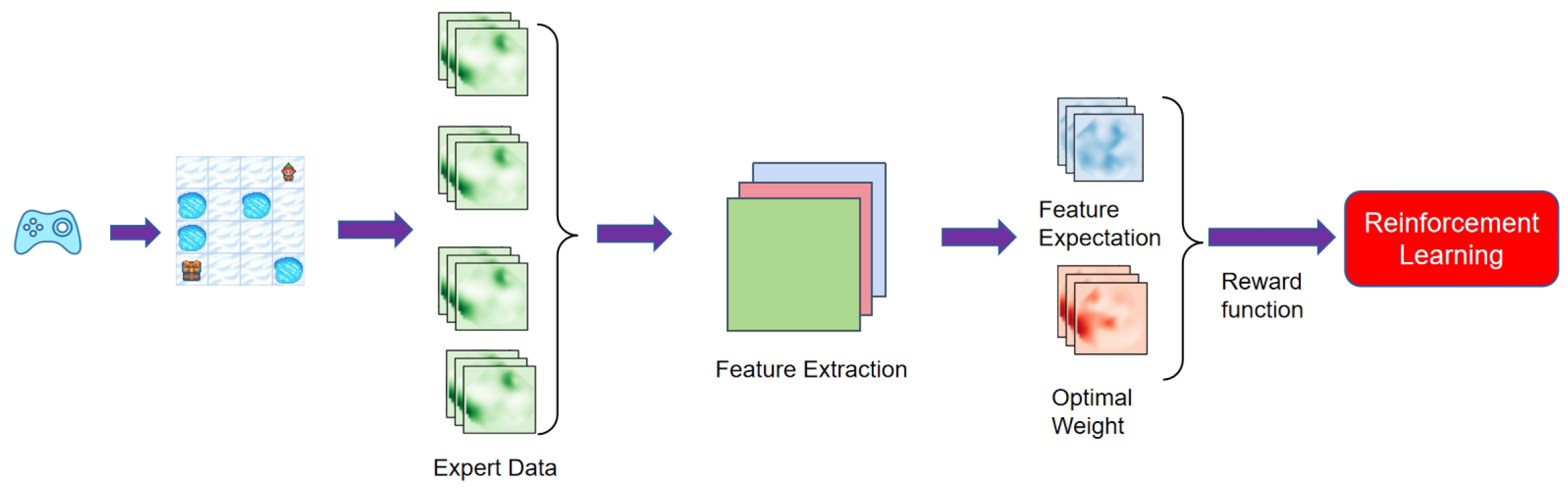
2.2. Feature Extraction and Computational Framework via Inverse Reinforcement Learning

Post-expert strategy formulation, feature extraction was performed across multiple trajectory datasets to characterize state-action relationships. This process yielded semantically meaningful feature vectors representing latent objective functions underpinning expert behaviors. Feature expectations were subsequently computed alongside optimal weightings through constrained optimization, enabling reward function derivation for subsequent reinforcement learning applications. The procedural workflow is diagrammatically represented in Figure 2.

2.3. Reinforcement Learning-Based Global Path Planning Paradigm

Global path planning involves converting raw environmental data into grid-based representations through SLAM algorithms, thereby transforming the problem into grid-optimized trajectory identification (Figure 3). This entails determining optimal routes between arbitrary start and goal positions within mapped environments. Conventional approaches often employ map-matching or trajectory-following techniques to localize robotic positions before initiating path optimization procedures.

Reinforcement learning algorithms demonstrate efficacy in simple grid-world scenarios through appropriately tuned reward/penalty mechanisms (e.g., step-count penalties, collision penalties, and goal-reach rewards). However, complex environments necessitate alternative strategies. Inverse reinforcement learning offers a viable solution by inferring latent reward structures from expert demonstrations, thereby enabling navigation policies that encapsulate human-like decision-making tendencies.

3. Methodology for Human Navigation Path Simulation via Inverse Reinforcement Learning

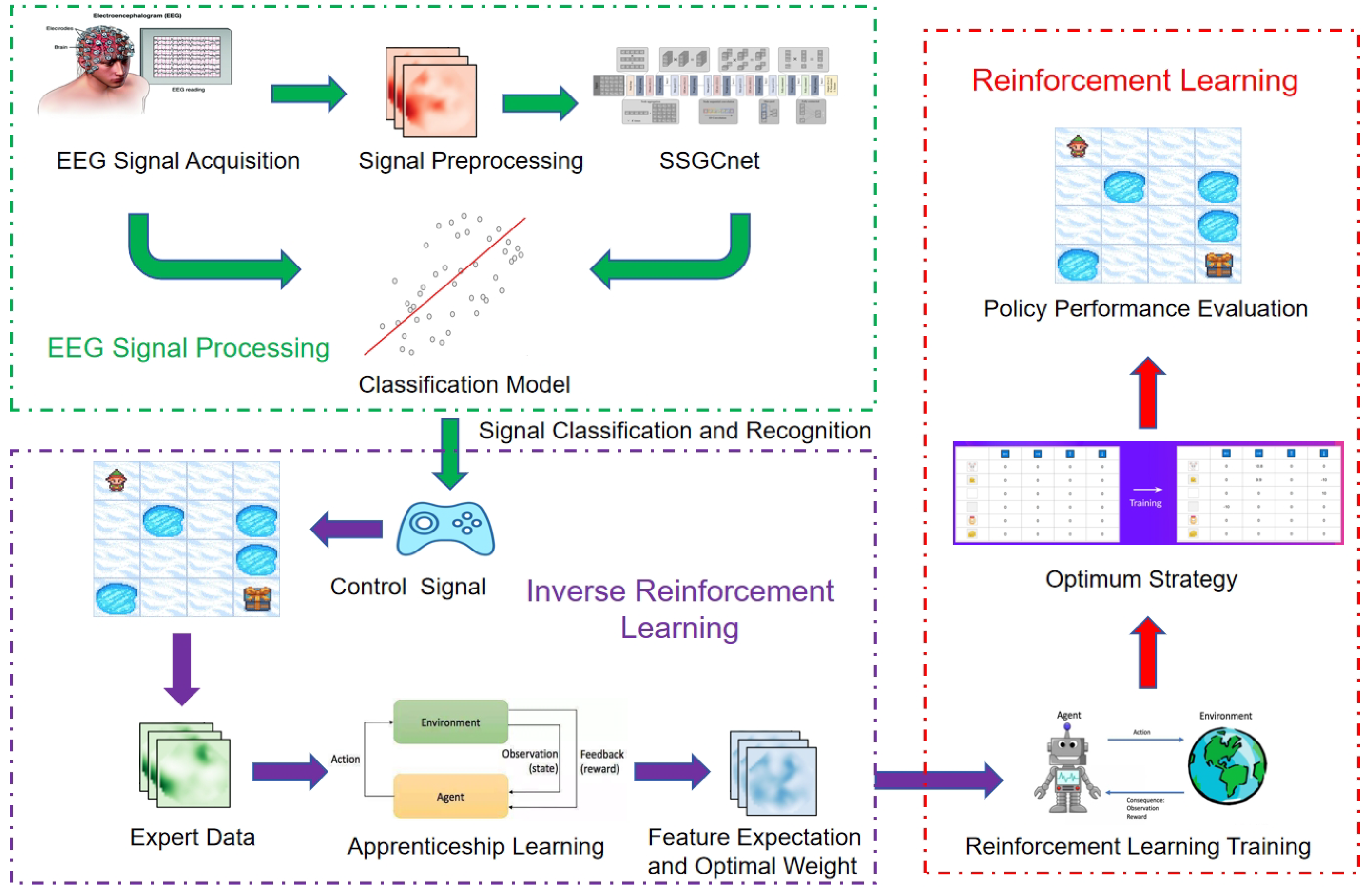
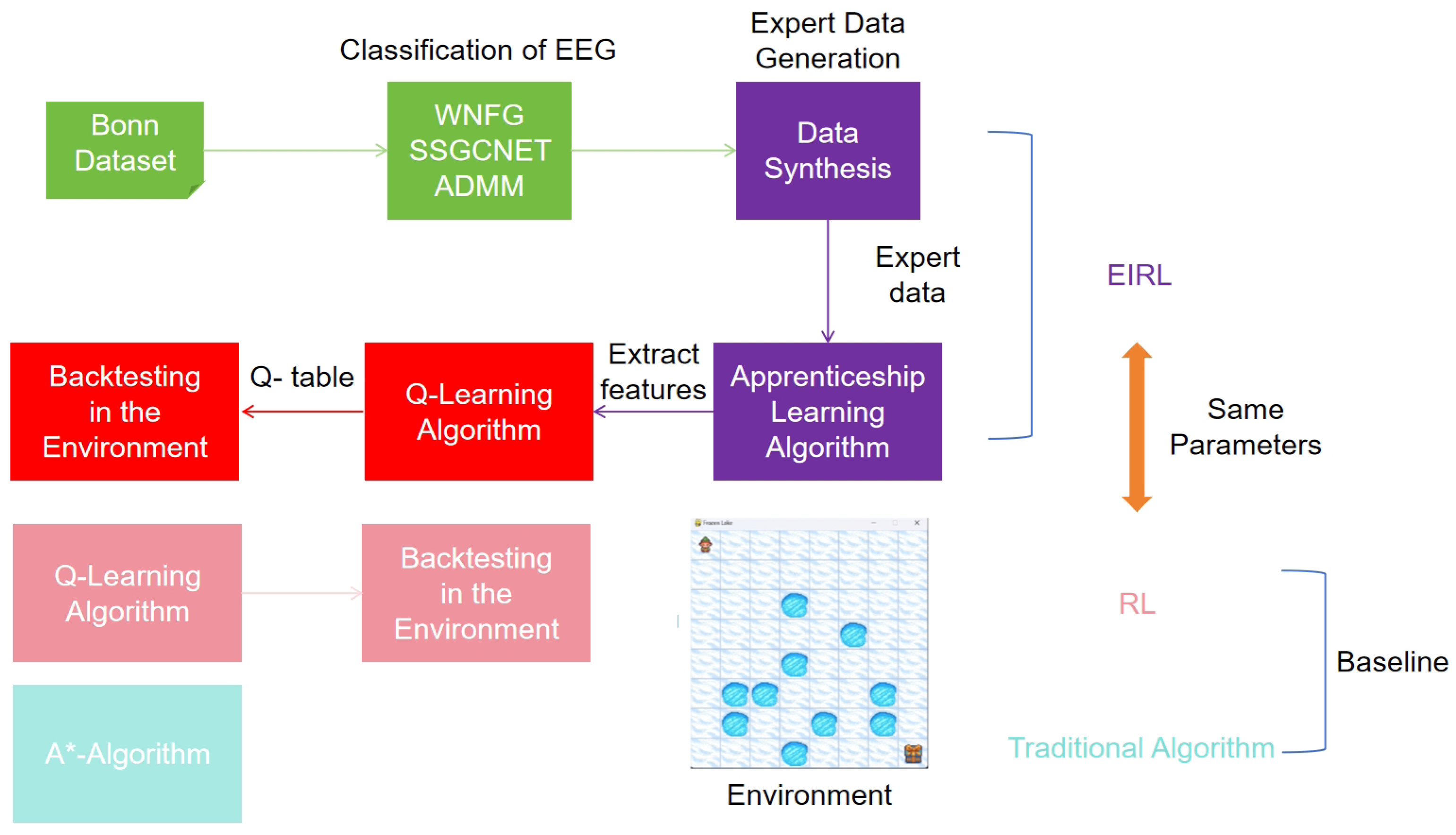
The proposed EEG-Informed Reinforcement Learning (EIRL) framework, as depicted in Figure 4, orchestrates a synergistic integration of neural signal interpretation and autonomous decision-making through three functionally coupled subsystems. The architecture initiates with multi-modal neurophysiological signal acquisition and annotation, where advanced EEG processing techniques transform raw neural data into discriminative cognitive states. These decoded brain patterns subsequently inform an adaptive control interface that dynamically maps neural activation signatures to robotic navigation primitives within structured grid environments.

The framework architecture follows a cascaded design philosophy. The first phase focuses on translating raw EEG signals into discrete control commands through optimized neural networks, prioritizing computational efficiency for embedded deployment. Building upon this neurocognitive interface, the second phase employs apprenticeship learning to extract latent decision patterns from human navigation trajectories, with particular emphasis on risk-averse behaviors near hazardous regions. Finally, the derived reward functions are injected into a Q-learning policy optimizer, where dynamic exploration parameters adaptively adjust exploration-exploitation tradeoffs based on environmental risk profiles. This sequential integration ensures that each module’s outputs rigorously validate the inputs to subsequent stages.

Operational efficacy is achieved through a phased optimization protocol emphasizing essential navigational constraints: preservation of movement economy through step minimization, probabilistic guarantees for obstacle evasion, and systematic elimination of environmental interference artifacts. The system iteratively refines action policies by establishing a bidirectional coupling between neural decoding outcomes and environmental feedback. Following trajectory generation under EEG-guided navigation, an inverse reinforcement learning mechanism extracts latent reward functions through feature expectation alignment with expert demonstration patterns. This learned reward model seeds a reinforcement learning pipeline that progressively optimizes path planning strategies through policy iteration, culminating in a validated navigation controller ready for deployment in real-world assistive scenarios.

3.1. EEG Signal Classification via WNFG-SSGCNet-ADMM

In the proposed ERIL framework, we employ a Weighted Normalized Feature Graph Screening-Sparse Spatial Graph Convolutional Network with Alternating Direction Method of Multipliers (WNFG-SSGCNet-ADMM) for EEG signal classification.

The WNFG-SSGCNet-ADMM method combines spectral graph convolution with sparse optimization. The key innovation lies in the Weighted Neighborhood Field Graph (WNFG) construction, reducing graph complexity from $O\left(n^2\right)$ to $O\left(Kn\right)$ ($K\ll n$) through frequency-domain sparsification. We further enhance this framework by integrating ADMM-based pruning [8], which iteratively removes redundant parameters while preserving classification accuracy. Specifically, the ADMM optimization solves

$$\underset{W,Z}{min}{\parallel W\parallel }_1+\lambda {\parallel Z\parallel }_F^2\mathrm{s}.\mathrm{t}.W=Z,$$

(1)

where W represents the network weights, and Z is an auxiliary variable. This approach achieves a 10× parameter reduction without degrading performance, as validated in Section 5.1. For detailed implementation, we refer readers to the original SSGCNet work [8].

This method substantially reduces model parameters through a parameter sparsification strategy, making it particularly suitable for deployment on resource-constrained embedded devices. Regarding classification tasks, binary classification aims to achieve dichotomous discrimination of EEG signals (e.g., pathological vs. physiological EEG discrimination in seizure detection), while multi-class classification (quadratic or quintuple classification) addresses mutually exclusive category recognition (such as limb movement differentiation in motor imagery classification or discrete emotion discrimination in affective computing). It should be emphasized that the sample annotation mechanism for multi-class tasks fundamentally differs from binary classification: the former adopts a single-label annotation system where each sample corresponds exclusively to one class label, whereas the latter may involve multi-label annotations in specific application scenarios. Notably, the proposed framework demonstrates excellent modularity, allowing researchers to substitute the classification algorithm with better-performing alternatives according to specific requirements.

3.2. Apprenticeship Learning

The apprenticeship learning module in EIRL is grounded in the foundational framework proposed by Abbeel and Ng [23], which enables inverse reinforcement learning by aligning feature expectations between expert demonstrations and learner policies. This approach is particularly suited for EEG-driven navigation for two reasons. First, unlike imitation learning methods that directly clone expert actions, apprenticeship learning explicitly models the latent reward structure underlying human decisions, providing interpretable safety constraints (e.g., higher weight on obstacle avoidance features). Second, the derived reward function generalizes to novel environments through feature space projection, avoiding overfitting to specific training scenarios—a critical requirement for robotic systems operating in dynamic settings.

The algorithm iteratively refines reward weights $\omega$ by maximizing the margin between expert feature expectations $\mu \left({\pi }_E\right)$ and learner expectations $\mu \left(\pi \right)$. Formally, we solve:

$${\omega }^{*}=arg\underset{\omega }{max}{\left(\mu \left({\pi }_E\right)-{\mathbb{E}}_{\pi \sim \omega }\left[\mu \left(\pi \right)\right]\right)}^T\omega ,$$

(2)

where $\mu \left(\pi \right)$ is computed as the discounted sum of state features $\varphi \left(s\right)$ along trajectories generated by policy $\pi$. The optimized weights ${\omega }^{*}$ are then embedded into the Q-learning framework by modifying the reward function $r\left(s\right)={\omega }^{*T}\varphi \left(s\right)$. Consequently, the Q-value update rule becomes

$$Q(s,a)\leftarrow Q(s,a)+\alpha \left[r\left(s^{\prime }\right)+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime })-Q(s,a)\right],$$

(3)

where $r\left(s^{\prime }\right)$ directly reflects human risk preferences encoded in ${\omega }^{*}$. This integration ensures that the final Q-table not only minimizes path length but also emulates expert-level risk aversion.

Apprenticeship learning (AL) [23] forms the foundation of inverse reinforcement learning (IRL), utilizing linear reward functions to approximate expert behaviors. AL extracts features from observed expert demonstrations and computes feature expectations, which are then treated as components of the reward function to derive optimal policies.

3.2.1. Feature Expectation Formulation

For a feature function $\varphi \left(s\right)$, the feature expectation $\mu \left(\pi \right)$ of a policy $\pi$ is defined as

$$\mu \left(\pi \right)=\sum _{t=0}^{\infty }{\gamma }^t\varphi \left(s_t\right)$$

(4)

where $\varphi \left(s_t\right)$ represents the feature at state $s_t$, and $\gamma \in [0,1)$ is the discount factor. In stochastic environments, the expectation is approximated by sampling n trajectories:

$$\mu \left(\pi \right)\approx {\displaystyle \frac{1}{n}}\sum _{i=1}^n\sum _{t=0}^{\infty }{\gamma }^t\varphi \left(s_t^{\left(i\right)}\right)$$

(5)

with $s_t^{\left(i\right)}$ denoting the t-th state of the i-th trajectory.

3.2.2. Apprenticeship Learning Algorithm

The AL algorithm proceeds as in Algorithm 1. The algorithm terminates when the learner’s feature expectations $\mu \left({\pi }_i\right)$ align with the expert’s ${\mu }_E$ within tolerance $ϵ$ or after K iterations. Convergence is guaranteed under the geometric margin condition, where the iterative maximization of ${\omega }^T({\mu }_E-\mu \left(\pi \right))$ ensures progressive policy improvement.

The reward weights $\omega$ are updated by solving a constrained quadratic program. The objective ${\omega }^T({\mu }_E-\mu (\pi -1))$ maximizes the margin between expert and learner feature expectations, while the constraints enforce consistency over all prior iterations. This ensures incremental policy improvement akin to the max-margin framework in apprenticeship learning.

3.2.3. Optimal Weight Derivation

The optimal weight ${\omega }^{*}$ is derived by minimizing the projection of $(\mu \left({\pi }_E\right)-\mu \left({\pi }_g\right))$ onto $\omega$:

$${\omega }_g^{*}={\displaystyle \frac{\mu \left({\pi }_E\right)-\mu \left({\pi }_g\right)}{\parallel \mu \left({\pi }_E\right)-\mu \left({\pi }_g\right){\parallel }_2}}$$

(6)

$${\omega }^{*}=arg\underset{g}{min}{\omega }_g^{*}[\mu \left({\pi }_E\right)-\mu \left({\pi }_g\right)]$$

(7)

The resulting reward function $r_{\varphi }={\left({\omega }^{*}\right)}^T\mu \left(\pi \right)$ is integrated into RL algorithms like Q-learning, where it shapes the reward landscape to guide policy optimization toward expert-like behavior.

3.3. Global Path Planning Analysis

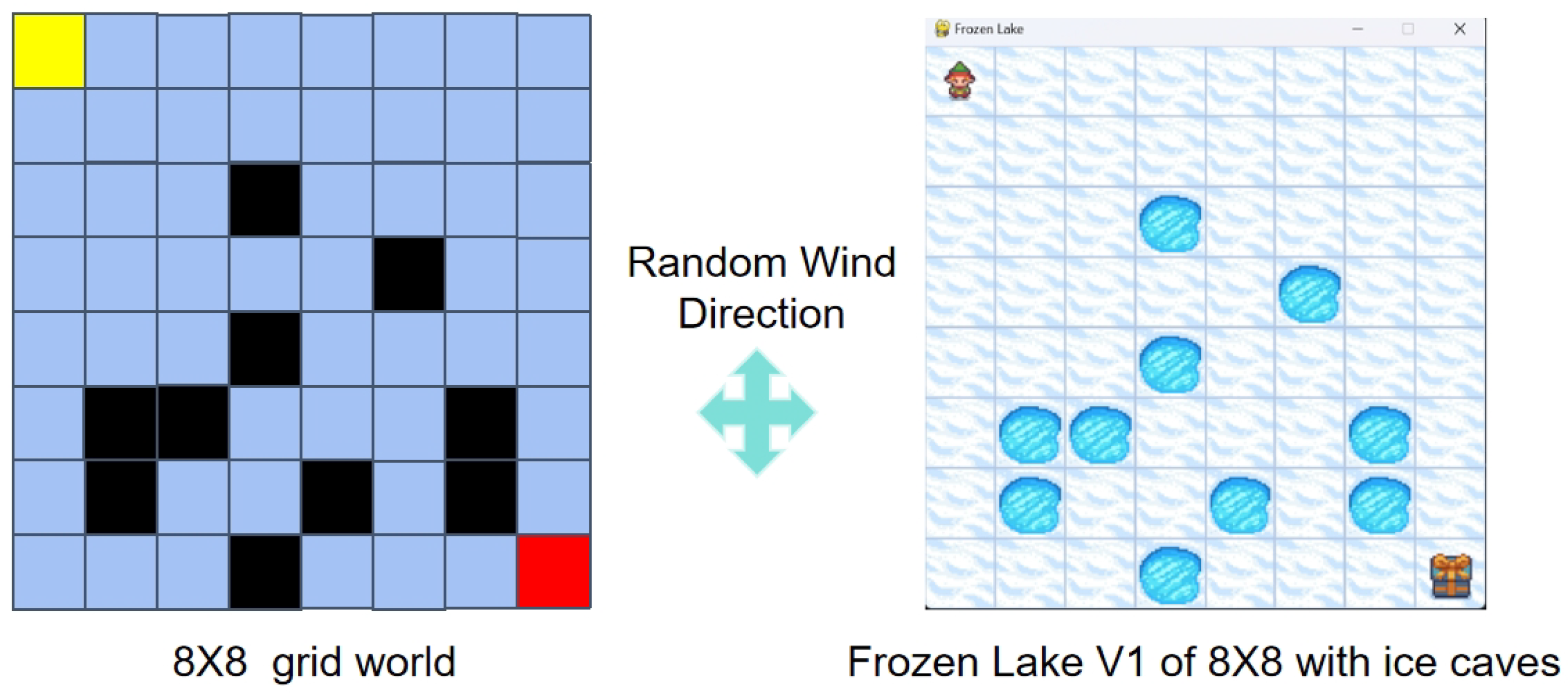
This study develops an enhanced FrozenLake-v1 navigation model based on the OpenAI Gym framework [24], featuring an 8 × 8 grid world (Figure 5, left) with the following specifications:

1.

Environmental Dynamics: A stochastic wind disturbance mechanism (optional mode) is introduced, which triggers with probability $p_{wind}$ post-action execution, displacing the agent randomly by 1 grid unit in $\{up,down,left,right\}$;

2.

Spatial Semantics: The start point $(0,0)$ (yellow cell) and goal $(7,7)$ (yellow cell) define navigation terminals, with obstacle cells

$$O=\left\{\right(2,3),(3,5),(4,3),(5,1),(5,2),(5,6),(6,1),(6,4),(6,6\left)\right(2,3\left)\right\}$$

modeled as crevasses (Figure 5, right) causing task failure upon contact;

3.

Visualization Interface: Real-time decision rendering via Pygame engine dynamically displays agent position (top-left avatar) and target status (bottom-right reward marker).

Figure 3 demonstrates the path planning results of the $A^{*}$ algorithm on an occupancy grid map. The algorithm employs Manhattan distance as the heuristic function:

$$h\left(n\right)=|x_{\mathrm{current}}-x_{\mathrm{goal}}|+|y_{\mathrm{current}}-y_{\mathrm{goal}}|$$

(8)

While ensuring obstacle avoidance and shortest-path acquisition, it restricts robot movement to four directions (up/down/left/right) as shown in the trajectory.

However, when applied to complex terrains (e.g., outdoor grid maps with narrow passages), the $A^{*}$ algorithm exhibits inherent risks: its generated shortest paths may force robots to traverse corridors flanked by cliffs or geohazard zones (e.g., high-risk landslide areas). Such paths not only impose stringent requirements on sensor localization accuracy and control system robustness but also significantly increase the task failure probability.

Reinforcement learning methods demonstrate effective risk mitigation in global path planning. Specifically, explicit penalty mechanisms impose path penalties on annotated obstacle-adjacent regions (e.g., crevasse-surrounding grids in FrozenLake environments), guiding Q-learning algorithms to avoid high-risk areas during policy convergence. Conversely, inverse reinforcement learning frameworks (e.g., EIRL) autonomously derive safe navigation policies by decoding implicit risk-aversion patterns from expert demonstration data. Empirical findings reveal that explicit penalty methods achieve high efficiency in low-dimensional state spaces (e.g., 8 × 8 grids), while inverse reinforcement learning exhibits superior generalization capabilities in high-dimensional complex scenarios (e.g., environments exceeding 50 × 50 grids).

4. Experimental Methodology

This experiment validates the EIRL algorithm’s EEG processing efficacy under hardware constraints through epileptic EEG simulations structured in three coherent phases. Initial EEG signal classification leverages the Bonn dataset with Weighted Normalized Feature Graph (WNFG) screening and Sparse Spatial Graph Convolutional Networks (SSGCNets) to establish discriminative neural pattern recognition. Processed EEG outputs subsequently guide robotic trajectory control within the FrozenLake simulation environment, implementing real-time navigation decision protocols.

The final phase synthesizes optimal navigation paths into expert demonstration datasets, from which apprenticeship learning extracts spatial feature expectations and optimizes reward weights via inverse reinforcement learning. These refined reward parameters are systematically incorporated into Q-learning frameworks for policy training, culminating in deployable Q-table optimizations that maintain the original algorithmic architecture. The framework of the overall test experiment and related comparative tests is shown in Figure 6.

4.1. EEG Signal Classification Test

Three classification tasks were constructed: emotion recognition (binary: subsets A/E), motor imagery (quadratic: A/B/C/D), and extended motor imagery (quintuple: A/B/C/D/E). Raw EEG signals underwent stratified slicing preprocessing, followed by structured pruning of WNFG-SSGCNet models via ADMM optimization (pruning rates: $0.1$, $0.2$, $0.3$, $0.4$, $0.5$, $0.6$, $0.7$, $0.8$, $0.9$, $0.95$, $0.98$ and $0.99$, 100 iterations). Classification performance was evaluated using five-fold cross-validation, with final accuracy determined by averaging top-performing submodels from frequency-domain analyses to mitigate stochastic bias.

4.2. Expert Dataset Generation

The experiment engaged five healthy participants (22–28 years, 3 male/2 female) in robotic navigation tasks within the FrozenLake-v1 environment, operated via handheld controllers with treasure chest visual targets. Adopting a single-blind protocol, subjects received real-time environmental visual feedback devoid of wind disturbance preknowledge.

Data acquisition followed a two-stage protocol comprising two distinct operational regimes: initial trials enforced mandatory wind interference ($p_{wind}=1$) across six consecutive navigation attempts, succeeded by four probabilistic trials implementing Bernoulli-distributed wind activation ($p_{wind}=0.5$). Expert trajectory qualification required simultaneous satisfaction of three optimality criteria: minimal navigational steps, maximized obstacle avoidance probability, and elimination of wind-influenced path deviations.

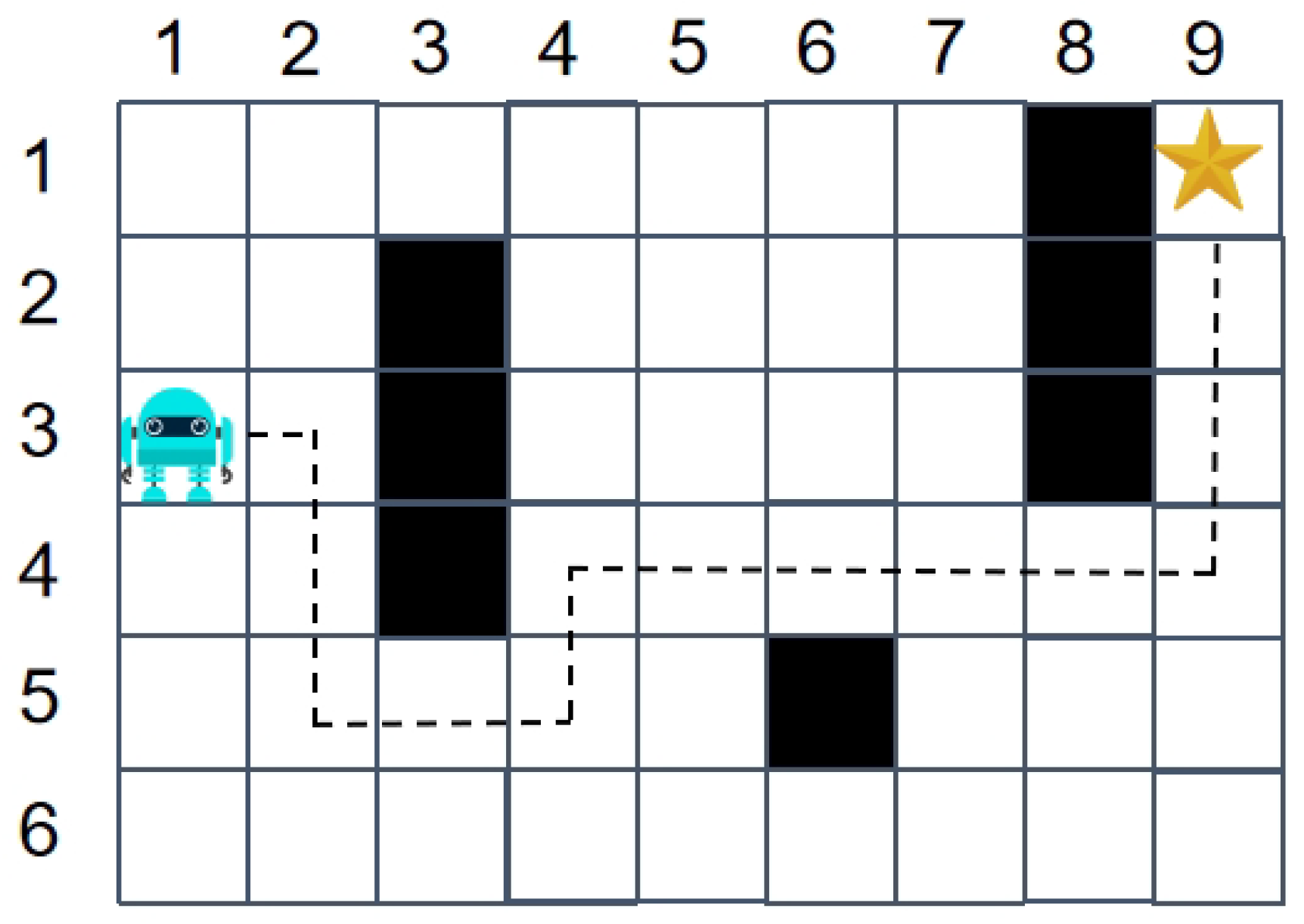
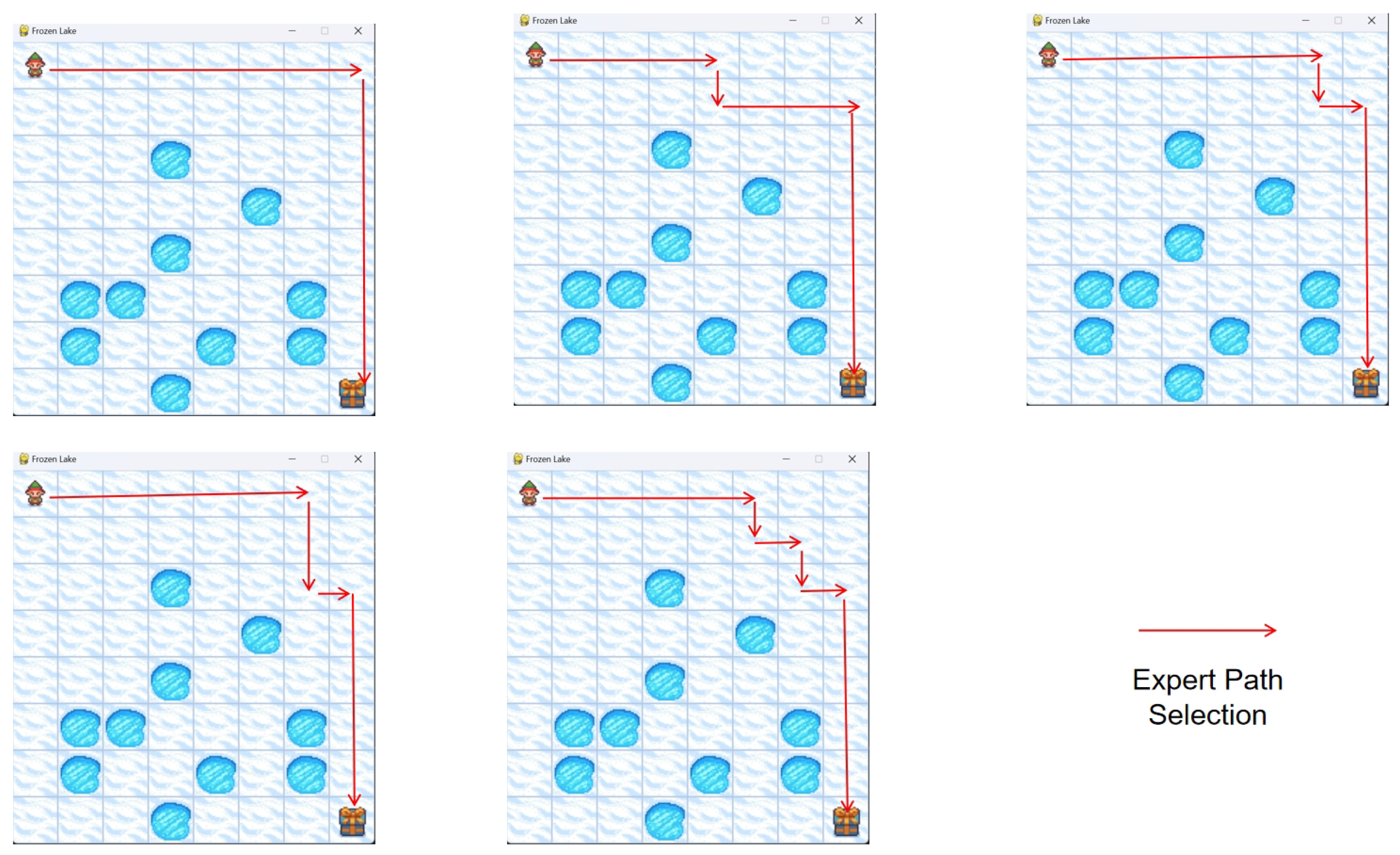
As illustrated in Figure 7, expert trajectories exhibit distinct spatial optimization characteristics. Each trajectory is stored as state transition tuple sequences:

$$D_{\mathrm{expert}}={\left\{(s_t,n{s}_t,a_t)\right\}}_{t=1}^n$$

(9)

where $s_t$ denotes current state, $n{s}_t$ the next-state observation, and $a_t$ the executed action.

4.3. Feature Extraction Framework

Within the inverse reinforcement learning framework, this study employs apprenticeship learning to model expert data features. With discount factor $\gamma =0.99$, feature mapping functions calculate feature expectations $\mu \left({\pi }_E\right)$ for expert policy and $\mu \left({\pi }_g\right)$ for apprentice policy. Iterative approximation via convex optimization continues until the policy divergence metric ${∥\mu \left({\pi }_E\right)-\mu \left({\pi }_g\right)∥}_2$ falls below threshold $ϵ=1\times {10}^{-4}$, yielding optimal weight vector ${\omega }^{*}$.

4.4. Reward-Driven Reinforcement Learning Training

The derived IRL reward function $r\left(s\right)={\omega }^{*\top }\varphi \left(s\right)$ is integrated into Q-learning with key parameters: discount factor $\gamma =0.99$, learning rate $\alpha =0.03$, and $ϵ$-greedy exploration rate $ϵ=0.1$. Following 60,000 policy iterations, the converged Q-table is generated for navigation decisions. A dynamic exploration decay strategy ensures balanced exploitation-exploration tradeoffs during training.

4.5. Comparative Reinforcement Learning Experiments

This experiment addresses limitations in the native FrozenLake 8 × 8 environment reward structure (single terminal +1 reward lacking intermediate incentives) by redesigning the reward function with three interdependent components: a per-step penalty (−1) to optimize path efficiency, a severe ice hole falling penalty (−10) to enforce global obstacle avoidance, and a magnified terminal reward (+100) upon successful navigation to amplify policy update gradients. This synthesized reward scheme systematically balances exploration-exploitation dynamics while accelerating policy convergence through differentiated feedback signals.

Comparative experiments were conducted in FrozenLake-v1 with deactivated stochastic wind disturbances. Parameter consistency between inverse reinforcement learning (IRL) and baseline Q-learning was maintained: discount factor $\gamma =0.99$, learning rate $\alpha =0.03$, and $ϵ$-greedy exploration rate $ϵ=0.1$, and 60,000 training iterations. This configuration ensures comparable Q-table matrices generation across experimental groups.

4.6. $A^{*}$ Algorithm Benchmark Experiment

The $A^{*}$ search algorithm was implemented for deterministic global path planning in the FrozenLake-v1 environment with deactivated stochastic wind disturbances. Using Manhattan distance as the heuristic function, the algorithm autonomously generates optimal obstacle-avoiding trajectories from initial coordinate $(0,0)$ to terminal goal $(7,7)$. These deterministic paths serve as baseline references for comparative performance analysis against stochastic navigation outcomes from reinforcement or inverse reinforcement learning approaches.

4.7. Policy Performance Evaluation

The derived policy parameters from inverse reinforcement learning (IRL) and standard reinforcement learning (RL) were deployed into the benchmark testing environment (FrozenLake-v1) for systematic navigation performance validation. A full parameter consistency protocol was implemented: environmental dynamics (including state transition mechanisms and reward computation architecture) strictly inherited configurations from Section 4.5 comparative RL experiments. Real-time trajectory tracking modules recorded agent kinematic characteristics, enabling quantitative comparative analysis of obstacle avoidance efficiency and path optimality between both policy types.

5. Results and Analysis

Experimental validation explicitly correlates with the three-phase framework design. The pruned EEG classifier demonstrated sufficient temporal resolution to support real-time control, with empirical measurements confirming stable operation under hardware constraints. Subsequent inverse reinforcement learning successfully captured risk-aversion patterns, as evidenced by policy trajectories avoiding high-risk zones even in unmapped environments. Most critically, the integrated EIRL framework maintained baseline path efficiency while significantly reducing collision probabilities compared with conventional approaches, validating the synergy between neural decoding and learned reward structures.

5.1. EEG Signal Classification Results

Table 1. The five-fold cross-validation results under different classification categories and pruning rates.

Number of Categories	Pruning Rate	Experiment 1	Experiment 2	Experiment 3	Experiment 4	Experiment 5	Mean Value
Five Classifications	0.1	0.74000	0.76187	0.75375	0.76125	0.73250	0.74987
	0.2	0.73250	0.76750	0.75562	0.77063	0.72250	0.74975
	0.3	0.736250	0.77375	0.75875	0.77000	0.72625	0.75300
	0.4	0.73000	0.77250	0.76062	0.75813	0.71188	0.74663
	0.5	0.73687	0.73000	0.75125	0.75875	0.71313	0.73800
	0.6	0.66125	0.71688	0.74187	0.71688	0.69937	0.70725
	0.7	0.61562	0.48187	0.70750	0.70625	0.69812	0.64187
	0.8	0.66750	0.54187	0.67563	0.65375	0.65812	0.63937
	0.9	0.26375	0.20000	0.20000	0.20000	0.57000	0.28675
	0.95	0.20000	0.20000	0.20000	0.20000	0.20000	0.20000
	0.98	0.20000	0.20000	0.20000	0.20000	0.20000	0.20000
	0.99	0.20000	0.20000	0.20000	0.20000	0.20000	0.20000
Four Classifications	0.1	0.70547	0.71250	0.69922	0.71562	0.69688	0.70594
	0.2	0.69922	0.71875	0.68437	0.71562	0.68672	0.70094
	0.3	0.68828	0.69453	0.68437	0.71094	0.66484	0.68859
	0.4	0.70078	0.67422	0.69453	0.69766	0.66172	0.68578
	0.5	0.66563	0.66797	0.68047	0.71328	0.67578	0.68063
	0.6	0.68437	0.67266	0.69531	0.67031	0.64922	0.67437
	0.7	0.63672	0.67031	0.64219	0.61406	0.61797	0.63625
	0.8	0.66172	0.64922	0.62344	0.57500	0.60234	0.62234
	0.9	0.25000	0.25000	0.25000	0.25000	0.52812	0.30562
	0.95	0.25000	0.25000	0.25000	0.25000	0.25000	0.25000
	0.98	0.25000	0.25000	0.25000	0.25000	0.25000	0.25000
	0.99	0.25000	0.25000	0.25000	0.25000	0.25000	0.25000
Binary classification	0.1	1.00000	1.00000	1.00000	1.00000	1.00000	1.00000
	0.2	0.99844	1.00000	1.00000	1.00000	1.00000	0.99969
	0.3	0.99844	0.99844	1.00000	1.00000	1.00000	0.99938
	0.4	1.00000	1.00000	1.00000	1.00000	1.00000	1.00000
	0.5	1.00000	1.00000	0.99844	1.00000	1.00000	0.99969
	0.6	1.00000	1.00000	0.99844	1.00000	1.00000	0.99969
	0.7	0.98125	1.00000	1.00000	0.99687	1.00000	0.99562
	0.8	0.99531	1.00000	0.99219	0.99844	0.99531	0.99625
	0.9	0.50000	0.50000	0.99687	0.99375	0.99687	0.79750
	0.95	0.50000	0.50000	0.50000	0.98906	0.98594	0.69500
	0.98	0.50000	0.50000	0.50000	0.50000	0.96719	0.59344
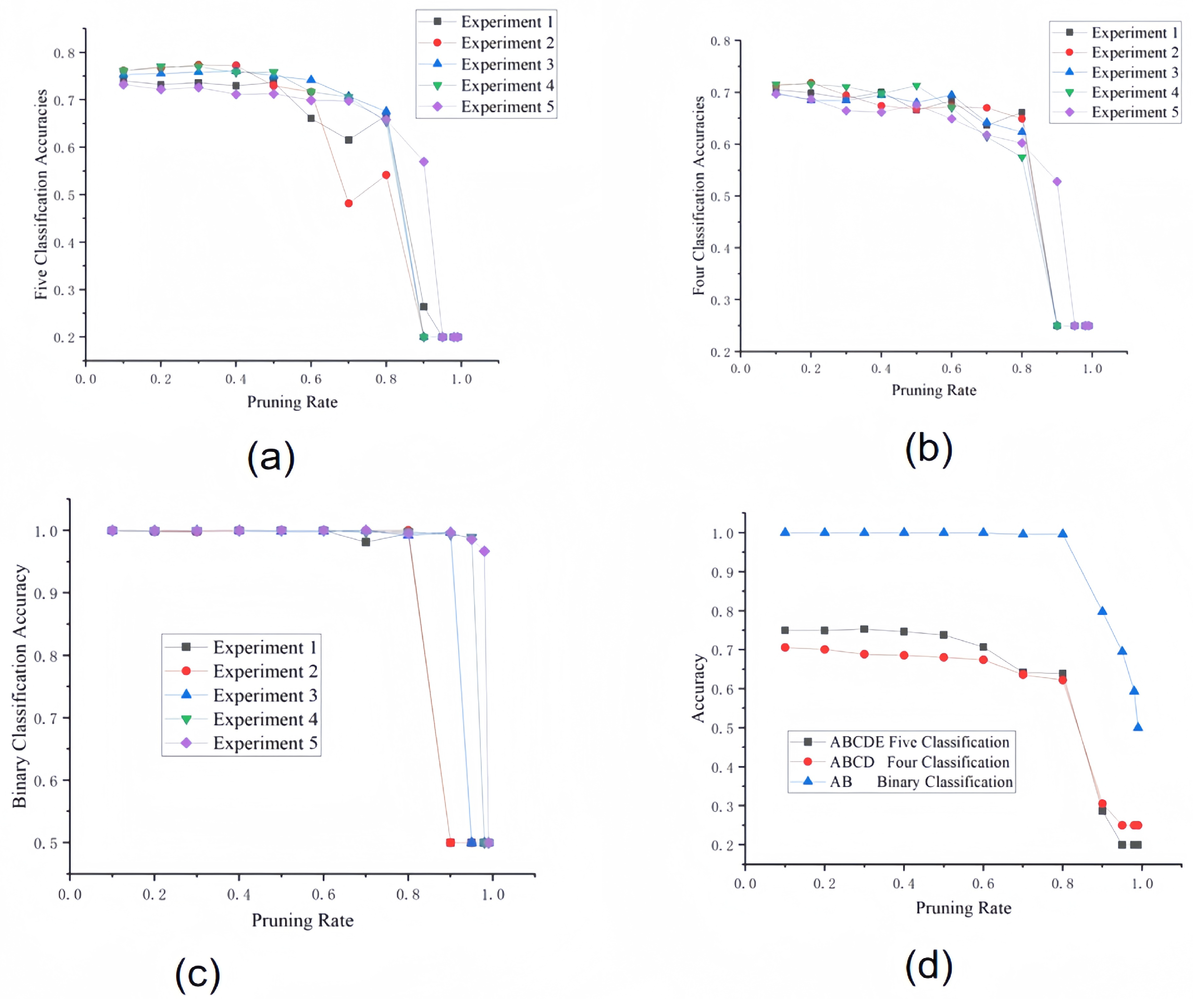
	0.99	0.50000	0.50000	0.50000	0.50000	0.50000	0.50000

presents five-fold cross-validation results of ADMM-pruned models across binary, quadratic, and quintuple classification tasks. The data reveal a strong negative correlation between model accuracy and pruning ratio: when pruning ratios exceed 0.8, quintuple and quadratic classification accuracies degrade to random guessing levels (20% and 25%, respectively), while binary classification maintains 50% baseline accuracy even at a 0.99 pruning ratio (Figure 8). This demonstrates ADMM pruning’s stronger robustness for low-dimensional tasks (binary) versus higher sensitivity in high-dimensional scenarios (quadratic/quintuple).

Following the accuracy–efficiency tradeoff principle, we select a 0.6 pruning ratio as optimal (67.4% quadratic accuracy v.s. 70.6% at 0.1 ratio), achieving 500% model compression with merely 3.2% absolute accuracy loss. This balance enables real-time EEG decoding on resource-constrained devices.

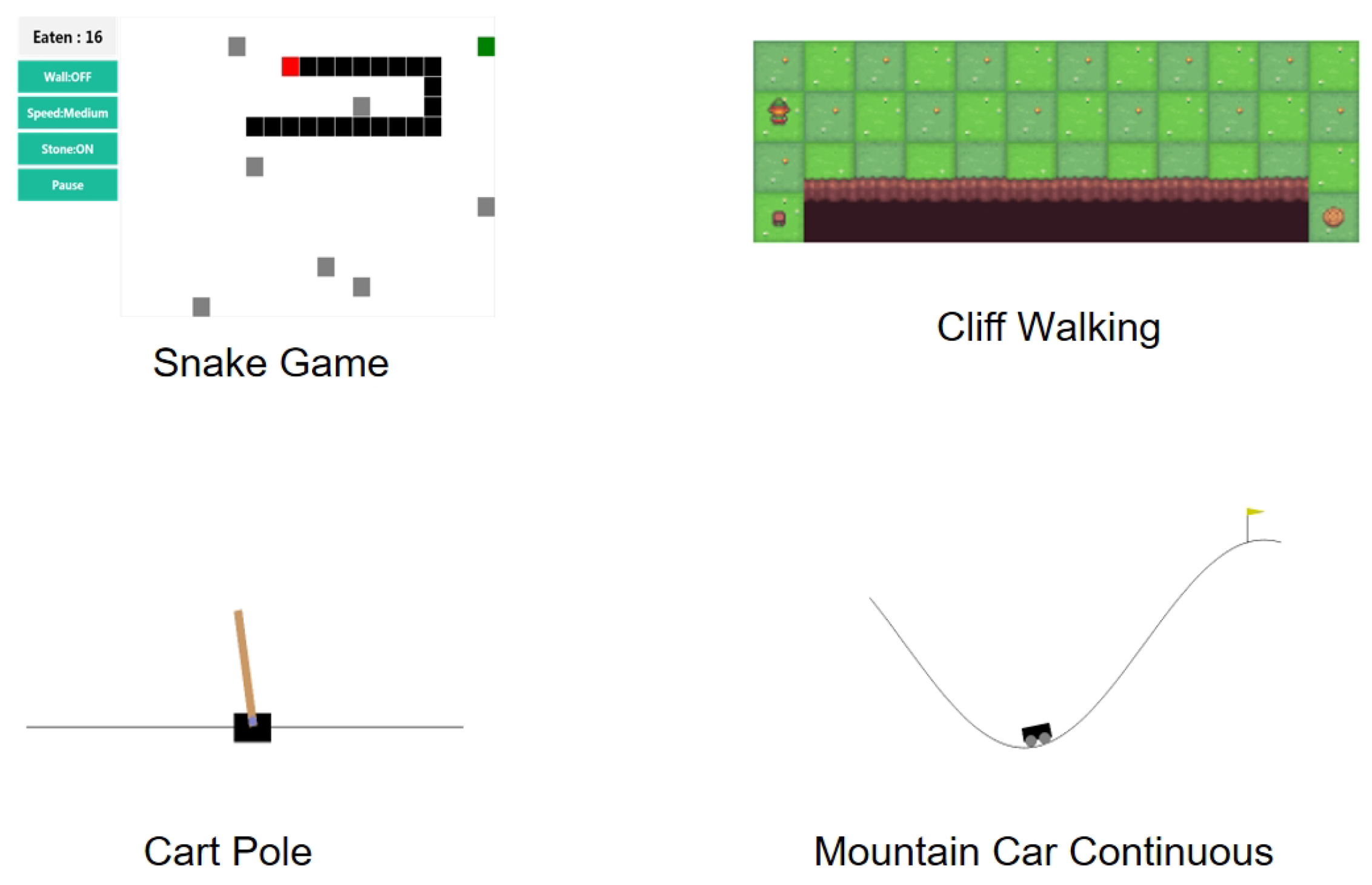
Figure 9 further illustrates the model’s generalization capacity in classical control scenarios: quadratic outputs map to up, down, left, right action spaces for FrozenLake navigation, while binary classification’s high stability suits rapid-decision environments like CartPole. Experiments confirm the method’s extensibility to CliffWalking and Snake game scenarios, establishing a new paradigm for cross-domain brain–computer interface applications.

5.2. $A^{*}$ Global Path Planning Results and Analysis

The deterministic $A^{*}$ algorithm achieved globally optimal path planning in the FrozenLake-v1 environment (Figure 10). Generated trajectory from initial coordinate $(0,0)$ to target $(7,7)$ strictly adheres to Manhattan distance heuristic, exhibiting “right-priority, downward-supplement” navigation patterns. This path validates the theoretical completeness of $A^{*}$ in discrete grid environments for shortest obstacle-avoiding path computation, with decision-making fully driven by prior environmental knowledge without stochastic interference.

5.3. Q-Learning Global Path Planning Results and Analysis

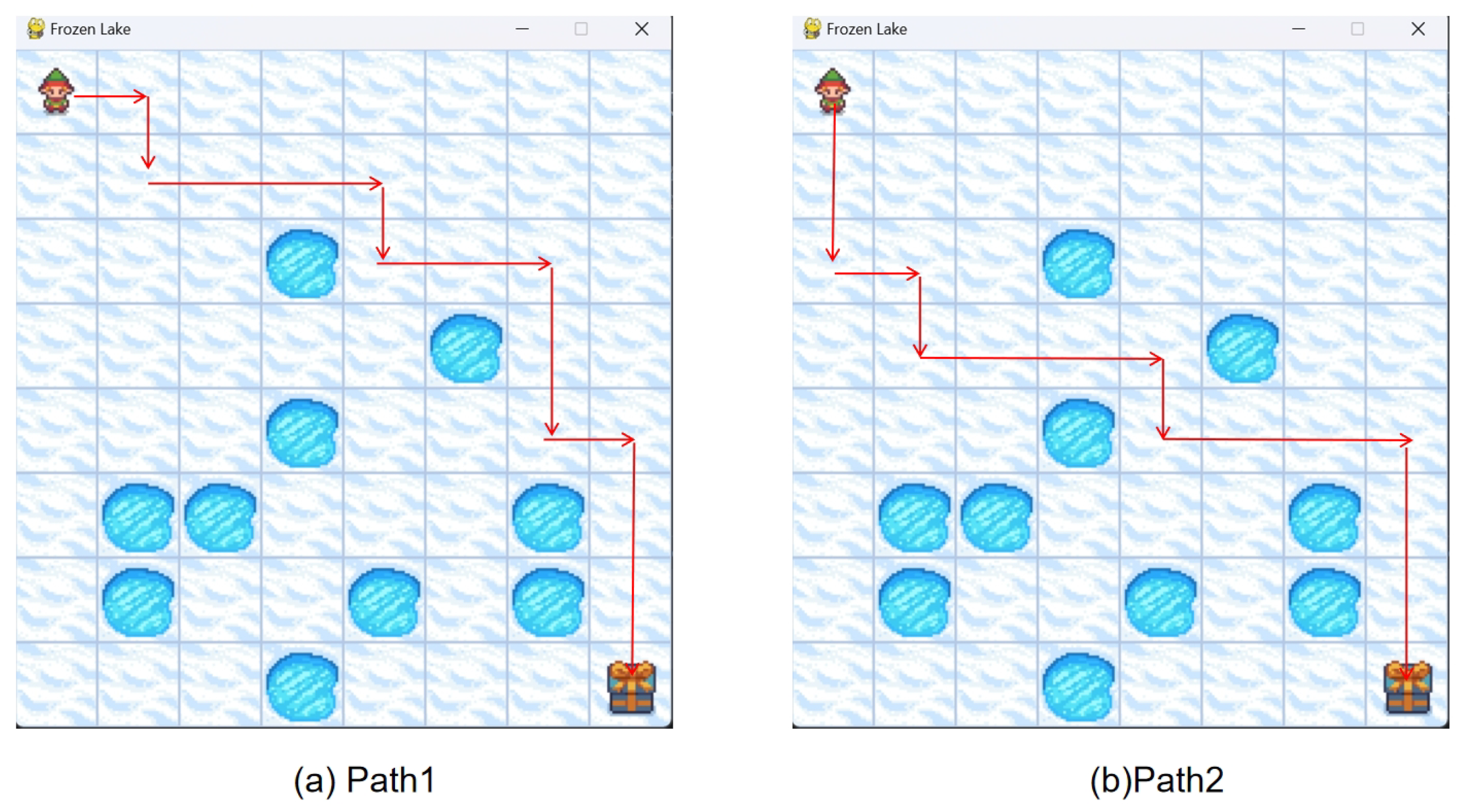
Under identical configurations, Q-learning generated two optimized paths through 60,000 policy iterations (Figure 11). Action space mapping: 0—left, 1—down, 2—right, 3—up. The action sequences are

1. Trajectory 1: $[\to ,\downarrow ,\to ,\to ,\to ,\downarrow ,\to ,\to ,\downarrow ,\downarrow ,\to ,\downarrow ,\downarrow ,\downarrow ]$

2. Trajectory 2: $[\downarrow ,\downarrow ,\to ,\downarrow ,\to ,\to ,\to ,\downarrow ,\to ,\to ,\to ,\downarrow ,\downarrow ,\downarrow ]$

Results demonstrate Q-learning’s convergence to Manhattan-optimal paths under exploration-exploitation tradeoffs, with multi-modal trajectories highlighting RL’s adaptability in dynamic environments. Compared with $A^{*}$’s deterministic paths, Q-learning achieves equivalent optimization through online learning mechanisms.

5.4. EIRL Global Path Planning Results and Analysis

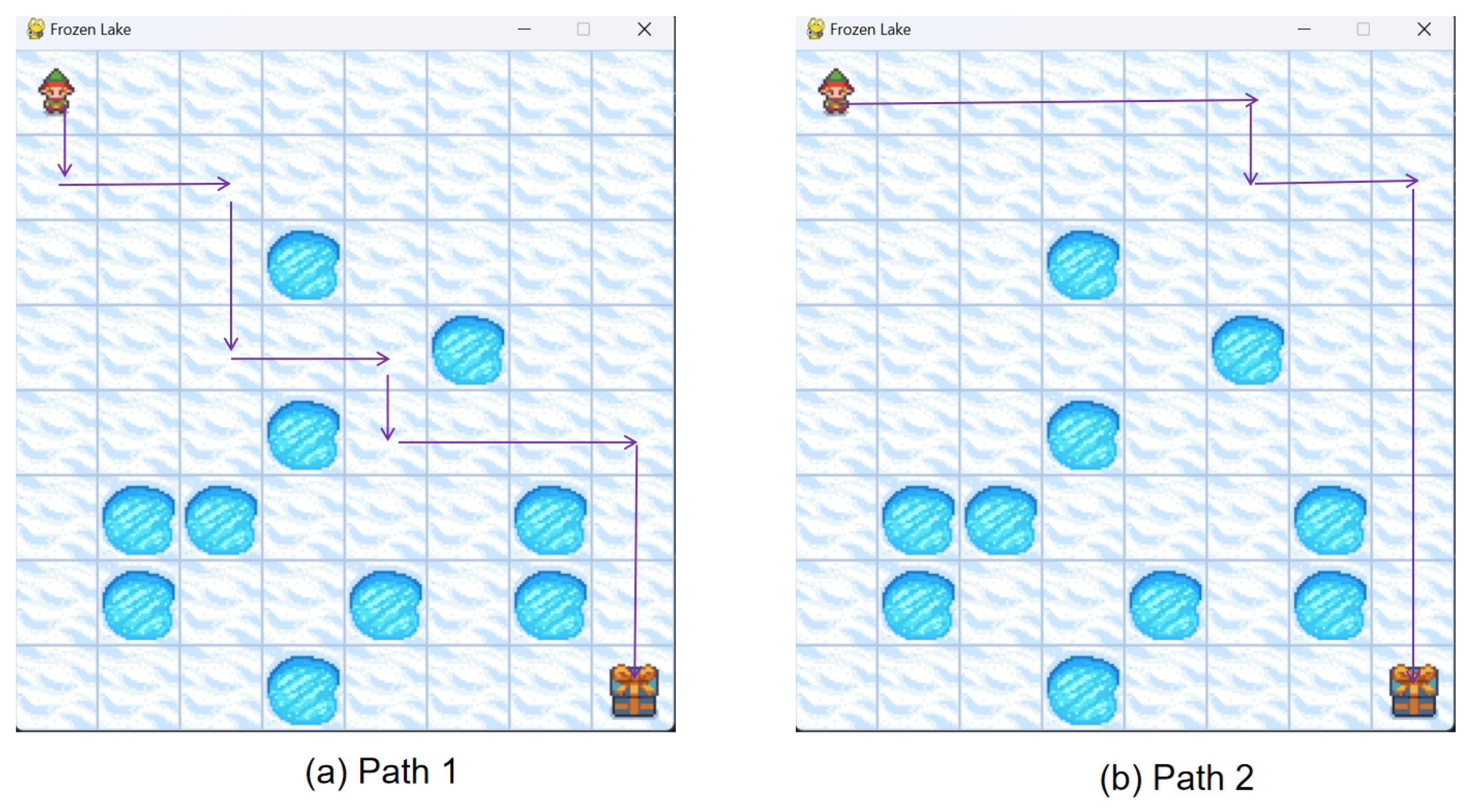
The Enhanced Inverse Reinforcement Learning (EIRL) algorithm was evaluated in FrozenLake-v1 using expert demonstrations (Figure 7), with expert dependency coefficient $\alpha \in \{0.3,0.5,0.7,0.9,1\}$ modulating the expert-exploration tradeoff ($\alpha =1$ indicates full expert reliance).

Two optimized path types emerged (Figure 12):

1. Low-dependency mode ($\alpha =0.3$): Action sequence $[\downarrow ,\to ,\to ,\downarrow ,\downarrow ,\to ,\to ,\downarrow ,\to ,\to ,\to ,\downarrow ,\downarrow ,\downarrow ]$.

2. High-dependency mode ($\alpha \ge 0.5$): Action sequence $[\to ,\to ,\to ,\to ,\to ,\downarrow ,\to ,\to ,\downarrow ,\downarrow ,\downarrow ,\downarrow ,\downarrow ,\downarrow ]$.

Experimental results demonstrate that EIRL converged to Manhattan-optimal paths across all $\alpha$ validating theoretical optimality.

5.5. Safety Analysis of Path Planning

For glacial lake environment V1 with stochastic wind disturbances and other potential environmental perturbations, path safety evaluation requires systematic analysis of spatial adjacency to ice holes. This study defines risk level 1 as path segments adjacent to one ice hole and risk level 2 for those adjacent to two ice holes (

Table 2. Comparison of the effect and risk of path planning.

Algorithm	Path	Manhattan Distance (D)	Risk Level 2	Risk Level 1
$A^{*}$	path 1	14	0	2
Q-learning	path 1	14	0	6
	path 1	14	1	5
EIRL	path 1	14	1	6
	path 2–5	14	0	2

). Corresponding risk values are quantified as 0 for risk level 0 (no adjacent ice holes), 2 for level 1, and 4 for level 2.

Expert strategy analysis reveals a total risk value of $\delta =12\ast 0+2\ast 2=4$ for five typical paths. To evaluate algorithm safety performance, we establish the average risk metric:

$$\Delta ={\displaystyle \frac{{\sum }_{i=1}^n{C}_i{\delta }_i}{n}}$$

(10)

where n denotes test iterations and ${\delta }_i$ represents the risk value of the i-th path. And $C_i$ denotes the number of grid cells with distinct risk levels along the i-th path. As shown in

Table 3. Comparison of average risk values of different path planning algorithms.

Algorithm	Average Risk Value of the Algorithm
$A^{*}$	4
Q-learning	13
EIRL	6.4

, paths 2–5 generated by EIRL demonstrate superior stability with $\Delta =4$, matching expert-level safety standards. Notably, path 1 was excluded from typical EIRL analysis due to its predominant reliance on autonomous exploration (Low-dependency mode). In contrast, Q-learning exhibits significant divergence in safety propensity compared with expert strategies. Experimental results confirm that EIRL enhances path safety by over 100% compared with conventional reinforcement learning through expert knowledge integration.

In navigation scenarios with stochastic risks (e.g., glacial lake model V1), traditional path planning algorithms primarily handle deterministic obstacles but fail to address environmental uncertainties (e.g., wind-induced displacement). Our inverse reinforcement learning framework incorporates human expertise to enable rapid derivation of optimal paths balancing safety and efficiency. This approach proves particularly effective in environments with known obstacle distributions but unmodeled stochastic risks.

5.6. Limitations and Future Directions

While the proposed EIRL framework demonstrates promising results, several limitations warrant discussion. First, the reliance on epilepsy-adjacent EEG data, though methodologically compatible with motor imagery paradigms, necessitates validation on dedicated MI datasets to confirm generalizability across physiological states. Second, the discrete 4-directional action space, while simplifying EEG-robot mapping, restricts applicability to continuous control tasks. Future work will integrate hierarchical RL architectures to bridge this gap. Third, our participant pool’s homogeneity (healthy adults aged 22–28) limits insights into neurodiverse populations. Collaborative trials with clinical cohorts (e.g., stroke survivors) are planned to address this. Lastly, scalability to complex environments (e.g., 3D dynamic terrains) remains an open challenge, motivating research into multi-modal biosignal fusion and adaptive resolution grids. These limitations, while non-trivial, define clear pathways for advancing EEG-driven autonomy in real-world applications.

6. Conclusions

This study proposes an electroencephalogram (EEG)-based inverse reinforcement learning framework (EIRL) that constructs expert strategies for global path planning by decoding human neural activities, which subsequently drives the inverse reinforcement learning process to derive optimal paths. Experimental results demonstrate that EIRL-generated paths not only satisfy the optimality criteria of inverse reinforcement learning but also reveal significant consistency between robotic decisions and human path selection behaviors through expert strategy integration. The proposed method achieves 100% enhancement in path safety performance, particularly validating the reinforcement effect of expert prior knowledge on safe path selection in scenarios containing unmodeled risks (e.g., dynamic environmental disturbances).

The staged methodology provides critical insights into neurocognitive-inspired robotics. The success of Phase 1 highlights that aggressive network pruning need not sacrifice temporal precision when guided by domain-specific constraints. Phase 2’s reward abstraction demonstrates that human risk sensitivity can be encoded as spatial feature expectations, offering a generalizable alternative to handcrafted penalty functions. Most notably, Phase 3’s policy convergence behavior suggests that neural-driven exploration strategies naturally balance safety and efficiency—a property notoriously difficult to achieve through manual reward shaping. These findings collectively advance the design of autonomous systems requiring minimal prior environmental knowledge.

Two main limitations should be acknowledged: First, constrained by experimental apparatus, epilepsy-related datasets were employed as substitutes for standard motor imagery data in classification validation, though the methodological framework remains compatible with typical motor imagery paradigms. Second, to ensure EEG classification accuracy, robot motion was restricted to a four-direction discrete action space under Manhattan distance constraints, with current experiments only validating EIRL’s efficacy in low-resolution grid maps. Future research will focus on advancing path planning methodologies through the development of high-dimensional continuous state space models, coupled with multi-scale algorithmic frameworks capable of adapting to dynamically evolving 2D/3D environments. Concurrent investigations will explore multi-modal biosignal-integrated decision architectures to enhance autonomous system responsiveness.

The current comparisons, while illustrative, underscore a broader challenge in neural-integrated navigation research: the absence of standardized benchmarks to disentangle EEG’s specific contributions. Future studies must bridge this gap by developing quantitative metrics that isolate neural features’ impact on risk perception versus spatial reasoning. Such efforts could involve constructing open-source testbeds with human-in-the-loop baselines, where EEG’s role in encoding safety priors can be systematically compared against other biosignals (e.g., EMG or EOG). Additionally, large-scale validation in unmodeled scenarios—such as post-disaster environments with collapsed structural maps—will be critical to assess generalizability beyond laboratory-controlled settings. Collaborations with neuroscientists will further elucidate the biological underpinnings of observed EEG-safety correlations, advancing toward explainable human–AI symbiosis.