A Method for Extracting Features of the Intrinsic Mode Function’s Energy Arrangement Entropy in the Shaft Frequency Electric Field of Vessels

Abstract

To address the challenge of detecting low-frequency electric field signals from vessels in complex marine environments, a vessel shaft frequency electric field feature extraction method based on intrinsic mode function energy arrangement entropy values is proposed, building upon a scaled model. This study initially establishes a measurement system for shaft frequency electric fields, utilizing a titanium-based oxide electrode to construct an equivalent dipole source simulating the shaft frequency electric field signals of different types of vessels. Subsequently, a comparative analysis of the time-domain and frequency-domain characteristics of signals after modal decomposition is conducted. A feature extraction method is then proposed that combines the maximum average energy of intrinsic mode functions with arrangement entropy values to achieve discrimination of target signals. Finally, the feasibility of the proposed method is validated through sea trials. The results indicate that the method can successfully screen different types of typical vessels and address the target screening failure caused by slight differences in the characteristic parameters of the shaft frequency electric field signal. The entropy difference has been improved from 0.05 to about 0.2, and the difference rate of the shaft frequency electric field signal has been improved by 75%. This has effectively reduced the false alarm rate of target detection.

1. Introduction

Owing to their low-frequency characteristics, slow attenuation rate, and rich spectral composition, ship shaft-rate electric field signals have emerged as a critical modality in underwater target detection following acoustic field-based approaches [1]. The spectral components primarily comprise static electric field frequencies and shaft-rate electric field frequencies. Static electric field components correlate with hull corrosion levels, while shaft-rate electric field components reflect the rotational dynamics of propeller systems. These distinct frequency signatures provide clear discriminative indicators for target presence detection in submerged environments. However, how to effectively extract target features in complex marine environments is a vital and hot issue in current research on underwater target detection. Traditional signal feature extraction methods mainly include time-domain signal structure, Fourier transform of time-domain signals, classical spectrum estimation, and wavelet transform. Vessel shaft frequency electric field signals have non-stationary and nonlinear characteristics, making it difficult to obtain effective parameters directly reflecting target features from the raw signals. Fourier transform integrates over the entire time domain of the signal, making it unable to reflect the time-varying characteristics of non-stationary electric signals clearly. Wavelet transform, influenced by wavelet basis functions, is prone to energy leakage issues in signals, thus failing to extract time-domain signal features accurately. In summary, traditional signal feature extraction methods can no longer solve the feature extraction problem for complex shaft frequency signals under low signal-to-noise ratio conditions [2,3].

In recent years, with the rapid development of signal decomposition algorithms and nonlinear dynamic analysis methods, the updating and improvement of signal processing techniques, especially signal feature extraction techniques have been accelerating [4,5,6]. On the one hand, nonlinear dynamic analysis methods can provide the nonlinear characteristics required by signal processing techniques, many of which have been proven more effective than traditional energy and frequency characteristics. On the other hand, signal decomposition algorithms can break down complex non-stationary signals into a series of sub-signals based on different criteria. This enriches the quantity of signal features and highlights the differences between sub-signals. Empirical Mode Decomposition (EMD), a classic signal decomposition algorithm based on the Fourier transform, decomposes signals based on the time-scale characteristics of the signals without the need for presetting basis functions. When performing multi-scale decomposition of non-stationery and time-varying signals, it exhibits adaptability compared to traditional wavelet transform methods [7]. Based on the EMD method, scholars have successively proposed Ensemble Empirical Mode Decomposition (EEMD) and Intrinsic Computing Expressive Empirical Mode Decomposition with Adaptive Noise (ICCEMDAN) to address issues such as signal mode mixing and residual noise signals, further improving the integrity of the decomposed signals [8,9,10]. However, these algorithms still suffer from a certain degree of mode mixing and are based on empirical rather than theoretical foundations. Gilles proposed Empirical Wavelet Transform (EWT) to address the above issues in 2013. By segmenting the Fourier spectrum of the target signal, it adaptively decomposes complex signals into empirical wavelet functions within specific frequency ranges [11]. However, the research above only analyzed the time-domain part of the signal without considering the frequency-domain part.

Currently, the integration of nonlinear dynamic analysis methods with signal decomposition algorithms in signal feature extraction techniques is widely applied in fault diagnosis [12,13], biomedicine [14,15,16], geophysics [17,18], underwater acoustic signal processing [19,20,21], and other fields. Permutation entropy (PE), as a nonlinear dynamic analysis method, serves as a tool for describing the complexity of time series. This method focuses solely on information within the time series, making it computationally simple, resistant to noise, and highly robust [22]. In traditional research on vessel noise radiation signal processing, EEMD and its analysis of energy differences between high- and low-frequency signals are used to extract signal features. Still, the complexity of time series, namely entropy values, is not considered [23]. In fault diagnosis and electroencephalography (EEG) medicine, modal decomposition and its extended methods combined with entropy values have been widely confirmed. Reverse Dispersion Entropy (RDE), as a nonlinear dynamic analysis method, combines with EWT to decompose complex non-stationary signals into empirical wavelet functions with compact support spectra [24]. In addition, methods combining modal decomposition with sample entropy, approximate entropy, and others have also been proven effective [25,26]. However, few research methods combine modal decomposition with entropy values for the feature extraction of vessel shaft frequency electric field signals. Therefore, targeted feature extraction for vessel target shaft frequency electric field signals is significant for target detection and recognition. Most vessel shaft frequency electric field signal feature extraction is based on the modal decomposition of the time-domain signal, and the problems of signal modal aliasing and noise signal residuals in modal decomposition have yet to be effectively solved. In addition, a single entropy calculation can only reflect the complexity of the time-domain signal and fails to extract the frequency-domain features effectively.

Therefore, considering the problem of joint time- and frequency-domain feature extraction, this paper proposes research on a feature extraction method for the vessel electric field based on the maximum energy arrangement entropy of the Intrinsic Mode Function (IMF) of EMD. Aiming at the problems of mode aliasing and noise signal residuals, firstly, by establishing a test system to simulate the shaft frequency signal, the collected non-smooth random shaft frequency signal is decomposed into a set of IMFs by using EMD to analyze the signal characteristics from the time-domain aspect. Secondly, on this basis, the energy size of each group of signal components is calculated, and the largest energy component is selected as a characteristic parameter to find its PE value and realize multi-target electric field signal differentiation. Finally, the method is verified by actual marine vessel data, confirming that the method can better distinguish E-field signals of different vessel shaft frequencies.

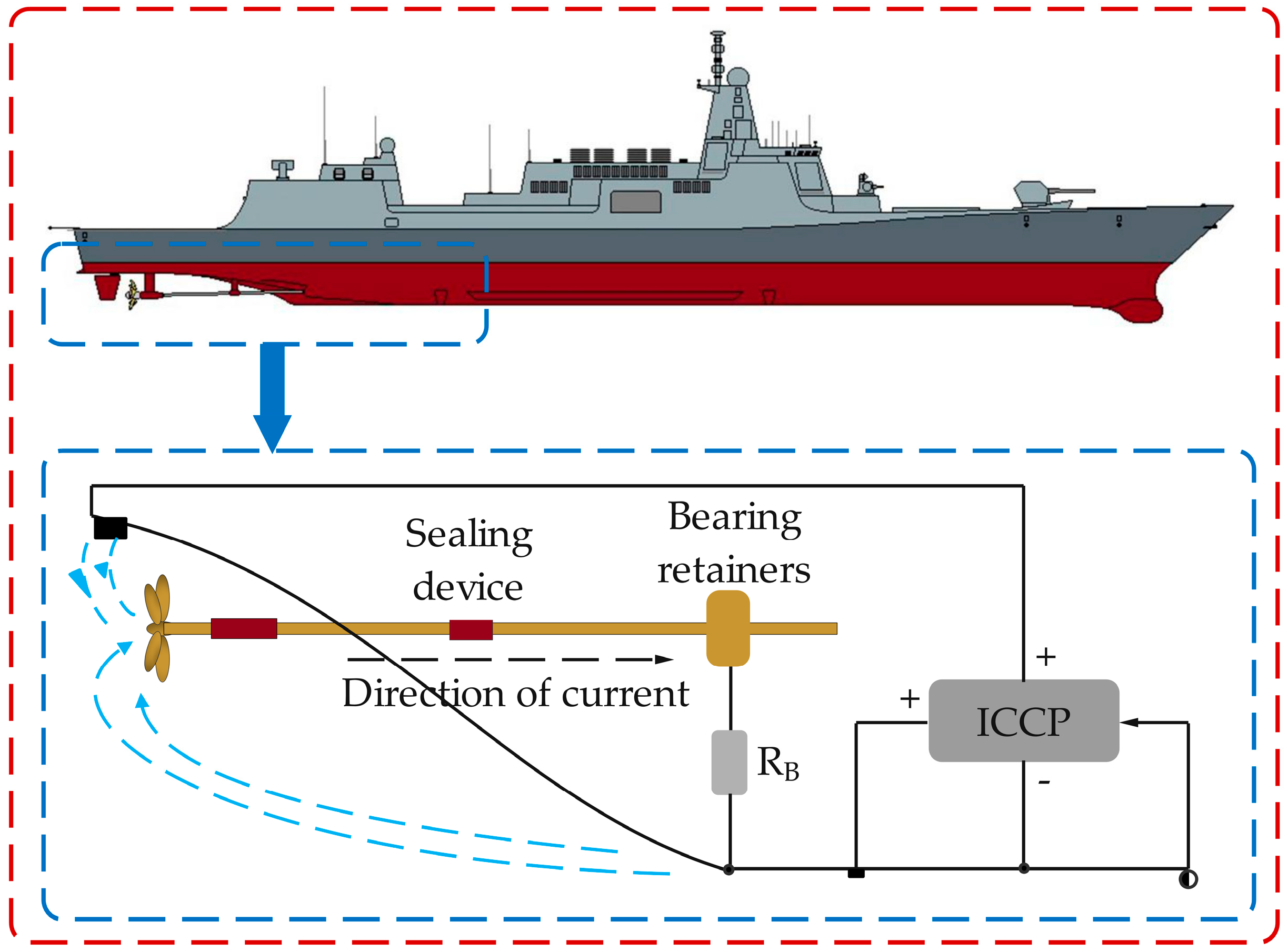
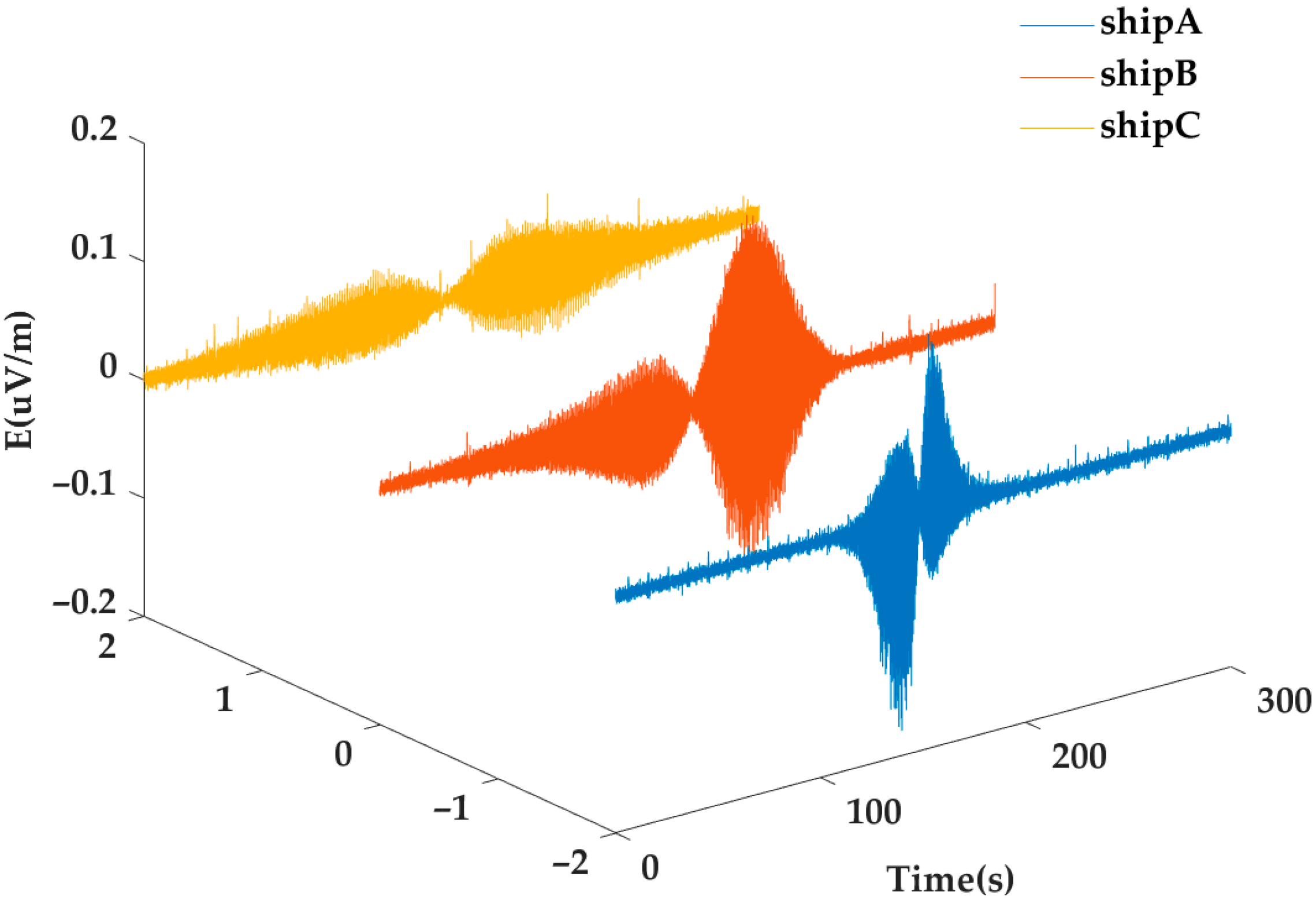
2. Mechanisms for Generating Shaft Frequency Signals of Vessels

When a vessel travels through seawater, the metal hull’s electrochemical corrosion and anti-corrosion measures generate a static electric field and an Extremely Low-Frequency Electric Field (ELFE). The ELFE, characterized by its low frequency, long underwater propagation distance, and distinct spectral features, is widely utilized for long-range underwater target detection [27]. Figure 1 illustrates the shaft frequency electric field’s generation principle and equivalent circuit diagram, where ICCP represents the impressed current cathodic protection system. Due to the potential of the metal hull being higher than that of the propeller, the hull, propeller, and seawater form a current loop. The equivalent impedance RB in the loop undergoes periodic changes with the rotation of propeller bearings. This leads to the demodulation of the current in the loop, generating a time-varying electric field signal around the vessel at the fundamental frequency of the propeller rotation, known as the shaft frequency signal [28].

The intensity of the shaft frequency electric field is correlated with variations in the grounding resistance of the shaft and the current density flowing through the propeller circuit. As a result, the magnitude difference in shaft frequency electric field signals between different types of vessels can be several times. Additionally, based on the propagation characteristics of the electric field in seawater, the intensity of the shaft frequency electric field is inversely proportional to the cube of the distance. The distance between the measurement point and the vessel target also determines the size of the shaft frequency electric field signal [29]. Therefore, in underwater electric field detection of vessels, the shaft-rate electric field serves as a critical characteristic signature. Figure 2 presents the shaft frequency signal recorded during the ship’s transit. The experimental setup utilized an Ag/AgCl electrode-based electric field measurement system with a sampling frequency of 100 Hz, deployed at a water depth of approximately 10 m. To enhance the temporal resolution and energy representation of target signals in the time-frequency spectrum, a computational framework was implemented using a 512-point sliding time window with a 64-sample overlap increment. From the analytical results, the three orthogonal components of the shaft-rate electric field (denoted as $E_x$, $E_y$, and $E_z$) exhibit distinct spectral signatures. Notably, between 200 s and 580 s, a pronounced energy amplification of the 4.7 Hz harmonic component is observed across all three field dimensions. Furthermore, ambient electromagnetic noise induced by oceanic dynamics—including tidal currents, wave motion, and hydrodynamic turbulence—constitutes the dominant interference source, significantly compromising the detectability of target-specific spectral features. This stochastic noise floor fundamentally limits the discriminative capability for identifying distinct target signatures due to spectral overlap between environmental noise and vessel-generated signals under typical operational conditions.

3. Experimental Analysis Based on Feature Extraction of Vessel Shaft Frequency Electric Field Signals

As per the findings in Section 1, it has been established that the shaft frequency electric field signal collected by the vessel’s underwater electric field detection system contains a complex and random background noise signal from the marine environment. To study the characteristics of the shaft frequency signal itself, the experiment in this paper constructs a system that uses various modal decomposition techniques to extract signal features from both the time and frequency domains. It also compares the ability of different modal decomposition algorithms to extract the target signal features from the random signals based on the adaptive line spectral energy analysis.

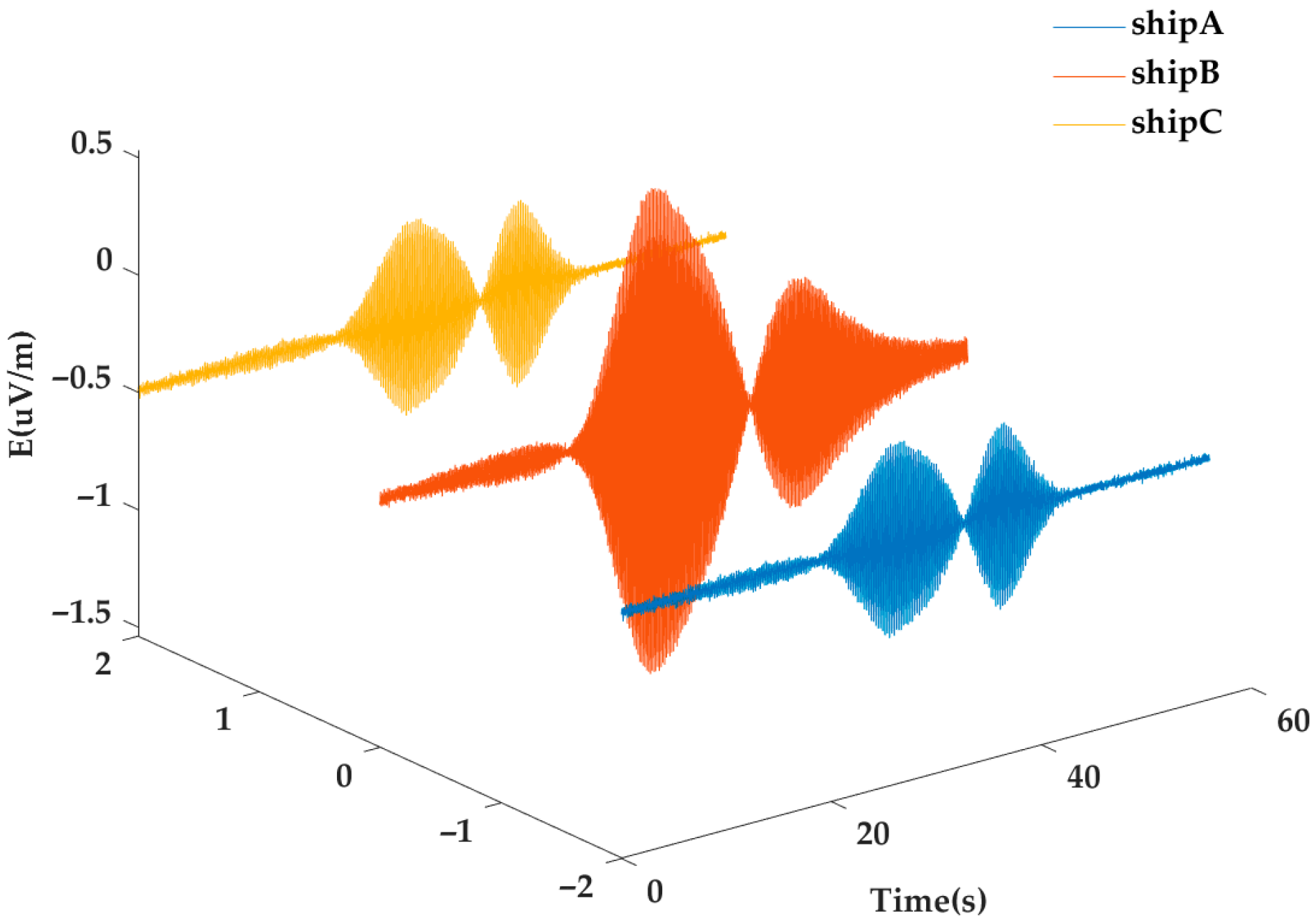
3.1. System Design and Construction

This section aims to study the characteristics of shaft frequency signals from different types of vessels. To achieve this, scaled-down model experiments are conducted based on the shaft frequency signal generation principle. The experiments simulate far-field measurement scenarios for typical vessels. The experimental system uses titanium-based oxide electrodes as the anode signal source to simulate the shaft frequency electric field generated by the vessel. Ag/AgCl electrodes are used as the electric field acquisition system at different underwater depths. Assuming a typical vessel with a length of 178.8 m, a width of 28 m, and a maximum speed of 18 knots, three anodes are used. An equivalent electric dipole source scaling model is established for different targets according to the ratio of 1:100, as shown in Figure 3.

In Figure 3, anodes 1, 2, and 3 are all made of titanium-based oxide and are equivalent to different dipoles simulating different types of vessels based on different power connections. In Figure 3a, anode 2 is connected to the positive pole of the power source, while anodes 1 and 3 are connected to the negative pole. In Figure 3b, anode 1 is connected to the positive pole of the power source, and anodes 2 and 3 are connected to the negative pole. In Figure 3c, anode 3 is connected to the positive pole of the power source, and anodes 1 and 2 are connected to the negative pole. The arrangement of sensors and simulated sources is shown in Figure 4. The electric field measurement system uses Ag/AgCl electrodes, with electrode distances set at 5 cm and measurement depths at 14 cm, 28 cm, and 42 cm. The sampling frequency is 200 Hz. Standard simulated sources are used as target source signals, fixed on the towing device, and moved at a speed of 5 cm/s. The water depth in the test area is approximately 0.9 m, the conductivity is 4.58 S/m, and the power source is a GS610 programmable current source with a signal fundamental frequency set at 4.73 Hz and a signal amplitude of 0.7 A.

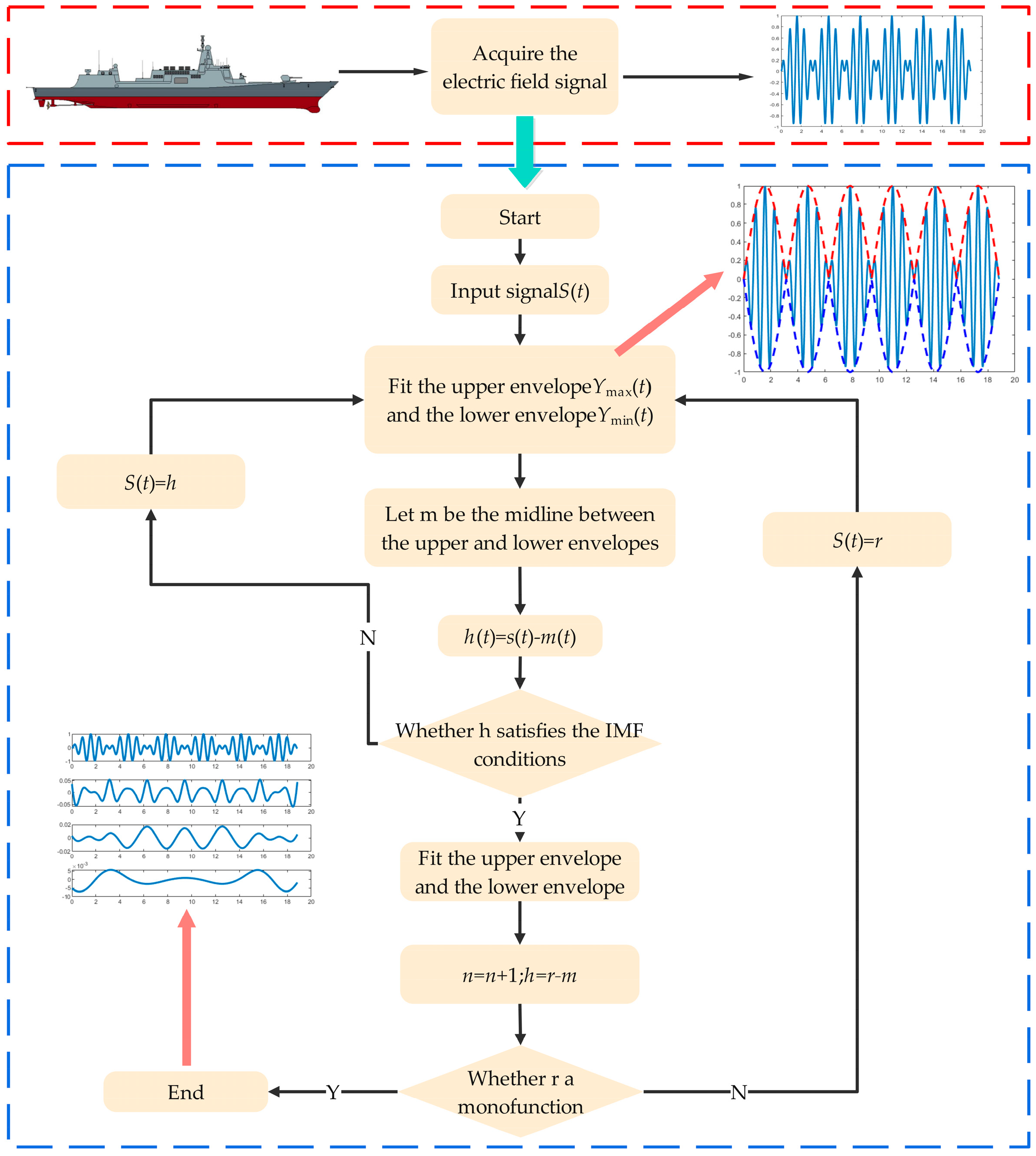
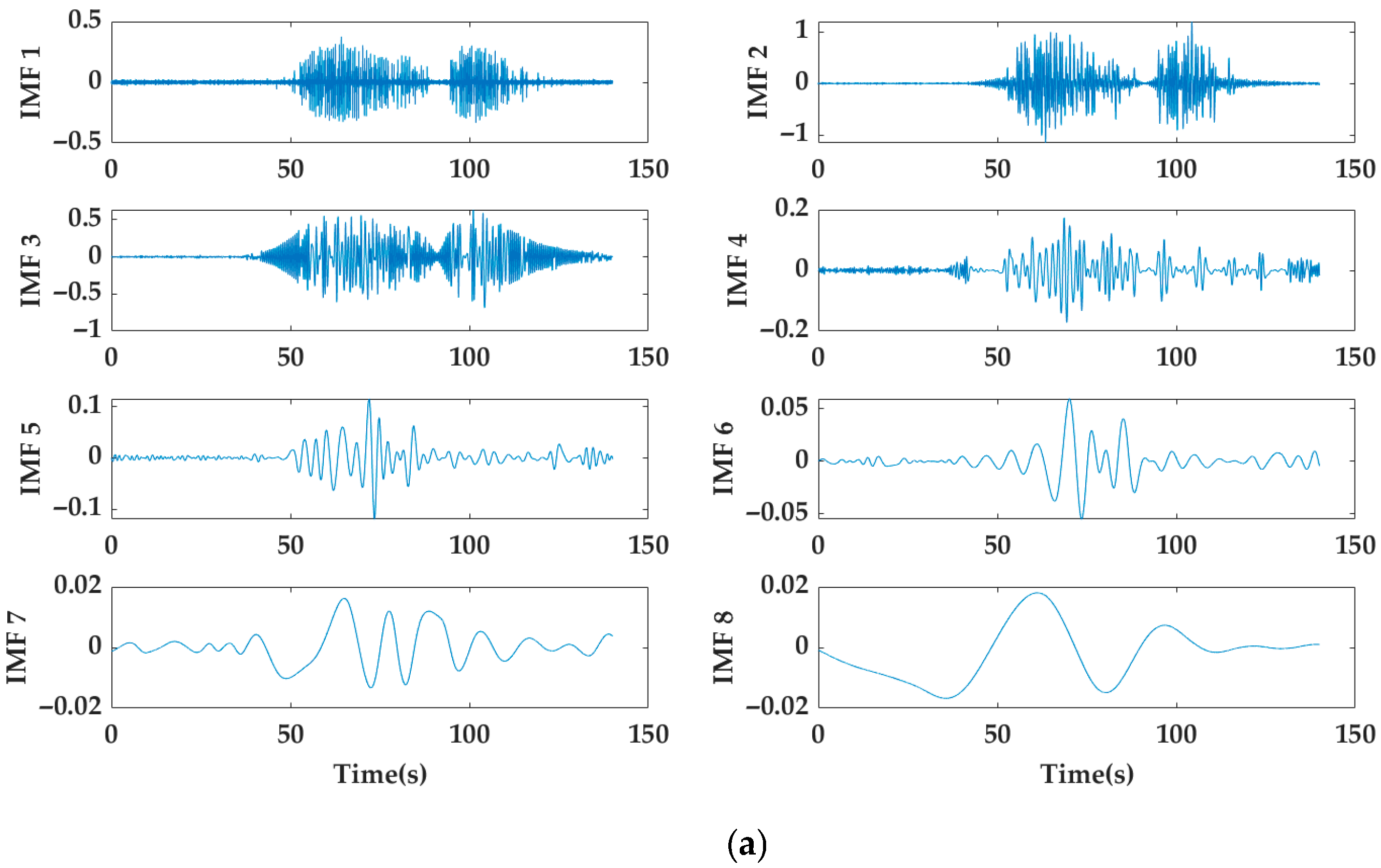
3.2. Method for Intrinsic Mode Function Extraction of Shaft Frequency Electric Field Signals

Signal decomposition algorithms break down the original signal into several Intrinsic Mode Functions (IMFs), a crucial step in preprocessing for signal feature extraction techniques. Empirical Mode Decomposition (EMD) is an adaptive sequential data decomposition algorithm primarily suitable for non-stationary and nonlinear sequences. It extracts information from the original signal itself, ensuring the maximum preservation of the original signal’s integrity. The decomposed IMF contains the local feature information of the original signal at different time scales, and the signal decomposition flowchart is shown in Figure 5.

The specific algorithm steps are as follows:

(1)

Input original time series signal $S(t)=\left\{s(t_1),s(t_2),\cdots ,s(t_n)\right\}\hspace{1em}n=1,2,\cdots N$ and employ cubic spline interpolation to obtain local maxima and minima, forming the upper and lower envelopes of the signal $Y(t)$;

(2)

From the upper envelope $Y_{\max }(t)=\left\{y_{\max }(t_1),y_{\max }(t_2),\cdots ,y_{\max }(t_i)\right\}$, fitted to the sequence of locally very large points, and the lower envelope $Y_{\min }(t)=\left\{y_{\min }(t_1),y_{\min }(t_2),\cdots ,y_{\min }(t_i)\right\}$, fitted to the sequence of locally very small points, find the average value $M(t)=\left\{m(t_1),m(t_2),\cdots ,m(t_i)\right\}$ of each extreme point in the sequence, and subsequently demean the raw signal through mean value subtraction, yielding the centered signal $h(t)$.

(3)

Check whether $h(t)$ satisfies the IMF conditions. There are two main conditions: firstly, the number of local extremum points and zero-crossings must be equal or differ by one; secondly, at any given moment, the average of the envelope of local maxima and the envelope of local minima must be zero. If the conditions are not met, use signal $h(t)$ as a basis and return to step (2) for further screening until the decomposed signal after $k$ iterations satisfies the IMF conditions. The first IMF component $h_k(t)$ of the original signal is represented as $c_1(t)$;

(4)

Subtract the first IMF component $r_1(t)$ from the original signal $S(t)$ leaving the residual signal $r_n(t)$ and repeat step (2) for decomposition. Continue this process until the residual signal $r_n(t)$ becomes a monotonic function that cannot be further decomposed. The sum of all IMF components and the residual component is the original signal $S(t)$, i.e.,

$$S(t)={\displaystyle \sum _{j=1}^N{c}_j(t)+r_n(t)}$$

(1)

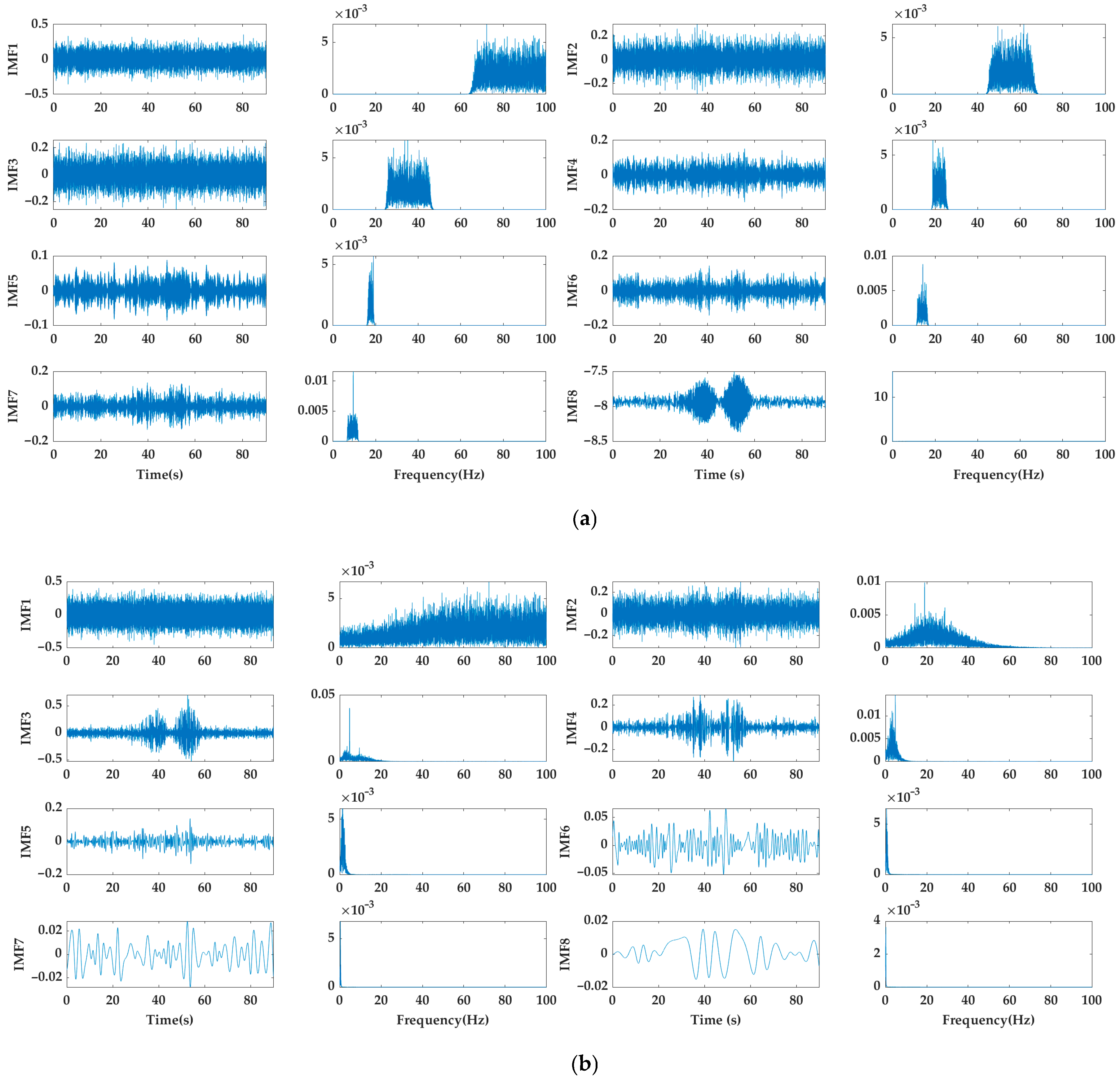
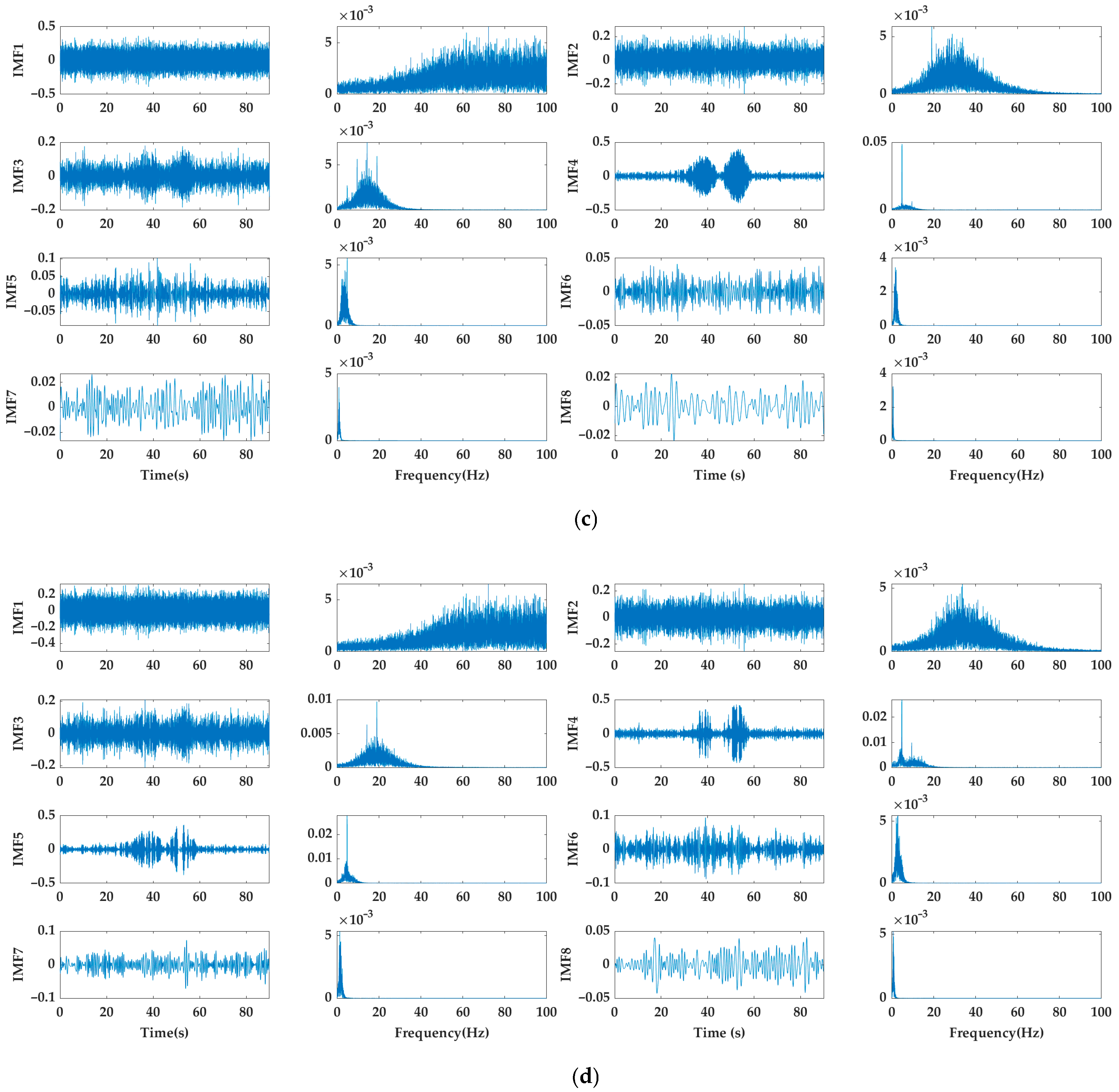
3.3. Comparison of Signal Decomposition Algorithms Based on Shaft Frequency Electric Field Experiments

To deeply investigate the vessel’s electric field signal extraction characteristics in different decomposition methods, the experiments based on the system acquisition of shaft frequency electric field signals in Section 3.1 and the four decomposition methods of EWT, EMD, EEMD, and ICCEMDAN are compared to decompose the signals into eight layers, i.e., components IMF1 to IMF8, to maximize the retention of the original signals and at the same time to extract the characteristics of each band. The time-domain waveforms and corresponding frequency spectra of signals processed through four distinct decomposition methodologies are comparatively presented in Figure 6.

From the analysis of Figure 6, it can be seen that after EWT decomposes the shaft frequency electric field in Figure 6a, the signal features are mainly concentrated in component IMF8. In contrast, no target signal frequency is found in the frequency-domain signal except for the DC component. This indicates that the EWT fails to effectively decompose and extract the vessel’s shaft frequency electric field signal features. Additionally, after EMD, EEMD, and ICEEMDAN, the time-domain features and energy of the shaft frequency E-field signal are mainly concentrated in components IMF3 and IMF4. From the frequency-domain perspective, the 4.73 Hz frequency signal in EMD appears in IMF3, which is the shaft frequency signal, and the 4.73 Hz frequency signal in EEMD appears in IMF3; the 4.73 Hz frequency signal in ICCEMAND decomposition appears in IMF3 and IMF4. In summary, comparing the four decomposition methods, in addition to the EWT decomposition method, the other three modal decomposition methods can initially extract the time-domain characteristics of the vessel’s shaft frequency electric field signals. In contrast, these methods are only for the same vessel signals, and they cannot be effectively differentiated for the different vessel target signals.

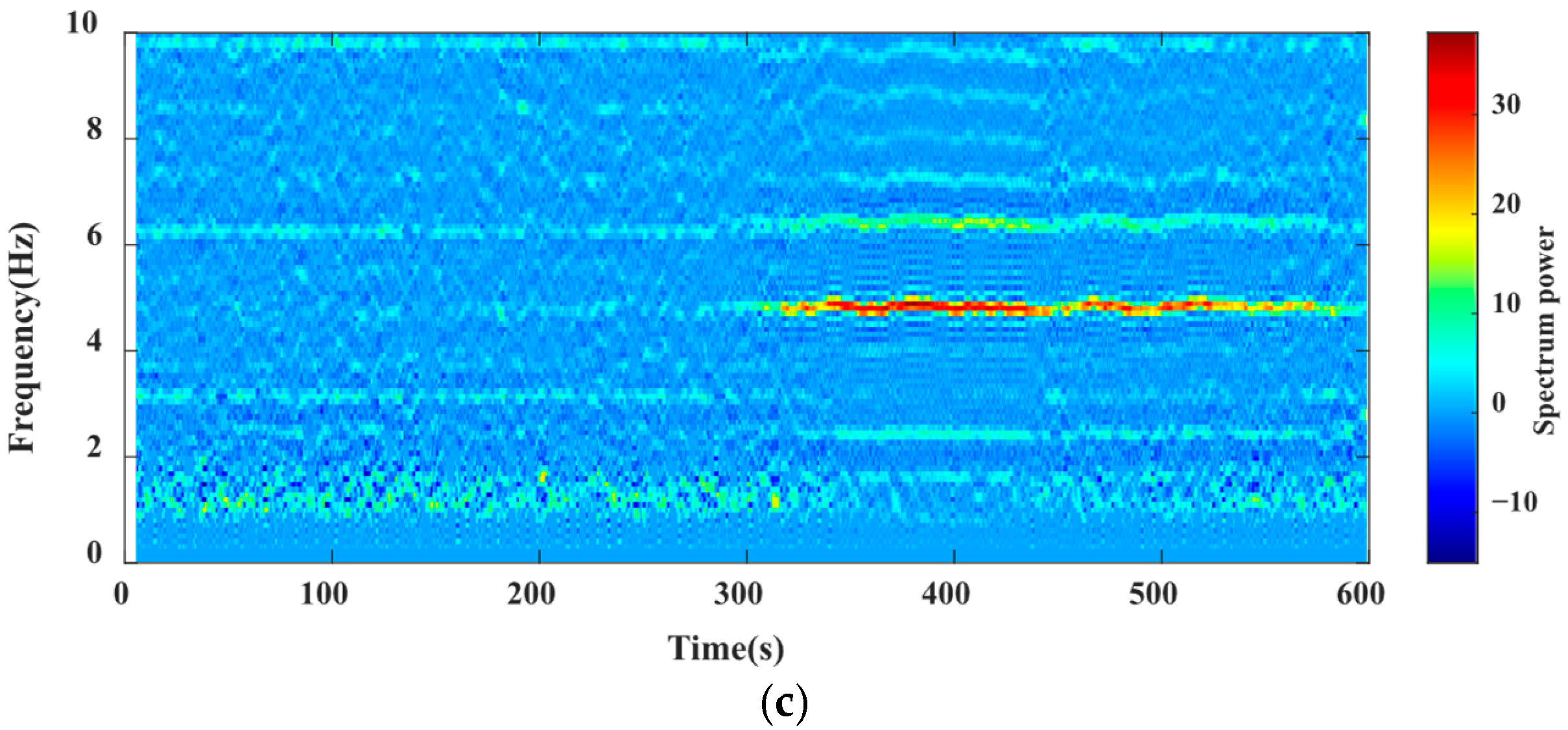
3.4. Adaptive Spectral Energy Detection

To comprehensively analyze the signal features and to further assess the effectiveness of the four different decomposition methods for signal feature extraction, the adaptive line spectrum energy detection method is adopted [30]. As analyzed in Section 3.2, signals decomposed by different methods are separated into multiple IMFs. After calculating the spectrum through the Fourier transform and comparing, it is observed that, apart from background noise, the signal exhibits distinct frequencies in IMF3 and IMF4. Therefore, based on the spectral detection method, a fixed threshold value is applied to detect signals in the decomposed signals. The experimental results are shown in Figure 7.

In Figure 7, the left side shows the time-domain signals obtained after applying four different decomposition algorithms, and the right side displays the time–frequency plots after spectral detection. The figure shows that the time-domain signal after EWT decomposition has distinct shaft frequency signal features in the IMF8 component, lasting approximately from 25 s to 60 s. In Figure 7b, the frequency duration spans about 15 s to 60 s. For the time-domain signal after EMD, as shown in Figure 7c, the target signal persists from around 30 s to 60 s, corresponding to the spectral plot of the target’s duration in Figure 7d. As for the EEMD and ICCEMDAN algorithms, the time-domain target signal is prominent, but the corresponding frequency spectra are mostly noise signals. In summary, the EMD signal algorithm more effectively extracts target signals from random signals in the time and frequency domains. It exhibits strong anti-interference capabilities and retains as much feature information from the target source as possible.

4. Signal Feature Extraction Method Based on Intrinsic Mode Function Energy Permutation Entropy

Comparing the four signal decomposition methods in Section 2, it can be seen that the line spectrum detection method based on EMD can realize the initial extraction of the target signal features but cannot identify the signal features between different vessels. To effectively extract different target signal features and solve the problem of screening different typical ship target signals, this paper proposes a kind of arrangement entropy based on EMD of IMF.

4.1. Permutation Entropy Algorithm Based on Intrinsic Mode Functions

Since the signal after EMD can be divided into multiple IMF time series, assume that the IMF of a certain time series signal after EMD is represented by function $C(t)=\left\{c(t_1),c(t_2),\cdots ,c(t_n)\right\}n=1,2,\cdots N$. The reconstructed space of this function can be defined as

$$\left[\begin{array}{l}c(1)\hspace{1em}\hspace{0.33em}c(1+\tau )\hspace{1em}\hspace{0.33em}\cdots \hspace{1em}\hspace{0.33em}c(1+(m-1)\tau )\\ \hspace{0.33em}\hspace{0.17em}⋮\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.17em}\hspace{1em}⋮\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ c(j)\hspace{1em}\hspace{0.33em}c(j+\tau )\hspace{0.17em}\hspace{0.33em}\hspace{0.17em} \hspace{0.33em}\cdots \hspace{1em}\hspace{0.33em}c(j+(m-1)\tau )\\ \hspace{0.33em}\hspace{0.17em}⋮\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.17em}\hspace{1em}⋮\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}⋮\\ c(K)\hspace{1em}c(K+\tau )\hspace{0.17em}\hspace{0.33em}\hspace{0.17em} \cdots \hspace{1em}c(K+(m-1)\tau )\end{array}\right]\hspace{1em}(j=1,2,\cdots ,K)$$

(2)

where $\tau$ is the time delay, and $m$ is the embedded dimension, corresponding to the number of elements in each row vector of the matrix. Each row vector in the matrix can serve as a reconstruction component, and $K$ denotes the number of reconstructed vector subsequences. The total number of reconstructed row vectors is $n-(m-1)\tau$ and each row vector is arranged in ascending order.

Next, each reconstructed subsequence is sorted in ascending order, i.e.,

$$c(i+(j_1-1)\tau )\le c(i+(j_2-1)\tau )\le \cdots \le c(i+(j_m-1)\tau )$$

(3)

If two subsequences in the vector are identical:

$$c(i+(j_1-1)\tau )=c(i+(j_2-1)\tau )$$

(4)

The original sequence can be sorted accordingly:

$$c(i+(j_1-1)\tau )\le c(i+(j_2-1)\tau )(j_1\le j_2)$$

(5)

In conclusion, any time series signal $C(t)$, it can be mapped to a symbol sequence:

$$S(g)=(j_1,j_2,\cdots ,j_m)$$

(6)

where $g=1,2,\cdots ,l$ and $l\le m!$ are one of the permutations among $j_1$ to $j_m$ in $m!$ arrangements, and each subsequence $c(t)$ of dimension $m$ can be mapped to the symbol function $S(g)$. If the probability distribution of all symbols is denoted as $p_1,p_2,\cdots p_l$, the probability entropy (PE) of the symbol sequence of the time series can be represented as follows:

$$H_p(m)=-{\displaystyle \sum _{j=1}^l{p}_j\ln p_j}$$

(7)

When $P_j=1/m!$ occurs, $H_p(m)$ reaches its maximum value $\ln m!$, and it is typically normalized as follows:

$$0\le H_p(m)/\ln m!\le 1$$

(8)

where the value of $H_p(m)$ represents the time series randomness. A lower value of $H_p$ indicates a more regular time series, while a higher value suggests a more irregular time series, containing a greater amount of information.

4.2. Permutation Entropy Analysis of Intrinsic Mode Functions

To validate the algorithm’s effectiveness, this section simulates three types of vessels using equivalent electric field dipole sources with three different connection methods. The experiments use the same frequency and amplitude signal as input, and the time-domain signals of the three electric fields are measured, as shown in Figure 8.

Figure 9 shows the EMD algorithm decomposing the electric field signals of the three vessel axes frequencies into ordered IMF results from high to low frequency. An analysis of the graph reveals that for Vessel A, the amplitude of the IMF1, IMF2, and IMF3 component signals is significantly higher than that of the other components, indicating the primary energy components of the signal features. Next, the primary energy of Vessel B is concentrated in IMF2 and IMF3. For Vessel C, the signal energy is concentrated in the IMF1, IMF2, and IMF3 components.

The PE values are calculated for each IMF decomposition to extract the signal characteristics of different components further. Two parameters are required for calculating PE: time delay $\tau$ and embedding dimension $m$. Considering the aim of retaining as many abrupt anomalies and feature parameters of the actual signal as possible, the time delay $\tau$ is set to 1, and the embedding dimension $m$ is set to 4 [31]. The PE calculation results for different vessels are shown in Figure 10. The X-axis represents the first to eighth IMF components after decomposing the electric field signal, while the Y-axis represents the PE values for each element.

As demonstrated in Figure 10, the permutation entropy (PE) values of intrinsic mode function (IMF) components for the shaft-rate electric field signals of the three vessel types (Vessel A, B, and C) exhibit a monotonic decline with increasing decomposition order. This trend indicates a progressive reduction in signal complexity at higher IMF orders, reflecting diminished discriminative information content pertaining to shaft-rate characteristics. Notably, the PE values across distinct vessels (A, B, and C) display insufficient statistical divergence at identical decomposition orders, thereby limiting the efficacy of conventional empirical mode decomposition (EMD) in differentiating vessel-specific signatures. Due to the slight differences in PE values for same-order components among different vessels, the IMFs are reorganized according to the energy sequence. Assuming the $j$-th IMF component after the decomposition of the original electric field signal has $N$ sampling points, where the instantaneous amplitude of the $n$-th sampling point is $c_j(n)$, its instantaneous energy is the following:

$$Q_j=c_j^2(n)$$

(9)

Therefore, the average energy of the $j$-th IMF component is the following:

$$\widehat{E}{n}_j={\displaystyle \sum _{n=1}^N{Q}_j(n)}/N$$

(10)

The energy values of each IMF component are calculated according to Equations (9) and (10), as shown in Figure 11. The X-axis represents the eight IMF components sorted in descending order of energy, and the Y-axis represents the PE values for each component.

The experimental results reveal no discernible systematic correlation between the signal energy levels and permutation entropy (PE) values of the intrinsic mode function (IMF) components. However, significant inter-vessel discrepancies in PE values are observed specifically within the first four energy-dominant IMF ranks. For distinct vessel types, the PE values of these primary energy tiers (IMF1–IMF4) exhibit marked differentiation, with higher energy levels corresponding to richer signal feature compositions. This empirical evidence substantiates that energy-based prioritization of shaft-rate electric field components enables selective extraction of discriminative electromagnetic signatures, thereby facilitating vessel classification through enhanced feature separability in the dominant energy regimes.

5. Signal Feature Extraction Methods for Different Vessels

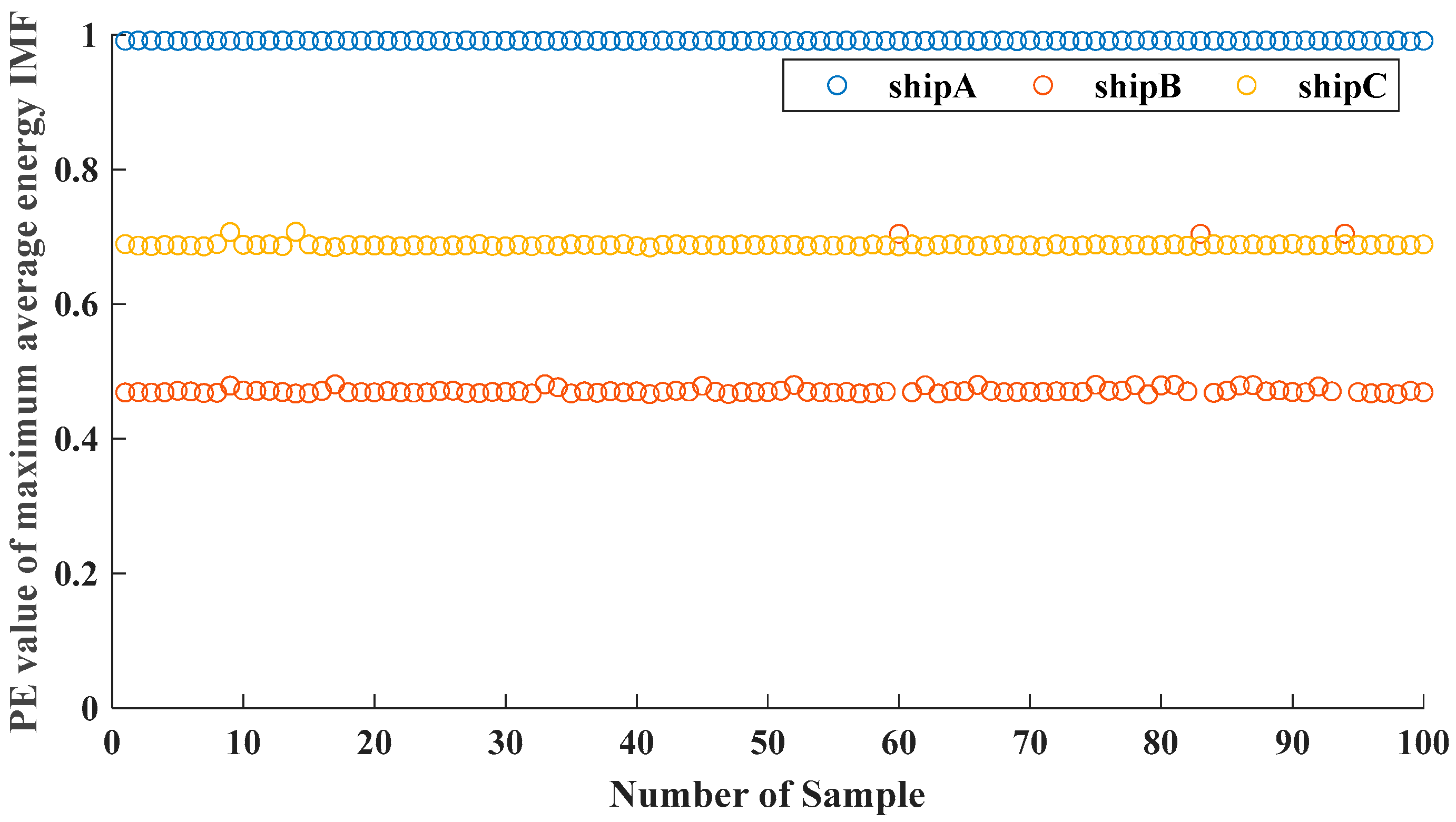
5.1. Feature Extraction Based on the PE Values of the IMF with the Highest Energy

The differences are primarily concentrated in the first three energy levels by analyzing the PE values of IMF components at various orders for the three different electric field signals. The IMF components in the first energy level contain the main features of the signal, and there are significant differences in PE values. Although the PE values for the second and third energy levels differ considerably, the comprehensive signal feature components are not as pronounced as in the first energy level. Therefore, this study utilizes the IMF components from the first energy level to determine their features.

$$\widehat{E}{n}_{\max }=\max \left\{\widehat{E}{n}_1,\widehat{E}{n}_2,\cdots ,\widehat{E}{n}_j\right\}$$

(11)

where $\widehat{E}$ represents the average energy of each IMF component after EMD. According to Equations (9)–(11), the highest average energy and PE values for each IMF component of Vessel A, Vessel B, and Vessel C are calculated and presented in

Table 1. PE values of components for three different types of vessels.

	Vessel A	Vessel B	Vessel C
Highest Energy Level	IMF2	IMF2	IMF3
Average Energy	0.04727	0.0653	0.0048
PE Values	0.6187	0.9883	0.3934

.

According to the analysis of Table 1, the maximum average energy levels of signals after decomposition are different for different vessels, with an average energy difference greater than 0.02 and a PE difference greater than 0.3.

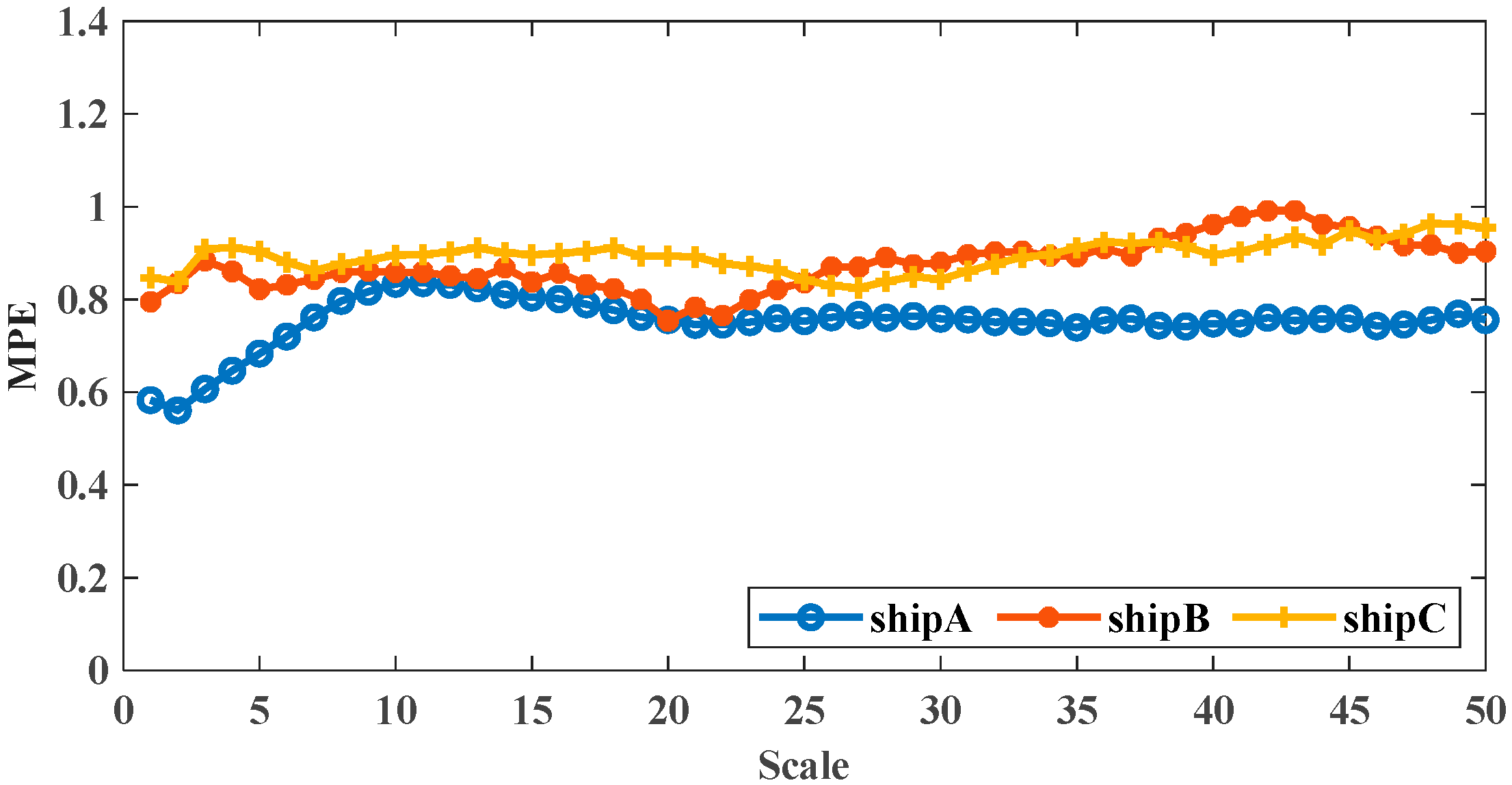
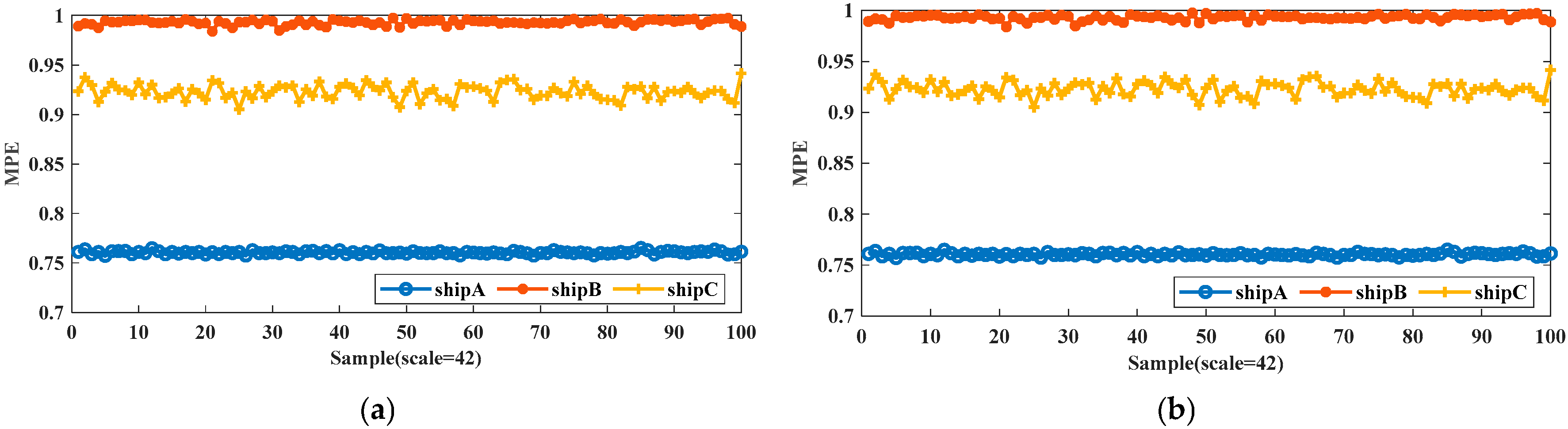
5.2. Feature Extraction Based on Multi-Scale Permutation Entropy

Due to the varying complexities of time series signals from different types of vessels in the same maritime area, this paper utilizes multiscale permutation entropy (MPE) to describe the complexity of time series at different scales, as shown in Figure 12. With an embedding dimension of 4 and a time delay of 1, the X-axis represents the time scale, and the Y-axis represents the entropy values corresponding to each time scale.

Figure 12 shows that with the increase in time scale, Vessel B and Vessel C fluctuate within a certain range, and the fluctuation amplitude is insignificant. In contrast, the fluctuation amplitude for Vessel A is quite noticeable. There are certain differences among the three signals at different time scales, with the largest difference observed at time scales 42 and 43.

Table 2. Entropy values at different time scales.

	Vessel A	Vessel B	Vessel C
Scale = 42	0.7611	0.9914	0.9184
Scale = 43	0.7542	0.9914	0.9344

analyzes the entropy values of the signals from the three vessels at time scales 42 and 43. Within the two sets of time scales, Vessel A exhibits significant differences in entropy values compared to the other two vessels, while the difference between Vessel B and Vessel C is slight. Looking at the overall data, the differences are not very pronounced, and separability requires further analysis.

5.3. Experimental Data Verification Based on PE of IMF with Maximum Average Energy

To validate the universality of the proposed method, 100 samples of different types of signals were taken as test data to compare the effectiveness of three feature extraction methods. The feature parameters extracted include the PE values of the original signals and the PE values of the IMF components with maximum average energy, as shown in Figure 13.

Analyzing Figure 13a, there is a noticeable difference between Vessel A and the other two vessels, approximately around 0.2. However, the difference between Vessel B and Vessel C is less than 0.05, making it challenging to distinguish their feature parameters. In Figure 13b, the entropy values of the IMF components with the maximum average energy for the same vessel are generally maintained at the same level. The PE values between different vessels differ by more than 0.2, indicating effective discrimination of the feature parameters of electric field signals from different vessel axis frequencies.

For different vessels at different time scales, as analyzed in Section 4.2, the entropy values show the maximum difference at time scales 42 and 43. Therefore, time scales 42 and 43 are selected, and the experimental results are shown in Figure 14.

6. Verification with Real Vessel Data

To further validate the effectiveness of the proposed method, offshore experiments were conducted near Zhifu Island, Yantai (with a water depth of approximately 17 m, seawater conductivity of about 3.5 S/m, longitude of 121.43°, and latitude of 37.58°), as shown in Figure 15. Ag/AgCl electrodes were used in the experiment, with an electrode distance of approximately 1 m and a sampling frequency of 100 Hz. The measurement system was arranged near the navigation channel. The basic parameters of three different types of vessels are shown in

Table 3. Information on three vessels.

Serial Number	Vessel Name	Speed (kn)	Orthogonal Distance (m)
Vessel A	BoHaiZuanZhu	16.8	198
Vessel B	TaiCheng29	11.7	187
Vessel C	ChangXiangLong	6	232

. The vessel speed was estimated from shore-based rangefinder measurements. The time-domain axis frequency signals are shown in Figure 16, and their entropy values are shown in Figure 17.

Based on actual vessel electric field signal data, the entropy values are calculated using the algorithm proposed in this paper. Analyzing the graph reveals a significant difference in PE values for different vessels. The difference between Vessel A and Vessel B is approximately 0.5, while the difference between Vessel A and Vessel C is around 0.3. This indicates that this paper’s proposed method can effectively distinguish target signals.

According to the data analysis in

Table 4. Feature parameters of electric field signals from different vessels.

	Vessel A	Vessel B	Vessel C
Variance of PE values for IMF with Maximum Average Energy	4.5134 × 10−8	1.3986 × 10−5	8.5552 × 10−8
Range of PE values for IMF with Maximum Average Energy	0.9909~0.9917	0.4667~0.4822	0.686~0.69
Variance of PE Values	8.0481 × 10−9	4.2267 × 10−8	4.6864 × 10−8
Range of PE Value	0.9993~0.9997	0.9980~0.9989	0.9941~0.9952
Variance of MPE Values	1.4947 × 10−8	8.09472 × 10−7	4.4766 × 10−7
(Time Scale = 42)	0.9992~0.9998	0.9837~0.9878	0.9819~0.9854
Variance of MPE Values	9.9759 × 10−9	1.4209 × 10−6	5.6725 × 10−7
(Time Scale = 43)	0.9992~0.9998	0.9811~0.9860	0.9836~0.9869

, the entropy variance of each vessel is very low across the three feature extraction methods of PE value, PE value of maximum mean energy IMFs, and MPE value. This suggests that the entropy value of different vessels is stable. Among them, the PE value feature parameter of the IMF with maximum average energy is in different fluctuation intervals. The range difference between vessels A and B is about 0.53, and the range difference between vessels A and C is about 0.22, indicating good differentiation. When only the PE value is used as a feature parameter, the maximum difference between vessel A and vessel C is only about 0.005, making it difficult to differentiate the signal characteristics of different vessels. However, when MPE is used as a feature parameter, the fluctuation ranges of vessel B and vessel C overlap partially when the time scale is 34, so they cannot be differentiated. In summary, the PE value of the IMF with maximum mean energy is the best feature extraction method as it can better distinguish the three signals than the other two methods.

7. Conclusions

For the feature extraction of different types of vessel shaft frequency electric field signals, this paper proposes a feature extraction method based on the generation mechanism of vessel target shaft frequency electric field signals, which arranges the intrinsic mode function energy and entropy. The feasibility of the method is verified by using the scaled model experiment. The feature extraction effect of different decomposition methods is analyzed from the two perspectives of the time domain and the frequency domain. On this basis, the maximum average energy component of the shaft frequency signal is used to calculate the entropy value to distinguish the non-smooth shaft frequency signals generated by different targets. Finally, the method is verified by using the real vessel data, and the conclusions are as follows:

(1)

For the traditional single modal decomposition, the EMD method is more suitable for shaft frequency electric field time-domain signal feature extraction than the three decomposition methods of EWT, EEMD, and ICCEMAND after the comparison of the line spectrum detection methods.

(2)

Based on the EMD algorithm, the modal decomposition and entropy value algorithm extract the signal features of the vessel’s shaft frequency electric field. A test system is built to simulate three different vessel shaft frequency electric field signals, and the PE value is analyzed to decrease significantly with the increase in the order of the IMF component after signal decomposition. To distinguish the shaft frequency E-field signals of different vessels, the IMF components are arranged in descending order of energy, and the PE value of the IMF with maximum energy is calculated. After analysis, it was found that the PE values of the three kinds of shaft frequency electric field signals have apparent differences.

(3)

Combined with the simulation experiment method, the PE values of the maximum average energy IMF of the three typical vessel shaft frequency electric field signals are used as the characteristic parameter, and 100 samples of shaft frequency electric field signals are taken, respectively, for comparison. The results show that the fluctuation range of the same type of E-field signals is minimal, with similar characteristic parameters. However, the typical parameters of the different kinds of E-field signals differ significantly and are well differentiated. Compared with the PE and MPE values of the original target signals, the PE value of the maximum mean energy IMF as a feature parameter can fully reflect the complexity of the target feature signals and has better discriminability.

Therefore, the PE value of the maximum mean energy IMF as a feature parameter has good discriminative ability for different vessel shaft frequency E-field signals. Although the feature extraction of different vessels is realized in this paper, the problem of recognizing different types of vessels is not considered. Future work will be to realize vessel-type recognition based on shaft frequency electric field feature extraction.