Dynamic Ensemble Selection for EEG Signal Classification in Distributed Data Environments

Abstract

This study presents a novel approach to EEG signal classification in distributed environments using dynamic ensemble selection. In scenarios where data dispersion arises due to privacy constraints or decentralized data collection, traditional global modelling is impractical. We propose a framework where classifiers are trained locally on independent subsets of EEG data without requiring centralized access. A dynamic coalition-based ensemble strategy is employed to integrate the outputs of these local models, enabling adaptive and instance-specific decision-making. Coalitions are formed based on conflict analysis between model predictions, allowing either consensus (unified) or diversity (diverse) to guide the ensemble structure. Experiments were conducted on two benchmark datasets: an epilepsy EEG dataset comprising 150 segmented EEG time series from ten patients, and the BCI Competition IV Dataset 1, with continuous recordings from seven subjects performing motor imagery tasks, for which a total of 1400 segments were extracted. In the study, we also evaluated the non-distributed (centralized) approach to provide a comprehensive performance baseline. Additionally, we tested a convolutional neural network specifically designed for EEG data, ensuring our results are compared against advanced deep learning methods. Gradient Boosting combined with measurement-level fusion and unified coalitions consistently achieved the highest performance, with an F1-score, accuracy, and balanced accuracy of 0.987 (for nine local tables). The results demonstrate the effectiveness and scalability of dynamic coalition-based ensembles for EEG diagnosis in distributed settings, highlighting their potential in privacy-sensitive clinical and telemedicine applications.

1. Introduction

Electroencephalography (EEG) is a non-invasive technique that records the electrical activity of the brain and is widely used in clinical diagnostics, especially for neurological disorders such as epilepsy. Accurate and timely classification of EEG signals is essential for effective diagnosis and intervention. However, in modern healthcare and research environments, EEG data are often collected across multiple centers, devices, or sessions, resulting in dispersed datasets. By this statement, we mean that EEG recordings may originate from different patients across multiple hospitals, but some patients may also be tested at various institutions. In many real-world scenarios, especially when data are collected across medical centers, patient identifiers are anonymized or protected due to privacy regulations. As a result, it is not possible to determine whether a given EEG signal comes from the same individual tested in different locations or from different individuals altogether. Our study operates under this constraint, treating the data as independent observations without attempting to resolve patient identity. All of these scenarios—multiple patients across centers, with some cases involving a single patient tested across sessions—are considered possible within our analysis. This fragmentation, coupled with privacy and regulatory concerns, limits the feasibility of centralized processing [1]. Consequently, there is a growing need for intelligent decision-making frameworks that can operate effectively under data distribution constraints while maintaining high diagnostic accuracy. Given the complexity of EEG signals, manual interpretation is a time-consuming task that demands substantial expertise [2]. Automated classification systems can offer consistent and fast support to neurologists, aiding in long-term monitoring, early diagnosis, and personalized therapy strategies.

According to the World Health Organization, epilepsy affects approximately 50 million people worldwide [3], and EEG remains the primary tool for its diagnosis. However, the increasing volume of EEG data collected from patients poses challenges for timely expert analysis. AI-based models, including deep learning and ensemble methods, have been explored to support clinical workflows by identifying abnormal patterns automatically [2,4]. In particular, our ensemble-based approach aims to improve robustness and adaptability across diverse EEG data distributions.

Previous studies have explored decision-making in scenarios involving dispersed or decentralized data, such as federated learning [5,6], local modeling [7,8], and ensemble-based techniques [9,10]. Federated learning approaches enable collaborative model training without direct data sharing, but they often require synchronization and substantial communication overhead. Alternatively, local modeling strategies independently train models on separate data partitions and aggregate their predictions using ensemble methods. While effective, traditional ensemble strategies like majority voting or static averaging do not account for the varying relevance or reliability of models across different input instances, especially in heterogeneous and non-iid data environments.

EEG signal classification has been extensively studied using a range of machine learning and deep learning techniques [11,12,13]. Common approaches include feature-based models utilizing statistical, spectral, and wavelet descriptors, as well as end-to-end deep learning architectures [14,15]. Boosting algorithms, such as AdaBoost and Gradient Boosting, have demonstrated strong performance due to their ability to focus on hard-to-classify instances [16,17]. However, many existing works assume access to a unified dataset and do not address the challenges associated with EEG data dispersion, such as feature inconsistency, sample variability, and localized context.

Despite growing interest in distributed machine learning, there remains a significant gap in effectively integrating classifier outputs from dispersed EEG datasets in a way that adapts to each decision context. Existing ensemble methods often treat all models equally, regardless of their relevance or agreement. Moreover, most EEG classification studies either disregard the implications of data decentralization or lack mechanisms to dynamically select models best suited to individual test cases. While various dynamic ensemble selection techniques have been proposed in the literature [18,19,20,21,22], their application to EEG signal classification remains largely unexplored.

To address these challenges, this study introduces a dynamic ensemble selection framework for EEG signal classification in dispersed data environments. Local models are trained independently on non-overlapping subsets of EEG data, simulating a decentralized scenario. At inference time, we dynamically form coalitions of models based on their predictive behavior for each test instance. These coalitions, formed through conflict analysis, represent either high consensus or high diversity. By using both measurement-level and abstract-level fusion strategies, we adaptively aggregate the most informative predictions. The novelty lies in the context-aware coalition formation and its application to EEG diagnosis under data fragmentation constraints.

The main contributions of this work are as follows:

• A comprehensive ensemble framework that supports EEG classification with dispersed data without centralized access.
• A novel coalition-based dynamic model selection mechanism using conflict metrics.
• An in-depth evaluation across multiple dispersion scenarios with various base classifiers.
• Empirical evidence showing that unified coalitions with measurement-level fusion achieve good performance, particularly with Gradient Boosting models.

EEG plays a pivotal role in clinical neurology by providing real-time insight into the brain’s electrical activity. In epilepsy diagnosis, EEG allows for the identification of seizure patterns across different stages of the condition, which is crucial for timely intervention and treatment. However, interpreting EEG signals remains a challenging task due to their complexity and variability across patients. In this context, improving the accuracy and robustness of EEG classification models directly benefits medical professionals by offering decision support tools that reduce diagnostic uncertainty. Moreover, such improvements are also vital for the development of brain–computer interfaces (BCIs), which depend on reliable EEG interpretation to enable communication and control in individuals with severe motor impairments. By proposing a framework suitable for distributed data environments, this study addresses real-world constraints, such as data privacy and institutional fragmentation, and aims to support scalable, accurate, and privacy-preserving EEG analysis for both diagnostic and assistive technologies.

The approach proposed in this paper introduces a dynamic ensemble classification framework that adapts to the varying quality and distribution of EEG signals without requiring centralized access to the full dataset. In contrast to existing methods that either assume access to homogeneous data or apply static ensemble techniques, our strategy dynamically selects and integrates classifier outputs based on the consistency or disagreement between models. The originality of the method lies in its coalition-based selection mechanism, which considers the local predictive behavior of models and builds consensus or diversity groups tailored to each test instance. This mechanism is applied to distributed EEG data representing seizure stages across different patients—addressing an important gap in the literature, where classifier integration is often simplistic and lacks adaptability to decentralized clinical data. The results suggest that our unified, context-aware ensemble strategy not only improves performance metrics but also supports realistic deployment scenarios, such as telemedicine and hospital networks, where data cannot be freely shared.

The remainder of this paper is structured as follows. Section 2 describes the materials and methods used, including the classifiers, and coalition formation strategies. Section 3 presents the experimental setup and results. Also, the dataset, feature extraction, and data preparation are discussed in this section. Section 4 discusses the implications of the findings and limitations. Section 5 concludes the paper with key findings and possible future directions.

2. Materials and Methods

In the context of EEG analysis, especially when handling data from multiple sources or collection sites, it is common to encounter dispersed data—datasets that differ in structure, either due to variations in feature representation or the distribution of examples. To address this, and to support privacy-preserving processing, we adopt a local modeling strategy, where models are trained independently on isolated subsets of the data, referred to as local tables. These subsets are processed without requiring global data access, allowing for modular and decentralized analysis.

Different machine learning classifiers could be used for the local table. In this study, to analyze and model localized segments of EEG signals, we systematically compare five widely recognized algorithms: Random Forest, AdaBoost, Gradient Boosting, k-Nearest Neighbours, and Logistic Regression. Each classifier is trained separately on a distinct local dataset, with each dataset comprising a unique subset of EEG recordings. This approach enables us to mimic an object-distributed environment, where data are stored initially across multiple sources or locations, and each model learns from its respective local data without access to the full dataset.

Each trained model outputs a class probability vector for a test instance $\widehat{x}$, structured as $[{\mu }_{i,1}\left(\widehat{x}\right),\dots ,{\mu }_{i,c}\left(\widehat{x}\right)]$, where ${\mu }_{i,j}\left(\widehat{x}\right)$ is the support for class j provided by model i, and c is the number of decision classes. These prediction vectors serve as the basis for our ensemble fusion framework.

To go beyond conventional majority voting, we implement a dynamic ensemble selection framework. This approach dynamically identifies, for each test instance, a subset of models—called a coalition—that will participate in the final decision. The coalition is constructed individually for every tested object, making the ensemble configuration adaptive and context-aware.

We formally represent each local dataset as a decision table: $D_i=(U_i,A_i,d)$ denotes the set of EEG signal instances, $A_i$ the features (e.g., statistical, spectral, or wavelet-based descriptors), and d the decision label (e.g., ictal vs. inter-ictal state). Due to the distributed nature of the data, features and samples may vary between tables. To form coalitions, we use a conflict matrix approach. Each model’s prediction vector is evaluated to determine its stance on each class. For a class v, a model’s support is encoded by a function $v\left(i\right)\in \{-1,0,1\}$ defined as follows:

$$v\left(i\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{the}\mathrm{coordinate}{\mu }_{i,v}\left(\widehat{x}\right)\mathrm{for}\mathrm{decision}v\mathrm{in}\mathrm{the}\mathrm{prediction}\mathrm{vector}\mathrm{of}\hfill \\ \hfill & \mathrm{model}i\mathrm{has}\mathrm{the}\mathrm{maximum}\mathrm{value}\mathrm{of}\mathrm{all}\mathrm{coordinates}\mathrm{in}\mathrm{this}\mathrm{vector}.\hfill \\ 0\hfill & \mathrm{if}\mathrm{the}\mathrm{coordinate}{\mu }_{i,v}\left(\widehat{x}\right)\mathrm{for}\mathrm{decision}v\mathrm{in}\mathrm{the}\mathrm{prediction}\mathrm{vector}\mathrm{of}\hfill \\ \hfill & \mathrm{model}i\mathrm{is}\mathrm{this}\mathrm{vector}’s\mathrm{second}\mathrm{highest}\mathrm{of}\mathrm{all}\mathrm{coordinates}.\hfill \\ -1\hfill & \mathrm{in}\mathrm{other}\mathrm{cases}\hfill \end{array}\right.$$

(1)

Using these encodings, a conflict function $\rho (i,j)$ measures the disagreement between models i and j as the proportion of decision classes where their opinions differ. Formally,

$$\rho (i,j)={\displaystyle \frac{card\{v\in V:v(i)\ne v(j\left)\right\}}{card\left\{V\right\}}},$$

(2)

where $card\left\{V\right\}$ is the cardinality of the set of decision classes and i and j are local models.

Two types of coalitions are constructed:

• Unified coalitions, where $\rho (i,j)<0.5$ for all pairs in the group, capturing groups of models that largely agree.
• Diverse coalitions, where $\rho (i,j)>0.5$, representing models with significantly differing perspectives.

These coalitions are generated dynamically per test instance, allowing the ensemble structure to adapt to each prediction task. Importantly, models may belong to multiple coalitions simultaneously, reflecting overlapping perspectives, as commonly seen in real-world ensemble behavior.

For decision-making, we focus on the strongest coalition—the one with the highest number of members. Two types of decision fusion are used:

• Measurement-level fusion: All prediction vectors from coalition members are summed. The final class is the one with the highest aggregated score.
• Abstract-level fusion: A simple majority vote is conducted among coalition members, based on their most confident class prediction.

In addition to coalition-based methods, we also evaluate traditional ensemble fusion strategies—simple sum of prediction vectors for measurement-level or simple voting for abstract-level from all local models.

By integrating these techniques, we explore both consensus-driven and diversity ensemble strategies for EEG signal classification under distributed constraints. This approach aligns well with clinical scenarios where data are fragmented across institutions or collection systems, and direct data sharing is restricted due to privacy, regulation, or logistical concerns.

3. Datasets and Experimental Results

The aim of this study is to investigate whether EEG data, when distributed across multiple sources, can be effectively utilized for classification using a dynamic ensemble selection approach. The experiments were conducted on two datasets.

The EEG Epilepsy dataset [23] contains exemplary segmented EEG time series recordings from ten epilepsy patients, collected at the Neurology & Sleep Centre in Hauz Khas, New Delhi. Data acquisition was performed using the Grass Telefactor Comet AS40 Amplification System, (manufactured by Grass Technologies, West Warwick, RI, USA). with a sampling frequency of 200 Hz. During the recordings, gold-plated scalp EEG electrodes were placed according to the standard 10–20 system. Although the publicly available dataset contains data for only one channel, the EEG signals were band-pass filtered between 0.5 and 70 Hz and then segmented into three seizure-related stages: pre-ictal, inter-ictal, and ictal. Each single-channel EEG segment was extracted from continuous recordings of multiple patients, and each segment was selected from different channels.

Each downloadable folder corresponds to one of these seizure stages and contains fifty MATLAB version 2022a .mat files. Each file includes a 1024-sample EEG time series segment, representing a 5.12 s duration. From the raw signals, 33 features were extracted per segment, in accordance with the feature extraction protocol described in [14]. These features include the following:

• Statistical features: mean, variance, skewness, kurtosis, root mean square (RMS), and zero crossings.
• Spectral power features: delta, theta, alpha, beta, gamma, and total power.
• Wavelet-based features: for decomposition levels 0 to 4, the mean, variance, skewness, and kurtosis of the wavelet coefficients were computed.

As was mentioned, each observation is a time series of 5.12 s at a frequency of 200 Hz, which gives 1024 points in time, and based on them, the time parameters for the object are calculated (one mat file). As a result, we obtain 150 objects in total. Although the data were originally provided as a single dataset, our objective was to evaluate the performance of a classification system based on distributed data sources, simulating scenarios where EEG data are decentralized. To this end, the original dataset was first split into two parts: a training set containing 120 observations and a test set of 30 observations. For the Epilepsy dataset, the classification was made for three classes—pre-ictal, ictal and post-ictal.

The BCI Competition IV Dataset 1 [24] contains EEG recordings from seven subjects performing motor imagery tasks (e.g., left hand, right hand, or foot) with both calibration and evaluation data. Calibration data include visual cues and labels, while evaluation data simulate real-world conditions with auditory cues and no labels. EEG signals were recorded from 59 channels at 1000 Hz. The dataset incorporates both real and artificially generated EEG data to assess the robustness of classification algorithms. The specific nature (real or artificial) of each dataset is undisclosed to participants. This dataset serves as a benchmark for developing and testing algorithms aimed at real-time, asynchronous detection of motor imagery in EEG signals, a critical component for practical BCI applications. The dataset with extracted features for BCI dataset contains 1400 objects with extracted features for each channel. The data were split into training (80%), evaluating (10%), and testing (10%) datasets. The data were split in a stratified way, preserving the relative proportions of each class.

Next, the training data were dispersed into multiple independent sources, referred to as local tables, to simulate distributed learning environments. To examine the scalability and robustness of the proposed dynamic ensemble selection model, we experimented with varying numbers of these local data sources. Specifically, we tested configurations with 3, 5, 7, 9, and 11 local tables. In each case, the training objects were randomly partitioned among the local tables using a stratified sampling strategy to preserve class distributions across all subsets.

To ensure the stability and reliability of the results, each experiment was repeated 10 times. Given the inherent randomness in some of the evaluated methods, a fixed set of 10 randomly selected seeds was used to enhance reproducibility. Each repetition was executed with a specific seed, consistently applied throughout the entire pipeline.

The evaluation of classification performance was conducted on the test set using a variety of metrics: Classification Accuracy (Acc), Recall, Precision (Prec.), Balanced Accuracy (BAcc), and the F1-score. To provide a more comprehensive assessment, two variants of the F1-score were calculated: macro-averaged F1, which treats all classes equally, and weighted F1, which accounts for class imbalance by weighting classes according to their support.

The results are summarized in

Table 1. Results of precision (Prec.), recall, F-measure (F-m.), balanced accuracy ($bacc$), and classification accuracy ($acc$) for the considered approaches for the EEG Epilepsy dataset Part 1. RF is the abbreviation Random Forest and kNN for k-Nearest Neighbors. (Blue text color represent best result).

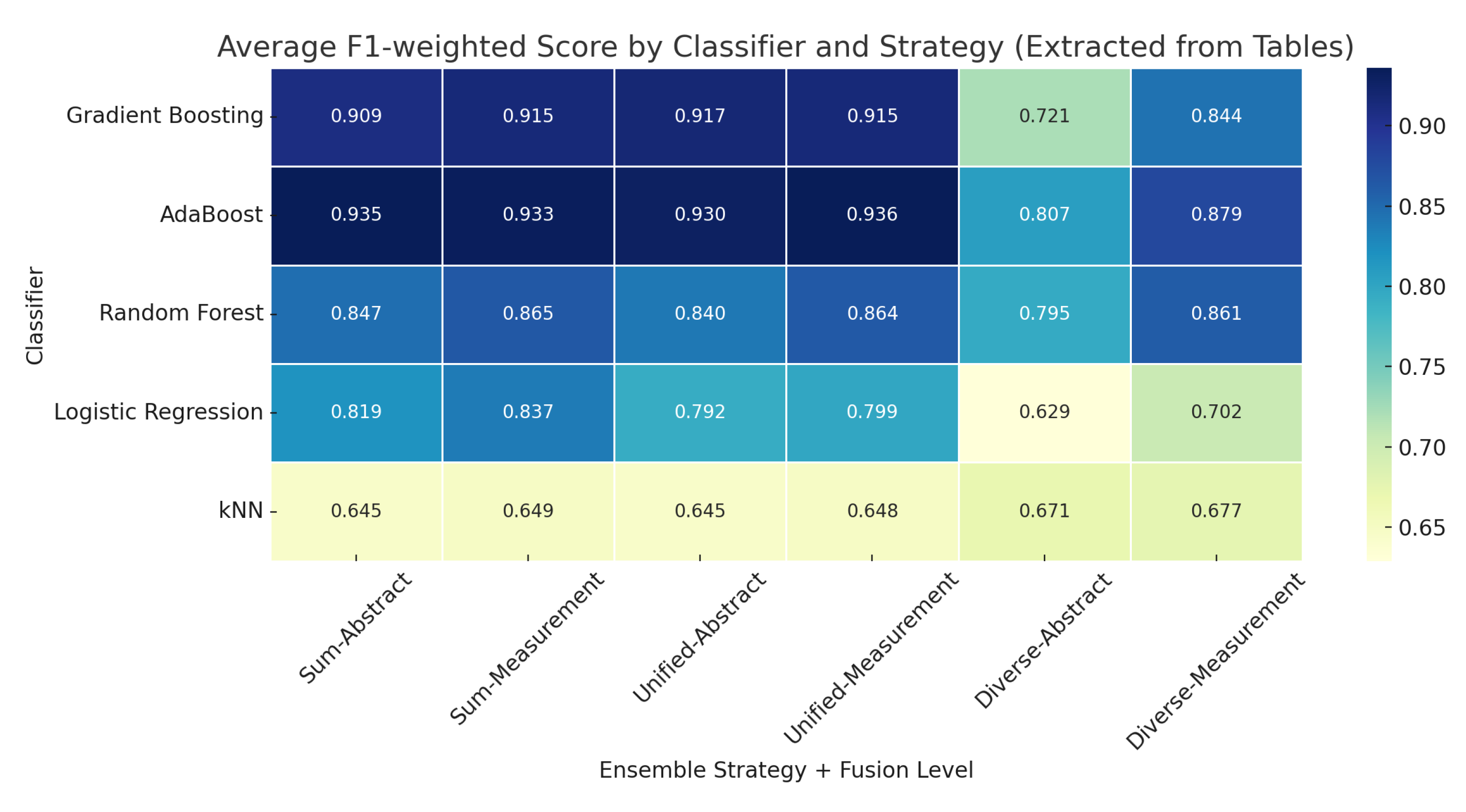
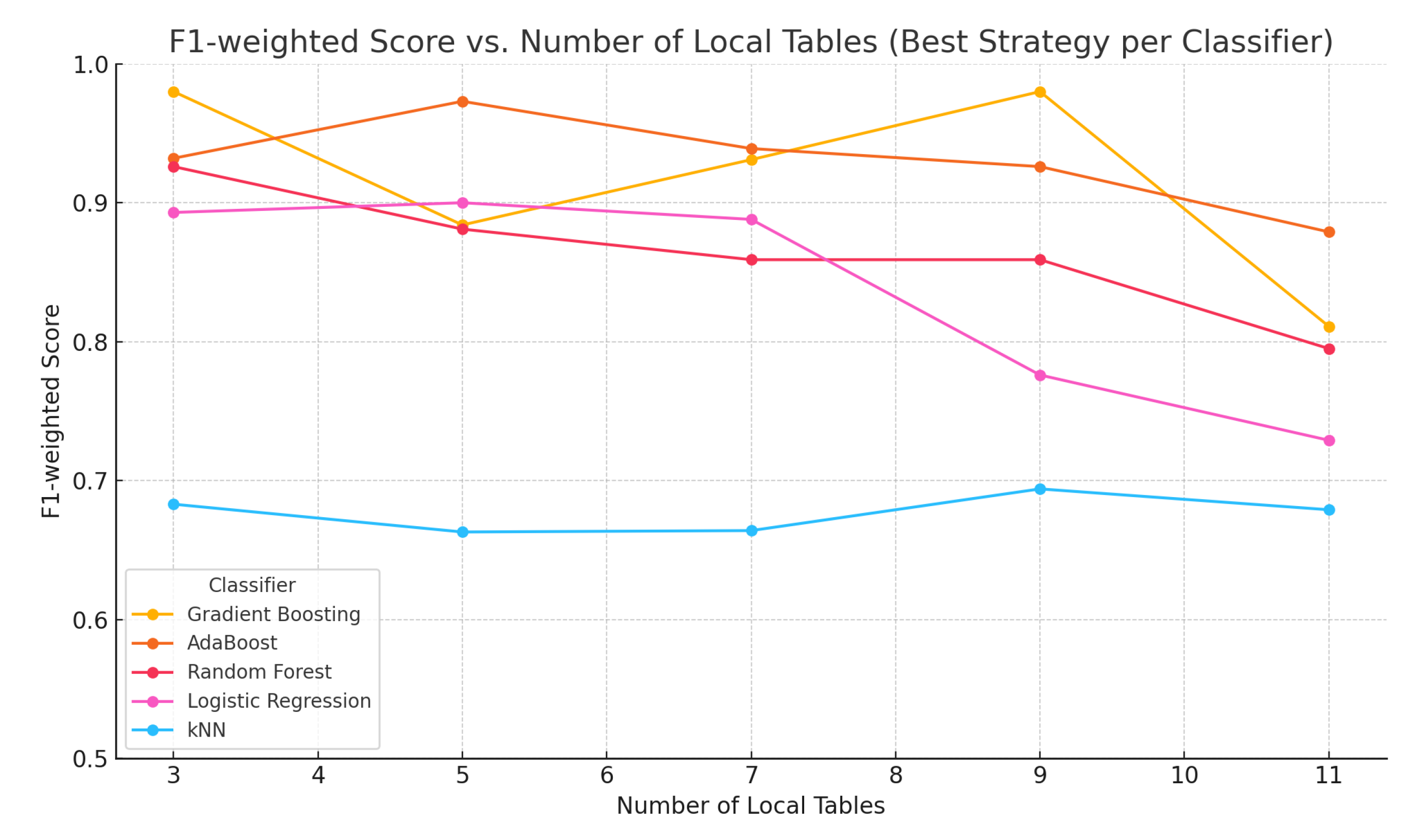
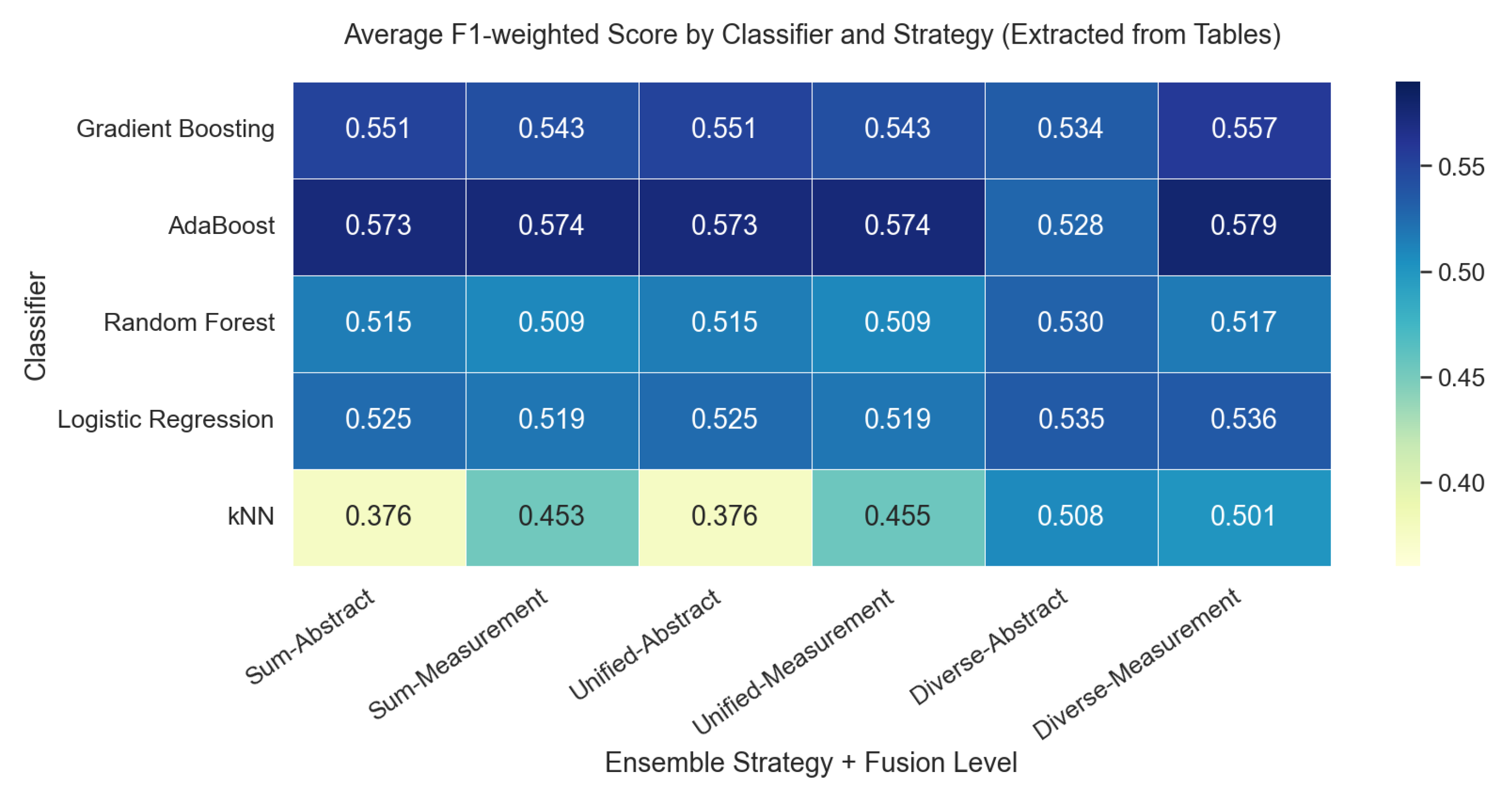
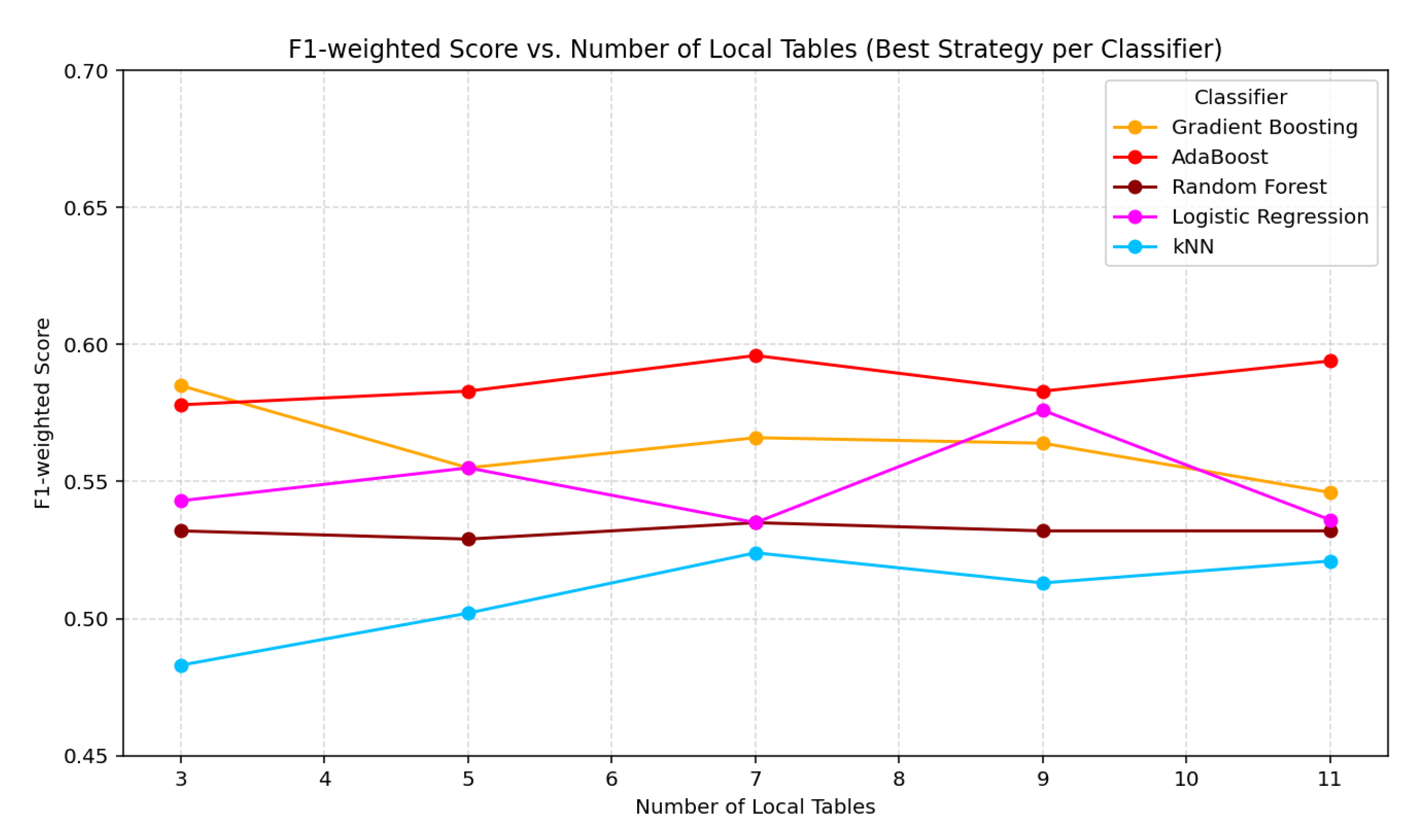
No. of Tables	Method/Model			F1	F1
		Prec.	Recall	(Weig.)	(Macro)	BAacc	Acc
3LT	Abstract level; sum; RF (100,gini)	0.903	0.893	0.892	0.892	0.893	0.893
	Measurement level; sum; RF (200,entropy)	0.94	0.927	0.926	0.926	0.927	0.927
	Unified groups; abstract level; RF (100,gini)	0.903	0.893	0.892	0.892	0.893	0.893
	Diverse groups; abstract level; RF (100,gini)	0.903	0.893	0.892	0.892	0.893	0.893
	Unified groups; measurement level; RF (200,entropy)	0.94	0.927	0.926	0.926	0.927	0.927
	Diverse groups; measurement level; RF (200,entropy)	0.94	0.927	0.926	0.926	0.927	0.927
	Abstract level; sum; kNN (2)	0.779	0.76	0.762	0.762	0.76	0.76
	Measurement level; sum; kNN (2)	0.746	0.727	0.723	0.723	0.727	0.727
	Unified groups; abstract level; kNN (2)	0.779	0.76	0.762	0.762	0.76	0.76
	Diverse groups; abstract level; kNN (2)	0.75	0.72	0.717	0.717	0.72	0.72
	Unified groups; measurement level; kNN (2)	0.736	0.72	0.721	0.721	0.72	0.72
	Diverse groups; measurement level; kNN (2)	0.712	0.68	0.683	0.683	0.68	0.68
	Abstract level; sum; AdaBoost (50)	0.946	0.933	0.932	0.932	0.933	0.933
	Measurement level; sum; AdaBoost (50)	0.946	0.933	0.932	0.932	0.933	0.933
	Unified groups; abstract level; AdaBoost (50)	0.946	0.933	0.932	0.932	0.933	0.933
	Diverse groups; abstract level; AdaBoost (50)	0.938	0.927	0.926	0.926	0.927	0.927
	Unified groups; measurement level; AdaBoost (50)	0.946	0.933	0.932	0.932	0.933	0.933
	Diverse groups; measurement level; AdaBoost (50)	0.946	0.933	0.932	0.932	0.933	0.933
	Abstract level; sum; Gradient Boosting (100)	0.972	0.967	0.966	0.966	0.967	0.967
	Measurement level; sum; Gradient Boosting (50)	0.961	0.953	0.953	0.953	0.953	0.953
	Unified groups; abstract level; Gradient Boosting (50)	0.983	0.98	0.98	0.98	0.98	0.98
	Diverse groups; abstract level; Gradient Boosting (50)	0.839	0.827	0.823	0.823	0.827	0.827
	Unified groups; measurement level; Gradient Boosting (50)	0.961	0.953	0.953	0.953	0.953	0.953
	Diverse groups; measurement level; Gradient Boosting (200)	0.902	0.893	0.892	0.892	0.893	0.893
	Abstract level; sum; Logistic Regression	0.878	0.873	0.874	0.874	0.873	0.873
	Measurement level; sum; Logistic Regression	0.899	0.893	0.893	0.893	0.893	0.893
	Unified groups; abstract level; Logistic Regression	0.878	0.873	0.874	0.874	0.873	0.873
	Diverse groups; abstract level; Logistic Regression	0.832	0.807	0.809	0.809	0.807	0.807
	Unified groups; measurement level; Logistic Regression	0.899	0.893	0.893	0.893	0.893	0.893
	Diverse groups; measurement level; Logistic Regression	0.87	0.853	0.855	0.855	0.853	0.853
5LT	Abstract level; sum; RF (10,entropy)	0.909	0.867	0.856	0.856	0.867	0.867
	Measurement level; sum; RF (10,gini)	0.918	0.887	0.882	0.882	0.887	0.887
	Unified groups; abstract level; RF (10,entropy)	0.909	0.867	0.856	0.856	0.867	0.867
	Diverse groups; abstract level; RF (20,gini)	0.866	0.82	0.807	0.807	0.82	0.82
	Unified groups; measurement level; RF (10,entropy)	0.919	0.887	0.881	0.881	0.887	0.887
	Diverse groups; measurement level; RF (50,gini)	0.9	0.867	0.86	0.86	0.867	0.867
	Abstract level; sum; kNN (2)	0.719	0.68	0.688	0.688	0.68	0.68
	Measurement level; sum; kNN (4)	0.715	0.673	0.681	0.681	0.673	0.673
	Unified groups; abstract level; kNN (2)	0.719	0.68	0.688	0.688	0.68	0.68
	Diverse groups; abstract level; kNN (4)	0.743	0.72	0.722	0.722	0.72	0.72
	Unified groups; measurement level; kNN (4)	0.715	0.673	0.681	0.681	0.673	0.673
	Diverse groups; measurement level; kNN (2)	0.705	0.673	0.663	0.663	0.673	0.673
	Abstract level; sum; AdaBoost (20)	0.957	0.947	0.946	0.946	0.947	0.947
	Measurement level; sum; AdaBoost (100)	0.963	0.953	0.952	0.952	0.953	0.953
	Unified groups; abstract level; AdaBoost (20)	0.978	0.973	0.973	0.973	0.973	0.973
	Diverse groups; abstract level; AdaBoost (10)	0.897	0.88	0.879	0.879	0.88	0.88
	Unified groups; measurement level; AdaBoost (20)	0.972	0.967	0.966	0.966	0.967	0.967
	Diverse groups; measurement level; AdaBoost (20)	0.91	0.893	0.891	0.891	0.893	0.893
	Abstract level; sum; Gradient Boosting (10)	0.899	0.867	0.857	0.857	0.867	0.867
	Measurement level; sum; Gradient Boosting (10)	0.907	0.893	0.892	0.892	0.893	0.893
	Unified groups; abstract level; Gradient Boosting (200)	0.9	0.887	0.884	0.884	0.887	0.887
	Diverse groups; abstract level; Gradient Boosting (200)	0.77	0.74	0.743	0.743	0.74	0.74
	Unified groups; measurement level; Gradient Boosting (10)	0.907	0.893	0.892	0.892	0.893	0.893
	Diverse groups; measurement level; Gradient Boosting (10)	0.878	0.86	0.859	0.859	0.86	0.86
	Abstract level; sum; Logistic Regression	0.9	0.86	0.86	0.86	0.86	0.86
	Measurement level; sum; Logistic Regression	0.927	0.9	0.9	0.9	0.9	0.9
	Unified groups; abstract level; Logistic Regression	0.874	0.84	0.836	0.836	0.84	0.84
	Diverse groups; abstract level; Logistic Regression	0.762	0.7	0.697	0.697	0.7	0.7
	Unified groups; measurement level; Logistic Regression	0.842	0.827	0.816	0.816	0.827	0.827
	Diverse groups; measurement level; Logistic Regression	0.874	0.847	0.847	0.847	0.847	0.847
7LT	Abstract level; sum; RF (20,gini)	0.853	0.827	0.818	0.818	0.827	0.827
	Measurement level; sum; RF (20,entropy)	0.913	0.88	0.875	0.875	0.88	0.88
	Unified groups; abstract level; RF (10,gini)	0.865	0.807	0.789	0.789	0.807	0.807
	Diverse groups; abstract level; RF (200,entropy)	0.778	0.76	0.753	0.753	0.76	0.76
	Unified groups; measurement level; RF (100,entropy)	0.907	0.867	0.859	0.859	0.867	0.867
	Diverse groups; measurement level; RF (20,entropy)	0.915	0.887	0.881	0.881	0.887	0.887
	Abstract level; sum; kNN (3)	0.619	0.58	0.582	0.582	0.58	0.58
	Measurement level; sum; kNN (3)	0.66	0.647	0.613	0.613	0.647	0.647
	Unified groups; abstract level; kNN (3)	0.619	0.58	0.582	0.582	0.58	0.58
	Diverse groups; abstract level; kNN (5)	0.663	0.633	0.595	0.595	0.633	0.633
	Unified groups; measurement level; kNN (3)	0.66	0.647	0.613	0.613	0.647	0.647
	Diverse groups; measurement level; kNN (3)	0.707	0.687	0.664	0.664	0.687	0.687
	Abstract level; sum; AdaBoost (100)	0.952	0.94	0.939	0.939	0.94	0.94
	Measurement level; sum; AdaBoost (50)	0.952	0.94	0.939	0.939	0.94	0.94
	Unified groups; abstract level; AdaBoost (20)	0.956	0.94	0.939	0.939	0.94	0.94
	Diverse groups; abstract level; AdaBoost (100)	0.899	0.88	0.878	0.878	0.88	0.88
	Unified groups; measurement level; AdaBoost (20)	0.957	0.947	0.945	0.945	0.947	0.947
	Diverse groups; measurement level; AdaBoost (100)	0.967	0.96	0.959	0.959	0.96	0.96
	Abstract level; sum; Gradient Boosting (10)	0.952	0.94	0.938	0.938	0.94	0.94
	Measurement level; sum; Gradient Boosting (100)	0.967	0.96	0.959	0.959	0.96	0.96
	Unified groups; abstract level; Gradient Boosting (10)	0.944	0.933	0.931	0.931	0.933	0.933
	Diverse groups; abstract level; Gradient Boosting (200)	0.76	0.733	0.717	0.717	0.733	0.733
	Unified groups; measurement level; Gradient Boosting (100)	0.963	0.953	0.95	0.95	0.953	0.953
	Diverse groups; measurement level; Gradient Boosting (200)	0.899	0.887	0.882	0.882	0.887	0.887
	Abstract level; sum; Logistic Regression	0.923	0.893	0.888	0.888	0.893	0.893
	Measurement level; sum; Logistic Regression	0.923	0.893	0.888	0.888	0.893	0.893
	Unified groups; abstract level; Logistic Regression	0.841	0.833	0.83	0.83	0.833	0.833
	Diverse groups; abstract level; Logistic Regression	0.663	0.593	0.574	0.574	0.593	0.593
	Unified groups; measurement level; Logistic Regression	0.865	0.86	0.858	0.858	0.86	0.86
	Diverse groups; measurement level; Logistic Regression	0.734	0.66	0.652	0.652	0.66	0.66

and

Table 2. Results of precision (Prec.), recall, F-measure (F-m.), balanced accuracy ($bacc$), and classification accuracy ($acc$) for the considered approaches for the EEG Epilepsy dataset Part 2. RF is the abbreviation Random Forest and kNN for k-Nearest Neighbors. (Blue text color and bold represent best result).

No. of Tables	Method/Model			F1	F1
		Prec.	Recall	(Weig.)	(Macro)	BAacc	Acc
9LT	Abstract level; sum; RF (200,gini)	0.918	0.887	0.882	0.882	0.887	0.887
	Measurement level; sum; RF (20,gini)	0.906	0.86	0.85	0.85	0.86	0.86
	Unified groups; abstract level; RF (200,gini)	0.918	0.887	0.882	0.882	0.887	0.887
	Diverse groups; abstract level; RF (200,gini)	0.849	0.827	0.824	0.824	0.827	0.827
	Unified groups; measurement level; RF (10,gini)	0.907	0.867	0.859	0.859	0.867	0.867
	Diverse groups; measurement level; RF (20,entropy)	0.884	0.84	0.83	0.83	0.84	0.84
	Abstract level; sum; kNN (6)	0.707	0.687	0.664	0.664	0.687	0.687
	Measurement level; sum; kNN (6)	0.776	0.687	0.664	0.664	0.687	0.687
	Unified groups; abstract level; kNN (6)	0.707	0.687	0.664	0.664	0.687	0.687
	Diverse groups; abstract level; kNN (6)	0.788	0.727	0.681	0.681	0.727	0.727
	Unified groups; measurement level; kNN (6)	0.776	0.687	0.664	0.664	0.687	0.687
	Diverse groups; measurement level; kNN (2)	0.727	0.687	0.694	0.694	0.687	0.687
	Abstract level; sum; AdaBoost (100)	0.953	0.94	0.939	0.939	0.94	0.94
	Measurement level; sum; AdaBoost (50)	0.934	0.927	0.926	0.926	0.927	0.927
	Unified groups; abstract level; AdaBoost (50)	0.938	0.927	0.926	0.926	0.927	0.927
	Diverse groups; abstract level; AdaBoost (100)	0.747	0.713	0.714	0.714	0.713	0.713
	Unified groups; measurement level; AdaBoost (20)	0.928	0.92	0.92	0.92	0.92	0.92
	Diverse groups; measurement level; AdaBoost (10)	0.912	0.893	0.892	0.892	0.893	0.893
	Abstract level; sum; Gradient Boosting (10)	0.967	0.96	0.959	0.959	0.96	0.96
	Measurement level; sum; Gradient Boosting (10)	0.964	0.953	0.952	0.952	0.953	0.953
	Unified groups; abstract level; Gradient Boosting (10)	0.985	0.98	0.98	0.98	0.98	0.98
	Diverse groups; abstract level; Gradient Boosting (20)	0.672	0.653	0.655	0.655	0.653	0.653
	Unified groups; measurement level; Gradient Boosting (10)	0.989	0.987	0.987	0.987	0.987	0.987
	Diverse groups; measurement level; Gradient Boosting (100)	0.763	0.733	0.738	0.738	0.733	0.733
	Abstract level; sum; Logistic Regression	0.782	0.767	0.765	0.765	0.767	0.767
	Measurement level; sum; Logistic Regression	0.791	0.78	0.776	0.776	0.78	0.78
	Unified groups; abstract level; Logistic Regression	0.771	0.74	0.742	0.742	0.74	0.74
	Diverse groups; abstract level; Logistic Regression	0.541	0.553	0.535	0.535	0.553	0.553
	Unified groups; measurement level; Logistic Regression	0.779	0.733	0.739	0.739	0.733	0.733
	Diverse groups; measurement level; Logistic Regression	0.712	0.58	0.577	0.577	0.58	0.58
11LT	Abstract level; sum; RF (100,entropy)	0.879	0.807	0.787	0.787	0.807	0.807
	Measurement level; sum; RF (10,gini)	0.882	0.82	0.793	0.793	0.82	0.82
	Unified groups; abstract level; RF (200,gini)	0.861	0.8	0.78	0.78	0.8	0.8
	Diverse groups; abstract level; RF (20,gini)	0.749	0.713	0.698	0.698	0.713	0.713
	Unified groups; measurement level; RF (100,gini)	0.882	0.813	0.795	0.795	0.813	0.813
	Diverse groups; measurement level; RF (100,entropy)	0.889	0.827	0.81	0.81	0.827	0.827
	Abstract level; sum; kNN (2)	0.742	0.62	0.527	0.527	0.62	0.62
	Measurement level; sum; kNN (5)	0.594	0.613	0.563	0.563	0.613	0.613
	Unified groups; abstract level; kNN (2)	0.742	0.62	0.527	0.527	0.62	0.62
	Diverse groups; abstract level; kNN (2)	0.673	0.64	0.641	0.641	0.64	0.64
	Unified groups; measurement level; kNN (5)	0.594	0.613	0.563	0.563	0.613	0.613
	Diverse groups; measurement level; kNN (3)	0.818	0.707	0.679	0.679	0.707	0.707
	Abstract level; sum; AdaBoost (50)	0.924	0.92	0.92	0.92	0.92	0.92
	Measurement level; sum; AdaBoost (100)	0.938	0.92	0.918	0.918	0.92	0.92
	Unified groups; abstract level; AdaBoost (50)	0.89	0.88	0.879	0.879	0.88	0.88
	Diverse groups; abstract level; AdaBoost (10)	0.709	0.64	0.637	0.637	0.64	0.64
	Unified groups; measurement level; AdaBoost (50)	0.932	0.92	0.918	0.918	0.92	0.92
	Diverse groups; measurement level; AdaBoost (20)	0.786	0.74	0.721	0.721	0.74	0.74
	Abstract level; sum; Gradient Boosting (10)	0.87	0.833	0.825	0.825	0.833	0.833
	Measurement level; sum; Gradient Boosting (20)	0.853	0.827	0.82	0.82	0.827	0.827
	Unified groups; abstract level; Gradient Boosting (10)	0.844	0.82	0.811	0.811	0.82	0.82
	Diverse groups; abstract level; Gradient Boosting (10)	0.685	0.673	0.665	0.665	0.673	0.673
	Unified groups; measurement level; Gradient Boosting (20)	0.813	0.8	0.793	0.793	0.8	0.8
	Diverse groups; measurement level; Gradient Boosting (20)	0.86	0.853	0.851	0.851	0.853	0.853
	Abstract level; sum; Logistic Regression	0.799	0.727	0.71	0.71	0.727	0.727
	Measurement level; sum; Logistic Regression	0.809	0.74	0.729	0.729	0.74	0.74
	Unified groups; abstract level; Logistic Regression	0.765	0.687	0.68	0.68	0.687	0.687
	Diverse groups; abstract level; Logistic Regression	0.585	0.54	0.529	0.529	0.54	0.54
	Unified groups; measurement level; Logistic Regression	0.777	0.707	0.687	0.687	0.707	0.707
	Diverse groups; measurement level; Logistic Regression	0.618	0.58	0.581	0.581	0.58	0.58

(for the EEG Epilepsy dataset) and

Table 3. Results of precision (Prec.), recall, F-measure (F-m.), balanced accuracy ($bacc$), and classification accuracy ($acc$) for the considered approaches for the BCI Competition IV Dataset 1 Part 1. RF is the abbreviation Random Forest and kNN for k-Nearest Neighbors. (Blue text color represent best result).

No. of Tables	Method/Model			F1	F1
		Prec.	Recall	(Weig.)	(Macro)	BAacc	Acc
3LT	Abstract level; sum; RF (10,gini)	0.533	0.533	0.532	0.532	0.533	0.533
	Measurement level; sum; RF (50,entropy)	0.52	0.519	0.518	0.518	0.519	0.519
	Unified groups; abstract level; RF (10,gini)	0.533	0.533	0.532	0.532	0.533	0.533
	Diverse groups; abstract level; RF (10,entropy)	0.523	0.523	0.522	0.522	0.523	0.523
	Unified groups; measurement level; RF (50,entropy)	0.52	0.519	0.518	0.518	0.519	0.519
	Diverse groups; measurement level; RF (50,gini)	0.521	0.52	0.518	0.518	0.52	0.52
	Abstract level; sum; kNN (2)	0.467	0.484	0.408	0.408	0.484	0.484
	Measurement level; sum; kNN (4)	0.473	0.474	0.466	0.466	0.474	0.474
	Unified groups; abstract level; kNN (2)	0.467	0.484	0.408	0.408	0.484	0.484
	Diverse groups; abstract level; kNN (2)	0.528	0.519	0.478	0.478	0.519	0.519
	Unified groups; measurement level; kNN (4)	0.468	0.468	0.467	0.467	0.468	0.468
	Diverse groups; measurement level; kNN (4)	0.483	0.484	0.483	0.483	0.484	0.484
	Abstract level; sum; AdaBoost (10)	0.574	0.571	0.566	0.566	0.571	0.571
	Measurement level; sum; AdaBoost (200)	0.582	0.58	0.578	0.578	0.58	0.58
	Unified groups; abstract level; AdaBoost (10)	0.574	0.571	0.566	0.566	0.571	0.571
	Diverse groups; abstract level; AdaBoost (10)	0.555	0.554	0.553	0.553	0.554	0.554
	Unified groups; measurement level; AdaBoost (200)	0.582	0.58	0.578	0.578	0.58	0.58
	Diverse groups; measurement level; AdaBoost (10)	0.581	0.58	0.578	0.578	0.58	0.58
	Abstract level; sum; Gradient Boosting (20)	0.586	0.586	0.585	0.585	0.586	0.586
	Measurement level; sum; Gradient Boosting (20)	0.561	0.56	0.559	0.559	0.56	0.56
	Unified groups; abstract level; Gradient Boosting (20)	0.586	0.586	0.585	0.585	0.586	0.586
	Diverse groups; abstract level; Gradient Boosting (20)	0.556	0.555	0.554	0.554	0.555	0.555
	Unified groups; measurement level; Gradient Boosting (20)	0.561	0.56	0.559	0.559	0.56	0.56
	Diverse groups; measurement level; Gradient Boosting (200)	0.558	0.556	0.554	0.554	0.556	0.556
	Abstract level; sum; Logistic Regression	0.537	0.536	0.536	0.536	0.536	0.536
	Measurement level; sum; Logistic Regression	0.519	0.519	0.519	0.519	0.519	0.519
	Unified groups; abstract level; Logistic Regression	0.537	0.536	0.536	0.536	0.536	0.536
	Diverse groups; abstract level; Logistic Regression	0.542	0.542	0.541	0.541	0.542	0.542
	Unified groups; measurement level; Logistic Regression	0.519	0.519	0.519	0.519	0.519	0.519
	Diverse groups; measurement level; Logistic Regression	0.544	0.544	0.543	0.543	0.544	0.544
5LT	Abstract level; sum; RF (10,entropy)	0.506	0.506	0.504	0.504	0.506	0.506
	Measurement level; sum; RF (20,entropy)	0.507	0.506	0.504	0.504	0.506	0.506
	Unified groups; abstract level; RF (10,entropy)	0.506	0.506	0.504	0.504	0.506	0.506
	Diverse groups; abstract level; RF (100,entropy)	0.53	0.53	0.529	0.529	0.53	0.53
	Unified groups; measurement level; RF (20,entropy)	0.507	0.506	0.504	0.504	0.506	0.506
	Diverse groups; measurement level; RF (200,entropy)	0.521	0.521	0.519	0.519	0.521	0.521
	Abstract level; sum; kNN (2)	0.421	0.476	0.368	0.368	0.476	0.476
	Measurement level; sum; kNN (3)	0.473	0.473	0.472	0.472	0.473	0.473
	Unified groups; abstract level; kNN (2)	0.421	0.476	0.368	0.368	0.476	0.476
	Diverse groups; abstract level; kNN (2)	0.517	0.516	0.502	0.502	0.516	0.516
	Unified groups; measurement level; kNN (3)	0.473	0.473	0.472	0.472	0.473	0.473
	Diverse groups; measurement level; kNN (6)	0.501	0.501	0.5	0.5	0.501	0.501
	Abstract level; sum; AdaBoost (200)	0.568	0.567	0.566	0.566	0.567	0.567
	Measurement level; sum; AdaBoost (20)	0.582	0.581	0.581	0.581	0.581	0.581
	Unified groups; abstract level; AdaBoost (200)	0.568	0.567	0.566	0.566	0.567	0.567
	Diverse groups; abstract level; AdaBoost (20)	0.521	0.521	0.52	0.52	0.521	0.521
	Unified groups; measurement level; AdaBoost (20)	0.582	0.581	0.581	0.581	0.581	0.581
	Diverse groups; measurement level; AdaBoost (20)	0.584	0.584	0.583	0.583	0.584	0.584
	Abstract level; sum; Gradient Boosting (20)	0.557	0.556	0.555	0.555	0.556	0.556
	Measurement level; sum; Gradient Boosting (10)	0.559	0.557	0.554	0.554	0.557	0.557
	Unified groups; abstract level; Gradient Boosting (20)	0.557	0.556	0.555	0.555	0.556	0.556
	Diverse groups; abstract level; Gradient Boosting (100)	0.534	0.534	0.533	0.533	0.534	0.534
	Unified groups; measurement level; Gradient Boosting (10)	0.559	0.557	0.554	0.554	0.557	0.557
	Diverse groups; measurement level; Gradient Boosting (50)	0.555	0.555	0.555	0.555	0.555	0.555
	Abstract level; sum; Logistic Regression	0.508	0.508	0.506	0.506	0.508	0.508
	Measurement level; sum; Logistic Regression	0.513	0.513	0.513	0.513	0.513	0.513
	Unified groups; abstract level; Logistic Regression	0.508	0.508	0.506	0.506	0.508	0.508
	Diverse groups; abstract level; Logistic Regression	0.531	0.531	0.529	0.529	0.531	0.531
	Unified groups; measurement level; Logistic Regression	0.513	0.513	0.513	0.513	0.513	0.513
	Diverse groups; measurement level; Logistic Regression	0.555	0.555	0.555	0.555	0.555	0.555
7LT	Abstract level; sum; RF (50,entropy)	0.521	0.521	0.52	0.52	0.521	0.521
	Measurement level; sum; RF (10,gini)	0.511	0.511	0.51	0.51	0.511	0.511
	Unified groups; abstract level; RF (50,entropy)	0.521	0.521	0.52	0.52	0.521	0.521
	Diverse groups; abstract level; RF (100,entropy)	0.537	0.536	0.535	0.535	0.536	0.536
	Unified groups; measurement level; RF (10,gini)	0.511	0.511	0.51	0.51	0.511	0.511
	Diverse groups; measurement level; RF (10,gini)	0.521	0.521	0.518	0.518	0.521	0.521
	Abstract level; sum; kNN (2)	0.419	0.483	0.357	0.357	0.483	0.483
	Measurement level; sum; kNN (2)	0.441	0.449	0.428	0.428	0.449	0.449
	Unified groups; abstract level; kNN (2)	0.419	0.483	0.357	0.357	0.483	0.483
	Diverse groups; abstract level; kNN (2)	0.531	0.529	0.524	0.524	0.529	0.529
	Unified groups; measurement level; kNN (2)	0.442	0.444	0.438	0.438	0.444	0.444
	Diverse groups; measurement level; kNN (5)	0.519	0.518	0.512	0.512	0.518	0.518
	Abstract level; sum; AdaBoost (10)	0.601	0.599	0.596	0.596	0.599	0.599
	Measurement level; sum; AdaBoost (50)	0.586	0.584	0.582	0.582	0.584	0.584
	Unified groups; abstract level; AdaBoost (10)	0.601	0.599	0.596	0.596	0.599	0.599
	Diverse groups; abstract level; AdaBoost (10)	0.524	0.524	0.524	0.524	0.524	0.524
	Unified groups; measurement level; AdaBoost (50)	0.586	0.584	0.582	0.582	0.584	0.584
	Diverse groups; measurement level; AdaBoost (10)	0.575	0.575	0.574	0.574	0.575	0.575
	Abstract level; sum; Gradient Boosting (50)	0.557	0.556	0.555	0.555	0.556	0.556
	Measurement level; sum; Gradient Boosting (50)	0.558	0.558	0.557	0.557	0.558	0.558
	Unified groups; abstract level; Gradient Boosting (50)	0.557	0.556	0.555	0.555	0.556	0.556
	Diverse groups; abstract level; Gradient Boosting (200)	0.529	0.529	0.528	0.528	0.529	0.529
	Unified groups; measurement level; Gradient Boosting (50)	0.558	0.558	0.557	0.557	0.558	0.558
	Diverse groups; measurement level; Gradient Boosting (20)	0.568	0.567	0.566	0.566	0.567	0.567
	Abstract level; sum; Logistic Regression	0.478	0.479	0.478	0.478	0.479	0.479
	Measurement level; sum; Logistic Regression	0.481	0.481	0.48	0.48	0.481	0.481
	Unified groups; abstract level; Logistic Regression	0.478	0.479	0.478	0.478	0.479	0.479
	Diverse groups; abstract level; Logistic Regression	0.536	0.536	0.534	0.534	0.536	0.536
	Unified groups; measurement level; Logistic Regression	0.481	0.481	0.48	0.48	0.481	0.481
	Diverse groups; measurement level; Logistic Regression	0.535	0.535	0.535	0.535	0.535	0.535

and

Table 4. Results of precision (Prec.), recall, F-measure (F-m.), balanced accuracy ($bacc$), and classification accuracy ($acc$) for the considered approaches for the BCI Competition IV Dataset 1 Part 2. RF is the abbreviation Random Forest and kNN for k-Nearest Neighbors. (Blue text color represent best result).

No. of Tables	Method/Model			F1	F1
		Prec.	Recall	(Weig.)	(Macro)	BAacc	Acc
9LT	Abstract level; sum; RF (10,gini)	0.509	0.509	0.507	0.507	0.509	0.509
	Measurement level; sum; RF (10,entropy)	0.518	0.518	0.516	0.516	0.518	0.518
	Unified groups; abstract level; RF (10,gini)	0.509	0.509	0.507	0.507	0.509	0.509
	Diverse groups; abstract level; RF (100,entropy)	0.533	0.533	0.532	0.532	0.533	0.533
	Unified groups; measurement level; RF (10,entropy)	0.518	0.518	0.516	0.516	0.518	0.518
	Diverse groups; measurement level; RF (10,entropy)	0.525	0.524	0.522	0.522	0.524	0.524
	Abstract level; sum; kNN (4)	0.473	0.496	0.371	0.371	0.496	0.496
	Measurement level; sum; kNN (5)	0.454	0.454	0.454	0.454	0.454	0.454
	Unified groups; abstract level; kNN (4)	0.473	0.496	0.371	0.371	0.496	0.496
	Diverse groups; abstract level; kNN (6)	0.514	0.514	0.513	0.513	0.514	0.514
	Unified groups; measurement level; kNN (5)	0.454	0.454	0.454	0.454	0.454	0.454
	Diverse groups; measurement level; kNN (5)	0.51	0.51	0.507	0.507	0.51	0.51
	Abstract level; sum; AdaBoost (100)	0.565	0.565	0.565	0.565	0.565	0.565
	Measurement level; sum; AdaBoost (100)	0.535	0.534	0.533	0.533	0.534	0.534
	Unified groups; abstract level; AdaBoost (100)	0.565	0.565	0.565	0.565	0.565	0.565
	Diverse groups; abstract level; AdaBoost (20)	0.52	0.52	0.52	0.52	0.52	0.52
	Unified groups; measurement level; AdaBoost (100)	0.535	0.534	0.533	0.533	0.534	0.534
	Diverse groups; measurement level; AdaBoost (50)	0.589	0.586	0.583	0.583	0.586	0.586
	Abstract level; sum; Gradient Boosting (10)	0.535	0.534	0.533	0.533	0.534	0.534
	Measurement level; sum; Gradient Boosting (20)	0.519	0.519	0.517	0.517	0.519	0.519
	Unified groups; abstract level; Gradient Boosting (20)	0.535	0.534	0.533	0.533	0.534	0.534
	Diverse groups; abstract level; Gradient Boosting (20)	0.529	0.529	0.528	0.528	0.529	0.529
	Unified groups; measurement level; Gradient Boosting (50)	0.519	0.519	0.517	0.517	0.519	0.519
	Diverse groups; measurement level; Gradient Boosting (20)	0.566	0.565	0.564	0.564	0.565	0.565
	Abstract level; sum; Logistic Regression	0.578	0.577	0.576	0.576	0.577	0.577
	Measurement level; sum; Logistic Regression	0.574	0.574	0.572	0.572	0.574	0.574
	Unified groups; abstract level; Logistic Regression	0.578	0.577	0.576	0.576	0.577	0.577
	Diverse groups; abstract level; Logistic Regression	0.539	0.539	0.537	0.537	0.539	0.539
	Unified groups; measurement level; Logistic Regression	0.574	0.574	0.572	0.572	0.574	0.574
	Diverse groups; measurement level; Logistic Regression	0.51	0.51	0.51	0.51	0.51	0.51
11LT	Abstract level; sum; RF (10,entropy)	0.517	0.516	0.51	0.51	0.516	0.516
	Measurement level; sum; RF (10,gini)	0.497	0.497	0.495	0.495	0.497	0.497
	Unified groups; abstract level; RF (10,entropy)	0.517	0.516	0.51	0.51	0.516	0.516
	Diverse groups; abstract level; RF (100,entropy)	0.533	0.533	0.532	0.532	0.533	0.533
	Unified groups; measurement level; RF (10,gini)	0.497	0.497	0.495	0.495	0.497	0.497
	Diverse groups; measurement level; RF (50,entropy)	0.521	0.519	0.51	0.51	0.519	0.519
	Abstract level; sum; kNN (4)	0.539	0.506	0.377	0.377	0.506	0.506
	Measurement level; sum; kNN (7)	0.451	0.454	0.445	0.445	0.454	0.454
	Unified groups; abstract level; kNN (4)	0.539	0.506	0.377	0.377	0.506	0.506
	Diverse groups; abstract level; kNN (2)	0.524	0.524	0.521	0.521	0.524	0.524
	Unified groups; measurement level; kNN (7)	0.451	0.454	0.445	0.445	0.454	0.454
	Diverse groups; measurement level; kNN (4)	0.503	0.503	0.502	0.502	0.503	0.503
	Abstract level; sum; AdaBoost (10)	0.579	0.577	0.574	0.574	0.577	0.577
	Measurement level; sum; AdaBoost (20)	0.6	0.597	0.594	0.594	0.597	0.597
	Unified groups; abstract level; AdaBoost (10)	0.579	0.577	0.574	0.574	0.577	0.577
	Diverse groups; abstract level; AdaBoost (10)	0.522	0.522	0.522	0.522	0.522	0.522
	Unified groups; measurement level; AdaBoost (20)	0.6	0.597	0.594	0.594	0.597	0.597
	Diverse groups; measurement level; AdaBoost (20)	0.579	0.576	0.573	0.573	0.576	0.576
	Abstract level; sum; Gradient Boosting (10)	0.528	0.528	0.527	0.527	0.528	0.528
	Measurement level; sum; Gradient Boosting (50)	0.527	0.526	0.526	0.526	0.526	0.526
	Unified groups; abstract level; Gradient Boosting (10)	0.528	0.528	0.527	0.527	0.528	0.528
	Diverse groups; abstract level; Gradient Boosting (200)	0.529	0.529	0.529	0.529	0.529	0.529
	Unified groups; measurement level; Gradient Boosting (50)	0.527	0.526	0.526	0.526	0.526	0.526
	Diverse groups; measurement level; Gradient Boosting (100)	0.548	0.548	0.546	0.546	0.548	0.548
	Abstract level; sum; Logistic Regression	0.528	0.528	0.527	0.527	0.528	0.528
	Measurement level; sum; Logistic Regression	0.513	0.513	0.511	0.511	0.513	0.513
	Unified groups; abstract level; Logistic Regression	0.528	0.528	0.527	0.527	0.528	0.528
	Diverse groups; abstract level; Logistic Regression	0.536	0.536	0.534	0.534	0.536	0.536
	Unified groups; measurement level; Logistic Regression	0.513	0.513	0.511	0.511	0.513	0.513
	Diverse groups; measurement level; Logistic Regression	0.54	0.539	0.536	0.536	0.539	0.539

(for the BCI Competition IV Dataset 1), presenting averaged metric values from all 10 achieved metrics. The dataset, characterized by varying degrees of dispersion (indicated by annotations such as ‘3LT’, meaning the dataset has been divided into three separate local tables), is evaluated using three approaches: without coalitions, with coalitions representing agents’ agreement, and with coalitions representing agents’ disagreement. The following notations are used:

• Abstract level, sum: Each local classifier (Random Forest, AdaBoost, Gradient Boosting, k-Nearest Neighbours, and Logistic Regression) makes an independent prediction, one decision class. The final decision is the result of majority voting.
• Probability level, sum: Each local classifier makes an independent prediction. The resulting probability vectors are summed element-wise, and the class with the highest aggregated score is selected as the final decision.
• Unified groups, abstract level: Models are grouped using compliance coalition formation. One strongest coalition makes the final decision by voting.
• Diverse groups, abstract level: Models are grouped using diversified coalition formation. One strongest coalition makes the final decision by voting.
• Unified groups, measurement level: Models are grouped using compliance coalition formation. One strongest coalition prediction vectors are summed. The final class is the one with the highest aggregated score.
• Diverse groups, measurement level: Models are grouped using diversified coalition formation. One strongest coalition prediction vectors are summed. The final class is the one with the highest aggregated score.

All methods and experiments were implemented in Python 3.12, utilizing the scikit-learn library for the implementation of classifiers such as Random Forest, AdaBoost, Gradient Boosting, and Logistic Regression, as well as NumPy and Pandas for efficient data processing and analysis. To assess the influence of hyperparameter settings on model performance, a comprehensive evaluation of selected configurations was conducted for each classification algorithm. The following ranges of hyperparameters were examined:

• Random Forest: The number of estimators (n_estimators) was varied among $\{10,20,50,$$100,200\}$. Two splitting criteria were evaluated: gini and entropy. The maximum depth of trees was fixed at max_depth = 6, while the minimum number of samples required to split an internal node (min_samples_split) was tested with values $\{2,3,4\}$.
• AdaBoost: The ensemble size was controlled by varying n_estimators in $\{10,20,50,$$100,200\}$. Two boosting algorithms were considered: SAMME and SAMME.R. Additionally, the learning_rate parameter was evaluated with values $\{0.1,0.5,$$1.0,1.5\}$ to control the contribution of each weak learner.
• Gradient Boosting: The number of boosting stages (n_estimators) was set to values among $\{10,20,50,$$100,200\}$, with the learning_rate adjusted across $\{0.1,0.5,1.0\}$. The maximum depth of each individual regression estimator (max_depth) was varied within $\{3,4,5,6\}$.
• Logistic Regression: The following solvers were evaluated: lbfgs, liblinear, sag, saga, and newton-cg. The class_weight parameter was set either to balanced or none to assess the impact of handling class imbalance. Regularization was controlled via the penalty parameter, which was tested with values l1, l2, and None.

The tables report the best performance achieved for each configuration, along with the corresponding number of estimators that obtained this result. For each dataset, the highest-performing outcome is indicated, with the best result highlighted to facilitate comparison across different configurations.

The experimental results for the EEG Epilepsy dataset presented in Table 1 and Table 2 provide clear evidence supporting the effectiveness of the proposed approach based on dynamic ensemble selection over distributed EEG data sources. Among the evaluated classifiers, Gradient Boosting demonstrated the most robust and consistently high performance across varying levels of data dispersion. Notably, the unified groups strategy, particularly when applied at the measurement level, achieved the highest classification scores. In the configuration with nine local tables (9LT), Gradient Boosting combined with measurement-level unified coalition selection achieved an F1-score of 0.987, balanced accuracy (BAacc) of 0.987, and overall classification accuracy of 0.987—the best results across all tested configurations.

AdaBoost also yielded high performance, particularly with three to seven local tables, achieving F1-scores above 0.93 in multiple scenarios. In contrast, Random Forest achieved moderately strong results but consistently lagged behind the boosting methods. Logistic Regression and k-Nearest Neighbors (kNN) exhibited significantly lower performance, especially as the number of local tables increased, indicating sensitivity to data sparsity and limitations in capturing complex patterns in a decentralized setting.

Figure 1 illustrates the comparative performance for the EEG Epilepsy dataset of various classifiers across different ensemble strategies and fusion levels. The x-axis represents the ensemble strategy combined with the fusion level (e.g., Sum–Abstract, Unified–Measurement, Diverse–Measurement), while the y-axis lists the classifiers evaluated (Gradient Boosting, AdaBoost, Random Forest, Logistic Regression, kNN). The color-coded values indicate the average F1-weighted score, computed across all levels of data dispersion (3 to 11 local tables). As shown, Gradient Boosting combined with the unified strategy consistently achieves the highest performance, clearly outperforming the other approaches.

A comparison of dynamic ensemble selection strategies with conflict analysis revealed that unified coalition approaches consistently outperformed both simple probability-based voting and diverse coalition models. While the probability sum method remained competitive in several configurations, it was outclassed by coalition-based strategies. In contrast, the diverse groups strategy, which aggregates classifiers with conflicting predictions, generally resulted in reduced classification performance across all metrics, especially when paired with weak learners or simple models.

Furthermore, measurement-level fusion of classifier outputs proved superior to abstract-level fusion. Access to the full probability distribution of predictions enabled more precise and informative coalition formation and decision-making, particularly benefiting complex ensemble techniques.

Importantly, the study demonstrates that the proposed framework is scalable and maintains high classification quality even with an increased number of data sources (up to 11 local tables), particularly when strong base learners are employed and appropriate ensemble strategies are selected.

Figure 2 presents a line chart illustrating the variation in F1-weighted scores across different levels of data dispersion and the EEG Epilepsy dataset (i.e., the number of local tables: 3, 5, 7, 9, 11) for each classifier, based on their best-performing ensemble strategy. The results reveal that Gradient Boosting demonstrates strong robustness to data distribution, achieving its highest performance at nine local tables (LT). AdaBoost maintains consistently high performance up to 7LT, followed by a slight decline. In contrast, Random Forest and Logistic Regression show a gradual decrease in classification quality as dispersion increases. k-Nearest Neighbors (kNN) exhibits the weakest but stable performance across all dispersion levels.

Comparing the results presented in Table 3 and Table 4 for the BCI Competition IV Dataset 1, one can notice small but systematic differences in the effectiveness of various approaches. Generally, the best results in both tables were obtained by AdaBoost and Gradient Boosting models, especially in combination with the measurement level and homogeneous groups. The F1 (weighted) values for these approaches ranged from approximately 0.57 to 0.59, without exceeding 0.6, which indicates a moderate difficulty of the dataset.

Although the differences between the tables are subtle, Table 4—corresponding to experiments with greater data dispersion (9LT and 11LT)—shows slightly higher F1 values for some configurations; e.g., for diverse groups at the measurement level with AdaBoost, an F1 of 0.589 was achieved with 9LT, while analogous approaches in Table 3 reached a maximum of 0.584 with 5LT. On the other hand, in Table 3, methods with fewer local tables (3LT–5LT) often performed better, suggesting that the increase in the number of data sources affects the results—both positively and negatively, depending on the configuration. Overall, however, none of the methods clearly dominated the others, and the classification performance remained at a similar level in all tested variants.

Figure 3 illustrates the comparative F1-measure for the BCI Competition IV Dataset 1 of various classifiers across different ensemble strategies and fusion levels. AdaBoost consistently achieves the highest F1-scores across all strategies, with values ranging from 0.528 to 0.579. The diverse-measurement fusion level brings the best overall score for AdaBoost (0.579), suggesting that incorporating diverse feature sources at the measurement level benefits this classifier the most. Gradient Boosting also performs strongly, with scores clustering around 0.543–0.557. The best result (0.557) is also seen under the diverse-measurement condition. Logistic Regression and Random Forest show more stable but slightly lower performance. Their F1-scores fluctuate minimally across strategies, indicating that their performance is less sensitive to the fusion strategy, with Logistic Regression the highest at 0.536 and Random Forest at 0.530. k-Nearest Neighbors yields the lowest performance, particularly under sum-abstract and unified-abstract, where the F1-score drops to 0.376. However, performance improves substantially under diverse-abstract and diverse-measurement strategies (0.508 and 0.501, respectively), highlighting kNN’s benefit from diversity in feature fusion.

Figure 4 presents a line chart illustrating the variation in F1-weighted scores across different levels of data dispersion and the BCI Competition IV Dataset 1 (i.e., the number of local tables: 3, 5, 7, 9, 11) for each classifier, based on their best-performing ensemble strategy. Among the classifiers, AdaBoost demonstrates the most consistently high performance across all dispersion levels. This stability indicates that AdaBoost is robust to distributional changes and can maintain reliable predictive quality even in more fragmented learning environments. Gradient Boosting starts with strong performance at three local tables, close to that of AdaBoost, but exhibits a gradual decline as the data become more dispersed. Random Forest shows relatively flat performance across all levels of dispersion. While not severely impacted by the increase in local tables, its performance does not reach the levels of the boosting methods, highlighting its limitations in capturing complex patterns in this BCI dataset under decentralized conditions. Logistic Regression exhibits more variability. Finally, k-Nearest Neighbors consistently achieves the lowest F1-weighted scores, although a slight upward trend is visible from three to seven local tables, after which performance plateaus. Overall, the results indicate that AdaBoost offers the most robust classification capability under distributed conditions, followed by Gradient Boosting, while Random Forest and kNN are less effective for this task.

Statistical tests were performed to confirm the observations and F1-weighted values were used for comparison. The F1-weighted values of all six approaches were compared: 1—Abstract level, sum; 2—Measurement level, sum; 3—Unified groups, abstract level; 4—Diverse groups, abstract level; 5—Unified groups, measurement level; 6—Diverse groups, measurement level. So, six dependent samples, each containing 50 observations, were created, representing the results presented in Table 1, Table 2, Table 3 and Table 4. The Friedman test was used to determine whether the differences in F1-weighted values among the approaches were statistically significant. The Friedman test indicated that there is a statistically significant difference in mean F1-weighted among the twenty approaches, ${\chi }^2(50,5)=14.24,p=0.014$. To pinpoint the specific differences, a post hoc Dunn–Bonferroni test was performed, with the significant results highlighted in blue in

Table 5. p-values for the post hoc Dunn–Bonferroni test for appeoaches: unified groups unweighted and weighted; diverse groups unweighted and weighted. (Blue text color represent best result).

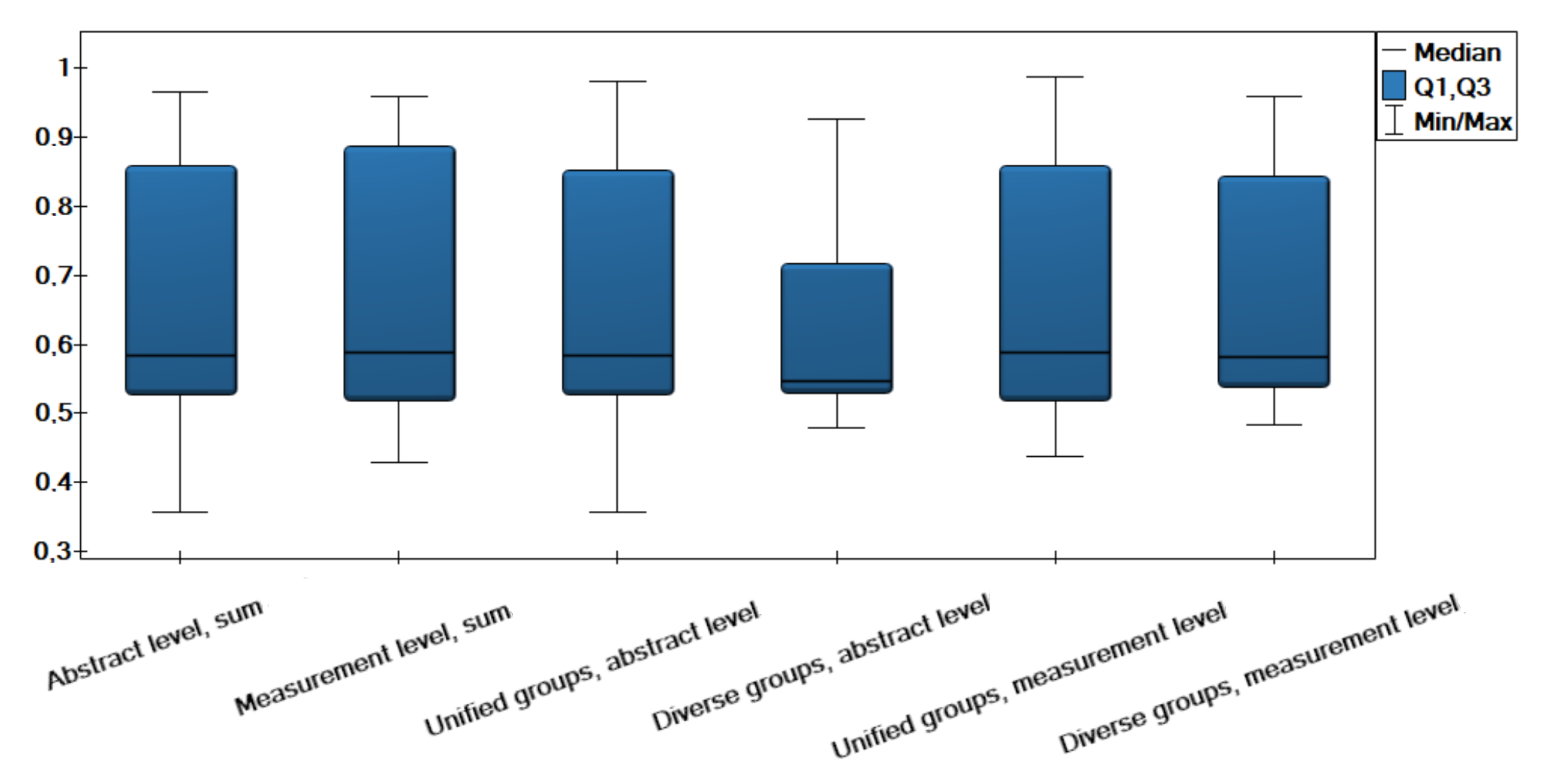
p-Value	Abstract Level Sum	Measurement Level Sum	Unified Groups Abstract Level	Diverse Groups Abstract Level	Unified Groups Measurement Level	Diverse Groups Measurement Level
Abstract level, sum		1	1	0.456	1	1
Measurement level, sum	1		1	0.132	1	1
Unified groups, abstract level	1	1		1	1	1
Diverse groups, abstract level	0.456	0.132	1		0.426	0.009
Unified groups, measurement level	1	1	1	0.426		1
Diverse groups, measurement level	1	1	1	0.009	1

. The test revealed significant differences between the diverse groups, abstract level approach, and the diverse groups, measurement level approach. A comparative box plot illustrating the F1-weighted results for the six approaches is provided in Figure 5. Based on the graph, it can be seen that worse results were achieved for the diverse groups with abstract level approach.

As can be seen, the observed performance differences across the two datasets highlight the importance of dataset-specific characteristics in model evaluation. The Epilepsy dataset was carefully curated and preprocessed by its authors to facilitate model training—signals were clearly segmented, of equal length, and correctly labeled for each mental state. In contrast, the BCI dataset was explicitly designed to be challenging: it comprises continuous, unsegmented signals with unknown transitions between mental states, variable trial durations (1.5–8 s), class imbalance, and artificially inserted “no control” periods. These differences substantially impact model performance and suggest that care must be taken when generalizing results across datasets with differing structures and assumptions.

The results presented above are compared to those obtained without applying distributed environments. Admittedly, this comparison is not entirely fair, as the non-dispersed approach allows the model access to all available knowledge simultaneously. Nevertheless, these experiments were conducted to determine whether dispersing knowledge significantly reduces classification quality. The results obtained for both datasets and the approaches used in the paper (Random Forest, AdaBoost, Gradient Boosting, Logistic Regression) are shown in

Table 6. Results of precision (Prec.), recall, F-measure (F-m.), balanced accuracy ($bacc$), and classification accuracy ($acc$) in the case where the distributed environments are not applied. RF is the abbreviation Random Forest and kNN stands for k-Nearest Neighbors. (Blue text color represent best result).

Data Set	Method/Model	Prec.	Recall	F1 (Weig.)	F1 (Macro)	BAacc	Acc
EEG Epilepsy	RF (200,gini)	0.946	0.933	0.932	0.932	0.933	0.933
	kNN (4)	0.782	0.74	0.716	0.716	0.74	0.74
	AdaBoost (20)	0.953	0.947	0.946	0.946	0.947	0.947
	Gradient Boosting (50)	0.946	0.933	0.932	0.932	0.933	0.933
	Logistic Regression	0.888	0.867	0.869	0.869	0.867	0.867
BCI Competition IV Dataset 1	RF (20,gini)	0.53	0.529	0.527	0.527	0.529	0.529
	kNN (2)	0.485	0.492	0.442	0.442	0.492	0.492
	AdaBoost (10)	0.606	0.604	0.603	0.603	0.604	0.604
	Gradient Boosting (20)	0.597	0.597	0.597	0.597	0.597	0.597
	Logistic Regression	0.542	0.541	0.541	0.541	0.541	0.541

. The procedure for optimizing the parameters mirrored the strategies employed in the approaches discussed earlier.

Comparing the results from the non-dispersed version (Table 6) with the dispersed approach shows that AdaBoost is the best-performing method overall. For the EEG Epilepsy dataset, the dispersed approach actually performs slightly better, with results like 0.983 accuracy and 0.98 for other metrics. This means that spreading the data out did not hurt the results—in fact, it may have helped a bit. For the BCI Competition IV Dataset 1, the distributed version scores just a little lower, with accuracy values between 0.596 and 0.601. However, this difference is very small and not really significant. Overall, using dispersed data does not reduce the quality of the results. In the case of the EEG Epilepsy data, it even improves it. For the BCI dataset, the drop in performance is so minor that it shows dispersion does not cause any real deterioration. On the contrary, distributed approaches can work just as well, or even better, depending on the dataset.

We also compared our results with state-of-the-art deep learning models commonly used in EEG classification. For this purpose, we selected the approach described in [25]. EEGNet is a lightweight convolutional neural network specifically designed for EEG signal analysis. Its architecture uses depthwise and separable convolutions, which allows it to efficiently capture both spatial and temporal features from EEG data while keeping the model compact and computationally efficient. EEGNet is known for its ability to generalize well across various EEG paradigms, such as P300, ERN, MRCP, and SMR, without the need for extensive task-specific adjustments. It also performs strongly when training data are limited and offers interpretable results, as the features it learns often correspond to known EEG patterns. Specifically, we used EEGNet-SSVEP, as it achieved the best performance on the analyzed datasets. The obtained results are presented in

Table 7. Results of precision (Prec.), recall, F-measure (F-m.), balanced accuracy ($bacc$), and classification accuracy ($acc$) for deep learning EEGNet-SSVEP model commonly used in EEG classification.

Data Set	Prec.	Recall	F1 (Weig.)	F1 (Macro)	BAacc	Acc
EEG Epilepsy	0.836	0.767	0.737	0.737	0.767	0.767
BCI Competition IV Dataset 1	0.516	0.516	0.513	0.513	0.516	0.516

.

As shown, the results obtained using a dedicated neural network are inferior to those achieved in the distributed environment.

4. Discussion

This study investigated the use of dynamic ensemble selection for EEG signal classification in scenarios where data are distributed due to privacy or logistical constraints. The experimental results across both the EEG Epilepsy dataset and the BCI Competition IV Dataset 1 indicate that the proposed approach—particularly when using Gradient Boosting and unified measurement-level coalitions—achieved consistently strong performance metrics. These outcomes suggest that the coalition-based strategy may offer advantages in adapting to the heterogeneity of EEG signals across distributed sources.

While the unified coalition strategy generally outperformed both diverse coalition and traditional ensemble methods, this should be interpreted within the context of the datasets and settings examined. The dynamic nature of the model selection process appears to support more adjusted decisions, especially when high agreement among local models can be obtained. Moreover, the benefit of measurement-level fusion over abstract-level fusion highlights the value of using detailed probability distributions rather than relying solely on class labels.

This study has several limitations that should be considered. First, the distributed environment was simulated by partitioning centralized EEG datasets, rather than using data collected from genuinely independent sources. This means that important real-world challenges were not fully addressed. Second, the experimental design assumed synchronous model training and evaluation, as well as balanced class distributions and uniform feature representation across all local sites. In real-world scenarios, data are often highly imbalanced or non-iid, and devices may operate asynchronously, which can introduce additional complexity and impact model robustness. Third, the study relied on a relatively small number of subjects and focused on two publicly available EEG datasets related to epilepsy and motor imagery. While stratified sampling was used to maintain class balance, the limited sample size and scope may restrict the generalizability of the findings to other patient populations or clinical applications. Finally, the feature extraction process was based on conventional statistical, spectral, and wavelet-based features. Incorporating more advanced feature representations, such as deep-learned embeddings, could potentially improve classification performance and should be explored in future research.

Despite these limitations, the proposed framework appears promising for applications where data decentralization is essential due to privacy, security, or logistical constraints—such as mobile health (mHealth) platforms, tele-neurology, and collaborative clinical research. Its modular design allows for integration with various base classifiers and coalition strategies and has shown the ability to scale with increasing numbers of distributed data sources in our experiments.

To contextualize our findings, we compared our best results with those reported in recent EEG-based epilepsy classification studies. For instance, Huang et al. [14] reported an F1-score of 0.9516 using a dual-attention deep learning framework on a similarly structured epilepsy dataset, while Kołodziej et al. [12] achieved an accuracy of approximately 0.95 using a CNN-based pipeline on intracranial EEG data. In our study, the unified coalition-based ensemble approach with Gradient Boosting achieved an F1-score and balanced accuracy of 0.987. While direct comparisons are limited by differences in datasets and experimental conditions, these results suggest that our method may offer competitive performance, even in a distributed data setting.

The reliability of EEG features across sessions is a well-documented challenge, particularly in clinical and cognitive applications that rely on single-session recordings for machine learning-based decision-making. Numerous studies have shown that EEG signals can exhibit substantial intra-individual variability across days, devices, or mental states, which may affect the replicability of model outputs [26,27,28].

In our study, this challenge also appears due to data privacy constraints. Because the data used in our decentralised learning framework originate from independent local sources and are subject to anonymisation, we cannot identify whether two recordings originate from the same patient across different sessions or institutions. As such, we cannot explicitly evaluate how likely it is that an AI model would assign the same diagnosis to two EEGs recorded on separate days from the same individual. This limitation reflects a broader issue in privacy-preserving medical AI, where the need to protect patient identity may restrict the evaluation of temporal reliability.

Nevertheless, the proposed dynamic ensemble strategy may help address some of these challenges. By training multiple local models on independently sourced EEG subsets and forming coalitions based on inter-model agreement or conflict, the approach aims to reduce dependence on any single, potentially noisy signal. This instance-specific selection mechanism may contribute to improved resilience against feature noise or anomalies in individual recordings.

In summary, while further refinement and validation in real-world settings are needed, the results suggest that this method could provide a useful foundation for developing distributed and adaptable EEG classification systems.

5. Conclusions

This paper introduced a dynamic ensemble selection framework for EEG signal classification in distributed data environments. The proposed method uses coalition formation based on conflict metrics to dynamically integrate predictions from locally trained models. Our findings suggest that the framework has potential for effective classification in scenarios where data centralization is infeasible.

In particular, unified coalitions at the measurement level consistently achieved strong results, especially when paired with Gradient Boosting classifiers. These results underscore the promise of context-aware ensemble strategies in handling data dispersion and heterogeneity—common challenges in clinical and telemedicine applications. The findings emphasize the following:

• Coalition-based ensemble models outperform traditional voting approaches.
• Measurement-level prediction aggregation preserves more discriminative information than abstract label-level fusion.
• Boosting methods (Gradient Boosting, AdaBoost) are suitable for decentralized EEG classification tasks.

While the results are encouraging, we acknowledge that further validation on larger and more diverse datasets is necessary to fully establish the generalizability of the approach. Future work will focus on expanding the framework to more complex clinical scenarios and integrating it with real-time EEG acquisition systems. Future work should also investigate the robustness of the proposed framework in the presence of noise, missing data, and high variability across different patients. Transfer learning or domain adaptation techniques could be incorporated to improve generalization in dispersed system. Overall, this study contributes to ongoing efforts in developing adaptive, privacy-aware EEG analysis methods, with potential applications in both telemedicine and decentralized healthcare infrastructures.