Analysis of Vibration Characteristics of the Grading Belt in Wolfberry Sorting Machines
Abstract
1. Introduction
2. Materials and Methods
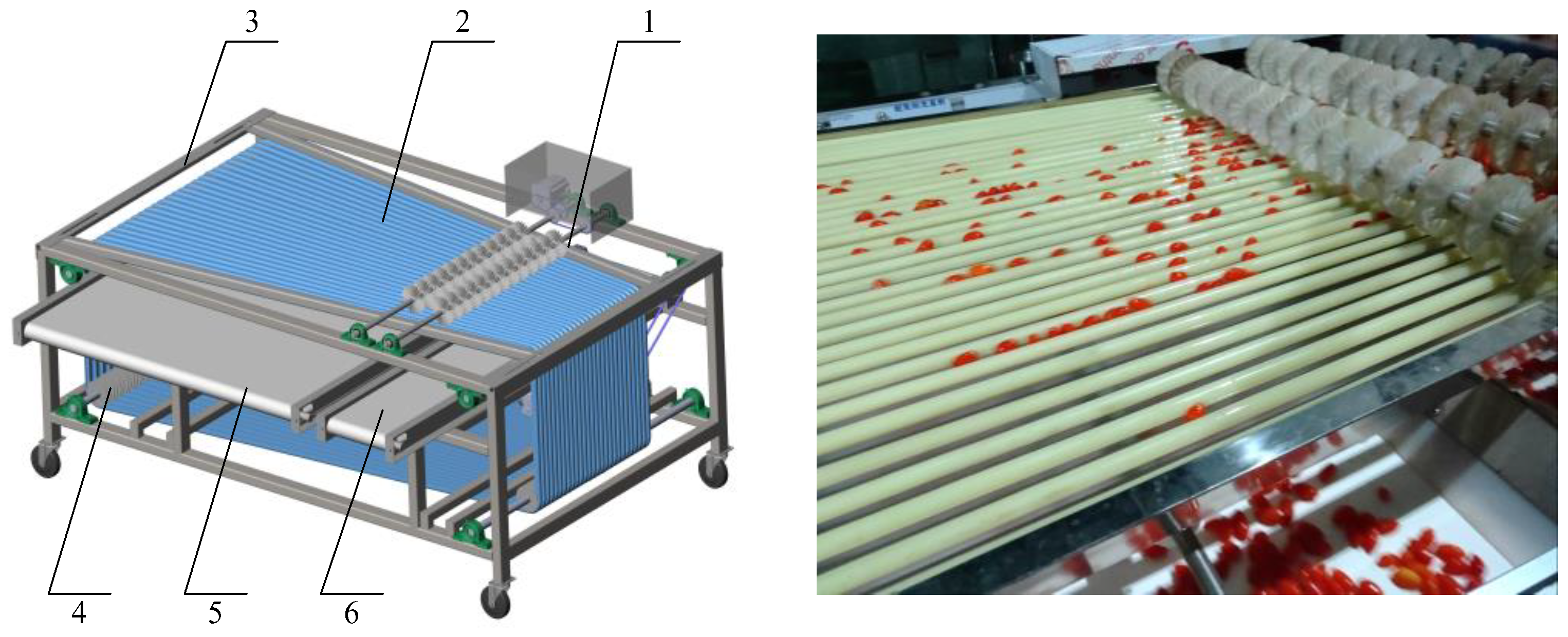
2.1. Structural Optimization Scheme Design
2.2. Transmission Modeling and Principles
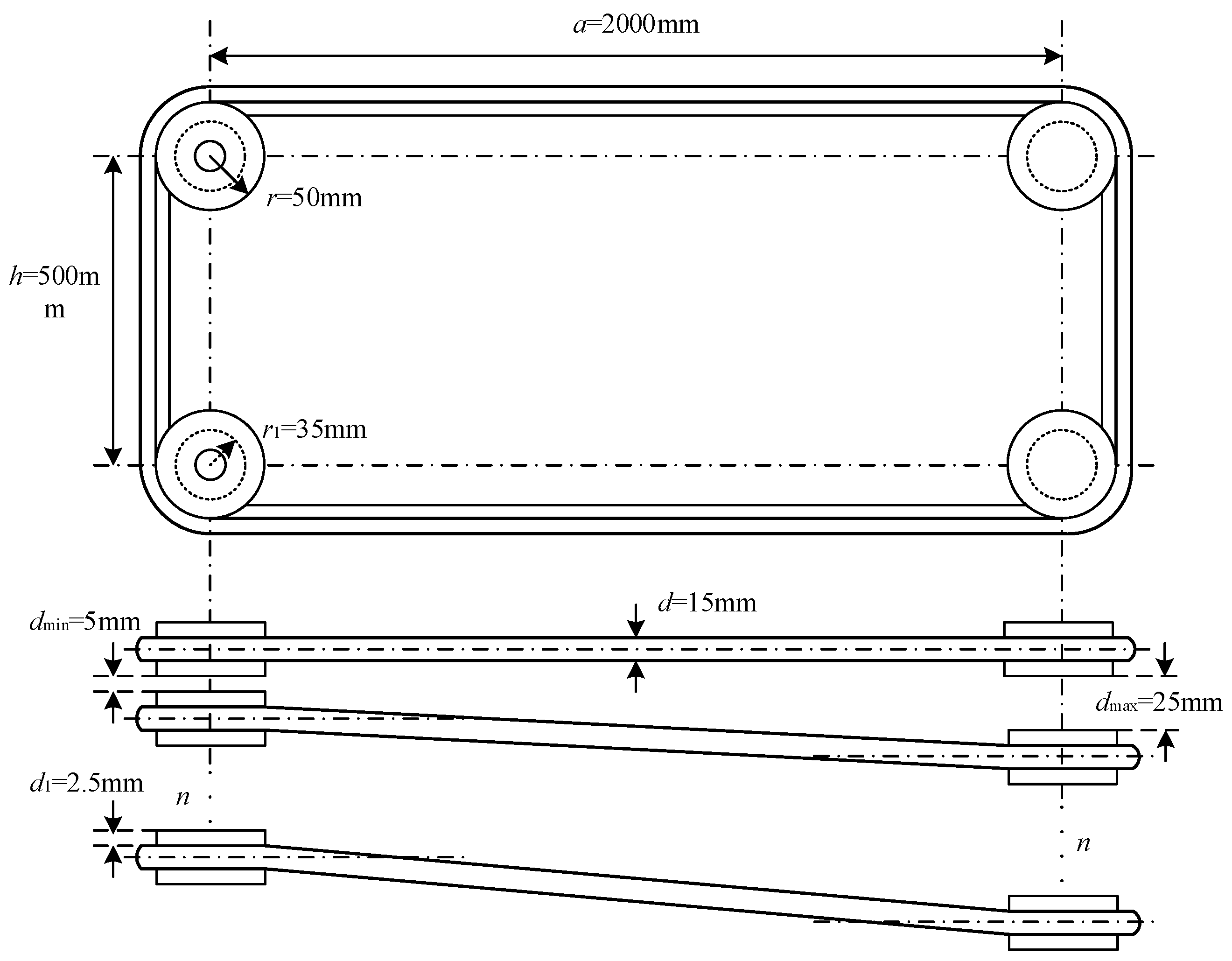
2.2.1. Structural Designs
- (1)
- Given the substantial variation in the size of individual fresh wolfberries, the machine must possess a high level of precision.
- (2)
- Considering the fragile nature of the outer skin of fresh wolfberries, mechanical damage must be minimized during the grading process.
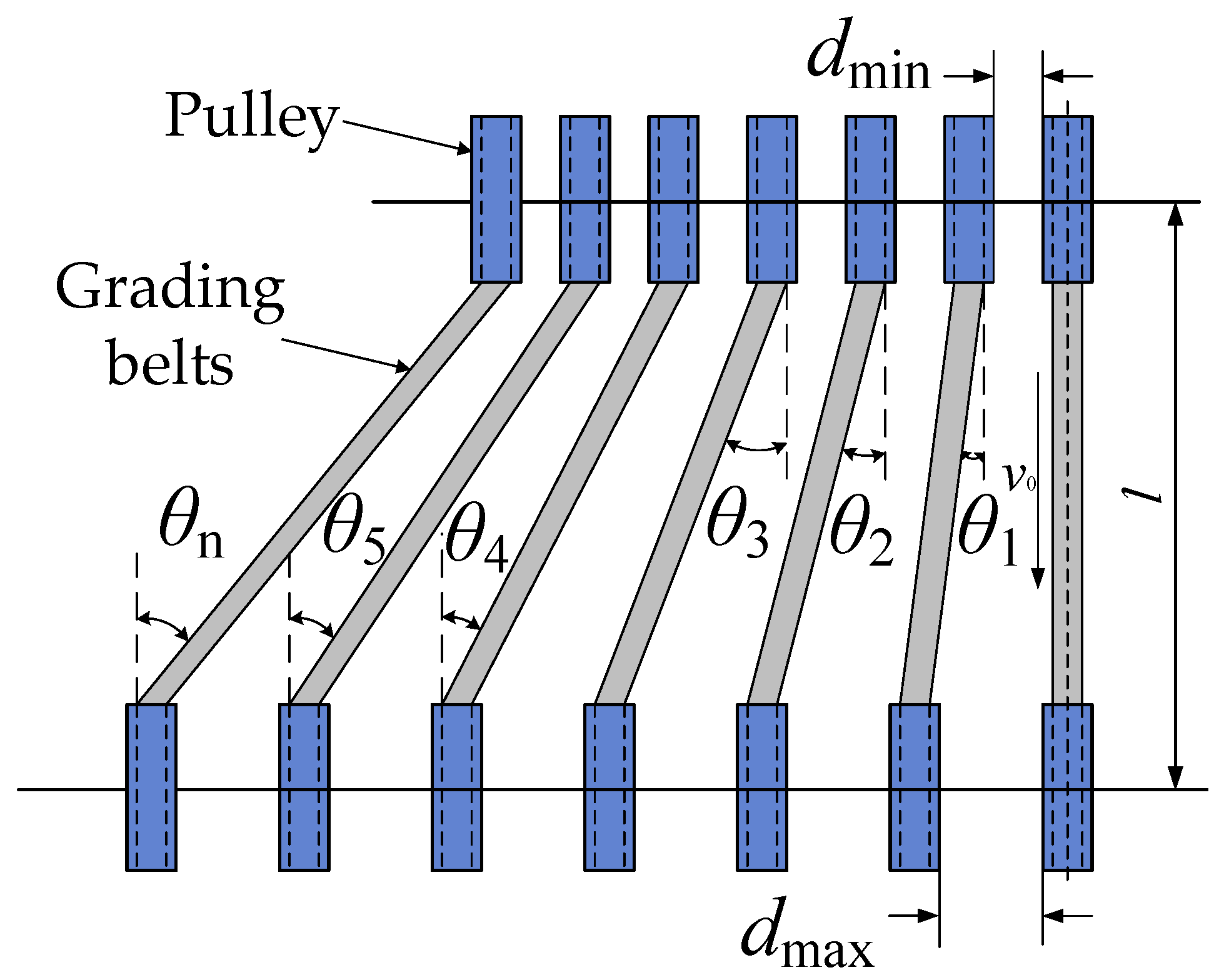
2.2.2. Working Principle and Existing Issues
2.3. Mechanical Modeling of Transverse Vibration of a Flat Belt
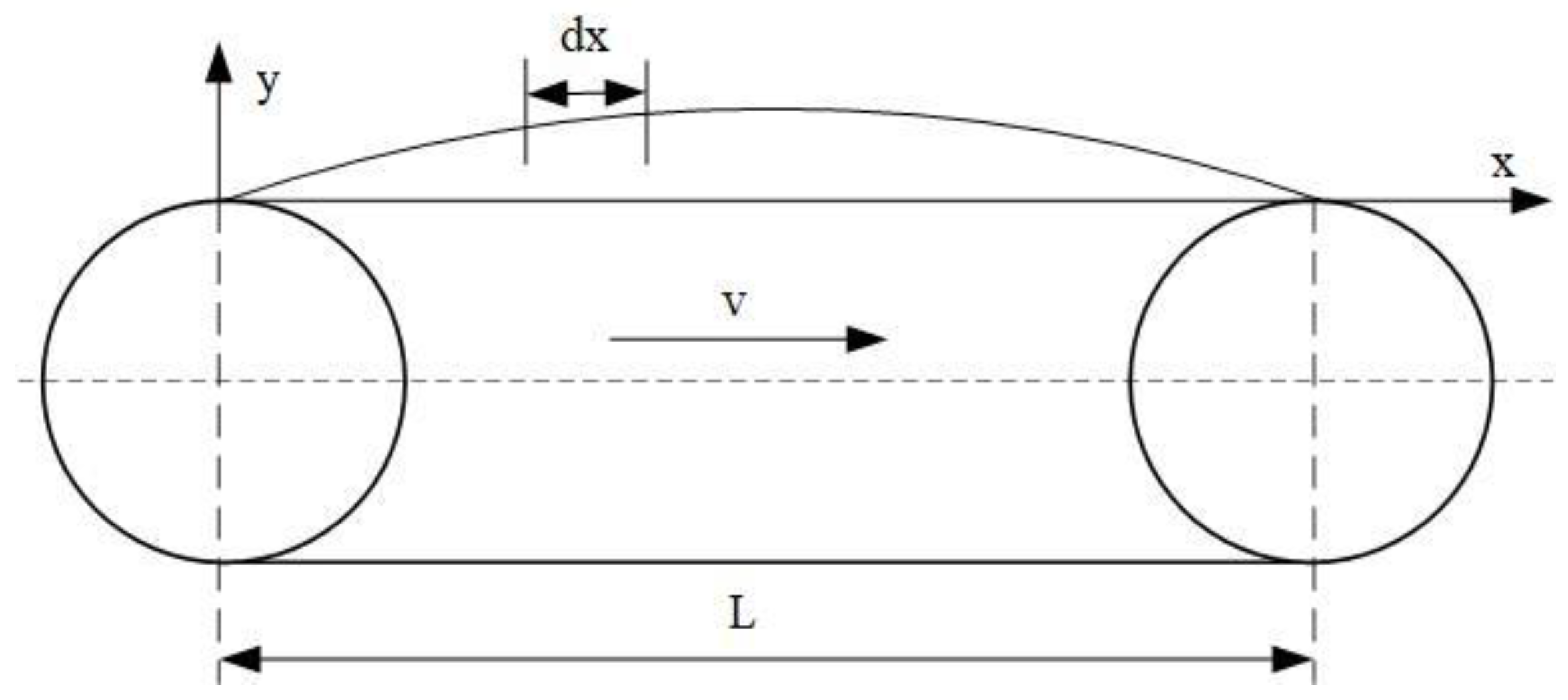
2.3.1. Analysis of Belt Drive Systems
2.3.2. Transverse Vibration Analysis of Belt Drives
2.4. Graded Flat-Band Dynamics Analysis
Belt Drive Modeling
- The vibration of the motor on the transmission device is relatively small and can be disregarded.
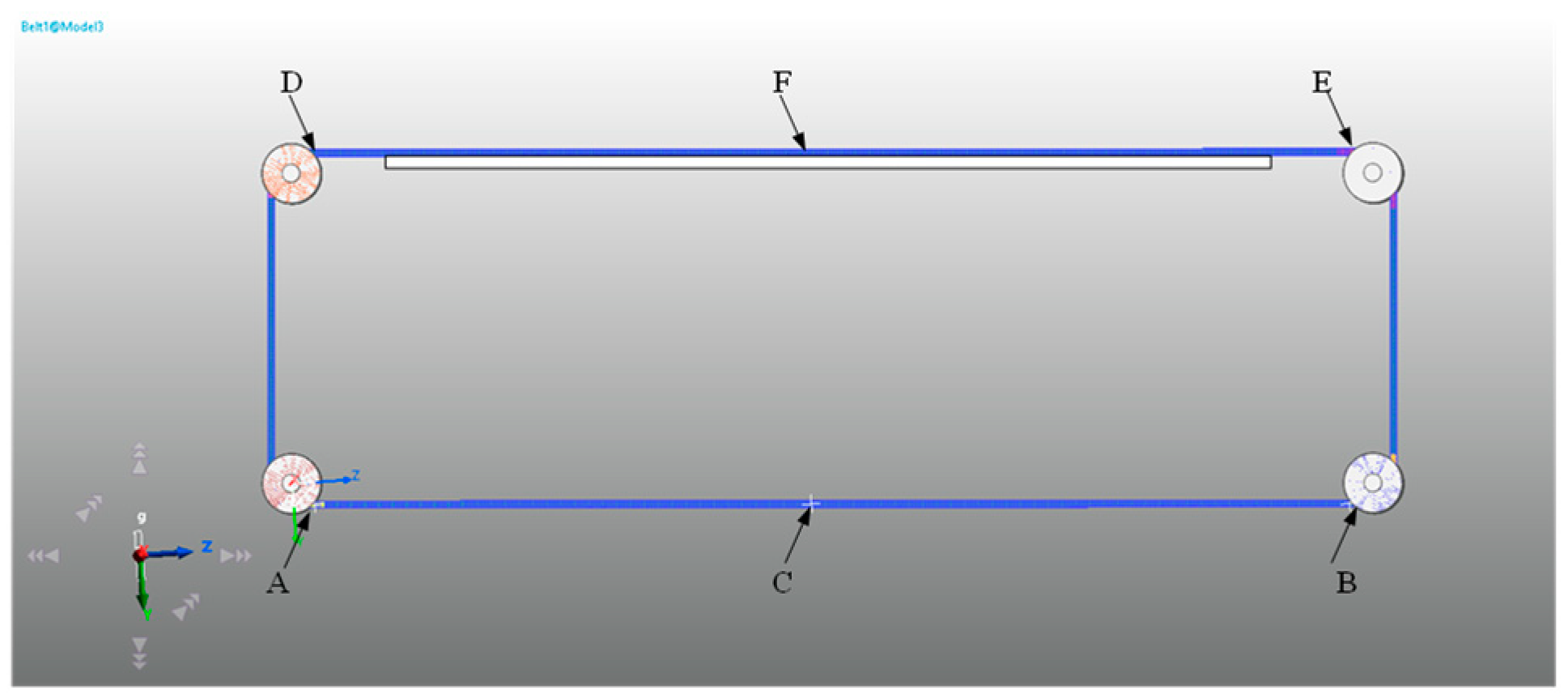
- The fixed device beneath the flexible belt has a considerable influence on the lateral vibration of the belt. The lateral vibration characteristics of the belt without this device added are mainly considered. It is simplified into two parts, namely, the driving wheel and the transmission belt [30]. The simplified model is shown in Figure 6.
2.5. Experimental Validation
2.6. Single-Factor Analysis
2.7. Response Surface Optimization
2.8. Structural Optimization Design
2.8.1. Transverse Vibration Response Analysis
2.8.2. Belt Pulley Process Optimization
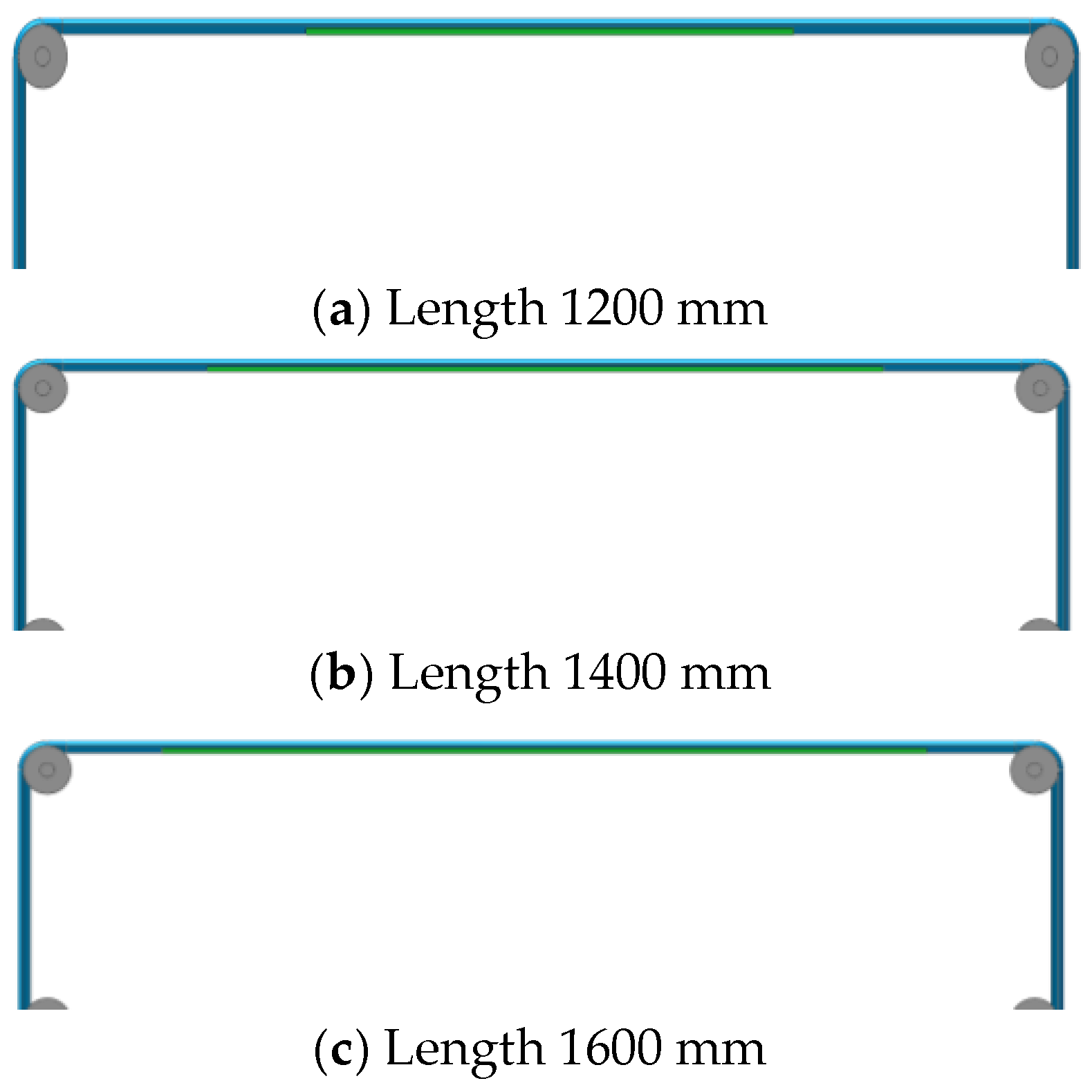
2.8.3. Fixture Length Optimization
3. Results and Discussion
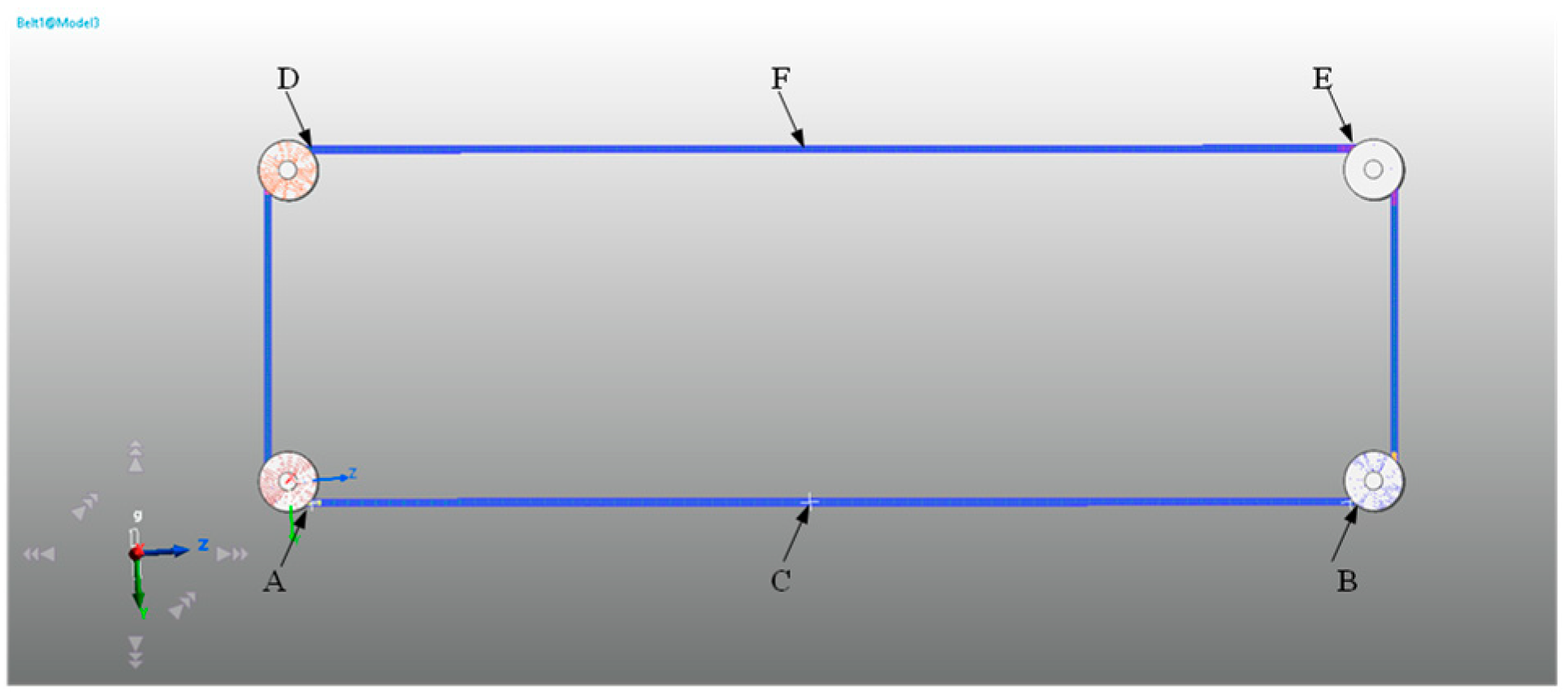
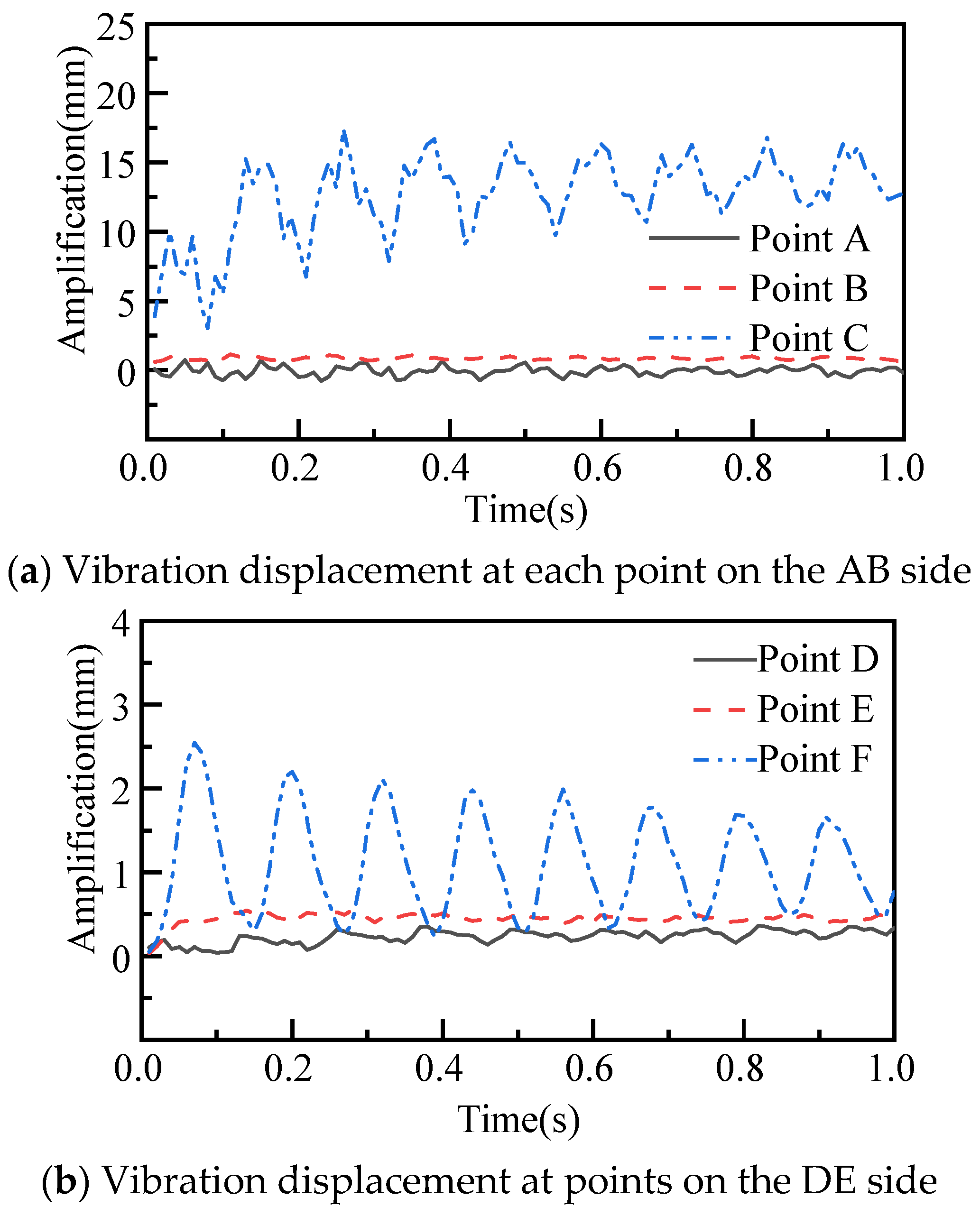
3.1. Belt Drive Simulation
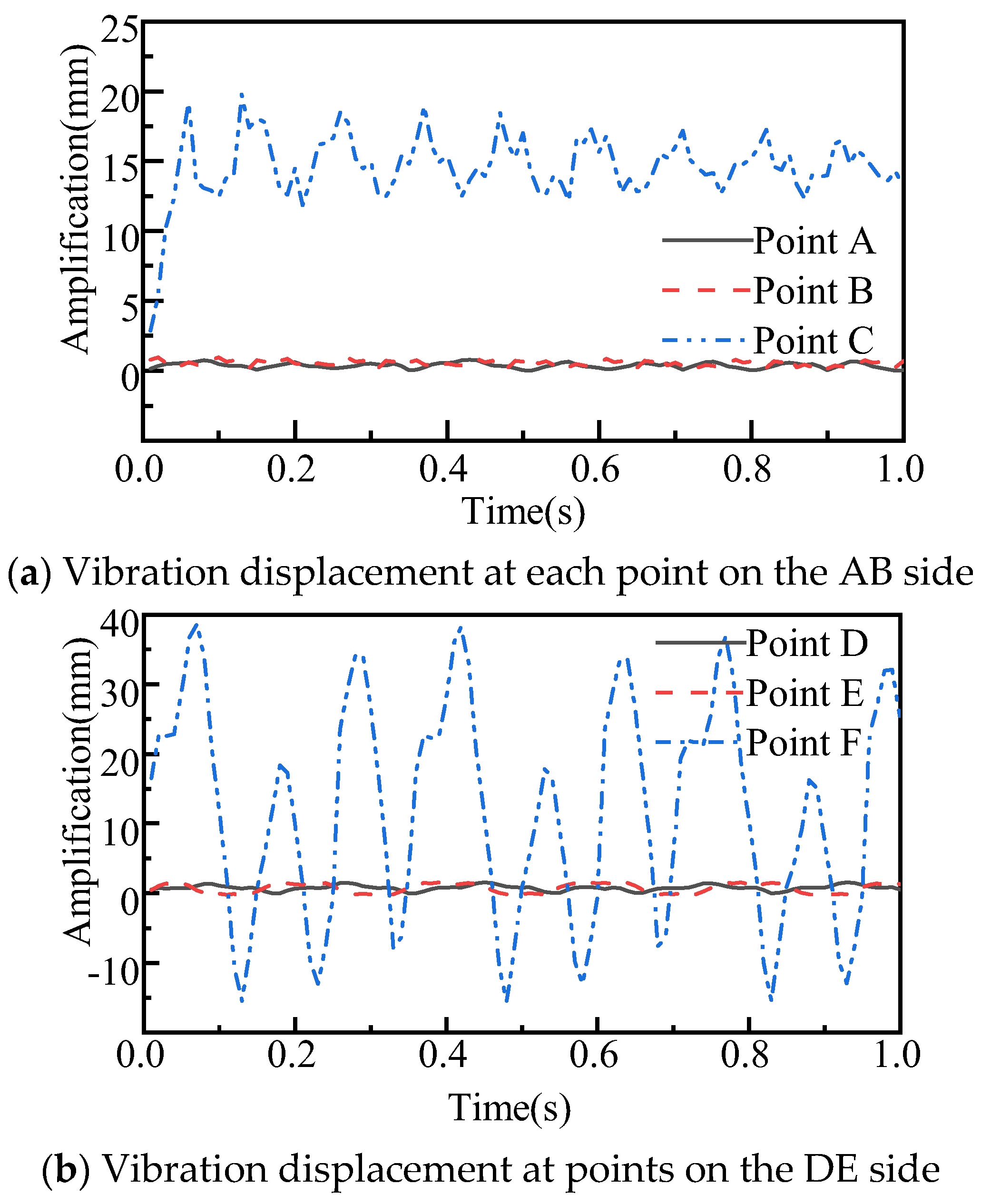
3.2. Experimental Results
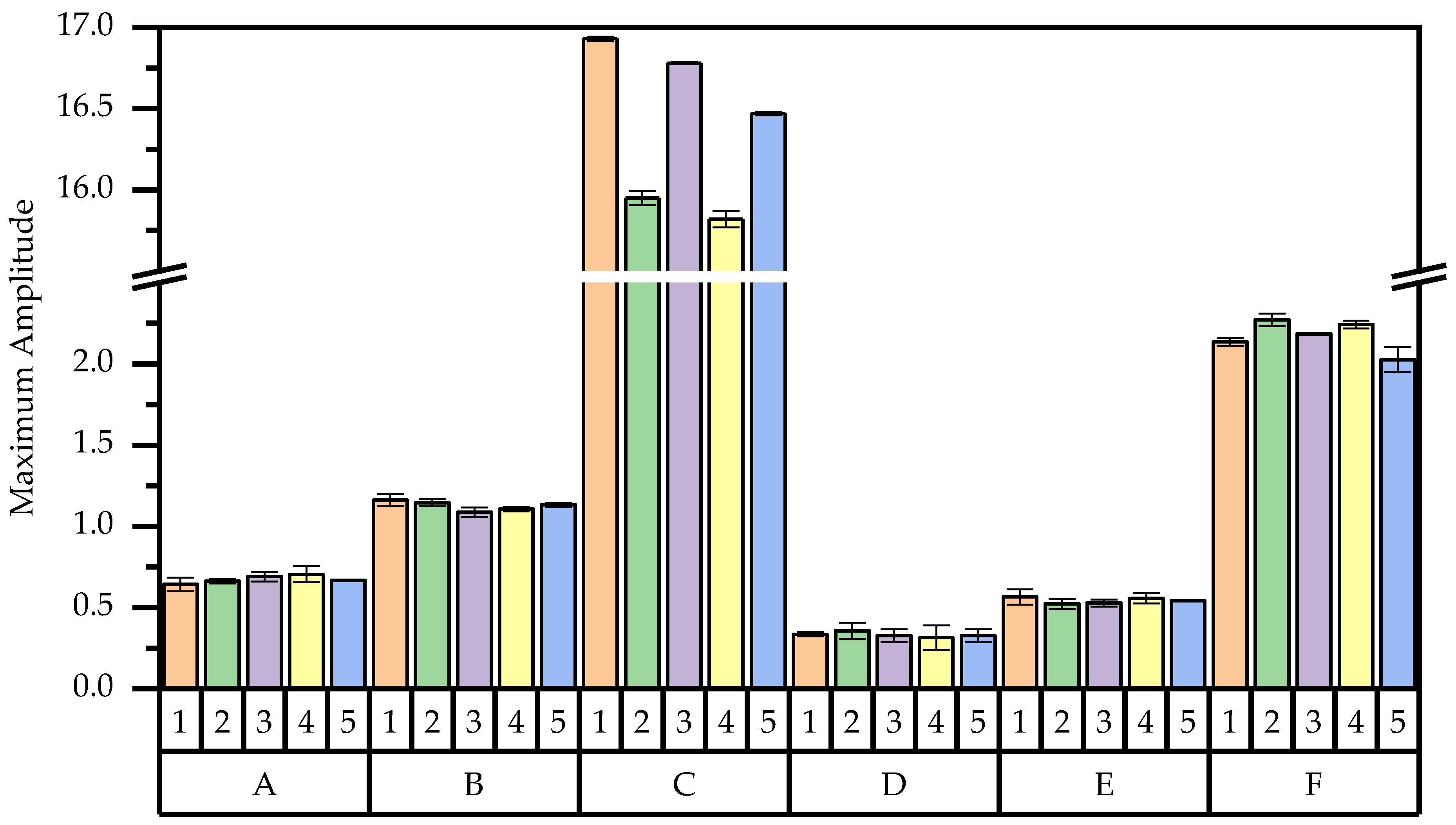
3.3. Single-Factor Analysis Results
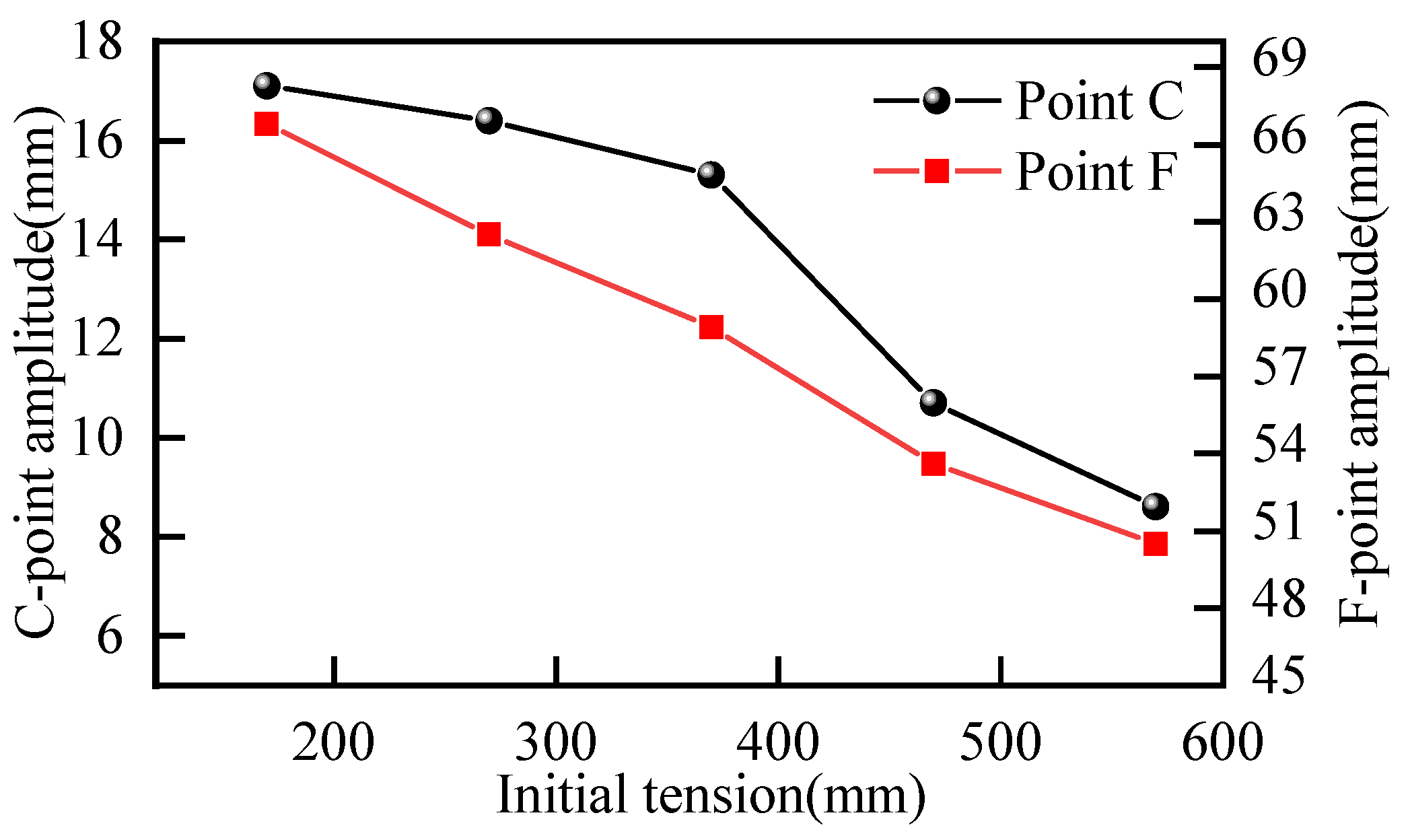
3.3.1. Analysis of Transverse Vibration Displacement Under Various Initial Tension Conditions
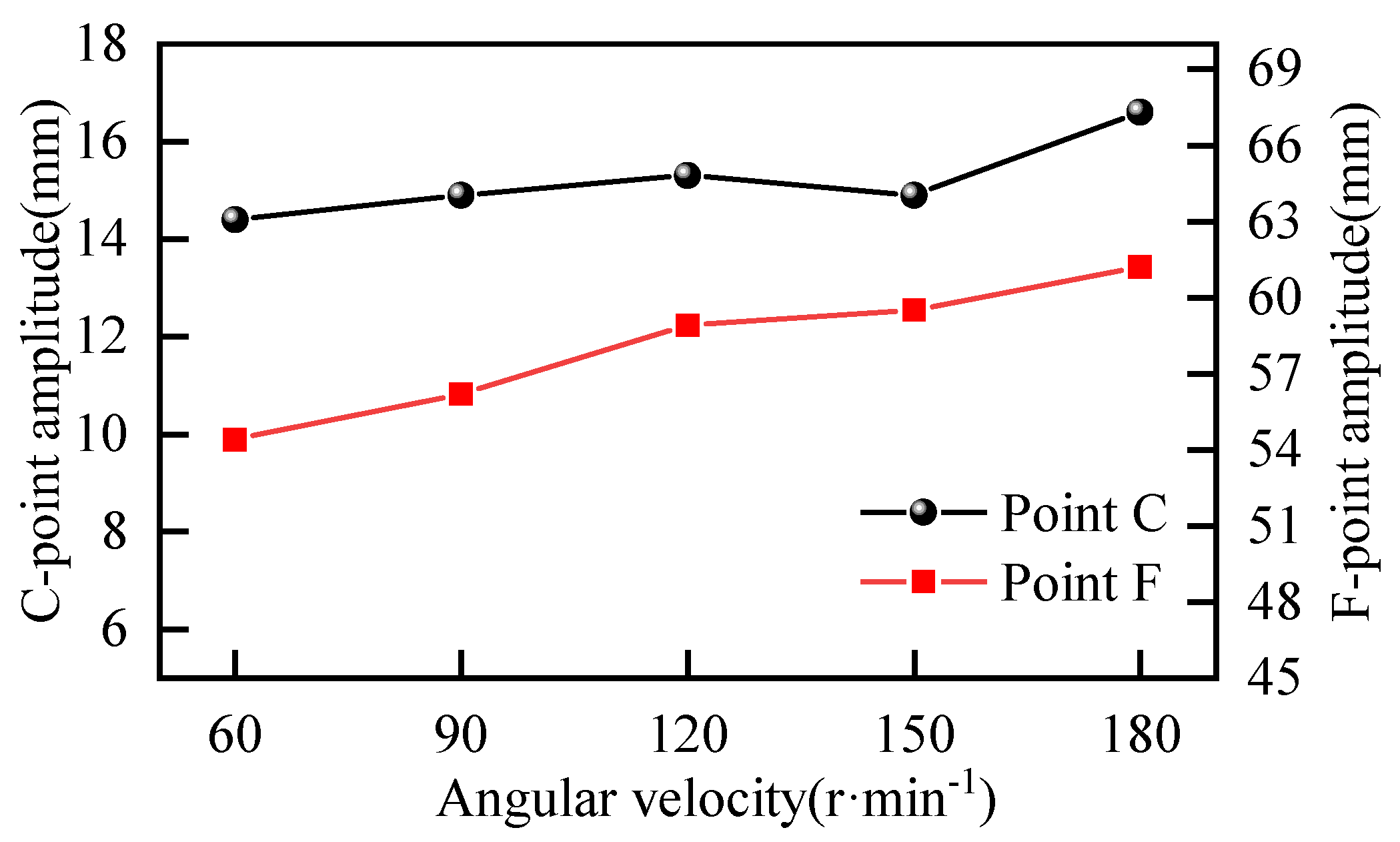
3.3.2. Analysis of Lateral Vibration Displacement Under Different Speed Conditions
3.3.3. Analysis of Lateral Vibration Displacement Under Different Skew Angle Conditions
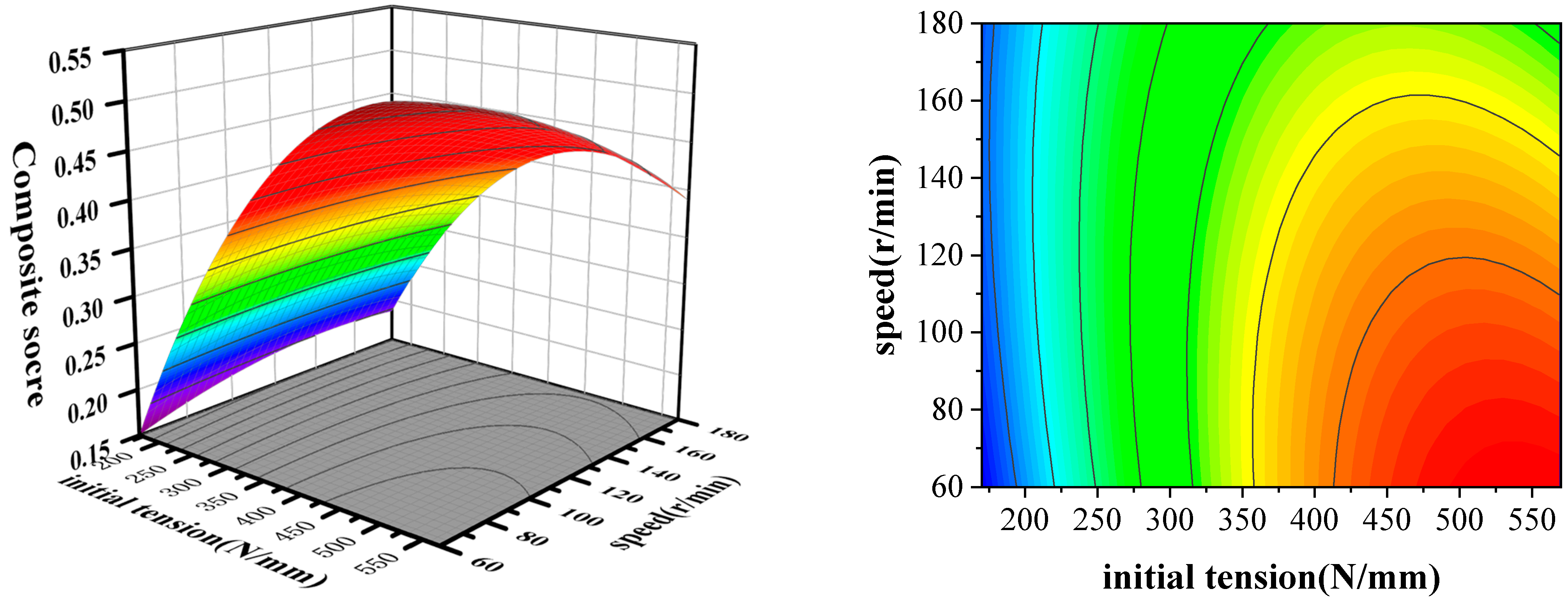
3.4. Response Surface Analysis Results
3.5. Analysis of the Results of Structural Optimization Design
3.5.1. Response Analysis Results
3.5.2. Belt Pulley Optimization Results
3.5.3. Optimum Fixture Length
4. Conclusions
- (1)
- To address the vibration issue of the transmission belt in the fresh wolfberry sorting machine, the lateral vibration theory was employed to develop relevant models and derive theoretical formulas. The analysis revealed that the primary factors influencing lateral vibration are initial tension, rotational speed, and center distance.
- (2)
- The feasibility of the model was validated through field experiments. The average error between the maximum amplitude in the simulation results and the actual measured maximum amplitude was 3%, indicating that the established dynamic model is reliable.
- (3)
- Based on the single-factor experiments, the response surface methodology (RSM) was employed to optimize the grading flat belt of the wolfberry sorter. The factors influencing the lateral vibration of the grading flat belt were ranked in descending order of their comprehensive impact as follows: initial tension > bias angle > rotational speed. In this study, a quadratic polynomial regression model to obtain a comprehensive score was established through response surface experiments. The results indicate that the lateral vibration displacement is minimized when the initial tensile force is 520 N/mm, the rotational speed of the transmission shaft is 60 min−1, and the deflection angle of the transmission mechanism is 5°.
- (4)
- Under the working conditions of an initial tension of 520 N/mm, a transmission shaft speed of 60 r/min, a transmission mechanism deflection angle of 5°, and a belt center distance of 2200 mm, harmonic response analysis was performed using the modal superposition method. Significant resonance responses were observed at excitation frequencies of 4 Hz and 8 Hz. Under these conditions, both the pulley structure and the fixing device were optimized. When the fillet radius of the pulley was set to 10 mm and the length of the fixing device was adjusted to 1600 mm, the lateral vibration of the belt was minimized, thereby reducing the impact of lateral vibration and improving the reliability of the goji berry sorter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Li, X.; Gao, S. Design and test of roller-type nylon brush potato cleaning and grading machine. Agric. Mech. Res. 2021, 43, 152–155+160. [Google Scholar]
- Liu, X. A new type of wolfberry sieving machine based on TRIZ innovation method. Sci. Technol. Innov. Appl. 2018, 15, 30–31. [Google Scholar]
- Laykin, S.; Alchanatis, V.; Fallik, E.; Edan, Y. Image–processing algorithms for tomato classification. Trans. ASAE 2002, 45, 851. [Google Scholar] [CrossRef]
- Heinemann, P.H.; Pathare, N.P.; Morrow, C.T. An automated inspection station for machine-vision grading of potatoes. Mach. Vis. Appl. 1996, 9, 14–19. [Google Scholar] [CrossRef]
- ElMasry, G.; Cubero, S.; Moltó, E.; Blasco, J. In-line sorting of irregular potatoes by using automated computer-based machine vision system. J. Food Eng. 2012, 112, 60–68. [Google Scholar] [CrossRef]
- Li, J.; Cao, W. Research and analysis of synchronous belt drive performance of intelligent terminal lifting and lowering integrated machine. Mech. Des. Manuf. Eng. 2023, 52, 115–120. [Google Scholar]
- Gou, H.; Yan, H.; Zhao, T.; Ban, X.; Meng, X.; Bao, Y. Dynamic response of high-speed train-track-bridge coupled system under combined wind and snow. Struct. Infrastruct. Eng. 2025, 21, 695–709. [Google Scholar] [CrossRef]
- Qin, S.A.; Zhou, P.; Zhou, Y.J.; Jiang, H.Y. Overview of the development status of belt drive industry. Mech. Drive 2020, 44, 8. [Google Scholar]
- Zhu, S.M.; Lu, S.M.; Yu, Y.D.; Guo, Y.F. Current status and prospects of belt drive theory and technology. Mech. Drive 2007, 31, 92–96. [Google Scholar]
- Wu, Y.Z. Research progress of new products of transmission belt. Mech. Transm. 2013, 37, 4–9. [Google Scholar]
- Yu, D.Z.; Yi, X.G.; Xin, C. Study of flat belt drive mechanics. Key Eng. Mater. 2009, 419–420, 265–268. [Google Scholar]
- Piotr, K.; Łukasz, W.; Grzegorz, D.; Matijošius, J. Development trends in belt transmissions with V-belt. MATEC Web Conf. 2022, 357, 01003. [Google Scholar]
- Yu, Y.; Ren, S.M.; Wei, Y.X.; Zhang, Z.L. Design of variable pitch type fresh wolfberry grader based on EDEM. Arid Reg. Agric. Res. 2023, 41, 266–273. [Google Scholar]
- Wei, M.Z. Analysis on skew of flat belts in two-pulley drives. J. Mech. Des. 2011, 133, 111001. [Google Scholar]
- Gong, S.M. Experimental Dynamics Analysis of Transverse Vibration of Drive Belt System. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2014. [Google Scholar]
- Xu, L.H. A graphical study of force relations in belt drives. Mech. Drive 2006, 30, 35–36. [Google Scholar]
- Li, X.X. Research on Reliability Analysis Method of Belt Drive Vibration Characteristics and Surface Defects. Master’s Thesis, Harbin University of Commerce, Harbin, China, 2022. [Google Scholar]
- Kou, B.; Liu, Q.; Li, N. Research on transverse vibration characteristics of rope change device with clamping chain transmission in lifting system. J. Vibroeng. 2017, 19, 894–907. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, W.D.; Fan, W. Dynamic modeling, simulation and experiment of power transmission belt drives: A systematic review. J. Sound Vib. 2021, 491, 115759. [Google Scholar] [CrossRef]
- Li, J.F. Research on the Vibration and Noise of Synchronous Belt Drive of Intelligent Terminal Lifting and Lowering Machine. Master’s Thesis, Yancheng Institute of Technology, Yancheng, China, 2023. [Google Scholar]
- Piotr, B.; Lech, G.; Robert, K.; Ozdoba, M. Models of transverse vibration in conveyor belt—Investigation and analysis. Energies 2021, 14, 4153. [Google Scholar] [CrossRef]
- Li, Z.G.; Chen, G.P.; Shi, Y.C. Experimental study on the smoothness of automotive synchronous belt drive. J. Shaoyang Univ. 2020, 17, 30–36. [Google Scholar]
- Zhu, H. Research on Nonlinear Vibration and Parameter Optimisation of Engine Front End Accessory Drive System. Master’s Thesis, Chongqing University, Chongqing, China, 2017. [Google Scholar]
- Nie, W.; Zheng, D. An approach of FEM analysis of the influence of pretension on the transverse vibration of belt drive. J. Phys. Conf. Ser. 2019, 1345, 032032. [Google Scholar] [CrossRef]
- Fujii, A.; Yonemoto, S.; Miyazaki, K.; Furumata, S.; Okuda, K.; Miyazawa, H. Analysis of the accessory belt lateral vibration in automotive engines. JSAE Rev. 2002, 23, 41–47. [Google Scholar] [CrossRef]
- Liu, Y. Recurdy Multibody Dynamics Simulation Basic Application and Improvement; Electronic Industry Press: Beijing, China, 2013. [Google Scholar]
- Li, T.T.; Guo, W.; Wang, C.C.; Zhang, X. Simulation and analysis of the dynamics of 2K-V reducer based on Recur Dyn. J. Eng. Res. Rep. 2024, 26, 60–68. [Google Scholar]
- Zhou, G.L.; Han, Z.H.; Guo, Y.C. Transverse vibration characteristics of conveyor belt based on Recur Dyn. J. Heilongjiang Univ. Sci. Technol. 2018, 28, 649–654. [Google Scholar]
- Sun, X.J.; Zhang, J.; Wang, Y. Dynamic simulation of Recur Dyn flat belt drive. J. Lanzhou Inst. Technol. 2012, 19, 36–39. [Google Scholar]
- Andrianov, V.I.; Horssen, V.T.W. On the transversal vibrations of a conveyor belt: Applicability of simplified models. J. Sound Vib. 2007, 313, 822–829. [Google Scholar] [CrossRef]
- Ma, D.Y.; Xiong, B.; Fang, F.T.; Pan, R.; Zhang, M. Simulation and analysis of Recur Dyn V-belt drive. Mech. Transm. 2014, 38, 118–122. [Google Scholar]
- Chen, N.X. Simulation Analysis and Experimental Research on the Performance of PM-Type Industrial Multiribbed Belt Drive; Changchun University of Science and Technology: Changchun, China, 2016. [Google Scholar]
- Xie, J.; Zhao, D.S.; Sha, H.Z.; Liang, J.T. Optimum design of toggle transmission system in double toggle mechanical press using response surface methodology combined with experimental design. Appl. Mech. Mater. 2011, 86, 858–862. [Google Scholar] [CrossRef]
- Wei, J.; Wang, E.J.; Wei, M.Q.; Zhang, X.J.; Chen, T.M. Optimisation of low temperature vacuum drying process of wolfberry based on response surface method. China Food Addit. 2024, 35, 138–145. [Google Scholar]
- Yu, Y.; Yu, M.Q.; Wang, E.J.; Chen, T. Optimisation and simulation of temperature field of wolfberry drying box. Food Mach. 2024, 40, 101–107+114. [Google Scholar]










| Name | Density | Poisson’s Ratio | Young’s Modulus |
|---|---|---|---|
| Parameters | 1.15 g/cm3 | 0.48 | 22 MPa |
| Damping coefficient | Stiffness coefficient | Dynamic friction coefficient | Static friction coefficient |
| 1 × 10−4 N·s/mm | 1000 N/mm | 0.4 | 0.65 |
| Level | Experimental Factors | ||
|---|---|---|---|
| A Initial Pull/ (N) | B Rotation Speed /(r·min−1) | C Declination /° | |
| −1 | 170 | 60 | 4.5 |
| 0 | 370 | 120 | 5 |
| 1 | 570 | 180 | 5.5 |
| Test Number | A | B | C | DE Edge Amplitude | AB Edge Amplitude | Overall Rating |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 50.5 | 8.6 | 0.786 |
| 2 | 0 | −1 | 1 | 54.4 | 14.4 | 0.571 |
| 3 | 1 | 1 | 0 | 38.0 | 16.7 | 0.724 |
| 4 | 0 | 0 | 0 | 40.3 | 19.2 | 0.6323 |
| 5 | 1 | 0 | −1 | 50.1 | 11.2 | 0.703 |
| 6 | 0 | 0 | 0 | 36.5 | 13.2 | 0.766 |
| 7 | −1 | 0 | −1 | 89.8 | 17.8 | 0.199 |
| 8 | 0 | −1 | −1 | 59.4 | 11.4 | 0.600 |
| 9 | −1 | 1 | 0 | 48.4 | 21.8 | 0.464 |
| 10 | 1 | −1 | 0 | 27.8 | 14.3 | 0.8321 |
| 11 | −1 | −1 | 0 | 44.1 | 22.6 | 0.421 |
| 12 | 0 | 1 | −1 | 62.6 | 12.1 | 0.554 |
| 13 | 0 | 0 | 0 | 35.9 | 14.9 | 0.727 |
| 14 | 0 | 1 | 1 | 49.5 | 11.9 | 0.691 |
| 15 | 0 | 0 | 0 | 34.2 | 16.3 | 0.799 |
| 16 | −1 | 0 | 1 | 66.8 | 17.1 | 0.469 |
| 17 | 0 | 0 | 0 | 38.7 | 14.1 | 0.732 |
| Position | Amplitude Value (mm) | |||||
|---|---|---|---|---|---|---|
| P0 | P1 | P2 | P3 | P4 | P5 | |
| A | 0.67 | 0.642 | 0.661 | 0.690 | 0.703 | 0.668 |
| B | 1.12 | 1.162 | 1.145 | 1.087 | 1.105 | 1.133 |
| C | 16.67 | 16.93 | 15.95 | 16.78 | 15.93 | 16.47 |
| D | 0.34 | 0.335 | 0.357 | 0.326 | 0.314 | 0.326 |
| E | 0.54 | 0.565 | 0.523 | 0.528 | 0.557 | 0.541 |
| F | 2.19 | 2.135 | 2.272 | 2.186 | 2.243 | 2.025 |
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Mold | 0.3933 | 9 | 0.0437 | 37.50 | 0.0004 | *** |
| A | 0.1659 | 1 | 0.1659 | 142.36 | 0.0078 | *** |
| B | 0.0032 | 1 | 0.0032 | 2.78 | 0.2694 | |
| C | 0.0743 | 1 | 0.0743 | 63.77 | 0.0064 | ** |
| AB | 0.0091 | 1 | 0.0091 | 7.83 | 0.0266 | |
| AC | 0.0593 | 1 | 0.0593 | 50.88 | 0.0002 | ** |
| BC | 0.0005 | 1 | 0.0005 | 0.4154 | 0.5398 | |
| A2 | 0.0509 | 1 | 0.0509 | 43.72 | 0.0003 | |
| B2 | 0.0013 | 1 | 0.0013 | 1.14 | 0.3214 | |
| C2 | 0.0229 | 1 | 0.0229 | 19.65 | 0.0030 | *** |
| residual | 0.0082 | 7 | 0.0042 | |||
| Misfit term | 0.0053 | 3 | 0.0061 | 2.52 | 0.1972 | |
| error term | 0.0280 | 4 | 0.0027 |
| Radius of a Rounded Corner R (mm) | Theoretical Reduction in Amplitude | F-Point Amplitude Simulation Reduced Value | Belt Deflection |
|---|---|---|---|
| 0 | 0% | 2.1 mm | 0.67 |
| 9 | 58.2% | 0.9 mm | 0.45 |
| 10 | 61.2% | 0.84 mm | 0.38 |
| 11 | 65.4% | 0.78 mm | 0.59 |
| 12 | 69.2% | 0.71 mm | 0.56 |
| 13 | 72.6% | 0.67 mm | 0.58 |
| Serial Number | Amplitude and Decay Rate at Each Point | |||||
|---|---|---|---|---|---|---|
| Point D | Attenuation Rate | Point F | Attenuation Rate | Point E | Attenuation Rate | |
| Length 1200 mm | 0.35 | 2.2 | 0.49 | |||
| Length 1400 mm | 0.29 | 17.1% | 2.08 | 5.5% | 0.34 | 30.6% |
| Length 1600 mm | 0.23 | 34.3% | 1.75 | 20.45% | 0.28 | 42.8% |
| Length 1800 mm | 0.30 | 14.3 | 1.87 | 15% | 0.35 | 28.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Su, Z.; Zhang, J.; Li, J.; Qin, W. Analysis of Vibration Characteristics of the Grading Belt in Wolfberry Sorting Machines. Appl. Sci. 2025, 15, 6022. https://doi.org/10.3390/app15116022
Yu Y, Su Z, Zhang J, Li J, Qin W. Analysis of Vibration Characteristics of the Grading Belt in Wolfberry Sorting Machines. Applied Sciences. 2025; 15(11):6022. https://doi.org/10.3390/app15116022
Chicago/Turabian StyleYu, Yang, Zhiwei Su, Junhao Zhang, Jinglong Li, and Wu Qin. 2025. "Analysis of Vibration Characteristics of the Grading Belt in Wolfberry Sorting Machines" Applied Sciences 15, no. 11: 6022. https://doi.org/10.3390/app15116022
APA StyleYu, Y., Su, Z., Zhang, J., Li, J., & Qin, W. (2025). Analysis of Vibration Characteristics of the Grading Belt in Wolfberry Sorting Machines. Applied Sciences, 15(11), 6022. https://doi.org/10.3390/app15116022






