Using Hybrid Feature and Classifier Fusion for an Asynchronous Brain–Computer Interface Framework Based on Steady-State Motion Visual Evoked Potentials

Abstract

This study proposes an asynchronous brain–computer interface (BCI) framework based on steady-state motion visual evoked potentials (SSMVEPs), designed to enhance the accuracy and robustness of control state recognition. The method integrates filter bank common spatial patterns (FBCSPs) and filter bank canonical correlation analysis (FBCCA) to extract complementary spatial and frequency domain features from EEG signals. These multimodal features are then fused and input into a dual-classifier structure consisting of a support vector machine (SVM) and extreme gradient boosting (XGBoost). A weighted fusion strategy is applied to combine the probabilistic outputs of both classifiers, allowing the system to leverage their respective strengths. Experimental results demonstrate that the fused FB(CSP + CCA)-(SVM + XGBoost) model achieves superior performance in distinguishing intentional control (IC) and non-control (NC) states compared to models using a single feature type or classifier. Furthermore, the visualization of feature distributions using UMAP shows improved inter-class separability when combining FBCSP and FBCCA features. These findings confirm the effectiveness of both feature-level and classifier-level fusion in asynchronous BCI systems. The proposed approach offers a promising and practical solution for developing more reliable and user-adaptive BCI applications, particularly in real-world environments requiring flexible control without external cues.

1. Introduction

Brain–computer interface (BCI) technology is a rapidly evolving interdisciplinary field that enables direct communication between the central nervous system (CNS) and external devices, bypassing traditional neuromuscular pathways [1,2]. By decoding brain signals into interpretable control commands, BCI systems have been widely applied in human–machine interaction, neurorehabilitation, and communication support for individuals with severe motor impairments [3,4,5].

Among various BCI paradigms, steady-state visual evoked potentials (SSVEPs) have been widely adopted due to their high signal-to-noise ratio (SNR), low training requirements, and strong cross-subject consistency [6,7,8]. In SSVEP-based systems, users focus on flickering visual stimuli to evoke frequency-specific EEG responses for multi-target selection. However, prolonged exposure to high-frequency flickering stimuli can induce visual fatigue, reducing user comfort and long-term usability [9]. To improve user experience, researchers have proposed the steady-state motion visual evoked potential (SSMVEP) paradigm. This approach uses periodic motion stimuli—such as expanding or contracting rings—instead of flashing lights, preserving the frequency-specific response while improving visual comfort [10]. Previous studies have shown that SSMVEPs are more suitable for long-term use, offering better user acceptance and greater signal stability in practical environments [11].

In terms of operational mode, BCI systems can be categorized into synchronous and asynchronous types [12]. Synchronous BCIs require users to issue commands within predefined temporal windows, which simplifies signal processing but limits user autonomy and interaction flexibility [13]. In contrast, asynchronous BCIs allow users to initiate commands at any arbitrary time, aligning more closely with natural interaction. However, such systems must continuously monitor EEG signals to distinguish between intentional control (IC) and non-control (NC) states in real time—a technically demanding task in real-world scenarios [14,15,16].

State detection methods for asynchronous BCIs can be broadly divided into threshold-based and classifier-based approaches [17]. Threshold-based methods, such as canonical correlation analysis (CCA), are efficient but sensitive to individual variability and environmental noise, which may degrade performance [18,19]. Recently, more studies have introduced supervised learning classifiers to enhance system adaptability and robustness. Existing methods have explored convolutional neural networks [20], complex network analysis [21], and multimodal feature fusion techniques [22]. For example, Zhang X et al. [20] proposed an FFT-CNN architecture that achieved improved accuracy in asynchronous SSVEP classification, but the model was prone to overfitting due to its high complexity. Zhang W et al. [21] employed filter banks and an optimized complex network (OCN) to extract attention-related features from multiband EEG data, followed by classification using a support vector machine (SVM). However, this approach focused primarily on attention state representation and did not fully leverage frequency-specific evoked responses inherent to SSVEP/SSMVEP paradigms. Du et al. [22] introduced a feature fusion technique combining task-related component analysis (TRCA) coefficients and power spectral density (PSD) features into a composite TRPSD descriptor, achieving enhanced performance with a stepwise linear discriminant analysis (SWLDA) classifier. Despite the progress in feature fusion techniques, many existing methods still rely on either spatial or frequency domain features alone, overlooking the benefits of their integration. Furthermore, the lack of consideration for the compatibility between specific feature types and classifier architectures often leads to suboptimal model performance.

In the context of SSMVEP-based asynchronous state detection, the core assumption is that NC-state EEG lacks pronounced frequency components corresponding to stimulus frequencies, whereas IC-state EEG exhibits clear responses at stimulus frequencies and their harmonics [23]. Therefore, a hybrid feature extraction strategy that integrates frequency domain correlation and spatial energy distribution is desirable. Canonical correlation analysis is particularly effective for quantifying the similarity between EEG signals and reference templates across multiple frequencies, requiring no training and offering high efficiency for real-time applications [24]. In parallel, the common spatial pattern (CSP) algorithm can identify spatial filters that maximize the variance difference between IC and NC states, enabling the extraction of discriminative spatial features [25]. Motivated by these insights, this study proposes a dual-feature fusion framework combining CCA and CSP-derived features, designed to capture both frequency and spatial domain information.

Moreover, different classifiers exhibit varying degrees of compatibility with different types of features [26]. SVMs have been widely applied to motor-related EEG classification tasks, showing robust performance in high-dimensional, sparse, and linearly separable data contexts [27]. In contrast, extreme gradient boosting (XGBoost) has demonstrated strong capability in modeling nonlinear relationships and handling redundant features, making it well suited for complex EEG tasks such as seizure detection and emotion recognition [28,29]. The features extracted by FBCSPs and FBCCA differ substantially in their statistical characteristics, representational structures, and dimensional profiles. FBCSPs extract channel-wise variance through linear spatial filtering, producing relatively low-dimensional features with a linear structure. These properties make FBCSP features well suited for boundary-based classifiers such as SVMs [30]. In contrast, FBCCA generates high-dimensional features by measuring frequency domain correlation with reference templates. These features are inherently nonlinear and more complex in structure, aligning well with XGBoost, which excels in nonlinear modeling and embedded feature selection [31]. The direct concatenation of these heterogeneous feature sets into a single classifier could introduce issues such as dimensionality mismatch, overfitting, and compromised generalization. To address this, the proposed framework adopts a structured feature–classifier pairing approach: the SVM is paired with FBCSP features, and XGBoost is paired with FBCCA features. This strategy leverages the strengths of each classifier in handling its respective feature type. A weighted probabilistic fusion mechanism is then employed to integrate the outputs from the two classifiers. This fusion enables the system to exploit the complementary strengths of both classifiers without diminishing discriminative capability. By employing this dual-branch classifier fusion scheme—an SVM for FBCSPs and XGBoost for FBCCA—the framework achieves both classifier-specific adaptability and coordinated optimization of feature–model compatibility, thereby enhancing robustness and generalization in asynchronous BCI state detection.

In summary, this study proposes a dual-level fusion framework for asynchronous SSMVEP-based BCI systems, incorporating a three-tier collaborative structure that integrates heterogeneous features, heterogeneous classifiers, and decision-level fusion. At the feature level, spatial–domain and frequency domain features are extracted using FBCSP and FBCCA, enabling joint modeling of spatial distributions and frequency-locked responses in EEG signals. At the classifier level, SVM and XGBoost are respectively employed to process the FBCSP and FBCCA features, and their outputs are combined using a weighted probabilistic fusion strategy to achieve structured feature–classifier alignment and collaborative optimization.

This study systematically introduces a novel dual-feature fusion mechanism based on FBCSPs and FBCCA into the asynchronous SSMVEP framework, achieving joint modeling of spatial and frequency information. Furthermore, a classifier ensemble is constructed based on feature–classifier compatibility, where an SVM and XGBoost are paired with their respective feature types, enhancing the model’s adaptability to heterogeneous features and improving generalization performance. The proposed method offers a novel and practical approach for developing high-performance, scalable asynchronous BCI systems.

2. Materials and Methods

2.1. Subjects

A total of 10 participants aged between 23 and 26 years were recruited for this study. All participants had normal or corrected-to-normal vision and no history of psychiatric disorders. Written informed consent was obtained from all participants after a full explanation of the experimental procedures.

2.2. Paradigm Design

This study employed a ring-shaped contraction–expansion SSMVEP paradigm. The SSMVEP paradigm consisted of a high-contrast background and a low-contrast annular stimulus. The primary parameters of the low-contrast ring included its inner and outer diameters. The high-contrast background determined the maximum diameter of the entire visual paradigm. The area ratio (C) between the ring and the background was defined as follows:

$$C={\displaystyle \frac{S_1}{S-S_1}}$$

(1)

In this equation, $S_1$ represents the total area of the annular stimulus, and $S$ denotes the total area of the background.

At the onset of the paradigm, the outer diameters of the concentric rings were arranged in an arithmetic sequence. Given the maximum diameter of the visual field ($r_{max}$), the outer diameter ($r_1^i$) and inner diameter ($r_2^i$) of each ring were related to the area as follows:

$$r_1^i=(2i-1)\ast r_{max}/2n$$

(2)

$$S^i=\pi {(r_1^i)}^2-\pi {(r_1^{i-1})}^2$$

(3)

$$S_1^i=\pi {(r_1^i)}^2-\pi {(r_2^i)}^2$$

(4)

In this equation, $i$ denotes the index of the $i$-th ring counted from the center outward, and $n$ represents the total number of rings. $S^i$ indicates the area enclosed between the outer diameter of the $i$-th ring and that of the ($i$ − 1)-th ring, while $S_1^i$ refers to the area of the $i$-th annular ring.

To ensure that the overall luminance of the paradigm remains constant during motion, the area ratio $C$ between the annular rings and the background must be maintained at a fixed value. Therefore, the inner diameter of each ring needs to be determined through calculation. Based on Equations (1)–(4), the inner diameter $r_2^i$ of the $i$-th ring can be computed as follows:

$$r_2^i=\sqrt{(1-C)\ast {(r_1^i)}^2+C{(r_1^{i-1})}^2}$$

(5)

Let the variation range of the outer diameter of each annular ring be defined as $[(i+1)\ast r_{max}/n,i\ast r_{max}/n]\mathrm{c}$. The outer diameter follows a sinusoidal motion trajectory. Accordingly, the time-dependent change in the outer diameter $r_1^i$ of the $i$-th ring can be expressed as:

$$r_1^i=i+1-cos(2\pi ft)\ast r_{max}/n$$

(6)

In this equation, $f$ represents the stimulation frequency, and $t$ denotes the stimulation time.

In this study, eight types of ring-shaped stimulation paradigms with distinct flickering frequencies (i.e., 3.00 Hz, 3.25 Hz, 3.50 Hz, 3.75 Hz, 4.00 Hz, 4.25 Hz, 4.50 Hz, and 4.75 Hz) were employed, as illustrated in Figure 1. In addition, to evaluate the proposed algorithm’s ability to distinguish between idle and control states, a designated idle region was included to collect EEG data corresponding to the idle state. Participants were instructed to fixate within a dashed rectangular frame during idle trials to ensure that no control commands were generated. As a result, a total of nine target classes were collected in this study, including eight stimulation conditions and one idle condition.

2.3. Data Acquisition

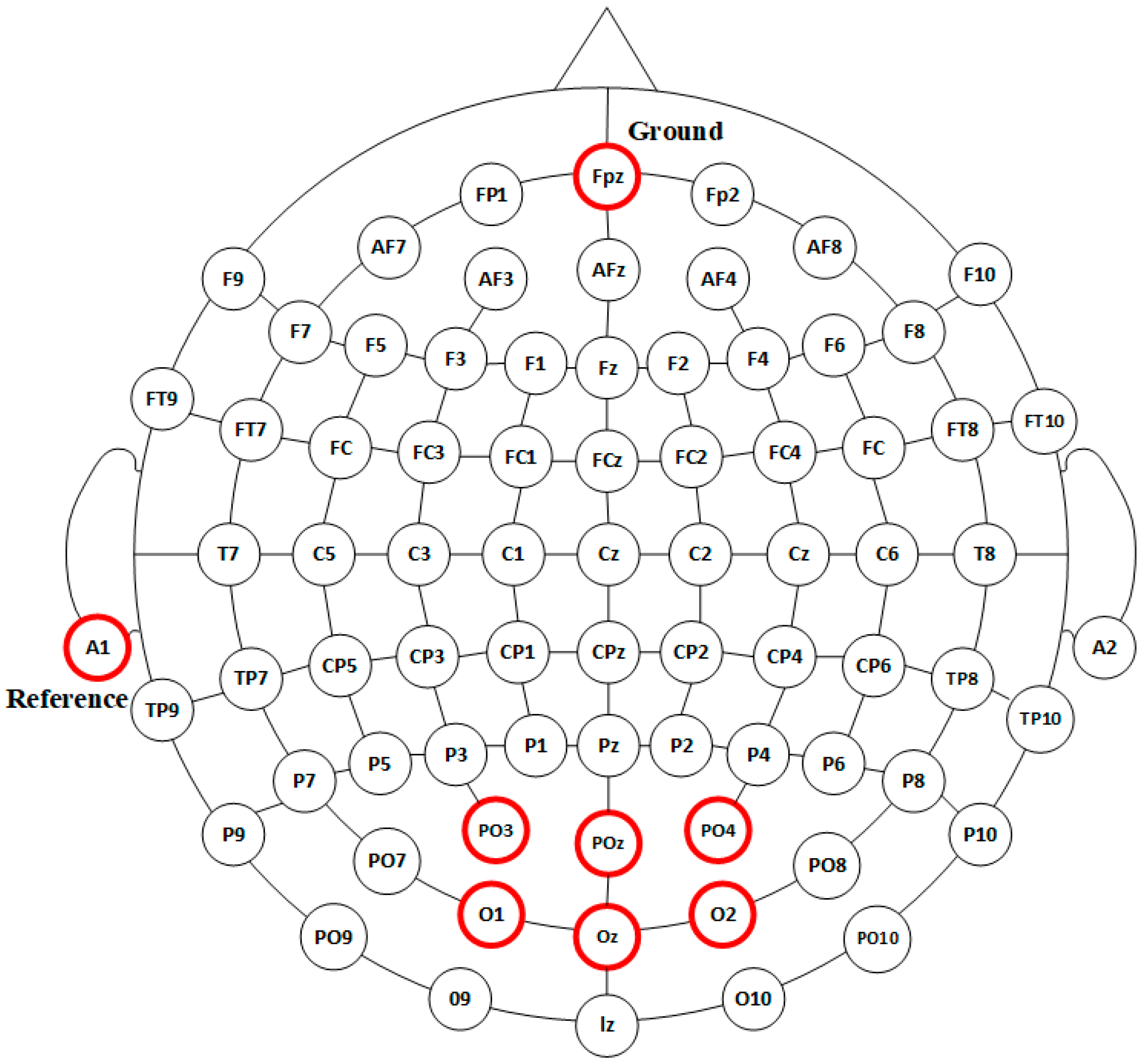
EEG signals were recorded using the g.USBamp system (The manufacturer of this device is g.tec medical engineering GmbH, Schiedlberg, Austria). EEG electrodes were positioned in accordance with the international 10–20 system. The reference electrode (A1) was placed on the unilateral earlobe of the subject, while the ground electrode was located at Fpz, on the prefrontal cortex. Since SSMVEPs elicit the strongest responses in the occipital region of the brain, six electrodes—O1, Oz, O2, PO3, POz, and PO4—were selected for data acquisition in this area, as illustrated in Figure 2. EEG signals were sampled at 1200 Hz, followed by preprocessing steps that included a 4th-order Butterworth notch filter (48–52 Hz) to eliminate powerline interference and an 8th-order Butterworth band-pass filter (2–100 Hz) to suppress low- and high-frequency noise. The filtered signals were subsequently downsampled to 240 Hz. Throughout the recording session, electrode impedance was maintained below 10 kΩ.

2.4. Experimental Procedure

During the experiment, participants were instructed to sequentially gaze at eight target stimuli, each corresponding to a different stimulation frequency (3.00 Hz, 3.25 Hz, 3.50 Hz, 3.75 Hz, 4.00 Hz, 4.25 Hz, and 4.75 Hz). Each frequency-specific target was presented 20 times, with idle fixation trials randomly interspersed among the eight stimulation conditions to simulate the non-control state. Each trial lasted 5 s, consisting of a 1 s cue period, a 3 s stimulation period, and a 1 s rest period. The entire experiment comprised 10 blocks, with each block containing 16 trials. After the completion of each block, participants were given a 2 min break to minimize fatigue.

2.5. Feature Extraction and Classification Algorithms

2.5.1. Common Spatial Patterns

The CSP is a spatial filtering algorithm specifically designed for binary classification tasks, and it is widely used in the field of brain signal processing. This algorithm effectively extracts spatial distribution features from multichannel EEG data. CSPs have been extensively applied in brain–computer interface systems and other neural signal analysis tasks, demonstrating particularly strong performance in decoding motor imagery, such as hand movement intentions. The core principle of CSPs involves the use of matrix diagonalization techniques to identify an optimal set of spatial filters. These filters are then used to project the EEG data in a way that maximizes the variance difference between two classes. This approach enables the extraction of feature vectors with enhanced class separability.

Assume two classes of EEG data, $X_1$ and $X_2$, with each trial having dimensions of N × T (number of channels × number of time points). By applying Equations (7) and (8) to $X_1$ and $X_2$, the average sample covariance matrices for the two classes, $\overline{R_1}$ and $\overline{R_2}$, can be obtained.

$$\overline{R_1}={\displaystyle \frac{1}{M_1}}{\displaystyle \sum _{i=1}^{M_1}\frac{X_{1,i}{X}_{1,i}^T}{trace(X_{1,i}{X}_{1,i}^T)}}$$

(7)

$$\overline{R_2}={\displaystyle \frac{1}{M_2}}{\displaystyle \sum _{i=1}^{M_2}\frac{X_{2,i}{X}_{2,i}^T}{trace(X_{2,i}{X}_{2,i}^T)}}$$

(8)

In these equations, $M_1$ and $M_2$ represent the total number of samples in $X_1$ and $X_2$, respectively. $X_{1,i}^T$ and $X_{2,i}^T$ denote the transpose of the $i$-th sample in $X_{1,i}$ and $X_{2,i}$, respectively. $trace(X)$ refers to the sum of the elements along the main diagonal of matrix $X$.

Next, the composite spatial covariance matrix is calculated using Equation (9), and eigenvalue decomposition is performed on the resulting composite covariance matrix $R$ using Equation (10):

$$R=\overline{R_1}+\overline{R_2}$$

(9)

$$R=U\lambda U^T$$

(10)

In this equation, $\lambda$ denotes the diagonal matrix of eigenvalues of the covariance matrix $R$, $U$ represents the matrix of corresponding eigenvectors, and $U^T$ is the transpose of $U$.

After obtaining the eigenvalue matrix $\lambda$ and eigenvector matrix $U$ through decomposition, the whitening transformation matrix $P$ is computed as follows:

$$P=\sqrt{\lambda }{U}^T$$

(11)

The whitening matrix $P$ is then applied to transform the average covariance matrix $\overline{R_1}$ and $\overline{R_2}$, as follows:

$$S_1=P\overline{R_1}{P}^T$$

(12)

$$S_2=P\overline{R_2}{P}^T$$

(13)

Subsequently, principal component decomposition is performed on $S_1$ and $S_2$.

$$S_1=B{\mathsf{\Lambda }}_1{B}^T$$

(14)

$$S_2=B{\mathsf{\Lambda }}_2{B}^T$$

(15)

Using Equations (14) and (15), it can be demonstrated that the eigenvector matrices of $S_1$ and $S_2$ are identical. Under this condition, the eigenvalue matrices of $S_1$ and $S_2$ satisfy the following relationship:

$${\mathsf{\Lambda }}_1+{\mathsf{\Lambda }}_2=I$$

(16)

According to Equation (16), the eigenvalue matrices of $S_1$ and $S_2$ are complementary and sum to the identity matrix. This implies that when an eigenvalue of $S_1$ reaches its maximum, the corresponding eigenvalue of $S_2$ attains its minimum. Therefore, the eigenvalues of $S_1$ are sorted in descending order, while those of $S_2$ are sorted in ascending order. The eigenvectors corresponding to the top mmm largest eigenvalues of $S_1$ and the top mmm smallest eigenvalues of $S_2$ are selected and combined to form $\widehat{B}$. Consequently, the final spatial filter projection matrix $W$ is obtained as:

$$W={\widehat{B}}^{T}P$$

(17)

Let $X$ denote the input EEG signal. By applying the spatial filter, the filtered signal $Z$ can be obtained as follows:

$$Z=WX$$

(18)

Subsequently, the variance of the filtered signal is calculated, normalized, and then log-transformed to obtain the corresponding feature vector $f$ for the input signal $X$, as shown below:

$$f=log{\displaystyle \frac{var(\mathrm{Z})}{sum(var(\mathrm{Z}))}}$$

(19)

In this equation, $var(\mathrm{Z})$ denotes the variance of the filtered signal $Z$.

2.5.2. Canonical Correlation Analysis

CCA is an unsupervised machine learning algorithm used to explore the relationship between two sets of variables, $X=(X_1,X_2,X_3,\dots ,X_n)$ and $Y=(Y_1,Y_2,Y_3,\dots ,Y_n)$. The fundamental idea of CCA is to find two sets of non-zero vectors, $\alpha =({\alpha }_1,{\alpha }_1,{\alpha }_1,{\alpha }_1,\dots {\alpha }_n)$ and $\beta =({\beta }_1,{\beta }_1,{\beta }_1,{\beta }_1,\dots {\beta }_n)$, which are used to linearly combine the variables in each set into new variables, $U$ and $V$. Specifically, the linear combinations are defined as $U={\alpha }_1{X}_1+{\alpha }_2{X}_2+\cdots +{\alpha }_n{X}_n$ and $V={\beta }_1{Y}_1+{\beta }_2{Y}_2+\cdots +{\beta }_n{Y}_n$. By applying the coefficient vectors $\alpha$ and $\beta$, the analysis shifts from examining the relationship between the original variable sets, $X$ and $Y$, to investigating the correlation between the derived variables, $U$ and $V$.

In the process of using CCA to identify SSMVEP signals, a set of sine and cosine functions must be constructed as reference signals, as defined by the following equation:

$$Y=\left(\begin{array}{c}\sin (2\pi f_{i}t)\\ \cos (2\pi f_{i}t)\\ ⋮\\ \sin (2\pi H{f}_{i}t)\end{array}\right),t=\left[\begin{array}{c}{\displaystyle \frac{1}{F_s}},{\displaystyle \frac{2}{F_s}},\dots ,{\displaystyle \frac{N}{F_s}}\end{array}\right]$$

(20)

In this equation, $H$ denotes the number of harmonics, $N$ represents the number of sampling points, and $F_s$ is the sampling frequency.

The recorded evoked EEG signal is denoted as $X=(X_1,X_2,X_3,\dots ,X_C)$, where $C$ is the number of electrode channels. By solving Equation (21), a set of canonical correlation coefficients between the EEG signal $X$ and the reference signal $Y$ can be obtained, represented as ${\rho }_{f_i}=({\rho }_1,{\rho }_2,{\rho }_3,\dots ,{\rho }_C)$.

$${\rho }_{(\mathrm{X},\mathrm{Y})}={\displaystyle \frac{E({\alpha }^{T}X{Y}^T\beta )}{\sqrt{E({\alpha }^{T}X{X}^T\alpha )E({\beta }^{T}Y{Y}^T\beta )}}}$$

(21)

After computing each set of data, four correlation coefficient vectors, ${\rho }_{f_i}$, are obtained, each corresponding to a specific flickering frequency, $f_i$, as shown in Equation (22). The frequency associated with the maximum correlation coefficient ${\rho }_{\mathrm{x}}$ in the vector ${\rho }_{f_i}$ is selected as the final identified target frequency, denoted as $f_{target}$.

$$f_{target}=\underset{f_i}{\mathrm{argmax}}{\rho }_{\mathrm{x}}$$

(22)

Since the CCA algorithm employs the correlation coefficient corresponding to each stimulus frequency as the basis for classification, its accuracy can to some extent reflect the quality of the evoked signals induced by the paradigm.

2.5.3. Filter Bank Combination Characteristics

Filter banks (FBs) are a commonly used signal processing technique that decomposes the input signal into multiple frequency sub-bands. It has been widely applied in EEG signal analysis and has given rise to algorithms such as filter bank common spatial patterns (FBCSPs) and filter bank canonical correlation analysis (FBCCA). In this approach, the EEG signal is first filtered into different frequency bands using a filter bank. The filter bank analysis decomposes the original EEG signal into five sub-band signals using a set of predefined band-pass filters. Each sub-band covers a specific frequency range and facilitates the effective extraction of frequency-specific neural activity features, while preserving the phase information of the signal. The selected five sub-bands span the frequency range of 2–40 Hz and are defined as follows: [2–8] Hz, [8–14] Hz, [14–20] Hz, [20–30] Hz, and [30–40] Hz. This configuration encompasses commonly observed EEG rhythms, including delta, theta, alpha, beta, and low-gamma bands, thereby providing a comprehensive frequency representation for subsequent feature extraction and classification tasks.

Features are then extracted from the filtered signals using CSP and CCA methods. Finally, the CSP and CCA features are combined through a cross-feature fusion strategy. The detailed procedure is as follows:

First, the input data $X$ are processed using a set of predefined filters, resulting in a filter bank denoted as $W_z$.

$$W_z=(w_1,w_2,\dots ,w_n)$$

(23)

In this equation, $w_i$ denotes the $i$-th filter, and $n$ represents the total number of filters in the filter bank.

The input data are then transformed using the filter bank $W_z$, resulting in the filtered data $X^{\prime }$, as expressed by the following equation:

$$X^{\prime }=W_{z}X$$

(24)

Feature extraction is performed on the filter bank outputs using the CCA algorithm (Equation (21)) and the CSP algorithm (Equation (19)), resulting in the following expression:

$$\rho (X\prime ,Y)=({\rho }_{(w_{1}X,Y)},\dots ,{\rho }_{(w_{n}X,Y)})$$

(25)

$$f_{(X^{\prime })}=(f_{(w_{1}X)},\dots ,f_{(w_{n}X)})$$

(26)

The combined feature $T_{f,\rho }$ is obtained by cross-fusing the features extracted using the CSP and CCA algorithms.

$$T_{f,\rho }=Concat(f_{(w_{1}X)},{\rho }_{(w_{1}X,Y)},\dots ,f_{(w_{n}X)},{\rho }_{(w_{n}X,Y)})$$

(27)

2.5.4. Classifier Design and Fusion Strategy

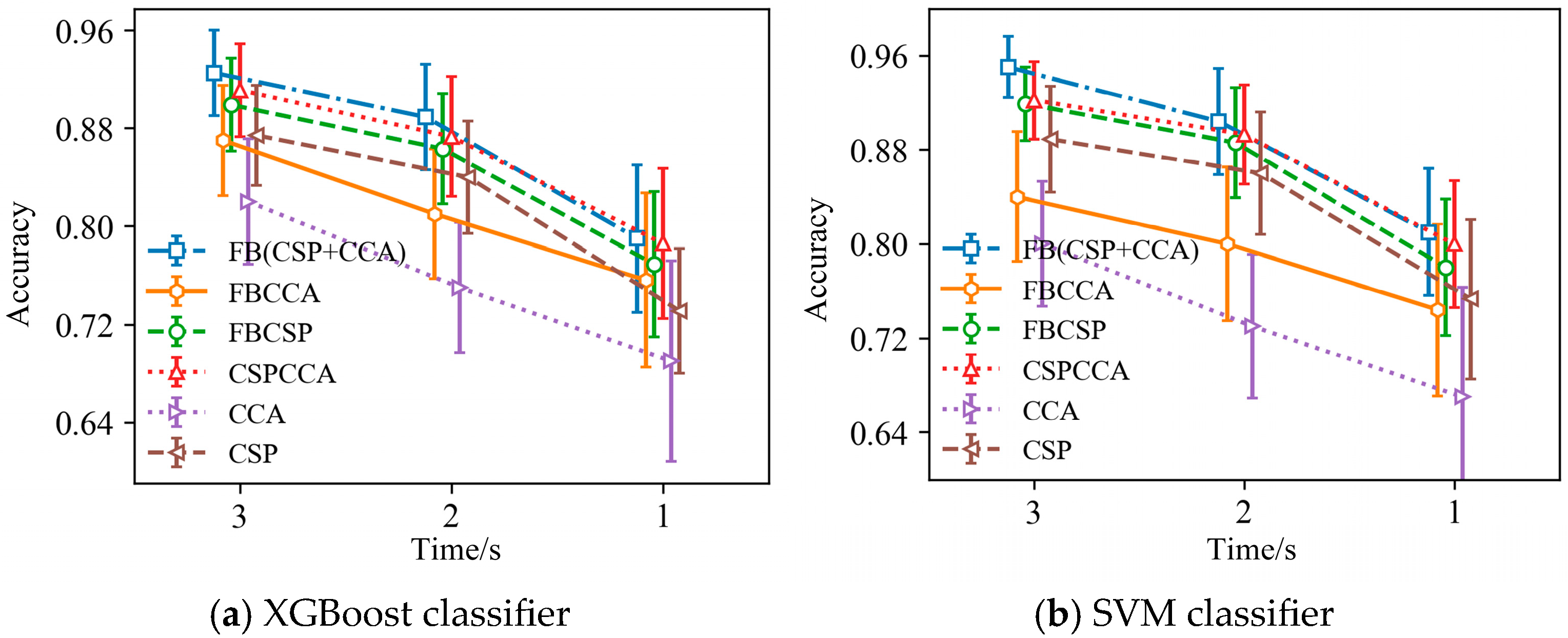
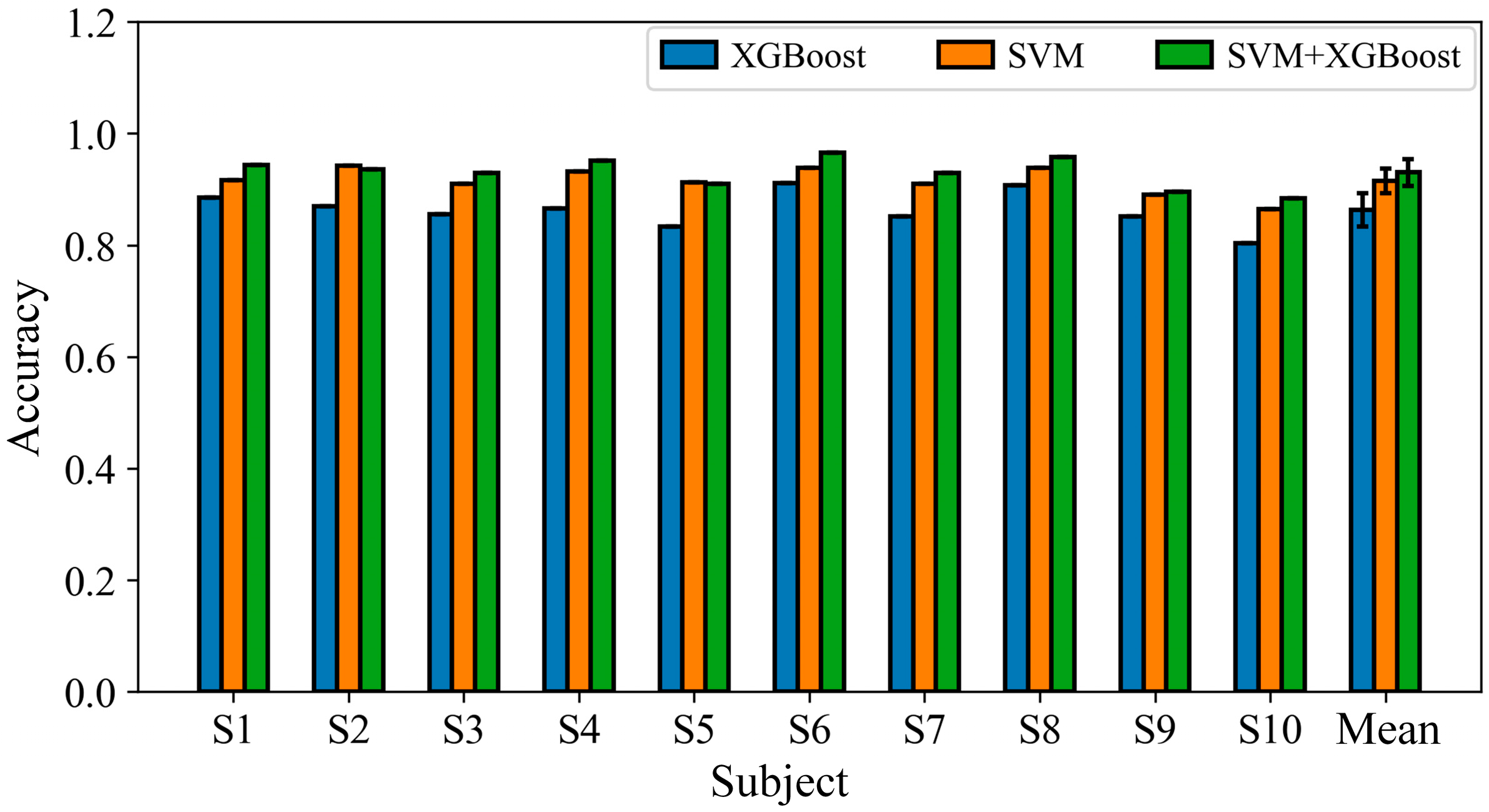
Considering that the extracted features require classification, two classifiers were selected based on the characteristics of the respective features. For features extracted using the CSP algorithm, SVM was adopted, as the CSP aims to maximize variance between two classes, making an SVM a suitable choice for binary classification. In contrast, the features derived from the CCA algorithm tend to have higher dimensionality due to the presence of multiple stimulation frequencies; therefore, the XGBoost algorithm, an ensemble learning method, was chosen to better handle this complexity. Accordingly, in this study, an SVM and XGBoost were used to classify features extracted by the CSP and CCA algorithms, respectively.

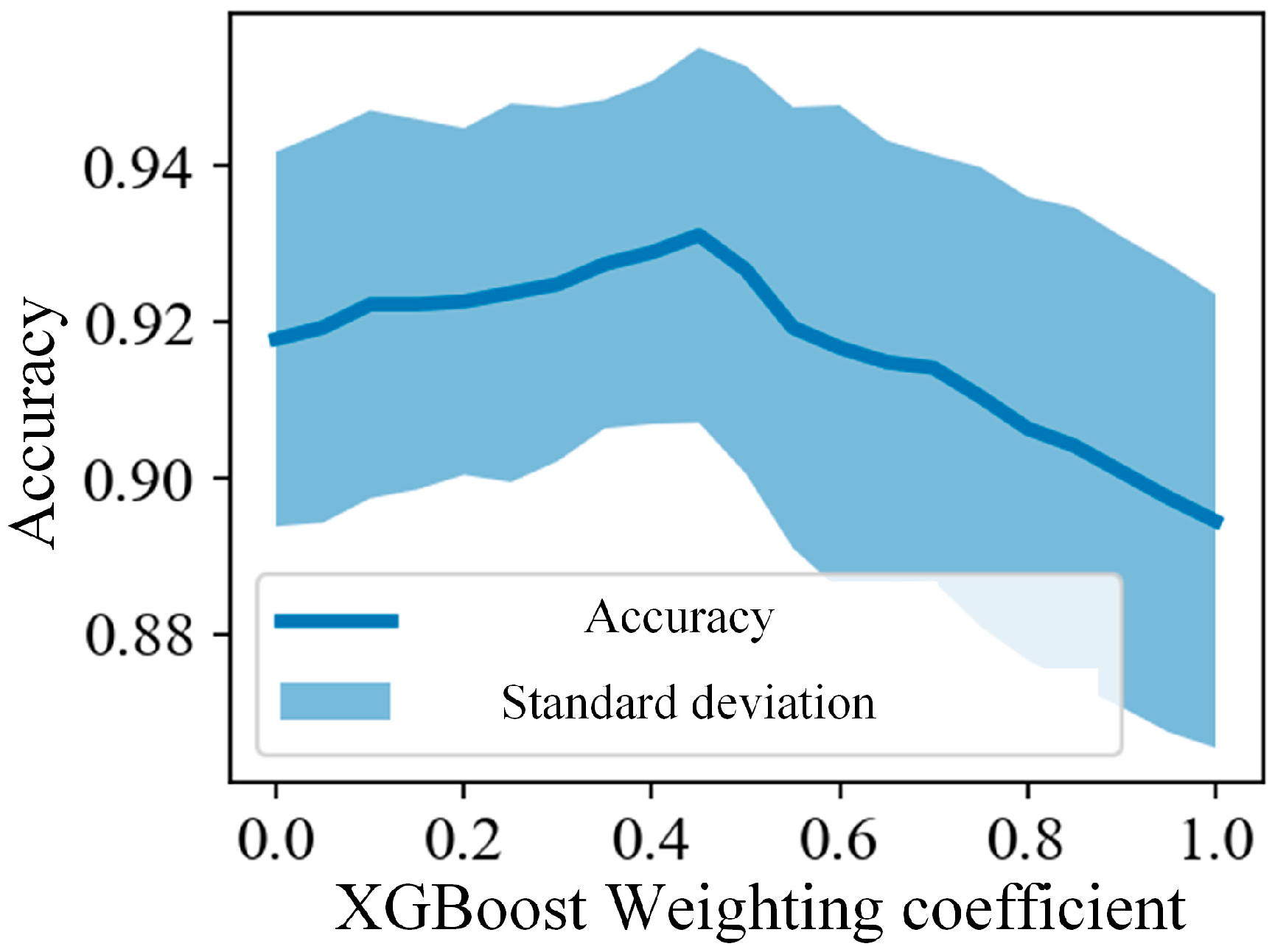
XGBoost is well suited for handling a large number of features and can automatically learn nonlinear relationships among them, making it particularly effective for complex and high-dimensional datasets. In contrast, SVMs excel at identifying optimal decision boundaries, especially in binary classification tasks. Given the nature of the combined features—CCA-derived features represent multi-class frequency information, while CSP-derived features capture binary spatial energy differences—XGBoost may outperform an SVM when classifying CCA features, whereas an SVM may be more effective than XGBoost for CSP features. Therefore, a weighted (SVM + XGBoost) classifier is proposed to predict the combined FB(CSP + CCA) features. This hybrid approach enables the classifier to learn the relative importance of different feature types, potentially enhancing the model’s ability to recognize asynchronous states. The detailed design is as follows:

$$p=(1-q)\ast SVM\left(T_{f,\rho }\right)+q\ast XGBoot\left(T_{f,\rho }\right)$$

(28)

In this equation, $p$ represents the final predicted probability for the combined feature $T_{f,\rho }$; $q$ denotes the weighting coefficient. $T_{f,\rho }$ is the fused feature vector constructed from both CSP and CCA features. $SVM\left(T_{f,\rho }\right)$ and $XGBoot\left(T_{f,\rho }\right)$ correspond to the predicted probabilities generated by the SVM and XGBoost classifiers, respectively, based on the input feature $T_{f,\rho }$.

2.6. Statistical Analyses

For the classification accuracy of different methods under each subject condition, we adopted the paired t-test to evaluate the statistical significance of the differences between the methods. And Bonferroni correction was adopted to adjust the p value. A corrected p value of less than 0.05 was taken as the criterion for judging that the difference was statistically significant.

3. Results

3.1. Combinatorial Characterization

First, the features extracted by the CCA algorithm using 2 s data segments were analyzed. Dimensionality reduction was performed using the UMAP algorithm on the feature sets derived from both CCA and FBCCA, and the results are shown in Figure 3. Figure 3a presents the reduced features obtained from the FBCCA algorithm, while Figure 3b illustrates those from the standard CCA algorithm. As shown in Figure 3a, although a small number of features corresponding to the eight stimulation frequencies and the idle state were confused, the FBCCA-derived features still exhibit relatively clear boundaries. In contrast, Figure 3b shows that the boundaries between features extracted by the CCA algorithm become more blurred, and the separation between different frequencies begins to fade. Overall, the features extracted by FBCCA demonstrate smaller intra-class distances and larger inter-class distances.

Subsequently, features extracted by the CSP algorithm using 2 s data segments were analyzed. UMAP was applied to both the CSP and FBCSP feature sets, and the results are shown in Figure 4. Figure 4a corresponds to the dimensionality-reduced features from the CSP, and Figure 4b corresponds to those from the FBCSP. As observed in Figure 4, both methods show some degree of boundary confusion between the idle and control states after dimensionality reduction. However, the FBCSP exhibits smaller intra-class distances and fewer instances of feature overlap, indicating better class separability compared to the CSP.

The features extracted by FBCSP and FBCCA were then standardized separately and fused. UMAP was applied to the combined features, and the results are presented in Figure 5. Compared to Figure 4a, Figure 5 shows that the class separability between different states improved significantly after combining FBCCA and FBCSP features, with an increase in inter-class distances and a reduction in feature confusion. This indicates that the fusion of features from FBCCA and the FBCSP yields superior results in the low-dimensional space.

This improvement can be attributed to the complementary nature of the two algorithms: the FBCSP emphasizes the spatial characteristics of EEG signals, while FBCCA focuses on frequency-specific information related to the stimulus response. Although the FBCSP can effectively distinguish between idle and control states based on spatial energy differences, it cannot explicitly determine whether these differences arise from stimulus-induced brain oscillations. In contrast, CCA can precisely capture correlations between EEG signals and target stimulation frequencies. Therefore, combining both algorithms leverages their respective strengths and results in better feature boundary formation in the dimensionality-reduced space than using either FBCCA or the FBCSP alone.

3.2. Analysis of Weighted Results

Following the above feature dimensionality reduction analysis, the FB(CSP + CCA) combination was shown to produce more discriminative low-dimensional features. To further evaluate the classification performance of the FB(CSP + CCA) features, both XGBoost and SVM classifiers were applied. The results are illustrated in Figure 6.

As shown in Figure 6a,b, the FB(CSP + CCA) features achieved the highest classification accuracy under both XGBoost and SVM classifiers when compared with other individual feature sets, which is consistent with the findings from the previous dimensionality reduction analysis. Furthermore, it can be observed that the classification performance of CCA and CSP features varies slightly depending on the classifier used. To further explore this effect, classification results for the same feature types under different classifiers were plotted in the same figure, as shown in Figure 7.

In Figure 7a, the classification accuracy of FBCSP-SVM can be seen to be higher than that of FBCSP-XGBoost, and CSP-SVM outperforms CSP-XGBoost. Conversely, in Figure 7b, FBCCA-XGBoost and CCA-XGBoost achieve higher accuracies than their respective SVM counterparts. These results suggest that for features extracted using CSPs and FBCSPs, the SVM provides a better classification performance, while for features extracted using CCA and FBCCA, XGBoost is more effective.

From a theoretical standpoint, an SVM utilizes kernel functions to map data into a higher-dimensional space, where it becomes linearly separable. CCA features, projected based on different stimulus frequencies, tend to be sparse in the original feature space. When these sparse features are mapped into a high-dimensional space, the increased sparsity may hinder the performance of the SVM in terms of learning and generalization. In contrast, CSP features are designed to maximize inter-class differences, making them well suited for binary classification. The distribution of CSP features is more compact in the feature space, thereby enhancing the effectiveness of SVM classification. On the other hand, XGBoost handles high-dimensional data more efficiently and captures complex nonlinear relationships through its tree-based structure, making it well suited for multi-frequency CCA-based feature vectors.

Considering the complementary strengths of the SVM and XGBoost for different types of features, a weighted ensemble classifier combining the outputs of both models was proposed. The combined output was calculated using a weighting coefficient, where the sum of the weights assigned to XGBoost and SVM equals 1. When the XGBoost weight was set to 1, the SVM weight was 0, and vice versa. The average classification performance for different XGBoost weights is shown in Figure 8.

As shown in Figure 8, the highest classification accuracy was achieved when the weight assigned to the XGBoost classifier was 0.45 and the weight assigned to the SVM classifier was 0.55. Based on this result, the ensemble model was configured with XGBoost and SVM weights set to 0.45 and 0.55, respectively.

The combined features were then classified using the SVM, XGBoost, and the weighted ensemble classifiers. The classification results are presented in Figure 9, and the average performance was statistically evaluated using a paired-sample t-test.

As shown in Figure 9, due to individual variability, the classification accuracy for participant S2 did not improve when using the SVM + XGBoost ensemble classifier; in fact, it was slightly lower than that achieved with the standalone SVM classifier. For all other participants, the ensemble classifier yielded a noticeable improvement. On average, the SVM + XGBoost classifier achieved an accuracy of 93.1%, representing a 1.5% improvement over the SVM classifier (p < 0.05) and a 3.7% improvement over the XGBoost classifier (p < 0.001).

These results indicate that the ensemble classifier combining the SVM and XGBoost significantly enhances the overall classification performance. This improvement can be attributed to the complementary strengths of the two classifiers: the SVM is particularly effective for binary spatial features extracted by CSPs, while XGBoost performs better on multi-frequency features derived from CCA. To further validate this observation, the classifiers were also applied to the raw EEG signals, and the results are shown in Figure 10.

As shown in Figure 10, for most participants, the highest classification accuracy was achieved using the SVM classifier. Only participant S1 showed a 1.9% improvement in accuracy when using the ensemble classifier. On average, the SVM classifier outperformed both the ensemble and the XGBoost classifiers, with the SVM + XGBoost ensemble achieving a mean accuracy of 74.9%, which was 2% lower than that of the SVM classifier alone (p < 0.05). These findings suggest that the ensemble classifier does not provide additional benefits when applied directly to raw EEG data and may, in fact, reduce model performance.

Furthermore, a comparison between classification results using fused features and those using raw EEG data demonstrates a significant performance gain. Specifically, the accuracy improved by 23.7% under XGBoost (p < 0.001), 14.8% under SVM (p < 0.001), and 18.3% under the SVM + XGBoost ensemble classifier (p < 0.001). These findings provide strong evidence that using fused FB(CCA + CSP) features as classifier inputs substantially improves classification accuracy compared to using raw EEG signals.

4. Discussion

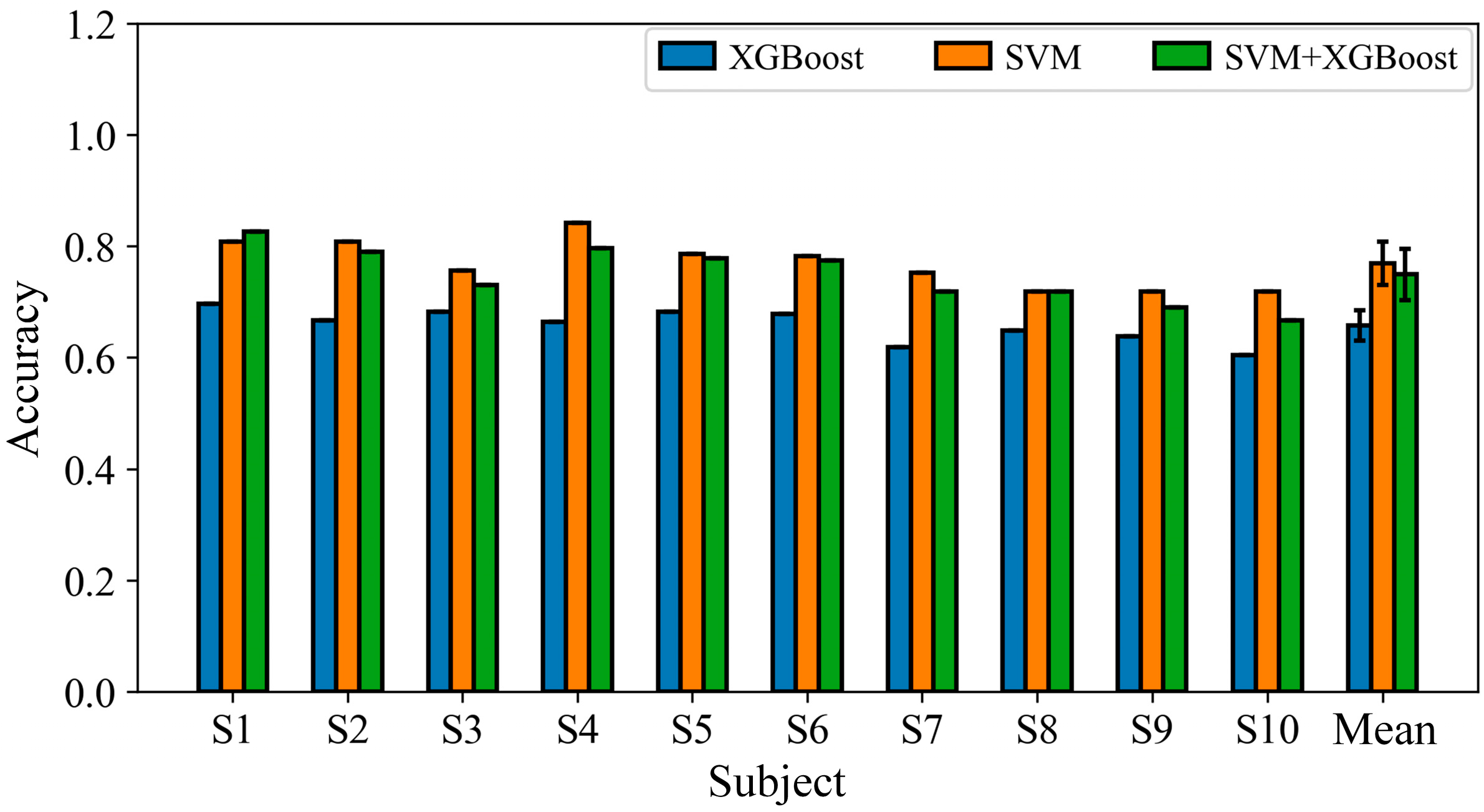
This study addresses the challenge of reliably distinguishing between IC and NC states in asynchronous BCIs. It proposes a hybrid SSMVEP-BCI system that integrates multidimensional features with a structurally complementary classification strategy. The system combines FBCSPs and FBCCA to jointly extract spatial and frequency information from EEG signals, effectively enhancing inter-class separability during the feature modeling phase. For classification, the SVM and XGBoost are fused with weighted integration to improve both the discriminative power and stability of the model. Experimental results demonstrate that under asynchronous conditions, the proposed system significantly outperforms methods based on single-feature extraction or traditional classification architectures, validating its effectiveness and practicality.

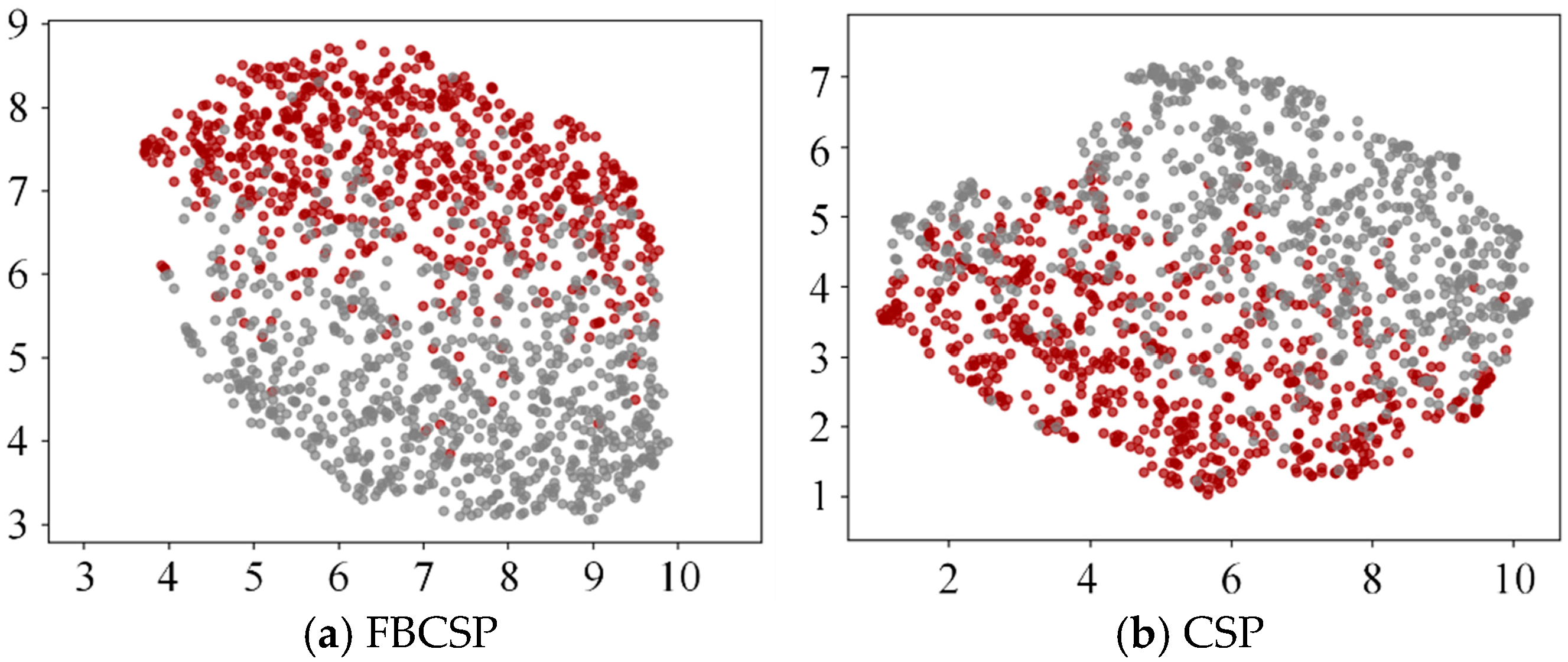
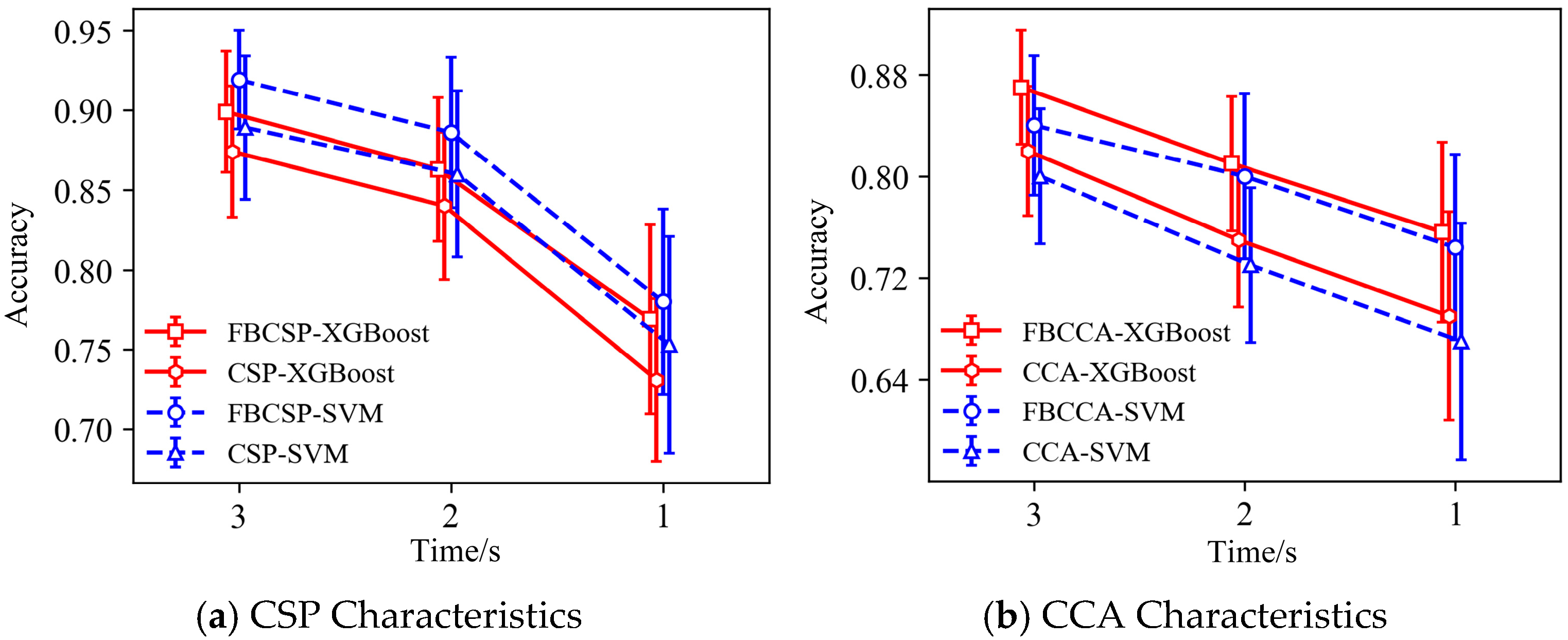
FBCSPs and FBCCA represent two fundamental processing pathways for extracting information from EEG signals: spatial patterns and frequency features, respectively. FBCSPs, which are derived from the CSP method, apply spatial filtering to maximize the covariance difference between two classes. This reflects category-specific differences in the spatial distribution of cortical activity and is particularly effective for capturing cooperative patterns across multiple channels in tasks such as attentional shifts or motor imagery [32,33]. FBCCA, on the other hand, is based on CCA, which assumes that the brain exhibits phase-locked responses at specific frequencies to periodic external stimuli (e.g., SSVEPs/SSMVEPs). It extracts neural coherence features by maximizing the correlation between EEG signals and reference sinusoidal sequences [34,35]. These two feature types model distinct neural mechanisms: FBCSPs focus on spatial distribution patterns, while FBCCA emphasizes frequency-locked coupling. They are not redundant but rather represent highly complementary neural encoding pathways.

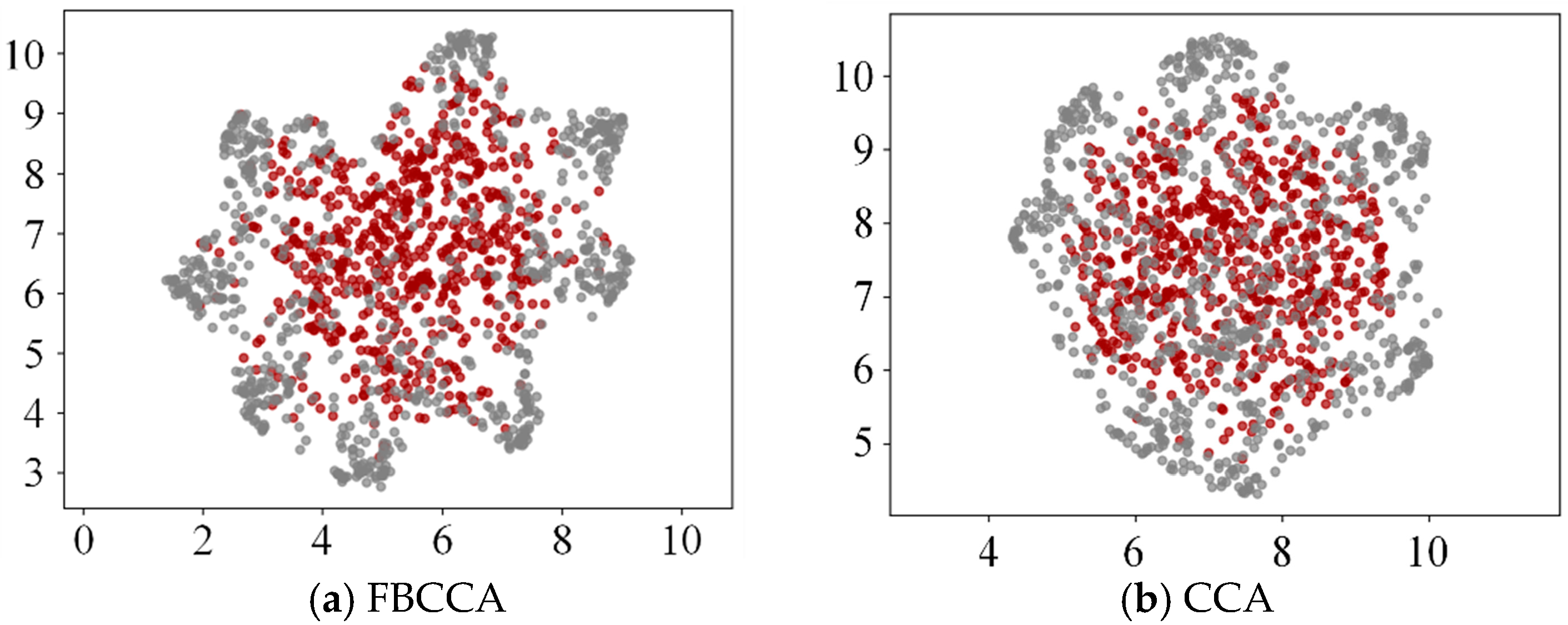
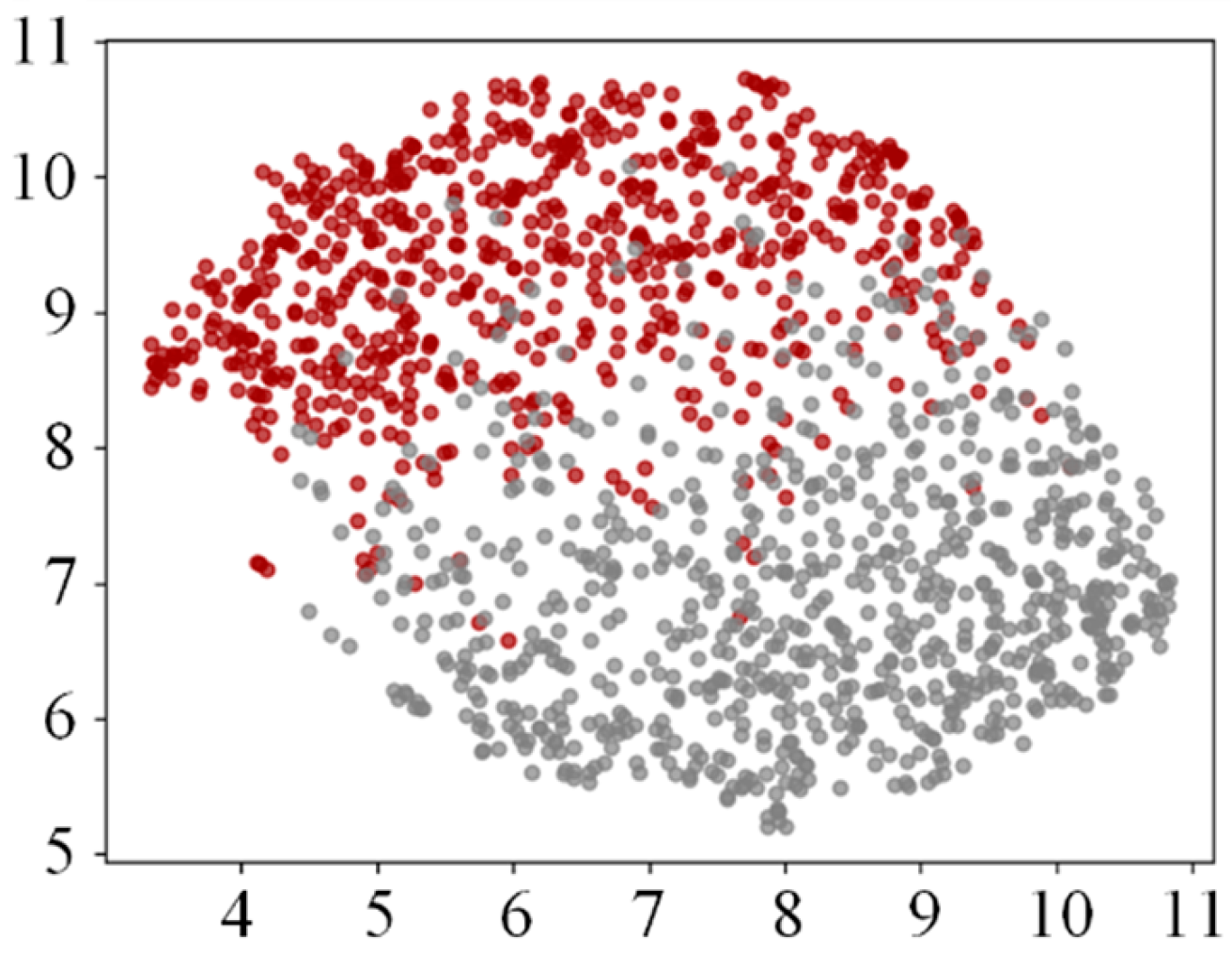
Moreover, both FBCSPs and FBCCA employ a filter bank strategy to decompose and reconstruct signals across multiple frequency sub-bands. This approach helps mitigate the distribution instability caused by individual frequency drift and channel jitter, and it has become a key trend in recent steady-state visual evoked potential (SSVEP) research [36,37]. By integrating features from different frequency bands and decoding pathways, this study achieves a robust and biologically grounded feature representation. This enriched signal foundation enhances the discrimination of complex IC/NC states in asynchronous tasks and improves resistance to noise. The fusion of FBCSPs and FBCCA enables synergistic modeling of the multichannel encoding characteristics in SSMVEP signals, enhancing the structural representation of neural information. Visualization results demonstrate superior inter-class separability for the fused features, supporting our modeling hypothesis regarding the spatial–frequency coupling mechanism. This study, based on the fusion idea of the complementarity of neural processing paths, has advantages in terms of physiological rationality and model interpretability.

In terms of classifier design, this study adopts the principle of feature structure–classifier preference matching to construct a dual-classifier framework integrating an SVM and XGBoost. The SVM, which is grounded in the theory of margin maximization, demonstrates a strong generalization ability when dealing with structured, low-dimensional, and boundary-concentrated data. It is particularly suited for spatially projected features that are linearly or nearly linearly separable [38]. In EEG signal processing, SVMs are widely used for classification tasks, such as motor imagery and SSVEP, due to their robustness and resistance to overfitting in high-dimensional spaces [39,40]. In contrast, XGBoost, as a representative of ensemble tree models, excels in handling nonlinear, high-dimensional data with strong feature interdependencies [41]. It is especially effective for modeling complex frequency domain features [42], such as the high-dimensional sub-band response features produced by FBCCA.

The weighted fusion mechanism we designed goes beyond traditional majority voting. Instead, it establishes a structurally synergistic decision-making process by analyzing the performance weights of each classifier across different feature types. This approach balances discriminative power and resistance to interference, avoiding the interpretability challenges often associated with deep learning models. Compared to recent “black-box” deep learning-based EEG decoding methods [43], our dual-classifier structure maintains high interpretability and flexible parameter tuning, making it particularly well suited for high-reliability, asynchronous systems where minimizing false activations is critical. SVMs excel at learning geometric boundaries in the low-dimensional space shaped by FBCSPs, while XGBoost effectively handles the high-dimensional, nonlinear feature distributions derived from FBCCA. By fusing the outputs of both classifiers with learned weights, the system achieves enhanced discriminative stability in high-dimensional feature space and avoids overfitting to specific feature sets that can occur with single models. This classifier fusion represents not only an improvement in model accuracy but also an architectural optimization of the fusion strategy, highlighting the system’s innovation in information integration mechanisms.

Despite the encouraging results achieved in this study, several issues remain that warrant further investigation. First, the current fusion weights are empirically set and cannot dynamically adapt to real-world interaction conditions such as user state fluctuations and signal variability. Future research could explore adaptive weighting mechanisms based on reinforcement learning, Bayesian optimization, or neural architecture search, aiming to enhance the system’s long-term applicability and robustness. Second, the system has not yet been deployed in a real-time asynchronous interaction environment, lacking comprehensive evaluation in terms of response latency, computational resource consumption, and user feedback. Asynchronous BCI systems are highly sensitive to response time [44]. Therefore, future efforts should focus on embedding the model into real-time systems and conducting system-level online testing.

The current experimental validation was conducted only with healthy subjects, and there is a lack of application evaluation in clinical populations such as individuals with motor disorders or cognitive impairments. Given the known differences in neural response timing and activation patterns among these groups [45,46], it is important to develop personalized EEG feature extraction strategies to improve the model’s generalizability across diverse populations. Additionally, this study has not yet conducted a direct quantitative comparison of classification performance with other mainstream methods, such as TRCA or CNN-based classifiers. Therefore, in future work, we plan to integrate our fusion strategy into more advanced models to evaluate its generalizability, robustness, and applicability across different classification frameworks. These insights would provide a theoretical foundation for developing highly trustworthy, interpretable, and auditable BCI systems.

In conclusion, this study demonstrates that combining multi-band EEG features (FBCSP and FBCCA) with dual classifier ensembles (SVM and XGBoost) provides a promising solution for improving asynchronous state detection in SSMVEP-BCI systems. The proposed methodology enhances feature separability and classification reliability, which is a key step in the development of practical, user-friendly, and high-performance asynchronous BCIs.

5. Conclusions

This study effectively tackled the challenge of accurately detecting control states in asynchronous BCI systems without relying on external cues, offering a valuable advancement in SSMVEP-based brain–computer interface research. The core innovation lies in the proposed dual-layer fusion framework, which systematically integrates filter bank CSP and CCA features with an ensemble classifier combining an SVM and XGBoost. This hybrid approach achieved a high average classification accuracy of 93.1% and significantly improved inter-class feature separability. Looking ahead, future work will explore the extension of this fusion strategy to multi-paradigm BCI systems and investigate adaptive weighting mechanisms to enhance system responsiveness and facilitate broader clinical applications.